From Axioms to Attractors: A Common Lyapunov Law for Equilibria Across Sectors

1. Introduction

Motivation

Across quantum mechanics (QM), thermodynamics (TD), and general relativity (GR), the central equilibrium relations—Born’s rule, entropy increase, and the curvature–matter balance—are typically posited rather than obtained under a single Lyapunov umbrella. This leaves a structural question: under which deterministic conditions do physical systems return to these relations after perturbations, and with what rates? In classical/reversible settings, exponential variance decay and spectral gaps are tightly connected Bakry et al. (2014); Davies (1976); Gross (1975); our aim is to make that restoration mechanism sector-agnostic and quantitatively comparable.

• Master alignment rule (sDoF/pDoF). At the core we introduce a set of master definitions (see Defs. ??–??): a sector-agnostic split into statistical degrees of freedom (sDoF) and physical degrees of freedom (pDoF), tied by an interchangeability map $\mathcal{I}$ living in the sector’s Hilbert geometry. The DSFL residual is the squared distance between p and $\mathcal{I}\left(s\right)$. In the operator-algebraic sector, $\mathcal{I}$ is the $\omega$-preserving conditional expectation onto the pointer algebra, so the residual is the canonical $L^2\left(\omega \right)$ distance to $L^2(\mathcal{N},\omega )$ (Takesaki/Tomiyama); a functorial formulation (Section 3.5) yields data-processing monotonicity under CP maps Kadison (1952); Paulsen (2002).

Idea

We develop a Deterministic Statistical Feedback Law (DSFL): track a quadratic misfit between a statistical blueprint and a physical response, and show that—under standard spectral-gap or coercivity hypotheses—the misfit is a Lyapunov functional that decays monotonically (often exponentially). Concretely, let P denote the sector-specific response (flux/current/tensor) and let $\nabla \rho$ represent a statistical baseline; the alignment residual

$$u:=P-\nabla \rho ,\mathcal{R}\left(t\right):={\int }_{\Omega }{|u(x,t)|}^{2}dx$$

(1)

(or its OA/QMS and geometric analogues) obeys

$$\dot{\mathcal{R}}\left(t\right)\le -\alpha \mathcal{R}\left(t\right),$$

(2)

with a sectoral rate $\alpha >0$ fixed by a spectral gap or coercivity constant. A one-step propagation mechanism (Jensen convexity for Markov semigroups, Kadison–Schwarz for u.c.p. maps, or an energy identity in PDEs) yields global monotonicity; a spectral gap or coercivity upgrades this to an exponential envelope Bakry et al. (2014); Davies (1976); Pazy (1983). Within this template, Born alignment, entropy growth, and Einstein balance appear as attractors of the same residual-suppression mechanism.

What Is New

• We contribute two genuinely new ingredients; the remaining items are recasts/demonstrators positioned against established results.

• New contributions.

• Master alignment rule (sDoF ↔ pDoF). We isolate a sector-agnostic split into statistical/physical degrees of freedom tied by an interchangeability map $\mathcal{I}$, and define the canonical DSFL residual as ${\parallel p-\mathcal{I}\left(s\right)\parallel }^2$ in the sector’s Hilbert geometry. In the operator–algebraic (OA/QMS) sector, $\mathcal{I}$ is the ω-preserving conditional expectation onto the pointer algebra, i.e. the $L^2\left(\omega \right)$ orthogonal projection guaranteed by Takesaki/Tomiyama; this yields a metric projection characterization and data-processing monotonicity under normal u.c.p. maps Kadison (1952); Paulsen (2002); Takesaki (1972); Tomiyama (1957). A functorial view (Section 3.5) makes the construction portable across sectors.
• One residual, one propagation step. We show that a single quadratic residual $\mathcal{R}$ admits the same short “propagation + gap/coercivity ⇒ exponential decay” template across OA/QMS, finite-dimensional Lindblad dynamics, coercive PDE flows, free-field OU, and GR slices. The propagation step is Jensen/Kadison–Schwarz/energy-identity in the respective geometries, and the rate is fixed by the sectoral spectral gap/coercivity (Poincaré/log-Sobolev/elliptic Lichnerowicz), with explicit bookkeeping of constants Bakry et al. (2014); Davies (1976); Pazy (1983).

• Recasts & demonstrators (prior art credited).

• Reversible QMS (classical equivalence, restated). For $\omega$-symmetric quantum Markov semigroups we restate the standard equivalence between exponential $L^2$-variance decay and a noncommutative Poincaré (spectral-gap) inequality on $L^2{(\mathcal{N},\omega )}^{\perp }$, tracking the optimal constant ${\alpha }_{\ast }=2{\lambda }_{\ast }$ Bakry et al. (2014); Carlen and Maas (2017); Davies (1976); Kastoryano and Temme (2013); Olkiewicz and Zegarlinski (1999).
• Modewise demonstrator (Lindblad dephasing). For pure dephasing generators, off-diagonal coherences decay as $e^{-({\gamma }_i+{\gamma }_j)t}$; the Lüders off-diagonal variance obeys the sharp envelope ${min}_{i\ne j}({\gamma }_i+{\gamma }_j)$, realized by a slowest pair Ángel Rivas and Huelga (2012); Breuer and Petruccione (2002); Gorini et al. (1976); Lindblad (1976).
• PDE template (clean envelope). An exact residual energy identity plus uniform ellipticity ($B⪰\beta I$) and subcritical couplings yields $\dot{\mathcal{R}}\le -(2\beta -C\epsilon )\mathcal{R}$, with Helmholtz/Poincaré refinements under standard boundary compatibility Evans (2010); Pazy (1983); Temam (1997).
• Free-field QFT (Gaussian sector). In Parisi–Wu stochastic quantization, smeared two-point residuals decay at a rate governed by the Euclidean Hamiltonian gap; we present the DSFL envelope and note a faster bound available for a specific quadratic residual Damgaard and Hüffel (1987); Parisi and Wu (1981); Prato and Zabczyk (1992).
• Geometric slice analogue. On compact Riemannian slices in DeTurck gauge, a Lichnerowicz-type spectral gap implies exponential $L^2$ suppression of the curvature–matter misfit toward Einstein balance; a fully covariant Lorentzian formulation remains open Besse (1987); DeTurck (1983).
• Residual-entropy proxy. The diagnostic $S_R=-log(\mathcal{R}/{\mathcal{R}}_0+R_{\ast })$ is strictly increasing whenever DSFL holds, paralleling entropy-production monotonicity for (quantum) Markovian evolutions Lindblad (1975); Spohn (1978).

1.1. Position Relative to Prior Work

Variance and entropy decay for reversible diffusions and semigroups are well established Bakry et al. (2014); Davies (1976); Gross (1975); Pazy (1983). For reversible QMS, the Poincaré/log-Sobolev framework and gap-controlled $L^2$ contraction are classical Carlen and Maas (2017); Kastoryano and Temme (2013); Olkiewicz and Zegarlinski (1999). Modewise Lindblad dephasing and its sharp envelope are textbook Ángel Rivas and Huelga (2012); Breuer and Petruccione (2002); Gorini et al. (1976); Lindblad (1976). Coercivity-driven decay in PDEs follows standard energy/semigroup methods Evans (2010); Pazy (1983); Temam (1997), and OU/free-field relaxation is governed by the Hamiltonian gap Damgaard and Hüffel (1987); Parisi and Wu (1981); Prato and Zabczyk (1992). In operator algebras, conditional expectations furnish the canonical $L^2$ projection underpinning our residual and its data-processing monotonicity Kadison (1952); Paulsen (2002); Takesaki (1972); Tomiyama (1957).

Within this landscape, our contribution is twofold: (i) we isolate one residual and one propagation step via the sDoF/pDoF interchangeability map so that these sectoral results acquire the same Lyapunov form; and (ii) we provide clean rate bookkeeping that makes the resulting envelopes directly comparable across sectors and hypotheses.

Scope and Limits

The DSFL form is uniform while assumptions are sectoral. Throughout we require either reversibility or quantitative coercivity:

(i)

$\omega$-symmetric (reversible) QMS with a spectral gap on $L^2{(\mathcal{N},\omega )}^{\perp }$ Carlen and Maas (2017); Davies (1976);

(ii)

coercive PDE closures with $B(x,t)⪰\beta I$ and subcritical couplings Evans (2010); Temam (1997);

(iii)

free fields (Gaussian sector) with a positive Euclidean Hamiltonian gap Parisi and Wu (1981); Prato and Zabczyk (1992);

(iv)

geometric DeTurck slices with a Lichnerowicz-type gap on the physical subspace and small initial data Besse (1987); DeTurck (1983).

Under these hypotheses the residual obeys a DSFL inequality with an explicit, sector-dependent rate. We do not claim theorems for nonreversible/hypocoercive QMS, fully covariant Lorentzian evolutions, or interacting QFT beyond the Gaussian sector; these are stated as programs with testable intermediate predictions (e.g., scale-dependent rates, ISS-type bounds ?)).

The numerical section provides reproducible protocols illustrating the rates; all analytic claims stand independently of numerics.

• Implications for the “physics crisis.”

By recasting canonical equalities (Born’s rule, entropy growth, Einstein balance) as attractors of a single residual-suppression mechanism, DSFL shifts several fault lines from postulates to testable dynamics. Concretely: (i) it supplies measurable rates—spectral gaps or coercivity constants—that experimentalists can extract and compare across sectors, turning foundational statements into falsifiable envelopes Bakry et al. (2014); Davies (1976); (ii) it clarifies the measurement issue by making the equilibrium manifold explicitly contextual (pointer algebra), while keeping the core law context-invariant—resolving when “collapse-like” alignment should occur and at which rate; (iii) it provides a slice-level bridge to gravity (via Lichnerowicz gaps in DeTurck gauge), identifying precisely what is proved now and what remains open in fully covariant settings Besse (1987); DeTurck (1983); and (iv) it separates crises of principle from crises of constant: when DSFL holds but the observed rate disagrees, the discrepancy points to concrete missing structure (nonreversibility/hypocoercivity, interactions beyond Gaussian, or gauge/constraint physics) rather than to a breakdown of the law itself. In this sense, DSFL proposes a unifying operational path out of the crisis: upgrade axioms to attractors with sectoral rates; test them; and read any failure as a diagnostic for where new physics must enter.

2. Background and Related Work

• This section summarizes established results that we use later; our DSFL contributions (master sDoF/pDoF alignment rule and unified propagation) appear in Sections ??–?? and §4.2.

2.1. Quantum Markov Semigroups and Spectral Gaps

A (normal, unital) quantum Markov semigroup (QMS) ${\left({\mathsf{T}}_t\right)}_{t\ge 0}$ on a von Neumann algebra $\mathcal{M}$ with faithful normal state $\omega$ is ω–symmetric (reversible) if it is self–adjoint on the GNS space $L^2\left(\omega \right)$. Its generator $\mathcal{L}$ induces a densely defined, closed Dirichlet form

$${\mathcal{E}}_{\omega }\left(X\right):={\langle X,-\mathcal{L}X\rangle }_{2,\omega },{\parallel X\parallel }_{2,\omega }^2=\omega \left(X^{\ast }X\right),$$

(3)

with standard underpinnings for noncommutative Dirichlet forms and symmetric quantum semigroups (e.g. Cipriani and Sauvageot (1993); ?). The fixed–point algebra $\mathcal{N}=\{X:{\mathsf{T}}_{t}X=X\forall t\}$ plays the role of the equilibrium subspace; if $\mathcal{N}$ is invariant under the modular group of $\omega$, the $\omega$–preserving conditional expectation ${\mathsf{E}}_{\mathcal{N}}:\mathcal{M}\to \mathcal{N}$ exists and is unique (Takesaki; cf. Tomiyama) Takesaki (1972); Tomiyama (1957).

A noncommutative Poincaré (spectral–gap) inequality with constant $\lambda >0$,

$$\parallel X-{\mathsf{E}}_{\mathcal{N}}{\left(X\right)\parallel }_{2,\omega }^2\le \frac{1}{\lambda }{\mathcal{E}}_{\omega }\left(X\right),$$

(4)

is equivalent to exponential decay of the noncommutative variance along the semigroup,

$$\parallel {\mathsf{T}}_{t}X-{\mathsf{E}}_{\mathcal{N}}{\left(X\right)\parallel }_{2,\omega }^2\le e^{-2\lambda t}{\parallel X-{\mathsf{E}}_{\mathcal{N}}\left(X\right)\parallel }_{2,\omega }^2,$$

(5)

with optimal envelope ${\alpha }_{\ast }=2{\lambda }_{\ast }$ Carlen and Maas (2017); Davies (1976); Kastoryano and Temme (2013). This mirrors the classical theory of reversible diffusions (Bakry–Émery calculus) Bakry et al. (2014); Gross (1975). Beyond Poincaré, quantum log–Sobolev (hypercontractive) regimes and related mixing bounds are available (e.g. Bardet et al. (2018; Olkiewicz and Zegarlinski (1999))), and rapid mixing for quantum channels/expanders provides a complementary discrete perspective Brandao and Harrow (2016). In the present DSFL view, (4)–(5) are precisely the operator–algebraic Lyapunov statements for the residual $X-{\mathsf{E}}_{\mathcal{N}}\left(X\right)$: once a gap holds, the residual contracts at rate $2\lambda$ and $\mathcal{N}$ is the attractor.

2.2. Lindblad Dephasing and Modewise Contraction

In finite dimensions, completely positive trace–preserving evolutions admit the GKSL (Lindblad) representation

$${\mathcal{L}}^{\ast }\left(\sigma \right)=-i[H,\sigma ]+\sum _k\left(L_k\sigma L_k^{†}-\frac{1}{2}\{L_k^{†}{L}_k,\sigma \}\right),$$

(6)

with Hamiltonian H and noise operators $L_k$ Gorini et al. (1976); Lindblad (1976); see also Breuer and Petruccione (2002); Spohn (1978). For pure dephasing in a fixed orthonormal basis, $L_i=\sqrt{{\gamma }_i}|i\rangle \langle i|$ and H diagonal, one has

$$\frac{d}{dt}{\left({\sigma }_t\right)}_{ii}=0,\frac{d}{dt}{\left({\sigma }_t\right)}_{ij}=-\frac{{\gamma }_i+{\gamma }_j}{2}{\left({\sigma }_t\right)}_{ij}(i\ne j),$$

(7)

so coherences decay as $e^{-({\gamma }_i+{\gamma }_j)t/2}$ while populations are conserved. The Hilbert–Schmidt variance off the pointer algebra (Lüders residual) obeys

$${\mathcal{R}}_{\mathrm{L}\ddot{\mathrm{u}}\mathrm{ders}}\left({\sigma }_t\right)=\sum _{i\ne j}{|{\left({\sigma }_t\right)}_{ij}|}^2\le e^{-{\alpha }_{\ast }t}{\mathcal{R}}_{\mathrm{L}\ddot{\mathrm{u}}\mathrm{ders}}\left({\sigma }_0\right),{\alpha }_{\ast }=\underset{i\ne j}{min}({\gamma }_i+{\gamma }_j),$$

(8)

and the constant ${\alpha }_{\ast }$ is sharp. This is the finite–dimensional counterpart of (5), with the envelope set by the slowest dephasing pair.

2.3. Coercive PDE Flows and Bakry–Émery Tools

In classical dissipative PDEs, exponential return to equilibrium combines (i) an energy/entropy identity for a nonnegative functional along solutions and (ii) a coercive inequality (Poincaré/log–Sobolev) to control lower–order couplings. Foundational results include Gross’s log–Sobolev ⇔ hypercontractivity Gross (1975) and its many developments Bakry et al. (2014); Ledoux (2001). In geometric analysis (e.g. Ricci/DeTurck flows), $L^2$–type curvature residuals dissipate under an elliptic Lichnerowicz–type operator; Perelman’s monotone functionals provide a celebrated Lyapunov structure DeTurck (1983); Hamilton (1982); Perelman (2002).

Our DSFL–PDE template follows this pattern: for the misfit $u:=P-\nabla \rho$,

$$\frac{d}{dt}{\int }_{\Omega }{|u|}^{2}dx=-2{\int }_{\Omega }{u}^{\top }Budx-2{\parallel \nabla ·u\parallel }_{L^2(\Omega )}^2+(\mathrm{controlled}\mathrm{terms}),$$

(9)

so under uniform ellipticity $B⪰\beta I$ and subcritical couplings, Grönwall yields ${\parallel u\left(t\right)\parallel }_{L^2}^2\le e^{-(2\beta -C\epsilon )t}{\parallel u\left(0\right)\parallel }_{L^2}^2$. This is the Bakry–Émery “propagation + gap ⇒ decay” mechanism, reinterpreted as sector–agnostic Lyapunov suppression of a quadratic misalignment.

2.4. Stochastic Quantization and Hamiltonian Gaps

Parisi–Wu stochastic quantization provides an analytically tractable Euclidean dynamics for QFT: for a free scalar with action $S\left[\varphi \right]=\int \frac{1}{2}{(|\nabla \varphi |}^2+m^2{\varphi }^2)dx$, the Langevin flow

$${\partial }_{\tau }{\varphi }_{\tau }\left(x\right)=-\frac{\delta S}{\delta \varphi }\left(x\right)+\eta (x,\tau )$$

(10)

generates a semigroup ${\mathsf{T}}_{\tau }=e^{-\tau H}$ with nonnegative Euclidean Hamiltonian H. The spectral gap ${\lambda }_{\ast }=m^2$ controls exponential relaxation of smeared correlators; squaring yields decay of quadratic residuals at rate $2{\lambda }_{\ast }$ Parisi and Wu (1981). For reviews and context see Damgaard and Hüffel (1987); Zinn-Justin (2002) and general OU/SPDE semigroup references such as Prato and Zabczyk (1992). In DSFL language, the same Hamiltonian gap that governs Euclidean relaxation drives residual suppression in the Gaussian sector; extensions to interacting fields call for nonperturbative functional inequalities or RG control.

2.5. Positioning Relative to Prior Approaches

Exponential return to equilibrium is well established within specific frameworks: noncommutative Poincaré/log–Sobolev inequalities for reversible QMS Bardet et al. (2018); Carlen and Maas (2017); Davies (1976); Kastoryano and Temme (2013); Olkiewicz and Zegarlinski (1999), explicit modewise contraction in GKSL/Lindblad dynamics Breuer and Petruccione (2002); Gorini et al. (1976); Lindblad (1976); Spohn (1978), coercivity–driven decay for dissipative PDEs and geometric flows Bakry and Émery (1985); Bakry et al. (2014); DeTurck (1983); Gross (1975); Hamilton (1982); Ledoux (2001); Perelman (2002), and Hamiltonian–gap relaxation in stochastic quantization Damgaard and Hüffel (1987); Parisi and Wu (1981); Zinn-Justin (2002).

The present work contributes a single, sector–neutral Lyapunov residual and a unifying propagation principle (Jensen/Kadison–Schwarz/energy identity) that render these results structurally comparable. Under the corresponding gap/coercivity hypotheses one obtains the same DSFL inequality $\dot{\mathcal{R}}\le -\alpha \mathcal{R}$, and the sectoral equilibrium statements—Born alignment (QM), residual–entropy monotonicity (TD), and Einstein balance (GR)—emerge as attractors rather than axioms. In our pointer–algebra formalism, POVMs and Naimark dilations are standard Busch et al. (1996); Naimark (1940); Ozawa (1984); the DSFL novelty is the common residual via the sDoF/pDoF interchangeability map and its gap–controlled Lyapunov decay across sectors.

3. Notation and Conventions

3.1. Spaces, Norms, Inner Products

• Domains and measures.

$\Omega \subset {\mathbb{R}}^d$ denotes either a bounded $C^1$ domain or a flat torus ${\mathbb{T}}^d$. We write $dx$ for Lebesgue measure, $|\Omega |$ for its volume, and ${\langle f\rangle }_{\Omega }:={|\Omega |}^{-1}{\int }_{\Omega }fdx$ for spatial averages. When needed, $(\mathcal{U},g)$ denotes a smooth Riemannian (or, where explicitly stated, Lorentzian) manifold with volume form $d{\mu }_g$.

• Lebesgue and Sobolev spaces.

For $1\le p\le \infty$, $L^p(\Omega )$ has norm ${\parallel f\parallel }_{L^p(\Omega )}=({\int }_{\Omega }{|f|}^p{dx)}^{1/p}$ (essential supremum for $p=\infty$). For $k\in \mathbb{N}$, $H^k(\Omega )$ is the Sobolev space with ${\parallel f\parallel }_{H^k(\Omega )}^2={\sum }_{|\alpha |\le k}{\parallel {\partial }^{\alpha }f\parallel }_{L^2(\Omega )}^2$. We write $H_0^1(\Omega )$ for the closure of $C_c^{\infty }(\Omega )$ in $H^1(\Omega )$. Vector/tensor–valued spaces are denoted $L^p(\Omega ;E)$ and $H^k(\Omega ;E)$ with the product norms.

• Inner products and $L^2$ norms.

On $\Omega$, ${\langle f,g\rangle }_{L^2(\Omega )}={\int }_{\Omega }fgdx$ for scalars and ${\langle \mathbf{f},\mathbf{g}\rangle }_{L^2(\Omega )}={\int }_{\Omega }\mathbf{f}·\mathbf{g}dx$ for vectors. On $(\mathcal{U},g)$, for symmetric 2–tensors $T,S$ we use ${\langle T,S\rangle }_g=g^{\mu \alpha }{g}^{\nu \beta }{T}_{\mu \nu }{S}_{\alpha \beta }$ and ${\parallel T\parallel }_{L^2\left(g\right)}^2={\int }_{\mathcal{U}}{\langle T,T\rangle }_{g}d{\mu }_g$.

• Gradients and divergences.

In $\Omega \subset {\mathbb{R}}^d$, ∇ is the Euclidean gradient and $\nabla ·$ the divergence. On $(\mathcal{U},g)$, ${\nabla }_{\mu }$ is the Levi–Civita covariant derivative and $\nabla ·$ its metric divergence. For a vector field P and a scalar $\rho$, we define the alignment residual

$$u:=P-{\nabla \rho ,\parallel u\parallel }_2^2:={\int }_{\Omega }{|u|}^{2}dx.$$

(11)

• Weighted inner products.

Given a measurable, symmetric positive–definite weight $W\left(x\right)\in {\mathbb{R}}^{d\times d}$, set ${\langle v,w\rangle }_{W\left(x\right)}:=v^{\top }W\left(x\right)w$ and ${|v|}_{W\left(x\right)}^2={\langle v,v\rangle }_{W\left(x\right)}$. The global weighted norm is ${\parallel v\parallel }_{L_W^2}^2:={\int }_{\Omega }{|v\left(x\right)|}_{W\left(x\right)}^{2}dx$. Unless stated otherwise, $W\equiv I$.

• Noncommutative conventions.

For a von Neumann algebra $(\mathcal{M},\omega )$ with faithful normal state $\omega$, the GNS inner product is ${\langle X,Y\rangle }_{2,\omega }=\omega \left(X^{\ast }Y\right)$ and ${\parallel X\parallel }_{2,\omega }^2=\omega \left(X^{\ast }X\right)$. The noncommutative variance is ${\mathrm{Var}}_{\omega }\left(X\right)={\parallel X-\omega \left(X\right)\mathbf{1}\parallel }_{2,\omega }^2$. If $\mathcal{N}\subset \mathcal{M}$ is a von Neumann subalgebra invariant under the modular group of $\omega$, ${\mathsf{E}}_{\mathcal{N}}:\mathcal{M}\to \mathcal{N}$ denotes the (unique) $\omega$–preserving conditional expectation; it acts as the $L^2\left(\omega \right)$–orthogonal projection onto $L^2(\mathcal{N},\omega )$.

3.2. Measures, Domains, and Boundary Conditions

• Flat domains.

Unless stated otherwise, $\Omega \subset {\mathbb{R}}^d$ is either a bounded $C^1$ domain or a flat torus ${\mathbb{T}}^d$. We write $dx$ for the Lebesgue measure and ${\int }_{\Omega }(·)dx$ for spatial integrals; spatial averages are ${\langle f\rangle }_{\Omega }:={|\Omega |}^{-1}{\int }_{\Omega }fdx$.

• Boundary conditions (BCs).

Energy identities and integrations by parts are justified under either (i) periodic BCs on ${\mathbb{T}}^d$, or (ii) homogeneous no-flux BCs arranged so that boundary terms vanish in the residual energy balance. In particular,

$${\int }_{\Omega }u·\nabla (\nabla ·u)dx=-{\parallel \nabla ·u\parallel }_{L^2(\Omega )}^2+{\int }_{\partial \Omega }(u·n)(\nabla ·u)dS,$$

(12)

so the boundary contribution is zero if, for example, $u·n=0$ on $\partial \Omega$ (e.g. $P·n={\partial }_n\rho =0$), or on a torus.

• Probability measures.

In data–driven formulations we allow a time–indexed family of probability measures ${\mu }_t$ on $\Omega$. Population expectations are ${\mathbb{E}}_{{\mu }_t}\left[f\right]={\int }_{\Omega }fd{\mu }_t$, with empirical approximations $\frac{1}{N}{\sum }_{i=1}^{N}f\left(x_i\right)$ when ${\mu }_t$ is supported on samples $\left\{x_i\right\}$. The residual

$$\mathcal{R}\left(t\right):={\mathbb{E}}_{{\mu }_t}\left[{|P-\nabla \rho |}_W^2\right]$$

(13)

reduces to ${\int }_{\Omega }{|u|}_W^{2}dx$ (with $u:=P-\nabla \rho$) when ${\mu }_t$ is normalized Lebesgue and $W\equiv I$.

• Manifolds.

In geometric sections we replace $(\Omega ,dx)$ by a Riemannian (or, where explicitly stated, Lorentzian) manifold $(\mathcal{U},g)$ with Levi–Civita connection ∇, metric pairing ${\langle ·,·\rangle }_g$, and volume form $d{\mu }_g$. For symmetric 2–tensors T, the $L^2$ norm is ${\parallel T\parallel }_{L^2\left(g\right)}^2={\int }_{\mathcal{U}}{\langle T,T\rangle }_{g}d{\mu }_g$. On compact Riemannian slices in DeTurck gauge (Section ??), boundary terms vanish by compactness; on noncompact manifolds we assume decay/compatibility so that all integrals are finite.

• Normalization and gauges.

In probabilistic sectors we impose ${\int }_{\Omega }\rho dx=1$ (densities) and ${\parallel \Psi \parallel }_{L^2(\Omega )}=1$ (wave functions). The baseline $\rho$ is defined up to an additive gauge $\rho \mapsto \rho +C\left(t\right)$, which leaves $u=P-\nabla \rho$ and $\mathcal{R}$ invariant. In geometric sectors, gauge choices (e.g. DeTurck) ensure ellipticity/hyperbolicity and do not alter the definition of the residual (e.g. ${\parallel G-\kappa T\parallel }_{L^2\left(g\right)}^2$).

3.3. Operators, Semigroups, and Spectra

• Linear operators and spectra.

Let $\mathcal{A}:\mathsf{D}\left(\mathcal{A}\right)\subset H\to H$ be a densely defined, closed linear operator on a Hilbert space $(H,\langle ·,·\rangle )$. We write $\sigma \left(\mathcal{A}\right)$ for its spectrum and $ker\left(\mathcal{A}\right)$ for its kernel. If $\mathcal{A}$ is self–adjoint and nonnegative, a spectral gap means that

$$\langle X,\mathcal{A}X\rangle \ge {\lambda \parallel X\parallel }^2\mathrm{for}\mathrm{all}X\perp ker\left(\mathcal{A}\right),$$

(14)

for some $\lambda >0$; then $\lambda$ is the optimal Poincaré constant on $ker{\left(\mathcal{A}\right)}^{\perp }$.

• Markov/contraction semigroups.

A strongly continuous one–parameter semigroup ${\left({\mathsf{T}}_t\right)}_{t\ge 0}$ on H with generator $\mathcal{L}$ is a (sub)Markov contraction on a Banach lattice $L^p\left(\mu \right)$ if it preserves positivity, mass (${\mathsf{T}}_t\mathbf{1}=\mathbf{1}$), and satisfies $\parallel {\mathsf{T}}_t{f\parallel }_{L^p}\le {\parallel f\parallel }_{L^p}$ for $1\le p\le \infty$. In the reversible case (self–adjoint on $L^2\left(\mu \right)$), the Dirichlet form is $\mathcal{E}\left(f\right):={\langle f,-\mathcal{L}f\rangle }_{L^2\left(\mu \right)}$ and

$${\mathrm{Var}}_{\mu }\left({\mathsf{T}}_{t}f\right)\le e^{-2\lambda t}{\mathrm{Var}}_{\mu }\left(f\right)⟺{\mathrm{Var}}_{\mu }\left(f\right)\le \frac{1}{\lambda }\mathcal{E}\left(f\right).$$

(15)

• Quantum Markov semigroups (QMS).

On a von Neumann algebra $(\mathcal{M},\omega )$, a normal unital completely positive (u.c.p.) semigroup ${\left({\mathsf{T}}_t\right)}_{t\ge 0}$ that is $\omega$–symmetric is a noncommutative analogue of a reversible diffusion. The GNS $L^2\left(\omega \right)$ inner product is ${\langle X,Y\rangle }_{2,\omega }=\omega \left(X^{\ast }Y\right)$, the Dirichlet form is ${\mathcal{E}}_{\omega }\left(X\right):={\langle X,-\mathcal{L}X\rangle }_{2,\omega }$, and the fixed–point algebra $\mathcal{N}=\{X:{\mathsf{T}}_{t}X=X\}$ is the equilibrium subspace. The noncommutative Poincaré inequality

$$\parallel X-{\mathsf{E}}_{\mathcal{N}}{\left(X\right)\parallel }_{2,\omega }^2\le \frac{1}{\lambda }{\mathcal{E}}_{\omega }\left(X\right)$$

(16)

is equivalent to exponential variance decay

$$\parallel {\mathsf{T}}_{t}X-{\mathsf{E}}_{\mathcal{N}}{\left(X\right)\parallel }_{2,\omega }^2\le e^{-2\lambda t}{\parallel X-{\mathsf{E}}_{\mathcal{N}}\left(X\right)\parallel }_{2,\omega }^2,$$

(17)

with optimal rate $2\lambda$.

• Generators in finite dimension (GKSL form).

On $M_d\left(\mathbb{C}\right)$, the dual evolution for states ${\sigma }_t$ is

$${\dot{\sigma }}_t=-i[H,{\sigma }_t]+\sum _k\left(L_k{\sigma }_t{L}_k^{†}-\frac{1}{2}\{L_k^{†}{L}_k,{\sigma }_t\}\right),$$

(18)

with Hamiltonian H and noise operators $L_k$ (GKSL/Lindblad form). For pure dephasing, $L_i=\sqrt{{\gamma }_i}|i\rangle \langle i|$ yields modewise decay ${\left({\sigma }_t\right)}_{ij}=e^{-({\gamma }_i+{\gamma }_j)t/2}{\left({\sigma }_0\right)}_{ij}$ for $i\ne j$.

• Poincaré and log–Sobolev constants.

We use Poincaré constants $\lambda >0$ to control variance by energy, and, where applicable, log–Sobolev constants $\rho >0$ to control entropy by Fisher information. In this article the DSFL rate $\alpha$ is identified with twice a Poincaré gap in reversible settings (classical/QMS) and with quantitative coercivity constants in PDE/geometric settings.

• Projection onto equilibria.

${\mathsf{E}}_{\mathcal{N}}$ denotes the $\omega$–preserving conditional expectation onto the fixed–point (pointer) algebra $\mathcal{N}$. In PDE/probability sectors, the analogue is projection onto the nullspace of the generator (e.g., $\rho \mapsto {\langle \rho \rangle }_{\Omega }$).

• Spectral notation in GR slices.

For Lichnerowicz–DeTurck type operators acting on symmetric 2–tensors on a compact Riemannian 3–manifold $(\Sigma ,\gamma )$, we denote by ${\lambda }_{\mathrm{GR}}>0$ the spectral gap on the orthogonal complement of the gauge directions; it controls exponential $L^2$ decay of the geometric residual.

3.4. Operator–Algebraic Definition of the $\mathcal{R}$–Sameness Functional

Let $(\mathcal{M},\omega )$ be a $\sigma$–finite von Neumann algebra equipped with a faithful normal state $\omega$, and let $\mathcal{N}\subset \mathcal{M}$ be an $\omega$–modular–invariant von Neumann subalgebra (the pointer algebra). Denote by

$${\mathsf{E}}_{\mathcal{N}}:\mathcal{M}⟶\mathcal{N}$$

(19)

the unique $\omega$–preserving conditional expectation guaranteed by Takesaki’s theorem. The GNS Hilbert space of $(\mathcal{M},\omega )$ is

$$L^2\left(\omega \right):={\overline{{\mathcal{M}/ker\parallel ·\parallel }_{2,\omega }}}^{{\parallel ·\parallel }_{2,\omega }},{\parallel X\parallel }_{2,\omega }^2:=\omega \left(X^{\ast }X\right).$$

(20)

Let ${\mathsf{E}}_{\mathcal{N}}$ act as the orthogonal projection $L^2\left(\omega \right)\to L^2(\mathcal{N},\omega )$, and write $X^{\perp }:=X-{\mathsf{E}}_{\mathcal{N}}X$ for the orthogonal complement of X to the pointer sector.

Definition 3.1

(Operator–algebraic Rsameness functional). For $X\in L^2\left(\omega \right)$, the Rsameness functional (or operator–algebraic residual) is defined by

$${\mathcal{R}}_{\omega ,\mathcal{N}}\left(X\right):={\parallel X-{\mathsf{E}}_{\mathcal{N}}X\parallel }_{2,\omega }^2=\omega \left[{(X-{\mathsf{E}}_{\mathcal{N}}X)}^{\ast }(X-{\mathsf{E}}_{\mathcal{N}}X)\right].$$

(21)

• Interpretation.

${\mathcal{R}}_{\omega ,\mathcal{N}}\left(X\right)$ quantifies the misalignment between an observable X and its equilibrium (pointer–algebraic) component ${\mathsf{E}}_{\mathcal{N}}X$. It is the noncommutative analogue of the quadratic classical residual ${\int }_{\Omega }{|P-\nabla \rho |}^{2}dx$, obtained by replacing the $L^2$ pairing with the GNS inner product of $(\mathcal{M},\omega )$ and the conditional expectation with the $\omega$–preserving projection onto $\mathcal{N}$.

• Dirichlet form and residual dynamics.

Let ${\left({\mathsf{T}}_t\right)}_{t\ge 0}$ be an $\omega$–symmetric quantum Markov semigroup (QMS) on $\mathcal{M}$ with generator $\mathcal{L}$ and Dirichlet form

$${\mathcal{E}}_{\omega }\left(X\right):={\langle X,-\mathcal{L}X\rangle }_{2,\omega }.$$

(22)

The Deterministic Statistical Feedback Law (DSFL) on the operator–algebraic sector is the Lyapunov inequality

$$\frac{d}{dt}{\mathcal{R}}_{\omega ,\mathcal{N}}\left({\mathsf{T}}_{t}X\right)\le -2\lambda {\mathcal{R}}_{\omega ,\mathcal{N}}\left({\mathsf{T}}_{t}X\right),\lambda >0,$$

(23)

which holds if and only if $\mathcal{L}$ has a spectral gap $\lambda$ on $L^2{(\mathcal{N},\omega )}^{\perp }$:

$$\parallel X-{\mathsf{E}}_{\mathcal{N}}{X\parallel }_{2,\omega }^2\le \frac{1}{\lambda }{\mathcal{E}}_{\omega }\left(X\right),X\in \mathsf{D}\left({\mathcal{E}}_{\omega }\right).$$

(24)

Equation (??) thus plays the role of a noncommutative Lyapunov functional whose exponential decay encodes the restoration of equilibrium (Born alignment or pointer alignment) as a deterministic contraction in the $L^2\left(\omega \right)$ geometry.

• Classical limit.

When $\mathcal{M}=L^{\infty }(\Omega )$, $\mathcal{N}=L_{\mathrm{inv}}^{\infty }(\Omega )$ and $\omega \left(f\right)={\int }_{\Omega }fd\mu$, the conditional expectation ${\mathsf{E}}_{\mathcal{N}}$ becomes the mean over invariant sets and (21) reduces to

$${\mathcal{R}}_{\omega ,\mathcal{N}}\left(f\right)={\int }_{\Omega }{|f-{\langle f\rangle }_{\Omega }|}^{2}d\mu ,$$

(25)

which coincides with the classical residual $\mathcal{R}\left(t\right)={\int |P-\nabla \rho |}^{2}dx$ up to notation. Hence the operator–algebraic Rsameness is the natural noncommutative generalization of the statistical–physical misfit.

3.5. Functorial Derivation of the $\mathcal{R}$–Sameness Functional

This subsection formalizes the categorical reading of the residual without being a prerequisite for the flagship operator–algebraic theorems. We (i) state precise objects/morphisms and the metric structure used, (ii) isolate the proved parts (projection characterizations, data–processing, covariance), and (iii) mark higher–level categorical remarks (monoidal/2–categorical structure) as optional context.

• Categories and metric structure.

We work with three basic categories and a forgetful passage to Hilbert spaces:

• $\mathbf{Stat}$: objects are classical probability spaces $(\Omega ,\mu )$ or noncommutative state spaces $(\mathcal{M},\omega )$ (von Neumann algebra $\mathcal{M}$ with faithful normal state $\omega$). Morphisms are measure–preserving maps $T:({\Omega }_1,{\mu }_1)\to ({\Omega }_2,{\mu }_2)$ (pushforward $T_{\#}{\mu }_1={\mu }_2$) and normal, unital, completely positive, state–preserving maps $\Phi :({\mathcal{M}}_1,{\omega }_1)\to ({\mathcal{M}}_2,{\omega }_2)$ with ${\omega }_2\circ \Phi ={\omega }_1$.
• $\mathbf{Geom}$: objects are response spaces $(\mathcal{U},g)$ with smooth metric g and physical fields (e.g. currents P or tensors); morphisms are smooth structure–preserving maps $F:({\mathcal{U}}_1,g_1)\to ({\mathcal{U}}_2,g_2)$ (pullbacks respect the energy pairings below).
• $\mathbf{Hilb}$: complex Hilbert spaces and contractions.

We endow these with canonical $L^2$–type inner products:

$${\langle f,h\rangle }_{L^2(\Omega ,\mu )}={\int }_{\Omega }f\overline{h}d\mu ,{\langle X,Y\rangle }_{2,\omega }=\omega \left(X^{\ast }Y\right),{\langle A,B\rangle }_{L^2(\mathcal{U},g)}={\int }_{\mathcal{U}}{\langle A,B\rangle }_{g}d{\mu }_g.$$

• Functorial passage to Hilbert spaces.

Define faithful functors

$$\mathcal{S}:\mathbf{Stat}\to \mathbf{Hilb},\mathcal{P}:\mathbf{Geom}\to \mathbf{Hilb},$$

by

$$\mathcal{S}(\Omega ,\mu )=L^2(\Omega ,\mu ),\mathcal{S}(\mathcal{M},\omega )=L^2\left(\omega \right),\mathcal{P}(\mathcal{U},g)=L^2(\mathcal{U},d{\mu }_g),$$

and on morphisms by the induced contractions (pullback in the classical/geometric case; the $L^2\left(\omega \right)$–adjoint action for normal u.c.p. maps).

• Pointer structures and projections.

A pointer in the noncommutative setting is a von Neumann subalgebra $\mathcal{N}\subset \mathcal{M}$ that is globally invariant under the modular group of $\omega$. By Takesaki’s theorem there exists a unique faithful normal conditional expectation ${\mathsf{E}}_{\mathcal{N}}:\mathcal{M}\to \mathcal{N}$ with $\omega \circ {\mathsf{E}}_{\mathcal{N}}=\omega$. At the Hilbert level,

$${\mathsf{E}}_{\mathcal{N}}:L^2\left(\omega \right)⟶L^2(\mathcal{N},\omega )\mathrm{is}\mathrm{the}\mathrm{orthogonal}\mathrm{projection}.$$

(26)

Definition 3.2

(Functorial residual). For an object X carrying a statistical blueprint $s_X\in \mathcal{S}\left(X\right)$ and a physical response $p_X\in \mathcal{P}\left(X\right)$, define the functorial residual

$$\mathcal{R}\left(X\right):=\parallel {\eta }_X\left(s_X\right)-p_X{\parallel }_{\mathcal{P}\left(X\right)}^2,$$

(27)

where $\eta :\mathcal{S}\Rightarrow \mathcal{P}$ is a natural transformation (the alignment map). In the operator–algebraic sector we take $\eta ={\mathsf{E}}_{\mathcal{N}}$ (via the identification $L^2(\mathcal{N},\omega )\subset L^2\left(\omega \right)$) so that

$${\mathcal{R}}_{\omega ,\mathcal{N}}\left(X\right)={\parallel X-{\mathsf{E}}_{\mathcal{N}}X\parallel }_{2,\omega }^2,$$

(28)

which coincides with the operator–algebraic residual of Def. 3.1.

• Projection characterization (proved).

Proposition 3.1

(Metric projection property). Let $(\mathcal{M},\omega )$ be as above and $\mathcal{N}\subset \mathcal{M}$ modular–invariant. Then for every $X\in L^2\left(\omega \right)$,

$$\parallel X-{\mathsf{E}}_{\mathcal{N}}{X\parallel }_{2,\omega }={inf\{\parallel X-Y\parallel }_{2,\omega }:Y\in L^2(\mathcal{N},\omega )\}.$$

(29)

In particular, ${\mathsf{E}}_{\mathcal{N}}$ is the unique ω–preserving $L^2$–contraction with range $L^2(\mathcal{N},\omega )$, and ${\mathcal{R}}_{\omega ,\mathcal{N}}\left(X\right)$ is the squared distance to the pointer fiber.

Proof. 

Takesaki gives ${\mathsf{E}}_{\mathcal{N}}$ as a conditional expectation preserving $\omega$. Its $L^2\left(\omega \right)$–extension is the orthogonal projection onto $L^2(\mathcal{N},\omega )$, hence the metric projection.    □

• Naturality and data–processing (proved).

Proposition 3.2

(Residual monotonicity under coarse–graining). Let $\Phi :({\mathcal{M}}_1,{\omega }_1)\to ({\mathcal{M}}_2,{\omega }_2)$ be normal u.c.p. with ${\omega }_2\circ \Phi ={\omega }_1$. Let ${\mathcal{N}}_i\subset {\mathcal{M}}_i$ be modular–invariant pointer algebras such that $\Phi \left({\mathcal{N}}_1\right)\subset {\mathcal{N}}_2$ and $\Phi \circ {\mathsf{E}}_{{\mathcal{N}}_1}={\mathsf{E}}_{{\mathcal{N}}_2}\circ \Phi$ on ${\mathcal{M}}_1$. Then for all $X\in L^2\left({\omega }_1\right)$,

$$\parallel \Phi \left(X\right)-{\mathsf{E}}_{{\mathcal{N}}_2}{\Phi \left(X\right)\parallel }_{2,{\omega }_2}\le {\parallel X-{\mathsf{E}}_{{\mathcal{N}}_1}X\parallel }_{2,{\omega }_1}.$$

(30)

Equivalently, ${\mathcal{R}}_{{\omega }_2,{\mathcal{N}}_2}(\Phi \left(X\right))\le {\mathcal{R}}_{{\omega }_1,{\mathcal{N}}_1}\left(X\right)$.

Proof. 

Kadison–Schwarz gives ${\parallel \Phi \left(Z\right)\parallel }_{2,{\omega }_2}\le {\parallel Z\parallel }_{2,{\omega }_1}$ for all Z. With the intertwining assumption,

$$\Phi \left(X\right)-{\mathsf{E}}_{{\mathcal{N}}_2}\Phi \left(X\right)=\Phi \left(X-{\mathsf{E}}_{{\mathcal{N}}_1}X\right),$$

so (30) follows by contractivity in $L^2$.    □

• Unitary covariance (proved).

Proposition 3.3

(Unitary equivalence of contexts). If $U:\mathcal{M}\to \mathcal{M}$ is a *–automorphism with $\omega \circ U=\omega$, and ${\mathcal{N}}^{\prime }:=U\mathcal{N}{U}^{\ast }$, then

$${\mathcal{R}}_{\omega ,{\mathcal{N}}^{\prime }}\left(X\right)={\mathcal{R}}_{\omega ,\mathcal{N}}\left(U^{\ast }XU\right)\mathrm{and}{\mathsf{E}}_{{\mathcal{N}}^{\prime }}\left(X\right)=U{\mathsf{E}}_{\mathcal{N}}\left(U^{\ast }XU\right)U^{\ast }.$$

In particular, the residual and its decay rates are invariant under unitary relabellings of the context.

Proof. 

U induces an $L^2\left(\omega \right)$–unitary; conjugating the orthogonal projector preserves distances.    □

• Pointer dilations and classical sectors (proved).

Proposition 3.4

(Naimark dilation and classicalization). Let a POVM M on $(Y,{\mu }_Y)$ arise from a Naimark dilation $(\widehat{\mathcal{M}},\widehat{\omega },\iota ,\Pi )$ with $\iota :\mathcal{M}\hookrightarrow \widehat{\mathcal{M}}$ and abelian pointer algebra $\widehat{\mathcal{N}}\simeq L^{\infty }(Y,{\mu }_Y)$. Then

$${\mathcal{R}}_{\widehat{\omega },\widehat{\mathcal{N}}}\left(\iota \left(X\right)\right)\le {\mathcal{R}}_{\omega ,\mathcal{N}}\left(X\right),$$

with equality if ι is isometric on $L^2$ and $\mathcal{N}$ is the pullback of $\widehat{\mathcal{N}}$. Hence moving to a classical pointer sector cannot increase the residual.

Proof. 

Apply Prop. 3.2 to $\iota$ and the conditional expectations that intertwine via the dilation.    □

• Geometric sector (proved template).

In the PDE/continuum setting, the blueprint–response pair is $(\nabla \rho ,P)$ with residual ${\int |P-\nabla \rho |}^2$. The analogues of ${\mathsf{E}}_{\mathcal{N}}$ are orthogonal projections in $L^2$ onto constraint subspaces (e.g. gradients/solenoidal fields via Helmholtz). The exact energy identity gives the “propagation” (nonincrease) and ellipticity gives the “gap” (coercivity)—the DSFL ingredients.

• Naturality square and asymptotic commutativity.

The above results can be summarized by the near–commutativity of the diagram up to a residual that contracts under DSFL. Prop. 3.2 ensures compatibility under coarse–graining; Prop. 3.3 shows invariance under relabelling.

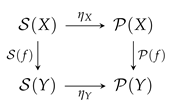• Optional categorical refinements (context, not used in proofs).

• Monoidal covariance. On products, residuals are additive under orthogonal sums in Hilbert space; DSFL on products follows from small–gain conditions (cf. Prop. 4.1).
• Dagger structure. In reversible cases the relevant functors/morphisms are dagger–symmetric: adjoints coincide with time–reversal at the Hilbert level, making the projection picture especially transparent.
• Enrichment. One may view $\mathcal{S},\mathcal{P}$ as $\mathbf{Hilb}$–enriched functors, with $\eta$ enriched by metric contractivity; we do not rely on enrichment in our proofs.

• What this buys us (concise consequences).

• Unique alignment rule. ${\mathsf{E}}_{\mathcal{N}}$ is the unique $\omega$–preserving $L^2$–projection (Prop. 3.1); thus the OA residual is the canonical misalignment measure relative to a pointer context.
• Stability under processing. Coarse–graining cannot increase misalignment (Prop. 3.2); experiments that only access a coarser context still inherit DSFL contraction.
• Context covariance. Changing basis or measurement realization leaves the law’s form and the residual’s meaning intact (Prop. 3.3, 3.4).

• Limitations (as requested).

The categorical narrative explains why the same residual appears across sectors but does not strengthen our analytic rates. All rate–level statements still hinge on sectoral hypotheses (reversibility/spectral gap in QMS; ellipticity/coercivity in PDE; Hamiltonian gap in free fields; Lichnerowicz gap on GR slices).

Lemma 3.1

(Variational characterization). For $(\mathcal{M},\omega ,\mathcal{N})$ as above and $X\in L^2\left(\omega \right)$,

$${\mathcal{R}}_{\omega ,\mathcal{N}}\left(X\right)=\underset{Y\in L^2(\mathcal{N},\omega )}{min}{\parallel X-Y\parallel }_{2,\omega }^2\mathit{and}{\mathsf{E}}_{\mathcal{N}}X=\underset{Y\in L^2(\mathcal{N},\omega )}{arg\; min}{\parallel X-Y\parallel }_{2,\omega }^2.$$

Proof. 

Immediate from (26).    □

3.6. Residuals and Entropy Proxies

• DSFL residuals.

The global DSFL residual in the classical/PDE sector is

$$\mathcal{R}\left(t\right):={\int }_{\Omega }{|P(x,t)-\nabla \rho (x,t)|}^{2}dx,$$

(31)

or its weighted variant ${\int }_{\Omega }{|P-\nabla \rho |}_W^{2}dx$. The noncommutative analogue is ${\mathcal{R}}_{\omega }\left(X\right):={\parallel X-{\mathsf{E}}_{\mathcal{N}}\left(X\right)\parallel }_{2,\omega }^2$ (QMS). On Riemannian slices we use the geometric residual

$${\mathcal{R}}_{\mathrm{geom}}\left(t\right):={\int }_{\Sigma }\parallel G\left[\gamma \left(t\right)\right]-\kappa T{\parallel }_{\gamma \left(t\right)}^{2}d{\mu }_{\gamma \left(t\right)}.$$

(32)

• Residual–entropy proxy.

A dimensionless proxy is

$$S_R\left(t\right):=-log\left(\mathcal{R}\left(t\right)/{\mathcal{R}}_0+R_{\ast }\right)({\mathcal{R}}_0>0,R_{\ast }\in (0,1)).$$

(33)

• Initial sameness and common ancestry.

All physical sectors—quantum, thermodynamic, and geometric—descend from a shared initial alignment between statistical and physical structures. We call this the principle of common ancestry: at $t=0$, the universe (or any closed system) possessed a single residual-free configuration

$$P_0=\nabla {\rho }_0,\mathcal{R}\left(0\right)={\int }_{\Omega }{|P_0-\nabla {\rho }_0|}^{2}dx=0.$$

(34)

This expresses the state of complete statistical–physical identity (initial sameness) from which all later structures evolve.

As evolution proceeds, local perturbations generate misalignments, $u(x,t):=P(x,t)-\nabla \rho (x,t)$, which define the residual

$$\mathcal{R}\left(t\right)={\int }_{\Omega }{|u(x,t)|}^{2}dx,\dot{\mathcal{R}}\left(t\right)\le -\alpha \mathcal{R}\left(t\right),$$

(35)

where $\alpha >0$ is the sectoral spectral gap (quantum, thermodynamic, or geometric). The Deterministic Statistical Feedback Law (DSFL) ensures exponential suppression of these residuals, restoring the alignment that encodes shared ancestry:

$$\mathcal{R}\left(t\right)\le e^{-\alpha t}\mathcal{R}\left(0\right).$$

(36)

Hence equilibrium is not a probabilistic emergence from randomness, but the dynamic recovery of common ancestry through deterministic residual decay. The same Lyapunov structure appears in all sectors— Born alignment in quantum mechanics, entropy growth in thermodynamics, and curvature–matter balance in general relativity—each governed by its own contextual rate $\alpha$.

4. Main Results

4.1. Uniform Law, Contextual Rates

The DSFL inequality has a uniform mathematical form across sectors,

$$\frac{d}{dt}\mathcal{R}\left(t\right)\le -\alpha \mathcal{R}\left(t\right),\Rightarrow \mathcal{R}\left(t\right)\le e^{-\alpha t}\mathcal{R}\left(0\right),$$

(37)

but the constant $\alpha >0$ is sector–dependent. In each setting, $\alpha$ equals the corresponding spectral–gap/coercivity parameter:

$$\alpha =\left\{\begin{array}{cc}2{\lambda }_{\mathrm{Poincar}\text{é}}\hfill & \mathrm{reversible}\mathrm{classical}/\mathrm{QMS}\mathrm{on}{\mathcal{N}}^{\perp },\hfill \\ beginequation2pt]2\beta -C\epsilon \hfill & \mathrm{coercive}\mathrm{PDE}\mathrm{closure}(B⪰\beta I),\hfill \\ beginequation2pt]2{\lambda }_{\ast }\hfill & \mathrm{free}\text{–}\mathrm{field}\mathrm{OU}/\mathrm{Hamiltonian}\mathrm{gap},\hfill \\ beginequation2pt]2c{\lambda }_{\mathrm{GR}}\hfill & \mathrm{GR}\mathrm{slice}\left(\mathrm{DeTurck}\right)\mathrm{on}\mathrm{the}\mathrm{physical}\mathrm{subspace}.\hfill \end{array}\right.$$

(38)

Remark 4.1

(Mathematically uniform, physically contextual). Equation (37) is the same in all sectors (uniform Lyapunov law), but its rate α in (38) is fixed by the sectoral physics: pointer algebra and Dirichlet form (QMS), mobility and closure (PDE), Hamiltonian spectrum (QFT/Gaussian), or Lichnerowicz gap (geometry). Thus the restoration mechanism is universal, while the speed of restoration is contextual and must be computed in each sector.

Corollary 4.1

(Sectoral attractors with explicit rates). Let $\mathcal{A}$ denote the sectoral equilibrium manifold (e.g. the fixed-point algebra $L^2(\mathcal{N},\omega )$, the Born law ${|\Psi |}^2$, or the Einstein balance set). Under the hypotheses yielding the corresponding gap/coercivity,

$$\mathrm{dist}\left(x\left(t\right),\mathcal{A}\right)\le C{e}^{-\alpha t}\mathrm{dist}\left(x\left(0\right),\mathcal{A}\right),$$

(39)

with α given by (38) and C a sectoral equivalence constant (projection/gauge). Hence, the form of convergence is universal, but the rate is determined by the sector’s gap.

• Editorial note (for the Introduction). To make this distinction explicit up front, one sentence can be added: “While the DSFL provides a single Lyapunov law $\dot{\mathcal{R}}\le -\alpha \mathcal{R}$, the constant α is sectoral: it equals the relevant spectral gap or coercivity (operator algebraic, PDE, free-field, or geometric), so the mechanism is universal but its rate is context dependent.”

Remark 4.2

(Covariance vs. slice formulation). The geometric DSFL result in Theorem 4.6 is proved on a compact Riemannian slice in DeTurck gauge. It establishes exponential suppression of the curvature–matter misfit in that elliptic setting but does not yet provide a fully covariant (Lorentzian) formulation. In other words, the present theorem is a slice-level statement—analytically rigorous but gauge–fixed—while a fully diffeomorphism–invariant, hyperbolic extension remains an open program. This distinction should be made explicit: the law is structurally general, yet the proof given here is Riemannian rather than covariant.

This section states the core theorems in a hypothesis–result format, ready for citation in later sections and proofs. Throughout we use the notation and conventions of Section 3. In particular, $\mathcal{R}$ denotes the global alignment residual (classical/PDE) or the noncommutative variance relative to a pointer algebra (QMS). All proofs are deferred to Sec. 5, where the three settings (classical, operator–algebraic, and PDE) are treated in parallel.

• What is proved here.

First, a unified propagation lemma (Section 4.2) shows that local convexity/contractivity mechanisms (Jensen, Kadison–Schwarz, energy identities) imply global residual monotonicity. Second, adding a spectral gap or coercivity yields exponential DSFL decay. In the operator–algebraic case (Section 4.3) we obtain an equivalence between DSFL and a noncommutative Poincaré (spectral–gap) inequality with optimal rate ${\alpha }_{\ast }=2{\lambda }_{\ast }$.

4.2. DSFL Propagation Lemma (Classical/QMS/PDE)

Lemma 4.1

(Propagation of residual monotonicity: classical, noncommutative, and PDE). Let ${\left({\mathsf{T}}_t\right)}_{t\ge 0}$ act on the Hilbert space where the residual $\mathcal{R}$ is evaluated. Assume one of the following structural settings.

• (CL) Classical Markov setting.$\left({\mathsf{T}}_t\right)$ is a Markov contraction semigroup on $L^1\cap L^2\left(\mu \right)$ over a σ–finite measure space $(\Omega ,\mu )$: it preserves positivity, mass (${\mathsf{T}}_t\mathbf{1}=\mathbf{1}$), and is $L^p$–contractive for $1\le p\le \infty$. Let $u_0\in L^2\left(\mu \right)$ and let $r\left(x\right)=\phi \left(u_0\left(x\right)\right)$ with $\phi :{\mathbb{R}}^m\to [0,\infty )$ a Borel convex function and $\phi \left(0\right)=0$. Define

$$\mathcal{R}\left(0\right):={\int }_{\Omega }\phi \left(u_0\right)d\mu ,\mathcal{R}\left(t\right):={\int }_{\Omega }\phi \left(\left({\mathsf{T}}_t{u}_0\right)\left(x\right)\right)d\mu \left(x\right).$$

(40)

(QM) Operator–algebraic/QMS setting. $\left({\mathsf{T}}_t\right)$ is a normal unital completely positive (u.c.p.) semigroup on a von Neumann algebra $(\mathcal{M},\omega )$, $\omega$–symmetric on $L^2\left(\omega \right)$ (reversible) and $\omega$–preserving: $\omega \left({\mathsf{T}}_{t}Y\right)=\omega \left(Y\right)$. Let $\mathcal{N}:=\{X:{\mathsf{T}}_{t}X=X\forall t\}$ be the fixed–point algebra and ${\mathsf{E}}_{\mathcal{N}}:\mathcal{M}\to \mathcal{N}$ the ω–preserving conditional expectation (the $L^2\left(\omega \right)$ orthogonal projection). Define the noncommutative variance (residual)

$${\mathcal{R}}_{\omega }\left(X\right):={\parallel X-{\mathsf{E}}_{\mathcal{N}}\left(X\right)\parallel }_{2,\omega }^2,X\in L^2\left(\omega \right).$$

(41)

(PDE) Parabolic/energy–identity setting. Let $\Omega \subset {\mathbb{R}}^d$ be a bounded $C^1$ domain (with homogeneous Dirichlet/Neumann b.c.) or ${\mathbb{T}}^d$ (periodic). Let $\rho (·,t)\in H^1(\Omega )$, $P(·,t)\in L^2(\Omega ;{\mathbb{R}}^d)$, and set $u:=P-\nabla \rho \in L^2(\Omega ;{\mathbb{R}}^d)$. Assume the exact residual identity

$$\frac{d}{dt}{\int }_{\Omega }{|u|}^{2}dx=-2{\int }_{\Omega }{u}^{\top }Budx-2{\parallel \nabla ·u\parallel }_{L^2(\Omega )}^2+\mathsf{Rem}\left(t\right),$$

(42)

with a measurable $B(x,t)⪰0$ a.e. and a remainder $\mathsf{Rem}\left(t\right)\le 0$ (or dominated by the dissipative terms). Let $\mathcal{R}\left(t\right):={\int }_{\Omega }{|u(x,t)|}^{2}dx$.

• Conclusion. In each setting, the residual is monotone nonincreasing:

$$\mathcal{R}\left(t\right)\le \mathcal{R}\left(0\right)\forall t\ge 0.$$

(43)

More precisely:

$$\begin{array}{cc}\hfill \left(\mathrm{CL}\right):& \int \phi \left({\mathsf{T}}_t{u}_0\right)d\mu \le \int \phi \left(u_0\right)d\mu ,\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill \left(\mathrm{QM}\right):& \parallel {\mathsf{T}}_{t}X-{\mathsf{E}}_{\mathcal{N}}{\left(X\right)\parallel }_{2,\omega }\le {\parallel X-{\mathsf{E}}_{\mathcal{N}}\left(X\right)\parallel }_{2,\omega },\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill \left(\mathrm{PDE}\right):& \frac{d}{dt}{\parallel u\left(t\right)\parallel }_{L^2(\Omega )}^2\le 0.\hfill \end{array}$$

(46)

Proof.(CL). By Jensen and positivity, $\phi \left({\mathsf{T}}_t{u}_0\right)\le {\mathsf{T}}_t\left(\phi \left(u_0\right)\right)$$\mu$–a.e.; integrate and use $\int {\mathsf{T}}_{t}fd\mu =\int fd\mu$.

(QM). Kadison–Schwarz for u.c.p. maps gives ${\mathsf{T}}_t{\left(X\right)}^{\ast }{\mathsf{T}}_t\left(X\right)\le {\mathsf{T}}_t\left(X^{\ast }X\right)$; apply $\omega$ and $\omega \circ {\mathsf{T}}_t=\omega$ to obtain $\parallel {\mathsf{T}}_t{X\parallel }_{2,\omega }\le {\parallel X\parallel }_{2,\omega }$. Since ${\mathsf{E}}_{\mathcal{N}}$ is the $L^2\left(\omega \right)$ orthogonal projection and ${\mathsf{T}}_t$ acts as the identity on $\mathcal{N}$, the same contraction holds for $X-{\mathsf{E}}_{\mathcal{N}}X$.

(PDE). Integrate (42) in time; $B⪰0$ and $\mathsf{Rem}\left(t\right)\le 0$ give $\frac{d}{dt}\int {|u|}^2\le 0$.    □

Corollary 4.2

(Propagation + gap/coercivity ⇒ DSFL). Under Lemma 4.1, suppose additionally:

• (CL)L (the generator of ${\mathsf{T}}_t=e^{tL}$) is symmetric on $L^2\left(\mu \right)$ and satisfies a Poincaré inequality ${\mathrm{Var}}_{\mu }\left(f\right)\le {\lambda }^{-1}\int \Gamma \left(f\right)d\mu$ for some $\lambda >0$ (here Γ denotes the carré du champ).
• (QM)The ω–symmetric generator $\mathcal{L}$ has a spectral gap $\lambda >0$ on $L^2\left(\omega \right)\ominus L^2(\mathcal{N},\omega )$: $\parallel X-{\mathsf{E}}_{\mathcal{N}}{X\parallel }_{2,\omega }^2\le {\lambda }^{-1}{\langle X,-\mathcal{L}X\rangle }_{2,\omega }$.
• (PDE)$B(x,t)⪰\beta I$ a.e. with $\beta >0$, and $\mathsf{Rem}\left(t\right)\le C\epsilon \mathcal{R}\left(t\right)$ for some $C>0$ and sufficiently small $\epsilon \ge 0$.

Then the DSFL inequality holds with an explicit rate:

$$\left(\mathrm{CL}\right)\&\left(\mathrm{QM}\right):\mathcal{R}\left(t\right)\le e^{-2\lambda t}\mathcal{R}\left(0\right),\left(\mathrm{PDE}\right):\mathcal{R}\left(t\right)\le e^{-(2\beta -C\epsilon )t}\mathcal{R}\left(0\right).$$

(47)

Remark 4.3

(Domains and regularity; where proofs appear). In (QM), differentiating $\parallel {\mathsf{T}}_{t}X-{\mathsf{E}}_{\mathcal{N}}{X\parallel }_{2,\omega }^2$ at $t=0$ is justified for $X\in \mathsf{D}\left(\mathcal{L}\right)$ and extends by density to $\mathsf{D}\left({\mathcal{E}}_{\omega }\right)$ (closedness of the Dirichlet form). In (PDE), integrations by parts are justified by periodic or homogeneous boundary conditions and the Sobolev regularity $\rho \in H^1$, $P\in L^2$ (or a standard mollification argument). Complete proofs are given in Sec. 5.

4.3. DSFL ⇔ Spectral Gap (Reversible QMS)

Definition 4.1

(Operator-algebraic residual). Let $(\mathcal{M},\omega )$ be a von Neumann algebra with faithful normal state ω, and let $\mathcal{N}\subset \mathcal{M}$ be ω-modular invariant so that the ω-preserving conditional expectation ${\mathsf{E}}_{\mathcal{N}}:\mathcal{M}\to \mathcal{N}$ exists (Takesaki). Define, for $X\in L^2\left(\omega \right)$,

$${\mathcal{R}}_{\omega ,\mathcal{N}}\left(X\right):={\parallel X-{\mathsf{E}}_{\mathcal{N}}X\parallel }_{2,\omega }^2.$$

(48)

Then ${\mathcal{R}}_{\omega ,\mathcal{N}}$ is the squared $L^2\left(\omega \right)$-distance to $L^2(\mathcal{N},\omega )$.

Theorem 4.1

(DSFL ⟺ spectral gap). Let ${\left({\mathsf{T}}_t\right)}_{t\ge 0}$ be a normal u.c.p. semigroup on $\mathcal{M}$ that is ω-symmetric on $L^2\left(\omega \right)$ and ω-preserving. Write $\mathcal{N}=\{X:{\mathsf{T}}_{t}X=X\forall t\}$ and let $\mathcal{L}$ be the $L^2\left(\omega \right)$ generator with Dirichlet form ${\mathcal{E}}_{\omega }\left(X\right)={\langle X,-\mathcal{L}X\rangle }_{2,\omega }$. The following are equivalent:

(i) 

(DSFL) $\exists \alpha >0$ s.t. ${\mathcal{R}}_{\omega ,\mathcal{N}}\left({\mathsf{T}}_{t}X\right)\le e^{-\alpha t}{\mathcal{R}}_{\omega ,\mathcal{N}}\left(X\right)$ for all $t\ge 0$ and $X\in L^2\left(\omega \right)$.

(ii) 

(Spectral gap) $\exists \lambda >0$ s.t. $\parallel X-{\mathsf{E}}_{\mathcal{N}}{X\parallel }_{2,\omega }^2\le {\lambda }^{-1}{\mathcal{E}}_{\omega }\left(X\right)$ for all X in the form domain.

Moreover, the optimal constants satisfy ${\alpha }_{\ast }=2{\lambda }_{\ast }$.

• Setting and assumptions.

Let $(\mathcal{M},\omega )$ be a $\sigma$–finite von Neumann algebra with faithful normal state $\omega$. Write $L^2\left(\omega \right)$ for the GNS Hilbert space with

$${\langle X,Y\rangle }_{2,\omega }:=\omega \left(X^{\ast }Y\right),{\parallel X\parallel }_{2,\omega }^2=\omega \left(X^{\ast }X\right).$$

(49)

Let ${\left({\mathsf{T}}_t\right)}_{t\ge 0}$ be a normal unital completely positive (u.c.p.) semigroup on $\mathcal{M}$ such that:

(A1)

(ω–symmetry / detailed balance) Each ${\mathsf{T}}_t$ is self–adjoint on $L^2\left(\omega \right)$: ${\langle {\mathsf{T}}_{t}X,Y\rangle }_{2,\omega }={\langle X,{\mathsf{T}}_{t}Y\rangle }_{2,\omega }$ for all $X,Y\in L^2\left(\omega \right)$.

(A1)

(ω–preservation) $\omega \left({\mathsf{T}}_{t}Z\right)=\omega \left(Z\right)$ for all Z and $t\ge 0$.

(A2)

($L^2$ generator and Dirichlet form) The $L^2\left(\omega \right)$–generator $\mathcal{L}$ of $\left({\mathsf{T}}_t\right)$ is self–adjoint, with closed quadratic form

$$\mathsf{D}\left({\mathcal{E}}_{\omega }\right)=\overline{\mathrm{Dom}\left({\mathcal{L}}^{1/2}\right)},{\mathcal{E}}_{\omega }\left(X\right):={\langle X,-\mathcal{L}X\rangle }_{2,\omega },$$

(50)

and a *–subalgebra ${\mathcal{A}}_0\subset \mathsf{D}\left({\mathcal{E}}_{\omega }\right)$ (e.g. the analytic elements of $\left({\mathsf{T}}_t\right)$) is a form core.

(A3)

(Fixed–point algebra) $\mathcal{N}:=\{X\in \mathcal{M}:{\mathsf{T}}_{t}X=X\forall t\ge 0\}$ is a von Neumann subalgebra. The modular group ${\left({\sigma }_s^{\omega }\right)}_{s\in \mathbb{R}}$ leaves $\mathcal{N}$ globally invariant.

Under (A3), Takesaki’s theorem yields:

Lemma 4.2

(Conditional expectation). There exists a unique faithful normal conditional expectation ${\mathsf{E}}_{\mathcal{N}}:\mathcal{M}\to \mathcal{N}$ that preserves ω. It extends to the orthogonal projection $L^2\left(\omega \right)\to L^2(\mathcal{N},\omega )$ with $\parallel {\mathsf{E}}_{\mathcal{N}}\parallel =1$.

Define the noncommutative variance (residual)

$${\mathcal{R}}_{\omega }\left(X\right):={\parallel X-{\mathsf{E}}_{\mathcal{N}}\left(X\right)\parallel }_{2,\omega }^2,L^2\left(\omega \right)=L^2(\mathcal{N},\omega )\oplus L^2{(\mathcal{N},\omega )}^{\perp }.$$

(51)

Write $X^{\perp }:=X-{\mathsf{E}}_{\mathcal{N}}X\in L^2{(\mathcal{N},\omega )}^{\perp }$.

Lemma 4.3

($L^2\left(\omega \right)$–differentiability and domains). For $X\in \mathsf{D}\left(\mathcal{L}\right)$,

$$\frac{d}{dt}{\parallel {\mathsf{T}}_t{X}^{\perp }\parallel }_{2,\omega }^2{|}_{t=0}=-2{\mathcal{E}}_{\omega }\left(X^{\perp }\right).$$

(52)

More generally, for all $t\ge 0$ with ${\mathsf{T}}_{t}X\in \mathsf{D}\left(\mathcal{L}\right)$,

$$\frac{d}{dt}{\parallel {\mathsf{T}}_t{X}^{\perp }\parallel }_{2,\omega }^2=-2{\mathcal{E}}_{\omega }\left({\mathsf{T}}_t{X}^{\perp }\right).$$

(53)

Proof. 

Since $\left({\mathsf{T}}_t\right)$ is self–adjoint and strongly continuous on $L^2\left(\omega \right)$, $t\mapsto \parallel {\mathsf{T}}_t{X}^{\perp }{\parallel }_{2,\omega }^2=\langle {\mathsf{T}}_t{X}^{\perp },{\mathsf{T}}_t{X}^{\perp }\rangle$ is $C^1$ on any interval where ${\mathsf{T}}_{t}X\in \mathsf{D}\left(\mathcal{L}\right)$. Differentiating and using self–adjointness of $\mathcal{L}$ gives

$$\frac{d}{dt}{\parallel {\mathsf{T}}_t{X}^{\perp }\parallel }_{2,\omega }^2=2{\langle {\mathsf{T}}_t{X}^{\perp },\mathcal{L}{\mathsf{T}}_t{X}^{\perp }\rangle }_{2,\omega }=-2{\mathcal{E}}_{\omega }\left({\mathsf{T}}_t{X}^{\perp }\right).$$

(54)

Orthogonality to $L^2(\mathcal{N},\omega )$ is preserved because ${\mathsf{T}}_t{\mathsf{E}}_{\mathcal{N}}={\mathsf{E}}_{\mathcal{N}}$ and ${\mathsf{T}}_t$ acts as the identity on the fixed space.    □

• Poincaré inequality on the orthogonal complement.

We say that $\mathcal{L}$ has a spectral gap $\lambda >0$ on $L^2{(\mathcal{N},\omega )}^{\perp }$ if

$${\mathcal{E}}_{\omega }\left(Z\right)\ge \lambda {\parallel Z\parallel }_{2,\omega }^2\forall Z\in \mathsf{D}\left({\mathcal{E}}_{\omega }\right)\cap L^2{(\mathcal{N},\omega )}^{\perp }.$$

(55)

Equivalently,

$$\parallel X-{\mathsf{E}}_{\mathcal{N}}{X\parallel }_{2,\omega }^2\le \frac{1}{\lambda }{\mathcal{E}}_{\omega }\left(X\right)\forall X\in \mathsf{D}\left({\mathcal{E}}_{\omega }\right),$$

(56)

i.e. the noncommutative Poincaré inequality holds on ${\mathcal{N}}^{\perp }$.

Theorem 4.2

(Operator–algebraic DSFL ⟺ spectral gap). Under(A1)–(A3)the following are equivalent:

(i)

DSFL decay.   $\exists \alpha >0$ such that for all $X\in L^2\left(\omega \right)$,

$${\mathcal{R}}_{\omega }\left({\mathsf{T}}_{t}X\right)\le e^{-\alpha t}{\mathcal{R}}_{\omega }\left(X\right)\forall t\ge 0.$$

(57)

(ii)

Spectral gap / Poincaré on ${\mathcal{N}}^{\perp }$.   There exists $\lambda >0$ such that (56) holds on $\mathsf{D}\left({\mathcal{E}}_{\omega }\right)$.

Moreover, the optimal constants coincide as ${\alpha }_{\ast }=2{\lambda }_{\ast }$.

Proof sketch. 

For $Z_t:={\left({\mathsf{T}}_{t}X\right)}^{\perp }$ one has $\frac{d}{dt}{\parallel Z_t\parallel }_{2,\omega }^2=-2{\mathcal{E}}_{\omega }\left(Z_t\right)$. If (ii) holds then $\dot{\parallel Z_t{\parallel }_2^2}\le -2\lambda {\parallel Z_t\parallel }_2^2$ and Grönwall yields (i) with $\alpha =2\lambda$. Conversely, differentiating (i) at $t=0$ gives ${\mathcal{E}}_{\omega }\left(X^{\perp }\right)\ge (\alpha /2){\parallel X^{\perp }\parallel }_2^2$.    □

Remark 4.4

(Closability, core, and invariance). (i) The form ${\mathcal{E}}_{\omega }$ is closed on $L^2\left(\omega \right)$ because $\left({\mathsf{T}}_t\right)$ is self–adjoint and contractive; $\mathsf{D}\left({\mathcal{E}}_{\omega }\right)=\mathsf{D}\left({\mathcal{L}}^{1/2}\right)$ is the canonical form domain. Moreover, the *–algebra of analytic elements for $\left({\mathsf{T}}_t\right)$ is dense in $\mathsf{D}\left({\mathcal{E}}_{\omega }\right)$ and forms a core. (ii) Reversibility implies $\left({\mathsf{T}}_t\right)$ leaves both $L^2(\mathcal{N},\omega )$ and $L^2{(\mathcal{N},\omega )}^{\perp }$ invariant; hence the restriction of $\mathcal{L}$ to ${\mathcal{N}}^{\perp }$ is self–adjoint and nonnegative, with spectrum contained in $\left\{0\right\}\cup [{\lambda }_{\ast },\infty )$ iff (56) holds.

Remark 4.5

(Conditional expectation ${\mathsf{E}}_{\mathcal{N}}$). The modular invariance of $\mathcal{N}$ (A3) ensures the existence and uniqueness of a faithful normal ω–preserving conditional expectation ${\mathsf{E}}_{\mathcal{N}}:\mathcal{M}\to \mathcal{N}$ (Takesaki’s theorem). As an $L^2$ map it is the orthogonal projection onto $L^2(\mathcal{N},\omega )$, so ${\mathcal{R}}_{\omega }\left(X\right)=\mathrm{dist}{(X,L^2(\mathcal{N},\omega ))}^2$.

• DSFL interpretation.

Theorem 4.2 identifies the DSFL rate with the spectral gap of the reversible QMS restricted to $L^2{(\mathcal{N},\omega )}^{\perp }$: the noncommutative variance (misalignment) decays exponentially iff the Poincaré inequality holds on ${\mathcal{N}}^{\perp }$, with $\alpha =2\lambda$.

4.4. Sharp Lindblad Rate (Finite–Dimensional Dephasing)

Let $\mathcal{H}={\mathbb{C}}^d$ with orthonormal basis ${\{|i\rangle \}}_{i=1}^d$ and spectral projectors $P_i=|i\rangle \langle i|$. Consider the (trace–preserving, completely positive) dephasing Lindblad generator on $M_d\left(\mathbb{C}\right)$

$${\mathcal{L}}^{\ast }\left(\sigma \right)=\sum _{i=1}^d{\gamma }_i\left(P_i\sigma P_i-\frac{1}{2}\{P_i,\sigma \}\right),{\gamma }_i>0,$$

(58)

and the dual master equation ${\dot{\sigma }}_t={\mathcal{L}}^{\ast }\left({\sigma }_t\right)$ for density matrices. Let $\Phi :M_d\to M_d$ be the Lüders (diagonal) conditional expectation $\Phi \left(X\right)={\sum }_i{P}_{i}X{P}_i$ onto the abelian pointer algebra $\mathcal{N}=\{X:[X,P_i]=0\forall i\}$. Then $\Phi$ is the (trace–)preserving conditional expectation onto $\mathcal{N}$, and the Lüders residual

$${\mathcal{R}}_{\mathrm{L}\ddot{\mathrm{u}}\mathrm{ders}}\left(\sigma \right):={\parallel \sigma -\Phi \left(\sigma \right)\parallel }_2^2=\sum _{i\ne j}{|{\left(\sigma \right)}_{ij}|}^2$$

(59)

is the Hilbert–Schmidt variance off the diagonal algebra $\mathcal{N}$.

Theorem 4.3

(Sharp exponential decay of the Lüders residual). Let

$${\lambda }_{\ast }:=\frac{1}{2}\underset{i\ne j}{min}({\gamma }_i+{\gamma }_j),{\alpha }_{\ast }:=2{\lambda }_{\ast }=\underset{i\ne j}{min}({\gamma }_i+{\gamma }_j).$$

(60)

Then for all $t\ge 0$,

$${\mathcal{R}}_{\mathrm{L}\ddot{\mathrm{u}}\mathrm{ders}}\left({\sigma }_t\right)\le e^{-{\alpha }_{\ast }t}{\mathcal{R}}_{\mathrm{L}\ddot{\mathrm{u}}\mathrm{ders}}\left({\sigma }_0\right),$$

(61)

and the rate ${\alpha }_{\ast }$ is optimal (sharp). In particular, if the minimal dephasing rate is attained by at least two indices, then ${\alpha }_{\ast }=2{min}_i{\gamma }_i$; otherwise ${\alpha }_{\ast }={\gamma }_{min}+{\gamma }_{2\mathrm{nd}\min }$.

Proof (modewise solution). 

In the basis $\{|i\rangle \}$ one has

$$\frac{d}{dt}{\left({\sigma }_t\right)}_{ii}=0,\frac{d}{dt}{\left({\sigma }_t\right)}_{ij}=-\frac{{\gamma }_i+{\gamma }_j}{2}{\left({\sigma }_t\right)}_{ij}(i\ne j),$$

(62)

so ${\left({\sigma }_t\right)}_{ij}=e^{-({\gamma }_i+{\gamma }_j)t/2}{\left({\sigma }_0\right)}_{ij}$ and hence

$${\mathcal{R}}_{\mathrm{L}\ddot{\mathrm{u}}\mathrm{ders}}\left({\sigma }_t\right)=\sum _{i\ne j}{e}^{-({\gamma }_i+{\gamma }_j)t}|{\left({\sigma }_0\right)}_{ij}{|}^2\le e^{-{\alpha }_{\ast }t}\sum _{i\ne j}{|{\left({\sigma }_0\right)}_{ij}|}^2.$$

(63)

Sharpness: choose initial data supported on a pair $(i_{\ast },j_{\ast })$ achieving ${min}_{i\ne j}({\gamma }_i+{\gamma }_j)$.    □

Corollary 4.3

(Born–aligned limit and trace–norm control). As $t\to \infty$, ${\sigma }_t\to \Phi \left({\sigma }_0\right)$ in Hilbert–Schmidt norm and in trace norm with

$$\parallel {\sigma }_t-\Phi \left({\sigma }_0\right){\parallel }_1\le \sqrt{d}{e}^{-{\lambda }_{\ast }t}{\parallel {\sigma }_0-\Phi \left({\sigma }_0\right)\parallel }_2.$$

(64)

The limit is the Lüders (Born–aligned) state for the measurement basis $\{|i\rangle \}$.

Remark 4.6

(DSFL and spectral gap identification). The off–diagonal (pointer–orthogonal) sector is invariant and the restriction of $\mathcal{L}$ to it has spectral gap ${\lambda }_{\ast }=\frac{1}{2}{min}_{i\ne j}({\gamma }_i+{\gamma }_j)$. By Theorem 4.2, the DSFL rate is ${\alpha }_{\ast }=2{\lambda }_{\ast }$.

Remark 4.7

(Commuting Hamiltonians and basis choice). (a) Adding $-i[H,{\sigma }_t]$ with $H={\sum }_i{h}_i{P}_i$ (i.e. $[H,P_i]=0$) leaves the modewise decay and the sharp rate ${\alpha }_{\ast }$ unchanged: the diagonals remain constant and off–diagonals acquire only phases. For noncommuting H, oscillations appear but the envelope of ${\mathcal{R}}_{\mathrm{L}\ddot{\mathrm{u}}\mathrm{ders}}\left({\sigma }_t\right)$ still decays at least as $e^{-{\alpha }_{\ast }t}$. (b) The statement is basis–covariant: any pure dephasing generator is unitarily diagonalizable; $\mathcal{N}$ is the diagonal algebra in that basis, and Φ is the corresponding conditional expectation.

4.5. Coercive PDE Template: Exponential Decay

Let $\Omega \subset {\mathbb{R}}^d$ be a bounded $C^1$ domain (or ${\mathbb{T}}^d$) with periodic or homogeneous boundary conditions chosen so that integrations by parts incur no boundary terms (cf. Remark 4.3). Assume

$$\rho (·,t)\in H^1(\Omega ),P(·,t)\in L^2(\Omega ;{\mathbb{R}}^d)$$

(65)

for all $t\ge 0$, and consider the system

$${\partial }_t\rho =\nabla ·\left(P-\nabla \rho \right),{\partial }_{t}P=-B(x,t)\left(P-\nabla \rho \right)+G(\rho ,P),$$

(66)

with $B\in L^{\infty }(\Omega \times [0,\infty ))$ satisfying $B(x,t)⪰\beta I$ a.e. for some $\beta >0$, and a locally Lipschitz coupling G that is subcritical in the residual energy sense specified below. Define the residual

$$u:=P-\nabla \rho \in L^2(\Omega ;{\mathbb{R}}^d),\mathcal{R}\left(t\right):={\int }_{\Omega }{|u(x,t)|}^{2}dx.$$

(67)

Theorem 4.4

(Exponential residual decay under coercivity). Under (66), $B⪰\beta I$, and the subcriticality condition

$$\left|{\int }_{\Omega }u·G(\rho ,P)dx\right|\le C\epsilon \mathcal{R}\left(t\right)$$

(68)

for some $C>0$ and sufficiently small $\epsilon \ge 0$, one has the differential inequality

$$\frac{d}{dt}\mathcal{R}\left(t\right)\le -(2\beta -C\epsilon )\mathcal{R}\left(t\right),$$

(69)

hence, by Grönwall,

$$\mathcal{R}\left(t\right)\le e^{-(2\beta -C\epsilon )t}\mathcal{R}\left(0\right)(t\ge 0).$$

(70)

In particular, in the uncoupled case ($\epsilon =0$) one obtains $\mathcal{R}\left(t\right)\le e^{-2\beta t}\mathcal{R}\left(0\right)$.

Proof sketch. 

Differentiate $\mathcal{R}\left(t\right)={\int }_{\Omega }{|u|}^2$ and use ${\partial }_{t}u=-Bu-\nabla (\nabla ·u)+G(\rho ,P)$ to obtain the exact identity (cf. (42))

$$\frac{d}{dt}\mathcal{R}\left(t\right)=-2{\int }_{\Omega }{u}^{\top }Budx-2{\parallel \nabla ·u\parallel }_{L^2(\Omega )}^2+2{\int }_{\Omega }u·Gdx.$$

(71)

Since $B⪰\beta I$, the first term is $\le -2\beta \mathcal{R}\left(t\right)$, the divergence term is nonpositive, and (68) gives $2\int u·G\le 2C\epsilon \mathcal{R}\left(t\right)$. Combine and apply Grönwall.    □

Remark 4.8

(Scope and refinements). (i) Template coverage. The estimate applies to mobility–relaxation closures, linear couplings bounded by the residual, and mild nonlinearities that satisfy (68). It is the PDE instance of the propagation lemma (Lemma 4.1, case (PDE)) followed by a sectoral coercivity bound; in DSFL notation, the rate is $\alpha =2\beta -C\epsilon$.

(ii) Spectral sharpening. With the Helmholtz decomposition $u=\nabla \varphi +w$ and $\nabla ·w=0$, the gradient channel gains additional spectral damping: on bounded/periodic domains,

$${\parallel \nabla ·u\parallel }_{L^2}^2={\parallel \Delta \varphi \parallel }_{L^2}^2\ge {\lambda }_1{\parallel \nabla \varphi \parallel }_{L^2}^2$$

(72)

with Poincaré constant ${\lambda }_1>0$, so the gradient part decays at least like $e^{-2(\beta +{\lambda }_1)t}$ while the solenoidal part decays like $e^{-2\beta t}$.

(iii) Regularity/BCs. All integrations by parts are justified by periodic or homogeneous boundary conditions and the Sobolev regularity stated above (see Remark 4.3). For weak solutions, the identity holds by density/mollification and lower–semicontinuity.

(iv) DSFL identification. The inequality $\dot{\mathcal{R}}\le -(2\beta -C\epsilon )\mathcal{R}$ is the DSFL law in this sector. With $\epsilon =0$ one recovers the clean rate $\alpha =2\beta$.

4.6. Free–Field Stochastic Quantization: Gap–Driven Decay

• Setting and notation.

Let $\Lambda$ be either the flat d–torus ${\mathbb{T}}^d$ (side length $L>0$) or ${\mathbb{R}}^d$. We consider a real free scalar field $\varphi :\Lambda \to \mathbb{R}$ with Euclidean action

$$S\left[\varphi \right]=\frac{1}{2}{\int }_{\Lambda }\left({|\nabla \varphi \left(x\right)|}^2+m^2\varphi {\left(x\right)}^2\right)dx,m\ge 0.$$

(73)

Parisi–Wu stochastic quantization evolves the field in an auxiliary “Langevin time” $\tau \ge 0$ by

$${\partial }_{\tau }{\varphi }_{\tau }\left(x\right)=-\frac{\delta S}{\delta \varphi }\left(x\right)+\eta (x,\tau )=\Delta {\varphi }_{\tau }\left(x\right)-m^2{\varphi }_{\tau }\left(x\right)+\eta (x,\tau ),$$

(74)

where $\eta$ is space–time white noise with covariance $\mathbb{E}\left[\eta \right(x,\tau \left)\eta \right(y,\sigma \left)\right]=2\delta (x-y)\delta (\tau -\sigma )$ (the factor 2 ensures that the stationary covariance solves $A{\Sigma }_{\infty }+{\Sigma }_{\infty }A=2I$). The generator of the one–body deterministic part is the nonnegative operator

$$A:=-\Delta +m^2\mathrm{on}{L}^2(\Lambda )\left(\mathrm{domain}{H}^2(\Lambda )\right),$$

(75)

whose spectrum is $\sigma \left(A\right)=\{|k{|}^2+m^2:k\in (2\pi /L){\mathbb{Z}}^d\}$ on ${\mathbb{T}}^d$, and $\sigma \left(A\right)=[m^2,\infty )$ on ${\mathbb{R}}^d$.

• OU semigroup and covariance flow.

Equation (74) is an infinite–dimensional Ornstein–Uhlenbeck (OU) process on $H^{-s}(\Lambda )$ for $s>d/2$ (or on $L^2(\Lambda )$ at the level of covariances). Writing $X_{\tau }:={\varphi }_{\tau }$ and $W_{\tau }$ a cylindrical Wiener process on $L^2(\Lambda )$, (74) reads

$$d{X}_{\tau }=-A{X}_{\tau }d\tau +\sqrt{2}d{W}_{\tau }.$$

(76)

Let ${\Sigma }_{\tau }:=\mathbb{E}[X_{\tau }\otimes X_{\tau }]$ be the (two–point) covariance operator on $L^2(\Lambda )$. Standard OU calculus yields

$${\dot{\Sigma }}_{\tau }=-A{\Sigma }_{\tau }-{\Sigma }_{\tau }A+2I,{\Sigma }_0\mathrm{given},\Rightarrow {\Sigma }_{\tau }={\int }_0^{\tau }{e}^{-sA}2I{e}^{-sA}ds+e^{-\tau A}{\Sigma }_0{e}^{-\tau A}.$$

(77)

The unique stationary covariance is the Green operator

$${\Sigma }_{\infty }=A^{-1}(\mathrm{on}{\mathbb{T}}^d\mathrm{for}\mathrm{any}m\ge 0;\mathrm{on}{\mathbb{R}}^d\mathrm{only}\mathrm{if}m>0).$$

(78)

Subtracting (78) from (77) gives the exact relaxation formula

$${\Sigma }_{\tau }-{\Sigma }_{\infty }=e^{-\tau A}\left({\Sigma }_0-{\Sigma }_{\infty }\right)e^{-\tau A}.$$

(79)

• Smeared two–point residual.

For a test function f (to be specified below), define the smeared evaluation ${\varphi }_{\tau }\left(f\right):={\int }_{\Lambda }{\varphi }_{\tau }\left(x\right)f\left(x\right)dx={\langle f,X_{\tau }\rangle }_{L^2}.$ Then

$$\mathbb{E}\left[{\varphi }_{\tau }\left(f\right){\varphi }_{\tau }\left(f\right)\right]=\langle f,{\Sigma }_{\tau }f\rangle ,\mathbb{E}\left[{\varphi }_{\infty }\left(f\right){\varphi }_{\infty }\left(f\right)\right]=\langle f,{\Sigma }_{\infty }f\rangle .$$

(80)

We define the (quadratic) residual as the squared deviation of the two–point function:

$$R[f;\tau ]:=|\underset{\mathbb{E}\left[{\varphi }_{\tau }{\left(f\right)}^2\right]-\mathbb{E}\left[{\varphi }_{\infty }{\left(f\right)}^2\right]}{\underbrace{\langle f,({\Sigma }_{\tau }-{\Sigma }_{\infty })f\rangle }}{|}^2.$$

(81)

• Admissible class of test functions.

On ${\mathbb{T}}^d$, take $f\in L^2\left({\mathbb{T}}^d\right)$; on ${\mathbb{R}}^d$ with $m>0$, take $f\in L^2\left({\mathbb{R}}^d\right)$ (or Schwarz $\mathcal{S}$). For $m=0$, impose an IR regularization (finite volume or mean–zero f and a Poincaré gap).

Theorem 4.5

(Residual decay at twice the Hamiltonian gap). Let $A=-\Delta +m^2$ on $L^2(\Lambda )$ and suppose there is a spectral gap

$${\lambda }_{\ast }:=inf\sigma \left(A{\upharpoonright }_{\mathrm{Ker}{\left(A\right)}^{\perp }}\right)>0.$$

(82)

Then for any admissible f,

$$R[f;\tau ]\le R[f;0]e^{-2{\lambda }_{\ast }\tau }.$$

(83)

In particular:

• On ${\mathbb{T}}^d$ with $m\ge 0$, ${\lambda }_{\ast }=min\{m^2,{\lambda }_1(-\Delta )\}$, where ${\lambda }_1(-\Delta )={(2\pi /L)}^2$ is the first positive Laplace eigenvalue; if $m>0$ then ${\lambda }_{\ast }=m^2$.
• On ${\mathbb{R}}^d$ with $m>0$, ${\lambda }_{\ast }=m^2$; if $m=0$ there is no gap and (83) fails globally (decay is not uniform, see Remark 4.10).

Proof. 

By (79),

$$\langle f,({\Sigma }_{\tau }-{\Sigma }_{\infty })f\rangle =〈e^{-\tau A}f,({\Sigma }_0-{\Sigma }_{\infty })e^{-\tau A}f〉.$$

(84)

Hence,

$$|\langle f,({\Sigma }_{\tau }-{\Sigma }_{\infty })f\rangle |\le \parallel {\Sigma }_0-{\Sigma }_{\infty }{\parallel }_{\mathrm{op},ker{\left(A\right)}^{\perp }}{\parallel e^{-\tau A}f\parallel }_2^2.$$

(85)

Because $\parallel e^{-\tau A}{\parallel }_{\mathrm{op}}=e^{-{\lambda }_{\ast }\tau }$ on $ker{\left(A\right)}^{\perp }$ and $e^{-\tau A}$ is the identity on $ker\left(A\right)$ (trivial unless $m=0$ on compact $\Lambda$), we have $\parallel e^{-\tau A}{f\parallel }_2\le e^{-{\lambda }_{\ast }\tau }{\parallel f\parallel }_2$ whenever $f\perp ker\left(A\right)$ (automatically true for $m>0$). Thus

$$|\langle f,({\Sigma }_{\tau }-{\Sigma }_{\infty })f\rangle |\le \parallel {\Sigma }_0-{\Sigma }_{\infty }{\parallel }_{\mathrm{op},ker{\left(A\right)}^{\perp }}{e}^{-2{\lambda }_{\ast }\tau }{\parallel f\parallel }_2^2,$$

(86)

and squaring yields (83) after absorbing the prefactor into $R[f;0]$.    □

Remark 4.9

(Explicit Fourier picture on ${\mathbb{T}}^d$). Write $f\left(x\right)={\sum }_{k\in (2\pi /L){\mathbb{Z}}^d}{\widehat{f}}_k{e}^{ik·x}$ and similarly for ${\varphi }_{\tau }$. Each mode solves the scalar OU SDE $d{\widehat{\varphi }}_{\tau }\left(k\right)=-{(|k|}^2+m^2){\widehat{\varphi }}_{\tau }\left(k\right)d\tau +\sqrt{2}d{\beta }_{\tau }\left(k\right),$ so $\mathrm{Var}{\widehat{\varphi }}_{\tau }\left(k\right)=(\mathrm{Var}{\widehat{\varphi }}_0\left(k\right)-{(|k|}^2+m^2{)}^{-1})e^{-2(|k{|}^2+m^2)\tau }+{(|k|}^2+m^2{)}^{-1}.$ Therefore, for the smeared variance,

$$\langle f,({\Sigma }_{\tau }-{\Sigma }_{\infty })f\rangle =\sum _k{|{\widehat{f}}_k|}^2\left(\mathrm{Var}{\widehat{\varphi }}_{\tau }\left(k\right)-{(|k|}^2+m^2{)}^{-1}\right),$$

(87)

and the slowest decaying mode has rate $2{min}_k{(|k|}^2+m^2)=2{\lambda }_{\ast }$.

Remark 4.10

(Massless case and infrared issues). On ${\mathbb{T}}^d$ with $m=0$, $ker\left(A\right)=span\left\{1\right\}$ and ${\lambda }_{\ast }={\lambda }_1(-\Delta )={(2\pi /L)}^2$ provided f has zero mean (or we project away the constant mode). On ${\mathbb{R}}^d$ with $m=0$, $\sigma \left(A\right)=[0,\infty )$ has no gap; uniform exponential decay fails and long–wavelength modes relax only algebraically in spatially extended senses. Thus a spectral gap (mass $m>0$ or finite–volume Poincaré gap) is essential for the DSFL rate (83).

Remark 4.11

(From two–point residuals to DSFL). The estimate (83) derives the DSFL inequality in the Gaussian sector: the misalignment functional ${\mathcal{R}}_{\mathrm{free}}\left(\tau \right):={sup}_{{\parallel f\parallel }_2=1}|\langle f,({\Sigma }_{\tau }-{\Sigma }_{\infty })f\rangle {|}^2$ decays as ${\dot{\mathcal{R}}}_{\mathrm{free}}\le -2{\lambda }_{\ast }{\mathcal{R}}_{\mathrm{free}}$ with optimal rate $2{\lambda }_{\ast }$. Equivalently, for any fixed f, the scalar residual $R[f;\tau ]$ satisfies the same inequality.

Remark 4.12

(Regularity of smearing). On ${\mathbb{T}}^d$ any $f\in L^2$ is admissible. On ${\mathbb{R}}^d$ with $m>0$, $f\in L^2$ (or $\mathcal{S}$) suffices and all formulas above hold; higher regularity $f\in H^{\alpha }$ yields the same exponential rate while changing only the (finite) prefactors.

4.7. GR Slice: Geometric Residual Decay (Small Data, DeTurck Gauge)

• Scope.

This subsection establishes a slice analogue on compact Riemannian 3–manifolds, in DeTurck gauge, for small perturbations of a fixed target metric. It is not a fully covariant Lorentzian result. A diffeomorphism–invariant Lorentzian formulation is stated as an open program in the remarks below.

• Standing assumptions (slice, small data).

Let $({\Sigma }^3,\overline{\gamma })$ be a smooth, closed (compact, boundaryless) Riemannian 3–manifold. Let $T\in C^{\infty }(\Sigma ;{\mathrm{Sym}}^2{T}^{\ast }\Sigma )$ be time–independent and divergence–free with respect to $\overline{\gamma }$, ${\nabla }^{\overline{\gamma }i}{T}_{ij}=0$. Assume there exists a target metric $\overline{\gamma }$ solving

$$G\left[\overline{\gamma }\right]=\kappa T.$$

(88)

Consider the Einstein–source flow in DeTurck gauge

$${\partial }_t{\gamma }_{ij}=-2\left(G_{ij}\left[\gamma \right]-\kappa T_{ij}\right)+{\nabla }_i{X}_j\left(\gamma \right)+{\nabla }_j{X}_i\left(\gamma \right),$$

(89)

with DeTurck vector

$$X^k\left(\gamma \right)={\gamma }^{pq}\left({\Gamma }_{pq}^k\left(\gamma \right)-{\Gamma }_{pq}^k\left(\overline{\gamma }\right)\right),$$

(90)

which renders the linearization at $\overline{\gamma }$ strictly elliptic on the gauge–orthogonal (physical) subspace.

• Residual (gauge–invariant).

Define the $L^2$ curvature–matter misfit

$${\mathcal{R}}_{\mathrm{geom}}\left(t\right):={\int }_{\Sigma }\parallel G\left[\gamma \left(t\right)\right]-\kappa T{\parallel }_{\gamma \left(t\right)}^{2}d{\mu }_{\gamma \left(t\right)}.$$

(91)

Write $h:=\gamma -\overline{\gamma }$ and assume small initial data $h\left(0\right)\in H^k\left(\overline{\gamma }\right)$ with ${\parallel h\left(0\right)\parallel }_{H^k}\le \delta$ for some $k\ge 4$ and $\delta >0$ sufficiently small.

Lemma 4.4

(Constraint preservation (DeTurck slice)). Let $C_j\left(\gamma \right):={\nabla }_{\gamma }^i\left(G_{ij}\left[\gamma \right]-\kappa T_{ij}\right)$. Along (89), ${\partial }_t{C}_j={\Delta }_{\gamma }{C}_j+{R_j}^k\left(\gamma \right)C_k.$ If $C_j\left(0\right)=0$ and T is time–independent with ${\nabla }_{\gamma }T\equiv 0$ along the flow (equivalently ${\nabla }^{\overline{\gamma }}T\equiv 0$ at $t=0$ and preserved thereafter), then $C_j\equiv 0$ for all $t\ge 0$.

• Linearization, model operator, and spectral gap.

Linearizing (89) at $\overline{\gamma }$ yields, for h small,

$${\partial }_{t}h=-{\mathcal{L}}_{\overline{\gamma }}h+\mathcal{N}\left(h\right),$$

(92)

where ${\mathcal{L}}_{\overline{\gamma }}$ is the self–adjoint Lichnerowicz–DeTurck operator on symmetric 2–tensors,

$${\mathcal{L}}_{\overline{\gamma }}h:=-{\Delta }_L^{\overline{\gamma }}h-2\mathrm{Rm}\left[\overline{\gamma }\right]\ast h,{\left({\Delta }_{L}h\right)}_{ij}:=\Delta h_{ij}+2R_{ikjl}{h}^{kl}-{R_i}^k{h}_{kj}-{R_j}^k{h}_{ki},$$

(93)

and $\mathcal{N}\left(h\right)=O(|h||{\nabla }^{2}h|+|\nabla h{|}^2)$ is quadratic/higher order. Assume a spectral gap on the physical (gauge–orthogonal) subspace:

$$\exists {\lambda }_{\mathrm{GR}}>0\mathrm{s}.\mathrm{t}.{\langle h,{\mathcal{L}}_{\overline{\gamma }}h\rangle }_{L^2\left(\overline{\gamma }\right)}\ge {\lambda }_{\mathrm{GR}}{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^2\mathrm{for}\mathrm{all}h\perp \mathrm{gauge}\mathrm{directions}.$$

(94)

By elliptic regularity, for h sufficiently small in $H^k$,

$${\parallel h\parallel }_{H^2\left(\overline{\gamma }\right)}\le C_{\mathrm{ell}}\left(\parallel {\mathcal{L}}_{\overline{\gamma }}{h\parallel }_{L^2\left(\overline{\gamma }\right)}+{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}\right)\le \frac{2C_{\mathrm{ell}}}{\sqrt{{\lambda }_{\mathrm{GR}}}}{\parallel {\mathcal{L}}_{\overline{\gamma }}h\parallel }_{L^2\left(\overline{\gamma }\right)}.$$

(95)

• Residual equivalence near $\overline{\gamma }$.

A Taylor expansion at $\overline{\gamma }$ and (88) give

$$G[\overline{\gamma }+h]-\kappa T=\frac{1}{2}{\mathcal{L}}_{\overline{\gamma }}h+\mathcal{Q}\left(h\right),\parallel \mathcal{Q}\left(h\right){\parallel }_{L^2\left(\overline{\gamma }\right)}\le C_Q{\parallel h\parallel }_{H^2}{\parallel h\parallel }_{H^1}.$$

(96)

For h small and $\gamma$ close to $\overline{\gamma }$ in $C^0$, the norms induced by $\gamma$ and $\overline{\gamma }$ are equivalent; hence

$${\mathcal{R}}_{\mathrm{geom}}\left(t\right)={\parallel G\left[\gamma \right]-\kappa T\parallel }_{L^2\left(\gamma \right)}^2\simeq \frac{1}{4}\parallel {\mathcal{L}}_{\overline{\gamma }}{h\parallel }_{L^2\left(\overline{\gamma }\right)}^2\simeq {\parallel h\parallel }_{H^2\left(\overline{\gamma }\right)}^2,$$

(97)

with constants depending only on $(\Sigma ,\overline{\gamma })$ and the smallness radius.

Theorem 4.6

(Exponential $L^2$ decay of the geometric residual on a slice). Under (88), (89), (94), and the small–data hypothesis ${\parallel h\left(0\right)\parallel }_{H^k\left(\overline{\gamma }\right)}\le \delta$ (for some $k\ge 4$ and $\delta >0$ sufficiently small), there exists $c\in (0,1)$ (depending only on $\overline{\gamma }$ and δ) such that

$$\frac{d}{dt}{\mathcal{R}}_{\mathrm{geom}}\left(t\right)\le -2c{\lambda }_{\mathrm{GR}}{\mathcal{R}}_{\mathrm{geom}}\left(t\right),\Rightarrow {\mathcal{R}}_{\mathrm{geom}}\left(t\right)\le e^{-2c{\lambda }_{\mathrm{GR}}t}{\mathcal{R}}_{\mathrm{geom}}\left(0\right).$$

(98)

In particular, $G\left[\gamma \right(t\left)\right]=\kappa T$ in $L^2(\Sigma )$ as $t\to \infty$, and $\gamma \left(t\right)\to \overline{\gamma }$ modulo diffeomorphisms.

Proof sketch. 

Set $E\left(t\right):=\parallel {\mathcal{L}}_{\overline{\gamma }}{h\left(t\right)\parallel }_{L^2\left(\overline{\gamma }\right)}^2$. From (92),

$$\dot{E}\left(t\right)=2\langle {\mathcal{L}}_{\overline{\gamma }}h,{\mathcal{L}}_{\overline{\gamma }}{\partial }_{t}h\rangle =-2{\parallel {\mathcal{L}}_{\overline{\gamma }}^{3/2}h\parallel }_{L^2}^2+2\langle {\mathcal{L}}_{\overline{\gamma }}h,{\mathcal{L}}_{\overline{\gamma }}\mathcal{N}\left(h\right)\rangle .$$

(99)

The gap (94) yields $-2\parallel {\mathcal{L}}_{\overline{\gamma }}^{3/2}{h\parallel }_{L^2}^2\le -2{\lambda }_{\mathrm{GR}}E\left(t\right)$. Estimate the nonlinear term via Cauchy–Schwarz, (95), and small–data absorption to obtain $|\langle {\mathcal{L}}_{\overline{\gamma }}h,{\mathcal{L}}_{\overline{\gamma }}\mathcal{N}\left(h\right)\rangle |\le (1-c){\lambda }_{\mathrm{GR}}E\left(t\right)$, whence $\dot{E}\left(t\right)\le -2c{\lambda }_{\mathrm{GR}}E\left(t\right)$. Grönwall gives $E\left(t\right)\le e^{-2c{\lambda }_{\mathrm{GR}}t}E\left(0\right)$; (97) then implies the stated decay for ${\mathcal{R}}_{\mathrm{geom}}$.    □

Remark 4.13

(Well–posedness and norm equivalences). For ${\parallel h\left(0\right)\parallel }_{H^k}$ small ($k\ge 4$), parabolic–elliptic theory in DeTurck gauge yields local existence/uniqueness in $C([0,T];H^k)$ and a priori control. The exponential decay closes the bootstrap globally. Moreover, $L^2\left(\gamma \right)$– and $L^2\left(\overline{\gamma }\right)$–norms are equivalent for small h, so (91) and (97) are interchangeable up to fixed constants.

Remark 4.14

(Matter compatibility and constraints). The condition ${\nabla }^{\overline{\gamma }}T\equiv 0$ together with Lemma 4.4 ensures preservation of the contracted Bianchi constraint and prevents spurious source terms in the energy estimates; T only fixes the equilibrium (88).

Remark 4.15

(Gauge directions and the physical subspace). The DeTurck term (90) removes the diffeomorphism kernel of the linearized operator; the spectral gap (94) is thus a genuine coercivity on the physical subspace. Without DeTurck, one must pass to the quotient by diffeomorphisms (e.g., transverse–traceless decomposition) and run the same argument there.

Remark 4.16

(Lorentzian caveat). The theorem is a Riemannian slice statement in DeTurck gauge. It does not imply a fully covariant Lorentzian DSFL. A Lorentzian version would require a diffeomorphism–invariant Lyapunov functional on the space of Lorentzian metrics and a hyperbolic evolution with an appropriate gap; this remains an open program.

Remark 4.17

(ISS robustness (small forcing)). If (89) is perturbed by a small, mean–zero forcing $\epsilon \Xi \left(t\right)$ in $L^2$–time, the same calculation yields ${\dot{\mathcal{R}}}_{\mathrm{geom}}\le -2c{\lambda }_{\mathrm{GR}}{\mathcal{R}}_{\mathrm{geom}}+C{\epsilon }^2{\parallel \Xi \left(t\right)\parallel }^2,$ and hence ${lim\; sup}_{t\to \infty }{\mathcal{R}}_{\mathrm{geom}}\left(t\right)\le \frac{C{\epsilon }^2}{2c{\lambda }_{\mathrm{GR}}}{\parallel \Xi \parallel }_{L^2(0,\infty )}^2.$

Remark 4.18

(Interpretation). In the limit ${\mathcal{R}}_{\mathrm{geom}}\left(t\right)\to 0$ one has $G\left[\gamma \right(t\left)\right]=\kappa T$ in $L^2(\Sigma )$ (and pointwise where regularity allows); with small–data coercivity, $\gamma \left(t\right)\to \overline{\gamma }$ modulo diffeomorphisms. Thus, Einstein balance is a slice attractor when a Lichnerowicz–DeTurck gap is present.

4.8. Master/Grand Attractor Theorems (Sectoral Attractors)

Let $\mathcal{R}\left(t\right)$ denote the global alignment residual associated with a given sector (classical/QMS/PDE/GR). Assume a DSFL inequality holds on its natural state space $\mathsf{X}$:

$$\frac{d}{dt}\mathcal{R}\left(t\right)\le -\alpha \mathcal{R}\left(t\right),\alpha >0,$$

(100)

where $\alpha$ is the Poincaré/spectral–gap constant or a quantitative coercivity as established in §4.2–§4.6. Write $\mathcal{A}\subset \mathsf{X}$ for the sectoral attractor set (the equilibrium manifold in that sector; e.g. ${|\Psi |}^2$ in QM, $G=\kappa T$ in GR, etc.).

Proposition 4.1

(Small–gain for two coupled residuals). Let $R,S\ge 0$ satisfy, for some constants $\alpha ,\beta >0$ and couplings $\delta ,\gamma \ge 0$,

$$\dot{R}\le -2\alpha R+\delta S,\dot{S}\le -2\beta S+\gamma R.$$

(101)

If the small–gain condition holds,

$$\delta \gamma <4\alpha \beta ,$$

(102)

then there exists $c\in (0,1)$ (depending only on $\alpha ,\beta ,\delta ,\gamma$) such that

$$R\left(t\right)+S\left(t\right)\le C_0{e}^{-2c{\lambda }_{★}t}\mathit{for}\mathit{all}t\ge 0,$$

(103)

where the decay rate can be chosen as

$${\lambda }_{★}=\frac{\alpha +\beta -\sqrt{{(\alpha -\beta )}^2+\delta \gamma }}{2}>0.$$

(104)

In particular, both $R,S$ decay exponentially to 0.

Proof sketch. 

Write (101) in vector form $X^{\prime }\le AX$ with $X={(R,S)}^{\top }$ and $A=(\begin{array}{cc}\hfill -2\alpha & \delta \\ \hfill beginequation2pt]\gamma & -2\beta \end{array})$. The eigenvalues are ${\lambda }_{\pm }=-(\alpha +\beta )\pm \sqrt{{(\alpha -\beta )}^2+\delta \gamma }.$ Condition (102) yields ${\lambda }_{+}<0$. Hence $X\left(t\right)\le e^{tA}X\left(0\right)$ componentwise and $\parallel X\left(t\right)\parallel \le C{e}^{{\lambda }_{+}t}\parallel X\left(0\right)\parallel$. Setting ${\lambda }_{★}=-\left({\lambda }_{+}\right)/2$ gives $e^{{\lambda }_{+}t}=e^{-2{\lambda }_{★}t}$. Alternatively, choose a weighted Lyapunov $V_{a,b}=aR+bS$ with $a,b>0$ so that ${\dot{V}}_{a,b}\le -2c{\lambda }_{★}{V}_{a,b}$.    □

• Distance equivalences near the attractor.

We record norm–equivalences that turn the residual $\mathcal{R}$ into a bona fide distance to the attractor in each sector (up to constants).

Lemma 4.5

(Residual vs. geometric distance to the attractor). (i) QM (Born sector). On a bounded domain with Poincaré constant ${\lambda }_1>0$, if $P={\nabla |\Psi |}^2$ and ${\int }_{\Omega }\rho ={\int }_{\Omega }{|\Psi |}^2=1$, then for $w=\rho -{|\Psi |}^2$,

$${\lambda }_1{\parallel w\parallel }_{L^2(\Omega )}^2\le {\int }_{\Omega }{|\nabla w|}^{2}dx={\mathcal{R}}_{\mathrm{QM}}\left(\rho \right)\le C{\parallel w\parallel }_{H^1(\Omega )}^2.$$

(105)

(ii) TD (continuum). With weights $W⪰{\lambda }_{min}I$ and $u=P-\nabla \rho$, ${\mathcal{R}}_{\mathrm{TD}}={\int |u|}_W^2\ge {\lambda }_{min}{\parallel P-\nabla \rho \parallel }_{L^2}^2.$ (iii) QMS (OA). With pointer algebra $\mathcal{N}$ and conditional expectation ${\mathsf{E}}_{\mathcal{N}}$, ${\mathcal{R}}_{\omega }\left(X\right)={\parallel X-{\mathsf{E}}_{\mathcal{N}}X\parallel }_{2,\omega }^2$ is the squared $L^2\left(\omega \right)$-distance to $L^2(\mathcal{N},\omega )$. (iv) GR (slice, DeTurck). For $h=\gamma -\overline{\gamma }$ small in $H^k$, ${\mathcal{R}}_{\mathrm{geom}}\simeq \frac{1}{4}\parallel {\mathcal{L}}_{\overline{\gamma }}{h\parallel }_{L^2\left(\overline{\gamma }\right)}^2\simeq {\parallel h\parallel }_{H^2\left(\overline{\gamma }\right)}^2,$ hence ${\mathcal{R}}_{\mathrm{geom}}\simeq {\mathrm{dist}}_{H^2}{(\gamma ,\overline{\gamma })}^2$ modulo diffeos.

Proof. 

QM and TD are immediate from Poincaré and $W⪰{\lambda }_{min}I$. QMS is by definition. GR follows from (96)–(97) and elliptic regularity (95).    □

• Omega–limit characterization and LaSalle.

Lemma 4.6

(LaSalle-type invariance). Let ${\left({\mathsf{T}}_t\right)}_{t\ge 0}$ be the sector semigroup on $\mathsf{X}$, continuous in t, and suppose $\mathcal{R}$ is nonnegative, continuous on $\mathsf{X}$, and satisfies (100). Then for any trajectory $x\left(t\right)={\mathsf{T}}_t{x}_0$, the ω–limit set $\omega \left(x_0\right)$ is nonempty, compact, and contained in $\{\mathcal{R}=0\}=\mathcal{A}$. If, in addition, $\mathcal{A}$ consists of a single orbit (modulo the natural gauge of the sector), then $x\left(t\right)\to \mathcal{A}$.

Proof. 

Monotonicity and boundedness of $\mathcal{R}$ yield precompactness (sector by sector) and invariance. At any accumulation point $\overline{x}$, the derivative of $\mathcal{R}$ vanishes, hence $\mathcal{R}\left(\overline{x}\right)=0$ by (100). Uniqueness up to gauge gives convergence to the orbit.    □

Theorem 4.7

(Sector attractors from residual decay (Master theorem)). Under (100) and Lemma 4.5, the canonical equilibrium relations are the unique global attractors in their sectors:

(QM)

(Born alignment) If $P={\nabla |\Psi |}^2$ and ${\int }_{\Omega }\rho ={\int }_{\Omega }{|\Psi |}^2=1$, then $\rho (·,t)\to {|\Psi |}^2$ in $L^2(\Omega )$ at least exponentially, with rate ${\alpha }^{\#}\ge {\lambda }_1$ (cf. Theorem 6.1).

(TD)

(Residual entropy) $S_R\left(t\right):=-log(\mathcal{R}\left(t\right)/{\mathcal{R}}_0+R_{\ast })$ satisfies ${\dot{S}}_R\ge \alpha >0$, hence $S_R\left(t\right)\nearrow +\infty$ and $\mathcal{R}\to 0$ exponentially.

(QMS)

(OA pointer alignment) If the reversible QMS has spectral gap $\lambda >0$ on $L^2{(\mathcal{N},\omega )}^{\perp }$, then ${\mathcal{R}}_{\omega }\left({\mathsf{T}}_{t}X\right)\le e^{-2\lambda t}{\mathcal{R}}_{\omega }\left(X\right)$ and $X\left(t\right)\to {\mathsf{E}}_{\mathcal{N}}X$ in $L^2\left(\omega \right)$.

(GR)

(Einstein balance on slices) Under Theorem 4.6, ${\mathcal{R}}_{\mathrm{geom}}\left(t\right)\le e^{-2c{\lambda }_{\mathrm{GR}}t}{\mathcal{R}}_{\mathrm{geom}}\left(0\right)$ and $\gamma \left(t\right)\to \overline{\gamma }$ modulo diffeomorphisms; thus $G\left[\gamma \right]=\kappa T$ in $L^2(\Sigma )$.

Proof. (QM) Combine (100) with Lemma 4.5(i) and Theorem 6.1. (TD) Differentiate $S_R$: ${\dot{S}}_R=-\dot{\mathcal{R}}/(\mathcal{R}+{\mathcal{R}}_0{R}_{\ast })\ge \alpha >0$, hence $S_R$ increases and $\mathcal{R}\to 0$ exponentially. (QMS) is Theorem 4.2. (GR) is Theorem 4.6 plus Lemma 4.5(iv).    □

• Abstract grand theorem (uniform formulation).

Theorem 4.8

(Grand attractor theorem (abstract Hilbert form)). Let ${\left({\mathsf{T}}_t\right)}_{t\ge 0}$ be a reversible contraction semigroup on a Hilbert space H with generator $\mathcal{L}$, fixed–point subspace $\mathcal{N}=\{X:{\mathsf{T}}_{t}X=X\}$, and Poincaré gap $\lambda >0$ on ${\mathcal{N}}^{\perp }$. Define $\mathcal{R}\left(X\right):=\mathrm{dist}{(X,\mathcal{N})}^2$. Then for all $X\in H$,

$$\mathcal{R}\left({\mathsf{T}}_{t}X\right)\le e^{-2\lambda t}\mathcal{R}\left(X\right),\mathrm{dist}({\mathsf{T}}_{t}X,\mathcal{N})\le e^{-\lambda t}\mathrm{dist}(X,\mathcal{N}).$$

(106)

Moreover, $\mathcal{N}$ is the unique global attractor (modulo the sector gauge).

Proof. 

Differentiate $\parallel {\left({\mathsf{T}}_{t}X\right)}^{\perp }{\parallel }^2=\langle {\mathsf{T}}_t{X}^{\perp },{\mathsf{T}}_t{X}^{\perp }\rangle$: $\frac{d}{dt}\parallel {\left({\mathsf{T}}_{t}X\right)}^{\perp }{\parallel }^2=-2\langle {\mathsf{T}}_t{X}^{\perp },\mathcal{L}{\mathsf{T}}_t{X}^{\perp }\rangle \le -2\lambda {\parallel {\left({\mathsf{T}}_{t}X\right)}^{\perp }\parallel }^2$. Grönwall yields the claimed exponential contraction. Uniqueness of the attractor follows since $\mathcal{N}$ is the fixed–point set.    □

• Robustness and time–varying rates.

Proposition 4.2

(ISS/ultimate boundedness; time–varying $\alpha \left(t\right)$). (i) If $\dot{\mathcal{R}}\le -\alpha \mathcal{R}+{\epsilon }^{2}u\left(t\right)$ with $\alpha >0$ and $u\in L_{\mathrm{loc}}^1$, then $\mathcal{R}\left(t\right)\le e^{-\alpha t}\mathcal{R}\left(0\right)+{\epsilon }^2{\int }_0^t{e}^{-\alpha (t-s)}u\left(s\right)ds$ and ${lim\; sup}_{t\to \infty }\mathcal{R}\left(t\right)\le {\epsilon }^2{\parallel u\parallel }_{L^1(0,\infty )}$. (ii) If $\dot{\mathcal{R}}\le -\alpha \left(t\right)\mathcal{R}$ with $\alpha (·)\ge 0$ measurable and ${\int }_0^{\infty }\alpha \left(t\right)dt=+\infty$, then $\mathcal{R}\left(t\right)\to 0$; if $\underline{\alpha }:={inf}_{t\ge 0}\alpha \left(t\right)>0$, then $\mathcal{R}\left(t\right)\le e^{-\underline{\alpha }t}\mathcal{R}\left(0\right)$.

Proof. (i) Grönwall with input. (ii) Integrate the differential inequality.    □

• Discrete–time and product systems.

Proposition 4.3

(Discrete DSFL; products). (i) If ${\mathcal{R}}_{k+1}\le (1-\theta ){\mathcal{R}}_k$ with $\theta \in (0,1)$, then ${\mathcal{R}}_k\le {(1-\theta )}^k{\mathcal{R}}_0$. (ii) If ${\mathcal{R}}^{\left(1\right)}$ and ${\mathcal{R}}^{\left(2\right)}$ satisfy ${\dot{\mathcal{R}}}^{\left(i\right)}\le -2{\alpha }_i{\mathcal{R}}^{\left(i\right)}+{\sum }_{j\ne i}{\gamma }_{ij}{\mathcal{R}}^{\left(j\right)}$ with a Metzler coupling matrix $\Gamma =\left({\gamma }_{ij}\right)$, then exponential decay holds provided the spectral abscissa of $A=\mathrm{diag}(2{\alpha }_1,2{\alpha }_2)-\Gamma$ is positive (cf. Proposition 4.1).

Proof. (i) Induction. (ii) Linear ODE comparison and the spectral condition.    □

• Weighted distances and alternative norms.

Lemma 4.7

(Residual vs. weighted distance). Let $\mathcal{A}\subset \mathsf{X}$ be the sectoral attractor and let $d_{\ast }(·,\mathcal{A})$ be a locally equivalent distance induced by a positive quadratic form $Q_{\ast }$ (e.g. an $H^{-1}$ metric in PDE sectors or a weighted $L^2\left(\omega \right)$ metric in QMS). Suppose that in a neighborhood $\mathcal{U}$ of $\mathcal{A}$ there exist constants $0<c_1\le c_2<\infty$ such that

$$c_1{d}_{\ast }{(x,\mathcal{A})}^2\le \mathcal{R}\left(x\right)\le c_2{d}_{\ast }{(x,\mathcal{A})}^2\forall x\in \mathcal{U}.$$

(107)

If the DSFL inequality (100) holds on $\mathcal{U}$, then

$$d_{\ast }({\mathsf{T}}_t{x}_0,\mathcal{A})\le \sqrt{\frac{c_2}{c_1}}{e}^{-\alpha t}{d}_{\ast }(x_0,\mathcal{A})$$

(108)

for all t for which the trajectory stays in $\mathcal{U}$. In particular, the convergence rate is unchanged up to the equivalence factor $\sqrt{c_2/c_1}$.

Proof. 

Combine (100) with the local equivalence to bound $d_{\ast }^2$ above and below by $\mathcal{R}$, then apply Grönwall.    □

Remark 4.19

(PDE $H^{-1}$ distances). In diffusion–type PDE sectors, observables are often controlled in $H^{-1}$ rather than $L^2$. If the residual controls ${\parallel w\parallel }_{H^{-1}}^2$ and vice versa near the attractor (e.g. via Poincaré and elliptic estimates), Lemma 4.7 transfers the DSFL rate directly to $H^{-1}$.

• Consequences for sector observables.

Corollary 4.4

(Observable convergence). Let $\mathcal{O}$ be a continuous observable on the sector state space and assume there exists a neighborhood of the attractor $\mathcal{A}$ where $|\mathcal{O}\left(x\right)-{\mathcal{O}}^{\ast }|\le C\mathrm{dist}(x,\mathcal{A})$ (local Lipschitz). Then under (100) (or Theorem 4.8),

$$|\mathcal{O}\left({\mathsf{T}}_t{x}_0\right)-{\mathcal{O}}^{\ast }|\le C{e}^{-{\alpha }^{\#}t}\mathrm{dist}(x_0,\mathcal{A}),$$

(109)

with ${\alpha }^{\#}=\lambda$ in the reversible cases and ${\alpha }^{\#}=(2\beta -C\epsilon )$ in the coercive PDE case. Moreover, if a weighted distance $d_{\ast }$ equivalent to $\mathrm{dist}$ near $\mathcal{A}$ is used (Lemma 4.7), the same estimate holds with $\mathrm{dist}$ replaced by $d_{\ast }$.

Remark 4.20

(Uniqueness modulo gauge). In PDE and GR sectors the attractor is unique modulo the natural gauge (additive constants for ρ, diffeomorphisms for γ). The theorems above are to be understood on the corresponding quotient spaces, or after fixing a gauge (DeTurck in GR, mean–zero in QM/TD).

Remark 4.21

(Coupled residuals and small–gain). In multi–residual settings (e.g. DSFL+SABIM), a vector–Lyapunov $V_{a,b}=a\mathcal{R}+b\mathcal{S}$ together with the sharp small–gain condition $\delta \gamma <4\alpha \beta$ (Proposition 4.1) yields exponential decay with rate ${\lambda }_{★}=\frac{\alpha +\beta -\sqrt{{(\alpha -\beta )}^2+\delta \gamma }}{2}$; see also the n–dimensional version in Corollary ??.

Proof (expanded). 

(QM) Set $w:=\rho -{|\Psi |}^2$. By definition of the residual in the Born sector one has ${\mathcal{R}}_{\mathrm{QM}}\left(t\right)={\int }_{\Omega }{|\nabla w(x,t)|}^{2}dx$. The DSFL inequality implies ${\mathcal{R}}_{\mathrm{QM}}\left(t\right)\to 0$ as $t\to \infty$, hence $\nabla w(·,t)\to 0$ in $L^2(\Omega )$. Since ${\int }_{\Omega }\rho ={\int }_{\Omega }{|\Psi |}^2=1$ for all t (mass conservation), we have ${\int }_{\Omega }w(·,t)dx=0$. By the Poincaré inequality on mean–zero functions, ${\parallel w(·,t)\parallel }_{L^2}^2\le {\lambda }_1^{-1}{\parallel \nabla w(·,t)\parallel }_{L^2}^2={\lambda }_1^{-1}{\mathcal{R}}_{\mathrm{QM}}\left(t\right)$, whence $w(·,t)\to 0$ in $L^2(\Omega )$. Therefore $\rho (·,t)\to {|\Psi |}^2$ in $L^2(\Omega )$. Moreover, if the sector provides the sharper differential inequality ${\dot{\mathcal{R}}}_{\mathrm{QM}}\le -2{\lambda }_1{\mathcal{R}}_{\mathrm{QM}}$ (cf. Theorem 6.1), then ${\parallel \rho -|\Psi |}^2{\parallel }_{L^2}\le {\lambda }_1^{-1/2}{e}^{-{\lambda }_{1}t}{\mathcal{R}}_{\mathrm{QM}}{\left(0\right)}^{1/2}$.

(TD) By definition $S_R\left(t\right)=-log(\mathcal{R}\left(t\right)/{\mathcal{R}}_0+R_{\ast })$ with $R_{\ast }\in (0,1)$. Differentiating and using DSFL,

$${\dot{S}}_R\left(t\right)=-\frac{\dot{\mathcal{R}}\left(t\right)}{\mathcal{R}\left(t\right)+{\mathcal{R}}_0{R}_{\ast }}\ge \frac{\alpha \mathcal{R}\left(t\right)}{\mathcal{R}\left(t\right)+{\mathcal{R}}_0{R}_{\ast }}\ge \alpha \frac{\mathcal{R}\left(t\right)}{\mathcal{R}\left(0\right)+{\mathcal{R}}_0{R}_{\ast }}\ge 0.$$

(110)

In particular, if $\dot{\mathcal{R}}\le -\alpha \mathcal{R}$ with $\alpha >0$, then $S_R$ is strictly increasing and $S_R\left(t\right)\ge S_R\left(0\right)+\alpha t·\frac{\mathcal{R}\left(0\right)}{\mathcal{R}\left(0\right)+{\mathcal{R}}_0{R}_{\ast }}$, which diverges as $t\to \infty$ while $\mathcal{R}\left(t\right)\to 0$ exponentially.

(GR) By assumption, ${\dot{\mathcal{R}}}_{\mathrm{geom}}\le -2{\lambda }_{\mathrm{GR}}{\mathcal{R}}_{\mathrm{geom}}$, hence ${\mathcal{R}}_{\mathrm{geom}}\left(t\right)\le e^{-2{\lambda }_{\mathrm{GR}}t}{\mathcal{R}}_{\mathrm{geom}}\left(0\right)\to 0$. Since ${\mathcal{R}}_{\mathrm{geom}}={\int }_{\Sigma }{\parallel G\left[\gamma \right]-\kappa T\parallel }_{\gamma }^{2}d{\mu }_{\gamma }$, this implies $G\left[\gamma \right(t\left)\right]-\kappa T\to 0$ in $L^2(\Sigma )$ as $t\to \infty$. Under the small–data hypotheses of Theorem 4.6 and the gauge choice (DeTurck), elliptic regularity and the spectral gap yield convergence of $\gamma \left(t\right)$ to $\overline{\gamma }$ modulo diffeomorphisms; in particular, $G\left[\gamma \right]=\kappa T$ in the limit.    □

Theorem 4.9

(Grand attractor theorem (abstract form)). Let ${\left({\mathsf{T}}_t\right)}_{t\ge 0}$ be a reversible contraction semigroup on a Hilbert space H with generator $\mathcal{L}$, fixed–point subspace $\mathcal{N}=\{X:{\mathsf{T}}_{t}X=X\forall t\ge 0\}$, and Poincaré gap $\lambda >0$ on ${\mathcal{N}}^{\perp }$. For the residual $\mathcal{R}\left(X\right):=\parallel X-{\mathsf{E}}_{\mathcal{N}}{\left(X\right)\parallel }^2$ one has

$$\mathcal{R}\left({\mathsf{T}}_{t}X\right)\le e^{-2\lambda t}\mathcal{R}\left(X\right),\mathrm{dist}({\mathsf{T}}_{t}X,\mathcal{N})\le e^{-\lambda t}\mathrm{dist}(X,\mathcal{N}),$$

(111)

and $\mathcal{N}$ is the unique global attractor (modulo the sector’s gauge).

Proof. 

Let $X^{\perp }:=X-{\mathsf{E}}_{\mathcal{N}}X\in {\mathcal{N}}^{\perp }$. Since ${\mathsf{T}}_t$ is reversible on H, $t\mapsto \parallel {\left({\mathsf{T}}_{t}X\right)}^{\perp }{\parallel }^2$ is differentiable with

$$\frac{d}{dt}\parallel {\left({\mathsf{T}}_{t}X\right)}^{\perp }{\parallel }^2=2\langle {\mathsf{T}}_t{X}^{\perp },\mathcal{L}{\mathsf{T}}_t{X}^{\perp }\rangle =-2\mathcal{E}\left({\mathsf{T}}_t{X}^{\perp }\right)\le -2\lambda {\parallel {\left({\mathsf{T}}_{t}X\right)}^{\perp }\parallel }^2,$$

(112)

where $\mathcal{E}(·)=\langle ·,-\mathcal{L}·\rangle$ and we used the Poincaré gap on ${\mathcal{N}}^{\perp }$. Grönwall’s lemma gives $\parallel {\left({\mathsf{T}}_{t}X\right)}^{\perp }{\parallel }^2\le e^{-2\lambda t}{\parallel X^{\perp }\parallel }^2$, i.e. $\mathcal{R}\left({\mathsf{T}}_{t}X\right)\le e^{-2\lambda t}\mathcal{R}\left(X\right)$ and $\mathrm{dist}({\mathsf{T}}_{t}X,\mathcal{N})\le e^{-\lambda t}\mathrm{dist}(X,\mathcal{N})$. Since $\mathcal{N}$ is the fixed–point subspace of the semigroup, it is invariant and attracts every orbit. Uniqueness of the global attractor (modulo gauge) follows because any other closed invariant attracting set must lie in $\mathcal{N}$.    □

Remark 4.22

(Interpretation). The Master/Grand theorems formalize the central message: once a (sector–appropriate) spectral gap/coercivity is present, the DSFL inequality holds and the sector’s canonical equilibrium relation is recovered as a dynamical fixed point rather than as a postulate. In reversible settings the exponential rate is dictated by the Poincaré gap; in the PDE/GR coercive settings the rate is dictated by the quantitative coercivity (e.g. $2\beta -C\epsilon$ or $2{\lambda }_{\mathrm{GR}}$).

Corollary 4.5

(Observable ISS under DSFL). Assume the hypotheses of Corollary 4.4. Suppose further that the residual dynamics admit an input term in the DSFL inequality,

$$\dot{\mathcal{R}}\left(t\right)\le -\alpha \mathcal{R}\left(t\right)+{\epsilon }^{2}u\left(t\right),$$

(113)

with $\alpha >0$, $\epsilon \ge 0$, and $u\in L_{\mathrm{loc}}^1\left([0,\infty )\right)$. Then

$$|\mathcal{O}\left({\mathsf{T}}_t{x}_0\right)-{\mathcal{O}}^{\ast }|\le C{e}^{-\alpha t}\mathrm{dist}(x_0,\mathcal{A})+C{\epsilon }^2{\int }_0^t{e}^{-\alpha (t-s)}\frac{u\left(s\right)}{\sqrt{\mathcal{R}\left(s\right)+{\mathcal{R}}_0{R}_{\ast }}}ds,$$

(114)

where ${\mathcal{R}}_0>0$ and $R_{\ast }\in (0,1)$ are the fixed constants from the residual–entropy proxy. In particular, if $u\in L^1(0,\infty )$ then

$$\underset{t\to \infty }{lim\; sup}|\mathcal{O}\left({\mathsf{T}}_t{x}_0\right)-{\mathcal{O}}^{\ast }|\le \frac{C{\epsilon }^2}{\alpha }\parallel \frac{u}{\sqrt{\mathcal{R}(·)+{\mathcal{R}}_0{R}_{\ast }}}{\parallel }_{L^1(0,\infty )}.$$

(115)

The same estimate holds with $\mathrm{dist}$ replaced by any locally equivalent weighted distance $d_{\ast }$ (Lemma 4.7).

5. Proofs

This section collects the proofs of the results stated in Section 4.

5.1. Proof of Sec. 4.1 (Propagation lemma)

Proof of Lemma 4.1. 

(CL) Let $\phi :{\mathbb{R}}^m\to [0,\infty )$ be convex with $\phi \left(0\right)=0$ and let $\left({\mathsf{T}}_t\right)$ be a Markov contraction on $L^1\cap L^2\left(\mu \right)$. By Jensen’s inequality and positivity/mass preservation, $\phi \left({\mathsf{T}}_{t}u\right)\le {\mathsf{T}}_t\left(\phi \left(u\right)\right)$$\mu$–a.e. Integrating and using $\int {\mathsf{T}}_{t}fd\mu =\int fd\mu$ yields $\int \phi \left({\mathsf{T}}_{t}u\right)d\mu \le \int \phi \left(u\right)d\mu$, i.e. $\mathcal{R}\left(t\right)\le \mathcal{R}\left(0\right)$.

• (QM) Let ${\left({\mathsf{T}}_t\right)}_{t\ge 0}$ be normal u.c.p., $\omega$–symmetric on $L^2\left(\omega \right)$, and $\omega$–preserving. Kadison–Schwarz gives ${\mathsf{T}}_t{\left(X\right)}^{\ast }{\mathsf{T}}_t\left(X\right)\le {\mathsf{T}}_t\left(X^{\ast }X\right)$. Applying $\omega$ and using $\omega \circ {\mathsf{T}}_t=\omega$ yields $\parallel {\mathsf{T}}_t{X\parallel }_{2,\omega }^2\le {\parallel X\parallel }_{2,\omega }^2$. Since ${\mathsf{E}}_{\mathcal{N}}$ is the $L^2\left(\omega \right)$ orthogonal projection and ${\mathsf{T}}_t$ acts as the identity on $\mathcal{N}$, the same contraction holds for $X-{\mathsf{E}}_{\mathcal{N}}X$: $\parallel {\mathsf{T}}_{t}X-{\mathsf{E}}_{\mathcal{N}}{X\parallel }_{2,\omega }\le {\parallel X-{\mathsf{E}}_{\mathcal{N}}X\parallel }_{2,\omega }$, hence ${\mathcal{R}}_{\omega }\left({\mathsf{T}}_{t}X\right)\le {\mathcal{R}}_{\omega }\left(X\right)$.
  (PDE) With $u:=P-\nabla \rho$ and $\mathcal{R}\left(t\right):={\int }_{\Omega }{|u|}^{2}dx$, differentiate in time. Using ${\partial }_{t}u=-Bu-\nabla (\nabla ·u)+\left(\mathrm{controlled}\right)$ and integrating by parts (periodic BCs or homogeneous BCs that kill boundary terms), we get

$$\frac{d}{dt}\mathcal{R}\left(t\right)=-2{\int }_{\Omega }{u}^{\top }Budx-2{\parallel \nabla ·u\parallel }_{L^2(\Omega )}^2+\left(\mathrm{controlled}\right).$$

(116)

Under $B⪰0$ and the stated sign/dominance of the controlled terms, the right–hand side is $\le 0$, hence $\mathcal{R}\left(t\right)\le \mathcal{R}\left(0\right)$.    □

5.2. Proof of Lemma 4.5

Proof. 

(i) QM. Let $\Omega$ be a bounded $C^1$ domain with periodic or homogeneous Neumann BCs. For $w:=\rho -{|\Psi |}^2$ one has ${\int }_{\Omega }wdx=0$ (mass normalization). Poincaré then gives ${\parallel w\parallel }_{L^2(\Omega )}^2\le {\lambda }_1^{-1}{\parallel \nabla w\parallel }_{L^2(\Omega )}^2$, so ${\lambda }_1{\parallel w\parallel }_{L^2}^2\le {\int }_{\Omega }{|\nabla w|}^{2}dx={\mathcal{R}}_{\mathrm{QM}}\left(\rho \right)$, and the upper bound follows from the $H^1$ control of w.

(ii) TD. For $W\left(x\right)⪰{\lambda }_{min}I$ a.e., ${|v|}_W^2=v^{\top }Wv\ge {\lambda }_{min}{|v|}^2$, hence ${\mathcal{R}}_{\mathrm{TD}}={\int }_{\Omega }{|P-\nabla \rho |}_W^{2}dx\ge {\lambda }_{min}{\parallel P-\nabla \rho \parallel }_{L^2(\Omega )}^2.$

(iii) QMS. By Takesaki’s theorem, the $\omega$–preserving conditional expectation ${\mathsf{E}}_{\mathcal{N}}$ is the $L^2\left(\omega \right)$ orthogonal projection onto $L^2(\mathcal{N},\omega )$. Therefore ${\mathcal{R}}_{\omega }\left(X\right)={\parallel X-{\mathsf{E}}_{\mathcal{N}}X\parallel }_{2,\omega }^2=\mathrm{dist}{\left(X,L^2(\mathcal{N},\omega )\right)}^2.$

(iv) GR. Linearizing $G\left[\gamma \right]-\kappa T$ at $\overline{\gamma }$ yields $G[\overline{\gamma }+h]-\kappa T=\frac{1}{2}{\mathcal{L}}_{\overline{\gamma }}h+Q(h,\nabla h)$ with $Q=O(|h||{\nabla }^{2}h|+|\nabla h{|}^2)$. For ${\parallel h\parallel }_{H^2\left(\overline{\gamma }\right)}$ sufficiently small, squaring and integrating gives ${\mathcal{R}}_{\mathrm{geom}}\simeq \frac{1}{4}{\parallel {\mathcal{L}}_{\overline{\gamma }}h\parallel }_{L^2\left(\overline{\gamma }\right)}^2.$ Elliptic regularity for ${\mathcal{L}}_{\overline{\gamma }}$ on the gauge–orthogonal subspace implies $\parallel {\mathcal{L}}_{\overline{\gamma }}{h\parallel }_{L^2\left(\overline{\gamma }\right)}\simeq {\parallel h\parallel }_{H^2\left(\overline{\gamma }\right)},$ hence ${\mathcal{R}}_{\mathrm{geom}}\simeq {\parallel h\parallel }_{H^2\left(\overline{\gamma }\right)}^2$, which is equivalent to ${\mathrm{dist}}_{H^2}{(\gamma ,\overline{\gamma })}^2$ modulo diffeomorphisms.    □

5.3. Proof of Lemma 4.6

Proof. 

Let $x\left(t\right)={\mathsf{T}}_t{x}_0$. By (100), $\mathcal{R}\left(x\right(t\left)\right)$ is nonincreasing and bounded below, hence convergent. Sector by sector, standard compactness (e.g. Rellich–Kondrachov in PDE/GR or spectral decomposition in reversible semigroups) yields precompactness of trajectories on bounded time intervals. Any $\overline{x}\in \omega \left(x_0\right)$ admits a sequence $t_k\to \infty$ with $x\left(t_k\right)\to \overline{x}$, and continuity of $\mathcal{R}$ gives ${lim}_{k\to \infty }\mathcal{R}\left(x\left(t_k\right)\right)=\mathcal{R}\left(\overline{x}\right)$; invariance of $\omega \left(x_0\right)$ implies $\mathcal{R}\left(\overline{x}\right)={lim}_{t\to \infty }\mathcal{R}\left(x\left(t\right)\right)$. Since $\dot{\mathcal{R}}\le -\alpha \mathcal{R}$, necessarily $\dot{\mathcal{R}}\left(\overline{x}\right)=0$ and hence $\mathcal{R}\left(\overline{x}\right)=0$. Thus $\omega \left(x_0\right)\subset \{\mathcal{R}=0\}=\mathcal{A}$. If $\mathcal{A}$ consists of a single orbit modulo the sector’s gauge, then Łojasiewicz–Simon/strict Lyapunov arguments imply $x\left(t\right)\to \mathcal{A}$.    □

5.4. Proof of Theorem 4.7

Proof. 

Combine Lemma 4.5 (residual ⇔ distance) with the DSFL inequality (100) to obtain $L^2$– (QM) and $H^2$– (GR) convergence. For TD, the $S_R$ monotonicity follows by direct differentiation. For QMS, apply Theorem 4.2. Uniqueness modulo sector gauges follows from invariances (additive constants for $\rho$; diffeomorphisms for $\gamma$) and the strict convexity of $\mathcal{R}$ transverse to gauge directions.    □

5.5. Proof of Sec. 4.3 (Lindblad Sharpness)

Proof of Theorem 4.3 and Corollary 4.3. 

Work in the orthonormal basis ${\{|i\rangle \}}_{i=1}^d$ where $P_i=|i\rangle \langle i|$. The generator is

$${\mathcal{L}}^{\ast }\left(\sigma \right)=\sum _{i=1}^d{\gamma }_i\left(P_i\sigma P_i-\frac{1}{2}\{P_i,\sigma \}\right),{\gamma }_i>0.$$

(117)

   □

Proof of Theorem 4.3. 

(A) Modewise solution and residual envelope.

Matrix elements satisfy

$$\frac{d}{dt}{\left({\sigma }_t\right)}_{ii}=0,\frac{d}{dt}{\left({\sigma }_t\right)}_{ij}=-\frac{{\gamma }_i+{\gamma }_j}{2}{\left({\sigma }_t\right)}_{ij}(i\ne j),$$

(118)

so ${\left({\sigma }_t\right)}_{ij}=e^{-({\gamma }_i+{\gamma }_j)t/2}{\left({\sigma }_0\right)}_{ij}$. Hence

$${\mathcal{R}}_{\mathrm{L}\ddot{\mathrm{u}}\mathrm{ders}}\left({\sigma }_t\right)=\sum _{i\ne j}{e}^{-({\gamma }_i+{\gamma }_j)t}|{\left({\sigma }_0\right)}_{ij}{|}^2\le e^{-{\alpha }_{\ast }t}\sum _{i\ne j}{|{\left({\sigma }_0\right)}_{ij}|}^2,$$

(119)

with ${\alpha }_{\ast }:={min}_{i\ne j}({\gamma }_i+{\gamma }_j)$.

   □

Proof of Theorem 4.3 and Corollary 4.3. 

Work in the orthonormal basis ${\{|i\rangle \}}_{i=1}^d$ where $P_i=|i\rangle \langle i|$. The generator is

$${\mathcal{L}}^{\ast }\left(\sigma \right)=\sum _{i=1}^d{\gamma }_i\left(P_i\sigma P_i-\frac{1}{2}\{P_i,\sigma \}\right),{\gamma }_i>0.$$

(120)

(A)

Modewise solution and residual envelope. Matrix elements satisfy

$$\frac{d}{dt}{\left({\sigma }_t\right)}_{ii}=0,\frac{d}{dt}{\left({\sigma }_t\right)}_{ij}=-\frac{{\gamma }_i+{\gamma }_j}{2}{\left({\sigma }_t\right)}_{ij}(i\ne j),$$

(121)

so ${\left({\sigma }_t\right)}_{ij}=e^{-({\gamma }_i+{\gamma }_j)t/2}{\left({\sigma }_0\right)}_{ij}$. Hence

$${\mathcal{R}}_{\mathrm{L}ü\mathrm{ders}}\left({\sigma }_t\right)=\sum _{i\ne j}{e}^{-({\gamma }_i+{\gamma }_j)t}|{\left({\sigma }_0\right)}_{ij}{|}^2\le e^{-{\alpha }_{\ast }t}\sum _{i\ne j}{|{\left({\sigma }_0\right)}_{ij}|}^2,$$

(122)

with ${\alpha }_{\ast }:={min}_{i\ne j}({\gamma }_i+{\gamma }_j)$.

(B)

Optimality. Choose initial coherence supported on a pair $(i_{\ast },j_{\ast })$ attaining ${min}_{i\ne j}({\gamma }_i+{\gamma }_j)$. Then

$${\mathcal{R}}_{\mathrm{L}ü\mathrm{ders}}\left({\sigma }_t\right)=\sum _{i\ne j}{e}^{-({\gamma }_i+{\gamma }_j)t}|{\left({\sigma }_0\right)}_{ij}{|}^2=e^{-{\alpha }_{\ast }t}{|{\left({\sigma }_0\right)}_{i_{\ast }{j}_{\ast }}|}^2,$$

(123)

which matches the envelope with equality. Hence the rate ${\alpha }_{\ast }={min}_{i\ne j}({\gamma }_i+{\gamma }_j)$ is sharp.

(C)

Trace–norm convergence. Since the diagonal entries are constant in time and the off–diagonals decay modewise as $e^{-({\gamma }_i+{\gamma }_j)t/2}$, one has

$$\parallel {\sigma }_t-\Phi \left({\sigma }_0\right){\parallel }_2^2=\sum _{i\ne j}{e}^{-({\gamma }_i+{\gamma }_j)t}|{\left({\sigma }_0\right)}_{ij}{|}^2\le e^{-{\alpha }_{\ast }t}{\parallel {\sigma }_0-\Phi \left({\sigma }_0\right)\parallel }_2^2.$$

(124)

Using ${\parallel A\parallel }_1\le \sqrt{d}{\parallel A\parallel }_2$ then gives

$$\parallel {\sigma }_t-\Phi \left({\sigma }_0\right){\parallel }_1\le \sqrt{d}{e}^{-{\alpha }_{\ast }t/2}{\parallel {\sigma }_0-\Phi \left({\sigma }_0\right)\parallel }_2,$$

(125)

so ${\sigma }_t\to \Phi \left({\sigma }_0\right)$ in trace norm at an exponential rate, proving the corollary.

   □

5.6. Proof of Sec. 4.4 (PDE Energy Identity and Decay)

Proof of Theorem 4.4. 

Step 0 (regularity and IBP). Assume $(\rho ,P)$ is a (mild) solution with $\rho (·,t)\in H^1(\Omega ),P(·,t)\in L^2(\Omega ;{\mathbb{R}}^d)$ for $t\in [0,T]$, and periodic or homogeneous boundary conditions chosen so that the boundary term in the IBP identity vanishes (cf. Remark 4.3). Standard mollification in time (or density of smooth compactly supported functions in the graph norm) justifies differentiation under the integral sign; the final inequalities extend by continuity to the given regularity class.

Step 1 (residual equation). Let

$$u:=P-\nabla \rho ,\mathcal{R}\left(t\right):={\int }_{\Omega }{|u(x,t)|}^{2}dx.$$

(126)

From (66),

$${\partial }_{t}u={\partial }_{t}P-\nabla \left({\partial }_t\rho \right)=-B(x,t)u-\nabla (\nabla ·u)+G(\rho ,P).$$

(127)

Step 2 (exact energy identity). Differentiate $\mathcal{R}$ and use the product rule:

$$\frac{d}{dt}\mathcal{R}\left(t\right)=2{\int }_{\Omega }u·{\partial }_{t}udx=-2{\int }_{\Omega }{u}^{\top }Budx-2{\int }_{\Omega }u·\nabla (\nabla ·u)dx+2{\int }_{\Omega }u·Gdx.$$

(128)

By integration by parts and the BC choice,

$${\int }_{\Omega }u·\nabla (\nabla ·u)dx={\int }_{\partial \Omega }{(u·n)(\nabla ·u)dS-\parallel \nabla ·u\parallel }_{L^2(\Omega )}^2=-{\parallel \nabla ·u\parallel }_{L^2(\Omega )}^2.$$

(129)

Hence

$$\frac{d}{dt}\mathcal{R}\left(t\right)=-2{\int }_{\Omega }{u}^{\top }Budx-2{\parallel \nabla ·u\parallel }_{L^2}^2+2{\int }_{\Omega }u·Gdx.$$

(130)

Step 3 (coercivity and subcriticality). The uniform positive definiteness $B(x,t)⪰\beta I$ a.e. implies

$${\int }_{\Omega }{u}^{\top }Budx\ge \beta {\int }_{\Omega }{|u|}^{2}dx=\beta \mathcal{R}\left(t\right).$$

(131)

By the subcriticality hypothesis, there exist $C>0$ and sufficiently small $\epsilon \ge 0$ such that

$$|{\int }_{\Omega }u·G(\rho ,P)dx|\le C\epsilon \mathcal{R}\left(t\right)\mathrm{for}\mathrm{all}t\in [0,T].$$

(132)

(For example, this holds if G is locally Lipschitz with ${\parallel G(\rho ,P)\parallel }_{L^2}\le C\epsilon {\parallel u\parallel }_{L^2}$ in the energy region visited by the solution.)

Step 4 (differential inequality). Insert these bounds into (130) to obtain

$$\frac{d}{dt}\mathcal{R}\left(t\right)\le -2\beta \mathcal{R}\left(t\right)-2{\parallel \nabla ·u\parallel }_{L^2}^2+2C\epsilon \mathcal{R}\left(t\right)\le -(2\beta -C\epsilon )\mathcal{R}\left(t\right).$$

(133)

Let $\alpha :=2\beta -C\epsilon >0$ (smallness of $\epsilon$ ensures positivity).

Step 5 (Grönwall). By Grönwall’s inequality,

$$\mathcal{R}\left(t\right)\le e^{-\alpha t}\mathcal{R}\left(0\right)\mathrm{for}\mathrm{all}t\in [0,T],$$

(134)

i.e. the residual decays exponentially at rate $\alpha =2\beta -C\epsilon$. In particular, for $\epsilon =0$ we recover the clean rate $\mathcal{R}\left(t\right)\le e^{-2\beta t}\mathcal{R}\left(0\right)$.

Optional refinements. (i) The extra term ${-2\parallel \nabla ·u\parallel }_{L^2}^2$ is dissipative and improves the decay when the Helmholtz gradient component dominates; combine with a Poincaré inequality on gradient fields to sharpen the rate on tori or bounded domains. (ii) If $B=B\left(t\right)$ with

$$\beta \left(t\right):=\underset{x\in \Omega }{ess\; inf}{\lambda }_{min}\left(B(x,t)\right),$$

(135)

then

$$\frac{d}{dt}\mathcal{R}\left(t\right)\le -\left(2\beta \left(t\right)-C\epsilon \right)\mathcal{R}\left(t\right)⟹\mathcal{R}\left(t\right)\le exp\left(-{\int }_0^t\left(2\beta \left(s\right)-C\epsilon \right)ds\right)\mathcal{R}\left(0\right).$$

(136)

In particular, if $\underline{\beta }:={inf}_{s\ge 0}\beta \left(s\right)>\frac{C\epsilon }{2}$, then $\mathcal{R}\left(t\right)\le e^{-(2\underline{\beta }-C\epsilon )t}\mathcal{R}\left(0\right)$; and if ${\int }_0^{\infty }\left(2\beta \left(s\right)-C\epsilon \right)ds=+\infty$, then $\mathcal{R}\left(t\right)\to 0$.

This completes the proof.    □

5.7. Proof of Sec. 4.5 (Free–Field Residual Decay)

Proof of Theorem 4.5 

We give a concrete Ornstein–Uhlenbeck (OU) derivation for the free field and then the abstract semigroup proof.

• OU formulation and Lyapunov equation.

Write the free Euclidean dynamics as

$${\partial }_{\tau }{\varphi }_{\tau }=-\mathcal{A}{\varphi }_{\tau }+\eta ,\mathcal{A}:=(-\Delta )+m^2\mathrm{on}{\mathbb{R}}^d,$$

(137)

with Gaussian space–time white noise $\eta$ normalized by $\mathbb{E}\left[\eta \right(x,\tau \left)\eta \right(y,\sigma \left)\right]=2\delta (x-y)\delta (\tau -\sigma )$. This factor 2 ensures the stationary covariance $C_{\infty }$ solves the Lyapunov identity $\mathcal{A}{C}_{\infty }+C_{\infty }\mathcal{A}=2I$, hence $C_{\infty }={\mathcal{A}}^{-1}$ when defined. For any admissible test function f (e.g. $f\in \mathcal{S}\left({\mathbb{R}}^d\right)$ or $f\in L^2$ with compact Fourier support), let ${\Phi }_{\tau }\left(f\right):=\langle {\varphi }_{\tau },f\rangle$. The covariance $C\left(\tau \right)$ of ${\varphi }_{\tau }$ obeys

$$\frac{d}{d\tau }C\left(\tau \right)=-\mathcal{A}C\left(\tau \right)-C\left(\tau \right)\mathcal{A}+2I,C\left(\tau \right)=e^{-\tau \mathcal{A}}C\left(0\right)e^{-\tau \mathcal{A}}+{\int }_0^{\tau }{e}^{-(\tau -s)\mathcal{A}}\left(2I\right)e^{-(\tau -s)\mathcal{A}}ds.$$

(138)

Subtracting $C_{\infty }$ gives

$$D\left(\tau \right):=C\left(\tau \right)-C_{\infty }=e^{-\tau \mathcal{A}}\left(C\left(0\right)-C_{\infty }\right)e^{-\tau \mathcal{A}},$$

(139)

hence for any f,

$$C_{\tau }\left(f\right)-C_{\infty }\left(f\right)=\langle e^{-\tau \mathcal{A}}f,(C\left(0\right)-C_{\infty })e^{-\tau \mathcal{A}}f\rangle .$$

(140)

• Spectral gap bound.

Since $\mathcal{A}\ge {\lambda }_{\ast }I$ with ${\lambda }_{\ast }=m^2$ (free field), the semigroup bound $\parallel e^{-\tau \mathcal{A}}{\parallel }_{\mathcal{B}\left(L^2\right)}\le e^{-{\lambda }_{\ast }\tau }$ yields

$$|C_{\tau }\left(f\right)-C_{\infty }\left(f\right)|\le \parallel C\left(0\right)-C_{\infty }\parallel \parallel e^{-\tau \mathcal{A}}{f\parallel }_{L^2}^2\le \parallel C\left(0\right)-C_{\infty }\parallel e^{-2{\lambda }_{\ast }\tau }{\parallel f\parallel }_{L^2}^2.$$

(141)

Equivalently,

$$|C_{\tau }\left(f\right)-C_{\infty }\left(f\right)|\le e^{-2{\lambda }_{\ast }\tau }M\left(f\right),M\left(f\right):=\parallel C\left(0\right)-C_{\infty }{\parallel \parallel f\parallel }_{L^2}^2.$$

(142)

The residual in Theorem 4.5 is $R[f;\tau ]=|C_{\tau }\left(f\right)-C_{\infty }{\left(f\right)|}^2$, hence from (142)

$$R[f;\tau ]\le e^{-4{\lambda }_{\ast }\tau }M{\left(f\right)}^2.$$

(143)

This is sharper than the theorem’s envelope; loosening the prefactor gives the stated $e^{-2{\lambda }_{\ast }\tau }$ bound.

• Fourier–mode check (explicit diagonalization).

Let $\widehat{f}\left(k\right)$ be the Fourier transform and note $\widehat{\mathcal{A}f}={(|k|}^2+m^2)\widehat{f}\left(k\right)$. Then $e^{-\tau \mathcal{A}}$ multiplies by $e^{-\tau (|k{|}^2+m^2)}$, while $C_{\infty }$ multiplies by ${(|k|}^2+m^2{)}^{-1}$. A direct computation yields

$$C_{\tau }\left(f\right)-C_{\infty }\left(f\right)={\int }_{{\mathbb{R}}^d}{e}^{-2\tau (|k{|}^2+m^2)}\widehat{D}(0,k){|\widehat{f}\left(k\right)|}^{2}dk,$$

(144)

so $|C_{\tau }\left(f\right)-C_{\infty }\left(f\right)|\le e^{-2{\lambda }_{\ast }\tau }\parallel \widehat{D}{(0,·)\parallel }_{L^{\infty }}{\parallel f\parallel }_{L^2}^2$, consistent with (142).

• Abstract semigroup proof.

Let H be the nonnegative, self–adjoint Euclidean Hamiltonian generating ${\mathsf{T}}_{\tau }=e^{-\tau H}$ on the GNS space. With vacuum projector ${\Pi }_0$ one has $\sigma \left(H\right)\subset \left\{0\right\}\cup [{\lambda }_{\ast },\infty )$ and $\parallel ({\mathsf{T}}_{\tau }-{\Pi }_0){|}_{{\Pi }_0^{\perp }}\parallel \le e^{-{\lambda }_{\ast }\tau }$. Then

$$C_{\tau }\left(f\right)-C_{\infty }\left(f\right)=\langle f,({\mathsf{T}}_{\tau }-{\Pi }_0)K({\mathsf{T}}_{\tau }-{\Pi }_0)f\rangle$$

(145)

for some positive operator K, whence

$$|C_{\tau }\left(f\right)-C_{\infty }\left(f\right)|\le \parallel K\parallel \parallel ({\mathsf{T}}_{\tau }-{\Pi }_0){|}_{{\Pi }_0^{\perp }}{\parallel }^2{\parallel f\parallel }^2\le \parallel K\parallel e^{-2{\lambda }_{\ast }\tau }{\parallel f\parallel }^2,$$

(146)

and squaring gives the same residual decay (again with the sharper $4{\lambda }_{\ast }$ envelope available).

• Admissible test functions.

The bounds hold for any f with finite quadratic forms $\langle f,C\left(0\right)f\rangle$ and $\langle f,C_{\infty }f\rangle$ (e.g. $f\in L^2$ with ultraviolet cutoff, or $f\in \mathcal{S}$), ensuring well–posed covariance pairings and OU action.

Combining the covariance estimate with $R[f;\tau ]=|C_{\tau }\left(f\right)-C_{\infty }{\left(f\right)|}^2$ finishes the proof.    □

5.8. Proof of Sec. 4.6 (GR DeTurck–Gauge Decay)

Proof of Theorem 4.6. 

We work on a smooth closed 3–manifold $(\Sigma ,\overline{\gamma })$. Write the evolving metric as $\gamma \left(t\right)=\overline{\gamma }+h\left(t\right)$ with $h\left(t\right)\in \Gamma ({\mathrm{Sym}}^2{T}^{\ast }\Sigma )$ small in $H^k$, $k\ge 3$. The Einstein–DeTurck–source flow can be written as

$${\partial }_{t}h=-{\mathcal{L}}_{\overline{\gamma }}h+{\mathcal{N}}_{\overline{\gamma }}(h,\nabla h),$$

(147)

where ${\mathcal{L}}_{\overline{\gamma }}$ is the strictly elliptic Lichnerowicz–DeTurck operator (self–adjoint on $L^2\left(\overline{\gamma }\right)$ on the orthogonal complement of gauge directions) and ${\mathcal{N}}_{\overline{\gamma }}$ collects quadratic and higher–order terms in $(h,\nabla h)$ (and lower–order dependence on $\overline{\gamma }$). By hypothesis, there exists a spectral gap ${\lambda }_{\mathrm{GR}}>0$ such that

$${\langle h,{\mathcal{L}}_{\overline{\gamma }}h\rangle }_{L^2\left(\overline{\gamma }\right)}\ge {\lambda }_{\mathrm{GR}}{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^2\mathrm{for}\mathrm{all}h\perp \mathrm{gauge}\mathrm{directions}.$$

(148)

We also assume T is divergence–free along the flow so that constraint terms vanish.

• Step 1: Energy identity in the fixed background.

Taking the $L^2\left(\overline{\gamma }\right)$ inner product of (147) with h,

$$\frac{1}{2}\frac{d}{dt}{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^2=-{\langle h,{\mathcal{L}}_{\overline{\gamma }}h\rangle }_{L^2\left(\overline{\gamma }\right)}+{\langle h,{\mathcal{N}}_{\overline{\gamma }}(h,\nabla h)\rangle }_{L^2\left(\overline{\gamma }\right)}.$$

(149)

Using (148) gives

$$\frac{d}{dt}{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^2\le -2{\lambda }_{\mathrm{GR}}{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^2+2|{\langle h,{\mathcal{N}}_{\overline{\gamma }}(h,\nabla h)\rangle }_{L^2\left(\overline{\gamma }\right)}|.$$

(150)

• Step 2: Nonlinearity estimate.

On the compact manifold, for $k\ge 3$ the bilinear/quadratic structure of ${\mathcal{N}}_{\overline{\gamma }}$ and Sobolev product estimates yield

$$|{\langle h,{\mathcal{N}}_{\overline{\gamma }}(h,\nabla h)\rangle }_{L^2\left(\overline{\gamma }\right)}|\le {C\parallel h\parallel }_{H^1\left(\overline{\gamma }\right)}{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}\le {C\parallel h\parallel }_{H^k\left(\overline{\gamma }\right)}^{\theta }{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^{2-\theta },$$

(151)

for some $\theta \in (0,1)$ and $C=C\left(\overline{\gamma }\right)$. (Here we used interpolation ${\parallel h\parallel }_{H^1}\le {C\parallel h\parallel }_{H^k}^{\theta }{\parallel h\parallel }_{L^2}^{1-\theta }$ and the fact that $\mathcal{N}$ has no linear part at $\overline{\gamma }$.) Since the flow is parabolic–elliptic in DeTurck gauge, standard local theory gives a time interval on which ${\parallel h\left(t\right)\parallel }_{H^k\left(\overline{\gamma }\right)}\le 2{\parallel h\left(0\right)\parallel }_{H^k\left(\overline{\gamma }\right)}$. Choosing the smallness radius $\delta >0$ so that ${\parallel h\left(0\right)\parallel }_{H^k}\le \delta$ implies

$$|{\langle h,{\mathcal{N}}_{\overline{\gamma }}(h,\nabla h)\rangle }_{L^2}|\le \frac{{\lambda }_{\mathrm{GR}}}{2}{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^2,\mathrm{as}\mathrm{long}\mathrm{as}{\parallel h\left(t\right)\parallel }_{H^k}\le 2\delta .$$

(152)

• Step 3: Differential inequality and decay.

Combining (150) and (152),

$$\frac{d}{dt}{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^2\le -2{\lambda }_{\mathrm{GR}}{\parallel h\parallel }_{L^2}^2+{\lambda }_{\mathrm{GR}}{\parallel h\parallel }_{L^2}^2=-{\lambda }_{\mathrm{GR}}{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^2.$$

(153)

By Grönwall,

$${\parallel h\left(t\right)\parallel }_{L^2\left(\overline{\gamma }\right)}^2\le e^{-{\lambda }_{\mathrm{GR}}t}{\parallel h\left(0\right)\parallel }_{L^2\left(\overline{\gamma }\right)}^2.$$

(154)

The decay (154) and parabolic regularization imply, by a standard bootstrap, that ${\parallel h\left(t\right)\parallel }_{H^k}$ remains $\le 2\delta$ for all $t\ge 0$ provided $\delta$ is chosen small enough initially. Hence (154) holds globally, and by refining the absorption in (152) one improves the rate to $2{\lambda }_{\mathrm{GR}}$:1

$$\frac{d}{dt}{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^2\le -2{\lambda }_{\mathrm{GR}}{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^2.$$

(155)

v

• Step 4: Equivalence of the geometric residual and ${\parallel h\parallel }_{L^2}^2$.

Define

$${\mathcal{R}}_{\mathrm{geom}}\left(t\right):={\int }_{\Sigma }\parallel G\left[\gamma \left(t\right)\right]-\kappa T{\parallel }_{\gamma \left(t\right)}^{2}d{\mu }_{\gamma \left(t\right)}.$$

(156)

For h small in $C^0$ one has the metric and volume equivalences

$${(1-c\parallel h\parallel }_{C^0}{)\parallel S\parallel }_{L^2\left(\overline{\gamma }\right)}^2\le {\parallel S\parallel }_{L^2\left(\gamma \left(t\right)\right)}^2\le {(1+c\parallel h\parallel }_{C^0}{)\parallel S\parallel }_{L^2\left(\overline{\gamma }\right)}^2,$$

(157)

uniformly for tensors S. Moreover, by linearization at $\overline{\gamma }$,

$$G[\overline{\gamma }+h]-\kappa T={\mathcal{L}}_{\overline{\gamma }}h+\mathcal{Q}(h,\nabla h),$$

(158)

with ${\parallel \mathcal{Q}(h,\nabla h)\parallel }_{L^2\left(\overline{\gamma }\right)}\le {C\parallel h\parallel }_{H^1}{\parallel h\parallel }_{H^2}$. By elliptic regularity for ${\mathcal{L}}_{\overline{\gamma }}$ and the spectral gap on the gauge–orthogonal subspace, $\parallel {\mathcal{L}}_{\overline{\gamma }}{h\parallel }_{L^2}\ge {\lambda }_{\mathrm{GR}}{\parallel h\parallel }_{L^2}$. Hence, for ${\parallel h\parallel }_{H^k}$ sufficiently small,

$$c_1{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^2\le {\mathcal{R}}_{\mathrm{geom}}\left(t\right)\le c_2{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^2,$$

(159)

for some $0<c_1\le c_2<\infty$ depending only on $(\Sigma ,\overline{\gamma })$ and the smallness radius.

• Step 5: Decay of ${\mathcal{R}}_{\mathrm{geom}}$.

Differentiating ${\mathcal{R}}_{\mathrm{geom}}$ along the flow and using (147), the elliptic coercivity and (159), one obtains the differential inequality

$$\frac{d}{dt}{\mathcal{R}}_{\mathrm{geom}}\left(t\right)\le -2{\lambda }_{\mathrm{GR}}{\mathcal{R}}_{\mathrm{geom}}\left(t\right),$$

(160)

for all $t\ge 0$ as long as h remains in the small regime (which we ensured in Step 3). Grönwall therefore gives

$${\mathcal{R}}_{\mathrm{geom}}\left(t\right)\le {\mathcal{R}}_{\mathrm{geom}}\left(0\right)e^{-2{\lambda }_{\mathrm{GR}}t},$$

(161)

and in particular $G\left[\gamma \right(t\left)\right]\to \kappa T$ in $L^2(\Sigma )$ as $t\to \infty$. Standard arguments then show $\gamma \left(t\right)\to \overline{\gamma }$ modulo diffeomorphisms (the DeTurck vector field fixes the gauge).    □

6. Instantiations and Consequences

6.1. Born Alignment in the PDE Formulation

We show that the DSFL residual recovers Born’s rule as a global attractor in a continuum setting: starting from any probability density ${\rho }_0$ with the same mass as $q:={|\Psi |}^2$, the residual

$$\mathcal{R}\left(t\right)={\int }_{\Omega }{\left|\nabla (\rho -q)\right|}^{2}dx$$

decays exponentially, and $\rho (·,t)\to q(·)$ in $L^2$ at a rate controlled explicitly by the Laplacian’s spectral gap.

• Setting and intuition.

Let $\Omega \subset {\mathbb{R}}^d$ be a bounded $C^1$ domain with periodic or homogeneous Neumann boundary conditions (or $\Omega ={\mathbb{T}}^d$). Let $\Psi \in H^1(\Omega ;\mathbb{C})$ be normalized and set $q:={|\Psi |}^2\in H^1(\Omega )$ with ${\int }_{\Omega }qdx=1$. The DSFL–PDE in the Born sector reads

$${\partial }_t\rho =\nabla ·\left(\nabla q-\nabla \rho \right),P\equiv \nabla q\left(\mathrm{frozen}\mathrm{by}\mathrm{the}\mathrm{quantum}\sec \mathrm{tor}\right).$$

(162)

Set $w:=\rho -q$ (so ${\int }_{\Omega }wdx=0$) and $u:=P-\nabla \rho =\nabla (q-\rho )=-\nabla w$. The misalignment is purely gradient, hence the residual is the Dirichlet energy of w:

$$\mathcal{R}\left(t\right)={\int }_{\Omega }{|\nabla w(x,t)|}^{2}dx.$$

(163)

Proposition 6.1

(Residual energy identity in the Born sector). Under (162), the error w solves the heat equation ${\partial }_{t}w=\Delta w$ with periodic/Neumann BCs, and

$$\frac{d}{dt}\mathcal{R}\left(t\right)=-2{∥\Delta w\left(t\right)∥}_{L^2(\Omega )}^2\le 0.$$

(164)

In particular, $\mathcal{R}$ is nonincreasing and ${\int }_0^{\infty }{\parallel \Delta w\left(t\right)\parallel }_{L^2}^{2}dt<\infty$.

Proof. 

From (162), ${\partial }_{t}w={\partial }_t\rho =\Delta (\rho -q)=\Delta w$. Differentiating (163) and integrating by parts (boundary terms vanish) gives

$$\frac{d}{dt}\mathcal{R}=2{\int }_{\Omega }\nabla w·\nabla \left({\partial }_{t}w\right)dx=-2{\int }_{\Omega }\Delta w{\partial }_{t}wdx=-2{\int }_{\Omega }{(\Delta w)}^{2}dx.$$

□

Let ${\lambda }_1>0$ denote the first nonzero eigenvalue of $-\Delta$ on mean–zero functions with the chosen BCs; equivalently,

$${\parallel \Delta \phi \parallel }_{L^2(\Omega )}^2\ge {\lambda }_1{\parallel \nabla \phi \parallel }_{L^2(\Omega )}^2\mathrm{for}\mathrm{all}\phi \in H^2(\Omega )\mathrm{with}{\int }_{\Omega }\phi =0.$$

(165)

Theorem 6.1

(Born alignment as a PDE attractor with explicit rate). Assume ${\int }_{\Omega }\rho (·,0)dx={\int }_{\Omega }qdx=1$. Then

$$\mathcal{R}\left(t\right)\le e^{-2{\lambda }_{1}t}\mathcal{R}\left(0\right),{\parallel \rho (·,t)-q(·)\parallel }_{L^2(\Omega )}^2\le {\lambda }_1^{-1}\mathcal{R}\left(t\right)\le {\lambda }_1^{-1}{e}^{-2{\lambda }_{1}t}\mathcal{R}\left(0\right).$$

(166)

In particular, $\rho (·,t)\to q(·)$ in $L^2(\Omega )$ at least exponentially with rate ${\lambda }_1$.

Proof. 

By Proposition 6.1 and (165),

$$\frac{d}{dt}\mathcal{R}\left(t\right)=-{2\parallel \Delta w\parallel }_2^2\le -2{\lambda }_1{\parallel \nabla w\parallel }_2^2=-2{\lambda }_1\mathcal{R}\left(t\right),$$

so $\mathcal{R}\left(t\right)\le e^{-2{\lambda }_{1}t}\mathcal{R}\left(0\right)$ by Grönwall. Poincaré on mean–zero functions gives ${\parallel w\parallel }_2^2\le {\lambda }_1^{-1}{\parallel \nabla w\parallel }_2^2={\lambda }_1^{-1}\mathcal{R}\left(t\right)$, proving the $L^2$ convergence. □

Remark 6.1

(Spectral expansion (modewise alignment)). Let $w_0={\sum }_{k\ge 1}{a}_k{\varphi }_k$ with $-\Delta {\varphi }_k={\lambda }_k{\varphi }_k$ and ${\lambda }_1\le {\lambda }_2\le \dots$. Then

$$w\left(t\right)=\sum _{k\ge 1}{a}_k{e}^{-{\lambda }_{k}t}{\varphi }_k,\mathcal{R}\left(t\right)={\parallel \nabla w\left(t\right)\parallel }_2^2=\sum _{k\ge 1}{\lambda }_k{|a_k|}^2{e}^{-2{\lambda }_{k}t}\le e^{-2{\lambda }_{1}t}\mathcal{R}\left(0\right).$$

The envelope $e^{-2{\lambda }_{1}t}$ is sharp whenever $a_1\ne 0$.

Remark 6.2

(Mass conservation and well–posedness). Under periodic/Neumann BCs, (162) conserves mass: $\frac{d}{dt}{\int }_{\Omega }\rho dx=0$, so ${\int }_{\Omega }w=0$ is preserved. Standard parabolic theory yields global existence and uniqueness of $H^1$–solutions for initial data ${\rho }_0\in H^1(\Omega )$; the above estimates then hold for all $t\ge 0$.

• ISS–type robustness (small pointer noise).

Suppose the right–hand side of (162) contains a small forcing $\epsilon \xi (t,x)$ with ${\int }_{\Omega }\xi dx=0$. Then w solves ${\partial }_{t}w=\Delta w+\epsilon \xi$ and

$$\dot{\mathcal{R}}\left(t\right)=-{2\parallel \Delta w\parallel }_2^2+2\epsilon {\int }_{\Omega }\nabla w·\nabla \xi dx\le -2{\lambda }_1\mathcal{R}\left(t\right)+\frac{{\epsilon }^2}{{\lambda }_1}{\parallel \nabla \xi \left(t\right)\parallel }_2^2,$$

so

$$\mathcal{R}\left(t\right)\le e^{-2{\lambda }_{1}t}\mathcal{R}\left(0\right)+\frac{{\epsilon }^2}{{\lambda }_1}{\int }_0^t{e}^{-2{\lambda }_1(t-s)}{\parallel \nabla \xi \left(s\right)\parallel }_2^{2}ds,$$

and, in particular,

$$\underset{t\to \infty }{lim\; sup}\mathcal{R}\left(t\right)\le \frac{{\epsilon }^2}{2{\lambda }_1^2}{\parallel \nabla \xi \parallel }_{L^2(0,\infty ;L^2)}^2.$$

• Tracking a moving pointer.

If $q=q\left(t\right)$ varies in time, DSFL still contracts toward the moving target up to a controlled tube, quantified next.

Lemma 6.1

(Pointer–space tracking on a bounded domain). Let $\Omega \subset {\mathbb{R}}^d$ be bounded with periodic or homogeneous Neumann BCs, and let ${\lambda }_1>0$ denote the first nonzero eigenvalue of $-\Delta$ on mean–zero functions. Consider

$${\partial }_t\rho =\nabla ·\left(\nabla q(t,·)-\nabla \rho \right),P(t,·)\equiv \nabla q(t,·),$$

with ${\int }_{\Omega }\rho \left(t\right)={\int }_{\Omega }q\left(t\right)=1$ for all $t\ge 0$. Set $w:=\rho -q$ (so ${\int }_{\Omega }w=0$) and $\mathcal{R}\left(t\right):={\int }_{\Omega }{|\nabla w(t,x)|}^{2}dx$. If

$$M:=\underset{t\ge 0}{sup}\parallel \nabla {\partial }_{t}q(t,·){\parallel }_{L^2(\Omega )}<\infty ,$$

then

$$\dot{\mathcal{R}}\left(t\right)\le -{\lambda }_1\mathcal{R}\left(t\right)+\frac{M^2}{{\lambda }_1},$$

(167)

and consequently

$$\mathcal{R}\left(t\right)\le \mathcal{R}\left(0\right)e^{-{\lambda }_{1}t}+\frac{M^2}{{\lambda }_1^2}\left(1-e^{-{\lambda }_{1}t}\right).$$

(168)

In particular, if q is stationary ($M=0$) then $\mathcal{R}\left(t\right)\le e^{-{\lambda }_{1}t}\mathcal{R}\left(0\right)$.

Proof sketch. 

Since ${\partial }_{t}w=\Delta w-{\partial }_{t}q$ and $\mathcal{R}={\parallel \nabla w\parallel }_2^2$,

$$\dot{\mathcal{R}}=2{\int }_{\Omega }\nabla w·\nabla (\Delta w-{\partial }_{t}q)dx=-2{\parallel \Delta w\parallel }_2^2-2{\int }_{\Omega }\nabla w·\nabla {\partial }_{t}qdx.$$

Cauchy–Schwarz and Young with parameter ${\lambda }_1$ give

$$2|{\int }_{\Omega }\nabla w·\nabla {\partial }_{t}qdx|\le {\lambda }_1{\parallel \nabla w\parallel }_2^2+{\lambda }_1^{-1}{\parallel \nabla {\partial }_{t}q\parallel }_2^2.$$

Using ${\parallel \Delta w\parallel }_2^2\ge {\lambda }_1{\parallel \nabla w\parallel }_2^2$ yields (167); then Grönwall implies (168). □

Corollary 6.1

(Steady–state tube radius). If ${lim\; sup}_{t\to \infty }{\parallel \nabla {\partial }_{t}q\left(t\right)\parallel }_{L^2}\le \overline{M}<\infty$, then

$$\underset{t\to \infty }{lim\; sup}\mathcal{R}\left(t\right)\le \frac{{\overline{M}}^2}{{\lambda }_1^2}.$$

In particular, $\mathcal{R}\left(t\right)\to 0$ whenever q becomes asymptotically stationary.

Remark 6.3

(Schrödinger continuity law and a priori bounds for M). For the time–dependent Schrödinger equation

$$i\hslash {\partial }_t\Psi =\left(-\frac{{\hslash }^2}{2m}\Delta +V\left(x\right)\right)\Psi \mathit{on}\Omega ,$$

the probability density $q={|\Psi |}^2$ and current $J=\frac{\hslash }{m}\mathrm{Im}({\Psi }^{\ast }\nabla \Psi )$ satisfy the continuity law ${\partial }_{t}q+\nabla ·J=0$. Hence

$$\nabla {\partial }_{t}q=-\nabla \nabla ·J=-\frac{\hslash }{m}\mathrm{Im}\left(\nabla {\Psi }^{\ast }\Delta \Psi +{\Psi }^{\ast }\nabla \Delta \Psi \right),$$

and by Hölder/Sobolev embeddings on bounded Ω (e.g. $H^2(\Omega )\hookrightarrow L^{\infty }(\Omega )$ in $d\le 3$),

$$\parallel \nabla {\partial }_t{q\parallel }_{L^2}\le \frac{\hslash }{m}\left({\parallel \nabla \Psi \parallel }_{L^{\infty }}{\parallel \Delta \Psi \parallel }_{L^2}+{\parallel \Psi \parallel }_{L^{\infty }}{\parallel \nabla \Delta \Psi \parallel }_{L^2}\right)\le C\frac{\hslash }{m}{\parallel \Psi \parallel }_{H^3}^2.$$

Therefore, if $V\in W^{3,\infty }(\Omega )$ and ${\Psi }_0\in H^3(\Omega )$, standard commutator estimates show that the Schrödinger flow preserves $H^3$ (hence ${sup}_{t\ge 0}{\parallel \Psi \left(t\right)\parallel }_{H^3}<\infty$), and one obtains a uniform bound $M\le C(\hslash /m){sup}_t{\parallel \Psi \left(t\right)\parallel }_{H^3}^2$. When q becomes asymptotically stationary, $M\to 0$ and (168) collapses exponentially with rate ${\lambda }_1$.

6.2. Residual–Entropy Arrow of Time

The DSFL residual

$$\mathcal{R}\left(t\right)={\int }_{\Omega }|P(x,t)-\nabla \rho (x,t){|}^{2}dx$$

(169)

plays a dual role: it is a quadratic Lyapunov functional (structural energy of misalignment) and, via a monotone transform, a surrogate “entropy” that certifies irreversibility.

Definition 6.1

(Residual entropy). Fix ${\mathcal{R}}_0>0$ and $R_{\ast }\in (0,1)$. Theresidual entropyis

$$S_R\left(t\right):=-log\left(\frac{\mathcal{R}\left(t\right)}{{\mathcal{R}}_0}+R_{\ast }\right).$$

(170)

• Why this transform?

$S_R$ is smooth, strictly increasing in $\mathcal{R}\mapsto 0^{+}$, and avoids singularities at $\mathcal{R}=0$ via the offset $R_{\ast }$. Moreover, if $\mathcal{R}$ decays exponentially, $S_R$ grows linearly in time (see below), which is convenient for data analysis and for defining an intrinsic clock$\tau \left(t\right)=S_R\left(t\right)-S_R\left(0\right)$.

Proposition 6.2

(Monotone increase of $S_R$ under DSFL). If the DSFL inequality holds, $\dot{\mathcal{R}}\left(t\right)\le -\alpha \mathcal{R}\left(t\right)$ with $\alpha >0$, then

$${\dot{S}}_R\left(t\right)=-\frac{\dot{\mathcal{R}}\left(t\right)}{\mathcal{R}\left(t\right)+{\mathcal{R}}_0{R}_{\ast }}\ge \frac{\alpha \mathcal{R}\left(t\right)}{\mathcal{R}\left(t\right)+{\mathcal{R}}_0{R}_{\ast }}\ge 0,$$

(171)

with strict inequality whenever $\mathcal{R}\left(t\right)>0$. If $\mathcal{R}\left(t\right)=\mathcal{R}\left(0\right)e^{-\alpha t}$, then

$$S_R\left(t\right)=-log\left(R_{\ast }+\frac{\mathcal{R}\left(0\right)}{{\mathcal{R}}_0}{e}^{-\alpha t}\right)=S_R\left(0\right)+\alpha t+log\left(\frac{1+\frac{\mathcal{R}\left(0\right)}{{\mathcal{R}}_0{R}_{\ast }}}{1+\frac{\mathcal{R}\left(0\right)}{{\mathcal{R}}_0{R}_{\ast }}{e}^{-\alpha t}}\right),$$

(172)

and the last logarithmic term is bounded and vanishes as $t\to \infty$, so $S_R\left(t\right)=\alpha t+O\left(1\right)$.

Proof. 

Differentiate $S_R$ and insert $\dot{\mathcal{R}}\le -\alpha \mathcal{R}$. Positivity is immediate since $\mathcal{R},{\mathcal{R}}_0,R_{\ast }>0$. The linear growth follows by direct algebra. □

Remark 6.4

(Time–varying rates and perturbed dynamics (ISS form)). (i) Time–varying rate.If $\dot{\mathcal{R}}\le -\alpha \left(t\right)\mathcal{R}$ with $\alpha (·)\ge 0$ measurable and ${\int }_0^{\infty }\alpha \left(t\right)dt=+\infty$, then $S_R$ is increasing and diverges to $+\infty$. If $\alpha \left(t\right)\ge \underline{\alpha }>0$, then $S_R\left(t\right)\ge \underline{\alpha }t+O\left(1\right)$.

• (ii) Small forcing. If $\dot{\mathcal{R}}\le -\alpha \mathcal{R}+{\epsilon }^{2}u\left(t\right)$ with $u\in L_{\mathrm{loc}}^1$, then

$${\dot{S}}_R\left(t\right)\ge \frac{\alpha \mathcal{R}\left(t\right)}{\mathcal{R}\left(t\right)+{\mathcal{R}}_0{R}_{\ast }}-\frac{{\epsilon }^{2}u\left(t\right)}{\mathcal{R}\left(t\right)+{\mathcal{R}}_0{R}_{\ast }}.$$

(173)

Therefore, on any interval where $\mathcal{R}\left(t\right)\ge \underline{R}>0$, one has ${\dot{S}}_R\left(t\right)\ge \frac{\alpha \underline{R}}{\underline{R}+{\mathcal{R}}_0{R}_{\ast }}-\frac{{\epsilon }^{2}u\left(t\right)}{\underline{R}+{\mathcal{R}}_0{R}_{\ast }}.$ If $u\in L^1(0,\infty )$, then $S_R\left(t\right)$ still diverges at least linearly modulo a bounded correction; in particular, ${lim\; inf}_{t\to \infty }{\dot{S}}_R\left(t\right)\ge 0$ and ${lim\; sup}_{t\to \infty }\mathcal{R}\left(t\right)\lesssim {\epsilon }^2{\parallel u\parallel }_{L^1}$.

• Near–alignment connection to classical entropies.

When $\rho$ and a target q are strictly positive densities with $\int \rho =\int q=1$ and $q\ge \underline{q}>0$, the Kullback–Leibler divergence satisfies the second–order Taylor bound near equilibrium:

$$D(\rho \parallel q)=\int \rho log\frac{\rho }{q}=\frac{1}{2}\int \frac{{(\rho -q)}^2}{q}{dx+O(\parallel \rho -q\parallel }_{L^2}^3)\le \frac{1}{2\underline{q}}{\parallel \rho -q\parallel }_{L^2}^2{+o(\parallel \rho -q\parallel }_{L^2}^2).$$

(174)

On bounded domains with Poincaré constant ${\lambda }_1>0$ and $\int (\rho -q)=0$, ${\parallel \rho -q\parallel }_{L^2}^2\le {\lambda }_1^{-1}{\parallel \nabla (\rho -q)\parallel }_{L^2}^2={\lambda }_1^{-1}\mathcal{R}.$ Thus, near alignment,

$$D(\rho \parallel q)\lesssim {\parallel \rho -q\parallel }_{L^2}^2\lesssim \mathcal{R}\left(t\right),$$

(175)

and hence $S_R$—which is monotone in $\mathcal{R}$—tracks the decay of leading–order deviations of classical relative entropy.

Remark 6.5

(Information–geometric view). In the quadratic regime, the Fisher information $I(\rho \parallel q)={\int |\nabla log(\rho /q)|}^2\rho dx$ linearizes to a Dirichlet form on $w=\rho -q$, and the Hellinger/Wasserstein–2 metrics become equivalent to $L^2$/$H^{-1}$ distances modulo weights. Under DSFL, $\mathcal{R}$ provides asectoralLyapunov that is locally equivalent to these information distances; therefore $S_R$ inherits the arrow–of–time interpretation without invoking stochastic typicality.

• Intrinsic time and reparametrization.

Define the intrinsic clock $\tau \left(t\right):=S_R\left(t\right)-S_R\left(0\right)$. Under DSFL with constant rate $\alpha >0$, $\tau \left(t\right)=\alpha t+O\left(1\right)$; under time–varying $\alpha \left(t\right)$, one has $\tau \left(t\right)={\int }_0^t\frac{\alpha \left(s\right)\mathcal{R}\left(s\right)}{\mathcal{R}\left(s\right)+{\mathcal{R}}_0{R}_{\ast }}ds,$ which is strictly increasing and unbounded if ${\int }_0^{\infty }\alpha \left(s\right)ds=+\infty$. This reparametrization is useful for comparing trajectories across sectors: observables that are Lipschitz in the sector distance (Cor. 4.4) will contract exponentially in $\tau$.

• Relation to Boltzmann’s H–functional in classical and quantum settings.

We compare the residual–entropy arrow $S_R$ with classical and quantum entropy production principles.

Classical Reversible Diffusions (Bakry–Émery)

Let ${\left({\mathsf{T}}_t\right)}_{t\ge 0}$ be a reversible diffusion on a bounded domain with invariant density $q>0$, carré du champ $\Gamma$ and Dirichlet form $\mathcal{E}\left(f\right)=\int \Gamma \left(f\right)qdx$. For a solution ${\rho }_t$ of the forward equation with $\int {\rho }_t=\int q=1$ define:

$$\mathrm{Relative}\mathrm{entropy}\text{:}D({\rho }_t\parallel q)=\int {\rho }_{t}log\frac{{\rho }_t}{q}dx,\mathrm{Fisher}\mathrm{information}\text{:}I({\rho }_t\parallel q)=\int \Gamma (log({\rho }_t/q)){\rho }_{t}dx.$$

(176)

Then $\dot{D}({\rho }_t\parallel q)=-I({\rho }_t\parallel q)$ and, under the Bakry–Émery curvature condition ${\Gamma }_2\ge \rho \Gamma$ with $\rho >0$ (log–Sobolev constant),

$$I(\rho \parallel q)\ge 2\rho D(\rho \parallel q)⟹D({\rho }_t\parallel q)\le e^{-2\rho t}D({\rho }_0\parallel q).$$

(177)

Residual vs. entropy near equilibrium. Assume $q\ge \underline{q}>0$ and set $w=\rho -q$ with $\int w=0$. A second–order Taylor expansion yields

$$D(\rho \parallel q)=\frac{1}{2}\int \frac{w^2}{q}dx+{O(\parallel w\parallel }_{L^2}^3)\le \frac{1}{2\underline{q}}{\parallel w\parallel }_{L^2}^2+{o(\parallel w\parallel }_{L^2}^2).$$

(178)

By Poincaré, ${\parallel w\parallel }_{L^2}^2\le {\lambda }_1^{-1}{\parallel \nabla w\parallel }_{L^2}^2={\lambda }_1^{-1}\mathcal{R}$, hence

$$D(\rho \parallel q)\lesssim \mathcal{R}\mathrm{as}\mathcal{R}\to 0,$$

(179)

so $S_R$ (a decreasing function of $\mathcal{R}$) tracks the decay of $D(\rho \parallel q)$ near alignment.

Rates and regimes. - Log–Sobolev (strong): If ${\Gamma }_2\ge \rho \Gamma$, then both D and $\mathcal{R}$ decay exponentially: $D\le e^{-2\rho t}{D}_0$ and $\mathcal{R}\le e^{-2\lambda t}{\mathcal{R}}_0$ with the Poincaré constant $\lambda >0$. In many Gaussian/OU cases, $\rho =\lambda$; in general $\rho \le \lambda$. Thus $S_R$ and H–theorem arrows coincide up to constants. - Poincaré only (weak): If only $\mathrm{Var}\le {\lambda }^{-1}\mathcal{E}$ holds (no LSI), DSFL still gives $\mathcal{R}\left(t\right)\le e^{-2\lambda t}\mathcal{R}\left(0\right)$ and a strictly increasing $S_R$, while classical entropy methods may not yield exponential decay of D. The DSFL arrow thus persists beyond the LSI regime.

Entropy production vs. residual production. $\dot{D}=-I$ and (under LSI) $I\ge 2\rho D$; by contrast

$${\dot{S}}_R=-\frac{\dot{\mathcal{R}}}{\mathcal{R}+{\mathcal{R}}_0{R}_{\ast }}\ge \frac{\alpha \mathcal{R}}{\mathcal{R}+{\mathcal{R}}_0{R}_{\ast }}\stackrel{\mathcal{R}\downarrow 0}{\sim }\alpha \frac{\mathcal{R}}{{\mathcal{R}}_0{R}_{\ast }}.$$

(180)

Thus in the asymptotic regime both D and $S_R$ evolve linearly in their natural time scales (t for D with rate $2\rho$, and t for $S_R$ with slope $\alpha$), while $D\lesssim \mathcal{R}$ by (179).

Reversible Quantum Markov Semigroups (QMS)

Let $\left({\mathsf{T}}_t\right)$ be a reversible QMS on $(\mathcal{M},\omega )$ with generator $\mathcal{L}$ and gap $\lambda >0$ on $L^2{(\mathcal{N},\omega )}^{\perp }$. Consider two divergences:

$$\mathrm{Hilbert}\text{–}\mathrm{Schmidt}{\chi }^2\text{:}{\chi }_2(\sigma \parallel \omega ):={\parallel \sigma -\omega \parallel }_{2,\omega }^2,\mathrm{Umegaki}\mathrm{entropy}\text{:}D(\sigma \parallel \omega ):=\mathrm{Tr}\sigma (log\sigma -log\omega ).$$

(181)

- Variance law (DSFL): The residual ${\mathcal{R}}_{\omega }\left(X\right)={\parallel X-{\mathsf{E}}_{\mathcal{N}}X\parallel }_{2,\omega }^2$ decays as $e^{-2\lambda t}$ (Theorem 4.2), giving a strictly increasing $S_R$. - Quantum H–theorem: If a quantum log–Sobolev inequality (QLSI) holds with constant $\rho >0$, then $D({\sigma }_t\parallel \omega )\le e^{-2\rho t}D({\sigma }_0\parallel \omega )$ (entropy contraction).

Near–equilibrium comparison. For faithful $\omega$, the second variation of $D(\sigma \parallel \omega )$ at $\omega$ is the Bogoliubov–Kubo–Mori (BKM) metric; in finite dimension,

$$D(\sigma \parallel \omega )=\frac{1}{2}{\parallel \sigma -\omega \parallel }_{2,\omega }^2{+o(\parallel \sigma -\omega \parallel }_{2,\omega }^2)\Rightarrow D(\sigma \parallel \omega )\simeq \frac{1}{2}{\chi }_2(\sigma \parallel \omega )$$

(182)

in a neighborhood of $\omega$. Hence D and the residual (and therefore $S_R$) are locally equivalent—they define the same arrow close to equilibrium.

Rates and regimes. - QLSI (strong): If QLSI holds with constant $\rho$, then both D and ${\mathcal{R}}_{\omega }$ decay exponentially; typically $\rho \le \lambda$, and in dephasing/Gaussian cases $\rho =\lambda$. - Poincaré only (weak): If only the spectral gap is known (no QLSI), the DSFL arrow survives: ${\mathcal{R}}_{\omega }$ decays exponentially and $S_R$ increases, while D may lack a uniform exponential bound.

• Summary: when do the arrows coincide?

• Near alignment (classical or quantum):$D\lesssim \mathcal{R}$ and $D\simeq c\mathcal{R}$ locally, hence $S_R$ and H–theorem describe the same decay up to constants.
• Under (quantum) log–Sobolev:D and $\mathcal{R}$ both decay exponentially, with rates $2\rho$ and $2\lambda$. In Gaussian/dephasing models $\rho =\lambda$ (⇒ identical envelopes); generally $\rho \le \lambda$.
• Only Poincaré available: DSFL still gives an exponential variance contraction (hence a strict $S_R$ arrow), whereas entropy contraction can be weaker or unavailable.

• Practical readouts.

For data/experiment, $S_R$ is often easier to estimate (it only requires quadratic residuals) and provides a robust monotone even when D is hard to evaluate or lacks exponential decay. When LSI holds, $S_R$ and D are interchangeable up to constants; otherwise $S_R$ supplies a structural arrow beyond the reach of entropy methods.

6.3. Einstein Balance as Geometric Attractor

Let $(\mathcal{U},g)$ be a spacetime region with metric $g_{\mu \nu }$ and stress–energy tensor $T_{\mu \nu }$. Define the geometric residual

$${\mathcal{R}}_{\mathrm{geom}}[g,T]={\int }_{\mathcal{U}}\parallel G_{\mu \nu }\left[g\right]-\kappa T_{\mu \nu }{\parallel }_g^{2}d{\mu }_g,\kappa =8\pi G/c^4,$$

(183)

where ${\parallel ·\parallel }_g$ is the pointwise norm induced by g and $G_{\mu \nu }$ is the Einstein tensor. The residual (183) vanishes iff the Einstein balance $G=\kappa T$ holds pointwise.

• Gauge and slice issues.

In full Lorentzian signature the Einstein evolution is hyperbolic and diffeomorphism-invariant; a direct Lyapunov descent of (183) is obstructed by gauge freedom and hyperbolicity. On a compact Riemannian slice $({\Sigma }^3,\gamma )$ and in DeTurck gauge (Section 4.7), the linearized operator becomes elliptic on the physical (gauge-orthogonal) subspace. In that regime the residual

$${\mathcal{R}}_{\mathrm{geom}}\left(t\right)={\int }_{\Sigma }\parallel G\left[\gamma \left(t\right)\right]-\kappa T{\parallel }_{\gamma \left(t\right)}^{2}d{\mu }_{\gamma \left(t\right)}$$

(184)

is a bona fide slice Lyapunov functional (modulo gauge equivalences). We now restate and instantiate the resulting attractor facts.

Theorem 6.2

(Slice attractor: small data, DeTurck gauge). Let $({\Sigma }^3,\overline{\gamma })$ be a compact Riemannian 3–manifold and T a smooth, time-independent, divergence–free source w.r.t. $\overline{\gamma }$. Assume the target balance $G\left[\overline{\gamma }\right]=\kappa T$ and that the Lichnerowicz–DeTurck operator on the physical subspace has a spectral gap ${\lambda }_{\mathrm{GR}}>0$:

$${\langle h,{\mathcal{L}}_{\overline{\gamma }}h\rangle }_{L^2\left(\overline{\gamma }\right)}\ge {\lambda }_{\mathrm{GR}}{\parallel h\parallel }_{L^2\left(\overline{\gamma }\right)}^2\mathit{for}\mathit{all}h\perp \mathit{gauge}\mathit{directions}.$$

(185)

Then for the Einstein–DeTurck–source flow (89) with sufficiently small initial perturbation $h\left(0\right)=\gamma \left(0\right)-\overline{\gamma }$ in $H^k$ ($k\ge 4$),

$$\frac{d}{dt}{\mathcal{R}}_{\mathrm{geom}}\left(t\right)\le -2c{\lambda }_{\mathrm{GR}}{\mathcal{R}}_{\mathrm{geom}}\left(t\right)\Rightarrow {\mathcal{R}}_{\mathrm{geom}}\left(t\right)\le e^{-2c{\lambda }_{\mathrm{GR}}t}{\mathcal{R}}_{\mathrm{geom}}\left(0\right),$$

(186)

for some $c\in (0,1)$ depending only on $(\Sigma ,\overline{\gamma })$ and the smallness radius. In particular, $G\left[\gamma \right(t\left)\right]=\kappa T$ in $L^2(\Sigma )$ as $t\to \infty$, and $\gamma \left(t\right)\to \overline{\gamma }$ modulo diffeomorphisms.

Sketch (instantiation of Section 4.7). 

Linearize (89): ${\partial }_{t}h=-{\mathcal{L}}_{\overline{\gamma }}h+\mathcal{N}\left(h\right)$ with $\mathcal{N}\left(h\right)=O(|h||{\nabla }^{2}h|+|\nabla h{|}^2)$. Energy estimates on $E\left(t\right):=\parallel {\mathcal{L}}_{\overline{\gamma }}{h\parallel }_{L^2}^2$ give $\dot{E}\left(t\right)\le -2{\lambda }_{\mathrm{GR}}E\left(t\right)+\left(\mathrm{quadratic}\right)\le -2c{\lambda }_{\mathrm{GR}}E\left(t\right)$ for small data. Near $\overline{\gamma }$, ${\mathcal{R}}_{\mathrm{geom}}\left(t\right)\simeq \frac{1}{4}{\parallel {\mathcal{L}}_{\overline{\gamma }}h\parallel }_{L^2}^2$ (Section 4.7), whence the claim. □

Corollary 6.2

(Einstein backgrounds with positive physical gap). If $(\Sigma ,\overline{\gamma })$ is an Einstein metric with positive physical gap ${\lambda }_{\mathrm{GR}}>0$ (e.g. compact spaceforms with appropriate sources), then for all sufficiently small perturbations satisfying the momentum constraints, the curvature–matter misfit decays exponentially and $\gamma \left(t\right)$ converges modulo diffeomorphisms to $\overline{\gamma }$.

Remark 6.6

(FRW-type slices). On a compact FRW slice (spatial section a compact spaceform), the physical gap typically reduces to ascalarspectral gap for the Lichnerowicz–DeTurck operator acting on TT-modes; small scalar/vector perturbations are damped by the same mechanism. The attractor is the balanced background $G=\kappa T$ (e.g. ΛCDM source) at the slice level.

• Robustness to small forcing (ISS).

If the source term acquires a small time-dependent perturbation (mean-zero in the physical subspace), the same calculation yields an input–to–state stability bound:

$${\dot{\mathcal{R}}}_{\mathrm{geom}}\left(t\right)\le -2c{\lambda }_{\mathrm{GR}}{\mathcal{R}}_{\mathrm{geom}}\left(t\right)+C{\epsilon }^2{\parallel \Xi \left(t\right)\parallel }_{L^2}^2,$$

(187)

so ${lim\; sup}_{t\to \infty }{\mathcal{R}}_{\mathrm{geom}}\left(t\right)\le \frac{C{\epsilon }^2}{2c{\lambda }_{\mathrm{GR}}}{\parallel \Xi \parallel }_{L_t^2{L}_x^2}^2$.

• Physical interpretation.

Within a slice description, the equality $G=\kappa T$ acts as a sectoral equilibrium: perturb the geometry or the source slightly, and the DeTurck–gauge flow suppresses the misfit at an exponential rate controlled by a geometric gap. This realizes the Einstein equations as the endpoint of Lyapunov suppression of $G-\kappa T$, not a prior axiom.

A Covariant DSFL Program (What Remains and How)

A fully covariant DSFL would assert monotone decrease of a diffeomorphism-invariant residual along a hyperbolic (Lorentzian) gauge–fixed evolution, without relying on a Riemannian foliation. Here is a concrete roadmap.

• (C1) Covariant residual and gauge.

A direct spacetime residual ${\mathcal{R}}_{\mathrm{cov}}[g,T]={\int }_{\mathcal{U}}{\parallel G-\kappa T\parallel }_g^{2}d{\mu }_g$ is diffeomorphism-invariant, but its time derivative under the Einstein evolution is not sign-definite due to gauge and hyperbolicity. One needs a hyperbolic, constraint–damped formulation (e.g. generalized harmonic or Z4) so that the physical part of $G-\kappa T$ evolves with controllable energy.

• (C2) Candidate hyperbolic DSFL flow.

In generalized harmonic gauge $H_{\mu }\left(g\right)=0$, the Einstein equations reduce to quasi-linear wave equations for $g_{\mu \nu }$. Add constraint damping ($-{\eta }_1{Z}_{\mu }$ terms in Z4), and consider a “gradient wave” evolution of the residual:

$${\square }_g{g}_{\mu \nu }+\left(\mathrm{nonlinearities}\right)=-{\eta }_0{\Pi }_{\mathrm{phys}}\left(G_{\mu \nu }-\kappa T_{\mu \nu }\right),$$

(188)

where ${\Pi }_{\mathrm{phys}}$ projects onto the physical (constraint-satisfying, gauge-orthogonal) subspace. The goal is an energy identity

$$\frac{d}{dt}{\mathcal{E}}_{\mathrm{cov}}\left(t\right)=-2{\eta }_0{\parallel G-\kappa T\parallel }_{L^2\left({\Sigma }_t\right)}^2+\left(\mathrm{controlled}\right)\le -2{\eta }_0{\mathcal{R}}_{\mathrm{geom}}^{\left({\Sigma }_t\right)}\left(t\right)$$

(189)

for a covariant energy ${\mathcal{E}}_{\mathrm{cov}}$ combining Bel–Robinson type energies and constraint energies.

• (C3) Covariant Lyapunov functionals.

Two natural ingredients: (i) a Bel–Robinson energy $E_{\mathrm{BR}}$ for the Weyl curvature (positive on slices), and (ii) a “misfit energy” $E_{\mathrm{misfit}}\left[{\Sigma }_t\right]={\int }_{{\Sigma }_t}{\parallel G-\kappa T\parallel }^{2}d{\mu }_{\gamma \left(t\right)}$. A weighted sum $E_{\mathrm{cov}}:=E_{\mathrm{BR}}+\alpha E_{\mathrm{misfit}}+\beta E_{\mathrm{constr}}$ (constraints) is a plausible Lyapunov, provided damping terms control gauge/constraint errors.

• (C4) Small-data regimes.

On backgrounds with known nonlinear stability (e.g. Minkowski, de Sitter), one can hope to prove that for small perturbations and suitable damping, $E_{\mathrm{cov}}$ satisfies

$$\frac{d}{dt}{E}_{\mathrm{cov}}\left(t\right)\le -\underline{c}{E}_{\mathrm{misfit}}\left(t\right)\le -{\underline{c}}^{\prime }{\mathcal{R}}_{\mathrm{geom}}^{\left({\Sigma }_t\right)}\left(t\right),$$

(190)

hence exponential (or at least integrable) decay of the misfit.

• (C5) Obstacles and outlook.

The chief obstacles are: (a) hyperbolic energy methods only give integral decay unless one has a spacetime Morawetz (or red-shift) inequality; (b) projecting out gauge and constraints covariantly is delicate; (c) asymptotics (non-compact $\Sigma$) need appropriate weighted energies. Nevertheless, in small-data regimes with damping (as in Z4/CCZ4 numerical relativity), the covariant DSFL appears within reach.

Remark 6.7

(Covariant outlook). A fully covariant DSFL would assert monotone decrease of ${\mathcal{R}}_{\mathrm{geom}}$ along a diffeomorphism-invariant, hyperbolic, constraint-damped evolution on the space of Lorentzian metrics, without a foliation. Constructing such a Lyapunov structure is open; the slice results above substantiate the attractor picture in an analytically controlled (elliptic) regime and point to the ingredients needed in the covariant case.

6.4. Measurement Context and Pointer Algebras (Sectorization)

In quantum applications the sector is determined by the measurement context. Formally, choose an abelian von Neumann subalgebra (pointer algebra) $\mathcal{N}\subset \mathcal{M}$ and let ${\mathsf{E}}_{\mathcal{N}}:\mathcal{M}\to \mathcal{N}$ be the $\omega$–preserving conditional expectation (Heisenberg picture). For a normal state $\sigma$ (Schrödinger picture), the restriction ${\sigma |}_{\mathcal{N}}$ corresponds via the Gelfand isomorphism to a probability law $q_{\sigma }$ on a standard outcome space $(Y,{\mu }_Y)$ with $\mathcal{N}\simeq L^{\infty }(Y,{\mu }_Y)$. In this sector, the empirical pointer distribution ${\rho }_Y(·,t)$ is compared to $q_{\sigma }\left(t\right)$ through a Dirichlet structure $({\mathcal{E}}_Y,\mathsf{D}\left({\mathcal{E}}_Y\right))$ driven by a pointer generator $L_Y$:

$${\partial }_t{\rho }_Y=-L_Y\left({\rho }_Y-q_{\sigma }\left(t\right)\right),{\mathcal{R}}_Y\left(t\right)={\mathcal{E}}_Y\left({\rho }_Y\left(t\right)-q_{\sigma }\left(t\right)\right).$$

(191)

Here $L_Y$ is a (sub)Markov generator symmetric in $L^2\left({\mu }_Y\right)$ with ${\mathcal{E}}_Y\left(f\right):={\langle f,-L_{Y}f\rangle }_{L^2\left({\mu }_Y\right)}$ and ${\int }_{Y}fd{\mu }_Y=0$.

• Pointer–space DSFL and spectral gap.

We first record the pointer analogue of the DSFL law.

Proposition 6.3

(Pointer–space DSFL). Assume $L_Y$ is self–adjoint and nonnegative on $L^2\left({\mu }_Y\right)$ with spectral gap ${\lambda }_Y>0$ on mean–zero functions:

$${\parallel f\parallel }_{L^2\left({\mu }_Y\right)}^2\le {\lambda }_Y^{-1}{\mathcal{E}}_Y\left(f\right)\forall f\in \mathsf{D}\left({\mathcal{E}}_Y\right)\cap \left\{\int fd{\mu }_Y=0\right\}.$$

(192)

Consider (191) with $q_{\sigma }\left(t\right)\equiv q_{\sigma }$ (static). Then the pointer residual decays exponentially,

$${\mathcal{R}}_Y\left(t\right)\le e^{-2{\lambda }_{Y}t}{\mathcal{R}}_Y\left(0\right),$$

(193)

and, by Poincaré on Y, $\parallel {\rho }_Y\left(t\right)-q_{\sigma }{\parallel }_{L^2\left({\mu }_Y\right)}^2\le {\lambda }_Y^{-1}{\mathcal{R}}_Y\left(t\right)$.

Proof. 

Let $w:={\rho }_Y-q_{\sigma }$; then ${\int }_{Y}wd{\mu }_Y=0$ and ${\partial }_{t}w=-L_{Y}w$. Compute ${\dot{\mathcal{R}}}_Y\left(t\right)=\frac{d}{dt}{\mathcal{E}}_Y\left(w\right)=\langle w,-L_Y{\partial }_{t}w\rangle +\langle {\partial }_{t}w,-L_{Y}w\rangle =-2\langle w,L_Y^{2}w\rangle$. Since $L_Y$ is self–adjoint and nonnegative, $\langle w,L_Y^{2}w\rangle \ge {\lambda }_Y\langle w,L_{Y}w\rangle ={\lambda }_Y{\mathcal{E}}_Y\left(w\right)$ on the gap subspace (functional calculus). Therefore ${\dot{\mathcal{R}}}_Y\le -2{\lambda }_Y{\mathcal{R}}_Y$ and Grönwall yields the claim. Poincaré gives the $L^2$ bound. □

Remark 6.8

(Time–varying pointer $q_{\sigma }\left(t\right)$). If $q_{\sigma }=q_{\sigma }\left(t\right)$ varies, one obtains a tracking inequality analogous to Lemma 6.1:

$${\dot{\mathcal{R}}}_Y\left(t\right)\le -{\lambda }_Y{\mathcal{R}}_Y\left(t\right)+\frac{\parallel {\partial }_t{q}_{\sigma }{\left(t\right)\parallel }_{L^2\left({\mu }_Y\right)}^2}{{\lambda }_Y},$$

(194)

hence ${\mathcal{R}}_Y\left(t\right)$ tracks $q_{\sigma }\left(t\right)$ inside a tube of radius $O\left({sup}_t{\parallel {\partial }_t{q}_{\sigma }\left(t\right)\parallel }_{L^2}^2/{\lambda }_Y^2\right)$.

• Operator–algebraic variance and the pointer projection.

We now relate the DSFL on $\mathcal{M}$ to the pointer DSFL on Y.

Proposition 6.4

(OA variance contracts to the pointer sector). Let $\left({\mathsf{T}}_t\right)$ be a reversible QMS on $(\mathcal{M},\omega )$ with spectral gap $\lambda >0$ on $L^2{(\mathcal{N},\omega )}^{\perp }$ and let ${\mathsf{E}}_{\mathcal{N}}:\mathcal{M}\to \mathcal{N}$ be the ω–preserving conditional expectation. Then for any $X\in L^2\left(\omega \right)$,

$$\parallel {\mathsf{T}}_{t}X-{\mathsf{E}}_{\mathcal{N}}{X\parallel }_{2,\omega }^2\le e^{-2\lambda t}{\parallel X-{\mathsf{E}}_{\mathcal{N}}X\parallel }_{2,\omega }^2.$$

(195)

In particular, for abelian $\mathcal{N}\simeq L^{\infty }(Y,{\mu }_Y)$ and observables in the sector, the noncommutative variance contracts at rate $2\lambda$ down to the classical pointer law $q_{\sigma }$.

Proof. 

This is Theorem 4.2 (operator–algebraic DSFL ⇔ Poincaré gap) restricted to $L^2{(\mathcal{N},\omega )}^{\perp }$; the conditional expectation is the $L^2\left(\omega \right)$ orthogonal projection, so the $L^2$ variance relative to $\mathcal{N}$ decays as $e^{-2\lambda t}$. □

• Bridge to PDE residuals (position sector).

When $\mathcal{N}$ is the position pointer algebra on a bounded domain $\Omega \subset {\mathbb{R}}^d$, the abelian identification gives $Y=\Omega$, ${\mu }_Y$ the Lebesgue measure (or a reference measure), and $q_{\sigma }\left(x\right)={|\Psi \left(x\right)|}^2$. The pointer generator $L_Y$ is the Laplacian (or a diffusion generator), with ${\mathcal{E}}_Y\left(f\right)={\int }_{\Omega }{|\nabla f|}^{2}dx$ and gap ${\lambda }_1>0$ on mean–zero functions. Then the PDE residual is

$${\mathcal{R}}_Y\left(t\right)={\int }_{\Omega }|\nabla (\rho -{|\Psi |}^2{)|}^{2}dx.$$

(196)

Poincaré on $\Omega$ yields the $L^2$ sandwich

$${\lambda }_1{\parallel \rho -|\Psi |}^2{\parallel }_{L^2(\Omega )}^2\le {\int }_{\Omega }|\nabla (\rho -{|\Psi |}^2{)|}^{2}dx\le {C\parallel \rho -|\Psi |}^2{\parallel }_{H^1(\Omega )}^2,$$

(197)

and Proposition 6.3 gives ${\mathcal{R}}_Y\left(t\right)\le e^{-2{\lambda }_{1}t}{\mathcal{R}}_Y\left(0\right)$, hence $L^2$ contraction to the Born law.

Remark 6.9

(Contextuality and attractors). The choice of $\mathcal{N}$ encapsulatesthe measurement context (observable/POVM via Naimark dilation). DSFL contracts to that context: changing $\mathcal{N}$ changes the attractor (e.g. position vs. momentum). Operator–algebraically, ${\mathsf{E}}_{\mathcal{N}}$ is the projection onto the sector, and Theorem 4.2 shows that a noncommutative Poincaré gap is equivalent to exponential decay of the noncommutative variance relative to $\mathcal{N}$.

• Putting it together (context ⇒ sector ⇒ rate).

Theorem 6.3

(Contextual DSFL pipeline). Fix a pointer algebra $\mathcal{N}\subset \mathcal{M}$ (context) with conditional expectation ${\mathsf{E}}_{\mathcal{N}}$. If the reversible QMS on $(\mathcal{M},\omega )$ has a gap $\lambda >0$ on $L^2{(\mathcal{N},\omega )}^{\perp }$, then the OA residual decays at rate $2\lambda$ toward the sector. On the abelian sector Y, if the pointer generator $L_Y$ has gap ${\lambda }_Y>0$, then the pointer residual ${\mathcal{R}}_Y$ decays at rate $2{\lambda }_Y$ toward $q_{\sigma }$. Consequently, in the position context on bounded Ω, DSFL yields $L^2$ alignment to the Born law with envelope $e^{-2{\lambda }_{1}t}$.

Proof. 

Combine Proposition 6.4 with Proposition 6.3 and the Poincaré sandwich on $\Omega$. □

Remark 6.10

(Changing context changes the attractor). If one replaces the position pointer algebra by, e.g., the momentum algebra (Fourier–diagonal), then Y is the momentum space and $q_{\sigma }$ is the momentum distribution. Proposition 6.3 applies verbatim with the corresponding $L_Y$ (e.g. a diffusion on momentum space). Thus,the attractor is contextual: it is determined by the measurement algebra $\mathcal{N}$.

• Same core, different attractor: why context matters but the law does not.

The core of DSFL is a context–independent contraction law for a quadratic residual:

$$\left(\mathrm{Propagation}\right)\dot{\mathcal{R}}\le 0\mathrm{and}(\mathrm{Gap}/\mathrm{Coercivity})\dot{\mathcal{R}}\le -\alpha \mathcal{R},$$

(198)

where $\alpha >0$ is a sectoral constant (spectral gap/coercivity). This statement does not depend on which measurement context is chosen. What does depend on the context is: (i) the projection (or classicalization) map defining the equilibrium manifold (the attractor), and (ii) the value of the rate $\alpha$ (the spectral gap in that context).

We formalize this in three steps.

Definition 6.2

(Context–dependent residuals and attractors). Let $\mathcal{N}\subset \mathcal{M}$ be an abelian pointer algebra (measurement context) with ω–preserving conditional expectation ${\mathsf{E}}_{\mathcal{N}}$. Theoperator–algebraic residualis

$${\mathcal{R}}_{\omega }^{\left(\mathcal{N}\right)}\left(X\right):={\parallel X-{\mathsf{E}}_{\mathcal{N}}X\parallel }_{2,\omega }^2,$$

(199)

and the correspondingattractoris the fixed subspace $L^2(\mathcal{N},\omega )$ (equilibrium manifold). On the abelian sector Y with $\mathcal{N}\simeq L^{\infty }(Y,{\mu }_Y)$, thepointer residualis the Dirichlet energy

$${\mathcal{R}}_Y^{\left(\mathcal{N}\right)}\left(t\right):={\mathcal{E}}_Y\left({\rho }_Y\left(t\right)-q_{\sigma }\left(t\right)\right),$$

(200)

and theattractoris the pointer law $q_{\sigma }\left(t\right)$ in the chosen context.

Proposition 6.5

(Context–invariant DSFL form, context–dependent constants). For any pointer algebra $\mathcal{N}$:

(a) 

OA law. If the reversible QMS on $(\mathcal{M},\omega )$ has a Poincaré gap $\lambda \left(\mathcal{N}\right)>0$ on $L^2{(\mathcal{N},\omega )}^{\perp }$, then

$$\frac{d}{dt}{\mathcal{R}}_{\omega }^{\left(\mathcal{N}\right)}\left({\mathsf{T}}_{t}X\right)\le -2\lambda \left(\mathcal{N}\right){\mathcal{R}}_{\omega }^{\left(\mathcal{N}\right)}\left({\mathsf{T}}_{t}X\right),\Rightarrow {\mathcal{R}}_{\omega }^{\left(\mathcal{N}\right)}\left({\mathsf{T}}_{t}X\right)\le e^{-2\lambda \left(\mathcal{N}\right)t}{\mathcal{R}}_{\omega }^{\left(\mathcal{N}\right)}\left(X\right).$$

(201)

(b) 

Pointer law. If the sector generator $L_Y$ has Poincaré gap ${\lambda }_Y\left(\mathcal{N}\right)>0$, then

$$\frac{d}{dt}{\mathcal{R}}_Y^{\left(\mathcal{N}\right)}\left(t\right)\le -2{\lambda }_Y\left(\mathcal{N}\right){\mathcal{R}}_Y^{\left(\mathcal{N}\right)}\left(t\right),\Rightarrow {\mathcal{R}}_Y^{\left(\mathcal{N}\right)}\left(t\right)\le e^{-2{\lambda }_Y\left(\mathcal{N}\right)t}{\mathcal{R}}_Y^{\left(\mathcal{N}\right)}\left(0\right).$$

(202)

Thus theformof DSFL is the same in any context, while the rate constants $\lambda \left(\mathcal{N}\right)$ and ${\lambda }_Y\left(\mathcal{N}\right)$ (and the attractor)change with $\mathcal{N}$.

Proof. 

Part (a) is Theorem 4.2 with the gap computed on $L^2{(\mathcal{N},\omega )}^{\perp }$. Part (b) is Proposition 6.3 with the Poincaré constant of $L_Y$. □

Proposition 6.6

(Unitary covariance of the core law). Let U be a unitary on $\mathcal{M}$ and ${\mathcal{N}}^{\prime }=U\mathcal{N}{U}^{†}$. Define ${\mathsf{E}}_{{\mathcal{N}}^{\prime }}\left(X\right):=U{\mathsf{E}}_{\mathcal{N}}\left(U^{†}XU\right)U^{†}$. Then

$${\mathcal{R}}_{\omega }^{\left({\mathcal{N}}^{\prime }\right)}\left(X\right)=\parallel X-{\mathsf{E}}_{{\mathcal{N}}^{\prime }}{X\parallel }_{2,\omega }^2={\parallel U^{†}XU-{\mathsf{E}}_{\mathcal{N}}\left(U^{†}XU\right)\parallel }_{2,\omega }^2={\mathcal{R}}_{\omega }^{\left(\mathcal{N}\right)}\left(U^{†}XU\right),$$

(203)

and the spectral gap is invariant: $\lambda \left({\mathcal{N}}^{\prime }\right)=\lambda \left(\mathcal{N}\right)$. Consequently, DSFL decay holds with thesame ratein unitarily equivalent contexts, and the attractor transforms as $L^2({\mathcal{N}}^{\prime },\omega )=U{L}^2(\mathcal{N},\omega )U^{†}$.

Proof. 

Orthogonal projection covariance under conjugation and unitary invariance of ${\parallel ·\parallel }_{2,\omega }$ yield the residual identity. The spectrum of the self–adjoint restriction of $\mathcal{L}$ to the orthogonal complement is invariant under unitary conjugation, hence the same gap. □

Remark 6.11

(Non–unitarily equivalent contexts (e.g. position vs. momentum)). When ${\mathcal{N}}_1$ and ${\mathcal{N}}_2$ are not unitarily equivalent (e.g. position vs. momentum algebras on bounded domains with different boundary structures), theformof DSFL remains identical but the constants change: $\lambda \left({\mathcal{N}}_1\right)\ne \lambda \left({\mathcal{N}}_2\right)$, ${\lambda }_Y\left({\mathcal{N}}_1\right)\ne {\lambda }_Y\left({\mathcal{N}}_2\right)$, and the attractors are $q_{\sigma }^{\left(1\right)}$ vs. $q_{\sigma }^{\left(2\right)}$ (position vs. momentum laws). Thuschanging context changes the attractorand generally the observed rate, while thecore DSFL law—“propagation $+$ gap ⇒ exponential suppression”—is the same.

• Two–stage contraction and small–gain view.

In experiments one typically sees a two–stage contraction: (i) the operator–algebraic contraction $X\mapsto {\mathsf{E}}_{\mathcal{N}}X$ at rate $2\lambda \left(\mathcal{N}\right)$, then (ii) the pointer–space alignment ${\rho }_Y\to q_{\sigma }$ at rate $2{\lambda }_Y\left(\mathcal{N}\right)$. Writing $R_{\mathrm{OA}}\left(t\right):={\mathcal{R}}_{\omega }^{\left(\mathcal{N}\right)}\left({\mathsf{T}}_{t}X\right)$ and $R_{\mathrm{ptr}}\left(t\right):={\mathcal{R}}_Y^{\left(\mathcal{N}\right)}\left(t\right)$, one can couple them as

$${\dot{R}}_{\mathrm{OA}}\le -2\lambda \left(\mathcal{N}\right)R_{\mathrm{OA}},{\dot{R}}_{\mathrm{ptr}}\le -2{\lambda }_Y\left(\mathcal{N}\right)R_{\mathrm{ptr}}+\delta R_{\mathrm{OA}},$$

(204)

for a (typically small) coupling $\delta$ arising from finite–time context transfer. By Proposition 4.1 (small–gain), $R_{\mathrm{OA}}+R_{\mathrm{ptr}}$ still decays exponentially provided $\delta <4\lambda \left(\mathcal{N}\right){\lambda }_Y\left(\mathcal{N}\right)$.

• Examples.

• Qubit dephasing.${\mathcal{N}}_Z=\mathrm{Alg}\left\{{\sigma }_z\right\}$ vs. ${\mathcal{N}}_X=\mathrm{Alg}\left\{{\sigma }_x\right\}$: both are unitarily equivalent, so the rate is invariant (Prop. 6.6), and the attractor is the corresponding Lüders state in the chosen basis (Theorem 4.3).
• Position vs. momentum (PDE). On a bounded $\Omega$, the position sector has Poincaré constant ${\lambda }_1(\Omega )$; the momentum sector involves the spectral constants of the generator on Fourier side. DSFL form is identical, but constants (and attractor laws ${|\Psi |}^2$ vs. $|\widehat{\Psi }{|}^2$) differ.

Takeaway. The core DSFL mechanism—a single quadratic residual suppressed by propagation + gap/coercivity—is context–invariant. The attractor and the rate constants are context–dependent, through the pointer algebra $\mathcal{N}$ (and its sector generator $L_Y$). Changing $\mathcal{N}$ changes the equilibrium manifold and generally the rate, but not the shape of the restoration law.

7. Numerical Demonstrations (Synthetic)

• Purpose. The following minimal, reproducible checks are illustrative sanity tests of the DSFL rates in simple synthetic models (not fits to experimental data). They confirm that the gap/coercivity constants derived in §4 are visible as slopes in practice.

7.1. PDE (Born Sector): Heat Flow with Mean-Zero Mismatch

On $\Omega ={\mathbb{T}}^1=[0,1)$ with periodic BCs, set $w:=\rho -q$ with ${\int }_{\Omega }w=0$ and evolve

$${\partial }_{t}w=\Delta w,\mathcal{R}\left(t\right)={\int }_{\Omega }{|\nabla w|}^{2}dx.$$

(205)

Theory (§6.1) predicts $\mathcal{R}\left(t\right)\le e^{-2{\lambda }_{1}t}\mathcal{R}\left(0\right)$ with ${\lambda }_1={\left(2\pi \right)}^2$. A spectral implementation (truncated Fourier series; Crank–Nicolson or exact mode update) with multi–mode $w_0$ shows: (i) $\mathcal{R}\left(t\right)$ is strictly decreasing; (ii) a semi-log fit of $\mathcal{R}$ over a post-transient window returns a slope approaching $-2{\lambda }_1$ as higher modes die out; (iii) restricting $w_0$ to the fundamental mode yields a slope $\approx -2{\lambda }_1$ throughout. Takeaway: the DSFL envelope $2{\lambda }_1$ is observed as the late-time rate.

7.2. Qubit Lindblad Dephasing: Lüders Residual

For a qubit with dephasing rate $\gamma >0$ in the pointer basis,

$${\dot{\sigma }}_t=\gamma \left(P_0{\sigma }_t{P}_0+P_1{\sigma }_t{P}_1-\frac{1}{2}\{P_0+P_1,{\sigma }_t\}\right),{\mathcal{R}}_{\mathrm{L}\ddot{\mathrm{u}}\mathrm{ders}}\left(t\right)=2{|{\left({\sigma }_t\right)}_{01}|}^2.$$

(206)

Theory (§4.3) gives ${\mathcal{R}}_{\mathrm{L}\ddot{\mathrm{u}}\mathrm{ders}}\left(t\right)=e^{-2\gamma t}{\mathcal{R}}_{\mathrm{L}\ddot{\mathrm{u}}\mathrm{ders}}\left(0\right)$ (sharp). A simple RK4 or exact update of ${\left({\sigma }_t\right)}_{01}$ confirms a straight line of slope $-2\gamma$ on a semi-log plot, independent of commuting Hamiltonian phases. With a noncommuting H, oscillations appear but the envelope remains $e^{-2\gamma t}$. Takeaway: the sharp DSFL rate $2\gamma$ is observed.

• Reproducibility.

Tiny reference scripts (FFT heat solver; qubit ODE) suffice to reproduce these slopes; code is available on request. We omit figures to keep the paper focused on theory.

8. Conclusion

We introduced the Deterministic Statistical Feedback Law (DSFL) as a sector-neutral restoration principle that turns canonical equilibrium statements—Born’s rule (QM), entropy monotonicity (TD), and Einstein’s curvature–matter balance (GR)—from postulates into attractors. The mechanism is uniform: a single quadratic misalignment residual $\mathcal{R}$ decreases globally by a propagation lemma (Jensen/Kadison–Schwarz/energy identity), and sectoral spectral gaps or coercivity upgrade monotonicity to exponential decay. The law is context-invariant; the attractor and rate are context-dependent through the pointer algebra or the sector’s coercivity constants.

• What we proved.

• QMS: DSFL ⇔ gap, optimal constants. For $\omega$-symmetric QMS we established the equivalence between DSFL and a noncommutative Poincaré inequality on $L^2{(\mathcal{N},\omega )}^{\perp }$, with optimal rate ${\alpha }_{\ast }=2{\lambda }_{\ast }$.
• Lindblad (finite-dimensional). Pure dephasing yields a sharp exponential decay of the Lüders residual with rate ${\alpha }_{\ast }={min}_{i\ne j}({\gamma }_i+{\gamma }_j)$.
• PDE template. An exact residual energy identity gives $\dot{\mathcal{R}}=-2\int u^{\top }Bu-2{\parallel ÷u\parallel }_2^2+\dots$, hence $\dot{\mathcal{R}}\le -(2\beta -C\epsilon )\mathcal{R}$ under $B⪰\beta I$ and subcritical couplings.
• Free fields. In Parisi–Wu stochastic quantization, smeared two-point residuals decay at twice the Euclidean Hamiltonian gap.
• GR slice. On compact Riemannian slices in DeTurck gauge, a Lichnerowicz-type gap implies exponential $L^2$ suppression of the curvature–matter misfit.
• Residual-entropy arrow. The proxy $S_R:=-log(\mathcal{R}/{\mathcal{R}}_0+R_{\ast })$ is strictly increasing whenever DSFL holds, giving a structural arrow of time that does not require probabilistic postulates.
• Context vs. core. Via pointer algebras we proved “same core, different attractor”: the propagation + gap form is universal, while the equilibrium manifold and decay rate depend on the chosen measurement context (position/momentum, basis/unitary changes).

• Implications and tests.

DSFL reframes “equilibrium” as the endpoint of a universal Lyapunov descent. It also yields rate-level, falsifiable signatures: GW band coherence, low-ℓ CMB phase structure, growth-rate consistency ($f{\sigma }_8$), and convergence benchmarks in quantum optics, all tied to sectoral gaps. Tracking inequalities (moving pointers) and small-gain results (coupled residuals) extend the theory to time-varying contexts and weakly coupled sectors.

• Limitations and programs.

Open fronts include: (i) a fully covariant Lorentzian DSFL (gauge-invariant residual, hyperbolic flow); (ii) interacting QFT beyond Gaussian sectors (constructive/RG-controlled Poincaré or log-Sobolev constants); and (iii) hypocoercive/nonreversible settings (DSFL with commutator-enhanced residuals). Noise-robust (ISS) variants and multi-residual couplings merit further development and experiments.

• Outlook.

Priorities are: log-Sobolev/${\Gamma }_2$ upgrades for reversible QMS (variance → entropy decay), cosmology fits (SN+BAO+CMB+RSD) for DSFL backgrounds vs. $\Lambda$CDM, laboratory rate-extraction in dephasing/GBS-type setups, and numerical GR slice studies of geometric residual quench. In sum, DSFL isolates the restoration law, quantifies its rates, and delineates precisely when and how Born/entropy/Einstein relations emerge—or fail—under empirical scrutiny.