Vibration Performance Improvement of Medical Rotating Systems Through Structural Parameter Optimization

1. Introduction

Medical rotating systems, including computed tomography (CT) gantries and other precision rotating assemblies, operate under strict vibration limits because mechanical motion directly affects signal stability, imaging consistency and long-term service reliability [1]. As operating speed increases, small geometric deviations, mass distribution errors, and stiffness variation can excite structural modes and amplify vibration displacement [2]. Excessive vibration not only degrades imaging quality but also accelerates wear in bearings and drive components, increasing maintenance requirements and reducing system availability [3]. Recent developments in clinical imaging systems indicate that mechanical layout and operating speed continue to evolve toward higher throughput and finer resolution, which places increasing demands on vibration performance over a wide speed range rather than at a single operating point [4]. In this context, recent studies on medical structural components have emphasized the importance of computational modeling in linking design parameters to mechanical performance under realistic service conditions [5]. Modeling-based investigations of medical welded structures have shown that local structural characteristics and parameter selection can significantly influence stress distribution and fatigue-related performance metrics, highlighting the value of simulation-driven design optimization in medical applications [6]. Although such studies focus on different structural forms, they underscore a common principle: reliable performance in medical systems increasingly depends on quantitative prediction and optimization of structural behavior rather than empirical adjustment [7].

Over the past decade, vibration improvement strategies for rotating systems have gradually shifted from the addition of damping devices toward design-stage optimization of structural parameters [8]. Finite element analysis is widely used to evaluate mode shapes, natural frequencies and dynamic response characteristics, while surrogate models are often introduced to reduce the computational cost associated with repeated simulations during optimization. Response surface methods have been applied to vibration-related design problems in rotating and high-speed structures, enabling efficient mapping between design variables and vibration response using a limited number of simulations [9]. To further improve efficiency and robustness, recent studies have reported adaptive and high-accuracy surrogate modeling strategies that better capture nonlinear behavior in complex design spaces and near resonant regions [10]. Parameter screening and sensitivity analysis have also become integral components of vibration-oriented optimization workflows [11]. By identifying parameters that exert the greatest influence on dynamic response, these methods reduce model dimensionality and improve optimization stability. Recent work has proposed sensitivity-based frameworks that relate parameter importance to vibration or displacement objectives, allowing designers to focus on a small set of effective variables while maintaining structural and functional constraints [12,13]. In parallel, hybrid optimization approaches that combine statistical regression with classical design-of-experiments techniques have been applied to rotating systems, offering a balance between physical interpretability and computational efficiency [14]. Broader reviews on vibration and noise control further emphasize that reliable surrogate models and consistent performance metrics are essential for translating optimization outcomes into practical engineering solutions [15].

Despite these advances, several limitations remain when vibration optimization methods are applied to medical rotating structures. First, many existing studies focus on general machinery or industrial frames, and their operating conditions do not fully reflect the speed range, assembly constraints, and reliability requirements characteristic of medical equipment. As a result, optimized parameters may not transfer directly to medical platforms [16]. Second, surrogate models are sometimes constructed using limited sampling plans, which may overlook nonlinear response behavior near resonant regions. This can lead to designs that perform well at sampled conditions but exhibit increased vibration under unsampled operating speeds [17]. Third, validation is often conducted at a small number of steady operating speeds, whereas medical rotating systems typically experience speed variation during start-up and shut-down. Although imbalance-related vibration has been widely investigated, systematic structural parameter optimization without reliance on additional damping devices remains relatively underexplored for medical rotating applications [18].

In this study, a structural parameter optimization framework is developed for medical rotating systems that integrates sensitivity-based parameter selection with response surface modeling. Finite element simulations are used to construct a surrogate model capturing the relationship between key structural parameters and vibration displacement over a broad operating speed range. Optimization is carried out across rotational speeds from 300 to 900 rpm, with the objective of reducing vibration displacement while maintaining structural stiffness within ±5% of the baseline design. By focusing on design-stage parameter adjustment rather than auxiliary damping measures, the proposed approach provides a practical and efficient solution for vibration reduction and supports systematic engineering iteration in medical rotating system design.

2. Materials and Methods

2.1. System description and study objects

The analysis was performed on a medical rotating structure typical of diagnostic imaging equipment. The system included a rotor, support frame, drive unit, and bearing assembly. One baseline configuration was defined according to a common clinical design. Based on this configuration, 48 structural variants were generated by adjusting selected geometric and material parameters within practical manufacturing limits. The rotational speed ranged from 300 to 900 rpm, covering normal operating conditions and regions close to resonance. All variants were analyzed using identical boundary conditions to allow direct comparison of vibration response.

2.2. Experimental design and control configuration

A design-based numerical study was carried out instead of physical testing. The baseline structure was treated as the control case, while the parameter-modified designs formed the comparison group. Design variables such as local thickness, support stiffness, and elastic modulus were chosen based on structural relevance and preliminary screening. Each design variant was evaluated independently using finite element analysis. This setup isolated the influence of structural parameters on vibration displacement without changing operating speed, boundary constraints, or introducing added damping elements.

2.3. Measurement methods and quality control

Dynamic behavior was obtained from finite element simulations that included mass distribution, stiffness, and rotational constraints. Modal analysis was first conducted to identify dominant modes within the target speed range. Harmonic response analysis was then used to calculate vibration displacement under rotational excitation. Mesh density was increased in regions of high stress and displacement to reduce numerical error. Convergence checks confirmed that vibration results were stable with respect to mesh size. Material properties and loading conditions were kept consistent across all simulations to ensure repeatability.

2.4. Data processing and model formulation

Post-processing focused on extracting the maximum vibration displacement at selected critical locations. A second-order response surface model was fitted to describe the relation between structural parameters and vibration response, given by

$$y={\beta }_0+\sum _{i=1}^n{\beta }_i{x}_i+\sum _{i=1}^n{\beta }_{\mathit{ii}}{x}_i^2+\sum _{i\text{<}j}{\beta }_{\mathit{ij}}{x}_i{x}_j,$$

Where$y$ represents vibration displacement, $x_i$ are normalized design variables, and $\beta$ are regression coefficients. Structural stiffness change was evaluated using

$$\Delta K={\displaystyle \frac{K-K_0}{K_0}}\text{×}100\%,$$

where $K_0$ is the stiffness of the baseline structure and$K$ is that of a modified design. These expressions allowed vibration reduction to be assessed together with stiffness preservation.

2.5. Optimization procedure and validation

The response surface model served as a surrogate in the optimization process. Vibration displacement was minimized subject to a stiffness constraint of ±5% relative to the baseline design. The search was carried out within predefined parameter bounds. The optimal design identified by the surrogate model was then reanalyzed using a full finite element simulation. Agreement between surrogate predictions and finite element results was used to verify the reliability of the optimization procedure for vibration improvement in medical rotating structures.

3. Results and Discussion

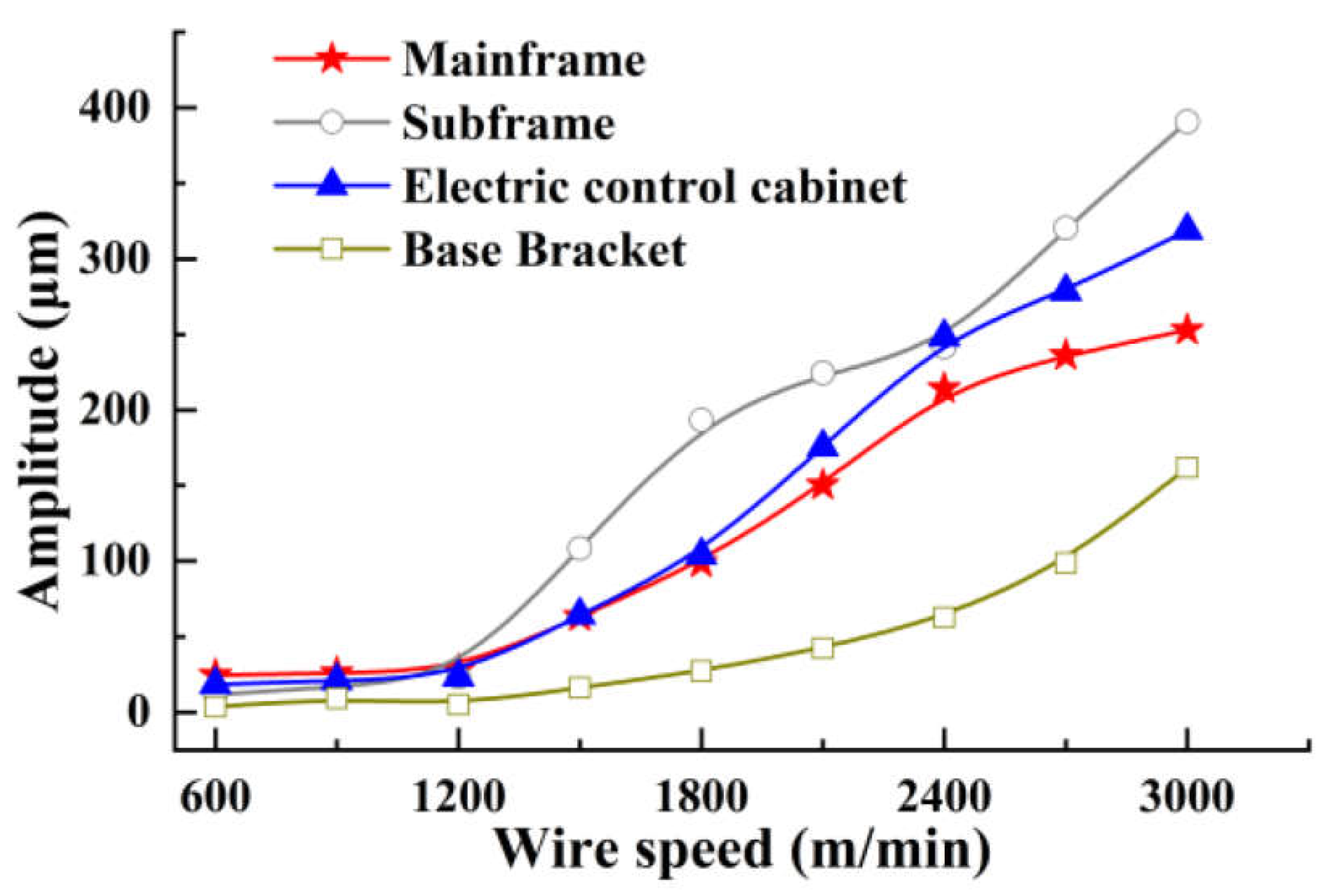
3.1. Vibration response of the baseline structure

The baseline design exhibited a clear increase in vibration displacement with rising rotational speed. At lower speeds, displacement grew gradually, while a faster rise occurred as the speed approached the dominant structural modes. The maximum displacement appeared at locations with reduced local stiffness, such as support transitions and connection regions, indicating that compliance distribution played a stronger role than mass variation alone. This speed-dependent response is typical for rotating structures operating near resonance. Similar amplitude growth trends have been reported in recent vibration studies based on response analysis under varying operating conditions, where displacement increases sharply once structural modes become active [19]. Figure 1 illustrates this behavior for the present medical rotating structure within the 300–900 rpm range.

3.2. Sensitivity results and dominant design parameters

Sensitivity analysis across the 48 design samples revealed that vibration displacement was governed by a limited number of structural parameters. Parameters related to local thickness along the main load path and stiffness in the support region produced the largest changes in displacement. In contrast, several geometric details had only minor influence within the tested ranges. This result indicates that vibration reduction can be achieved by targeting specific compliance-sensitive regions rather than modifying a large number of design variables. Similar findings have been reported in response-surface-based vibration optimization studies, where sensitivity screening is used to reduce the design space and improve robustness of the surrogate model [20]. These results justify the parameter selection adopted in the present optimization framework.

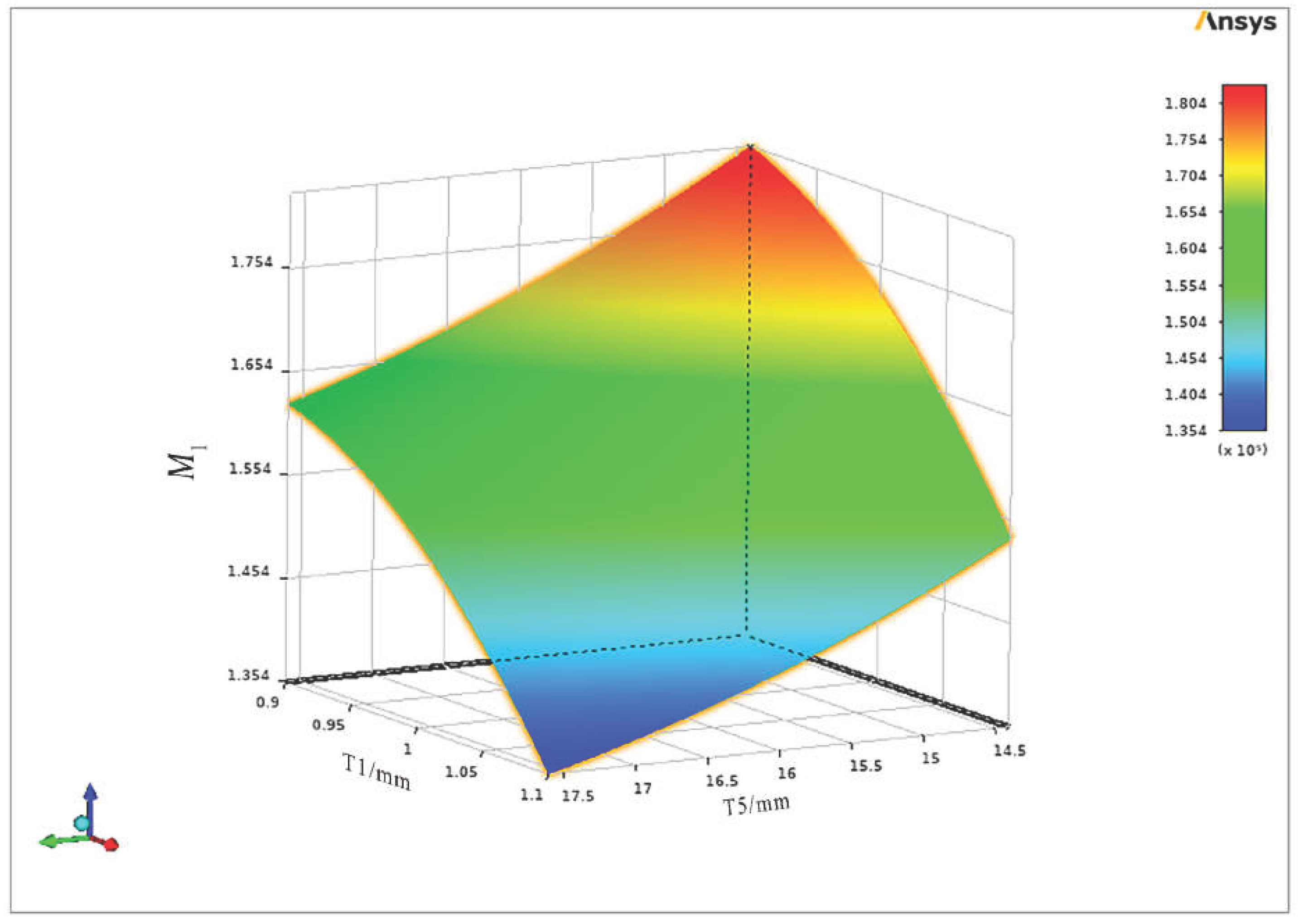
3.3. Response surface behavior and parameter interaction

The second-order response surface model provided a stable description of the relationship between structural parameters and vibration displacement. The fitted surface captured both nonlinear trends of individual parameters and interaction effects between parameter pairs. The strongest interaction was observed between local thickness near the support region and the global stiffness parameter, where increasing thickness led to a larger displacement reduction when stiffness was simultaneously increased. This interaction explains why one-parameter tuning is insufficient for vibration control in compact rotating structures. Response surface representations have been widely used to reveal such coupled effects in structural optimization problems, as shown in recent studies on vibration-oriented surrogate modeling [21]. Figure 2 presents the response surface obtained in this study and highlights the coupled influence of key parameters on peak vibration displacement.

3.4. Optimization outcome and comparison with published studies

After optimization, the maximum vibration displacement was reduced by 31.2% across the operating speed range, while the stiffness variation remained within ±5% of the baseline design. The improvement was most pronounced near the peak-response region, where moderate stiffness enhancement produced a clear reduction in displacement. This result is consistent with published optimization studies showing that response-based objectives are more effective for vibration reduction than frequency-shift-only strategies, particularly when resonance cannot be avoided [22]. Compared with recent response-surface-driven vibration optimization workflows, the achieved reduction level falls within the reported improvement range, while maintaining a tighter stiffness constraint suitable for medical rotating equipment. These results indicate that the proposed parameter optimization approach is effective for vibration control without introducing additional damping devices.

4. Conclusion

This work studied vibration reduction in medical rotating systems using structural parameter optimization based on sensitivity analysis and response surface modeling. The results indicate that vibration displacement is mainly controlled by a small set of stiffness- and thickness-related parameters along the primary load paths. Adjusting these parameters leads to a clear reduction in vibration without adding damping devices or changing operating conditions. Using a finite-element-based surrogate optimization approach, the maximum vibration displacement was reduced by 31.2%, while the overall structural stiffness remained within ±5% of the original design. The study shows how interactions between key structural parameters influence vibration response in compact rotating systems. It also confirms that response-based optimization is more effective than strategies that rely only on shifting natural frequencies.