Suppression of Residual Unbalance Moments in Rotating Medical Structures Using Adaptive Control

1. Introduction

Rotating medical equipment, including high-speed centrifuges, computed tomography gantries, rotary blood pumps and precision surgical spindles, is required to operate under stringent limits on vibration, noise and mechanical reliability [1]. Even after conventional static and dynamic balancing procedures, residual unbalance moments commonly persist as a result of assembly tolerances, thermal deformation, component replacement and gradual wear during service [2]. These residual moments generate synchronous excitation at the rotating frequency, which can lead to excessive vibration when structural resonances are involved. Such vibration degrades operational stability and functional accuracy, accelerates bearing wear, and shortens service life, thereby increasing maintenance cost and the risk of unplanned shutdowns in clinical environments [3,4]. With the growing demand for higher rotational speed and tighter performance margins, unbalance-induced vibration has become a critical constraint in the development of advanced rotating medical systems. Recent studies on rotating medical structures have emphasized that vibration response cannot be attributed solely to mass eccentricity, but is strongly influenced by structural dynamics, support conditions and control strategy [5]. Investigations combining system-level dynamic modeling with balance control analysis have shown that residual unbalance moments interact with flexible modes and can significantly amplify vibration near critical speeds, even when nominal unbalance levels are small [6]. These findings indicate that effective vibration suppression requires coordinated consideration of unbalance distribution, structural characteristics, and control design, rather than isolated tuning of individual components.

In recent years, extensive research efforts have been devoted to suppressing unbalance-induced vibration in rotating systems [7]. One major research direction focuses on active balancing and force-based compensation using controlled actuators. Linear quadratic regulator techniques and model-based feedback control strategies have been applied to rotor systems with time delay and parametric uncertainty, demonstrating that closed-loop control can attenuate synchronous vibration when phase characteristics are properly addressed [8,9]. Active magnetic bearing systems have also been widely investigated for vibration suppression in high-speed rotors, as they allow direct modulation of bearing forces without mechanical contact [10]. Although these approaches offer high control authority, their effectiveness often depends on accurate system models, stable operating conditions, and relatively complex hardware integration. Another important research trend involves adaptive and signal-based control methods designed to accommodate speed variation and uncertain disturbance characteristics [11]. Adaptive notch filters and synchronous vibration controllers have been proposed to track rotating frequency in real time and suppress dominant harmonic components over a wide speed range [12]. Compared with fixed-frequency approaches, adaptive schemes maintain suppression performance during acceleration and deceleration. In addition, learning-based methods such as iterative learning control and adaptive disturbance observers have been developed to compensate periodic disturbances associated with unbalance and related faults [13]. While these methods improve adaptability, practical implementation may be challenged by slow convergence, sensitivity to noise and robustness issues under rapidly changing operating conditions.

Despite these advances, several limitations remain, particularly for rotating medical devices. Many existing studies are validated under limited operating conditions or on simplified laboratory rigs that do not fully represent the structural complexity and environmental variability of clinical equipment [14]. Performance degradation is frequently observed when rotational speed varies rapidly or when unbalance is distributed across multiple components rather than concentrated at a single location [15]. Moreover, a substantial portion of the literature relies primarily on displacement measurements, whereas acceleration sensors are more commonly adopted in compact medical systems due to their small size, ease of installation, and broader frequency bandwidth. The higher noise level inherent in acceleration signals introduces additional challenges for stable adaptive control, which have not been sufficiently addressed in current studies [16]. Another unresolved issue concerns the physical modeling of residual unbalance moments. Many control strategies treat unbalance as a single harmonic disturbance without explicitly linking it to the underlying distribution of mass eccentricity. This simplification limits physical interpretability and often results in heuristic parameter tuning. Furthermore, frequency-domain suppression techniques may reduce vibration at a specific measurement location while unintentionally amplifying vibration elsewhere because of unmodeled structural coupling [17]. These shortcomings highlight the need for control approaches that combine physically meaningful unbalance modeling with adaptive capability and sensing schemes suitable for practical medical equipment.

In this study, an adaptive control framework is developed for suppressing residual unbalance moments in rotating medical structures using real-time vibration feedback. A rotating structure model is formulated to represent distributed mass eccentricity and its contribution to unbalance moments, allowing the disturbance to be described in a physically interpretable manner. Based on this model, adaptive gain tuning is implemented using high-frequency acceleration signals, enabling effective suppression of synchronous vibration under varying operating conditions. Through numerical analysis and representative test scenarios, the proposed approach is evaluated with respect to vibration reduction performance, stability under speed variation, and robustness to sensor noise. The results demonstrate that the proposed framework provides reliable vibration suppression across different unbalance levels and operating regimes, offering a practical solution for improving the operational performance and reliability of rotating medical equipment.

2. Materials and Methods

2.1. Samples and Study Object Description

The study examined a rotating structure representative of medical equipment used for precision motion, such as centrifuges and imaging subsystems. The structure consisted of a rigid shaft supported by rolling bearings and driven by an electric motor. Residual unbalance was introduced using calibrated masses attached at fixed radial positions. Three unbalance levels were considered: 120, 220, and 350 g·mm. For each level, tests were conducted at three constant rotational speeds, resulting in nine operating conditions. All experiments were performed indoors at an ambient temperature of 23 ± 1 °C. The rotational speed deviation during steady operation was maintained within ±0.5%. The selected structure and operating range reflect common mass distribution and stiffness characteristics observed in medical rotating devices.

2.2. Experimental Design and Control Configuration

Two control configurations were examined: an adaptive feedback configuration and a fixed-gain configuration used as a reference. In the adaptive configuration, controller gains were adjusted online based on measured vibration response. In the reference configuration, gains remained constant and were tuned using nominal system parameters. Both configurations were tested under identical unbalance conditions and speed settings. This design ensured that differences in vibration response could be attributed to the control strategy rather than mechanical or environmental factors. Each operating condition was repeated three times to reduce the influence of random variation.

2.3. Measurement Method and Quality Control

Vibration was measured using a tri-axial piezoelectric accelerometer mounted on the bearing housing along the radial direction. The sensor had a sensitivity of 100 mV/g and a frequency range up to 5 kHz. Acceleration signals were sampled at 2 kHz using a 16-bit data acquisition system. Before testing, sensor calibration was checked using a reference excitation source. Data collected during startup and shutdown were excluded. Only steady-state segments longer than 10 s were used for analysis. Signal quality was verified by inspecting time histories and frequency spectra to confirm the absence of saturation and abnormal spikes.

2.4. Data Processing and Model Formulation

Measured acceleration signals were first detrended to remove low-frequency bias. A band-pass filter centered on the rotational frequency was then applied to isolate the synchronous vibration component. Vibration intensity was quantified using the root mean square value, defined as [17]:

$$a_{\mathrm{RMS}}=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{a}_i^2},$$

where $a_i$​ denotes the sampled acceleration and $N$ is the number of samples. The feedback gain was updated according to the vibration level using:

$$K_{t+1}=K_t+\alpha a_{\mathrm{RMS},t},$$

where $K_t$ is the gain at time step $t$ and $\alpha$ is a constant adaptation factor. This update rule allowed the control effort to vary with vibration magnitude without explicit estimation of unbalance parameters.

2.5. Performance Indicators and Data Analysis

Control performance was evaluated by comparing vibration levels obtained under adaptive and fixed-gain configurations. The vibration reduction rate was calculated as [18]:

$$R={\displaystyle \frac{a_{\mathrm{ref}}-a_{\mathrm{ctrl}}}{a_{\mathrm{ref}}}}\times 100\%,$$

where $a_{\mathrm{ref}}$​ and $a_{\mathrm{ctrl}}$​represent the RMS acceleration for the reference and adaptive cases, respectively. Mean values and standard deviations were computed across repeated tests to assess consistency. Additional tests were conducted under small speed fluctuations and additive measurement noise to examine stability under non-ideal conditions. All signal processing and calculations were carried out using MATLAB with identical settings for all datasets.

3. Results and Discussion

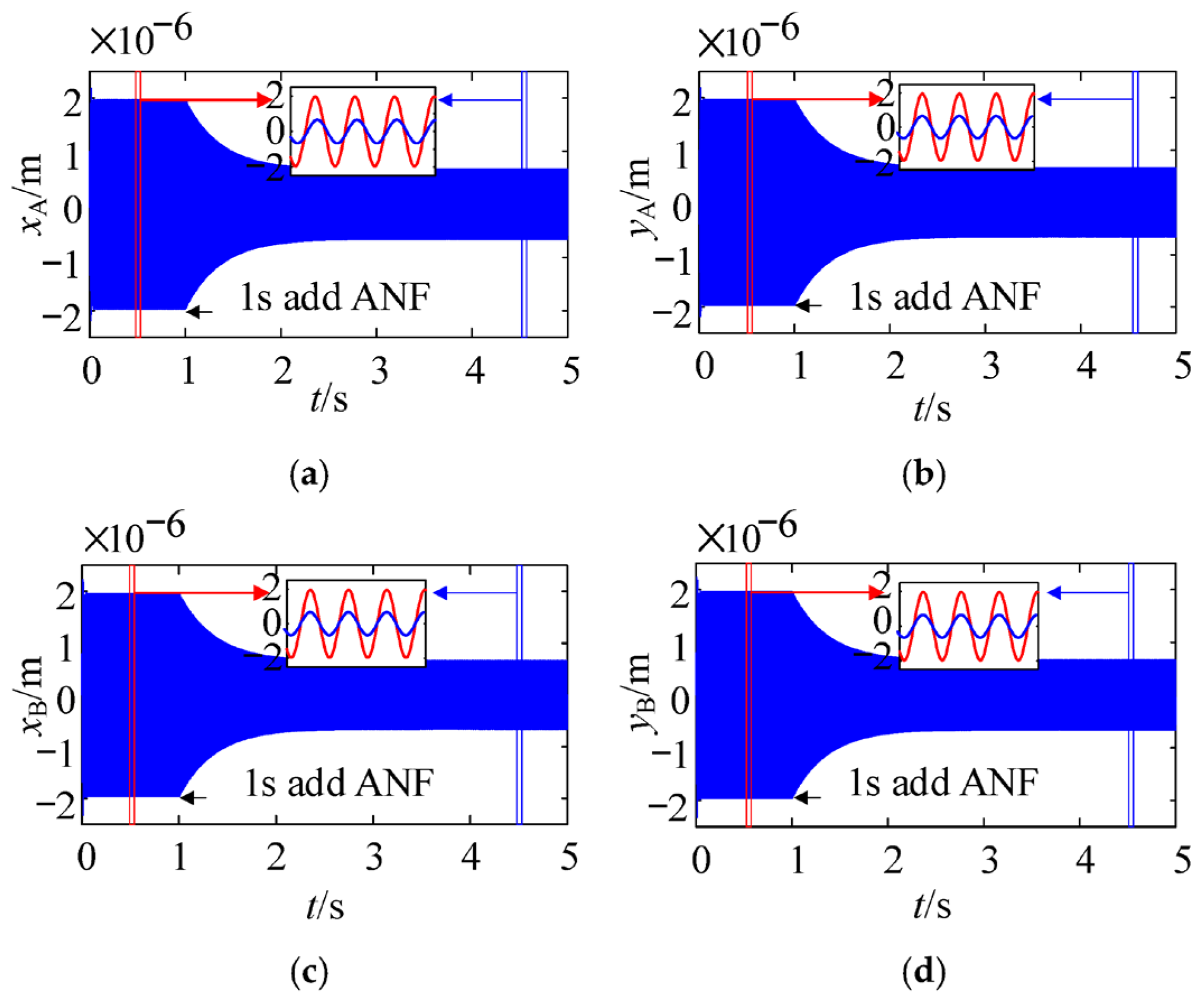
3.1. Response Reduction Under Different Residual Unbalance Levels

The vibration response decreased under all tested residual unbalance levels after the adaptive controller reached steady operation. As illustrated in Figure 1, the peak radial acceleration declined from 1.42 m/s² in the reference case to 0.79 m/s² when adaptive gain adjustment was applied. This reduction corresponds to an average decrease of 44.4% across the three unbalance conditions. The reduction trend remained similar as the unbalance magnitude increased from 120 to 350 g·mm, indicating that the control response was not limited to a single operating point. The dominant change was observed at the synchronous frequency, while the broadband vibration level showed only minor variation. This behavior suggests that the gain update mainly influenced the periodic excitation associated with residual unbalance rather than altering the overall structural response [19].

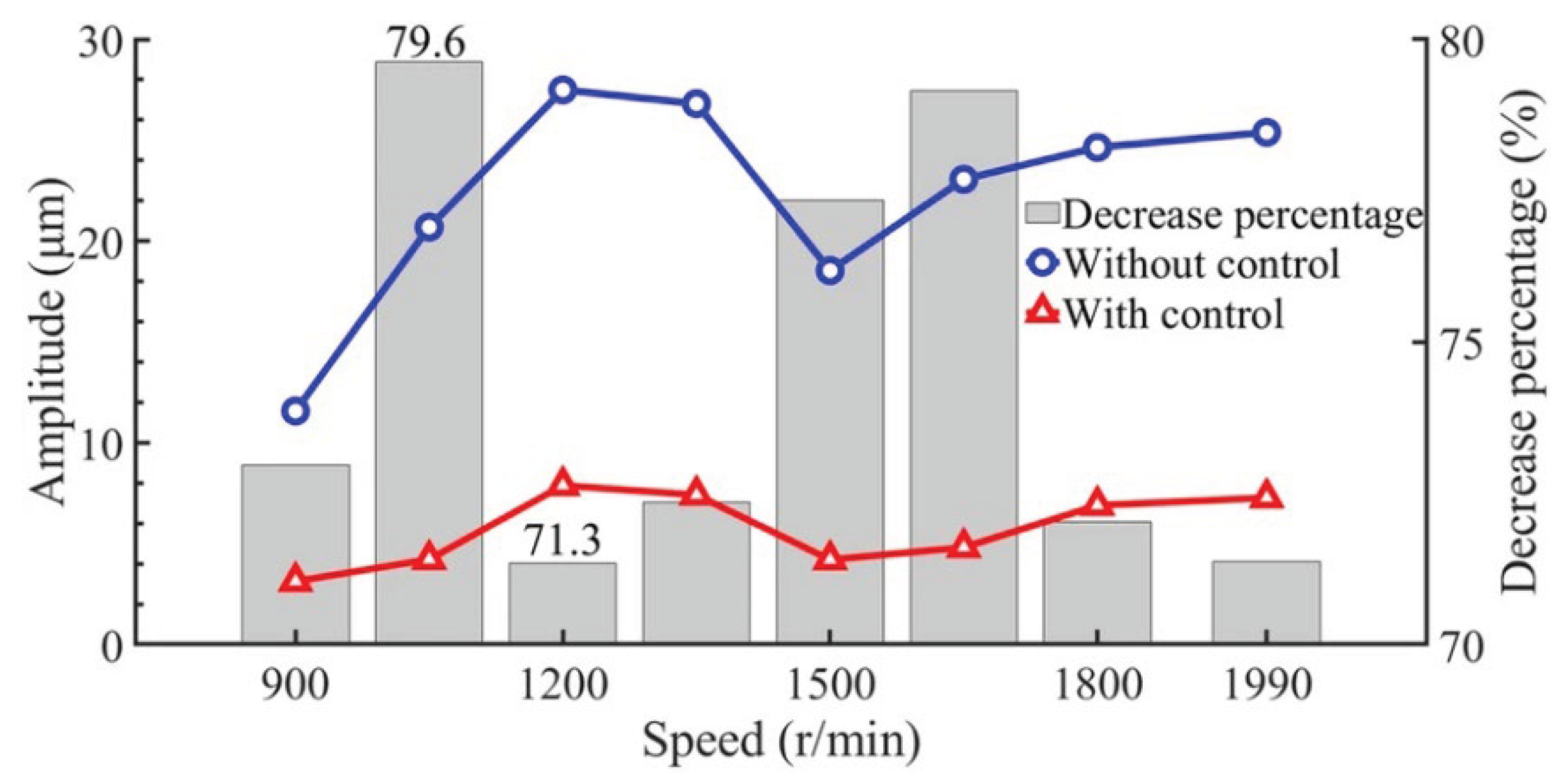
3.2. Influence of Rotational Speed Variation

The vibration response under varying rotational speed is shown in Figure 2. In the reference configuration, speed variation caused noticeable fluctuation in vibration amplitude, particularly near the transition regions. After adaptive control was enabled, the vibration level remained lower throughout the speed range. This outcome indicates that the controller responded to changes in excitation conditions without requiring a fixed disturbance frequency. In comparison, several reported approaches rely on frequency-locked filters or predefined speed information, which may lose alignment during speed transitions [20]. Iterative learning and notch-filter-based methods reported in recent studies show similar trends but often require additional synchronization mechanisms to maintain stability when speed changes [21]. The present results show that direct adaptation based on measured vibration amplitude can reduce sensitivity to speed variation within the tested range.

3.3. Effect of Measurement Noise on Control Performance

When measurement noise was added to the acceleration signal, the adaptive controller continued to reduce the primary vibration component, as shown in Figure 2, although the reduction margin became smaller. This outcome reflects the inherent sensitivity of acceleration-based feedback to noise, especially when the control gain is updated online. The applied sampling rate and steady-state evaluation window limited the influence of transient noise spikes. In contrast, displacement-based feedback used in some magnetic bearing systems benefits from higher signal-to-noise ratios but requires more complex sensing hardware. Previous studies have noted that periodic disturbance suppression can be affected by noise accumulation, which is why additional filtering or observer layers are often introduced [22]. The present results indicate that acceptable suppression can still be achieved with standard acceleration sensors when conservative gain adaptation is applied.

3.4. Comparison with Existing Studies and Practical Implications

Compared with recent rotor vibration control studies, the achieved reduction level is moderate but consistent across unbalance magnitude, speed variation, and noisy measurements [23]. Studies using active magnetic bearings or high-authority actuators often report larger reductions, but these systems rely on specialized hardware and displacement sensing that may not be available in compact medical devices. The current approach operates with housing-mounted accelerometers and does not require explicit unbalance identification or frequency estimation. This characteristic makes it suitable for medical rotating equipment where installation space and system modification are limited. At the same time, the results indicate that performance depends on the observability of the vibration mode at the measurement location. Future studies should therefore consider multi-point sensing and longer-duration tests to address structural coupling and operational drift that occur in extended clinical use.

4. Conclusion

This work investigated the reduction of residual unbalance moments in rotating medical structures using vibration-based gain adjustment. The experimental results show that peak radial acceleration was reduced by an average of 44.4% across multiple unbalance levels, and the reduction was maintained when rotational speed varied and measurement noise was present. The control scheme relies on acceleration feedback and does not require displacement sensors or explicit estimation of unbalance parameters, which fits the sensing and integration constraints of compact medical equipment. The results indicate that adjusting feedback gains in response to measured vibration can suppress synchronous excitation while preserving the overall dynamic behavior of the structure. From an application perspective, the method provides a practical option for vibration mitigation in rotating medical devices where hardware modification is limited. The present study is restricted to a single structural setup and a limited operating range. Further investigations should include different device configurations, extended operating periods, and multi-point measurements to evaluate long-term stability and structural coupling effects under clinical conditions.