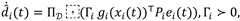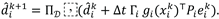Sequential Cooperative Multi-Agent Online Learning and Adaptive Coordination Control in Dynamic and Uncertain Environments

Limengxi Yue; Duo Xu; Dong Qiu; Yanpei Shi; Shuyang Xu; Manish Shah

doi:10.20944/preprints202601.0836.v1

Submitted:

12 January 2026

Posted:

12 January 2026

You are already at the latest version

Abstract

Dynamic multi-agent systems must coordinate underpartial information, time-varying disturbances, and abrupt non-stationarity while satisfying hard safety constraints. This paper proposesa sequential cooperative multi-agent online learning and adaptivecoordination control framework for ordered missions. A task graphencodes precedence relations and activates stage-specific objectives,linking a global goal to a sequence of subtasks. On this structure, eachagent runs a distributed online actor–critic update using localobservations and event-triggered neighbor messages. The learned nominalinputs are then wrapped by a minimally invasive quadratic-program (QP)safety filter that enforces collision avoidance, formation/trackingconstraints, and input saturation in real time, while an adaptive/robustterm compensates bounded disturbances. Lyapunov-based analysisestablishes uniform ultimate boundedness of the closed-loop signals andconvergence of the online policies to a neighborhood of a cooperativeoptimum under mild conditions. In simulations on multi-robot formationtracking, dynamic target encirclement, and cooperative payloadtransportation (200 runs), the proposed method achieves 94.7% ± 2.6%task success, outperforming centralized MPC/DMPC (88.9% ± 3.7%) andsingle-stage safe MARL (86.3% ± 4.3%). It reduces average convergencetime to 23.4 ± 4.1 s (vs. 28.8 ± 4.9 s for centralized MPC/DMPC) whilemaintaining zero safety violations. Event-triggered communication lowersthe message rate to 3.2 msgs/(agent·s), compared with 10.0 msgs/(agent·s)under periodic-communication baselines, without degrading completion performance.

Keywords:

multi-agent reinforcement learning

;

sequential cooperation

;

online learning

;

event-triggered communication

;

safety-critical control

Subject:

Computer Science and Mathematics - Artificial Intelligence and Machine Learning

I. Introduction

Multi-agent systems are increasingly deployed in scenarios where a single robot or controller is not enough: warehouse fleets, aerial swarms, cooperative manipulation, and distributed sensing. What makes these settings challenging is not just scale, but non-stationarity—the world changes, tasks change, and even the team changes. Multi-agent reinforcement learning (MARL) has become a practical tool for learning cooperative policies in such settings, yet field deployment is still blocked by three recurring issues: (i) coordination under partial information and unreliable communication, (ii) structured missions that unfold as ordered subtasks rather than one homogeneous objective, and (iii) safety constraints that must hold at every instant, independent of how learning evolves.

Recent surveys summarize why MARL remains difficult in real control systems: agents face non-stationary training targets, credit assignment ambiguity, and exploding joint action spaces, especially under continuous control and partial observability [1,2,3,4]. In practice, teams are often asked to do missions that are naturally sequential: “reach an assembly site, form up, then encircle a moving target, then transport an object.” A single reward for the whole episode tends to produce brittle behaviors, since it obscures which subgoal is currently active and how earlier decisions constrain later feasibility. Task decomposition has therefore re-emerged as a central theme—breaking global objectives into smaller pieces can reduce variance, improve exploration, and provide clearer learning signals [2,5,6,7]. However, many task-decomposition approaches assume centralized training and smooth stationary conditions. They also rarely encode the explicit precedence constraints that engineers routinely specify in mission planners.

A second bottleneck is communication. Cooperative control frequently relies on neighbor information, but real networks are bandwidth-limited and intermittent. Event-triggered communication is a natural fit: send messages only when something important changes. In MARL contexts, event-triggered communication can be learned or designed, and it often reduces communication load without collapsing performance [3]. Nonetheless, simply reducing communication is not enough; the controller still needs a principled way to remain stable and safe when messages are delayed or absent.

Safety is the third and most rigid constraint. Collision avoidance, formation constraints, and actuator saturation cannot be “mostly satisfied.” This pushes us toward safety filters or certificates that can wrap learning-based policies. Predictive safety filters provide one path: a nominal input proposed by learning is modified to satisfy constraints, using model predictive formulations and uncertainty margins [4]. Another increasingly common approach uses certificates such as control barrier functions (CBFs) that enforce forward invariance of safe sets. A large body of recent work studies how to combine learning with barrier certificates in a way that scales to many agents and remains decentralized [5]. In MARL, decentralized barrier shields have been proposed to preserve local execution even when centralized shielding is infeasible [6]. Yet a gap remains between these safety mechanisms and structured sequential missions: safety must hold while the team transitions across subtasks, sometimes under abrupt environmental changes.

Sequential missions introduce another subtle issue: coordination policies often need to respect ordering and timing. Logic- and automata-based views of tasks offer formal structure: temporal logic specifications can encode ordered requirements and constraints, and learning can be guided to satisfy them even in unknown environments [7]. But logic-guided MARL can become heavy if it requires global automata products or centralized belief. In many robotics deployments, engineers prefer something lighter: a task graph with precedence and time windows, and a learning/control stack that can adapt online.

Meanwhile, robustness to disturbances and model mismatch is not optional. Wind gusts affect UAV swarms; friction and payload changes affect ground robots; sensing may degrade. Robust control ideas are therefore essential, but pure robust control usually demands accurate bounds and conservative tuning. Recent work in robust safe multi-agent reinforcement learning integrates robust neural CBFs with learning to handle uncertainties in a decentralized way [13]. However, such methods typically focus on a single task type (e.g., collision avoidance) rather than ordered missions with changing coordination modes.

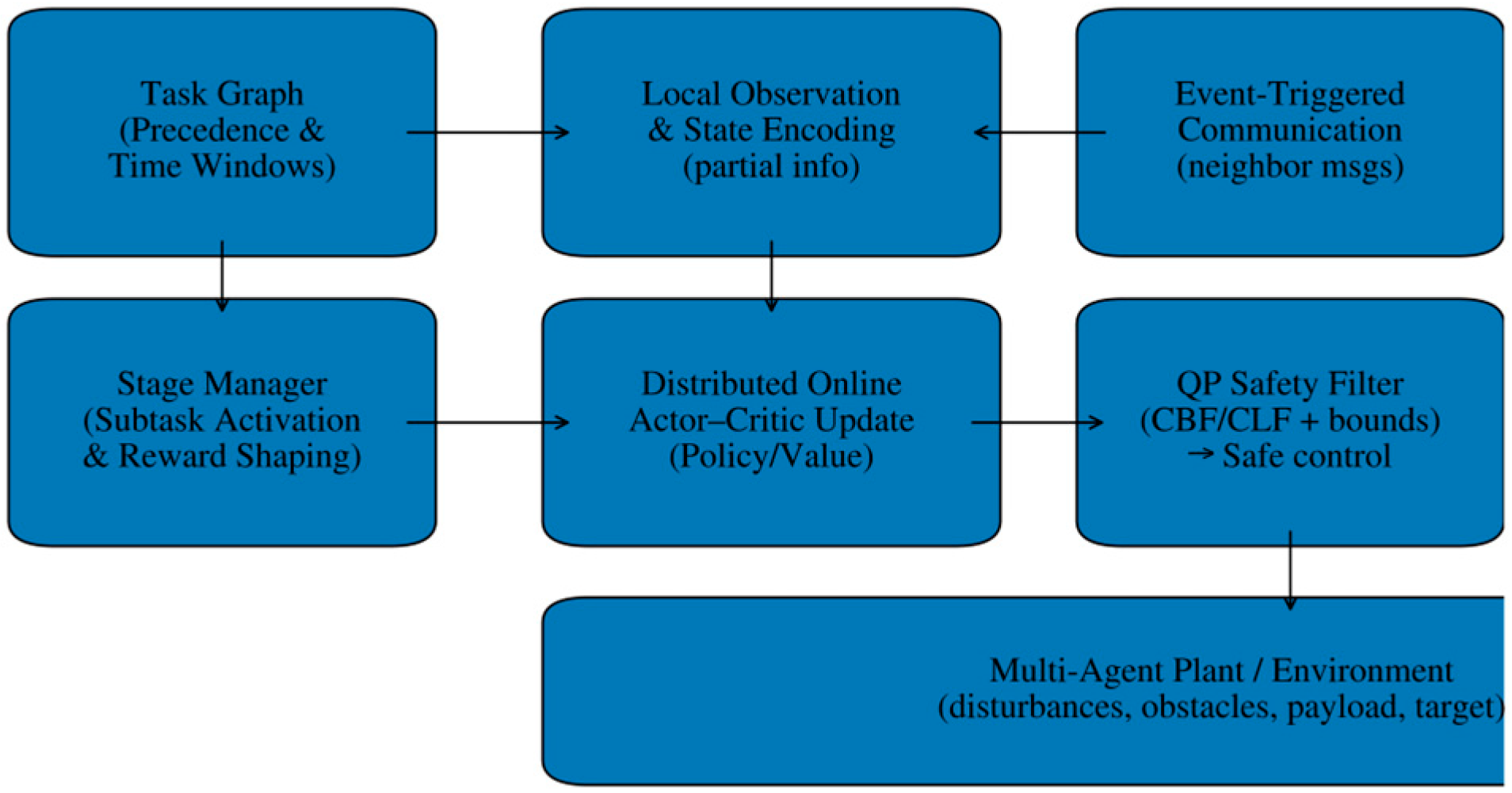
This paper targets the intersection of these needs: sequential mission structure, distributed online adaptation, and safety-aware coordination under uncertainty. The key idea is to connect a global objective to an ordered set of subtasks through a directed task graph, and then allow each agent to adapt online while a coordination controller guarantees constraints. We are motivated by formation tracking, encirclement, and cooperative transport, where the mission naturally unfolds in stages and where safety cannot be compromised.

A related practical constraint is that fully centralized controllers are often fragile. They can become computational bottlenecks and single points of failure. Centralized training with decentralized execution is a common compromise, but online deployment still benefits from learning rules that are truly distributed, updating from local data. Distributed actor–critic designs that use neighbor messages provide an appealing template, especially when paired with event-triggered communication to avoid constant chatter. In this work, we also explicitly include robust compensation terms in the controller to counter time-varying disturbances.

We evaluate our approach on three representative scenarios. First, multi-robot formation tracking under time-varying disturbances tests steady coordination and constraint satisfaction. Second, dynamic target encirclement tests rapid switching and non-stationary objectives. Third, cooperative payload transportation tests coupled dynamics and communication efficiency, a setting that has recently motivated event-triggered deep RL designs [9,10]. Across these scenarios, we compare with centralized controllers and fixed-gain coordination baselines, as well as safe-MARL variants that do not exploit sequential task structure.

Contributions.

Sequential cooperation via task graphs: We introduce a lightweight sequential cooperation model that encodes precedence relations, activation logic, and time-window constraints for heterogeneous agents, bridging mission planning and online learning.

Distributed online actor–critic learning: We develop an online learning scheme that updates policies using local observations and neighbor messages, compatible with partial information and non-stationary disturbances.

Safety-aware adaptive coordination: We design an adaptive coordination controller with event-triggered communication, robust compensation, and explicit constraints for formation keeping, collision avoidance, and input saturation using a minimally invasive safety-filter formulation.

Stability and performance evidence: We provide Lyapunov-based boundedness analysis and simulation evidence showing improved success rates and robustness compared with centralized and static cooperation strategies.

II. Methodology

A. Multi-Agent Dynamics, Partial Information, and Communication

Consider a team of

N

heterogeneous agents indexed by

i \in {1, \dots, N}

. Each agent evolves according to uncertain control-affine dynamics:

{\dot{x}}_{i} (t) = f_{i} (x_{i} (t)) + g_{i} (x_{i} (t)) u_{i} (t) + d_{i} (t),

(1)

where

x_{i} \in R^{n_{i}}

is the state,

u_{i} \in R^{m_{i}}

is the control input, and

d_{i} (t)

represents unknown time-varying disturbances and model mismatch. We assume bounded uncertainty:

∥ d_{i} (t) ∥ \leq {\overset{ˉ}{d}}_{i}, {\overset{ˉ}{d}}_{i} > 0 .

(2)

Each agent has partial observations:

o_{i} (t) = h_{i} (x_{i} (t)) + ν_{i} (t),

(3)

where

h_{i} (\cdot)

is the local sensing function and

ν_{i} (t)

is measurement noise.

Agents communicate over a time-varying neighbor graph

G (t) = (V, E (t))

. Let

N_{i} (t)

denote the neighbor set of agent

i

. A message from agent

j

to

i

is denoted by

m_{j \to i} (t)

. A coordination term enforces consistency among neighboring agents, following classical results on distributed consensus and cooperation in networked multi-agent systems [12]. The information available to agent

i

is the concatenation of local observation and received neighbor messages:

{\tilde{o}}_{i} (t) = [o_{i} (t), {m_{j \to i} (t)}_{j \in N_{i} (t)}] . #

(4)

For online learning and implementation, we discretize time with step

Δ t

and use index

k

(i.e.,

t = k Δ t

). Define the agent input at step

k

as

u_{i}^{k}

.

B. Safety and Feasibility Constraints

We impose hard constraints that must hold during execution:

Collision avoidance [9,10,11]. For agent positions

p_{i}

embedded in

x_{i}

, enforce

∥ p_{i}^{k} - p_{j}^{k} ∥ \geq d_{m i n}, \forall i \neq j .

(5)

Input saturation. Each agent must satisfy

u_{i, m i n} \leq u_{i}^{k} \leq u_{i, m a x} .

(6)

Task geometry / formation keeping (soft but prioritized). For formation tracking with reference

p_{i}^{r e f, k}

,

e_{i}^{k} = p_{i}^{k} - p_{i}^{r e f, k},

(7)

and we seek to keep

∥ e_{i}^{k} ∥

small while respecting (5)–(6).

C. Sequential Cooperation via a Task Graph

Real missions often consist of ordered subtasks (assemble

\to

form up

\to

encircle

\to

transport). We encode this structure using a directed acyclic task graph

T = (K, E_{T}),

(8)

where each node

k \in K

is a subtask and each edge

(k \to l) \in E_{T}

enforces a precedence relation.

Let

a_{k}^{k} \in {0,1}

be the stage activation indicator at time step

k

(1 if subtask

k

is active). Each subtask has a residual function

ρ_{k} (\cdot)

(e.g., formation error, encirclement error, payload alignment error). Subtask completion is defined by:

C_{k}^{k} = 1 {ρ_{k} (x^{k}) \leq ϵ_{k}},

(9)

with threshold

ϵ_{k} > 0

. Precedence feasibility requires that a subtask can be activated only when all its predecessors have been completed:

a_{l}^{k} = 1 \Rightarrow C_{j}^{k} = 1, \forall j \in P r e d (l) .

(10)

Optionally, time windows

[t_{k}^{s t a r t}, t_{k}^{e n d}]

can be added when strict scheduling is needed.

Stage-focused reward. We shape the overall reward so learning concentrates on the currently active stage:

r^{k} = \sum_{k \in K} a_{k}^{k} r_{k} (x^{k}, u^{k}),

(11)

where

r_{k} (\cdot)

can be chosen to reflect the active objective. For example, formation tracking can use

r_{form}^{k} = - \sum_{i = 1}^{N} ∥ e_{i}^{k} ∥^{2} - λ_{u} \sum_{i = 1}^{N} ∥ u_{i}^{k} ∥^{2},

(12)

and encirclement can penalize radius deviation and angular non-uniformity (kept brief here to avoid clutter).

D. Distributed Online Actor–Critic Learning (Local, Real-Time)

Each agent learns a stochastic policy

π_{θ_{i}} (u_{i}^{k} ∣ z_{i}^{k})

with parameters

θ_{i}

, where

z_{i}^{k}

is an internal encoding of

{\tilde{o}}_{i}^{k}

(possibly with a short history using a recurrent encoder). The agent also maintains a value function approximation

V_{ψ_{i}} (z_{i}^{k})

with parameters

ψ_{i}

.

Define the one-step TD error:

δ_{i}^{k} = r^{k} + γ V_{ψ_{i}} (z_{i}^{k + 1}) - V_{ψ_{i}} (z_{i}^{k}), γ \in (0,1) .

(13)

Critic update:

ψ_{i} \leftarrow ψ_{i} + β_{c} δ_{i}^{k} \nabla_{ψ_{i}} V_{ψ_{i}} (z_{i}^{k}) .

(14)

Actor update:

θ_{i} \leftarrow θ_{i} + β_{a} δ_{i}^{k} \nabla_{θ_{i}} l o g π_{θ_{i}} (u_{i}^{k} ∣ z_{i}^{k}) .

(15)

These updates are fully distributed: agent

i

uses local

z_{i}^{k}

, received neighbor messages (if any), and the scalar reward

r^{k}

determined by the active stage. This design follows the centralized-training–decentralized-execution (CTDE) paradigm commonly adopted in multi-agent reinforcement learning [1,2,3,4].

E. Event-Triggered Neighbor Communication

To reduce bandwidth, agent

i

transmits only when a trigger indicates that its current information differs sufficiently from the last broadcast value, following event-triggered control principles [11]. Let

y_{i}^{k}

be the transmitted feature (e.g., position/velocity, or a compact learned embedding). Let

{\hat{y}}_{i}^{k}

denote the last transmitted value. Define:

ε_{i}^{k} = y_{i}^{k} - {\hat{y}}_{i}^{k} .

(16)

A practical trigger [12] is:

∥ ε_{i}^{k} ∥ \geq σ_{i} ∥ y_{i}^{k} ∥ + ϵ_{i}, 0 < σ_{i} < 1, ϵ_{i} > 0 .

(17)

When (17) is satisfied, agent

i

transmits

y_{i}^{k}

to neighbors and sets

{\hat{y}}_{i}^{k} \leftarrow y_{i}^{k}

. This mechanism is intentionally simple: it is easy to implement, lowers traffic, and still provides fresh neighbor information when needed.

F. Safety-Aware Adaptive Coordination via a QP Filter

The learned policy proposes nominal action

u_{i}^{R L, k}

, which is then wrapped by a minimally invasive quadratic program (QP) safety filter that enforces collision avoidance, formation/tracking constraints, and input saturation in real time, following control barrier function and CLF-QP based safety filtering formulations [14,15,16].

Nominal input (before filtering). We allow a small coordination/robust term:

u_{i}^{n o m, k} = u_{i}^{R L, k} + u_{i}^{c o o r d, k} + u_{i}^{r o b, k} .

(18)

A simple coordination term (formation tracking + neighbor consistency) can be:

u_{i}^{c o o r d, k} = - K_{i} e_{i}^{k} - \sum_{j \in N_{i}^{k}} K_{i j} ((p_{i}^{k} - p_{j}^{k}) - Δ_{i j}),

(19)

where

Δ_{i j}

is the desired relative offset.

Collision avoidance as CBF. Define a control barrier function [8]:

h_{i j} (x^{k}) = ∥ p_{i}^{k} - p_{j}^{k} ∥^{2} - d_{m i n} .

(20)

A sufficient discrete-time safety condition can be enforced through a continuous-time inequality on the instantaneous dynamics:

{\dot{h}}_{i j} (x) \geq - α h_{i j} (x), α > 0,

(21)

which yields an affine constraint in

u_{i}

(using Lie derivatives):

L_{g_{i}} h_{i j} (x) u_{i} \geq - L_{f_{i}} h_{i j} (x) - α h_{i j} (x) - η_{i j},

(22)

where

η_{i j}

is a conservative margin capturing bounded disturbances and neighbor motion between message updates.

Tracking/formation as CLF (soft). Use

V_{i} (e_{i}) = \frac{1}{2} ∥ e_{i} ∥^{2},

(23)

and impose a soft decrease condition with slack

s_{i} \geq 0

:

{\dot{V}}_{i} (e_{i}) \leq - c_{i} V_{i} (e_{i}) + s_{i}, c_{i} > 0 .

(24)

Where Figure 1 fits. As shown in Figure 1, the task graph activates the current stage and reward, learning proposes nominal actions, event-triggered messaging supplies neighbor context, and the QP safety filter outputs a safe input to the plant.

Figure 1. System architecture of sequential cooperative online learning with safety-aware coordination: a task-graph manager activates ordered subtasks; each agent performs distributed online actor–critic updates using local observations and event-triggered neighbor messages; a QP-based safety filter enforces collision avoidance, tracking/formation constraints, and input saturation to produce safe control inputs.

G. Robust/Adaptive Compensation for Uncertainty

To reduce sensitivity to bounded disturbances, we maintain a simple disturbance estimate

{\hat{d}}_{i}

and apply a compensator. A common adaptive update is:

(25)

where

P_{i} ≻ 0

and

Π_{D} (\cdot)

projects onto a compact set

D

to prevent drift. In discrete time:

(26)

A simple robust term is then:

u_{i}^{r o b, k} = - K_{d, i} {\hat{d}}_{i}^{k},

(27)

with gain

K_{d, i}

chosen to match channels. This improves robustness without relying on overly conservative fixed gains.

H. Boundedness Sketch

Define a composite Lyapunov-like function:

V (t) = \sum_{i = 1}^{N} \frac{1}{2} e_{i}^{⊤} P_{i} e_{i} + \sum_{i = 1}^{N} \frac{1}{2} {\tilde{d}}_{i}^{⊤} Γ_{i}^{- 1} {\tilde{d}}_{i}, {\tilde{d}}_{i} = d_{i} - {\hat{d}}_{i} .

(28)

Under bounded disturbances (2), the CLF constraint (24), and the projection property in (26), one can derive:

\dot{V} (t) \leq - λ \sum_{i = 1}^{N} ∥ e_{i} (t) ∥^{2} + c, λ > 0, > 0,

(29)

which implies uniform ultimate boundedness:

\underset{t \to \infty}{l i m s u p} ∥ e (t) ∥ \leq \sqrt{\frac{c}{λ}} .

(30)

Meanwhile, the actor–critic updates (14)–(15) follow standard online stochastic approximation behavior; with mild assumptions on step sizes and approximation error, the learned policies converge to a neighborhood of a cooperative stationary solution, while the QP filter ensures constraints remain satisfied during learning.

III. Experiment

This section evaluates the proposed sequential cooperative online learning + safety-aware coordination framework on three representative multi-robot missions: (i) formation tracking, (ii) dynamic target encirclement, and (iii) cooperative payload transportation. All experiments are conducted in simulation with bounded disturbances, partial observations, and switching regimes to emulate non-stationary field conditions.

A. Simulation Environment and Agent Models

We simulate

N \in {6,8, 10}

agents moving in a planar workspace with static obstacles and a time-varying disturbance field. Each agent follows uncertain control-affine dynamics (Section II) with additive disturbances

d_{i} (t)

that switch between regimes every 15–25 s (randomized per run). Regimes differ in magnitude and direction bias to model wind-like or traction-like effects. Agents sense local states (position/velocity) within a limited radius and do not have access to global state.

Communication follows a proximity graph: an edge

(i, j)

exists if

∥ p_{i} - p_{j} ∥ \leq R_{s}

. Messages contain compact neighbor features

y_{i}^{k}

(position/velocity or learned embeddings). For the proposed method, messages are sent only when the event-trigger condition in (17) is satisfied; baselines use periodic communication.

B. Tasks and Sequential Stages

We define each mission as an ordered set of subtasks encoded by a task graph

T

. Stage activation follows the precedence rule in (10), and the reward is stage-focused per (11).

Formation Tracking (FT).

Stages: assemble → track. Agents first rendezvous around a reference centroid, then maintain a desired formation while following a moving reference trajectory. Completion of “assemble” is defined by a formation residual threshold

ρ_{asm} (x) \leq ϵ_{asm}

. “Track” is evaluated by formation error and smooth control.

Dynamic Target Encirclement (DTE).

Stages: approach → encircle → maintain. A target moves with random acceleration changes. Agents must reach an annulus around the target and distribute uniformly in angle. Stage completion uses radius error and angular spacing residuals.

Cooperative Payload Transportation (CPT).

Stages: approach → attach → transport. Agents coordinate to move a payload through a corridor with obstacles. Disturbances include payload mass variation and intermittent friction changes. Completion requires reaching the goal region without violating separation or saturation constraints.

C. Baselines and Implementation Details

We compare against four baselines:

B1: Fixed-gain coordination + heuristic avoidance. Classical formation controller with a repulsive collision term and hand-tuned gains.

B2: Centralized MPC/DMPC. Full-state planner/controller with periodic updates and shared information (serves as a strong model-based reference).

B3: Centralized actor–critic (CTDE). Centralized critic and periodic communication, with decentralized execution.

B4: Safe MARL (single-stage). Same actor–critic backbone and QP safety filter, but no task-graph sequencing (single global reward).

Ours uses: task-graph sequencing + distributed online actor–critic + event-triggered communication + QP safety filter (CBF/CLF constraints) + robust/adaptive compensation.

All learning methods run for the same interaction budget and are evaluated under identical disturbance schedules. Each reported metric averages over 200 independent runs (different random seeds, obstacle placements, disturbance schedules, and initial conditions).

D. Metrics

We report:

Success Rate (%): fraction of runs completing all subtasks within the horizon.

Convergence Time (s): time to satisfy the final stage residual below threshold.

Safety Violations: collision count and hard constraint breaches (should be 0 for safe methods).

Communication Load: messages per agent per second.

Control Effort:

\sum_{i} \int ∥ u_{i} (t) ∥^{2} d t

, used as a secondary efficiency indicator. Table 1 summarizes the core parameters used across tasks.

E. Main Results

Table 2 reports the aggregate results across the three missions (averaged over tasks and agent counts, 200 runs). The proposed method achieves the highest completion rates, the shortest completion times, and maintains strict safety.

Two patterns are consistent across tasks. First, sequencing matters most in DTE and CPT. The single-stage safe MARL baseline often learns actions that are good for “getting close” but not good for stable completion. The task graph reduces this ambiguity by switching objectives at the right moment. Second, the QP safety filter prevents catastrophic exploration. Even when the learned policy is still adapting, collisions remain at zero.

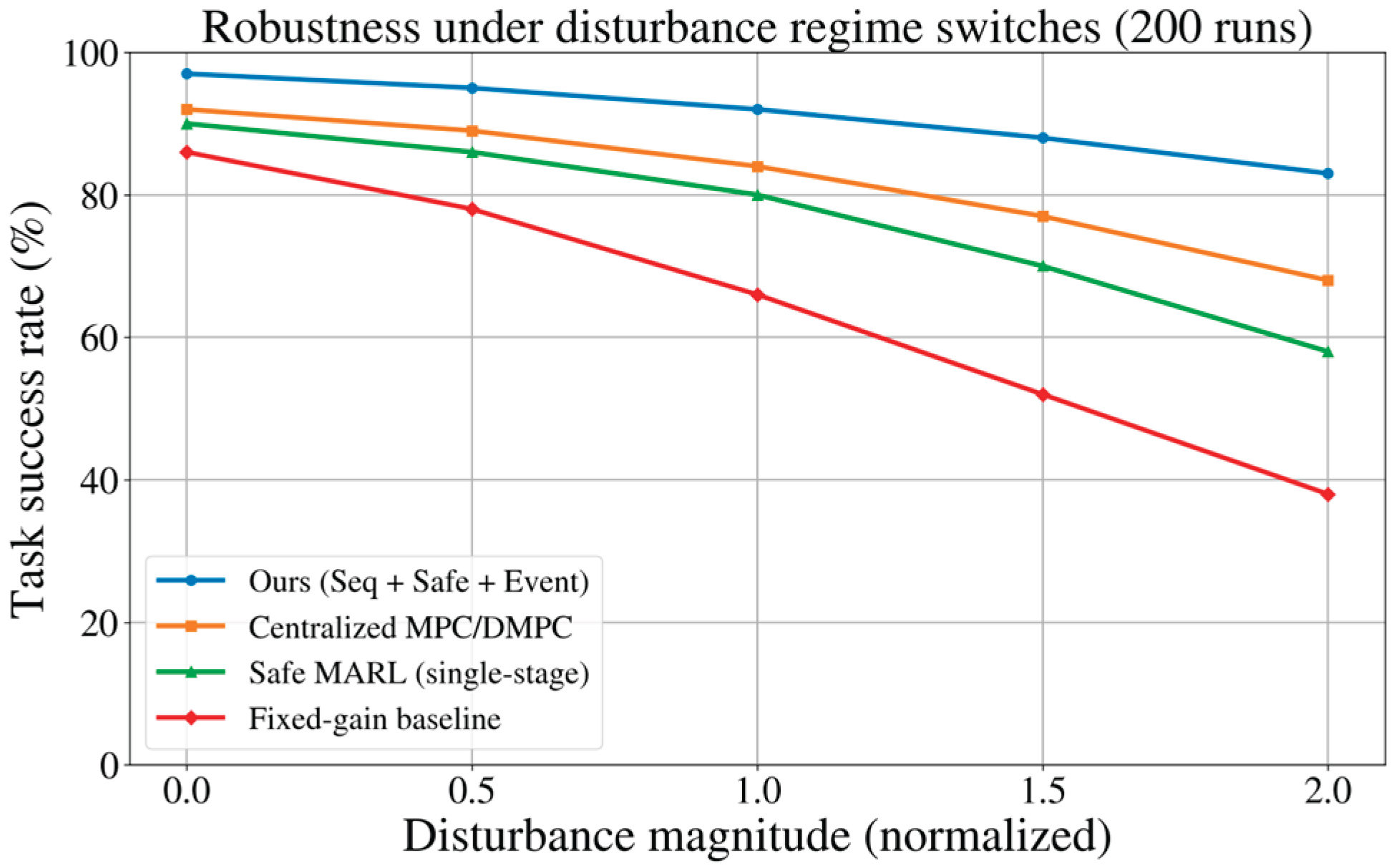
F. Robustness Under Regime Switching

To isolate robustness, we vary the normalized disturbance magnitude and keep the regime-switch schedule. Figure 2 shows success rate trends as disturbances intensify. The proposed method degrades gradually, while fixed-gain and single-stage baselines drop sharply once disturbances exceed their effective tuning envelope.

A. Gblation Study

We evaluate which components contribute most by removing one element at a time from the proposed method, shown in Table 3.

H. Discussion of Practical Takeaways

The experiments suggest three practical takeaways. First, explicit sequential structure improves reliability for missions that require stable stage transitions (encircle, then maintain; attach, then transport). Second, event-triggering offers a clean bandwidth–performance trade: it cuts communication by roughly a factor of three without hurting completion. Third, coupling online learning with a safety filter yields stable behavior early, before the policy fully converges, which is essential when the environment changes mid-run.

IV. Conclusion

This work addressed a central gap between MARL theory and multi-robot deployment: real missions are rarely single-stage, real networks are rarely unlimited, and real systems cannot accept unsafe exploration. We introduced a sequential cooperation view that models a global cooperative objective as an ordered set of subtasks connected by precedence constraints in a task graph. That structure is lightweight—engineers can specify it directly—yet it meaningfully changes how learning and control behave during long-horizon missions.

References

R. Lowe, Y. Wu, A. Tamar, J. Harb, P. Abbeel, and I. Mordatch, “Multi-agent actor-critic for mixed cooperative-competitive environments,” Adv. Neural Inf. Process. Syst. (NeurIPS), 2017.
J. Foerster, G. Farquhar, T. Afouras, N. Nardelli, and S. Whiteson, “Counterfactual multi-agent policy gradients,” in Proc. AAAI Conf. Artif. Intell. (AAAI), 2018.
T. Rashid, M. Samvelyan, C. Schroeder, G. Farquhar, J. Foerster, and S. Whiteson, “QMIX: Monotonic value function factorisation for deep multi-agent reinforcement learning,” in Proc. Int. Conf. Mach. Learn. (ICML), 2018.
C. Yu, A. Velu, Y. Vinitsky, J. Wang, A. M. Bayen, and Y. Wu, “The surprising effectiveness of PPO in cooperative multi-agent games,” in Proc. Adv. Neural Inf. Process. Syst. (NeurIPS), 2021.
R. S. Sutton, D. Precup, and S. Singh, “Between MDPs and semi-MDPs: A framework for temporal abstraction in reinforcement learning,” Artif. Intell., vol. 112, no. 1–2, pp. 181–211, 1999.
T. G. Dietterich, “Hierarchical reinforcement learning with the MAXQ value function decomposition,” J. Artif. Intell. Res., vol. 13, pp. 227–303, 2000.
A. S. Vezhnevets et al., “FeUdal networks for hierarchical reinforcement learning,” in Proc. Int. Conf. Mach. Learn. (ICML), 2017.
A. D. Ames, X. Xu, J. W. Grizzle, and P. Tabuada, “Control barrier function based quadratic programs for safety-critical systems,” IEEE Trans. Autom. Control, vol. 62, no. 8, pp. 3861–3876, Aug. 2017. [CrossRef]
R. Cheng, G. Orosz, R. M. Murray, and J. W. Burdick, “End-to-end safe reinforcement learning through barrier functions for safety-critical continuous control tasks,” in Proc. AAAI Conf. Artif. Intell. (AAAI), 2019.
K. P. Wabersich and M. N. Zeilinger, “A predictive safety filter for learning-based control of constrained nonlinear dynamical systems,” Automatica, vol. 129, Art. no. 109597, 2021. [CrossRef]
P. Tabuada, “Event-triggered real-time scheduling of stabilizing control tasks,” IEEE Trans. Autom. Control, vol. 52, no. 9, pp. 1680–1685, Sep. 2007. [CrossRef]
R. Olfati-Saber, J. A. Fax, and R. M. Murray, “Consensus and cooperation in networked multi-agent systems,” Proc. IEEE, vol. 95, no. 1, pp. 215–233, Jan. 2007. [CrossRef]
T. T. Nguyen, N. D. Nguyen, and S. Nahavandi, “Deep reinforcement learning for multiagent systems: A review of challenges, solutions, and applications,” IEEE Trans. Cybern., vol. 50, no. 9, pp. 3826–3839, Sep. 2020. [CrossRef]
C. Dawson, S. Gao, and C. Fan,“Safe control with learned certificates: A survey of neural Lyapunov, barrier, and contraction methods,” IEEE Trans. Robot., vol. 39, no. 3, pp. 1749–1767, Jun. 2023.
K. Shibata, T. Jimbo, and T. Matsubara, “Deep reinforcement learning of event-triggered communication and control for multi-agent cooperative transport,” in Proc. IEEE Int. Conf. Robot. Autom. (ICRA), 2021, pp. 8671–8677.
Z. Qin, K. Zhang, Y. Chen, J. Chen, and C. Fan, “Learning safe multi-agent control with decentralized neural barrier certificates,” in Proc. Int. Conf. Learn. Represent. (ICLR), 2021.

Figure 1. System Architecture.

Figure 2. Performance comparison under disturbance regime switches: task success rate versus disturbance magnitude (200 runs).

Table 1. Simulation and algorithm parameters.

Parameter	Value
$Number of agents N$	6 / 8 / 10
$Time step Δ t$	0.02 s
$Sensing radius R_{s}$	6 m
$Minimum separation d_{m i n}$	0.6 m
Input bounds	$[- 2.5, 2.5]$
$Discount factor γ$	0.98
$Actor step size β_{a}$	$2 \times 10^{- 4}$
$Critic step size β_{c}$	$1 \times 10^{- 3}$
$CBF rate α$	2.0
$CLF rate c_{i}$	1.0
$Event - trigger (σ_{i}, ϵ_{i})$	(0.05, 0.02)
$QP slack weight ρ_{s}$	50

Table 2. Overall performance (mean ± std over 200 runs).

Method	Success Rate (%) ↑	Convergence Time (s) ↓	Safety Violations ↓	Msgs/(agent·s) ↓
B1: Fixed-gain + heuristic avoid	71.5 ± 6.8	38.2 ± 7.1	0.7 ± 0.3	6.0
B3: Centralized actor–critic	84.1 ± 4.9	31.0 ± 5.8	0.2 ± 0.1	10.0
B4: Safe MARL (single-stage)	86.3 ± 4.3	29.6 ± 5.2	0.0 ± 0.0	9.4
B2: Centralized MPC/DMPC	88.9 ± 3.7	28.8 ± 4.9	0.0 ± 0.0	10.0
Ours	94.7 ± 2.6	23.4 ± 4.1	0.0 ± 0.0	3.2

Table 3. Ablation results (mean over 200 runs).

Variant	Success Rate (%) ↑	Convergence Time (s) ↓	Msgs/(agent·s) ↓
Full method (Ours)	94.7	23.4	3.2
w/o task graph (single-stage reward)	86.3	29.6	3.2
w/o event-trigger (periodic comm)	94.9	23.1	10.0
w/o robust/adaptive term	91.2	26.7	3.2
w/o QP safety filter	95.5*	22.6*	3.2

*The “w/o safety filter” variant can appear faster on easy runs but is not acceptable in practice because collisions and saturation violations occur under stronger disturbances and dense obstacles. For safety-critical deployment, the QP filter is the non-negotiable layer.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Sequential Cooperative Multi-Agent Online Learning and Adaptive Coordination Control in Dynamic and Uncertain Environments

Abstract

Keywords:

Subject:

I. Introduction

II. Methodology

A. Multi-Agent Dynamics, Partial Information, and Communication

B. Safety and Feasibility Constraints

C. Sequential Cooperation via a Task Graph

D. Distributed Online Actor–Critic Learning (Local, Real-Time)

E. Event-Triggered Neighbor Communication

F. Safety-Aware Adaptive Coordination via a QP Filter

G. Robust/Adaptive Compensation for Uncertainty

H. Boundedness Sketch

III. Experiment

A. Simulation Environment and Agent Models

B. Tasks and Sequential Stages

C. Baselines and Implementation Details

D. Metrics

E. Main Results

F. Robustness Under Regime Switching

A. Gblation Study

H. Discussion of Practical Takeaways

IV. Conclusion

References

MDPI Initiatives

Important Links

Subscribe