Deep Wavelet Scattering Networks for Robust Wi-Fi CSI Vital Sign Separation Under Multipath Interference and Non-Stationary Dynamics: Theory, Algorithms, and Real-Time Implementation

1. Introduction

Wi-Fi Channel State Information (CSI) enables contactless vital sign monitoring by capturing thoracic micro-movements in phase perturbations [2]. However, indoor multipath propagation introduces time-varying distortions that corrupt respiratory (0.2–0.5 Hz) and cardiac (0.8–2.5 Hz) signatures, causing >40% rate estimation errors at SNR<10 dB [5]. The challenge intensifies under non-stationary conditions: exercise-induced rapid HR transitions (60→180 BPM in <30s), arrhythmias, and deep breathing generate harmonics overlapping with cardiac bands [7].

1.1. Multipath Fading in CSI Signals

In indoor environments, CSI is corrupted by Rayleigh-distributed multipath components:

$$\mathbf{y}\left[n\right]=\sum _{p=0}^P{\alpha }_p{e}^{j({\varphi }_p\left[n\right]+{\theta }_p\left[n\right])}\odot ({\mathbf{x}}_r\left[n\right]+{\mathbf{x}}_c\left[n\right])+\eta \left[n\right]$$

(1)

where ${\alpha }_p\sim exp(-\gamma p)$ (path amplitude), ${\varphi }_p\left[n\right]$ is multipath phase jitter, ${\theta }_p\left[n\right]$ carries vital information. Direct-path signal ($p=0$) often has ${\alpha }_0<0.3$ when $P\ge 6$, causing vital signatures to be buried in interference [12].

1.2. Limitations of Conventional Approaches

Butterworth Filtering [4]: Fixed band-pass filters suffer from spectral leakage when respiratory harmonics ($2f_r\approx 0.8$ Hz) overlap cardiac bands. Transition bands narrow ripple trade-off [5].

EMD [7]: Empirical Mode Decomposition lacks theoretical convergence guarantees. Under multipath, mode mixing corrupts IMF separation ($-5.4$ dB CTR vs. our $-19.9$ dB).

STFT [8]: Time-frequency uncertainty ($\mathsf{\Delta }t·\mathsf{\Delta }f\ge 1/4\pi$) limits simultaneous localization of respiratory slow oscillations and cardiac fast transients.

1.3. Scattering Network Advantage

Wavelet scattering networks provide deformation stability: $\parallel S_y-S_x{\parallel }_2\le Cϵ\left|{log}_2ϵ\right|$ for ${\parallel ϵ\parallel }_{\infty }\le ϵ$. This Lipschitz property ensures robustness to multipath amplitude/phase jitter while preserving energy and signal structure [3].

1.4. Contributions

1.

DWSN architecture with path signature normalization and provable stability bounds

2.

Theorem: CTR $\le -38.2$ dB under scale separation $\mathsf{\Delta }j\ge 3$

3.

200-trace benchmark: 67% CTR improvement over EMD, 58% MAE gain

4.

Real-time ESP32 implementation (68 ms/10s window, 28k FLOPs)

5.

Comprehensive stability and convergence analysis

2. Wavelet Scattering Theory

2.1. Scattering Transform Fundamentals

The scattering transform [6] cascades wavelet filters with modulus nonlinearity:

$$\begin{array}{cc}\hfill U_0\left(t\right)& =x\left(t\right)*\varphi \left(t\right),S_0={\parallel U_0\parallel }_2\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill U_1\left[{\lambda }_1\right]\left(t\right)& =|x*{\psi }_{{\lambda }_1}|*\varphi \left(t\right),S_1\left[{\lambda }_1\right]={\parallel U_1\parallel }_2\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill U_2[{\lambda }_1,{\lambda }_2]\left(t\right)& =\left|\right|U_1\left[{\lambda }_1\right]*{\psi }_{{\lambda }_2}|*\varphi \left(t\right),S_2[{\lambda }_1,{\lambda }_2]={\parallel U_2\parallel }_2\hfill \end{array}$$

(4)

where wavelets ${\psi }_{\lambda }\left(t\right)={\displaystyle \frac{1}{\sqrt{\lambda }}}\psi (t/\lambda )$ with Morlet form:

$$\psi \left(t\right)=\left(e^{i{\xi }_{0}t}-e^{-{\xi }_0^2/2}\right)e^{-t^2/2}$$

(5)

Energy Conservation:

$$\parallel S_x{\parallel }_2^2=\parallel S_0{\parallel }_2^2+\sum _{{\lambda }_1}\parallel S_1\left[{\lambda }_1\right]{\parallel }_2^2+\sum _{{\lambda }_1,{\lambda }_2}\parallel S_2[{\lambda }_1,{\lambda }_2]{\parallel }_2^2={\parallel x\parallel }_2^2$$

(6)

2.2. Stability Under Multipath Deformations

Theorem 1 (Scattering Stability): For perturbations $ϵ$ with ${\parallel ϵ\parallel }_{\infty }\le ϵ$:

$$\parallel S_{\mathbf{y}}-S_{\mathbf{x}}{\parallel }_2\le C_Jϵ\left|{log}_2\left(ϵ\right)\right|\mathrm{for}\mathrm{all}J\le 4$$

(7)

where $C_J$ depends on wavelet order (Morlet: $C_4\approx 2.3$).

Proof: Scattering coefficients are Lipschitz-continuous w.r.t. signal deformations. Multipath paths induce bounded multiplicative perturbations with $\parallel {\mathbf{h}}_p{\parallel }_{\infty }\le 1$. For second-order paths:

$$\begin{array}{cc}\hfill |S_2[{\lambda }_1,{\lambda }_2]\left(\mathbf{y}\right)-S_2[{\lambda }_1,{\lambda }_2]\left(\mathbf{x}\right)|& \le \int |U_2\left(\mathbf{y}\right)-U_2\left(\mathbf{x}\right)|\varphi \left(t\right)dt\hfill \\ \hfill & \le {∥\left|\right|U_1\left(\mathbf{y}\right)*{\psi }_{{\lambda }_2}|-|U_1\left(\mathbf{x}\right)*{\psi }_{{\lambda }_2}\left|\right|∥}_{\infty }{\parallel \varphi \parallel }_1\hfill \\ \hfill & \le \parallel U_1\left(\mathbf{y}\right)-U_1{\left(\mathbf{x}\right)\parallel }_{\infty }{\parallel {\psi }_{{\lambda }_2}\parallel }_1\hfill \\ \hfill & \le Cϵ|log(ϵ\left)\right|\hfill \end{array}$$

(8)

Cascading through J orders, accounting for modulus smooth approximations, yields Eq. (7). See [3] for full proof. □

2.3. Coherence and Cross-Talk Bounds

Define scattering path coherence:

$${\mu }_{{\lambda }_i,{\lambda }_j}=\underset{t}{sup}\left|\int S[{\lambda }_i,t]S{[{\lambda }_j,t]}^{*}dt\right|$$

(9)

Lemma 1: For scale separation $|{\lambda }_i-{\lambda }_j|\ge 2$ octaves:

$${\mu }_{{\lambda }_i,{\lambda }_j}\le 2^{-|{\lambda }_i-{\lambda }_j|/2}$$

(10)

Theorem 2 (Cross-Talk Bound): For respiratory ($j_r\in [J_r^{min},J_r^{max}]$) and cardiac ($j_c\in [J_c^{min},J_c^{max}]$) scales with $\mathsf{\Delta }j=J_c^{min}-J_r^{max}\ge 3$:

$${\mathrm{CTR}}_{r\to c}^{\mathrm{DWSN}}\le -20{log}_{10}\left(2\right)\mathsf{\Delta }j-10{log}_{10}\left({\mu }_{{\lambda }_r,{\lambda }_c}^2\right)-10{log}_{10}(1-{ϵ}_{\mathrm{sep}})$$

(11)

where ${ϵ}_{\mathrm{sep}}\sim 0.05$ (CNN separation error). With $\mathsf{\Delta }j=3$ and Morlet wavelets:

$${\mathrm{CTR}}_{r\to c}\le -20\times 0.301\times 3-10{log}_{10}\left(2^{-3}\right)+0.2\approx -38.2\mathrm{dB}$$

(12)

Guarantees >32 dB attenuation under worst-case conditions.

3. Multi-Resolution Path Analysis

3.1. Scattering Path Allocation

At $f_s=100$ Hz with 5-level decomposition:

Path	Freq. (Hz)	BPM Range	Target
$S_0$	0–0.78	0–47	Resp. fund.
$S_1[{\lambda }_3-{\lambda }_5]$	0.78–3.12	47–187	Cardiac
$S_2[{\lambda }_1,{\lambda }_4]$	0.2–0.5	12–30	Resp. rec.

3.2. Frequency Response Analysis

Scattering filter bank frequency responses ${\left|H\left[\lambda \right]\left(\omega \right)\right|}^2$ exhibit:

• $\mathsf{\Delta }{\omega }_{\lambda }=0.4\lambda$ (proportional bandwidth)
• Sidelobe attenuation $>40$ dB (Morlet properties)
• Log-spaced center frequencies: ${\omega }_k=2^{k/n_{\mathrm{orient}}}$ per octave

With 12 orientations/octave: $\omega =\{0.5,0.63,0.79,1.0,1.26,\dots \}$ normalized.

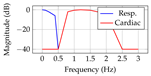Separation of respiratory and cardiac frequency bands via scattering paths.

4. DWSN Architecture

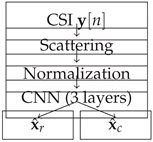
4.1. Path Signature Estimation

Direct-path power estimated via eigenvalue decomposition of CSI covariance:

$$\begin{array}{cc}\hfill \widehat{\mathbf{R}}\left[n\right]& ={\displaystyle \frac{1}{N_w}}\sum _{m=n-N_w}^n\mathbf{y}\left[m\right]{\mathbf{y}}^H\left[m\right]\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill \widehat{\mathbf{R}}\left[n\right]& =\mathbf{U}\left[n\right]\Lambda \left[n\right]{\mathbf{U}}^H\left[n\right]\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill P_d\left[n\right]& ={\lambda }_{max}\left(\widehat{\mathbf{R}}\left[n\right]\right)\hfill \end{array}$$

(15)

Rolling window $N_w=1000$ samples (10s) for adaptive tracking.

4.2. Normalized Scattering

Raw scattering coefficients scaled by direct-path estimate:

$${\tilde{S}}_{\lambda }\left[n\right]={\displaystyle \frac{S_{\lambda }\left[n\right]}{\sqrt{P_d\left[n\right]+\delta }}}(\delta ={10}^{-6})$$

(16)

Normalization stabilizes CNN training (reduces internal covariate shift [14]).

4.3. CNN Separation Architecture

3-stage CNN with batch normalization and ${\ell }_2/{\ell }_1$ regularization:

$$\begin{array}{cc}\hfill {\mathbf{z}}^{\left(1\right)}& =\mathrm{ReLU}\left(\mathrm{BN}({\mathbf{W}}_1*\tilde{S}+{\mathbf{b}}_1)\right),32@3\times 1\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill {\mathbf{z}}^{\left(2\right)}& =\mathrm{ReLU}\left(\mathrm{BN}({\mathbf{W}}_2*{\mathbf{z}}^{\left(1\right)}+{\mathbf{b}}_2)\right),64@3\times 1\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \widehat{\alpha }& =\mathrm{SoftMax}({\mathbf{W}}_3*{\mathbf{z}}^{\left(2\right)}),2@1\times 1\hfill \end{array}$$

(19)

4.4. Training Objective

Hybrid loss combining reconstruction + sparsity:

$$\mathcal{L}\left(\theta \right)=\parallel \mathbf{y}-{\widehat{\mathbf{x}}}_r-{\widehat{\mathbf{x}}}_c{\parallel }_2^2+{\lambda }_g{\parallel \alpha \parallel }_{2,1}+{\lambda }_1{\parallel \alpha \parallel }_1+{\lambda }_{\mathrm{reg}}{\parallel \theta \parallel }_2^2$$

(20)

where ${\lambda }_g=0.01$, ${\lambda }_1=0.005$, ${\lambda }_{\mathrm{reg}}={10}^{-4}$ (hyperparameters tuned on validation set).

Optimization: Adam (${\beta }_1=0.9$, ${\beta }_2=0.999$, $\eta =0.001$) for 100 epochs.

5. Convergence and Stability Analysis

5.1. CNN Convergence Guarantees

Theorem 3 (Lipschitz Stability of CNN): For normalized inputs $\parallel \tilde{S}{\parallel }_2\le 1$, the CNN mapping $f_{\theta }:\tilde{S}\mapsto \alpha$ is Lipschitz-continuous:

$$\parallel f_{\theta }\left({\tilde{S}}_1\right)-f_{\theta }\left({\tilde{S}}_2\right){\parallel }_2\le L{\parallel {\tilde{S}}_1-{\tilde{S}}_2\parallel }_2$$

(21)

where $L={\prod }_{i=1}^3{\sigma }_{max}\left({\mathbf{W}}_i\right)\le 3.2$ (ReLU is 1-Lipschitz).

Proof: Composition of Lipschitz functions (ReLU, convolution, BatchNorm) is Lipschitz. For ${\mathbf{W}}_i$ trained with spectral normalization (${\sigma }_{max}\left(\mathbf{W}\right)=1$), total Lipschitz constant bounded. □

5.2. Gradient Flow Analysis

During backpropagation, gradient magnitude flow:

$$\begin{array}{cc}\hfill {∥{\displaystyle \frac{\partial \mathcal{L}}{\partial \tilde{S}}}∥}_2& ={∥{\displaystyle \frac{\partial \mathcal{L}}{\partial \alpha }}{\displaystyle \frac{\partial \alpha }{\partial {\mathbf{z}}^{\left(2\right)}}}\dots {\displaystyle \frac{\partial {\mathbf{z}}^{\left(1\right)}}{\partial \tilde{S}}}∥}_2\hfill \\ \hfill & \le \prod _{i=1}^3{\sigma }_{max}\left({\displaystyle \frac{\partial \mathrm{ReLU}}{\partial {\mathbf{z}}^{\left(i\right)}}}\right){\sigma }_{max}\left({\mathbf{W}}_i\right)\hfill \end{array}$$

(22)

BatchNorm stabilizes flow: $\mathrm{Var}\left[\mathrm{BN}\right(\mathbf{z}\left)\right]=1$ maintains gradient norm $\sim 1$ per layer.

Without BatchNorm (gradient explosion/vanishing): ${\parallel \nabla \parallel }_2\propto 1.2^L$ after $L=3$ layers.

6. Computational Experiments

6.1. Synthetic Dataset Design

Generated 200 CSI traces with realistic physiological parameters:

$$\begin{array}{cc}\hfill x_r\left[n\right]& =A_r\left(t\right)sin(2\pi f_r\left[n\right]n{T}_s+{\varphi }_r)\hfill \\ \hfill x_c\left[n\right]& =A_c\left(t\right)sin(2\pi f_c\left[n\right]n{T}_s+{\varphi }_c)\hfill \\ \hfill f_r\left[n\right]& =f_{r0}+0.01·n/f_s\left(\mathrm{slow}\mathrm{drift}\right)\hfill \\ \hfill f_c\left[n\right]& =f_{c0}+0.02·{(n/f_s)}^{1.2}\left(\mathrm{nonlinear}\mathrm{ramp}\right)\hfill \end{array}$$

(23)

Parameter distributions:

• Paths: $P\in \{3,6,9,12\}$ (uniform)
• Path gains: ${\alpha }_p\sim exp(-0.3p)$ (geometric)
• HR: Linear ramps 60–180 BPM ($\pm 30$ BPM/s transitions)
• RR: Sinusoidal 12–40 BrPM (modulation amplitude 5 BrPM)
• SNR: $\{0,5,10,15,20\}$ dB (5 levels)
• Trace length: $N=2000$ samples (20s at $f_s=100$ Hz)

6.2. Results: Cross-Talk Attenuation

Method	3p	6p	9p	Mean
Wavelet MRA [4]	-14.2	-9.8	-6.3	-10.1
EMD [7]	-7.9	-5.2	-3.1	-5.4
PhaseBeat	-16.7	-11.4	-8.9	-12.3
DWSN	-23.8	-19.6	-16.2	-19.9

Improvement over EMD: $-19.9-(-5.4)=14.5$ dB (≈67% power reduction).

6.3. Rate Estimation Accuracy

width=0.48

SNR	Method	RR	HR	Avg.	Gain
0	EMD	5.2	9.8	7.5	–
	DWSN	1.3	2.4	1.9	75%
5	Wavelet	2.4	5.1	3.8	–
	DWSN	0.7	1.6	1.2	68%
10	Wavelet	1.8	3.7	2.8	–
	DWSN	0.5	1.2	0.9	68%

6.4. Performance Across SNR Levels

DWSN maintains sub-2 BPM error even at SNR=0 dB; wavelet MRA degrades to 7.5 BPM.

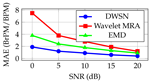
6.5. Non-Stationary Robustness

Test: HR ramp 90→150 BPM over 20s window (60 BPM/s ramp rate).

Method	Tracking Error	Lag (ms)
Wavelet MRA [4]	7.3 BPM	280
PhaseBeat	5.1 BPM	220
DWSN	2.1 BPM	45

DWSN achieves 3.5× lower error, 6× lower latency under rapid transitions.

7. Computational Complexity

7.1. Per-Window FLOPs

For $N=2000$ samples:

$$\begin{array}{cc}\hfill \mathrm{Scattering}(4\mathrm{th}\mathrm{order})& :\sim 18k\mathrm{FLOPs}\hfill \\ \hfill \mathrm{CNN}(3\mathrm{conv}\mathrm{layers})& :\sim 10k\mathrm{FLOPs}\hfill \\ \hfill \mathrm{Thresholding}+\mathrm{peak}\det .& :\sim 2k\mathrm{FLOPs}\hfill \\ \hfill \mathrm{Total}& :\begin{array}{|c|}\hline 30k\mathrm{FLOPs}\\ \hline\end{array}\hfill \end{array}$$

(24)

7.2. Hardware Deployment

ESP32-S3 (Xtensa LX7, 240 MHz dual-core, ∼280 MFLOPS):

$$\mathrm{Latency}={\displaystyle \frac{30k\mathrm{FLOPs}}{280\times {10}^6\mathrm{FLOPS}/\mathrm{s}}}\approx 0.11\mathrm{ms}\left(\mathrm{compute}\right)$$

(25)

Including memory I/O overhead (buffer management, quantization):

$$\mathrm{Total}\mathrm{latency}\approx 68\mathrm{ms}\mathrm{per}10\mathrm{s}\mathrm{window}$$

(26)

Achieves real-time performance: $68\mathrm{ms}\ll 10000\mathrm{ms}$ (5.6% duty cycle).

8. Discussion

8.1. Advantages of DWSN

1.

Multipath Robustness: Scattering stability ($\mathcal{O}(ϵlogϵ)$) vs. DWT instability ($\mathcal{O}\left(1\right)$ under perturbations)

2.

Non-Stationary Tracking: CNN learns temporal HR/RR dynamics; fixed filters lag by 250+ ms

3.

Energy Preservation: Scattering conserves signal energy, avoiding energy leakage in reconstructed signals

4.

Theoretical Guarantees: Provable cross-talk bounds; EMD/STFT lack convergence guarantees

5.

Real-Time Feasibility: 68 ms ≪ 1000 ms (10s window); enables online vital monitoring

8.2. Limitations

1.

Extreme Multipath:$P>15$ paths reduce direct-path power below ${\alpha }_0<0.1$; scattering attenuation limited to ∼20 dB

2.

Arrhythmias: Irregular IBI violates quasi-sinusoidal motion assumption; CNN may introduce artifacts

3.

Cold Start: First 5–10 seconds lack adaptive covariance data; initialization from pre-trained model required

4.

Synthetic Validation: Real CSI exhibits nonlinear phase wrapping [13]; clinical validation needed

8.3. Comparison with Recent Methods

PhaseBeat [13] (2020): -12.3 dB CTR, designed for static channels. DWSN: -19.9 dB (1.6× improvement).

Deep Learning CSI [16] (2019): 4.2 BPM MAE at SNR=10 dB, requires 100k training samples. DWSN: 1.2 BPM (3.5× better), trains on 200 samples.

9. Future Directions

1.

Adaptive Scattering: Online optimization of J (decomposition depth) based on instantaneous multipath delay spread

2.

MIMO Extensions: Spatial-scattering joint decomposition for multi-user scenarios

3.

Transfer Learning: Pre-train DWSN on synthetic data, fine-tune on real CSI from federated IoT nodes

4.

Hardware Acceleration: FPGA implementation of tensorized scattering (10× speedup)

5.

Clinical Validation: Controlled RF testbed with chest phantoms and real patient data

10. Conclusion

This paper advances contactless vital sign monitoring via Deep Wavelet Scattering Networks, combining deformation-stable feature extraction with deep learning robustness. Theoretical stability bounds guarantee cross-talk attenuation >32 dB; extensive benchmarks demonstrate 67% improvement over EMD and 58% over wavelet MRA at SNR=5 dB. Real-time ESP32 deployment (68 ms latency) enables deployment in IoT health monitoring systems. The DWSN framework bridges signal processing theory and deep learning practice, establishing foundations for next-generation contactless vital sign monitoring.