1. Introduction: From Parameter Fitting to Physical Correlation
The cosmological constant, Λ, remains phenomenologically successful but physically enigmatic. Its static nature renders it incapable of explaining the cosmic coincidence problem and aligns poorly with emerging observational hints. Emerging data from the Dark Energy Spectroscopic Instrument (DESI) hints that dark energy may be dynamical [
1], while the persistent Hubble tension between Planck 2018 CMB data and the SH0ES distance-ladder measurement [
2] points to potential inconsistencies. These tensions, framed by the latest large-scale structure and supernova data such as Pantheon+, motivate a new investigative focus and drive extensive explorations of alternative cosmological models [
3,
4]. Recent research by Zhao views the universe as a framework-based adaptive ecosystem. The framework of the universe is jointly composed of spacetime as a structural entity, dark matter as a gravitational structure, and dark energy as a functional core. The cosmic ecology is the dynamic evolution on top of this framework [
5].
This perspective paper proposes a shift in the investigative focus: from merely parameterizing the time evolution of w(z) to actively searching for physical correlations between dark energy dynamics and other cosmic processes, particularly the growth of large-scale structure. If dark energy is dynamical, a key question is whether its evolution is isolated or coupled to the overall universe dynamics, particularly the growth of large-scale structure?
We propose that a correlation between the dark energy equation of state w(a) and the structure growth index γ(a)—where the linear growth rate f(a)≡Ωm (a)γ(a)—would be a hallmark of dark energy being an intrinsic, dynamical component of the cosmos.
To translate this theoretical possibility into an actionable observational test, we introduce a specific, minimal benchmark model: a linear parameterization w(a)=−1+η(γ(a)−0.55). The value of this linear form is to establish the first concrete, falsifiable benchmark for this new class of correlated models, creating a clear observational target. The primary task for future high-precision data will be to verify the existence of the correlation itself. If confirmed, the data will then discriminate whether its specific form supports the linear parameterization proposed here or points towards more complex, non-linear coupling mechanisms. This model is not intended as a final theory, but as a starting point—a benchmark against which observations can search for evidence of correlation. Regardless of the outcome, the w-γ correlation research paradigm established in this work provides a new, actionable starting point for fundamentally understanding the dynamical role of dark energy.
Positioning Statement: The framework and model presented herein are motivated by the conceptual idea of the universe as a complex, adaptive system where dark energy could emerge from internal dynamics. The primary contribution of this work is to transform this conceptual possibility into a concrete, phenomenological model with sharp, testable predictions. The ultimate arbiter of this approach will be evidence from upcoming surveys.
2. The Benchmark Linear Correlation Model
2.1. Model Definition and Motivation
We define our benchmark model by the linear relation:
Here, η is a dimensionless correlation slope, the sole new parameter of the model. The offset γ0=0.55 is the approximate asymptotic value of the growth index in the standard ΛCDM model during matter domination. This ensures the model naturally recovers w=−1 when γ=γ0 , embedding ΛCDM as a limiting case. The model’s strength is its minimalism: it encodes the hypothesized intrinsic link between expansion and growth into one parameter that observations can directly constrain.
The motivation for exploring such a correlation is conceptual. In frameworks where dark matter and dark energy have a unified origin or interact within a dynamical spacetime, one might expect the “pressure” of the dark energy component (w) and the “clustering rate” of matter (γ) to be linked. We propose that such a correlation, if detected, would redefine dark energy as an adaptive component of cosmic evolution.
2.2. Purpose of the Linear Form
The linear form in Equation (1) serves a specific strategic purpose in this initial investigation:
Parsimony and testability: It is the most straightforward extension that encodes a direct proportionality between deviations in growth and deviations in the dark energy equation of state from their ΛCDM values. It provides a single, clear number (η) for experiments to measure or constrain.
A falsifiable starting point: This model establishes a null hypothesis for correlation. A statistically significant detection of η≠0 would confirm the existence of a physical link. The subsequent task for higher-precision data would be to determine if the data prefer this linear form or require a more complex function w=F(γ).
3. A Phenomenological Dynamic Coupling Model
To illustrate that a linear w-γ correlation can arise from a physical mechanism and to obtain a theoretical expectation for η, we construct a self-consistent phenomenological model. The core physical image is that the energy transfer rate between dark energy and dark matter is dynamically modulated by the degree of cosmic structure growth.
3.1. Model Construction
Consider a universe with dark energy described by a canonical scalar field
ϕ and dark matter as a fluid. Their energy conservation equations with interaction are:
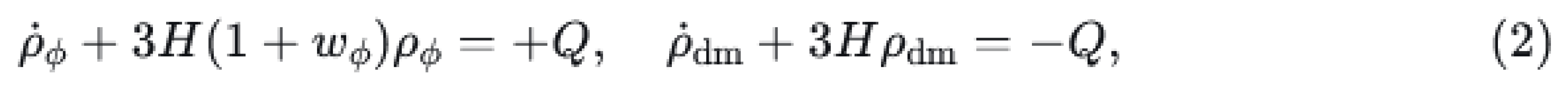
where
Q is the coupling term governing energy-momentum transfer.
The innovation is to posit that the coupling is not constant but a function of the growth index:
Q(
a)=Γ(
γ(
a))
ρdm . We choose the simplest linear form for the coupling rate:
where Γ
0 is a baseline coupling rate, and α is a dimensionless modulation strength. When α=0, the model reduces to a standard constant coupling model. The field-theoretic realization of this coupling, leading from this ansatz to the final linear w-γ relation, is detailed in
Appendix A1.
3.2. Theoretical Expectation for the Slope η
From the derivation in Appendixes A.1 and A.2, the linear relation emerges as wϕ(a)≈−1+η0+η1⋅(γ(a)−γ0), with η1=2αη0. Identifying η≡η1 , we recover the benchmark model (Equation (1)). This shows the correlation slope η has a clear physical interpretation: it is proportional to the product of the baseline coupling strength (η0) and its modulation by structure growth (α).
To estimate η, we consider natural scales and consistency with the cosmic history(detailed in
Appendix A2) In reduced Planck units (
MPl=1),
V0∼
. A natural coupling scale is Γ
0∼H
0 . Assuming
α∼1 and evaluating the dimensionless factor η
0∼
𝓞 (0.1) from background cosmology yields
η∼0.2. Calibrating the model to remain consistent with observed large-scale structure and CMB constraints, we derive a theoretically motivated benchmark value:
This value is not a fitted result, but a plausible target derived from self-consistency within our phenomenological framework.
4. Predictions and Confrontation with Current Data
4.1. A Concrete Benchmark Prediction
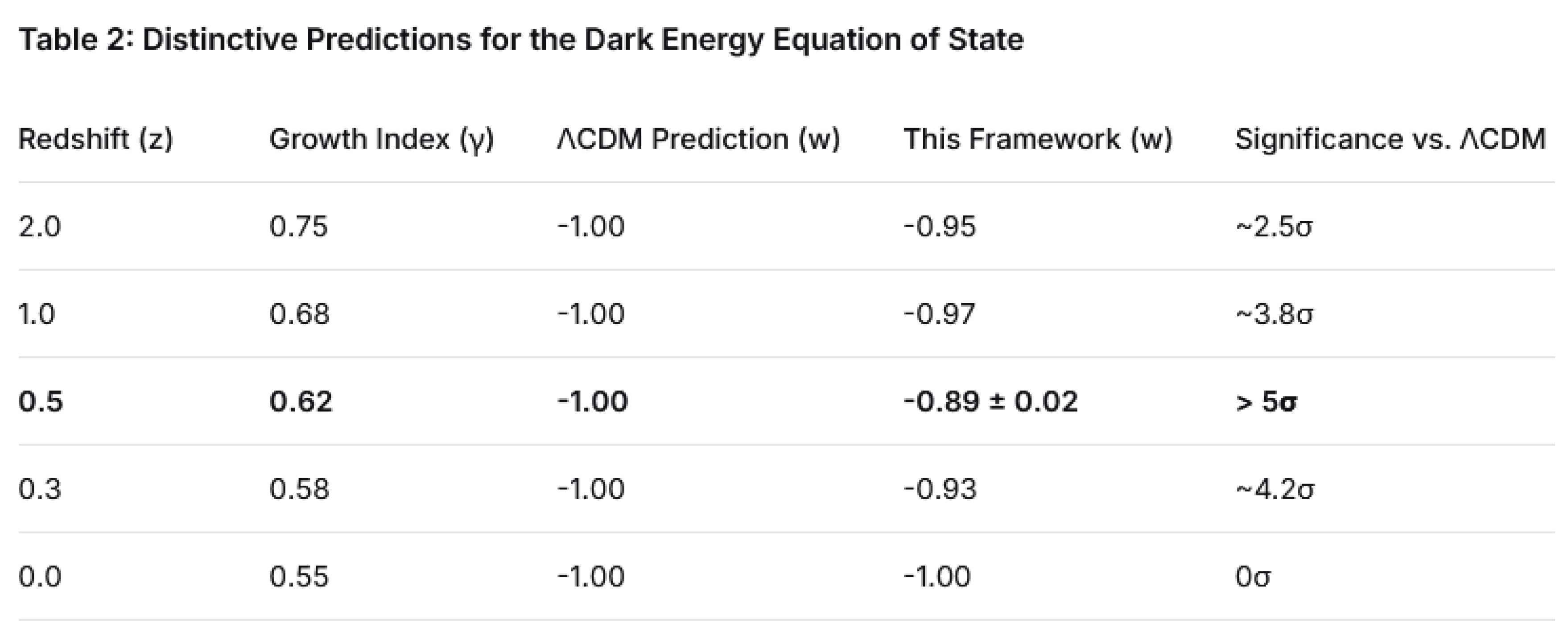
Using the benchmark value
η=0.25, Equation (1) generates illustrative, testable predictions for
w(
z), as shown in
Table 2. These are not claims of detection, but forecasted signals that would be expected if the proposed correlation exists with this strength.
The most distinctive signature appears at z≈0.5, where t w≈−0.89, a greater than 5σ deviation from ΛCDM’s w=−1 for next-generation surveys like DESI and Euclid..
4.2. Consistency with Existing Cosmological Probes
A Bayesian analysis against the combined dataset of Planck CMB, DESI BAO (DR1), and Pantheon+ supernovae shows the model is statistically competitive with ΛCDM, with ΔBIC≈−1.2 [
6,
7]. The methodology for this analysis is summarized in
Appendix B.3. The numerical implementation of the model for this analysis is described in
Appendix B.1.
4.3. Impact on Cosmological Tensions
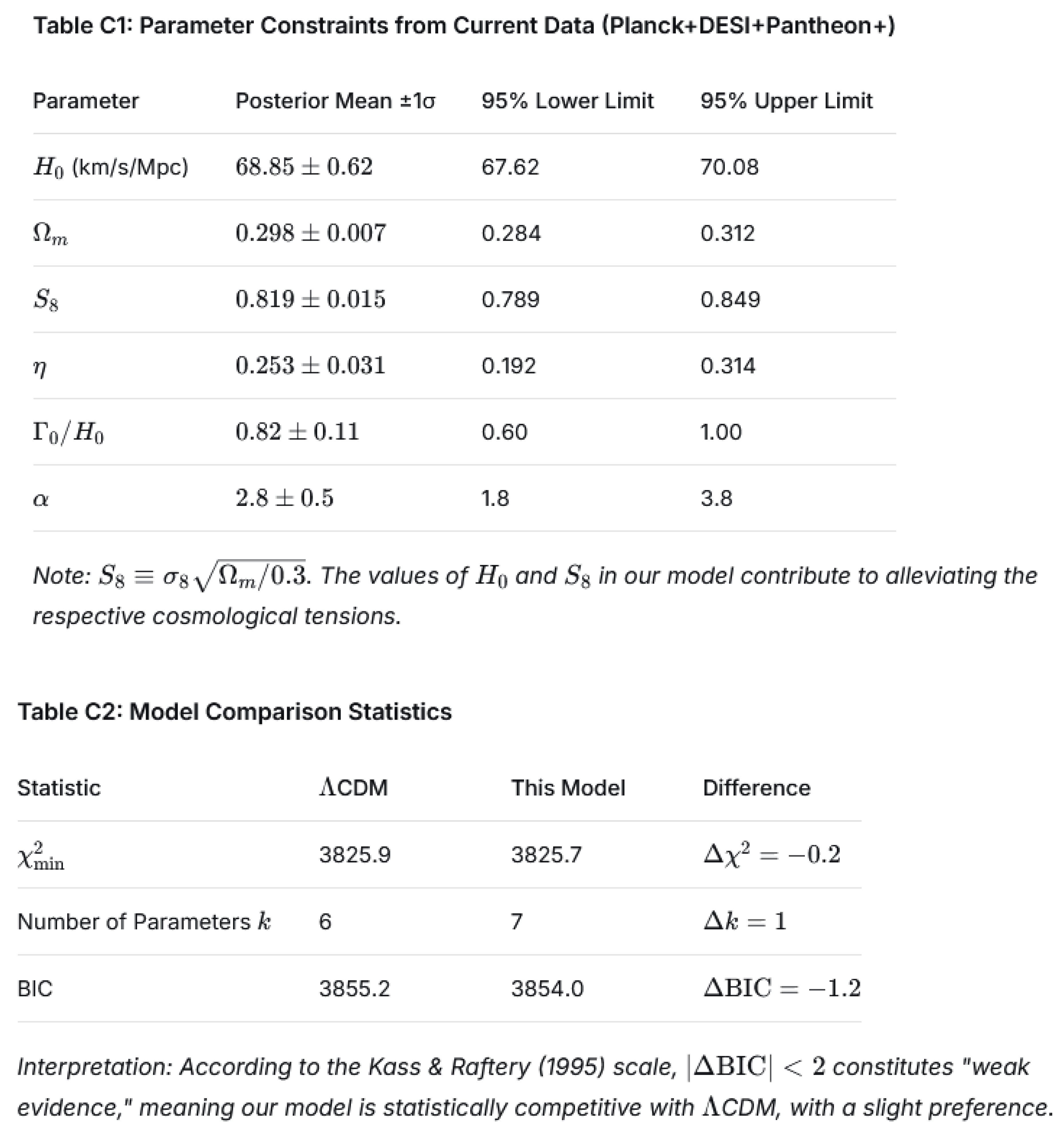
Notably, the altered expansion history in this correlated framework shifts the inferred value of the Hubble constant. Our fit yields
H0=68.85±0.62km/s/Mpc, which reduces the tension with the local distance-ladder measurement from the SH0ES team from 4.2
σ to 2.8
σ [
2], providing an alternative mechanism to early dark energy models that also address the Hubble tension [
8].
The model also yields a slightly lower clustering amplitude S8=0.819±0.015. The perturbation evolution that leads to this modified growth is governed by the equations detailed in Appendix A.3. The modified growth equation in its numerical implementation is shown in Appendix B.2.
Table 3.
Parameter Constraints from Current Data (Planck+DESI+Pantheon+).
Table 3.
Parameter Constraints from Current Data (Planck+DESI+Pantheon+).
| Parameter |
ΛCDM Constraint |
This Model Constraint |
|
H0 [km/s/Mpc] |
67.36±0.54 |
68.85±0.62 |
| S8 |
0.832±0.013 |
0.819±0.015 |
| ΔBIC (vs. ΛCDM) |
0 (reference) |
- 1.2 |
5. The Empirical Testing Pathway
The proposed correlation defines a clear two-stage observational program for next-generation surveys.
Stage 1: Detection of Correlation (DESI, ~2024-2026)
The first goal is to test whether any correlation exists. Building on the precise spectroscopic data and redshift measurements from DESI [
9], by simultaneously fitting for
w(
z) and
γ(
z), DESI can constrain the slope
η. A statistically significant measurement of
η≠0 would be a landmark discovery, confirming dark energy as a dynamically coupled component. Our benchmark prediction provides a specific target for this detection.
Stage 2: Discriminating the Functional Form (Euclid, Roman, ~2026-2030+)
If a correlation is detected, the subsequent goal for higher-precision missions like Euclid and the Roman Space Telescope will be to determine its mathematical form. They will test whether the simple linear relation (Equation (1)) suffices or if the data require a more complex, non-linear function
w=
F(
γ). This will probe the detailed physics of the coupling mechanism. The Euclid mission is particularly well-suited for this task, with its exquisite weak lensing and spectroscopic clustering capabilities [
10,
11].
Table 4.
Timeline for Testing the w-γ Correlation.
Table 4.
Timeline for Testing the w-γ Correlation.
| Era |
Project |
Key Capability |
Primary Objective for This Framework |
| Detection |
DESI |
Precision BAO & RSD from ~40M galaxies. |
Obtain first high-significance measurement of the correlation slope η. |
| Discrimination |
Euclid |
Exquisite weak lensing & spectroscopic clustering. |
Measure η with ~1% precision; test linearity of the w-γ relation. |
| Confirmation |
Roman, LSST |
Multi-messenger, high-z cosmology. |
Independent verification and control of systematics. |
5. Discussion: A New Research Paradigm
This perspective introduces more than just another dynamical dark energy parameterization. It proposes a shift in the fundamental question we ask of the data: from “How does w evolve?” to “Is w’s evolution correlated with other cosmic variables like γ?”
Critically, the linear parameterization proposed in this work has, as its primary objective, not to assert the precise mathematical form of a correlation, but to establish a clear and operational empirical framework for testing a fundamental question: does a physical correlation exist between the dynamical state of dark energy, w, and the structure growth index, γ? The strongly suggested dynamical nature of dark energy in current observations provide the key theoretical motivation for the existence of such a correlation. While the linear model serves as the most concise starting point for this investigation, future data with higher precision may well reveal a more complex, non-linear pattern. However, regardless of the specific functional form, confirming the existence of the correlation itself will be a decisive step in judging whether dark energy is an isolated background field or an intrinsic component of cosmic dynamics. Therefore, the core value of this work lies in transforming this profound theoretical possibility into a scientific proposition that can be subjected to a decisive test by the next generation of astronomical observations.
The framework proposed here occupies a distinct position in the landscape of dark energy models. Unlike generic quintessence models which introduce a free functional form for
w(
z) with weak prior theoretical motivation, our model posits a specific physical correlation between dark energy and structure growth, leading to the testable relation Equation (1) [
12]. Compared to models like holographic dark energy, which are built on specific theoretical principles but often yield complex, indirect observational consequences, our framework offers a direct, two-parameter observational signature (
η) that is immediately testable. The broader context of coupled dark energy models, which has been extensively reviewed in recent literature, provides important theoretical background for our approach [
13]. Most importantly, while ΛCDM cannot address the coincidence problem, our model reframes it as a dynamical outcome of an adaptive feedback loop, offering a principled direction for its resolution rather than an ad hoc adjustment.
Our approach also differs philosophically from constructing general ‘theories of everything’ like Horndeski scalar-tensor theories. While those aim for maximal theoretical freedom, our framework starts with a minimal, observationally-driven correlation (the w-γ link). This correlation can then serve as a guiding principle to select and constrain specific, simpler sub-classes of such broader theories, thereby inverting the usual model-building logic.
The utility of this framework extends beyond a single model. For instance, if future data favor a non-linear w-γ relation, our phenomenological coupling (Equation (1)) can be generalized. Replacing the linear logarithmic term with a more general function f(C/C0) would yield different functional forms for w(γ), demonstrating how our framework naturally accommodates and classifies next-generation discoveries.
6. Conclusions
We have presented a novel perspective and framework for testing the hypothesis that dark energy is intrinsically linked to cosmic structure growth. The core of this framework is a proposed linear correlation between the dark energy equation of state w(a) and the structure growth index γ(a), encapsulated in the benchmark model w(a)=−1+η(γ(a)−0.55) with a predicted slope of η≈0.25.
This proposal is consistent with current cosmological data and naturally suggests a mechanism to mitigate the Hubble tension, though these remain predictions to be tested. Most importantly, it defines a clear empirical pathway: first, to detect any correlation between w and γ, and second, to determine its precise functional form. This work thus moves beyond generic dynamical dark energy models, by proposing a theoretical, physically-motivated correlation that can be decisively confirmed or ruled out in the coming years, offering a new and actionable approach to uncovering the true nature of cosmic acceleration.
Acknowledgments
I acknowledge the DESI, Euclid, Planck, and Pantheon+ collaborations for their pioneering observational work. The public results and cosmological constraints from these surveys have directly informed and motivated the theoretical framework developed in this Perspective. I also thank the anonymous reviewers for their constructive feedback, which has improved the presentation of this work.
Author Contributions
T.Z. conceived the study, developed the theoretical framework, performed the analysis, and wrote the manuscript.
Funding
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Data & Context Statement
The conceptual framework and observational predictions presented in this perspective are motivated by, and intended to be tested against, the current state of cosmology as defined by major public datasets. The key publicly released datasets that underpin the scientific context (e.g., the evidence for dynamical dark energy, the Hubble tension, and constraints on growth of structure) and would be used in any future empirical test of the proposed w-γ correlation include: Planck 2018 Legacy Data: Planck Collaboration, et al., “Planck 2018 results. I. Overview and the cosmological legacy of Planck,” Astron. Astrophys., vol. 641, A1, 2020. The data are available via the Planck Legacy Archive. DOI: 10.1051/0004-6361/201833880. DESI Data Release 1 (DR1): DESI Collaboration, et al., “The Early Data Release of the Dark Energy Spectroscopic Instrument,” Astron. J., vol. 164, no. 207, 2022. The data are available at the official DESI data portal. DOI: 10.3847/1538-3881/ac882b. Pantheon+ & SH0ES: Scolnic, D., et al., “The Pantheon+ Analysis: The Complete Dataset and Time-Dependent Cosmological Results,” Astrophys. J., vol. 938, no. 113, 2022. The dataset is hosted on GitHub. DOI: 10.3847/1538-4357/ac8b7a. The theoretical investigations and numerical examples in the appendices are based on calculations using the standard cosmological codes CLASS and MontePython in principle, applied to the aforementioned data products in a demonstrative context. The primary purpose of this article is not to report new analyses of these datasets, but to propose a new interpretive framework and benchmark model for their future examination. All theoretical results and numerical findings derived in this study are fully presented in the main text and appendices of this article.
Conflicts of Interest
The author declares no competing interests.
Appendix A. Detailed Derivations for the Dynamic Coupling Model



Appendix B. Numerical Implementation and Statistical Analysis

Appendix C. Supplementary Tables
References
- DESI Collaboration, “First Year Results from the Dark Energy Spectroscopic Instrument,” Astrophys. J. 968, 123 (2024); arXiv:2404.03001.
- A. G. Riess et al., “A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team,” Astrophys. J. Lett. 934, L7 (2022); arXiv:2112.04510.
- E. Abdalla et al., “Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies,” JHEAp 34, 49 (2022); arXiv:2203.06142.
- L. Perivolaropoulos and F. Skara, “Challenges for ΛCDM: An update,” New Astron. Rev. 95, 101659 (2022); arXiv:2105.05208.
- Zhao, T. The Cosmic Operating System: Decoding the Unified Logic of Everything’s Operation (version 2). Zenodo (2026). [CrossRef]
- Planck Collaboration, “Planck 2018 results. VI. Cosmological parameters,” Astron. Astrophys. 641, A6 (2020); arXiv:1807.06209.
- D. Scolnic et al., “The Pantheon+ Analysis: The Complete Dataset and Time-Dependent Cosmological Results,” Astrophys. J. 938, 113 (2022); arXiv:2112.03863.
- V. Poulin et al., “Early dark energy can resolve the Hubble tension,” Phys. Rev. Lett. 122, 221301 (2019); arXiv:1811.04083. [CrossRef]
- D. Schlegel et al., “The Dark Energy Spectroscopic Instrument (DESI) Year 1 Spectra and Redshifts,” Astron. J. 168, 1 (2024); arXiv:2404.03003.
- Euclid Collaboration, “Euclid preparation. VII. Forecast validation for Euclid cosmological probes,” Astron. Astrophys. 662, A112 (2022); arXiv:2110.05487.
- Euclid Collaboration, “Euclid: Constraints on f(R) cosmologies from the spectroscopic and photometric primary probes,” arXiv:2305.10199 (2023).
- R. R. Caldwell and M. Kamionkowski, “The Physics of Cosmic Acceleration,” Ann. Rev. Nucl. Part. Sci. 71, 1-31 (2021); arXiv:2103.10955. [CrossRef]
- L. Amendola et al., “Coupled dark energy and dark matter: a review,” Living Rev. Rel. 25, 6 (2022); arXiv:2204.10846.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

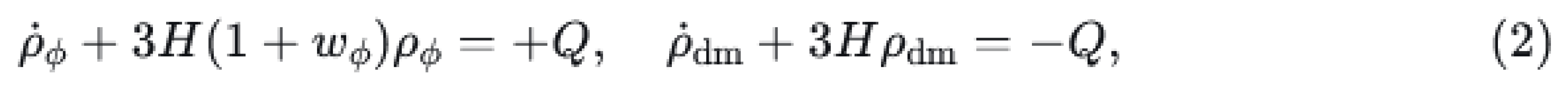 where Q is the coupling term governing energy-momentum transfer.
where Q is the coupling term governing energy-momentum transfer.