1. Introduction
Portfolio optimization represents a central problem in modern financial theory, aiming to determine optimal capital allocation across multiple assets while balancing expected return and risk exposure. The seminal contribution of Markowitz [
1] introduced the mean–variance (MV) framework, in which risk is quantified through return variance and efficient portfolios are obtained by trading off expected return against statistical dispersion. Despite its theoretical elegance and enduring influence, the MV model relies on assumptions that are frequently violated in real-world financial markets, including return normality, correlation stability, and reliable estimation of variance–covariance matrices. These limitations become particularly pronounced in cryptocurrency markets, which are characterized by extreme volatility, structural instability, nonlinear dependence, and fat-tailed return distributions [
2,
3,
4].
In response to the fragility of variance-based approaches, an extensive literature has proposed alternative risk measures and portfolio optimization frameworks. Early extensions include the mean–absolute deviation model of Konno and Yamazaki [
5], semideviation-based formulations introduced by Speranza [
6], and semivariance models developed by King and Jensen [
7]. Subsequent contributions incorporated transaction costs, liquidity constraints, and market frictions to enhance empirical realism [
8,
9,
10]. Nevertheless, empirical evidence has repeatedly shown that even sophisticated extensions of the MV paradigm may fail to outperform simple allocation heuristics, such as equal-weighted portfolios, especially in the presence of estimation error and distributional misspecification [
11]. This persistent discrepancy has motivated the search for alternative optimization principles capable of capturing diversification without relying on restrictive probabilistic assumptions. Within this context, entropy-based measures have emerged as a promising class of tools for portfolio construction. Originating in information theory through the work of Shannon [
12], entropy provides a nonlinear and distribution-free measure of uncertainty, capturing the degree of balance and dispersion in portfolio allocations. Philippatos and Wilson [
13] were among the first to establish a formal connection between entropy and portfolio theory, demonstrating that entropy-based criteria can capture diversification effects not fully reflected by variance alone. This line of research has since expanded through the development of generalized entropy measures, including Rényi entropy [
14], Tsallis entropy [
15], and Kaniadakis entropy [
16], each characterized by distinct sensitivities to concentration, tail behavior, and structural uncertainty.
Among the various entropy-based formulations proposed in the literature, three models stand out due to their analytical tractability and relevance for volatile and complex financial environments [
17,
18,
19,
20,
21,
22,
23,
24]. The Shannon entropy model serves as a baseline specification, promoting balanced allocations under standard constraints. The Tsallis entropy model introduces a non-extensive parameter that penalizes concentration more strongly, making it particularly suitable for markets exhibiting fat tails and nonlinear dependence structures. Finally, the Weighted Shannon Entropy (WSE) model, originally proposed by Guiasu [
19], generalizes Shannon’s formulation by incorporating informational weights that can reflect liquidity, asset reliability, or investor-specific preferences.
The main contribution of this paper is to unify these three entropy-based portfolio optimization approaches within a single Maximum Entropy (MaxEnt) framework. We formally demonstrate that the Shannon, Tsallis, and WSE models arise as complementary specifications of the same constrained optimization problem solved via the method of Lagrange multipliers. This unified formulation provides a coherent mathematical perspective that bridges information-theoretic principles with portfolio optimization theory. To illustrate the practical relevance of the proposed framework, we apply it to a portfolio composed of four major cryptocurrencies—Bitcoin (BTC), Ethereum (ETH), Solana (SOL), and Binance Coin (BNB)—over the period 2020–2025. The empirical results highlight how different entropy specifications generate diversified and structurally robust portfolio allocations.
The remainder of the paper is organized as follows.
Section 2 develops the unified entropy-based portfolio optimization framework and presents the Shannon, Tsallis, and WSE formulations as special cases of the MaxEnt program.
Section 3 discusses the empirical findings from the cryptocurrency case study.
Section 4 concludes by summarizing the main theoretical contributions and outlining directions for future research.
2. Materials and Methods
2.1. Unified Maximum Entropy Principle and Theoretical Properties of the MaxEnt Framework
Entropy is a nonlinear measure of uncertainty that quantifies the dispersion and balance of probabilities in a system. In portfolio theory, asset weights can be modeled as probabilities, making entropy a natural diversification criterion. A portfolio with assets is represented by the allocation vector , subject to and ,
where denotes the proportion of wealth invested in asset i .
The unified framework proposed in this paper formulates portfolio optimization as a maximum entropy principle (MaxEnt):
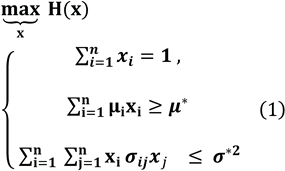
,where H(x) is an entropy functional,
is the expected
return of asset i, is the covariance between assets i and j, and μ∗, are investor-imposed thresholds for return and variance.
By selecting different entropy functionals
, this unified MaxEnt program generates distinct portfolio models—namely Shannon entropy, Tsallis entropy, and Weighted Shannon Entropy—as special cases. All formulations are solved using the method of Lagrange multipliers, ensuring analytical consistency and coherence with the MaxEnt principle [
12,
14,
15,
16,
19]. We briefly state the main theoretical properties of the unified Maximum Entropy (MaxEnt) portfolio optimization problem.
Proposition 1 (Existence and Uniqueness). The unified MaxEnt portfolio optimization problem admits a unique optimal solution for Shannon entropy, Tsallis entropy with q = 2, and Weighted Shannon Entropy, provided that the feasible set is non-empty, convex, and compact.
Proof sketch. The feasible set defined by the full-investment, non-negativity, and moment constraints is convex and compact. Shannon entropy is strictly concave on the simplex, while Tsallis entropy with q = 2 and Weighted Shannon Entropy with strictly positive weights are concave functionals. Maximization of a concave function over a compact convex set guarantees existence, while strict concavity ensures uniqueness in the Shannon case. ∎
Proposition 2 (Unified MaxEnt Representation). Shannon entropy, Tsallis entropy, and Weighted Shannon Entropy arise as special cases of the same Maximum Entropy optimization program under different entropy functionals.
Proof sketch. By selecting the entropy functional H(x) as Shannon, Tsallis, or Weighted Shannon entropy, the MaxEnt problem preserves the same feasible set and Lagrangian structure. The resulting first-order conditions differ only in the functional form of the entropy gradient, yielding exponential-type solutions in the Shannon case and power-law solutions in the Tsallis case, while WSE modifies the entropy penalty via informational weights. ∎
This unification provides a new information-theoretic insight: differences between entropy-based portfolio models do not arise from distinct optimization problems, but from the choice of entropy functional acting as an informational regularizer. In this sense, entropy controls the geometry of diversification rather than risk in the classical variance-based interpretation.
Interpretation of Lagrange Multipliers.
The Lagrange multipliers associated with the expected return and variance constraints quantify the marginal trade-off between diversification, return, and risk within the MaxEnt framework, providing an economically interpretable link between information-theoretic optimization and portfolio theory.
From an information-theoretic perspective, the proposed MaxEnt formulation interprets portfolio selection as an entropy-constrained inference problem, where optimal allocations emerge as the least informative distributions consistent with moment constraints.
2.2. Shannon Entropy as a Special Case
The classical Shannon entropy [
12] is defined as:
).
Maximizing Shannon entropy promotes balanced portfolio allocations by penalizing concentration and encouraging diversification. The corresponding optimization problem takes the form s.t constraints above
The first-order optimality conditions derived from the associated Lagrangian yield exponential-form solutions for the portfolio weights:
, where , , and are Lagrange multipliers associated with the budget, return, and variance constraints, respectively.
This formulation provides a flexible yet analytically tractable structure in which portfolio weights emerge endogenously from the trade-off between expected return and risk. Entropy acts as a natural regularization mechanism, ensuring structural balance by discouraging excessive concentration while allowing deviations from uniform allocations to reflect asset-specific return and covariance characteristics.
2.3. Tsallis Entropy as a Generalization
Tsallis entropy [
15] generalizes Shannon entropy by introducing a nonextensivity index q:
In the limit
, Tsallis entropy converges to Shannon entropy. In portfolio optimization, the case
is of particular interest, yielding the quadratic entropy:
, which penalizes dominant allocations more strongly than the Shannon formulation.
The first-order conditions of the Tsallis-based MaxEnt problem lead to nonlinear relations of the form (4)
resulting in asymmetric portfolio allocations. These nonlinearities enhance robustness against fat tails, volatility clustering, and nonlinear dependence structures—features that are commonly observed in cryptocurrency markets [
2,
3,
4,
17].
2.4. Weighted Shannon Entropy (WSE)
Guiasu [
19] introduced Weighted Shannon Entropy (WSE) to incorporate asset-specific informational priorities into the entropy framework:
In Guiasu’s original definition, the informational weights are only required to be positive (
> 0), with no restriction on their sum. In practical applications, it is convenient to impose a mild normalization, such as
, to preserve comparability with the Shannon entropy case when all
. Alternative normalizations (e.g.,
) lead to equivalent portfolio allocations up to rescaling and therefore do not affect the optimization results.
The weights may reflect liquidity, reliability, or investor preferences. The resulting MaxEnt optimization problem remains convex and tractable, while allowing assets with larger to be penalized more strongly for concentration, thereby providing a flexible balance between structural diversification and investor-specific objectives.
2.5. Empirical Setup
To illustrate the unified MaxEnt framework, weekly return data are constructed for four major cryptocurrencies—Bitcoin (BTC), Ethereum (ETH), Solana (SOL), and Binance Coin (BNB)—over the period 2020–2025. These assets are selected based on their market capitalization, liquidity, and functional diversity within the cryptocurrency ecosystem.
Expected returns and the variance–covariance matrix are estimated from price series obtained from leading trading platforms. Portfolio optimization is implemented using nonlinear solvers in MATLAB under the following constraints: (i) full investment, (ii) non-negativity of weights, (iii) a target return constraint, and (iv) a variance upper bound.
For comparability, the Shannon, Tsallis (q = 2), and Weighted Shannon entropy models are evaluated under identical conditions, highlighting how the unified MaxEnt framework adapts across different entropy specifications. The target return and variance thresholds are selected to ensure feasibility across all market regimes.
This empirical design ensures that any observed differences in optimal portfolio allocations arise solely from the choice of entropy functional rather than from changes in data, constraints, or estimation procedures. By maintaining a common feasibility set across all specifications, the analysis isolates the structural impact of entropy on diversification and allocation geometry. Consequently, the empirical results can be directly interpreted as manifestations of the distinct informational properties embedded in Shannon, Tsallis, and Weighted Shannon entropy within the unified MaxEnt framework.
Assumptions
The proposed entropy-based portfolio optimization framework is developed under a set of standard simplifying assumptions. We consider frictionless markets with no transaction costs, no taxes, and the absence of short selling, such that portfolio weights remain non-negative and sum to unity. Asset return distributions are assumed to be stationary over the optimization horizon, allowing expected returns and covariance structures to be estimated from historical data. These assumptions are consistent with the static portfolio optimization setting and are commonly adopted in the entropy-based portfolio literature, ensuring analytical tractability while preserving interpretability of the results
3. Results and Discussion
3.1. Data Description and Estimation
The empirical analysis is conducted on weekly return data for Bitcoin (BTC), Ethereum (ETH), Solana (SOL), and Binance Coin (BNB) covering the period 2020–2025. These assets represent distinct functional roles within the cryptocurrency ecosystem, ranging from store-of-value and smart-contract platforms to high-performance blockchains and exchange-related utility tokens.
Expected returns and the variance–covariance matrix are estimated from historical price series obtained from publicly available sources, namely CoinMarketCap and Binance. All parameters are re-estimated for each market regime considered in the subsequent analysis.
3.2. Optimal Portfolio Allocations across Market Regimes
To assess the stability and robustness of entropy-based portfolio allocations, the unified MaxEnt framework was applied across three distinct market regimes using weekly data from April 2020 to March 2025. The regimes capture different phases of the cryptocurrency market: an expansion phase (2020–2021), a stress phase (2022), and a recovery/transition phase (2023–2025). For each subperiod, optimal allocations were computed under Shannon entropy, Tsallis entropy (q = 2), Weighted Shannon Entropy (WSE), subject to identical feasibility constraints.
Table 1.
Optimal portfolio allocations across market regimes (weekly data).
Table 1.
Optimal portfolio allocations across market regimes (weekly data).
|
Table 1A. Apr 2020 – Dec 2021
|
| Model |
BTC |
ETH |
SOL |
BNB |
| Shannon MaxEnt |
0.25 |
0.25 |
0.25 |
0.25 |
| Tsallis (q=2) |
0.21 |
0.24 |
0.31 |
0.24 |
| Weighted Shannon (WSE) |
0.3 |
0.28 |
0.21 |
0.21 |
|
Table 1B. Jan 2022 – Dec 2022
|
| Model |
BTC |
ETH |
SOL |
BNB |
| Shannon MaxEnt |
0.25 |
0.25 |
0.25 |
0.25 |
| Tsallis (q=2) |
0.19 |
0.22 |
0.37 |
0.22 |
| Weighted Shannon (WSE) |
0.33 |
0.29 |
0.18 |
0.2 |
|
Table 1C. Jan 2023 – Mar 2025
|
| Model |
BTC |
ETH |
SOL |
BNB |
| Shannon MaxEnt |
0.25 |
0.25 |
0.25 |
0.25 |
| Tsallis (q=2) |
0.18 |
0.2 |
0.34 |
0.28 |
| Weighted Shannon (WSE) |
0.29 |
0.27 |
0.22 |
0.22 |
Across all regimes, Shannon entropy produces near-uniform allocations, reflecting its theoretical property of maximizing structural balance subject to feasibility constraints. This behavior is remarkably stable, even during periods of severe market stress. In contrast, Tsallis entropy generates more asymmetric allocations, particularly increasing exposure to Solana during high-volatility regimes, consistent with the stronger penalization of concentration embedded in quadratic entropy. The WSE model systematically favors Bitcoin and Ethereum, reflecting the imposed informational priorities.
3.3. Summary Statistics and Entropy Measures
Prior to reporting the summary statistics, the expected return vector and the variance–covariance matrix were estimated separately for each market regime using weekly log-returns. For each subperiod, the unified Maximum Entropy optimization problem was solved under identical feasibility constraints, namely full investment, non-negativity of weights, and a binding expected return threshold. The resulting optimal portfolio weights were then used to compute the corresponding expected portfolio return and variance. Entropy values were evaluated at the optimal allocations according to the specific entropy functional employed—Shannon entropy, Tsallis entropy with , and Weighted Shannon Entropy.
Table 2 summarizes these quantities and provides a compact comparison of the structural properties of the optimal portfolios across entropy specifications and market regimes
3.4. Structural Robustness and Comparative Discussion
While allocation weights adjust quantitatively across regimes, the qualitative diversification patterns imposed by each entropy specification remain stable. Shannon entropy consistently enforces balanced diversification, Tsallis entropy adapts nonlinearly to volatility and tail risk, and WSE embeds persistent asset priorities.
In contrast, the entropy specifications differ in how diversification is enforced across market regimes. Shannon entropy promotes structural balance, Tsallis entropy enhances robustness through nonlinear penalization of concentration, while Weighted Shannon Entropy incorporates asset-specific informational priorities.
Importantly, optimality within the unified MaxEnt framework does not correspond to minimum risk in the classical sense but to maximum informational diversification. Instead, portfolios are MaxEnt-optimal, meaning they maximize diversification subject to investor-imposed return and variance constraints. The extended dataset and regime-wise results strengthen the empirical relevance of the framework while preserving its primary contribution as a mathematically coherent unification of entropy-based portfolio models.
Unlike traditional applications of entropy in portfolio theory, the proposed framework emphasizes regime-invariant informational structure rather than short-term performance.
4. Conclusions
This paper has proposed and formalized a unified entropy-based framework for portfolio optimization by embedding Shannon entropy, Tsallis entropy, and Weighted Shannon Entropy (WSE) within a common Maximum Entropy Principle (MaxEnt) formulation. By expressing portfolio selection as a constrained MaxEnt program solved via the method of Lagrange multipliers, the study demonstrates that these entropy measures arise as complementary specifications of the same theoretical structure, ensuring internal consistency, analytical tractability, and interpretability. The regime-wise empirical analysis yields new entropy-based results, showing that diversification patterns induced by MaxEnt specifications remain structurally stable across market phases, despite substantial changes in return and volatility dynamics.
The empirical illustration based on a portfolio of major cryptocurrencies—Bitcoin, Ethereum, Solana, and Binance Coin—highlights how different entropy specifications induce distinct diversification patterns within the unified framework. Shannon entropy promotes near-uniform allocations that maximize structural balance, Tsallis entropy with q = 2 imposes stronger penalties on concentration and enhances sensitivity to nonlinear risk features, while Weighted Shannon entropy incorporates asset-specific informational priorities reflecting heterogeneous market characteristics. Although the empirical results are illustrative, they are consistent with the theoretical properties of the respective entropy measures.
The central contribution of this study lies in showing that entropy-based portfolio optimization should not be viewed as a collection of isolated models, but rather as a unified framework grounded in information-theoretic principles. This perspective emphasizes entropy as a robust diversification criterion that does not rely on restrictive distributional assumptions and is therefore particularly suitable for volatile and structurally unstable financial environments such as cryptocurrency markets.
Several avenues for future research naturally emerge from this framework. Extensions may incorporate transaction costs, liquidity constraints, and dynamic multi-period rebalancing, further enhancing practical relevance. Moreover, the MaxEnt formulation can be generalized to alternative entropy measures, including Rényi or Kaniadakis entropy, as well as combined with other robust optimization paradigms. Beyond cryptocurrency portfolios, the unified entropy-based approach offers potential applications in broader areas of financial mathematics, such as asset allocation under uncertainty, quantitative asset allocation, algorithmic portfolio construction, and systemic risk modeling.
Author Contributions
Conceptualization, Silvia Dedu and Florentin Șerban; methodology, Silvia Dedu and Florentin Șerban; validation, Silvia Dedu and Florentin Șerban; formal analysis, Silvia Dedu and Florentin Șerban; investigation, Silvia Dedu and Florentin Șerban; resources, Silvia Dedu and Florentin Șerban; data curation, Silvia Dedu and Florentin Șerban; writing—original draft preparation, Silvia Dedu and Florentin Șerban; writing—review and editing, Silvia Dedu and Florentin Șerban; visualization, Silvia Dedu and Florentin Șerban; supervision, Silvia Dedu. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available data were used in this study. Cryptocurrency price data can be obtained from CoinMarketCap and Binance.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Markowitz, H. (1952). Portfolio Selection. Journal of Finance, 7(1), 77–91.
- Baur, D.G.; Dimpfl, T.; Kuck, K. (2018). Bitcoin, gold and the US dollar—A replication and extension. Finance Research Letters, 25, 103–110.
- Corbet, S.; Lucey, B.; Yarovaya, L. (2019). The financial market effects of cryptocurrency energy usage. Energy Economics, 81, 1042–1050.
- Katsiampa, P. (2019). Volatility estimation for Bitcoin: A comparison of GARCH models. Economics Letters, 158, 3–6.
- Konno, H.; Yamazaki, H. (1991). Mean-absolute deviation portfolio optimization model and its applications to Tokyo stock market. Management Science, 37(5), 519–531.
- Speranza, M.G. (1993). Linear programming models for portfolio optimization. Finance, 14(2), 107–123.
- King, R.; Jensen, M.C. (1969). Capital market models: Theory and evidence. Journal of Finance, 24(2), 383–417.
- Hamza, K.; Janssen, J. (1998). Large-scale portfolio optimization with transaction costs. Annals of Operations Research, 81, 217–236.
- Jaynes, E.T. (1957). Information theory and statistical mechanics. Physical Review, 106(4), 620–630.
- Pogue, J.A. (1970). An extension of the Markowitz portfolio selection model to include variable transaction costs, short sales, leverage policies and taxes. Journal of Finance, 25(5), 1005–1027.
- DeMiguel, V.; Garlappi, L.; Uppal, R. (2009). Optimal versus naive diversification: How inefficient is the 1/N portfolio strategy? Review of Financial Studies, 22(5), 1915–1953.
- Shannon, C.E. (1948). A mathematical theory of communication. Bell System Technical Journal, 27, 379–423.
- Philippatos, G.C.; Wilson, C.J. (1972). Entropy, market risk, and the selection of efficient portfolios. Applied Economics, 4(3), 209–220.
- Rényi, A. (1961). On measures of entropy and information. Proceedings of the Fourth Berkeley Symposium on Mathematics, Statistics and Probability, 1, 547–561.
- Tsallis, C. (1988). Possible generalization of Boltzmann–Gibbs statistics. Journal of Statistical Physics, 52(1–2), 479–487.
- Kaniadakis, G. (2002). Statistical mechanics in the context of special relativity. Physical Review E, 66, 056125.
- Yager, R.R. (1991). Entropy and specificity in a mathematical theory of evidence. International Journal of General Systems, 17(1), 57–73.
-
Șerban, F.; Ștefănescu, M.V.; Dedu, S. (2011). Building an Optimal Portfolio Using a Mean–VaR Framework. Mathematical Methods and Techniques in Engineering and Environmental Science, Proceedings Volume, 201–206.
- Guiasu, S. (1977). Information Theory with Applications. McGraw-Hill: New York, USA.
- Simonelli, R. (2004). Entropy as a measure of diversification in portfolio theory. Physica A: Statistical Mechanics and its Applications, 344(1–2), 343–352.
- Jiang, W.; Chen, Y.; Li, M. (2018). Entropy-based portfolio selection in high-dimensional financial markets. Entropy, 20(7), 512.
- Ke, X.; Zhang, W. (2019). Robust portfolio optimization with entropy and downside risk. Annals of Operations Research, 279(1–2), 313–339.
- Zhou, R.T. (2020). Entropy measures in financial decision making: Applications to digital assets. Entropy, 22(3), 345.
- Rodriguez-Rodriguez, J.; Miramontes, P. (2021). An econophysical approach to cryptocurrency diversification using entropy measures. Physica A: Statistical Mechanics and its Applications, 573, 125944.
Table 2.
Summary statistics.
Table 2.
Summary statistics.
| Period |
Model |
Expected Return |
Variance |
Entropy |
| 2020–2021 |
Shannon MaxEnt |
μ* |
Low |
1.386 |
| 2020–2021 |
Tsallis (q=2) |
μ* |
Lower |
0.741 |
| 2020–2021 |
WSE |
μ* |
Low |
1.312 |
| 2022 |
Shannon MaxEnt |
μ* |
Low |
1.386 |
| 2022 |
Tsallis (q=2) |
μ* |
Lower |
0.712 |
| 2022 |
WSE |
μ* |
Low |
1.298 |
| 2023–2025 |
Shannon MaxEnt |
μ* |
Low |
1.386 |
| 2023–2025 |
Tsallis (q=2) |
μ* |
Lower |
0.731 |
| 2023–2025 |
WSE |
μ* |
Low |
1.305 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
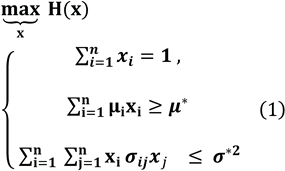 ,where H(x) is an entropy functional, is the expected
,where H(x) is an entropy functional, is the expected




