Hybrid Plasmonic–Photonic Panda-Ring Antenna Embedded with a Gold Grating for Dual-Mode Transmission

1. Introduction

The rapid evolution of wireless and optical communication systems has led to increasing demand for high-frequency, high-efficiency antennas supporting multi-band operation with minimal losses. Millimeter-wave (mmWave) antennas are crucial enablers for fifth-generation (5G) systems due to their high-speed and low-latency connectivity requirements; however, they also present significant design challenges, including miniaturization and fabrication precision at higher frequencies [1]. Terahertz (THz) frequency bands have been identified as promising candidates for future sixth-generation (6G) communication systems, offering vast bandwidth and ultrahigh data rates, while simultaneously imposing severe challenges related to high propagation loss and compact high-gain antenna realization [2,3]. Next-generation 5G/6G antennas for embedded and Internet-of-Things (IoT) applications further emphasize compact size, reliability, and energy-efficient performance, motivating extensive research into advanced compact and plasmonic antenna architectures [4]. Consequently, emerging design paradigms such as plasmonic antennas are being actively explored for integration into mmWave and THz systems to provide subwavelength confinement, improved gain, and reconfigurable resonance behavior [5].

Plasmonic antennas and related nanostructures have attracted considerable attention due to their ability to manipulate electromagnetic energy at nanometric scales through surface plasmon polaritons (SPPs), enabling enhanced near-field localization and tailored radiation characteristics for high-frequency applications. Several plasmonic heterostructures and nanoantenna configurations have been reviewed for telecommunication purposes, including beam steering, wave guiding, and signal modulation in emerging 6G systems [6]. Plasmonic antennas supporting intense electric or magnetic field hot spots have also been theoretically investigated, highlighting their potential for strong electromagnetic field control despite intrinsic ohmic losses [7]. To mitigate the limitations of purely plasmonic devices, hybrid plasmonic–photonic waveguide structures have been proposed, combining dielectric waveguide modes with surface plasmon modes to balance field confinement and propagation loss [8] Furthermore, integration strategies that merge plasmonic elements with dielectric photonic circuits demonstrate how hybrid designs can exploit the advantages of both domains, which is essential for efficient optical communication systems [9].

Among various resonant structures, the Panda-ring resonator [10,11,12,13,14,15,16]—a derivative of the microring resonator [17,18,19,20]—has attracted significant attention due to its capability to support Whispering Gallery Modes (WGMs), which enhance optical field confinement and coupling efficiency. WGMs enable high-Q resonances through total internal reflection along curved dielectric interfaces, allowing precise control of resonant wavelengths and power distribution among multiple ports. Integrating plasmonic elements such as metallic gratings into these dielectric resonators further improves light–matter interaction, facilitating hybrid SPP–WGM coupling and enhancing radiation efficiency [21,22]. This hybridization forms the foundation of dual-mode plasmonic operation, where both plasmonic and photonic modes coexist and can be selectively excited depending on system requirements. Dual-mode architectures are particularly advantageous in next-generation communication systems, enabling seamless transitions between wired (fiber-optic) and wireless (Li-Fi or THz) transmission [23]. Compared with conventional microring, disk, and metamaterial resonators, the Panda-ring resonator offers enhanced modal controllability, high-Q whispering gallery confinement, and precise multi-port power routing [24,25]. Its multi-ring topology provides a versatile platform for hybrid plasmonic–photonic integration, enabling efficient dual-mode operation with improved radiation efficiency and sub-wavelength field confinement. These characteristics make the Panda-ring resonator particularly suitable for next-generation Li-Fi and terahertz (THz) communication systems [6,26,27].

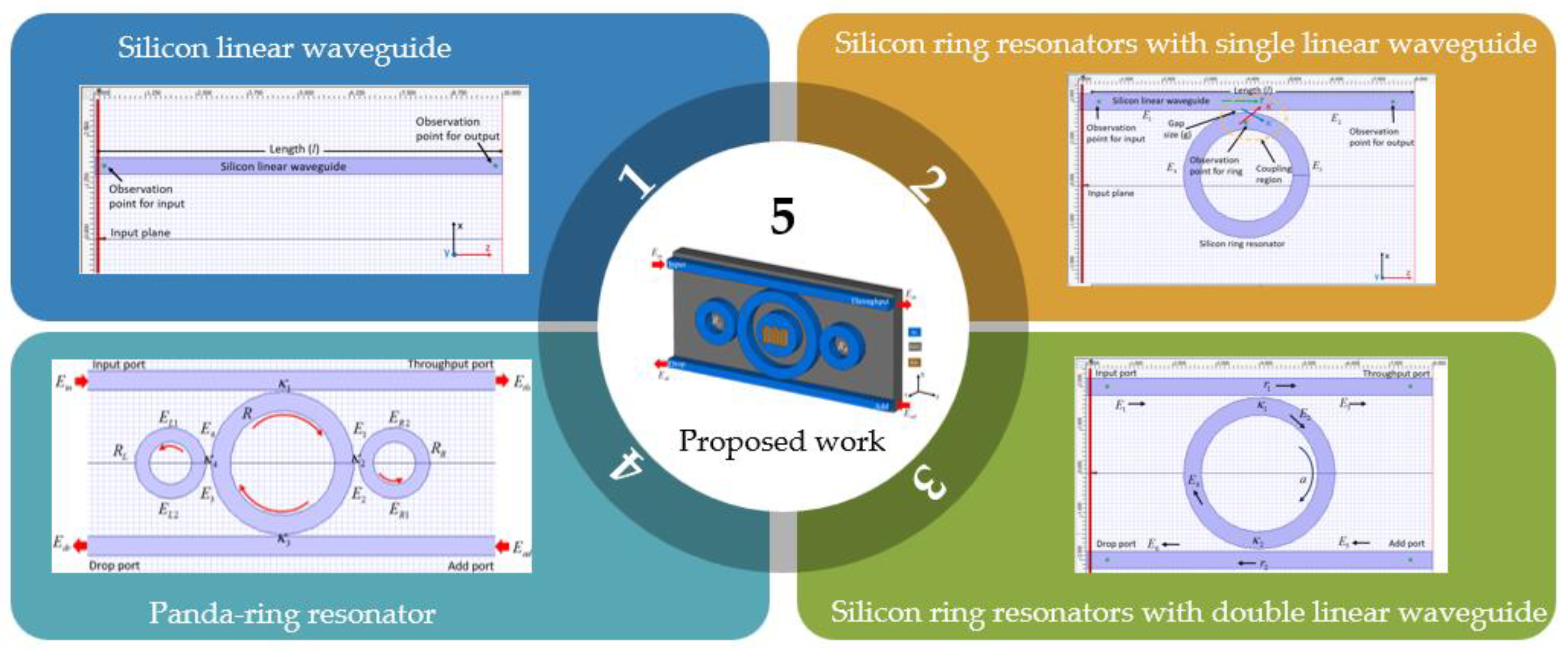
Building upon these principles, this study proposes a computationally optimized plasmonic Panda-ring antenna embedded with a gold grating, designed to enhance both near-field confinement and far-field radiation characteristics through a hybrid plasmonic–photonic approach. To systematically investigate the evolution of mode confinement and coupling behavior, the proposed design is developed through a hierarchical resonator architecture, starting from a conventional silicon linear waveguide, followed by silicon ring resonators coupled to single and double linear waveguides. These intermediate configurations provide fundamental insight into power routing, resonance stability, and mode interaction within photonic resonator systems. Based on this progression, the final Panda-ring structure integrates a central microring with two side rings and an embedded gold grating, forming a hybrid antenna capable of supporting strong Whispering Gallery Mode (WGM) resonance and efficient surface plasmon polariton (SPP) excitation. The overall structural evolution and the final proposed configuration are illustrated in Figure 1.

The embedded gold grating strengthens plasmonic field excitation at the metal–dielectric interface while maintaining high-Q WGM confinement within the silicon waveguide network. This synergy between SPPs and WGMs enables stable dual-mode operation, facilitating high-gain performance across optical and terahertz frequency bands. In addition, the proposed design addresses key limitations of conventional plasmonic antennas by improving impedance matching, expanding operational bandwidth, and reducing propagation loss. Comprehensive numerical simulations using Optiwave FDTD and CST Microwave Studio are performed to analyze the antenna’s spectral response, field distribution, gain, and directivity. The simulation results demonstrate that the proposed Panda-ring configuration achieves stable dual-mode transmission with enhanced radiation efficiency, making it well suited for integration into Li-Fi transmitters, 6G communication modules, and hybrid photonic–plasmonic circuits.

2. Materials and Methods

This section presents the theoretical basis, structural design, and computational approach used to analyze the proposed plasmonic Panda-ring antenna embedded with a gold grating. The study combines analytical modeling and numerical simulations to investigate the antenna’s dual-mode plasmonic behavior, governed by the interaction between surface plasmon polaritons (SPPs) and Whispering Gallery Modes (WGMs).

The gold grating enhances plasmonic confinement at the metal–dielectric interface, while the Panda-ring configuration supports high-Q optical resonance and efficient mode coupling. Full-wave simulations using Optiwave FDTD and CST Microwave Studio are performed to evaluate spectral response, field distribution, and radiation characteristics. The following subsections describe the theoretical foundation, material parameters, and computational setup employed in this work.

2.1. Theoretical Foundation

This section presents the theoretical framework, structural design, and computational methodology used to analyze the proposed plasmonic Panda-ring antenna embedded with a gold grating. The study integrates analytical modeling with full-wave numerical simulations to investigate the dual-mode plasmonic behavior arising from hybrid surface plasmon polariton (SPP) and Whispering Gallery Mode (WGM) interactions. In the proposed architecture, the embedded gold grating enhances plasmonic field confinement at the metal–dielectric interface, while the Panda-ring resonator supports high-Q optical resonances and efficient mode coupling. Full-wave simulations using Optiwave finite-difference time-domain (FDTD) and CST Microwave Studio are conducted to evaluate the spectral response, near-field distribution, and far-field radiation characteristics. The following subsections describe the physical principles, material properties, structural configuration, and computational setup employed in this work.

2.1.1. Surface Plasmon Polaritons (SPPs)

SPPs are electromagnetic waves that propagate along the interface between a metal and a dielectric, resulting from the collective oscillation of free electrons in the metal when excited by incident light. This interaction allows subwavelength field confinement and enhanced near-field coupling [28,29]. The dispersion relation of SPPs is given by:

$$\beta =k_0\sqrt{{\displaystyle \frac{{\epsilon }_m{\epsilon }_d}{{\epsilon }_m+{\epsilon }_d}}}$$

(1)

where $\beta$ is the propagation constant of the SPP, $k_0$ is the free-space wavevector, and ${\epsilon }_m$ and ${\epsilon }_d$ represent the complex permittivities of the metal and dielectric, respectively. SPPs exist when the real part of ${\epsilon }_m$ is negative, a condition typically satisfied by noble metals such as gold (Au) and silver (Ag) in the optical and terahertz (THz) frequency ranges. The dielectric function of gold is modeled using the Drude model [30,31], which describes the frequency-dependent behavior of conduction electrons as:

$${\epsilon }_m\left(\omega \right)={\epsilon }_{\infty }-{\displaystyle \frac{{\omega }_p^2}{{\omega }^2+j\omega \gamma }}$$

(2)

where ${\epsilon }_{\infty }$ is the high-frequency permittivity, ${\omega }_p$ is the plasma frequency, and $\gamma$ represents the damping constant associated with electron collisions. This formulation enables accurate modeling of plasmonic resonance within the gold grating structure, which plays a critical role in enhancing field confinement and radiation efficiency.

2.1.2. Whispering Gallery Modes (WGMs)

WGMs arise when light is confined within a circular dielectric resonator through total internal reflection, forming standing waves that circulate along the perimeter of the resonator. These modes support high quality factors (Q-factors), enabling strong optical confinement and resonance stability [32,33]. The resonance wavelength condition of a WGM is expressed as:

$${\lambda }_m={\displaystyle \frac{2\pi r{n}_{eff}}{m}}$$

(3)

where ${\lambda }_m$ is the resonant wavelength, $r$ is the radius of the microring, $n_{eff}$ is the effective refractive index, and $m$ denotes the mode number. In the proposed design, WGMs are excited within the Panda-ring structure composed of a central microring coupled with two side rings. This configuration enhances resonance control and stability, supporting efficient optical energy exchange among the input, throughput, add, and drop ports.

By embedding a gold grating within the central microring, strong hybrid coupling between SPPs and WGMs is achieved [9,23,24]. The metallic grating perturbs the dielectric resonance field, allowing simultaneous excitation of plasmonic and photonic modes, which results in dual-mode transmission. The interaction between these modes improves impedance matching and enhances radiation gain. Moreover, the hybrid coupling minimizes propagation losses by redistributing the electromagnetic field energy between the plasmonic (metallic) and photonic (dielectric) domains [34]. This dual-mode mechanism forms the theoretical basis of the proposed antenna, enabling efficient mode conversion between plasmonic and photonic channels — a key feature for high-performance Li-Fi, 6G, and on-chip optical communication applications [5,9].

2.2. Structural Design of the Proposed Antenna

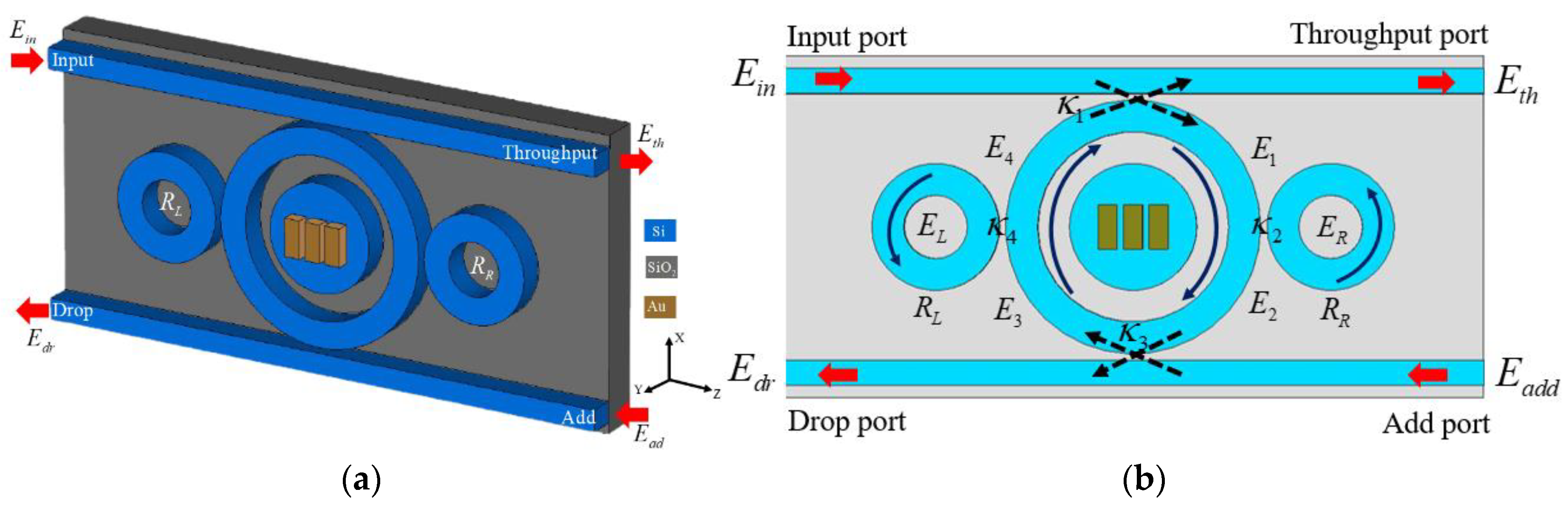
The proposed plasmonic Panda-ring antenna is designed to achieve strong electromagnetic field confinement and efficient radiation by integrating plasmonic and photonic mechanisms within a compact resonator-based architecture. The structural configuration, illustrated in Figure 2, is based on a Panda-ring resonator circuit composed of a central microring coupled to two side rings and double linear waveguides. This multi-ring topology enhances modal interaction, resonance controllability, and power routing capability, while maintaining compact dimensions suitable for optical and terahertz-frequency operation.

As shown in Figure 2(a), the structure is implemented on a silicon (Si) waveguide platform supported by a silicon dioxide (SiO₂) substrate. A gold (Au) grating is embedded at the center of the main ring, forming a plasmonic island that enables strong surface plasmon polariton (SPP) excitation at the metal–dielectric interface. The propagation of SPP waves occurs along the metal–dielectric boundary with an evanescent decay in the transverse direction, where the collective oscillation of free electrons in the metal is described by the Drude model. The resulting plasmonic modes exhibit transverse magnetic (TM) polarization and strong field localization, which are essential for efficient near-field enhancement and plasmonic radiation. The Panda-ring resonator supports whispering gallery modes (WGMs) within the dielectric microring structure, where optical fields circulate along the curved interfaces through total internal reflection. In this work, the resonant (plasma) frequency associated with plasmonic excitation is identified from the WGM spectral response, enabling effective hybridization between photonic WGMs and plasmonic SPPs. This hybrid SPP–WGM interaction forms the basis of dual-mode operation, where confined photonic energy and localized plasmonic fields coexist and interact coherently within the same structure.

The optical input field E_in is launched through the linear Si waveguide and distributed among the throughput (Eth), drop (E_dr), and add (E_ad) ports. The coupling behavior between the rings and the waveguide is determined by coupling coefficients, which govern energy transfer and resonance balance within the structure. This configuration ensures stable resonance behavior, low insertion loss, and strong interaction between neighboring resonators. A summary of the key design parameters and material properties used in the computational modeling is presented in Table 1.

Based on the structural configuration shown in Figure 2(b), the electric-field evolution within the Panda-ring resonator circuit can be described using a coupled-mode analytical model [35]. The field amplitudes at the throughput, drop, and add ports are governed by the coupling coefficients, insertion losses, and phase accumulation along each ring, and can be expressed as follows:

$$E_{th}=\sqrt{1-{\gamma }_1}\left(\sqrt{1-{\kappa }_1}{E}_{i1}+j\sqrt{{\kappa }_1}{E}_4{e}^{-{\displaystyle \frac{\alpha }{2}}{\displaystyle \frac{L_D}{4}}-j{k}_n{\displaystyle \frac{L_D}{4}}}\right)$$

(4)

$$E_{dr}=\sqrt{1-{\gamma }_3}\left(\sqrt{1-{\kappa }_3}{E}_{i2}+j\sqrt{{\kappa }_3}{E}_2{e}^{-{\displaystyle \frac{\alpha }{2}}{\displaystyle \frac{L_D}{4}}-j{k}_n{\displaystyle \frac{L_D}{4}}}\right)$$

(5)

$$E_{ad}=\sqrt{1-{\gamma }_3}\left(\sqrt{1-{\kappa }_3}{E}_d+j\sqrt{{\kappa }_3}{E}_2{e}^{-{\displaystyle \frac{\alpha }{2}}{\displaystyle \frac{L_D}{4}}-j{k}_n{\displaystyle \frac{L_D}{4}}}\right)$$

(6)

where,

$$E_1=\sqrt{1-{\gamma }_1}\left(\sqrt{1-{\kappa }_1}{E}_4{e}^{-{\displaystyle \frac{\alpha }{2}}{\displaystyle \frac{L_D}{2}}-j{k}_n{\displaystyle \frac{L_D}{2}}}+j\sqrt{{\kappa }_1}{E}_{i1}{e}^{-{\displaystyle \frac{\alpha }{2}}{\displaystyle \frac{L_D}{4}}-j{k}_n{\displaystyle \frac{L_D}{4}}}\right)$$

(7)

$$E_2=\sqrt{1-{\gamma }_2}\left(\sqrt{1-{\kappa }_2}{E}_1+j\sqrt{{\kappa }_2}{E}_{R1}{e}^{-{\displaystyle \frac{\alpha }{2}}{L}_R-j{k}_n{L}_R}\right)$$

(8)

$$E_3=\sqrt{1-{\gamma }_3}\left(\sqrt{1-{\kappa }_3}{E}_2{e}^{-{\displaystyle \frac{\alpha }{2}}{\displaystyle \frac{L_D}{2}}-j{k}_n{\displaystyle \frac{L_D}{2}}}+j\sqrt{{\kappa }_3}{E}_{i2}{e}^{-{\displaystyle \frac{\alpha }{2}}{\displaystyle \frac{L_D}{4}}-j{k}_n{\displaystyle \frac{L_D}{4}}}\right)$$

(9)

$$E_4=\sqrt{1-{\gamma }_4}\left(\sqrt{1-{\kappa }_4}{E}_3+j\sqrt{{\kappa }_4}{E}_{L1}{e}^{-{\displaystyle \frac{\alpha }{2}}{L}_L-j{k}_n{L}_L}\right)$$

(10)

Where $\gamma ,\kappa$ and $\alpha$ are insertion loss coefficient of the directional coupler, the coupling factor and attenuation coefficient of the ring. In additional, L_D is the circumference of the center ring, L_R is the circumference of the right ring, L_L is the circumference of the left ring and $k_n=2\pi n_{eff}$. To evaluate the power intensity presented in Section 3.2, the optical intensity at each port is derived from the corresponding electric-field amplitude obtained from numerical simulations. Under harmonic steady-state conditions, the optical intensity is proportional to the squared magnitude of the electric field and can be expressed as

$$I={\displaystyle \frac{1}{2}}{n}_{eff}c{\epsilon }_0\left|E^2\right|$$

(11)

where $n_{eff}$ is the effective refractive index of the guiding medium, ${\epsilon }_0$ is the vacuum permittivity, $c$ is the speed of light in free space, and $E$ denotes the complex electric-field amplitude at the observation port. This relation is applied consistently to all ports of the resonator structures, including the throughput, drop, and add ports.

2.3. Computational Modeling and Simulation Setup

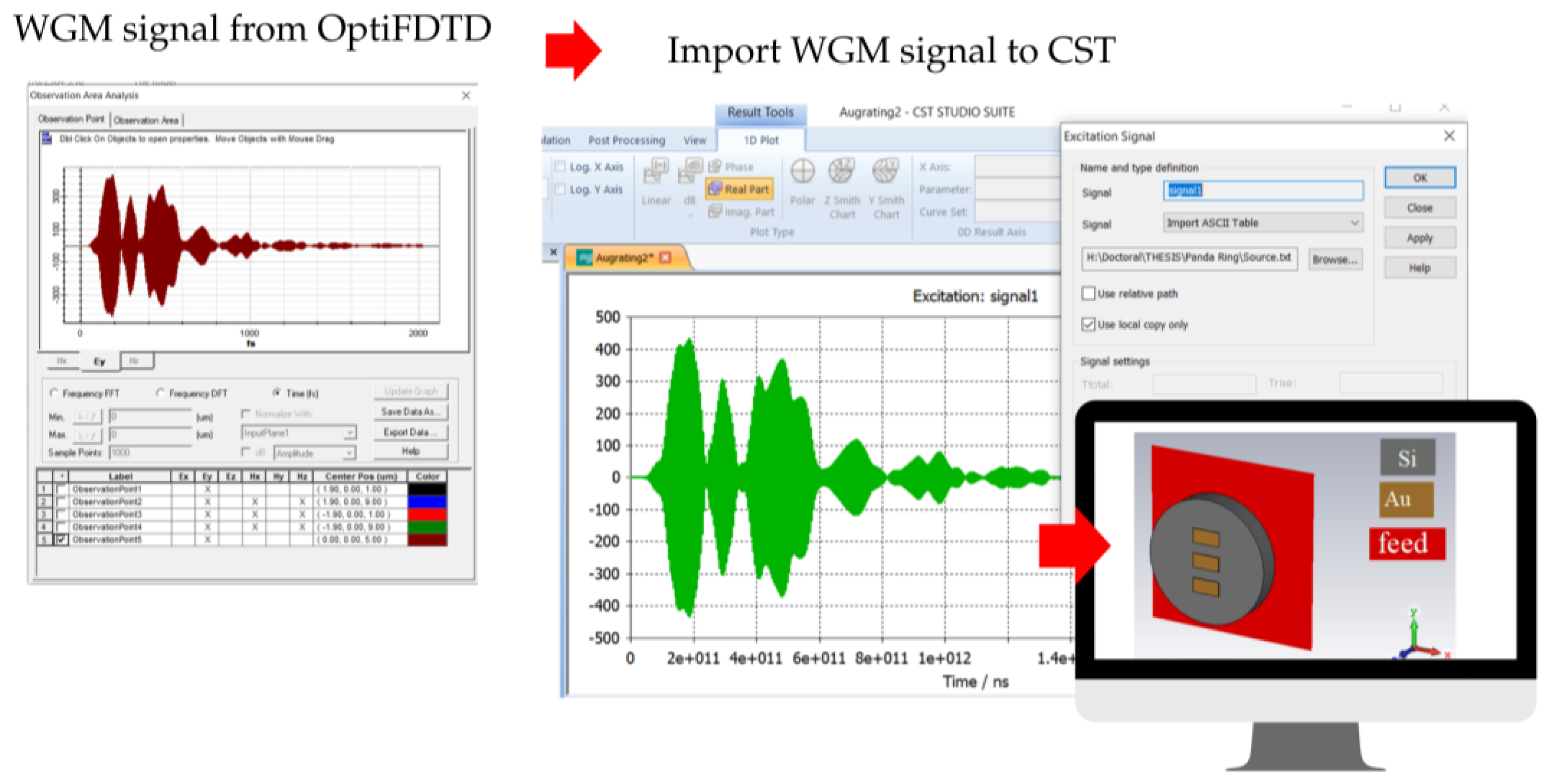
To comprehensively investigate the dual-mode plasmonic behavior of the proposed Panda-ring antenna embedded with a gold grating, full-wave numerical simulations were conducted using two complementary electromagnetic solvers: Optiwave Finite-Difference Time-Domain (FDTD) and CST Microwave Studio. This combined approach enables accurate characterization of near-field photonic–plasmonic interactions in the optical domain as well as far-field radiation performance in the terahertz regime.

Optiwave FDTD was employed to model the optical-domain behavior of the resonator-based structures, to suppress artificial boundary reflections, anisotropic perfectly matched layer (APML) boundary conditions are applied in all directions. The APML consists of 15 absorbing layers with a reflection coefficient of approximately 1.0×10⁻¹², providing effective absorption of both propagating and evanescent plasmonic waves. A uniform spatial discretization of Δx=Δy=Δz= 0.045 µm is employed to accurately resolve subwavelength field confinement at the metal–dielectric interface. The computational domain comprises 308×55×353 mesh cells along the X, Y, and Z-axes, respectively. A Gaussian pulse centered at 1.55 µm is launched through the silicon linear waveguide. Time-domain electric-field responses are recorded at the throughput, drop, add, and central ring regions, and subsequently transformed into the spectral domain using discrete Fourier transform (DFT) analysis. To achieve steady-state resonance, the simulation is performed over 20,000 round trips. This configuration provides reliable evaluation of electric-field distributions and spectral power characteristics, forming the basis for subsequent WGM-based excitation and far-field radiation analysis. To investigate the antenna radiation characteristics, including gain, and far-field patterns, CST Microwave Studio was utilized. In this stage, the optical WGM output obtained from the resonator analysis was employed as the excitation source for the plasmonic antenna structure. This approach allows direct translation of near-field energy confinement into radiating modes, enabling realistic evaluation of antenna performance under WGM-driven excitation. Frequency-domain solvers were used to compute far-field radiation patterns at selected operating frequencies corresponding to the dominant resonant wavelengths identified in the optical simulations.

Figure 3. Procedure for WGM-based excitation signal transfer from Optiwave FDTD to CST Microwave Studio: the time-domain WGM electric-field signal extracted from the central Panda-ring resonator is exported from OptiFDTD and subsequently imported as the excitation source in CST to drive the plasmonic antenna for far-field radiation and gain analysis.

Figure 3. Procedure for WGM-based excitation signal transfer from Optiwave FDTD to CST Microwave Studio: the time-domain WGM electric-field signal extracted from the central Panda-ring resonator is exported from OptiFDTD and subsequently imported as the excitation source in CST to drive the plasmonic antenna for far-field radiation and gain analysis.

The combination of Optiwave FDTD and CST Microwave Studio provides a unified computational framework that bridges photonic resonance behavior and antenna radiation analysis. This multi-scale simulation strategy ensures physical consistency between near-field plasmonic–photonic interactions and far-field electromagnetic radiation, thereby enabling reliable assessment of the proposed antenna’s dual-mode transmission capability. The simulation methodology adopted in this work directly supports the electric-field, power intensity, and radiation results discussed in Section 3, confirming the effectiveness of the proposed hybrid plasmonic–photonic Panda-ring antenna design.

3. Results

This section presents the numerical results of the proposed plasmonic Panda-ring antenna, focusing on the evolution of electromagnetic behavior from resonator-based photonic structures to the hybrid plasmonic–photonic configuration. The analysis includes electric-field distributions, spectral power intensity responses, and far-field radiation characteristics, providing insight into the hybrid SPP–WGM coupling mechanism and its role in enabling dual-mode transmission and enhanced antenna performance.

3.1. Electric-Field Distribution in Resonator-Based Structures

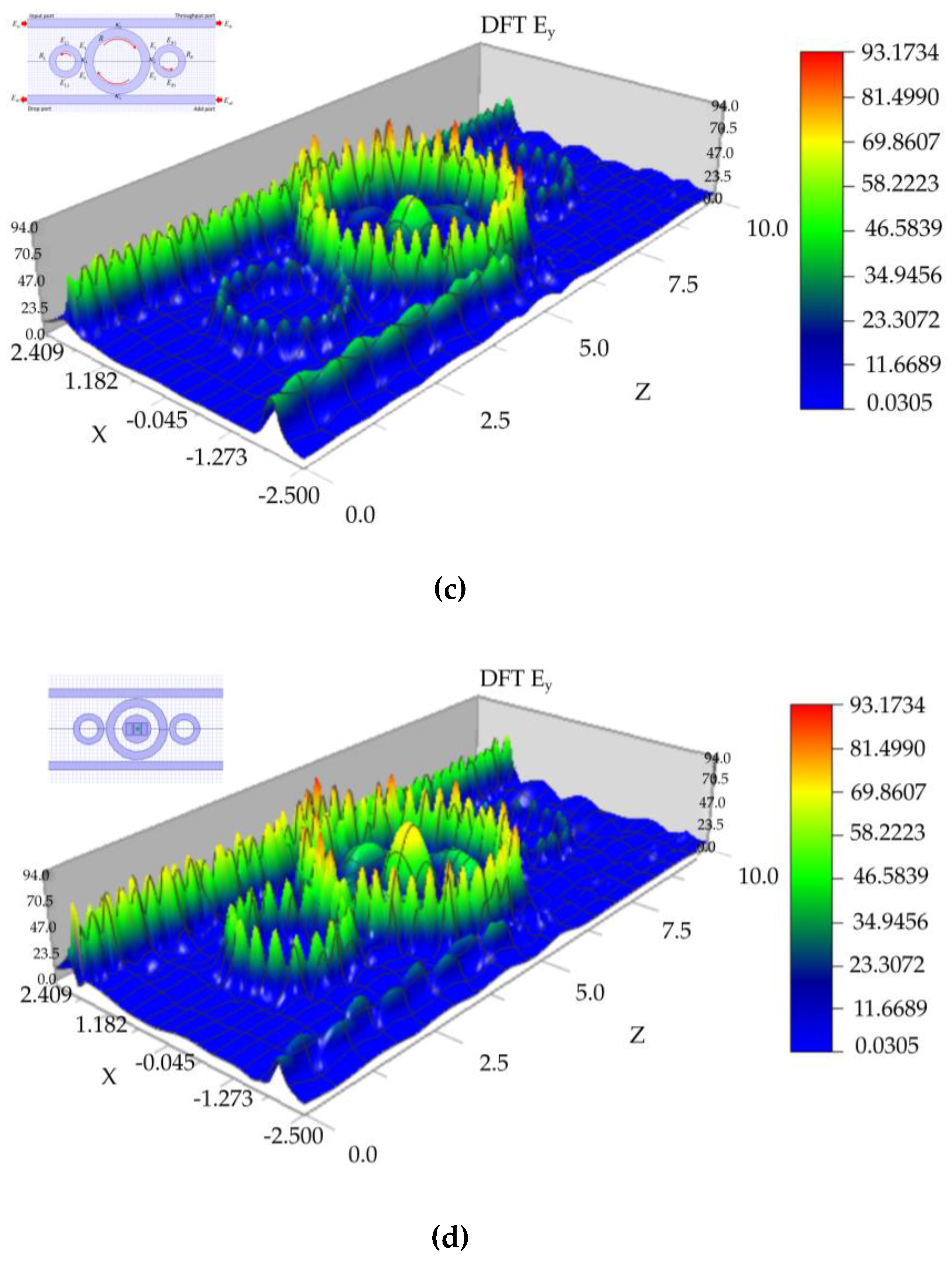
The electric-field distributions of the resonator-based configurations and the proposed structure are summarized in Figure 4 to provide a comparative visualization of field confinement, coupling behavior, and resonant mode evolution as the structural complexity increases. Unlike the linear waveguide baseline, which primarily supports forward-guided propagation with limited field localization, the resonator-based structures exhibit pronounced field enhancement arising from resonant circulation and evanescent coupling mechanisms. This progressive evolution of field distribution plays a critical role in establishing the hybrid plasmonic–photonic response and dual-mode operation of the proposed antenna. For Structure 1, which consists of a simple silicon linear waveguide, no detailed electric-field distribution analysis is presented. In general, propagation loss in a straight waveguide accumulates with transmission length due to material absorption and scattering effects. However, in this work the waveguide length is intentionally designed to be extremely short, on the order of a few micrometers, resulting in negligible attenuation over the propagation distance considered. Consequently, the linear waveguide primarily serves as a reference for guided-wave transmission rather than a resonant structure. The subsequent analysis therefore focuses on resonator-based configurations (Structures 2–5), where field localization, resonant buildup, and coupling-induced redistribution dominate the electromagnetic behavior and are directly relevant to the dual-mode operation of the proposed antenna.

For the silicon ring resonator coupled to a single linear waveguide (Structure 2), the electric-field distribution demonstrates a clear buildup of circulating fields along the ring perimeter, indicating the excitation of whispering-gallery-like resonant modes. Strong field localization is observed near the coupling region between the straight waveguide and the ring, confirming efficient evanescent coupling and power transfer from the bus waveguide into the resonator cavity. Outside the coupling zone, the field intensity decays rapidly, highlighting effective spatial confinement within the resonator. This configuration represents the fundamental resonant behavior, where energy is primarily stored and recirculated within a single ring, providing a baseline for subsequent multi-resonator coupling analysis. When the resonator topology is extended to include a double linear waveguide configuration (Structure 3), the electric-field distribution reveals a more complex coupling pattern. In addition to the circulating field within the ring, enhanced field intensity appears along both bus waveguides, indicating bidirectional energy exchange through multiple coupling interfaces. The presence of two waveguides introduces additional coupling paths, leading to increased field redistribution and partial symmetry breaking in the spatial field profile. This configuration enables more flexible power routing between input, throughput, drop, and add ports, while maintaining strong resonant confinement inside the ring. The resulting field pattern illustrates how multi-port access can be achieved without significantly degrading resonance stability, an essential feature for integrated photonic circuits and antenna feeding networks. Further enhancement of resonant interaction is observed in the Panda-ring resonator configuration without plasmonic loading (Structure 4), where a central ring is coupled to two side rings. The electric-field distribution shows strong field localization not only within the main ring but also in the adjacent side rings, indicating efficient inter-ring coupling and collective mode formation. The coupled-ring topology promotes energy exchange among the resonators, leading to extended field circulation paths and increased effective interaction length. As a result, higher field intensity and improved confinement are achieved compared with single-ring configurations. The presence of multiple resonant pathways also facilitates mode splitting and stabilization, which is advantageous for achieving controlled resonance behavior and enhanced spectral selectivity.

The most significant modification of the electric-field distribution occurs in the proposed hybrid plasmonic–photonic Panda-ring structure embedded with a gold grating (Structure 5). As shown in Figure 4, the field intensity is strongly enhanced at the central ring region where the metallic grating is embedded, while high-intensity circulating fields are preserved along the dielectric ring perimeter. This behavior indicates the simultaneous excitation of whispering gallery modes within the dielectric resonator and surface plasmon polaritons at the metal–dielectric interface. The strong spatial overlap between the evanescent plasmonic field supported by the gold grating and the circulating WGM field confined in the silicon ring confirms the formation of hybrid SPP–WGM coupling. The hybrid coupling mechanism fundamentally alters the field distribution by redistributing electromagnetic energy between plasmonic and photonic domains. While the dielectric resonator maintains high-Q confinement and stable circulation, the metallic grating introduces localized plasmonic hotspots that enhance near-field intensity and facilitate controlled radiative leakage.

This dual behavior enables efficient conversion between guided photonic modes and radiative plasmonic modes, thereby supporting dual-mode transmission. The resulting field pattern exhibits both strong near-field localization, characteristic of plasmonic excitation, and extended circulating fields associated with photonic resonance, providing a physical basis for the observed improvements in radiation efficiency and gain. Comparing the field distributions across all resonator-based structures highlights the critical role of structural evolution in enabling dual-mode operation. Single-ring and multi-bus configurations primarily enhance photonic resonance and power routing, whereas the Panda-ring topology introduces cooperative resonant coupling that strengthens field confinement. The integration of the gold grating further extends this capability by activating plasmonic modes that interact constructively with WGMs. This synergy enhances impedance matching, reduces propagation loss through energy redistribution, and improves far-field radiation characteristics without sacrificing resonance stability.

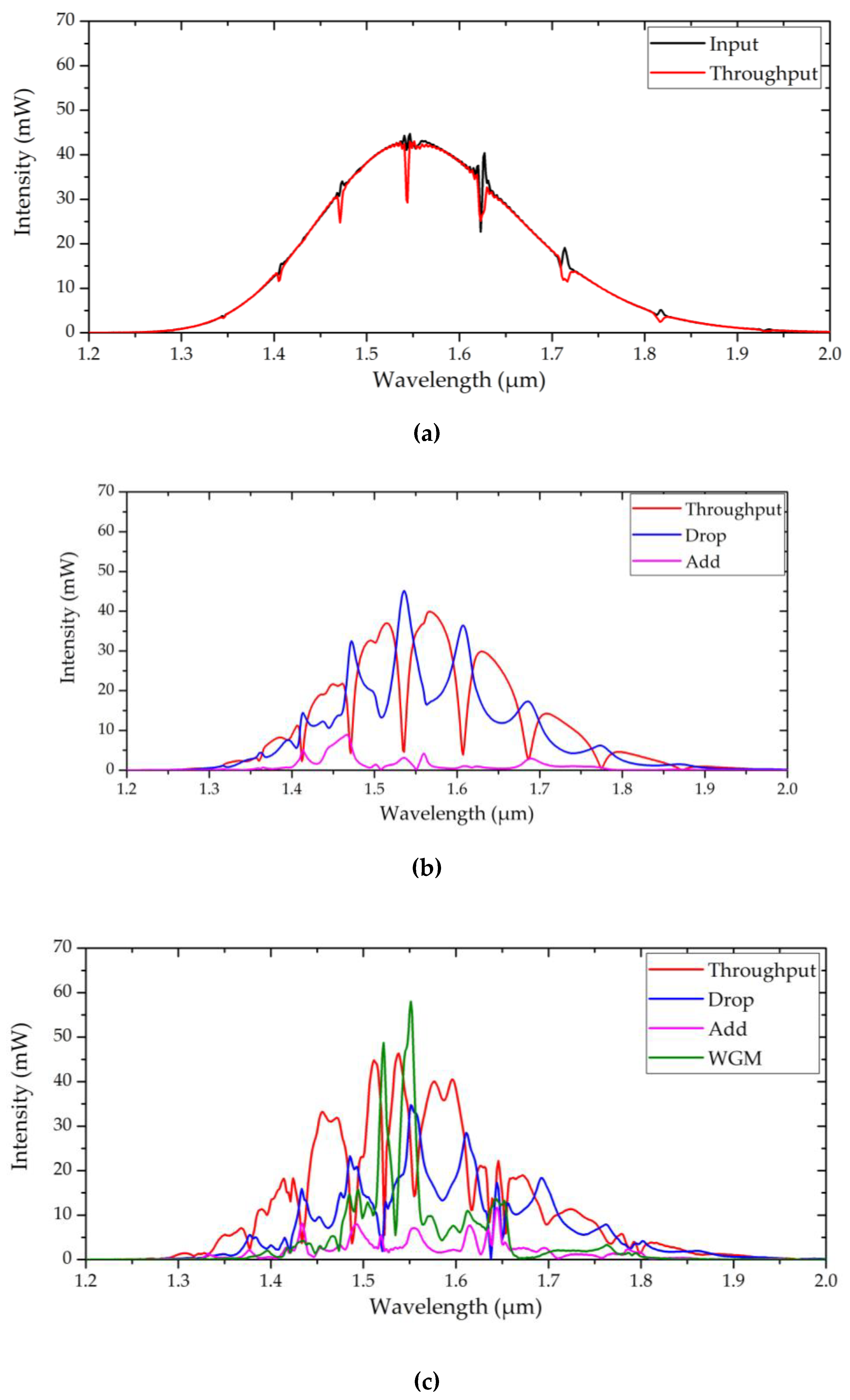
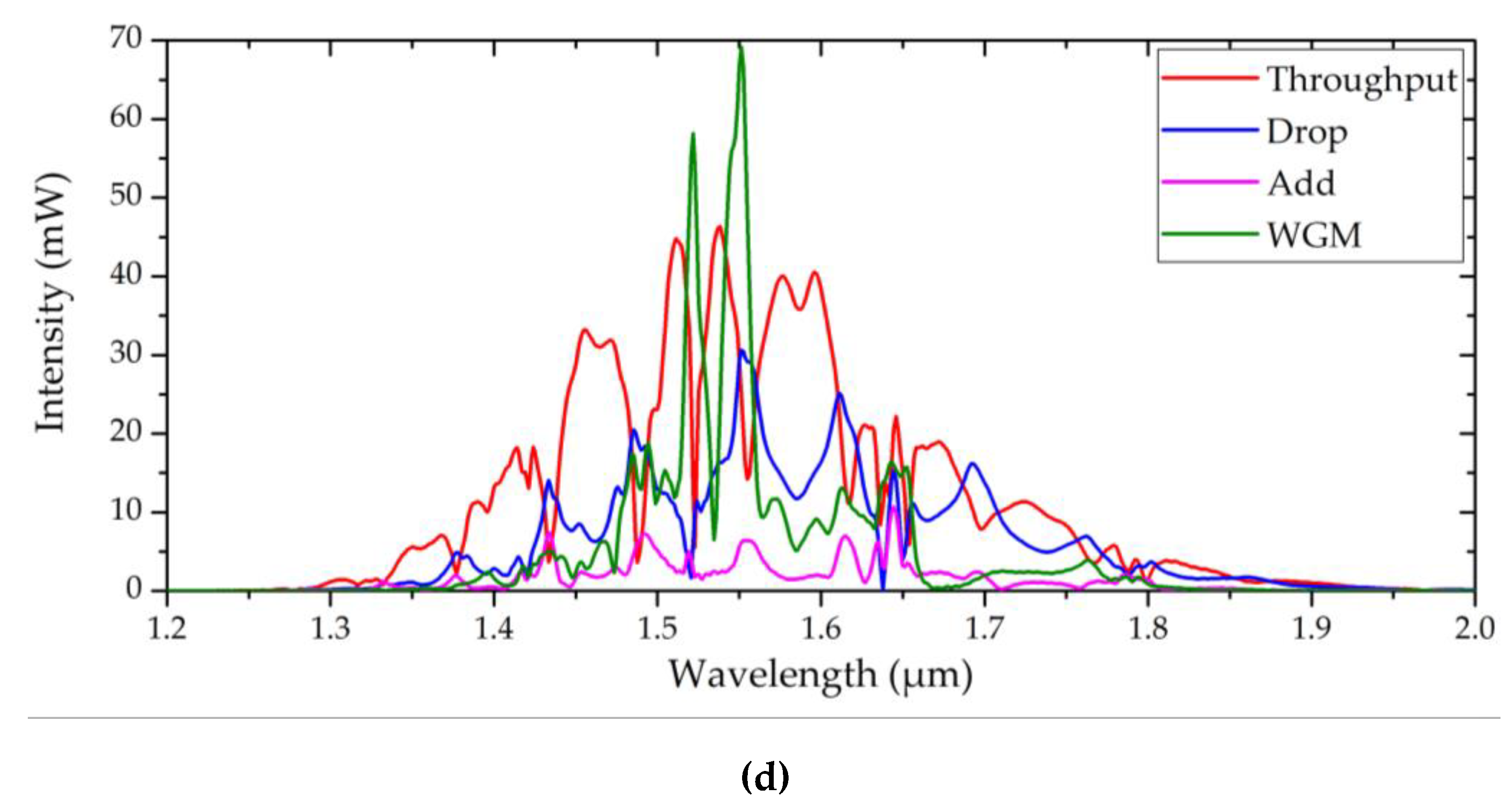
3.2. Spectral Power Intensity Analysis of Resonator-Based Structures

Figure 5 presents the simulated power intensity spectra of the resonator-based configurations, illustrating the evolution of spectral characteristics from purely photonic resonators to the proposed hybrid plasmonic Panda-ring antenna. The results provide insight into wavelength-dependent power redistribution, resonant mode formation, and the transition toward dual-mode operation governed by hybrid surface plasmon polariton (SPP) and whispering gallery mode (WGM) coupling. For Structure 2, which consists of a silicon ring resonator coupled to a single linear waveguide, the power intensity response is dominated by fundamental WGM resonances. As shown in Figure 5(a), the throughput port exhibits attenuation notches at resonance wavelengths, corresponding to efficient coupling of optical energy into the ring cavity. The complementary behavior observed at the drop port in Figure 5(b) confirms selective wavelength extraction characteristic of add–drop filter operation. In this configuration, energy redistribution is primarily controlled by photonic resonance, with limited modal interaction and negligible add-port excitation.

The introduction of a second linear waveguide in Structure 3 significantly modifies the spectral response. As illustrated in Figure 5(b), the throughput, drop, and add ports simultaneously exhibit pronounced resonance features. The presence of dual bus waveguides enables bidirectional coupling and increases the number of accessible coupling paths, resulting in enhanced power routing flexibility. Compared with the single-waveguide configuration, Structure 3 demonstrates increased resonance density and stronger port-to-port interaction, indicating improved controllability of photonic power flow while maintaining stable WGM confinement. Figure 5(c) shows the power intensity spectra of Structure 4, employing a Panda-ring resonator composed of a central microring coupled to two auxiliary side rings. The multi-ring topology introduces coherent inter-ring coupling, leading to mode splitting and resonance broadening across the wavelength spectrum. Strong WGM intensity peaks are observed, accompanied by deeper attenuation at the throughput port and enhanced extraction at the drop port. The add port also exhibits noticeable modulation, reflecting bidirectional energy exchange enabled by the coupled resonator system. These results confirm that the Panda-ring architecture significantly enhances modal interaction and resonance controllability compared with conventional single-ring configurations, serving as a critical intermediate step toward hybrid plasmonic integration. The spectral response of the proposed Structure 5, shown in Figure 5(d), reveals a marked enhancement in power intensity characteristics due to the incorporation of a gold grating within the Panda-ring resonator. Sharp and high-amplitude WGM peaks appear near the central resonance wavelengths, indicating strong electromagnetic field localization induced by efficient SPP excitation at the metal–dielectric interface. Compared with the purely photonic Panda-ring, the hybrid structure exhibits deeper throughput attenuation, stronger drop-port extraction, and increased add-port modulation, demonstrating effective hybridization between plasmonic and photonic modes.

The coexistence of enhanced WGM resonances and redistributed port intensities confirms the realization of dual-mode operation in Structure 5. In this regime, photonic WGMs provide resonance stability and efficient power routing, while plasmonic SPPs contribute sub-wavelength field confinement and localized field enhancement. The hybrid SPP–WGM interaction improves impedance matching and energy transfer efficiency, resulting in superior spectral selectivity and power redistribution compared with all preceding configurations.

3.3. Far-Field Radiation and Gain Characteristics Under WGM Excitation

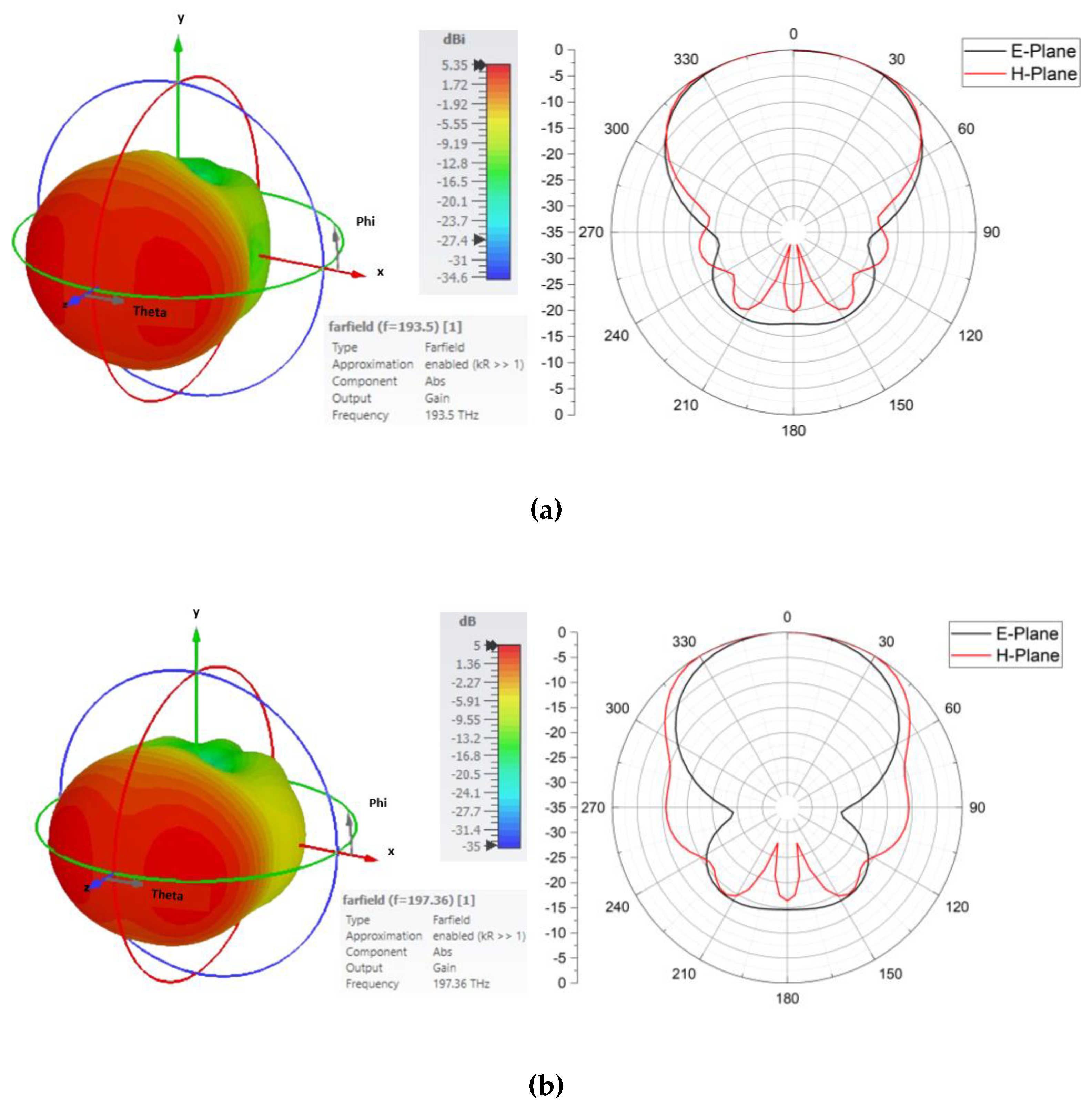
In this subsection, the far-field radiation characteristics and antenna gain of the proposed hybrid plasmonic Panda-ring antenna are analyzed under Whispering Gallery Mode (WGM)-based excitation. Unlike conventional antenna excitation schemes that rely on direct port feeding, the proposed approach employs the WGM signal extracted from Structure 4 as the excitation source, which is subsequently injected into the central plasmonic region of the antenna in CST Microwave Studio. This excitation strategy enables the conversion of confined photonic energy into radiated electromagnetic waves, thereby realizing a unique WGM-driven antenna operation.

Figure 6(a) illustrates the three-dimensional far-field radiation pattern and corresponding E-plane and H-plane cuts at a frequency of 193.5 THz. The radiation pattern exhibits a dominant main lobe with relatively symmetric angular distribution, indicating effective radiation from the plasmonic antenna structure. The maximum realized gain reaches approximately 5.35 dBi, demonstrating that the confined WGM energy can be efficiently transformed into far-field radiation through the hybrid plasmonic–photonic architecture. The E-plane and H-plane patterns further confirm stable radiation characteristics, with comparable beamwidths and controlled sidelobe levels, reflecting balanced mode conversion and radiation efficiency. Figure 6(b) presents the radiation characteristics at a higher operating frequency of 197.36 THz. At this frequency, the antenna maintains a well-defined radiation pattern with a peak gain of approximately 5.0 dBi. Although a slight reduction in gain is observed compared with the lower-frequency case, the radiation remains directive and stable, indicating broadband operation enabled by the hybrid resonant structure. The consistency of the E-plane and H-plane patterns across both frequencies highlights the robustness of the WGM-based excitation mechanism and its ability to sustain efficient radiation over a wide spectral range.

The observed radiation behavior can be attributed to the hybrid coupling between WGMs and surface plasmon polaritons (SPPs) within the antenna. The WGM excitation provides high-Q energy storage and stable resonance inside the Panda-ring structure, while the embedded gold grating facilitates strong plasmonic field localization and momentum matching at the metal–dielectric interface. This hybrid SPP–WGM interaction enables efficient out-coupling of electromagnetic energy from the near-field region into free space, resulting in enhanced gain and improved radiation efficiency compared with purely photonic or purely plasmonic antenna configurations. Furthermore, the directional radiation patterns observed in both E-plane and H-plane cuts confirm that the proposed antenna supports controlled radiation rather than isotropic scattering, which is a common limitation in many nanoscale plasmonic antennas. The combination of multi-ring resonant confinement and plasmonic perturbation allows effective shaping of the radiation characteristics, making the antenna suitable for high-frequency wireless and optical communication applications.

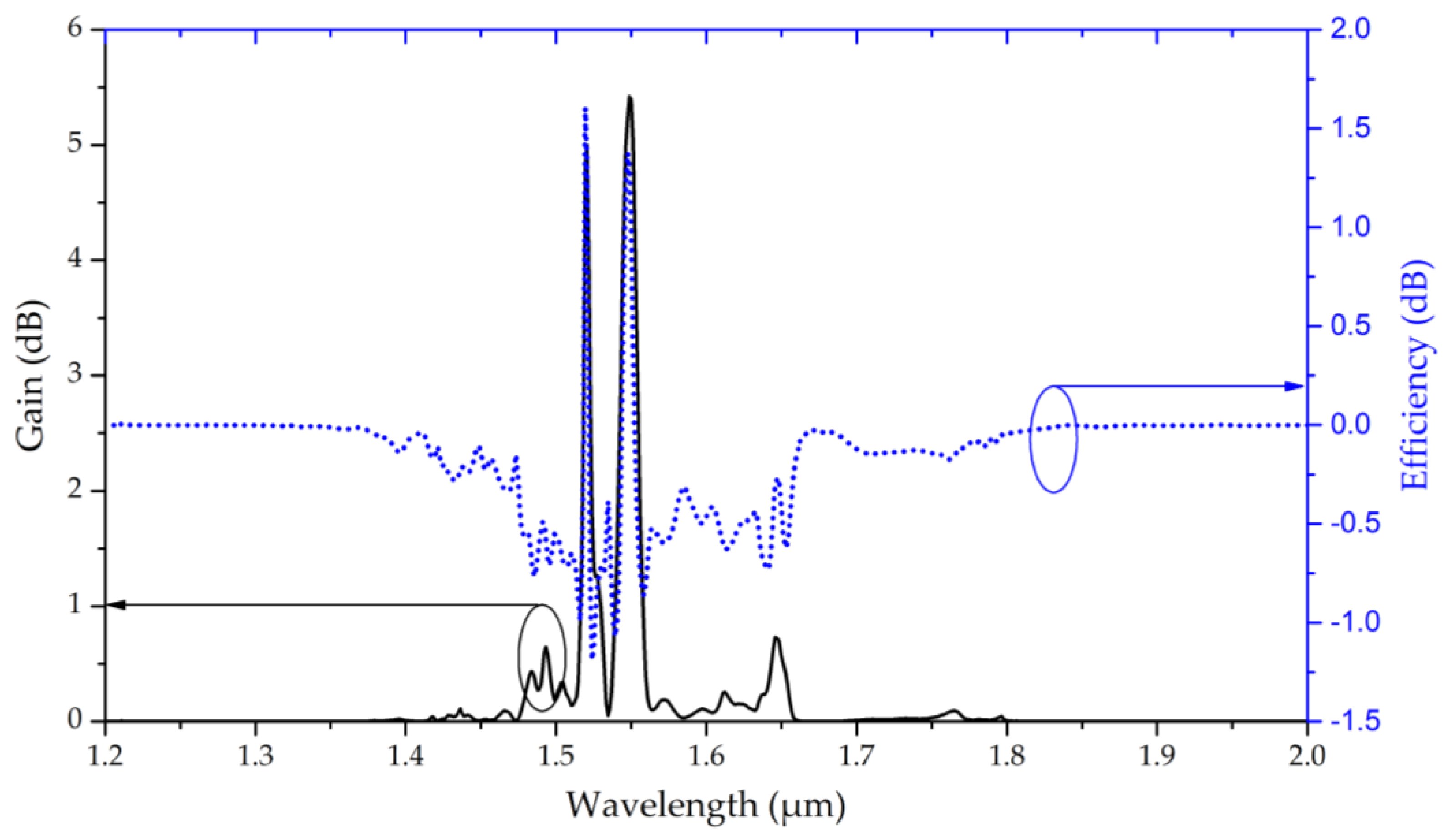
Following the far-field radiation analysis, the wavelength-dependent gain and radiation efficiency of the proposed antenna under WGM excitation are further evaluated, as illustrated in Figure 7. The results provide additional insight into the relationship between resonant photonic confinement and radiative performance across the optical band. the antenna gain exhibits pronounced peaks in the vicinity of the dominant WGM resonant wavelengths, particularly at 1.52 and 1.55 µm, where the gain reaches values exceeding 5 dB. These sharp gain enhancements coincide with the spectral positions where strong WGM confinement and efficient hybrid SPP–WGM coupling occur within the Panda-ring structure. At these wavelengths, the stored electromagnetic energy inside the resonator is effectively transferred to radiating modes through the embedded gold grating, resulting in a significant increase in far-field radiation strength. The radiation efficiency curve, plotted simultaneously in Figure 7, remains relatively stable over a broad wavelength range, with only moderate fluctuations near the resonance region. Although a slight efficiency reduction is observed at the exact resonance wavelengths due to increased plasmonic absorption and ohmic losses in the metallic grating, the overall efficiency remains close to 0 dB, indicating that a substantial portion of the input energy is successfully converted into radiated power. This behavior reflects the inherent trade-off between field confinement and radiation loss in hybrid plasmonic systems, where enhanced localization is accompanied by increased metallic dissipation.

Notably, the coexistence of high gain and acceptable radiation efficiency near the WGM resonances confirms the effectiveness of the proposed dual-mode operating mechanism. The Panda-ring resonator provides high-Q photonic energy storage through WGMs, while the gold grating introduces controlled plasmonic perturbation that enables momentum matching and efficient out-coupling to free space. This synergistic interaction allows the antenna to achieve gain enhancement without severe degradation of radiation efficiency, overcoming a common limitation of purely plasmonic nanoantennas. Overall, the spectral gain and efficiency characteristics demonstrate that the proposed hybrid plasmonic–photonic Panda-ring antenna supports stable and efficient radiation over a broad optical wavelength range, with peak performance governed by WGM-assisted excitation. These results further validate the suitability of the proposed design for high-frequency optical wireless links, Li-Fi transmitters, and integrated photonic–plasmonic communication systems requiring compact form factors and dual-mode transmission capability.

4. Discussion

This section discusses the physical implications and performance trends observed from the comparative analysis of the five investigated structures, as summarized in Table 2, with particular emphasis on the transition from purely photonic guiding systems to the proposed hybrid plasmonic–photonic Panda-ring antenna. The discussion highlights how incremental structural modifications influence field confinement, spectral behavior, and radiation capability, ultimately enabling efficient dual-mode transmission suitable for high-frequency Li-Fi and terahertz (THz) applications

4.1. Evolution from Linear Photonic Guiding to Resonator-Based Confinement

The linear silicon waveguide (Structure 1) serves as a fundamental reference, supporting guided-wave propagation without resonant enhancement. Due to the absence of feedback or modal confinement mechanisms, electromagnetic energy remains weakly confined and does not contribute to effective radiation. While such structures are indispensable as optical interconnects and excitation channels in integrated photonic systems, their functionality is limited to signal transport rather than energy manipulation or radiation [36,37,38]. Consequently, Structure 1 is excluded from detailed field or radiation analysis and is used solely as a baseline for comparison. Introducing a ring resonator with a single bus waveguide (Structure 2) enables whispering gallery mode (WGM) formation through total internal reflection along the curved dielectric interface [32,36,39]. This configuration significantly enhances optical field confinement compared with linear waveguides; however, the energy remains largely trapped within the resonator due to its high-Q nature and minimal radiation leakage. As a result, this structure is well suited for optical filtering and refractive-index sensing applications but remains ineffective as a radiating element [33,40,41].

The dual-bus (add-drop) ring resonator (Structure 3) extends this concept by providing controlled power routing through distinct throughput and drop ports [33]. Although spectral selectivity and functional versatility improve, the dominant physical mechanism remains linear WGM confinement. Radiation leakage is still weak and unintentional, confirming that conventional add-drop resonators are not inherently suitable for antenna operation [17,18,19,20,42].

4.2. Panda-Ring Resonator as a High-Q WGM Excitation Platform

The Panda-ring resonator (Structure 4), composed of a central ring coupled with two auxiliary side rings, represents a significant advancement in modal controllability and resonance stability. The multi-ring topology supports strongly coupled WGMs with enhanced quality factors, enabling precise control over resonance conditions and power distribution among multiple ports [10,11,12,14,15,16]. Despite these advantages, the structure remains predominantly non-radiative due to strong optical confinement. Importantly, the Panda-ring configuration demonstrates its value as an efficient WGM excitation source, rather than a direct radiator. The high stored electromagnetic energy and stable resonance behavior make it particularly suitable for feeding downstream radiating structures, optical signal processing, and nonlinear photonic applications [13,15,35]. This observation forms a crucial bridge between photonic resonators and antenna systems, enabling the transition from confined optical modes to radiative electromagnetic modes.

4.3. Hybrid SPP–WGM Coupling and Dual-Mode Radiation Mechanism

The proposed structure (Structure 5) introduces a fundamental shift in physical behavior by embedding a gold (Au) grating into the Panda-ring resonator. This modification facilitates strong coupling between WGMs and surface plasmon polaritons (SPPs) at the metal–dielectric interface [28,29,30], resulting in a hybrid plasmonic–photonic system. Unlike purely photonic resonators, this hybrid configuration enables sub-wavelength field confinement and efficient momentum matching, allowing confined energy to couple into free-space radiation modes [22,23]. The electric-field and power-intensity distributions demonstrate pronounced localization at the Au grating region, confirming the excitation of plasmonic modes. When driven by WGM-based excitation from Structure 4, the proposed antenna exhibits stable and directional far-field radiation with enhanced gain across multiple optical and THz frequencies. This behavior validates the proposed dual-mode transmission mechanism, where photonic WGMs provide high-Q energy storage and plasmonic SPPs act as an efficient radiation channel [10,11,24]. The observed conversion of WGM-confined energy into directional radiation can be interpreted through plasmon-mediated emission dynamics, analogous to propagating surface plasmon induced photon emission processes previously reported in quantum emitter–plasmon systems [44]. Compared with conventional plasmonic antennas, which often suffer from excessive ohmic losses and poor impedance matching [6,7], the proposed hybrid architecture balances confinement and radiation efficiency through coordinated photonic–plasmonic interaction. The Panda-ring topology ensures resonance stability, while the embedded grating enables controlled radiative leakage. This synergy results in superior performance relative to both purely photonic and purely plasmonic designs [8,9,25,26]

From an application perspective, the comparative analysis clearly illustrates that only the proposed hybrid Panda-ring antenna achieves the necessary combination of field confinement, spectral controllability, and radiation capability required for next-generation communication systems. Structures 1–3 are limited to guided-wave or resonator-based photonic applications, while Structure 4 functions optimally as a non-radiative WGM excitation platform. In contrast, Structure 5 enables direct conversion of confined optical energy into directional electromagnetic radiation. These characteristics make the proposed antenna particularly attractive for Li-Fi transmitters, THz wireless links, and photonic–plasmonic transceivers, where seamless integration between optical signal processing and wireless radiation is required. Furthermore, the computational design framework adopted in this work allows scalable optimization across frequency bands, supporting future extensions toward tunable or reconfigurable hybrid antenna systems.

5. Conclusions

This work has presented a comprehensive investigation and computational demonstration of a hybrid plasmonic–photonic Panda-ring antenna embedded with a metallic gold grating, aimed at enabling efficient dual-mode transmission for high-frequency optical and terahertz communication systems. By systematically evolving the structural configuration from a linear silicon waveguide to progressively more complex resonator-based architectures, the physical mechanisms governing electromagnetic field confinement, spectral behavior, and radiation capability were clearly elucidated. The comparative analysis confirms that conventional photonic structures—including single-ring and add-drop microring resonators—primarily support whispering gallery mode (WGM) confinement with negligible radiation, rendering them unsuitable for antenna applications despite their effectiveness in filtering and sensing. The Panda-ring resonator, composed of three coupled rings, significantly enhances modal controllability and resonance stability, functioning as a high-Q WGM excitation and energy storage platform rather than a direct radiator. A fundamental transition is achieved by embedding a gold grating into the central Panda-ring resonator, thereby activating strong hybrid coupling between WGMs and surface plasmon polaritons (SPPs). This hybrid SPP–WGM interaction enables sub-wavelength field confinement while simultaneously facilitating efficient momentum matching and controlled radiative leakage. As a result, WGM-confined photonic energy is effectively converted into directional free-space radiation, realizing a dual-mode operating mechanism that bridges guided optical modes and radiating electromagnetic modes within a single compact structure.

Full-wave simulations using Optiwave FDTD and CST Microwave Studio demonstrate that the proposed hybrid Panda-ring antenna achieves stable far-field radiation with peak realized gains exceeding 5 dBi at resonant optical frequencies around 1.52–1.55 µm, while maintaining acceptable radiation efficiency despite intrinsic plasmonic losses. The observed radiation behavior is attributed to plasmon-mediated emission dynamics enabled by the embedded metallic grating, which acts as a controlled out-coupling interface rather than a passive scattering element. Compared with purely plasmonic or purely photonic antenna designs, the proposed architecture achieves a favorable balance between strong field confinement, spectral selectivity, and radiation efficiency. Overall, the results confirm that the hybrid plasmonic–photonic Panda-ring antenna uniquely combines the advantages of high-Q photonic resonators and plasmonic radiators, overcoming key limitations associated with each individual domain. The proposed design is therefore well suited for next-generation Li-Fi transmitters, terahertz wireless links, and integrated photonic–plasmonic transceivers requiring compact form factors, directional radiation, and seamless optical-to-wireless mode conversion.