1. Introduction
Currently, M-sequences are widely used in radar systems [
1,
2], where they generate probing signals. These signals improve the accuracy of distance measurement to objects and ensure reliable detection by distinguishing the useful echo signal from noise. In communication systems, they serve to encode data in order to provide reliable synchronization between transmitting and receiving communication equipment. M-sequences also play an important role in the design of multi-position onboard control systems used in remote sensing aviation equipment [
3,
4,
5,
6,
7,
8,
9,
10,
11].
In order to form radar situational awareness using networks of small aerial vehicles equipped with compact on-board radar stations (CORS), it is necessary for each station to emit a unique phase-coded probing signal. This requirement arises from the need for unambiguous identification of CORS emission sources in a common radio channel and accurate determination of the reflection of signals from corresponding transmitting-receiving positions in the system.
High levels of side lobes (SL) in the autocorrelation function (ACF) can negatively affect the proper functioning of CORS detection systems [
12,
13,
14]. Therefore, the current task is to find new complex sequences that have lower SL levels in the normalized autocorrelation function (NACF) while maintaining the same structure for the positions of positive and negative elements as traditional M-sequences. This reduction in the side lobe levels of NACF is achieved by searching for new complex values in the sequence structure by replacing the traditional symmetric alphabet of positive and negative ones with an asymmetric one.
The goal of this study is to search for new complex M-sequences where the SL of the NACF are lower than those of the traditional M-sequences, but with the same structure of positive and negative element positions. This reduction in side lobes is achieved by finding new complex values in the sequence structure through replacing the conventional symmetric alphabet of positive and negative ones with an asymmetric one.
To achieve the stated goal, the paper considers two cases of element substitution in the traditional sequence. In the first case, only the negative one is replaced with the sought-after complex number. In the second case, both the negative and positive ones in the M-sequence structure are replaced. Within this study, it is necessary to analyze how the SL of the NACF change and identify the complex values at which the side lobes of the NACF will be minimized for the new complex M-sequences.
Numerical methods are employed to search for complex values of sequences for both cases. Computer experiments are conducted to evaluate the SL of the NACF. These experiments are based on the analysis of the expressions obtained that describe how each side lobe of the NACF changes as a function of the complex value assigned to the code element. Furthermore, phase modulation of the signal with the generated complex sequence is studied, and the correlation properties of the resulting signals are analyzed.
In
Section 2, the aperiodic and periodic ACFs of traditional M-sequences are analyzed. The process for deriving expressions for the lobes is presented, from which graphs describing the sidelobe levels as a function of the introduced parameter are built for both the aperiodic and periodic ACFs in further research.
In
Section 3, dependencies of the side lobe levels of the periodic and aperiodic NACFs of the complex M-sequences are studied in relation to the new alphabet: {1; –exp(φi)} in the first case, and {exp(φ1i); –exp(φ2i)} in the second case. The values of the parameter φ vary in the range from 0° to 360°. Graphs illustrating the dependencies of the side lobes of the NACF on the parameter φ are provided. The minimal possible level of the side lobes of the NACF for the investigated M-sequences is identified.
In
Section 4, phase modulation of the probing signal with the generated complex M-sequences is carried out. Graphs of the NACF of the resulting signal are constructed. The minimum side lobe level of the NACF for the signal, corresponding to the minimum side lobe level of the complex M-sequence, is found, confirming proper phase modulation of the probing signal.
In
Section 5, the obtained results are discussed, further development recommendations are formulated, and areas for further application of the results in various fields are identified.
In Section 6, the findings of the research are summarized, and the scientific and technical novelty of the results is highlighted.
2. Autocorrelation Function of the M-Sequences
One of the reasons for the demand for M-sequences in radar systems is their correlation characteristics [
15,
16,
17,
18,
19]. When selecting sequences, preference is often given to those with the lowest SL in the NACF. For M-sequences, the maximum value of the ACF occurs only at a zero shift, while for any other shifts, the correlation approaches zero.
The ACF of the sequence x(n) is denoted as R(k) and is computed using expression (1) for the periodic ACF (PACF) of sequences, and expression (2) for the aperiodic ACF (AACF) [
20].
It should be noted that for constructing a multi-position CORS system, code-modulated signals are used, both when selecting the probing signal and when selecting the synchronizing signal used in the frame preamble, which is necessary for organizing communication channels between the group of CORS, as well as for their management [
21,
22,
23,
24,
25,
26].
Therefore, both the properties of the AACF and PACF need to be studied. The AACF should be analyzed for implementing earth’s surface probing modes, including group modes where modulated signals are used. The PACF should be studied when organizing communication channels between elements of the group, i.e., when combining several CORS into an interacting group.
For the PACF calculation:
where n varies from 0 to N-1, and x(n+k) is the sequence element shifted by k positions. If the sequence element with index n+k goes beyond the sequence length, periodic continuation of the sequence is used.
For the calculation of the AACF:
where k varies from 0 to N-1, and n varies from 0 to N-k-1. In this case, the summation is performed only over those n indices for which n+k remains within the sequence length N.
In general form, the process of obtaining expressions describing the sidelobes of the AACF and PACF is presented in
Table 1 and
Table 2, respectively. This example is presented for an M-sequence of length N = 4. The number of sidelobes of the ACF can be calculated using expression (3):
For convenience, each sidelobe of the ACF is assigned an index m, with the main lobe having index 0, and the SL having indices –3, –2, –1, 1, 2, 3. As seen from
Table 1 and
Table 2, there is a relationship between the analytical expressions for the main lobe and the SL of the ACF, which can be expressed using equation (4):
where m is the index of the autocorrelation function lobe. rp(m) is the value of the m-th SL of the PACF, r(m) is the value of the m-th SL of the AACF, and N is the sequence length.
In this context, the CORS hardware is subject to specific requirements related to the choice of the probing signal, for which the levels of the SL of the AACF are directly influenced by the specifics of the task being solved [
27,
28,
29]. For earth’s surface probing modes, the analysis of the AACF is of paramount importance. Its key advantage is a well-defined main lobe at zero shift combined with the minimal SL levels, which ensures high resolution in the range coordinate.
For ensuring interference-resistant data exchange in wireless communication channels between CORS positions, the PACF should be analyzed. The PACF analysis will improve the survivability and fault tolerance of the data exchange system within the interacting group of CORS [
30].
Thus, the analysis of the AACF properties is necessary for implementing group probing signal modes, while the corresponding analysis of the PACF is necessary for implementing communication channels. This will allow the creation of multi-position radar systems optimally combining location and information exchange functions within the interacting group. Such a combination will expand the functional capabilities of individual CORS units, and therefore, the search for new signal-code constructions, both for probing and data exchange, is a modern and relevant task.
3. Search for New Complex M-Sequences
When studying M-sequences, it is necessary to minimize the level of SL of the NACF. This can be achieved by searching for new values in its code structure [
31]. This study proposes replacing the elements of the existing traditional symmetric alphabet {1; –1} in the M-sequence structure with an asymmetric alphabet that can consist of both real and complex values. In complex form, the exponential form of the code elements is used in the form exp(φi), where φ is the angle of the unit vector on the complex plane. φ can also be used as the initial phase for phase modulation of elementary pulses when forming a signal-code structure [
32,
33,
34,
35,
36].
Next, traditional M-sequences of length N = 7, 15, 31, 63, 127, 255, 511 are examined as an example (see
Table 3) illustrating the process of modifying code values to a complex version, using four M-sequences (two M-sequences of length 7 and 15).
Table 3 lists the generator polynomials [
37,
38,
39] and the traditional sequences generated from them with a symmetric alphabet consisting of -1 and +1.
In [
40], optimal replacements of negative ones with the real element “a” in the structures of M-sequences of length N = 15, 31, 63, 127, 255, 511 were determined. Below, two options for changing the traditional alphabet {1; –1} of M-sequences to: {1; –exp(φi)} and {exp(φ1i); –exp(φ2i)}, respectively, will be considered.
3.1. Replacing One Negative Element in the Alphabet of Traditional M-Sequences with a Complex Value
In the first variant, the negative 1 in the code structure is replaced with a complex value – «–exp(φi)», while the positive 1 remains in its place without changing its value. An example of such a replacement of the alphabet of sequences from
Table 3 is presented in
Table 4.
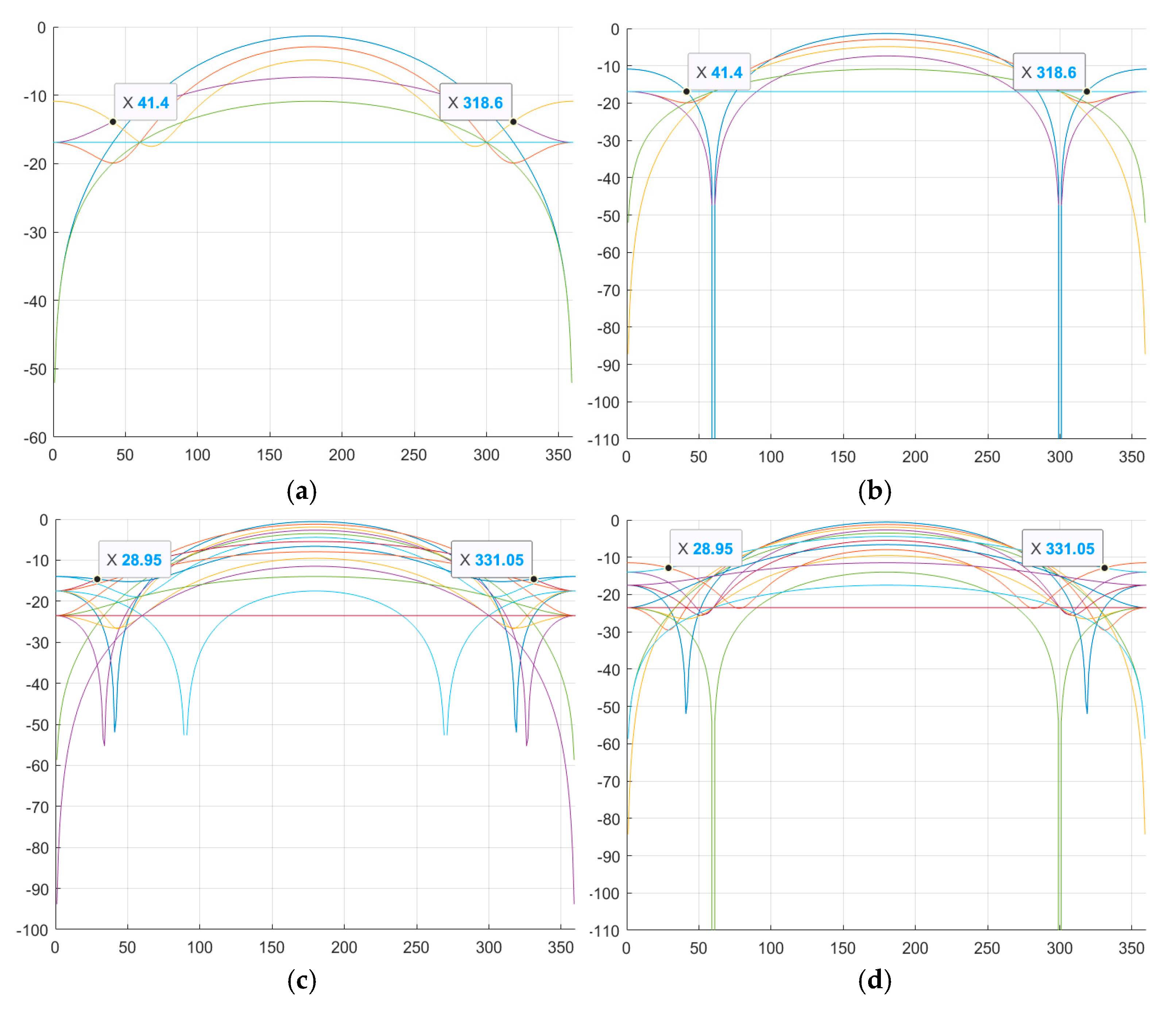
Next, it is necessary to find the optimal value of φ at which the SL of the NACF level is lowest. That is, to search for and determine the specific φ value from the 0-360° range at which the SL will have the minimum level. Graphical representation of the SL levels of the aperiodic NACF of M-sequences from
Table 4 with the alphabet {1; –exp(φi)} is shown in
Figure 1. The horizontal axis shows the value of φ from the range 0-360°, the vertical axis shows the value of SL of the NACF in decibels.
As can be seen from
Figure 1, for M-sequences of the same length, the optimal values of φ are the same initial phases: φ1 = 41.4° and φ2 = 318.6° for N = 7, φ1 = 28.95° and φ2 = 331.05° for N = 15.
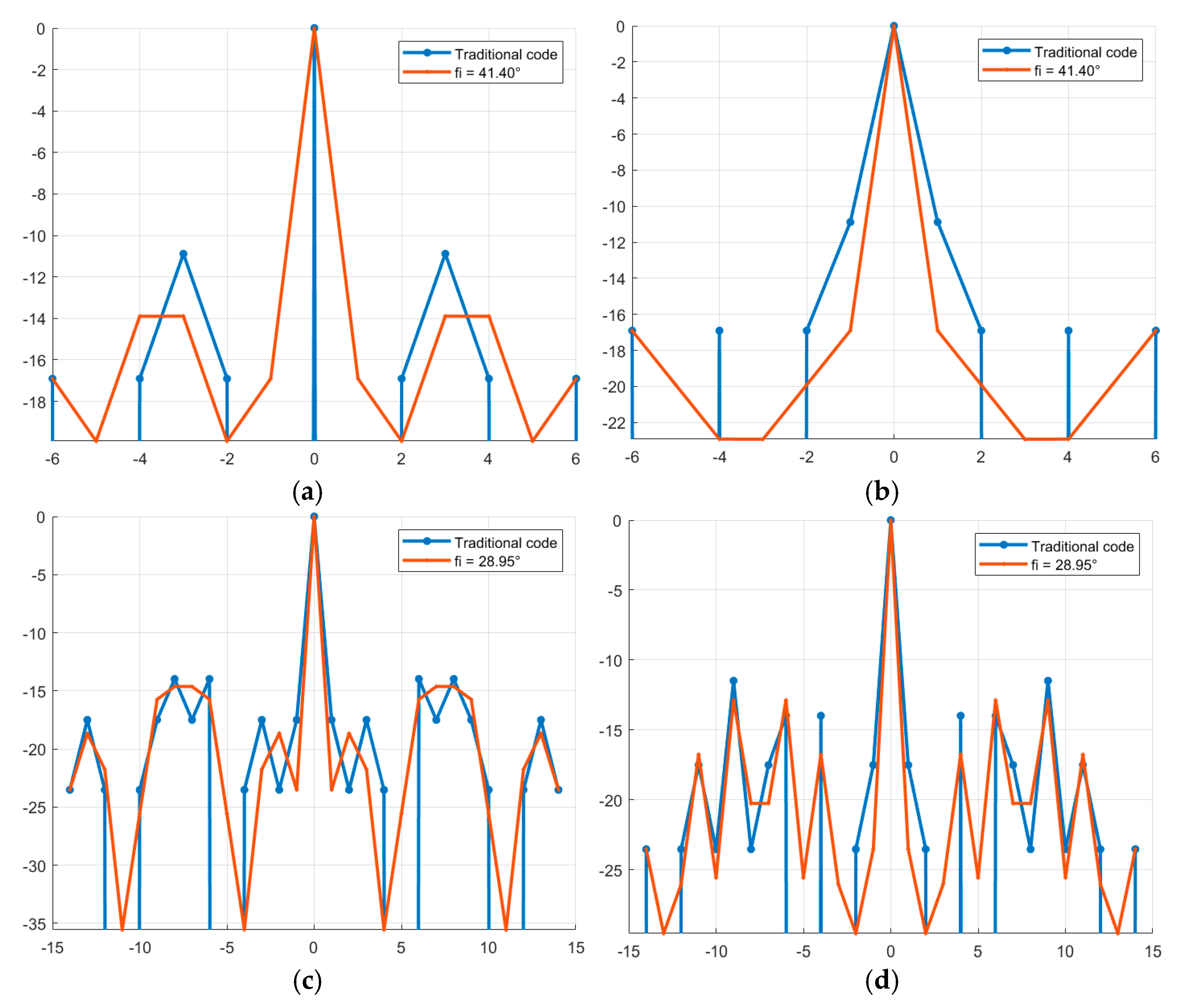
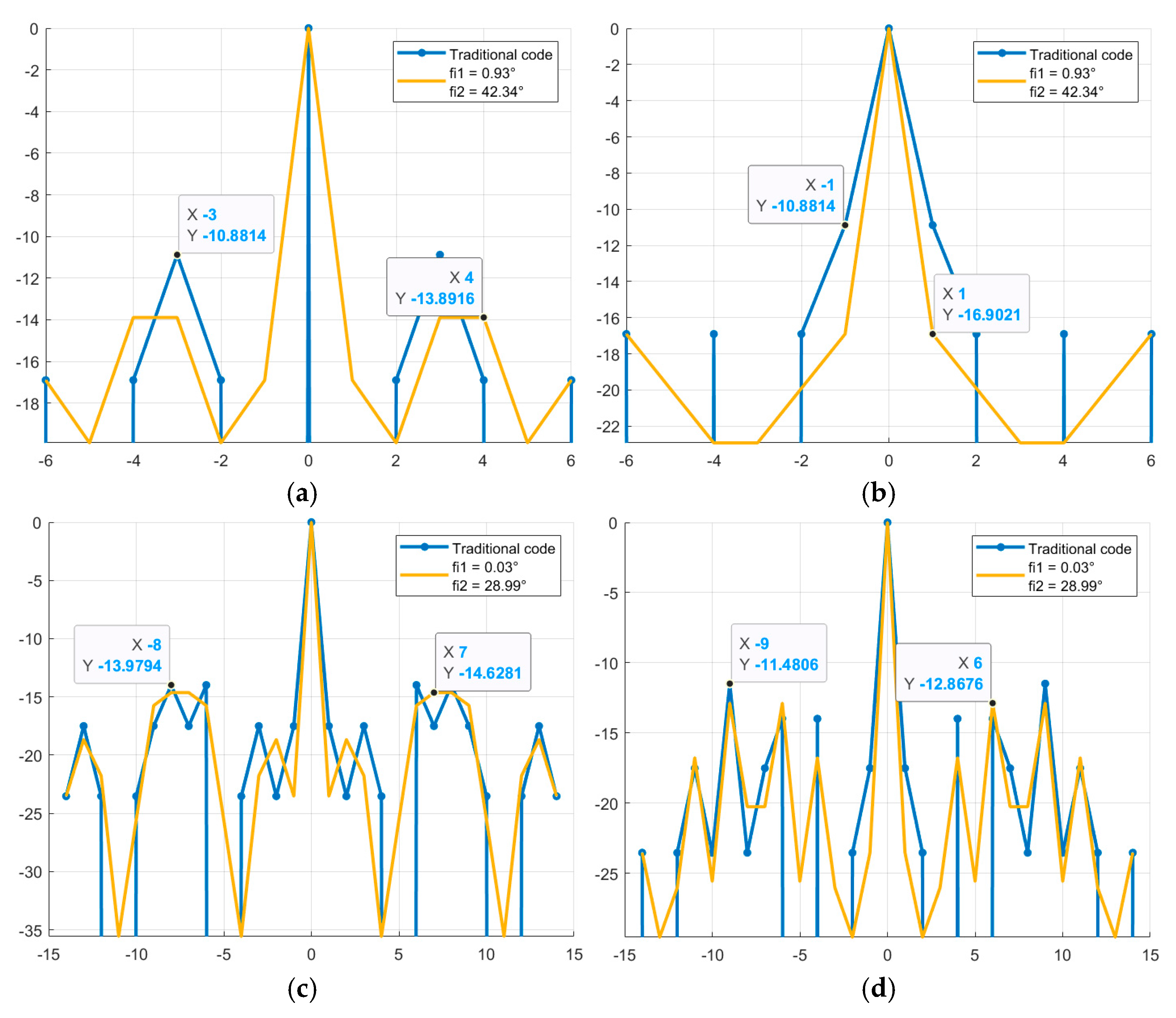
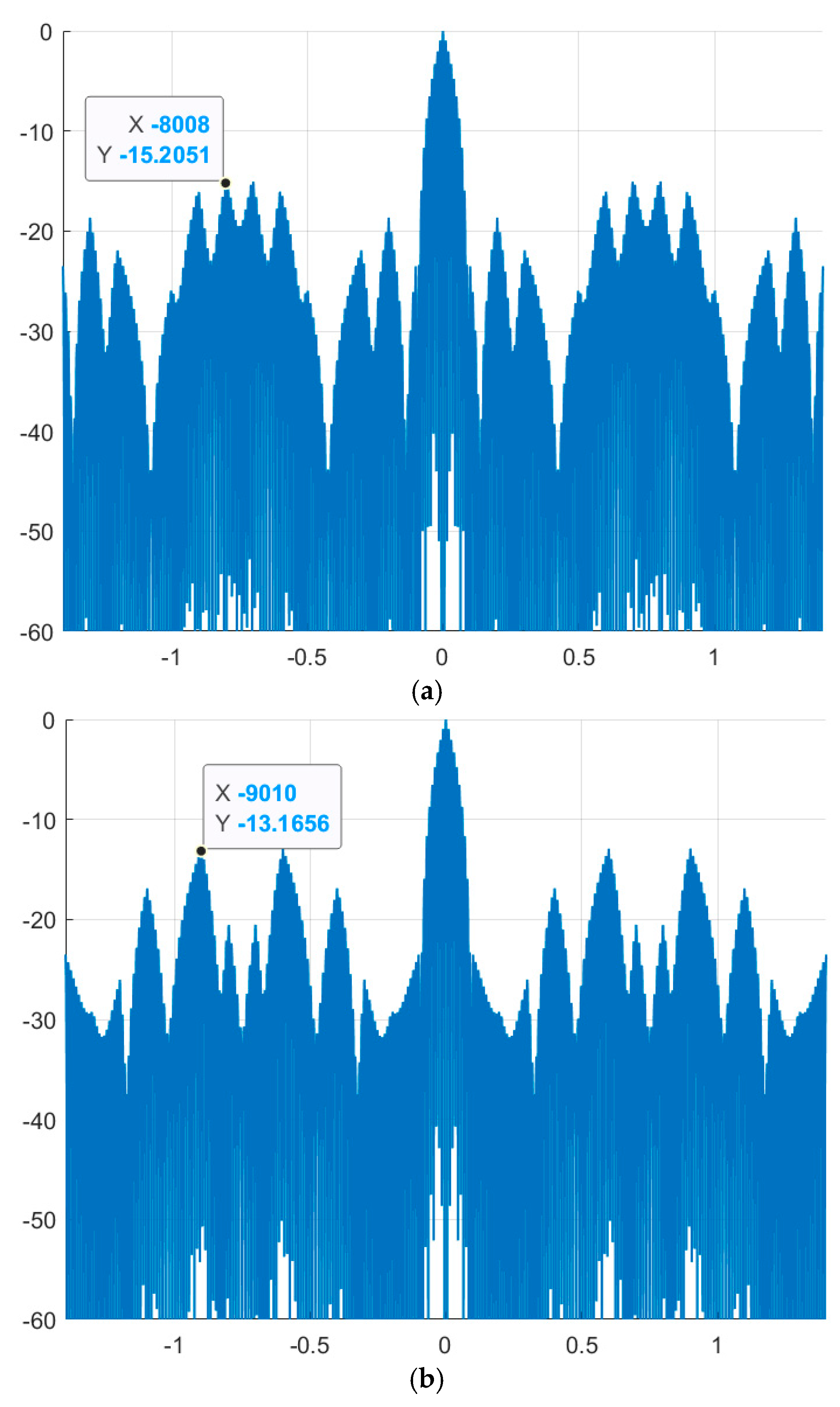
Figure 2 shows a comparison of the aperiodic NACF with traditional M-sequences. The horizontal axis shows the indices of the m petals, and the vertical axis shows the values of the petal levels of the NACF of the sequences in decibels.
As can be seen from the graphs in
Figure 2, certain values of the parameter φ make it possible to reduce the SL of the NACF of traditional M-sequences. Thus, for the traditional M-sequence of length 7, the SL of the NACF level is –10.88, and for the obtained complex M-sequences, the SL of the NACF level is –15.39, therefore, the difference between the values is 4.51. For M-sequences of length 15, the difference between the values is 1.02 (–12.73 for the traditional sequence and –13.75 for the complex one). Similar to the studies carried out above for the aperiodic NACF,
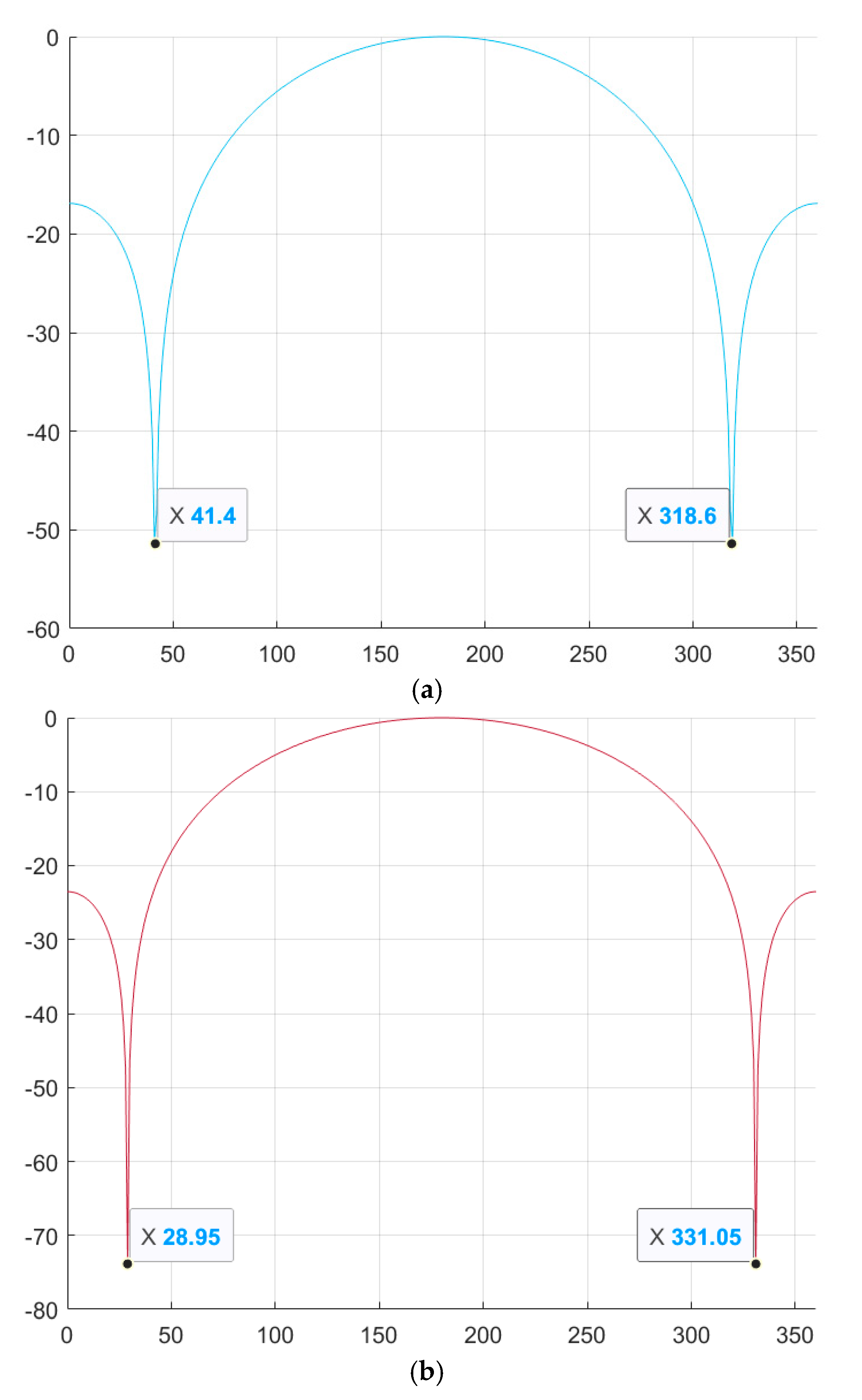
Figure 3 shows the change in the SL of the NACF level of the periodic M-sequence. Similar to
Figure 1, on the horizontal axis of
Figure 3 displays the value of φ, on the vertical line – the value of the SL of the NACF in decibels.
As can be seen from
Figure 3, for the periodic NACF, the optimal values are φ1 = 41.4° and φ2 = 318.6° for the M-sequence with length N = 7 and φ1 = 28.95° and φ2 = 331.05° for the M-sequence with length N = 15. Thus, the optimal values for the periodic NACF coincide with the optimal values for the aperiodic NACF.
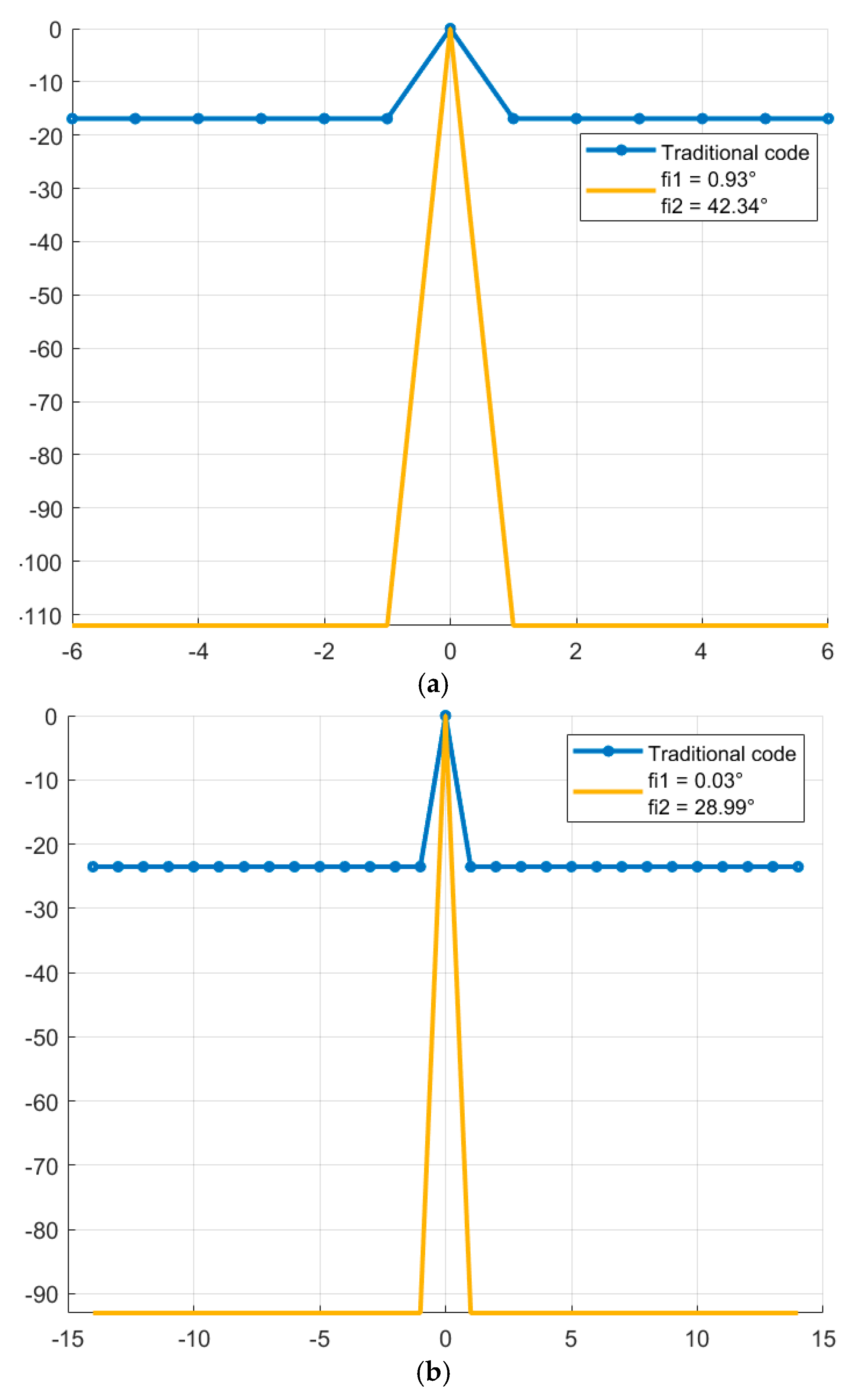
Figure 4 shows a comparison of the BL level of the periodic NACF of the traditional and complex M-sequences.
As can be seen from
Figure 4, complex M-sequences can significantly reduce the level of SL of the NACF. For the traditional M-sequence of length N = 7, the SL of the NACF level is –16.90, and for the obtained complex M-sequences, the SL of the NACF level is –112.04, therefore, the difference between the values is 95.14. For M-sequences of length N = 15, the difference between the values is 69.77 (the SL of the NACF level is –23.52 for the traditional sequence and –93.29 for the complex one).
3.2. Replacing Two Elements in the Alphabet of Traditional M-Sequences with Complex Values
The second variant of replacing the alphabet of M-sequences replaces the positive 1 with «–exp(φ
1i)» and the negative 1 with «exp(φ
2i)». An example of replacing the alphabet of the previously discussed sequences is presented in
Table 5.
Similar to the variant with the replacement of one alphabet element, it is necessary to determine the optimal values of the pair {φ
1 φ
2} from the range 0-360°, at which the SL of the NACF level is the lowest. A graphical representation of the SL of the NACF level for M-sequences is shown in
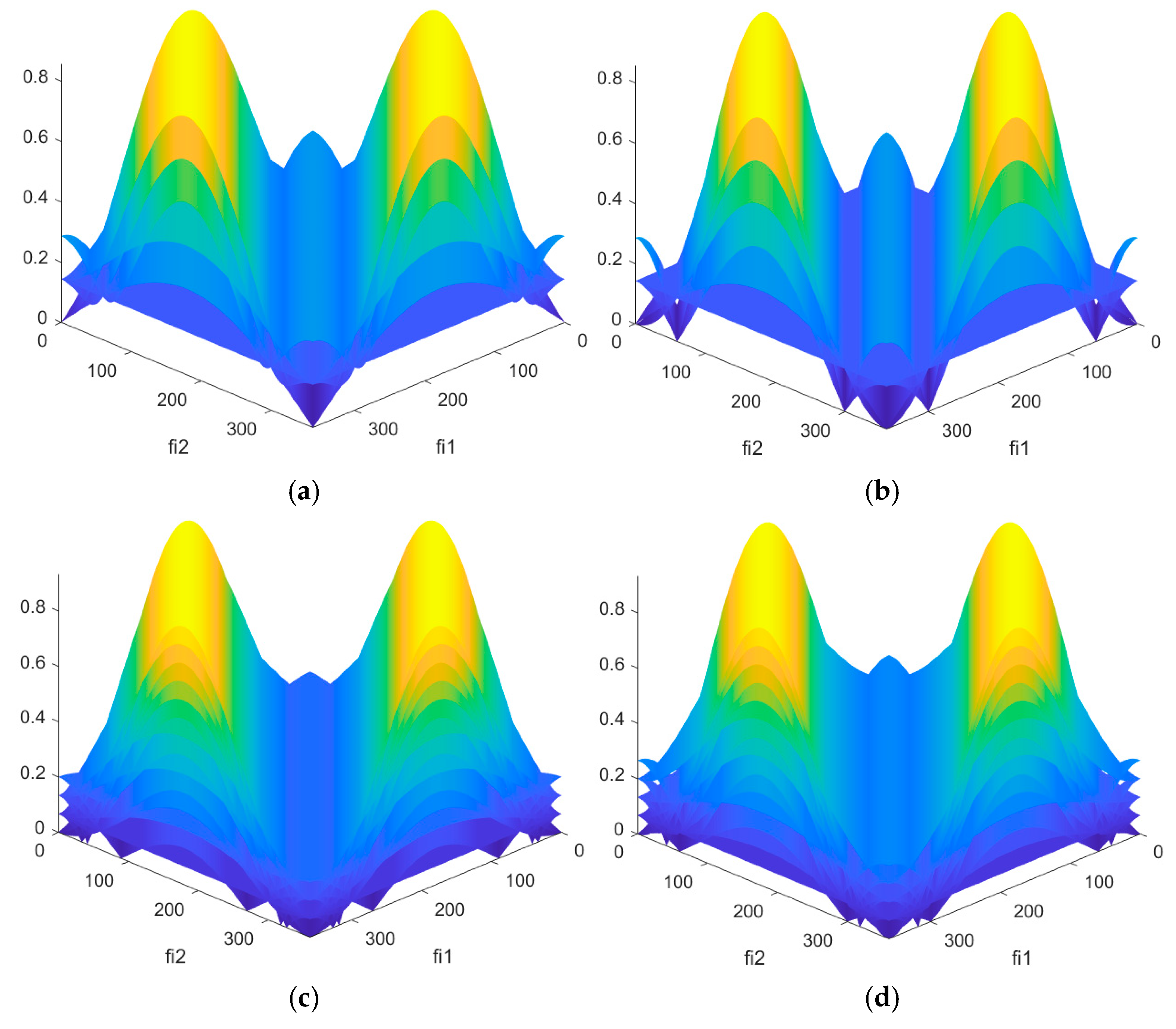
Figure 5. The vertical axis shows the values of the SL of the NACF for φ
1 and φ
2.
When replacing two elements from the M-sequence alphabet, the optimal values of φ
1 and φ
2 are significantly greater than when replacing a single element. Thus, for M-sequences of length N = 7, the number of pairs { φ
1, φ
2} exceeds 700. An important pattern is observed: for all the resulting optimal pairs {φ
1, φ
2}, the difference between their values is, on average, 42, i.e., |φ
1 – φ
2| ≈ 42. To check the reduction of the SL of the NACF, the first found pairs {φ
1 φ
2} are used (
Figure 6).
Figure 7 shows a comparison of the SL of the periodic NACF of a traditional and complex M-sequence, depending on two parameters.
As can be seen from the study, the reduction in the SL of the NACF of M-sequences when replacing either one or two alphabet elements occurs by approximately the same values, which is also confirmed by the experimental results presented in
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6 and
Figure 7. Below is the average reduction in the SL level for M-sequences of length N = 31, 63, 127, 255, 511.
Table 6 presents the studied M-sequences whose length exceeds 15, and
Table 7 presents the reduction in the SL level of the NACF for all sequences.
An analysis of the numerical results in
Table 7 shows that using certain complex M-sequences, it was possible to reduce the SL level of the normalized aperiodic and periodic ACF compared to the same level obtained using traditional representations of this code.
Therefore, for example, the greatest decrease in the maximum SL for the normalized AACF was 4.51 dB, while for the normalized PACF it was 95.14 dB for an M-sequence of length N = 7. With an increase in the length of the M-sequence, the level of SL of the NACF decreases, which will increase the probability of correct signal detection for a given probability of false alarm, that is, against the background of internal noise of the receiving device. Based on this, it should be concluded that it is advisable to use new complex element values to modify M-sequences.
4. Phase Modulation of a Signal by Complex M-Sequences
In modern SSARS, one of the main requirements is to increase the range resolution. For this purpose, complex broad-spectrum probing signals are used in practice, which improves the accuracy and reliability of range estimation to ground targets [
41,
42,
43,
44,
45,
46].
The choice of signal modulation type is also important, as it affects the range resolution when detecting ground targets.
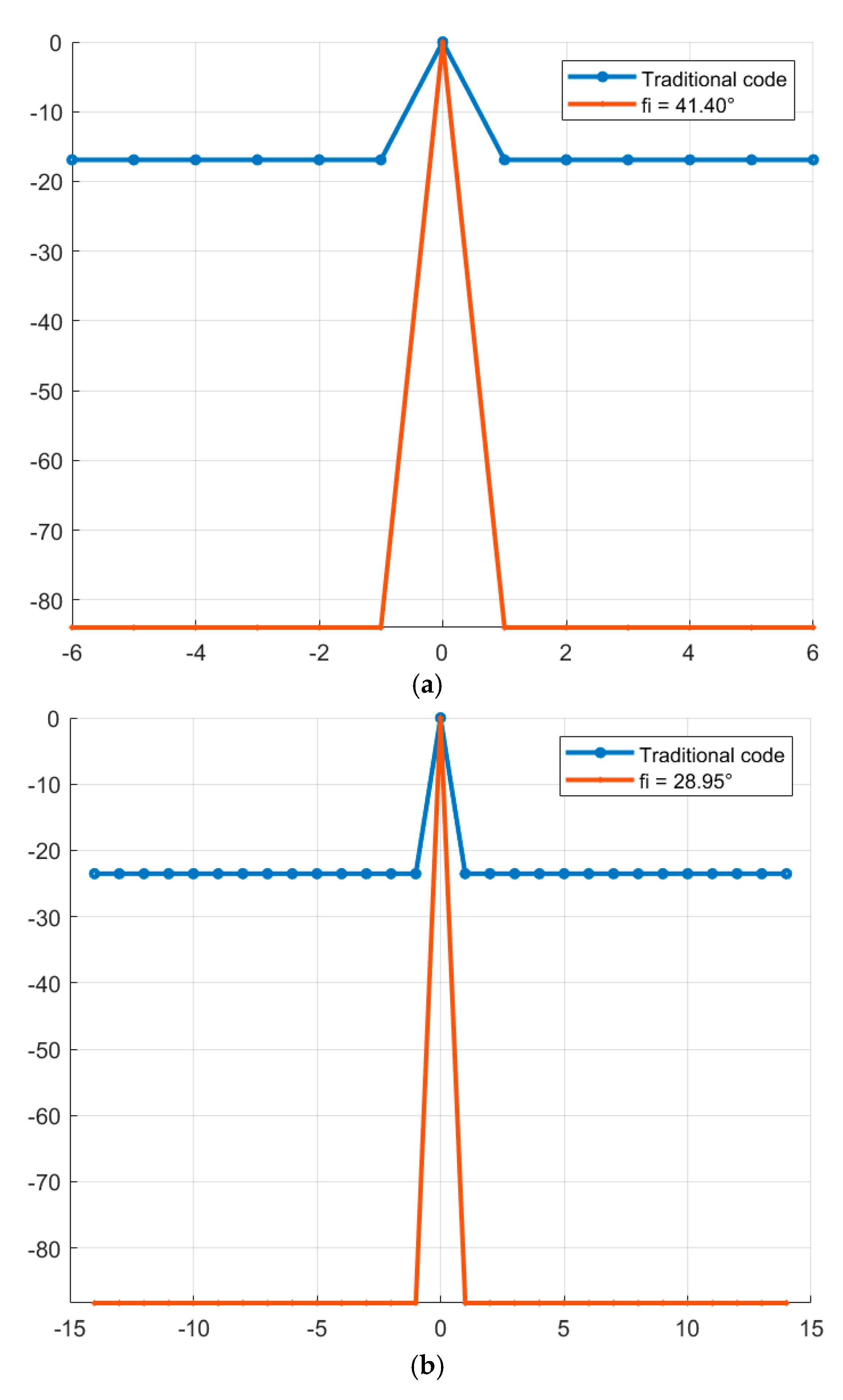
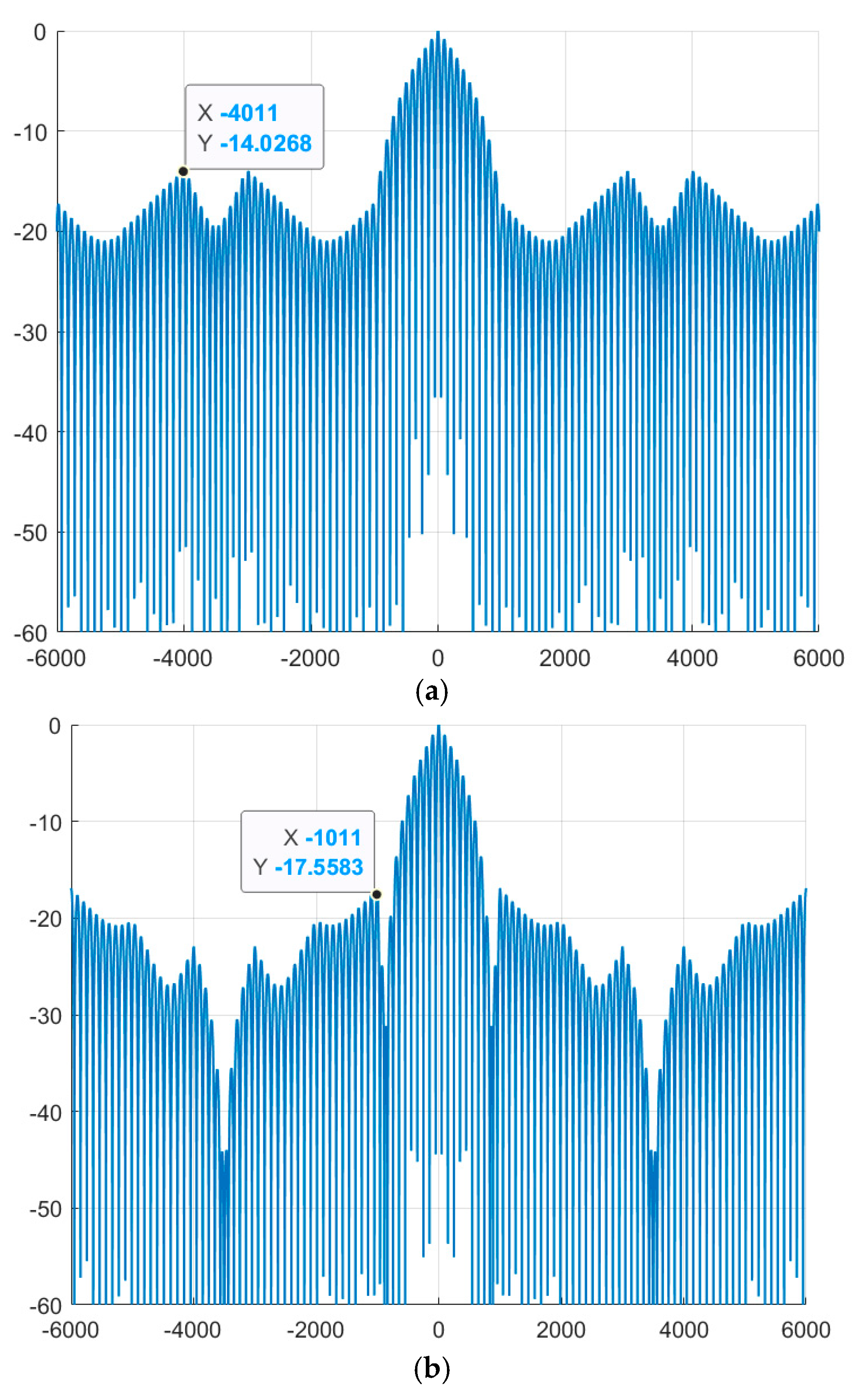
Next, we consider the process of generating and analyzing the correlation properties of signals phase-modulated by new complex M-sequences. The previously obtained initial phase values φ of the new sequences make it possible to generate phase-modulated signals with lower levels of SL of the NACF compared to traditional ones. As an example (
Figure 8), complex M-sequences of length N = 7 with the alphabet {1; –exp(φi)} are used for signal modulation. The vertical axis shows the values of the SL of the NACF of the signals, and the horizontal axis shows the time samples.
Similar to
Figure 8, complex M-sequences of length N = 15 with the alphabet {1; – exp(φi)} are considered below (
Figure 9).
Comparing
Figure 2 and
Figure 8, and 9, it is clear that the maximum level of the SL of the aperiodic NACF of the complex M-sequence and the phase-modulated signal based on it coincide within the computational error, indicating that the signals were generated correctly.
4. Discussion
In addition to low SL of the periodic and aperiodic ACF of complex M-sequences, it is also possible to achieve a fairly low level of the cross-correlation function (CCF) of complex M-sequences. In this regard, future research aims to find values of φ that would ensure not only low levels of sidelobes of the normalized autocorrelation function, but also the required low level of cross-correlation lobes between several M-sequences of the same length, but formed by different generator polynomials. A key requirement is maintaining a balance between these parameters to ensure the possibility of using multiple signals in a single radar channel. Therefore, further research may be directed toward searching for marked signal-code structures modulated simultaneously by several parameters (e.g., phase, frequency, and amplitude). In this case, the search should be carried out taking into account that these signal-code structures should have a low level of SL of the ACF and at the same time have a lobe level of the CCF, which will be lower than that of the ACF. Such an improvement can be used to implement an aviation swarm system of group interaction with SSARS.
The approach presented in this paper for finding new values for M-sequence constructions can also be used as a direction for further research. This approach can be applied to finding new values for other types of sequences, such as pseudorandom sequences, both binary and with a larger number of parameters in their alphabet.
In addition to communications, radar, and radio navigation, these signals can be used to implement group interactions between land-, sea-, and underwater-based swarms. Further research can be aimed at modifying the code structure to ensure both low SL of the NACF and low mutual interference in a single channel.
5. Conclusions
The study resulted in an assessment of the properties of the autocorrelation functions of complex M-sequences, including an analysis of their periodic and aperiodic components. An approach based on replacing the traditional sequence alphabet with an asymmetric complex one was developed, which significantly reduced the level of sidelobes in the autocorrelation function.
The practical significance of the obtained results lies in their application to improving the quality of airborne radar and communication systems, where minimizing the level of SL of the NACF is a key requirement. The newly discovered complex M-sequences demonstrated high efficiency in computer experiments, which will further enable the generation of signal-code structures used in group systems for airborne monitoring of the earth’s surface.
Thus, the use of complex M-sequences and signals modulated by them confirmed the improvement of their correlation properties by searching for new values in the structure of the M-sequence by replacing the traditional alphabet {1; –1} with an asymmetric complex one.
The obtained results are intended to stimulate research in the field of changing the algorithms for generating and processing signals, increasing the reliability of detecting a useful signal in conditions of interference in radar channels when implementing a swarm of SSARS, united in an interacting group.
Author Contributions
Conceptualization, V.A.N., R.I.C., S.A.N., A.R.B. and V.P.K.; methodology, V.A.N., R.I.C., S.A.N., A.R.B. and V.P.K.; software, R.I.C.; validation, S.A.N., A.R.B. and V.P.K.; formal analysis, V.A.N., R.I.C., S.A.N., A.R.B. and V.P.K.; investigation, V.A.N., R.I.C., S.A.N., A.R.B. and V.P.K.; resources, V.A.N., R.I.C., S.A.N., A.R.B. and V.P.K.; data curation, V.A.N., R.I.C., S.A.N., A.R.B. and V.P.K.; writing—original draft preparation, V.A.N., R.I.C., S.A.N., and V.P.K.; writing—review and editing, V.A.N., R.I.C., S.A.N., A.R.B. and V.P.K.; visualization, V.A.N., R.I.C., S.A.N., A.R.B. and V.P.K.; supervision, V.A.N.; project administration, V.A.N.; funding acquisition, V.A.N. All authors have read and agreed to the published version of the manuscript.
Funding
The study was supported by a grant from the Russian Science Foundation (project No. 24-79-10259).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable
Data Availability Statement
All data supporting the reported results are public.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACF |
Autocorrelation function |
| AACF |
Aperiodic autocorrelation function |
| NACF |
Normalized autocorrelation function |
| CCF |
Cross-correlation function |
| PACF |
Periodic autocorrelation function |
| SL |
Side lobe |
| SSARS |
Small-sized airborne radar systems |
References
- Pankratov, D.Yu.; Gorovenko, A.V. Using space-time multiplexing to improve information security in mobile radio networks. Systems for synchronization, generation and processing of signals. 2023. Vol. 14, No. 1, 49–54.
- Kognovitsky, O.S.; Kukunin, D.S. Application of the dual basis for processing M-sequences over a field with double extension. Electrosvyaz. 2023, No. 10, 34–42.
- Timofeev, A.L.; Sultanov, A.Kh.; Meshkov, I.K.; Gizatulin, A.R. Radar with holographic coding of the probing signal. Journal of Radio Electronics. 2024, No. 3, 1–15.
- Ipanov, R.N.; Komarov, A.A. Application of probing FKM signals with zero autocorrelation zone to improve the quality of measurements in SAR. Journal of Radio Electronics. 2024, No. 1, 1–34.
- Lapchinsky, E.N; Faleeva, E.V. Application of software for processing Earth remote sensing data. Scientific, technical and economic cooperation of Asia-Pacific countries in the 21st century. 2023, Vol. 2, 523–528.
- Kalacheva, O.A. Using remote sensing data when working with information systems. Organization of production, economics and management: Proceedings of the V student scientific and practical conference, Voronezh, June 10, 2024. Voronezh: Rostov State University of Railway Engineering. 2024, 184–187.
- Nenashev, V.A.; Shepeta, A.P.; Kryachko, A.F. Fusion Radar and Optical Information in Multi-Position On-Board Location Systems. 2020 Wave Electronics and its Application in Information and Telecommunication Systems (WECONF), St. Petersburg, Russia, 2020, 1–5.
- Nenashev, V.A.; Khanykov I.G. Formation of a complex image of the earth’s surface based on clustering of pixels of location images in a multi-position onboard system. Informatics and Automation. 2021, Vol. 20, No. 2, 302–340.
- Karin, S.A.; Karin, A.I. Method for increasing the efficiency of complex processing of Earth remote sensing data in solving problems of monitoring spatial objects. Scientific and Technical Bulletin of Information Technologies, Mechanics and Optics. 2022, Vol. 22, No. 4, 691–698.
- Nenashev, V.A.; Khanykov, I.G.; Kharinov, M.V. A Model of Pixel and Superpixel Clustering for Object Detection. Journal of Imaging. 2022; 8(10):274.
- Nenashev, V.A.; Shepeta, D.A. Мathematical models and algorithms for modeling the location signals reflected from the underlying surfaces of the earth, sea, and coastal waters. Proc. SPIE 11150, Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2019, 111501V (14 October 2019).
- Sergeev, A.; Nenashev, V.; Vostrikov, A.; Shepeta, A.; Kurtyanik, D. (2019). Discovering and Analyzing Binary Codes Basedon Monocyclic Quasi-Orthogonal Matrices. In: Czarnowski, I.; Howlett, R.; Jain, L. (eds) Intelligent Decision Technologies 2019. Smart Innovation, Systems and Technologies, vol 143. Springer, Singapore. [CrossRef]
- Vadim A. Nenashev; Alexander F. Kryachko; Alexander P. Shepeta and Dmitry A. Burylev “Features of information processing in the onboard two-position small-sized radar based on UAVs”, Proc. SPIE 11197, SPIE Future Sensing Technologies, 111970X (12 November 2019). [CrossRef]
- Li, J.; Ye, L.; Wang, W. A Radar Waveform Design Method Based on Multicarrier Phase Coding for Suppressing Autocorrelation Sidelobes. Sensors 2025, 25, 5801. [CrossRef]
- Morozov, O.G.; Morozov, G.A.; Ilyin, G.I.; Nureyev, I.I.; Sakhabutdinov, A.ZH.; Rostokin, I.N.; Ivanov, A.A.; Lustina, A.A.; Denisenko, E.P.; Denisenko, P.E.; Andreev, V.D. Radiophotonic method for determining the angle of arrival of a reflected radar signal based on tandem amplitude-phase modulation. Bulletin of the Volga Region State Technological University. Series: Radio engineering and infocommunication systems. 2021, No. 1 (49), 50–62.
- Opalikhina, O.V. Formation of an m-sequence over a Galois residue field. Bulletin of the Voronezh State University. Series: Systems Analysis and Information Technologies. 2023, No. 2, 77–90.
- Krasnikov, Yu.V.; Kalashnikov, R.V.; Smolin, R.V. Study of the influence of the Doppler frequency additive on the level of side lobes along the range of a nonlinear frequency-modulated signal. Bulletin of the Yaroslavl Higher Military School of Air Defense. 2023, No. 1 (20), 4–8.
- Morozov, O.G.; Ivanov, A.A.; Lustina, A.A.; Andreev, V.D. Method for determining the angle of arrival of a reflected radar signal based on radiophotonics technologies. Radio wave propagation: Proceedings of the XXVII All-Russian open scientific conference, Kaliningrad, June 28 – March 2021. Kaliningrad: Immanuel Kant Baltic Federal University. 2021, 613–618.
- Urambekov, E.B. Development of a phase-shift keyed signal function model to improve the resolution of an airborne radar station. International Journal of Information Technology and Energy Efficiency. 2024, Vol. 9 No. 4(42), 156–162.
- Changjie Wang; Hao Zhang; Wei Ren; Quanhua Liu. Design of polyphase sequence sets with good correlation properties under spectral distortion via majorization-minimization framework. Digital Signal Processing. Volume 145, 2024, Article 104284. ISSN 1051-2004.
- Bogdanov, A. V.; Kazakevich, E. V. Determination of the communication range when using flight and lifting equipment in hard-to-reach areas // SPbNTORES: proceedings of the annual STC. 2022, No. 1 (77), 139–140.
- Yu, L.; Shao, Q.; Guo, Y.; Xie, X.; Liang, M.; Hong, W. Complex-Valued U-Net with Capsule Embedded for Semantic Segmentation of PolSAR Image. Remote Sens. 2023, 15, 1371. [CrossRef]
- Adil, M.; Buono, A.; Nunziata, F.; Ferrentino, E.; Velotto, D.; Migliaccio, M. On the Effects of the Incidence Angle on the L-Band Multi-Polarisation Scattering of a Small Ship. Remote Sens. 2022, 14, 5813. [CrossRef]
- Qu, C.; Li, J.; Bao, J.; Zhu, Z. Design and Development of Array POS for Airborne Remote Sensing Motion Compensation. Remote Sens. 2022, 14, 3420. [CrossRef]
- Kyzivat, E.D.; Smith, L.C.; Pitcher, L.H.; Fayne, J.V.; Cooley, S.W.; Cooper, M.G.; Topp, S.N.; Langhorst, T.; Harlan, M.E.; Horvat, C.; et al. A High-Resolution Airborne Color-Infrared Camera Water Mask for the NASA ABoVE Campaign. Remote Sens. 2019, 11, 2163. [CrossRef]
- Zhang, Y.; Zou, H.; Luo, T.; Qin, X.; Zhou, S.; Ji, K. A Fast Superpixel Segmentation Algorithm for PolSAR Images Based on Edge Refinement and Revised Wishart Distance. Sensors 2016, 16, 1687. [CrossRef]
- Yu, J.; Bai, J.; Huang, J.; Wang, X.; Feng, J.; Xia, F.; Zheng, Z. End-to-End Constellation Mapping and Demapping for Integrated Sensing and Communications. Electronics 2025, 14, 4070. [CrossRef]
- Zhang, K.; Li, Y.; Wang, X.; Yang, Z.; Zhang, F.; Wang, K.; Zhao, Z.; Wang, Y. Three-Dimensional Non-Stationary MIMO Channel Modeling for UAV-Based Terahertz Wireless Communication Systems. Entropy 2025, 27, 788. [CrossRef]
- Oulaid, B.; Harris, P.; Maas, E.; Fakeye, I.A.; Baker, C. Geographically Weighted Quantile Machine Learning for Probabilistic Soil Moisture Prediction from Spatially Resolved Remote Sensing. Remote Sens. 2025, 17, 2907. [CrossRef]
- Yan, J.; Xin, L.; Fang, H.; Zhou, H. On-Site Localization of Unmanned Vehicles in Large-Scale Outdoor Environments. World Electr. Veh. J. 2025, 16, 650. [CrossRef]
- Evgeniy K. Grigoriev; Vadim A. Nenashev; Alexander M. Sergeev and Sergey A. Nenashev “Research and analysis of methods forgenerating and processing new code structures for the problems of detection,synchronization and noise-resistant coding”, Proc. SPIE 11533, Image andSignal Processing for Remote Sensing XXVI, 115331L (20 September 2020). [CrossRef]
- Buren, G.A.; Polevoda, Yu.A. Principles of amplitude-phase modulation. Fundamental, exploratory, applied research and innovative projects: Collection of works of the National scientific and practical conference, Moscow, December 7–8, 2023. Moscow: Association of graduates and employees of VVIA named after professor N.E. Zhukovsky for the preservation of the historical and scientific heritage of VVIA named after professor N.E. Zhukovsky. 2023, 34–351.
- Vakhtin, V.E.; Lebedev, E.S.; Bobrov, D.A. Signal modulation and its types, comparison. Text: direct. Young scientist. 2023, No. 33 (480), 66–68.
- Levin, D.V.; Makarenkov, V.V.; Parshutkin, A.V. Study of the possibilities of implementing multi-position radar based on complex processing of signals from multi-range radar stations. Radar study of natural environments: Proceedings of the XXXIII All-Russian symposium dedicated to the 100th anniversary of the birth of Doctor of Technical Sciences, Professor Nikolai Fomich Klyuev, St. Petersburg, April 19–20, 2023. St. Petersburg: A.F. Mozhaisky Military Space Academy. 2024, 348–354.
- Zhukova, I.N.; Bystrov, N.E. Specifics of using window functions in processing signals with a pseudo-random law of amplitude-phase manipulation. Bulletin of Novgorod State University. 2023, No. 5 (134), 708–715.
- Mikhalitsyn, E.A. Radiophotonic phase direction finder with a Doppler frequency shift meter for radio signals. Mathematical methods in technology and engineering. 2023, No. 6, 52–56.
- Patent №. 2709666 C1 Russian Federation, IPC H03M 1/24. Pseudo-random code scale: No. 2019103609: declared 02/08/2019: published 12/19/2019 / A.A. Ozhiganov, P.A. Pribytkin; applicant Open Joint-Stock Company “Avan-garde”.
- Zakharov, I.D.; Ozhiganov, A.A. Using generating polynomials of m-sequences in constructing pseudo-random code scales // Instrument engineering. 2011, No. 6, 49–55.
- Nenashev, V.A.; Nenashev, S.A. Search and Study of Marked Code Structures for a Spatially Distributed System of Small-Sized Airborne Radars. Sensors 2023, 23, 6835.
- Nenashev, V.A.; Bestugin, A.R.; Rabin, A.V.; Solenyi, S.V.; Nenashev, S.A. Modified Nested Barker Codes for Ultra-Wideband Signal-Code Constructions. Sensors, 23, no. 23: 9528. 2023.
- Bogatyrev, E.V.; Galeev, R.G.; Ivanov, V.E.; Kudinov, S.I.; Malygin, I.V.; Noskov, V.Y.; Chernykh, O.A. Doppler method for determining the motion parameters of an aerological probe of a radar system. Advances in modern radio electronics. 2025, V. 79, No. 2, 39–51.
- Wang, L.; Liu, Y.; Chen, Q.; Zhou, X.; Zhu, S.; Chen, S. Airborne Short-Baseline Millimeter Wave InSAR System Analysis and Experimental Results. Remote Sens. 2024, 16, 1020.
- Adil, M.; Buono, A.; Nunziata, F.; Ferrentino, E.; Velotto, D.; Migliaccio, M. On the Effects of the Incidence Angle on the L-Band Multi-Polarisation Scattering of a Small Ship. Remote Sens. 2022, 14, 5813.
- Mazuro, M.; Skokowski, P.; Kelner, J.M. Coordinated Radio Emitter Detection Process Using Group of Unmanned Aerial Vehicles. Sensors 2025, 25, 7298. [CrossRef]
- Chen, L.; Wan, H.; Hu, H.; Zhang, H.; Liu, L.; Xu, L.; Jiang, Z.; Sroczyńska, J. Correlation Analysis Between Everyday Public Space and Urban Built Environment and a Study of Its Evaluation Framework: Taking Tianjin as an Example. Buildings 2025, 15, 4348. [CrossRef]
- Wang, Z.; Shao, Z.; Chen, R.; Zhao, M.; Jia, Z.; Ma, Y.; Xie, W.; Zhang, Y.; Zhang, B. NRBO-XGBoost-Optimized High-Fidelity Temperature Correction for UAV-Based TIR Imagery and Its Application for Monitoring Coal Fire. Fire 2025, 8, 462. [CrossRef]
Figure 1.
Dependence of the aperiodic NACF of a complex M-sequence on the parameter φ: (a) M-sequence №1; (b) M-sequence №2; (c) M-sequence №3; (d) M-sequence №4.
Figure 1.
Dependence of the aperiodic NACF of a complex M-sequence on the parameter φ: (a) M-sequence №1; (b) M-sequence №2; (c) M-sequence №3; (d) M-sequence №4.
Figure 2.
Comparison of the level of aperiodic NACF of the traditional M-sequence and its complex version depending on the parameter φ: (a) M-sequence №1; (b) M-sequence №2; (c) M-sequence №3; (d) M-sequence №4.
Figure 2.
Comparison of the level of aperiodic NACF of the traditional M-sequence and its complex version depending on the parameter φ: (a) M-sequence №1; (b) M-sequence №2; (c) M-sequence №3; (d) M-sequence №4.
Figure 3.
Dependence of the periodic NACF of a complex M-sequence on the parameter φ: (a) M-sequence of length N = 7; (b) M-sequence of length N = 15.
Figure 3.
Dependence of the periodic NACF of a complex M-sequence on the parameter φ: (a) M-sequence of length N = 7; (b) M-sequence of length N = 15.
Figure 4.
Comparison of the level of the periodic NACF of the traditional M-sequence and its complex version depending on the parameter φ: (a) M-sequence of length N = 7; (b) M-sequence of length N = 15.
Figure 4.
Comparison of the level of the periodic NACF of the traditional M-sequence and its complex version depending on the parameter φ: (a) M-sequence of length N = 7; (b) M-sequence of length N = 15.
Figure 5.
Dependence of the aperiodic NACF of a complex M-sequence on the parameters φ1 and φ2: (a) M-sequence №1; (b) M-sequence №2; (c) M-sequence №3; (d) M-sequence №4.
Figure 5.
Dependence of the aperiodic NACF of a complex M-sequence on the parameters φ1 and φ2: (a) M-sequence №1; (b) M-sequence №2; (c) M-sequence №3; (d) M-sequence №4.
Figure 6.
Comparison of the level of aperiodic NACF of the traditional M-sequence and its complex version depending on the parameters φ1 and φ2: (a) M-sequence №1; (b) M-sequence №2; (c) M-sequence №3; (d) M-sequence №4.
Figure 6.
Comparison of the level of aperiodic NACF of the traditional M-sequence and its complex version depending on the parameters φ1 and φ2: (a) M-sequence №1; (b) M-sequence №2; (c) M-sequence №3; (d) M-sequence №4.
Figure 7.
Comparison of the level of the periodic NACF of the traditional M-sequence and its complex version depending on the parameters φ1 and φ2: (a) M-sequence of length N = 7; (b) M-sequence of length N = 15.
Figure 7.
Comparison of the level of the periodic NACF of the traditional M-sequence and its complex version depending on the parameters φ1 and φ2: (a) M-sequence of length N = 7; (b) M-sequence of length N = 15.
Figure 8.
Phase modulation of a signal by an aperiodic complex M-sequence: (a) M-sequence №1; (b) M-sequence №2.
Figure 8.
Phase modulation of a signal by an aperiodic complex M-sequence: (a) M-sequence №1; (b) M-sequence №2.
Figure 9.
Phase modulation of a signal by an aperiodic complex M-sequence: (a) M-sequence №3; (b) M-sequence №4.
Figure 9.
Phase modulation of a signal by an aperiodic complex M-sequence: (a) M-sequence №3; (b) M-sequence №4.
Table 1.
Process of obtaining expressions for the sidelobes of the AACF.
Table 1.
Process of obtaining expressions for the sidelobes of the AACF.
| |
a1
|
a2
|
a3
|
a4
|
|
|
|
| m |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
| a4*
|
a1* a4*
|
a2* a4*
|
a3* a4*
|
a4* a4*
|
|
|
|
| a3*
|
|
a1* a3*
|
a2* a3*
|
a3* a3*
|
a4* a3*
|
|
|
| a2*
|
|
|
a1* a2*
|
a2* a2*
|
a3* a2*
|
a4* a2*
|
|
| a1*
|
|
|
|
a1* a1*
|
a2* a1*
|
a3* a1*
|
a4* a1*
|
| |
a1* a4*
|
a2* a4* + a1* a3*
|
a3* a4* + a2* a3* + a1* a2*
|
a4* a4* + a3* a3* + a2* a2* + a1* a1*
|
a4* a3* + a3* a2* + a2* a1*
|
a4* a2* + a3* a1*
|
a4* a1*
|
Table 2.
Process of obtaining expressions for the sidelobes of the PACF.
Table 2.
Process of obtaining expressions for the sidelobes of the PACF.
| |
a1
|
a2
|
a3
|
a4
|
|
|
|
| m |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
| a4*
|
a1* a4*
|
a2* a4*
|
a3* a4*
|
a4* a4*
|
a1* a4*
|
a2* a4*
|
a3* a4*
|
| a3*
|
a4* a3*
|
a1* a3*
|
a2* a3*
|
a3* a3*
|
a4* a3*
|
a1* a3*
|
a2* a3*
|
| a2*
|
a3* a2*
|
a4* a2*
|
a1* a2*
|
a2* a2*
|
a3* a2*
|
a4* a2*
|
a1* a2*
|
| a1*
|
a2* a1*
|
a3* a1*
|
a4* a1*
|
a1* a1*
|
a2* a1*
|
a3* a1*
|
a4* a1*
|
| |
a1* a4* + a4* a3* + a3* a2* + a2* a1*
|
a2* a4* + a1* a3* + a4* a2* + a3* a1*
|
a3* a4* + a2* a3* + a1* a2* + a4* a1*
|
a4* a4* + a3* a3* + a2* a2* + a1* a1*
|
a1* a4* + a4* a3* + a3* a2* + a2* a1*
|
a2* a4* + a1* a3* + a4* a2* + a3* a1*
|
a3* a4* + a2* a3* + a1* a2* + a1* a1*
|
Table 3.
M-sequences and the polynomials that generate them.
Table 3.
M-sequences and the polynomials that generate them.
| № |
Length |
Generating polynomial |
M-sequence |
| 1 |
7 |
x3 + x2 + 1 |
–1 –1 1 1 1 –1 1 |
| 2 |
7 |
x3 + x + 1 |
1 1 –1 –1 1 –1 1 |
| 3 |
15 |
x4 + x + 1 |
1 –1 1 –1 1 1 1 1 –1 –1 –1 1 –1 –1 1 |
| 4 |
15 |
x4 + x3 + 1 |
–1 –1 1 1 1 1 –1 1 –1 1 1 –1 –1 1 –1 |
Table 4.
M-sequences with alphabet {1; –exp(φi)}.
Table 4.
M-sequences with alphabet {1; –exp(φi)}.
| № |
Length |
M-sequence |
| 1 |
7 |
–exp(φi) –exp(φi) 1 1 1 –exp(φi) 1 |
| 2 |
7 |
1 1 –exp(φi) –exp(φi) 1 –exp(φi) 1 |
| 3 |
15 |
1 –exp(φi) 1 –exp(φi) 1 1 1 1 –exp(φi) –exp(φi) –exp(φi) 1 –exp(φi) –exp(φi) 1 |
| 4 |
15 |
–exp(φi) –exp(φi) 1 1 1 1 –exp(φi) 1 –exp(φi) 1 1 –exp(φi) –exp(φi) 1 –exp(φi) |
Table 5.
M-sequences with alphabet {exp(φ1i); –exp(φ2i)}.
Table 5.
M-sequences with alphabet {exp(φ1i); –exp(φ2i)}.
| № |
Length |
M-sequence |
| 1 |
7 |
–exp(φ2i) –exp(φ2i) exp(φ1i) exp(φ1i) exp(φ1i) –exp(φ2i) exp(φ1i) |
| 2 |
7 |
exp(φ1i) exp(φ1i) –exp(φ2i) –exp(φ2i) exp(φ1i) –exp(φ2i) exp(φ1i) |
| 3 |
15 |
exp(φ1i) –exp(φ2i) exp(φ1i) –exp(φ2i) exp(φ1i) exp(φ1i) exp(φ1i) exp(φ1i) –exp(φ2i) –exp(φ2i) –exp(φ2i) exp(φ1i) –exp(φ2i) –exp(φ2i) exp(φ1i) |
| 4 |
15 |
–exp(φ2i) –exp(φ2i) exp(φ1i) exp(φ1i) exp(φ1i) exp(φ1i) –exp(φ2i) exp(φ1i) –exp(φ2i) exp(φ1i) exp(φ1i) –exp(φ2i) –exp(φ2i) exp(φ1i) –exp(φ2i) |
Table 6.
M-sequences of length N = 31, 63, 127, 255, 511.
Table 6.
M-sequences of length N = 31, 63, 127, 255, 511.
| Length |
Traditional M-sequence |
| 31 |
–1 1 1 –1 1 –1 –1 –1 –1 1 1 –1 –1 1 –1 –1 1 1 1 1 1 –1 1 1 1 –1 –1 –1 1 –1 1 |
| 63 |
–1 1 –1 –1 –1 1 1 1 –1 –1 1 –1 –1 1 –1 1 1 –1 1 1 1 –1 1 1 –1 –1 1 1 –1 1 –1 1 –1 1 1 1 1 1 1 –1 –1 –1 –1 –1 1 –1 –1 –1 –1 1 1 –1 –1 –1 1 –1 1 –1 –1 1 1 1 1 |
| 127 |
–1 –1 1 –1 –1 –1 1 1 –1 1 –1 1 1 –1 –1 1 1 1 –1 –1 1 1 –1 –1 1 –1 1 1 1 1 –1 1 –1 1 –1 –1 1 –1 1 –1 1 –1 1 1 1 –1 –1 –1 1 1 1 1 1 –1 1 1 1 1 1 1 1 –1 –1 1 –1 –1 1 –1 –1 –1 –1 1 1 –1 –1 –1 –1 –1 –1 1 –1 1 1 –1 1 1 –1 –1 –1 1 –1 1 –1 –1 –1 –1 –1 1 1 1 –1 1 1 –1 1 –1 –1 1 1 1 1 –1 –1 –1 –1 1 –1 –1 1 1 –1 1 1 1 –1 1 –1 |
| 255 |
1 –1 –1 1 –1 –1 –1 1 –1 –1 –1 1 1 –1 1 1 –1 1 1 1 –1 –1 –1 1 –1 1 1 –1 –1 1 1 –1 –1 1 –1 1 1 –1 1 1 –1 –1 1 –1 –1 1 1 1 –1 1 –1 1 –1 1 –1 1 1 1 –1 1 1 –1 1 –1 1 1 –1 1 –1 –1 1 1 1 1 1 1 1 1 –1 –1 1 1 –1 1 1 1 1 –1 1 1 1 –1 1 –1 –1 –1 –1 –1 –1 –1 1 –1 1 –1 1 1 –1 –1 –1 1 1 –1 –1 1 1 1 –1 –1 –1 –1 –1 –1 1 1 1 1 1 –1 1 –1 –1 1 –1 1 –1 1 –1 –1 1 –1 –1 –1 –1 –1 1 –1 –1 –1 –1 1 1 1 –1 1 1 1 1 1 1 –1 1 1 –1 –1 –1 –1 1 1 –1 –1 –1 1 –1 –1 1 1 –1 –1 –1 –1 –1 1 1 –1 1 –1 –1 –1 1 –1 1 –1 –1 1 1 –1 1 –1 1 –1 –1 –1 –1 1 –1 1 1 1 –1 –1 1 1 1 1 –1 1 –1 1 1 1 1 1 –1 –1 –1 1 1 1 –1 –1 1 –1 1 –1 –1 –1 1 1 1 1 –1 –1 –1 –1 1 –1 –1 1 –1 –1 1 –1 1 1 1 |
| 511 |
–1 1 –1 –1 1 –1 –1 –1 1 1 1 1 –1 –1 –1 –1 –1 –1 1 1 –1 1 1 1 –1 –1 1 –1 –1 –1 –1 1 1 –1 –1 1 1 1 –1 –1 1 1 –1 –1 1 1 –1 1 1 1 1 1 –1 –1 –1 1 –1 –1 –1 1 1 –1 –1 1 –1 –1 1 –1 1 –1 –1 1 –1 –1 1 –1 –1 1 1 1 –1 1 1 1 1 –1 –1 –1 1 1 1 1 1 1 1 –1 –1 1 1 –1 1 –1 –1 –1 1 –1 1 –1 –1 1 1 1 –1 –1 –1 –1 1 –1 1 –1 –1 –1 –1 –1 –1 –1 1 –1 –1 1 –1 1 1 1 –1 –1 –1 –1 –1 1 –1 –1 –1 1 –1 1 1 1 –1 1 1 1 –1 1 1 –1 1 –1 1 –1 –1 –1 –1 1 1 1 1 –1 1 1 1 –1 –1 –1 1 1 –1 –1 –1 1 1 1 –1 –1 –1 1 –1 1 1 –1 1 –1 1 1 1 1 –1 1 –1 1 –1 1 –1 –1 –1 1 –1 –1 1 1 1 1 –1 –1 1 1 1 –1 1 –1 –1 –1 –1 –1 1 1 –1 –1 –1 –1 –1 –1 –1 –1 1 1 1 –1 –1 1 –1 1 1 1 1 1 1 –1 –1 –1 –1 1 1 –1 1 –1 –1 1 –1 1 1 –1 1 1 –1 –1 1 1 1 1 1 –1 1 –1 1 1 –1 1 –1 –1 –1 –1 1 –1 –1 –1 –1 1 –1 1 1 1 1 –1 –1 1 –1 –1 1 1 –1 1 –1 1 1 –1 –1 1 1 –1 –1 –1 –1 1 1 1 –1 1 –1 1 1 1 –1 1 –1 –1 1 1 1 1 1 1 –1 1 1 1 1 1 1 1 1 1 –1 1 –1 –1 –1 1 1 –1 1 –1 1 –1 1 1 1 1 1 –1 1 1 –1 –1 –1 1 1 –1 1 1 –1 1 1 1 –1 1 –1 1 –1 –1 1 1 –1 1 1 –1 –1 –1 –1 –1 1 1 1 1 1 –1 –1 1 –1 1 –1 –1 –1 1 1 1 –1 1 1 –1 –1 1 –1 –1 –1 1 –1 –1 –1 –1 –1 1 –1 1 1 –1 –1 1 –1 1 1 –1 –1 –1 1 –1 1 –1 1 –1 –1 1 –1 1 –1 1 –1 1 –1 1 1 –1 –1 –1 –1 1 –1 –1 1 1 –1 –1 1 –1 1 –1 1 1 –1 1 1 1 1 –1 1 1 –1 1 1 –1 1 –1 –1 1 1 –1 –1 –1 1 –1 –1 1 –1 –1 –1 –1 –1 –1 1 –1 1 –1 1 1 1 –1 –1 1 1 1 1 |
Table 7.
Comparison of SL of the NACF levels.
Table 7.
Comparison of SL of the NACF levels.
| Length |
Average level of NACF M-sequences, dB |
| Aperiodic |
Periodic |
| Traditional |
Complex |
Difference |
Traditional |
Complex |
Difference |
| 7 |
–10.88 |
–15.39 |
4.51 |
–16.90 |
–112.04 |
95.14 |
| 15 |
–12.73 |
–13.75 |
1.02 |
–23.52 |
–93.29 |
69.77 |
| 31 |
–15.85 |
–16.58 |
0.73 |
–29.82 |
–97.72 |
67.90 |
| 63 |
–15.16 |
–15.85 |
0.69 |
–35.97 |
–95.65 |
69.68 |
| 127 |
–19.16 |
–20.24 |
1.08 |
–42.05 |
–100.92 |
58.74 |
| 255 |
–23.53 |
–23.82 |
0.29 |
–48.18 |
–102.73 |
54.55 |
| 511 |
–26.94 |
–27.15 |
0.21 |
–53.98 |
–110.17 |
56.19 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |