Adiabatic Perturbation of Two-Level Ultralight Dark Matter Soliton Core in Baryonic Dehnen γ Potential (Part I)

1. Introduction

Ultralight Dark matter (ULDM), fuzzy dark matter or bosonic dark matter with mass $m\sim {10}^{-22}\mathrm{eV}$, successfully explains galactic and sub-galactic dynamics. In the weak field limit, the complex wavefunction $\mathsf{\Psi }$ satisfies the Gross-Pitaevskii-Poisson equation (GPP) [1]:

$$i\hslash {\displaystyle \frac{\partial \mathsf{\Psi }}{\partial t}}=\left[-{\displaystyle \frac{{\hslash }^2}{2m}}{\nabla }^2+m\mathsf{\Phi }+g{\left|\mathsf{\Psi }\right|}^2\right]\mathsf{\Psi }$$

(1)

$${\nabla }^2\mathsf{\Phi }=4\pi Gm{\left|\mathsf{\Psi }\right|}^2$$

(2)

where $\mathsf{\Phi }$ is the Newtonian potential for dark matter (DM) only case, and g is the self-interaction coupling constant. Cosmological simulations have shown that the virialized dark matter haloes have a solitonic core of radius $\sim {\lambda }_{dB}$, and surrounded by cold dark matter (CDM)-like envelopes described by the NFW profile [2,3]. The gravitational atom (see [4,5] solutions with populated excited states have been widely studied, but without a proper treatment of baryons as time-dependent perturbation. In dwarf galaxies, stars, gas and other baryonic matter contribute to the potential and evolve on timescales which are longer compared to the dynamical time of the core. In this work we construct a two-level harmonic oscillator description of the ULDM solitonic core surrounded by a baryonic potential. The dark matter-only core is the ground state of a harmonic potential defined by the central density ${\rho }_0$, and the first radial s-wave excitation as second basis state, projecting our dark matter system onto the two-dimensional Hilbert Space. We introduce baryonic Dehnen $\gamma$ potential as adiabatic perturbation [6]. The baryonic matter couple to the dakr matter soliton core through the overlap integral $J_{ij}(\gamma ,\alpha )$ which is evaluated for general value of $\gamma$ in the limit $R_c\lesssim a_b$. The $2\times 2$ Hamiltonian expresses the dynamics with a baryon dependent level splitting and off diagonal mixing. As baryons evolve slowly, the ULDM core remains in it’s instantaneous eigen-state and acquires a finite accumulation of first radial excitation. In this part, we focus on the formalism and develop a toy model for a dwarf galaxy. We also give a general ovrview of the dynamics of first excited state with dipole like excitation. In part II we test this framework with real dwarf spheroidal galaxies and stellar kinematic data.

2. Two–Level Solitonic Core

We consider the dark matter only case (without baryons) first with spherical symmetry near the center of the dark matter halo. The Poisson equation takes the form:

$${\displaystyle \frac{1}{r^2}}\frac{\mathrm{d}}{\mathrm{d}r}\left(r^2\frac{\mathrm{d}\mathsf{\Phi }}{\mathrm{d}r}\right)=4\pi Gm{\left|\mathsf{\Psi }\left(r\right)\right|}^2\equiv 4\pi G\rho \left(r\right)$$

(3)

Assuming that near the soliton core, density is approximately constant

$$\rho \left(r\right)\simeq {\rho }_0\mathrm{for}r\ll R_c$$

(4)

Here, $R_c$ is the soliton core radius. The Poisson equation reduces to

$$\frac{\mathrm{d}}{\mathrm{d}r}\left(r^2\frac{\mathrm{d}\mathsf{\Phi }}{\mathrm{d}r}\right)\simeq 4\pi G{\rho }_0$$

(5)

Integrating this equation twice gives the harmonic potential near the center:

$$\mathsf{\Phi }\left(r\right)\simeq \mathsf{\Phi }\left(0\right)+{\displaystyle \frac{2\pi G{\rho }_0}{3}}{r}^2.$$

(6)

The potential for a particle of mass m is $V\left(r\right)$ given by:

$$V\left(r\right)\simeq m\mathsf{\Phi }\left(0\right)+{\displaystyle \frac{1}{2}}m{\omega }_{\mathrm{eff}}^2{r}^2,$$

(7)

The effective oscillation frequency is given by:

$${\omega }_{\mathrm{eff}}^2={\displaystyle \frac{4\pi G{\rho }_0}{3}}.$$

(8)

We omit the constant $m\mathsf{\Phi }\left(0\right)$ and define the effective oscillator length (in this case, the core radius $R_c$) as:

$$R_c\equiv \sqrt{{\displaystyle \frac{\hslash }{m{\omega }_{\mathrm{eff}}}}}$$

(9)

The Hamiltonian for single dark matter particle is approximated as:

$${\hat{H}}_0=-{\displaystyle \frac{{\hslash }^2}{2m}}{\nabla }^2+{\displaystyle \frac{1}{2}}m{\omega }_{\mathrm{eff}}^2{r}^2.$$

(10)

The eigenstates corresponding to this hamiltonian are the quantum states of a 3D isotropic harmonic oscillator. We can write the s–wave eigenfunctions as:

$${\psi }_{n0}\left(\mathbf{x}\right)=R_{n0}\left(r\right)Y_0^0(\theta ,\phi ),Y_0^0={\displaystyle \frac{1}{\sqrt{4\pi }}},$$

(11)

with radial functions $R_{n0}\left(r\right)$. We are only concerned with the ground state and the first radial s–wave excitation, which forms our two level basis. For a quantum mechanical overview the readers can consult Refs.[7,8].

2.1. Ground and First Radial Excitation Modes

The radial wavefunction of the 3D harmonic oscillator ground state ($n=0,l=0$) is:

$$R_0\left(r\right)={\displaystyle \frac{2}{{\pi }^{1/4}{R}_c^{3/2}}}exp\left(-{\displaystyle \frac{r^2}{2R_c^2}}\right),$$

(12)

The first radial excited s–wave mode is:

$$R_1\left(r\right)=\sqrt{6}\left({\displaystyle \frac{r^2}{3R_c^2}}-{\displaystyle \frac{1}{2}}\right)R_0\left(r\right).$$

(13)

These satisfy the orthonormality conditions:

$${\int }_0^{\infty }{R}_i\left(r\right)R_j\left(r\right)r^{2}r={\delta }_{ij},$$

(14)

which are the two lowest s– wave levels of the isotropic harmonic oscillator.

The single particle energies corresponding to the two quantum states (s–wave modes) are:

$$\begin{array}{cccc}\hfill E_0& ={\displaystyle \frac{3}{2}}\hslash {\omega }_{\mathrm{eff}},\hfill & \hfill E_1& ={\displaystyle \frac{7}{2}}\hslash {\omega }_{\mathrm{eff}},\hfill \end{array}$$

(15)

with dark–matter–only energy level spacing is:

$${\Delta }_0\equiv E_1-E_0=2\hslash {\omega }_{\mathrm{eff}}.$$

(16)

In our GPP-system self-gravity and self-interaction modify the spectrum, so $E_0,E_1$ and ${\Delta }_0$ are our effective parameters which encode these corrections.

2.2. Two–Level Truncation

The total wavefunction of the ULDM particle for the two s–wave modes is:

$$\mathsf{\Psi }(t,\mathbf{x})=c_0\left(t\right){\psi }_0\left(\mathbf{x}\right)+c_1\left(t\right){\psi }_1\left(\mathbf{x}\right),$$

(17)

with

$${\psi }_i\left(\mathbf{x}\right)=R_i\left(r\right)Y_0^0(\theta ,\phi ),i=0,1.$$

(18)

The amplitudes $c_0,c_1$ satisfy the condition: $|c_0{|}^2+{\left|c_1\right|}^2=N_{core}$, where $N_{core}$ is the total number of ULDM particles in the solitonic core.

The two-level Hamiltonian for the dark matter-only case is:

$${\hat{H}}_{\mathrm{DM}}^{\left(0\right)}=E_0|0⟩⟨0+E_1|1⟩⟨1|,$$

(19)

With the energy gap ${\Delta }_0$ given by 16. The nonlinear self-interactions renormalize $E_0$ and $E_1$ and we focus on the linear baryon-induced perturbations. The ground state soliton density profile, with soliton mass $M_{sol}$, is given by:

$${\rho }_{\mathrm{sol}}^{\left(0\right)}\left(r\right)={\displaystyle \frac{M_{\mathrm{sol}}}{{\pi }^{3/2}{R}_c^3}}exp\left(-{\displaystyle \frac{r^2}{R_c^2}}\right),$$

(20)

We see that at $r=0$ we get the expression for ${\rho }_0$ which is the density near the center of the solitonic core.

3. Adiabatic Perturbation by Dehnen $\gamma$ Baryons

The spherical baryonic density distribution given by the Dehnen $\gamma$-model [9,10] is:

$${\rho }_b\left(r\right)={\displaystyle \frac{(3-\gamma )M_b}{4\pi }}{\displaystyle \frac{a_b}{r^{\gamma }{(r+a_b)}^{4-\gamma }}},0\le \gamma <3,$$

(21)

Here, $M_b$ is the total baryonic mass, $a_b$ is the scale radius. The corresponding gravitational potential is:

$${\mathsf{\Phi }}_b\left(r\right)=-{\displaystyle \frac{G{M}_b}{(2-\gamma )a_b}}\left[1-{\left({\displaystyle \frac{r}{r+a_b}}\right)}^{2-\gamma }\right],\gamma \ne 2.$$

(22)

For a detailed discussion of distribution functions for spherical systems see [11]. Here we externally specify ${\rho }_b$ and ${\mathsf{\Phi }}_b$ and impose the time dependence by adiabatically varying $M_b\left(t\right)$ and $a_b\left(t\right)$.

We add baryons into the two-level system as an adibatic perturbation, so that the total Hamiltonian density gets an extra term as:

$$\Delta {\mathcal{H}}_{\mathcal{b}}=m{\mathsf{\Phi }}_b(r,t){\left|\mathsf{\Psi }\right|}^2$$

(23)

Projecting onto the level system with the basis $\{0,1\}$:

$$\begin{array}{cc}\hfill V_{ij}\left(t\right)& =m\int d^{3}x{\psi }_i^{*}\left(\mathbf{x}\right){\mathsf{\Phi }}_b(r,t){\psi }_j\left(\mathbf{x}\right)\hfill \\ \hfill & =m{\int }_0^{\infty }{R}_i\left(r\right)R_j\left(r\right){\mathsf{\Phi }}_b(r,t)r^{2}dr.\hfill \end{array}$$

(24)

Using the equation 22 and the radial orthonormality condition for the wavefunctions we get:

$$V_{ij}\left(t\right)=-{\displaystyle \frac{mG{M}_b\left(t\right)}{(2-\gamma )a_b}}{\delta }_{ij}+{\displaystyle \frac{mG{M}_b\left(t\right)}{(2-\gamma )a_b}}{J}_{ij}(\gamma ,\alpha )$$

(25)

Here, the first term produces an overall energy shift and the second term is physically relevant baryonic perturbation (relative matrix element):

$$V_{ij}^{\left(rel\right)}\left(t\right)={\displaystyle \frac{mG{M}_b\left(t\right)}{(2-\gamma )a_b}}{J}_{ij}(\gamma ,\alpha )$$

(26)

where $J_{ij}(\gamma ,\alpha )$ is the dimensionless baryon overlap integral given by:

$$J_{ij}(\gamma ,\alpha )={\int }_0^{\infty }{y}^2{f}_i\left(y\right)f_j\left(y\right){\left({\displaystyle \frac{\alpha y}{1+\alpha y}}\right)}^{2-\gamma }dy,$$

(27)

Here, $y=r/R_c$, $\alpha \equiv R_c/a_b$ and $f_i$ the dimensionless radial profiles defined via $R_i\left(r\right)=R_c^{-3/2}{f}_i\left(y\right)$. The core in dwarf galaxy is more compact [12,13] than the baryonic distribution: $R_c\ll a_b$ so that $\alpha \ll 1$. So we expand:

$${\left({\displaystyle \frac{\alpha y}{1+\alpha y}}\right)}^{2-\gamma }={\alpha }^{2-\gamma }{y}^{2-\gamma }\left[1+\mathcal{O}\left(\alpha y\right)\right],$$

(28)

leads to the scaling relation

$$J_{ij}(\gamma ,\alpha )\simeq {\alpha }^{2-\gamma }{C}_{ij}\left(\gamma \right),$$

(29)

where

$$C_{ij}\left(\gamma \right)\equiv {\int }_0^{\infty }{y}^{4-\gamma }{f}_i\left(y\right)f_j\left(y\right)dy.$$

(30)

The coefficients $C_{ij}\left(\gamma \right)$ can be evaluated in terms of the gamma function. The coefficients corresponding to the overlap integral i.e overlap coefficients have been calculated in the Appendix A.

3.1. Effective Two–Level Baryon Induced Hamiltonian and Mixing Angle

We construct two-level Hamiltonian including baryonic perturbation. Baryons add $V_{ij}^{rel}$ given by the equation 26 to the DM-only Hamiltonian in equation 19. The total perturbed Hamiltonian in the two-state basis is:

$$H\left(t\right)=\left(\begin{array}{cc}{E}_0+V_{00}^{\left(\mathrm{rel}\right)}\left(t\right)& V_{01}^{\left(\mathrm{rel}\right)}\left(t\right)\\ V_{01}^{\left(\mathrm{rel}\right)}\left(t\right)& E_1+V_{11}^{\left(\mathrm{rel}\right)}\left(t\right)\end{array}\right).$$

(31)

and define

$$\begin{array}{cc}\hfill \overline{E}\left(t\right)& \equiv {\displaystyle \frac{1}{2}}\left[E_0+E_1+V_{00}^{\left(\mathrm{rel}\right)}\left(t\right)+V_{11}^{\left(\mathrm{rel}\right)}\left(t\right)\right]\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill \Delta \left(t\right)& \equiv \left[E_1+V_{11}^{\left(\mathrm{rel}\right)}\left(t\right)\right]-\left[E_0+V_{00}^{\left(\mathrm{rel}\right)}\left(t\right)\right]={\Delta }_0+{\displaystyle \frac{mG{M}_b\left(t\right)}{(2-\gamma )a_b}}\left[J_{11}(\gamma ,\alpha )-J_{00}(\gamma ,\alpha )\right]\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill J\left(t\right)& \equiv V_{01}^{\left(\mathrm{rel}\right)}\left(t\right)={\displaystyle \frac{mG{M}_b\left(t\right)}{(2-\gamma )a_b}}{J}_{01}(\gamma ,\alpha ).\hfill \end{array}$$

(34)

The relative Hamiltonian takes the form:

$$H_{\mathrm{rel}}\left(t\right)={\displaystyle \frac{\Delta \left(t\right)}{2}}{\sigma }_z+J\left(t\right){\sigma }_x.$$

(35)

Lets conveniently define

$$\begin{array}{cc}\hfill {\kappa }_{\Delta }(\gamma ,\alpha )& \equiv {\displaystyle \frac{mG}{(2-\gamma )a_b}}\left[J_{11}(\gamma ,\alpha )-J_{00}(\gamma ,\alpha )\right],\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill {\kappa }_J(\gamma ,\alpha )& \equiv {\displaystyle \frac{mG}{(2-\gamma )a_b}}{J}_{01}(\gamma ,\alpha ),\hfill \end{array}$$

(37)

so that we get compact form for $\Delta \left(t\right)$ and $J\left(t\right)$ as:

$$\begin{array}{cc}\hfill \Delta \left(t\right)& ={\Delta }_0+{\kappa }_{\Delta }{M}_b\left(t\right),\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill J\left(t\right)& ={\kappa }_J{M}_b\left(t\right).\hfill \end{array}$$

(39)

Thus the instantaneous eigen values of the $H_{rel}$ are:

$$E_{\pm }\left(t\right)=\pm {\displaystyle \frac{1}{2}}\sqrt{\Delta {\left(t\right)}^2+4J{\left(t\right)}^2},$$

(40)

and the mixing angle is defined as:

$$tan2\theta \left(t\right)={\displaystyle \frac{2J\left(t\right)}{\Delta \left(t\right)}}.$$

(41)

A convenient way to express the instantaneous eigens tates is:

$$\begin{array}{cc}|+(t)⟩& =cos\theta \left(t\right)|1⟩+sin\theta (t\left)\right|0⟩,\hfill \end{array}$$

(42)

$$\begin{array}{cc}|-(t)⟩& =-sin\theta \left(t\right)|1⟩+cos\theta (t\left)\right|0⟩,\hfill \end{array}$$

(43)

so that $H_{\mathrm{rel}}\left(t\right)\pm \left(t\right)=E_{\pm }\left(t\right)\pm \left(t\right)$. The expectation value of the relative Hamiltonian is a bounded function of the mixing angle. This can also be proven by using the Hardy-Littlewood-Sobolev (HLS) inequality (see [14,15]). The adiabatic perturbation theory implies that the baryonic component grows slowly in comparison to the dynamical time due to which the two-state soliton wavefunction remains at the eigenstate up to a phase of the time dependent $2\times 2$ Hamiltonian given by the equation 35. The adiabatic condition can be written as:

$$\begin{array}{|c|}\hline \left|{\displaystyle \frac{-\left(t\right){\dot{H}}_{\mathrm{rel}}\left(t\right)+\left(t\right)}{{\left[E_{+}\left(t\right)-E_{-}\left(t\right)\right]}^2}}\right|\ll 1.\\ \hline\end{array}$$

(44)

The mixed ground-radial state density corresponding to the instantaneous lower and upper eigenstates can be written in the form:

$${\rho }_{-}(r;M_b)={\displaystyle \frac{M_{\mathrm{sol}}}{4\pi }}{\left[cos\theta \left(M_b\right)R_0\left(r\right)-sin\theta \left(M_b\right)R_1\left(r\right)\right]}^2.$$

(45)

and

$${\rho }_{+}(r;M_b)={\displaystyle \frac{M_{\mathrm{sol}}}{4\pi }}{\left[sin\theta \left(M_b\right)R_0\left(r\right)+sin\theta \left(M_b\right)R_1\left(r\right)\right]}^2$$

(46)

We can easily show that $\int {\rho }_{+}(r;M_b)dV=\int {\rho }_{+}(r;M_b)dV=M_{sol}$ for any $\theta \left(M_b\right)$ because the transformation bewteen the $\{0,1\}$ and $\{+,-\}$ basis is unitary.

4. Dwarf Galaxy: A Toy Model

In this section we develop and test adiabatic formalism, we consider am idealized dwarf galaxy whose dark matter distribution is dominated by ULDM solitonic core and the baryonic matter in this galaxy follow Dehnen-$\gamma$ profile. The self-gravitating core at the center of the halo is natural in this model and is a well-motivated framework for dwarf galaxy dynamics. The numerical values of all the parameters in this setup are taken from ( [10,16,17,18,19,20,21]).

4.1. Solitonic Core and DM–Only Level Spacing

We model the solitonic core as 3D harmonic oscillator near the center. Our choice of values are:

$$\begin{array}{cc}\hfill m& ={10}^{-22}\mathrm{eV},\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill M_{\mathrm{sol}}& ={10}^8{M}_{\odot },\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill R_c& =0.5\mathrm{kpc},\hfill \end{array}$$

(49)

Here, m is the dark matter particle mass, $M_{\mathrm{sol}}$ is the soliton mass and $R_c$ is the core radius. We calculate the values of effective frequency ${\omega }_{eff}$ and the energy gap between the ground state and the first radial excitation as:

$$\begin{array}{cc}\hfill {\omega }_{\mathrm{eff}}& \simeq 1.9\times {10}^{-15}{\mathrm{s}}^{-1},\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill {\Delta }_0& \simeq 4.0\times {10}^{-49}\mathrm{J}\simeq 2.5\times {10}^{-30}\mathrm{eV}.\hfill \end{array}$$

(51)

For the cuspy $\gamma =1$ and cored $\gamma =0$ baryonic component we take the values for final baryonic mass and baryon scale radius $a_b$ as:

$$\begin{array}{cc}\hfill M_{b,\mathrm{final}}& =3\times {10}^7{M}_{\odot },\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill a_b& =0.8\mathrm{kpc},\hfill \end{array}$$

(53)

We see that the baryon distribution scale is larger than for the solitonic core, which is true for a typical dwarf galaxy.

4.2. Baryon–Induced Shifts and Mixing

For the calculation of energy shifts and energy level mixing due to baryons we take the following numerical values.

$$\begin{array}{cc}\hfill m& ={10}^{-22}\mathrm{eV}\simeq 1.78\times {10}^{-58}\mathrm{kg},\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill a_b& =0.8\mathrm{kpc}\simeq 2.47\times {10}^{19}\mathrm{m},\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill G& =6.67\times {10}^{-11}{\mathrm{m}}^3{\mathrm{kg}}^{-1}{\mathrm{s}}^{-2},\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill \alpha & =0.625,\hfill \end{array}$$

(57)

and numerically we have,

$$\begin{array}{cc}\hfill \gamma =1:& {\kappa }_{\Delta }(1,\alpha )\approx 1.70\times {10}^{-88}\mathrm{J}/\mathrm{kg},\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill & {\kappa }_J(1,\alpha )\approx 1.39\times {10}^{-88}\mathrm{J}/\mathrm{kg},\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill \gamma =0:& {\kappa }_{\Delta }(0,\alpha )\approx 1.88\times {10}^{-88}\mathrm{J}/\mathrm{kg},\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill & {\kappa }_J(0,\alpha )\approx 1.15\times {10}^{-88}\mathrm{J}/\mathrm{kg}.\hfill \end{array}$$

(61)

The final baryonic mass is:

$$M_{b,\mathrm{final}}=3\times {10}^7{M}_{\odot }\simeq 5.97\times {10}^{37}\mathrm{kg},$$

(62)

4.3. Dimensionless Parametrization for the Two–Level ULDM System

For our numerical work we choose the following dimensionless quantites:

$$E_0={\Delta }_0,M_0=M_{b,\mathrm{final}},$$

(63)

and we define the baryon mass fraction as a function of time:

$$\mu \left(t\right)\equiv {\displaystyle \frac{M_b\left(t\right)}{M_{b,\mathrm{final}}}}\in [0,1].$$

(64)

We express:

$$\begin{array}{cc}\hfill {\Delta }_{\gamma }\left(t\right)& ={\Delta }_0\left[1+A_{\gamma }\mu \left(t\right)\right],\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill J_{\gamma }\left(t\right)& ={\Delta }_0{B}_{\gamma }\mu \left(t\right),\hfill \end{array}$$

(66)

for general value of $\gamma$

$$A_{\gamma }\equiv {\displaystyle \frac{{\kappa }_{\Delta }(\gamma ,\alpha )M_{b,\mathrm{final}}}{{\Delta }_0}},B_{\gamma }\equiv {\displaystyle \frac{{\kappa }_J(\gamma ,\alpha )M_{b,\mathrm{final}}}{{\Delta }_0}}.$$

(67)

For specific values of $\gamma$ i.e for both the Plummer model ($\gamma =0$) and Hernquist-like ($\gamma =1$) model, numerically:

$$\begin{array}{cc}\hfill \gamma =1:& A_1\simeq 0.0253,B_1\simeq 0.0206,\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill \gamma =0:& A_0\simeq 0.0280,B_0\simeq 0.0172.\hfill \end{array}$$

(69)

For the Hernquist-like model:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\Delta }_1\left(t\right)}{{\Delta }_0}}& =1+0.0253\mu \left(t\right),\hfill \end{array}$$

(70)

$$\begin{array}{cc}\hfill {\displaystyle \frac{J_1\left(t\right)}{{\Delta }_0}}& =0.0206\mu \left(t\right),\hfill \end{array}$$

(71)

For the more symmetric Plummer-model for baryons:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\Delta }_0\left(t\right)}{{\Delta }_0}}& =1+0.0280\mu \left(t\right),\hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill {\displaystyle \frac{J_0\left(t\right)}{{\Delta }_0}}& =0.0172\mu \left(t\right),\hfill \end{array}$$

(73)

In the simulation we are considering a smooth adiabatic growth of baryons via

$$\mu \left(t\right)={sin}^2\left({\displaystyle \frac{\pi t}{2T_{\mathrm{ramp}}}}\right),0\le t\le T_{\mathrm{ramp}},$$

(74)

so that the baryonic mass and the baryon-induced mixings grow slowly. The baryon mass and the mixing of the states is switched on slowly (i.e adiabatically) with stationary points at $t=0$ and $t=T_{ramp}$. This model provides a controlled and natural setting to study how the baryonic growth dirves the adiabatic mixing between the ground and the first radial excited state and soliton core deformation.

Figure 1. The corresponding dimensionless profiles $f_0\left(y\right)$ and $f_1\left(y\right)$ are shown.

Figure 1. The corresponding dimensionless profiles $f_0\left(y\right)$ and $f_1\left(y\right)$ are shown.

Figure 2. Dimensionless radial density profiles of the instantaneous lower − and upper + as baryon mass grows adiabatically. The curves remain nearly identical for all $\mu \left(t\right)$, implying a tiny excited state population of ULDM particles

Figure 2. Dimensionless radial density profiles of the instantaneous lower − and upper + as baryon mass grows adiabatically. The curves remain nearly identical for all $\mu \left(t\right)$, implying a tiny excited state population of ULDM particles

Figure 3. Two dimensional slices of the normalized density $\rho (x,y)/{\rho }_{max}$ when $\mu \left(t\right)$ increase from 0 to 1 for Dehnen-$\gamma$.

Figure 3. Two dimensional slices of the normalized density $\rho (x,y)/{\rho }_{max}$ when $\mu \left(t\right)$ increase from 0 to 1 for Dehnen-$\gamma$.

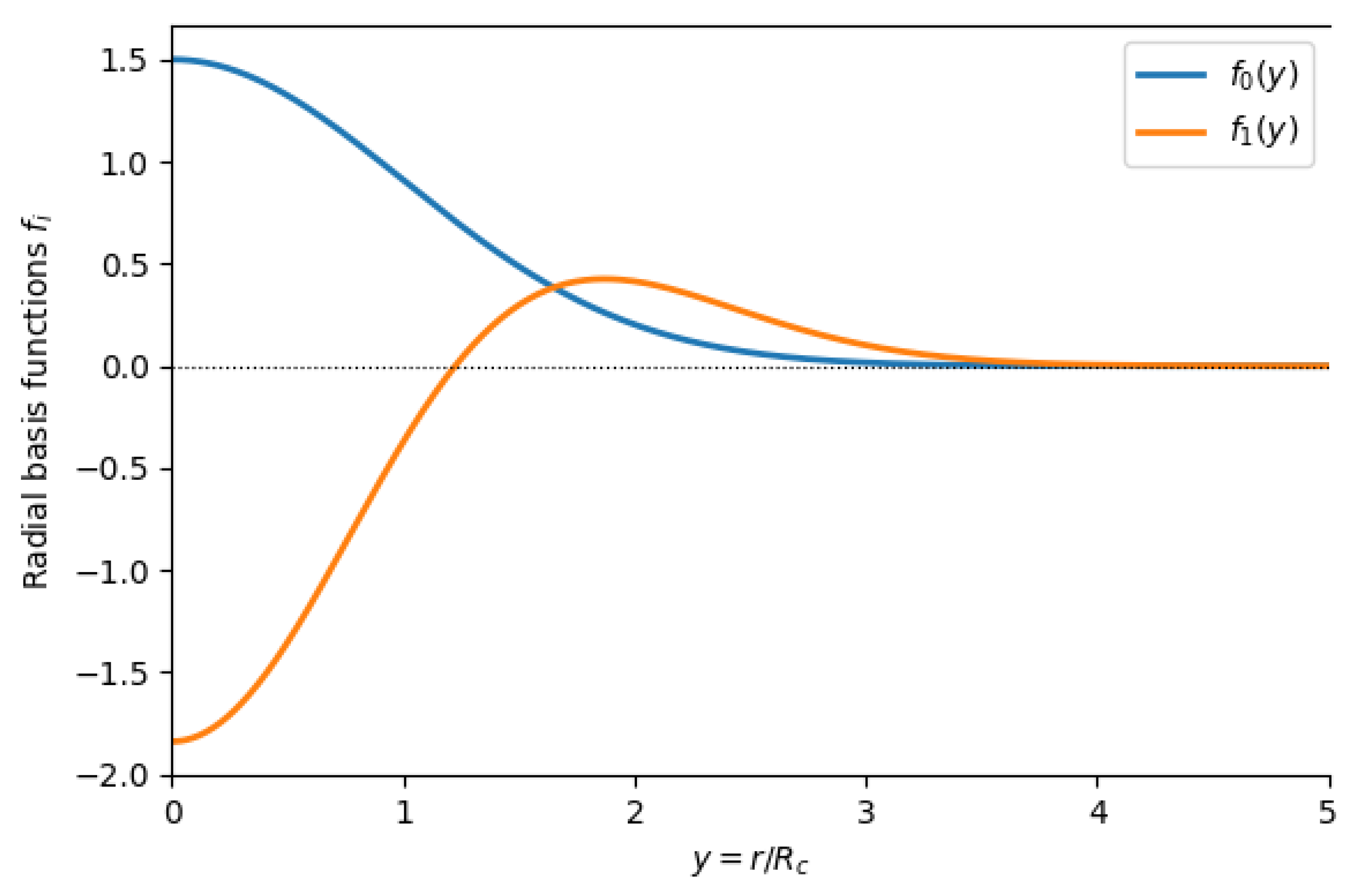
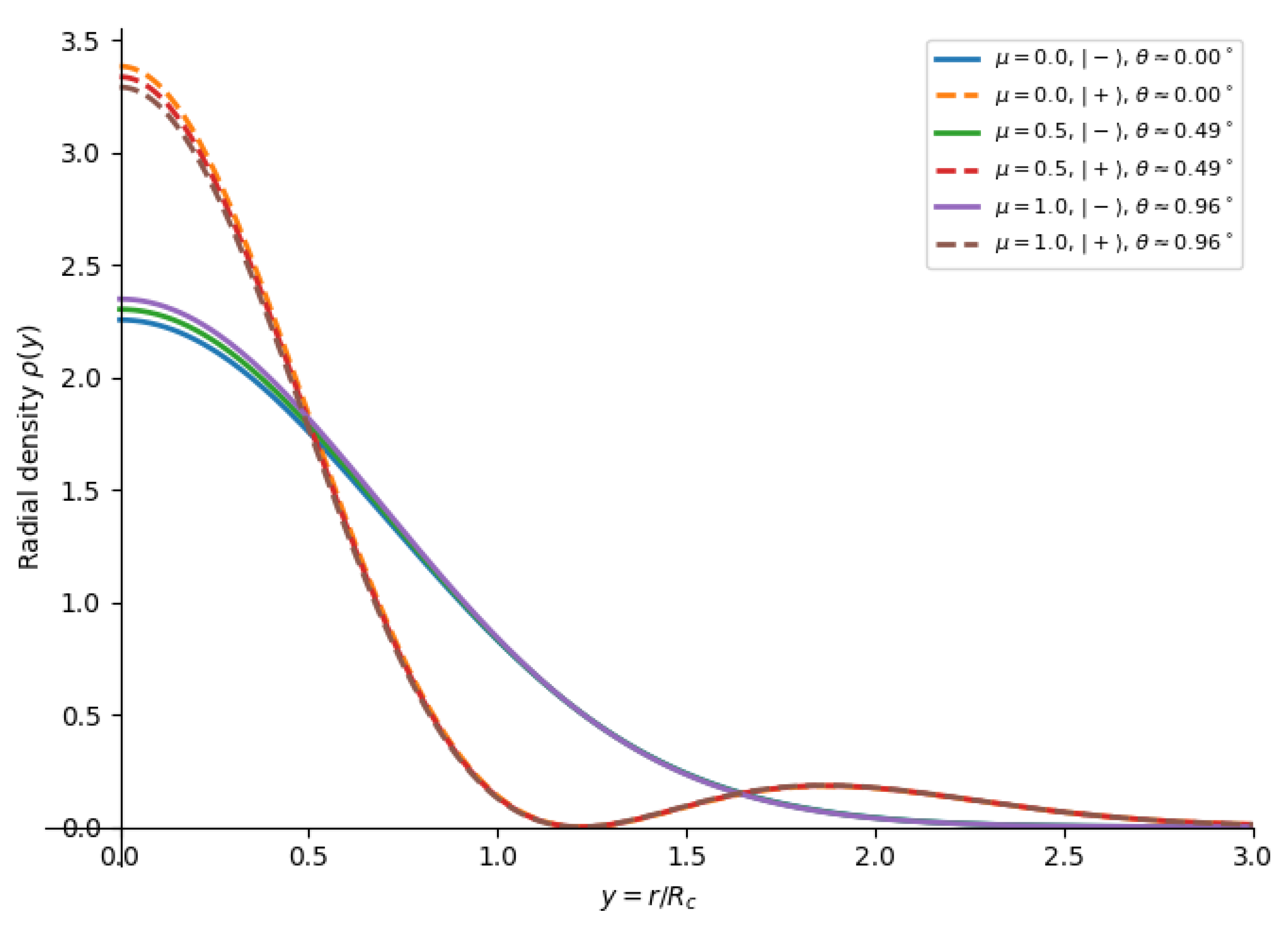
5. Summary and Outlook

In this work we presented a two–level harmonic oscillator like model for describing the ULDM solitonic core in the presence of Dehnen baryonic matter for $\gamma$ = 0 and 1. We proved that resulting core dynamics due to the baryonic adiabatic perturbation is governed by two–level relative Hamiltonian $H_{\mathrm{rel}}$ leading to the deformation of the density profile. In our toy dwarf–galaxy, adiabatic evolution of baryonic matter cannot generate any substantial excited state occupation number i.e only $4\times {10}^{-4}$ fraction of particles is in the excited state. The normalized density distribution function for ULDM particles remains almost symmetric during the baryonic evolution In (Part–II) companion paper we will consider higher number of excited states and also use this framework with real dwarf spheroidal galaxies, using observed baryonic profiles and stellar kinematics to study the baryon induced shifts in the core radius and infer other ULDM parameters including the dark matter particle mass. We will also study Gaffe–like($\gamma \to 2$) distribution model as a limiting case in the Dehnen-$\gamma$ baryon distribution.