Analysis of Telegraph Equation for Propagating Waves with Dispersion and Attenuation

1. Introduction

As a partial differential equation (PDE) [1,2], the telegraph equation is used as a model for the dynamics of electric potential and electric current on a lossy transmission line [3,4,5]. From broader perspectives, telegraph-like equations describe diverse phenomena in nature, biology, and industrial devices, for instance: [i] dispersion in turbulent flows [6], [ii] flows through hollow tubes [7,8], [iii] structural dynamics [9,10,11,12], [iv] vibration of a string, say, of a guitar [13,14,15,16], [v] signal transmission through biological neurons [17,18,19], [vi] population dynamics [20], [vi] heat conduction with Fourier-Cattaneo or Maxwell-Cattaneo law containing slight wave propagations [21,22], [vii] quantum electrodynamics [23], to name a few.

From theoretical perspectives, telegraph-like equations harbor several key features of temporal transients, reaction or leakage, diffusion, propagating waves [24,25], sources and sinks. A variety of analytical and semi-analytical solutions to telegraph-like equations have so far been developed [21,26,27]. Many numerical solutions to telegraph-like equations have been published as well [14,15,28]. Especially, our dimensional analysis of telegraph equations uncovered hitherto neglected mechanisms [17].

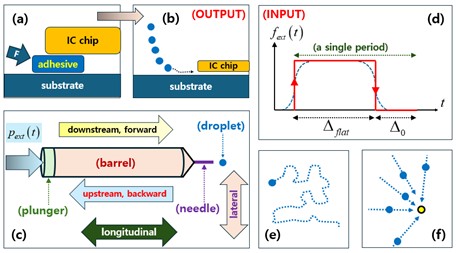
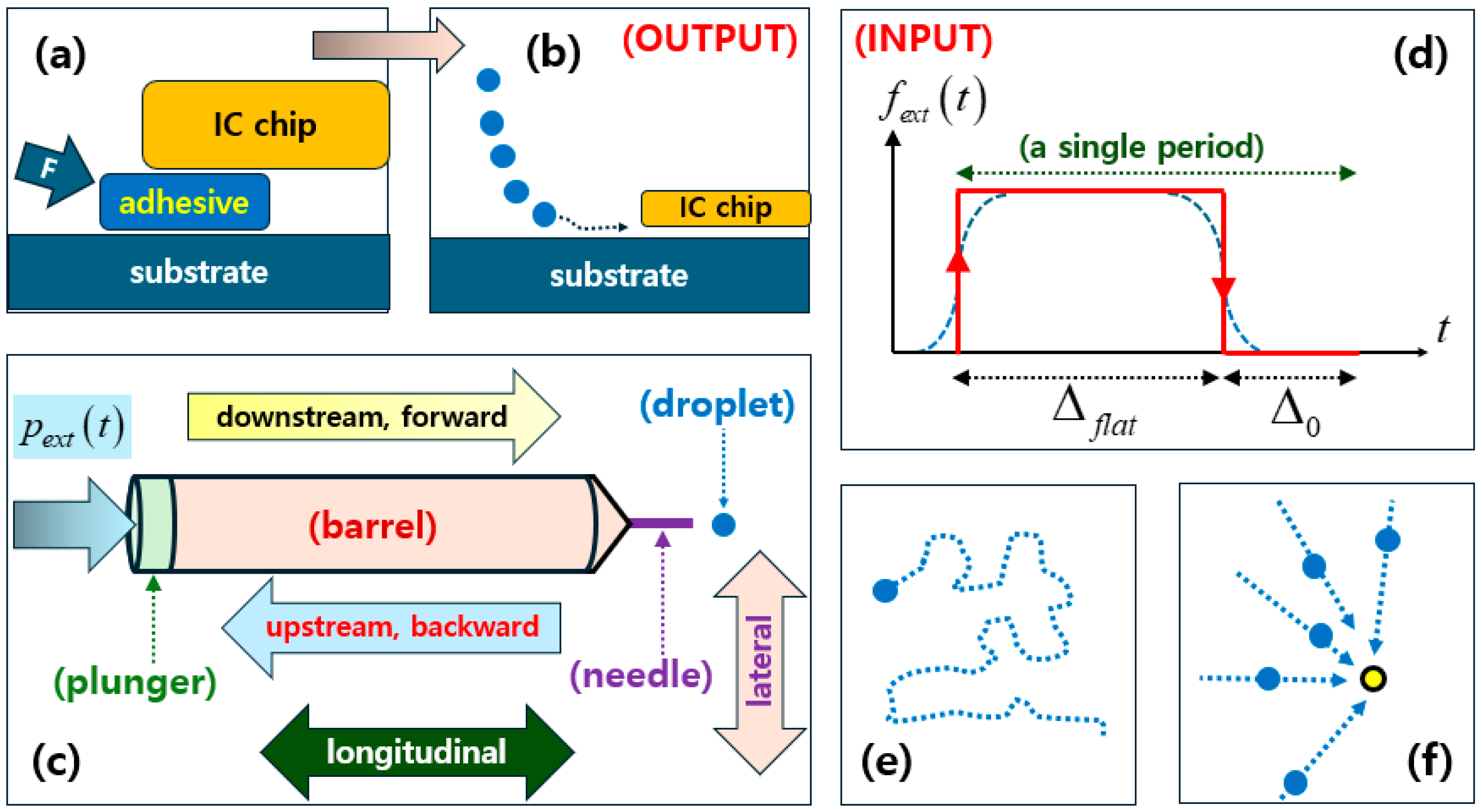
Meanwhile, let us turn our attention to our on-going research project. Here, we are assigned to help perform efficient underfill encapsulation for electronics industry. Figure 1(a,b) depict typical underfill encapsulation situations [29,30]. The goal is to provide adhesive solutions underneath an integrated circuit (IC) chip that is to be bonded to the underlying substrate. The overlapping arrow from Figure 1(a,b) indicates a decreasing feature size of an IC chip.

In older days, a bulk of adhesive fluid could have been pushed into the wide gap by an external force marked by ‘F’ on Figure 1(a). Conventional jetting of rather long liquid mass as illustrated on Figure 1(a) may be still employed for relatively coarse three-dimensional (3-D) printing [31]. When a miniature 3-D printer is employed for filling, say, very tiny holes, continuous liquid flow cannot fill in those holes because of large flow resistance per volume.

In recent days with ever-increasing miniaturization, the gap between IC chips and a substrate is so narrow that epoxy jetting or forced injection as shown on Figure 1(a) cannot accomplish adequate underfill encapsulation. Therefore, only sufficiently tiny droplets of adhesive solution are sucked into those thin gaps thanks to favorable capillary pulling force as shown on Figure 1(b) [29,30,32].

Concerning the modern-day underfill encapsulation illustrated on Figure 1(b), our task is to measure and control at real time the droplet dynamics of droplet dispensers so that certain specified volumes of droplets are ejected on demand [30,33,34].

Our experimental data let us believe that the dynamics at hand encompasses both fluid flows and structural deformation of a droplet dispenser on equal footing. Interactions between these two branches of mechanics are quite complicated so that we cannot analytically solve the relevant dynamics with high precision. Detailed numerical simulations are now available in literature on the whole or partial processes of droplet dispensing [7,30,35]. Although those details help us to understand what is going on, they cannot be utilized for real-time control of droplet dispensing [30].

Therefore, we decided to seek a simpler physical model for droplet dispensing. After several trials, we have learned that a telegraph-like equation and its solution could provide us with necessary clues as to the real-time controllability of a whole dispenser. Especially, the electric-circuit interpretation of the solutions to telegraph-like equations could help us to construct proper real-time measurement and/or control circuits [31,33,36].

In this connection, vibration control is an enabling technique not only in transportation vehicles and structural dynamics but also in manufacturing of semiconductor and precision machines [37]. In this respect, one of the goals of this study is to lay foundations on analytical tools that arise from telegraph-like equations. Such analytical tools could be utilized to enhance the functionalities of pertinent real-time control devices based on electric circuits that emulate telegraph equations [38].

Once those control devices are conFigured, we are trying to implement modern algorithms for physics-informed neural network (PINN) and/or physical AI (artificial intelligence) [32,39,40]. That is why we are frequently referring in this study to fundamental concepts underlying biological neuroscience [25,41]. We hope that this study contributes ultimately to realizing neuromorphic circuits [42].

Figure 1(c) illustrates a process of a single immunization shot administered through a medical syringe. Here, the driving force is exerted by hand pressure as given on Figure 1(c,d) [7,31,43]. For a proper injection shot, a nurse may have been trained, say, for a couple of months. Our droplet dispenser requires a certain total volume of droplets to be dropped over the chip area, after which the droplet dispenser is moved to another location over a substrate as shown by the trajectory on Figure 1(e). The whole encapsulation process is desired to be real-time automated. Consequently, our droplet dispensers are much harder to control than a single immunization injector shown on Figure 1(c).

Especially, the dynamics of droplet breakup and ejection should be adequately examined by taking into consideration capillarity, wetting, surface tension, and gravity [7,15,24,30,35,44,45]. Table 1 makes comparison among several fluid-ejection devices.

Here in this study, we will consider the fundamental aspects of the frequency dispersion relations of telegraph equations over infinite one-dimensional (1-D) domain [46]. Some of the characteristics found for telegraph equations are well-known. Notwithstanding, we focus on deriving those features not only from theorists’ perspectives but also from the perspective of practicing engineers.

Along this line of reasoning, section 2 provides reasons for why we examine telegraph equations from fresh look. Section 3 repeats the derivations of 1-D telegraph-like equations along with some reduced forms. Section 4 reexamines a 3-D telegraph equation for comparison to 1-D equations. Section 5 provides solutions to the well-known dispersion relation for the leaky telegraph equation. In addition, new findings including crossovers are offered for the dispersion relation of a leak-free telegraph equation. Section 6 handles the response functions for typical circuit configurations, thus showing features of low-pass filters. Section 7 offers some relevant discussions, followed by conclusions in section 8. Appendices are provided at the end to make this manuscript self-contained.

2. Motivation for this Study

As depicted on Figure 1(c), a droplet dispenser consists roughly of a plunger, a barrel, and a (contracting) nozzle [7]. An external forcing, say, compressed-air pressure is acting on the outside face of a plunger as illustrated on the left portion of Figure 1(c). Notice that the compressed-air excitation is just one of widely employed methods of periodically driving droplet dispensers [33,39,47]. As depicted on Figure 1(b), a droplet dispenser is employed for generating a stream of droplets of epoxy solution (being an electric insulator). This succession of droplets is dropped down on an electronic chip undergoing encapsulation process [30].

Let us denote the excitation by $f_{ext}\left(t\right)$ with $t$ being time. An idealized form of $f_{ext}\left(t\right)$ is displayed on Figure 1(d), where a single period out of repeated train of excitations is indicated by four segments of red lines [48]. As an initial stage, the infinitesimally short step-up event corresponds to pressurization. During the upper flat period ${\mathsf{\Delta }}_{flat}$, a main event of droplet ejection takes place. Afterwards, an infinitely short step-down event is enforced during which the ejection of a droplet is initiated and then terminated [31]. During the dormant or rest period ${\mathsf{\Delta }}_0$, the droplet dispenser is moved to another position over a substrate as illustrated on Figure 1(e). Such a four-step process is repeated as designed. In our experimental runs, ${\mathsf{\Delta }}_{flat}\approx 2\frac{1}{2}s$ and ${\mathsf{\Delta }}_0\approx \frac{1}{2}s$, respectively.

Meanwhile, let us consider side conditions that consist of initial conditions (ICs) and boundary conditions (BCs) [1,2,19]. The damped vibration of a string of finite longitudinal length requires specifying certain valid boundary conditions (BCs). In addition, proper initial conditions are required for analytic solutions to telegraph equations [4,22,28,49,50]. Such Cauchy problems (PDEs and side conditions) for telegraph equations over finite 1-D domain will be handled in a separate publication.

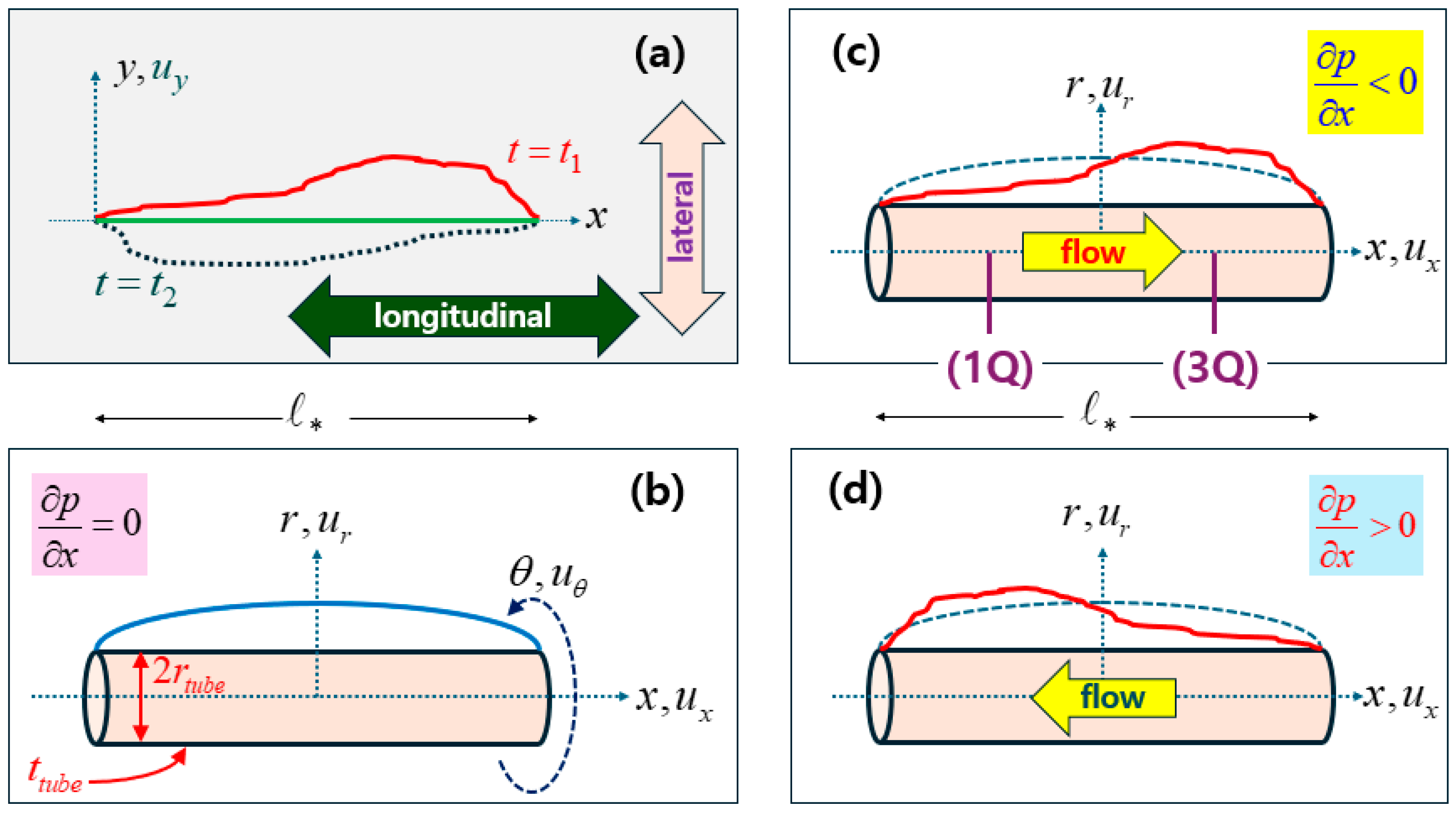
In the meantime, Figure 2(a) illustrates a string of finite length ${\ell }_{\ast }$, where a string in a quiescent state is just the horizontal green line along the longitudinal $x$-direction (indicated by the horizontal double-headed arrow).

We will consider henceforth an infinite 1-D domain $-\infty <x<\infty$, although a finite length ${\ell }_{\ast }$ is introduced on Figure 2 for an illustrative purpose. Over time $t$, this string could undergo lateral deformation $u_y\left(t,x\right)$ in the lateral direction (indicated by the vertical double-headed arrow) perpendicular to the $x$-direction. For instance, $u_y\left(t_1,x\right)$ and $u_y\left(t_2,x\right)$ indicate such lateral displacements at distinct times $t_1$ and $t_2$ on Figure 2(a). Both ends of the string are held fixed solely for illustrative purposes [14,15].

Let us copy the telegraph equation presented in [15] with slight alterations in notation as follows.

$$\sigma {\displaystyle \frac{\partial u_y}{\partial t}}+{\displaystyle \frac{{\partial }^2{u}_y}{\partial t^2}}={\displaystyle \frac{T}{\mu }}{\displaystyle \frac{{\partial }^2{u}_y}{\partial x^2}}-{\displaystyle \frac{\pi E{r}_{string}^4}{4\mu }}{\displaystyle \frac{{\partial }^4{u}_y}{\partial x^4}}$$

(1)

Here, $\sigma$ is an internal damping and $E$ is Young’s modulus. In addition, the string parameters $\left\{T,\mu ,r_{string}\right\}$ are the longitudinal tension, the mass per unit length, and the radius of a circular cross section of a string, respectively [16].

The first term on the left-hand side (LHS) of equation (1) signifies temporal decay. The wave equation made of two nearby terms $\left({\partial }^2{u}_y/\partial t^2\right)=\left(T/\mu \right)\left({\partial }^2{u}_y/\partial x^2\right)$ on both sides of equality sign helps to determine the sound velocity $a_{string}=\sqrt{T/\mu }$ of a string. This wave equation gives rise to propagating solutions consisting of a pair of functions $u_y\propto g\left(x\pm at\right)$ for suitably differentiable forms of $g\left(\circ \right)$ [2,14,19,25,27]. The last fourth-order term proportional to $\left({\partial }^4{u}_y/\partial x^4\right)$ on the RHS stands for flexural (or bending) stiffness due to finite-sized cross section [7,10,11,12,14,24]. If this flexure term is neglected, equation (1) is reduced to the following.

$$\sigma {\displaystyle \frac{\partial u_y}{\partial t}}+{\displaystyle \frac{{\partial }^2{u}_y}{\partial t^2}}=a_{string}^2{\displaystyle \frac{{\partial }^2{u}_y}{\partial x^2}}$$

(2)

Transient damping of a solid string of a finite radius could occur due to surrounding viscous incompressible fluid [13,22]. Here, one-way influence of a surrounding fluid flow on a string is assumed. Viscous drag by fluid on a solid gives rise to the first-order temporal-derivative term $\sigma \left(\partial u_y/\partial t\right)$ appearing in the above simpler telegraph equation. Furthermore, two-way fluid-structure interactions are handled in [8], where nonlinearities are hardly avoided. Such fluid-structure interactions play a crucial role also in underfill encapsulation [30], where thermal mismatches become often problematic.

Meanwhile, the influence of solid-tube deformation on the flow inside a tube is exploited for nondestructive ultrasonic measurement. Collapsible tube deformations that are dramatically larger than our minute deformations have been measured by ultrasonic techniques, where flows are maintained by applied pressure gradient as on Figure 1(c), Figure 2(b), Figure 2(c) and Figure 2(d) [51].

Pressure waves propagating through incompressible inviscid fluid inside a cylindrical elastic tube have been examined from diverse perspectives [8]. In this connection, let us turn to Figure 2(b–d), each of which displays a circular hollow tube of finite radius.

In terms of Cartesian $xyz$-coordinates as on Figure 2(a), any radial direction on the $yz$-plane is called a lateral direction. In the cylindrical $r\theta x$-coordinate as on Figure 2(b–d), the axial direction is pointing in the $x$-coordinate, while the radial direction is pointing in the $r$-coordinate. Inside each hollow tube lies a volume of fluid. The displacement components $\left\{u_x,u_r\right\}$ are provided along with their corresponding coordinates $\left\{x,r\right\}$. In addition, the usual circumferential (azimuthal or angular) symmetry is assumed so that $u_{\theta }\equiv 0$ and the $\theta$-dependences are suppressed.

Figure 2(b–d) correspond to distinct states of fluid flows and longitudinal pressure gradients as marked on each subfigure and summarized on Table 2. These pressure gradients result from the compressed-air excitation as depicted on Figure 1(c,d).

It is difficult in general to find analytical solutions to the fluid flow through a circular hollow tube of finite longitudinal length [4]. In this connection, recall that the solution to the unsteady Poiseuille flow has been constructed solely over a circular tube of infinite longitudinal length [52]. This fact makes all practical problems involved in droplet dispensers extremely difficult. Meanwhile, the momentum loss due to the shear stress between the inner wall of a cylindrical tube and internally flowing fluid can be considered as kind of leakage from the viewpoint of flowing fluid.

With both ends assumed fixed, no-flow case on Figure 2(b) exhibits a displacement profile that is symmetric across the central lateral plane. If downstream flow is set up as on Figure 2(c) thanks to favorable pressure gradient $\left(\partial p/\partial x\right)<0$, the lateral displacements on the downstream half are greater on average than those on the upstream half. If upstream flow is set up as on Figure 2(d) due to unfavorable pressure gradient $\left(\partial p/\partial x\right)>0$, the lateral displacements on the downstream half are smaller on average than those on the upstream half.

If temporal delay is neglected for simplicity, $\left(\partial p/\partial x\right)<0$ corresponds roughly to pressurization period, while $\left(\partial p/\partial x\right)>0$ corresponds roughly to depressurization period. Such periodic cycles consisting of pressurization and depressurization are executed by a pneumatic device for a droplet dispenser that is set up in our laboratory [33,34].

During unsteady transient processes as in our situations, Darcy-Weissbach law (the average longitudinal pressure gradient being proportional to the average fluid velocity squared) breaks down [51], thereby rendering extremely unpredictable the fluid flows inside a tube.

On Figure 2(c), we have illustrated the lateral displacements at two distinct locations, namely, $u_r\left(t,x=\frac{1}{4}{\ell }_{\ast }\right)$ and $u_r\left(t,x=\frac{3}{4}{\ell }_{\ast }\right)$ as indicated by the thick vertical lines and marked with 1Q (the first quadrant) and 3Q (the third quarter). To this end, we employed a modern nanoscopic optical displacement sensor, thereby measuring displacements on the order of sub-micrometer. In addition, the difference $u_r\left(t,x=\frac{3}{4}{\ell }_{\ast }\right)-u_r\left(t,x=\frac{1}{4}{\ell }_{\ast }\right)$ turns out to be temporally periodic as a response to periodic compress-air excitation.

Let us examine more closely the displacement fields of a circular tube as depicted on Figure 2(b–d). Also shown on Figure 2(b) are the radius $r_{tube}$ (not a coordinate) of a tube and the tube thickness $t_{tube}$ (not time). Suppose that $t_{tube}<<r_{tube}$ such that the tube is relatively thin in comparison to its radius. Although the tube thickness is still accounted for, the displacement fields can be taken as being $r$-independent. In this situation, the governing PDEs are the elastodynamic Navier equations [9,12].

In the thin-tube limit $t_{tube}<<r_{tube}$, Navier equations can be reduced to thin-plate equations for the two displacement components $\left\{u_x,u_r\right\}$, which depend only on $\left\{t,x\right\}$ [10]. Such thin-plate equations play a crucial role in handling not only structural dynamics but also semiconductor thin films [50]. In our droplet dispensers, we expect $\left|u_x\right|<<\left|u_r\right|$ so that we illustrate only $u_x$ on Figure 2(b–d). With these approximations, $u_r$ being of our primary concern stands for a bending mode, whereas $u_x$ stands for a pressure (‘p’ for short) mode. In comparison, a shear (‘s’ for short) mode is missing since we assumed $u_{\theta }=0$ [10]. Alternatively, $u_r$ is called an ‘out-of-plane displacement’, whereas $u_x$ is called an ‘in-plane displacement’.

Let us give a rough description of the reduced Navier thin-plate equations. Most importantly, these thin-plate equations possess the features of temporal transient, wave phenomenon, diffusion, leakage, and external source, namely, all features exhibited by the telegraph equation presented in equation (1). However, these reduced Navier equations contain partial differentials $\left\{{\partial }^4\left(\circ \right)/\partial x^4,{\partial }^4\left(\circ \right)/\partial t^2\partial x^2,\partial \left(\circ \right)/\partial x\right\}$ in addition to those partial differentials shown in equation (1). In other words, these reduced Navier equations are second order in time whilst they are fourth order in space in great distinction to the generix telegraph equations [7,24].

Quite importantly, the first-order derivative $\partial \left(\circ \right)/\partial x$ arises from the one-way fluid flows as depicted on Figure 2(c,d) during unsteady states. This presence of $\partial \left(\circ \right)/\partial x$ popping up in the reduced Navier equations lets the problem at hand be asymmetrical across the central lateral plane as illustrated by the spatial profile of the lateral displacement $u_r\left(t,x\right)$ on Figure 2(c,d) [10].

However, both establishing proper BCs and finding associated analytical solutions to the thin-plate equations turn out to be significantly complicated. This is why we decided to examine a simpler telegraph equation in this study to explore the afore-mentioned compound effects. In this sense, we are seeking a ‘computationally minimal model’ for droplet dispensers [39].

3. Derivation of One-Dimensional (1-D) Telegraph Equation

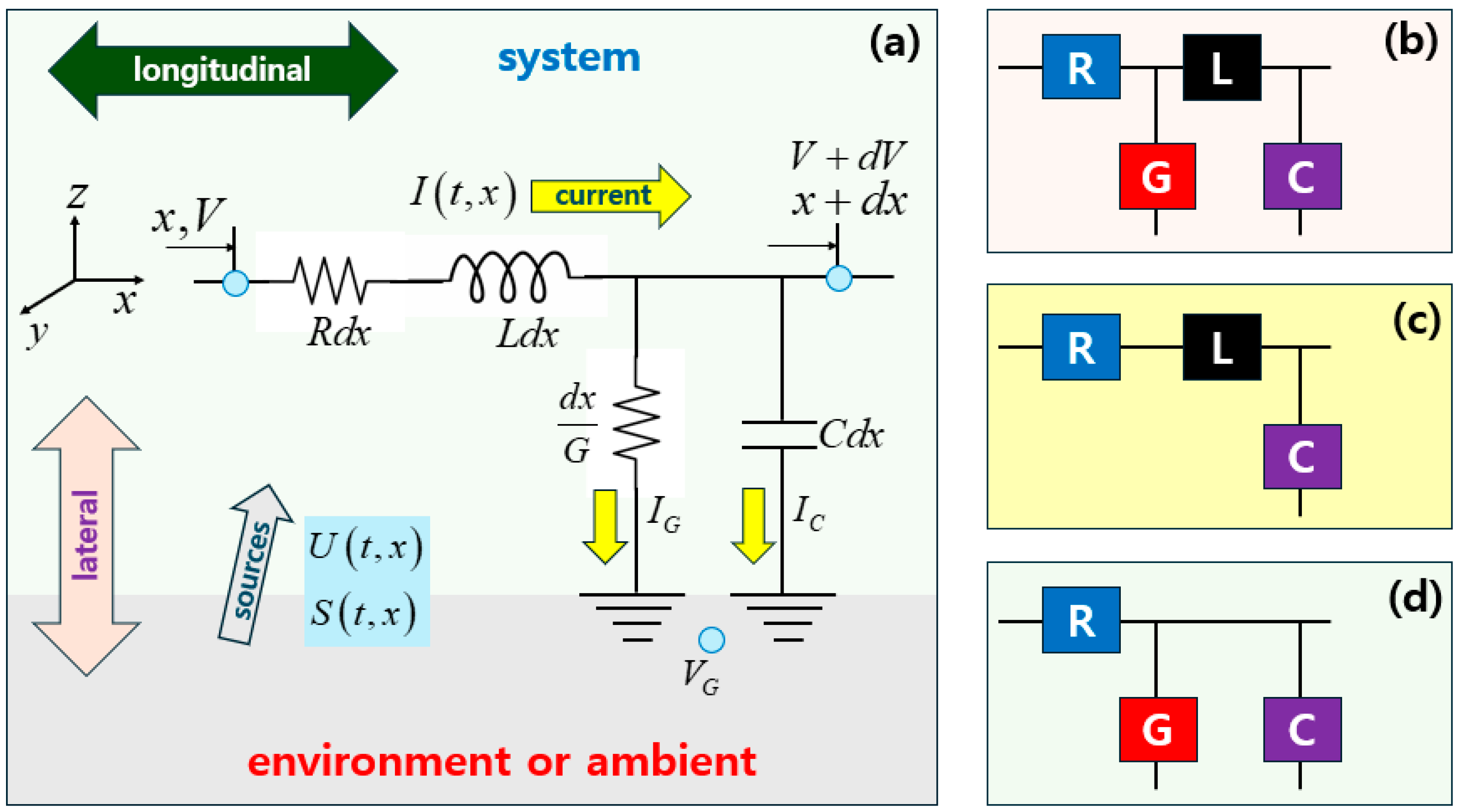
We are taking conventional steps to derive a telegraph equation with the help of the electric circuit displayed on Figure 3(a) [31].

Figure 3(a) exhibits an electric circuit employed to derive a telegraph (a.k.a. telegrapher) equation [26]. Let us explain how this electric circuit is constructed in terms of electric potential $V\left(t,x\right)$ and electric current $I\left(t,x\right)$ from a generic perspective. From a narrower perspective of biological neurons, we can deal with the transmembrane potential and ionic current, respectively [38,39]. We assume that $I\left(t,x\right)$ flow from left to right. Figure 3(a) shows an elemental domain over $\left(x,x+dx\right)$, where $x$ is the 1-D coordinate pointing to the right.

On Figure 3(a), there are four electric components: [i] a resistor of resistance $R$, [ii] an inductor of (self-) inductance $L$ [3], [iii] a capacitor of capacitance $C$, and [iv] an electric shunt conductor of the (leak) conductance $G$ (or the inverse of shunt resistance) [38,53]. They are also listed on Table 3 for summary.

Both $R$ and $L$ are longitudinally arranged, while $C$ and $G$ are laterally extended. An electric substrate can be considered as an environment, whereas the four-element circuit can be taken as a system. In case with usual electric chips, the conductance is considered as an unwanted leakage from a system to an environment. In fact, the encapsulation of electronic chips on a substrate serves two purposes: [i] a mechanical bonding, and [ii] an electronic insulation with selectively local electric conductions.

In this sense, our droplet dispensers need to properly establish encapsulation of electric chips onto a substrate as indicated by the trajectory of a dispenser on Figure 1(e). The electric conductance $G$ would be the resistance between those chips and a substrate.

Conductance plays also a key role in the analysis of neuronal signal transmission [25,41]. In terms of a biological neuron, an axon is directed along the longitudinal $x$-direction, whereas a system normally implies the inside of an axon. The conductance $G$ accounts for the ions undergoing Ohmic processes through the transmembrane channels that connect laterally the inside of an axon and the environment consisting of extracellular space (ECS) [18,48]. While an axon can be considered as a system, the ECS can be taken as an environment. Meanwhile, the notion of ‘environment’ began to appear in [38].

From another viewpoint, a biological substrate can serve as an environment [45]. The system-environment interaction (SEI) is enabled by the transmembrane ion channels that laterally straddle the membranes of an axon. The inside of an axon is normally modeled as a cylindrical tube, the radius of which is normally much greater than the typical radius of ion channels. In practice, the membranes separating the inside of an axon from the ECS can be considered as porous walls.

In this respect, waves propagating through cortical circuits in-vitro experiments are believed to arise from synaptic interactions and the intrinsic behavior of local neuronal circuitry. This fact gives another credence to the validity of SEIs considered in this study [19].

The system consists of the resistor-inductor pair with $\left\{R,L\right\}$, while the environment is everything other than the system as illustrated on Figure 3(a). Meanwhile, the capacitor-conductor pair with $\left\{C,G\right\}$ serves as bridges between the system and the environment, which is called in this study a ‘system-environment interaction (SEI)’. On Figure 3(a), both $\left\{R,L\right\}$ of the system elements are serially connected, whereas both $\left\{C,G\right\}$ of the SEI elements are arranged in parallel to each other.

Let us employ the symbol $\left[\circ \right]$ for a physical quantity ‘$\circ$’. Because resistance $R$ and conductance $G$ are of inverse dimensions of each other, their product $RG$ is dimensionless [17]. In Appendix A, we have proved that the following three products are of the following dimensions, where ‘$s$’ is ‘second’ as a temporal unit.

$$\left[RG\right]=1\equiv s^0,\begin{array}{c}\end{array}\left[RC\right]=\left[LG\right]=s,\begin{array}{c}\end{array}\left[LC\right]=s^2$$

(3)

It is worth stressing that the properties $\left\{R,L,G,C\right\}$ employed in this study are total values, which specify the off-the-shelf commodities available in stores selling electric components. In neuroscience, where the condition $L=0$ is mostly met, $RC$ is called a ‘membrane time constant’ according to the dimension in equation (3).

For comparison with the data in literature, we define the per-unit-length properties $\left\{\overline{R},\overline{L},\overline{G},\overline{C}\right\}$ as follows.

$$\overline{R}\equiv {\displaystyle \frac{R}{\ell }},\begin{array}{c}\end{array}\overline{L}\equiv {\displaystyle \frac{L}{\ell }},\begin{array}{c}\end{array}\overline{G}\equiv {\displaystyle \frac{G}{\ell }},\begin{array}{c}\end{array}\overline{C}\equiv {\displaystyle \frac{C}{\ell }}$$

(4)

Throughout this study, $\ell$ is a certain constant length [20,25]. See Appendix A for numerical data of $\left\{\overline{R},\overline{L},\overline{G},\overline{C}\right\}$.

Meanwhile, Figure 2(a) shows ${\ell }_{\ast }$ as the string length measured in the $x$-direction. In general, $\ell \ne {\ell }_{\ast }$. The length $\ell$ is missing in almost all open literature available these days [20,26]. We find notwithstanding that the introduction of $\ell$ is necessary for setting up dimensionally correct formulas [17].

The electric potential $V\left(t,x\right)$ undergoes reductions by $\left(R/\ell \right)Idx$ due to a system resistor and by $\left(L/\ell \right)\left(\partial I/\partial t\right)dx$ due to a system inductor. Meanwhile, the electric charge $dq$ stored on the capacitor is given by $dq=\left(C/\ell \right)Vdx$. Therefore, the electric current through the capacitor is given by $\left(C/\ell \right)\left(\partial V/\partial t\right)dx$ as the time-rate of charge. Likewise, for the (leak) conductance $G$ (or the inverse of shunt resistance [38,53], the electric current is given by $\left(G/\ell \right)Vdx$ [40]. It is crucial to notice that both leakage current components are directed from the system out to the environment. That is, we encounter two components $\left\{C\left(\partial V/\partial t\right),GV\right\}$ of leakage (or escape) currents.

Resultantly, both $dV\left(t,x\right)$ and $dI\left(t,x\right)$ are governed by the first-order differentials over the length increment $dx$ [25].

$$\left\{\begin{array}{l}dV=-{\displaystyle \frac{R}{\ell }}Idx-{\displaystyle \frac{L}{\ell }}{\displaystyle \frac{\partial I}{\partial t}}dx+{\displaystyle \frac{U}{\ell }}dx\\ dI=-{\displaystyle \frac{C}{\ell }}{\displaystyle \frac{\partial V}{\partial t}}dx-{\displaystyle \frac{G}{\ell }}Vdx+{\displaystyle \frac{S}{\ell }}dx\end{array}\right.\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\left\{\begin{array}{l}\ell {\displaystyle \frac{\partial V}{\partial x}}=-RI-L{\displaystyle \frac{\partial I}{\partial t}}+U\\ \ell {\displaystyle \frac{\partial I}{\partial x}}=-C{\displaystyle \frac{\partial V}{\partial t}}-GV+S\end{array}\right.$$

(5)

Here, we have added external distributed sources for potential $U\left(t,x\right)$ and for current $S\left(t,x\right)$ that are directed from the environment into the system [48,53]. For instance, $S\left(t,x\right)$ is imposed by a patch electrode in neuroscience [39].

Combining both relationships in equation (5) leads to the following pair of second-order PDEs [1,2,26].

$$\left\{\begin{array}{l}\left(RC+LG\right){\displaystyle \frac{\partial V}{\partial t}}+LC{\displaystyle \frac{{\partial }^{2}V}{\partial t^2}}={\ell }^2{\displaystyle \frac{{\partial }^{2}V}{\partial x^2}}-RGV-\ell {\displaystyle \frac{\partial U}{\partial x}}+\left(RS+L{\displaystyle \frac{\partial S}{\partial t}}\right)\\ \left(RC+LG\right){\displaystyle \frac{\partial I}{\partial t}}+LC{\displaystyle \frac{{\partial }^{2}I}{\partial t^2}}={\ell }^2{\displaystyle \frac{{\partial }^{2}I}{\partial x^2}}-RGI+\left(C{\displaystyle \frac{\partial U}{\partial t}}+GU\right)-\ell {\displaystyle \frac{\partial S}{\partial x}}\end{array}\right.$$

(6)

Here on the LHSs, the first terms $\left(RC+LG\right)\left(\partial \left\{V,I\right\}/\partial t\right)$ stand for dissipation, while the second terms $\left(LC\right)\left({\partial }^2\left\{V,I\right\}/\partial t^2\right)$ imply acceleration terms. On the right-hand sides (RHSs), the first terms ${\ell }^2\left({\partial }^2\left\{V,I\right\}/\partial x^2\right)$ signify diffusion, whereas the second terms $RG\left\{V,I\right\}$ refer to either leakage or forward reaction.

Such leakage is supposed to take place in the lateral direction as marked by the vertical double-headed arrow on Figure 1(c), Figure 2(a) and Figure 3(a). Since equation (6) contains diffusion only the longitudinal $x$-direction, any lateral diffusion is not accounted for unlike the case in [27]. It is natural that the terms on each relation in equation (6) are of the same dimension. Meanwhile, $R$ is called a ‘membrane resistance’ especially for the term $RS$ appearing in equation (6) [25].

When $V\left(t,x\right)$ in equation (6) is interpreted to be a flow velocity as on Figure 2(b–d), the potential source $U\left(t,x\right)$ can be taken to be proportional to the pressure $p$, while $\partial U/\partial x$ is proportional to a pressure gradient $\partial p/\partial x$. In this situation, the pressure $p\left(t,x=0\right)=p_{ext}$ at the entrance to the syringe of a droplet dispenser would be the excitation function $f_{ext}\left(t\right)$ depicted on Figure 1(c). In this study, the current source can be set to zero, i.e., $S\left(t,x\right)=0$.

Let us define a ‘full leaky RLGC circuit’, where a circuit with $RLGC\ne 0$ is differentiated from other circuits. A proper reference time ${\tau }_{RLGC}$ for a full leaky RLGC circuit can be established in two ways when comparing two pairs of terms in the generic telegraph equation (6) as follows.

$$\begin{array}{l}\left\{\begin{array}{l}\left\{\left(RC+LG\right){\displaystyle \frac{\partial V}{\partial t}},LC{\displaystyle \frac{{\partial }^{2}V}{\partial t^2}}\right\}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}{\tau }_{RLGC}^{12}\equiv {\displaystyle \frac{LC}{RC+LG}}\\ \begin{array}{c}\end{array}\left\{\left(RC+LG\right){\displaystyle \frac{\partial V}{\partial t}},RGV\right\}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}{\tau }_{RLGC}^{10}\equiv {\displaystyle \frac{RC+LG}{RG}}\end{array}\right.\\ \begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\left\{\begin{array}{l}\left[{\tau }_{RLGC}^{12}\right]\equiv {\displaystyle \frac{\left[LC\right]}{\left[RC+LG\right]}}={\displaystyle \frac{s^2}{s}}=s\\ \left[{\tau }_{RLGC}^{10}\right]\equiv {\displaystyle \frac{\left[RC+LG\right]}{\left[RG\right]}}={\displaystyle \frac{s}{1}}=s\end{array}\right.\end{array}$$

(7)

Here, superscript ‘$12$’ and ‘$10$’ signify the orders of the participating differentials, respectively.

Therefore, the strength of the leakage term $RGV$ can measured, in one way, by the above delay (or decay) time ${\tau }_{RLGC}^{10}$ in equation (7) [4,7,19,38,53,54]. The dimensionalities listed in equation (3) can be employed to verify that the delay times $\left\{{\tau }_{RLGC}^{12},{\tau }_{RLGC}^{10}\right\}$ carry indeed the dimension of time as shown in equation (7). Besides, ${\tau }_{RLGC}^{10}$ corresponds to ${\sigma }^{-1}$ in equation (2].

Decay and delay are biologically plausible [38,48,55]. The numerator $RC+LG$ of ${\tau }_{RLGC}^{10}$ consists of two terms, where each term is a product of a system parameter and a SEI parameter. Even the denominator $RG$ of ${\tau }_{RLGC}^{10}$ is another product of the two.

For the desired reference time ${\tau }_{RLGC}$, we can reconcile the two distinct reference times $\left\{{\tau }_{RLGC}^{12},{\tau }_{RLGC}^{10}\right\}$ in equation (7) by taking their geometric average in the following manner.

$${\tau }_{RLGC}\equiv \sqrt{{\tau }_{RLGC}^{12}{\tau }_{RLGC}^{10}}\equiv \sqrt{{\displaystyle \frac{LC}{RC+LG}}{\displaystyle \frac{RC+LG}{RG}}}=\sqrt{{\displaystyle \frac{LC}{RG}}}$$

(8)

This process of logically deriving a reference time ${\tau }_{RLGC}$ has not been explicitly attempted elsewhere as far as we know. Since $\left[RG\right]=1$ as a dimension, $\left[{\tau }_{RLGC}\right]\equiv \left[\sqrt{LC}\right]=s$ in agreement with the last formula in equation (3).

When source terms vanish, namely, $S=U=0$, equation (6) is reduced to the following source-free ‘generic telegraph equations‘ [20,23].

$$\left\{\begin{array}{l}\left(RC+LG\right){\displaystyle \frac{\partial V}{\partial t}}+LC{\displaystyle \frac{{\partial }^{2}V}{\partial t^2}}={\ell }^2{\displaystyle \frac{{\partial }^{2}V}{\partial x^2}}-RGV\\ \left(RC+LG\right){\displaystyle \frac{\partial I}{\partial t}}+LC{\displaystyle \frac{{\partial }^{2}I}{\partial t^2}}={\ell }^2{\displaystyle \frac{{\partial }^{2}I}{\partial x^2}}-RGI\end{array}\right.$$

(9)

Here, the two source-free equations are decoupled. Therefore, we will henceforth treat the first relation for the electric potential $V$ for convenience. The arrangement corresponding to equation (9) is schematically illustrated on Figure 3(b).

Equation (9) can be considered as either [i] diffusion equations contaminated by propagating waves [19], or [ii] wave equations contaminated by attenuation or damping [22,28]. Equation (9] is alternatively called a ‘propagative diffusion equation’ from the first viewpoint, whereas it is alternatively called a ‘damped wave equation’ from the second perspective [5].

Equation (9) can be alternatively cast into the following more familiar form when divided by $LC$ [26,27].

$$\begin{array}{l}LC\ne 0:\begin{array}{c}\end{array}\left({\displaystyle \frac{R}{L}}+{\displaystyle \frac{G}{C}}\right){\displaystyle \frac{\partial V}{\partial t}}+{\displaystyle \frac{{\partial }^{2}V}{\partial t^2}}={\displaystyle \frac{{\ell }^2}{LC}}{\displaystyle \frac{{\partial }^{2}V}{\partial x^2}}-{\displaystyle \frac{R}{L}}{\displaystyle \frac{G}{C}}V\\ \alpha \equiv {\displaystyle \frac{R}{L}},\begin{array}{c}\end{array}\beta \equiv {\displaystyle \frac{G}{C}},\begin{array}{c}\end{array}a\equiv {\displaystyle \frac{\ell }{\sqrt{LC}}}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\left(\alpha +\beta \right){\displaystyle \frac{\partial V}{\partial t}}+{\displaystyle \frac{{\partial }^{2}V}{\partial t^2}}=a^2{\displaystyle \frac{{\partial }^{2}V}{\partial x^2}}-\alpha \beta V\end{array}$$

(10)

Here, the conventional pair $\left\{\alpha ,\beta \right\}$ together with the signal velocity $a$ are defined. This equation is essentially identical to the simplified telegraph equation (2) valid for string vibration, except for the leakage term $-\alpha \beta V$ on the RHS of equation (10).

As summarized on Table 3, the ratios $R/L$ is a property of a system, whereas $G/C$ is a property of an SEI. Although these two ratios $\left\{R/L,G/C\right\}$ have already been identified in [26], their associations with a system and an SEI have never been properly entertained. Besides, both $L$ and $C$ belong to reactance.

Therefore, the product $\alpha \beta$ on the RHS of the last term $-\alpha \beta V$ in equation (10) is another manifestation of relative attenuation. In fact, $\alpha \beta V$ corresponds to losses due to displacement-dependent lateral force for string vibration, but not due to externally applied lateral load for string vibration [37].

To cope with the pair $\left\{R/L,G/C\right\}$ more systematically, let us examine their ratio $q$and the subsequent linear combination $\eta$ as follows.

$$RLGC\ne 0:\begin{array}{c}\end{array}q\equiv \sqrt{{\displaystyle \frac{G/C}{R/L}}}=\sqrt{{\displaystyle \frac{LG}{RC}}},\begin{array}{c}\end{array}\eta \equiv {\displaystyle \frac{1}{2}}\left(q+{\displaystyle \frac{1}{q}}\right)$$

(11)

Let us find the range of $\eta$ defined in equation (11) in the following manner.

$$\begin{array}{l}q\equiv \sqrt{{\displaystyle \frac{LG}{RC}}}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}0<q<\infty ;\begin{array}{c}\end{array}{\displaystyle \frac{\partial \eta }{\partial q}}={\displaystyle \frac{1}{2}}\left(1-{\displaystyle \frac{1}{q^2}}\right)=0\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}{q}_{\min }=1\\ {\eta }_{\min }={\displaystyle \frac{1}{2}}\left(q_{\min }+{\displaystyle \frac{1}{q_{\min }}}\right)={\displaystyle \frac{1}{2}}\left(1+{\displaystyle \frac{1}{1}}\right)=1\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\eta \ge 1\end{array}$$

(12)

Resultantly, $\eta \ge 1$ for $0<q<\infty$. Typical values of $\left\{q,\eta \right\}$ are evaluated for exemplary data in Appendix A [20].

By means of the parameters defined in equations (11) along with the properties in equation (12), we thus find that the condition $\eta =1$ is equivalent to the following alternatives.

$$\begin{array}{l}RLGC\ne 0:\begin{array}{c}\end{array}\eta =1\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}q\equiv \sqrt{{\displaystyle \frac{LG}{RC}}}=1\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}{\displaystyle \frac{LG}{RC}}=1\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ {\displaystyle \frac{R}{L}}={\displaystyle \frac{G}{C}},\begin{array}{c}\end{array}{\displaystyle \frac{L}{C}}={\displaystyle \frac{R}{G}}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ {\alpha }^2-4\beta ={\left({\displaystyle \frac{R}{L}}+{\displaystyle \frac{G}{C}}\right)}^2-4{\displaystyle \frac{R}{L}}{\displaystyle \frac{G}{C}}={\left({\displaystyle \frac{R}{L}}-{\displaystyle \frac{G}{C}}\right)}^2=0\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}{\alpha }^2=4{\beta }^2\end{array}$$

(13)

Here, $\left\{\alpha ,\beta \right\}$ have been introduced in equation (10). Therefore, $\eta =1$ is equivalent to the equality $\left(L/C\right)=\left(R/G\right)$, which is called the condition for ‘distortion-less propagation (but still not attenuation-less)‘ by [5].

Consequently, the condition $\eta =1$ of distortion-less propagation does not hold true in the special data of [56], which is experimentally measured for polyethylene insulated cable. A way of reaching the condition $\left(R/L\right)=\left(G/C\right)$ is to increase $L$, which can be realized from the perspectives provided in Appendix B.

In this connection, let us take the following ratio between the two reference times ${\tau }_{RLGC}^{10}$ and ${\tau }_{RLGC}$ presented respectively in equations (7) and (8).

$$\begin{array}{l}{\tau }_{RLGC}^{10}\equiv {\displaystyle \frac{RC+LG}{RG}},\begin{array}{c}\end{array}{\tau }_{RLGC}\equiv \sqrt{{\displaystyle \frac{LC}{RG}}}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ {\displaystyle \frac{{\tau }_{RLGC}^{10}}{{\tau }_{RLGC}}}\equiv {\displaystyle \frac{RC+LG}{RG}}\sqrt{{\displaystyle \frac{RG}{LC}}}={\displaystyle \frac{RC+LG}{\sqrt{RLGC}}}=\sqrt{{\displaystyle \frac{LG}{RC}}}+\sqrt{{\displaystyle \frac{RC}{LG}}}=2\eta \end{array}$$

(14)

Here, $\eta$ is defined in equation (11).

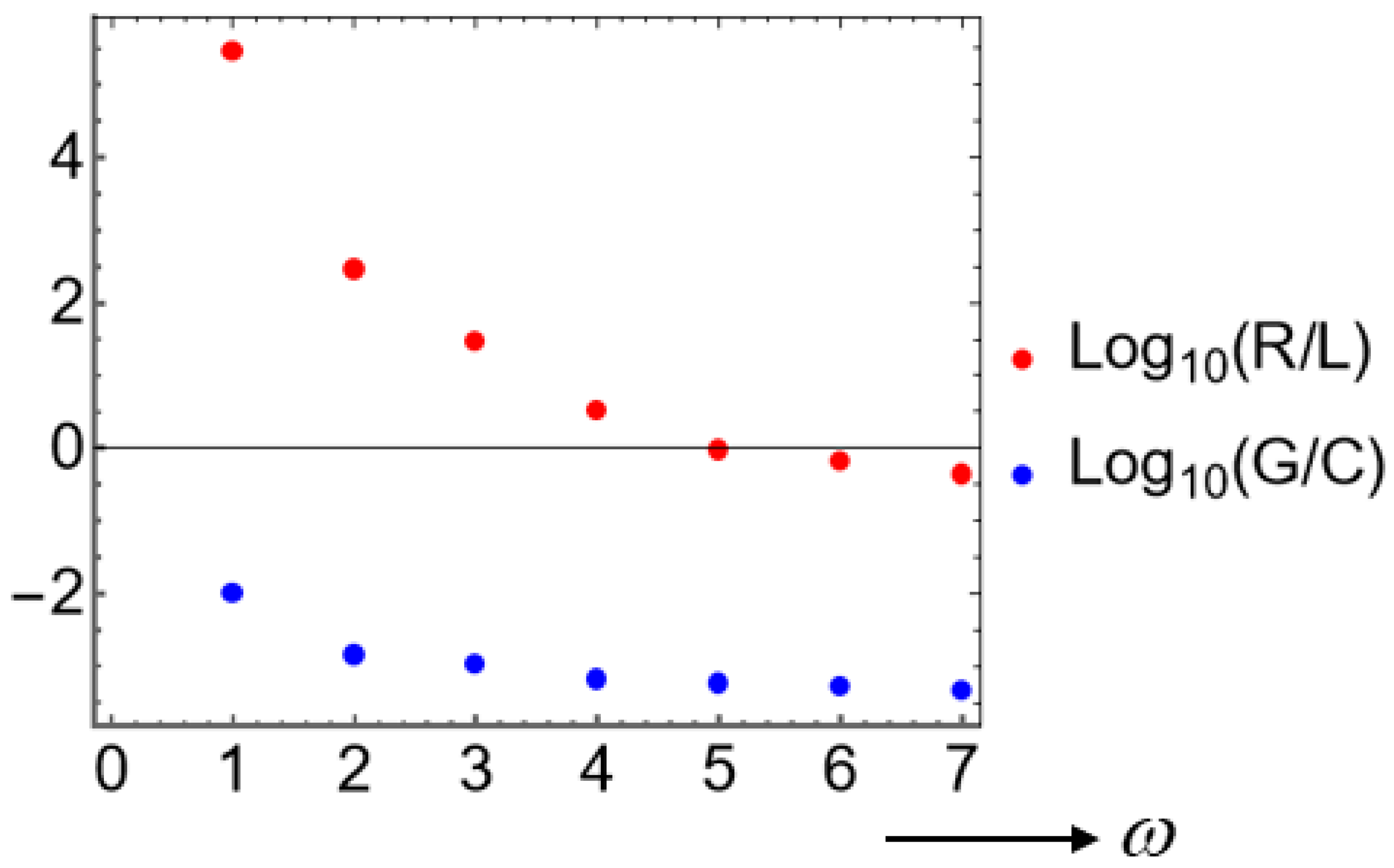
In this respect, let us compare the magnitude of $\left\{R/L,G/C\right\}$. To this end, we have drawn Figure 4 based on the data of [56], which are per-unit-length properties $\left\{\overline{R},\overline{L},\overline{C},\overline{G}\right\}$ introduced in equations (4) and (5). Hence, $R/L=\overline{R}/\overline{L}$ and $G/C=\overline{G}/\overline{C}$. We find here that $0<\left(G/C\right)<<\left(R/L\right)$ approximately by two orders of magnitude.

Comparing equations (2) and (10), we ascertain the following correspondences.

$$\left({\displaystyle \frac{R}{L}}+{\displaystyle \frac{G}{C}}\right)\begin{array}{c}\end{array}\leftrightarrow \begin{array}{c}\end{array}\sigma ,\begin{array}{cc}& \end{array}{a}^2\equiv {\displaystyle \frac{{\ell }^2}{LC}}\begin{array}{c}\end{array}\leftrightarrow \begin{array}{c}\end{array}{\displaystyle \frac{T}{\mu }}\equiv a_{string}^2$$

(15)

In the spirit of introducing $\ell$ in equations (4) and (5), the signal velocity $a\equiv \ell /\sqrt{LC}$ is employed throughout this study, where $\left[a\right]\equiv \left[\ell \right]/\left[\sqrt{LC}\right]=m/s$ in view of $\left[\sqrt{LC}\right]=s$ in equation (3). In comparison, the formula $a\equiv 1/\sqrt{\overline{L}\overline{C}}$ widely employed in most of open literature employs the per-unit-length properties $\overline{L}\equiv L/\ell$ and $\overline{C}\equiv C/\ell$ in terms of our notation [26]. See Appendix A, which employs the per-unit-length properties of [20] for exemplary numerical evaluations.

It is crucial to notice in equation (15) that the tension $T$ is directed along the length of a string, while $\mu$ is the mass per unit longitudinal length [12]. Let us interpret the correspondence ${\ell }^2/\left(LC\right)\leftrightarrow T/\mu$ appearing in equation (15). The mass (inertia) per unit length carries the correspondence $C/{\ell }^2\leftrightarrow \mu$, where the capacitance $C$ per unit area ${\ell }^2$ is understood as sort of electric inertance. The remaining correspondence $1/L\leftrightarrow T$ signifies the dynamical nature of both inductance $L$ and string tension $T$.

Table 4 lists several relations reducible from equation (6).

As another easiest reduced case, consider the circuit with both internal-loss-free ($R=0$) and leak-free ($G=0$) properties. This wholly loss-free case is expected to cause no attenuation. In this case, the source-free generic telegraph equation (9) is further reduced to the following wave equation [2,12,55].

$$\left\{\begin{array}{l}R=G=0\\ LC\ne 0\end{array}\right.:\begin{array}{c}\end{array}LC{\displaystyle \frac{{\partial }^{2}V}{\partial t^2}}={\ell }^2{\displaystyle \frac{{\partial }^{2}V}{\partial x^2}}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}{\displaystyle \frac{\ell }{\sqrt{LC}}}\equiv a={\displaystyle \frac{\ell }{{\tau }_{LC}}},\begin{array}{c}\end{array}{\tau }_{LC}\equiv \sqrt{LC}$$

(16)

We call this PDE the ‘canonical wave equation’ [1,2]. Additionally, it is super-important to keep a non-zero capacitance $C\ne 0$ and non-zero inductance $L\ne 0$ in this case. Here, we have introduced a reference ‘LC time’${\tau }_{LC}\equiv \sqrt{LC}$, where the subscript ‘$LC$’ implies that $LC\ne 0$. With reference to equations (15) and (16) for $a\equiv \ell /\sqrt{LC}$, $\left[{\tau }_{LC}\right]=\left[\sqrt{LC}\right]=s$ according to equation (3).

Consider the following equation.

$$LC{\displaystyle \frac{{\partial }^{2}V}{\partial t^2}}=-RGV\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}{\displaystyle \frac{{\partial }^{2}V}{\partial t^2}}=-{\displaystyle \frac{RG}{LC}}V$$

(17)

According to the four-element electric circuit depicted on Figure 3(a), equation (17) is at most hypothetical, since $RLGC\ne 0$ assumed for equation (17) requires that $RC+LG=0$ in equation (6). However, $RC+LG=0$ is impossible to achieve since $R,L,G,C>0$.

Although this hypothetical equation (17) is not reducible from equation (9) by taking any proper combinations of the parameters $\left\{R,L,G,C\right\}$, it shed light on further meaning of $\left(RG\right)/\left(LC\right)=\left(R/L\right)\left(G/C\right)\equiv \alpha \beta$. As listed on Table 3, $\left(R/L\right)\left(G/C\right)$ is the product of the two relative losses that represent respectively a system and a SEI.

Equation (17) is a simple harmonic equation described by, say, Hook’s law. Here, $LC$ serves as an inertance (viz., effective mass) [37], while $RG$ serves as an effective spring constant [12]. In this perspective, $-RGV$ acts as a restoring force. Although the role of capacitance $C$ as an inertance is well-known, the role of $L$ as another inertance is less well-known.

The remaining special reduced case is the leak-free RLC circuit with $G=0$ (but not with $RG=0$), whereby the source-free generic telegraph equation (9) is reduced to the following [4,13,22,49].

$$\left\{\begin{array}{l}G=0\\ RLC\ne 0\end{array}\right.:\begin{array}{c}\end{array}RC{\displaystyle \frac{\partial V}{\partial t}}+LC{\displaystyle \frac{{\partial }^{2}V}{\partial t^2}}={\ell }^2{\displaystyle \frac{{\partial }^{2}V}{\partial x^2}}$$

(18)

Let us call this equation a ‘leak-free diffusion-wave equation’, since it exhibits both diffusion and wave phenomena. Notice that there is still a loss due to the non-zero system loss, namely, $R\ne 0$. The absence of a leakage term $-RGV$ in equation (18) corresponds to missing forward-reaction, if equation (18) is interpreted as a reaction-diffusion equation [38]. The arrangement corresponding to equation (18) is schematically illustrated on Figure 3(c).

Meanwhile, according to Figure 4, $\left(G/C\right)<<\left(R/L\right)$ for a certain material. Therefore, the leak-free RLC circuit with $G=0$ is indeed an interesting limit case, identification of which is our own contribution.

Equation (18) has been derived by the analysis of two-dimensional (2-D) geometry in [3]. In addition to the longitudinal refence length $\ell \equiv {\ell }_x$, let ${\ell }_z$ be the lateral reference length. It is assumed in [3] that $L\propto \left({\ell }_x/{\ell }_z\right)$ and $C\propto {\ell }_x{\ell }_z$ under the approximation ${\ell }_x>>{\ell }_z$. Resultantly, $LC\propto {\ell }_x^2\equiv {\ell }^2$, thereby getting in conformity with the expected dimension of ${\ell }^2\left({\partial }^{2}V/\partial x^2\right)$ on the RHS in equation (18).

In this connection, both equations (9) and (18) are 1-D hyperbolic-parabolic second-order equations [1,2,26], where wave propagations are implied by the adjective ‘hyperbolic’ and diffusion is implied by the adjective ‘parabolic’. The wave nature of the telegraph-like equations is what we are going to expand on in this study.

Let us reduce equation (6) into the following rotation-free (induction-free) leaky circuit with $L=0$ [17].

$$L=0:\begin{array}{c}\end{array}\left\{\begin{array}{l}RC{\displaystyle \frac{\partial V}{\partial t}}={\ell }^2{\displaystyle \frac{{\partial }^{2}V}{\partial x^2}}-RGV+RS-\ell {\displaystyle \frac{\partial U}{\partial x}}\\ RC{\displaystyle \frac{\partial I}{\partial t}}={\ell }^2{\displaystyle \frac{{\partial }^{2}I}{\partial x^2}}-RGI+\left(C{\displaystyle \frac{\partial U}{\partial t}}+GU\right)-\ell {\displaystyle \frac{\partial S}{\partial x}}\end{array}\right.$$

(19)

Hence, a wave-propagation feature is absent since $L=0$, whence the signal velocity $a\equiv \ell /\sqrt{LC}$ in equations (15) and (16) gets undefined. The PDEs in equation (19) are reaction-diffusion (a.k.a. diffusion-leak) equations, which are thus alternatively known as a ‘cable equation’ [25]. Notice in equation (19) that the second-order time derivatives ${\partial }^{2}V/\partial t^2$ and ${\partial }^{2}I/\partial t^2$ are absent. The arrangement corresponding to equation (19) is schematically illustrated on Figure 3(d).

The fact that the rotation-free leaky circuit with $L=0$ is apparently free of propagating waves as in equation (19) is suggestive of the fact that a non-zero inductance ($L\ne 0$) is instrumental to supporting propagating waves [18,46]. As another example, dual propagation velocities (of different magnitudes but of the same sign) could prevail without attenuation in case with soliton flows involving surface tension [24].

In neuroscience, magnetic effects are normally neglected so that $L=0$ [48], albeit they are non-negligible in rare situations. Consider in equation (19) a special case that $S=0$ but $U\ne 0$ for neuronal signal transmission. Furthermore, let us assume that $U\left(t,x\right)\equiv U_0\left(t\right)\delta \left(x\right)$ with $\delta \left(x\right)$ being a (spatially localized) delta function [19]. When the temporal portion is modeled by $U_0\left(t\right)\equiv f_{ext}\left(t\right)$, where $f_{ext}\left(t\right)$ is what is shown on Figure 1(d). The resulting solution $V\left(t,x\right)$ sought over a semi-infinite 1-D domain $0\le x<\infty$ looks almost like what is presented in [48]. Notwithstanding, these solutions in [48] do not account for the termination stage involving drop ejection process [19].

A multi-variable extension of equation (19) with proper forms of excitations $\left\{U,S\right\}$ is well-known as a ‘leaky integrate-and-fire (LIF)’ model in neuroscience, where terms $\left\{-RGV,-RGI\right\}$ are leakage terms [19,25,36,38,39,41,42,53,54,57]. In case with the LIF model, the current source $S$ consists of either the sum or the integral from many other nearby neurons as depicted on Figure 1(f) showing convergent trajectories [19,25]. Here lies the connection between the subjects of droplet dispersers handled in our study and multi-layered neural network.

A heavily investigated form of equation (19) is its source-free diffusion-leak (reaction-diffusion) equation with $L=U=S=0$ as given below for an electric potential.

$$\begin{array}{l}L=U=S=0:\begin{array}{c}\end{array}RC{\displaystyle \frac{\partial V}{\partial t}}={\ell }^2{\displaystyle \frac{{\partial }^{2}V}{\partial x^2}}-RGV\\ \begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\left\{\begin{array}{l}{\tau }_{RC}\equiv RC\\ \left[{\tau }_{RC}\right]\equiv \left[RC\right]=s\end{array}\right.\end{array}$$

(20)

This special form of telegraph equation has also been extensively investigated as equation (19). This is also known as a ‘leaky heat equation’ [5], for which a heat-transfer aspect of the product $RG$ is described in Appendix C [58].

We can define from equation (20) the ‘RC time’ ${\tau }_{RC}\equiv RC$ by comparing the two terms $RC\left(\partial V/\partial t\right)$ and $RGV$. The dimension $\left[{\tau }_{RC}\right]\equiv \left[RC\right]=s$ from equation (3).

4. Derivation of Three-Dimensional (3-D) Telegraph Equation

As the last issue of the PDE, the telegraph equation (10) can be extended into 3-D space as follows in terms of conventional notation.

$$\begin{array}{l}LC\ne 0:\begin{array}{c}\end{array}\left({\displaystyle \frac{R}{L}}+{\displaystyle \frac{G}{C}}\right){\displaystyle \frac{\partial V}{\partial t}}+{\displaystyle \frac{{\partial }^{2}V}{\partial t^2}}={\displaystyle \frac{{\ell }^2}{LC}}\left({\displaystyle \frac{{\partial }^{2}V}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}V}{\partial y^2}}+{\displaystyle \frac{{\partial }^{2}V}{\partial z^2}}\right)-{\displaystyle \frac{R}{L}}{\displaystyle \frac{G}{C}}V\\ A\equiv {\displaystyle \frac{R}{L}}+{\displaystyle \frac{G}{C}},\begin{array}{c}\end{array}B\equiv {\displaystyle \frac{R}{L}}{\displaystyle \frac{G}{C}}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}A{\displaystyle \frac{\partial V}{\partial t}}+{\displaystyle \frac{{\partial }^{2}V}{\partial t^2}}=a^2\left({\displaystyle \frac{{\partial }^{2}V}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}V}{\partial y^2}}+{\displaystyle \frac{{\partial }^{2}V}{\partial z^2}}\right)-BV\end{array}$$

(21)

Here, $a^2\equiv {\ell }^2/\left(LC\right)$ introduced in equations (15) and (16). In addition, the $x$-coordinate is along the longitudinal direction as marked by the horizontal double-headed arrow on Figure 1(c), Figure 2(a) and Figure 3(a). Therefore, the $yz$-plane is a lateral plane, being perpendicular to the longitudinal $x$-axis. Besides, any radial direction on the $yz$-plane is a lateral direction. For equation (21) and the following relevant treatment, we closely follow [27].

Let us introduce below several parameters.

$${\xi }_{\pm }\equiv x\mp at,\begin{array}{c}\end{array}\left\{\begin{array}{l}\gamma =const\\ \lambda \equiv {\displaystyle \frac{A+4\gamma }{a}}\end{array}\right.,\begin{array}{c}\end{array}\left\{\begin{array}{l}{p}_{+}={\displaystyle \frac{B+A\gamma }{a^2\lambda }}={\displaystyle \frac{1}{a}}{\displaystyle \frac{B+A\gamma }{A+4\gamma }}\\ p_{-}={\displaystyle \frac{\gamma }{a}}\end{array}\right.$$

(22)

Here, ${\xi }_{\pm }\equiv x\mp at$ form a complementary pair of characteristic curves, which stands for propagating waves [2]. Besides, $\gamma \in ℝ$ is a real constant.

The solution to equation (21) assumes the following Ansatz of product form [57].

$$\left\{\begin{array}{l}V\left(t,x,y,z\right)\equiv f\left({\xi }_{+},y,z\right)g\left({\xi }_{+},{\xi }_{-}\right)\\ g\left({\xi }_{+},{\xi }_{-}\right)\equiv \exp \left(p_{+}{\xi }_{+}+p_{-}{\xi }_{-}\right)\end{array}\right.$$

(23)

We are looking for a solution in the following special form.

$$\lambda {\displaystyle \frac{\partial f}{\partial {\xi }_{+}}}=-\left({\displaystyle \frac{{\partial }^{2}f}{\partial y^2}}+{\displaystyle \frac{{\partial }^{2}f}{\partial z^2}}\right)+0\times f$$

(24)

This special form is satisfied for the parameters defined in equation (22), which help eliminate the term proportional $f$ in equation (24) as intentionally indicated by $0\times f$. This missing $f$-term is indicative of leakage, the elimination of which corresponds to introducing an integrating factor for a differential equation as in [48].

Equation (24) is now handled with a method of separation of variables, thereby resulting in the following equation [2,52].

$$f\left({\xi }_{+},y,z\right)=f_y\left({\xi }_{+},y\right)f_z\left({\xi }_{+},z\right)\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\lambda {\displaystyle \frac{\partial f_j}{\partial {\xi }_{+}}}=-{\displaystyle \frac{{\partial }^2{f}_j}{\partial y^2}},\begin{array}{c}\end{array}j=y,z$$

(25)

This special form is satisfied for the parameters defined in equation (22).

Equation (25) can be solved to provide a solution, whence the solution to $V\left(t,x,y,z\right)$ can be further constructed according to equation (23).

$$\begin{array}{l}V\left(t,x,y,z\right)=Ai\left[{\left(\frac{1}{2}{a}_y{\lambda }^2\right)}^{1/3}\left(y+\frac{1}{2}{a}_y{\xi }_{+}^2\right)\right]\\ \begin{array}{cc}& \end{array}\times Ai\left[{\left(\frac{1}{2}{a}_z{\lambda }^2\right)}^{1/3}\left(z+\frac{1}{2}{a}_z{\xi }_{+}^2\right)\right]\\ \begin{array}{cc}& \end{array}\times \exp \left\{-\frac{1}{2}\lambda {\xi }_{+}\left[a_{y}y+a_{z}z+\frac{1}{3}\left(a_y^2+a_z^2\right){\xi }_{+}^2\right]+{\displaystyle \frac{B+A\gamma }{a^2\lambda }}{\xi }_{+}+{\displaystyle \frac{\gamma }{a}}{\xi }_{-}\right\}\end{array}$$

(26)

Here, $\left\{a_y,a_z\right\}\in ℝ$ is yet another pair of constants.

Meanwhile, $Ai\left(\circ \right)$ is the Airy function. Since Airy function is either sinusoidally attenuating or uniformly attenuating with increasing magnitude of its argument, the solution $V\left(t,x,y,z\right)$ in equation (26) properly account for the spatially evanescent waves in the lateral direction as $\left|y\right|,\left|z\right|\to \infty$. In this connection, notice in equation (24) that the sum $\left({\partial }^{2}f/\partial y^2\right)+\left({\partial }^{2}f/\partial z^2\right)$ represents the diffusion on the lateral $yz$-plane.

Of course, there are both forward waves implied by ${\xi }_{+}$ and backward waves implied by ${\xi }_{-}$ in the solution presented in equation (26) [19,46]. Since equation (21) is symmetric in $x$, we can easily come up with another equation involving $\partial f/\partial {\xi }_{-}$ instead of $\partial f/\partial {\xi }_{+}$ in equation (24) by replacing $x$ with $-x$ in equation (21).

Both equations (20] and (25) are diffusion equations, where the longitudinal characteristic variable ${\xi }_{+}$ in equation (25) is time-like. As regards equation (9), we have already pointed out that telegraph equations harbor both features of diffusion and wave propagation.

A Cauchy problem for the diffusion-leak equation (19) has been solved with an appropriate set of side conditions early in 1946 by [48]. Although that diffusion-leak equation does not explicitly contain wave-propagation terms, the resulting solution in [48] contains implicit wave-propagation factors. Notwithstanding, the associated characteristic curves in [44] are not of the form ${\xi }_{\pm }\equiv x\mp at$ but of nonlinear form in $\left\{t,x\right\}$.

Notice furthermore that $f\left({\xi }_{+},y,z\right)$ in equation (23) serves as sort of envelope function, which takes a slightly different form in [48] as well. In addition, it is worth recognizing that ${\xi }_{\pm }\equiv x\mp at$ in equation (26) shows itself up not only in linear form but also in squared form.

Meanwhile, diffusion in equation (26) is manifested mostly by the Airy functions. In comparison, wave propagation is manifested by the two characteristic curves of ${\xi }_{\pm }$, that appears not only in the Airy functions but also in the exponential function.

For a 1-D problem, equation (24) becomes $\lambda \left(\partial f/\partial {\xi }_{+}\right)=0$, thus giving rise to a trivial solution $f\left({\xi }_{+},y,z\right)=const$ for equation (23). For this 1-D problem, the solution in equation (26) is reduced to the following.

$$V\left(t,x\right)\propto \exp \left(p_{+}{\xi }_{+}+p_{+}{\xi }_{-}\right)\equiv \exp \left({\displaystyle \frac{B+A\gamma }{a^2\lambda }}{\xi }_{+}+{\displaystyle \frac{\gamma }{a}}{\xi }_{-}\right)$$

(27)

In comparison, the simplest wave equation $\left(LC\right)\left({\partial }^{2}V/\partial t^2\right)={\ell }^2\left({\partial }^{2}V/\partial x^2\right)$ in equation (16) admits a generic solution in the form of D'Alembert formula $V=V_{+}{g}_{+}\left(x-at\right)+V_{-}{g}_{-}\left(x+at\right)$ [1,2]. Here, $g_{\pm }\left(\circ \right)$ are certain differentiable functions, while $V_{\pm }$ are certain constants depending on appropriate side conditions [4]. Consequently, the amplitude ratio between the forward waves with $V_{+}{g}_{+}\left(x-at\right)$ and the backward waves with $V_{-}{g}_{-}\left(x+at\right)$ will depend on the appropriate side conditions at hand [19].

Other 3-D effects of inductors and capacitors are summarized in Appendix B [18,49,59,60]. In addition, Appendix B offers basics of memristors, since excitation-response relations such as shown on Figure 1 and Figure 2 are partially explainable [40,43,50,61,62].

5. Derivation and Analysis of Dispersion Relations

We mean by resonance the source-free conditions $U=S=0$, for which the generic telegraph equation (9) is employed. Moreover, the wave amplitude on resonance is undetermined [46,57]. In this situation, in equation (9) are decoupled so that let us consider henceforth only $V$.

Consider the Ansatz $V\left(t,x\right)\propto \exp \left[i\left(\omega t-\kappa x\right)\right]$ for propagating waves over the infinite domain $-\infty <x<\infty$. Here, $i$ denotes an imaginary unit such that $i^2=-1$. In addition, $\omega$ and $\kappa$ are temporal frequency and spatial wave number, respectively [46,63]. As an aside, $\omega t-\kappa x$ is called an ‘eikonal’ [63]. For example, small lateral displacements of a hollow tube in dynamic states as mentioned in section 2 guarantee the applicability of the above Ansatz $V\propto \exp \left[i\left(\omega t-\kappa x\right)\right]$ [8,10].

There are two kinds of approaches to handling the propagation factor $\exp \left[i\left(\omega t-\kappa x\right)\right]$ [12]: [i] the spatially attenuated and temporally periodic (SATP) approach [10,20,22,46], and [ii] the temporally attenuated and spatially per$\left\{V,I\right\}$iodic (TASP) approach [11,20,63]. In brief,

$$\left\{\begin{array}{l}SATP:\begin{array}{c}\end{array}\left\{\begin{array}{l}\omega \in ℝ\\ \kappa \in ℂ\end{array}\right.,\begin{array}{c}\end{array}\kappa \equiv {\kappa }_r+i{\kappa }_i\equiv \mathrm{Re}\left(\kappa \right)+i\mathrm{Im}\left(\kappa \right)\\ TASP:\begin{array}{c}\end{array}\left\{\begin{array}{l}\omega \in ℂ\\ \kappa \in ℝ\end{array}\right.,\begin{array}{c}\end{array}\omega \equiv {\omega }_r+i{\omega }_i\equiv \mathrm{Re}\left(\omega \right)+i\mathrm{Im}\left(\omega \right)\end{array}\right.$$

(28)

Here, $ℝ$ and $ℂ$ denote the real and complex spaces, respectively. Besides, the subscripts ‘$r$’ and ‘$i$’ denote the real and imaginary parts, respectively.

From our detailed study, the overall characteristics of the SATP approach turn out to be quite different from those of the TASP approach. The relevant algebra for the SATP approach is largely more complicated than that for the TASP approach [22].

With the TASP approach, we let $\omega$ be complex while keeping $\kappa$ real, viz., $\omega \in ℂ$ and $\kappa \in ℝ$. With this TASP approach, problems valid over a finite 1-D domain such as on Figure 2 are easier to handle. One reason is that BCs at both ends are easier to specify [10,13] so that relevant boundary-value problems (BVPs) are easier to handle with the TASP approach.

With the TASP approach fully adopted, we have found many interesting phenomena. Among others, we rediscovered the well-known dual (double) attenuation rates for non-propagating stationary waves in addition to propagating waves [10,24,46,57,60]. Notwithstanding, finite-domain 1-D problems will be examined in a forthcoming publication, since the analysis is rather tricky. It is because several key findings such as cutoffs and crossovers would depend on the types of applicable side conditions.

In comparison, one of the advantages of the SATP approach in comparison to the TASP approach is the fact that temporally imposed functions such as displayed on Figure 1(d) can be easily resolved by way of, say, Fourier transform in $\omega \in ℝ$ with respect to $t$.

Let us focus more on the SATP approach, for which we let $\kappa$ be complex while keeping $\omega$ real [10,49].

$$\begin{array}{l}SATP:\begin{array}{c}\end{array}\left\{\begin{array}{l}\omega \in ℝ\\ \kappa \in ℂ\end{array}\right.,\begin{array}{c}\end{array}\left\{\begin{array}{l}\kappa \equiv {\kappa }_r+i{\kappa }_i\equiv \mathrm{Re}\left(\kappa \right)+i\mathrm{Im}\left(\kappa \right)\\ t,\omega \ge 0\end{array}\right.\\ \begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\exp \left[i\left(\omega t-\kappa x\right)\right]=\exp \left[i\left(\omega t-{\kappa }_{r}x\right)\right]\exp \left({\kappa }_{i}x\right)\end{array}$$

(29)

Here, the inequality $t\ge 0$ leads to the restriction that $\omega >0$. Furthermore, notice that ${\kappa }_r$ is the longitudinal wave number (a.k.a. propagation constant) directed along the longitudinal direction as marked by the horizontal double-headed arrow on Figure 1(c), Figure 2(a) and Figure 3(a).

With $\exp \left[i\left(\omega t-\kappa x\right)\right]$, we are looking for the existence of traveling waves [57]. Meanwhile, let us examine the propagation factor $\exp \left[i\left(\omega t-{\kappa }_{r}x\right)\right]\exp \left({\kappa }_{i}x\right)$ in more detail. On one hand, suppose that ${\kappa }_r>0$, whereby $\exp \left[i\left(\omega t-{\kappa }_{r}x\right)\right]$ implies waves propagating into the positive $x$-direction. Wave stability requires that ${\kappa }_i<0$ as it progresses in view of the spatial-attenuation factor $\exp \left({\kappa }_{i}x\right)$ [11,13,20,22,57,63].

On the other hand, suppose the opposite case that ${\kappa }_r<0$, whereby $\exp \left[i\left(\omega t-{\kappa }_{r}x\right)\right]$ implies waves propagating into the negative $x$-direction. This negative propagation should carry ${\kappa }_r>0$. In brief, we should have ${\kappa }_r{\kappa }_i<0$ in any case. The cases ${\kappa }_r>0$ and ${\kappa }_r<0$ are henceforth defined to correspond respectively to forward (propagating) waves and backward (propagating) waves. This way of interpreting the two cases ${\kappa }_r>0$ and ${\kappa }_r<0$ was exactly what has been adopted in [48].

Let us summarize below these two waves.

$$\left\{\begin{array}{l}\kappa \in ℂ\\ {\kappa }_r{\kappa }_i<0\end{array}\right.,\begin{array}{c}\end{array}\left\{\begin{array}{l}\left\{\begin{array}{l}{\kappa }_r>0\\ {\kappa }_i<0\end{array}\right.:\begin{array}{c}\end{array}\left(forward\begin{array}{c}\end{array}waves\right)\\ \left\{\begin{array}{l}{\kappa }_r<0\\ {\kappa }_i>0\end{array}\right.:\begin{array}{c}\end{array}\left(backward\begin{array}{c}\end{array}waves\right)\end{array}\right.$$

(30)

Telegraph-like equations and their solutions offer far-reaching applications in both mechanics and electric circuits. Suppose that the reaction-diffusion (or diffusion-leak) equation (18) is slightly modified by the addition of wave-propagation features exhibited by telegraph-like equations. Such slight addition would give rise to both forward and backward wave propagations as classified in equation (30) [25]. Here lies a possibility of arousing slight backpropagation in the characteristics exhibited by the conventional diffusion-leak equations [42].

Meanwhile, with this SATP approach, we could discover spatially evanescent modes if they are circumstantially admissible as discussed in the preceding section 4 [10]. In the sequel publication, our focus will be laid on how strong forward waves are in comparison to backward waves [19].

When the Ansatz $V\propto \exp \left[i\left(\omega t-\kappa x\right)\right]$ in equation (29) is substituted into the source-free generic telegraph equation (9) [10], the following dispersion relation $\omega =\omega \left(\kappa \right)$ is obtained in two equivalent forms [22,46].

$$\left\{\begin{array}{l}LC{\omega }^2-\left(RC+LG\right)i\omega -{\ell }^2{\kappa }^2-RG=0\\ {\ell }^2{\kappa }^2=-\left(R+i\omega L\right)\left(G+i\omega C\right)=LC{\omega }^2-\left(RC+LG\right)i\omega -RG\end{array}\right.$$

(31)

The arrangement corresponding to equation (31) is schematically illustrated on Figure 3(b).

It takes us by surprise that the generation of double (dual) attenuation peaks is hinged upon the resonance coupling between longitudinal and transverse (viz., lateral) resonators in the context of metamaterials consisting of simultaneous mass and stiffness [46]. In this regard, it is shown in [46] that the dual (double) attenuation rates carry two distinct contributions: [i] one rate stemming solely from system parameters that act in the longitudinal direction, and [ii] the other rate stemming from SEI parameters that account for both longitudinal and lateral dynamics.

It is rather disappointing to us that such a distinction made between a system and an SEI has not been explicitly recognized in [46].

Likewise, the dispersion relation ${\ell }^2{\kappa }^2=-\left(R+i\omega L\right)\left(G+i\omega C\right)$ in equation (31) exhibits a perfect symmetry between $R+i\omega L$ and $G+i\omega C$ so that the longitudinal system dynamics (represented by $R+i\omega L$) lies in interaction with the lateral SEI (represented by $G+i\omega C$). Moreover, in the interpretation by Hooke’s law in equation (17), the product $LC$ ($L$ from a system and $C$ from an SEI) serves as a mass and the other product $RG$ ($R$ from a system and $G$ from an SEI) acts as stiffness. See Table 3 for a summary in this respect.

At this juncture, let us introduce the following set of reference quantities $\left\{{\tau }_{RLGC},{\ell }_{RLGC}\right\}$ and corresponding dimensionless parameters under the assumption of$RLGC\ne 0$ for a full leaky RLGC circuit.

$$\begin{array}{l}RLGC\ne 0:\begin{array}{c}\end{array}\left\{\begin{array}{l}{\tau }_{RLGC}\equiv \sqrt{{\displaystyle \frac{LC}{RG}}}\\ {\ell }_{RLGC}\equiv {\displaystyle \frac{\ell }{\sqrt{RG}}}\end{array}\right.\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\left\{\begin{array}{l}\mathsf{\Omega }\equiv {\tau }_{RLGC}\omega \\ K\equiv {\ell }_{RLGC}\kappa \end{array}\right.\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\left\{\begin{array}{l}{\rm Y}\equiv {\displaystyle \frac{t}{{\tau }_{RLGC}}}\\ X\equiv {\displaystyle \frac{x}{{\ell }_{RLGC}}}\end{array}\right.\\ \begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\exp \left[i\left(\omega t-\kappa x\right)\right]\equiv \exp \left[\mathrm{i}\left(\mathsf{\Omega }{\rm Y}-KX\right)\right]\end{array}$$

(32)

Here, $\left\{{\rm Y},X\right\}$ are dimensionless time and 1-D coordinate, respectively, while $\left\{\mathsf{\Omega },K\right\}$ are dimensionless frequency and wave number, respectively.

As the most easily conceivable reduced case [19], the full leaky RLGC circuit with $RLGC\ne 0$ as illustrated on Figure 3(a) becomes a leak-free RLC circuit if $G=0$ and $RLC\ne 0$ for which equation (18) holds true [49]. Let us examine the dispersion relation for this leak-free RLC circuit by setting $G=0$ in the generic equation (31) as follows.

$$\left\{\begin{array}{l}G=0\\ RLC\ne 0\end{array}\right.:\begin{array}{c}\end{array}{\ell }^2{\kappa }^2=LC{\omega }^2-RCi\omega$$

(33)

This circuit with $G=0$ corresponds to an ideal perfect insulator, for which the shunt resistance $R_{shunt}\equiv 1/G$ becomes infinite [49]. Part of the reason why we examine this leak-free RLC circuit is the property $\left(R/L\right)>>\left(G/C\right)$ as displayed on Figure 4. The arrangement corresponding to equation (33) is schematically illustrated on Figure 3(c).

As we did in equation (32), let us introduce a new pair $\left\{{\tau }_{RLC},{\ell }_{RLC}\right\}$ of references and corresponding dimensionless parameters under the assumption of $G=0$ and $RLC\ne 0$ for a leak-free RLC circuit.

$$\begin{array}{l}\left\{\begin{array}{l}G=0\\ RLC\ne 0\end{array}\right.:\begin{array}{c}\end{array}\zeta \equiv {\displaystyle \frac{R^{2}C}{L}}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ \left\{\begin{array}{l}{\tau }_{RLC}\equiv {\displaystyle \frac{L}{R}}\\ {\ell }_{RLC}\equiv {\displaystyle \frac{\begin{array}{c}\ell \end{array}}{\sqrt{\zeta }}}\end{array}\right.\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\left\{\begin{array}{l}\tilde{\mathsf{\Omega }}\equiv {\tau }_{RLC}\omega \\ \tilde{K}\equiv {\ell }_{RLC}\kappa \end{array}\right.,\begin{array}{c}\end{array}\left\{\begin{array}{l}\widetilde{{\rm Y}}\equiv {\displaystyle \frac{t}{{\tau }_{RLC}}}={\displaystyle \frac{R}{L}}t\\ \tilde{X}\equiv {\displaystyle \frac{x}{{\ell }_{RLC}}}\equiv {\displaystyle \frac{\sqrt{\zeta }}{\ell }}x\end{array}\right.\\ \begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\exp \left[i\left(\omega t-\kappa x\right)\right]\equiv \exp \left[i\left(\tilde{\mathsf{\Omega }}\widetilde{{\rm Y}}-\tilde{K}\tilde{X}\right)\right]\end{array}$$

(34)

Here, the tilde ‘~’ is employed as an overbar. Hence, $\left\{\widetilde{{\rm Y}},\tilde{X}\right\}$ are dimensionless time and 1-D coordinate, respectively, while $\left\{\tilde{\mathsf{\Omega }},\tilde{K}\right\}$ are dimensionless frequency and wave number, respectively.

It is appropriate to examine the special ratio $\zeta$ previously introduced in equation (34) in the following way.

$$\left\{\begin{array}{l}{\tau }_{RC}\equiv RC\\ {\tau }_{RLC}\equiv {\displaystyle \frac{L}{R}}\end{array}\right.\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\zeta \equiv {\displaystyle \frac{{\tau }_{RC}}{{\tau }_{RLC}}}\equiv {\displaystyle \frac{R}{L}}RC\equiv {\displaystyle \frac{R^{2}C}{L}}$$

(35)

Here, ${\tau }_{RC}\equiv RC$ is the RC time previously defined in equation (20). Moreover, the reference-time ratio $\zeta$ appearing in equations (34) and (35) complements the previously introduced ratio ${\tau }_{RLGC}^{10}/{\tau }_{RLGC}\equiv 2\eta$ in equation (14).

Here, the reference time ${\tau }_{RLC}\equiv L/R$ is identifiable also from equation (18) as another ratio ${\tau }_{RLC}\equiv \left(LC\right)/\left(RC\right)$ in [22]. Besides, ${\tau }_{RLC}\equiv L/R$ is alternatively called ‘an inverse of bandwidth’. In addition, ${\tau }_{LRC}\equiv L/R$ has been identified in the context of interelectrode electric potential [49]. From mechanics viewpoint, ${\tau }_{RLC}\equiv L/R$ is linked to viscous air resistance exerted on a vibrating string as illustrated on Figure 2(a).

In the meantime, the signal velocity $a\equiv \ell /\sqrt{LC}$ employed in the simple wave equation (16) is linked to the following parameters respectively for the full leaky RLGC circuit and the leak-free RLC circuit.

$$\begin{array}{l}RLGC\ne 0:\begin{array}{c}\end{array}a\equiv {\displaystyle \frac{\ell }{\sqrt{LC}}}={\displaystyle \frac{\frac{\ell }{\sqrt{RG}}}{\sqrt{\frac{LC}{RG}}}}\equiv {\displaystyle \frac{{\ell }_{RLGC}}{{\tau }_{RLGC}}}\\ \left\{\begin{array}{l}G=0\\ RLC\ne 0\end{array}\right.:\begin{array}{c}\end{array}a\equiv {\displaystyle \frac{\ell }{\sqrt{LC}}}={\displaystyle \frac{\frac{\begin{array}{c}\ell \end{array}}{\sqrt{\frac{R^{2}C}{L}}}}{\frac{L}{R}}}={\displaystyle \frac{\frac{\begin{array}{c}\ell \end{array}}{\sqrt{\zeta }}}{\frac{L}{R}}}\equiv {\displaystyle \frac{{\ell }_{RLC}}{{\tau }_{RLC}}}\end{array}$$

(36)

Here, reference times and reference lengths are read respectively from equations (32) and (34).

Meanwhile, equations (31) and (33) are reduced to the following dimensionless forms respectively of $K\left(\mathsf{\Omega }\right)$ and $\tilde{K}\left(\tilde{\mathsf{\Omega }}\right)$

$$\begin{array}{l}RLGC\ne 0:\begin{array}{c}\end{array}K\left(\mathsf{\Omega };\eta \right)=\sqrt{{\mathsf{\Omega }}^2-2\eta i\mathsf{\Omega }-1}\\ \left\{\begin{array}{l}G=0\\ RLC\ne 0\end{array}\right.:\begin{array}{c}\end{array}\tilde{K}\left(\tilde{\mathsf{\Omega }}\right)=\sqrt{\tilde{\mathsf{\Omega }}\left(\tilde{\mathsf{\Omega }}-i\right)}\end{array}$$

(37)

Here, the parameter $\eta$ has already been defined in equation (11) with attendant properties in equation (12).

We have started with the four parameters $\left\{R,L,G,C\right\}$ in the PDE (9), which are readily reduced to two parameters $\left\{R/L,G/C\right\}$ in the PDE (10) [20]. We have identified in equation (37) that $K\left(\mathsf{\Omega };\eta \right)=\sqrt{{\mathsf{\Omega }}^2-2\eta i\mathsf{\Omega }-1}$ depends solely on a single parameter $\eta$. Even better is the fact that $\tilde{K}\left(\tilde{\mathsf{\Omega }}\right)=\sqrt{\tilde{\mathsf{\Omega }}\left(\tilde{\mathsf{\Omega }}-i\right)}$ is parameter-free.

Meanwhile, we resort to the following generic solution to $\sqrt{a+ib}$ for a generic $z\in ℂ$ [49].

$$\begin{array}{l}\left\{\begin{array}{l}a,b\in ℝ\\ z\in ℂ\end{array}\right.:\begin{array}{c}\end{array}\left\{\begin{array}{l}z\equiv a+ib\\ \left|z\right|=\sqrt{a^2+b^2}\end{array}\right.\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ \sqrt{z}=\sqrt{a+ib}=\pm \left[\sqrt{\frac{1}{2}\left(\left|z\right|+a\right)}+i\mathrm{sgn}\left(b\right)\sqrt{\frac{1}{2}\left(\left|z\right|-a\right)}\right]\end{array}$$

(38)

When this formula is applied to equation (37), we obtain the following pair of solutions $K_r+i{K}_i$ and ${\tilde{K}}_r+i{\tilde{K}}_i$ [49].

$$\begin{array}{l}RLGC\ne 0:\begin{array}{c}\end{array}\left\{\begin{array}{l}K\equiv K_r+i{K}_i\equiv \mathrm{Re}\left(K\right)+i\mathrm{Im}\left(K\right),\begin{array}{c}\end{array}{K}_r{K}_i<0\\ \left\{\begin{array}{l}{K}_r=\sqrt{\frac{1}{2}}\sqrt{\sqrt{{\left({\mathsf{\Omega }}^2-1\right)}^2+4{\eta }^2{\mathsf{\Omega }}^2}+\left({\mathsf{\Omega }}^2-1\right)}\\ K_i=-\sqrt{\frac{1}{2}}\sqrt{\sqrt{{\left({\mathsf{\Omega }}^2-1\right)}^2+4{\eta }^2{\mathsf{\Omega }}^2}-\left({\mathsf{\Omega }}^2-1\right)}\end{array}\right.\end{array}\right.\\ \left\{\begin{array}{l}G=0\\ RLC\ne 0\end{array}\right.:\begin{array}{c}\end{array}\left\{\begin{array}{l}\tilde{K}\equiv {\tilde{K}}_r+i{\tilde{K}}_i\equiv \mathrm{Re}\left(\tilde{K}\right)+i\mathrm{Im}\left(\tilde{K}\right),\begin{array}{c}\end{array}{\tilde{K}}_r{\tilde{K}}_i<0\\ \left\{\begin{array}{l}{\tilde{K}}_r=\sqrt{\tilde{\mathsf{\Omega }}}\sqrt{\frac{1}{2}}\sqrt{\sqrt{{\tilde{\mathsf{\Omega }}}^2+1}+\tilde{\mathsf{\Omega }}}\\ {\tilde{K}}_i=-\sqrt{\tilde{\mathsf{\Omega }}}\sqrt{\frac{1}{2}}\sqrt{\sqrt{{\tilde{\mathsf{\Omega }}}^2+1}-\tilde{\mathsf{\Omega }}}\end{array}\right.\end{array}\right.\end{array}$$

(39)

Notice here that $\mathsf{\Omega }\in ℝ$, while $K\equiv K_r+i{K}_i\equiv \mathrm{Re}\left(K\right)+i\mathrm{Im}\left(K\right)$ according to equation (29). Hence, the condition $K_r{K}_i<0$ in equation (30) is satisfied. According to the generic formula in (38), the other solution $-K_r-i{K}_i$ is acceptable as well since $\left(-K_r\right)\left(-K_i\right)<0$. Therefore, we will stick to the solutions presented in equation (39) to fix the idea. Likewise, $\tilde{K}\equiv {\tilde{K}}_r+i{\tilde{K}}_i\equiv \mathrm{Re}\left(\tilde{K}\right)+i\mathrm{Im}\left(\tilde{K}\right)$ with ${\tilde{K}}_r{\tilde{K}}_i<0$.

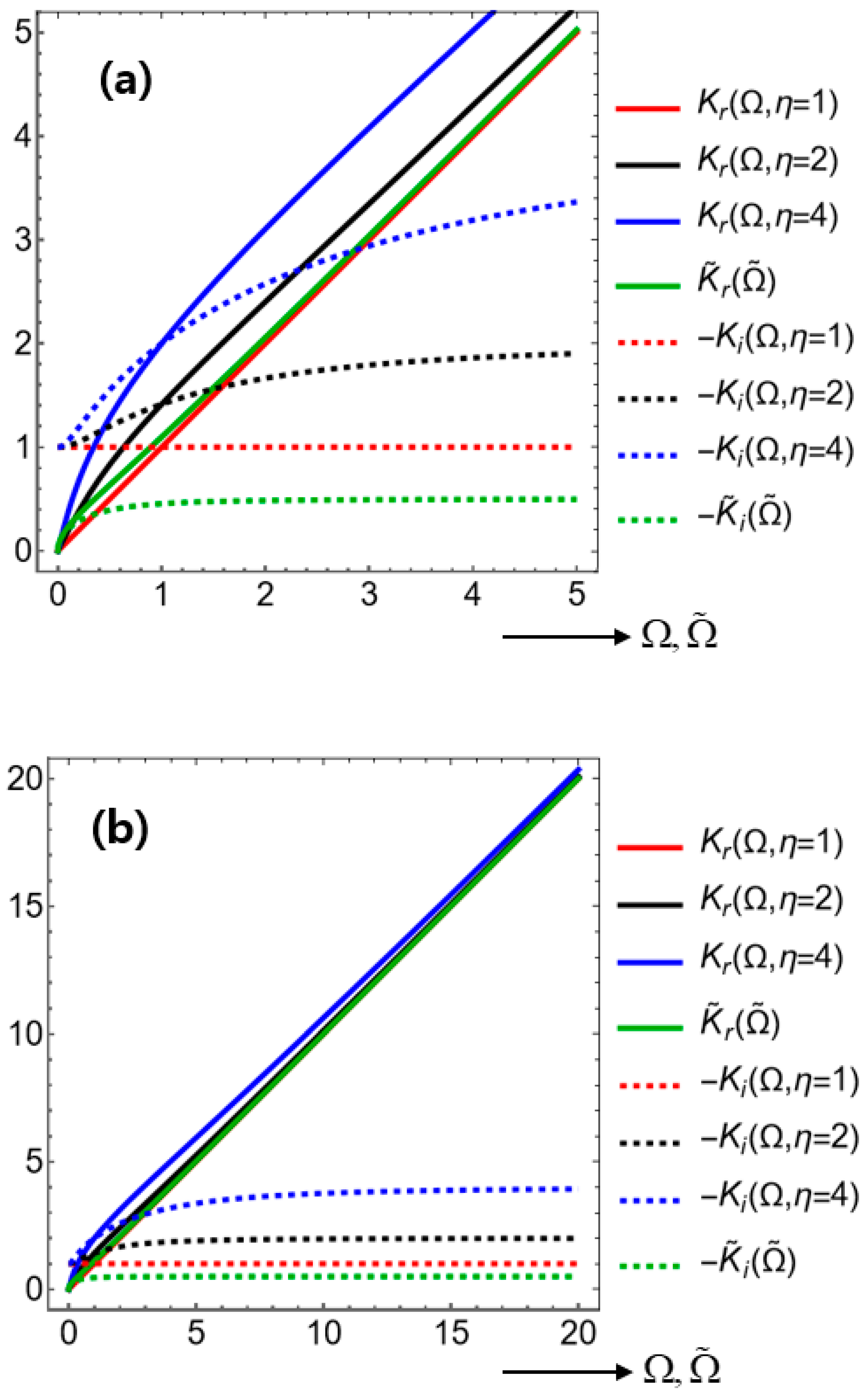
Figure 5(a) displays two kinds of curves on the same display panel: [i] $K_r\left(\mathsf{\Omega };\eta \right)$ and $-K_i\left(\mathsf{\Omega };\eta \right)$ in case of the full leaky RLGC circuit, and [ii] ${\tilde{K}}_r\left(\tilde{\mathsf{\Omega }}\right)$ and $-{\tilde{K}}_i\left(\tilde{\mathsf{\Omega }}\right)$ in case of the leak-free RLC circuit. In addition, solid curves are drawn for the wave number or propagation constants $K_r\left(\mathsf{\Omega };\eta \right)$ and ${\tilde{K}}_r\left(\tilde{\mathsf{\Omega }}\right)$, while dashed curves are drawn for the attenuation rates $-K_i\left(\mathsf{\Omega };\eta \right)$ and $-{\tilde{K}}_i\left(\tilde{\mathsf{\Omega }}\right)$. Figure 5(a) is a zoomed-out version of Figure 5(a).

On one hand, let us examine the real parts $K_r\left(\mathsf{\Omega };\eta \right)$ and ${\tilde{K}}_r\left(\tilde{\mathsf{\Omega }}\right)$ on solid curves. Both $K_r\left(\mathsf{\Omega };\eta \right)$ and ${\tilde{K}}_r\left(\tilde{\mathsf{\Omega }}\right)$ are increasing with respective increasing frequencies. Meanwhile, notice from equation (12) that $1\le \eta <\infty$. In this connection, ${\tilde{K}}_r\left(\tilde{\mathsf{\Omega }}\right)$ does not appear to be obtainable either from the $\eta \downarrow 1$ limit or from the $\eta \uparrow \infty$ limit of $K_r\left(\mathsf{\Omega };\eta \right)$. It is because the curve of ${\tilde{K}}_r\left(\tilde{\mathsf{\Omega }}\right)$ lies between the curve of $K_r\left(\mathsf{\Omega };\eta =1\right)$ and $K_r\left(\mathsf{\Omega };\eta =2\right)$.

On the other hand, let us examine the imaginary parts $-K_i\left(\mathsf{\Omega };\eta \right)$ and $-{\tilde{K}}_i\left(\tilde{\mathsf{\Omega }}\right)$ on dashed curves. Once again, $-{\tilde{K}}_i\left(\tilde{\mathsf{\Omega }}\right)$ does not appear to be obtainable either from the $\eta \downarrow 1$ limit or from the $\eta \uparrow \infty$ limit of$-K_i\left(\mathsf{\Omega };\eta \right)$. One aspect of these discrepancies is the following small-frequency limits as seen from equation (39).

$$\begin{array}{l}RLGC\ne 0:\begin{array}{c}\end{array}\left\{\begin{array}{l}{K}_r\left(\mathsf{\Omega }=0;\eta \right)=0\\ K_i\left(\mathsf{\Omega }=0;\eta \right)=-1\end{array}\right.\\ \left\{\begin{array}{l}G=0\\ RLC\ne 0\end{array}\right.:\begin{array}{c}\end{array}\left\{\begin{array}{l}{\tilde{K}}_r\left(\mathsf{\Omega }=0\right)=0\\ {\tilde{K}}_i\left(\mathsf{\Omega }=0\right)=0\end{array}\right.\end{array}$$

(40)

Therefore, only $-K_i\left(\mathsf{\Omega }=0;\eta \right)=1$ is non-zero for any $\eta$ over $1\le \eta <\infty$, while other small-frequency limits vanish. These small-frequency limits $K_r\left(\mathsf{\Omega }=0;\eta \right)=0$ and $-K_i\left(\mathsf{\Omega }=0;\eta \right)=1$ for any values of $\eta$ can be alternatively called ‘stationarity limits’ instead. These stationarity limits exhibit a significant phenomenon, since $K_r\left(\mathsf{\Omega }=0;\eta \right)=0$ stands for non-propagating stationary state, which still undergoes spatial attenuation due to $-K_i\left(\mathsf{\Omega }=0;\eta \right)=1\ne 0$.

Recall that $K_r\to 0$ in the limit $\mathsf{\Omega }\to 0$ as shown in equation (40) by the SATP approach. We have carried out a separate analysis via the TASP approach (to be separately published) to find that ${\mathsf{\Omega }}_r\to 0$ in the limit $K\to 0$ is also achieved. Notwithstanding, we learn from the TASP approach a new phenomenon that there is a certain finite low-$K$zone $0\le K\le K_{cutoff}\left(\eta \right)$ where ${\mathsf{\Omega }}_r=0$. The TASP approach also revealed bifurcation phenomena for attenuation rates as well [19,57]. Such a finite forbidden wave-number zone cannot be seen via the current SATP approach. However, the significantly distinct behaviors between $K_i\left(\mathsf{\Omega }=0;\eta \right)=-1$ and ${\tilde{K}}_i\left(\mathsf{\Omega }=0\right)=0$ in equation (40) are the symptom of the existence of such forbidden zones.

For the full leaky RLGC circuit, the following limits hold true for $\eta =1$ from the equation (39).

$$\left\{\begin{array}{l}{K}_r\left(\mathsf{\Omega },\eta =1\right)=\mathsf{\Omega }\\ K_i\left(\mathsf{\Omega },\eta =1\right)=1\end{array}\right.$$

(41)

Therefore, $K_r\left(\mathsf{\Omega },\eta =1\right)=\mathsf{\Omega }$ is a straight line, while $-K_i\left(\mathsf{\Omega },\eta =1\right)=1$ is a constant horizontal line as displayed by the red curves on Figure 5.

In brief, the curves of ${\tilde{K}}_r\left(\tilde{\mathsf{\Omega }}\right)$ and $-{\tilde{K}}_i\left(\tilde{\mathsf{\Omega }}\right)$ exhibit rather distinct features in comparison to those of $K_r\left(\mathsf{\Omega };\eta \right)$ and $-K_i\left(\mathsf{\Omega };\eta \right)$. Especially, stationary non-propagating states do not appear to exist for the leak-free RLC circuit. The reason may be ascribed to the absence of dissipative SEIs for the leak-free RLC circuit with $G=0$, namely, ${\tilde{K}}_r\left(\tilde{\mathsf{\Omega }}=0\right)=0$ and $-{\tilde{K}}_i\left(\tilde{\mathsf{\Omega }}=0\right)=0$ [57].

This absence of stationary non-propagating states leads us to ask a self-question: “When an electric circuit is sufficiently insulated from an environment and hence an electric grounding is almost perfect, would then electric waves almost be always propagative rather than stationary?”. If this question were affirmatively answered, we might conjecture that ACs (alternating currents) will be better propagative through telegraph transmission lines than DCs (direct currents).

With reference to Figure 3(a), Table 5 makes comparison of several dispersion relations and corresponding key characteristics for the full leaky RLGC circuit with $RLGC\ne 0$ and other reduced circuits. Notice the reference length $\ell$ is undetermined. With a certain reference time $\tau$, the ratio $\ell /\tau$ becomes a reference velocity.

In the meantime, the phase velocities $\left\{W_p\left(\mathsf{\Omega };\eta \right),{\tilde{W}}_p\left(\tilde{\mathsf{\Omega }}\right)\right\}$ and the group velocities $\left\{W_g\left(\mathsf{\Omega };\eta \right),{\tilde{W}}_g\left(\tilde{\mathsf{\Omega }}\right)\right\}$ are evaluated from equation (39) respectively via the following formulas [20,24,46,49,63].

$$\begin{array}{l}RLGC\ne 0:\begin{array}{c}\end{array}\\ \left\{\begin{array}{l}{W}_p\equiv {\displaystyle \frac{\mathsf{\Omega }}{K_r}}={\displaystyle \frac{\sqrt{2}\mathsf{\Omega }}{\sqrt{\sqrt{{\left({\mathsf{\Omega }}^2-1\right)}^2+4{\eta }^2{\mathsf{\Omega }}^2}+\left({\mathsf{\Omega }}^2-1\right)}}}\\ W_g\equiv {\left({\displaystyle \frac{\partial K_r}{\partial \mathsf{\Omega }}}\right)}^{-1}={\displaystyle \frac{\sqrt{2}}{\mathsf{\Omega }}}\sqrt{\sqrt{{\left({\mathsf{\Omega }}^2-1\right)}^2+4{\eta }^2{\mathsf{\Omega }}^2}+{\mathsf{\Omega }}^2-1}\\ \begin{array}{cc}& \end{array}\times {\displaystyle \frac{\sqrt{{\left({\mathsf{\Omega }}^2-1\right)}^2+4{\eta }^2{\mathsf{\Omega }}^2}}{\sqrt{{\left({\mathsf{\Omega }}^2-1\right)}^2+4{\eta }^2{\mathsf{\Omega }}^2}+{\mathsf{\Omega }}^2-1+2{\eta }^2}}\end{array}\right.\\ \left\{\begin{array}{l}G=0\\ RLC\ne 0\end{array}\right.:\begin{array}{c}\end{array}\left\{\begin{array}{l}{\tilde{W}}_p\equiv {\displaystyle \frac{\tilde{\mathsf{\Omega }}}{{\tilde{K}}_r}}={\displaystyle \frac{\sqrt{2}\tilde{\mathsf{\Omega }}}{\sqrt{\sqrt{{\tilde{\mathsf{\Omega }}}^2+1}+\tilde{\mathsf{\Omega }}}}}\\ {\tilde{W}}_g\equiv {\left({\displaystyle \frac{d{\tilde{K}}_r}{d\mathsf{\Omega }}}\right)}^{-1}={\displaystyle \frac{2\sqrt{2}\sqrt{\tilde{\mathsf{\Omega }}}\sqrt{{\tilde{\mathsf{\Omega }}}^2+1}}{{\left(\sqrt{{\tilde{\mathsf{\Omega }}}^2+1}+\tilde{\mathsf{\Omega }}\right)}^{3/2}}}\end{array}\right.\end{array}$$

(42)

Figure 6(a) displays two kinds of curves on the same display panel: [i] $W_p\left(\mathsf{\Omega };\eta \right)$ and $W_g\left(\mathsf{\Omega };\eta \right)$ for the full leaky RLGC circuit, and [ii] ${\tilde{W}}_p\left(\tilde{\mathsf{\Omega }}\right)$ and ${\tilde{W}}_g\left(\tilde{\mathsf{\Omega }}\right)$ for the leak-free RLC circuit. Here, $W_p\left(\mathsf{\Omega };\eta \right)$ and ${\tilde{W}}_p\left(\tilde{\mathsf{\Omega }}\right)$ are phase velocities displayed on solid curves, while $W_g\left(\mathsf{\Omega };\eta \right)$ and ${\tilde{W}}_g\left(\tilde{\mathsf{\Omega }}\right)$ are group velocities shown on dashed curves.

Overall, all solid curves increase uniformly with increasing frequencies, while all dashed curves exhibit local maxima at certain frequencies. For instance, a local maximum is pointed to by the green blank arrow on Figure 6(a) for ${\tilde{W}}_g\left(\tilde{\mathsf{\Omega }}\right)$. Such a maximum feature in the group velocity is not uncommon [49].

The curve of $W_p\left(\mathsf{\Omega };\eta =1\right)=1$ indicates a luminal phase velocity. All other phase velocities stay subluminal. In case with phase velocities, the inequality $W_p\left(\mathsf{\Omega };\eta =2\right)<{\tilde{W}}_p\left(\tilde{\mathsf{\Omega }}\right)<W_p\left(\mathsf{\Omega };\eta =1\right)$ holds true over most of higher frequency zones except near zero frequency. However, such comparison between $\left\{W_p\left(\mathsf{\Omega };\eta \right),{\tilde{W}}_p\left(\tilde{\mathsf{\Omega }}\right)\right\}$ is not to be trusted due to distinct reference quantities listed in equations (32) and (34).

Each curve of group velocity exhibits a single crossover across the horizontal luminal line, e.g., as indicated by the green filled arrow on Figure 6(a) for ${\tilde{W}}_g\left(\tilde{\mathsf{\Omega }}\right)$. In other words, ${\tilde{W}}_g\left(\tilde{\mathsf{\Omega }}\right)<1$ (subluminal) over $0\le \tilde{\mathsf{\Omega }}<{\tilde{\mathsf{\Omega }}}_{crit}$, while ${\tilde{W}}_g\left(\tilde{\mathsf{\Omega }}\right)>1$ (superluminal) over ${\tilde{\mathsf{\Omega }}}_{crit}<\tilde{\mathsf{\Omega }}$. Here,${\tilde{\mathsf{\Omega }}}_{crit}$ is a certain constant. Likewise, $W_g<1$ (subluminal) over $0\le \mathsf{\Omega }<{\mathsf{\Omega }}_{crit}\left(\eta \right)$, whereas $W_g>1$ (superluminal) over ${\mathsf{\Omega }}_{crit}\left(\eta \right)<\mathsf{\Omega }<\infty$. The critical frequency ${\mathsf{\Omega }}_{crit}\left(\eta \right)$ appears to increase with increasing $\eta$ [19]. Besides, $W_g\left(\mathsf{\Omega }\right)$ also displays a local maximum with respect to $\mathsf{\Omega }$ as clearly seen on Figure 6(b).

We can easily evaluate the zero-frequency limits of the phase and group velocities as follows based on equation (42).

$$\left\{\begin{array}{l}\underset{\mathsf{\Omega }\to 0}{\lim }{W}_p=\underset{\mathsf{\Omega }\to 0}{\lim }{W}_g={\displaystyle \frac{1}{\eta }}\\ \underset{\tilde{\mathsf{\Omega }}\to 0}{\lim }{\tilde{W}}_p=\underset{\tilde{\mathsf{\Omega }}\to 0}{\lim }{\tilde{W}}_g=0\end{array}\right.$$

(43)

We can confirm these limits easily on Figure 6(b). For instance, $W_p\left(\mathsf{\Omega }=0,\eta =4\right)=W_g\left(\mathsf{\Omega }=0,\eta =4\right)=\frac{1}{4}$ as indicated by the horizontal solid blue arrow on Figure 6(b). Also indicated by the green arrow near the coordinate origin is the limit ${\tilde{W}}_p\left(\tilde{\mathsf{\Omega }}=0\right)={\tilde{W}}_g\left(\tilde{\mathsf{\Omega }}=0\right)=0$. In addition, we have anomalous dispersion, namely, $W_p\left(\mathsf{\Omega };\eta \right)<W_g\left(\mathsf{\Omega };\eta \right)$ for $\eta >1$ and ${\tilde{W}}_p\left(\tilde{\mathsf{\Omega }}\right)<{\tilde{W}}_g\left(\tilde{\mathsf{\Omega }}\right)$ for all cases.

Meanwhile, consider the rotation-free leaky circuit with $L=0$ and $RGC\ne 0$ as presented in equation (20). This circuit is devoid of wave propagation, since it is just a diffusion-leak equation. Therefore, the Ansatz $V\left(t,x\right)\propto \exp \left[i\left(\omega t-\kappa x\right)\right]$ is not applicable. Yet, let us continue to perform the following analysis of dispersion relation to see what kinds of difference exist between diffusion and wave propagation.

$$\left\{\begin{array}{l}L=0\\ RGC\ne 0\end{array}\right.:\begin{array}{c}\end{array}{\ell }^2{\kappa }^2=-RCi\omega -RG$$

(44)

Here, $\kappa \left(\omega \right)$ on the RHS is linear in $\omega$, while $\kappa \left(\omega \right)$’s on the RHSs of both equations (31) and (33) are quadratic in $\omega$. This difference will lead to quite distinct behaviors of the respective dispersion relations. The arrangement corresponding to equation (44) is schematically illustrated on Figure 3(d).

Furthermore, let us handle the rotation-free (induction-free) leaky circuit with $L=0$ and $RGC\ne 0$ as presented in equations (20) and (44) to prepare the following.

$$\begin{array}{l}\left\{\begin{array}{l}L=0\\ RGC\ne 0\end{array}\right.:\begin{array}{c}\end{array}\left\{\begin{array}{l}{\tau }_{RGC}\equiv {\displaystyle \frac{C}{G}}\\ {\ell }_{RGC}\equiv {\displaystyle \frac{\ell }{\sqrt{RG}}}\end{array}\right.,\begin{array}{c}\end{array}\left\{\begin{array}{l}\widehat{\mathsf{\Omega }}\equiv {\tau }_{RGC}\omega \\ \widehat{K}\equiv {\ell }_{RGC}\kappa \end{array}\right.,\begin{array}{c}\end{array}\left\{\begin{array}{l}\widehat{{\rm Y}}\equiv {\displaystyle \frac{t}{{\tau }_{RGC}}}={\displaystyle \frac{G}{C}}t\\ \widehat{X}\equiv {\displaystyle \frac{x}{{\ell }_{RGC}}}\equiv {\displaystyle \frac{\sqrt{RG}}{\ell }}x\end{array}\right.\\ \begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\exp \left[i\left(\omega t-\kappa x\right)\right]\equiv \exp \left[i\left(\widehat{\mathsf{\Omega }}\widehat{{\rm Y}}-\widehat{K}\widehat{X}\right)\right]\end{array}$$

(45)

Here, we have introduced a ‘caret’ notation for this circuit. Additionally, we have introduced additional reference quantities $\left\{{\tau }_{RGC},{\ell }_{RGC}\right\}$. As discussed for Figure 4, $\left[C/G\right]=s$, while $\left[RG\right]$ is dimensionless as discussed in Appendix A.

We have examined in equation (36) whether the reference velocities ${\ell }_{RLGC}/{\tau }_{RLGC}$ and ${\ell }_{RLC}/{\tau }_{RLC}$ are equal to the well-known signal velocity $a\equiv \ell /\sqrt{LC}$. Therefore, making such comparisons with the help of ${\ell }_{RGC}/{\tau }_{RGC}$ in equation (45) turns out futile, because $a\equiv \ell /\sqrt{LC}$ is undefined with $L=0$. Therefore, conventional discussion in terms of subluminal, luminal, and superluminal states will become unfounded.

However, we can go on to find the dimensionless dispersion relation as follows based on equations (44) and (45).

$$\left\{\begin{array}{l}L=0\\ RGC\ne 0\end{array}\right.:\begin{array}{c}\end{array}\left\{\begin{array}{l}{\widehat{K}}^2=-1-i\widehat{\mathsf{\Omega }}\\ \widehat{K}=\sqrt{-1-i\widehat{\mathsf{\Omega }}}\end{array}\right.\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\left\{\begin{array}{l}{\widehat{K}}_r=\sqrt{\frac{1}{2}}\sqrt{\sqrt{1+{\widehat{\mathsf{\Omega }}}^2}-1}\\ {\widehat{K}}_i=-\sqrt{\frac{1}{2}}\sqrt{\sqrt{1+{\widehat{\mathsf{\Omega }}}^2}+1}\end{array}\right.$$

(46)

Here, we have applied the square-root formula in equation (38), to explicitly find ${\widehat{K}}_r\left(\widehat{\mathsf{\Omega }}\right)$ and ${\widehat{K}}_i\left(\widehat{\mathsf{\Omega }}\right)$ as we have done in equation (39).

Based on equation (46), let us find the following pair of phase and group velocities as in equation (42).

$$\left\{\begin{array}{l}L=0\\ RGC\ne 0\end{array}\right.:\begin{array}{c}\end{array}\left\{\begin{array}{l}{\widehat{W}}_p\equiv {\displaystyle \frac{\widehat{\mathsf{\Omega }}}{{\widehat{K}}_r}}={\displaystyle \frac{\sqrt{2}\widehat{\mathsf{\Omega }}}{\sqrt{\sqrt{1+{\widehat{\mathsf{\Omega }}}^2}-1}}}\\ {\widehat{W}}_p\equiv {\left({\displaystyle \frac{d{\widehat{K}}_r}{d\widehat{\mathsf{\Omega }}}}\right)}^{-1}={\displaystyle \frac{2\sqrt{2}\sqrt{1+{\widehat{\mathsf{\Omega }}}^2}\sqrt{\sqrt{1+{\widehat{\mathsf{\Omega }}}^2}-1}}{\widehat{\mathsf{\Omega }}}}\end{array}\right.$$

(47)

Hence, we can easily come up with the following limit behaviors.

$$\left\{\begin{array}{l}L=0\\ RGC\ne 0\end{array}\right.:\begin{array}{c}\end{array}\left\{\begin{array}{l}\left\{\begin{array}{l}{\widehat{K}}_r\left(\widehat{\mathsf{\Omega }}=0\right)=0\\ {\widehat{K}}_i\left(\widehat{\mathsf{\Omega }}=0\right)=-1\end{array}\right.,\begin{array}{c}\end{array}\left\{\begin{array}{l}\underset{\widehat{\mathsf{\Omega }}\to \infty }{\lim }{\widehat{K}}_r=\sqrt{\frac{1}{2}}\sqrt{\widehat{\mathsf{\Omega }}}\\ \underset{\widehat{\mathsf{\Omega }}\to \infty }{\lim }{\widehat{K}}_i=-\sqrt{\frac{1}{2}}\sqrt{\widehat{\mathsf{\Omega }}}\end{array}\right.\\ \left\{\begin{array}{l}{\widehat{W}}_p\left(\widehat{\mathsf{\Omega }}=0\right)=0\\ {\widehat{W}}_g\left(\widehat{\mathsf{\Omega }}=0\right)=2\end{array}\right.,\begin{array}{c}\end{array}\left\{\begin{array}{l}\underset{\widehat{\mathsf{\Omega }}\to \infty }{\lim }{\widehat{W}}_p=\sqrt{2}\sqrt{\widehat{\mathsf{\Omega }}}\\ \underset{\widehat{\mathsf{\Omega }}\to \infty }{\lim }{\widehat{W}}_g=2\sqrt{2}\sqrt{\widehat{\mathsf{\Omega }}}\end{array}\right.\end{array}\right.$$

(48)

Here, the limit ${\widehat{W}}_g\left(\widehat{\mathsf{\Omega }}=0\right)=2$ requires a bit of care in its derivation.

Figure 7 displays the dispersion characteristics $\left\{{\widehat{K}}_r,-{\widehat{K}}_i,{\widehat{W}}_p,{\widehat{W}}_g\right\}$ against the dimensionless frequency $\widehat{\mathsf{\Omega }}$. All members of $\left\{{\widehat{K}}_r,-{\widehat{K}}_i,{\widehat{W}}_p,{\widehat{W}}_g\right\}$ increase uniformly with increasing $\widehat{\mathsf{\Omega }}$ without limits.

Notice that equation (20) is a diffusion-leak equation, thereby being endowed with no wave propagation. Therefore, both $\left\{{\widehat{W}}_p,{\widehat{W}}_g\right\}$ going without bounds as $\widehat{\mathsf{\Omega }}\to \infty$ is indicative of infinite propagation velocity of signals especially for high frequencies. Such infinite propagation velocities are in conformance with, say, thermal heating being sensed instantly everywhere no matter how those senses are infinitesimally small. It is because governing equation for temperature is analogous to equation (20).

In mathematical languages, activities of parabolic PDEs carry infinite signal velocity. In comparison, hyperbolic PDEs such as in equations (9) and (18) are accompanied by finite propagation velocities as examined not only in equation (42) but also on Figure 5 and Figure 6 [1,2].

Such infinite propagation velocities are also in agreement with the finite group velocity ${\widehat{W}}_g\left(\widehat{\mathsf{\Omega }}=0\right)=2$ in equation (48) at a stationary state. It is because a group velocity is sort of energy-transmission velocity, by which wave energy is steadily supplied for all temporally neighboring transient states of non-zero frequencies. The non-zero finite attenuation rate ${\widehat{K}}_i\left(\widehat{\mathsf{\Omega }}=0\right)=-1$ in equation (48) at a steady state also agrees with such energy transfer in low frequencies beginning with zero frequency.

A further reduction of the case with $L=0$ is that $L=G=0$ for the rotation-free and leak-free circuit. For this circuit, equation (31) is reduced to provide the following.

$$\begin{array}{l}\left\{\begin{array}{l}L=G=0\\ RC\ne 0\end{array}\right.:\begin{array}{c}\end{array}{\ell }^2{\kappa }^2=RCi\omega \begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\left\{\begin{array}{l}{\tau }_{RC}\equiv RC\\ {\ell }_{RC}\equiv \ell \end{array}\right.,\begin{array}{c}\end{array}\left\{\begin{array}{l}\stackrel{⌣}{\mathsf{\Omega }}\equiv {\tau }_{RC}\omega \\ \stackrel{⌣}{K}\equiv {\ell }_{RC}\kappa \end{array}\right.\\ \begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}{\stackrel{⌣}{K}}^2=-i\stackrel{⌣}{\mathsf{\Omega }}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}a\equiv {\displaystyle \frac{\ell }{\sqrt{LC}}}\ne {\displaystyle \frac{\ell }{RC}}\equiv {\displaystyle \frac{{\ell }_{RC}}{{\tau }_{RC}}}\end{array}$$

(49)

Here, we have introduced yet another set of notations $\left\{\stackrel{⌣}{K},\stackrel{⌣}{\mathsf{\Omega }}\right\}$ with inverted arc.

Moreover, a new reference time ${\tau }_{RC}\equiv RC$ is defined. This time ${\tau }_{RC}\equiv RC$ is deducible from equation (33) such that it been conventionally called an ‘RC (membrane) time’ in the context of neuroscience [38,39] and diffusive memristors [43]. This nomenclature is made in comparison to the LC time ${\tau }_{LC}\equiv \sqrt{LC}$ inequation (16), which is also easily deducible from equation (33) on dimensional ground.

Furthermore, we have pointed out that the absence of $L$ in equation (49) leads to a different signal velocity ${\ell }_{RC}/{\tau }_{RC}$ as for the rotation-free laky circuit discussed in equation (45).

We can easily find the solution to ${\stackrel{⌣}{K}}^2=-i\stackrel{⌣}{\mathsf{\Omega }}$ in equation (49) as follow by way of the generic formula in equation (38).

$$\begin{array}{l}\left\{\begin{array}{l}L=G=0\\ RC\ne 0\end{array}\right.:\begin{array}{c}\end{array}\stackrel{⌣}{K}=\sqrt{-i\stackrel{⌣}{\mathsf{\Omega }}}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ \stackrel{⌣}{K}=\frac{1}{\sqrt{2}}\stackrel{⌣}{\mathsf{\Omega }}-i\frac{1}{\sqrt{2}}\stackrel{⌣}{\mathsf{\Omega }}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\left\{\begin{array}{l}{\stackrel{⌣}{W}}_p\equiv {\displaystyle \frac{\stackrel{⌣}{\mathsf{\Omega }}}{{\stackrel{⌣}{K}}_r}}=\sqrt{2}\\ {\widehat{W}}_g\equiv {\left({\displaystyle \frac{d{\stackrel{⌣}{K}}_r}{d\stackrel{⌣}{\mathsf{\Omega }}}}\right)}^{-1}=\sqrt{2}\end{array}\right.\end{array}$$

(50)

Here, the solution $\stackrel{⌣}{K}=\frac{1}{\sqrt{2}}\stackrel{⌣}{\mathsf{\Omega }}-i\frac{1}{\sqrt{2}}\stackrel{⌣}{\mathsf{\Omega }}$ led easily to the corresponding phase and group velocities given above. Resultantly, both phase and group velocities are constant with respect to the non-dimensional scheme provided in equation (49).

Starting with equation (31), we process for the internal-loss-free and leak-free circuit with $R=G=0$ and $LC\ne 0$ to obtain the following.

$$\begin{array}{l}\left\{\begin{array}{l}R=G=0\\ LC\ne 0\end{array}\right.:\begin{array}{c}\end{array}{\ell }^2{\kappa }^2=LC{\omega }^2\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ \left\{\begin{array}{l}{\tau }_{LC}\equiv \sqrt{LC}\\ {\ell }_{LC}\equiv \ell \end{array}\right.,\begin{array}{c}\end{array}\left\{\begin{array}{l}\overline{\mathsf{\Omega }}\equiv {\tau }_{LC}\omega \\ \overline{K}\equiv {\ell }_{LC}\kappa \end{array}\right.\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\overline{K}=\overline{\mathsf{\Omega }}\end{array}$$

(51)

These results are simpler than those in equations (49) and (50). The linear dispersion relation $\overline{K}=\overline{\mathsf{\Omega }}$ is what we have discussed in equation (16) for the canonical wave equation.

$$\left\{\begin{array}{l}R=G=0\\ LC\ne 0\end{array}\right.:\begin{array}{c}\end{array}a\equiv {\displaystyle \frac{\ell }{\sqrt{LC}}}\equiv {\displaystyle \frac{{\ell }_{LC}}{{\tau }_{LC}}},\begin{array}{c}\end{array}\left\{\begin{array}{l}{\overline{W}}_p\equiv {\displaystyle \frac{\overline{\mathsf{\Omega }}}{\overline{K}}}={\displaystyle \frac{\overline{\mathsf{\Omega }}}{\overline{\mathsf{\Omega }}}}=1\\ {\overline{W}}_g\equiv {\left({\displaystyle \frac{d{\overline{K}}_r}{d\overline{\mathsf{\Omega }}}}\right)}^{-1}=1\end{array}\right.$$

(52)

In this case, we end up with the ratio ${\ell }_{LC}/{\tau }_{LC}=a$, thus being the signal velocity introduced in equation (16). Resultantly, both phase and group velocities are luminal for all frequencies.

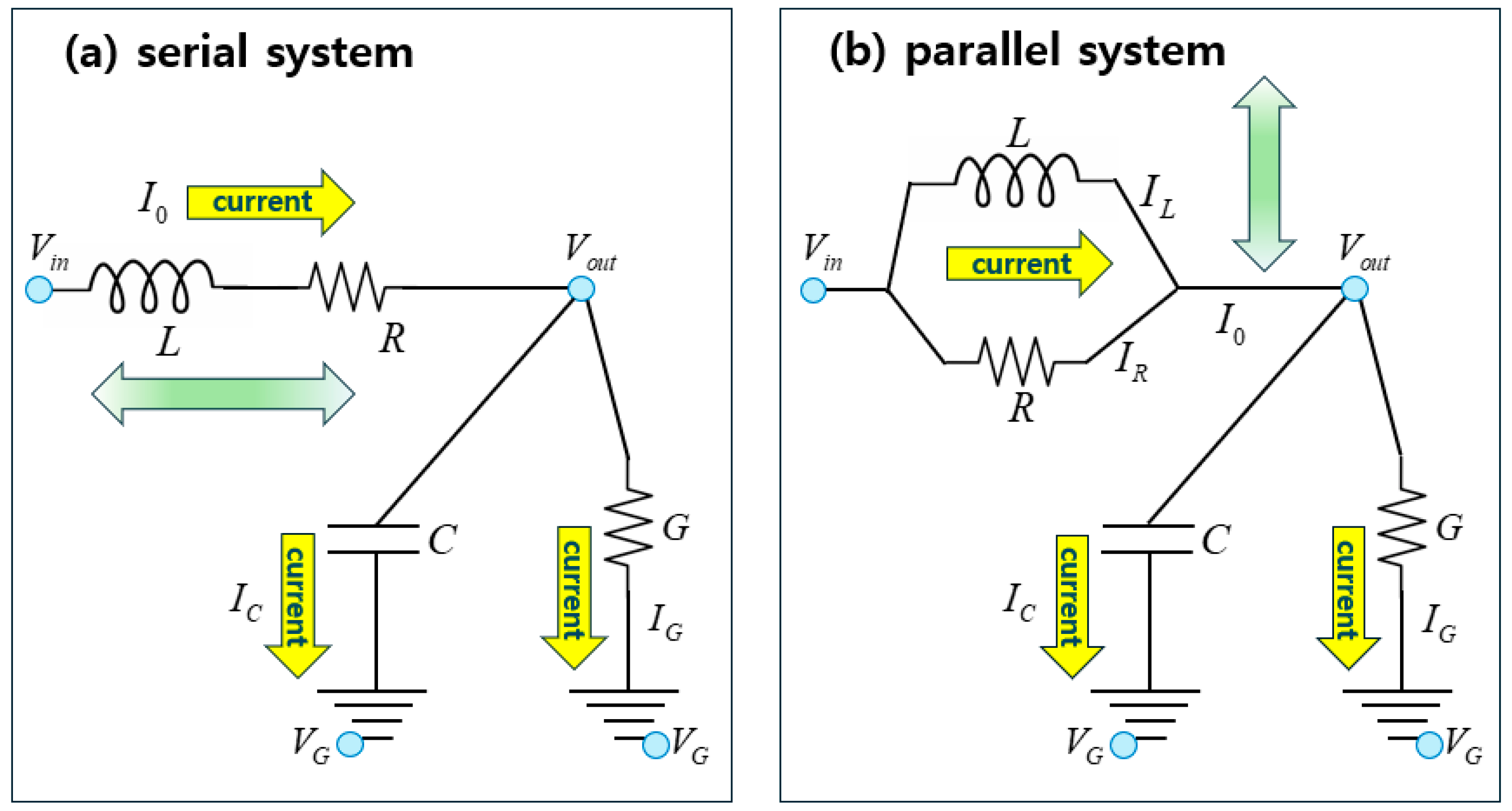
6. Response Functions of Single Four-Element Electric Circuits

Let us consider another leaky circuit consisting of four discrete electric elements $\left\{R,L,G,C\right\}$ with $RLGC\ne 0$. Figure 8 illustrates two distinct circuit arrangements, which are variants of the full leaky RLGC circuit displayed on Figure 3(a). Both arrangements in Figure 8 share the same pairs of SEI components, namely, a capacitor with $C$ and a conductor with $G$ that are connected in parallel to each other. This $C-G$ subcircuit is then linked to a system consisting of an inductor with $L$ and a resistor with $R$. The difference is that $R$ and $L$ within a system are connected in series with each other on Figure 8(a), while they are arranged in parallel to each other on Figure 8(b).

See equation (4) for the relationships between dimensional and dimensionless parameters. While the per-unit-length properties $\left\{\overline{R},\overline{L},\overline{G},\overline{C}\right\}$ are appropriate for the continuous electric circuit on Figure 3(a), the total properties $\left\{R,L,G,C\right\}$ are certainly appropriate for the discrete electric circuit on Figure 8.

For each configuration, our goal is to find the (frequency) response function $\left(V_{out}-V_G\right)/\left(V_{in}-V_G\right)$, being the ratio of the output electric potential $V_{out}$ against the input electric potential $V_{in}$. Here, $V_G$ is a common ground potential, being held constant [38]. For simplicity, we neglect any spatial dependences unlike the case with Figure 3(a) so that only temporal dynamics will be considered. We thus do not need a reference length $\ell$ here.

In addition, notice that the two SEI elements $\left\{G,C\right\}$ carry electric currents $\left\{I_G,I_C\right\}$, respectively. According to Kirchhoff’s circuit law of conservation of electric currents, we have $I_0=I_C+I_G$. Hence, the following pair of relations hold true [38].

$$\begin{array}{l}\left\{\begin{array}{l}{I}_C=C{\displaystyle \frac{d\left(V_{out}-V_G\right)}{dt}}\\ I_G=G\left(V_{out}-V_G\right)\end{array}\right.,\begin{array}{c}\end{array}{V}_{in},V_{out},I_0,I_C,I_G\propto e^{i\omega }\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\left\{\begin{array}{l}{I}_C=i\omega C\left(V_{out}-V_G\right)\\ I_G=G\left(V_{out}-V_G\right)\end{array}\right.\\ I_0=I_C+I_G\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}i\omega C\left(V_{out}-V_G\right)+G\left(V_{out}-V_G\right)=I_0\end{array}$$

(53)

Here, we have applied the Ansatz $V_{in},V_{out},I_0,I_C,I_G\propto e^{i\omega }$ for temporal periodicity of dynamics.

Let us make analysis of the serial system shown on Figure 8(a) as in equation (53).

$$V_{in}-V_{out}=R{I}_0+L{\displaystyle \frac{d{I}_0}{dt}}=R{I}_0+i\omega L{I}_0\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}{I}_0={\displaystyle \frac{V_{in}-V_{out}}{R+i\omega L}}$$

(54)

Combining $I_C+I_G=I_0$ in equation (53) and $I_0$ in equation (54) leads to the following response function.

$$\begin{array}{l}\mathrm{i}\omega C\left(V_{out}-V_G\right)+G\left(V_{out}-V_G\right)=I_0={\displaystyle \frac{V_{in}-V_G-\left(V_{out}-V_G\right)}{R+\mathrm{i}\omega L}}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ \left[1+\left(R+\mathrm{i}\omega L\right)\left(G+\mathrm{i}\omega C\right)\right]\left(V_{out}-V_G\right)=V_{in}-V_G\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ {\mathsf{\Gamma }}_s\equiv {\displaystyle \frac{V_{out}-V_G}{V_{in}-V_G}}={\displaystyle \frac{1}{1+\left(R+\mathrm{i}\omega L\right)\left(G+i\omega C\right)}}={\displaystyle \frac{1}{1+RG+\left(RC+LG\right)i\omega -LC{\omega }^2}}\end{array}$$

(55)

Let us turn to the parallel system displayed on Figure 8(b) as follows by way of $I_R+I_L=I_0$, being different from equation (54).

$$\begin{array}{l}\left\{\begin{array}{l}{V}_{in}-V_{out}=R{I}_R\\ V_{in}-V_{out}=L{\displaystyle \frac{d{I}_L}{dt}}\end{array}\right.\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\left\{\begin{array}{l}{V}_{in}-V_{out}=R{I}_R\\ V_{in}-V_{out}=Li\omega I_L\end{array}\right.\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ I_R+I_L=I_0\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}{\displaystyle \frac{V_{in}-V_{out}}{R}}+{\displaystyle \frac{V_{in}-V_{out}}{i\omega L}}=I_0\end{array}$$

(56)

Combining $I_C+I_G=I_0$ in equation (53) and $I_R+I_L=I_0$ in equation (56) leads to the following response function for the parallel system.

$$\begin{array}{l}i\omega C\left(V_{out}-V_G\right)+G\left(V_{out}-V_G\right)=I_0={\displaystyle \frac{V_{in}-V_{out}}{R}}+{\displaystyle \frac{V_{in}-V_{out}}{i\omega L}}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ RLi\omega \left(G+i\omega C\right)\left(V_{out}-V_G\right)=\left(R+i\omega L\right)\left(V_{in}-V_{out}\right)\\ \begin{array}{cc}& \end{array}=\left(R+i\omega L\right)\left[V_{in}-V_G-\left(V_{out}-V_G\right)\right]\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ {\mathsf{\Gamma }}_p\equiv {\displaystyle \frac{V_{out}-V_G}{V_{in}-V_G}}={\displaystyle \frac{R+i\omega L}{R+i\omega L+RLi\omega \left(G+i\omega C\right)}}={\displaystyle \frac{R+i\omega L}{R+\left(1+RG\right)i\omega L-RLC{\omega }^2}}\end{array}$$

(57)

Meanwhile, let us invert $\eta \equiv \frac{1}{2}\left(q+q^{-1}\right)$ in equation (11) as follows.

$$\eta \equiv {\displaystyle \frac{1}{2}}\left(q+{\displaystyle \frac{1}{q}}\right)\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}{q}^2-2\eta q+1=0\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}q=\eta \pm \sqrt{{\eta }^2-1}$$

(58)

Therefore, $\eta$ is doubly valued in $q$. Hence, it will be better to employ $q$ whenever both of $\left\{q,\eta \right\}$ show up in the forthcoming formulas.

Let us make dimensionless both complex response functions ${\mathsf{\Gamma }}_s$ (for serial system) and ${\mathsf{\Gamma }}_p$ (for parallel system), respectively in equations (55) and (57) as follows [19].

$$\left\{\begin{array}{l}serial:\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}{\mathsf{\Gamma }}_s={\displaystyle \frac{1}{1+RG\left(1-{\mathsf{\Omega }}^2\right)+RG\left(q+q^{-1}\right)i\mathsf{\Omega }}}\\ parallel:\begin{array}{c}\end{array}{\mathsf{\Gamma }}_p={\displaystyle \frac{1+iq\mathsf{\Omega }}{1-RG{\mathsf{\Omega }}^2+\left(1+RG\right)iq\mathsf{\Omega }}}\end{array}\right.$$

(59)

Here, we have employed the following intermediate relationships based on the various parameters presented in equations (11) and (32).

$$\left\{\begin{array}{l}LC{\omega }^2=RG{\displaystyle \frac{LC}{RG}}{\omega }^2=RG{\mathsf{\Omega }}^2\\ q\equiv \sqrt{{\displaystyle \frac{LG}{RC}}}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}{\displaystyle \frac{L}{R}}\omega ={\displaystyle \frac{L}{R}}\sqrt{{\displaystyle \frac{RG}{LC}}}\sqrt{{\displaystyle \frac{LC}{RG}}}\omega \equiv \sqrt{{\displaystyle \frac{LG}{RC}}}\mathsf{\Omega }\equiv q\mathsf{\Omega }\\ \left(RC+LG\right)\omega =\sqrt{{\displaystyle \frac{RG}{LC}}}\left(RC+LG\right)\sqrt{{\displaystyle \frac{LC}{RG}}}\omega \equiv RG{\displaystyle \frac{RC+LG}{\sqrt{RLGC}}}\mathsf{\Omega }\equiv RG\left(q+q^{-1}\right)\mathsf{\Omega }\end{array}\right.$$

(60)

Notice again that the product $RG$ is dimensionless as provided in equation (3). This way of comparing serial and parallel circuits is crucial to properly assessing the performances of electrical devices useful in practice [62].

Normally, what we need are the following magnitudes.

$$\left\{\begin{array}{l}serial:\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\left|{\mathsf{\Gamma }}_s\right|={\displaystyle \frac{1}{\sqrt{{\left[1+RG\left(1-{\mathsf{\Omega }}^2\right)\right]}^2+{\left[RG\left(q+q^{-1}\right)\mathsf{\Omega }\right]}^2}}}\\ parallel:\begin{array}{c}\end{array}\left|{\mathsf{\Gamma }}_p\right|={\displaystyle \frac{\sqrt{1+{\left(q\mathsf{\Omega }\right)}^2}}{\sqrt{{\left(1-RG{\mathsf{\Omega }}^2\right)}^2+{\left[\left(1+RG\right)q\mathsf{\Omega }\right]}^2}}}\end{array}\right.$$

(61)

Large-$\mathsf{\Omega }$ limits are easily found below.

$$\left\{\begin{array}{l}serial:\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\underset{\mathsf{\Omega }\to \infty }{\lim }\left|{\mathsf{\Gamma }}_s\right|={\displaystyle \frac{1}{RG}}{\displaystyle \frac{1}{{\mathsf{\Omega }}^2}}\\ parallel:\begin{array}{c}\end{array}\underset{\mathsf{\Omega }\to \infty }{\lim }\left|{\mathsf{\Gamma }}_p\right|={\displaystyle \frac{q\mathsf{\Omega }}{RG{\mathsf{\Omega }}^2}}={\displaystyle \frac{q}{RG}}{\displaystyle \frac{1}{\mathsf{\Omega }}}\end{array}\right.$$

(62)

Hence, the serial system exhibits an inversely linear behavior with respect to $\mathsf{\Omega }$, while the parallel system exhibits an inversely quadratic behavior with respect to $\mathsf{\Omega }$.

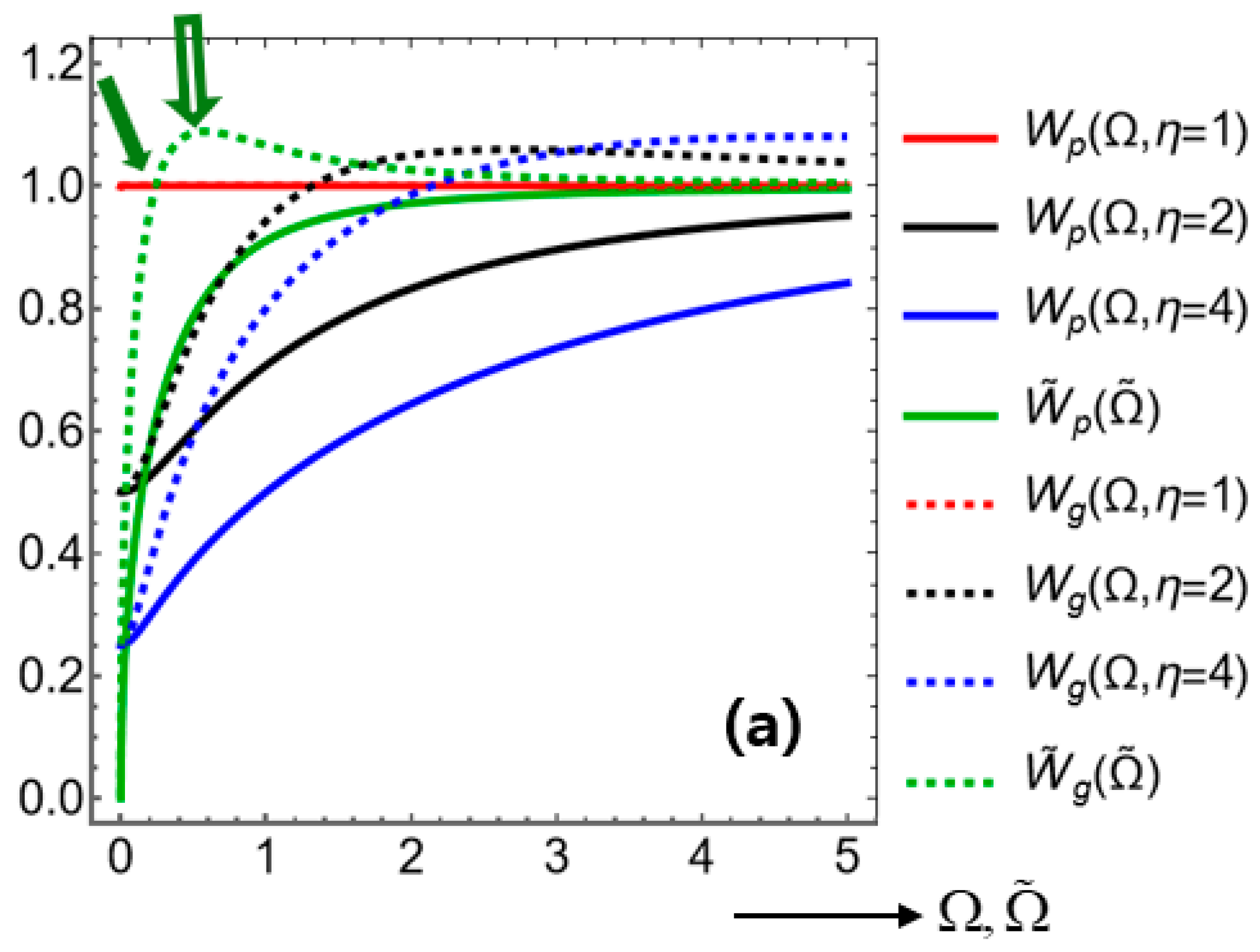
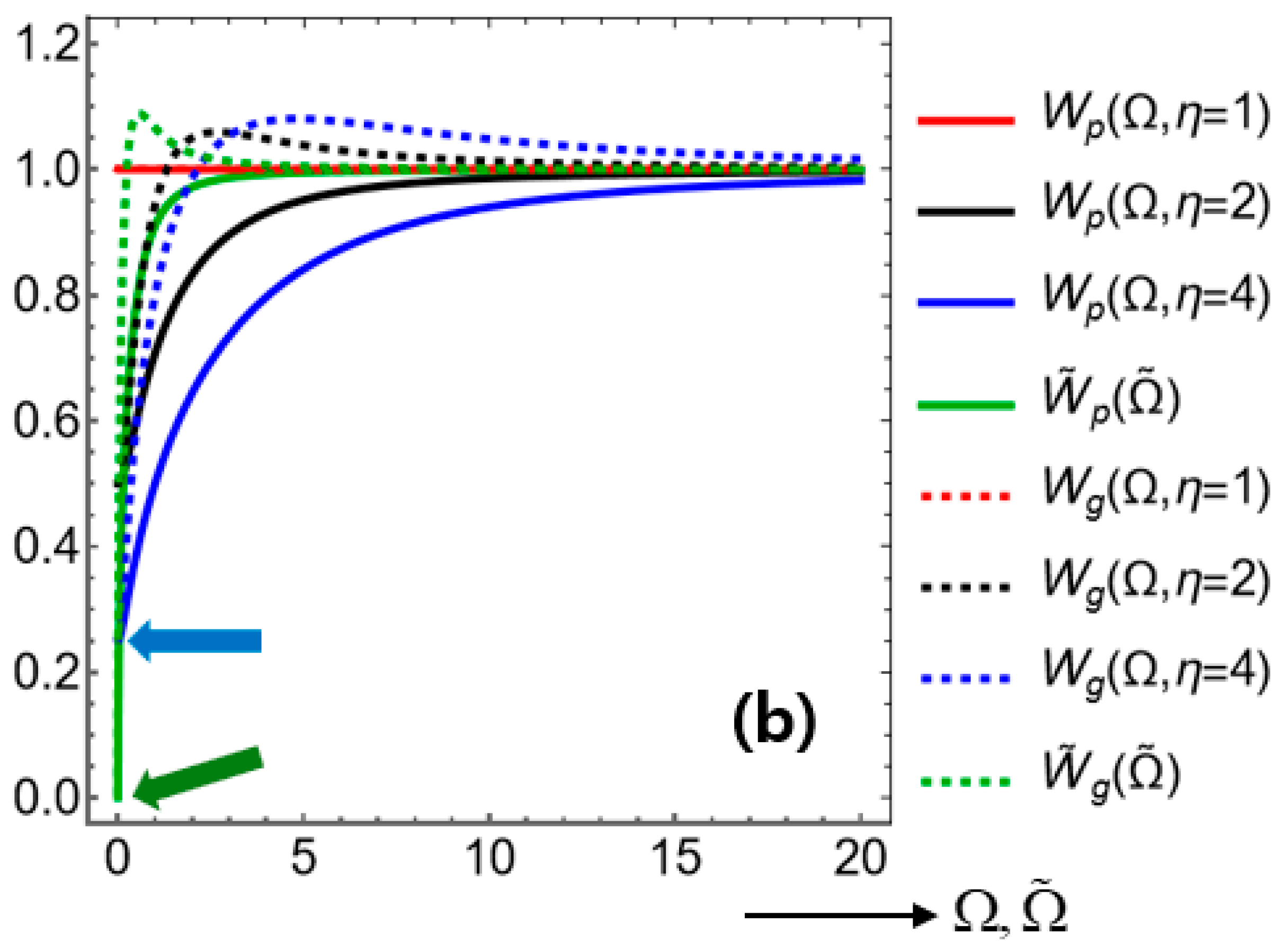
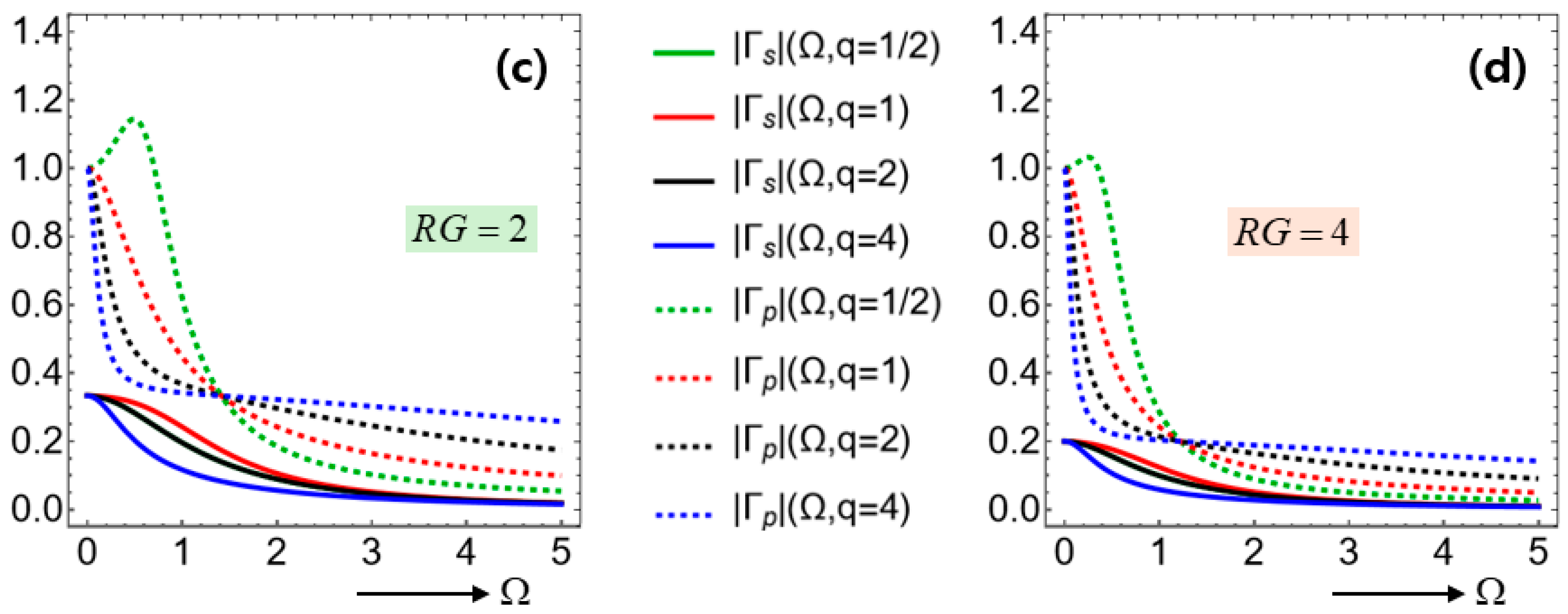
Figure 9 shows the magnitudes of response functions $\left\{\left|{\mathsf{\Gamma }}_s\right|,\left|{\mathsf{\Gamma }}_p\right|\right\}$ plotted against the dimensionless frequency $\mathsf{\Omega }$ for varying values of $q=\frac{1}{2},1,2,4$. For a given value of $RG$, each subfigure displays that $\left|{\mathsf{\Gamma }}_s\right|<\left|{\mathsf{\Gamma }}_p\right|$ over all range of $\mathsf{\Omega }$. In words, a parallel system undergoes a less potential drop than a serial system while the SEIs remain the same.

Most of the response functions exhibit maxima at zero frequencies (namely, static states), thus standing for low-pass filters [10]. One exception is the dotted green curves for $\left|{\mathsf{\Gamma }}_p\right|$ with $q=\frac{1}{2}<1$, where a maximum takes place at a non-zero finite $\mathsf{\Omega }$. Other curves of red, black, and blue colors exhibit uniform decreases with increasing $\mathsf{\Omega }$. Besides, the curves of $\left|{\mathsf{\Gamma }}_s\right|\left(\mathsf{\Omega },RG,q\right)$ are identical with those of $\left|{\mathsf{\Gamma }}_s\right|\left(\mathsf{\Omega },RG,q^{-1}\right)$ thanks to the factor $\left(q+q^{-1}\right)$ appearing in equation (61).

The four subfigures of Figure 9 show that the high-frequency components are especially damped with increasing $RG$ as also observed by [38] in their numerical solution with a LIF model. Leakages help a system under consideration to become robust (namely, stable) against perturbations although leaks are incurred [57].

In this regard, consider a temporally periodic function where each cycle consists of two step changes and a flat period in between, followed by a dormant period as displayed on Figure 1(d). Suppose further that such temporal discontinuities are resolved into various frequency components according to Fourier decomposition [62]. In view of Gibbs’ phenomenon for such a decomposition, there appear unwanted high-frequency components that get stronger across discontinuities [31]. The low-pass (temporal) filter as shown on Figure 9 dampens faster-oscillating components by greater amount than slower oscillating components [25].

In this respect, the large-$\mathsf{\Omega }$ behaviors in equation (62) are also visible on Figure 9, where stronger temporal attenuations with increasing $\mathsf{\Omega }$ are exhibited for a serial system in comparison to a parallel system. Such a low-pass filter capability would have been associated with non-zero values of the inductance $L$. This reasoning is based on the dispersion features displayed on Figure 7 obtained for the rotation-free leaky circuit with $L=0$ and $RGC\ne 0$, where ever-increasing relation ${\widehat{K}}_r\left(\widehat{\mathsf{\Omega }}\right)$ is shown up to infinitely high frequencies.

The discontinuous step-up and step-down processes illustrated by the red lines on Figure 1(d) model an idealistic situation. Instead, we suppose in practical situations that continuous ramp-up and ramp-down processes indicated by the blue dotted curves on Figure 1(d) are more likely to take place [33,40,50,51,62]. For that kind of temporally continuous forcing, the portion of the high-frequency response will be of less nuisance. A disadvantage is that the entire analysis would require numerical solutions for such continuous forcing functions.

It is seen from Figure 9 that a parallel system is more efficient than a serial system in acting as a low-pass filter. In this respect, it is well-known that a central processing unit (CPU) works mostly via serial processing, while a graphical processing unit (GPU) functions via parallel processing. We are then faced with our own question as to whether a GPU serves as a generically better low-pass filter than a CPU. This question remains to be answered in our future publications.

In this respect, let us consider the serial system displayed on Figure 8(a), where the two elements $R-L$ are repeated in a serial manner as indicated by the horizontal double-headed green arrow. To find the pertinent response function, we need to modify the system given in equations (53), (54), and (55) in the following manner.

$$\begin{array}{l}i\omega C\left(V_{out}-V_G\right)+G\left(V_{out}-V_G\right)=I_0={\displaystyle \frac{V_{in}-V_{out}}{n\left(R+\mathrm{i}\omega L\right)}}\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ {\mathsf{\Gamma }}_s^n\equiv {\displaystyle \frac{V_{out}-V_G}{V_{in}-V_G}}={\displaystyle \frac{1}{1+nRG+\left(nRC+nLG\right)i\omega -nLC{\omega }^2}}\end{array}$$

(63)

Here, the superscript ‘$n$’ indicates a repetition number.

We find that ${\mathsf{\Gamma }}_s$ in equation (63) is obtainable by making substitutions $R\to nR$ and $L\to nL$ into ${\mathsf{\Gamma }}_s$ in equation (55), thereby satisfying the usual recipe for serial extension.

Likewise, let us consider the parallel system displayed on Figure 8(b), where the two elements $R-L$ are repeated in a parallel manner as indicated by the vertical double-headed green arrow. To find the pertinent response function, we need just to modify the system given in equations (56) and (57) in the following manner.

$$\begin{array}{l}i\omega C\left(V_{out}-V_G\right)+G\left(V_{out}-V_G\right)=I_0=n\left({\displaystyle \frac{V_{in}-V_{out}}{R}}+{\displaystyle \frac{V_{in}-V_{out}}{\mathrm{i}\omega L}}\right)\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ {\mathsf{\Gamma }}_p^n\equiv {\displaystyle \frac{V_{out}-V_G}{V_{in}-V_G}}={\displaystyle \frac{n\left(R+\mathrm{i}\omega L\right)}{nR+\left(n+RG\right)i\omega L-RLC{\omega }^2}}\end{array}$$

(64)

Therefore, ${\mathsf{\Gamma }}_p$ in equation (64) is obtainable by making substitutions $G\to n^{-1}G$ and $C\to n^{-1}C$ into ${\mathsf{\Gamma }}_p$ in equation (57), thereby conforming to the usual recipe for parallel juxtaposition.

According to the ways that $\mathsf{\Omega }$ and $q$ are defined respectively in equation (11) and (32), both $\mathsf{\Omega }$ and $q$ remain unaltered even under the serial extension and the parallel juxtaposition. Consequently, the dimensionless forms in equations (63) and (64) are easily modified to the following.

$$\begin{array}{l}\left\{\begin{array}{l}serial:\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}{\mathsf{\Gamma }}_s^n={\displaystyle \frac{1}{1+nRG\left(1-{\mathsf{\Omega }}^2\right)+nRG\left(q+q^{-1}\right)i\mathsf{\Omega }}}\\ parallel:\begin{array}{c}\end{array}{\mathsf{\Gamma }}_p^n={\displaystyle \frac{n\left(1+iq\mathsf{\Omega }\right)}{n-RG{\mathsf{\Omega }}^2+\left(n+RG\right)iq\mathsf{\Omega }}}\end{array}\right.\begin{array}{c}\end{array}\Rightarrow \begin{array}{c}\end{array}\\ \left\{\begin{array}{l}serial:\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\left|{\mathsf{\Gamma }}_s^n\right|={\displaystyle \frac{1}{\sqrt{{\left[1+nRG\left(1-{\mathsf{\Omega }}^2\right)\right]}^2+{\left[nRG\left(q+q^{-1}\right)\mathsf{\Omega }\right]}^2}}}\\ parallel:\begin{array}{c}\end{array}\left|{\mathsf{\Gamma }}_p^n\right|={\displaystyle \frac{n\sqrt{1+{\left(q\mathsf{\Omega }\right)}^2}}{\sqrt{{\left(n-RG{\mathsf{\Omega }}^2\right)}^2+{\left[\left(n+RG\right)q\mathsf{\Omega }\right]}^2}}}\end{array}\right.\end{array}$$

(65)

Hence, we get to the following large-$\mathsf{\Omega }$ limits.

$$\left\{\begin{array}{l}serial:\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\underset{\mathsf{\Omega }\to \infty }{\lim }\left|{\mathsf{\Gamma }}_s^n\right|={\displaystyle \frac{1}{nRG{\mathsf{\Omega }}^2}}={\displaystyle \frac{1}{n}}{\displaystyle \frac{1}{RG}}{\displaystyle \frac{1}{{\mathsf{\Omega }}^2}}\equiv {\displaystyle \frac{1}{n}}\underset{\mathsf{\Omega }\to \infty }{\lim }\left|{\mathsf{\Gamma }}_s^1\right|\\ parallel:\begin{array}{c}\end{array}\underset{\mathsf{\Omega }\to \infty }{\lim }\left|{\mathsf{\Gamma }}_p^n\right|={\displaystyle \frac{nq\mathsf{\Omega }}{RG{\mathsf{\Omega }}^2}}=n{\displaystyle \frac{q}{RG}}{\displaystyle \frac{1}{\mathsf{\Omega }}}\equiv n\underset{\mathsf{\Omega }\to \infty }{\lim }\left|{\mathsf{\Gamma }}_p^1\right|\end{array}\right.$$

(66)

Here, $\left|{\mathsf{\Gamma }}_s^1\right|$ and $\left|{\mathsf{\Gamma }}_p^1\right|$ are what have already been presented in equation (62), which corresponds to $n=1$ with a single pair of $\left\{R,L\right\}$.

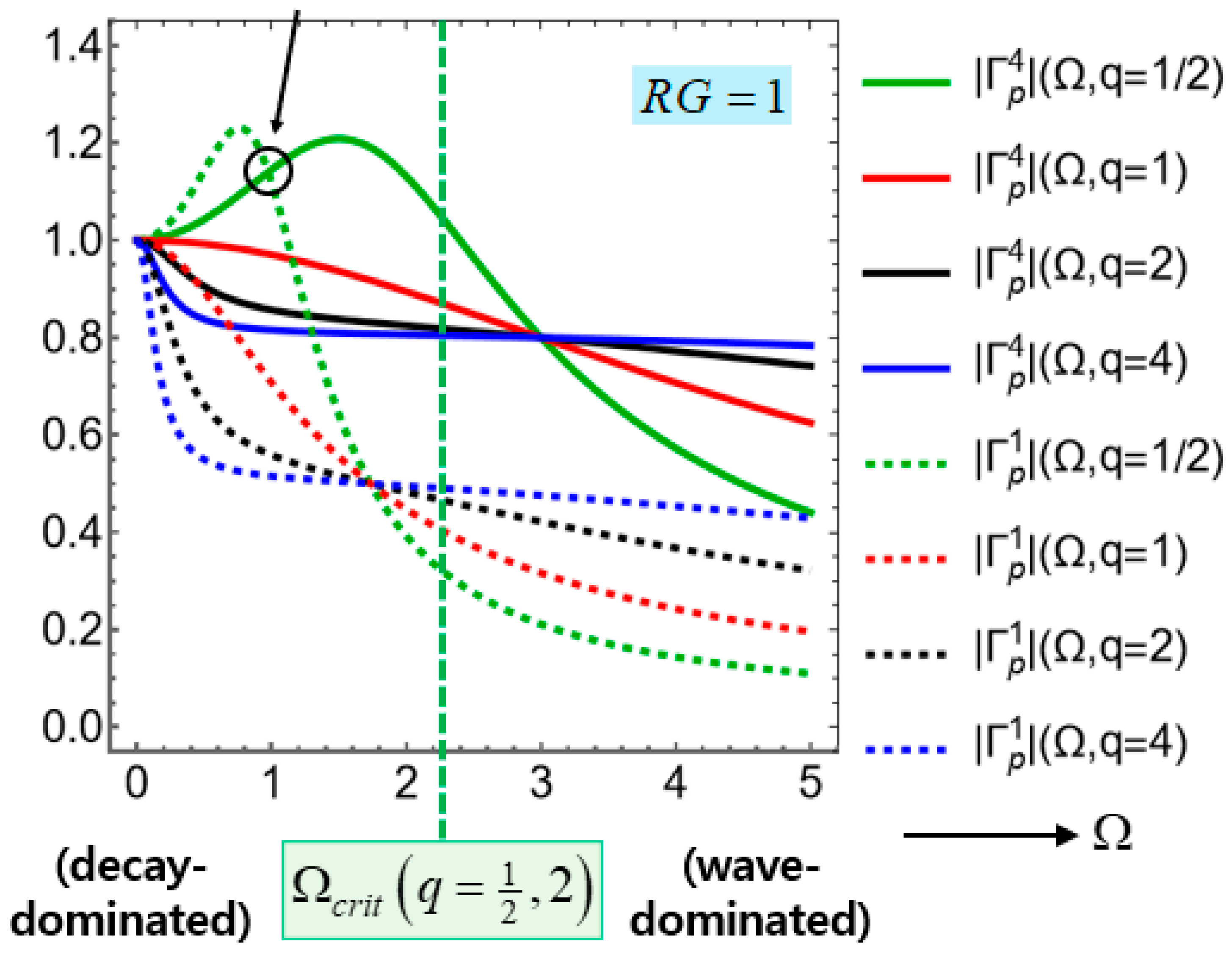
Notice that the response functions $\left|{\mathsf{\Gamma }}_s^n\right|$ and $\left|{\mathsf{\Gamma }}_p^n\right|$ have been derived by neglecting all spatial variations, while keeping only temporal variations. Notwithstanding, the error incurred by the serial extension for $n>1$ gets more serious due to, say, the temporal delay ${\tau }_{RLGC}^{10}$ presented in equation (7). In comparison, the error incurred by the parallel juxtaposition for $n>1$ would become minimal thanks to the same longitudinal extension. Therefore, $\left|{\mathsf{\Gamma }}_s^n\right|$ becomes less reliable as $n$ is increased, while $\left|{\mathsf{\Gamma }}_p^n\right|$ stays relatively reliable even with creasing $n$.

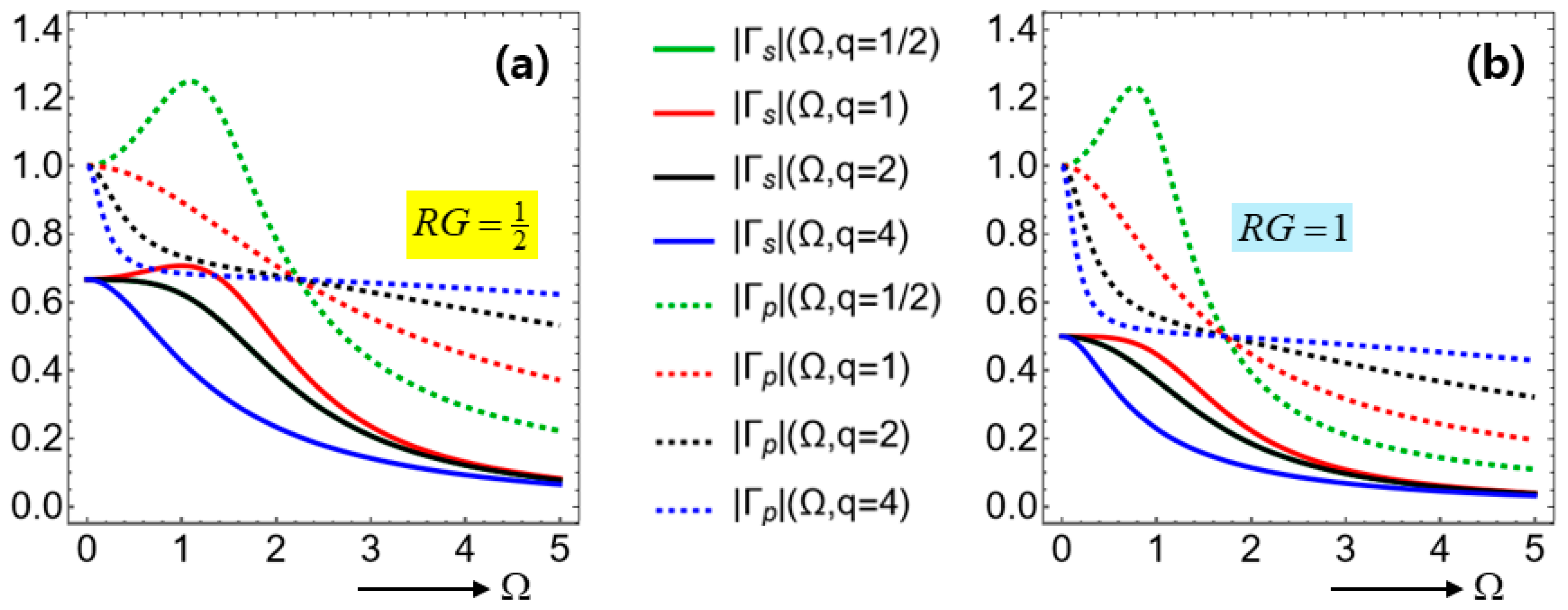
Equations (65) and (66) tell that $\left|{\mathsf{\Gamma }}_s^n\right|$ is uniformly decreasing with increasing $n$. In comparison, $\left|{\mathsf{\Gamma }}_p^n\right|$ appears to be rather fuzzy with varying $n$. Therefore, Figure 10 displays $\left|{\mathsf{\Gamma }}_p^n\right|$ with two values of $n=1,4$. We learn from Figure 10 that $\left|{\mathsf{\Gamma }}_p^1\right|<\left|{\mathsf{\Gamma }}_p^4\right|$ if $q>1$. In comparison, $\left|{\mathsf{\Gamma }}_p^1\right|$ and $\left|{\mathsf{\Gamma }}_p^4\right|$ undergo a crossover with varying $\mathsf{\Omega }$ if $q=\frac{1}{2}<1$ as seen by the pair of green curves, which is marked by a black blank circle and pointed to by a black solid downward arrow on Figure 10.

We have examined the balance between $\left(RC+LG\right)\left(\partial V/\partial t\right)$ and $\left(LC\right)\left({\partial }^{2}V/\partial t^2\right)$ in equation (7) in coming up with ${\tau }_{RLGC}^{12}$. Let us find below the condition that these two terms are equal in magnitudes in terms of the frequency $\mathsf{\Omega }\equiv {\tau }_{RLGC}\omega$ defined in equation (32).

$$\begin{array}{l}\left|{\displaystyle \frac{LC\frac{{\partial }^{2}V}{\partial t^2}}{\left(RC+LG\right)\frac{\partial V}{\partial t}}}\right|\propto \left|{\displaystyle \frac{LC{\omega }^2}{\left(RC+LG\right)\omega }}\right|={\displaystyle \frac{LC}{RC+LG}}\sqrt{{\displaystyle \frac{RG}{LC}}}\sqrt{{\displaystyle \frac{LC}{RG}}}\omega \\ \begin{array}{cc}& \end{array}={\displaystyle \frac{\sqrt{RLGC}}{RC+LG}}\mathsf{\Omega }={\displaystyle \frac{1}{\sqrt{\frac{LG}{RC}}+\sqrt{\frac{RC}{LG}}}}\mathsf{\Omega }={\displaystyle \frac{1}{2\eta }}={\displaystyle \frac{1}{q+\frac{1}{q}}}\mathsf{\Omega }\end{array}$$

(67)

Here, we have utilized ${\tau }_{RLGC}\equiv \sqrt{\left(LC\right)/\left(RG\right)}$ and $q\equiv \sqrt{\left(LG\right)/\left(RC\right)}$, which have been introduced in equation (32). Therefore,

$$\begin{array}{l}{\mathsf{\Omega }}_{crit}\equiv 2\eta \equiv q+q^{-1}\\ \left\{\begin{array}{l}\mathsf{\Omega }<{\mathsf{\Omega }}_{crit}:\begin{array}{c}\end{array}\left|LC{\displaystyle \frac{{\partial }^{2}V}{\partial t^2}}\right|<\left|\left(RC+LG\right){\displaystyle \frac{\partial V}{\partial t}}\right|\\ \mathsf{\Omega }>{\mathsf{\Omega }}_{crit}:\begin{array}{c}\end{array}\left|LC{\displaystyle \frac{{\partial }^{2}V}{\partial t^2}}\right|>\left|\left(RC+LG\right){\displaystyle \frac{\partial V}{\partial t}}\right|\end{array}\right.\end{array}$$

(68)

The critical frequency is evaluated below for example.

$${\mathsf{\Omega }}_{crit}\equiv 2\eta \equiv q+q^{-1}:\begin{array}{cc}& \end{array}\left\{\begin{array}{l}q=1:\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}{\mathsf{\Omega }}_{crit}=2\\ q=\frac{1}{2},2:\begin{array}{c}\end{array}{\mathsf{\Omega }}_{crit}=2\frac{1}{2}=\frac{5}{2}\\ q=\frac{1}{4},4:\begin{array}{c}\end{array}{\mathsf{\Omega }}_{crit}=4\frac{1}{4}=\frac{17}{4}\end{array}\right.$$

(69)

Let us take $q=\frac{1}{2},2$ for both of which ${\mathsf{\Omega }}_{crit}=2\frac{1}{2}=\frac{5}{2}$. This dividing critical frequency is indicated on Figure 10 by the green vertical dotted line. Figure 10 marks the left region $\mathsf{\Omega }<{\mathsf{\Omega }}_{crit}=\frac{5}{2}$ by ‘decay-dominated’, while it marks the right region $\mathsf{\Omega }>{\mathsf{\Omega }}_{crit}=\frac{5}{2}$ by ‘wave-dominated’. In brief, low-pass filters favor decay-dominated temporal dynamics.

7. Discussion

To get closer to reality, we need to consider telegraph equations over a finite 1-D domain as on Figure 2 [49]. For that purpose, proper boundary conditions (BCs) should be assigned for problems valid over a finite 1-D domain [28,50]. To this goal, in-depth analysis of the relevant BCs is required to reflect the physical situation at hand in our project [4].

What we expect from the resulting solutions to the telegraph equation over a finite 1-D domain is the relative strength between forward waves and backward waves [42]. From this viewpoint, the unequal strengths of forward and backward waves are determined by the ratio between $\left\{\left|p_{+}\right|,\left|p_{-}\right|\right\}$ in equation (27). This ratio is undetermined since $\gamma$ in equation (27) is still undetermined. Actual values of $\gamma$ should be determined by applying appropriate side conditions [42].

Such distinct wave velocities are in sharp contrast to the form $V\propto g\left(x\pm at\right)$ as a solution to the idealized hypothetical equation (16). We suppose that a proper set of BCs at both ends of a finite-length tube such as on Figure 2(b–d) should properly reflect the moving plunger at the upstream and the droplet ejection dynamics at the downstream end as depicted on Figure 1(c). Following an analogous line of reasoning, we conjecture that backward waves are associated with the backlash occurring with 3-D printing [32] and/or the suck-back phenomenon associated with the end-phase ejection of droplets being issued outward from droplet dispensers [7].

In this connection, the forward wave is generated by stimulating a previously inactive region, whereas the backward (reverse) wave is initiated by removing stimulation from a previously active region [19].

As crudes approximations, either Neumann condition or Dirichlet condition could be chosen [2,12,28]. However, when a mixed-type BC with generic complex coefficients is admitted, selections of physically admissible BC will get intricate. Here comes the notion of feedback due to the BC at the downstream end, by which the whole upstream dynamics may be significantly affected [45]. Moreover, the tube displacements $u_r$ shown on Figure 2(b–d) in the longitudinal direction should also be accounted for in a more realistic situation [12], thereby demanding more delicate BCs.

Solving the 3-D telegraph equation valid over the whole space as discussed in section 4 will be challenging when a problem domain is chosen either the inside or the outside of a circular cylindrical hollow tube of finite axial length. In this case, the Cartesian coordinates employed in section 4 should be replaced with cylindrical coordinates in handling the pertinent differential equations. Even the circumferential independence is assumed, this 3-D telegraph equation will be hard to solve depending on the necessary side conditions.

Last but not the least, the telegraph equations modified for droplet dispensers will be examined by consulting our experimental measurement data in a separate publication.

8. Conclusions

We have not only collected well-known fundamental properties of telegraph equations but also identified so-far hidden characteristics. Interactions between a system and an environment shed new light on the notion of leakage not only in mechanical vibration but also electric circuits. Especially, crossovers are found to take place for the phase and group velocities. We hope this study will help us in the future to set up real-time control devices and attendant control software for droplet dispensers employable for practical underfill encapsulation of integrated circuit chips. In this respect, we performed fundamental studies on propagating waves that carry information back and forth with unavoidable decays.