Deformed Special Relativity in Light of Unruh Effect

1. Introduction

The well-known Unruh effect[1,2,3,4] is a theoretical prediction in quantum field theory (QFT). It suggests that an observer who accelerates with a constant accelaration a through the empty space perceives a background thermal radiation, unlike a non-accelerating observer who would perceive a pure vacuum state without radiation as if it were at the zero absolute temperature ($T=0$K).

The temperature T of the background thermal bath is directly proportional to the observer’s proper acceleration (a), so that it is given by the famous formula $T={\displaystyle \frac{\hslash a}{2\pi c{k}_B}}$[1,2,3,4]. Such effect is seen as a connection between quantum mechanics, thermodynamics and general relativity. It is related to Hawking radiation from black holes. Direct experimental verification is challenging due to the extremely high accelerations required, but analog systems are being investigated.

In this paper, we will investigate a deformed relativistic dynamics due to the existence of background thermal vacuum whose emitted radiation is connected to a temperature T caused by an accelerated particle that feels a thermal bath according to Unruh effect, thus leading to a correction on the energy $E=m{c}^2=\gamma m{c}^2$. Due to such correction that consider a background thermal bath for the accelerated particle, we bring back the idea of an ultra-referential (a preferred frame), so that the velocity and acceleration of a particle is always given with respect to such privileged reference frame.

The concept of an absolute space is central to debates in classical and relativistic physics, particularly concerning the nature and origin of inertia. Mach[5] and Sciama[6] addressed this in the context of Mach’s principle, while Schrödinger’s work[7], primarily in quantum mechanics, operates within a framework that generally dispenses with an absolute frame, consistent with relativity principles.

In modern cosmology, the well-known CMB radiation provides an isotropic background reference frame, often referred to as the “cosmic rest frame" or preferred reference frame for cosmological observations. Observers moving relative to this frame can measure their velocity by observing the anisotropy (temperature variations) of the CMB. While this frame is a natural choice for describing the large-scale universe, general relativity ensures the laws of physics are the same in all inertial reference frames.

Deformed special relativity (DSR) in light of Unruh effect brings back an absolute reference frame as being a thermal vacuum. Of couse it is not the classical absolute space (an enpty space) conceived by Newton.

Actually, we think that the energy of a particle presents a non-local origin that comes from an interaction with a background thermal energy representing the whole universe. This means that the free energy $m{c}^2$ is now coupled to a background thermal field, thus leading to a correction on the energy $m{c}^2$ given in function of the background temperature T.

In a simple cosmological scenario, when we consider only one particle that accelerates with respect to the preferred frame and thus perceives a thermal bath, we will also show that the speed of light c is interpreted as an effective speed $c^{\prime }>c$ that depends on the background temperature T . Of course, it is also an effect of the own acceleration of the particle according to Unruh effect, leading to an effective energy $m{c}^{\prime 2}$ that diverges at the Planck temperature. In view of this, we will obtain the correction for the speed of ligh, namely $c\left(T\right)$, where T comes from the Unruh effect. We will show that $c\left(T\right)$ reduces drastically during the inflationary period, so that the so-called horizon problem will be discussed.

2. Modified Energy Equation in the Presence of a Thermal Field

According to special relativity (SR), the mass of a particle is $m=\gamma m_0$, where $m_0$ is the rest mass and $\gamma =1/\sqrt{1-v^2/c^2}$. On the other hand, if we think about the Newton second law applied to the relativistic momentum, we obtain $F=d\left(\gamma m_{0}v\right)/dt=\left(m_0{\gamma }^3\right)dv/dt=m_0{(1-v^2/c^2)}^{-3/2}dv/dt$. Here, we have in mind that $m_0{\gamma }^3$ is an inertial mass ($m_i$). We should realize that the inertial mass $m_i$ is larger than the relativistic mass $m(=\gamma m_0)$. The difference between them is still a controversial question [8,9,10,11,12,13]. Actually, the inertia is the resistance to acceleration ($m_i$), which is not in agreement with the relativistic mass ($m_r$). Therefore, in general we cannot consider $\overrightarrow{F}=m_r\overrightarrow{a}$. An interesting explanation for the difference between $m_i$ and $m=\left(m_r\right)$ could be the influence of an isotropic background field[14]. This universal field interacts with the particle, in such a way that it dresses the relativistic mass, leading to an effective mass $m^{*}(=m_{effective})$ that works like a dressed mass and then plays the role of the own inertial mass $m_i(>m_r)$. Thus we write $m^{*}=m_i={\gamma }^2{m}_r={\gamma }^{2}m$, and finally we can conclude that $m^{*}$ presents a non-local origin given in the scenario of Sciama[6]. Actually, it works like an interaction with a background field associated with a preferred frame[14]. This concept is also within the scenario of Schrödinger[15] and Mach[5] as already discussed before.

Now let us define the factor $\mathrm{\Gamma }={\gamma }^2$, so that we obtain

$$m^{*}=\mathrm{\Gamma }m,$$

(1)

where $\mathrm{\Gamma }$ is a factor that describes a non-local effect due to the isotropic background field in relation to which the particle is moving with speed v[14][16]. So, based on this reasoning, we conclude that the particle is not free, so that the presence of the whole universe modifies its energy, as follows:

$$E^{*}=\mathrm{\Gamma }m{c}^2,$$

(2)

where the modified energy $E^{*}$ is the energy E of the free particle moving in a empty space (without temperature) plus the increment $\delta E$ that represents a non-local interaction of the particle with the whole universe given by a thermal vacuum, so that we write $E^{*}=\mathrm{\Gamma }E=E+\delta E$.

Actually, we are now considering that $\delta E$ comes from the thermal background field of the whole universe. Therefore, there should be an equivalence between the dynamical and thermal approaches in obtaining the deformed relativistic energy, so that we can make the following assumption for the factor $\mathrm{\Gamma }$, namely:

$$\mathrm{\Gamma }\left(v\right)={\left(1-{\displaystyle \frac{v^2}{c^2}}\right)}^{-1}\equiv \mathrm{\Gamma }\left(T\right)={\left(1-{\displaystyle \frac{\frac{m_P{v}^2}{K_B}}{\frac{m_P{c}^2}{K_B}}}\right)}^{-1},$$

(3)

where we get $\mathrm{\Gamma }\left(T\right)={(1-T/T_P)}^{-1}$.

The Planck temperature is $T_P(=m_P{c}^2/K_B\sim {10}^{32}$K) associated with the Planck radius (length $L_P$) $R_P=L_P\sim {10}^{-35}$m in the early universe with Planck energy $E_P(=m_P{c}^2\sim {10}^{19}$GeV). The Planck mass is $m_P(\sim {10}^{-7}$kg).

According to Eq.(3), if $T\to T_P$, $\mathrm{\Gamma }\left(T\right)$ diverges.

Introducing the thermal approach given in Eq.(3) into Eq.(2), we obtain the modified relativistic energy, namely:

$$E=\mathrm{\Gamma }\left(T\right)m{c}^2={\displaystyle \frac{m{c}^2}{\left(1-\frac{T}{T_P}\right)}}={\displaystyle \frac{m_0{c}^2}{\left(1-\frac{T}{T_P}\right)\sqrt{1-\frac{v^2}{c^2}}}},$$

(4)

where we are now using the notation $E^{*}=E$ only for the purpose of simplification in the notation. We have $m=\gamma m_0=m_0/\sqrt{1-v^2/c^2}$.

Here it is important to call attention to the fact that the speed v is given with respect to a thermal background field as for instance the cosmic microwave background (CMB) frame or any other frame related to a background thermal field. However, this research brings novelty in the sense that such issue about thermal vacuum and its influence on the relativistic dynamics will be better understood when we implement the Unruh effect into Eq.(4) given in a previous paper[17].

3. Modified Energy Equation in Light of Unruh Effect

Now let us consider that the temperature T in Eq.(4) is the result of a background thermal bath felt by the particle, which experiences an acceleration a through the preferred frame related to the thermal vacuum, according to Unruh effect, namely:

$$T={\displaystyle \frac{\hslash a}{2\pi K_{B}c}},$$

(5)

where

$$T_P={\displaystyle \frac{\hslash a_P}{2\pi K_{B}c}},$$

(6)

where $a_P\sim {10}^{51}m/s^2$ is the order of magnitute of the Planck acceleration (the maximum aceleration), which is defined as $a_P=c/t_P$. The time $t_P=\sqrt{G\hslash /c^5}\sim {10}^{-43}$s is the Planck time (the minimum time).

Thus, by substituting Eq.(5) and Eq.(6) in Eq.(4), we rewrite Eq.(4) in the following way:

$$E={\displaystyle \frac{m{c}^2}{\left(1-\frac{a}{a_P}\right)}},$$

(7)

where $m=\gamma m_0$.

Eq.(7) should be interpreted as the deformed relativistic energy due to the Unruh effect. This equation shows that the energy of the particle increases when it presents an acceleration a with respect to the preferred frame associated with the thermal background field, so that its temperature T is the effect of the acceleration a of the particle.

The energy of the particle diverges close to the Planck acceleration $a_P$ related to the Planck temperature $T_P$.

Now, according to Eq.(7) based on the Unruh effect, it is easy to understand that the motion of the particle, both its speed v and acceleration a are given in relation to a cosmic background frame represented by a thermal vacuum.

As we find the ratios $E/E_P=K_{B}T/K_B{T}_P=T/T_P=a/a_P$ when dividing Eq.(5) by Eq.(6), it easy to see that Eq.(7) can be rewritten as follows:

$$E={\displaystyle \frac{m{c}^2}{\left(1-\frac{E}{E_P}\right)}},$$

(8)

where $E=K_{B}T$ and $E_P=K_B{T}_P\sim {10}^{19}$GeV, that is the Planck energy scale associated with the Planck temperature $T_P\sim {10}^{32}$K.

It is interesting to realize that Eq.(8) has the same form as the Magueijo-Smolin equation[18] with an invariant Planck energy scale. However, we should perceive that the invariance of $E_P$ originates from an extremely hot background thermal field (a very high vacuum energy density) with Planck temperature $T_P$ due to the Planck acceleration $a_P$ within the Unruh scenario. This is a fundamental explanation for understanding the divergence of the energy at the Planck scale based on thermal vacuum with Planck temperature, which represents the early universe at the Planck scale and the inflationary period due to a very high vacuum energy density, which is justified by an extremely high initial acceleration as is the Planck acceleration $a_P$.

4. Deformed Dispersion Relation

The deformed momentum of a single accelerated particle in the presence of a thermal vacuum due to Unruh effect is as follows:

$$P=\mathrm{\Gamma }mv{\displaystyle \frac{mv}{\left(1-\frac{T}{T_P}\right)}},$$

(9)

or

$$P={\displaystyle \frac{mv}{\left(1-\frac{E}{E_P}\right)}},$$

(10)

or even

$$P={\displaystyle \frac{mv}{\left(1-\frac{a}{a_P}\right)}},$$

(11)

where $m=\gamma m_0$ and $a=2\pi K_{B}cT/\hslash =2\pi Ec/\hslash$, with $E=K_{B}T$.

Now let us we introduce the deformed 4-momentum due to Unruh effect, namely:

$$P^{\mu }=[P^0,P^{\alpha }]=\left[{\displaystyle \frac{\gamma m_{0}c}{\left(1-\frac{T}{T_P}\right)}},{\displaystyle \frac{\gamma m_0{v}^{\alpha }}{\left(1-\frac{T}{T_P}\right)}}\right],$$

(12)

or

$$P^{\mu }=[P^0,P^{\alpha }]=\left[{\displaystyle \frac{\gamma m_{0}c}{\left(1-\frac{E}{E_P}\right)}},{\displaystyle \frac{\gamma m_0{v}^{\alpha }}{\left(1-\frac{E}{E_P}\right)}}\right]$$

(13)

or even

$$P^{\mu }=[P^0,P^{\alpha }]=\left[{\displaystyle \frac{\gamma m_{0}c}{\left(1-\frac{a}{a_P}\right)}},{\displaystyle \frac{\gamma m_0{v}^{\alpha }}{\left(1-\frac{a}{a_P}\right)}}\right],$$

(14)

where the deformed energy is $E=c{P}^0=\gamma m_0{c}^2/(1-T/T_P)=\gamma m_0{c}^2/(1-E/E_P)=\gamma m_0{c}^2/(1-a/a_P)$ and the spatial momentum is $P^{\alpha }=\gamma m_0{v}^{\alpha }/(1-T/T_P)=\gamma m_0{v}^{\alpha }/(1-E/E_P)=\gamma m_0{v}^{\alpha }/(1-a/a_P)$, with $\alpha =1,2,3$.

The quantity $P^{\mu }{P}_{\mu }$ is the deformed energy-momentum relation, namely:

$$P^{\mu }{P}_{\mu }={\displaystyle \frac{E^2}{c^2}}-P^2={\mathrm{\Gamma }}^2{m}_0^2{c}^2,$$

(15)

where we obtain

$$E^2={\displaystyle \frac{m^2{c}^4}{{\left(1-\frac{T}{T_P}\right)}^2}}=c^2{P}^2+{\mathrm{\Gamma }}^2{m}_0^2{c}^4,$$

(16)

or

$$E^2={\displaystyle \frac{m^2{c}^4}{{\left(1-\frac{E}{E_P}\right)}^2}}=c^2{P}^2+{\mathrm{\Gamma }}^2{m}_0^2{c}^4,$$

(17)

or even

$$E^2={\displaystyle \frac{m^2{c}^4}{{\left(1-\frac{a}{a_P}\right)}^2}}=c^2{P}^2+{\mathrm{\Gamma }}^2{m}_0^2{c}^4,$$

(18)

where ${\mathrm{\Gamma }}^2={(1-T/T_P)}^{-2}={(1-E/E_P)}^{-2}={(1-a/a_P)}^{-2}$.

Eq.(16), Eq.(17) and Eq.(18) are equivalent deformed energy-momentum relations due to Unruh effect.

5. Varying Speed of Light in Light of Unruh Effect

The factor $\mathrm{\Gamma }\left(T\right)$ is given for a background temperature detected by an accelerated single particle. Now, let us admit that $\mathrm{\Gamma }$ acts on the speed of light c instead of the mass m, whereas the well-known factor $\gamma$ acts only on the relativistic mass. Hence, we redefine Eq.(4), namely:

$$E=m\left[\mathrm{\Gamma }\left(T\right)c^2\right]=mc{\left(T\right)}^2,$$

(19)

where the factor $\mathrm{\Gamma }\left(T\right)$ is now applied on c instead of m, so that we have $c^{\prime }=c\left(T\right)=\mathrm{\Gamma }c$.

Eq.(19) leads to the following variation on the speed of light c, as follows:

$$c^{\prime }={\displaystyle \frac{c}{\sqrt{1-\frac{T}{T_P}}}},$$

(20)

which was obtained in a previous paper[17].

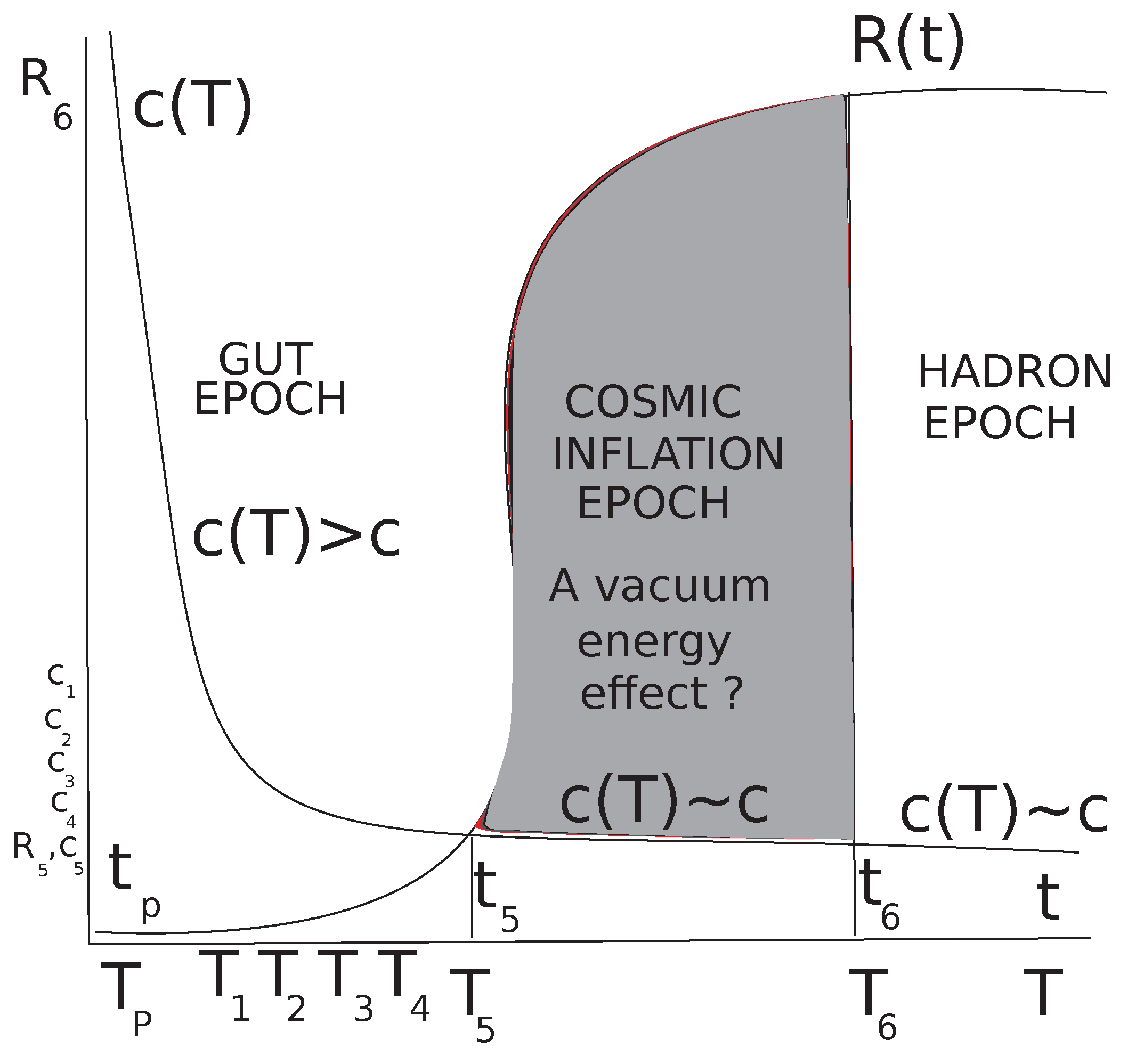
Figure 1 shows the simulations of the variation of values of $c\left(T\right)$ in the origin of the universe compared with the rapid increase of its radius due to cosmic inflation.

Keeping in mind that $T/T_P=E/E_P=a/a_P$ according to Unruh effect shown in Eq.(5) and Eq.(6), then Eq.(20) can be also written, namely:

$$c^{\prime }=c\left(E\right)={\displaystyle \frac{c}{\sqrt{1-\frac{E}{E_P}}}},$$

(21)

or even

$$c^{\prime }=c\left(a\right)={\displaystyle \frac{c}{\sqrt{1-\frac{a}{a_P}}}},$$

(22)

so that, in the limit $T\to T_P$ or $E\to E_P$ or even $a\to a_P$, which could be thought of as the beginning of the inflationary period for an accelerated single particle, the speed of light has diverged and after rapidly slowed down.

The variation of the speed of light due to the accelerated particle involved by a background thermal bath with temperatute T in a cosmological scenario is

$$\delta c=c^{\prime }-c=\left({\displaystyle \frac{1}{\sqrt{1-\frac{T}{T_P}}}}-1\right)c,$$

(23)

or

$$\delta c=\left({\displaystyle \frac{1}{\sqrt{1-\frac{E}{E_P}}}}-1\right)c,$$

(24)

or even

$$\delta c=\left({\displaystyle \frac{1}{\sqrt{1-\frac{a}{a_P}}}}-1\right)c,$$

(25)

where, for $T<<T_P$ or $E<<E_P$ or even $a<<a_P$, we have $\delta c\approx 0$.

Eq.(23), Eq.(24) or even Eq.(25) indicate that the variation $\delta c$, which was infinite at the Planck scale $L_P(\sim {10}^{-35}m$) with Planck energy $E_P(\sim {10}^{19}GeV)$, having an inflationary acceleration of expansion (Planck acceleration $a_p\sim {10}^{51}m/s^2$) reduced abruptly and still led to a very rapid increase in the radius of the universe according to the inflationary model.

The result above for $c\left(T\right)$ or $\delta c$ strongly contradict the VSL theories[19,20,21,22,23,24] that are used in order to try to explain the horizon problem. Such result was investigated in detail in a previous paper[17] without violating the postulate of special relativity (SR), as the speed of light was too large only in the early universe close to the Planck temperature. Therefore, VSL theories should be questioned[17].

6. Some Interesting Questions and Perspectives

According to the Unruh effect ($T=\hslash a/2\pi K_{B}c$), the hypothesis of a null acceleration, i.e., $a=0$ would lead to a vacuum with zero absolute temperature ($T=0$K). However, such vacuum would be something immaterial (empty space) or even metaphysical like Newton’s absolute space, which does not exist. Therefore the absolute zero temperature is prevented in order to avoid the unattainable limit of Newton’s absolute space, so that all particles must be accelerated in order to generate a thermal vacuum, which would be a quantum vacuum where the presence of gravity is unavoidable to accelerate particles. Due to this reasoning, a first interesting question arises: Is there an invariant minimum acceleration contrary to the Planck acceleration in order to prevent the absolute zero temperature according to Unruh effect? If we admit this, for the sake of symmetry, thus another curious question arises: Could we think that the thermal vacuum is associated with a privileged reference frame for an invariant minimum speed as is also the speed of light? So, we are led to build a deformed relativity with four invariants, namely two velocities and two accelerations. However, we must point out that we are already halfway to this goal, since a deformed special relativity (DSR) with two limits of speed denominated as symmetrical special relativity (SSR) that postulates a minimum limit of speed V at quantum level, has already been explored in a recent paper[25]. Therefore, now the main goal is to search for a deformed symmetrical special relativity (DSSR) in light of Unruh effect, where a minimum acceleration is also included. Such DSSR with four invariants will be deeply investigated in a future work. However, here let us first introduce some aspects of SSR already explored in the literature[25,26,27,28,29,30] in order to indicate the future challenge in searching for DSSR.

6.1. Relativistic Momentum and Energy in SSR

Let us first identify the new four-velocity vector in SSR. In this case, we have obtained the components:

$$\begin{array}{cc}\hfill & U^0=\mathrm{\Psi }c\hfill \\ \hfill & U^a=\mathrm{\Psi }{v}^a\hfill \\ \hfill & U^{\mu }=[U^0,U^a]=[\mathrm{\Psi }c,\mathrm{\Psi }{v}^a],\hfill \end{array}$$

(26)

where the factor

$$\mathrm{\Psi }={\displaystyle \frac{\sqrt{1-\frac{V^2}{v^2}}}{\sqrt{1-\frac{v^2}{c^2}}}},$$

(27)

where V is the invariant minimum speed[25,26,27,28,29,30].

The 4-velocity of SSR reduces to 4-velocity of SR, namely $U^{\mu }=[\gamma c,\gamma v^{\alpha }]$ when $V\to 0$ or $v\gg V$, being $\alpha =1,2,3$ the spatial components.

We are now ready to obtain the 4-momentum $p^{\mu }$ of SSR. So, by using the definition $p^{\mu }=m_0{U}^{\mu }$ and substituting Eq.(26), we find

$$p^{\mu }=\left[{\displaystyle \frac{E}{c}},p^{\alpha }\right]=[\mathrm{\Psi }{m}_{0}c,\mathrm{\Psi }{m}_0{v}^{\alpha }],$$

(28)

from where we obtain the energy E in SSR, namely:

$$E=\mathrm{\Psi }{m}_0{c}^2=m_0{c}^2{\displaystyle \frac{\sqrt{1-\frac{V^2}{v^2}}}{\sqrt{1-\frac{v^2}{c^2}}}}$$

(29)

and the momentum p, as follows:

$$p=\mathrm{\Psi }{m}_{0}v=m_{0}v{\displaystyle \frac{\sqrt{1-\frac{V^2}{v^2}}}{\sqrt{1-\frac{v^2}{c^2}}}},$$

(30)

so that we recover $E=\gamma m_0{c}^2$ and $p=\gamma m_{0}v$ of SR in the limit $V\to 0$.

6.2. Searching for the Momentum and Energy in DSSR

We know that SSR[25,26,27,28,29,30] has two invariant speeds, namely the speed of light c and a invariant minimum speed V. In this paper, we have shown a deformed SR (DSR) in view of a background thermal vacuum due to Unruh effect. Our next step is to search for a deformed SSR (DSSR) with a background thermal vacuum due to Unruh effect, however DSSR needs also a minimum acceleration and a minimum temperature to be investigated in a future work. Therefore, we will intend to search for a general factor $\mathrm{\Gamma }(T,T_P,T_{min})$, where a minimum temperature $T_{min}$ very close to zero should be implemented within the Unruh scenario, so that the 4-momentum in DSSR should be of the form

$$p^{\mu }=[\mathrm{\Gamma }(T,T_P,T_{min})\mathrm{\Psi }{m}_{0}c,\mathrm{\Gamma }(T,T_P,T_{min})\mathrm{\Psi }{m}_0{v}^{\alpha }],$$

(31)

where the energy in DSSR is of the form

$$E=\mathrm{\Gamma }(T,T_P,T_{min})\mathrm{\Psi }{m}_0{c}^2$$

(32)

and the momentum is of the form

$$p=\mathrm{\Gamma }(T,T_P,T_{min})\mathrm{\Psi }{m}_{0}v,$$

(33)

where $\mathrm{\Gamma }(T,T_P,T_{min})=?$. This is our challenge to be deeply investigated in a future work in order to build a DSSR with four (4) invariants, namely two speeds (c and V) and two accelerations ($a_P$ and $a_{min}=?$) connected with two temperatures ($T_P$ and $T_{min}=?$) according to Unruh effect.