Development and Validation of a Magnetic Sensor Array for Battery Diagnostics

1. Introduction

Magnetic field sensing plays a vital role across a broad spectrum of scientific and industrial applications, including geophysical exploration, biomedical diagnostics, navigation, and electromagnetic compatibility testing [1]. In recent years, the demand for compact, high-resolution, and low-noise magnetic sensor arrays has grown considerably, particularly in contexts that require precise spatial mapping of magnetic fields [2,3,4,5]. Beyond traditional domains, magnetic sensing has gained attention as a noninvasive approach for inspecting lithium-ion batteries (LiBs), offering promising capabilities for onboard battery identification [6] as well as noninvasive health monitoring and defect detection [7,8,9]. These techniques have demonstrated the ability to identify manufacturing anomalies such as tab or weld faults, irregular current paths, and localized short circuits. In some cases, magnetic measurements can even correlate with a battery state of charge (SOC) [10].

In many battery-powered systems, safety and performance monitoring vary depending on the application. Larger and more complex systems, such as electric vehicles, typically rely on a Battery Management System (BMS) [11,12], though access to their data is not always assured. Smaller devices such as e-bikes and scooters generally integrate a BMS as well [13], but the level of sophistication can differ, and lower-cost or poorly manufactured batteries may omit proper management circuits, creating safety risks. Modern power tools and consumer electronics also rely on embedded battery management, though in these cases the systems are often simplified, focusing on essential protections such as overcharge, over-discharge, and thermal cutoffs rather than full diagnostic capabilities. Critically, once a battery is removed from its host system for storage, servicing, recycling, or emergency handling, it is usually disconnected from the BMS. Under such circumstances, first responders and personnel responsible for handling, transporting, or storing batteries often lack the necessary information to assess battery safety, posing potential hazards [14] and complicating compliance with regulatory standards [15]. In such cases, magnetic sensing may offer a compelling alternative. By detecting internal current distributions and magnetic field anomalies, magnetic diagnostics can help identify faults that might not produce immediate thermal signatures or be visible through conventional inspection methods

Magnetic diagnostics are not intended to replace established tools like infrared (IR) thermal cameras [16,17], which remain essential for detecting abnormal temperature rises in LiBs [18] and ensuring safety in environments such manufacturing plants, storage centers, garages, mechanical workshops, dismantling facilities, and recycling sites. However, thermal imaging faces notable limitations [19]. Its accuracy can be influenced by environmental conditions [20], it may fail to promptly capture rapid combustion events, and it often requires trained personnel and regular maintenance. Moreover, its diagnostic capability remains constrained, as nonuniform temperature patterns observed in prior studies often stem from variations in thermal conductivity across active materials and current collectors rather than reflecting internal defects or cell states [21]. Surface temperature profiles also do not reliably represent the true internal temperature or correlate strongly with SOC [22], reducing the relevance of infrared measurements for fault detection. Although IR cameras can roughly identify regions of excessive heat from exothermic side reactions, they lack the precision to pinpoint or trace defect spots, limiting their effectiveness for early-stage diagnostics. In contrast, magnetic sensing provides direct information on internal current distribution and field anomalies [23,24,25], enabling the detection of faults that may not produce immediate thermal signatures [26,27]. This distinction highlights the complementary role of magnetic diagnostics, which can strengthen early warning systems and improve situational awareness, whereas IR imaging remains most effective in situ during thermal runaway, when “hot spots” initiating self-heating can be clearly identified.

In this context, magnetic sensing should be viewed as a complementary tool that enhances battery surveillance capabilities, by adding layers of information such as internal current distribution and magnetic field anomalies that thermal diagnostics alone cannot provide. This dual-modality approach strengthens early warning systems and situational awareness, especially when conventional data are limited. Although many techniques were not initially designed to fill diagnostic gaps, they can be repurposed effectively for fault detection and performance assessment [28]. Early studies showed that mapping magnetic fields leaking from cells revealed conductivity loss and short circuits, linking reduced conductivity to cycle deterioration [29]. One-dimensional scanning methods extended this work to diagnose capacity consistency across packs by detecting current imbalances [30], while sensor arrays and finite element simulations reconstructed current density maps and identified SOC anomalies such as dendrite formation [25]. Magnetic imaging also proved effective for collector defect detection [26]. More advanced three-dimensional electrochemical-magnetic-thermal models captured short circuits and cracks through distinct signatures [24], and gradient-based analysis distinguished internal faults from general degradation [26]. Instrumentation systems with hundreds of magnetic pixels refined spatial resolution, uncovering exponential current profiles and recording transient equalization events [31]. Most recently, real-time magnetic field imaging introduced destructive interference techniques to accentuate defect spots and classify failure modes such as tab connection faults or electrode misalignment [23].

However, most of the works discussed above rely upon mechanical scanning to move sensors across the battery surface. Motor-driven scanning is limited by mechanical complexity, slower sequential acquisition, and difficulty in detecting transient events, particularly when scaled to larger systems. In contrast, static sensor grids eliminate moving parts and enable simultaneous, high-resolution measurements across the battery surface, supporting real-time monitoring and improved fault detection. While grids require greater investment in hardware, synchronization, and data processing, they deliver superior scalability and reliability. Building on this, our device employs a 4×4 sensor grid as an initial testbed, with the goal of upscaling to larger arrays in the future. Combined with the interpolation procedure introduced in this paper, the approach is expected to enhance diagnostic resolution and robustness, advancing battery safety through improved detection of internal faults and anomalies. Although the motivation for this development is battery diagnostics, the array can capture spatial magnetic field distributions across a planar surface, enabling applications such as magnetic imaging [32], material characterization [33], and environmental field mapping [34,35].

This paper presents a dual objective. First, it details the design and implementation of the magnetic sensor array (MSA) and compares theoretical predictions with experimental measurements of magnetic fields generated by two planar copper conductors under a constant current. Once validated, the MSA is applied to monitor the magnetic field near the surface of a commercially available lithium-polymer (LiPo) pouch cell during controlled charge and discharge cycles. The results demonstrate the array’s potential for capturing magnetic signatures associated with battery operation. A follow-up study will explore its use in identifying faulty conditions in LiBs.

The structure of the paper is as follows. Section 2 describes the materials and methods, detailing the design of the MSA, the sample configurations, the measurement protocol, and the theoretical approach used for validation. Section 3 presents and analyzes both experimental and numerical results, including the application of the MSA to characterize the magnetic field distribution on a LiPo pouch cell. Finally, Section 4 concludes the study and outlines future directions.

2. Materials and Methods

Section 2.1 provides a detailed description of the MSA. Section 2.2 presents the samples under investigation, followed by the experimental procedure in Section 2.3. The data post--processing approach is introduced in Section 2.4, and the numerical framework employed for validation is outlined in Section 2.5.

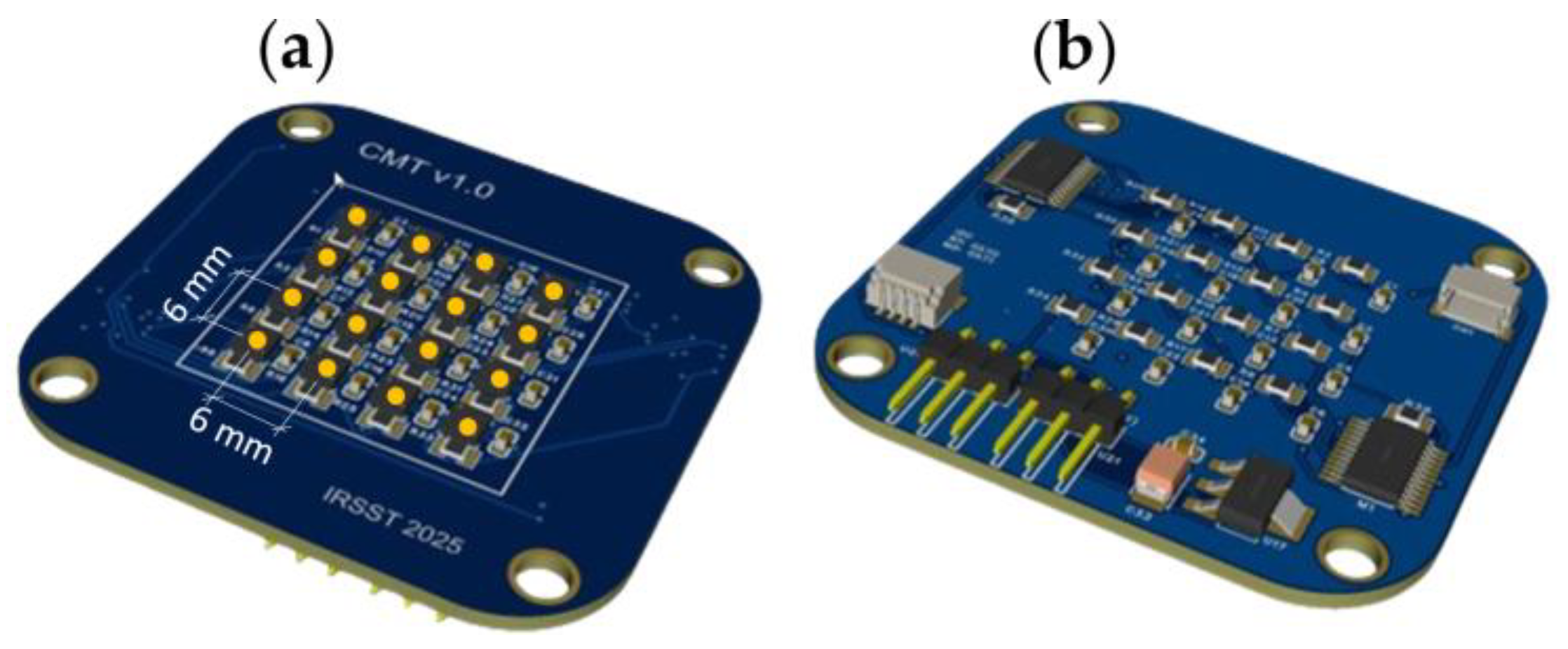
2.1. The Magnetic Sensor Array (MSA)

Figure 1 shows the MSA used to measure local magnetic fields near the surface of the samples. The array consists of a 4×4 grid of MMC5983MA sensors from MEMSIC [36], which are 3-axis anisotropic magnetoresistive magnetometers offering 18-bit resolution, a ±800 µT full-scale range and a maximum output data rate of 1kHz. The sensors actually measure the three components of the magnetic flux density vector, B, which we will refer to by magnetic field or B field, for short. These specifications make the system well-suited for precision magnetic field mapping. The sensors also feature integrated temperature sensing and built-in degaussing circuitry, which improve measurement stability and accuracy in environments with variable thermal or magnetic conditions. The MMC5983MA is packaged in a 16--pin Land Grid Array (LGA) with dimensions of 3.0 × 3.0 × 1.0 mm. Sensors are arranged on a rigid PCB with 6 mm center-to-center spacing in both directions, Figure 1(a). Future work may focus on developing sensor grids on flexible substrates [37], enabling measurements across nonplanar or irregular sample surfaces. Therefore, the array of magnetometers can be represented by a square of 16 dots, where each dot represents a sensor, separated vertically and horizontally from each other by 6 mm. It captures the magnetic field components B_x, B_y within the plane of the MSA, while B_z is measured perpendicular to the plane.

Since the MMC5983MA has only one fixed I²C address (0x30), to operate multiple sensors sharing the same I²C address simultaneously, the MSA architecture incorporates two TCA9548A multiplexers, configured at addresses 0x70 and 0x71. Each TCA9548A controls eight independent channels, allowing a total of sixteen sensors to be managed. The MSA is connected to the ESP32 microcontroller, that dynamically drives these channels, ensuring that only one sensor communicates on the I²C bus at a time. This approach prevents address conflicts while maintaining consistent and reliable data flow. Sequential data acquisition is optimized to minimize switching delays and deliver continuous, precise, and perfectly synchronized magnetic measurements. Additionally, a graphical user interface (GUI) was developed for this project to facilitate the selection of the communication port with the ESP32, as well as the real-time visualization and recording of the system’s generated data. The result is a modular, extensible, and interactive measurement platform, specifically designed for spatial magnetic field mapping.

The accuracy of the MSA sensors was validated using a magnetic field generated by Helmholtz coils and measured with a Wavecontrol SMP3 equipped with a WPH-DC probe (0.1 µT resolution). For all 16 sensors, the relative deviation between measured sensor values (B_s) and expected values (B_e), ΔB(%) = |B_s − B_e|/B_e × 100, was under 1% throughout the 10–100 µT range. The experimental resolution of the MSA is approximately 1 µT. Based on the sensor datasheet, the MSA’s estimated per--axis noise density falls within the nT/√Hz range. All measurements were conducted at room temperature, around 22 °C.

2.2. The Examined Samples

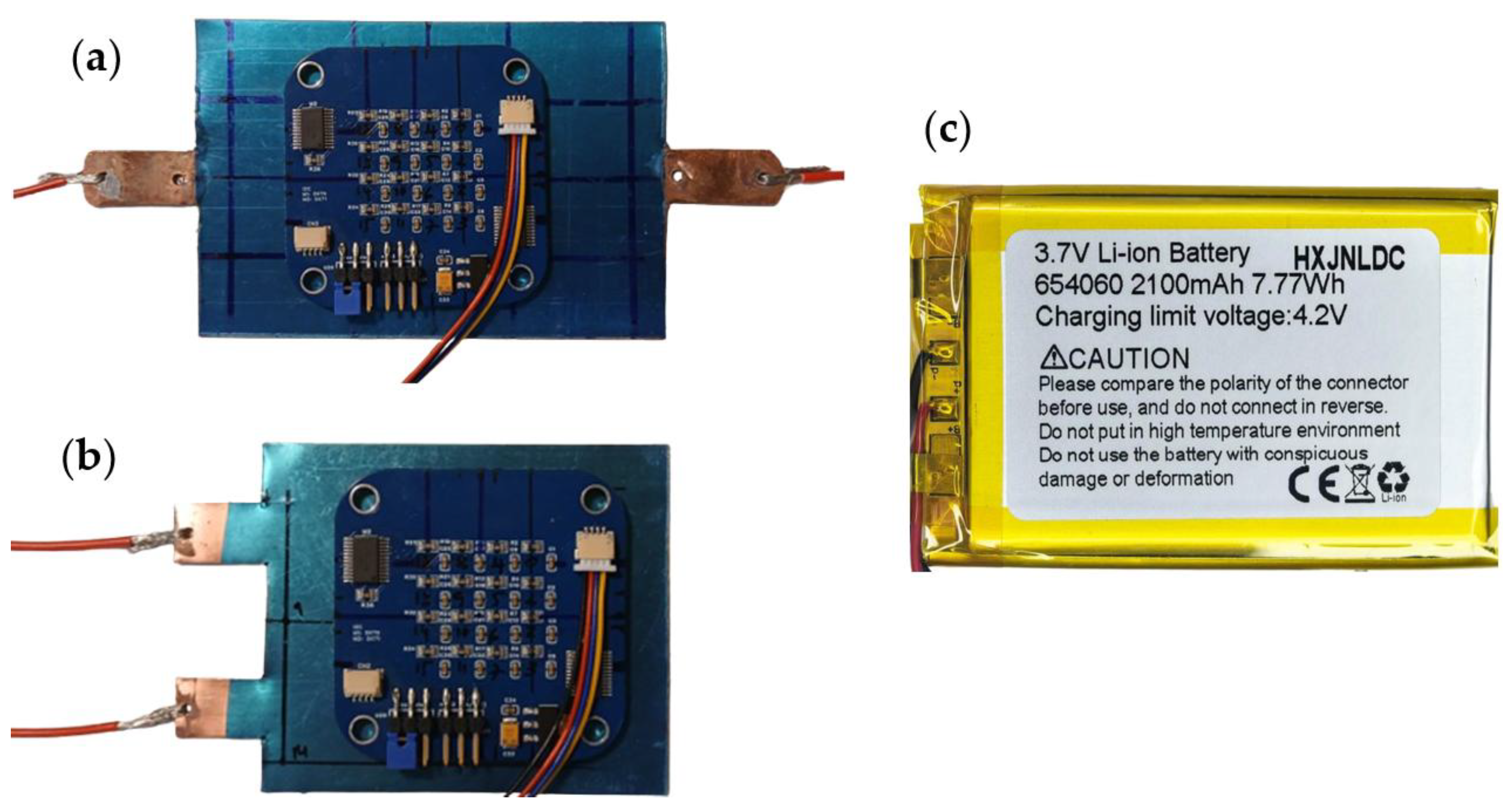
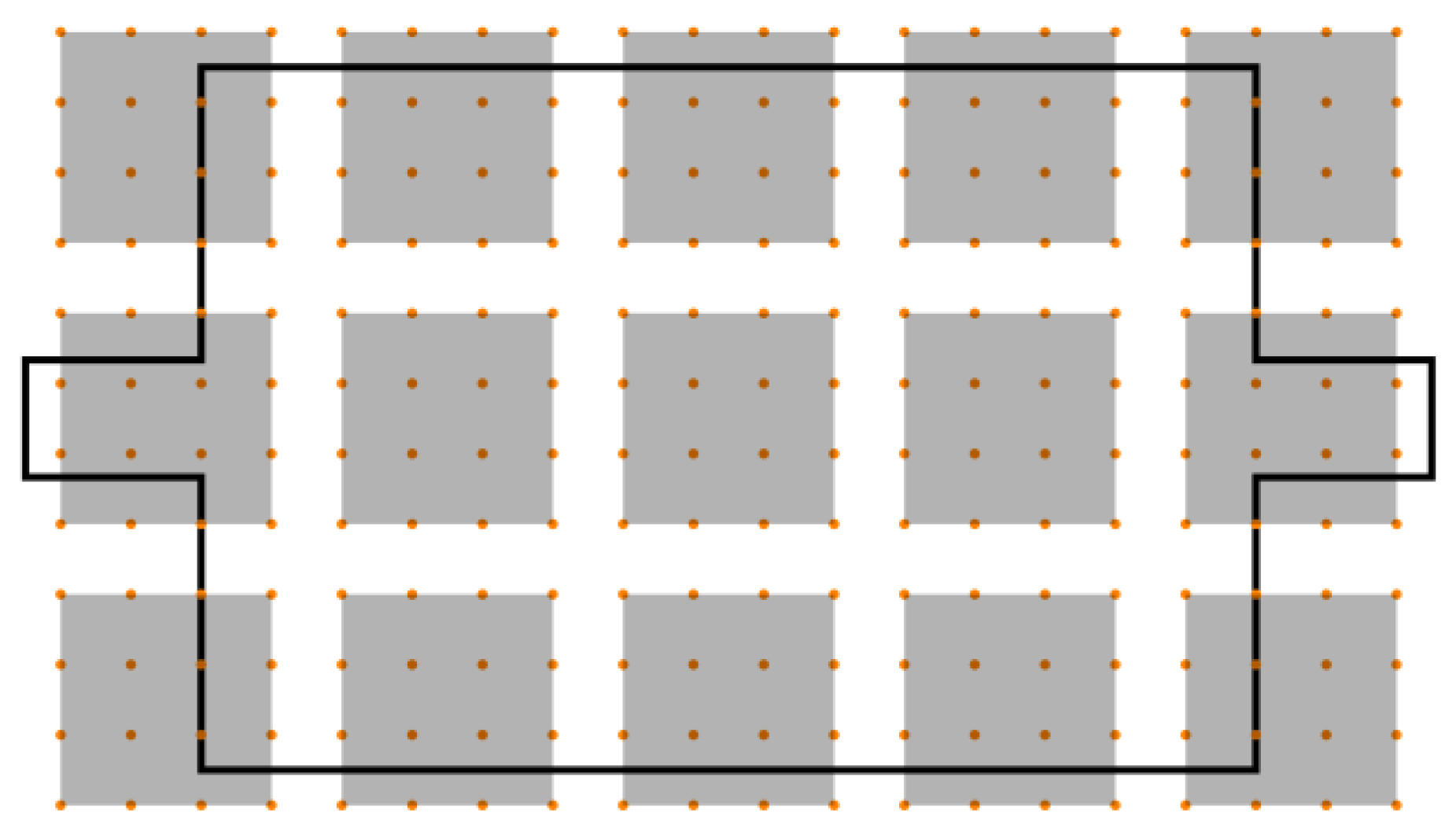
2.2.1. Planar Copper Conductors

Figure 2(a) and 2(b) show the copper samples used to evaluate the array’s ability to accurately map the magnetic fields across a surface. For clarity, we refer to these samples as CuA and CuB, respectively. Each sample is composed of copper approximately 0.6 mm thick. CuA measures 90 × 60 mm, while CuB measures 55 × 60 mm. In Figure 2(a), the current collectors are center-aligned and placed on opposite sides, whereas in Figure 2(b), they are located on the same side. This difference in configuration leads to distinct magnetic field distributions for each sample. During the experiments, both samples were subjected to a direct current of 1 A.

2.2.2. Lithium-Polymer (LiPo) Battery

To illustrate the use of the MSA in evaluating battery safety, we monitored the magnetic field near the surface of a LiPo cell under active discharge and charge conditions. The test subject was a 3.7 V, 2100 mAh, 654060 pouch-type battery with nominal dimensions of approximately 6.5 × 40 × 60 mm, Figure 2(c). This type of rechargeable cell is commonly found in DIY electronics, portable devices, and other low-power applications. Discharging and charging tests were both conducted at 1 A (0.5C) and 2 A (1C) at constant current condition. At a 1C rate, the battery discharged from 4 V to 3.3 V over approximately 22 minutes, providing a discharge capacity of 730 mAh and delivering about 2.4 Wh of energy.

2.3. The Measurement Procedure

Prior to each measurement, background magnetic fields, originating from Earth’s geomagnetic field and surrounding equipment, were removed by zeroing the field readings of each sensor through an offset calibration procedure. Next, the samples CuA and CuB were subjected to a 1 A direct current, and the resulting three components of B at the surface were measured. The MSA covers an 18 × 18 mm area consisting of 16 points spaced 6 mm apart, Figure 1(a). Therefore, to scan the entire CuA and CuB samples surface, the MSA was manually repositioned across 15 distinct locations, yielding measurements at 240 points in total, Figure 3. An improved version of the MSA, designed to measure the entire surface of this kind of sample without requiring sensor repositioning, is currently under development. In Figure 3, each gray rectangle represents a measurement position of the MSA for sample CuA (the same procedure was applied to the sample CuB). Since three B-field components were recorded at each point, the data set includes a total of 720 individual parameters. At each location, the MSA collected data for approximately one minute. Given the experimental acquisition rate of roughly 600 ms, each session yielded 100 data samples per component of B for each of the 16 sensors. The final experimental values represent the average of these 100 readings for each component of B.

The procedure to measure the battery’s generated B field mirrored that used for copper samples. Because the battery surface area is smaller than that of the copper samples, nine distinct measurement points were sufficient to scan its surface. The B field has been recorded during both charging and discharging phases at constant currents of 1 A and 2 A (0.5C and 1C respectively), using an EBC-A20 Battery Tester. Notably, a residual magnetic field distribution was observed at the surface of the battery even when it was disconnected, likely originating from trace magnetic elements in the cathode material or from the wiring and terminal connections. The residual field measured prior to and following discharge appears either unaffected by the battery’s SOC or reflects polarization--related magnetic fields [26] that cannot be resolved by the MSA. Additional research is needed to substantiate this interpretation. Consequently, the battery’s B field data presented in the following section collected during active charging and discharging is the result of the subtraction of this residual field.

2.4. Post-Treatment of the Experimental Data

Once the in-plane components of B (B_x and B_y) were measured at each point of the surface (as illustrated by the dots in Figure 3 for the sample CuA), a 3rd-order interpolation function, based on cubic polynomials in each spatial dimension [38], was applied to smoothly estimate values between the measured data points. This procedure was applied to both the copper samples and the battery. The B_z component was not analyzed in this work. Wolfram Mathematica 14.3.0 was employed to perform interpolation and create 2D field distributions and vector plots.

2.5. Numerical Computation of the B Field for the Copper Samples

The components of the B field were computed for the samples CuA and CuB. As an initial step, a DC voltage is applied across the sample terminals to establish a constant current of 1 A. This produces a current density vector, J, that varies with the spatial coordinates x and y. Because no potential difference exists along the thickness (z-axis), the out--of--plane component J_z can be disregarded. To perform these calculations, we have used FEMM 4.2 software [39], a finite element package designed for solving two-dimensional magnetostatic and low-frequency electromagnetic problems. After determining the components J_x and J_y as functions of x and y over the sample geometry, the magnetic field components B_x, B_y and B_z were computed via numerical integration of the Biot-Savart equation across the surface defined by − 65 mm < x < 65 mm and − 40 mm < y < 40 mm. To account for sensor thickness, the plane used for field calculations was positioned at z = 0.5 mm from the surface of the sample. The Fortran code used for evaluating the double integrals of the Biot–Savart law was revised with the assistance of GenAI (Copilot).

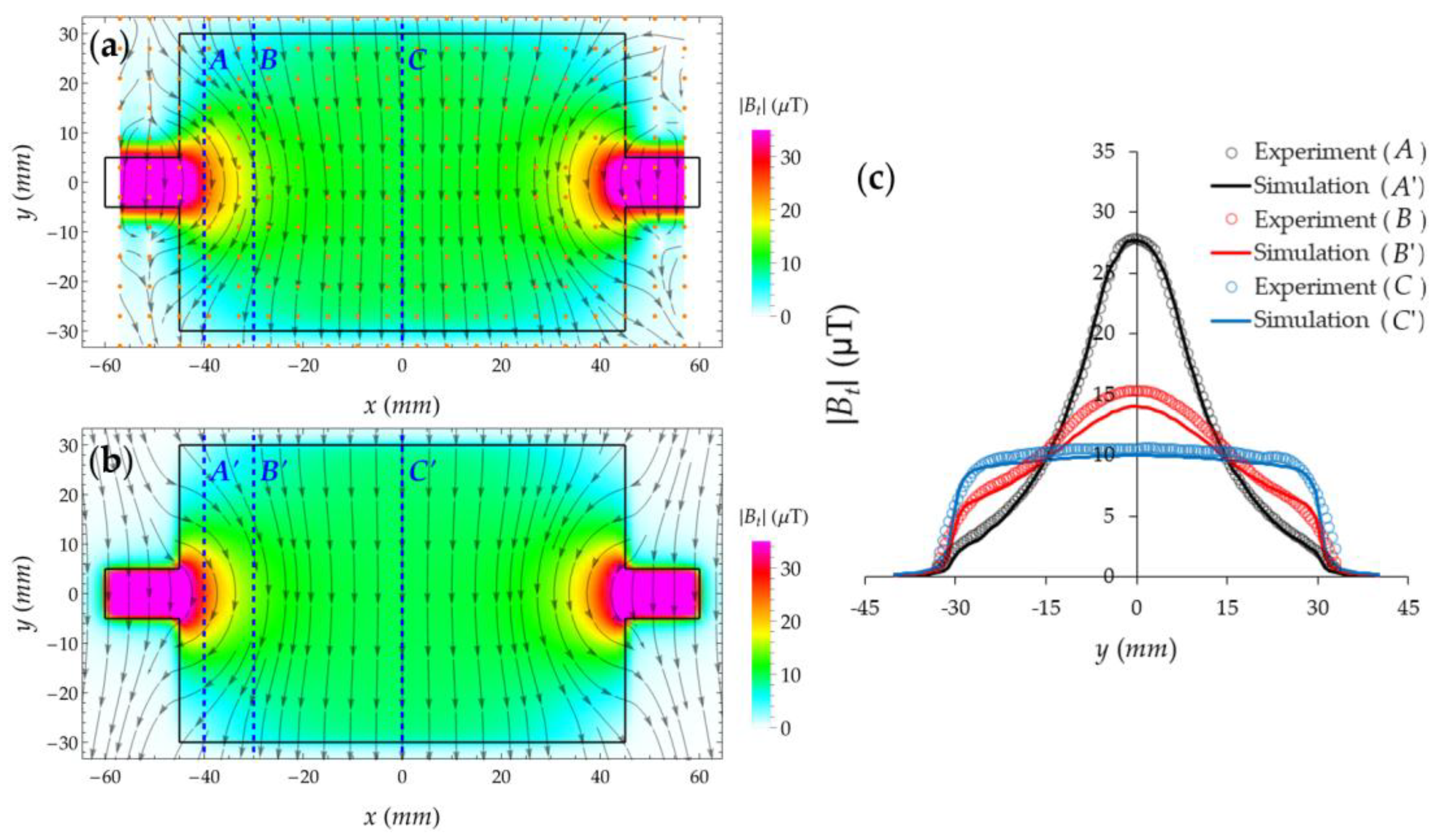
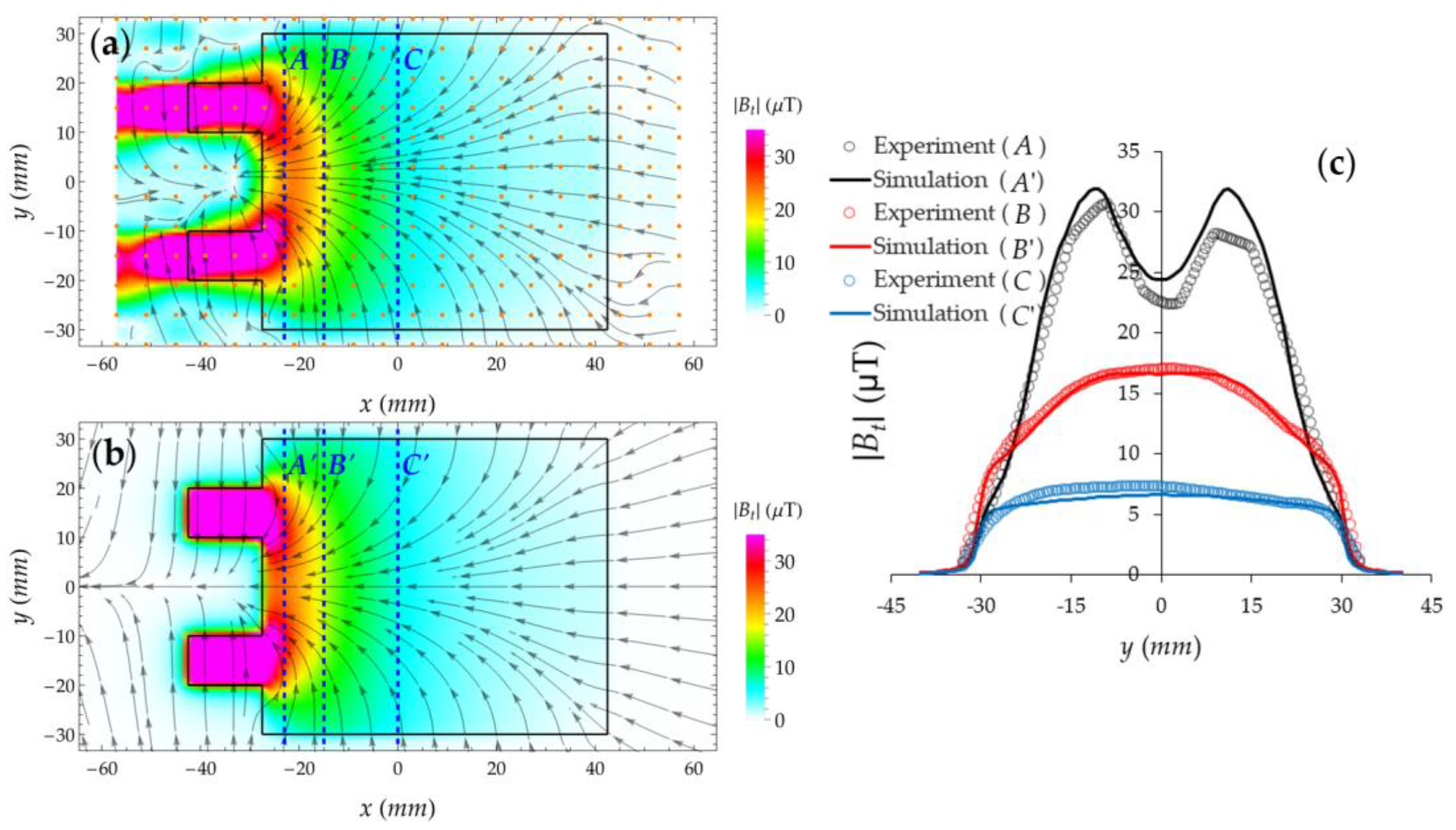
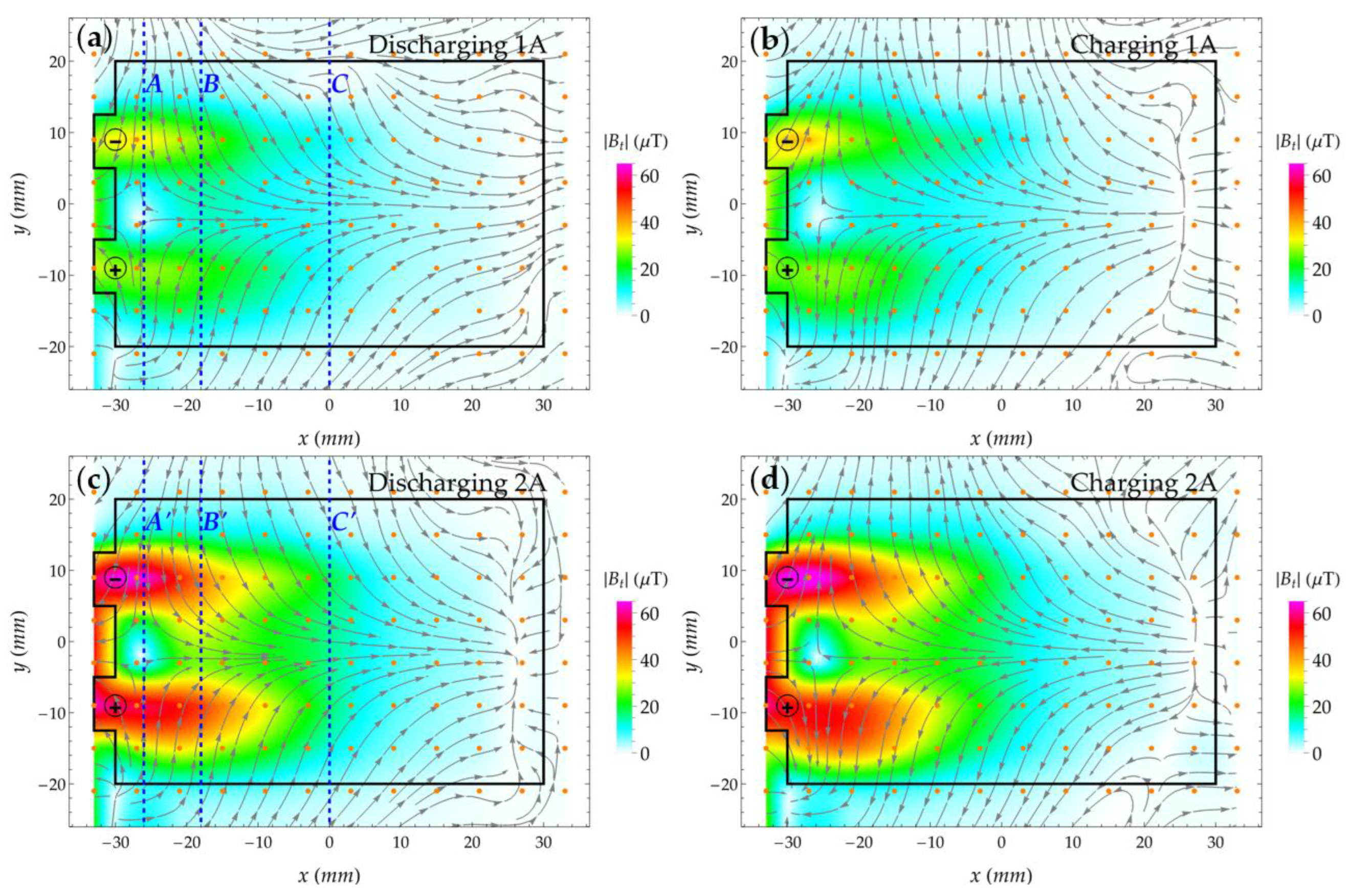
3. Results and Discussion

This section presents both experimental and numerical results. Section 3.1 focuses on the analysis of samples CuA and CuB to evaluate the MSA capability to measure B at the sample surface. Section 3.2 then examines the magnetic field measurements obtained from the battery.

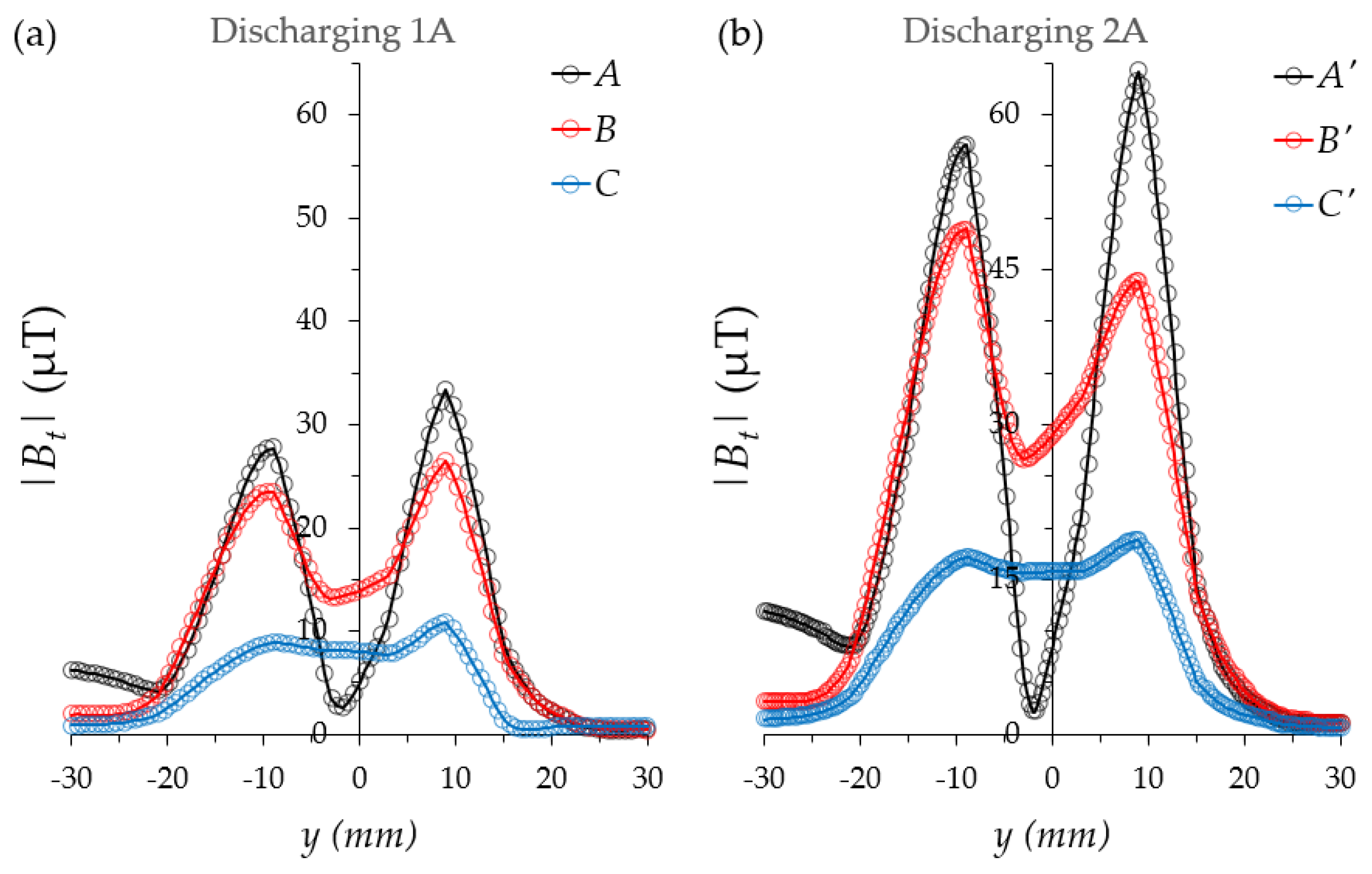
3.1. Magnetic Field of Copper Samples

Figure 4(a) and 4(b) show the experimental and simulated distributions of B at the surface of the CuA sample, subjected to a 1 A direct current flowing from the left to the right terminal. The color scale represents the magnitude of the in-plane component of B, |B_t|= (B_x² + B_y²)^1/2, which spans from zero up to approximately 54 µT near the terminals, but has been clipped at 35 µT to enhance visual clarity. Arrows in both figures depict the vector field formed by the B_x and B_y components.

Clearly, the component B_y is predominant as a result of the primarily horizontal current distribution, which is dictated by the conductor’s geometry. In Figure 4(a), orange dots mark the measurement locations of the components of B, as detailed in Section 2.3. The numerical data shown in Figure 4(b) were generated according to the methodology described in Section 2.5. Figure 4(c) displays the magnetic field variation along the vertical axis (y) at three fixed horizontal positions: x = −40 mm, −30 mm, and 0 mm, corresponding to the dotted vertical lines labeled A, B, and C in Figure 4(a) and A’, B’, and C’ in Figure 4(b). The comparison indicates that, overall, only minor discrepancies exist between the experimental measurements and the simulation results. These findings are also in qualitative agreement with those previously reported by Lee et al. [23].

A similar analysis was conducted on sample CuB, which was likewise exposed to a 1 A direct current. Figure 5(a) and 5(b) display the spatial distribution of |B_t| at the surface of the sample, obtained from both experimental measurement and simulation, with current flowing from the upper to the lower terminal. As in Figure 4, the maximum |B_t| was capped at 35 µT for visual clarity. In both figures, arrows illustrate the vector field distribution. In Figure 5(a), the orange dots, spaced 6 mm apart both vertically and horizontally, indicate the 240 measurement locations used to reconstruct the full surface distribution via interpolation, as previously described. The figures show a B field distribution consistent with a current entering through the upper terminal, predominantly flowing in the vertical direction, and exiting through the lower terminal. The slight field irregularities observed near the current pads in Figure 5(a) may be attributed to the imperfect geometry of the sample, as well as interpolation errors in measured regions with significant field variation. Figure 5(a) also shows a high field pattern extending beyond the sample boundaries, which originates from the wires connecting the sample to the current power supply, as Figure 2(b) shows. Figure 5(c) shows the magnetic field variation along y at x = −23 mm, −15 mm, and 0 mm, corresponding to the dotted lines labeled A, B, and C in Figure 5(a) and A’, B’, and C’ in Figure 5(b). Slight discrepancies between the numerical calculations and experimental results are noted, mainly due to the factors mentioned above and the displacement of the sensor grid over the sample, as outlined in Section 2.3. Similar to the previous sample, the overall distribution of |B_t| observed here is in qualitative agreement with that reported in [23].

Figure 4 and Figure 5 demonstrate that the MSA reliably measures the magnetic field in the µT range near the surface of a planar sample. The sensor shows consistent performance in detecting both the y and x components of the B field, as highlighted by the dominant field orientations in samples CuA and CuB. Additionally, the results show that the sensors are highly sensitive, capable of detecting small field variations and measuring fields below 5 µT. In summary, the measurements and numerical simulations conducted on the copper samples have enabled us to assess and validate both the capabilities and limitations of the MSA. Despite several experimental sources of error—including low magnetic fields below the resolution threshold of ±1 µT, a 6 mm physical spacing between sensors, misalignment from manually shifting the MSA across the 15 positions illustrated in Figure 3, and interpolation errors particularly in regions with steep field gradients—the sensors demonstrate sufficient reliability for investigating surface magnetic fields ranging from 1 µT to several tens of µT. In the next section, the MSA and the established measurement procedure are employed to examine the B field characteristics of a LiPo battery during operation.

3.2. Magnetic Field of a LiPo Battery

Figure 6 illustrates the measured B field near the battery surface under various conditions. For visual clarity, the maximum B field values have been capped at 65 µT. Figure 6(a) and 6(b) depict discharging and charging at a constant current of 1 A, while Figure 6(c) and 6(d) show the same processes at 2 A. In each figure, color shading represents the magnitude of the tangential component of B, |B_t| (as defined in Section 3.1), arrows indicate the direction of the field lines, and the + and − symbols denote the battery’s positive and negative terminals. Additionally, the orange dots, arranged in a grid with 6 mm spacing in both vertical and horizontal directions, represent the 144 measurement points employed to reconstruct the complete surface distribution through interpolation, as previously outlined.

The vector field pattern indicates a complex internal current flow within the battery. During discharging, as displayed in Figure 6(a) and 6(c), where current exits through the positive terminal, the magnetic field near the terminals is predominantly vertical, as anticipated. However, farther from the terminals, particularly near the horizontal axis at the center of the battery, the rightward field suggests an upward vertical current path. Unlike the present case, the sample in Figure 5(a) and 5(b) exhibits a leftward magnetic field near the horizontal axis at its center, despite sharing a similar geometry and current path from the lower terminal. Analogous reasoning is also valid for the charging mode shown in Figure 6(b) and 6(d). This intricate behavior reflects the specific internal architecture of the battery, the analysis of which lies beyond the scope of this study.

The vertical lines labeled A, B, C in Figure 6(a) and A’, B’, C’ in Figure 6(c) correspond to positions at x = 26 mm, –18 mm, and 0 mm. The field values along these lines, plotted as functions of y, are presented in Figure 7(a) and 7(b). These plots reveal a slightly asymmetrical double-peak structure in the field near the terminals, as illustrated by curves A and B in Figure 7(a) and A’ and B’ in Figure 7(b). Batteries with counter--side central alignment tabs have shown a similar effect, as noted in [23]. Such asymmetry likely arises from several factors: the configuration of internal current paths and electrode geometry, variations in conductivity and microstructure between anode and cathode materials that affect current distribution across the surface, and design elements such as external wiring and pad placement, which can further introduce imbalances in the magnetic field intensity [8]. Comparison of the field values during discharge at 1 A and 2 A indicates that the amplitude observed at 2 A is approximately twice that measured at 1 A, is agreement with the linear dependence of field intensity on current magnitude predicted by theory.

Furthermore (not shown), no significant quantitative difference in the field values has been observed between the discharging and charging modes, indicating that the observed magnetic field behavior is predominantly governed by the charging/discharging current magnitude rather than the direction of charge transfer, as mentioned in Section 2.3. However, a transient phenomenon known as the recovery effect, where the battery voltage rises toward an equilibrium level after discharge and disconnection, is likely to produce a subtle magnetic signature in the pT range [40]. Ongoing work is focused on adapting the present system to measure magnetic susceptibility, thereby enhancing sensitivity into the pT/√Hz range.

The results presented in this section further demonstrate that the MSA can measure the magnetic field distribution near the surface of a battery. From these measurements, the corresponding current distribution in the battery can be reconstructed using an inverse problem approach [41,42,43,44]. This analysis lies beyond the scope of the present work and will be pursued in future studies. As part of these efforts, we will also employ magnetic field measurements to characterize defects and critical internal behaviors in LiBs, particularly those associated with localized heating and potential thermal runaway. An innovative visualization method was proposed in [23], where the current--induced magnetic field of the operating battery is canceled by the opposing field of a conductor with identical geometry placed beneath the cell and carrying the same current in the opposite direction. This suppression isolates the defect--related magnetic field, and future work will focus on implementing and evaluating this technique. In contrast to invasive diagnostic methods such as voltage monitoring or impedance spectroscopy, magnetic sensors offer a nonintrusive means of monitoring batteries across charging, discharging, and resting states. Furthermore, by associating magnetic field magnitude and direction with current distribution and electrochemical dynamics, SOC estimation can be achieved with greater precision under variable conditions.

4. Conclusions

We have presented the magnetic sample array (MSA), consisting of 16 commercially available, high--sensitivity magnetometers arranged in a 4×4 grid. This system is designed to capture all three components of the magnetic field, B, within the microtesla (µT) range, at 16 spatially distinct points separated by 6 mm both vertically and horizontally. In this work, we focus on mapping the magnetic field distribution near the surface of two planar copper samples and a low--power LiPo pouch battery. An experimental procedure was implemented to scan surfaces of samples larger than the array and interpolate field values between grid points.

The B field of copper samples was numerically simulated using finite element analysis. The strong agreement between simulated and experimental measurements validated the accuracy of both the device and the experimental procedure, enabling reliable evaluation of the unknown magnetic field of a battery under both charging and discharging conditions. The device operated effectively without requiring a magnetic shield, owing to its built--in set/reset de--gaussing function, which facilitates future deployment in field applications.

Future developments will involve increasing the sensor count in the MSA, thereby facilitating the study of larger samples and enabling detection of temporal fluctuations in the magnetic field. Therefore, the expanded sensor area will further allow comprehensive surface mapping of samples smaller than the grid dimensions. Also, we intend to extend this research by characterizing battery ageing and state of health via magnetic field measurements. Batteries will be subjected to controlled external abuses (thermal, mechanical, and electrical) while monitoring the B field. The correlations between unstable behavior and magnetic signatures are expected to strengthen the case for the MSA as a promising tool in battery security diagnostics.