Theory of Geodesic Paths of Miracle and Nature: A Geometric Framework Unifying Law and Will

1. Introduction

1.1. The Paradox of Miracle and Nature

The relationship between deterministic natural law and spontaneous miracles has been a central issue in the philosophies of science, theology, and metaphysics for millennia. According to classical determinism, epitomized by Laplace's demon, all phenomena are governed by immutable natural laws [1]. Conversely, many religious and philosophical traditions maintain that divine will or human agency can alter outcomes in ways that transcend ordinary causality [2,3]. This disagreement is elegantly resolved in Jewish mystical thought, particularly in Rav Kook's concept that "the miracle is the soul of nature" [4], suggesting that miraculous and natural phenomena exist along a continuum, rather than as separate categories.

Although classical approaches separate natural law from miraculous deviation, whether conscious intention might influence physical or probabilistic outcomes has been studied in several empirical research programs. Notably, in 1997, studies from the Princeton Engineering Anomalies Research (PEAR) laboratory reported small but statistically significant deviations in random physical systems under directed human intention [5]. Later research examined whether focused attention can influence quantum systems, including double-slit interference patterns; mixed but intriguing results were obtained in this regard [6,7]. While interpretations remain debated, these results suggest that volition may introduce subtle biases into probabilistic processes, possibly interacting with fundamental indeterminacy at the quantum level. Such findings provide a preliminary empirical context for exploring how consciousness might influence events, thereby supporting a reformulation in which "miracle" is considered not a violation of natural law but an extreme curvature within an underlying probability landscape shaped by will.

The advent of quantum mechanics introduced fundamental indeterminacy into physics [8], opening a conceptual avenue for free will and observer effects. The collapse of a wavefunction remains one of the most debated topics in quantum foundations [9,10,11]. While measurement outcomes are treated as objectively probabilistic in standard quantum mechanics, several interpretations, including the von Neumann–Wigner consciousness-collapse and the Penrose–Hameroff orchestrated objective reduction, suggest that consciousness may play an active role in determining quantum events.

1.2. Historical and Empirical Context

The possibility that consciousness may influence physical systems has a controversial but scientifically documented history. Early pioneers of quantum mechanics, including Heisenberg and von Neumann, recognized that the observer's role in measurements cannot be entirely eliminated from formalism. The quantum Zeno effect [12] further demonstrates how observation can influence quantum evolution, showing that frequent measurements can effectively “freeze” a quantum system. Wigner (1961)[10] explicitly proposed that consciousness might collapse the wave function, a view later developed by Stapp [13,14] within an explicit quantum-mechanical framework.

Recent empirical investigations have explored whether human intention might influence quantum or random processes. Extensive studies were conducted in The PEAR Laboratory on human–machine interactions, and small but statistically significant deviations from chance in random event generators were reported under conscious intention [5,15]. Radin et al. [6,7] examined whether focused attention can influence quantum systems, including double-slit interference patterns, with mixed but notable results. Bierman and Radin (1997)[16] demonstrated presentiment effects, defined as physiological responses occurring before random stimulus presentation, which in turn suggests potential retrocausal or anticipatory phenomena.

Although these findings remain contested, they highlight a central question: Can consciousness systematically influence probabilistic outcomes in a manner that can be detected under controlled conditions? The theoretical framework and experimental proposal in this study should extend this line of inquiry by providing a geometric interpretation and a protocol designed to resolve prior methodological limitations.

To quantify consciousness within our framework, we adopt the Integrated Information Theory (IIT), which characterizes consciousness by a scalar Φ that reflects the irreducibility of a system's cause–effect structure [17]. We further propose that Φ functions as a coupling constant linking conscious integration to event-space curvature, such that measurable effects arise only above a threshold Φc value. This connection is developed in detail in Section 2.5.

1.3. Philosophical Frameworks and Conceptual Motivations

Philosophically, we distinguish three modes of reality (Table 1 in Section 2.5) :

• Nature (Deterministic or Stochastic Law): Outcomes governed entirely by physical laws without volitional influence.
• Choice: Local influence of conscious intention on probabilistic outcomes within the constraints of physical possibility.
• Miracle: Radical restructuring of probabilities, defined as events that appear highly improbable under baseline natural conditions but become significantly more likely under intense will or divine intervention.

Traditional metaphysics treats these as separate ontological categories. Conversely, we propose that they represent different degrees of curvature in a unified geometric structure: the personal event-space metric.

1.4. Objectives and Structure

This paper aims to:

• Develop a geometric framework in which event-space probabilities curve in a manner analogous to mass curving spacetime.
• Connect this framework to IIT, and propose that curvature effects scale with integrated information Φ.
• Develop a detailed experimental protocol using quantum photon routing via retinal absorption, which avoids the dual metric problem by ensuring collapse occurs within the subject's integrated neural system (detailed in Section 4.1).
• Address the methodological challenge of ensuring quantum collapse occurs within the subject's personal metric rather than that in external measurement devices—the "dual metric problem" detailed in Section 4.1—and provide comprehensive statistical, ethical, and methodological considerations.

2. Theoretical Framework

2.1. The Personal Event-Space Metric

We propose that each conscious observer possesses a personal metric g_μν(x, Φ) defined over "event space," which is a probabilistic manifold representing all possible outcomes. This metric encodes how distances between events are measured from the observer's perspective. Unlike spacetime, which is shared across all observers in general relativity, event space is inherently subjective. Different observers may assign different probabilities, and therefore different distances, to the same outcome.

In the absence of any volitional influence, the metric reduces to a baseline form g⁰_μν(x), which corresponds to standard quantum probabilities. When an observer exerts will, defined as a conscious intention directed toward a specific outcome, the metric curves and alters geodesic paths throughout the event space.

2.2. Geodesics as Paths of Reality

According to general relativity, free particles follow geodesics, which are the straightest possible paths through curved spacetime. In a recent study, the concept of geodesic paths has been extended to quantum many-body systems [18], suggesting that geometric approaches can elucidate quantum dynamics. Similarly, we propose that reality evolves along geodesics in event space. An event is more likely to occur if it lies along or near a geodesic path defined by the observer's personal metrics.

More formally, let γ(λ) be a path in event space parameterized by λ. The geodesic equations are as follows.

$${\displaystyle \frac{d^2{x}^{\mathsf{\mu }}}{d{\mathsf{\lambda }}^2}}+{\mathsf{\Gamma }}_{\mathsf{\alpha }\mathsf{\beta }}^{\mathsf{\mu }}{\displaystyle \frac{d{x}^{\mathsf{\alpha }}}{d\mathsf{\lambda }}}{\displaystyle \frac{d{x}^{\mathsf{\beta }}}{d\mathsf{\lambda }}}=0,$$

(1)

where Γ^μ_αβ are the Christoffel symbols derived from the metric g_μν. The curvature of the metric determines which outcomes are "geodesically proximate," and hence, more probable.

2.3. Will as a Curvature Field

We model a field that curves the event-space metric analogous to how mass–energy curves spacetime in Einstein's field equations [19]. We write:

$$g_{\mathsf{\mu }\mathsf{\nu }}\left(x,\mathsf{\Phi }\right)=g_{\mathsf{\mu }\mathsf{\nu }}^0\left(x\right)+h_{\mathsf{\mu }\mathsf{\nu }}\left(x,\mathsf{\Phi }\right),$$

(2)

where h_μν(x, Φ) is the perturbation induced by the observer's will, modulated by their level of integrated information Φ. The greater the Φ, the stronger is the curvature effect.

2.4. The Three Regimes

• Nature (h_μν ≈ 0): Characterized by minimal or no curvature; reality follows baseline geodesics determined by physical law alone.
• Choice (small but nonzero h_μν): Characterized by subtle curvature; conscious intention gently biases probabilities within narrow margins.
• Miracle (large h_μν): Characterized by extreme curvature; the probability landscape is dramatically reshaped, enabling outcomes that are vanishingly unlikely under baseline conditions.

2.5. Connection to Integrated Information Theory

IIT quantifies consciousness through the scalar Φ, which measures the irreducibility of a system's cause–effect structure [17,20,21]. We propose that Φ functions as the coupling constant between consciousness and metric curvature:

$$h_{\left(\mu \nu \right)}\left(x,\Phi \right)\propto f\left(\Phi \right)·T_{\left(\mu \nu \right)}^{\left(will\right)}\left(x\right)$$

(3)

where T^will_μν is a "stress-energy tensor of will"—a mathematical object encoding the intensity and directionality of intention— and f(Φ) is a monotonically increasing function with threshold behavior:

$$f\left(\mathsf{\Phi }\right)\approx 0\hspace{1em}\mathrm{for}\mathsf{\Phi }<{\mathsf{\Phi }}_c,\hspace{1em}\hspace{1em}f\left(\mathsf{\Phi }\right)>0\hspace{1em}\mathrm{for}\mathsf{\Phi }\ge {\mathsf{\Phi }}_c$$

While systems lack sufficient integration to induce measurable curvature below the threshold Φ_c, curvature effects emerge above this threshold.

Table 1. Comparison of the three regimes in the geometric framework.

Regime	Will Intensity	Metric Curvature	Phenomenological Description
Nature	Φ ≈ 0	|Δgμν| ≈ 0	Governed entirely by baseline physical law, no volitional influence
Choice	Φ moderate	0 < |Δgμν| < δc	Subtle local curvature; gentle probability bias within narrow margins
Miracle	Φ very large	|Δgμν| ≫ δc	Extreme curvature; dramatic reshaping of the probability landscape

Table 1. Comparison of the three regimes in the geometric framework.

Regime	Will Intensity	Metric Curvature	Phenomenological Description
Nature	Φ ≈ 0	|Δgμν| ≈ 0	Governed entirely by baseline physical law, no volitional influence
Choice	Φ moderate	0 < |Δgμν| < δc	Subtle local curvature; gentle probability bias within narrow margins
Miracle	Φ very large	|Δgμν| ≫ δc	Extreme curvature; dramatic reshaping of the probability landscape

3. Mathematical Formalism

3.1. Event-Space as a Probabilistic Manifold

We model event space as a smooth manifold $ℳ$ with local coordinates x^μ that represent possible outcomes. Each point in $ℳ$ corresponds to a distinct quantum state or a macroscopic event. The personal metric g_μν(x, Φ) defines a Riemannian structure on $ℳ$ and determines the distances among outcomes.

The probability densities are related to the metric via the volume form. The outcome at x has the following probability density:

$$\mathsf{\rho }\left(x\right)\propto \sqrt{\det g_{\mathsf{\mu }\mathsf{\nu }}\left(x,\mathsf{\Phi }\right)}\hspace{0.17em}{e}^{-S\left(x\right)},$$

(4)

where S(x) denotes an action or information function. Geodesic proximity corresponds to higher probability, because outcomes that lie along or near geodesics have lower action and therefore higher probability.

3.2. Field Equations for the Personal Metric

By analogy to Einstein's field equations, we propose:

$$R_{\mathsf{\mu }\mathsf{\nu }}-{\displaystyle \frac{1}{2}}R\hspace{0.17em}{g}_{\mathsf{\mu }\mathsf{\nu }}=\mathsf{\kappa }\hspace{0.17em}{T}_{\mathsf{\mu }\mathsf{\nu }}^{\mathrm{will}}\left(\mathsf{\Phi }\right),$$

(5)

where R_μν is the Ricci curvature tensor, R is the Ricci scalar, and κ is a coupling constant analogous to Newton's gravitational constant. The term $T_{\mathsf{\mu }\mathsf{\nu }}^{\mathrm{will}}\left(\mathsf{\Phi }\right)$ encodes the "energy-momentum" of conscious intention.

This equation is heuristic rather than derived from first principles, representing a conceptual analogy rather than a fully specified dynamical law. We address this and related theoretical limitations in Section 5, where we outline how the metric's functional dependence on Φ may be formalized in future studies. Nonetheless, the structure mirrors general relativity and provides a conceptual scaffold for this theoretical framework.

3.3. Quantum Probabilities and Geodesic Deviation

In standard quantum mechanics, the probability of outcome x is given by the Born rule as follows:

$$P\left(x\right)={\left|⟨x|\mathsf{\psi }⟩\right|}^2.$$

(6)

We propose that the personal metric modulates this probability:

$$P\left(x|\mathsf{\Phi }\right)=\mathcal{N}\hspace{0.17em}{\left|⟨x|\mathsf{\psi }⟩\right|}^2\hspace{0.17em}\exp \left(-{\displaystyle \frac{d_g{\left(x,x_{\mathrm{intent}}\right)}^2}{2{\mathsf{\sigma }}^2}}\right),$$

(7)

where d_g(x, x_intent) is the geodesic distance (in the metric g_μν) between the outcome x and the observer's intended outcome $x_{\mathrm{intent}}$, σ is a dispersion parameter, and $𝒩$ is a normalization constant.

This formulation implies that outcomes that are geodesically closer to the observer's intention receive an exponential increase in probability while maintaining overall normalization. The effect size depends on Φ, the strength of will, and the baseline quantum probabilities.

3.4. Coupling to Quantum Collapse

We hypothesize that metric curvature influences the wavefunction collapse. In standard collapse theories, such as the Ghirardi–Rimini–Weber (GRW) theory, collapse occurs stochastically with probabilities given by the Born rule, which states that the probability of a measurement outcome equals the squared magnitude of the system's wavefunction amplitude. In our framework, the collapse probabilities are biased by the observer's personal metric.

$$P_{\mathrm{collapse}}\left(x\right)={\displaystyle \frac{{\left|⟨x|\mathsf{\psi }⟩\right|}^2\hspace{0.17em}W\left(x,\mathsf{\Phi }\right)}{{\sum }_{x^{\prime }}{\left|⟨x^{\prime }|\mathsf{\psi }⟩\right|}^2\hspace{0.17em}W\left(x^{\prime },\mathsf{\Phi }\right)}}$$

(8)

The function W(x, Φ) is a will weighting function that increases with proximity to $x_{\mathrm{intent}}$ and with increasing Φ. This provides a formal mechanism for the influence of volition on quantum outcomes without violating energy-momentum conservation at the macroscopic level.

4. Experimental Protocol: Quantum Photon Routing via Retinal Absorption

4.1. The "Dual Metric Problem" and Choice of Retinal Absorption

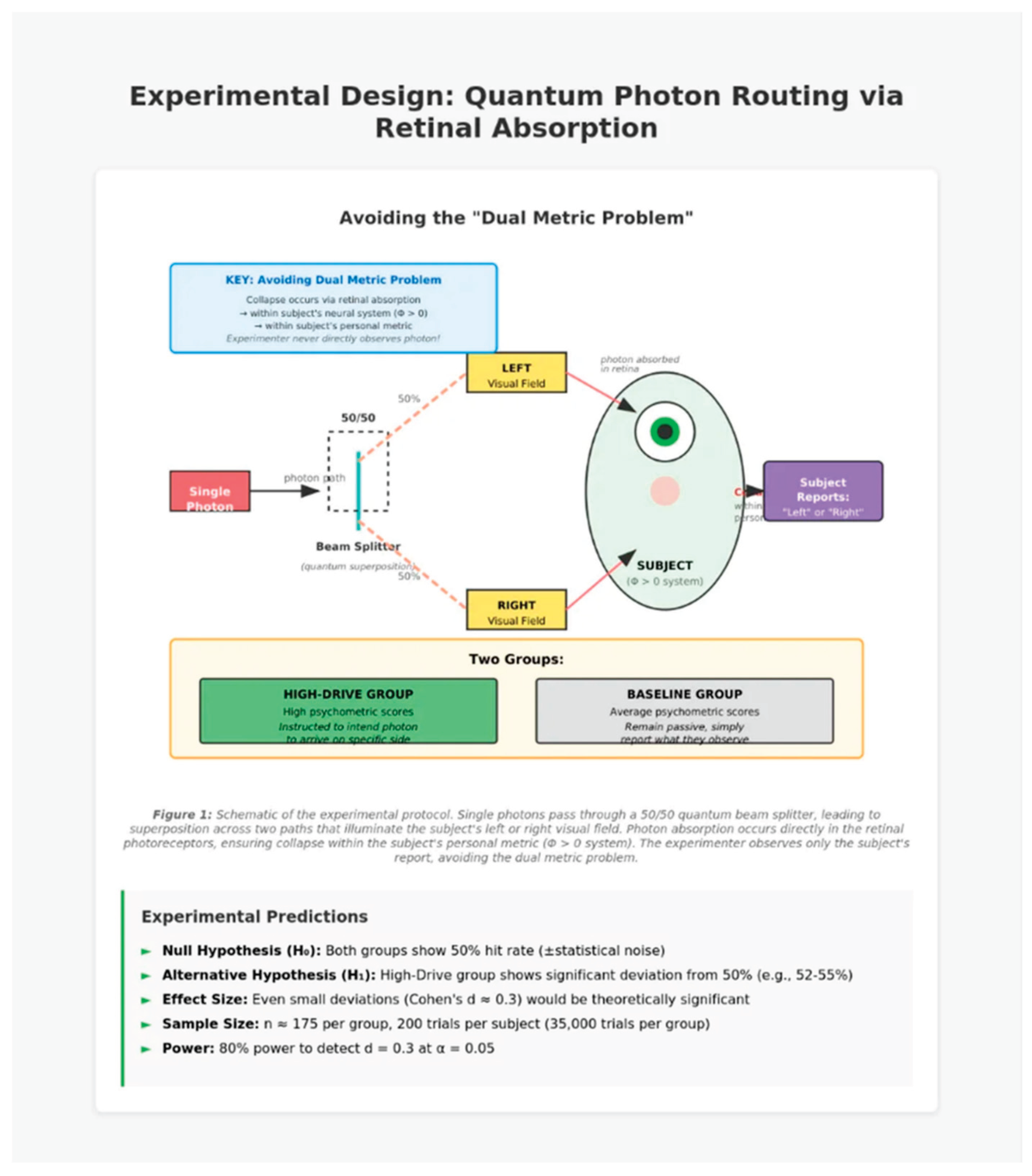
A fundamental challenge associated with testing this framework concerns the scope of volitional influence across metric boundaries. According to our theory, each conscious system with Φ > 0 possesses its own personal event-space metric. This raises a critical question: can an observer's will influence quantum collapse events that occur within a different system's metric? Consider an experiment using an external electronic detector with its own integrated information (Φdetector > 0). If the photon collapses in the detector's metric before reaching the subject, two problems arise. First, any measured deviation can reflect the experimenter's (or detector's) influence rather than the subject's intention—the classic dual metric problem. Second, and more fundamentally, it remains unclear whether the conscious will can traverse metric boundaries to influence collapse events occurring in external systems with their own Φ. The theory proposes that will curves one's personal event-space metric, but does not specify mechanisms for cross-metric influence. To avoid both issues, we designed an experiment where quantum collapse occurs directly within the subject's own integrated neural system. When a photon is absorbed by rhodopsin molecules in retinal photoreceptors, the collapse occurs within the subject's personal metric (Φsubject). The observer's will acts upon an event occurring within their own probabilistic manifold, not across metric boundaries. This design represents the most direct and theory-consistent test: conscious intention influencing quantum outcomes within the same integrated system. External sensors (e.g., electroretinography) capture only post-collapse biosignals, analogous to detecting the point where a photon has struck a screen following collapse in the double-slit experiment. The quantum event itself—photon absorption and wavefunction collapse—occurs entirely within the subject's personal metric, ensuring clean isolation of the predicted effect. If this within-metric experiment succeeds, future studies can explore the possibility of cross-metric. However, testing the core prediction requires first demonstrating the effect within a single, unambiguous metric framework.

4.2. Experimental Design

Hypothesis: Subjects with high volitional drive, quantified using validated psychometric instruments including measures of achievement motivation [22], Grit Scale [23], BIS/BAS [24], and Self-Efficacy Scale [25], will report detection distributions that differ significantly from those of baseline subjects, such as differences in spatial location or timing, even when photons are routed through quantum indeterminate paths such as beam splitters.

Figure 1. Schematic of the experimental protocol. Single photons pass through a 50/50 beam splitter, creating a superposition across two paths that illuminate the subject's left or right visual field. Photon absorption occurs in the retinal photoreceptors, which ensures collapse within the subject's personal metric (Φ > 0) and avoids the dual metric problem.

Figure 1. Schematic of the experimental protocol. Single photons pass through a 50/50 beam splitter, creating a superposition across two paths that illuminate the subject's left or right visual field. Photon absorption occurs in the retinal photoreceptors, which ensures collapse within the subject's personal metric (Φ > 0) and avoids the dual metric problem.

Setup:

• Single photons are generated using a heralded photon source (e.g., spontaneous parametric down-conversion).
• Each photon passes through a 50/50 quantum beam splitter, which produces two spatially separated paths positioned to illuminate the subject's left or right visual fields.
• Photons are directly absorbed by the retinal photoreceptors of the subject, triggering a neural response.
• The subject reports on which side (left or right) they perceived the photon.

Key Manipulation: Subjects are divided into two groups:

High-Drive Group: Pre-selected participants are chosen based on high scores on psychometric measures of volitional traits, including BIS/BAS, grit, and self-efficacy. They are instructed to intend for photons to arrive on a specific side, such as the right, and to maintain focused attention on this intention throughout each trial block.

Baseline Group: Participants with average scores on psychometric measures are instructed to remain passive and to simply report what they observe without attempting to influence the outcome.

4.3. Dependent Variable and Predictions

Primary Dependent Variable: The proportion of trials in which the subject reports detecting the photon on their intended side for the high-drive group, or on a randomly pre-assigned target side for the baseline group.

Predictions:

• Null Hypothesis (H₀): Both groups show a 50% hit rate (within statistical noise), consistent with unbiased quantum collapse.
• Alternative Hypothesis (H₁): The High-Drive group shows a statistically significant deviation from 50% (e.g., 52–55%), while the Baseline group remains at ~50%.

Even a small effect size, such as Cohen's d ≈ 0.3, would be theoretically significant because it suggests that high Φ and volitional focus can systematically bias quantum collapse probabilities.

4.4. Sample Size and Power Analysis

Using G*Power 3 [26], we calculate the sample sizes required for detecting a small-to-medium effect (d = 0.3) with 80% power at α = 0.05:

• Per-group sample size: n ≈ 175 subjects
• Trials per subject: 200 trials (to detect within-subject consistency)
• Total trials: 70,000 (175 × 2 groups × 200 trials)

This design balances feasibility with statistical power, ensuring sufficient data to detect subtle deviations from chance.

The sample will be recruited from diverse populations to ensure generalizability beyond WEIRD (Western, Educated, Industrialized, Rich, Democratic) populations [27].

4.5. Controls and Blinding

• Double-Blind Protocol: Experimenters who record the responses do not know which group the subject belongs to or what the subject's intended direction is.
• Randomization: Trial order and target side assignments are randomized across sessions.
• Control for Sensory Biases: Photon sources are balanced across both visual fields; any hardware asymmetries are calibrated and corrected.
• Pre-Registration: The hypotheses, sample size, and analysis plan are pre-registered in the Open Science Framework (OSF.io) before data collection begins.

4.6. Statistical Analysis

In the primary analysis, a two-sample t-test is used to compare the hit rates between the High-Drive and Baseline groups. The secondary analyses include the following:

• Correlation between individual Φ proxies (psychometric scores) and hit rate.
• Bayesian analysis to quantify evidence for or against alternative hypotheses.
• Time-series analysis to detect fatigue or learning effects across trial blocks.

4.7. Ethical Considerations

• Informed consent is obtained from all participants after clearly explaining that the study tests a speculative hypothesis.
• Light exposure is maintained within safe limits (scotopic conditions and brief flashes).
• Subjects are debriefed and allowed to withdraw their data post-experiment.
• The study is approved by the Institutional Review Board (IRB) before commencement.

4.8. Addressing the Dual Metric Problem

By ensuring that photon collapse occurs via retinal absorption within the subject's neural system, we avoid the dual metric problem. The experimenter never directly observes the photon's path and instead studies only the subject's report. Since the subject's retina is part of their integrated Φ > 0 system, collapse occurs within their personal metric. This design feature is essential for experimental validity.

5. Discussion

5.1. Interpretation of Potential Results

If the High-Drive group shows a statistically significant deviation from 50%, whereas the baseline group does not, this would constitute preliminary evidence of metric-based will-curvature effects. Conversely, if both groups remain at 50%, the null hypothesis would be supported, suggesting that

• The effect size is too small to detect using current methods, or
• The theoretical framework requires revision or abandonment.

Given the speculative nature of the hypothesis, negative results would not necessarily falsify the broader framework but would constrain the magnitude of any putative effect.

5.2. Broader Implications for Physics and Neuroscience

If empirically supported, this framework can have profound implications:

• Quantum Foundations: The results would suggest that consciousness plays a more active role in wavefunction collapse than is acknowledged in mainstream interpretations.
• Neuroscience and IIT: The findings would link Φ, a measure of consciousness, to empirically detectable physical effects and provide a new avenue for testing IIT.
• Philosophy of the Mind: The results would support non-epiphenomenal views of consciousness, in which subjective experience has causal efficacy.

5.3. Comparison to Alternative Models

Our framework has some conceptual similarities with several existing approaches, but also offers certain distinct features:

Von Neumann–Wigner Consciousness-Collapse: Similar to Wigner (1961) [10], we propose that consciousness influences collapse. However, we extend this view by introducing a geometric metric structure and connecting it to the Φ value of IIT. Our model also specifies a testable mechanism, the geodesic bias, rather than relying on a purely interpretational stance.

Stapp's Mind–Matter Interaction: Stapp [13,14] developed a quantum-mechanical framework for free will based on Heisenberg's Process 1 (measurement) and Process 2 (evolution). Our approach is compatible with that of Stapp, but adds a geometric layer—will as metric curvature—and proposes a specific experimental protocol to test it.

Penrose–Hameroff Orchestrated Objective Reduction (Orch OR): The Orch OR theory [28] posits that quantum coherence in microtubules undergoes objective reduction tied to space–time geometry. While Orch’s OR focuses on the physical basis of consciousness, our framework focuses on the influence of consciousness on probability distributions. The two are potentially complementary, i.e., Orch OR can provide the mechanism for consciousness itself, while our model describes how consciousness curves event space.

Objective Collapse Models (GRW, CSL): These models (Ghirardi–Rimini–Weber, continuous spontaneous localization) introduce stochastic collapse without invoking consciousness. Our model differs fundamentally: we propose that collapse probabilities are observer-dependent and modulated by Φ. However, if the objective collapse models are correct, and consciousness plays no role, our experimental predictions will fail.

Many-Worlds Interpretation (Everett): In Everett's framework, there is no collapse, only branching. Our model assumes collapse and is therefore incompatible with a pure many-worlds interpretation. However, our framework can be interpreted in Everettian terms, in which observers with high Φ experience branches with different measure weights that effectively steer their experienced branch. This reinterpretation would require significant theoretical development.

Ultimately, our framework is most compatible with consciousness-involved collapse theories but offers a novel geometric and IIT-based articulation. It differs from existing models in that it proposes personal metrics as the key mathematical structure and explicitly connects will curvature to integrated information.

5.4. Philosophical Implications

If empirically supported, this framework can suggest the following:

• Soft Agency: Conscious will has real but subtle physical consequences, not via "force" but via geometric influence on probability.
• Unified Causality: "Miracle" and "nature" are not ontologically distinct—they are degrees of curvature within the same geometric structure.
• Observer-Participatory Universe: Echoing Wheeler's "participatory anthropic principle," observers help shape the probabilistic fabric of reality rather than passively observing it.

5.5. Limitations of the Theory

Several conceptual and practical limitations remain:

• Mathematical Rigor: The current formalism is heuristic. A fully rigorous mathematical framework, such as a fiber bundle formulation and a precise definition of the event-space topology, remains to be developed.
• Mechanistic Gap: We have not specified the physical mechanism by which Φ couples to quantum probabilities. This is analogous to the status of general relativity before the development of quantum field theory, in which field equations existed without an underlying quantum mechanism.
• Threshold Ambiguity: The precise value of Φ_c and the form of f(Φ) are uncertain and must be determined empirically.
• Scope Limitations: The model applies only to systems with Φ > 0 and does not claim to replace standard physics for inanimate matter.
• Interpretational Flexibility: The geometric languages are largely metaphorical. Future studies must be aimed at clarifying whether an event space is a physical manifold or a mathematical tool for organizing probabilistic intuitions.

6. Conclusions

Herein, we have proposed a theoretical framework in which consciousness curves a personal event-space metric, thereby influencing the probabilities of quantum outcomes in a manner analogous to how mass curves spacetime in general relativity. This account offers a unified perspective on law and agency, determinism and choice, and physics and phenomenology.

The accompanying experimental design, which measures quantum photon routing through retinal absorption under intention-based conditions, provides a concrete and falsifiable prediction. Although speculative, the framework draws on established work in physics, including general relativity, as well as neuroscience via Integrated Information Theory and quantum mechanics. It seeks to connect philosophical questions with empirical methodologies in a manner that permits systematic testing.

Irrespective of whether the proposal is confirmed or rejected, we hope these findings will encourage further dialogue at the intersection of consciousness studies, quantum foundations, and the philosophy of physics. In keeping with scientific practice, we look forward to an empirical assessment of these proposals.