Motion out of Time: Single Speed Hypothesis

1. Introduction

The conventional understanding of motion, rooted in Newton’s laws of motion [1], defines velocity as the rate of change of position with respect to time, expressed as $v={\displaystyle \frac{d}{t}}$. This relationship underpins classical mechanics and is refined in Einstein’s special relativity [2], where the finite speed of light ($c=\mathrm{299,792,458}$ m/s) and time dilation govern the dynamics of moving bodies. Time, in these frameworks, is a continuous parameter over which motion occurs. However, we propose a radical alternative: motion is inherently instantaneous in the absence of interrupting factors, and the time we observe reflects periods of "stopping" rather than continuous traversal.

This hypothesis, termed "Motion Out of Time," posits that all objects—whether massless, like photons, or massive, like macroscopic bodies—share an intrinsic ability to move between points without elapsing time. Observed time arises from intermittent stops, potentially caused by external forces (e.g., friction, gravity) or intrinsic properties (e.g., mass, quantum interactions). Inspired by thought experiments, this idea challenges foundational assumptions and invites reinterpretation of phenomena across physics. While speculative, it aligns conceptually with aspects of relativity and quantum mechanics, as discussed later, drawing on works like Hartle’s exploration of spacetime [3] and Rovelli’s studies of time in quantum gravity [4].

2. Thought Experiment: Photon vs. Marble

To elucidate this hypothesis, consider a thought experiment in a vacuum: a photon and a marble travel 100 meters in a straight line (see Figure 1). The photon, moving at $c$, completes the distance in:

$$t_p={\displaystyle \frac{d}{c}}={\displaystyle \frac{100}{\mathrm{299,478,458}}}\approx 3.336\times {10}^{-7}seconds$$

The marble, traveling at $v_m$ = 40m/s, takes:

$$t_m={\displaystyle \frac{d}{v_m}}={\displaystyle \frac{100}{40}}=2.5seconds$$

Conventionally, as established in Newton’s laws [1] and refined by special relativity [2], the disparity in travel times—$t_m=2.5seconds$ for the marble and $t_p\approx 3.336\times {10}^{-7}seconds$ for the photon—is explained by their differing velocities, where $v={\displaystyle \frac{d}{t}}$ treats time as a continuous parameter of motion. In contrast, this hypothesis posits that all objects possess an intrinsic capacity for "instantaneous motion" between two points, occurring "out of time" when unimpeded. The observed travel times, we suggest, arise not from continuous traversal but from discrete "stops" induced by external forces or intrinsic properties, such as mass.

We propose that both the photon and the marble could, in an idealized state free of interruptions, cover the 100 meters with no elapsed time. For the photon, the observed $t_p=3.336\times {10}^{-7}seconds$ might reflect minimal stops, potentially linked to the uniform structure of spacetime as explored in later sections (see Section 4). For the marble, the 2.5 seconds could result from a greater accumulation of stops, possibly due to mass-related interactions (e.g., with the Higgs field [5]) or other unspecified factors in this vacuum scenario.

Imagine two messengers tasked with delivering a message over the same distance. One returns immediately, while the other is delayed by interruptions—rests, obstacles, or detours. This analogy, though simplified, underscores the hypothesis that time emerges from interruptions rather than motion itself.

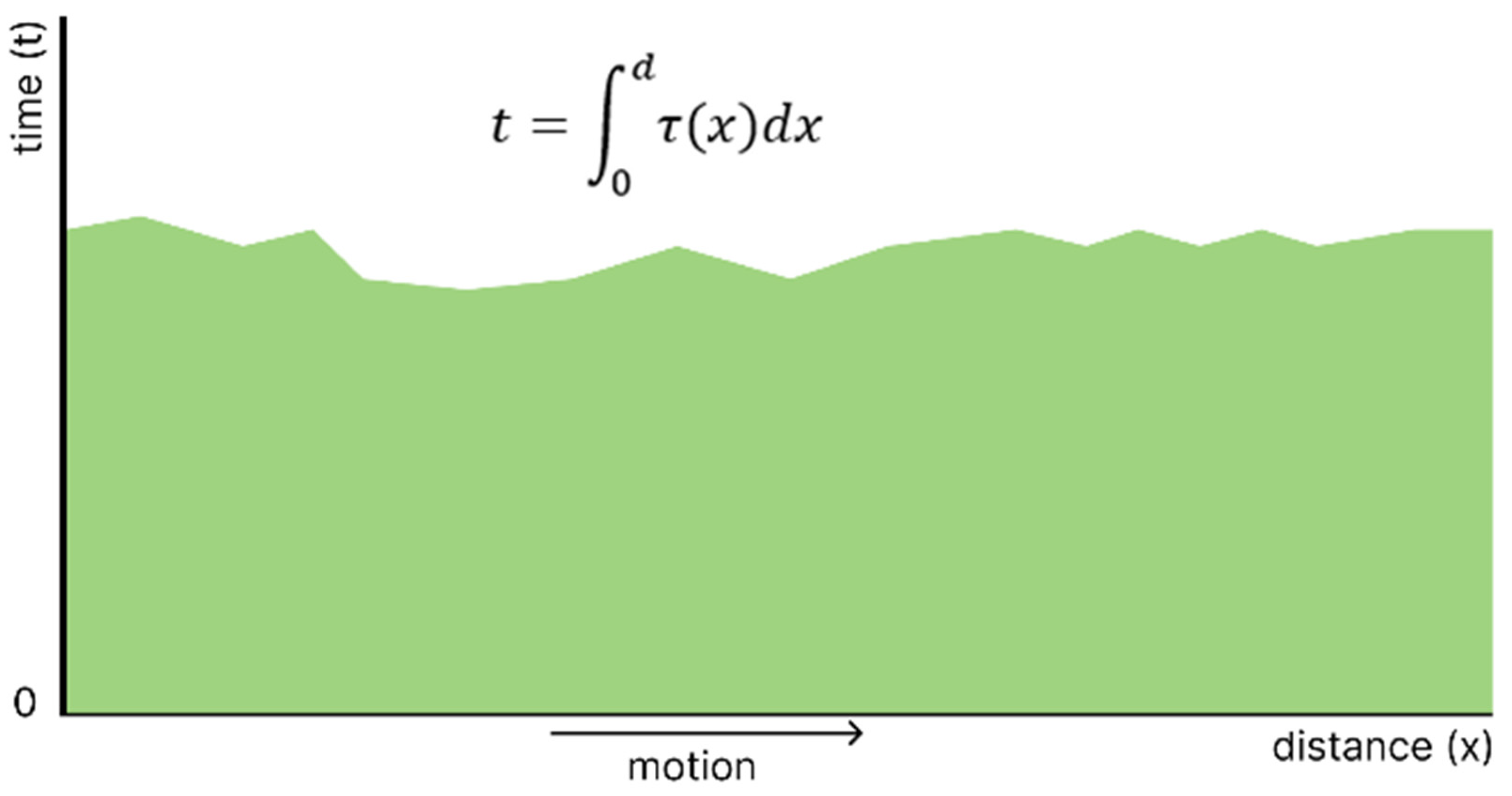
3. Conceptual Framework

We define "intrinsic motion" as the capacity of an object to traverse a distance instantaneously when unimpeded. Observed time $t$ is the sum of discrete stop times ${\tau }_i$, where stops are induced by external forces or intrinsic properties:

$$t=\sum _{i=1}^n{\tau }_i$$

The effective velocity becomes:

$$v={\displaystyle \frac{d}{t}}={\displaystyle \frac{d}{{\sum }_{i-1}^n{\tau }_i}}$$

Here, $n$ represents the number of hypothetical stops, and ${\tau }_i$ denotes the duration of each stop. For a photon traveling at the speed of light ($c=\mathrm{299,792,458}$), the observed coordinate time $t_p\approx 3.336\times {10}^{-7}second$ over 100 meters (as calculated in Section 2) is proposed, within this hypothesis, to result from the cumulative effect of discrete stops. While the photon’s proper time in relativity is zero ($\tau =0$) [2], we speculate that this coordinate time might arise from a constant series of interruptions attributed to the uniform structure of spacetime, possibly linked to vacuum fluctuations or the discrete nature of spacetime suggested by loop quantum gravity [4]. These interruptions are hypothesized to be uniform across space, involving a large number of extremely brief events ($n$ is large, ${\tau }_i$ is small), such that:

$$t_p=\sum _{i=1}^n{\tau }_i\approx 3.336\times {10}^{-7}seconds$$

which could, in this speculative model, contribute to the invariant speed of light $c={\displaystyle \raisebox{1ex}{$d$}\!\left/ \!\raisebox{-1ex}{$\sum {\tau }_i$}\right.}$. For massive objects like the marble, the total observed time is significantly larger, amounting to 2.5 seconds over the same distance, which we attribute to the cumulative effect of stops influenced by factors such as mass or interactions (e.g., with the Higgs field [5]). The photon’s interruptions, if real, would differ, possibly reflecting a fundamental spacetime property, though this remains unverified. This framework is entirely conceptual and not a predictive theory; rigorous experimental evidence and quantification of $n$ and ${\tau }_i$ are needed, potentially through quantum field theory or quantum gravity [4,6].

To complement the discrete formulation $t={\sum }_{i=1}^n{\tau }_i$, we propose a continuous model where stops occur across the distance $d$, with the total observed time derived from integration over the path (see Figure 2). At each infinitesimal segment $dx$, an object may experience either zero stop time—corresponding to instantaneous motion "out of time"—or a finite duration due to physical interactions, contributing to the observed time. We define $\tau (x)$ as the stop duration per unit distance (in $s/m$), such that:

$$t={\int }_0^d\tau (x)dx$$

The effective velocity is then:

$$v={\displaystyle \frac{d}{{\int }_0^d\tau (x)dx}}$$

This model posits that $\tau (x)$ may vanish in an idealized, unimpeded state, consistent with the hypothesis of intrinsic instantaneous motion (Section 1), or take positive values in real spacetime due to properties such as mass or energy interactions. To formulate $\tau (x)$, we propose a model rooted in Planck-scale physics and relativistic mass-energy effects, drawing inspiration from quantum gravity [4] and particle physics [5]:

$$\tau \left(x\right)={\displaystyle \frac{t_p}{I_p}}·\left(1+\alpha ·{\displaystyle \frac{m{c}^2}{E-m{c}^2}}\right)$$

Here, $t_p=5.391\times {10}^{-44}s$ is the Planck time, $I_p=1.616\times {10}^{-35}m$ is the Planck length, and ${\displaystyle \frac{t_p}{I_p}}\approx 3.34\times {10}^{-9}s/m$ represents a minimal stop duration density, hypothesized as a spacetime baseline [4]. The factor $1+\alpha ·{\displaystyle \frac{m{c}^2}{E-m{c}^2}}$ incorporates a mass-dependent contribution, where $m{c}^2$ is the rest energy (in joules), $E=\mathsf{\gamma }m{c}^2$ is the total relativistic energy with $\mathsf{\gamma }={\left(1-{\displaystyle \frac{v^2}{c^2}}\right)}^{-1/2}$, $E-m{c}^2$ is the relativistic kinetic energy (in joules), and $\alpha$ is a dimensionless coupling constant. This expression assumes that stops scale with inertial mass, potentially via Higgs interactions [5], and are reduced by relativistic energy, aligning with the role of energy in mitigating temporal delays (Section 6).

For the photon (Section 2: $d=100m,t=3.336\times {10}^{-7}s,m=0,v=c$):

$$\tau \left(x\right)={\displaystyle \frac{t_p}{I_p}}·\left(1+0\right)\approx 3.34\times {10}^{-9}s/m$$

$$t={\int }_0^{100}3.34\times {10}^{-9}dx=3.34\times {10}^{-7}s\approx 3.336\times {10}^{-7}s$$

This matches the observed coordinate time, suggesting that massless particles experience a uniform, minimal stop duration, possibly linked to spacetime granularity [4], resulting in $v=c$. For the marble ($m=0.02kg,v=40m/s$, $t=2.5s$):

$$E_k={\displaystyle \frac{1}{2}}m{v}^2={\displaystyle \frac{1}{2}}·0.02·{\left(40\right)}^2=16J$$

$$m{c}^2=0.02·{\left(3\times {10}^8\right)}^2=1.8\times {10}^{15}J$$

Given $v\ll \mathrm{c},\mathsf{\gamma }\approx 1$, so $E\approx m{c}^2+E_k$, and $E-m{c}^2\approx E_k=16J$:

$${\displaystyle \frac{m{c}^2}{E-m{c}^2}}={\displaystyle \frac{1.8\times {10}^{15}}{16}}=1.125\times {10}^{14}$$

$$t=d·\tau \left(x\right)=100·{3.34\times 10}^{-9}·\left(1+\alpha ·1.125\times {10}^{14}\right)=2.5$$

$$1+\alpha ·1.125\times {10}^{14}={\displaystyle \frac{2.5}{100·{3.34\times 10}^{-9}}}\approx 7.485\times {10}^6$$

$$\alpha \approx {\displaystyle \frac{7.485\times {10}^6}{1.125\times {10}^{14}}}\approx 6.65\times {10}^{-8}$$

Thus, $\tau \left(x\right)\approx 0.025s/m$ and $t=100·0.025=2.5s$, consistent with the marble’s observed time. This indicates a significant mass-induced increase in stop duration, supporting the hypothesis that massive objects experience greater delays (Section 2). However, $\alpha$ is specific to this example and not universal; its value depends on system-specific parameters and requires further investigation.

The baseline ${\displaystyle \frac{t_p}{I_p}}$ is derived from Planck units, widely accepted as fundamental scales in quantum gravity [4], though its interpretation as a stop duration remains speculative. The term ${\displaystyle \frac{m{c}^2}{E-m{c}^2}}$ is dimensionless, ensuring $\tau \left(x\right)$ retains units of $s/m$, and provides a physically grounded dependence on relativistic energy, surpassing the ad hoc nature of the original formulation. The coupling constant $\alpha$ adjusts the magnitude of the mass effect, potentially tied to mass-energy interactions (e.g., Higgs field [5]), but its general applicability across diverse systems remains untested (Section 6). In an idealized limit where $m=0$ or $E\to \infty$, $\tau (x)\to {\displaystyle \frac{t_p}{I_p}}$, approaching photon-like behavior, though observed finite times indicate non-zero contributions in practice.

This continuous model refines the discrete approach by treating stops as a distributed effect, with $\tau (x)$ reflecting either zero or finite stop time based on physical conditions. It aligns with speculations of spacetime discreteness [4] and mass-energy dynamics (Section 4), suggesting that photon stops stem from a universal spacetime property, while marble stops scale with mass. The exact form of $\tau (x)$ remains provisional, as $\alpha$’s value and the mechanisms driving stops (e.g., quantum fluctuations [6]) await theoretical refinement and experimental validation (Section 6), advancing this framework toward a testable hypothesis.

4. Connection to Established Physics

In the framework of special relativity, the proper time $\tau$ for an object traversing a distance $d$ over a coordinate time $t$ is defined as:

$$\tau =\sqrt{t^2-{\left({\displaystyle \frac{d}{c}}\right)}^2}$$

For a photon, where $d=ct$, the proper time evaluates to $\tau =0$, indicating no proper time is experienced during its propagation [3]. Within our hypothesis, the photon’s motion is postulated to be instantaneous between hypothetical interruptions, with its observed coordinate time—exemplified by $3.34\times {10}^{-7}s$ over $100m$—attributed to a consistent sequence of brief interruptions. These may arise from the uniform structure of spacetime, potentially linked to vacuum fluctuations or the discrete spacetime framework of loop quantum gravity [4]. This speculative model suggests that the invariant speed of light emerges as:

$$c={\displaystyle \frac{d}{{\int }_0^d\tau (x)dx}}$$

where $\tau \left(x\right)={\displaystyle \frac{t_p}{I_p}}$ for a photon ($m=0$), as derived in Section 3, offering a reinterpretation of relativistic velocity limits without contradicting established theory. For massive objects, $\tau >0$, which we hypothesize reflects the cumulative effect of more frequent or prolonged interruptions, possibly due to mass-dependent interactions such as those with the Higgs field [5].

Barbour’s work on timeless physics [7] posits that time emerges from change rather than existing as an inherent parameter. Our hypothesis extends this idea, proposing that motion is timeless between interruptions, with spacetime-induced events giving rise to perceived temporal progression. This perspective aligns conceptually with the discrete spacetime hypothesis of loop quantum gravity [4], where interruptions might correspond to quantized interactions, though empirical verification remains pending.

5. Reinterpretation of Quantum Phenomena

The "Motion Out of Time" hypothesis, initially formulated through classical thought experiments involving a photon and a marble (Section 2), extends its speculative reach into quantum mechanics, offering novel reinterpretations of foundational phenomena. This framework posits that all motion occurs instantaneously "out of time" in the absence of interruptions, with observed temporal effects arising from "stops" induced by external forces or intrinsic properties. In the quantum domain, these stops align with measurement or interaction events, providing a qualitative lens through which to view wave-particle duality, superposition, and entanglement. Building on the continuous stop model from Section 3, where travel time is expressed as:

$$t={\int }_0^d\tau (x)dx$$

with:

$$\tau \left(x\right)={\displaystyle \frac{t_p}{I_p}}·\left(1+\alpha ·{\displaystyle \frac{m{c}^2}{E-m{c}^2}}\right)$$

where $t_p=5.391\times {10}^{-44}s$, $I_p=1.616\times {10}^{-35}m$, $E=\mathsf{\gamma }m{c}^2$, $\mathsf{\gamma }={\left(1-{\displaystyle \frac{v^2}{c^2}}\right)}^{-1/2}$ and $\alpha$ is a dimensionless coupling constant, this section formalizes these ideas mathematically. It draws parallels to the photon’s motion and the marble’s interrupted journey, acknowledging the speculative nature of these reinterpretations and their need for future mathematical rigor and empirical validation (Section 6).

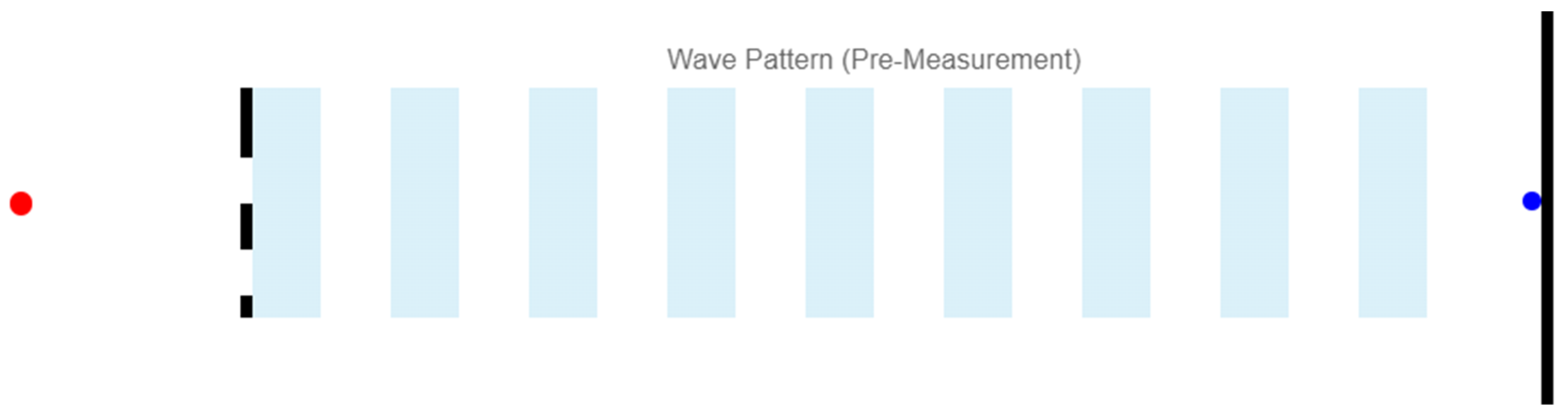
5.1. Wave-Particle Duality

The double-slit experiment exemplifies wave-particle duality: a quantum particle, such as an electron, produces an interference pattern when unobserved, yet manifests as a discrete entity when measured at a slit [8]. Conventionally, this behavior is attributed to the wavefunction’s evolution, governed by:

$$\mathit{i}\mathit{\hslash }{\displaystyle \frac{\partial \psi }{\partial t}}=-{\displaystyle \frac{{\hslash }^2}{2m}}{\displaystyle \frac{{\partial }^2\psi }{{\partial x}^2}}+V(x)\psi$$

and subsequent collapse (see Figure 3). Within the "Motion Out of Time" hypothesis, the particle is conceived as moving "out of time" across all possible paths simultaneously when unimpeded. The interference pattern reflects this timeless exploration of trajectories, with the observed time to the screen (LLL) given by:

$$t={\int }_0^L\tau (x)dx$$

For an electron ($m_e=9.11\times {10}^{-31}kg$, ${v\approx 10}^{6}m/s,E_k\approx {4.555\times 10}^{-19}J$, $L=1m$), unobserved:

$${\displaystyle \frac{m_e{c}^2}{E-m_e{c}^2}}\approx 1.8\times {10}^5$$

$$\tau \left(x\right)={3.34\times 10}^{-9}·\left(1+\alpha ·1.8\times {10}^5\right)$$

Given $t\approx {10}^{-6}s$:

$$1+\alpha ·1.8\times {10}^5={\displaystyle \frac{{10}^{-6}}{{3.34\times 10}^{-9}}}\approx 299.4$$

$$\alpha \approx {1.66\times 10}^{-3}$$

Measurement imposes a stop, collapsing $\psi (x)\to \delta (x-x_s)$, with ${\tau }_{meas}\approx {\displaystyle \frac{\mathit{\hslash }}{E_{int}}}$(e.g., $E_{int}\approx {10}^{-18}J,$ ${\tau }_{meas}\approx {10}^{-16}s$). This resonates with Wheeler’s delayed-choice experiments [9], where the choice of measurement retroactively influences behavior. The particle’s state remains undefined across all paths until a stop, induced by observation, determines its trajectory, suggesting a retro-causal interplay consistent with stops as temporal anchors.

5.2. Superposition

Quantum superposition permits a system to occupy multiple states concurrently until measurement resolves it into a definite state [10], described as:

$$\left|\psi \right.⟩=c_1\left|x_1\right.⟩+c_2\left|x_2\right.⟩$$

Where ${\left|c_1\right|}^2+{\left|c_2\right|}^2=1$. Under the hypothesis, a particle in superposition exists in a timeless condition, instantaneously encompassing all possible states, much like the marble’s capacity to traverse its path "out of time" absent interruptions (Section 2). The observed time over $d$ is:

$$t={\int }_0^d\tau (x)dx$$

For a cold atom ($m\approx {10}^{-25}kg$, $v\approx 1m/s$, $d=0.01m$, $t\approx {10}^{-3}s$):

$${\displaystyle \frac{m{c}^2}{E-m{c}^2}}\approx 1.8\times {10}^{41}$$

$$t=0.01·3.34\times {10}^{-9}·\left(1+\alpha ·1.8\times {10}^{41}\right)={10}^{-3}$$

$$\alpha \approx 1.66\times {10}^{-34}$$

Measurement introduces a stop, collapsing $\left|\psi \right.⟩$ to $\left|x_1\right.⟩$, with ${\tau }_{meas}\approx {\displaystyle \frac{\mathit{\hslash }}{∆E}}$ (e.g., $∆E\approx {10}^{-26}J,{\tau }_{meas}\approx {10}^{-8}s$). From the particle’s perspective, we consider that it always occupies a single position; the illusion of multiple locations arises from its motion “out of time.” This suggests time manifests through interruptions, not as a backdrop to state evolution, offering a qualitative analogy to the quantum-classical transition without resolving the measurement problem.

5.3. Entanglement

Entanglement manifests as instantaneous correlations between spatially separated particles, defying classical locality [11], with the state:

$$\left|\psi \right.⟩={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|\uparrow \right.⟩A\left|\downarrow \right.⟩B-\left|\downarrow \right.⟩A\left|\uparrow \right.⟩B\right)$$

The hypothesis proposes that entangled particles share a timeless connection "out of time" until a measurement imposes a stop, resolving their properties simultaneously, transcending temporal separation. Travel times to detectors are:

$$t_A={\int }_0^{d_A}\tau \left(x\right)dx,t_B={\int }_0^{d_B}\tau \left(x\right)dx$$

For photons ($m=0,\tau \left(x\right)={\displaystyle \frac{t_p}{I_p}}$ ), $t_A=d_A/c$, consistent with relativity [2]. Measurement imposes ${\tau }_{meas}\approx {\displaystyle \frac{\mathbf{\hslash }}{E_{int}}}$ (e.g., $E_{int}\approx {10}^{-19}J,{\tau }_{meas}\approx {10}^{-15}s$), collapsing $\left|\psi \right.⟩$ instantly. This likens entanglement to the marble’s instantaneous motion between stops (Section 2), with the entangled state persisting timelessly until halted, offering a conceptual analogy for non-locality without challenging the no-signaling principle [11].

5.4. Conceptual Note

These reinterpretations are speculative, designed to provoke discussion rather than supplant established quantum theory [8,10,11]. By positing that quantum phenomena occur "out of time" until stops impose temporal structure, the hypothesis aligns with inquiries into time’s role in quantum mechanics [12]. The model $\tau (x)$ extends the photon’s zero proper time and marble’s delays (Section 4), with $\alpha$ (e.g., $1.66\times {10}^{-34}$ for the atom) as a provisional constant needing refinement, possibly through quantum gravity insights [4]. Lacking the precision and grounding for a formal theory, it invites exploration of emergent time frameworks [7], building on the paper’s earlier arguments.

6. Implications and Challenges

If the "Motion Out of Time" hypothesis proves valid, it offers a transformative perspective on motion, time, and their interplay across classical and quantum domains. However, its development into a robust theory faces substantial conceptual and practical hurdles.

6.1. Implications

• Velocity as a Reflection of Stop Distribution: The hypothesis redefines velocity not as a measure of continuous motion but as an emergent property determined by the distribution and duration of stops along a path. For instance, in the thought experiment from Section 2, the marble’s slower effective speed ($v=40m/s$) compared to the photon’s ($v=c$) arises from a greater accumulation of stop durations, as modeled by $\tau (x)$, rather than a difference in intrinsic motion capability. Acceleration, in turn, becomes a mechanism that reduces the stop duration per unit distance, thereby increasing an object’s effective speed.
• Energy and Stop Mitigation: Energy, particularly relativistic energy, may play a critical role in mitigating stops, akin to overcoming inertia in classical mechanics. The updated model $\tau \left(x\right)={\displaystyle \frac{t_p}{I_p}}·\left(1+\alpha ·{\displaystyle \frac{m{c}^2}{E-m{c}^2}}\right)$ suggests that higher energy $(E)$ reduces $\tau (x)$, decreasing total travel time. In the quantum realm, as explored in Section 5, this could manifest as particles tunneling through potential barriers, effectively bypassing stops that would otherwise anchor their states, suggesting a reinterpretation of energy as a modulator of temporal interruptions.
• Quantum Measurement as Stops: Building on Section 5’s exploration of quantum phenomena, the hypothesis posits that measurement events act as stops, collapsing quantum superpositions or resolving entangled states. This provides a speculative lens on the measurement problem, framing stops as the points where timeless quantum behavior interfaces with observable temporality, entering the time domain we perceive.

6.2. Challenges

• Mathematical Rigor: A primary obstacle is developing a mathematical framework to quantify $\tau (x)$ across diverse systems. For macroscopic objects, this might involve parameters like mass, velocity, or external interactions, while in quantum systems, stops could correlate with quantum states or decoherence effects. The current model relies on a provisional coupling constant $\alpha$, which varies by example (e.g., $6.65\times {10}^{-8}$ for the marble, $1.66\times {10}^{-34}$ for a cold atom), necessitating a predictive formulation—potentially informed by quantum field theory [6].
• Relativity Compatibility: The hypothesis should align with special relativity, particularly the finite speed of light and the zero proper time of photons. It suggests photons experience minimal stops ($\tau \left(x\right)={\displaystyle \frac{t_p}{I_p}}$), yielding $t=d/c$, while massive objects incur greater delays due to mass-dependent terms. This should ensure observed coordinate times remain consistent with relativistic predictions, and reconciling the continuous stop model with spacetime geometry poses a formidable challenge.
• Testability and Distinction from Standard Physics: Experimental validation requires detecting stop-like behaviors, such as anomalies in high-precision timing of particle motion or quantum state transitions. Distinguishing these from established phenomena—like quantum fluctuations or relativistic time dilation—is a significant hurdle. The hypothesis must propose unique, observable signatures, potentially tied to variations in $\tau \left(x\right)$, to differentiate itself from current theories.

6.3. Future Research Directions

Future investigations could explore connections to quantum gravity [4], where discrete spacetime structures might naturally accommodate stop-like interruptions, or emergent time theories [7], which question time’s fundamental status. Advances in particle physics [5], particularly regarding mass-energy interactions, may elucidate the mechanisms driving stops, enhancing the hypothesis’s theoretical foundation.

To assess the hypothesis, we propose three experimental tests:

• Ultra-Precise Particle Timing: High-frequency atomic clocks or optical lattice clocks can measure travel times of photons and massive particles over fixed distances. Deviations from expected times correlated with mass or energy could support the hypothesis.
• Interferometry for Quantum Stopping Events: Using Mach-Zehnder interferometry, unexpected phase shifts or coherence losses in quantum particles may indicate discrete stopping events.
• High-Energy Particle Accelerators: Analyzing time-of-flight data for particles at varying energy levels may reveal that increased energy reduces stop durations, altering effective velocity beyond relativistic predictions.

These experiments could be conducted at facilities like NIST, CERN, and LIGO, leveraging their ultra-precise timing and interferometric capabilities.

7. Conclusions

The "Motion Out of Time" hypothesis argues that objects possess an intrinsic capacity for instantaneous motion, with observed travel times arising from stops modeled continuously across a path, as demonstrated by thought experiments with a photon and a marble (Section 2). This framework challenges conventional views of motion and time, finding resonance with special relativity—where photons exhibit zero proper time ($\tau \left(x\right)={\displaystyle \frac{t_p}{I_p}}$, yielding $t=d/c$)—and extending into quantum mechanics, where stops reinterpret measurement-induced collapse and entanglement dynamics (Section 5). Despite its potential to bridge classical and quantum perspectives and align with emergent time theories [7] and quantum gravity [4], the hypothesis is in its preliminary phase and calls for the empirical validation essential for its development into a robust scientific theory. Advancing it requires a rigorous model for $\tau \left(x\right)$, potentially leveraging quantum field theory [6] or discrete spacetime concepts [4], alongside experiments using ultra-precise particle timing or quantum transitions to detect interruptions influenced by mass and energy. Building on foundational works [1,2] and modern inquiries [4,7,12], this hypothesis invites further exploration of its implications for motion and time.