Clarifying the Chaotic Range in Systemic Tau: The Intermediate Volatility Zone (|τₛ| < 0.41) and Its Implications for Complex Chaotic Systems

1. Introduction

Systemic Tau (${\tau }_s$) was introduced as a universal, noise-robust stability metric for complex chaotic systems through ordinal correlation analysis of multisite time series [1,2]. Validated empirically in Aedes aegypti population dynamics at Caño Martín Peña, Puerto Rico [1], and extended to fractional anti-synchronization of physical attractors [3], ${\tau }_s$ consistently identifies:

• Stable synchronized regimes: ${\tau }_s\in [0.5,0.6]$
• Onset of bifurcation: ${\tau }_s<0.41$
• Robust anti-synchronization: ${\tau }_s<-0.41$

Although the bounding thresholds $\pm 0.41$ have been repeatedly confirmed, the intermediate zone $|{\tau }_s|<0.41$ — characterized by maximal volatility and near-zero ordinal correlation — has remained conceptually implicit. This technical note explicitly defines this region as the chaotic range, bridging order and disorder in a manner consistent with stochastic self-organization principles [4].

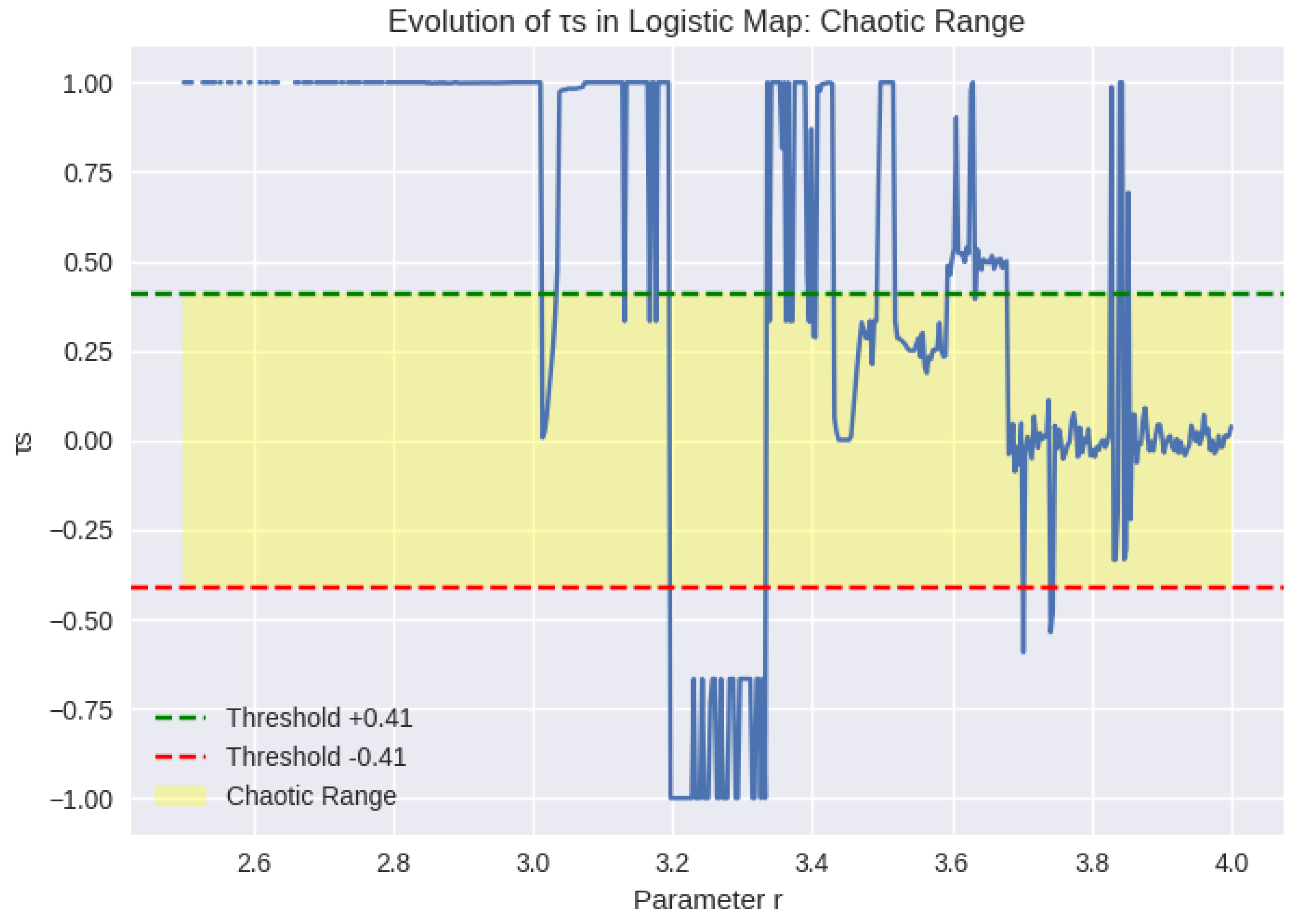
2. The Chaotic Range: Definition and Properties

The chaotic range is formally defined as:

$$|{\tau }_s|<0.41$$

Within this interval:

• Ordinal correlations collapse toward zero
• Sensitivity to initial conditions and noise is maximized
• Active bifurcations dominate system evolution
• Variance obeys ${\sigma }^2\le 1/N$ scaling
• Noise tolerance remains high (10–15%)

Table 1. Systemic Tau regimes and their interpretation.

${\mathit{\tau }}_{\mathit{s}}$ Range	Regime	Key Characteristics	Representative Systems
$>0.41$	Synchronized Stability	Strong positive ordinal agreement	Stable mosquito populations [1], convergent AI training [3]
$|{\tau }_s|<0.41$	Chaotic Range	Maximal volatility, weak/no correlation	Lorenz attractor bifurcations [4], critical climate transitions
$<-0.41$	Anti-Synchronized Divergence	Strong inverse ordinal agreement	Ecological anti-phase under stress [2], secure communication [4]

Table 1. Systemic Tau regimes and their interpretation.

${\mathit{\tau }}_{\mathit{s}}$ Range	Regime	Key Characteristics	Representative Systems
$>0.41$	Synchronized Stability	Strong positive ordinal agreement	Stable mosquito populations [1], convergent AI training [3]
$|{\tau }_s|<0.41$	Chaotic Range	Maximal volatility, weak/no correlation	Lorenz attractor bifurcations [4], critical climate transitions
$<-0.41$	Anti-Synchronized Divergence	Strong inverse ordinal agreement	Ecological anti-phase under stress [2], secure communication [4]

Figure 1 was produced with the following reproducible Python code:

Figure 1. Evolution of Systemic Tau in the logistic map ($x_{n+1}=r{x}_n(1-x_n)$) using paired trajectories with slight initial perturbation ($\Delta x_0=0.01$). The yellow shaded region ($|{\tau }_s|<0.41$) corresponds to the chaotic range. Generated with 1000 iterations (200 transient discarded).

Figure 1. Evolution of Systemic Tau in the logistic map ($x_{n+1}=r{x}_n(1-x_n)$) using paired trajectories with slight initial perturbation ($\Delta x_0=0.01$). The yellow shaded region ($|{\tau }_s|<0.41$) corresponds to the chaotic range. Generated with 1000 iterations (200 transient discarded).

3. Implications and Interdisciplinary Applications

Recognition of the chaotic range significantly enhances early-warning capacity across domains:

• Ecology & Public Health: Predicts Aedes aegypti outbreak risk when ${\tau }_s$ enters the chaotic range
• Climate & Earth Systems: Detects tipping points in noisy paleoclimate proxies
• Artificial Intelligence: Monitors training instability and catastrophic forgetting
• Cardiology: Tracks progression from sinus rhythm to ventricular fibrillation
• Materials Engineering: Forecasts failure cascades via logistic-map analogs of crack propagation
• Social Systems: Identifies correlation collapse in opinion dynamics or epidemic spreading networks
• Strategic Forecasting: Signals regime shifts in geopolitical or military simulations

4. Conclusion

The chaotic range ($|{\tau }_s|<0.41$) constitutes a fundamental dynamical regime within the Systemic Tau framework, representing the zone of purest chaos flanked by ordered (synchronized or anti-synchronized) states. Its explicit recognition completes the theoretical structure initiated in 2022–2025 works and opens immediate practical applications in prediction and control of complex systems.

Future releases of the open-source Systemic Tau toolkit will include automated chaotic-range detection flags.