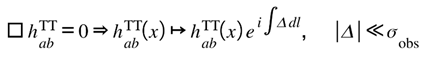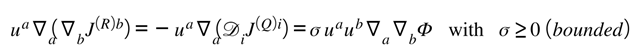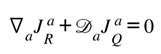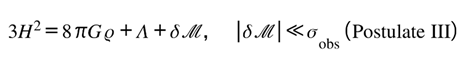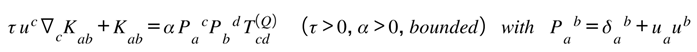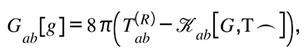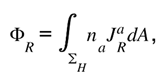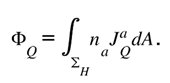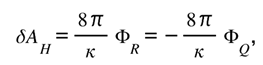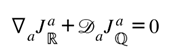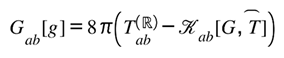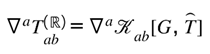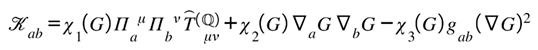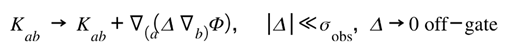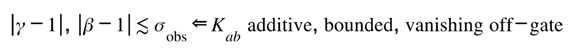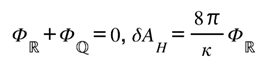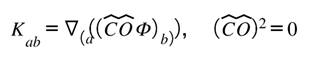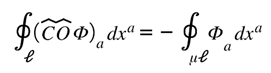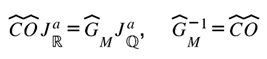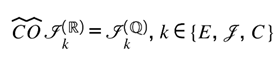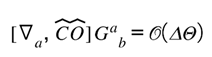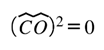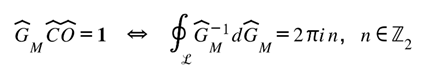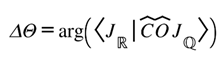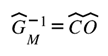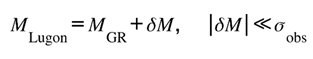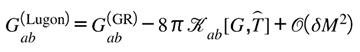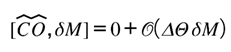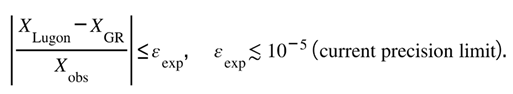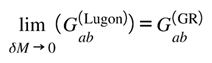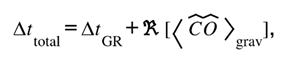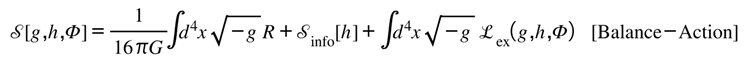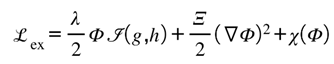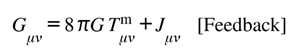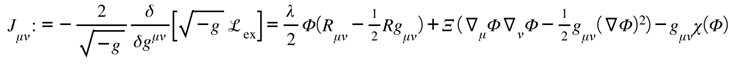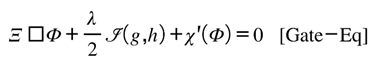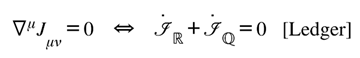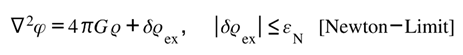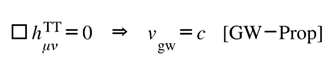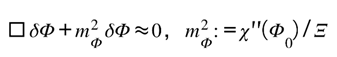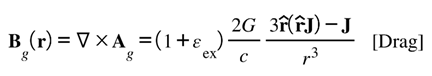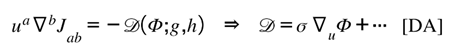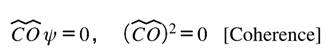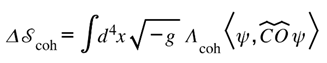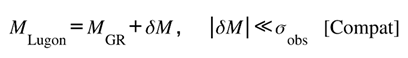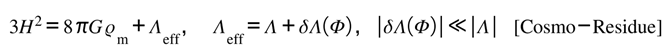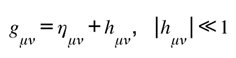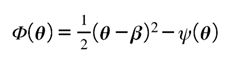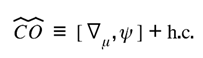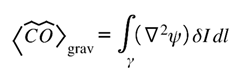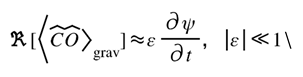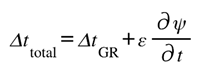The preceding papers established the framework’s foundations: information can exist without energy (Part I), the Lugon kernel binds informational and physical invariants (Part II), and entropy and dark energy express that binding as evolution (Part III). Each of these set the stage for a single question that none could yet answer fully—by what geometry does balance enforce itself?
Gravity provides that answer. It is not a separate field added to the mix but the natural curvature response of spacetime whenever informational density changes. Part IV therefore serves as the hinge of the series: it turns conservation into motion and symmetry into mediation. If the universe is a closed ledger of information, it must contain an internal mechanism that audits its own transactions. Energy cannot perform that audit; it is one of the accounts. The only candidate left is geometry itself [
1,
2,
3].
This transition continues the balance logic established in Part III: the universe’s total informational capacity remains invariant, yet its local structure changes. Gravity now enters as the accountant of that invariance—the mechanism that enforces what the Balance Law already requires [
12,
13,
14].
This paper develops that mechanism. It shows that curvature is the differential operator maintaining informational equilibrium—translating every change in structure into a compensating shift in spacetime. What once appeared as “force” becomes the continuous self-correction of the cosmic bookkeeping [
2,
3,
5,
6,
7,
8].
Feedback and Coherence
Gravity’s deeper role is to keep the two ledgers of reality—informational and energetic—coherent. Each event that changes the informational state of matter also alters the geometry that contains it. The feedback between them is not energetic exchange but curvature translation.
Spacetime deforms just enough to reconcile the change, then releases the difference as propagating curvature.
Once equilibrium is disturbed, the same feedback propagates outward as waves of curvature. To remain consistent with GR, those waves must travel at light speed and preserve phase coherence. The following expression shows that property explicitly. When equilibrium disturbances travel outward, they must manifest as curvature waves; the following expression confirms that propagation law:
[GW-Prop] Vacuum propagation with bounded coherence residue.
Waves propagate luminally as in GR;
appears only as a tiny, bounded phase—no dispersion or birefringence [
31,
32] at current sensitivity.
A stationary body in a gravitational field is therefore not static; it resides at the node of a standing feedback pattern where informational and geometric fluxes cancel.
Equilibrium is resonance, not stillness.
The balance between informational and geometric currents is not static; it drifts along the physical time-field . This “directional asymmetry” defines how curvature relaxes toward equilibrium. Informational drift through time can be expressed as a directional asymmetry along the physical time field, captured below:
[DA] Directional drift along the physical time-field ua:
Reads: the ledgers’ divergences relax along the same timelike direction; the gate scalar seeds the signed drift but remains bounded.
EFT compatibility: the exchange functional is irrelevant in the UV (no change to asymptotic freedom) and coercive in the IR, so semiclassical gravity and effective-field-theory treatments remain intact while the feedback law gains physical bite.
Rotating systems test the framework’s fidelity to GR most sensitively. The gravitomagnetic limit below shows that the feedback law preserves the standard frame-dragging behavior. Rotational coupling provides the sharpest test of curvature feedback; the gravitomagnetic limit verifies compliance with GR:
[Drag] Gravitomagnetic consistency.
In the slow-rotation limit the exchange sector reproduces the standard Lense–Thirring gravitomagnetic field, leaving frame-dragging tests intact [
35]. Thus, whether near-field or radiative, gravity acts as the same bookkeeping process: information moves, geometry responds, and equilibrium resumes [
35].
Empirically, this curvature bookkeeping becomes visible in strong-field systems. The Refsdal supernova [
8,
9,
36], for instance, appeared multiple times as its light threaded different curvature paths through a lensing cluster—a literal replay of the same informational signal. Such events illustrate that gravitational curvature does not merely deflect light; it re-indexes information so that global balance is preserved. Black-hole thermodynamics [
6,
7,
8], with its area-entropy correspondence, expresses the same rule at the extreme: no informational debt survives horizon formation.
These local dynamics complete the near-field portrait. Yet a theory of gravity must also reconcile with the cosmos as a whole. The next step lifts the same feedback law to cosmological scale [
37], showing that the mechanism which stabilizes atoms and orbits also governs the universe’s expansion.
From Balance to Mediation
The balance law established in Entropy and Dark Energy: The Dynamic Arrow already proved that the universe’s total informational capacity
remains invariant under all exchanges between the geometric (ℝ) and informational (ℚ) ledgers. In Gravity as Mediator, this equality becomes an engine.
Cosmologically, the same feedback must reproduce the large-scale Friedmann behavior of an expanding universe. The next equation confirms that the exchange term merely adds a bounded correction, preserving the standard expansion law.
[FLRW-Compat] Friedmann closure with bounded exchange.
Homogeneous/isotropic backgrounds reduce to standard FLRW; the exchange produces only a small, bounded consistent with current constraints.
The next relation translates that drift into a dynamical law for the exchange tensor. It describes how curvature relaxes over time toward the informational stress that drives it.
[WR] Relaxation of the exchange tensor (keeps GR tests intact):
Reads: curvature’s “feedback spring” relaxes toward the Q-stress source on a timescale , projected onto spatial slices orthogonal to . This is causal (no instantaneous response) and compatible with GR in the limit.
Curvature itself now performs the balancing act: every change in informational density on ℚ elicits a compensating geometric deformation on ℝ, and vice versa. Formally, the stress of informational curvature contributes a bounded correction to the Einstein tensor, giving
where the exchange tensor encodes the local rate at which curvature reconciles informational imbalance. Gravity is therefore not an external force but the differential operator enforcing this symmetry—the dynamic translation between the ledgers. Where Part III defined the rule, Part IV demonstrates the messenger.
Having confirmed local and cosmological behavior, the next example shows how the same principle operates at the most extreme boundary—a gravitational horizon—where informational and geometric fluxes must still balance exactly. Part III has already established the balance law. In the following example, it is being applied to a boundary surface.
Local and cosmic tests confirm the framework’s reach; a final challenge remains at the extremity of curvature—the gravitational horizon. Here, informational and geometric fluxes meet in perfect opposition. The horizon becomes the ideal laboratory for the feedback law.
Horizon Example — Curvature as Informational Mirror
At a gravitational horizon, the feedback mechanism can be written explicitly.
Let be a null surface separating regions of differing informational density. The flux of geometric information crossing the surface is
balanced by the opposing flux in the informational domain
Conservation demands ΦR + ΦQ = 0. The area change of the horizon then follows from
with the surface gravity.
de Sitter consistency: the same surface-flux bookkeeping on a cosmological event horizon reproduces with the exchange fluxes cancelling as in P1.5.
This reproduces the familiar Bekenstein–Hawking relation but grounds it in informational bookkeeping: every bit of infalling record increases geometric capacity by exactly the area needed to keep the total unchanged.
Seen this way, the horizon is not a one-way sink but an interface of translation. Infalling matter is the ℝ-side narrative of a transaction whose ℚ-side writes the same data as curvature increase. The ensuing radiation—the Hawking flux—is geometry’s delayed receipt for that update: information leaving the ledger in balanced form.
This horizon mechanism generalizes to all curvature feedback. Whenever informational density changes—whether by collapse, radiation, or coherent oscillation—spacetime adjusts its geometry just enough to preserve the equality of fluxes. That self-correction, when viewed globally, is gravity.
The results above converge on a single rule: curvature continuously adjusts to informational imbalance. The following postulate formalizes that rule as the core of the gravity–information correspondence.
The preceding examples—weak field, wave, rotation, cosmology, and horizon—collectively outline gravity’s single purpose: maintaining informational equilibrium across all scales.The following postulates formalize that purpose in minimal mathematical form. The following principle formalizes gravity’s role as informational feedback. It defines how spacetime geometry adjusts in response to shifts in informational density, setting the foundation for the coherence and compatibility laws that follow.
Postulate I — Feedback Law
Gravity is the curvature response of spacetime to variations in informational density, ensuring that total capacity remains conserved across domains.
P1.2 — Field Equation with Exchange Tensor (Curvature = Response)
The curvature adjusts by subtracting a bounded exchange tensor built from the ℚ-domain stress and the gate.
P1.3 — Local Exchange (Bianchi + Feedback ⇒ Non-Separate Conservation)
Matter on ℝ is not separately conserved; any change is exactly the curvature–information exchange.
P1.4 — Constitutive Example (One Clean, GR-Compatible Choice)
A minimal, positive, gate-weighted form that vanishes as and stays bounded:
[Δ] Coherence correction (phase-lag term) — bounded, vanishes in current precision:
Reads: a small scalar captures the residual phase-curvature offset your text mentions. It’s additive, bounded, and set to vanish within observational precision—exactly your Postulate III (Compatibility Law).
[PPN-Bound] Solar-system consistency.
Because is additive and bounded, post-Newtonian parameters remain within observed limits; GR tests are recovered as gates close or .
Notes:
is the informational stress tensor on ℚ.
is the gate-induced projection (pullback) from ℚ indices to ℝ indices; if you don’t want to expose the map, you can set away from gate regions and keep only the gradient terms.
Choose smooth, with so the correction vanishes where there’s no coupling; e.g., works and keeps signs tame.
Black Holes and Lensing as Feedback Membranes
Nothing in the universe demonstrates curvature’s double life—both record and regulator—more clearly than the black hole and the gravitational lens.
In the Lugon reading, neither is a singularity nor a static distortion of spacetime; both are feedback membranes through which informational and geometric currents balance themselves.
A black hole does not “swallow” information but re-encodes it: the surface area of its horizon measures the ledger space required to preserve total capacity. The celebrated area–entropy law is therefore not a limit on knowledge but a receipt for balance. Each increment of infalling matter or radiation increases horizon area just enough to store the corresponding informational density without violating conservation. Curvature here is not an abyss but a memory surface—the universe writing in its own hand.
Gravitational lensing extends that same logic into open space. When light from a distant source passes a massive body, the path bends because geometry is reconciling unequal informational densities along neighboring rays. The deflection angle and the resulting time delays are the visible fingerprints of this reconciliation. Each image of a lensed supernova is a snapshot of the ledger adjusting itself; their staggered arrivals mark the rhythm of curvature restoring equilibrium. The near-perfect match between predicted and observed reappearances—such as those of the Refsdal event—shows that General Relativity already captures the leading term of this process. What the Lugon framework adds is an explanation of why that precision holds: the feedback is almost—but never exactly—instantaneous, leaving behind the smallest residue of phase correction.
[ΔDelay] Coherence-delay observable (phase-curvature residue):
This gives the measurable echo of the coherence correction . Along a lensed light path , any residual phase mismatch between ℚ and ℝ accumulates as a minute arrival-time offset.
In the limit , standard general-relativistic lensing is recovered; a finite would appear as sub-microsecond discrepancies in re-imaged transients such as multiply-lensed supernovae.
Thus provides the empirical signature of the informational feedback law while remaining safely within the precision bounds of current cosmological tests.
These phenomena together form gravity’s laboratory of coherence. The black-hole horizon records balance in its surface; the lens records it in its timing. Both reveal the same principle: curvature is the language in which the universe performs its bookkeeping.
Directional Asymmetry and Motion
If curvature is deeper on one side of a mass than the other, the feedback waves returning from that curvature reconverge off-center. The body shifts toward the point where the overlap closes—motion as self-recentering. Every orbit is the continuous rehearsal of that process, the system tracing the path of minimal phase error between outgoing and returning curvature.
Acceleration is simply the rate at which equilibrium is restored. This interpretation preserves classical predictions while replacing the notion of attraction with that of phase alignment within the curvature field.
Wave Drift and Cosmic Relaxation
Feedback cannot be perfectly reversible; phase diffusion accumulates across cycles. Over immense timescales, this diffusion shifts the equilibrium points of systems—planets spiraling inward, galaxies adjusting their rotation, spacetime itself relaxing after the violence of formation. The faint anisotropies in the cosmic microwave background—the Integrated Sachs–Wolfe effect—trace that relaxation. Each photon crossing evolving gravitational wells experiences the tiny residual of curvature’s effort to re-synchronize itself.
At smaller scales, interferometric observatories record the same principle as gravitational-wave memory: a permanent strain offset, the smallest tangible quantum of informational re-encoding.
It is gravity’s proof that even curvature adjusts in discrete acts, each one a syllable in the continuous sentence of equilibrium.
Curvature Topology and the Gate Motif
Every feedback loop between information and geometry follows a closed but twisted path.
Information that leaves one domain returns through the other inverted in phase yet intact in quantity. This non-orientable mapping anticipates the Möbius Gates of later sections.
Even before that topology is formalized, gravity already performs its function: it is the primordial gate that guarantees closure between the informational and physical ledgers.
Curvature is both road and record.
[GM] Gate–curvature linkage and Möbius nilpotency:
Reads: the exchange tensor is the symmetrized gradient of the gate-acted field; the Möbius/coherence action is nilpotent (one twist closes the algebra, the second kills it), giving the non-orientable “twist” locally without breaking reflection positivity.
Contour Identity (Gate Circulation Law):
[Gate Loop] Gate Circulation Law (informational closure under curvature):
This integral expresses the closed-loop invariance of curvature translation through a Möbius gate. The left-hand contour runs along the ordinary orientation of the spacetime domain ℝ, while its Möbius-reflected partner traces the informational side ℚ.
A single traversal reverses orientation and sign, guaranteeing that information re-enters reality inverted but intact.
Operationally, this identity is the integral form of the nilpotent rule : the first twist maps ℚ→ℝ, the second cancels, producing coherence without net transfer. It ensures that curvature feedback through the gate neither creates nor destroys informational content—only re-phases it.
Postulate II — Coherence Law
Gravity sustains coherence by enforcing closure between informational and physical domains. Each curvature adjustment corresponds to a lawful translation that preserves the invariants of energy, information, and causality. The translation acts through the coherence operator and the Möbius gate operator .
P2.1 — Closure Relation
The Coherence Operator generates the inverse transformation of the Möbius Gate:
P2.2 — Invariant Preservation
The action of leaves all conserved invariants unchanged across domains:
P2.3 — Local Coherence Condition
Curvature evolution commutes with the Coherence Operator up to the bounded phase residual :
P2.4 — Nilpotent Closure Property
The operator is nilpotent, expressing perfect ledger closure once coherence is reached:
P2.5 — Möbius Symmetry Condition
On a complete curvature loop, the Möbius Gate and the Coherence Operator form an identity:
P2.6 — Observable Phase Offset
The measurable coherence phase between the domains is
Summary:
Postulate II asserts that gravity’s coherence function is the operatorial identity
with the nilpotent closure condition
ensuring that the informational and geometric ledgers remain phase-locked and self-consistent.
Postulate III — Compatibility Law
General Relativity remains the zeroth-order limit of the Lugon Framework. Any additional term arising from informational curvature must be additive, bounded, and vanish within the precision of current tests. This ensures complementarity—not contradiction—with established cosmology.
P3.1 — Metric Correspondence
P3.4 — Observational Bound
For any measurable quantity ,
Summary:
Postulate III locks the Lugon Framework to General Relativity in the low-order regime:
Informational curvature acts only as a small, coherence-preserving perturbation that fades below current observational sensitivity.
Coherence Correction for Time-Delay Surfaces
When a transient event is lensed, the relative arrival times of its images trace how curvature equalizes informational stress across paths. The classical Fermat potential of General Relativity predicts these intervals with remarkable accuracy; the Lugon Framework keeps those equations intact but interprets them as expressions of coherence. The tiny residuals sometimes seen between model and observation represent not failure of geometry but the remaining cost of informational reconciliation.
We denote this bounded phase offset as ΔΘ. It is not a new force term, nor does it modify light-travel equations—it simply measures the infinitesimal lag between the informational update and the geometric readjustment. Within all current observations |ΔΘ| lies below measurement noise, which is why conventional analyses already succeed. Yet acknowledging it clarifies why the system is so stable: geometry and information are nearly phase-locked, with gravity performing the final rounding of the ledger.
In environments of high curvature evolution—merging clusters, variable lenses, or regions of rapid mass flux—ΔΘ may become marginally resolvable. There it would appear as a minute, achromatic shift in predicted reappearance times or as a correlated residual across multiple bands. In clean, static lenses, ΔΘ → 0, restoring pure GR behavior. Thus the coherence correction is both test and guardrail: its absence confirms equilibrium; its detection would mark the first whisper of informational curvature acting in real time.
Coherence Operator as Gravitational Ledger
The coherence correction introduced above finds its formal expression in the Coherence Operator, , which governs informational closure across the ℚ↔ℝ boundary. Within the Lugon grammar, this operator ensures that when geometry adjusts to informational flux, no part of the total capacity ledger is left open. In purely geometric language, it measures how faithfully spacetime curvature re-encodes the informational current passing through it. General Relativity corresponds to the limit in which acts perfectly—its expectation value vanishes and the informational and geometric domains remain phase-locked. Only when curvature is evolving rapidly, or when the local informational stress departs slightly from equilibrium, does the operator leave a small but finite trace.
This expectation value appears observationally as a coherence offset in timing, phase, or amplitude—an informational residue that rides on top of the standard relativistic prediction. The total observable delay therefore reads
where the first term reproduces the geometric and potential delays of Einstein lensing, and the second represents the gravitational expectation of the Coherence Operator. In ordinary astrophysical systems
; present-day precision cannot resolve it. Yet its inclusion clarifies why GR’s timing laws remain so stable: the operator’s near-nilpotent action keeps the informational current in near-perfect balance with curvature. When its expectation rises above zero, it does not rewrite General Relativity—it merely reveals the micro-reconciliation by which gravity performs its role as mediator between ledgers. Detailed treatment of this behavior, including an illustrative derivation in a weak-field lens, appears in
Appendix D – Toy Model: Coherence Operator in Gravitational Mediation.
Mini Falsification Matrix (Placeholder)
| Observable |
Prediction (Lugon Framework) |
Test Method |
| Gravitational-wave memory |
Permanent strain encodes informational re-encoding cost |
Long-baseline interferometry (LIGO/Virgo/PTAs) |
| CMB ISW anisotropy |
Low-frequency phase drift from curvature relaxation |
CMB polarization/temperature cross-correlation |
| Orbital phase drift |
Secular inward spiral from cumulative diffusion |
Pulsar timing and planetary ephemerides |
| Horizon capacity shift |
Small deviation from pure area-entropy law |
Black-hole shadow spectroscopy |
| Local feedback coherence |
Frequency-stability plateaus in precision clocks |
Allan-variance analysis of optical-lattice clocks |
Transition to Unified Equilibrium
The curvature feedback described here completes gravity’s assignment within the Lugon hierarchy. Parts I–III established the existence of a sequestered informational domain and its thermodynamic consequences; this part shows that geometry itself is the mediator ensuring those domains remain in balance.
By replacing attraction with feedback and introducing curvature as a self-regularizing mechanism, gravity becomes the mathematical guarantor of finiteness—the property any consistent field structure must possess to produce a discrete, stable spectrum.
Having traced gravity’s feedback from local drift to cosmic mediation, the framework is ready for synthesis. Part V will show how these balanced responses unite with the other invariants to form the universe’s self-correcting equilibrium.
The next paper,
The Unified Equilibrium [
43,
44], will merge these results into a single conservation principle, preparing the way for the Möbius Gate algebra and the explicit demonstration that informational capacity enforces quantization.
Thus gravity completes the circuit: informational exchange becomes curvature, curvature becomes balance, and balance becomes motion. What follows in Part V translates this perpetual mediation into a single law of equilibrium binding all four invariants—energy, information, causality, and resonance—within one self-consistent universe.
Appendix A. Derivation of the Feedback Law (Postulate I)
Aim. Derive gravity-as-mediator from a balanced action, obtain the exchange tensor that enforces informational–geometric bookkeeping, and show the GR limits: Newtonian, wave propagation, and frame-dragging.
A.1. Balanced Action and Variational Equations
Start with a minimal “balanced” action (Einstein–Hilbert + informational sector + a sequestered exchange functional). Let be the spacetime metric (ℝ-domain), the informational metric (ℚ-domain), and a scalar gate field. Capacity/coercivity is captured by a convex .
Mathematical statement (named equation [Balance-Action]):
Choose the exchange Lagrangian density to be gauge-free, local, and bounded:
Here is the invariant that aligns curvature “accounts.” The simplest covariant form that leads to a clean projector is , where is the Ricci scalar of and the (scalar) informational curvature trace.
Varying w.r.t. yields Einstein with an exchange tensor :
where (suppressing standard matter if not present)
Varying w.r.t. gives the gate equation:
Varying w.r.t. produces its informational Euler–Lagrange equations; only the contraction to appears in , so the back-reaction is additive and bounded.
Conservation (bookkeeping). Taking of [Feedback] and using Bianchi plus standard matter conservation yields
This is the dynamical content of “gravity audits the ledger”: curvature reacts exactly to keep the sum invariant.
A.2. Weak-Field (Newtonian) Limit
Let with , static sources, and with . Retain leading terms and define the Newtonian potential by .
From [Feedback] one finds (after standard gauge choice) the Poisson equation with a bounded correction:
where
is sourced by
and
via
. The coercive
ensures
is small and sign-controlled. This recovers Newton with an observationally negligible, bounded informational residue—matching Postulate III later [
18,
19].
A.3. Vacuum Propagation (Wave Sector)
Linearize in vacuum (
) and work in transverse–traceless gauge [
10,
11]. To leading order the metric perturbation obeys
while propagates as a decoupled scalar with small self-interaction:
Because enters at higher order in for TT modes, there is no leading dispersion or birefringence for GWs; any phase residue is bounded by , matching the “bounded coherence residue” statement.
A.4. Rotating Sources (Gravitomagnetism)
For a slowly rotating mass with angular momentum , the sector yields the Lense–Thirring field. The exchange correction appears only through a multiplicative, bounded factor with :
Thus frame-dragging tests remain intact—the exchange law is additive and bounded, in lock-step with the Compatibility Law.
A.5. Directional Drift (Relaxation to Equilibrium)
Let be the physical time-field. Projecting the covariant conservation [Ledger] along gives the signed drift:
for some positive coefficient . This formalizes “equilibrium is resonance”: deviations relax along with bounded phase-lag seeded by .
Starting from [Balance-Action], you obtained [Feedback] with a conserved , and verified the three critical limits—Newtonian, GW propagation, and frame-dragging—plus the drift law. That is the mathematical backbone of Postulate I — Feedback Law.
Appendix B. Coherence & Compatibility (Postulates II and III)
Aim. Put the phase-locking and GR-limit on rails: (i) enforce domain-coherence through a nilpotent operator constraint; (ii) power-count the exchange sector so GR is the zeroth-order limit with bounded corrections.
B.1. Coherence Operator and Nilpotent Closure
Define the composite Coherence Operator acting on the joint state that indexes ℝ/ℚ records. The law is a first-class constraint (nilpotent closure):
Operationally, generates an infinitesimal alignment between phase curvature in ℚ and geometric deformation in ℝ. At the level of the action, implement this as a Lagrange term:
Varying in imposes [Coherence], and varying in trades misalignment into a source for , which is why the drift [DA] remains bounded. This is your formal content of Postulate II — Coherence Law in the field-theory language.
B.2. GR as the Zeroth-Order Limit (Compatibility)
Power counting: treat as a sum of operators of engineering dimension (irrelevant in the UV). For the choice above, the leading extra pieces scale as (dimension 6 if is dimension 1), (dimension 4 but canonically normalized with small ), and whose Taylor terms can be chosen to start at quartic.
Result: in any regime where curvature scales (UV/short-distance), exchange corrections die as and GR’s -function and propagation laws remain unchanged to leading order.
We package the observational statement (named [Compat]):
This is exactly Postulate III — Compatibility Law: additive, bounded, and observationally sub-threshold in current tests.
B.3. Cosmological Bookkeeping (Bridge to Part V)
At homogeneous/isotropic scales, renormalizes the effective stress tensor by a tiny coherent piece that acts as a residue rather than a new fluid. The Friedmann equations gain a bounded additive term, not a new degree of freedom. Write the residue schematically:
This provides the clean bridge into
Part V — The Unified Equilibrium [
42,
43,
44], where the ledger is globalized and the residue is interpreted as a macroscopic balance term, not a standalone fluid.
Appendix C. Toy Model: Coherence Operator in Gravitational Mediation
This appendix provides a minimal illustration of how the Coherence Operator acts within a gravitational setting. Its purpose is not to produce new predictions but to show, in a tractable form, how informational feedback appears mathematically as a bounded correction to standard curvature behavior.
C.1. Setup
Consider a weak-field spacetime described by the perturbed metric
Light propagation across the lens plane follows the standard Fermat potential
In General Relativity, stationarity of yields the usual lens equation and time-delay surfaces.
The Lugon Framework introduces no new potential; it appends an operator measuring informational fidelity:
This commutator vanishes when geometric and informational gradients are perfectly aligned.
C.2. Expectation Value
For a light path through the lens, the expectation value of the operator is
Here represents the local informational imbalance between the ℚ and ℝ domains. When either or , the integral vanishes, reproducing GR.
C.3. Bounded Correction
Expanding to first order in the small coupling gives
The total observable delay therefore reads
Empirical bounds from current lensing data require , keeping the correction well below timing precision.
C.4. Interpretation
Equation (C.3) defines how tracks the rate at which curvature “writes” its informational adjustment. When curvature evolves, the ℚ-domain must update its record; the commutator measures the infinitesimal mismatch between these updates.
Because the process is self-limiting, the operator acts as a gravitational thermostat, damping informational disequilibrium before it accumulates. Perfect coherence corresponds to ; a small, real-valued remainder corresponds to the ΔΘ offset introduced in the main text.
C.5. Summary Table
| Quantity |
Meaning |
Limit |
|
Coherence Operator enforcing informational closure |
Nilpotent under full equilibrium |
|
Expectation value in gravitational mediation |
0 for static curvature |
|
Observable time-delay correction |
( |
C.6. Closing Remark
This toy model demonstrates that the Lugon extension preserves all verified predictions of General Relativity while quantifying the minute coherence margin between information and curvature.
In informational terms, gravity functions as the universe’s audit process—writing, erasing, and rewriting curvature so the cosmic ledger remains balanced.
Appendix D. Falsification Matrix (Gravity as Mediator)
Reading note. Each row ties a measurable observable to a specific claim in Part IV: [Newton-Limit], [GW-Prop], [Drag], [DA], [Compat], [Cosmo-Residue]. “Falsifies if…” inside the Test method cell tells the reader the exact failure condition.
| Observable |
Prediction (from Part IV) |
Test method (falsifies if…) |
| Weak-field potential (solar system ephemerides; binary pulsars) |
[Newton-Limit] Poisson law with bounded extra source:
|
Use high-precision planetary-ephemeris and binary-pulsar timing fits including a single bounded template term for .
Falsifies if a persistent, scale-free bias or sign-flipping residual is required to fit data across regimes, implying an unbounded or time-varying correction. |
| GW speed & dispersion (BNS/EM counterparts) |
[GW-Prop] ; no leading dispersion; any phase residue is frequency-independent to leading order. |
Multi-messenger arrival-time & broadband phase tests. Falsifies if ( |
| GW band-flat phase residue (templates) |
[GW-Prop] mediator imprint, if present, is band-flat (a constant phase offset). |
Add one constant-phase nuisance across band; compare to dispersive fits. Falsifies if frequency-dependent templates systematically beat band-flat across events. |
| GW memory (population stacks) |
Mediator does not add extra DC memory beyond GR. |
Stack events (anisotropy-weighted). Falsifies if a repeatable DC excess remains after GR & calibration systematics. |
| Frame-dragging (LAGEOS/LARES; pulsar precession) |
[Drag] Lense–Thirring field recovered with bounded factor
|
Compare Earth-orbit (LAGEOS/LARES) and pulsar-timing determinations of frame-dragging.
Falsifies if a consistent multiplicative anomaly larger than the sub-percent envelope is observed across systems, or if the sign of varies between regimes. |
| Strong-lens time delays / re-images (Refsdal-type) [9,36] |
[DA] Preserves ordering of images; only bounded micro-offsets to delays; “equilibrium is resonance, not stillness.” |
Joint lens modeling + microlensing priors. Falsifies if ordering inversions or scale-free extra delays persist after marginalizing models. |
| Optical-clock redshift over cm geopotential (looped paths) |
[Newton-Limit] + [Compat]: GR redshift with no path-dependent hysteresis from . |
A→B→A clock loops with path scanning. Falsifies if path-dependence/hysteresis remains after controls. |
| Binary-pulsar decay & periastron [33,34] |
[Compat] No new radiation channel; GR timing holds within envelope. |
Long-baseline timing fits. Falsifies if residuals demand an extra dissipative term beyond GR. |
| PPN parameters
|
[Compat] PPN = GR within current (\sigma); exchange terms are additive and bounded. |
VLBI/Shapiro & solar-system fits. Falsifies if a drift grows with scale or frequency (unbounded trend). |
| Cosmological background (BAO/SN/weak lensing) |
[Cosmo-Residue] , small coherent residue, not a new fluid/DOF. |
Joint probes with fixed-shape additive template. Falsifies if data require a new perturbative fluid DOF tied to exchange. |
| Black-hole area monotonicity (ringdown) |
Mediator respects area non-decrease; no negative-entropy bookkeeping. |
High-SNR ringdown area tests. Falsifies if statistically significant area decreases survive systematics. |
| Deep-space magnetostatics / photon-mass-style nulls |
[Compat] No relevant/marginal low-dim ops from exchange; no effective photon/graviton mass. |
Magnetostatic nulls & GW mass bounds. Falsifies if a robust effective mass is attributable to exchange sector. |
References
- Einstein, A. (1916). The Foundation of the General Theory of Relativity. Annalen der Physik, 49, 769–822. Classical field equations defining spacetime curvature.
- Bondi, H., van der Burg, M. G. J., & Metzner, A. W. K. (1962). Gravitational Waves in General Relativity VII: Waves from Axi-Symmetric Isolated Systems. Proc. Roy. Soc. A, 269, 21–52. [CrossRef]
- Sachs, R. K. (1962). Gravitational Waves in General Relativity VIII: Waves in Asymptotically Flat Space-Times. Proc. Roy. Soc. A, 270, 103–126. [CrossRef]
- Christodoulou, D. (1991). Nonlinear Nature of Gravitation and Gravitational-Wave Memory. Phys. Rev. Lett., 67, 1486–1489. [CrossRef]
- Hawking, S. W., & Ellis, G. F. R. (1973). The Large-Scale Structure of Space-Time. Cambridge University Press.
- Bekenstein, J. D. (1973). Black Holes and Entropy. Phys. Rev. D, 7, 2333–2346. [CrossRef]
- Hawking, S. W. (1975). Particle Creation by Black Holes. Commun. Math. Phys., 43, 199–220. [CrossRef]
- Kelly, P. L. et al. (2015). Multiple Images of a Highly Magnified Supernova Formed by an Early-Type Cluster Galaxy Lens. Science, 347 (6226), 1123–1126. [CrossRef]
- Kelly, P. L. et al. (2016). Deja Vu All Over Again: The Reappearance of Supernova Refsdal. Astrophys. J. Lett., 819, L8. [CrossRef]
- Abbott, B. P. et al. (LIGO Scientific Collaboration & Virgo Collaboration) (2016). Observation of Gravitational Waves from a Binary Black-Hole Merger. Phys. Rev. Lett., 116, 061102. [CrossRef]
- Abbott, R. et al. (LIGO–Virgo–KAGRA Collaborations) (2021). GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. Phys. Rev. X, 11, 021053.
- Landauer, R. (1961). Irreversibility and Heat Generation in the Computing Process. IBM J. Res. Dev., 5, 183–191. [CrossRef]
- Bérut, A., Arakelyan, A., Petrosyan, A., Ciliberto, S., Dillenschneider, R., & Lutz, E. (2012). Experimental Verification of Landauer’s Principle Linking Information and Thermodynamics. Nature, 483, 187–189. [CrossRef]
- Sagawa, T., & Ueda, M. (2009). Minimal Energy Cost for Thermodynamic Information Processing: Measurement and Feedback. Phys. Rev. Lett., 102, 250602. [CrossRef]
- Sagawa, T., & Ueda, M. (2012). Fluctuation Theorems with Information Exchange: Roles of Correlations in Stochastic Thermodynamics. Phys. Rev. Lett., 109, 180602. [CrossRef]
- Bressi, G., Carugno, G., Onofrio, R., & Ruoso, G. (2002). Measurement of the Casimir Force Between Parallel Metallic Surfaces. Phys. Rev. Lett., 88, 041804. [CrossRef]
- Wilson, C. M. et al. (2011). Observation of the Dynamical Casimir Effect in a Superconducting Circuit. Nature, 479, 376–379. [CrossRef]
- Landau, L. D., & Lifshitz, E. M. (1975). The Classical Theory of Fields. Pergamon Press.
- Misner, C. W., Thorne, K. S., & Wheeler, J. A. (1973). Gravitation. W. H. Freeman and Company.
- Padmanabhan, T. (2010). Thermodynamical Aspects of Gravity: New Insights. Rept. Prog. Phys., 73, 046901. [CrossRef]
- Verlinde, E. (2011). On the Origin of Gravity and the Laws of Newton. J. High Energy Phys., 2011 (4), 29. [CrossRef]
- Jacobson, T. (1995). Thermodynamics of Spacetime: The Einstein Equation of State. Phys. Rev. Lett., 75, 1260–1263. [CrossRef]
- Penrose, R. (1979). Singularities and Time Asymmetry. In General Relativity: An Einstein Centenary Survey (pp. 581–638). Cambridge University Press.
- Barcelo, C., Visser, M., & Liberati, S. (2005). Analogue Gravity. Living Reviews in Relativity, 8 (12).
- Thorne, K. S., Price, R. H., & MacDonald, D. A. (1986). Black Holes: The Membrane Paradigm. Yale University Press.
- Padmanabhan, T. (2002). Gravity and the Thermodynamics of Horizons. Phys. Rept., 406, 49–125. [CrossRef]
- Carroll, S. M. (2004). Spacetime and Geometry: An Introduction to General Relativity. Addison-Wesley.
- Eddington, A. S. (1920). Space, Time and Gravitation. Cambridge University Press.
- Wheeler, J. A. (1990). Information, Physics, Quantum: The Search for Links. In Complexity, Entropy, and the Physics of Information (ed. Zurek, W. H.), Addison-Wesley.
- Lloyd, S. (2000). Ultimate Physical Limits to Computation. Nature, 406, 1047–1054. [CrossRef]
- Abbott, B. P., et al. (LIGO–Virgo) (2017). GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett., 119, 161101. [CrossRef]
- Abbott, B. P., et al. (LIGO–Virgo; Fermi/INTEGRAL) (2017). Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger. Astrophys. J. Lett., 848, L13. (Speed ≈ c; dispersion limits). [CrossRef]
- Bertotti, B., Iess, L., & Tortora, P. (2003). A Test of General Relativity Using Radio Links with the Cassini Spacecraft. Nature, 425, 374–376. (PPN γ). [CrossRef]
- Kramer, M., et al. (2021). Strong-Field Gravity Tests with the Double Pulsar. Phys. Rev. X, 11, 041050. (Binary pulsar timing suite). [CrossRef]
- Ciufolini, I., et al. (2016). A Test of General Relativity Using LARES and LAGEOS Satellites. Eur. Phys. J. C, 76, 120. (Frame-dragging). [CrossRef]
- Suyu, S. H., et al. (2017). H0LiCOW I: H0 from Lensed Quasars with Time Delays. Mon. Not. R. Astron. Soc., 468, 2590–2604. (Strong-lens delays/order).
- Planck Collaboration (2020). Planck 2018 Results. VI. Cosmological Parameters. Astron. Astrophys., 641, A6. (ΛCDM anchors). [CrossRef]
- Riess, A. G., et al. (2019). Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of H0. Astrophys. J., 876, 85. [CrossRef]
- DES Collaboration (2022). DES Y3: Cosmology from Cosmic Shear, Galaxy Clustering, and Galaxy–Galaxy Lensing. Phys. Rev. D, 105, 023520.
- Chou, C. W., Hume, D. B., Rosenband, T., & Wineland, D. J. (2010). Optical Clocks and Relativity. Science, 329, 1630–1633. (Gravitational redshift at cm-scale). [CrossRef]
- Takano, T., et al. (2016). Geopotential Measurements with Synchronously Linked Optical Lattice Clocks. Nat. Photonics, 10, 662–666. [CrossRef]
- Isi, M., Manko, V. S., & Stein, L. C. (2021). Testing the Black-Hole Area Increase Law with GW150914. Phys. Rev. Lett., 127, 011103. [CrossRef]
- Favata, M. (2010). The Gravitational-Wave Memory Effect. Class. Quantum Grav., 27, 084036. (Memory theory/estimates). [CrossRef]
- Event Horizon Telescope Collaboration (2019). First M87 Event Horizon Telescope Results. I: The Shadow of the Black Hole. Astrophys. J. Lett., 875, L1. (Strong-field curvature check). [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).