Submitted:
27 November 2025
Posted:
28 November 2025
You are already at the latest version
Abstract
A recent theoretical study of CsMnF4 under pressure [Inorg. Chem. 2024, 63(29), 13231] presents conclusions on its structural, optical, and magnetic behavior that conflict with established experimental evidence. Crucially, this work omits key prior experimental results on CsMnF4 and related Mn3+ fluorides under pressure. This perspective examines the resulting discrepancies, arguing that the omissions of this data undermines the theoretical estimates and methodological validity of Ref. [1]. This paper provides a critical overview centered on two main points: the contested nature of the pressure-induced high-spin to low-spin transition observed in CsMnF4 at ~37 GPa and a detailed discussion of Jahn-Teller physics in this archetypal system. By reconciling the existing literature with the new theoretical claims, this work aims to clarify the high-pressure behavior of CsMnF4.
Keywords:
1. Introduction
2. Results and Discussions
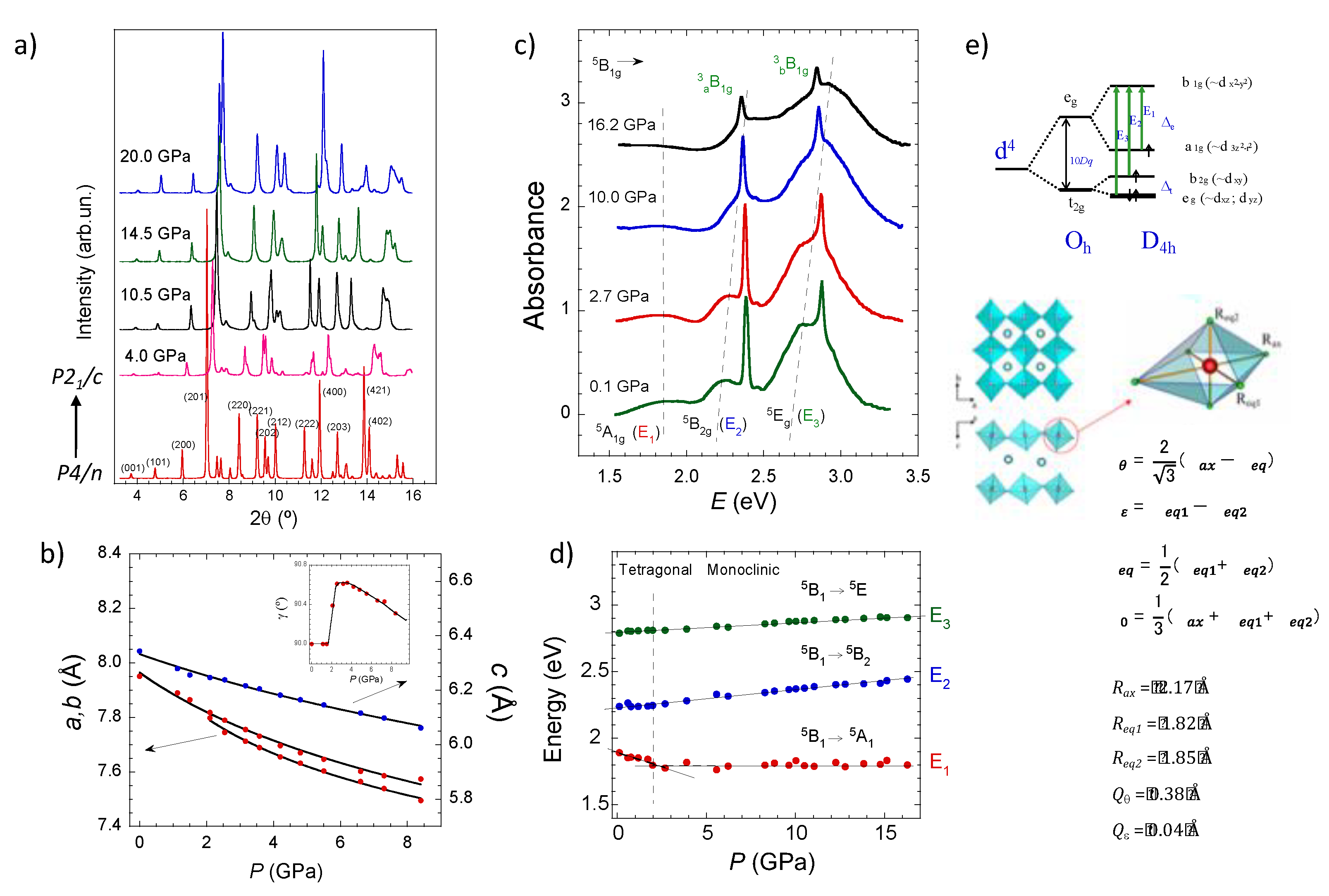
2.1. Structure of CsMnF4
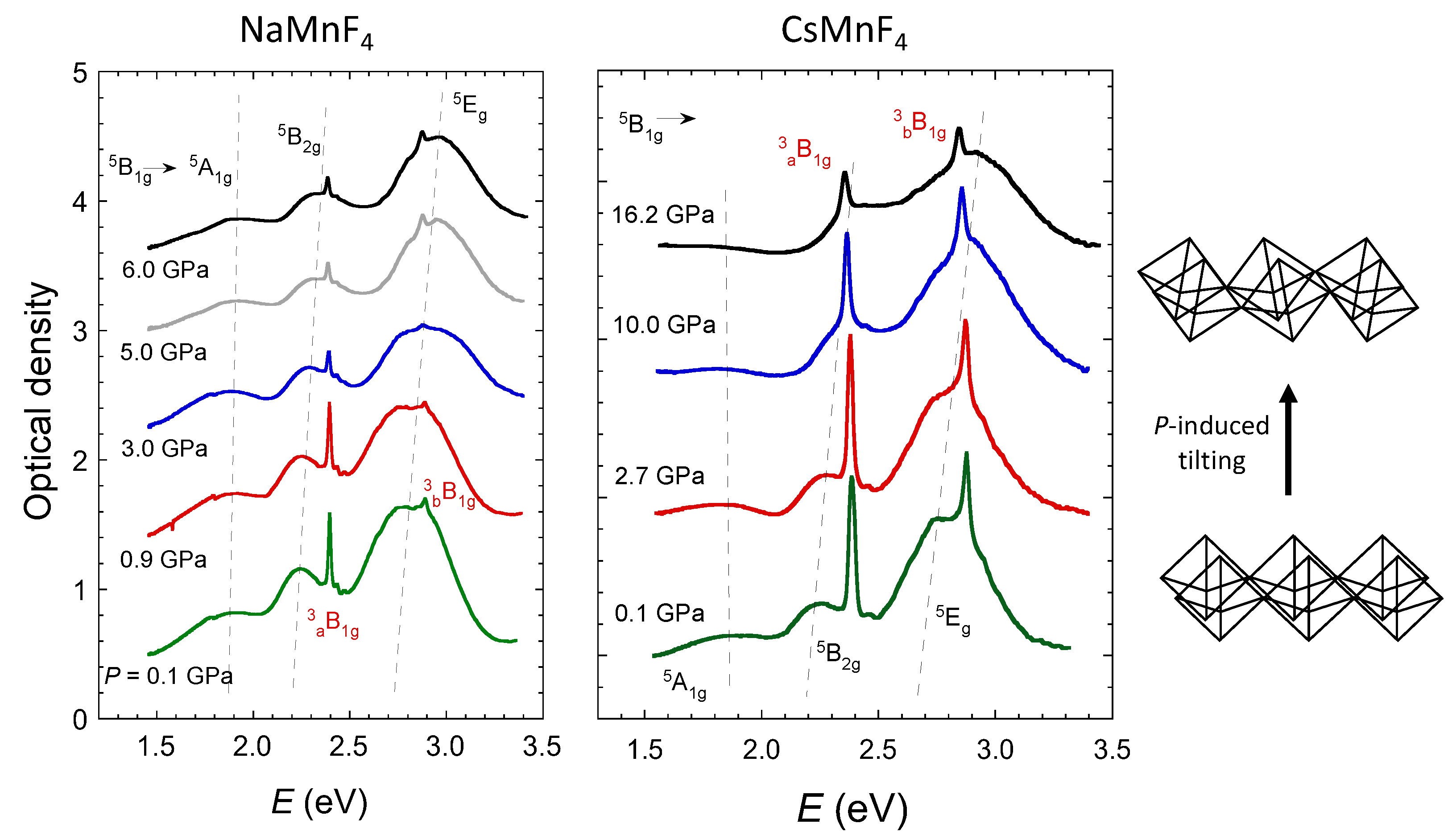
2.2. Pressure Dependence of the Optical and Electronic Properties
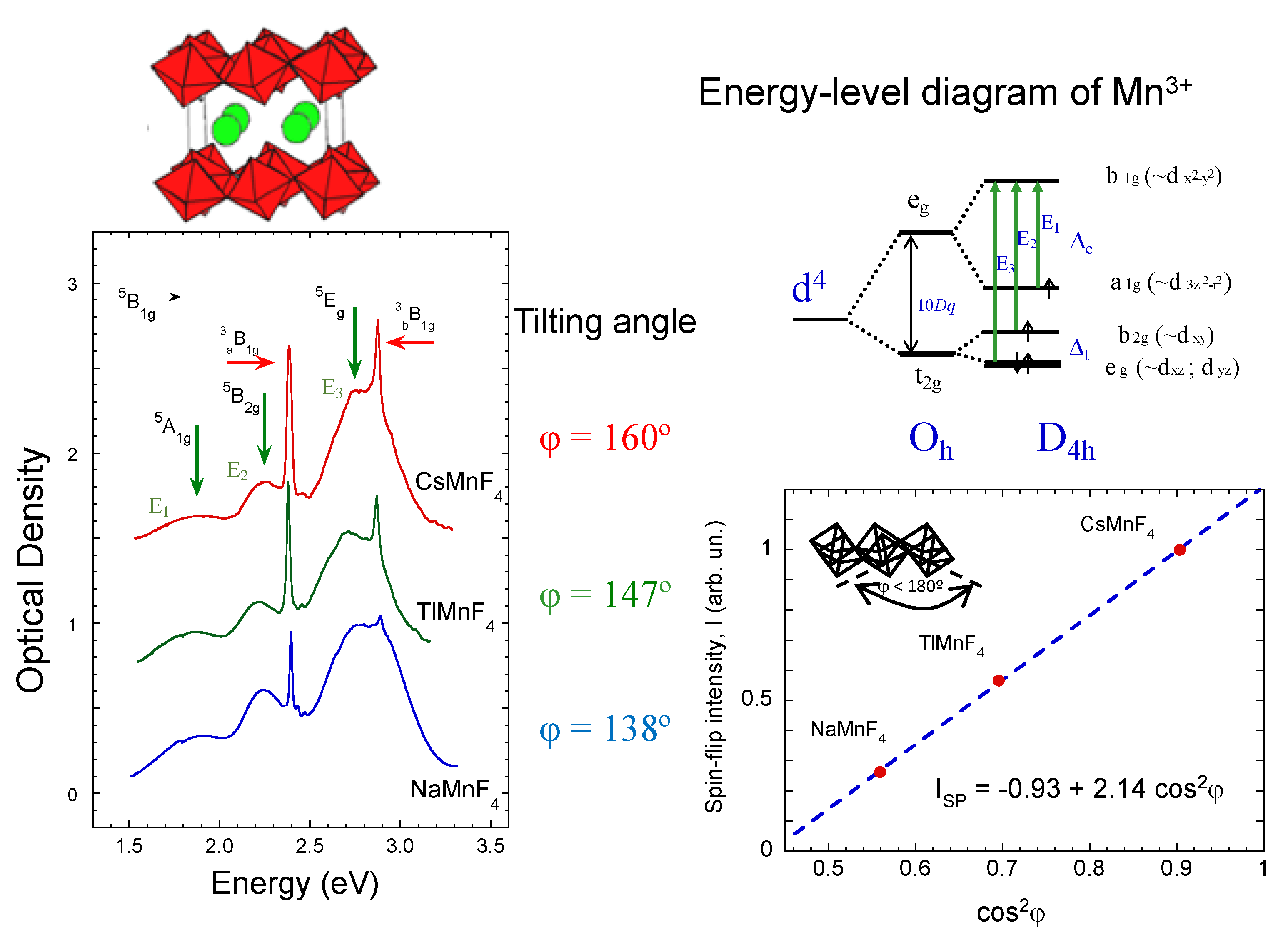
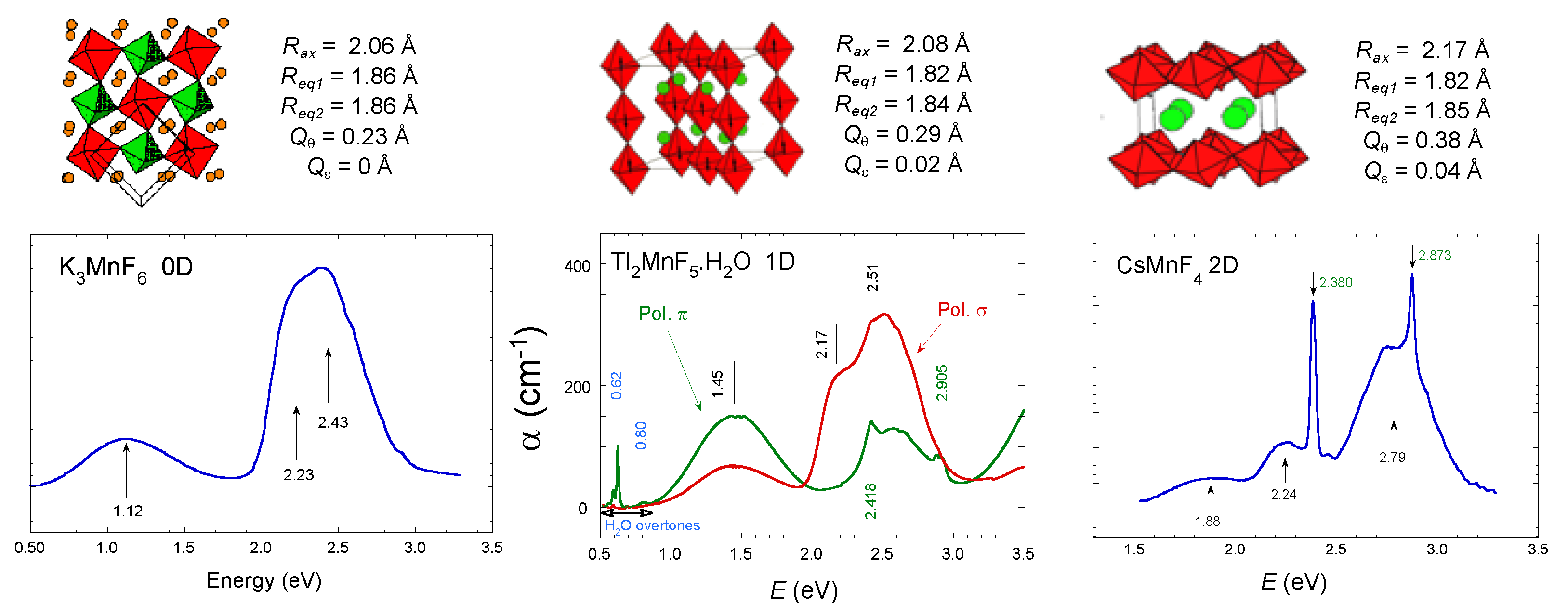
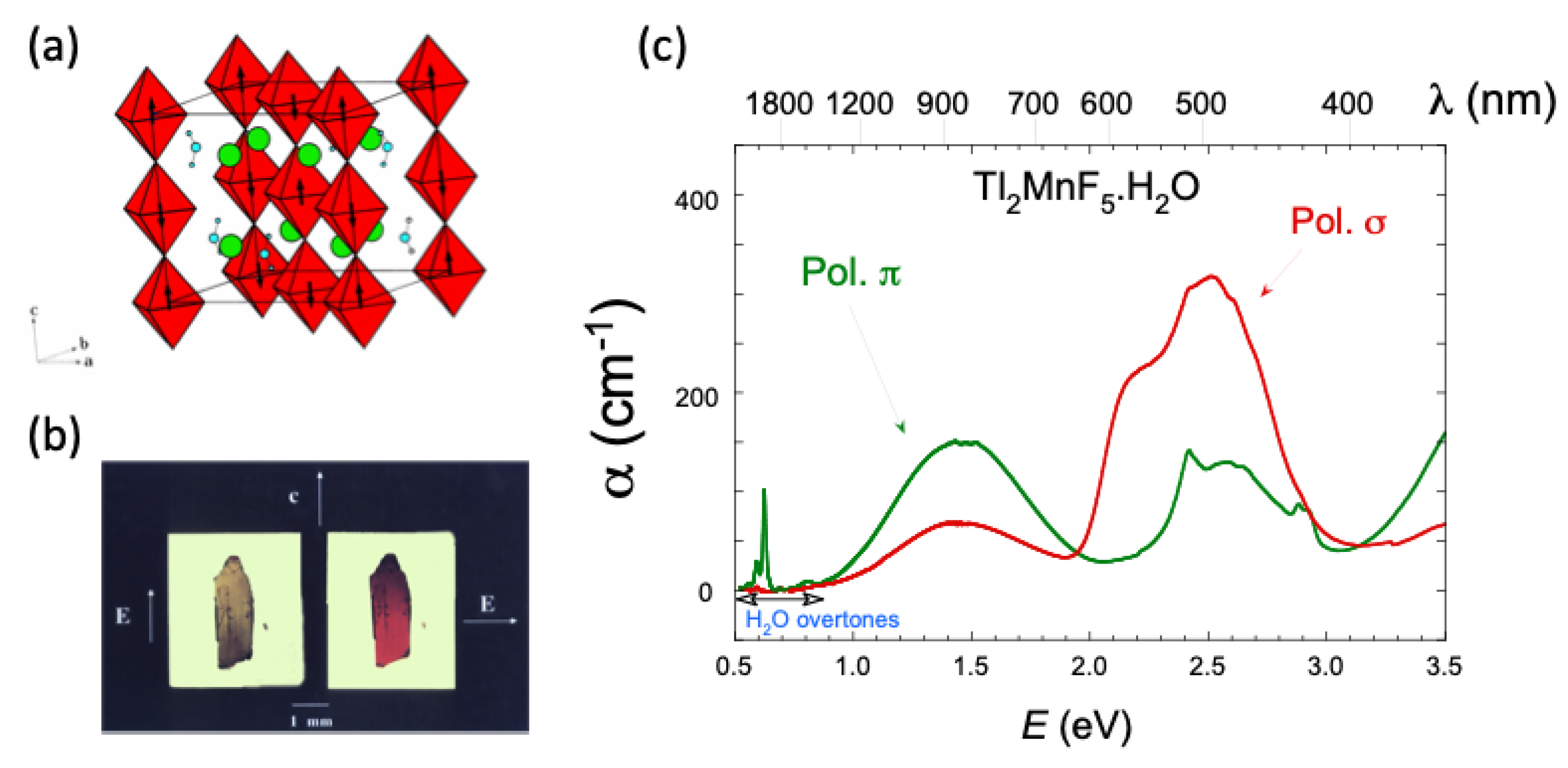
2.3. Optical Band Assignment of Mn3+ Fluorides
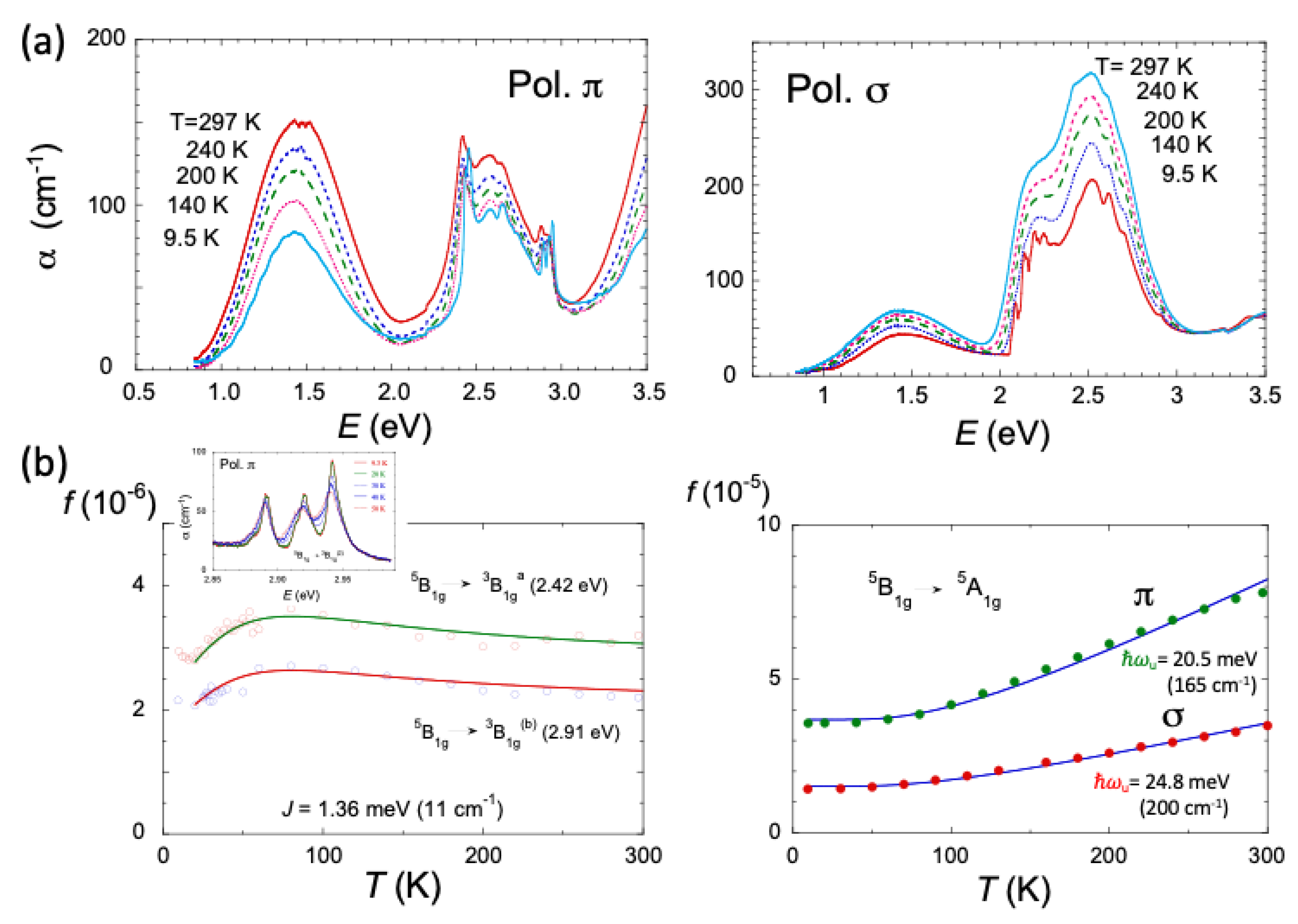
2.4. Magnetic Properties of CsMnF4
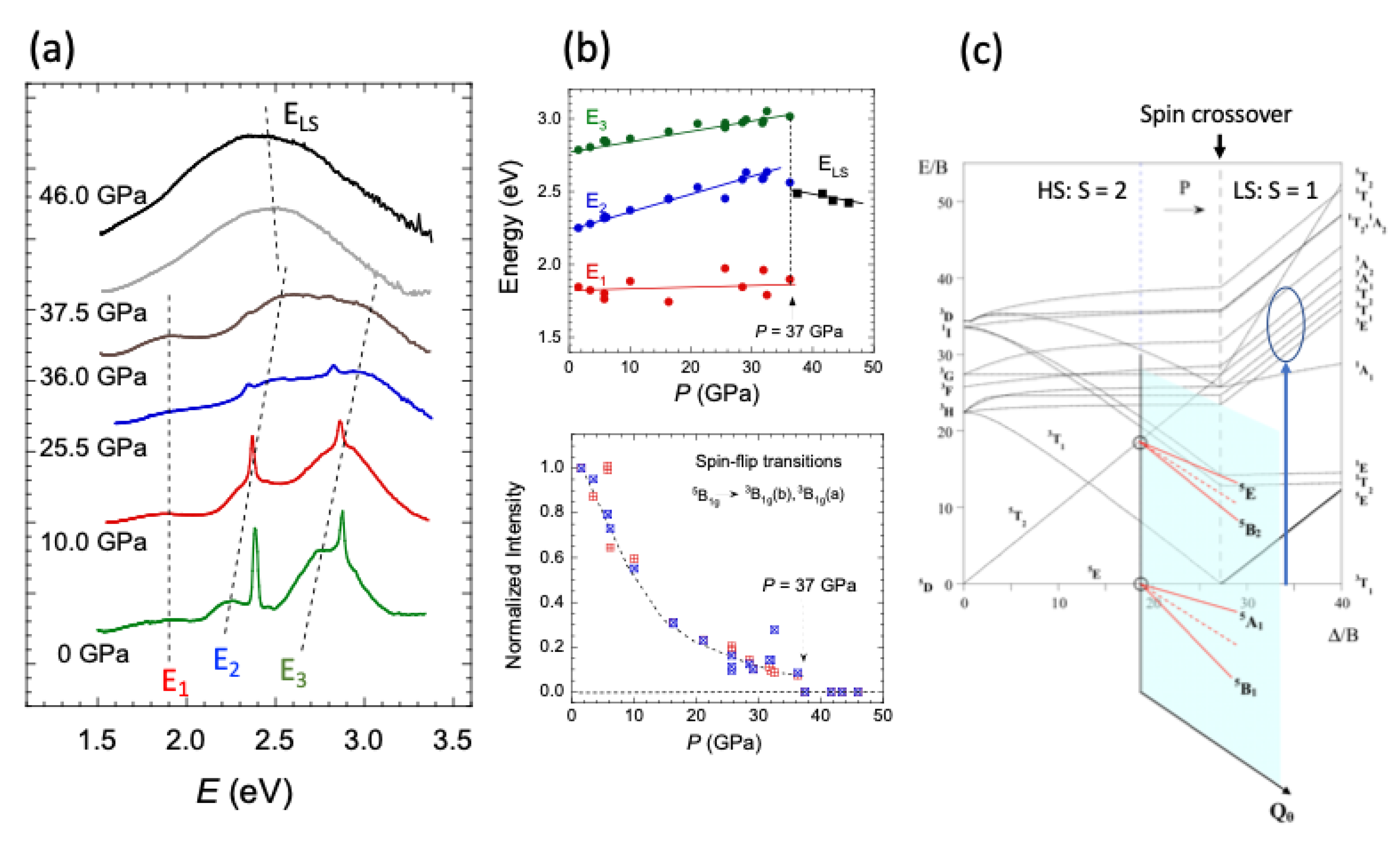
2.5. High-Spin to Low-Spin Transition at 37 GPa
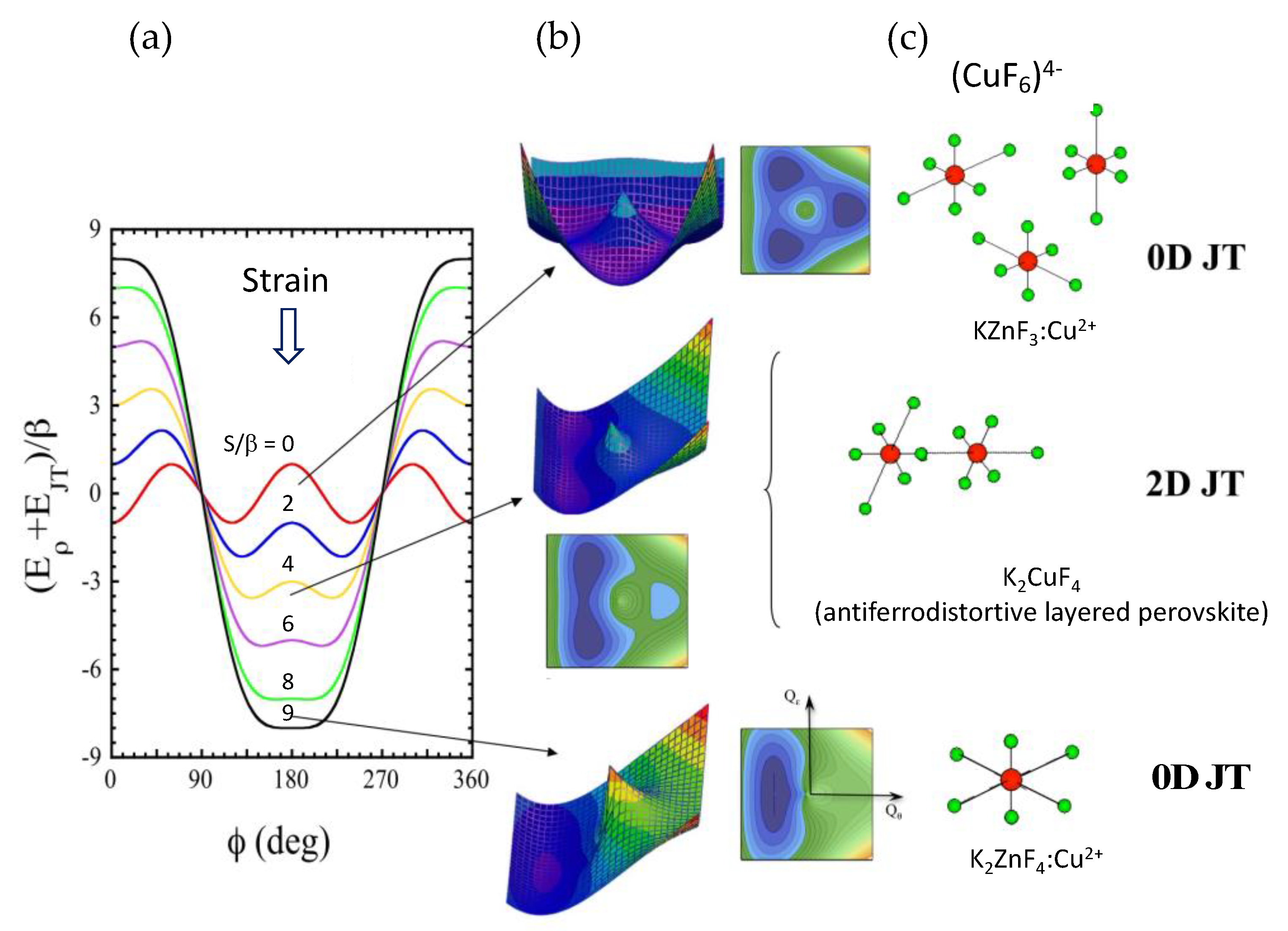
2.6. The Jahn-Teller Effect: Theorem, Theory, and Molecular Distortion
3. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| JT | Jahn-Teller |
| XRD | X-ray diffraction |
| LD | Linear dichroism |
| HS | High Spin |
| LS | Low Spin |
| nD | n Dimensional |
Appendix A
References
- Santamaría, G. , Fernández-Ruiz, T., García-Lastra, J. M., García-Fernández, P., Sánchez-Movellán, I., Moreno, M., & Aramburu, J. A. Understanding Pressure Effects on Structural, Optical, and Magnetic Properties of CsMnF4 and Other 3dn Compounds. Inorg. Chem. 2024, 63, 13231–13243. [Google Scholar] [CrossRef] [PubMed]
- Morón, M. C. , Palacio, F., Clark, S. M., & Paduan-Filho, A. Structural and magnetic behavior of the S= 2 layered ferromagnet CsMnF4 under hydrostatic pressure. Phys. Rev. B (Rapid Comm.) 1995, 51, 8660. [Google Scholar] [CrossRef]
- Morón, M. C. , Palacio, F., & Clark, S. M. Pressure-induced structural phase transitions in the AMnF4 series (A= Cs, Rb, K) studied by synchrotron x-ray powder diffraction: Correlation between hydrostatic and chemical pressure. Phys. Rev. B 1996, 54, 7052. [Google Scholar] [CrossRef]
- Rodríguez, F. , Aguado, F., Itie, J. P., & Hanfland, M. Structural Correlation in Jahn–Teller Systems of Cu2+ and Mn3+ under Pressure. J. Phys. Soc. Jpn. 2007, 76, 1–4. [Google Scholar] [CrossRef]
- Aguado, F. , Rodríguez, F., Valiente, R., Señas, A., Goncharenko, I. Three-dimensional magnetic ordering in the Rb2CuCl4 layer perovskite—structural correlations. J. Phys.: Cond. Matter 2004, 16, 1927. [Google Scholar] [CrossRef]
- Santamaría Fernández, G. Propiedades estructurales, magnéticas y ópticas del material en capas CsMnF₄ reanalizadas a la luz de simulaciones de primeros principios, Bachelor Thesis, University of Cantabria, 2021. http://hdl.handle.net/10902/23584. 1090. [Google Scholar]
- Aguado, F. , Rodriguez, F., Núñez, P. Pressure-induced Jahn-Teller suppression and simultaneous high-spin to low-spin transition in the layered perovskite CsMnF4. Phys. Rev. B 2007, 76, 094417. [Google Scholar] [CrossRef]
- Rodríguez, F. , Aguado, F. Correlations between structure and optical properties in Jahn–Teller Mn3+ fluorides: A study of TlMnF4 and NaMnF4 under pressure. J. Chem. Phys. 2003, 118, 10867–10875. [Google Scholar] [CrossRef]
- Aguado, F. , Rodríguez, F., & Núñez, P. Pressure effects on NaMnF4: Structural correlations and Jahn-Teller effect from crystal-field spectroscopy. Phys. Rev. B 2003, 67, 205101. [Google Scholar] [CrossRef]
- Rodríguez, F. , Núñez, P., & De Lucas, M. Polarized optical absorption spectroscopy of the Tl2MnF5.H2O 1D manganese(III) single crystal. J. Sol. St. Chem. 1994, 110, 370–383. [Google Scholar] [CrossRef]
- Ishizuka, M. , Henmi, S., Endo, S., Morón, M. C., & Palacio, F. Magnetic behavior of CsMnF4 under high pressure. J. Magn. Magn. Mat. 1999, 196, 440–442. [Google Scholar] [CrossRef]
- Candela, M. T. , Jara, E., Aguado, F., Valiente, R., & Rodríguez, F. Structural Correlations in Jahn–Teller Systems of Mn3+ and Cu2+: Unraveling Local Structures through Spectroscopic Techniques. J. Phys. Chem. C 2020, 124, 22692–22703. [Google Scholar] [CrossRef]
- Tanabe, Y. , & Sugano, S. On the Absorption Spectra of Complex Ions. I. J. Phys. Soc. Jpn. 1954, 9, 753–766. [Google Scholar] [CrossRef]
- Griffith, J. S. The Theory of Transition Metal Ions, Cambridge University Press, 1980, pp. 261, 412, 413.
- Tsuchiya, T. , Wentzcovitch, R. M., Da Silva, C. R., De Gironcoli, S., & Tsuchiya, J. Pressure induced high spin to low spin transition in magnesiowüstite. physica status solidi (b) 2006, 243, 2111–2116. [Google Scholar] [CrossRef]
- Hsu, H. , Umemoto, K., Cococcioni, M., & Wentzcovitch, R. First-principles study for low-spin LaCoO3 with a structurally consistent Hubbard U. Phys. Rev. B 2009, 79, 125124. [Google Scholar] [CrossRef]
- Hauser, A. Ligand field theoretical considerations. Spin Crossover in Transition Metal Compounds I, Gütlich, P., & Goodwin, H. A. (Eds.), Springer Science & Business Media, 2004, pp. 49-58.
- Gütlich, P. , Gaspar, A. B., & Garcia, Y. Spin state switching in iron coordination compounds. Beilstein J. Org. Chem. 2013, 9, 342–391. [Google Scholar] [CrossRef] [PubMed]
- Seredyuk, M.L. , Znovjyak, K.O., & Fritsky, I.O. Influence of Cooperative Interactions on the Spin Crossover Phenomenon in Iron(II) Complexes: A Review. Theor. Exp. Chem. 2022, 58, 75–89. [Google Scholar] [CrossRef]
- Jahn, H. A. , & Teller, E. Stability of Polyatomic Molecules in Degenerate Electronic States I. Orbital Degeneracy. Proc. R. Soc. A 1937, 161, 220–235. [Google Scholar] [CrossRef]
- Öpik, U. , & Pryce, M. H. L. Studies of the Jahn-Teller effect. I. A survey of the static problem. Proc. Roy. Soc. A. 1957, 238, 425–447. [Google Scholar] [CrossRef]
- Hitchman, M. A. The influence of vibronic coupling on the spectroscopic properties and stereochemistry of simple 4- and 6- coordinate copper (II) complexes. Comments Inorg. Chem. 1994, 15, 197–254. [Google Scholar] [CrossRef]
- Riley, M. J. Geometric and Electronic Information from the Spectroscopy of Six-Coordinate Copper(II) Compounds. In Transition Metal and Rare Earth Compounds; Yersin, H., Ed.; Springer: 2001; pp 57–80.
- Reinen, D. The modulation of Jahn-Teller coupling by elastic and binding strain perturbations – a novel view on an old phenomenon and examples from solid-state chemistry. Inorg. Chem. 2012, 51, 4458–4472. [Google Scholar] [CrossRef]
- Rodríguez, F. Unveiling the Local Structure of Cu2+ Ions from d-Orbital Splitting. Application to K2ZnF4: Cu2+ and KZnF3: Cu2+. Inorg. Chem. 2017, 56, 2029–2036. [Google Scholar] [CrossRef] [PubMed]
- Gaažo, J. , Bersuker, I.B., Garaj, J., Kabesova, M., Kohout, J., Langfelderova, H., Melnik, M., Serator, M., & Valach, F. Plasticity of the coordination sphere of copper(II) complexes, its manifestation and causes. Coord. Chem. Rev. 1976, 19, 253–297. [Google Scholar]
- Polinger, V. , & Bersuker, I. B. (2024). Orientational polarizability of solids induced by the Jahn-Teller and pseudo-Jahn-Teller effects. Phys. Rev. B 2024, 109, 224207. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




