GEOmetric Laws of Tectonic Motion: The First Law

1. Introduction

It is known that the Earth’s surface can be approximated by a geometrically regular figure of an ellipsoid of revolution. The elliptical shape of the planet is explained by the result of the combined action of gravitational and inertial forces due to the Earth’s rotation, which allows for the determination of a numerical value for the flattening and fixes the orientation of the flattening axis relative to the rotation axis. It is also known that the Earth’s rotation rate changes over time, and the rotation axis constantly moves relative to the Earth’s body, which inevitably should lead to a corresponding displacement of the flattening axis and a change in the flattening coefficient. The fact that all recent realizations of international reference systems (ITRF2014, ITRF2008, ITRF2000, etc.) rely on the lithospheric plate tectonics model indicates that, to date, there is no theory that can correctly describe the motion of the variable flattening axis on a deformable ellipsoid, since the kinematics of lithospheric plates is only realizable on an ideal sphere (Khain and Lomize, 2005). Leonhard Euler developed the theory of rotation of an absolutely rigid body. His theory consists of two parts: kinematic and dynamic. The concept of an "absolutely rigid body" was defined by him in a geometric sense, as a body in which the distance between any two points does not change over time. S. Newcomb explained the difference between the values of the Euler and Chandler periods by the fact that the Earth is not "absolutely rigid," although the kinematic basis in his studies remained unchanged (Avsyuk and Gerasimov, 1999). Today, we have instrumental observation data indicating that distances between points on Earth change over time, which requires a revision of the very geometry of the problem (IERS, n.d.; Gross, 2007). The proposed approach is based on a kinematic theory that generalizes Leonhard Euler’s rigid-body rotation theory to the case of describing rotations on an arbitrarily deformable ellipsoid. Furthermore, the use of a deformable reference surface requires no assumptions about the material composition or aggregate state of the Earth’s interior.

2. Solution of the Generalized Copernicus Problem on the Complex Spheroid

2.1. Copernicus’ Problem

Let us turn to the primary source – "On the Revolutions of the Heavenly Spheres" – where Chapter XI, "Proof of the Earth’s Triple Motion," presents Copernicus’ solution to the problem (Copernicus, 1543). The very title of the chapter indicates the geophysical nature of the problem. The proof consists of two parts. In the first part, the Earth’s motion is considered from the perspective of an observer on its surface, and in the second – in a heliocentric reference frame, from the standpoint of an imaginary celestial being. The main mathematical idea of Copernicus’ solution is analysis and synthesis, or the decomposition of observed motions into elementary geometric rotations, followed by the construction of a composition from the found elementary rotations that approximates the observations. Let us repeat the solution to his problem using modern mathematical tools.

2.2. Stereographic Projection

Let us use the method of complex coordination of the sphere’s surface, first proposed by Bernhard Riemann (Riemann, 1851). The method involves associating points on the sphere with points on a plane, where complex coordinates are defined, using stereographic projection (Figure 1). The sphere touches the plane at the south pole. Rays are drawn from the north pole of the sphere, intersecting the surface of the sphere and the plane. Each point on the sphere corresponds one-to-one to a point on the plane, except for the north pole. The north pole is associated with the point at infinity on the plane. Such a plane, equipped with a single point at infinity, is called the extended complex plane and is denoted as Ĉ, while the complex sphere is also called the Riemann sphere. Using stereographic projection, complex coordinates on the sphere can be calculated using the following formula:

$$\mathrm{z}= \cot {\displaystyle \frac{\phi }{2}}\ast e^{-i\ast \theta },$$

where:

z – complex coordinate;

φ – geodetic latitude, in radians;

θ – geodetic longitude, in radians;

This construction can easily be generalized to the case of complex coordination of a spheroid. Here and hereafter, a spheroid will refer to a sphere compressed into an ellipsoid relative to an arbitrarily oriented axis, with an arbitrary degree of compression. On a complex spheroid, functions describing the motion of its points can be introduced. To do this, we transfer the motion patterns from the plane to the spheroid using the same stereographic projection. Now, we project onto the spheroid’s surface not individual points of the plane, but lines and systems of lines described by functions of a complex variable. Of particular interest are functions that induce motion patterns on the spheroid, i.e., transformations of the surface that describe the intrinsic motions of the spheroid. 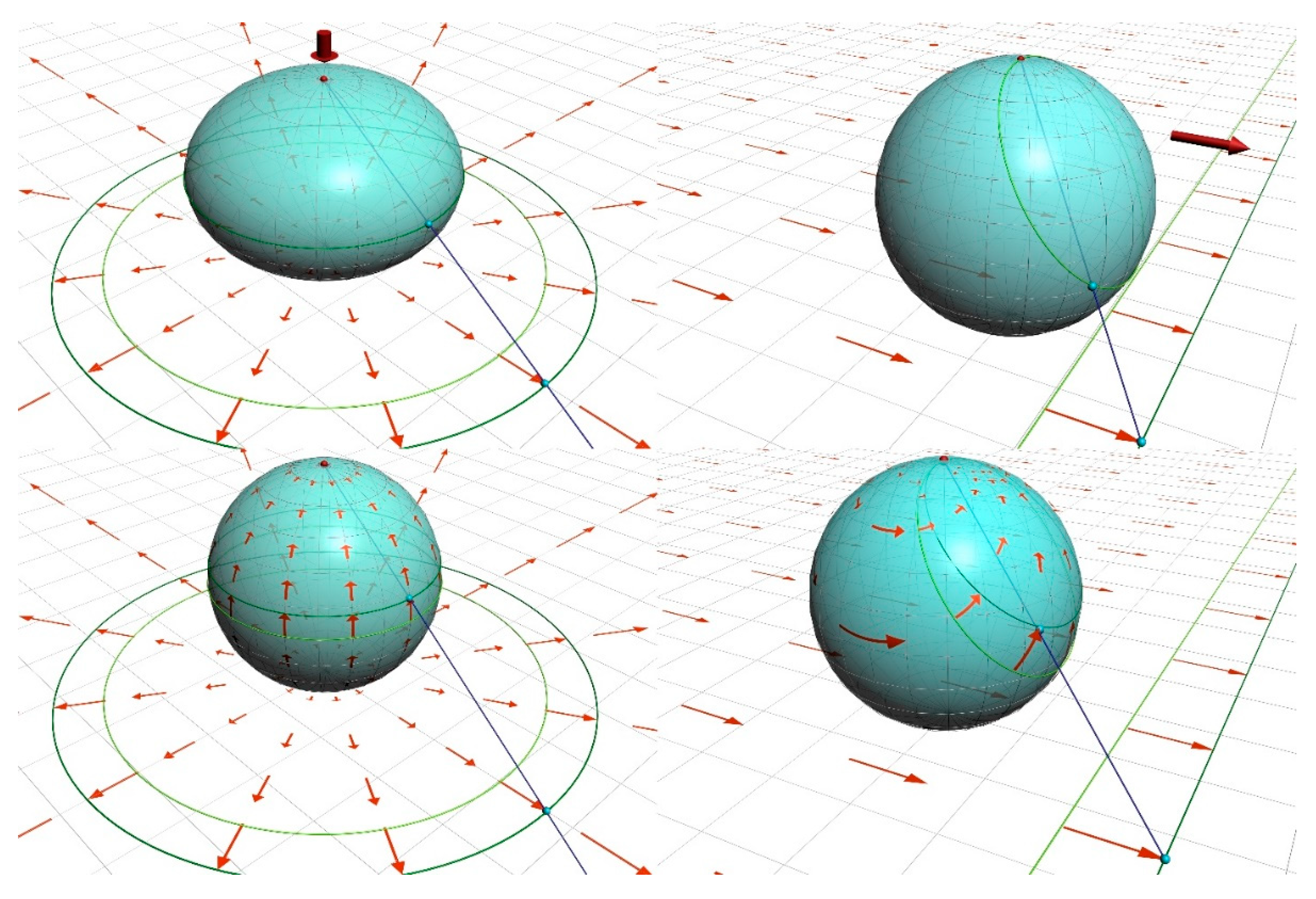Figure 1 illustrates the method for obtaining two elementary transformations of the spheroid: boost and isotropic rotation. A boost is obtained by uniformly stretching the projection plane. A boost can also be constructed by compressing the sphere into an ellipsoid of revolution along the projection axis. Isotropic rotation is obtained when the sphere moves relative to the projection plane. In both cases, an external transformation – compression and motion of the spheroid in space – can be one-to-one associated with a differential motion of the spheroid’s surface itself. This method allows for the introduction of complex coordination not only on a sphere but also on an arbitrarily compressed spheroid.

Figure 1. Construction of differential motions of the sphere using stereographic projection.

Figure 1. Construction of differential motions of the sphere using stereographic projection.

2.3. Möbius Transformations

In the mid-19th century, the German mathematician August Ferdinand Möbius (1790–1868) first systematically studied fractional-linear transformations on the extended complex plane (Möbius, 1855). These transformations, now called "Möbius transformations," have the form:

$$z\to {\displaystyle \frac{az+b}{cz+d}}$$

where a,b,c,d ∈ C, ad−bc=0,

Möbius transformations possess several important properties:

• They are conformal, meaning they preserve angles (like the stereographic projection itself);
• They form a group under composition (each transformation is invertible);
• Geometrically, they map circles and lines to circles or lines.

2.4. Analysis. Decomposition into Elementary Rotations

Analysis of the algebraic structure of the fractional-linear transformation shows that it can be represented as a composition of elementary functions corresponding to simple geometric transformations: translation, homothety, rotation, and inversion. However, such a decomposition is unsuitable for our purposes due to the presence of a transformation that is not a continuous motion (inversion). There exists another way to decompose the Möbius group into elementary rotations, which are given by the following formulas:

a) $w_i= {\displaystyle \frac{z_i\ast \cos \left(\frac{\alpha }{2}\right) + i\ast sin\left(\frac{\alpha }{2}\right)}{z_i\ast i\ast sin\left(\frac{\alpha }{2}\right)+ \cos \left(\frac{\alpha }{2}\right)}}$;

b) $w_i= z_i\ast e^{-i\ast \beta }$;

c) $w_i= \gamma \ast z_i$;

d) $w_i= z_i + \delta$;

where: α, β, γ, δ – parameters of elementary rotations (real numbers); -α, -β, ${\displaystyle \frac{1}{\mathsf{\gamma }}}$, -δ – inverse parameters of elementary rotations;

The first two are classical rigid-body rotations, while the last two define scaling (homothety) and shift on the complex plane, which, as we saw earlier (Figure 1), generate boost and isotropic rotation on the complex spheroid.

2.5. Coverings

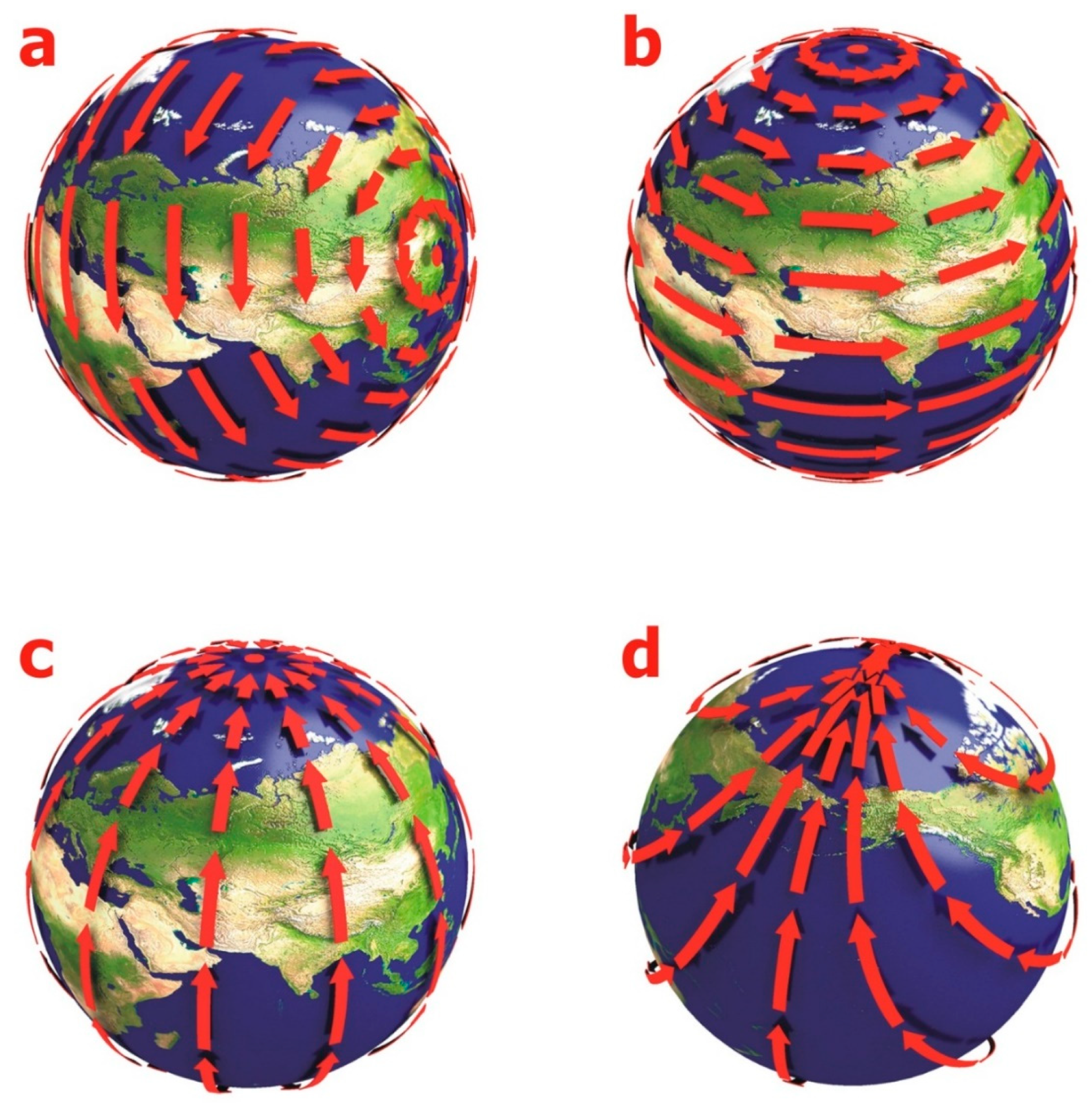
Let us now proceed to the main research question – the connection between tectonic motions and the Earth’s motion in space. Consider the coverings of geographical map images by vector fields of differential rotations (Figure 2):

a)

Rotation of the sphere around a diameter perpendicular to the stereographic projection axis – describes the motion of the geographic poles within the Earth’s body (Gross, 2007; IERS, n.d.). The direction of motion of points on the Earth’s surface is opposite to the direction of the North Geographic Pole’s trajectory.

b)

Rotation of the sphere around the polar axis. The direction of motion coincides with the direction of the Earth’s daily rotation. The contribution of this motion to the rotation composition manifests in the displacement of small sections of continental crust relative to larger ones. Many researchers note an interesting pattern – all islands with signs of continental crust are located along the eastern margins of continents.

c)

The south-to-north direction of the orbits approximates the motion of sections of the Earth’s crust over large time intervals. Currently, geology raises the question of the existence of a northern component of continental drift (Avsyuk and Gerasimov, 1999; Munk and MacDonald, 1975). The regular displacement of continental crust from south to north, which resulted in the separation of the single supercontinent (Pangea) into modern continents, was noted by Alfred Wegener, who postulated the existence of so-called pole-fleeing forces. This approximation also explains the regularities of J. Gregory: the triangular shape of continents and the orientation of the triangles with one vertex toward the South Geographic Pole. To monitor changes in the position of the Earth’s rotation axis, the International Latitude Service (now IERS) was established in the early 20th century, with all its stations located at the same latitude. After the first two years of the ILS operation, the Japanese astronomer Kimura discovered the so-called non-polar latitude variations (Munk and MacDonald, 1975). Currently, the change in station latitude is determined using the Kostinsky formula:

∆φ=xcosλ+ysinλ+z+ψ

where x – pole displacement along the Greenwich meridian, y – pole displacement in the direction 90° west of Greenwich, z – correction term introduced by Kimura, ψ – remaining variations not correlated from station to station. The term introduced by Kimura represents a non-polar latitude change, as if the latitudes of all ILS stations increased or decreased simultaneously. It is noted that the z-term has the same sign in both hemispheres. Non-polar latitude changes refer to systematic deviations from the existing theoretical model that could not be explained by instrumental measurement errors. In full accordance with Kimura’s description of non-polar increments, all points at the same latitude will have identical increments, and the direction of displacement will coincide in both hemispheres.

d)

Isotropic rotation describes the motion of observation surface points during the Earth’s motion in space. The direction of the orbits is determined by the patterns of distribution of extension and compression zones in the Earth’s crust. The field of isotropic rotation approximates global tectonic systems: rifts, island arcs (Ricard et al., 2022; Spada, 2022). The pole of isotropic rotation coincides with the North Geographic Pole, and the arc of maximum values of the vector field is oriented along the meridian passing through the Atlantic Rift. This region of the planet contains tectonic systems of extension, so the vector fields diverge here. On the other side of the planet, the tectonic structure of the Pacific Ocean floor shows signs of compression. The figure shows that the vector distributions in this hemisphere converge, and the field lines of isotropic rotation coincide in shape and symmetry with the system of island arcs in the Pacific Ocean. The amplitude of the isotropic rotation field vectors increases from north to south, fully consistent with the pattern of increasing displacement amplitudes of the "diverging" continental coastlines.

Figure 2. Elements of the extended group of Earth’s motions considering differential rotations.

Figure 2. Elements of the extended group of Earth’s motions considering differential rotations.

2.6. Signature

We can now introduce an important characteristic of the Earth’s surface - the signature. The signature defines the orientation of the surface and represents a sequence of plus and minus signs. In our chosen sequence of group elements and the defined orbit directions on the map, the signature will have the symbolic notation (++++) and the name "canonical". If we reverse the direction of time, the velocities of tectonic motions will also reverse their directions, so the signature will take the form (----). The signature serves as a powerful tool for comparative planetology. For instance, the signature of Venus would be fundamentally different, notably (+-++), primarily due to its retrograde rotation. This highlights how the signature captures the fundamental kinematic state of a planetary body. As a modeling tool, the signature is useful for solving problems of tectonic motion reconstruction.

2.7. Generalization of Copernicus’ Problem

Let us return to Copernicus’ problem and try to fill the gap in illustrating the proof of the Earth’s triple motion. It is known that the Earth performs two motions with daily and annual periods, which Copernicus transformed into two rotations around the polar axis and around the Sun. Additionally, our planet performs complex motions that were unknown to medieval astronomers. The question arises - what is the third motion of the Earth that is being referred to? Copernicus called the third motion "declinational", since it represents a combination of orbital and daily rotation due to the inclination of the Earth’s polar axis to the orbital plane. The declinational motion manifests itself in the change of seasons and has an annual period. We can compose the first two rotations and decompose the Earth’s motion into three motions - two elementary rotations and their combination. These rotations exhaust all motions of the sphere as a rigid surface. But the considered group contains two more rotations that, at first glance, could be discarded as byproducts of mathematical constructions. For a long time, physicists treated solutions of motion equations with values in the domain of imaginary and complex numbers in a similar way, until it was discovered that complex solutions have not only mathematical but also physical meaning. This remarkable fact underlies the theoretical prediction of physical phenomena. We cannot exclude the possibility that additional rotation fields correspond to reality. When modeling the Earth’s motion, it is necessary to account for the geoid’s compression, which is described by a boost. Isotropic rotation and its compositions will be needed to describe the Earth’s motion in space. Moreover, the third and fourth rotations represent differential motions of the sphere, which are indispensable for reconstructing the Earth’s crust in the geological past.

2.8. Synthesis. Compositions of Elementary Rotations

Let us now proceed to synthesize complex tectonic motion from simple elements. Our immediate task is to find compositions of simple rotations that approximate the empirical patterns of tectonic motion on the ellipsoid. Consider, as an example, the composition c^-ac (other compositions are constructed similarly). The first element of the operator transforms the elliptical surface of the Earth into a sphere, the next element shifts the origin of motion, and the last element compresses the sphere back into an ellipsoid of revolution. In Euclidean "reality," phenomena such as the deformation of the Earth’s ellipsoid of revolution into a spheroid are not observed; however, we can represent discrete operations on images as continuous transformations that describe motions without contradicting observations. To do this, we must transfer the resulting vector field from the complex plane to the ellipsoid. As a result, we will see a picture of continuous bending of the ellipsoid of revolution onto itself from the perspective of a celestial observer. From the perspective of an observer on Earth, we will see the displacement of the compression axis within the Earth’s body. It is known that the Earth is flattened at the poles due to centrifugal forces arising from rotation. If the rotation axis changes its position within the Earth’s body, the compression axis must shift to align with the rotation axis; that is, the Earth’s figure must adjust to the new position of the rotation axis. The theory of rigid-body rotation cannot describe this phenomenon by definition. Now, we can reconcile the motions of both axes within a unified model of a deformable Earth. Most importantly, tectonic motions describing the deformation of the Earth’s surface become a necessary consequence in the considered model, and instrumental observation data receive theoretical justification.

All the considered motions and their combinations possess a number of remarkable properties that allow them to be united into a group. All the listed motions are conformal, have a fixed point, and their orbits are circles. Any arbitrarily complex motion of a sphere can be decomposed into elementary rotations and associated with fractional-linear functions on the complex plane. Thus, the constructed model contains all the necessary elements for building a geophysical model that includes the astronomical one as a special case of the complex motion of the Earth.

2.9. Reference Systems for Earth’s Motion. Tectonic Time

To correctly describe motion, it is necessary to introduce at least two reference systems: a moving (or current) one with the North Pole coinciding with the current position of the North Geographic Pole (rotation axis), and a fixed one with the North Pole located on the trajectory of the pole’s motion and rigidly connected to a fixed point on the observation surface. There are infinitely many fixed reference systems, and all lie on the trajectory of the North Pole on the observation surface. The distances between points on the trajectory marked by astronomical time are not equal, so it becomes necessary to introduce tectonic time. The flow of tectonic time is determined by the parameter of the first elementary rotation in the group. The speed of tectonic motion is determined at each point of the Earth’s surface on the tangent vector to the local motion trajectory per unit time. The second derivative with respect to time of the magnitude of the coordinate increment of a surface point has the physical meaning of acceleration of tectonic motion. When determining the units of tectonic time, it is convenient to use its main property - cyclicity. One of the units of tectonic time can be taken as the period of the spiral trajectory of the North Pole’s motion - 6 years. The concepts of tectonic and geological time should not be identified. On geological time scales, it is impossible to determine quantitative directed quantities that have the physical meaning of velocity, acceleration, and derivatives of energy, momentum, etc. The geological scale is a copy of the historical time scale, measured in the decimal system. Geological time is not connected to any natural cycles, and its connection to the concepts of solar and astronomical time is not justified by geometric constructions.

3. Analogues. Prototype. Historical Problem Statement

3.1. Modern Model of Lithospheric Plate Motion

In patenting inventions, there is a strict rule: before describing a new solution, it is necessary to identify similar methods and select the closest analogue (prototype) among them. This allows immediately determining the state of the art and ensuring that further development proceeds in the fundamentally correct direction. A similar approach is appropriate here—when analyzing the existing geophysical paradigm.

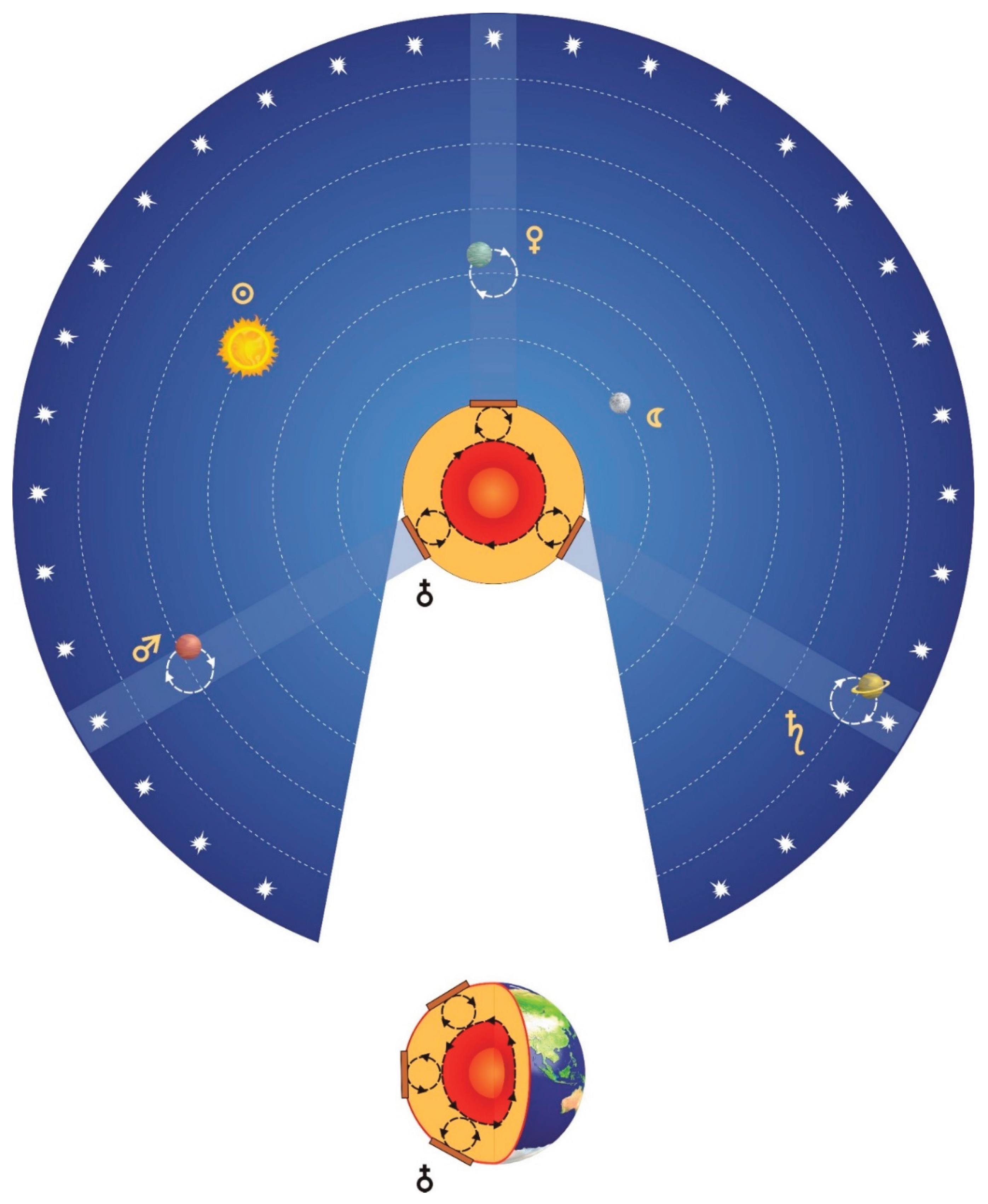
The latest achievement of geophysical science—the model of lithospheric plate motion—fits perfectly into Claudius Ptolemy’s system of the world (Figure 3). The kinematic scheme of convection of molten asthenospheric material easily reveals elements of the medieval model of celestial sphere rotation. The concentric, stationary system of geospheres complements ideas about celestial and sublunar worlds with their own special and independent laws of motion. Convective cells of the asthenosphere are analogues of planetary epicycles. The lexicon of geophysics lacks concepts of motion reference systems, and specialists are guided by the following definitions: "Geological space is a metric Euclidean space, however, some reservations must be made here. First of all, when studying it, a geocentric coordinate system should be used, with the origin rigidly attached to some point on our planet. In global constructions, it is convenient to place the origin at the Earth’s center, and in regional ones—at any point on its surface, sea level surface, or other surface convenient for certain reasons. The geocentricity of coordinates makes tectonic constructions independent of the Earth’s rotation and its motion in space" (Kosygin, 1983). Galileo’s opponents asserted the same, considering Nicholas Copernicus’ theory as nothing more than a mental exercise, justified only in the process of mathematical computation of planetary motion parameters. Based on such observation documentation, it is impossible to adequately depict geological space, describe processes of geological motion, and meaningfully solve earthquake prediction problems.

3.2. Analysis of Methodological Approaches from Historical Perspectives

In the era of Copernicus and Galileo, scientists were no longer satisfied with naive ideas about planetary motion, according to which celestial bodies supposedly moved through space pushed by angels. To explain the observed motions, medieval astronomers argued about the structure of the celestial firmament and concluded that it was made of pure crystal. Only much later did it become clear that no solid sphere existed and the space between planets was a vacuum.

Today we argue about the composition of the mantle and core, believing that without precise knowledge of these properties it is impossible to correctly describe tectonic motions. What once hindered understanding the structure of the Solar System now prevents us from understanding the Earth’s motion. We are repeating the same historical cycle: trying to explain motions through "driving forces" without first constructing the kinematics itself (Varga et al., 2022; Zhong and Liu, 2022). We are trying to explain what has not even been described yet. We are searching for forces without building a correct reference system, without analyzing observation data, and without identifying motion invariants. History shows the right path. Neither Copernicus, nor Kepler, nor Newton required knowledge about the structure of celestial spheres, their material, or physical composition.

4. Laws of Tectonic Motion

4.1. Energy Basis of Tectonic Processes

Any motion requires an energy source. The prevailing plate tectonics paradigm postulates a hypothetical source—thermal energy from mantle convection. However, energy analysis reveals a fundamental contradiction: according to (Riguzzi et al., 2010), the thermal flux can provide only 39–106 "Tsar Bombas" per day (where the unit is defined as the energy of the largest thermonuclear device ever tested—58.6 megatons of TNT equivalent), while the estimated efficiency of such a process yields physically unrealistic values exceeding 100%.

In contrast, our model relies on an observable and measurable source—the Earth’s rotational energy. Direct calculations based on IERS data (Semashev, 2025) show that variations in rotational kinetic energy create a power flux of ~2794 "Tsar Bombas" per day. Only 4–7% of this energy is required to sustain tectonic activity—a physically realistic efficiency comparable to natural processes.

Critically, rotational energy exceeds all alternative sources by orders of magnitude. Thus, it represents the only quantitatively confirmed candidate capable of explaining global tectonic activity without invoking hypothetical mechanisms with inherently overestimated efficiency.

4.2. The First Law of Tectonic Motion

Today we possess a vast amount of instrumental observations about the motion of the Earth’s surface, but we have yet to extract the main thing from them—those geometric patterns that must underlie any motion. In geophysics, the very question of the existence of laws of tectonic motion has not even been raised. The accepted concept of mantle convection suggests that lithospheric plates move chaotically, under the influence of local flows of molten material, and therefore are not obliged to obey any global patterns.

However, before us lies an obvious fact that we have grown accustomed to overlooking: no matter how the Earth’s appearance has changed over time, no matter how continents have moved, no matter how oceans have been rearranged, the Earth has always maintained the shape of a compressed spheroid. Thus, we can establish the first law of tectonic motion as follows:

The trajectories of tectonic motion of any point on the Earth’s surface are orbits of the action of the conformal Möbius group on the complex spheroid. Any such motion can be decomposed into a composition of four elementary rotations.

Over hundreds of millions of years, despite continental drift, the breakup of supercontinents, the opening and closing of oceans, the planet remains a geometrically simple figure—a spheroid flattened at the poles. This is not a random feature. This is a geometric invariant of the motion of the Earth as a deformable rotating body. Its existence means that tectonic motions cannot be chaotic: behind them must lie a strict kinematic structure. It is such invariants that form the foundation for future "laws of tectonic motion"—analogues of Kepler’s laws for the motion of the Earth’s surface. Based on the presented kinematic model, it is already possible today to quantitatively calculate the components of the geodynamic field and build forecasts of seismic hazard, without involving hypotheses about the Earth’s internal structure (Semashev, 2006; Semashev and Semashev, 2024). Just as Kepler once discovered the hidden order in planetary motion following Copernicus, so we today stand on the threshold of discovering the hidden order in tectonics, which becomes visible only after choosing the correct reference frame and recalculating observations. This will be the subject of discussion in the second part of the trilogy—" GEOmetric Laws of Tectonic Motion. Part II: Evidence of the Second Law of Tectonic Motion."

5. Conclusions

Based on the solution of the generalized Copernicus-Euler problem for a deformable spheroid, a new kinematic model has been developed that for the first time organically unites astronomical and tectonic motions into a single mathematical system. The main results of the work are as follows:

• The group structure of tectonic motions has been established. It has been shown that motions of the Earth’s surface are orbits of the action of the conformal Möbius group on a complex spheroid, and any complex motion can be decomposed into a composition of four types of elementary rotations.
• The First Law of Tectonic Motion has been established. By analogy with Kepler’s laws in celestial mechanics, this law reveals a fundamental geometric invariant—the preservation of the conformal structure on a deformable spheroid, manifested in the conservation of angles between lines on its surface and the overall spheroidal figure of the Earth despite continuous tectonic deformations. This opens the way to creating a new axiomatics of geodynamics, free from hypotheses about the planet’s internal structure.
• A new methodological approach has been proposed. The model demonstrates that a correct description of the kinematics of the Earth’s surface requires accounting for its deformability and motion in reference systems connected with the rotation axis and the planet’s figure, rather than with arbitrarily chosen points of the Earth’s crust.
• A complete energy basis for tectonic processes has been provided, establishing that the previously unaccounted energy of Earth’s rotation [Semashev, 2024] creates a power flux (~2794 "Tsar Bombas" per day), offering an observationally grounded alternative to hypothetical deep-Earth energy sources.
• Practical significance has been shown. The constructed kinematic model creates the basis for the quantitative calculation of geodynamic field components and the development of physically based methods for seismic hazard prediction, as confirmed by a patent for the corresponding method [Semashev and Semashev, 2024].
• The work revives the scientific program of Copernicus, Kepler, and Newton, transferring its principles—first the search for geometric laws of motion, and only then the transition to dynamics with the discovery of a physical law, as Newton did.
• This study opens a new research direction and challenges the scientific community to discover the subsequent laws of tectonic motion—the Second and Third, which, akin to Kepler’s laws, will complete the creation of the kinematic foundation of tectonics as an exact science and pave the way for the future discovery of its "law of universal gravitation."

Thus, this research lays the foundation for revising the methodological foundations of tectonics, bridging the long-standing gap between astronomy and geology and returning geodynamics to the mainstream of fundamental physics and geometric group theory.