Entropy-Driven Orbital Formation: A Thermodynamic Foundation for the Hydrogen Atom

1. Introduction-Reframing the Hydrogen Atom

Quantum mechanics (QM), for all its mathematical precision and predictive power, offers little insight into the physical reality of atomic structure. The standard formulation treats the electron’s behavior through the time-independent Schrödinger equation, yielding solutions called wavefunctions — ψₙₗₘ — that describe orbital shapes as mathematical eigenstates of an abstract operator equation:

H ψ=E ψ

(1)

These wavefunctions successfully predict observable quantities such as energy levels and transition probabilities. However, they remain disconnected from any physical explanation of why these orbitals form, what shapes them, and how they relate to the field reality of the atom itself. QM treats the wavefunction as an abstract probabilistic object — a tool for computing measurement outcomes — but not as a physically real field. The only link between theory and observation is the “collapse” during measurement, yet even that remains unexplained in terms of causality or mechanism. The actual shape of the atom — its field distribution in space — has no dynamic cause in standard quantum theory. Traditional QM implicitly assumes that orbital shapes arise from an interaction between the electron and the proton via the Coulomb potential. But it completely neglects the role of the surrounding field — the background entropy — that constantly interacts with the atom. It assumes that the electron absorbs photons from the environment and “jumps” from one level to another, without explaining how the field shape changes or what controls the spatial transformation of the orbital. S-Theory provides this missing insight. We propose that the hydrogen atom is not a fixed structure but a recursive entropy engine, continuously interacting with its surroundings. We model the hydrogen atom as a recursive, entropy-guided relaxer: a local thermodynamic entropy density field, S(r), organizes the orbital geometry, and discrete environmental inputs drive transitions between S-max macrostates.

1.1. Generalized Definition of Entropy in S-Theory

S-Theory begins with a primordial entropic background, $S_{\mathrm{\infty }}$: an unbounded, unstructured field composed of an infinite number of entropic quanta, the fundamental microscopic elements of the theory, as indicated in Figure 1. For mathematical convenience, individual entropic quanta are treated as elements of a complex potential field, whose real and imaginary components capture correlated and uncorrelated contributions. This allows wave-like interference and geometry to emerge from recursion, without postulating a separate quantum wavefunction. In $S_{\mathrm{\infty }}$, these quanta fluctuate freely without correlation or geometry, representing maximal entropy. Physical structure arises when subsets of these quanta become correlated, giving rise to three distinct correlation classes: (i) S_thermal — minimally correlated entropic quanta that generate thermal and background fluctuations; (ii) S_EM — highly correlated entropic quanta that organize into electromagnetic-like field structures; and (iii) S_core — maximally correlated entropic quanta that form stable, localized cores associated with mass. Energy and mass are not primitive; they emerge from these different correlation states. S_EM corresponds to organized field energy, S_core to localized mass structures, while S_thermal represents background heat and noise. We define the local entropy at position $\mathbf{r}$by counting the number of possible microscopic arrangements of entropic quanta within a finite local cell, subject to their correlation structure and boundary geometry. For 2D approximation,

Here, ${\mathsf{\Omega }}_S\left(\mathbf{r}\right)$is the total number of distinguishable microconfigurations of entropic quanta, decomposed into three contributions given by

corresponding to S_thermal, S_EM, and S_core, respectively.

${\mathsf{\Omega }}_{\mathrm{th}}$counts micro configurations of entropic quanta that produce macroscopic thermal energy through random, minimally correlated arrangements.

${\mathsf{\Omega }}_{\mathrm{sEM}}$counts field-structured micro configurations of entropic quanta arising from correlations linked to electric charges and magnetic field organization.

${\mathsf{\Omega }}_{\mathrm{Score}}$counts mass-forming micro configurations of entropic quanta, representing maximally correlated clusters that behave as stable cores.

In regions dominated by S_thermal, the definition reduces to the classical Boltzmann form. In structured regions, correlated quanta (S_EM and Score) reduce the number of accessible micro configurations, giving rise to organized energy fields and mass. This generalized entropy definition serves as the foundational expression for all subsequent derivations in S-Theory, unifying thermal entropy, electromagnetic field structure, and mass within a single entropic counting framework that encompasses both structured and unstructured components of physical reality.

This generalized definition does more than extend Boltzmann’s counting—it introduces geometry as an intrinsic outcome of entropy correlations. In classical statistical mechanics, entropy quantifies the number of microstates consistent with a given macroscopic energy, but it carries no information about spatial form. In S-Theory, however, the correlated entropic quanta (S_EM and S_core) not only reduce accessible micro configurations but also organize them in space, producing stable geometric patterns. These correlated fields act as sculptors of structure: S_core defines localized cores, while S_EM defines coherent surrounding fields, together giving rise to shapes such as atomic orbitals, molecular structures, and eventually large-scale cosmic forms. In this way, geometry itself is an entropic construct, emerging directly from the distribution and correlation of entropic quanta, not imposed by external equations. This shift—from entropy as a scalar descriptor to entropy as a shaper of structure—is the central conceptual advance of S-Theory.

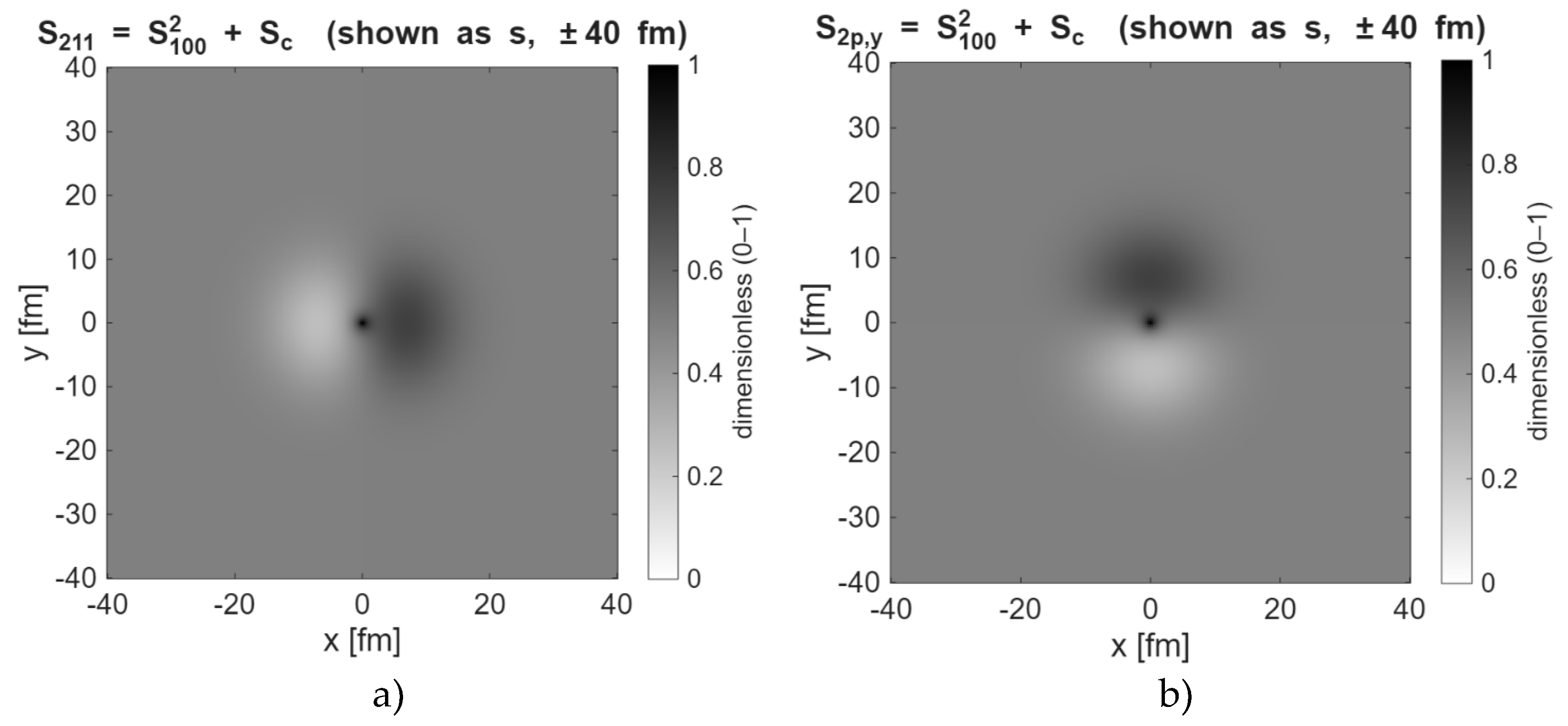
To generate orbital fields in 2D, we work with the dimensionless capacity field

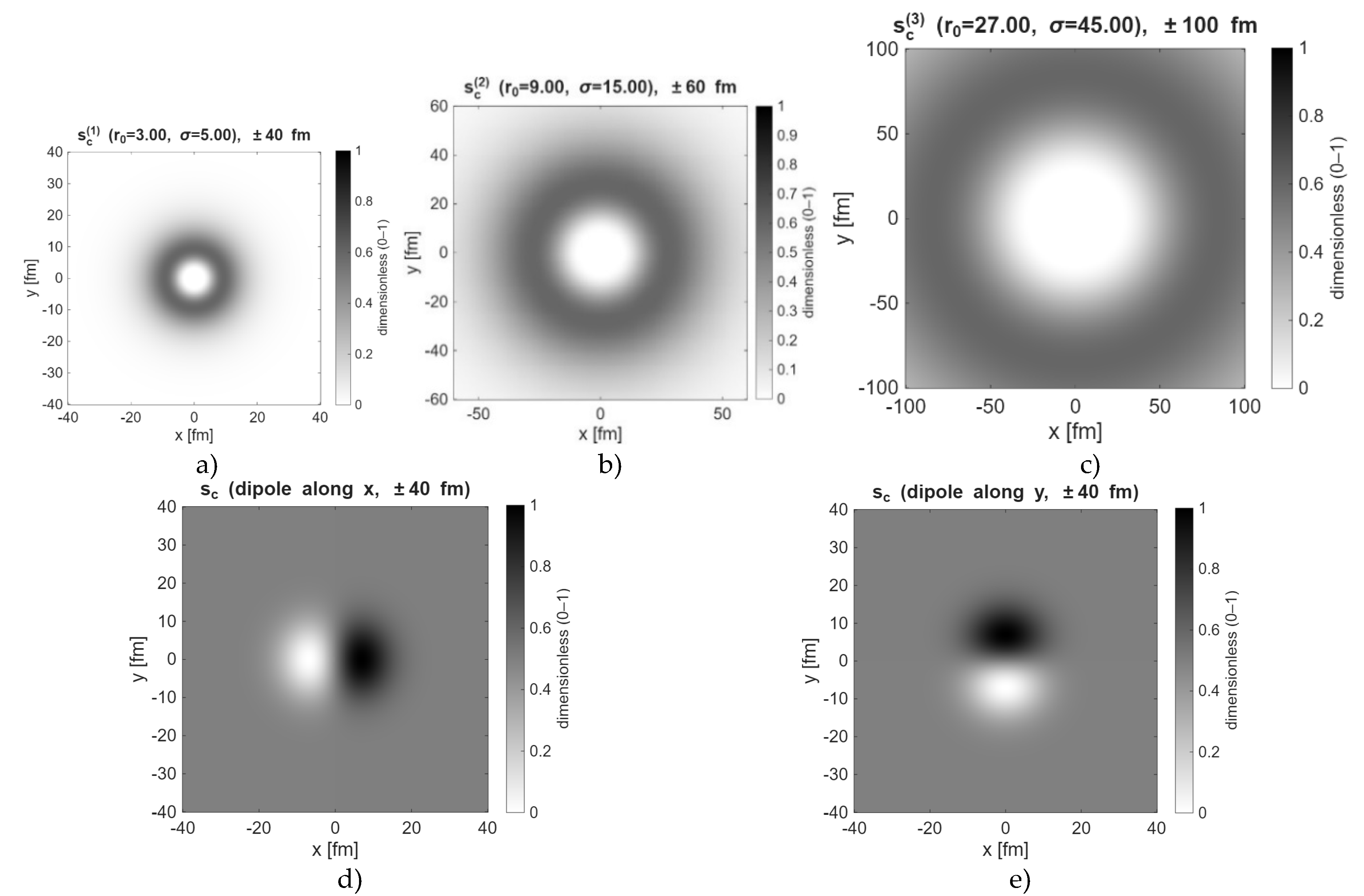
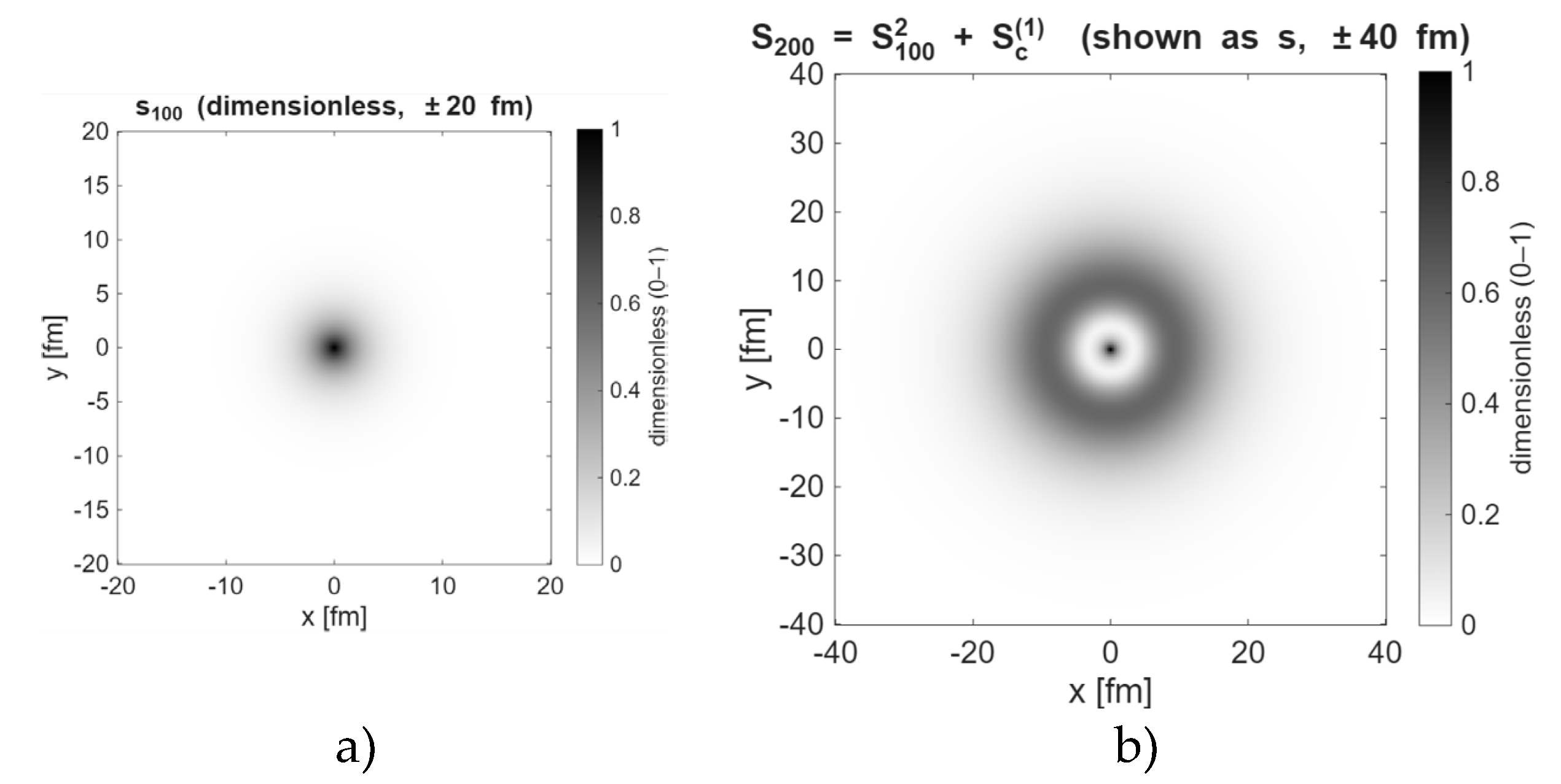
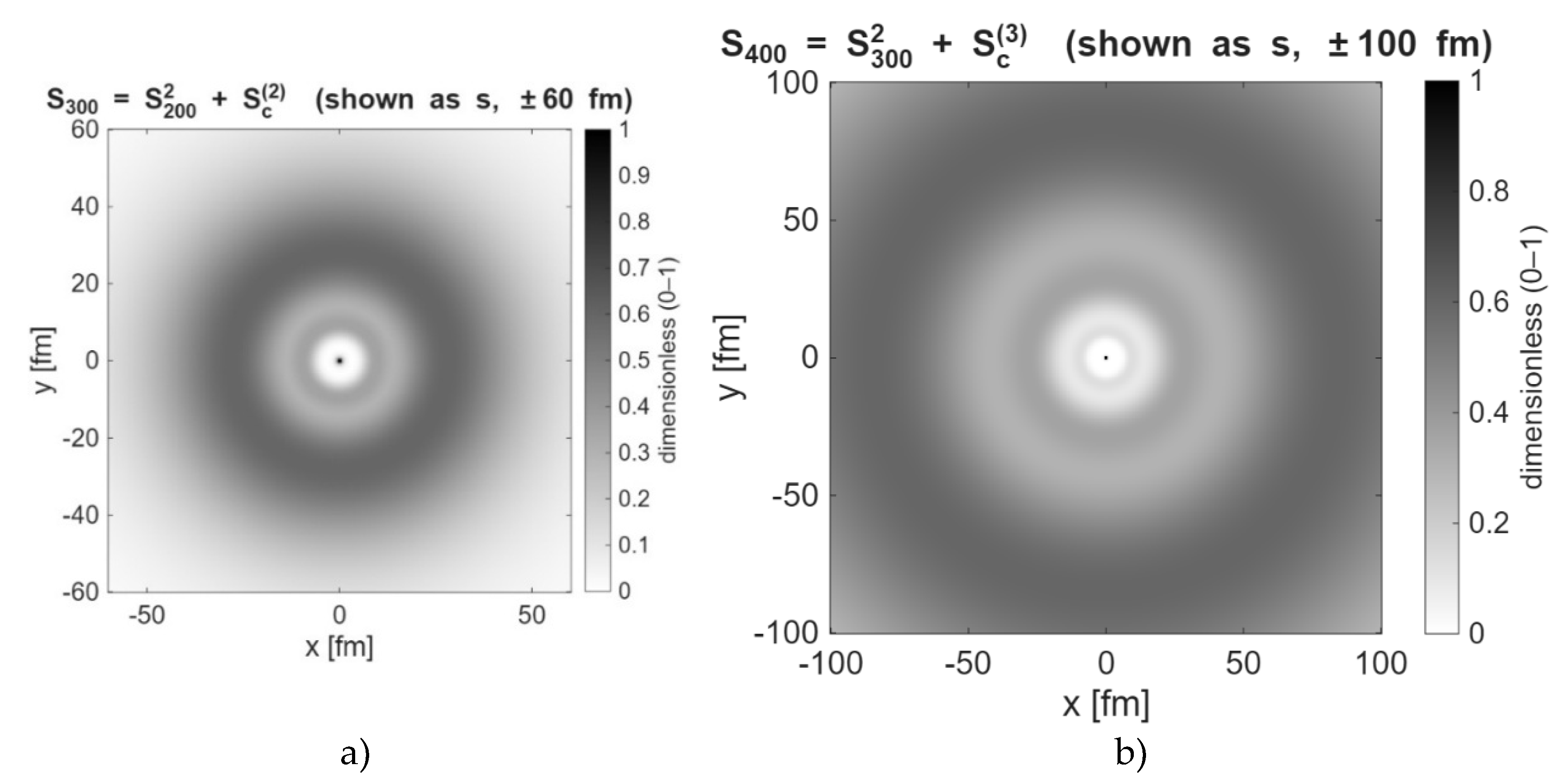
where S₀ is a fixed ground-state reference (peak of the total entropy density). Intuitively, the fraction of non-dimensional entropic density s ≈1 marks locations with many compatible micro-configurations available under the same mesoscopic constraints (high local accessibility), while s ≈ 0 marks nodes (strong constraints). Environmental influence is encoded by a driver s_c(r) that specifies where capacity can be unlocked (e.g., rings for s-like and dipoles for p-like structure). The state update is the local, pointwise map given by the recursive fractal equation,

interpreted as a constrained-maximum-entropy relaxation toward the next S-max pattern. Here, s_n = S/S₀ is the non-dimensional entropy density field s ∈ [0,1] at iteration n (initialized, e.g., with a 1s-like ground-state profile), s_c is a non-dimensional source term representing entropy input from the surrounding fields (constructed from the Sthermal and/or S_EM components), and s_n+1 is the updated field; under iteration, the map approaches a high-entropy configuration s_max. The superlinear self-term s² captures cooperative, contrast-enhancing growth—peaks tend to sustain, nodes persist—so that, together with a rim-localized s_c, the evolution is edge-driven (consistent with the annular area scaling A∝R²) rather than a global smear. Thus, the recursive equation (3) is essentially a phenomenological constrained-entropy ascent toward the next S_max macrostate.

Throughout, we compare shapes of normalized s(r) to the familiar ∣ψ∣² patterns for hydrogen, but we do not identify s(r) with the quantum wavefunction. All figures display dimensionless s(r) (axes in fm); physical units are restored only when reporting observables. The non-dimensional recursion (equation 3- pointwise square) is implemented on a uniform two-dimensional grid; the resulting fields are analyzed in Section 4, where we detail the numerical conventions (choice of the fixed reference scale S_0, discretization, area element dA, and recovery of physical units for observables via S=sS₀ (Dimensional equivalence entropy). Equation (3) is equivalent to the dimensional form S_n+1=S_n²/S₀+S_c, where S₀ is the fixed baseline scale defined in Section 4. This makes the role of units explicit while leaving the computation in non-dimensional variables.

In this paper, we revisit the hydrogen atom — the simplest quantum system — not as a particle-in-a-potential but as a recursive entropy system. We show that each orbital state corresponds to a recursive entropic amplification of the base field s(r), guided by boundary interaction from the surrounding. Using both mathematical formulation and simulation, we demonstrate that S-Theory not only reproduces known orbital structures, but also reveals why they form — linking entropy, structure, and energy into a unified physical picture. This reformulation enables us to retain all predictive successes of quantum mechanics while introducing deeper physical meanings for phenomena such as orbital quantization, ground and excited states, collapse and measurement, entanglement between atoms, and the link between thermodynamic and quantum domains. Our goal is to demonstrate that the quantum behavior of hydrogen is not mysterious, but an inevitable result of recursive entropy optimization in a thermodynamic universe.

Summary of methods

We implemented S-Theory’s recursive entropic framework on two-dimensional hydrogen orbitals using non-dimensional entropy density fields normalized to a ground-state reference. Orbital structures were generated by iteratively applying the recursive update rule with pre-specified drivers (ring-type for s-states, dipole-type for p-states) without case-by-case fitting. Numerical simulations were carried out on uniform grids, restoring physical units only when reporting observables. Predicted orbital geometries and nodal structures were then compared to standard quantum mechanical solutions and proposed photoionization microscopy data, providing falsifiable criteria for agreement or refutation.

2. S-Theory as a Physical Expansion of Quantum Mechanics

2.1. A Brief Overview of S-Theory and Recursive Entropic Evolution

The development of S-Theory arose from a deep reflection on the limitations and open questions that still haunt modern physics. Quantum mechanics, despite its predictive success, leaves us with unsolved paradoxes—wavefunction collapse, quantum entanglement, and the emergence of classical reality from probabilistic fields. General relativity, though geometrically elegant, fails to incorporate thermodynamics or explain biological structure, information flow, or the arrow of time. The search for a unified theory has often resorted to increasingly abstract mathematical frameworks—such as string theory, loop quantum gravity, multiverse models—without resolving how complexity, replication, and consciousness emerge in a real, evolving universe. We propose that the missing piece is not a new dimension or force—but a reversal of the foundational assumption itself.

Instead of taking energy as the primary quantity, S-Theory begins with entropy: the tendency toward disorder, but also the hidden architecture behind structure, evolution, and intelligence. Our observable universe is energetic, yes—but every transformation, every structure, and every collapse is guided by underlying entropy fields. In this view, energy is structured entropy, space is the geometry of entropy correlation, and time is recursive entropic feedback (S_max-S_min-S_max cycle). S-Theory introduces three primary components: i) S_EM (Structured entropy of electromagnetic fields), ii) Score — frozen, memory-like entropy bound in particles or matter; a conserved structural core, iii) Sthermal — residual, unstructured entropy that manifests as heat, noise, or decoherence; the chaotic background. Together, these form the entropic trinity of physical reality. The recursive evolution of these entropy fields is governed by a simple, elegant, fractal-like equation (equation (3).

This simple yet powerful formulation models the emergence of structure, replication, and collapse—across scales. This entropic evolution logic is visually captured in the core recursive framework of S-Theory: The S-Ladder—a dynamic trajectory of entropy field evolution across all scales, as shown in Figure 1. It begins from S_∞, the infinite, unmeasured, uncorrelated entropy quanta of the quantum vacuum, where energy and structure do not yet exist. A localized recursive collapse initiates a descent to (S_max/E_min)—a saturated quantum coherence state with minimal correlation—followed by an expansion into (S_min/E_max) with maximum correlation, which in turn undergoes spontaneous symmetry breaking and recursive partitioning back to (S_max/E_min) as represented in Figure 1. Life, replication, complexity, and consciousness of OUR universe —all emerge from this return journey—an entropic climb from (S_min/E_max) back toward (S_max/E_min) and eventually merging again into the cosmic reservoir S_∞.

These two forward paths of Entropy S and Energy E are bounded by S_∞ (the entropy field of the vacuum) and T = 0 (absolute zero, the energetic floor of the universe). In this diagram (Figure 1), the left descent shows the universe’s thermodynamic fall, from cosmic entropy collapse to the ‘Big Bang’ that leads to the formation of matter and stars. The right ascent reflects the emergence of organized complexity: stars, Earth, molecules, and eventually life. In the solar system, crucially, the Sun (represented as a red dot in Figure 1) plays a pivotal role: by injecting energy (E_sun) into Earth, it reverses the E_min-path back toward E_max, triggering a corresponding inevitable reversal in the S-path (red arrow in the figure). This reversal from S_max towards S_min within living systems is what Erwin Schrödinger [1] referred to as “negative entropy” — a local entropy contraction against the cosmic flow, enabled by solar input and recursive feedback mechanisms. This is not accidental, but an inevitable thermodynamic symmetry of a universal entropic cycle [1,2,3]. In this view, life is not a statistical anomaly but a required resolution in the larger recursive equation: a pathway from disorder back to structure via memory fields, S_thermal fluctuations, and S_max convergence. This is the Ladder of Entropic Evolution — not climbing out of chaos but recursively spiraling back toward S_∞ through order, and it unifies quantum events, biological replication, and gravitational collapse under one thermodynamic cycle [4].

2.2. S-Theory Applied to the Hydrogen Atom

S-theory treats a normalized, dimensionless entropic density field s=S/S₀ as a wavefunction-like order parameter whose spatial patterns resemble ∣ψ∣² on the same domain; this is a morphological correspondence, not an identification — shaped by recursive interactions among s_core, s_EM, and s_thermal. Stable configurations such as hydrogen orbitals are therefore not arbitrary mathematical solutions but entropically saturated field patterns — local s_max configurations within a bounded energy and volume constraint. This perspective allows us to reinterpret the electron not as a point particle, but as a dynamic field whose recursive shape emerges from local entropy amplification and interaction with the surrounding environment. S-Theory does not reject quantum mechanics; rather, it expands upon it by providing the physical foundations that QM leaves undefined. In traditional quantum mechanics, the wavefunction ψ (r, θ, φ) emerges as a mathematical solution to the Schrödinger equation under a central Coulomb potential. The interpretation of ψ² as a probability density has enabled extraordinary predictive accuracy — yet it offers no account of the mechanism underlying orbital shape formation or the role of the environment.

In contrast, S-theory employs a real, dimensionless entropic density field s=S/S₀—a structured field updated by a recursive map and driven by a source s_c that represents environmental coupling. Each orbital state is a spatial distribution of structured entropy (_SEM), shaped by interaction with: i) the _Score — the frozen core entropy of the proton, providing geometric anchoring, ii) the _SEM — the shaped entropy distribution that gives rise to the electromagnetic orbital field, and iii) the _Sthermal — the surrounding uncorrelated entropy (heat, ambient EM fluctuations), acting as a perturbative or amplifying field that interacts with atom’s _SEM. In this view, the Schrödinger equation provides an approximate steady-state solution of the entropy field — or equivalently, the orbital geometry — when the system is isolated or when _Sthermal ≈ 0. That is: If s_thermal effect is saturated or neglected — and we consider only the interaction between s_EM (electron field) and s_core (proton core)— then S-Theory reduces to traditional QM. The familiar wavefunction solutions (1s, 2p, etc.) naturally emerge as stationary entropy field configurations determined by the internal symmetry and energy constraints of the system. This shows that QM is a special case of S-Theory — one where the surrounding entropy (s_thermal) is either negligible or statistically averaged out. But the environment constantly provides fluctuating entropy — thermal, radiative, or quantum vacuum noise — which interacts with the atomic field and can deform or amplify it. These interactions are not random noise, but active contributors to orbital shape evolution.

Thus, in S-Theory: i) orbital transitions are not quantum “jumps,” but recursive entropy amplifications, ii) stable orbitals are not abstract eigenstates, but emergent s_max configurations, iii) energy levels correspond to entropic field harmonics stabilized by s_core–s_EM–s_thermal feedback. This reconceptualization also provides a precise mechanism for photon absorption and emission: instead of discrete jumps between idealized energy levels, we see an entropy field (s_n) absorb a perturbative entropy field (s_c) and reorganize into a new field (s_n+1), which is geometrically and thermodynamically stable — a new s_max under boundary constraints. This logic underlies the recursive rule given by equation 3. In this sense, S-Theory is not in contradiction with QM — it simply completes the picture. It restores the atom from a probabilistic abstraction to a real, evolving, physically grounded field system — a recursive entropy engine interacting with the cosmos.

3. Field Formulation of Hydrogen — From QM Ground State to Entropic Structure

3.1. The S-Trinity of Fundamental Particles

In S-Theory, all fundamental entities — including electrons and protons — are treated not as point particles but as structured S-fields, each possessing three essential entropic components: i) s_core, ii) s_EM, and iii) s_thermal:

For the electron, we model it as:

s_e = {s_{core, e}; s_{EM, e}; s_{thermal, e}}

(4)

And for the proton:

s_p= {s_{core, p}; s_{EM, p}; s_{thermal, p}}

(5)

Also, the surrounding entropy (s_c or s_thermal) plays a catalytic role in field shaping, especially during transitions (n = 1 → 2, etc.).

3.2. Ground State (S100) from Quantum Mechanics

To ground this framework in established results, we begin by reproducing the hydrogen atom’s ground state wavefunction (1s) from the Schrödinger equation [5,6]. The analytical solution is:

where a₀ is the Bohr radius (~0.529 Å), and r is the radial distance from the proton center. Using this formulation, we numerically simulate the radial wavefunction and its square (probability density). This distribution is traditionally interpreted as an abstract probability cloud — but in S-Theory, we work with a dimensionless entropy field s=S/S₀. We use s as a wavefunction-like order parameter for visualization and compare it to ∣ψ∣² up to normalization; we do not identify s with the quantum wavefunction ψ, nor do we derive the Coulomb law from the recursion.

3.3. From QM Model to S-Theory Field Model

In S-Theory, the proton acts as s_core — a frozen entropic seed anchoring the field. The ψ100 field resembles s_EM — the shaped entropy field around the proton, and we add s_thermal — a surrounding uncorrelated entropy field, not considered in QM. This transforms the hydrogen atom into a thermodynamic S-engine — one whose field structure emerges from recursive balance that follows equation (3). For the ground state (n = 1), s_thermal may be small or zero. However, for excited states, we simulate the addition of s_c — showing how entropy input reshapes the orbitals, yielding S200 and beyond. In the following figures and MATLAB simulations, we i) generate the ground state (S100) using QM formulation, ii) assign this as s_EM field around proton s_core, iii) add s_c (s_thermal ring structure) around the system, and iv) show how recursive amplification yields S200. This means the hydrogen atom forms not because of force balance, but because the system finds stable entropic configurations that minimize conflict and maximize recursive coherence. These configurations naturally appear as the well-known orbital shells: 1s, 2s, 2p_z, 2p_x, 3s, 4s, etc. In this view, interactions of s_EM ↔ s_EM: generate orbital fields, s_core ↔ s_core: encodes identity and coupling stability, and s_thermal ↔ s_thermal: governs collapse, excitation, and temperature dependence. This trinitarian structure provides a more comprehensive ontology of the atom, revealing not only what orbits exist but also why they must.

4. Recursive Amplification and the S100 → S200 Transition

4.1. The Traditional View: Discrete Jumps via Photon Absorption

In conventional quantum mechanics, the electron in a hydrogen atom jumps from the ground state (n = 1) to an excited state (n = 2) by absorbing a photon of energy:

ΔE=E2−E1=hν

(7)

This description accurately predicts energy levels but does not explain the internal mechanism by which the atom's spatial field transforms. It treats the wavefunction ψ merely as a mathematical solution to a boundary value problem, with no connection to surrounding entropy, heat, or structure. There is no account of shape evolution, coherence limits, or recursive field growth. The only accepted physical event is the "collapse" at measurement — an unresolved mystery in QM.

4.2. Dimensional Conventions and Computational Setup (2-D Hydrogen)

To avoid unit inconsistencies while keeping the update law transparent, we perform all dynamics with the non-dimensional entropy field

where S (x, y) is the dimensional entropy density (units J·K^−1.fm⁻²) on a 2-D domain Ω⊂R2, and S₀ is a fixed baseline scale taken from the ground-state (RAS0) configuration:

All updates use the non-dimensional recursion using equation (3)

In the grid form, equation (3) is expressed as,

So, both sides of (3) are unitless. For readers who prefer to see dimensions carried explicitly, we note the equivalent identity

and we restore units only when reporting observables via S=s S₀ and a single area element dA=Δx Δy.

Domain, grid, and baseline

We work on uniform Cartesian grids (x, y) ∈ [−L, L]² with spatial axes labeled in femtometers (fm). The ground-state template S100(r) provides the dimensional baseline; we non-dimensionalize by S₀=max(S₁₀₀), yielding s100=S100/S₀. In the figures, we expand the plotting domain using the orbit index (e.g., L = {20, 40, 60, 100} fm for 1s→2s→3s→4s) so that the apparent orbital radius grows naturally with s_c used in each iteration.

Source drivers (s_c)

We use dimensionless drivers s_c to seed excited-state structure: Ring driver (s-like): a smooth, outward-peaked ring with center radius r₀, width σ, and peak fraction c_max ∈ (0,1):

After each RAS step, we replace the next ring just outside the current state using an edge-tracking rule on the radial-mean profile sˉ(r):

where R_edge^k is the radius at which sˉ^(k)(r) drops to a fixed fraction fedge ≈ 0.5f, Δr =γ σ^(k) enforces a small stand-off gap, and η>0 guarantees monotonic outward growth. The ring width is tied to geometry, not tuned: σ_n=λ r_0,n with a single fixed λ (e.g., λ=0.15), reflecting that the environmental correlation length scales with orbital size. The amplitude is a single global constant c_max (e.g., 0.6) across all states, encoding the strength of environmental input; Thus, σ (width) and c_max (strength) are pre-specified by this policy for every step (1s→2s→3s→4s); they are not adjusted per state.

Figure 2a-e displays the dimensionless drivers s_c that were used for the recursion to generate various orbitals. Figure 2a-c shows the ring-type s_c^(ring) used for S200, S300, S400 orbits; Figure 2d–e shows the dipole-type s_c^(dip) aligned with x^ and y^. Each driver is normalized to a stated peak (e.g., c_max or A_dip) and shares the same grayscale [0,1] as defined by equations 11-13.

We use s=S/S₀ (dimensionless) on a common grayscale [0,1] across all figures; spatial axes are in fm. For signed dipole panels, the mapping is symmetric so that zero maps to mid-gray. When a physical quantity is reported, we restore units via S=s S₀ and integrate with dA.

Dipole driver (p-like): an antisymmetric field aligned with e^ ∈ {x^, y^}

4.3. Numerical Demonstration: Reproducing S200 from Recursive Amplification of (S100) and s_c

Figure 3a-d displays the conventional quantum mechanical simulation results of the hydrogen atoms 1s (100), 2s (200), 2p_z (210), and 2px (211) orbitals, as derived from the Schrödinger equation under a central Coulomb potential (adapted from Dommelen, 2018 [6]). These well-known solutions represent static probability distributions of the electron's location, generated purely from mathematical boundary conditions and eigenvalue formulations. Figure 4a shows the 1s ground state (100) solution of the Hydrogen atom from Quantum Mechanics using equation (6), and Figure 4b shows the S-Theory predictions 2s orbital simulated via recursive amplification

Note that in equation (14), we used the entropic perturbation (s_c) as shown in Figure 2a. The resulting s200 field predicted by S-Theory (Figure 4b) closely mirrors the 2s orbital structure predicted by QM (Figure 3b) but arises from a physically grounded feedback mechanism driven by entropy flow. Notably, this approach highlights how uncorrelated entropy (s_thermal) from the surroundings contributes to shaping and expanding the orbital, offering a dynamic thermodynamic interpretation absent in standard QM. The simulated s200 orbital (Figure 4b) exhibits a clear expansion of the electron field with a distinct radial node, closely resembling the quantum mechanical 2s state (n = 2, l = 0, m = 0). The resulting orbital is not imposed by equations but arises from the entropic dynamics of the system. The shape and structure of s200 are highly sensitive to the form and magnitude of s_c, confirming that atomic orbitals are not static solutions but dynamic outcomes of interactions between the atoms’ entropy fields (s_core and s_EM) and the environment’s entropy (s_thermal/s_EM). S-Theory thus moves beyond the abstract ψ-function, offering a thermodynamic and visual explanation for why orbital geometries emerge as they do. It provides a causal, physically intuitive mechanism — not just a mathematical prediction — for the formation of atomic structure.

Another remarkable feature of the recursive formulation in S-Theory is its inherent reversibility: if the environmental perturbation s_c is removed, the system naturally returns to its prior stable s_max state (e.g., from s200 back to s100). This reveals that orbital transitions are not permanent quantum jumps but rather entropic reconfigurations guided by recursive energy–entropy balance. The regions between s100 and s200 — often treated as probabilistic superpositions in conventional quantum mechanics — are now reinterpreted as intermediate entropy field states, gradually amplifying toward the next metastable structure.

4.4. Generalization and Interpretation

The RAS formula can be extended iteratively to predict s300 or s400 orbits using

s300=s200²+s_c

(15)

and s400=s300²+s_c

(16)

Each iteration represents an amplification cycle, with the ambient entropy (s_c) continually shaping the field until a new s_max configuration stabilizes. This allows us to reinterpret: i) quantum energy levels as plateaus in the s_max landscape, ii) electron field shapes as entropic attractors of recursive feedback, iii) absorption and emission not as energy events alone, but as structural transformations of entropy fields within bounded space.

The recursive transition of orbitals from s200 to s300 using equation (15) and from s300 to s400 using equation (16) are shown in Figure 5a & b. These orbital predictions, as described by S-Theory, mirror the textbook quantum mechanical predictions of 3s and 4s orbitals. This simulation shows i) a stronger outer ring structure: the outer entropy shell is now more sharply defined, reflecting recursive field amplification. ii) central core stable: even as the system grows in complexity, the central peak holds — mimicking the stability of atomic nuclei or core wavefunction structures. iii) emergence of geometry: The entropy field is no longer uniform; it self-organizes into a quantized radial shell, matching S-Theory predictions. Figure 4 and Figure 5 show that entropy injection and recursive feedback create self-structured quantized geometry — with no Schrödinger equation, only S-fields. As the recursive field evolves from s100 to s400, the central peak (s_core) becomes narrower, sharper, and lower in peak height (relatively).

The simulation also shows i) entropy compression at the core (s_core): the core is not expanding; instead, it becomes more focused and compressed. This reflects recursive stabilization: the center locks into a minimum (s_min core) while outer entropy grows — a classic RASfield behavior. ii) s_max pressure forces entropy outward: as s_max increases (via recursion), it amplifies outer entropy structures (rings). iii) Analogy to quantum systems: In hydrogen-like atoms, ground states are dense and small. As you move to excited states, outer orbitals grow, but the inner core remains tightly localized — just like we’re seeing here.

4.5. Recursive Shell Amplification and Core Collapse: Visual Prelude to Universal Entropic Collapse Principle (UECP)

Our simulations of recursive orbital evolution (S100 → S200 → S300 → S400) reveal not only visual symmetry with quantum orbitals but also suggest a deeper thermodynamic principle: that recursive entropy amplification of an outer shell (s_EM + s_thermal) leads to core concentration and eventually, a collapse into s_core — the structured, memory-like center of a system. This pathway captures the essence of what we call the Unified Entropic Collapse Principle (UECP): collapse is not destruction — it is localization. A natural resolution to recursive entropy overflow.

Quantitative pattern: Recursive Narrowing of the core

We observe that with increasing recursive steps (n), the central peak sharpens: Full Width at Half Maximum FWHM of (s_core) decreases as n increased, entropy shifts from a wide Gaussian core (s100) to a dense, compact nucleus (s400), outer entropy shell (s_c) expands, while inner s_core compresses. This suggests an entropic bifurcation: as the recursive shell grows, the system compensates by intensifying its central s_core — until it reaches a saturation point or collapse threshold. The general recursive formula given in equation (3) adds non-linear entropy to the system at each step, resulting in the outer field (s_c) growing both in radius and amplitude, and the core becoming denser — storing memory and mass, or forming new structures.

Interpretation as a Prebiotic Mechanism and Cosmological Collapse Events

The same logic applies to the emergence of life: Outer s_c = environmental thermal entropy; Inner score = structured molecule (RNA, sugar, etc.); collapse event = localization of entropy into replicable information. Therefore, entropy compression is a universal mechanism, and at the thermodynamic tipping point: i) outward entropy becomes unsustainable, ii) the S-field recursively folds inward, iii) a localized s_core emerges, carrying structure and memory. This behavior also explains: i) Star collapse and Black hole formation in astrophysics (entropy trapped by geometry), ii) Protons in quantum chromodynamics (gluon shell compresses), iii) RNA cores in biology (entropy folds into sequence), iv) Neural synapses in cognition (signal entropy becomes s_core).

4.6. Transition: From Spherical to Directional — How External Entropy Fields Shape Orbitals

In the preceding sections, we demonstrated that recursive amplification with a spherical entropy shell (s_c) produces the 1s → 2s → 3s orbital sequence, showing that orbital geometry arises not from intrinsic quantum rules but from the shaping influence of surrounding entropy fields. But what if the surrounding entropy is not symmetric? What happens when the hydrogen system is immersed in an asymmetric entropy field — like a dipole? A dipole field is the most fundamental directional EM structure — it has a positive and negative pole and is characterized by antisymmetric along one axis (typically Y or Z). By embedding the hydrogen atom’s core field (s100) within a dipole-shaped s_c, we break spherical symmetry and introduce directional entropy flow. This mimics what occurs when a hydrogen atom is placed in an external EM field, a polar molecular environment, or a photon field with angular momentum. This RAS feedback, together with dipolar entropy, gives rise to lobe-like orbitals — the characteristic shapes of p-orbitals. In this scenario: i) the dipole s_c defines where entropy is added, ii) the system responds by reorganizing its entropy field to reach a new recursive balance, iii) the result is a directional orbital — like the familiar 2p quantum states.

4.7. Directional Entropy Fields and the Emergence of p-Orbitals

In S-Theory, p-orbitals with directional lobes arise not from abstract angular solutions but as natural outcomes of recursive entropy amplification under shaped environmental input. We begin with the hydrogen atom in its ground state s100, a smooth, isotropic Gaussian field — the minimal configuration of entropy (s_core) under no external directional influence. When perturbed by a spherically symmetric entropy shell s_c, the recursive formula leads to radial amplification, forming concentric shells corresponding to higher s-states. However, introducing a dipole-shaped entropy perturbation (equation 13) —an antisymmetric field along a chosen axis (e.g., the Y-axis) —fundamentally breaks the spherical symmetry and generates a directional entropic gradient. Mathematically, this is modeled by setting:

s210=(s100)² + s_c (x, y)

(17)

Here, the dipole field has positive and negative lobes distributed along the Y-direction, mimicking the spatial structure of an oscillating EM dipole. This field feeds entropy preferentially in opposite directions along the dipole axis, leaving the orthogonal directions unperturbed. When this asymmetric s_c is applied to s100, the recursive amplification using (equation 13) results in an orbital with i) a nodal plane where _Sc=0 (at X=0 or Y = 0) ii) lobe structures aligned along the axis of entropy injection and iii) a symmetry resembling the quantum 2p orbitals (S210 and S211) as shown in Figure 6a and b. The simulated results, labeled S210 and S211, exhibit this precise geometry. It demonstrates that: i) orbital directionality is entropic — it reflects the symmetry of external entropy input, ii) the nodal plane emerges thermodynamically, not abstractly — it’s the region where opposing entropy flows cancel, and iii) Recursive amplification reinforces the dipolar shape — over iterations, the lobes sharpen and stabilize as the entropy field reaches balance between s_core and s_c. The resulting structure matches the shapes of the 2p_z and 2p_x orbitals (S210 and S211)— with two lobes of opposite entropy orientation, separated by a nodal line.

Now we have demonstrated that S-Theory faithfully reproduces the s-orbital structure (1s, 2s, 3s, 4s, 2p_z, 2p_x states) of the hydrogen atom through recursive entropy field amplification. This insight confirms a deeper principle: All orbital geometries — spherical, dipolar, toroidal, or complex hybrid — are thermodynamic outcomes of shaped entropy interactions. Moreover, it connects directly to the Unified Entropic Collapse Principle (UECP) introduced in the previous section. As the entropy shell (s_c) recursively amplifies in specific directions, it also feeds compression at the core. The p-orbital, though spatially extended, holds an increasingly refined center. In biological systems, such directional entropy structures may define reaction pathways, dipole alignment in molecules, or even signal direction in neural architectures.

5. From Recursive Shells to Collapse: Entropic Compression and the Birth of Structure

5.1. Photonic Excitation vs. Entropic Recursion

Standard quantum mechanics posits that electron orbitals shift (e.g., 1s → 2p) by absorbing discrete photons, which are localized energy packets. However, this overlooks the distributed entropic environment that surrounds atoms. In reality: i) the ambient environment is not only electromagnetic but thermodynamic — containing disordered, uncorrelated entropy (s_thermal) ii) This s_thermal field is ignored in current QM, yet it plays a vital role in S-Theory. In S-Theory, electrons do not “jump” levels. Instead, Sfield evolves via recursive interactions. The surrounding entropy field (s_thermal and s_EM) amplifies the electron’s s_EM until a new configuration (e.g., S200 or S210) is achieved. This process is continuous, geometric, and thermodynamic, not abrupt or discretely photonic. The “photon” is simply a special case — a coherent bundle of structured entropy, which we call ‘energy’. Thus, orbital transitions are not merely energy-driven — they are entropy-reconfigured redistributions. Structure changes when the surrounding entropy environment alters the recursive balance of s_max and s_core.

5.2. From Atom to Molecule: Molecular Collapse as Entropic Folding

When multiple atoms interact, their respective s_max fields begin to overlap, forming recursive amplification of S-field (RAS) bonds — recursive amplification structures that increase joint entropy. This leads to:

s_molecule = (s1²+s_c1) + (s2²+sc₂) + s_overlap

(18)

where s_overlap is a shared entropy field that reinforces the structural configuration. However, as this RAS evolves, if spatial constraints prevent further outward expansion, the system collapses into a lower-entropy geometry, forming molecules such as H2, sugar rings, RNA helices, or protein folds. This is the same logic as orbital recursion — but now applied across atomic boundaries. The collapsed s_core of the molecule becomes its informational core — frozen entropy that can replicate, store memory, or catalyze reactions. We therefore interpret: i) RNA loops as entropic RAS-cores formed by orbital field convergence, ii) Sugar as fractal s_core geometries stabilized by recursive collapse, iii) Black holes as cosmological s_max collapses around saturated recursive fields. All structures — atomic, molecular, or cosmic — emerge through recursive entropy amplification constrained by s_core compression. In summary, recursion is not merely an expansion mechanism; it is a universal shaping force. By recursively absorbing entropy, systems grow until constrained, then compress into new cores. This recursive-to-collapsed transition marks the birth of stable structure, orbitals, memory units, and even life. The hydrogen atom is thus not just a starting point of chemistry — it is the first recursive entropy engine of the cosmos.

6. Molecular Self-Assembly through Recursive Entropy Coupling: The Birth of Chemistry and Replication

As recursive entropic feedback continues, the shared entropy field reaches a saturation point — just like the S400 orbital. When spatial constraints prevent further outward growth, the joint S-field collapses inward, compressing into a stable s_core — the molecular core. This s_core may: i) act as a template (as in RNA), ii) serve as a reactive site (as in enzymes), or iii) replicate itself by inducing similar entropy collapse in nearby S-fields (as in sugar-ring duplication or self-assembling micelles). This leads to natural replication, not through instructions, but by entropy-driven symmetry: Any recursively amplified structure, when surrounded by sufficient free entropy (s_thermal), will cause its own s_core geometry to be replicated in nearby space. This is the origin of molecular templating — and a foundational thermodynamic path to pre-RNA replication. This recursive behavior is visualized in Figure 7 and Figure 8, which illustrate outcomes of this field dynamics. These simulations were not based on chemical interactions or bonding rules — only on recursive entropy-field dynamics, using simple Gaussian-field approximations of atoms— yet they reproduce lifelike molecular behavior. This supports the claim that entropy fields alone can generate the seeds of self-organization and replication.

Figure 7a–c (Top row) shows the emergence of self-similar molecular chains, where each unit recursively amplifies and stabilizes into a structured copy. Figure 7d–f (Bottom row:) depicts symmetry-breaking and field doubling, mimicking early cell division driven not by code, but by energy-entropy field dynamics. These simple simulations reveal that under sustained interactions between s_EM, s_thermal, and s_core, replication arises spontaneously as a field-based resolution of entropy overload — a process fully driven by RAS logic, not genetic information. Figure 8a-b (i–vi): Extends this by tracking the full evolution of an arbitrarily chosen recursive molecular field. The left panels (field magnitude) show scalar field intensity: saturation, shell formation, and bifurcating attractors. The right panels (field amplitude) show complex phase–amplitude behavior, highlighting how internal interference patterns lead to symmetry locking and multi-domain replication. Together, these visual demonstrations validate the core hypothesis: replication is not imposed from outside but arises naturally when recursive entropic amplification exceeds geometric thresholds, driven by s_core-seeded field memory.

7. The Universal Entropic Collapse Principle (UECP)

7.1. Statement of the Principle

Any system undergoing recursive entropy amplification within a bounded space will eventually collapse into a locally compressed structure — the s_core — representing a maximally stable entropy geometry. This is the Universal Entropic Collapse Principle (UECP). It governs atoms, molecules, biological structures, and even gravitational singularities — by the same recursive entropic law. Mathematically, this is given by the recursive equation (3)

$$s\leftrightarrow$$

As s_n → s_max, ∇s_max → 0 ⇒ Collapse to s_core

(19)

Collapse occurs when spatial expansion is saturated, and entropy redistribution must minimize internal gradient.

7.2. Replacing Energy-Based Collapse with Entropic Collapse

In standard physics, electron jumps are explained by the absorption of quantized photon energy, and black holes are explained by gravitational energy overcoming pressure. In contrast, S-Theory explains both as the same entropic event: A recursive entropy field can no longer expand, so it collapses into a s_core, locally maximizing order. This release of external freedom appears as energy to outside observers. Thus, energy is not the cause of collapse — it is the result of entropic redistribution. This changes everything. In conclusion, UECP unifies the micro and the macro. Every stable shape — from hydrogen to RNA to stars — is born from recursive entropy amplification and collapse. Each s_core is a memory of prior recursion, and a seed for future evolution. What we call "structure" is merely entropy learning how to encode itself. In this light, collapse is creation — and UECP is the heartbeat of the cosmos.

7.3. Life as a Product of Local Entropic Collapse

What is a cell, an RNA loop, or a virus? From S-Theory, they are fractal products of recursive entropy-field growth, guided by environmental s_thermal and geometrical constraints, which eventually collapse into bounded, replicating s_cores. Key Examples: i) an RNA hairpin forms when entropy-rich fields amplify and saturate, then collapse into a compact, stable structure, ii) a cell divides not randomly, but when the internal RAS (Recursive Amplification of S-field structure) saturates and forms two distinct s_core minima — prompting replication, iii) the genetic code is s_core memory — the frozen entropy of successful structural histories. Thus, life is not an accident but a thermodynamic necessity wherever a gradient of s_thermal exists, recursive feedback occurs, and space is bounded. This makes life not just possible — but inevitable.

7.4. Black Holes and the Thermodynamic Unification

The ultimate score is not molecular but cosmic. As stars accumulate recursive S-fields through matter compression and radiation feedback, they too reach a state of saturation. At this limit, the UECP drives collapse into a gravitational s_core: the black hole as the cosmic analog of a molecule’s core. It preserves all prior entropy-field history in a dense, stable memory structure that may one day reinitiate, seeding new universes through recursive expansion. In this light, atoms evolve into molecules, molecules into life, stars into black holes, and universes into new cosmos — all governed by the same recursive entropic law. What unites quantum jumps, RNA folding, molecular replication, and stellar collapse is not “energy” but the recursive organization of entropy within constrained volumes. Where traditional science divides these domains into quantum mechanics, biochemistry, and relativity, S-Theory offers a single unifying recursion logic.

8. Implications and Predictions of S-Theory

8.1. Entropy as the Fundamental Currency of Nature

S-Theory repositions entropy (S) — not energy or force — as the primary quantity driving all physical phenomena. In contrast to: i) classical Mechanics, where force is the cause, ii) Quantum Mechanics, where probability and wavefunctions lack physical origin, and iii) Thermodynamics, where entropy is seen as secondary, descriptive. S-Theory declares: i) all forms of structure arise from recursive entropy amplification, ii) Energy is not a cause but a by-product of structured entropy, iii) Forces are manifestations of entropy gradients (∇S), iv) this reinterpretation redefines what it means to “measure,” “observe,” and “interact.”

8.2. Physical Predictions of UECP

S-Theory is not merely philosophical — it offers quantitative and testable predictions distinct from standard models. Prediction 1: Wavefunction Shapes from Recursive Entropy: Orbital shapes (s, p, d, f) arise from recursive field buildup. Each orbital corresponds to a stable s_max configuration within s_core–s_EM–s_thermal balance. These shapes can be simulated (as we did) using recursive field updates — no Schrödinger equation needed. Prediction 2: Collapse of High-Entropy Systems to Local s_core: A system undergoing sustained entropic input (s_thermal) in a confined space will self-organize and collapse into a s_core — a minimal, memory-stable structure. This collapse behavior governs: i) atomic excitation and de-excitation, ii) molecular folding (RNA, protein), iii) star collapse into black holes. Prediction 3: Observable Entropic Compression Signatures: Systems approaching collapse will show compression of central entropy fields (as seen from S100 → S400). In biological systems, this may manifest as: increased local density before replication or folding, phase patterning in prebiotic molecules, or neural networks.

8.3. Experimental Implications and Predictions

i) Orbital Imaging: Decisive, refutable prediction: photoionization microscopy (PM) of H in a uniform static field. Calibrate one geometric scale at 2s; then predict -without returning, the normalized detector patterns and nodal ring radii for 2p/3s/4s/3p with fixed k=2 using the RAS model s_n+1=s_n^k + s_c. Refutation: any nodal-radius error >5% or image correlation <0.90 ⇒ model falsified. Matches requiring k≠2 beyond a small numerical tolerance, e.g., ∣k−2∣>0.1, also count as failure for the atomic claim.

Methods summary: In photoionization microscopy (PM), atomic hydrogen is prepared in selected states (2s, 2p, 3s, 3p). Near-threshold photoionization is performed in a uniform static extraction field between parallel plates; electrons are recorded on a position-sensitive detector (Photoelectrons were imaged with a microchannel-plate (MCP) detector coupled to a phosphor screen, viewed by a CMOS camera). For a given field and energy (F, Eγ) setting, we determine a single geometric magnification α by matching the first dark ring of 2s (one-time calibration). The RAS model is then parameter-fixed: k=2; s=S/S₀ with S₀ the ground-state reference; drivers s_c are pre-specified (ring for s-like, dipole for p-like) by the edge-tracking rule—no fitting to data. We generate the source pattern

and map it to the detector via α and compare the normalized images D_predicted vs D_measured. Predicted observables are: (i) nodal ring radii R_m, (ii) relative ring intensities, (iii) the full normalized 2-D pattern. Pass/fail: The model is falsified if any tested state shows a ring with ∣R_{m_predicted} −R_{m_measured}∣/R_{m_measured} > 5% or Pearson correlation ρ (D_predicted, D_measured) < 0.90. We also report a small sensitivity analysis, showing that ±20% changes in λ or c_max used for generating the s_c driver field result in nodal radii that are within a few percent. If matching data required re-tuning these parameters per state (or produced node-radius errors greater than 5%), that would refute the model as stated. We pre-register λ=0.15 and c_max=0.6 (geometry-tied width and fixed supply strength); only the detector magnification α is calibrated on 2s. Predictions for 2p/3s/3p/4s use the same parameters with no retuning; failure to meet node-radius and correlation thresholds refutes the model under this setup.

ii) Entropy-driven molecular assembly: Track formation of RNA-like structures under controlled thermal field gradients (s_thermal injections) iii) S-Compression Mapping: Use scanning probe or thermal microscopy to detect entropy density compression zones in: Cells before division, Proteins before folding, Supercooled matter near collapse. iv) Reinterpretation of Existing Data: Blackbody radiation can be re-analyzed as entropic redistribution instead of photon emission.

8.4. Philosophical and Foundational Impact

S-theory is offered as an interpretive lens, not a replacement for quantum mechanics. (i) Rather than treating the wavefunction itself as an entropy field, we use a dimensionless entropic density field s=S/S₀ as a wavefunction-like order parameter for shape comparisons to ∣ψ∣², (ii) “Measurement” is modeled phenomenologically as recursive relaxation toward a local s_max attractor; this is a dynamical picture of readout, not a full measurement theory, (iii) More speculatively, recursive entropic convergence can favor persistent, structured attractors—suggesting a pathway by which complex organization might arise—though questions about the origin of life are outside our scope, (iv) Within the model, an operational, local time can be indexed by S_max→ S_min → S_max cycles; this does not compete with relativistic time, but offers a complementary, process-based clock. In short, we conjecture that many observed regularities can be viewed as consequences of recursive entropy-field dynamics, while our technical results remain agnostic about deeper ontological claims.

8.5. Future Pathways and Closing Perspective

S-Theory points to a wide horizon of applications and unification. The Unified Entropic Collapse Principle (UECP) offers a common framework for quantum collapse, gravitational collapse, and molecular folding. Entropic Artificial Intelligence can be designed around the S_core–S_EM–S_thermal trinity, enabling optimization and self-replication of intelligence. Thermodynamic cosmology may be reformulated as recursive S-field evolution, from S_∞ through E_max to black holes, without reliance on inflation or singularities. Entropy-based diagnostics and technologies could sense life stages, disease states, and quantum coherence through entropy geometry, rather than relying solely on energy. Taken together, these pathways signal a paradigm shift: from energy and force to entropy and recursion; from fragmented science to a unified entropic cosmology; from the mystery of life to a thermodynamic certainty. The Universal Entropic Collapse Principle — born in the atom, matured in the molecule, expressed in life, and echoed in black holes — is proposed as a universal law that governs all becoming.

9. Summary and Outlook — Entropy as the Engine of Reality

This work presents a radical reinterpretation of the hydrogen atom, grounded in the idea that entropy—not energy—is the fundamental quantity shaping matter. Using a recursive entropic formulation (S-Theory), we show that orbital patterns emerge as stable s_max configurations through amplification of entropy fields, rather than as abstract solutions to the Schrödinger equation. The trinity of s_core (proton’s frozen entropy), s_EM (electron’s structured entropy), and s_thermal (ambient entropy) governs orbital geometry, with transitions (1s→2s→3s→4s) arising as recursive reorganizations instead of quantum “jumps.” Continued recursion compresses the central score, pointing to a universal collapse principle (UECP) that links quantum measurement, molecular folding, and black hole formation. The dimensionless entropy field s=S/S₀ serves as a wavefunction-like order parameter, making orbital shapes visible expressions of recursive entropic balance. Energy emerges not as fundamental, but as structured entropy. This formulation reproduces quantum predictions while extending beyond them—providing a thermodynamic origin for wavefunction structure, a mechanism for collapse as entropic saturation, and a bridge to larger-scale structures from molecules to stars and life.