Nonlocal Boundary Value Problems for Systems of Ordinary Integrodifferential Equations

1. Introduction

Boundary value problems for ordinary differential equations, due to their importance in science and engineering, have been studied extensively by many researchers. Among others, Kiguradze [1] considered the general boundary value problem for a system of linear ordinary differential equations,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dx}{dt}}& =& P\left(t\right)x+q\left(t\right),\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill \mathit{l}\left(x\right)& =& c_0,\hfill \end{array}$$

(2)

where $P\in L([a,b];{\mathbf{R}}^{n\times n})$, $q\in L([a,b];{\mathbf{R}}^n)$, $c_0\in {\mathbf{R}}^n$ and $\mathit{l}:C([a,b];{\mathbf{R}}^n)\to {\mathbf{R}}^n$ is a continuous linear transformation, and the corresponding homogeneous system

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dx}{dt}}& =& P\left(t\right)x,\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \mathit{l}\left(x\right)& =& 0.\hfill \end{array}$$

(4)

He proved that the problem (1), (2) is uniquely solvable if and only if

$$det\mathit{l}\left(Y\right)\ne 0,$$

(5)

where Y is the fundamental matrix of the system (3) satisfying the condition

$$Y\left(a\right)=E,$$

where E is the identity matrix. If (5) holds, then the solution x of the problem (1), (2) has the representation

$$x\left(t\right)=x_0\left(t\right)+{\int }_a^{b}G(t,\tau )q\left(\tau \right)d\tau ,$$

where $x_0$ is the solution of the problem (3), (2) and G is the Greens’ matrix of the homogeneous problem (3), (4).

In this paper, we extend these results to the case of nonlocal boundary value problems for a system of linear ordinary integrodifferential equations,

$$\begin{array}{ccc}\hfill x^{\prime }\left(t\right)-A\left(t\right)x\left(t\right)-G\left(t\right)\eta \left(x\right)& =& f\left(t\right),a\le t\le b,\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill \theta \left(x\right)& =& c,\hfill \end{array}$$

(7)

where

$$x\left(t\right)=\left(\begin{array}{c}{x}_1\left(t\right)\\ ⋮\\ x_n\left(t\right)\end{array}\right),x^{\prime }\left(t\right)={\displaystyle \frac{d}{dt}}x\left(t\right)=\left(\begin{array}{c}{x}_1^{\prime }\left(t\right)\\ ⋮\\ x_n^{\prime }\left(t\right)\end{array}\right),$$

are $n\times 1$ vectors of the unknown functions $x_1\left(t\right),\dots ,x_n\left(t\right)$ and their first-order derivatives, respectively,

$$A\left(t\right)=\left[\begin{array}{ccc}{a}_{11}\left(t\right)& \dots & a_{1n}\left(t\right)\\ ⋮& & ⋮\\ a_{n1}\left(t\right)& \dots & a_{nn}\left(t\right)\end{array}\right],G\left(t\right)=\left[\begin{array}{ccc}{g}_{11}\left(t\right)& \dots & g_{1m}\left(t\right)\\ ⋮& & ⋮\\ g_{n1}\left(t\right)& \dots & g_{nm}\left(t\right)\end{array}\right],$$

are, respectively, $n\times n$ and $n\times m$ matrices of given functions,

$$\eta \left(x\right)=\left(\begin{array}{c}{\eta }_1\left(x\right)\\ ⋮\\ {\eta }_m\left(x\right)\end{array}\right),\theta \left(x\right)=\left(\begin{array}{c}{\theta }_1\left(x\right)\\ ⋮\\ {\theta }_n\left(x\right)\end{array}\right),$$

are $m\times 1$ and $n\times 1$ vectors of the values of the linear bounded functionals ${\eta }_j,j=1,\dots ,m,$ and ${\theta }_i,i=1,\dots ,n,$ on $x\left(t\right)$, respectively, and

$$f\left(t\right)=\left(\begin{array}{c}{f}_1\left(t\right)\\ ⋮\\ f_n\left(t\right)\end{array}\right),c=\left(\begin{array}{c}{c}_1\\ ⋮\\ c_n\end{array}\right),$$

denote a $n\times 1$ vector of given forcing functions and a $n\times 1$ vector of constants, respectively. Also, throughout this paper, $I_n$ denotes the $n\times n$ identity matrix and 0 is used to denote the scalar zero and the all-zero vector or matrix, as appropriate, without confusion.

It is note that, although only integrodifferential equations are investigated here, the Equations (6), (7) are more general and describe various types of nonlocal boundary value problems. Specifically, in the case where the functionals ${\eta }_j$ are integrals with fixed limits of the unknown vector x then (6) is a system of Fredholm Integro-Differential Equations (FIDEs). When the functionals ${\eta }_j$ are values of x at certain fixed points $\check{t}\in [a,b]$ then (6) is a system of Differential-Boundary Equations [2] or Loaded Differential Equations (LDEs) [3]. In the case that ${\eta }_j\equiv 0,j=1,\dots ,m$, or $G\left(t\right)\equiv 0$, then (6) reduces to a system of Differential Equations (DEs).

The boundary functionals ${\theta }_i,i=1,\dots ,n,$ describe classical initial and boundary conditions and nonlocal conditions, which may be mixed and nonseparable conditions, multipoint boundary conditions involving a number of points in $[a,b]$, and integral conditions. They can take the general form

$$\sum _{j=1}^{{\ell }_1}{A}_{j}x\left(t_j\right)+\sum _{j=1}^{{\ell }_2}{B}_j{\int }_{{\xi }_j}^{{\xi }_{j+1}}{C}_j\left(s\right)x\left(s\right)ds=c,$$

where $C_j\left(t\right)$ are $n\times n$ matrices of continuous functions on $[a,b]$, $A_j,B_j$ are $n\times n$ constant matrices, c is an n-dimensional constant vector, $a=t_1<t_2<\dots <t_{{\ell }_1-1}<t_{{\ell }_1}=b$ and $a={\xi }_1<{\xi }_2<\dots <{\xi }_{{\ell }_2}<{\xi }_{{\ell }_2+1}=b$. The necessity and development of non-local boundary conditions in the modeling of complex physical situations is discussed in [4,5,6,7].

We prove existence and uniqueness criteria and provide a formula for the closed-form solution of the problem (6), (7). The analysis is based on the fundamental matrix Z of the homogeneous differential system $x^{\prime }-A\left(t\right)x=0$. From a practical point of view, Z can always computed when the matrix A has constant coefficients and in several cases with variable coefficients. Solvability criteria of general linear boundary value problems for systems of Fredholm-type integrodifferential equations with degenerate kernels by other methods have also been reported in [8,9,10,11]. Closed-form solutions for nth-order FIDEs with nonlocal boundary conditions have been investigated in [12,13]. The exact solution to systems of first-order FIDEs with constant coefficients under general boundary conditions based on the matrix exponential has been studied in [14]. Approximate numerical methods for solving nonlocal boundary value problems for systems of FIDEs can be found in [15,16,17,18] and the references therein.

The paper is organized as follows. In Section 2, the problem is formulated in an operator form in a Banach space and some preliminary results are presented. The main results are given in Section 3 where two key theorems for the solvability of the problem are proved and a symbolic procedure for constructing the solution is presented. In Section 4, several examples are solved to demonstrate the application and effectiveness of the proposed technique. The conclusions are drawn in Section 5.

2. Preliminaries

Let $\mathbb{X}$ denote a Banach space, namely the space of continuous functions $C[a,b]$ or the Lebesgue space $L_p(a,b)$, with $a,b\in \mathbb{R}$.

Let ${\mathbb{X}}_n$ be the n-dimensional vector space of all column vectors $x\left(t\right)={\left(x_1\left(t\right),\dots ,x_n\left(t\right)\right)}^T$ with $x_i\left(t\right)\in \mathbb{X},i=1,\dots ,n$, and ${\mathbb{X}}_n^1$ denote the space all x that have continuous first derivatives $C_n^1[a,b]$ or the Sobolev space $W_{p_n}^1(a,b)$.

Let ${\left[{\mathbb{X}}_n\right]}^{*}$ be the dual space of ${\mathbb{X}}_n$, i.e. the set of all linear bounded functionals ${\varphi }_i$ defined on ${\mathbb{X}}_n$. We denote by ${\varphi }_i\left(x\right)$ the value of ${\varphi }_i$ at $x\in {\mathbb{X}}_n$ and

$$\varphi \left(x\right)=\left(\begin{array}{c}{\varphi }_1\left(x\right)\\ ⋮\\ {\varphi }_n\left(x\right)\end{array}\right),\varphi \left(Z\right)=\left[\begin{array}{ccc}\varphi \left(z_1\right)& \dots & \varphi \left(z_n\right)\end{array}\right]$$

where Z is $n\times n$ matrix of functions with the column vectors $z_1,\dots ,z_n\in {\mathbb{X}}_n$. Note that for any $n\times 1$ constant vector c

$$\varphi \left(Zc\right)=\varphi \left(Z\right)c.$$

(8)

Let the operator $\mathcal{A}:{\mathbb{X}}_n\to {\mathbb{X}}_n$ and $\mathfrak{D}\left(\mathcal{A}\right)$ and $\mathfrak{R}\left(\mathcal{A}\right)$ be its domain and range, respectively. The operator $\mathcal{A}$ is said to be injective or uniquelly solvable if for all $x,y\in \mathfrak{D}\left(\mathcal{A}\right)$ such that $\mathcal{A}x=\mathcal{A}y$, follows that $x=y.$ Recall that a linear operator $\mathcal{A}$ is injective if and only if $ker\mathcal{A}=\left\{0\right\}.$ The operator $\mathcal{A}$ is called surjective or everywhere solvable if $\mathfrak{R}\left(\mathcal{A}\right)={\mathbb{X}}_n.$ The operator $\mathcal{A}$ is called bijective if $\mathcal{A}$ is both injective and surjective.

Definition 1. 

The operator $\mathcal{A}$ is said to be correct if $\mathcal{A}$ is bijective and its inverse ${\mathcal{A}}^{-1}$ is bounded on $\mathfrak{R}\left(\mathcal{A}\right)={\mathbb{X}}_n$.

Definition 2. 

The problem $\mathcal{A}x=f,f\in {\mathbb{X}}_n,$ is said to be well posed and hence uniquely and everywhere solvable, if the operator $\mathcal{A}$ is correct.

Lemma 1. 

Let the operator $\mathcal{A}:{\mathbb{X}}_n\to {\mathbb{X}}_n$ be defined by

$$\mathcal{A}x=x^{\prime }-A\left(t\right)x,\mathfrak{D}\left(\mathcal{A}\right)=\left\{x\in {\mathbb{X}}_n^1\right\},$$

(9)

where $A\left(t\right)$ is a $n\times n$ matrix of functions $a_{ij}\left(t\right)\in \mathbb{X},i,j=1,\dots ,n$, and the boundary functional vector $\widehat{\theta }\in {\left[{\mathbb{X}}_n\right]}^{*}$. Let $Z\left(t\right)$ be a fundamental matrix of the homogeneous equation $\mathcal{A}x=0$ satisfying $\widehat{\theta }\left(Z\right)=I_n$, where $I_n$ denotes the $n\times n$ identity matrix. Then:

(i) 

The operator $\widehat{\mathcal{A}}:{\mathbb{X}}_n\to {\mathbb{X}}_n$ defined by

$$\widehat{\mathcal{A}}x=\mathcal{A}x,\mathfrak{D}\left(\widehat{\mathcal{A}}\right)=\left\{x\in \mathfrak{D}\left(\mathcal{A}\right):\widehat{\theta }\left(x\right)=0\right\}$$

is correct and the unique solution of the equation $\widehat{\mathcal{A}}x=f$ for any $f\in {\mathbb{X}}_n$ is given by

$$x={\widehat{\mathcal{A}}}^{-1}f=Z\left(t\right){\int }_{t_0}^t{Z}^{-1}\left(s\right)f\left(s\right)ds-Z\left(t\right)\widehat{\theta }\left(Z\left(t\right){\int }_{t_0}^t{Z}^{-1}\left(s\right)f\left(s\right)ds\right),$$

(10)

where $t_0$ is a fixed point in $[a,b]$.

(ii) 

In the case that $\widehat{\theta }\left(x\right)=x\left(t_0\right)$,

$$x={\widehat{\mathcal{A}}}^{-1}f=Z\left(t\right){\int }_{t_0}^t{Z}^{-1}\left(s\right)f\left(s\right)ds.$$

(11)

Proof. (i) It is well known that every solution of $\mathcal{A}x=f$ is given by

$$x=Z\left(t\right){\int }_{t_0}^t{Z}^{-1}\left(s\right)f\left(s\right)ds+Z\left(t\right)c,$$

(12)

where c is a column vector of n arbitrary constants. Acting by the vector $\widehat{\theta }$ on both sides of (12) and taking into account that $\widehat{\theta }\left(x\right)=0$ and $\widehat{\theta }\left(Z\right)=I_n$, we obtain

$$\begin{array}{ccc}\hfill \widehat{\theta }\left(x\right)& =& \widehat{\theta }\left(Z\left(t\right){\int }_{t_0}^t{Z}^{-1}\left(s\right)f\left(s\right)ds\right)+c=0,\hfill \\ \hfill c& =& -\widehat{\theta }\left(Z\left(t\right){\int }_{t_0}^t{Z}^{-1}\left(s\right)f\left(s\right)ds\right).\hfill \end{array}$$

Substituting c into (12), we get (10). Since (10) holds for any $f\in \mathfrak{R}\left(\widehat{\mathcal{A}}\right)={\mathbb{X}}_n$ and $\widehat{\theta }$ is bounded it is concluded that ${\widehat{\mathcal{A}}}^{-1}$ is bounded on $\mathfrak{R}\left(\widehat{\mathcal{A}}\right)={\mathbb{X}}_n$ and hence the operator $\widehat{\mathcal{A}}$ is correct.

(ii) Equation (11) follows immediately from (10) since $\widehat{\theta }\left(x\right)=x\left(t_0\right)$. □

3. Main Results

Let the operator $\mathcal{B}:{\mathbb{X}}_n\to {\mathbb{X}}_n$ be defined by

$$\mathcal{B}x=\mathcal{A}x-G\left(t\right)\eta \left(x\right),\mathfrak{D}\left(\mathcal{B}\right)=\left\{x\in {\mathbb{X}}_n^1:\theta \left(x\right)=c\right\},$$

(13)

where the operator $\mathcal{A}$ is defined in (9), $G\left(t\right)$ denotes a $n\times m$ matrix of functions $g_{ij}\left(t\right)\in \mathbb{X},$$i=1,\dots ,n,j=1,\dots ,m$, $\eta \left(x\right)$ is a $m\times 1$ vector of the values ${\eta }_j\left(x\right)$ of the functionals ${\eta }_j\in {\left[{\mathbb{X}}_n\right]}^{*},$$j=1,\dots ,m$ at x, $\theta \left(x\right)$ is a $n\times 1$ vector of the values ${\theta }_i\left(x\right)$ of the boundary functionals ${\theta }_i,i=1,\dots ,n$ at x, and c is vector of n arbitrary constants. Then the problem (6), (7) can be expressed compactly as follows

$$\mathcal{B}x=f,f\in {\mathbb{X}}_n.$$

(14)

We first consider the case with homogeneous boundary conditions $c\equiv 0$. The following theorem provides conditions for the existence and uniqueness of the solution and the solution itself for this problem.

Theorem 1. 

Let Lemma 1 holds. Let the operator ${\mathcal{B}}_0:{\mathbb{X}}_n\to {\mathbb{X}}_n$ be defined by

$${\mathcal{B}}_{0}x=\mathcal{A}x-G\left(t\right)\eta \left(x\right),\mathfrak{D}\left({\mathcal{B}}_0\right)=\left\{x\in {\mathbb{X}}_n^1:\theta \left(x\right)=0\right\}.$$

(15)

Then:

(i) 

The operator ${\mathcal{B}}_0$ is injective if and only if

$$detW=det\left[\begin{array}{cc}\theta \left(Z\right)& \theta \left({\widehat{\mathcal{A}}}^{-1}G\right)\\ -\eta \left(Z\right)& I_m-\eta \left({\widehat{\mathcal{A}}}^{-1}G\right)\end{array}\right]\ne 0,$$

(16)

where W is a square matrix of order $n+m$ and the inverse operator ${\widehat{\mathcal{A}}}^{-1}$ is given in Lemma 1.

(ii) 

When (16) holds, the unique solution of the problem ${\mathcal{B}}_{0}x=f$ for any $f\in {\mathbb{X}}_n$ is given by

$$\begin{array}{ccc}\hfill x& =& {\mathcal{B}}_0^{-1}f\hfill \\ & =& {\widehat{\mathcal{A}}}^{-1}f-\left[\begin{array}{cc}Z\left(t\right)& {\widehat{\mathcal{A}}}^{-1}G\left(t\right)\end{array}\right]W^{-1}\left(\begin{array}{c}\theta \left({\widehat{\mathcal{A}}}^{-1}f\right)\\ -\eta \left({\widehat{\mathcal{A}}}^{-1}f\right)\end{array}\right).\hfill \end{array}$$

(17)

Proof. (i) Assume that $detW\ne 0$. Let the element $x\in ker{B}_0$. Then

$$\begin{array}{ccc}\hfill {\mathcal{B}}_{0}x& =& \mathcal{A}x-G\left(t\right)\eta \left(x\right)\hfill \\ & =& \mathcal{A}\left(x-Z\left(t\right)\widehat{\theta }\left(x\right)\right)-G\left(t\right)\eta \left(x\right)\hfill \\ & =& \widehat{\mathcal{A}}\left(x-Z\left(t\right)\widehat{\theta }\left(x\right)\right)-G\left(t\right)\eta \left(x\right)=0,\hfill \end{array}$$

(18)

since $\mathcal{A}\left(Z\left(t\right)\widehat{\theta }\left(x\right)\right)=0$ and the element $y=x-Z\left(t\right)\widehat{\theta }\left(x\right)\in \mathfrak{D}\left(\widehat{\mathcal{A}}\right)\subset \mathfrak{D}\left(\mathcal{A}\right)$ because $\widehat{\theta }(x-Z{\widehat{\theta }}_0\left(x\right))=\widehat{\theta }\left(x\right)-\widehat{\theta }\left(Z\right)\widehat{\theta }\left(x\right)=\widehat{\theta }\left(x\right)-I_n\widehat{\theta }\left(x\right)=0$ by using (8) and the relation $\widehat{\theta }\left(Z\right)=I_n$.

Multiplying (18) by ${\widehat{\mathcal{A}}}^{-1}$ and rearranging terms we get

$$x=Z\left(t\right)\widehat{\theta }\left(x\right)+{\widehat{\mathcal{A}}}^{-1}G\left(t\right)\eta \left(x\right).$$

(19)

Acting on (19) by the boundary functional vector $\theta$ and using (8) we get

$$\theta \left(x\right)=\theta \left(Z\right)\widehat{\theta }\left(x\right)+\theta \left({\widehat{\mathcal{A}}}^{-1}G\right)\eta \left(x\right),$$

and from (15)

$$\theta \left(Z\right)\widehat{\theta }\left(x\right)+\theta \left({\widehat{\mathcal{A}}}^{-1}G\right)\eta \left(x\right)=0.$$

(20)

Furthermore, acting on (19) by the functional vector $\eta$ and making use of (8) we obtain

$$\eta \left(x\right)=\eta \left(Z\right)\widehat{\theta }\left(x\right)+\eta \left({\widehat{\mathcal{A}}}^{-1}G\right)\eta \left(x\right),$$

and hence

$$-\eta \left(Z\right)\widehat{\theta }\left(x\right)+\left[I_m-\eta \left({\widehat{A}}^{-1}G\right)\right]\eta \left(x\right)=0.$$

(21)

From (20) and (21) we construct the system of algebraic equations

$$\left[\begin{array}{cc}\theta \left(Z\right)& \theta \left({\widehat{\mathcal{A}}}^{-1}G\right)\\ -\eta \left(Z\right)& I_m-\eta \left({\widehat{\mathcal{A}}}^{-1}G\right)\end{array}\right]\left(\begin{array}{c}\widehat{\theta }\left(x\right)\\ \eta \left(x\right)\end{array}\right)=0,$$

(22)

or

$$W\left(\begin{array}{c}\widehat{\theta }\left(x\right)\\ \eta \left(x\right)\end{array}\right)=0,$$

(23)

where W is as in (16). Since $detW\ne 0$ it follows from (23) that $\widehat{\theta }\left(x\right)=0$ and $\eta \left(x\right)=0$, so from (19) it is implied that $x=0$ and hence $ker{\mathcal{B}}_0=\left\{0\right\}$, i.e. ${\mathcal{B}}_0$ is injective.

Conversely, let $detW=0$. Then there exists a nonzero constant vector $(c_{\theta }^T,c_{\eta }^T)=(c_{{\theta }_1},\dots ,c_{{\theta }_n},c_{{\eta }_1},\dots ,c_{{\eta }_m})$ such that

$$W\left(\begin{array}{c}{c}_{\theta }\\ c_{\eta }\end{array}\right)=0.$$

(24)

Consider the element $y=Z\left(t\right)c_{\theta }+{\widehat{\mathcal{A}}}^{-1}G\left(t\right)c_{\eta }\in \mathfrak{D}\left(\mathcal{A}\right)={\mathbb{X}}_n$ and note that $y\ne 0$ since $ker\mathcal{A}\cap \mathfrak{D}\left(\widehat{\mathcal{A}}\right)=\varnothing$[19]. Moreover, $y\in \mathfrak{D}\left({\mathcal{B}}_0\right)$ since from (24)

$$\theta \left(y\right)=\theta \left(Z\right)c_{\theta }+\theta \left({\widehat{\mathcal{A}}}^{-1}G\right)c_{\eta }=0,$$

and also

$$\begin{array}{ccc}\hfill {\mathcal{B}}_{0}y& =& \mathcal{A}y-G\left(t\right)\eta \left(y\right),\hfill \\ & =& G\left(t\right)\left[-\eta \left(Z\right)c_{\theta }+\left[I_m-\eta \left({\widehat{\mathcal{A}}}^{-1}G\right)\right]c_{\eta }\right]=0.\hfill \end{array}$$

(25)

This means that $y\in ker{\mathcal{B}}_0$ and hence the operator is not injective. Thus ${\mathcal{B}}_0$ is injective if and only if $detW\ne 0$.

(ii) We consider the nonhomogeneous system

$${\mathcal{B}}_{0}x=\mathcal{A}x-G\left(t\right)\eta \left(x\right)=f,f\in {\mathbb{X}}_n.$$

Then

$$\mathcal{A}x-G\left(t\right)\eta \left(x\right)=\widehat{\mathcal{A}}\left(x-Z\left(t\right)\widehat{\theta }\left(x\right)\right)-G\left(t\right)\eta \left(x\right)=f,$$

(26)

since the element $y=x-Z\left(t\right)\widehat{\theta }\left(x\right)\in \mathfrak{D}\left(\widehat{\mathcal{A}}\right)\subset \mathfrak{D}\left(\mathcal{A}\right)$. Multiplying (26) by ${\widehat{\mathcal{A}}}^{-1}$ and solving with respect to x we get

$$x={\widehat{\mathcal{A}}}^{-1}f+Z\left(t\right)\widehat{\theta }\left(x\right)+{\widehat{\mathcal{A}}}^{-1}G\left(t\right)\eta \left(x\right).$$

(27)

Acting on (27) by the boundary functional vector $\theta$ we get

$$\theta \left(x\right)=\theta \left({\widehat{\mathcal{A}}}^{-1}f\right)+\theta \left(Z\right)\widehat{\theta }\left(x\right)+\theta \left({\widehat{\mathcal{A}}}^{-1}G\right)\eta \left(x\right),$$

and from (15)

$$\theta \left(Z\right)\widehat{\theta }\left(x\right)+\theta \left({\widehat{\mathcal{A}}}^{-1}G\right)\eta \left(x\right)=-\theta \left({\widehat{\mathcal{A}}}^{-1}f\right).$$

(28)

Similarly, acting on (27) by the functional vector $\eta$ we have

$$-\eta \left(Z\right)\widehat{\theta }\left(x\right)+\left[I_m-\eta \left({\widehat{A}}^{-1}G\right)\right]\eta \left(x\right)=\eta \left({\widehat{\mathcal{A}}}^{-1}f\right).$$

(29)

We write (28) and (29) in the form

$$W\left(\begin{array}{c}\widehat{\theta }\left(x\right)\\ \eta \left(x\right)\end{array}\right)=\left(\begin{array}{c}-\theta \left({\widehat{\mathcal{A}}}^{-1}f\right)\\ \eta \left({\widehat{\mathcal{A}}}^{-1}f\right)\end{array}\right),$$

(30)

where W is given in (16). Since $detW\ne 0$ equation (30) can be inverted to obtain $\widehat{\theta }\left(x\right)$ and $\eta \left(x\right)$. Substitution then into (27) yields (17). □

We now prove the main theorem for the solution of the fully nonhomogeneous problem (14).

Theorem 2. 

Let Lemma 1 holds and let the operator

$$\mathcal{B}x=\mathcal{A}x-G\left(t\right)\eta \left(x\right),\mathfrak{D}\left(\mathcal{B}\right)=\left\{x\in {\mathbb{X}}_n^1:\theta \left(x\right)=c\right\}.$$

(31)

Then:

(i)

The operator $\mathcal{B}$ is injective if and only if

$$detW=det\left[\begin{array}{cc}\theta \left(Z\right)& \theta \left({\widehat{\mathcal{A}}}^{-1}G\right)\\ -\eta \left(Z\right)& I_m-\eta \left({\widehat{\mathcal{A}}}^{-1}G\right)\end{array}\right]\ne 0,$$

(32)

where W is a square matrix of order $n+m$ and the inverse operator ${\widehat{\mathcal{A}}}^{-1}$ is given in Lemma 1.

(ii) 

When (32) holds, the unique solution of the nonhomogeneous problem $\mathcal{B}x=f$ for any $f\in {\mathbb{X}}_n$ is given by

$$\begin{array}{ccc}\hfill x& =& {\mathcal{B}}^{-1}f\hfill \\ & =& {\widehat{\mathcal{A}}}^{-1}f-\left[\begin{array}{cc}Z\left(t\right)& {\widehat{\mathcal{A}}}^{-1}G\left(t\right)\end{array}\right]W^{-1}\left(\begin{array}{c}\theta \left({\widehat{\mathcal{A}}}^{-1}f\right)-c\\ -\eta \left({\widehat{\mathcal{A}}}^{-1}f\right)\end{array}\right).\hfill \end{array}$$

(33)

Proof. 

Assume $detW\ne 0$. Let any $u,v\in \mathfrak{D}\left(\mathcal{B}\right)$ such that $\mathcal{B}u=\mathcal{B}v$. Then

$$\begin{array}{ccc}\hfill \mathcal{A}u-G\left(t\right)\eta \left(u\right)& =& \mathcal{A}v-G\left(t\right)\eta \left(v\right),\hfill \\ \hfill \theta \left(u\right)& =& \theta \left(v\right),\hfill \end{array}$$

whence it follows that

$$\begin{array}{ccc}\hfill \mathcal{A}(u-v)-G\left(t\right)\eta (u-v)& =& 0,\hfill \\ \hfill \theta (u-v)& =& 0,\hfill \end{array}$$

or

$${\mathcal{B}}_0(u-v)=0.$$

(34)

From Theorem 1 it follows that $u-v=0$ and therefore $u=v$ which means that the operator $\mathcal{B}$ is injective.

Conversely, assume $detW=0$. Let as above any $u,v\in \mathfrak{D}\left(\mathcal{B}\right)$ such that $\mathcal{B}u=\mathcal{B}v$. Then from (34) and Theorem 1 we conclude that $B_0$ is not injective. This means there is at least an element $u-v\in \mathfrak{D}\left({\mathcal{B}}_0\right)$ with $u-v\ne 0$, or equivalently $u\ne v$, satisfying (34). Hence, the operator $\mathcal{B}$ is not injective.

(ii) The solution of the nonhomogeneous problem $\mathcal{B}x=f$ can be obtained via the principle of superposition, i.e. as the sum of the solution of the problem ${\mathcal{B}}_{0}x=f$ and the solution of homogeneous problem $\mathcal{B}x=0$. The former is given in (17) and latter is now computed below.

We write the homogeneous system as follows

$$\begin{array}{ccc}\hfill \mathcal{B}x& =& \mathcal{A}x-G\left(t\right)\eta \left(x\right)\hfill \\ & =& \widehat{\mathcal{A}}\left(x-Z\left(t\right)\widehat{\theta }\left(x\right)\right)-G\left(t\right)\eta \left(x\right)=0,\hfill \end{array}$$

(35)

from the fact that the element $y=x-Z\left(t\right)\widehat{\theta }\left(x\right)\in \mathfrak{D}\left(\widehat{\mathcal{A}}\right)\subset \mathfrak{D}\left(\mathcal{A}\right)$ and the assumptions of Lemma 1 hold. Multiplying by ${\widehat{\mathcal{A}}}^{-1}$ and rearranging yields

$$x=Z\left(t\right)\widehat{\theta }\left(x\right)+{\widehat{\mathcal{A}}}^{-1}G\left(t\right)\eta \left(x\right).$$

(36)

Acting on (36) by the functional vectors $\eta$ and $\theta$ and from (31) we get, respectively,

$$-\eta \left(Z\right)\widehat{\theta }\left(x\right)+\left[I_m-\eta \left({\widehat{A}}^{-1}G\right)\right]\eta \left(x\right)=0,$$

(37)

and

$$\theta \left(x\right)=\theta \left(Z\right)\widehat{\theta }\left(x\right)+\theta \left({\widehat{\mathcal{A}}}^{-1}G\right)\eta \left(x\right)=c.$$

(38)

Writing (37) and (38) in matrix form, we have

$$W\left(\begin{array}{c}\widehat{\theta }\left(x\right)\\ \eta \left(x\right)\end{array}\right)=\left(\begin{array}{c}c\\ 0\end{array}\right).$$

(39)

Since $detW\ne 0$, equation (39) can be inverted to find ${[\widehat{\theta }\left(x\right),\eta \left(x\right)]}^T$ and after substituting into (36) we get the solution

$$x=\left[\begin{array}{cc}Z\left(t\right)& {\widehat{\mathcal{A}}}^{-1}G\left(t\right)\end{array}\right]W^{-1}\left(\begin{array}{c}c\\ 0\end{array}\right).$$

(40)

Finally, by the principle of superposition from (17) and (40) we get (33). □

In the case where the operator $\mathcal{B}$ is just a differential operator of first order, i.e. when $G\left(t\right)\equiv 0$ and $\eta \left(x\right)\equiv 0$, the following corollary holds.

Corollary 1. 

Let the operator ${\mathcal{B}}_d:{\mathbb{X}}_n\to {\mathbb{X}}_n$ be defined by

$${\mathcal{B}}_{d}x=\mathcal{A}x,\mathfrak{D}\left({\mathcal{B}}_d\right)=\{x\in {\mathbb{X}}_n^1:\theta \left(x\right)=c\}.$$

Then:

(i) 

The operator ${\mathcal{B}}_d$ is injective if and only if

$$det{W}_d=det\theta \left(Z\right)\ne 0,$$

(41)

where $W_d$ is square matrix of order n.

(ii) 

Additionally, when (41) holds, the unique solution of ${\mathcal{B}}_{d}x=f$ for any $f\in {\mathbb{X}}_n$ is given by

$$\begin{array}{ccc}\hfill x& =& {\mathcal{B}}_d^{-1}f\hfill \\ & =& {\widehat{\mathcal{A}}}^{-1}f-Z{W}_d^{-1}\left(\begin{array}{c}\theta \left({\widehat{\mathcal{A}}}^{-1}f\right)-c\end{array}\right).\hfill \end{array}$$

(42)

Finally, for the efficient implementation of Theorem 2 we provide the algorithm in Listing Listing 1.

Listing 1. Algorithm for solving nonlocal linear boundary value problems in closed form.

4. Examples

In this section, selected nonlocal boundary value problems for differential and integrodifferential equations are solved to demonstrate the application of the method and its effectiveness. All calculations and visualizations were performed in the free, open-source computer algebra system Maxima.

4.1. Differential Equations

Example DE.1 The first problem we consider is a three-point boundary value problem presented by Na [20] and concerns the distribution of shear deformation $\psi$ of sandwich beams governed by the ordinary differential equation

$${\psi }^{\prime \prime \prime }-k^2{\psi }^{\prime }+a=0,$$

(43)

where k and a are physical constants related to elastic properties of the beam, under the boundary conditions

$${\psi }^{\prime }\left(0\right)={\psi }^{\prime }\left(1\right)=0,\psi \left({\displaystyle \frac{1}{2}}\right)=0,$$

(44)

corresponding to zero shear bimoment at the two free ends and the symmetry condition, respectively. This problem with $k=5$ and $a=1$ is used as a benchmark for validating numerical methods for multipoint boundary value problems in many studies [21,22,23].

By setting $x_1\left(t\right)=\psi ,x_2\left(t\right)={\psi }^{\prime }$ and $x_3\left(t\right)={\psi }^{\prime \prime }$ the problem (43), (44) can be written as the system of three first-order differential equations

$$\begin{array}{ccc}\hfill x_1^{\prime }\left(t\right)-x_2\left(t\right)& =& 0,\hfill \\ \hfill x_2^{\prime }\left(t\right)-x_3\left(t\right)& =& 0,\hfill \\ \hfill x_3^{\prime }\left(t\right)-k^2{x}_2\left(t\right)& =& -a,\hfill \end{array}$$

(45)

subject to homogeneous boundary conditions

$$x_2\left(0\right)=x_2\left(1\right)=0,x_1\left({\displaystyle \frac{1}{2}}\right)=0.$$

(46)

To solve the system of equations (45), (46), we take $n=3$, $\mathbb{X}=C[0,1]$ and write it in the operator form as in Corollary 1

$${\mathcal{B}}_{d}x=\mathcal{A}x=f\left(t\right),\mathfrak{D}\left({\mathcal{B}}_d\right)=\{x\in {\mathbb{X}}_3^1:\theta \left(x\right)=c\},$$

where

$$\begin{array}{ccc}\hfill x\left(t\right)& =& {\left(\begin{array}{ccc}{x}_1\left(t\right)& x_2\left(t\right)& x_3\left(t\right)\end{array}\right)}^T,f\left(t\right)={\left(\begin{array}{ccc}0& 0& -a\end{array}\right)}^T,\hfill \\ \hfill \mathcal{A}x& =& x^{\prime }-A\left(t\right)x=x^{\prime }-\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& k^2& 0\end{array}\right]x,\hfill \\ \hfill \theta \left(x\right)& =& \left(\begin{array}{c}{x}_2\left(0\right)\\ x_2\left(1\right)\\ x_1\left({\displaystyle \frac{1}{2}}\right)\end{array}\right)=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]x\left(0\right)+\left[\begin{array}{ccc}0& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right]x\left(1\right)+\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 1& 0& 0\end{array}\right]x\left({\displaystyle \frac{1}{2}}\right),\hfill \\ \hfill c& =& {\left(\begin{array}{ccc}0& 0& 0\end{array}\right)}^T.\hfill \end{array}$$

We consider the auxiliary correct system as in Lemma 1

$$\widehat{\mathcal{A}}x=\mathcal{A}x=f\left(x\right),\mathfrak{D}\left(\widehat{\mathcal{A}}\right)=\left\{x\in {\mathbb{X}}_3^1:\widehat{\theta }\left(x\right)=x\left(0\right)=0\right\}.$$

Since $\mathcal{A}x=0$ is a system of linear differential equations with constant coefficients, it is easy to find a fundamental matrix, for example,

$$Z\left(t\right)=\left[\begin{array}{ccc}1& {\displaystyle \frac{1}{k}}sinh\left(kt\right)& {\displaystyle \frac{1}{k^2}}(cosh\left(kt\right)-1)\\ 0& cosh\left(kt\right)& {\displaystyle \frac{1}{k}}sinh\left(kt\right)\\ 0& ksinh\left(kt\right)& cosh\left(kt\right)\end{array}\right],k\ne 0,$$

which satisfies the equation $\widehat{\theta }\left(Z\right)=I_3$.

Then, from the proposed algorithm, it follows that the system (45), (46) has a unique solution when

$$det{W}_d={\displaystyle \frac{sinh\left(k\right)}{k}}\ne 0,$$

and in this case we get

$$x_1\left(t\right):={\displaystyle \frac{a}{k^3}}\left(sinh\left({\displaystyle \frac{k}{2}}\right)-sinh\left(kt\right)\right)+{\displaystyle \frac{a}{k^2}}\left(t-{\displaystyle \frac{1}{2}}\right)+{\displaystyle \frac{a}{k^3}}tanh\left({\displaystyle \frac{k}{2}}\right)\left(cosh\left(kt\right)-cosh\left({\displaystyle \frac{k}{2}}\right)\right),$$

which is the solution $\psi =x_1\left(t\right)$ of the original boundary value problem (43), (44).

Example DE.2 Consider the system of two differential equations with variable coefficients,

$$\begin{array}{ccc}\hfill (t^2+1)x_1^{\prime }\left(t\right)-t{x}_1\left(t\right)+x_2\left(t\right)& =& 2t^4+4t^2-3,\hfill \\ \hfill (t^2+1)x_2^{\prime }\left(t\right)-x_1\left(t\right)-t{x}_2\left(t\right)& =& 5t,\hfill \end{array}$$

(47)

for $0\le t\le 1$, subject to the boundary conditions

$$\begin{array}{ccc}\hfill x_1\left(0\right)+x_2\left({\displaystyle \frac{1}{2}}\right)-2{\int }_{3/4}^{1}s{x}_1\left(s\right)ds& =& -{\displaystyle \frac{2183}{7680}},\hfill \\ \hfill x_1\left({\displaystyle \frac{1}{2}}\right)-4x_2\left(1\right)+{\int }_0^{1/4}\left(x_1\left(s\right)+2x_2\left(s\right)\right)ds& =& {\displaystyle \frac{4835}{3072}}.\hfill \end{array}$$

(48)

We take $n=2$, $\mathbb{X}=C[0,1]$ and put the system (47), (48) in the operator form as in Corollary 1

$${\mathcal{B}}_{d}x=\mathcal{A}x=f\left(t\right),\mathfrak{D}\left({\mathcal{B}}_d\right)=\{x\in {\mathbb{X}}_2^1:\theta \left(x\right)=c\},$$

where

$$\begin{array}{ccc}\hfill x\left(t\right)& =& {\left(\begin{array}{cc}{x}_1\left(t\right)& x_2\left(t\right)\end{array}\right)}^T,f\left(t\right)={\left(\begin{array}{cc}{\displaystyle \frac{2t^4+4t^2-3}{t^2+1}}& {\displaystyle \frac{5t}{t^2+1}}\end{array}\right)}^T,\hfill \\ \hfill \mathcal{A}x& =& x^{\prime }-A\left(t\right)x=x^{\prime }-\left[\begin{array}{cc}{\displaystyle \frac{t}{t^2+1}}& {\displaystyle \frac{-1}{t^2+1}}\\ {\displaystyle \frac{1}{t^2+1}}& {\displaystyle \frac{t}{t^2+1}}\end{array}\right]x,\hfill \\ \hfill \theta \left(x\right)& =& \left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]x\left(0\right)+\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]x\left({\displaystyle \frac{1}{2}}\right)+\left[\begin{array}{cc}0& 0\\ 0& -4\end{array}\right]x\left(1\right)\hfill \\ & & +{\int }_0^{1/4}\left[\begin{array}{cc}0& 0\\ 1& 2\end{array}\right]x\left(s\right)ds+{\int }_{3/4}^1\left[\begin{array}{cc}-2s& 0\\ 0& 0\end{array}\right]x\left(s\right)ds,\hfill \\ \hfill c& =& {\left(\begin{array}{cc}-{\displaystyle \frac{2183}{7680}}& {\displaystyle \frac{4835}{3072}}\end{array}\right)}^T.\hfill \end{array}$$

Consider the complementary system as in Lemma 1

$$\widehat{\mathcal{A}}x=\mathcal{A}x=f\left(x\right),\mathfrak{D}\left(\widehat{\mathcal{A}}\right)=\left\{x\in {\mathbb{X}}_2^1:\widehat{\theta }\left(x\right)=x\left(0\right)=0\right\}.$$

It is known that the homogeneous system $\mathcal{A}x=0$ has the fundamental matrix

$$Z\left(t\right)=\left[\begin{array}{cc}1& -t\\ t& 1\end{array}\right],$$

which satisfies the equation $\widehat{\theta }\left(Z\right)=I_2$, see, for example, [24].

Then, from the proposed algorithm, we obtain

$$det{W}_d=-{\displaystyle \frac{1279}{384}}\ne 0,$$

which ensures that the system (47), (48) has a unique solution which is

$$x_1\left(t\right)=t^3-2t,x_2\left(t\right)=t^2-1.$$

4.2. Integrodifferential Equations

Example IDE.1 In [25], a second order control problem for the dynamics of the rocket bank reduces to the second-order Fredholm integrodifferential equation

$${\chi }^{\prime \prime }\left(t\right)+\nu {\chi }^{\prime }\left(t\right)+\mu {\int }_0^{T}K\left(s\right)\chi \left(s\right)ds=\mathfrak{f}\left(t\right),$$

(49)

with the boundary conditions

$$T\chi \left(0\right)+{\int }_0^T\chi \left(t\right)dt=0,{\chi }^{\prime }\left(T\right)=\phi ,$$

(50)

where $K\left(s\right),\mathfrak{f}\left(t\right)\in C[0,T]$, $\nu =1/T_0$, $\mu =\left(k_0{k}_1\right)/T_0$, $T_0,k_0,k_1,\phi$ are constants and $T>T_0$.

With the transformation $\chi \left(t\right)=x_1\left(t\right)$ and ${\chi }^{\prime }\left(t\right)=x_2\left(t\right)$ we can reduce the problem (49), (50) to the following system of two first-order integrodifferential equations

$$\begin{array}{ccc}\hfill x_1^{\prime }\left(t\right)-x_2\left(t\right)& =& 0,\hfill \\ \hfill x_2^{\prime }\left(t\right)+\nu x_2\left(t\right)+\mu {\int }_0^{T}K\left(s\right)x_1\left(s\right)ds& =& \mathfrak{f}\left(t\right),\hfill \end{array}$$

(51)

subject to the boundary conditions

$$T{x}_1\left(0\right)+{\int }_0^T{x}_1\left(s\right)ds=0,x_2\left(T\right)=\phi .$$

(52)

We set $\mathbb{X}=C[0,T]$, $n=2$ and $m=1$ and write the boundary value problem (51), (52) in the operator form

$$\begin{array}{c}\hfill \mathcal{B}x=\mathcal{A}x-G\left(t\right)\eta \left(x\right),\mathfrak{D}\left(\mathcal{B}\right)=\left\{x\in {\mathbb{X}}_2^1:\theta \left(x\right)=c\right\},\end{array}$$

(53)

where

$$\begin{array}{ccc}\hfill x\left(t\right)& =& {\left(\begin{array}{cc}{x}_1\left(t\right)& x_2\left(t\right)\end{array}\right)}^T,f\left(t\right)={\left(\begin{array}{cc}0& \mathfrak{f}\left(t\right)\end{array}\right)}^T,\hfill \\ \hfill \mathcal{A}x& =& x^{\prime }-A\left(t\right)x=x^{\prime }-\left[\begin{array}{cc}0& 1\\ 0& -\nu \end{array}\right]x,\hfill \\ \hfill G\left(t\right)& =& \left[\begin{array}{c}0\\ -\mu \end{array}\right],\eta \left(x\right)=\left(\begin{array}{c}{\int }_0^T\left[\begin{array}{cc}K\left(s\right)& 0\end{array}\right]x\left(s\right)ds\end{array}\right),\hfill \\ \hfill \theta \left(x\right)& =& \left[\begin{array}{cc}T& 0\\ 0& 0\end{array}\right]x\left(0\right)+\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]x\left(T\right)+{\int }_0^T\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]x\left(s\right)ds,\hfill \\ \hfill c& =& {\left(\begin{array}{cc}0& \phi \end{array}\right)}^T,\hfill \end{array}$$

Let the complementary system in Lemma 1 be defined by

$$\widehat{\mathcal{A}}x=\mathcal{A}x=f\left(x\right),\mathfrak{D}\left(\widehat{\mathcal{A}}\right)=\left\{x\in {\mathbb{X}}_2^1:\widehat{\theta }\left(x\right)=x\left(0\right)=0\right\}.$$

The fundamental matrix of the homogeneous system $\mathcal{A}x=0$ is

$$Z\left(t\right)=\left[\begin{array}{cc}1& {\displaystyle \frac{1-e^{-\nu t}}{\nu }}\\ 0& e^{-\nu t}\end{array}\right],$$

which satisfies $\widehat{\theta }\left(Z\right)=I_2$.

Substituting into the Algorithm, we obtain that the system (51), (52) has a unique solution if and only if

$$detW=2T{e}^{-T\nu }\left(1-{\displaystyle \frac{\mu }{\nu }}{\int }_0^{T}K\left(s\right)[{\displaystyle \frac{T}{4}}-s-{\displaystyle \frac{1}{2T{\nu }^2}}+({\displaystyle \frac{1}{2T\nu }}-e^{-s\nu }+{\displaystyle \frac{1}{2}}){\displaystyle \frac{e^{T\nu }}{\nu }}]ds\right)\ne 0.$$

As a simple example, let $K\left(s\right)=1$, $\mathfrak{f}\left(t\right)=1$, $\nu =1/5$, $\phi =1$ and $T=10$. In this case the exact solution of the boundary value problem (49), (50) is

$$\chi \left(t\right)={\displaystyle \frac{e^{-\frac{t}{5}}\left(\left(\left(\left(125e^2+125\right)\mu -10\right)t-1250e^2\mu +30e^2+15\right)e^{\frac{t}{5}}+1250e^2\mu -40e^2\right)}{\left(125e^2-125\right)\mu -2}}.$$

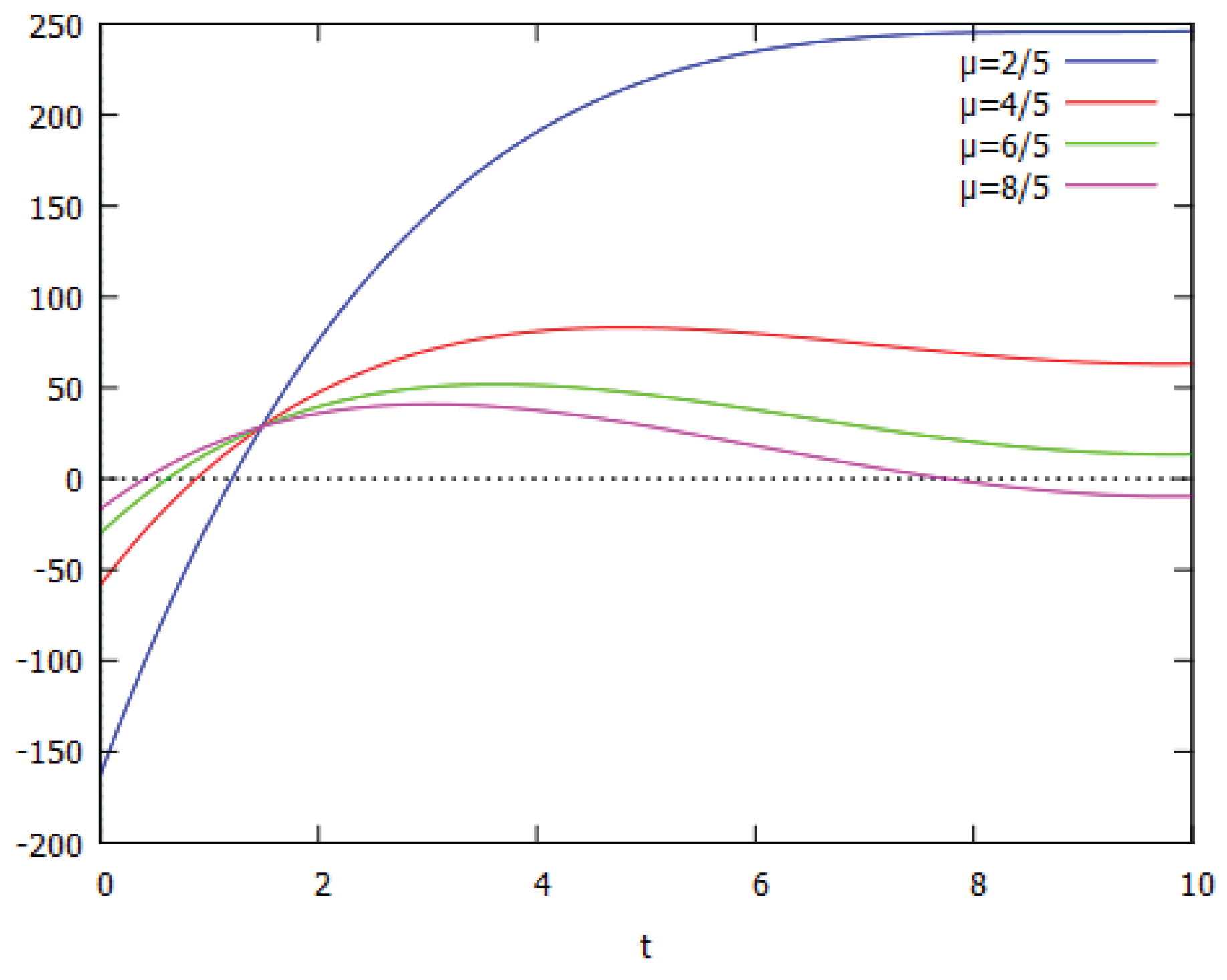
In the more complicated case for $K\left(s\right)=e^{-\nu t}/10$ and $\mathfrak{f}\left(t\right)=2t$ the solution is illustrated for different values of $\mu$ in Figure 1.

Example IDE.2 Consider the following system of two second-order linear Fredholm integrodifferential equations

$$\begin{array}{ccc}\hfill u_1^{\prime \prime }\left(t\right)+u_2^{\prime }\left(t\right)+{\int }_0^{1}2ts[u_1\left(s\right)-3u_2\left(s\right)]ds& =& 3t^2+{\displaystyle \frac{3t}{10}}+8,\hfill \\ \hfill u_1^{\prime }\left(t\right)+u_2^{\prime \prime }\left(t\right)+{\int }_0^{1}3(2t+s^2)[u_1\left(s\right)-2u_2\left(s\right)]ds& =& 21t+{\displaystyle \frac{4}{5}},\hfill \end{array}$$

(54)

subject to the boundary conditions

$$\begin{array}{ccc}\hfill u_1\left(0\right)+u_1^{\prime }\left(0\right)& =& 1,\hfill \\ \hfill u_1\left(1\right)+u_1^{\prime }\left(1\right)& =& 10,\hfill \\ \hfill u_2\left(0\right)+u_2^{\prime }\left(0\right)& =& 1,\hfill \\ \hfill u_2\left(1\right)+u_2^{\prime }\left(1\right)& =& 7.\hfill \end{array}$$

(55)

This problem is solved numerically by the Tau method in [18].

To construct the exact solution by the method presented in the previous sections we use the transformation $u_1\left(t\right)=x_1\left(t\right)$, $u_2\left(t\right)=x_2\left(t\right)$, $u_1^{\prime }\left(t\right)=x_3\left(t\right)$ and $u_2^{\prime }\left(t\right)=x_4\left(t\right)$ and write the boundary value problem (54), (55) as a system of four first-order integrodifferential equations,

$$\begin{array}{ccc}\hfill x_1^{\prime }-x_3& =& 0,\hfill \\ \hfill x_2^{\prime }-x_4& =& 0,\hfill \\ \hfill x_3^{\prime }+x_4+2t{\int }_0^{1}s\left(x_1\left(s\right)-3x_2\left(s\right)\right)ds& =& 3t^2+{\displaystyle \frac{3t}{10}}+8,\hfill \\ \hfill x_4^{\prime }+x_3+6t{\int }_0^1\left(x_1\left(s\right)-2x_2\left(s\right)\right)ds+3{\int }_0^1{s}^2\left(x_1\left(s\right)-2x_2\left(s\right)\right)ds& =& 21t+{\displaystyle \frac{4}{5}},\hfill \end{array}$$

(56)

with the boundary conditions

$$\begin{array}{ccc}\hfill x_1\left(0\right)+x_3\left(0\right)& =& 1,\hfill \\ \hfill x_1\left(1\right)+x_3\left(1\right)& =& 10,\hfill \\ \hfill x_2\left(0\right)+x_4\left(0\right)& =& 1,\hfill \\ \hfill x_2\left(1\right)+x_4\left(1\right)& =& 7.\hfill \end{array}$$

(57)

In the space $\mathbb{X}=C[0,1]$ and for $n=4$ and $m=3$, we write the boundary value problem (56), (57) in the operator form as in Theorem 2:

$$\mathcal{B}x=\mathcal{A}x-G\left(t\right)\eta \left(x\right),\mathfrak{D}\left(\mathcal{B}\right)=\left\{x\in {\mathbb{X}}_4^1:\theta \left(x\right)=c\right\}.$$

where

$$\begin{array}{ccc}\hfill x\left(t\right)& =& {\left(\begin{array}{cccc}{x}_1\left(t\right)& x_2\left(t\right)& x_3\left(t\right)& x_4\left(t\right)\end{array}\right)}^T,f\left(t\right)={\left(\begin{array}{cccc}0& 0& 3t^2+{\displaystyle \frac{3t}{10}}+8& 21t+{\displaystyle \frac{4}{5}}\end{array}\right)}^T,\hfill \\ \hfill \mathcal{A}x& =& x^{\prime }-A\left(t\right)x=x^{\prime }-\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ 0& 0& 0& -1\\ 0& 0& -1& 0\end{array}\right]x,\hfill \\ \hfill G\left(t\right)& =& \left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& -2t& 0\\ -6t& 0& -3\end{array}\right],\eta \left(x\right)=\left(\begin{array}{c}{\int }_0^1\left[\begin{array}{cccc}1& -2& 0& 0\\ s& -3s& 0& 0\\ s^2& -2s^2& 0& 0\end{array}\right]x\left(s\right)ds\end{array}\right),\hfill \\ \hfill \theta \left(x\right)& =& \left[\begin{array}{cccc}1& 0& 1& 0\\ 0& 0& 0& 0\\ 0& 1& 0& 1\\ 0& 0& 0& 0\end{array}\right]x\left(0\right)+\left[\begin{array}{cccc}0& 0& 0& 0\\ 1& 0& 1& 0\\ 0& 0& 0& 0\\ 0& 1& 0& 1\end{array}\right]x\left(1\right),c=\left(\begin{array}{c}1\\ 10\\ 1\\ 7\end{array}\right),\hfill \end{array}$$

Let the complementary system in Lemma 1 be defined by

$$\widehat{\mathcal{A}}x=\mathcal{A}x=f\left(x\right),\mathfrak{D}\left(\widehat{\mathcal{A}}\right)=\left\{x\in {\mathbb{X}}_4^1:\widehat{\theta }\left(x\right)=x\left(0\right)=0\right\},$$

where, since the matrix A is constant, it is easy to construct a fundamental set of solutions of the homogeneous system $\mathcal{A}x=0$, namely

$$Z\left(t\right)=\left[\begin{array}{cccc}1& 0& sinh\left(t\right)& 1-cosh\left(t\right)\\ 0& 1& 1-cosh\left(t\right)& sinh\left(t\right)\\ 0& 0& cosh\left(t\right)& -sinh\left(t\right)\\ 0& 0& -sinh\left(t\right)& cosh\left(t\right)\end{array}\right],$$

which satisfies the equation $\widehat{\theta }\left(Z\right)=I_4$.

By substituting into Algorithm, we directly obtain the unique solution of the system (56), (57),

$$x\left(t\right)={\left(\begin{array}{cccc}3t^2+1& t^3+2t-1& 6t& 3t^2+2\end{array}\right)}^T,$$

and hence the exact solution of the original boundary value problem (54), (55) $u_1\left(t\right)=3t^2+1$ and $u_2\left(t\right)=t^3+2t-1$.

5. Conclusions

Solvability criteria for general nonlocal boundary value problems for systems of linear ordinary integrodifferential equations of Fredholm type have been derived in a computationally convenient matrix form. A direct operator method for constructing their exact solution has also been presented. The method can be easily implemented in any Computer Algebra System (CAS). The main advantage is its ease of use and efficiency. Its disadvantage is the requirement of the fundamental matrix of the corresponding homogeneous differential system, which limits its application to cases where the matrix of coefficients is constant or is a matrix with variable coefficients of a special form [26].

The proposed method will be useful to many researchers as well as educational professionals in teaching advanced mathematics. Exact solutions are always necessary to validate numerical methods such as the finite element method [27,28,29,30,31], and others. The solvability criteria and the solution method derived here are equally applicable to nonlocal boundary value problems for linear ordinary loaded differential and integrodifferential equations and their systems.