fσ8 as a Probe of Future-Singularity Dark Energy Models and ΛCDM

1. Introduction

On cosmological scales, our present knowledge of the late–time expansion is still dominated by purely background, or geometrical, measurements. These include the Type Ia supernova Hubble diagram, which constrains the luminosity distance–redshift relation [1,2,3,4], the baryon acoustic oscillation scale imprinted in the clustering of galaxies [5,6,7,8,9], and the CMB–based scaled distance indicators to the last–scattering surface, such as $\mathcal{R}$ and $l_a$ [10,11,12]. Taken together, these probes have firmly established the presence of a dark-energy–like component, allow us to infer its overall abundance, and provide tight constraints on the background expansion history $H\left(z\right)$ [13,14,15]. At the same time, because they are sensitive only to the integrated geometry, they have limited ability to reveal the physical origin of the accelerated expansion. Within general relativity, they do not allow us to clearly distinguish between a cosmological constant (the standard $\mathrm{\Lambda }$CDM scenario) and a dynamical dark-energy fluid, and in a broader theoretical setting they are not sufficient to decide between GR and modified–gravity explanations.

A complementary avenue is provided by dynamical probes, which track the evolution of inhomogeneities through the growth of the matter density contrast, ${\delta }_m\left(z\right)\equiv \delta {\rho }_m\left(z\right)/{\rho }_m\left(z\right)$. Current measurements of the growth rate are still relatively weak, so taken in isolation they do not yet impose very stringent bounds on many cosmological parameters, nor do they strongly discriminate among the broad zoo of dark-energy and modified–gravity models proposed in the literature (see, e.g., [16,17,18,19,20] and references therein). However, when growoh information is combined with the geometrical data, the constraining power increases significantly. In particular, joint analyses of background probes with ${\delta }_m\left(z\right)$–based observables (or derived quantities such as $f{\sigma }_8$) sharpen our ability to distinguish between dark-energy scenarios and modified–gravity models (including $f\left(R\right)$ theories and the Dvali–Gabadadze–Porrati (DGP) model) and the reference $\mathrm{\Lambda }$CDM cosmology [21,22,23,24] far more effectively than either geometrical or dynamical probes considered separately.

The lack of a firm explanation of the origin of the present universe accelerated expansion led to the formulation of different scenarios of modified gravity models or dynamical dark energy models among which, within general relativity, some foresaw different types of singularities in a finite future time. In this latter field, models describing a Big Rip (BR), a Sudden Future Singularity (SFS), also known as Type II singularities [25,26,27,28], a Generalized Sudden Future Singularity (GSFS), a Finite Scale Factor Singularity (FSFS), also known as Type III singularities [28,29], a Big-Separation Singularity (BS) [28] and w-singularities [30] gained some attention among cosmologists.

The new generation of large–scale structure surveys, such as DESI1 [31], Euclid2 [32,33,34,35] and space missions of the Roman (formerly WFIRST–2.4)3 type, are designed to deliver high–precision measurements of both background and growth observables. By jointly constraining geometrical quantities (such as distance–redshift relations) and dynamical quantities (encoding the evolution of density perturbations), these experiments are expected to significantly enhance our ability to distinguish a pure cosmological constant from time–varying dark energy scenarios.

In parallel, planned and proposed observations of the cosmic microwave background across microwave to far–infrared frequencies, in both temperature and polarization, will provide complementary information on the dark sector. In particular, mission concepts like PRISM (Polarized Radiation and Imaging Spectroscopy) [36] and the Cosmic Origins Explorer (CoRE) satellite [37], which aim at extremely accurate polarization measurements of the microwave sky, are forecast to tighten constraints on dark energy and possible deviations from $\mathrm{\Lambda }$CDM [38,39], thereby contributing to a clearer picture of the origin of cosmic acceleration.

DESI has already completed its first year of observations and delivered high–precision measurements of both BAO and the growth rate $f{\sigma }_8\left(z\right)$, which are broadly consistent with the standard $\mathrm{\Lambda }$CDM scenario and general relativity within current uncertainties, while approaching the regime where scale–dependent growth effects could be detected [40,41,42]. The Euclid mission has been successfully launched and has entered its main survey phase, with early data releases – including the Early Release Observations (ERO) and the first Quick Data Release (Q1) – demonstrating excellent control of systematics in weak–lensing and large–scale–structure measurements [43,44,45,46], although the full tomographic cosmological constraints are still forthcoming. At the same time, some of the CMB polarization concepts mentioned above (PRISM, CoRE) have remained at the level of mission studies rather than operational satellites. These developments confirm the basic premise of our analysis – that forthcoming large–scale–structure surveys are capable of tightly constraining any non–standard, potentially scale–dependent growth – while, at present, showing no compelling observational need to depart from the standard $\mathrm{\Lambda }$CDM growth history.

In Section 2 we present the background evolution together with the Einstein equations for linear perturbations in the Newtonian gauge. In Section 3 we give a short description of the dynamical dark energy models with the SFS and the FSFS. In Section 4 we describe the compilation of current $f{\sigma }_8$ measurements and the ${\chi }^2$ methodology used to confront the models with the data. Finally, in Section 5 we present the results of this comparison.

2. Growth Function

In this section we summarize and adapt the perturbation formalism for the scale-dependent growth function developed in our previous analysis of $\mathrm{\Lambda }$CDM with future galaxy surveys [47].

The growth of matter inhomogeneities provides a powerful dynamical diagnostic of the expansion history. A convenient quantity is the (logarithmic) growth rate f, defined by

$$f\left(a\right)\equiv {\displaystyle \frac{dln{\delta }_m\left(a\right)}{dlna}},$$

(2.1)

where ${\delta }_m$ denotes the matter density contrast. In many applications one adopts the phenomenological ansatz

$$f\left(a\right)={\mathrm{\Omega }}_m{\left(a\right)}^{\gamma },$$

(2.2)

where a is the scale factor, $\gamma$ is the so–called growth index, and ${\mathrm{\Omega }}_m\left(a\right)$ is the matter density parameter as a function of time,

$${\mathrm{\Omega }}_m\left(a\right)\equiv {\displaystyle \frac{H_0^2{\mathrm{\Omega }}_{m,0}{a}^{-3}}{H{\left(a\right)}^2}},$$

(2.3)

with ${\mathrm{\Omega }}_{m,0}$ the present–day matter density parameter, $H\left(a\right)=\dot{a}/a$ the Hubble expansion rate, and $H_0$ its value today. The parameterization (2.2) provides an approximate solution of the scale–independent growth equation [48,49],

$$f^{\prime }+f^2+f\left({\displaystyle \frac{\dot{H}}{H^2}}+2\right)={\displaystyle \frac{3}{2}}{\mathrm{\Omega }}_m,$$

(2.4)

where a prime denotes $\prime \equiv d/dlna$, and which in turn follows from the familiar second–order differential equation for the matter density contrast,

$${\ddot{\delta }}_m+2H{\dot{\delta }}_m-4\pi G{\rho }_m{\delta }_m=0,$$

(2.5)

after changing the independent variable from cosmic time t to $lna$. Here overdots denote time derivatives and ${\rho }_m$ is the background matter density.

For the standard $\mathrm{\Lambda }$CDM cosmology one finds $\gamma =6/11$ [23,50,51], while current data yield an observational estimate $\gamma =0.665\pm 0.0669$ [52]. In the case of dark energy models with a slowly varying equation of state, the approximation (2.2) remains accurate, with the growth index given by

$$\gamma ={\displaystyle \frac{3(w_0-1)}{6w_0-5}},$$

(2.6)

where $w_0\equiv w\left(a\right)=p/\rho$ denotes the dark energy equation of state (with $w_0=-1$ for $\mathrm{\Lambda }$CDM). For such slowly varying dark energy scenarios, $\gamma$ is expected to be nearly constant in time, with any redshift dependence typically at the level of only a few percent [49,53]. This is no longer true in generic modified gravity models: there the growth index can have a nontrivial time evolution. A well–known example is the Dvali–Gabadadze–Porrati (DGP) model, for which $\gamma \simeq 0.68$, and a more faithful description of the full system (2.10)–(2.12) requires an explicitly redshift–dependent parameterization of $\gamma \left(z\right)$. Several such parameterizations have been proposed in the literature [23,24,54,55,56].

Beyond the scale–independent approximation, it has been shown [48,49,53] that the exact general–relativistic treatment of linear perturbations yields a scale dependence of the growth on sufficiently large scales, already for $\mathrm{\Lambda }$CDM, with noticeable effects for wavelengths $\gtrsim 100h^{-1}\mathrm{Mpc}$. The usual scale–independent treatment assumes that the perturbation modes of interest lie well inside the Hubble radius (sub–Hubble regime). However, this assumption can break down at comparatively modest scales, of order $200h^{-1}\mathrm{Mpc}$ in the early universe, even though the Hubble radius today is of order $3000h^{-1}\mathrm{Mpc}$. The same considerations apply to the $\mathrm{\Lambda }$CDM model and to the future–singularity dark energy models studied in this work [48,49,53,57].

Furthermore, Denkiewicz [57] showed that dynamical dark energy models with future singularities can exhibit a nontrivial dependence on the perturbation wavenumber: there exists a characteristic scale at which the dark energy perturbations become comparable in amplitude to the matter perturbations. More generally, for any given model one can identify a limiting wavelength below which dark energy perturbations are tightly coupled to matter perturbations and cannot be neglected. While for canonical quintessence fields dark energy inhomogeneities are relevant only on scales comparable to the Hubble radius, models with noncanonical kinetic terms or very small dark energy sound speed, $c_s\ll 1$, can develop dark energy perturbations that trace the matter perturbations even on scales significantly smaller than the Hubble radius [57,58,59,60]. The two singular models considered here should be viewed as specific examples within this broader class of possibilities.

In the present analysis we focus on the evolution of dark matter perturbations. We work with the full scale–dependent system of linear perturbation equations for both the FSFS and SFS scenarios, and compare the resulting growth with that obtained in a reference $\mathrm{\Lambda }$CDM cosmology constructed under the same general assumptions.

We adopt the Newtonian gauge for scalar perturbations and assume negligible anisotropic stress, so that the perturbed line element can be written as

$$d{s}^2=-(1+2\mathrm{\Phi })d{t}^2+(1-2\mathrm{\Phi })a^2{\gamma }_{ij}d{x}^{i}d{x}^j,$$

(2.7)

where ${\gamma }_{ij}$ denotes the spatial metric and $\mathrm{\Phi }$ is the Newtonian potential. For a spatially flat universe filled with pressureless, nonrelativistic dark matter with density ${\rho }_m$ and an exotic dark energy component with density ${\rho }_{de}$, the background dynamics is described by the Friedmann and continuity equations,

$$\begin{array}{ccc}\hfill H^2& =& {\displaystyle \frac{8\pi G}{3}}({\rho }_m+{\rho }_{de}),\hfill \end{array}$$

(2.8)

$$\begin{array}{ccc}\hfill \dot{\rho }& =& -3H(\rho +p),\hfill \end{array}$$

(2.9)

where $\rho ={\rho }_m+{\rho }_{de}$ and p is the total pressure.

Linearizing Einstein’s equations around this background in the Newtonian gauge yields, after some algebra, the following evolution equations for the potential $\mathrm{\Phi }$, the matter density contrast $\delta \equiv \delta {\rho }_m/{\rho }_m$, and the velocity potential of dark matter (encoded in $v_f\equiv -va$):

$$\begin{array}{ccc}\hfill \ddot{\mathrm{\Phi }}& =& -4H\dot{\mathrm{\Phi }}+8\pi G{\rho }_{de}{w}_{de}\mathrm{\Phi },\hfill \end{array}$$

(2.10)

$$\begin{array}{ccc}\hfill \dot{\delta }& =& 3\dot{\mathrm{\Phi }}+{\displaystyle \frac{k^2}{a^2}}{v}_f,\hfill \end{array}$$

(2.11)

$$\begin{array}{ccc}\hfill {\dot{v}}_f& =& -\mathrm{\Phi },\hfill \end{array}$$

(2.12)

subject to the constraint equations

$$\begin{array}{ccc}\hfill 3H(H\mathrm{\Phi }+\dot{\mathrm{\Phi }})+{\displaystyle \frac{k^2}{a^2}}\mathrm{\Phi }& =& -4\pi G\delta {\rho }_m,\hfill \end{array}$$

(2.13)

$$\begin{array}{ccc}\hfill (H\mathrm{\Phi }+\dot{\mathrm{\Phi }})& =& -4\pi G{\rho }_m{v}_f.\hfill \end{array}$$

(2.14)

Here k denotes the comoving wavenumber of the perturbation mode.

If one assumes that the relevant modes are well inside the Hubble radius, $k^2/a^2\gg H^2$, and that the gravitational potential varies slowly in time, the system above reduces to the scale–independent evolution equation (2.5) for ${\delta }_m$. Relaxing only the sub–Hubble assumption, while still keeping the potential quasi–static, leads instead to a scale–dependent growth equation [49,53],

$$\begin{array}{c}\hfill {\ddot{\delta }}_m+2H{\dot{\delta }}_m-{\displaystyle \frac{4\pi G{\rho }_m{\delta }_m}{1+\xi (a,k)}}=0,\end{array}$$

(2.15)

where the function

$$\begin{array}{c}\hfill \xi (a,k)={\displaystyle \frac{3a^{2}H{\left(a\right)}^2}{k^2}}\end{array}$$

(2.16)

encodes the departure from the sub–Hubble limit.

Equation (2.15) can be rewritten in terms of the growth rate $f=dln{\delta }_m/dlna$ as

$$\begin{array}{c}\hfill f^{\prime }+f^2+\left(2-{\displaystyle \frac{3}{2}}{\mathrm{\Omega }}_m\left(a\right)\right)f={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mathrm{\Omega }}_m\left(a\right)}{1+\xi (a,k)}},\end{array}$$

(2.17)

with $\prime \equiv d/dlna$ and, in this expression, assuming the $\mathrm{\Lambda }$CDM background for $H\left(a\right)$. A useful approximate solution of (2.17) is given by

$$f(k,a)={\displaystyle \frac{{\mathrm{\Omega }}_m{\left(a\right)}^{\gamma }}{1+{\displaystyle \frac{3H_0^2{\mathrm{\Omega }}_{m,0}}{a{k}^2}}}},$$

(2.18)

which reduces to the standard scale–independent form when $\xi (a,k)\to 0$. In this limit, (2.17) collapses to (2.4), whose solution is well approximated by (2.2) with $\gamma =6/11$. It has been shown [49,53] that the scale–dependent equation (2.15) reproduces the full general–relativistic system (2.10)–(2.12) with good accuracy up to scales comparable to the horizon; on even larger scales, however, the time evolution of the potential $\mathrm{\Phi }$ can no longer be neglected.

For the purposes of this work, it is crucial to emphasize that we do not employ either of the approximations mentioned above. In our numerical analysis we solve the complete set of linear perturbation equations without assuming the sub–Hubble limit or a slowly varying gravitational potential.

3. FSFS and SFS as Dynamical Dark Energy Candidates

The SFS and FSFS show up within the framework of the Einstein–Friedmann cosmology governed by the standard field equations, Equations (2.8), and the energy-momentum conservation law, Equation (2.9). We get the SFS and FSFS scenarios with the scale factor in the following form:

$$a\left(t\right)=a_s\left[b+\left(1-b\right){\left({\displaystyle \frac{t}{t_s}}\right)}^m-b{\left(1-{\displaystyle \frac{t}{t_s}}\right)}^n\right].$$

(3.1)

An appropriate choice of the constants $(b,t_s,a_s,m,n)$ is necessary [25,61]. For both cases, the SFS as well as the FSFS model, the evolution starts with the standard big-bang singularity at $t=0$$(a=0)$, and evolves to an exotic singularity for $t=t_s$, where $a=a_s\equiv a\left(t_s\right)$ is a constant. Accelerated expansion in an SFS universe is assured with a negative b, while for a FSFS universe b has to be positive. In order to have the SFS, n has to be within the range $1<n<2$; while for an FSFS, n has to obey the condition $0<n<1$. For the SFS at $t=t_s$, $a\to a_s$, $\varrho \to {\varrho }_s=\mathrm{const}.$, $p\to \infty$; while for an FSFS the energy density $\rho$ also diverges and one has: for $t\to t_s$, $a\to a_s$, $\rho \to \infty$, and $p\to \infty$, where $a_s,t_s$ are constants and $a_s\ne 0$. In both scenarios the non-relativistic matter scales as $a^{-3}$, i.e.

$${\rho }_m={\mathrm{\Omega }}_{m,0}{\rho }_0{\left({\displaystyle \frac{a_0}{a}}\right)}^3,$$

(3.2)

and the evolution of the exotic (dark energy) fluid ${\rho }_{de}$, can be determined by taking the difference between the total energy density $\rho$, and the energy density of the non-relativistic matter, i.e.

$${\rho }_{de}=\rho -{\rho }_m.$$

(3.3)

In those scenarios the dark energy component is also responsible for the exotic singularity at $t\to t_s$. The dimensionless energy densities are defined in a standard way as

$${\mathrm{\Omega }}_m={\displaystyle \frac{{\rho }_m}{\rho }},{\mathrm{\Omega }}_{de}={\displaystyle \frac{{\rho }_{de}}{\rho }}.$$

(3.4)

For the dimensionless exotic dark energy density we have the following expression

$${\mathrm{\Omega }}_{de}=1-{\mathrm{\Omega }}_{m,0}{\displaystyle \frac{H_0^2}{H^2\left(t\right)}}{\left({\displaystyle \frac{a_0}{a\left(t\right)}}\right)}^3=1-{\mathrm{\Omega }}_m.$$

(3.5)

The barotropic index of the equation of state for the dark energy is defined as

$$w_{de}=p_{de}/{\rho }_{de}.$$

(3.6)

The singularity scenarios considered in this work were also tested as candidates for dynamical fine structure cosmology [62]. In that approach, the dark energy is sourced by a scalar field which couples to the electromagnetic sector of the theory; the knowledge about the effective evolution of the dark energy density and the dark energy equation of state evolution is sufficient to estimate the resulting fine structure evolution.

4. $f{\sigma }_8$ Data and ${\chi }^2$ Methodology

In order to confront our models with large-scale-structure measurements, we use the growth observable $f{\sigma }_8\left(z\right)$ and a standard ${\chi }^2$ methodology.

4.1. Fiducial Cosmological Background

In order to specify the background cosmology for the reference $\mathrm{\Lambda }$CDM model, we adopt the best-fit Planck 2018 TT,TE,EE+lowE $\mathrm{\Lambda }$CDM parameters [8] as our fiducial background; the corresponding values are listed in Table 1. In the present analysis these parameters are kept fixed, and Planck data are not included in the $f{\sigma }_8$ likelihood.

The evolution of the matter density contrast is computed by numerically integrating the system of Equations (2.10)–(2.12), subject to the constraint relations (2.13)–(2.14). Throughout this work, the matter contrast ${\delta }_m$ is normalized to unity at $a=1$.

4.2. Compilation of Current $f{\sigma }_8$ Measurements

To confront the models with observations we use a compilation of $N=22$ measurements of the growth observable $f{\sigma }_8\left(z\right)$ obtained from redshift-space distortions (RSD) in galaxy surveys. Our data set coincides with the compilation constructed in Sagredo et al. [19], which is based on the “Gold-2017” sample of 18 independent measurements introduced in Nesseris et al. [20] and supplemented by four additional BOSS and VIPERS points. Our implementation follows closely that of Sagredo et al. [19]: we adopt the same data points, redshifts and covariance prescriptions, including the geometrical rescaling factors; see Sagredo et al. [19], Nesseris et al. [20] and the references therein for further details.

Each entry in the compilation provides the effective redshift $z_i$, the measured value ${\left[f{\sigma }_8\right]}_i^{\mathrm{obs}}$, the quoted $1\sigma$ error ${\sigma }_i$, and the matter density parameter of the fiducial cosmology assumed in that analysis, ${\mathrm{\Omega }}_{m,0}^{\mathrm{fid}}$.4 In addition, the compilation includes non-trivial covariance among the three WiggleZ points and among the four SDSS-IV measurements; we encode these correlations in a $22\times 22$ covariance matrix $C_{ij}$, with the remaining entries taken to be diagonal, i.e. $C_{ij}={\sigma }_i^2{\delta }_{ij}$ for all other data points.

4.3. Geometrical Rescaling and ${\chi }^2$ Definition

Following standard practice, we account for the fact that each RSD measurement was obtained assuming a particular fiducial background when mapping observed angles and redshifts to comoving distances. Denoting by $E_{\mathrm{fid}}\left(z\right)$ and $D_{A,\mathrm{fid}}\left(z\right)$ the dimensionless Hubble parameter and angular diameter distance in the fiducial cosmology used for a given measurement, and by $E\left(z\right)$ and $D_A\left(z\right)$ the corresponding quantities in the model under consideration, the leading geometrical correction enters through the combination (see e.g.[20,63]).

$$R(z;{\mathrm{\Omega }}_{m,0}^{\mathrm{fid}})\equiv {\displaystyle \frac{E\left(z\right)D_A\left(z\right)}{E_{\mathrm{fid}}(z;{\mathrm{\Omega }}_{m,0}^{\mathrm{fid}})D_{A,\mathrm{fid}}(z;{\mathrm{\Omega }}_{m,0}^{\mathrm{fid}})}}.$$

(4.1)

Given the theoretical prediction $f{\sigma }_8^{\mathrm{th}}\left(z\right)$ for a model with background $E\left(z\right)$ and $D_A\left(z\right)$, the quantity to be compared to the published measurement is then

$${\left[f{\sigma }_8\right]}_i^{\mathrm{model}}=R\left(z_i;{\mathrm{\Omega }}_{m,0}^{\mathrm{fid}}\left(i\right)\right)f{\sigma }_8^{\mathrm{th}}\left(z_i\right),$$

(4.2)

where ${\mathrm{\Omega }}_{m,0}^{\mathrm{fid}}\left(i\right)$ is the fiducial matter density parameter used in the i-th RSD analysis.

We assemble the data–theory residual vector

$$V_i\equiv {\left[f{\sigma }_8\right]}_i^{\mathrm{obs}}-{\left[f{\sigma }_8\right]}_i^{\mathrm{model}},i=1,\dots ,N,$$

(4.3)

and define the total ${\chi }^2$ as

$${\chi }^2=\sum _{i,j=1}^N{V}_i{\left(C^{-1}\right)}_{ij}{V}_j,$$

(4.4)

where $C_{ij}$ is the full covariance matrix described above.

In this work we evaluate ${\chi }^2$ for three fixed cosmological models: (i) a reference $\mathrm{\Lambda }$CDM background calibrated on the Planck 2018 parameters of Table 1, treated here as a fixed model with no additional free parameters; (ii) a sudden future singularity (SFS) model with parameters $(m,n,b,y_0)$ chosen to satisfy geometrical probes; and (iii) a finite scale factor singularity (FSFS) model with an analogous parameter choice. In all cases we solve the full scale-dependent perturbation equations presented in Section 2, and construct $f{\sigma }_8^{\mathrm{th}}\left(z\right)$ from the synchronous-gauge matter contrast as described in Section 2. We do not perform a full multi-parameter MCMC fit; the present analysis is instead a proof-of-concept comparison of fixed, geometry-motivated models against current growth data. We also report the corresponding p-values and the Akaike and Bayesian information criteria (AIC and BIC) under simple assumptions about the effective number of free parameters in each model.

Figure 1. Growth-rate observable $f{\sigma }_8\left(z\right)$ compared with the “Gold” compilation of 22 redshift-space-distortion measurements. Black points with $1\sigma$ error bars show the observational data, while the curves denote the theoretical predictions at $k=0.1h{\mathrm{Mpc}}^{-1}$ for the three fixed backgrounds considered in this work: $\mathrm{\Lambda }$CDM calibrated to the Planck 2018 fiducial cosmology (solid black), the sudden future singularity (SFS) model (black dashed), and the finite scale factor singularity (FSFS) model (grey dotted). For each model we solve the full scale-dependent linear perturbation equations without invoking the sub-Hubble or slowly varying potential approximations, and consistently rescale each data point to the corresponding background geometry via the standard $E\left(z\right)D_A\left(z\right)$ correction.

Figure 1. Growth-rate observable $f{\sigma }_8\left(z\right)$ compared with the “Gold” compilation of 22 redshift-space-distortion measurements. Black points with $1\sigma$ error bars show the observational data, while the curves denote the theoretical predictions at $k=0.1h{\mathrm{Mpc}}^{-1}$ for the three fixed backgrounds considered in this work: $\mathrm{\Lambda }$CDM calibrated to the Planck 2018 fiducial cosmology (solid black), the sudden future singularity (SFS) model (black dashed), and the finite scale factor singularity (FSFS) model (grey dotted). For each model we solve the full scale-dependent linear perturbation equations without invoking the sub-Hubble or slowly varying potential approximations, and consistently rescale each data point to the corresponding background geometry via the standard $E\left(z\right)D_A\left(z\right)$ correction.

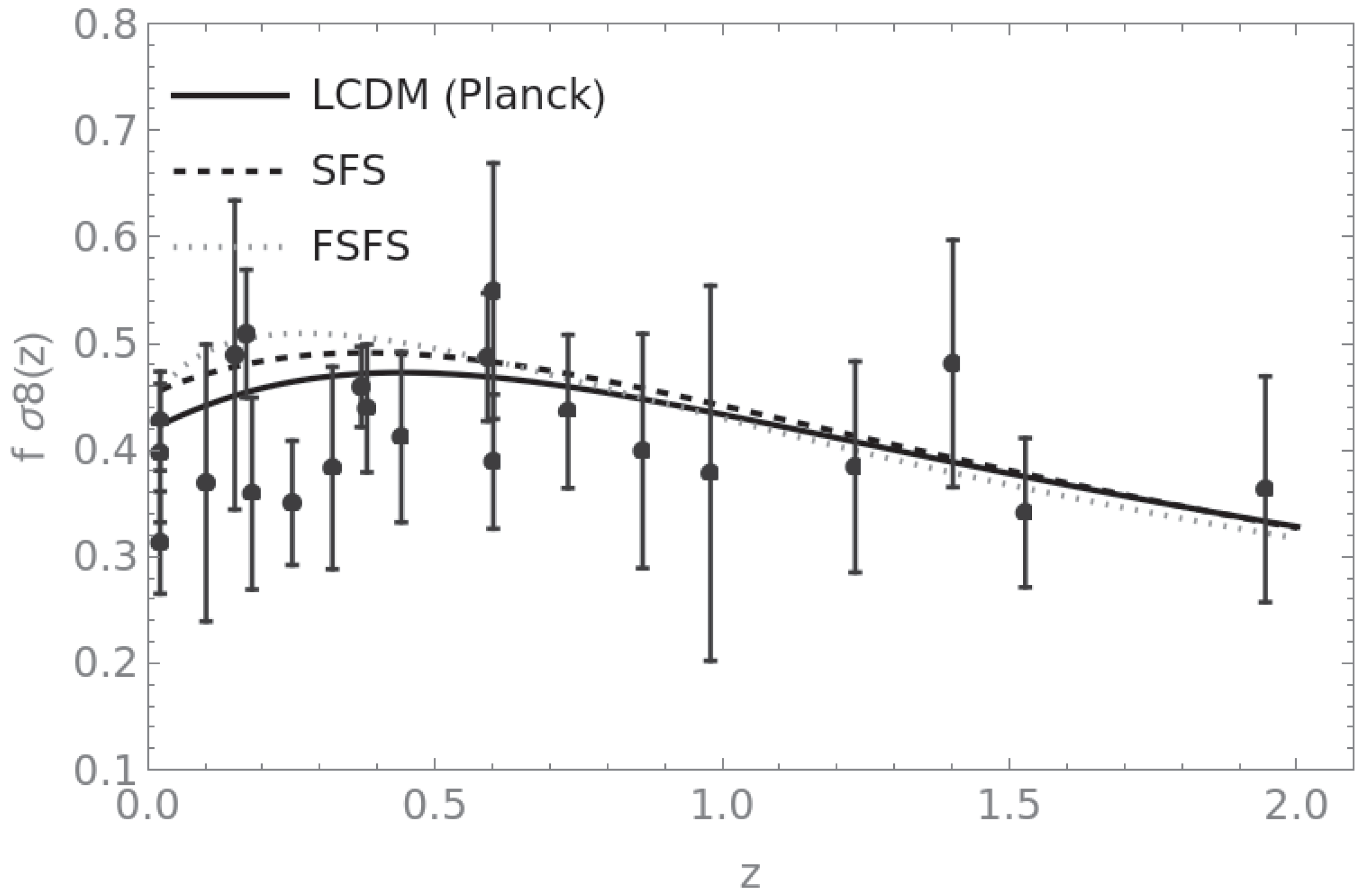
5. Results and Conclusions

Using the methodology of Section 4 we first evaluate the growth observable $f{\sigma }_8\left(z\right)$ in the reference $\mathrm{\Lambda }$CDM model and in the two future-singularity scenarios (SFS and FSFS), for a representative linear scale $k=0.1h{\mathrm{Mpc}}^{-1}$. For each model we then compute the residual vector $V_i$ and the corresponding ${\chi }^2$ for the $N=22$ data points in our $f{\sigma }_8$ compilation.

For the fixed SFS parameter set used in previous geometrical analyses,5 we obtain

$${\chi }_{\mathrm{SFS}}^2\simeq 26.5\mathrm{for}N=22.$$

(5.1)

If we treat this as a pure goodness-of-fit test with $\nu =N$ degrees of freedom, the corresponding p-value is

$$p_{\mathrm{SFS}}\simeq 0.23,$$

(5.2)

so the SFS template provides an acceptable fit to the current $f{\sigma }_8$ data. The reduced chi-squared is

$${\chi }_{\nu ,\mathrm{SFS}}^2\equiv {\displaystyle \frac{{\chi }_{\mathrm{SFS}}^2}{N}}\simeq 1.21,$$

(5.3)

or, if one subtracts an effective number of free parameters $k_{\mathrm{SFS}}=4$ from the data points, ${\chi }_{\nu ,\mathrm{SFS}}^2\simeq 1.47$ for $\nu =22-4$.

For the reference $\mathrm{\Lambda }$CDM model fixed to the Planck 2018 best-fit parameters, solving the full scale-dependent perturbation equations yields

$${\chi }_{\mathrm{\Lambda }\mathrm{CDM}}^2\simeq 17.5,$$

(5.4)

corresponding to a p-value

$$p_{\mathrm{\Lambda }\mathrm{CDM}}\simeq 0.74,$$

(5.5)

i.e. the $f{\sigma }_8$ data show no tension with this particular growth history. The reduced chi-squared is

$${\chi }_{\nu ,\mathrm{\Lambda }\mathrm{CDM}}^2\simeq 0.79(\nu =22),$$

(5.6)

or ${\chi }_{\nu ,\mathrm{\Lambda }\mathrm{CDM}}^2\simeq 0.87$ if one subtracts two effective parameters $k_{\mathrm{\Lambda }\mathrm{CDM}}=2$ (for ${\mathrm{\Omega }}_{m,0}$ and ${\sigma }_{8,0}$) and uses $\nu =22-2$.

The difference

$$\Delta {\chi }_{\mathrm{SFS}-\mathrm{\Lambda }\mathrm{CDM}}^2\equiv {\chi }_{\mathrm{SFS}}^2-{\chi }_{\mathrm{\Lambda }\mathrm{CDM}}^2\simeq 9.1$$

(5.7)

quantifies the degradation in the goodness-of-fit when going from the Planck $\mathrm{\Lambda }$CDM background to the SFS model, for the same $N=22$ data points and without any parameter fitting. While both models yield acceptable absolute p-values, the SFS template is clearly disfavoured in a relative sense.

We have performed an analogous calculation for a representative FSFS parameter set compatible with geometrical probes. In this case the best-fit chi-squared remains larger than in the $\mathrm{\Lambda }$CDM reference,

$${\chi }_{\mathrm{FSFS}}^2\simeq 34.3,$$

(5.8)

which for $N=22$ data points corresponds to a p-value,

$$p_{\mathrm{FSFS}}\simeq 0.05.$$

(5.9)

The reduced chi-squared is ${\chi }_{\nu ,\mathrm{FSFS}}^2\simeq 3.34$ (or $\simeq 4.08$ if we subtract $k_{\mathrm{FSFS}}=4$ from the degrees of freedom), shows that the FSFS benchmark provides noticeably worse fit to the growth data than the Planck$\mathrm{\Lambda }$CDM, but does not reach the level of decisive exclusion. Relative to $\mathrm{\Lambda }$CDM the degradation in the fit is

$$\Delta {\chi }_{\mathrm{FSFS}-\mathrm{\Lambda }\mathrm{CDM}}^2\simeq 16.8.$$

(5.10)

To provide a rough model-comparison diagnostic, we also evaluate the Akaike and Bayesian information criteria,

$$\mathrm{AIC}={\chi }^2+2k,\mathrm{BIC}={\chi }^2+klnN,$$

(5.11)

where k is the effective number of free parameters entering the $f{\sigma }_8$ prediction. Taking $k_{\mathrm{\Lambda }\mathrm{CDM}}=2$ and $k_{\mathrm{SFS}}=k_{\mathrm{FSFS}}=4$, we find for the SFS model

$$\Delta {\mathrm{AIC}}_{\mathrm{SFS}-\mathrm{\Lambda }\mathrm{CDM}}\simeq 13.1,\Delta {\mathrm{BIC}}_{\mathrm{SFS}-\mathrm{\Lambda }\mathrm{CDM}}\simeq 15.3,$$

(5.12)

and for the FSFS model

$$\Delta {\mathrm{AIC}}_{\mathrm{FSFS}-\mathrm{\Lambda }\mathrm{CDM}}\simeq 20,\Delta {\mathrm{BIC}}_{\mathrm{FSFS}-\mathrm{\Lambda }\mathrm{CDM}}\simeq 23.$$

(5.13)

In both cases the information criteria prefer the standard $\mathrm{\Lambda }$CDM model over the singularity scenarios; according to common interpretative scales, $\Delta \mathrm{BIC}\gtrsim 10$ already corresponds to “very strong” evidence against the more complex model.

Overall, our analysis shows that:

(i)

For the particular fixed parameter sets considered in this work, the SFS and FSFS benchmarks are disfavoured to different degrees with respect to the Planck-2018–calibrated $\mathrm{\Lambda }$CDM reference model once model complexity is taken into account.

(ii)

The FSFS benchmark considered here yelds a poorer fit to the $f{\sigma }_8$ data than Planck$\mathrm{\Lambda }$CDM and is disfavoured by the information criteria, but it is not decisively ruled out by growth measurements.

We emphasise that these conclusions are based on fixed parameter choices and on a single $f{\sigma }_8$ compilation, and that we have not performed a joint likelihood analysis including geometrical probes, CMB anisotropies, and the latest full-shape clustering measurements (e.g. DESI DR2). A fully consistent global fit, including a detailed treatment of the DESI and Euclid likelihoods and of possible non-linear and biasing systematics, is beyond the scope of this work and is left for future studies. Nevertheless, the present results demonstrate that current growth-of-structure measurements already provide a non-trivial consistency test for future-singularity dark energy models, and that the particular SFS and FSFS templates examined here are not favoured over the standard $\mathrm{\Lambda }$CDM cosmology.