The Quantum Emergent Vacuum: A Spectrally Bounded Framework for Physical Unification

1. Introduction

In conventional quantum field theory, the vacuum is treated as a continuous and unbounded energetic background [2,7]. All possible fluctuation modes, extending up to arbitrarily high energies, contribute to the vacuum energy. This leads to the well-known discrepancy between the theoretically predicted vacuum energy density and the observed value of the cosmological constant, representing one of the central tensions in modern theoretical physics [3]. In this work we develop a unified theoretical framework, referred to as the Quantum Emergent Vacuum (QEV) model Ref. [1]. The QEV model describes the vacuum as a spectrally bounded medium whose physical properties, particle content, coupling structure and gravitational response all arise from its internal spectral organization.

Vacuum fluctuations are allowed only within a finite energy interval, bounded above by a hadronic limit (the QCD confinement scale) and below by a thermal limit (a critical temperature associated with hadronic matter formation) [4]. Within these boundaries, we introduce a spectral density and a discrete set of energy levels, and we propose the hypothesis that the stable particles of the Standard Model can be interpreted as excitations of this bounded vacuum spectrum. Gauge symmetries and coupling constants appear in this picture as emergent properties of the internal spectral structure.

Furthermore, we connect the spectral description of the vacuum to a thermodynamic formulation by introducing a spectral entropy and an effective temperature. This allows a thermodynamic interpretation of gravity as a response of the bounded vacuum spectrum to matter-energy, in the spirit of induced and entropic gravity scenarios [3,5,6]. The goal of this article is to systematically formulate this emergent spectral vacuum model and to examine its implications for vacuum energy, particle physics, and gravitational phenomena.

2. Hypothesis and Model Framework

The QEV model, as an extension of the SBV+QEV construction in Ref. [1], is based on the central hypothesis that the physical vacuum is not an unbounded quantum background but a spectrally constrained medium characterized by two physically motivated bounds.

2.1. Central Hypothesis

The central hypothesis of this work is that the physical vacuum is not an unbounded quantum background, but a spectrally bounded medium in which vacuum fluctuations occur only within a finite energy range:

$$E_{min}\le E\le E_{max}.$$

(1)

Here,

• $E_{max}$ is set by the hadronic confinement scale (approximately the QCD scale, $L_{\mathrm{QCD}}\approx 1\mathrm{fm}$), which prevents vacuum fluctuations from accessing unphysical, deconfined quark states [4];
• $E_{min}$ is determined by the thermal transition scale associated with hadronic matter formation (with a critical temperature of approximately 30–$34\mathrm{K}$), below which vacuum excitations become thermally suppressed or “frozen out”.

This establishes a naturally bounded spectral domain governing all vacuum dynamics, without requiring ultraviolet extrapolation or fine-tuned high-energy parameters.

2.2. Definition of the Spectral Vacuum

2.2.1. Spectral Density

The vacuum is described by a spectral density $\rho \left(E\right)$ satisfying

$$\rho \left(E\right)=0\mathrm{for}E<E_{min},\rho \left(E\right)=0\mathrm{for}E>E_{max}.$$

(2)

Within the physical interval, we write

$$\rho \left(E\right)={\rho }_{0}f\left(E\right),$$

(3)

where ${\rho }_0$ is a normalization factor and $f\left(E\right)$ is a dimensionless shape function capturing the internal structure of the spectrum.

The vacuum energy density follows from

$${\rho }_{\mathrm{vac}}={\int }_{E_{min}}^{E_{max}}E\rho \left(E\right)\mathrm{d}E.$$

(4)

This finite integral replaces the divergences encountered in standard quantum field theory [2,7].

2.3. Discrete Energy Levels and Vacuum Modes

To model physical excitations, we introduce a discrete set of vacuum modes,

$$\left\{E_n\right\},n=1,2,3,\dots ,$$

(5)

with

$$E_{min}\le E_1\le E_2\le \dots \le E_{max}.$$

(6)

The spectral density may then be written as

$$\rho \left(E\right)=\sum _n{g}_n\delta (E-E_n),$$

(7)

where $g_n$ is the degeneracy of level n.

The vacuum energy density in discrete form becomes

$${\rho }_{\mathrm{vac}}=\sum _n{g}_n{E}_n.$$

(8)

The central physical claim is:

Each stable particle of the Standard Model corresponds to a specific excitation level $E_n$ of the bounded vacuum spectrum, with an associated degeneracy $g_n$ and transformation properties.

The rest mass of mode n follows from

$$m_n{c}^2=E_n(k=0).$$

(9)

2.4. Dispersion Relations and Field Representation

Each mode n is equipped with a dispersion relation of the form

$$E_n\left(k\right)=\sqrt{{\left(m_n{c}^2\right)}^2+{(\hslash ck)}^2},$$

(10)

analogous to standard relativistic field excitations [7]. The spatial realization of mode n is represented by a field amplitude ${\mathsf{\Phi }}_n\left(x\right)$, and the total field is written as

$${\mathsf{\Phi }}_{\mathrm{total}}\left(x\right)=\sum _n{\mathsf{\Phi }}_n\left(x\right)u_n\left(x\right),$$

(11)

where $u_n\left(x\right)$ are basis functions of the allowed spectral modes.

The effective Lagrangian is

$${\mathcal{L}}_{\mathrm{eff}}=\sum _n\left({\mathcal{L}}_{\mathrm{kin}}\left({\mathsf{\Phi }}_n\right)-V_n\left({\mathsf{\Phi }}_n\right)\right)+\sum _{n,m}{\mathcal{L}}_{\mathrm{int}}({\mathsf{\Phi }}_n,{\mathsf{\Phi }}_m),$$

(12)

with interactions arising from spectral overlap.

2.5. Emergent Gauge Symmetries

Degeneracies in the spectrum define internal symmetry spaces. If level $E_n$ has degeneracy $g_n$, the associated Hilbert space ${\mathcal{H}}_n$ is $g_n$-dimensional. Symmetry transformations acting within this space satisfy

$$G_n\subset U\left(g_n\right).$$

(13)

Thus,

Gauge symmetries emerge as symmetry groups of degenerate spectral subspaces.

This yields naturally:

• $\mathrm{SU}\left(3\right)$ as the symmetry of color triplet modes,
• $\mathrm{SU}\left(2\right)$ for weak doublets,
• $\mathrm{U}\left(1\right)$ as global phase invariance,

in line with the structure of the Standard Model [7].

The full Standard Model gauge group

$$\mathrm{SU}\left(3\right)\times \mathrm{SU}\left(2\right)\times \mathrm{U}\left(1\right)$$

(14)

therefore emerges from the vacuum spectrum.

2.6. Coupling Constants from Spectral Overlap

Interactions arise from overlap integrals in spectral space:

$$g_{nm}\propto \int f_n\left(E\right)f_m\left(E\right)W\left(E\right)\mathrm{d}E,$$

(15)

where $f_n\left(E\right)$ describes the spectral structure of mode n and $W\left(E\right)$ encodes vacuum-weighting.

Thus,

Coupling constants are geometric properties of the spectral vacuum.

This provides a natural route to understanding parameter hierarchies in terms of the underlying vacuum structure.

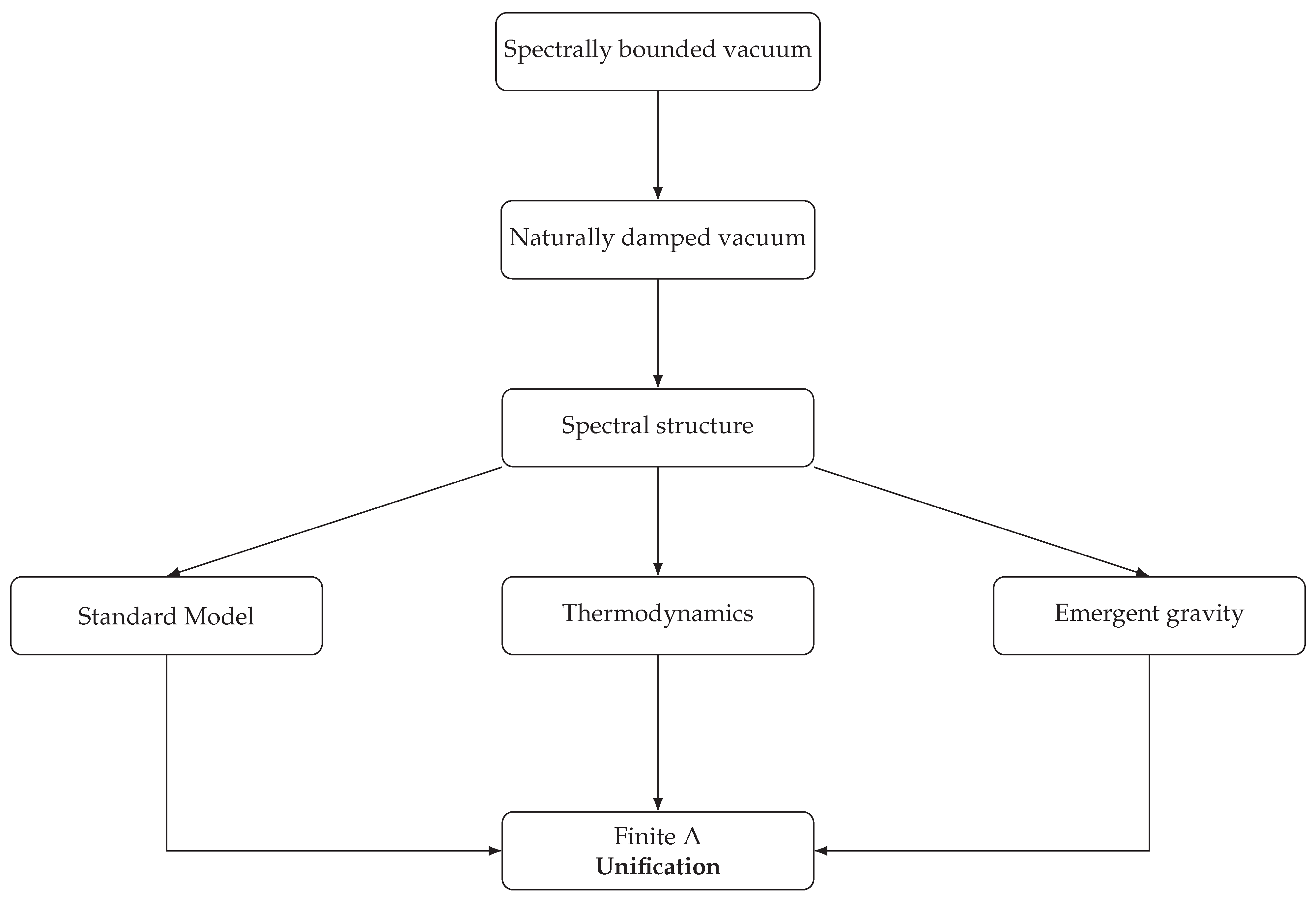
2.7. Conceptual Overview of Unification

Figure 1. Conceptual overview of a spectrally bounded and naturally damped vacuum leading to the Standard Model, thermodynamic behaviour and to a unified description of a finite vacuum energy $\mathsf{\Lambda }$ without fine-tuning

Figure 1. Conceptual overview of a spectrally bounded and naturally damped vacuum leading to the Standard Model, thermodynamic behaviour and to a unified description of a finite vacuum energy $\mathsf{\Lambda }$ without fine-tuning

3. Spectral Bounds and Physical Scaling

In the QEV model, the spectral window $[E_{min},E_{max}]$ determines the full physical content of the vacuum, including its energy density and its emergent excitations. In this section we estimate the physical scales associated with both limits and evaluate their implications for the resulting vacuum energy density.

3.1. Upper Bound: Hadronic Confinement Scale

The upper bound $E_{max}$ is set by the QCD confinement length, typically taken to be of order

$$L_{\mathrm{QCD}}\approx 1\mathrm{fm},$$

(16)

corresponding to an energy scale

$$E_{max}\sim {\displaystyle \frac{\hslash c}{L_{\mathrm{QCD}}}}\approx 200\mathrm{MeV},$$

(17)

consistent with hadronic phenomenology [4]. Modes above this scale would correspond to unphysical, deconfined quark excitations, which are excluded by color confinement. This motivates a hard spectral cutoff at the confinement boundary.

3.2. Lower Bound: Thermal Transition Scale

The lower bound is set by a critical temperature associated with the formation of hadronic matter. Below

$$T_{\mathrm{crit}}\approx 30-34\mathrm{K},$$

(18)

vacuum excitations become thermally suppressed, implying a minimum energy

$$E_{min}\sim k_{\mathrm{B}}{T}_{\mathrm{crit}}\approx 3\mathrm{meV}.$$

(19)

3.3. Finite Vacuum Energy Without Fine-Tuning

The vacuum energy density becomes

$${\rho }_{\mathrm{vac}}={\int }_{E_{min}}^{E_{max}}E\rho \left(E\right)\mathrm{d}E,$$

(20)

which is automatically finite. For reasonable spectral shapes $f\left(E\right)$, the predicted energy density can be brought close to the observed cosmological constant,

$${\rho }_{\mathsf{\Lambda }}\sim {\left(2\mathrm{meV}\right)}^4,$$

(21)

without requiring fine-tuning [3]. This suggests that the observed vacuum energy may arise as a consequence of the bounded spectral interval itself, rooted in hadronic and thermal physics [2,4].

4. Implications for the Standard Model

In the QEV model, the discrete spectral structure provides a natural route for understanding the particle content and gauge symmetries of the Standard Model as emergent features of the vacuum.

4.1. Particle Spectrum as Vacuum Excitations

Each stable particle species is associated with a discrete spectral level $E_n$, with rest mass

$$m_n{c}^2=E_n(k=0).$$

(22)

Degeneracies $g_n$ correspond to internal degrees of freedom such as color or weak isospin. This offers an organizing principle for the Standard Model spectrum without freely chosen parameters, complementing the usual quantum field theoretic view [7].

4.2. Emergence of Gauge Symmetries

If level $E_n$ has degeneracy $g_n$, its symmetry group is a subgroup of $U\left(g_n\right)$,

$$G_n\subseteq U\left(g_n\right).$$

(23)

This produces the full gauge group of the Standard Model:

• $SU\left(3\right)$ from triplet degeneracy of color modes,
• $SU\left(2\right)$ from doublet degeneracy of weak modes,
• $U\left(1\right)$ from global phase freedom.

Thus the gauge structure is not fundamental but emergent from the spectral vacuum.

4.3. Coupling Constants as Geometric Quantities

Couplings arise from overlap integrals in spectral space:

$$g_{nm}\propto \int f_n\left(E\right)f_m\left(E\right)W\left(E\right)\mathrm{d}E.$$

(24)

Their relative magnitudes therefore reflect geometric properties of the vacuum spectrum, providing a natural explanation for hierarchy patterns in the Standard Model and offering an alternative to conventional parameterization [3].

5. Thermodynamic Response and Emergent Gravity

A key feature of the QEV model is that gravity arises as a thermodynamic response of the spectrally bounded vacuum, rather than as a fundamental interaction. The spectral vacuum supports a thermodynamic interpretation based on a spectral entropy,

$$S_{\mathrm{spec}}=-\int P\left(E\right)lnP\left(E\right)\mathrm{d}E,$$

(25)

where $P\left(E\right)$ is the normalized population of spectral modes.

5.1. Macroscopic Dynamics from Entropy Variations

With the Boltzmann-like distribution

$$P\left(E\right)\propto \rho \left(E\right)exp\left(-{\displaystyle \frac{E}{k_{\mathrm{B}}{T}_{\mathrm{eff}}}}\right),$$

(26)

the extremization condition

$$\delta S_{\mathrm{spec}}+\beta \delta E_{\mathrm{total}}=0$$

(27)

leads to macroscopic dynamical equations analogous to gravitational behavior. Gravity arises not as a fundamental field but as a thermodynamic response of the vacuum, in the spirit of induced gravity and entropic gravity frameworks [3,5,6].

5.2. Connection to Cosmological Acceleration

The finite spectral interval naturally yields:

• a positive vacuum energy density,
• a late-time acceleration of the universe,
• a scale comparable to the observed cosmological constant.

This suggests that cosmic acceleration may be rooted in the spectral structure of the vacuum itself, without invoking dark energy as an independent entity [3].

6. Comparison with Existing Approaches

The QEV model occupies a distinct conceptual position relative to standard quantum field theory, string theory, and existing emergent gravity proposals. The idea of a structured vacuum has appeared in various forms throughout theoretical physics. In this section we compare the bounded spectral vacuum framework with several established approaches, highlighting similarities, differences, and potential advantages. The full overview of this comparison is given in Table 2.

6.1. Quantum Field Theory and the Cosmological Constant Problem

In conventional quantum field theory, vacuum energy is computed by summing zero-point energies of all modes up to an ultraviolet cutoff [2,7]. This leads to a theoretical prediction for ${\rho }_{\mathrm{vac}}$ that exceeds observations by up to 120 orders of magnitude.

Unlike the standard QFT approach:

• the bounded spectral model has no ultraviolet limit extending to infinity;
• the QCD scale itself provides a physical upper bound [4];
• the thermal lower bound suppresses infrared contributions;
• the resulting vacuum energy is automatically finite and observationally compatible.

Thus the model avoids the cosmological constant problem by construction, without invoking renormalization or fine-tuning [3].

6.2. String Theory and Higher-Dimensional Frameworks

String theory attempts to unify interactions by introducing extended objects and higher-dimensional compactified spaces. In contrast:

• The bounded spectral model makes no reference to higher dimensions.
• All physical structure arises from internal spectral organization of the vacuum.
• Gauge symmetries emerge from spectral degeneracies rather than from compactification.
• The particle spectrum is encoded in discrete vacuum levels rather than in vibrational string modes.

Whereas string theory introduces a vast “landscape” of possible vacua, the bounded spectral vacuum is minimalistic, tied directly to measurable scales such as $L_{\mathrm{QCD}}$ and $T_{\mathrm{crit}}$.

6.3. Induced Gravity and Entropic Gravity

Sakharov’s induced gravity [5] and Verlinde’s entropic gravity [6] both treat gravity as an emergent phenomenon. The present framework aligns with these ideas through:

• the thermodynamic interpretation of spectral entropy,
• the emergence of gravitational dynamics from entropy gradients,
• the lack of a fundamental gravitational field.

However, it differs in two essential points:

• Emergence is tied directly to spectral bounds rather than geometric microstates.
• Vacuum energy and gravity share a unified spectral origin.

6.4. QCD Vacuum Models

The QCD vacuum is known to possess condensates and non-trivial structure [4]. In this respect the QEV model is consistent with:

• confinement generating a physical upper bound,
• thermal transitions generating a physical lower bound,
• hadronic physics determining vacuum properties.

However, the present model extends beyond QCD by treating the entire Standard Model and gravity as emergent from the same spectral structure.

7. Discussion

The QEV model offers several conceptual advantages, but it also raises open questions that require further mathematical and phenomenological refinement.

7.1. Naturalness and Physical Motivation

A key strength of the model is that the spectral bounds are grounded in well-established physics:

• The QCD confinement scale sets a physical upper limit.
• A critical thermal scale sets a physical lower limit.

No arbitrary high-energy assumptions are needed, in contrast to theories relying on unknown Planck-scale physics.

7.2. Origin of Spectral Degeneracies

The emergence of gauge symmetries from spectral degeneracies provides a physically compelling alternative to traditional symmetry postulates [7]. Yet several questions remain:

• What determines the exact degeneracies of each level?
• Why do these degeneracies align with the structure of the Standard Model?
• Can symmetry breaking (e.g., electroweak symmetry breaking) be described purely spectrally?

These questions point toward possible deeper mathematical constraints on the spectral density.

7.3. Dynamical Behavior of the Vacuum Spectrum

The current formulation treats the vacuum spectrum as static, but cosmological evolution suggests that:

• $E_{min}$ may have evolved with cosmic temperature,
• the spectral distribution may have undergone phase transitions,
• gravitational fields may locally deform the spectrum.

Including such dynamics may yield new insights into structure formation and cosmic history.

7.4. Relation to Observables

The model makes several qualitative predictions:

• a specific scale for vacuum energy density,
• hierarchical coupling strengths,
• emergent gauge symmetries,
• thermodynamic gravitational behavior,
• potential spectral signatures in particle masses.

A key next step is to derive quantitative predictions that can be confronted with observational and experimental data.

8. Conclusions

The Quantum Emergent Vacuum (QEV) model presented here extends the spectrally bounded vacuum picture of Ref. [1] from a present-day description of vacuum energy to a broader framework in which particle content, gauge symmetries and gravity share a common spectral origin.

The central features of this framework are:

• A natural upper bound given by the QCD confinement scale.
• A natural lower bound given by a thermal transition scale.
• A finite vacuum energy density consistent with cosmology.
• Discrete spectral levels corresponding to particle species.
• Emergent gauge symmetries arising from spectral degeneracies.
• Geometric coupling constants obtained from spectral overlap.
• A thermodynamic interpretation of gravity based on spectral entropy.

Together, these features provide a unified way to interpret vacuum energy, particle physics, and gravitation within a single coherent model. While the present work establishes the conceptual foundation, several open questions remain:

• the detailed mathematical structure of the spectral density,
• the origin of exact Standard Model degeneracies,
• dynamical evolution of spectral bounds,
• quantitative predictions for particle masses and coupling constants.

Nevertheless, the bounded spectral vacuum offers a compelling alternative to existing high-energy frameworks, requiring no fine-tuning, no higher dimensions, and no ultraviolet extrapolation. The QEV model thus provides a physically grounded and observationally compatible alternative to ultraviolet-based unification programs.

Appendix N.1 Spectral Clustering for Three Lepton Families

We assume that, within the QEV spectral window $[E_{min},E_{max}]$, there exists a band of levels predominantly associated with leptonic excitations. We model this band as three closely spaced “family clusters”,

$${\mathcal{L}}_e,{\mathcal{L}}_{\mu },{\mathcal{L}}_{\tau },$$

each containing a weak doublet-like structure.

For each family $i=e,\mu ,\tau$ we introduce a pair of levels

$$E_{{\nu }_i},E_{{\ell }_i},$$

with degeneracy pattern

$$g_{{\nu }_i}=1,g_{{\ell }_i}=1,$$

but where the pair transforms as an $SU\left(2\right)$ doublet in the internal spectral space. We represent this schematically as

$$\left(\begin{array}{c}{\nu }_i\\ {\ell }_i\end{array}\right)\in {\mathcal{H}}_i^{\left(2\right)},$$

where ${\mathcal{H}}_i^{\left(2\right)}$ is a two-dimensional subspace associated with family i. The $SU\left(2\right)$ structure emerges from the symmetry group acting on ${\mathcal{H}}_i^{\left(2\right)}$.

Appendix N.2 Masses as Shifted Spectral Levels

Within the QEV framework, masses correspond to the rest energies of the excitations:

$$m_{{\nu }_i}{c}^2=E_{{\nu }_i}(k=0),m_{{\ell }_i}{c}^2=E_{{\ell }_i}(k=0).$$

We assume that, to leading order, the three families share a common family-independent base energy $E_0$ for their doublet:

$$E_{{\nu }_i}^{\left(0\right)}\approx E_{{\ell }_i}^{\left(0\right)}\approx E_0,$$

and that the observed mass hierarchy arises from small family-dependent spectral shifts $\delta E_i$ and intra-doublet splittings ${\Delta }_i$:

$$E_{{\nu }_i}=E_0+\delta E_i-{\Delta }_i,E_{{\ell }_i}=E_0+\delta E_i+{\Delta }_i.$$

The three families are then distinguished by the pattern

$$\delta E_e<\delta E_{\mu }<\delta E_{\tau },$$

while the small parameters ${\Delta }_i$ control the neutrino masses relative to their charged partners.

In this toy construction, the ordering

$$m_e<m_{\mu }<m_{\tau }$$

arises naturally from

$$m_{{\ell }_i}\propto E_0+\delta E_i+{\Delta }_i,$$

with

$$\delta E_e<\delta E_{\mu }<\delta E_{\tau }.$$

Appendix N.3 Spectral Wavefunctions and Weak Interactions

To describe weak interactions, we associate to each family i a pair of spectral wavefunctions $f_{{\nu }_i}\left(E\right)$ and $f_{{\ell }_i}\left(E\right)$, peaked around $E_{{\nu }_i}$ and $E_{{\ell }_i}$ respectively. The weak interaction strength between these modes is encoded in an overlap integral of the form

$$g_{\mathrm{weak}}^{\left(i\right)}\propto {\int }_{E_{min}}^{E_{max}}{f}_{{\nu }_i}\left(E\right)f_{{\ell }_i}\left(E\right)W_{\mathrm{weak}}\left(E\right)\mathrm{d}E,$$

where $W_{\mathrm{weak}}\left(E\right)$ is a weight function capturing the coupling of the spectral band to the emergent weak gauge field.

If the three families are associated with slightly different regions of the spectrum, then the integrals $g_{\mathrm{weak}}^{\left(i\right)}$ may differ slightly, providing a spectral origin for small family-dependent effects.

Appendix N.4 Neutrino Masses and Mixing

In the QEV model, neutrino masses can be interpreted as arising from tiny spectral shifts ${\Delta }_i$ and possible mixing among the ${\nu }_i$ levels. We introduce a small off-diagonal spectral mixing matrix

$$H_{\nu }=\left(\begin{array}{ccc}{E}_{{\nu }_e}& {ϵ}_{e\mu }& {ϵ}_{e\tau }\\ {ϵ}_{e\mu }& E_{{\nu }_{\mu }}& {ϵ}_{\mu \tau }\\ {ϵ}_{e\tau }& {ϵ}_{\mu \tau }& E_{{\nu }_{\tau }}\end{array}\right),$$

with ${ϵ}_{ij}\ll |E_{{\nu }_i}-E_{{\nu }_j}|$.

Diagonalizing $H_{\nu }$ yields mass eigenvalues $m_{{\nu }_1},m_{{\nu }_2},m_{{\nu }_3}$ and a mixing matrix $U_{\mathrm{PMNS}}$, which in principle can be related to the underlying spectral structure via

$$H_{\nu }=U_{\mathrm{PMNS}}\left(\begin{array}{ccc}{m}_{{\nu }_1}{c}^2& 0& 0\\ 0& m_{{\nu }_2}{c}^2& 0\\ 0& 0& m_{{\nu }_3}{c}^2\end{array}\right)U_{\mathrm{PMNS}}^{†}.$$

Although we do not attempt a quantitative fit here, this illustrates how neutrino masses and mixing can be treated as second-order effects of the QEV spectral structure.

Appendix N.5 Summary of the Toy Construction

This toy example shows how:

• three lepton families can be associated with three spectral clusters,
• each family corresponds to a doublet-like subspace in the QEV spectrum,
• charged lepton masses arise from family-dependent spectral shifts,
• neutrino masses and mixing follow from small splittings and mixing in the neutrino subsector.

A full quantitative implementation would require a specific choice of spectral density, explicit forms for $f_{{\nu }_i}\left(E\right)$ and $f_{{\ell }_i}\left(E\right)$, and a detailed construction of the weak interaction weight $W_{\mathrm{weak}}\left(E\right)$. Nevertheless, this example demonstrates that the QEV framework is structurally capable of accommodating the observed lepton sector as emergent spectral excitations.

Appendix N.6 Short Intuitive Explanation of the Lepton Construction

This appendix illustrates how the three lepton families (electron, muon, tau and their corresponding neutrinos) can emerge from the discrete energy levels of the QEV model. The goal is not to provide a full numerical derivation, but to present a simple and transparent mechanism that shows how the structure of the Standard Model lepton sector can arise from a spectrally bounded vacuum.

Appendix N.6.1 Three Families as Three Spectral Clusters

Within the QEV energy window, we assume a set of levels associated with leptonic excitations. These levels naturally group into three tightly spaced clusters: one for the electron family, one for the muon family, and one for the tau family. Each cluster corresponds to a distinct lepton generation.

Appendix N.6.2 SU(2) Doublets from Spectral Structure

Each family cluster contains two levels: one associated with the neutrino and one associated with the charged lepton. Together these form a spectral SU(2) doublet, because the two levels share an internal symmetry structure encoded in the QEV spectrum. This reproduces the familiar pattern $({\nu }_e,e)$, $({\nu }_{\mu },\mu )$, $({\nu }_{\tau },\tau )$ of the Standard Model.

Appendix N.6.3 Mass Hierarchy from Small Spectral Shifts

The three lepton families are assumed to lie near a common base energy, but each family is shifted slightly by a small amount. These shifts generate the observed mass hierarchy: the smallest shift corresponds to the lightest charged lepton (electron), an intermediate shift to the muon, and the largest shift to the tau. Neutrinos remain extremely light because their spectral levels lie only slightly below the neutral baseline of each doublet. In this way, the mass ordering arises directly from the pattern of spectral shifts.

Appendix N.6.4 Weak Interactions from Wavefunction Overlap

Each energy level has an associated spectral wavefunction. The strength of the weak interaction between members of a doublet is governed by the overlap integral of these wavefunctions with a weak-interaction weight function. Thus, the weak force emerges naturally from the internal structure of the QEV spectrum, without the need to introduce additional fundamental ingredients beyond the spectral vacuum itself.

Appendix N.6.5 Neutrino Mixing from Cross-Family Couplings

If the three neutrino levels carry small off-diagonal couplings, their eigenstates mix and form three neutrino mass eigenstates. This mixing produces the PMNS matrix and neutrino oscillations. In the QEV picture, neutrino mixing appears as a direct consequence of tiny couplings between the spectral clusters associated with the three lepton families.

Appendix N.6.6 Key Idea

This toy example shows that three lepton generations, their SU(2) pairing, their mass hierarchy, and neutrino mixing can all emerge naturally from the spectral organisation of the QEV vacuum. It demonstrates that the QEV framework is structurally capable of reproducing the lepton sector of the Standard Model as a set of emergent spectral excitations.

Appendix O.1 Short Intuitive Explanation of the Quark / SU(3) Sector

In this section we extend the intuitive picture developed for the lepton doublets to the quark sector. The aim is to illustrate how the QEV spectrum can naturally generate the internal colour symmetry, the existence of six quark flavours, and the hierarchical structure of their masses.

Appendix O.2 Colour as a Three-Fold Spectral Degeneracy

Within the QEV framework, quarks correspond to spectral excitations that exhibit a three-fold degeneracy:

$$g_q=3.$$

This degeneracy is interpreted as an internal symmetry acting on a three-dimensional subspace of the spectral Hilbert space. The associated symmetry group is the unitary group of this subspace, which naturally gives rise to

$$SU{\left(3\right)}_{\mathrm{colour}}.$$

Each quark flavour thus appears as a triplet of spectral states

$$\left\{\right|q_r\rangle ,|q_g\rangle ,|q_b\rangle \},$$

corresponding to the three colour charges.

Appendix O.3 Flavours from Distinct Spectral Clusters

As with leptons, the six quark flavours

$$u,d,c,s,t,b$$

are associated with six distinct spectral clusters. Each cluster has internal colour-triplet structure, but the central energies of the clusters differ, leading to the observed mass pattern.

We assume a set of six clusters

$${\mathcal{Q}}_u,{\mathcal{Q}}_d,{\mathcal{Q}}_c,{\mathcal{Q}}_s,{\mathcal{Q}}_t,{\mathcal{Q}}_b,$$

with centroid energies

$$E_u<E_d<E_s<E_c<E_b<E_t.$$

The exact ordering can be modelled by a combination of QEV spectral shifts and interactions with the hadronic cutoff scale.

Appendix O.4 Mass Hierarchy from Family-Dependent Spectral Shifts

The quark masses arise from the centroid energies of their associated spectral clusters:

$$m_q{c}^2\sim E_q.$$

Small shifts in the spectral density near each cluster produce the widely spaced mass hierarchy observed in nature. For example, the large mass of the top quark reflects a significant upward spectral displacement in the highest-energy quark cluster ${\mathcal{Q}}_t$.

The QEV picture therefore explains the extreme quark mass hierarchy as a natural consequence of the distribution of spectral shifts near the upper part of the QEV energy window.

Appendix O.5 Strong Interactions from Spectral Overlap

For each quark flavour q, the three colour states have closely aligned spectral wavefunctions

$$f_{q,r}\left(E\right),f_{q,g}\left(E\right),f_{q,b}\left(E\right),$$

whose overlap encodes the strength of the strong interaction. We model the emergent $SU\left(3\right)$ gauge coupling through a spectral integral:

$$g_s\propto \int f_{q,i}\left(E\right)f_{q,j}\left(E\right)W_{\mathrm{colour}}\left(E\right)\mathrm{d}E,$$

where $W_{\mathrm{colour}}\left(E\right)$ characterises the coupling of the spectral band to the emergent colour gauge field.

Because the three colour wavefunctions are nearly identical within each cluster, this leads naturally to an $SU\left(3\right)$-symmetric interaction.

Appendix O.6 Quark Mixing from Weak-Transition Couplings

The weak interaction couples the left-handed quark doublets

$$(u,d),(c,s),(t,b).$$

In the QEV model, these weak transitions arise from small off-diagonal spectral couplings between the corresponding cluster pairs. Writing the spectral Hamiltonian for the charge $+2/3$ quarks as

$$H_{u,c,t}=\left(\begin{array}{ccc}{E}_u& {ϵ}_{uc}& {ϵ}_{ut}\\ {ϵ}_{uc}& E_c& {ϵ}_{ct}\\ {ϵ}_{ut}& {ϵ}_{ct}& E_t\end{array}\right),$$

and similarly for the down-type quarks, the CKM mixing matrix appears upon diagonalisation:

$$H_{u,c,t}=V_{\mathrm{CKM}}\left(\begin{array}{ccc}{m}_u{c}^2& 0& 0\\ 0& m_c{c}^2& 0\\ 0& 0& m_t{c}^2\end{array}\right)V_{\mathrm{CKM}}^{†}.$$

Thus, quark mixing corresponds to cross-cluster couplings in the QEV spectrum.

Appendix O.7 Key Idea

This construction shows that:

• the colour symmetry $SU\left(3\right)$ arises from a threefold spectral degeneracy,
• six quark flavours correspond to six spectral clusters,
• quark masses reflect the centroid energies of these clusters,
• the strong interaction follows from spectral overlap within each triplet,
• and quark mixing (CKM) arises from small cross-cluster couplings.

Together, these features demonstrate that the QEV model provides a natural and unified mechanism for reproducing the quark sector and its gauge symmetry structure as emergent spectral phenomena.

Appendix O.8 Short English Explanation: Quark Sector and SU(3) from the QEV Spectrum

The quark sector of the Standard Model can be naturally interpreted within the QEV framework as a consequence of the spectral structure of the vacuum. Where leptons arise from doublets, quarks appear as triply degenerate spectral levels, giving rise to colour and the $SU\left(3\right)$ symmetry of the strong interaction.

Appendix O.8.1 Colour from a Three-Fold Spectral Degeneracy

A quark corresponds to an energy level in the QEV spectrum with three identical states. This triple degeneracy forms an internal symmetry whose natural mathematical structure is $SU\left(3\right)$. The three colour charges (red, green, blue) represent the three basis states of this degenerate subspace.

Thus, the QEV model explains why quarks carry colour and why the strong force follows an $SU\left(3\right)$ gauge symmetry.

Appendix O.8.2 Six Quark Flavours as Six Spectral Clusters

The six quark flavours

$$u,d,c,s,t,b$$

arise from six distinct spectral clusters. The centroid energy of each cluster determines the quark mass: low-energy clusters correspond to light quarks (u, d), intermediate clusters to $s,c,b$, and the highest-energy cluster to the top quark.

The strong mass hierarchy reflects the spacing between these clusters.

Appendix O.8.3 Masses from Family-Dependent Spectral Shifts

Quark masses are governed by the centroid energy of each cluster and by small internal shifts within the cluster. Because clusters can be widely separated in the QEV spectrum, the framework naturally yields the extremely large spread of quark masses, including the unusually heavy top quark.

Appendix O.8.4 Strong Interactions from Overlap of Spectral Wavefunctions

The three colour states of each quark have nearly overlapping spectral wavefunctions. The overlap among these functions determines the strength of gluon couplings, colour conservation and the emergent $SU\left(3\right)$ symmetry of the strong interaction. Thus, the strong force arises directly from the internal structure of the QEV spectrum.

Appendix O.8.5 Quark Mixing from Weak-Induced Cross-Cluster Couplings

Weak transitions couple up-type $(u,c,t)$ to down-type $(d,s,b)$ quarks. In the QEV picture, this mixing arises from small off-diagonal spectral couplings between the corresponding spectral clusters. Diagonalising the resulting matrices naturally produces the CKM matrix, quark mixing and CP violation.

Appendix O.8.6 Key Idea

The QEV model offers a coherent and unified mechanism in which:

• $SU\left(3\right)$ emerges from a triple spectral degeneracy,
• six quark flavours correspond to six spectral clusters,
• mass hierarchies follow from cluster energies,
• the strong interaction arises from spectral overlap,
• and CKM mixing results from cross-cluster couplings.

This example shows that the full quark sector can be viewed as an emergent set of spectral excitations of the Quantum Emergent Vacuum.

Table A2. Positioning of the QEV model relative to existing theoretical frameworks.

Framework	Vacuum picture	Gravity	Gauge symmetries & particles	Cosmological constant / dark energy	Unification status
QEV model (this work)	Spectrally bounded vacuum with hadronic upper bound and thermal lower bound; discrete levels with degeneracies.	Emergent, thermodynamic response of the spectral vacuum (entropy gradients).	Emergent from spectral degeneracies (SU(3), SU(2), U(1)); particles as vacuum excitations.	Finite vacuum energy from the bounded spectral window; no fine-tuning, dark energy not fundamental.	Single spectral mechanism for vacuum energy, particle content, gauge symmetries and gravity.
Standard QFT + $\mathsf{\Lambda }$CDM	Continuous UV-extended quantum vacuum; renormalised.	Fundamental GR added by hand; independent of vacuum structure.	Gauge symmetries postulated; particle content encoded manually.	$\mathsf{\Lambda }$ inserted as parameter; huge mismatch with QFT vacuum estimate.	No full unification; successful phenomenology but conceptual tension in vacuum physics.
String theory / higher dimensions	Vacuum based on higher-dimensional geometry; large landscape of possible vacua.	Typically fundamental; emerges from low-energy string limit.	Gauge groups and spectra from compactification; model-dependent.	Vacuum energy tied to moduli/fluxes; requires delicate tuning.	Ambitious unified framework, but predictive power limited by landscape.
Sakharov-induced gravity	Vacuum fluctuations induce gravity as an effective action.	Emergent, but depends on QFT content.	Gauge groups and particles external input.	Still suffers from vacuum energy problem.	Partial unification (gravity from matter), but SM structure unexplained.
Entropic gravity (Verlinde)	Vacuum as information-bearing medium; entropic/holographic structure.	Emergent: gravity as entropic force.	Gauge sector borrowed from QFT; not derived.	Reinterprets dark matter/energy as entropy effects.	Unifies gravity with thermodynamics, not with SM.
QCD vacuum models	Non-trivial QCD condensates, flux tubes and confinement vacuum.	Within GR; modifications can mimic gravitational effects.	Explains strong sector; SU(3) taken as input.	Modifies vacuum energy but no full solution.	Clarifies strong force, not a unification model.

Table A2. Positioning of the QEV model relative to existing theoretical frameworks.

Framework	Vacuum picture	Gravity	Gauge symmetries & particles	Cosmological constant / dark energy	Unification status
QEV model (this work)	Spectrally bounded vacuum with hadronic upper bound and thermal lower bound; discrete levels with degeneracies.	Emergent, thermodynamic response of the spectral vacuum (entropy gradients).	Emergent from spectral degeneracies (SU(3), SU(2), U(1)); particles as vacuum excitations.	Finite vacuum energy from the bounded spectral window; no fine-tuning, dark energy not fundamental.	Single spectral mechanism for vacuum energy, particle content, gauge symmetries and gravity.
Standard QFT + $\mathsf{\Lambda }$CDM	Continuous UV-extended quantum vacuum; renormalised.	Fundamental GR added by hand; independent of vacuum structure.	Gauge symmetries postulated; particle content encoded manually.	$\mathsf{\Lambda }$ inserted as parameter; huge mismatch with QFT vacuum estimate.	No full unification; successful phenomenology but conceptual tension in vacuum physics.
String theory / higher dimensions	Vacuum based on higher-dimensional geometry; large landscape of possible vacua.	Typically fundamental; emerges from low-energy string limit.	Gauge groups and spectra from compactification; model-dependent.	Vacuum energy tied to moduli/fluxes; requires delicate tuning.	Ambitious unified framework, but predictive power limited by landscape.
Sakharov-induced gravity	Vacuum fluctuations induce gravity as an effective action.	Emergent, but depends on QFT content.	Gauge groups and particles external input.	Still suffers from vacuum energy problem.	Partial unification (gravity from matter), but SM structure unexplained.
Entropic gravity (Verlinde)	Vacuum as information-bearing medium; entropic/holographic structure.	Emergent: gravity as entropic force.	Gauge sector borrowed from QFT; not derived.	Reinterprets dark matter/energy as entropy effects.	Unifies gravity with thermodynamics, not with SM.
QCD vacuum models	Non-trivial QCD condensates, flux tubes and confinement vacuum.	Within GR; modifications can mimic gravitational effects.	Explains strong sector; SU(3) taken as input.	Modifies vacuum energy but no full solution.	Clarifies strong force, not a unification model.