Timeless Counterspace & Shadow Gravity—A Unified Framework Foundational Consistency, Metamathematical Boundaries, and Cartographic Inquiries

1. Introduction

Modern cosmology and theoretical physics face an accumulation of anomalies that are increasingly addressed by adding baroque “dark sectors” or parallel conceptual universes. Popular expositions drift toward “mirror worlds” and multiverse speculations. This paper takes the opposite route: change ontology, not entities. We posit that the 3-D world is a shadow manifold embedded in a 4-D counterspace that contains the full content of reality. Time is not ontic; it is the parameterization of a comparison between admissible projections of one 4-D whole. “Motion” is how changes in the source layer register as geometry/inertia in the shadow.

This manuscript provides the definitive formulation of the “Timeless Counterspace & Shadow Gravity” (TCGS) framework. Beyond the physical derivations, we explicate the metamathematical logic that underpins the theory. By adopting a “cartographic, not falsificationist” methodology, we align the physical problem of dark matter with the logical problem of incompleteness. We argue that the 3-D observable universe is to the 4-D counterspace what a formal system is to a standard model in logic: capable of internal consistency but inherently unable to define its own truth [15,17].

1.0.0.1. Contributions

We: (i) codify and justify the axioms, including identity-of-source (one origin for all singularities), (ii) formalize the metamathematical boundary between the 4-D “Territory” and the 3-D “Map,” (iii) establish the homology between physical and biological artifacts (Sequention), (iv) derive GR as a relational, timeless limit, (v) introduce a single extrinsic response law replacing dark halos, and (vi) supply explicit constraints for cartographic validation.

2. Ontology and Axioms: Justification of the TCGS-SEQUENTION Framework

The TCGS framework is built upon four foundational axioms that invert the standard cosmological ontology. The central argument is that the observable three-dimensional ($\Sigma$) world is fundamentally incomplete and must be understood as a geometric projection of a higher-dimensional, static source manifold ($\mathcal{C}$).

2.1. Axiom A1: The Whole Content ($\mathcal{C}$) and the Necessity of Counterspace

A1 (Whole Content): There exists a smooth 4-D counterspace $(\mathcal{C},G_{AB},\Psi )$ with metric G and global content field(s) $\Psi$, containing the full content of all “time stages” simultaneously.

The proposal of a counter-spatial dimension is not merely natural but necessary; it emerges from an elementary analysis of three-dimensional phenomenology, its constraints, and its internal dynamics. The existence of $\mathcal{C}$ is the non-metaphysical resolution to a topological inconsistency within the observable 3D manifold $\Sigma$.

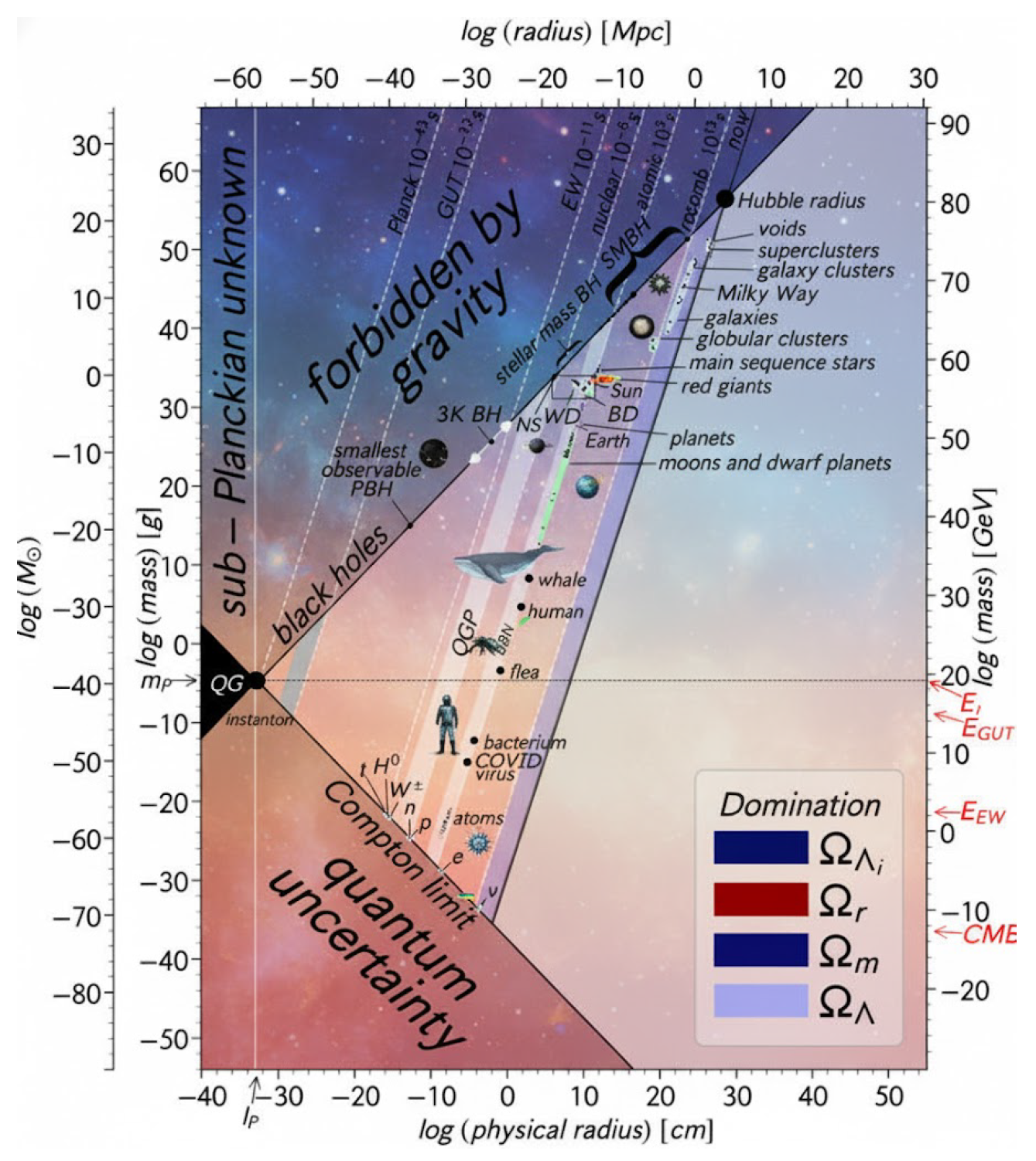
2.1.0.2. The Topological Inconsistency of $\Sigma$

The reference literature associated with the theory, specifically the Lineweaver-Patel mass-radius cartography, demonstrates that the space of all physical entities in $\Sigma$ is rigidly bounded by two antagonistic geometric limits:

(1)

The Schwarzschild Boundary (${\mathbf{r}}_{\mathbf{s}}$): The region forbidden by gravitation ($r_s=2Gm/c^2$).

(1)

The Compton Boundary (${\lambda }_{\mathbf{c}}$): The region forbidden by quantum uncertainty (${\lambda }_c=\hslash /mc$).

A truly fundamental, self-contained 3D space should be scale-invariant, lacking such rigid internal boundaries. The presence of these boundaries (see Figure 1) is the definitive geometric signature of an embedding. The observable 3D world is the "cone of admissibility" defined by the constraints imposed by the higher-dimensional source $\mathcal{C}$. These forbidden regions are not empty parameter spaces, but the projective limits of the immersion map $X:\Sigma \to \mathcal{C}$.

2.1.0.3. Measurement, Waves, and the Reverse Side

The necessity of $\mathcal{C}$ is further confirmed by the nature of measurement. When we discuss waves, we are not referring to "things" but to properties. The fact that a measurement is never identical to the object it seeks to characterize suggests the object’s fundamental geometry is richer than the 3D measurement apparatus can capture. The “reverse side” of a wave alludes to the configuration of fields required for a measurement to acquire physical meaning. This reverse side is precisely the segment of the 4D content field $\Psi$ in $\mathcal{C}$ that remains inaccessible during the instantaneous 3D slice $\Sigma$.

2.1.0.4. Counterspace is Necessary, Not Metaphysical

Those who assume that this component introduces a metaphysical inflection into the system misinterpret its nature. The metaphysical tint does not arise from the model, but rather from the impossibility of denying or dismissing the properties of Counterspace. Everything is reduced, by necessity, to the observation of its shadow (science as we know it): what can be parametrically measured.

2.2. Axiom A2: Identity of Source and Conserved Singularities

A2 (Identity of Source): There is a distinguished point $p_0\in \mathcal{C}$ and an automorphism group $Aut(\mathcal{C},G,\Psi )$ such that $S=Orb\left(p_0\right)$ is the fundamental singular set; all shadow singularities descend from $p_0$.

This axiom establishes the deep coherence of the framework by proposing a single, unified geometric origin ($p_0$, the Instanton) for all extreme gravitational phenomena. In General Relativity, a singularity is a physical breakdown. In TCGS, it is a conserved geometric feature. The formation of a black hole in the shadow $\Sigma$ is the critical event where the projection map X intersects the fundamental geometric boundary S within $\mathcal{C}$. It is entirely feasible that singularities are extreme manifestations of this counter-space, transforming catastrophic physical failure into a predictable geometric trace of the fixed 4D source.

2.3. Axiom A3: Shadow Realization ($\Sigma$) and Gauge Time

A3 (Shadow Realization): The observable world is a 3-manifold $\Sigma$ embedded by $X:\Sigma \to \mathcal{C}$; observables are pullbacks $(g,\psi )=(X^{*}G,X^{*}\Psi )$. “Time” is gauge (no ontic status).

This axiom is the geometric definition of the shadow: the observed 3D metric g and fields $\psi$ are simply the pullbacks of the 4D source G and $\Psi$. The key implication is the re-classification of time.

2.3.0.5. Time as a Foliation Artifact

If $\mathcal{C}$ is a static, complete 4D content, then apparent evolution is a foliation artifact—the result of slicing a fixed block. Time is merely the label parameterizing the comparison between admissible 3-geometries ($\Sigma$). This position is secured mathematically by the BSW (Baierlein–Sharp–Wheeler) action [4], which recovers the dynamics of GR not from a fundamental time, but from the reparameterization invariance of the 3-geometries.

2.4. Axiom A4: Parsimony and Extrinsic Response

A4 (Parsimony): No dark species; apparent dark effects arise from projection geometry encoded by one constitutive law.

This axiom enforces geometric parsimony. The observed phenomena attributed to “dark matter” are not new particles or fluids, but an informational deficit arising from describing a 4D geometry using a constrained 3D manifold. This deficit is encoded by a single, non-linear Extrinsic Constitutive Law (detailed in Section 6) that modifies the weak-field gravitational response on the shadow $\Sigma$, replacing dark halos with the projection operator $\mu$.

3. The Metamathematical Lens: Truth vs. Provability

A defining feature of the TCGS framework is its explicit alignment with the limitative theorems of mathematical logic. To fully explain the axiomatic system, we must define the conceptual boundary between the framework’s ontology and its epistemology.

3.1. The Gödelian Gap as a Physical Analogy

We posit a structural isomorphism between the physical TCGS system and the logical systems defined by Gödel and Tarski [15,17].

• The “Territory” (4D Counterspace $\mathcal{C}$): This corresponds to Tarskian Semantic Truth or the standard model $\mathfrak{N}$. It contains the “Whole Content” and is the domain of “what is,” independent of observation.
• The “Map” (3D Shadow $\Sigma$ & Predictions): This corresponds to Syntactic Provability within a formal system T. It is the computable, accessible domain of scientific laws and observations.

Just as Tarski’s Undefinability Theorem states that a system cannot define its own truth [16], Axiom A3 implies that the 3D shadow cannot fully define the 4D counterspace. The “truth” of the 4D geometry is transcendent to the 3D “object language.”

3.2. Cartography vs. Falsification

This analogy creates a non-Popperian, “cartographic” epistemology. Since the 3D map is a projection of a richer 4D truth, any specific mathematical map (like the $\mu$-function) is formally incomplete. A prediction failure (e.g., a mismatch in lensing offsets) does not falsify the territory (the existence of $\mathcal{C}$); rather, it is a “Gödel sentence”—a discovery of a geometric truth that the current map could not prove. Science is thus redefined as the infinite, incompletable process of mapping the complexity of the Counterspace.

4. The Unified Ontology: Physics and Biology Homology

The axiomatic rigor of TCGS extends beyond physics. By adhering to the Identity of Source (A2) and Parsimony (A4), the framework reveals a deep homology between "Dark Matter" in physics and "Teleology" or "Chance" in biology. Both are identified as artifacts of projecting a 4D static structure onto a 3D evolving slice.

Table 1 formalizes this unified ontology, demonstrating how the Extrinsic Constitutive Law operates identically across domains.

In the biological sector (SEQUENTION), “Darwinian chance” is re-defined as a "foliation artifact." Just as the weak-field regime in physics creates the illusion of dark matter, the "time-elapsed" regime in biology creates the illusion of random selection. The framework asserts that biological forms are 3D cross-sections of invariant 4D geometric structures, governed by ${\mu }_{bio}$ rather than historical contingency.

5. Geometry of the Shadow and Holography

5.1. Reconstruction

On $\mathcal{C}\setminus S$, the content field obeys a source equation with singular support on S,

$${\Delta }_G\Psi ={\int }_{S}q\left(y\right){\delta }_y\mu \left(y\right),{\int }_{S}q\mu =Q_0,$$

(1)

with $\mu$ invariant under $Aut(\mathcal{C},G,\Psi )$. Observables $(g,\psi )$ are uniquely fixed by $(S,\mathrm{bdry}\mathrm{data})$.

5.2. Space Has no Intrinsic Properties

All geometric structure on the shadow is inherited from $(\mathcal{C},X)$; the shadow has no independent ontic degrees of freedom. This aligns with the metamathematical view that syntactic theorems have no meaning without a semantic model.

6. GR as a Relational Limit (BSW/ADM Without Ontic Time)

We use the BSW Jacobi action to recover dynamics without assuming time as a fundamental variable [4,6].

$$S_{\mathrm{BSW}}={\displaystyle \frac{1}{16\pi G}}\int s{\int }_{\Sigma }^{3}x\sqrt{g}\sqrt{\mathcal{R}-2\Lambda }\sqrt{\mathcal{T}},$$

(2)

with $\mathcal{T}=G^{ijkl}({\dot{g}}_{ij}-{\mathcal{L}}_{\beta }{g}_{ij})({\dot{g}}_{kl}-{\mathcal{L}}_{\beta }{g}_{kl})$, $G^{ijkl}=g^{ik}{g}^{jl}-g^{ij}{g}^{kl}$. Variation yields the ADM constraints and an emergent lapse $N\propto \sqrt{\mathcal{T}/(\mathcal{R}-2\Lambda )}$, reconstructing a 4-metric $g_{\mu \nu }$ that obeys Einstein’s equations [5].

Theorem 1. 

Assuming locality, ultralocal kinetic metric, and scalar potential $\propto \mathcal{R}-2\Lambda$, reparameterization invariance on 3-geometries yields the ADM/Hamilton constraints and Einstein equations.

This derivation is crucial: it proves that "gravity" is the method by which the 3D shadow maintains consistency as it evolves through the 4D block.

7. Projection Geometry: The Extrinsic Constitutive Law

The weak-field response on the shadow obeys the modified Poisson equation derived from the projection geometry:

$$\nabla ·\left[\mu \left({\displaystyle \frac{|\nabla \Phi |}{a_{*}}}\right)\nabla \Phi \right]=4\pi G{\rho }_b,$$

(3)

with $\mu \left(y\right)\to 1$ for $y\gg 1$ and $\mu \left(y\right)\to y$ for $y\ll 1$. The geometric scale $a_{*}$ is an embedding invariant (e.g., $a_{*}=\xi c^2{\langle \left|H\right|\rangle }_{\Sigma }$). This single law replaces the need for dark matter halos [9,10,11].

8. Model Calibration: The Foundational Scale

The phenomenological success of TCGS hinges on the calibration of $a_{*}$.

Table 2. Minimal Calibration and Foundational Scales of the Extrinsic Response.

Parameter / Function	Value / Form	Contextual Justification
Invariant Scale ($a_{*}$)	$\approx 1.2\times {10}^{-10}\mathrm{m}/{\mathrm{s}}^2$	Universal transition acceleration determined by galactic kinematics.
Response Function ($\mu \left(y\right)$)	$\mu \left(y\right)=y/\sqrt{1+y^2}$	Simplest $C^1$ form satisfying asymptotic limits for GR and BTFR.
Dimensionless Variable (y)	$y=|\nabla \Phi |/a_{*}$	Ratio of observed acceleration to global geometric scale.

Table 2. Minimal Calibration and Foundational Scales of the Extrinsic Response.

Parameter / Function	Value / Form	Contextual Justification
Invariant Scale ($a_{*}$)	$\approx 1.2\times {10}^{-10}\mathrm{m}/{\mathrm{s}}^2$	Universal transition acceleration determined by galactic kinematics.
Response Function ($\mu \left(y\right)$)	$\mu \left(y\right)=y/\sqrt{1+y^2}$	Simplest $C^1$ form satisfying asymptotic limits for GR and BTFR.
Dimensionless Variable (y)	$y=|\nabla \Phi |/a_{*}$	Ratio of observed acceleration to global geometric scale.

8.1. Justification of the $\mu \left(y\right)$ Form

The chosen function $\mu \left(y\right)=y/\sqrt{1+y^2}$ is selected based on Axiom A4 (Parsimony).

• High-Acceleration Limit ($\mathbf{y}\gg \mathbf{1}$):$\mu \left(y\right)\to 1$. We recover standard GR.
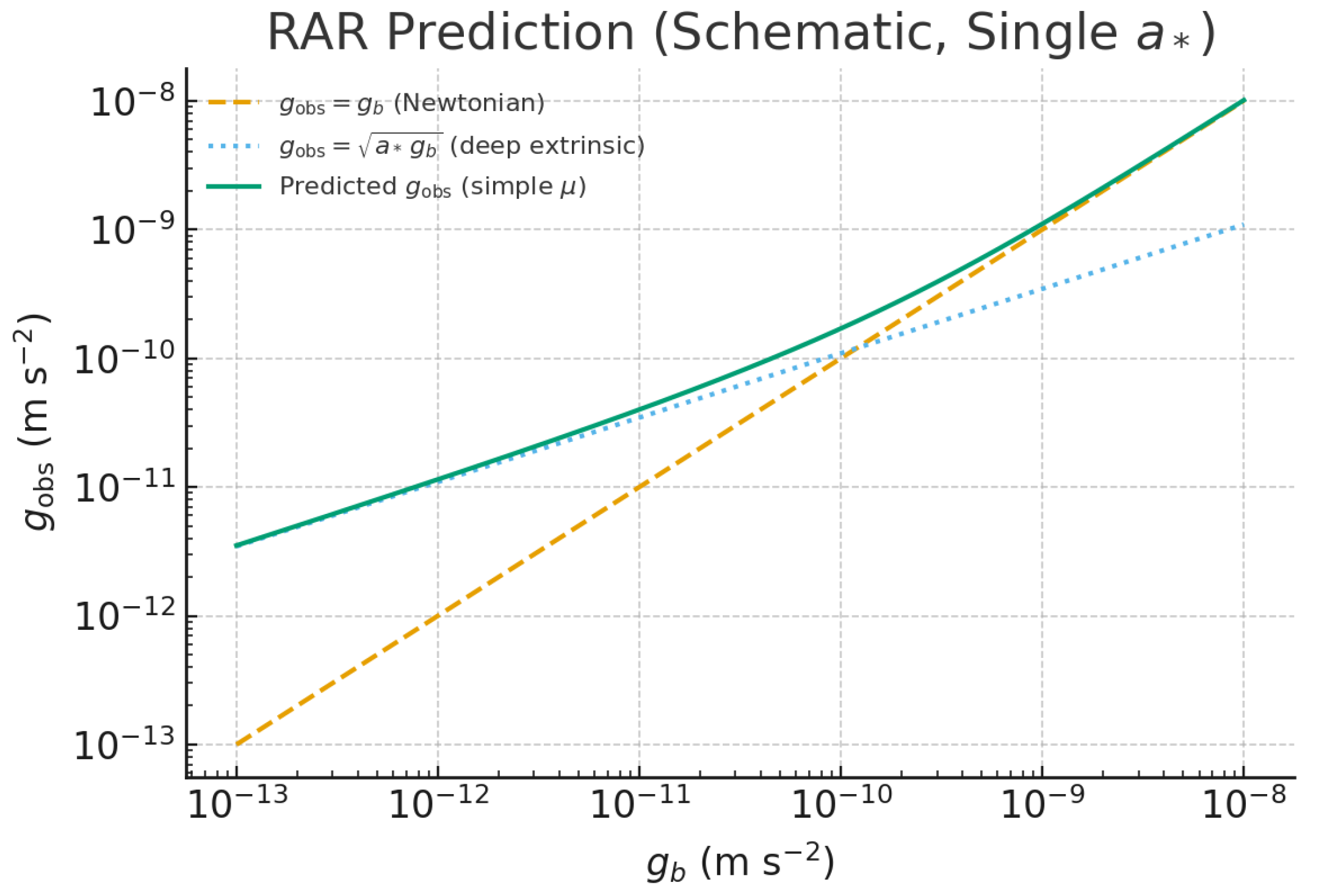
• Low-Acceleration Limit ($\mathbf{y}\ll \mathbf{1}$):$\mu \left(y\right)\to y$. This yields $\nabla ·(y\nabla \Phi )\approx 4\pi G{\rho }_b$, directly producing the Baryonic Tully-Fisher Law ($v^4\propto M_b$) and the Radial Acceleration Relation (RAR).

This calibration is the "Map" which we test against the "Territory."

9. Foundational Consistency

9.1. Constraint Algebra Closure

The hypersurface-deformation algebra is recovered from the BSW construction; the emergent lapse/shift ensure closure of $\{\mathcal{H},{\mathcal{H}}_i\}$ under Poisson brackets, securing diffeomorphism invariance [6,7].

9.2. PPN/Solar-System Bounds

In regions where $|\nabla \Phi |\gg a_{*}$, $\mu \to 1$ and the metric perturbations obey GR. Linearizing yields Post-Newtonian parameters $\gamma =\beta =1+O(a_{*}/g)$; tight bounds follow wherever $g\gg a_{*}$.

9.3. PDE Well-Posedness

Let $\mu \left(y\right)$ be $C^1$, strictly increasing, with $0<{\mu }_0\le \mu \left(y\right)\le {\mu }_1<\infty$ and $y{\mu }^{\prime }\left(y\right)$ bounded. Then the operator is uniformly elliptic; Lax–Milgram yields existence/uniqueness.

10. Worked Profiles and Figures

10.1. Galaxy-Scale: RAR and BTFR

For spherical symmetry, $\mu (g/a_{*})g=g_b\left(r\right)=G{M}_b\left(r\right)/r^2$, producing the branches $g\simeq g_b$ and $g=\sqrt{a_{*}{g}_b}$; hence $v^4=G{a}_{*}{M}_b$ (BTFR) and the RAR. See Figure 2.

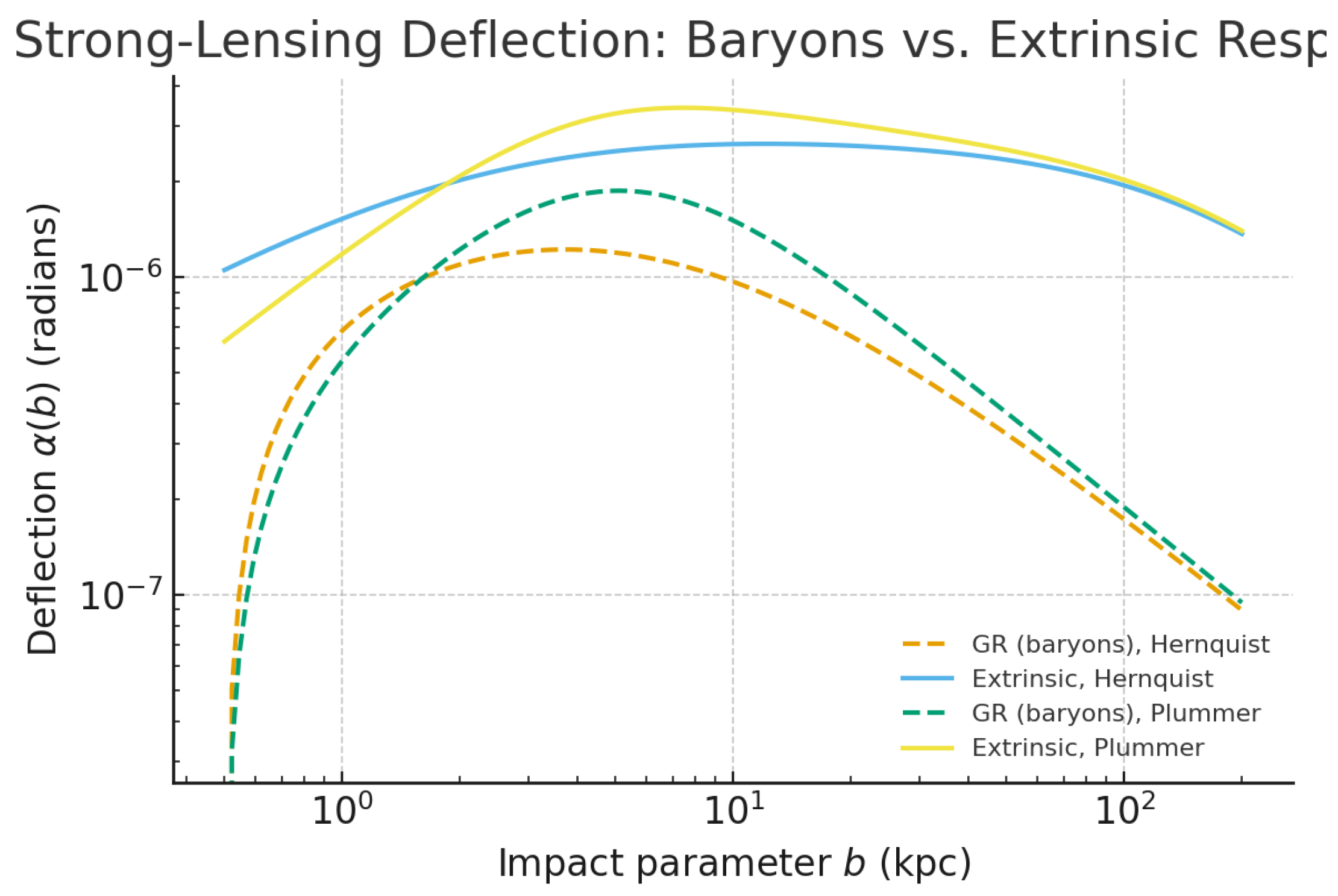
10.2. Strong Lensing: Hernquist and Plummer Baryons

The deflection in the extrinsic regime is $\alpha \left(b\right)=\frac{2b}{c^2}\int (g\left(r\right)/r)z$. fig:lens contrasts the prediction with GR (baryons only).

Figure 3. Deflection profiles for Hernquist and Plummer baryons ($M={10}^{11}{M}_{\odot }$, $a=5$ kpc). Dashed: GR with baryons only; solid: extrinsic response with the same $a_{*}$. The extrinsic model yields a quasi-constant tail, enabling strong lensing without dark halos.

Figure 3. Deflection profiles for Hernquist and Plummer baryons ($M={10}^{11}{M}_{\odot }$, $a=5$ kpc). Dashed: GR with baryons only; solid: extrinsic response with the same $a_{*}$. The extrinsic model yields a quasi-constant tail, enabling strong lensing without dark halos.

11. Cosmology Without Time

Cosmological observables are re-expressed as slice invariants of $(\mathcal{C},G,\Psi )$ (acoustic scales, BBN yields) [2,3]. Late-time “acceleration” is a foliation artifact of slicing a fixed content, not a fluid. This applies equally to the biological history; the apparent "evolution" of complexity is a slice invariant of the 4D biological content field.

12. Empirical Program: A Cartographic Survey

This program is cartographic, not falsificationist. In line with the Gödelian logic formalized in Section 3, a mismatch between prediction and observation does not falsify the core axioms (A1-A3) or the parsimony axiom (A4). Instead, it proves our mathematicalmap(the specific $\mu$-function) is incomplete, and we must draw a new one to match the “geometric complexity” of the territory.

The survey tasks are: (1) Single-scale galaxy fits for $a_{*}$; (2) joint kinematics–lensing without halo parameters; (3) merging-cluster offset morphology; (4) large-scale gravitational slip; (5) cosmological slice-invariant checks.

13. Conclusions

A timeless, identity-of-source framework yields GR as a limit and replaces dark sectors with a single, well-posed extrinsic response. We have demonstrated that this physical structure is formally analogous to the Tarskian distinction between semantic truth and syntactic provability. The program is empirically mappable and, through its parallel structure with SEQUENTION, offers a unified geometric resolution to the problems of Dark Matter and Darwinian Chance.