A Fundamental Solution of the Hubble Tension

1. Introduction

The properties of space are essential for theories, see e. g. Newton [1], Maxwell [2], Einstein [3], Minkowski [4], Einstein [5], Hilbert [6], Hubble [7], Lamb and Retherford [8], Casimir [9], Zeldovich [10], Perlmutter et al. [11], Smoot [12] and Riess et al. [13]. Thereby, outer space is a relatively ideal form of space in the universe, as outer space is hardly disturbed by molecules or other objects. Hereby, the universe consists of space and of the objects in space.

Moreover, the properties of space are important for applications such as space navigation, see for instance Soffel [14], telecommunication, quantum cryptography or quantum computer networks.

In order to understand space, it is essential to understand that space has a nonzero energy density $u_{DE}$ or $u_{\Lambda }$. It has essentially been proposed by Einstein [15] in terms of a cosmological constant $\Lambda$. And its value has been measured by Perlmutter et al. [11], Riess and others [16], Smoot [12].

Furthermore, space was not given in advance. Instead, space expanded from the Big Bang until today, and space will expand in the future, see Friedmann [17], Wirtz [18], Lemaître [19], Hubble [7], Hobson et al. [20], Workman and others [21], Planck Collaboration [22]. Thereby, the measurable present-day rate $H_0$ of increase of the space exhibits a problem, the $H_0$ - tension: Measurements provide different values of $H_0$ at the 5 $\sigma$ confidence level, see Riess and others [13].

This problem is explained here at the level of first principles and a founded and critically reflected scientific method, see sections (Section 1.1, Section 1.1.1).

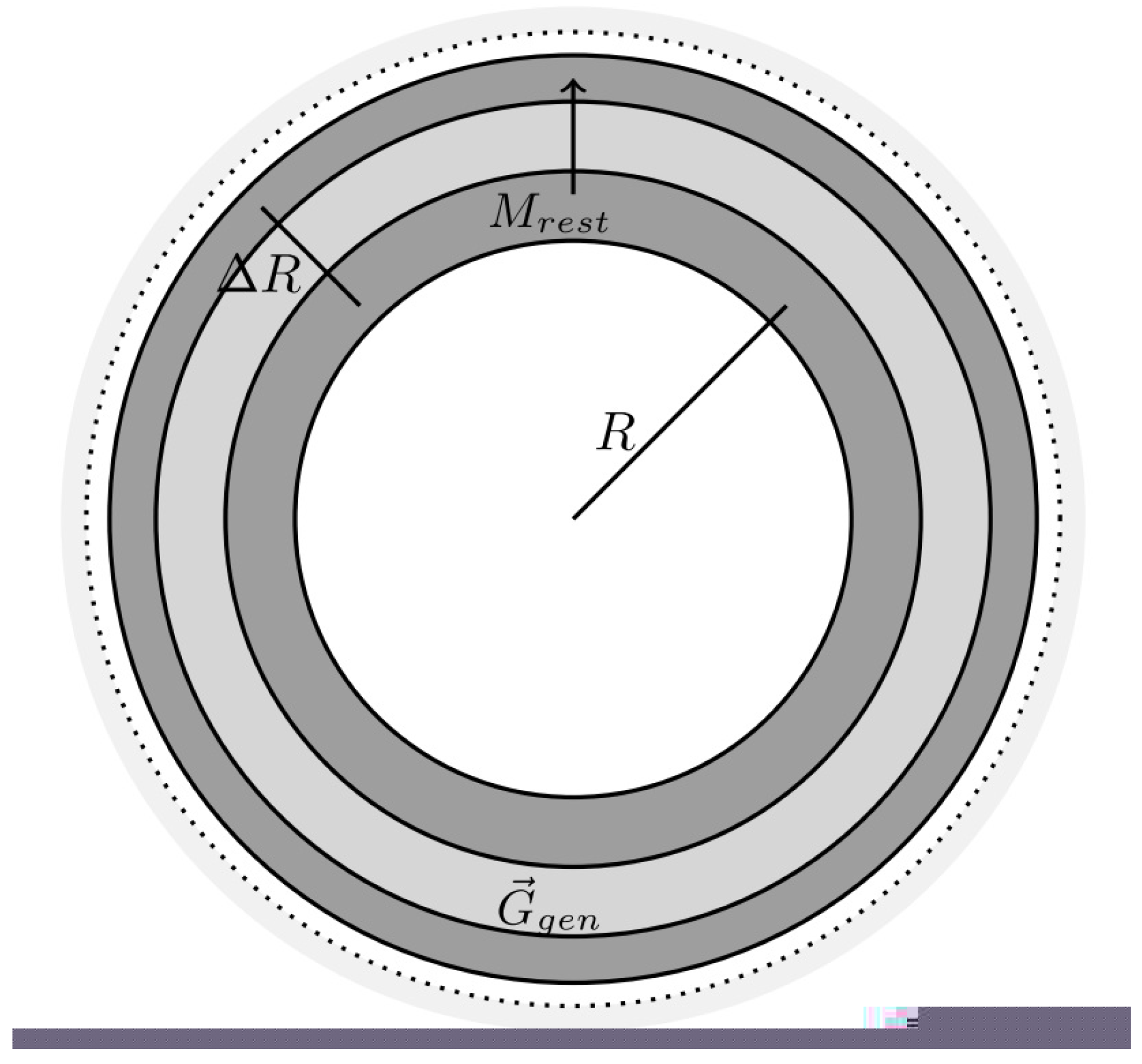
Firstly, an idealization of space is identified with help of a paradox. The idealization is that in present-day science space as a single entity. With help of a founded derivation, this idealization is overcome: Homogeneous space is a stochastic average of indivisible volume portions.

Secondly, a volume dynamics is derived for these volume portions.

Thirdly, the quantum postulates, gravity, and the Local Formation of Volume (LFV) are derived from this volume dynamics.

Fourthly, based on these founded and derived dynamical processes, the energy density of volume is derived for the case of a homogeneous universe. For that case, this energy density is called $u_{vol}$. It is in precise accordance with the observed value of the early universe, which was very homogeneous. Moreover, for this homogeneous case, the corresponding $H_0$ value is identified, in precise accordance with observation.

Of course, the universe is heterogeneous. Accordingly, the heterogeneity is analyzed in addition to the homogeneous universe. As a result, the $H_0$ value of the late universe, which is very heterogeneous, is derived. This result is in precise accordance with observation.

These results provide a very convincing evidence for the concept that homogeneous space is a stochastic average of indivisible volume portions. Moreover, these results represent a very clear evidence that the $H_0$ - tension is explained by the gradual evolution of heterogeneity in the universe. These two fundamental insights improve the present-day model of cosmology, the $\Lambda$CDM model. Additionally, these findings can be applied to space navigation and exploration, see Carmesin [23,24].

1.1. Hypothetic Deductive Method

In this paper, the results are obtained by the hypothetic deductive method, see Popper [25,26], Niiniluoto, Sintonen and Wolenski [27]. Hereby, the following hypotheses are used:

1.1.1. Used Hypotheses

In this section, the hypotheses are presented that are used in the hypothetic deductive method. Thereby, these hypotheses are very founded. Therefore, the risk of failure is very small.

(1) The space, that can be observed in the whole volume V ranging from Earth to the light horizon, is isotropic and homogeneous at this universal scale. Local heterogeneities are possible, for instance near a mass M, see Schwarzschild [28], Dyson, Eddington and Davidson [29,30]. This has been observed, see Planck Collaboration [22].

(1.1) Moreover, there is natural space that is very homogeneous and isotropic at small scales. For instance, natural space is very homogeneous and isotropic in a void, see Zeldovich, Einasto and Shandarin [31], Contarini et al. [32], and natural space was very homogeneous and isotropic in the early universe, see Planck Collaboration [22].

(1.2) Furthermore, in the heterogeneous universe, natural space can exhibit slight heterogeneity, additionally. For instance, in the heterogeneous universe, Abbott et al. [33] observed the merger of a binary stellar-mass black hole system, and the gravitational waves emitted thereby. These gravitational waves can be interpreted as coherent states that cannot be emitted in a natural homogeneous universe without heterogeneity, as only an appropriate heterogeneity can emit coherent states.

(2) Space has a positive energy density $u_{DE}$, it is the dark energy density. It is the density of the energy E of the volume V of the space in part (1), divided by this volume:

$$u_{DE}={\displaystyle \frac{E}{V}}.$$

(1)

This has been discovered by Perlmutter et al. [11], Riess and others [16], Smoot [12].

(3) The energy speed relation of special relativity theory (SRT) holds, see Einstein [3], Hobson et al. [20]: In general, an object with an energy E has a velocity $\overrightarrow{v}$ relative to a mass $m_{ref}$, that is used as a reference. Its absolute value is called speed $v=|\overrightarrow{v}|$. In the case of zero speed, $v=0$, the energy is called rest energy $E_0$. The energy speed relation of SRT is as follows:

$$E_0^2=E^2·\left(1-{\displaystyle \frac{v^2}{c^2}}\right)$$

(2)

In the case $v<c$, the relation has the following equivalent form:

$$E^2={\displaystyle \frac{E_0^2}{1-\frac{v^2}{c^2}}}$$

(3)

Hereby and in the following, the velocity is determined relative to an adequate coordinate system of relativity theory, for details see section (Section 1.1.5).

(4) Each volume or volume portion $\Delta V$ of space has zero rest energy $E_0$, and it has zero rest mass $m_0=E_0/c^2$.

$$m_0\left(V\right)=0=E_0\left(V\right).$$

(4)

This is shown in section (Section 1.1.2).

(5) In a process of increase of volume or space, the dark energy density $u_{DE}$ is a nonzero constant, whereby only very small variations might occur. This approximate constancy has been observed for the expansion of space since the Big Bang, see Planck Collaboration [22], Riess et al. [13]. Additionally, that constancy has been proposed by general relativity theory and cosmology, see Einstein [15], Friedmann [17], Lemaître [19], Hobson et al. [20]. Furthermore, the value of $u_{DE}$ is derived here, and the results are additional evidence for this approximate constancy.

The above very founded hypotheses (1) to (5) will be used for deductions in this paper.

1.1.2. Why Volume Has no Rest Mass

In this section, it is shown that volume has zero rest mass $m_0$.

In the vicinity of a mass M, there occurs additional volume $\delta V$, see section (Section 1.1.4) or Figure 1. If that additional volume would have a rest energy $m_0\left(\delta V\right)>0$, then there would be an additional rest mass $m_0$ in the vicinity of each mass M. Such an additional rest mass has never been observed, see e. g. Landau and Lifschitz [34], Workman et al. [21], Planck Collaboration [22], Zogg [35]. For instance, if there would be such an additional rest mass $m_0$, then this $m_0$ would modify the orbits of the GPS satellites, and this would have been observed, but this has not been observed. Consequently, additional volume $\delta V$ has no rest mass.

Moreover, the additional volume in the vicinity of a mass is the same type of volume as the usual volume that occurs without any mass. this is confirmed by the observation that only one type of volume has been observed, see e. g. Workman et al. [21], Planck Collaboration [22], Casimir [9], Zeldovich [10], Perlmutter et al. [11]. Therefore, in general, volume has no rest mass.

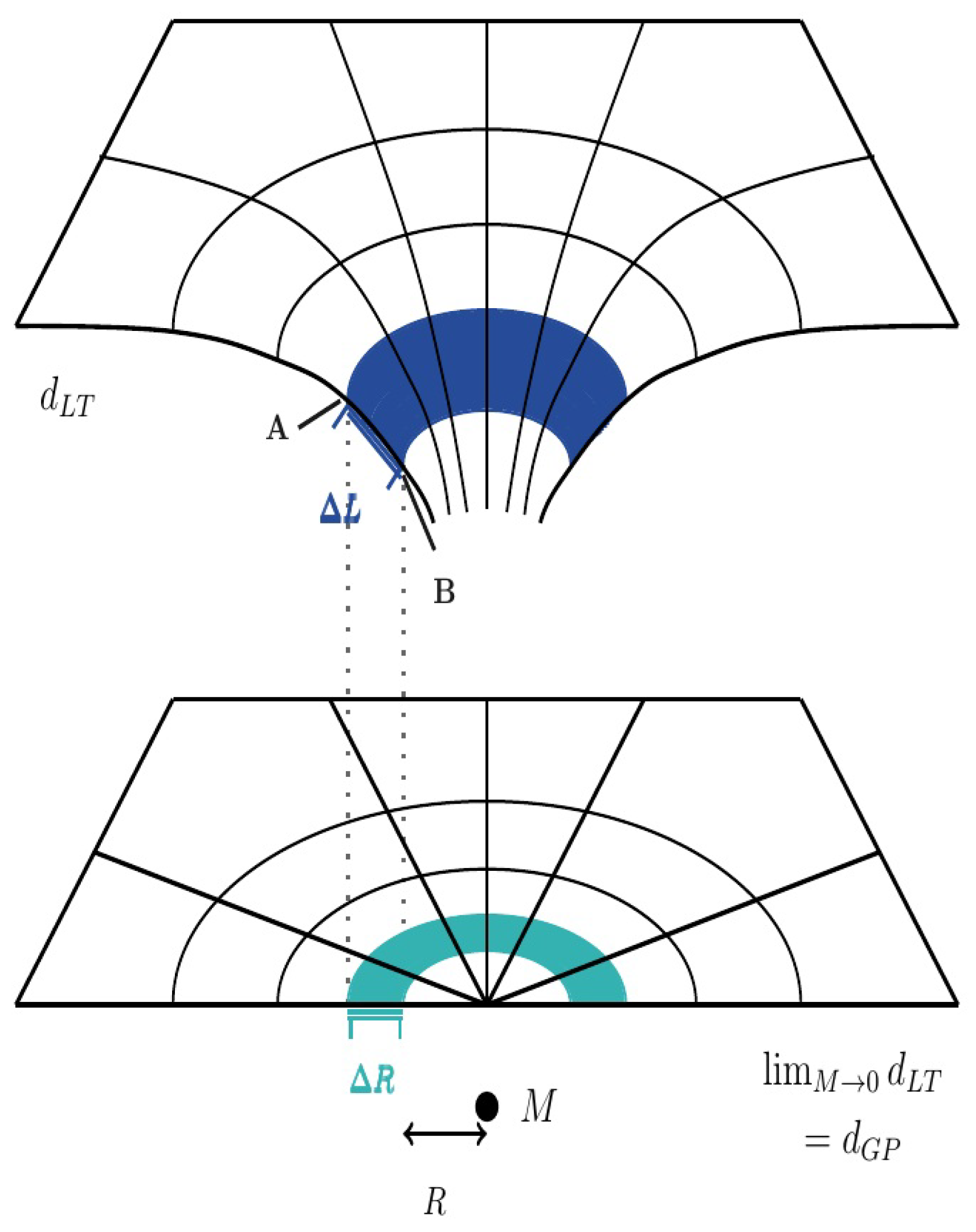
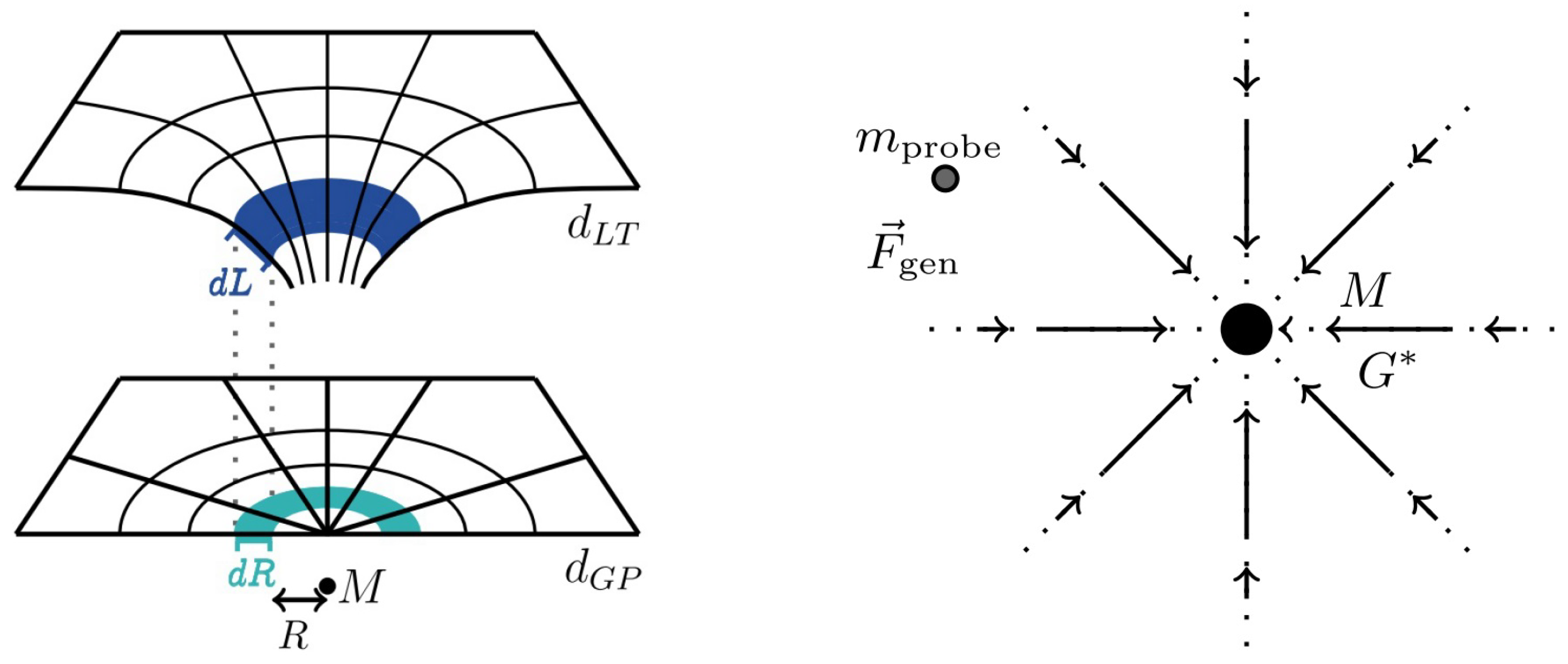
1.1.3. Mass Causes an Increase of Radial Light Travel Distance

In this section, it is shown that a mass M causes an increase of the radial distance R to M. This increase occurs at each radial difference $\Delta R$, see Figure 1.

For instance, in the vicinity of a mass M, an original (at $M=0$) radial distance $\Delta R$ is increased by the square root $\sqrt{g_{RR}}$ of the radial element $g_{RR}$ of the metric tensor to a value $\Delta L$, see Figure 1,

$$\Delta L=\Delta R·\sqrt{g_{RR}}.$$

(5)

Hereby, the value $\Delta L$ can be measured as a light travel distance$d_{LT}$, see Hobson et al. [20]. Similarly, the original value $\Delta R$ can be measured with help of two hand leads, the distance is called gravitational parallax distance, see Carmesin [23,36].

As a consequence of general relativity, see Einstein [5], Hilbert [6], Hobson et al. [20], at each radial coordinate (or gravitational parallax distance) R, the radial element $g_{RR}$ of the metric tensor can be expressed with help of the Schwarzschild [28] radius $R_S$:

$$g_{RR}={\displaystyle \frac{1}{1-\frac{R_S}{R}}},\mathrm{with}{R}_S={\displaystyle \frac{2G·M}{c^2}}$$

(6)

These relations are in precise accordance with observation, see e. g. Dyson, Eddington and Davidson [29], Pound and Rebka [30], Will [37].

According to the Hacking [38] criterion of reality, this increase of radial light travel distance $\Delta L$ is real, as it can be manipulated as follows: The mass M can be increased, and this causes an increase of radial light travel distance $\Delta L$, see Eqs. (5 and 6).

Moreover, also the gravitational parallax distance $\Delta R$ is real, as it can be manipulated as well: For instance, in Figure 1, $\Delta R$ is the distance between the points A and B. If B moves towards A, then $\Delta R$ decreases. Next, the corresponding volume is analyzed:

1.1.4. Mass Causes an Increase of Volume

In this section, the following is shown: In the vicinity of a mass M, the increase of the radial length $\Delta L$ causes an increase of the volume.

Without loss of generality, an portion of volume $\Delta V_R=\Delta R·\Delta x·\Delta y$ is used with $|\Delta R|=|\Delta x|$ and $|\Delta R|=|\Delta y|$.

In the vicinity of a mass M, the radial distance $\Delta R$ is increased to the respective light travel distance $\Delta L$ by the factor $\sqrt{g_{RR}}$, while $\Delta x$ and $\Delta y$ are not changed by M. Consequently, the volume $\Delta V_R$ is increased to the respective volume $\Delta V_L$ by the factor $\sqrt{g_{RR}}$, see Eq. (5):

$$\Delta V_L=\Delta L·\Delta x·\Delta y=\Delta R·\Delta x·\Delta y·g_{RR}=\Delta V_R·g_{RR}.$$

(7)

The difference of the volume $\Delta V_R$ measured with the gravitational parallax distance and the volume $\Delta V_L$ measured with the light travel distance is called additional volume$\delta V$:

$$\delta V:=\Delta V_L-\Delta V_R.$$

(8)

The ratio $\delta V/\Delta V_L$ is called relative additional volume ${\epsilon }_L$:

$${\epsilon }_L:={\displaystyle \frac{\delta V}{\Delta V_L}}.$$

(9)

1.1.5. On the Adequate Coordinate Systems

In the theory of relativity, a time interval $t_{sa{t}_E}$ of a clock onboard a satellite E and a time interval $t_{sa{t}_F}$ of a clock onboard a satellite F exhibit the phenomenon of kinematic time dilation. Thereby, relativity theory states: Between two events A and B, a clock in a laboratory coordinate system exhibits a time $t_{lab}$, a clock onboard the satellite E exhibits a time $t_{sa{t}_E}$, and a clock onboard the satellite F exhibits a time $t_{sa{t}_F}$ as follows:

$$t_{lab}=t_{sa{t}_E}·{\displaystyle \frac{1}{\sqrt{1-v_{E,lab}^2/c^2}}}\mathrm{and}{t}_{lab}=t_{sa{t}_F}·{\displaystyle \frac{1}{\sqrt{1-v_{F,lab}^2/c^2}}}.$$

(10)

Hereby, $v_{E,lab}=\left|{\overrightarrow{v}}_{E,lab}\right|$ is the speed of the satellite E relative to the laboratory coordinate system, and $v_{F,lab}=\left|{\overrightarrow{v}}_{F,lab}\right|$ is the speed of the satellite F relative to the laboratory coordinate system. However, the International Astronomical Union (IAU) realized that relativity theory does not provide information about the choice of an adequate laboratory coordinate system or laboratory frame. Such information about the frame is essential for predicting the times shown by the above clocks, and it is important for space navigation. The IAU called this lack of information the problem of finding an adequate coordinate system (ACS), see Soffel [14].

The problem of finding an adequate coordinate system (ACS) has been solved [23,24,39].

Thereby, for each point P in the universe, the following has been shown:

(1) An ACS exists.

(2) The ACS has a uniquely determined velocity ${\overrightarrow{v}}_{ACS,CS}$, relative to an arbitrarily chosen coordinate system $CS$.

(3) ${\overrightarrow{v}}_{ACS,CS}$ can be measured, and procedures of measurement are provided.

(4) ${\overrightarrow{v}}_{ACS,CS}$ can be predicted and calculated, and procedures for it are provided.

(5) The equations of time dilation in Eq. (10), as well as the energy speed relation in Eqs. (2 and 3) hold, when the ACS is used. Moreover, the typical results of relativity hold, when the ACS is used.

(6) There exists an absolute zero of the fractional kinematic time difference

$$\delta t_{kin,frac}:={\displaystyle \frac{t_{sa{t}_E}-t_{lab}}{t_{lab}}}\le 0,$$

(11)

whereby the chosen laboratory coordinate system is equal to the ACS.

In this paper, the ACS is used. Therefore, the derived results have clearly defined conditions.

1.2. Observed Energy Density of Volume

In outer space, Perlmutter et al. [11] and Riess et al. [16] discovered the accelerated rate of expansion of the universe. Based on the Friedmann Lemaître equation (FLE), this implies a nonzero energy density of empty space, see e. g. Friedmann [17], Lemaître [19], Hobson et al. [20], Carmesin [40]. It is called density $u_{\Lambda }$ of the cosmological constant $\Lambda$ or density $u_{DE}$ of the dark energy density [10,15,20,41]. An actual value observed with help of the Cosmic Microwave Background (CMB) is as follows: [22,23,40]

$$u_{\Lambda ,obs}=5.133(\pm 0.2432)·{10}^{-10}{\displaystyle \frac{\mathrm{J}}{{\mathrm{m}}^3}}=u_{DE,obs}.$$

(12)

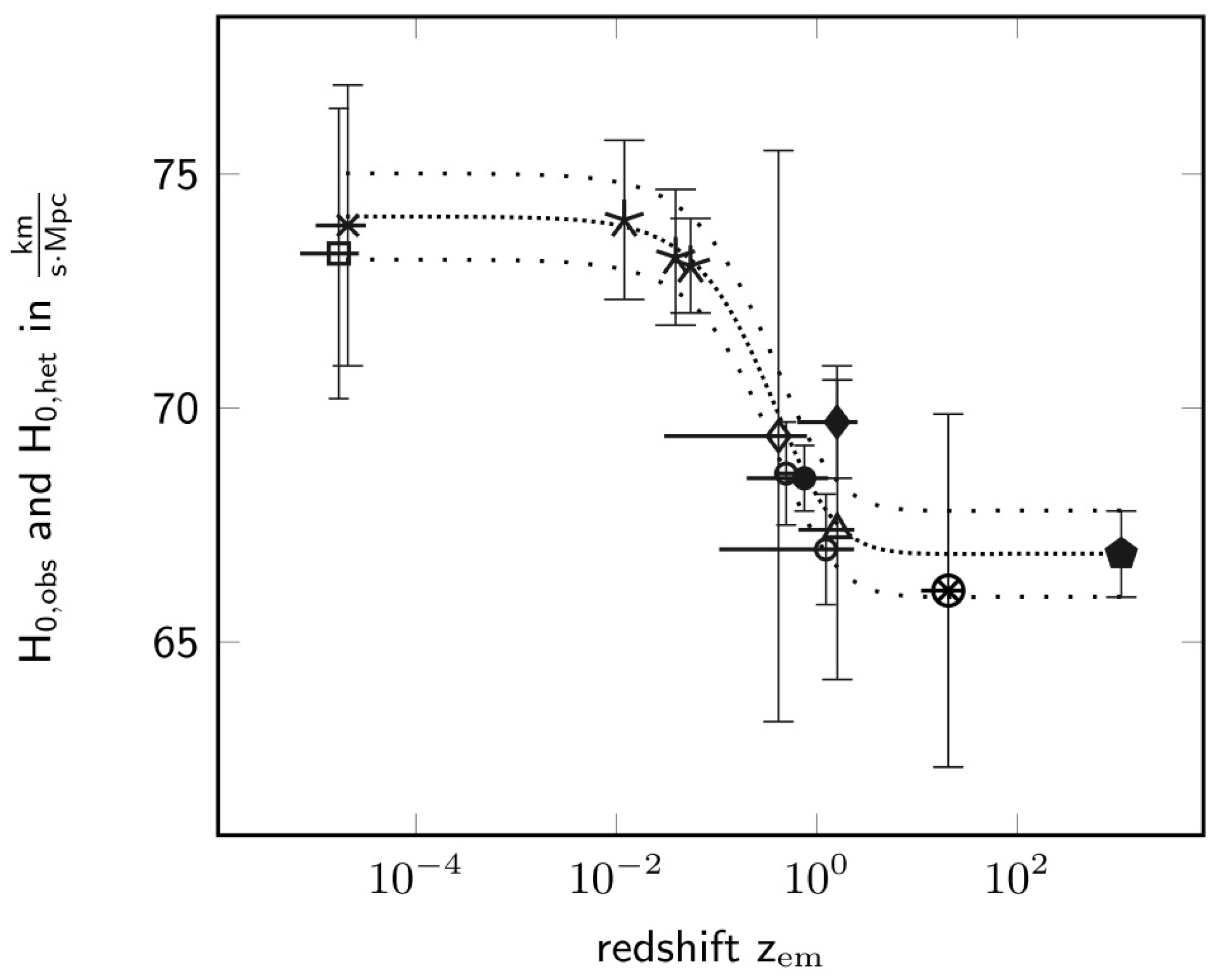
2. Problem of the Hubble Tension

In this section, we summarize a very interesting problem of modern physics. In particular, this problem is a discrepancy of two observed values that should be equal according to the $\Lambda$CDM model of present-day physics, see e. g. Hobson et al. [20]. Consequently, this discrepancy falsifies the $\Lambda$CDM model. In general, according to the hypothetic deductive method, a solution of such a falsification-problem provides the chance to improve concepts of physics [25,26]. In this paper, we will use the problem in order to develop founded and essential improvements of present-day physics.

Hubble [7] discovered the present-day rate of expansion of space since the Big Bang, the Hubble constant $H_0$. In general, the Hubble constant is measured by utilizing signals that have been emitted at a time $t_{em}$ or at a corresponding redshift $z_{em}$, see e. g. Hobson et al. [20].

Penzias and Wilson [42] discovered the cosmic microwave background (CMB), a radiation that has been emitted in the early universe, at $t_{em}=380000\mathrm{years}$ after the Big Bang. Utilizing that radiation, the Planck Collaboration [22] observed the corresponding value of the Hubble constant:

$$H_{0,obs,CMB}=66.88(\pm 0.92){\displaystyle \frac{\mathrm{km}}{\mathrm{s}·\mathrm{Mpc}}}$$

(13)

Hereby, the redshift of emission is $z_{em}=z_{CMB}=1090.3\pm 0.41$. In the measurement, the so-called temperature - temperature correlation, TT, has been used[22] table 2, column 1.

As another example, Riess et al. [13] utilized radiation emitted from supernovae of type Ia in near galaxies and obtained the following observed $H_0$ - value:

$$H_{0,obs,near,Ia}=73.04(\pm 1.01){\displaystyle \frac{\mathrm{km}}{\mathrm{s}·\mathrm{Mpc}}}$$

(14)

Thereby, many galaxies with different redshift values $z_{em}$ have been observed. Accordingly, the redshift $z_{em}$ of emission is described by the average of the redshift values of the observed[13] sections 5.1 and 5.2 galaxies, $\langle z\rangle =0.055$.

Riess et al. [13] observed a discrepancy between the $H_0$ - value based on the CMB and the $H_0$ - value based on near galaxies. Such a discrepancy is called Hubble tension or $H_0$ tension, see e. g. Planck Collaboration [22]. That discrepancy is at the five $\sigma$ confidence level. Consequently, that discrepancy can be regarded and named as a scientific result [13]. This result falsifies the $\Lambda$CDM model, as this model states that the value of $H_0$ should not depend on the redshift value of observed objects. Based on such a falsification of a model, that model can be interpreted as an idealization, see e. g. Shech [45], Song et al. [46]. Consequently, the idealization of the ΛCDM model is identified:

The Hubble tension falsifies the $\Lambda$CDM model. Accordingly, the $\Lambda$CDM model is an idealization.

Therefore, the Hubble tension or $H_0$ tension is a founded scientific problem. A fundamental solution of this problem is derived in this paper. Hereby, no fit is executed, no unfounded hypothesis is proposed, and a precise accordance with observation is achieved, and predictions are derived.

Moreover, the value of the Hubble constant $H_{0,obs,CMB}$ of the early universe is a $H_0$ - value of a nearly homogeneous universe, since the early universe was nearly homogeneous [22]. In contrast, $H_{0,obs,near,Ia}$ is a $H_0$ - value of the late universe, as the observed supernovae occured in the late universe. Additionally, $H_{0,obs,near,Ia}$ is a value of the heterogenous universe, as the late universe is very heterogeneous [22,47,48].

As the Hubble constant describes the rate of expansion of space since the Big Bang, we analyze the properties of space in more detail. For it, in section (Section 3), we show that the present-day view of space includes a paradox, the so-called space paradox. Moreover, we derive a solution of that space paradox. With it, we will explain and derive the Hubble tension. This solves the problem of the Hubble tension.

3. Space paradox

In general, a paradox provides the chance to develop a deep insight [49]. In this section, we will derive a paradox, and we will use it in order to develop a deep insight.

In the following, the space, that can be observed in the whole volume V ranging from Earth to the light horizon, is considered. For instance, this space has been observed [22].

In physical concepts that are commonly used at the present-day, the space with its volume V is considered as a single entity, see e. g. Newton [1], Maxwell [2], Einstein [5,17], Lemaître [19], Landau and Lifschitz [50], Hobson et al. [20], Planck Collaboration [22].

That space has a positive energy density $u_{DE}$, see Eq. (1):

$$u_{DE}={\displaystyle \frac{E}{V}}.$$

(15)

As a consequence of SRT, the volume V with its energy E of space, velocity $\overrightarrow{v}$, and speed $|\overrightarrow{v}|=v$, obey the energy speed relation, see Eqs. (2 and 3)

$$E^2={\displaystyle \frac{E_0^2}{1-\frac{v^2}{c^2}}}\mathrm{or}{E}^2·\left(1-{\displaystyle \frac{v^2}{c^2}}\right)=E_0^2.$$

(16)

As the energy density is nonzero, the energy E is nonzero. Thus, the above relation can be divided by $E^2$. Therefore, the following form of the energy momentum relation holds:

$$1-{\displaystyle \frac{v^2}{c^2}}={\displaystyle \frac{E_0^2}{E^2}}.$$

(17)

As a consequence of the zero rest energy $E_0$ of V, see Eq. (4), the right hand side in Eq. (17) is zero. Consequently, the volume V with its energy E has the speed c of light in vacuum.

$$v=c=v\left(V\right)=v\left(E\right).$$

(18)

3.1. The paradox

In physical concepts that are commonly used at the present-day, the volume is considered as a single entity, see e. g. Newton [1], Maxwell [2], Einstein [5], Friedmann [17], Lemaître [19], Landau and Lifschitz [50], Hobson et al. [20], Planck Collaboration [22]. In such a concept of volume, that whole volume would move parallel to some unit direction vector ${\overrightarrow{e}}_v$ and with the speed of light, $\overrightarrow{v}=c·{\overrightarrow{e}}_v$, see Eq. (18).

However, that velocity $\overrightarrow{v}$ would break the isotropy of space observed at a universal scale [22]. This is a contradiction. In general, a paradox is a contradiction, the solution of which provides a deeper insight [49]. The above contradiction is called the space paradox. It is solved next:

3.2. A solution of the space paradox in natural homogeneous space

(1) The space paradox has five premises: There are four founded premises about space and its volume V, see section (Section 1.1), parts (1) - (4), part (5) is not used here: isotropy, the positive dark energy density, the energy speed relation of SRT (which is correct in the used ACS, see Section 1.1.5), and the zero rest energy $E_0$. And there is one hardly founded premise (see the beginning of Section 3.1): the concept of space as a single entity. Therefore, space is not a single entity.

As space is not a single object, it must consist of many parts of the volume V. These parts $\delta V$ are analyzed next. Thereby, a part of the space with its volume V is called a volume portion (VP).

Hereby, parts of volume with at least one local maximum of volume are analyzed. Thereby, for each part, one such maximum is used in order to localize that part $\delta V$. Such a part is called a localized VP.

Since the energy and volume of space have the speed $v=c$, the above parts $\delta V$ must have the same speed. For instance, each part $\delta V_j$ has its speed

$$v_j=c.$$

(19)

In general, a part of volume is called volume portion.

(2) Next, for the case of a homogeneous universe and space, and for the case of a usual density ${\rho }_{hom}$, The following question is analyzed:

Can such a part $\delta V_j$ with $v_j=c$ consist of smaller parts $\delta V_k$?

Hereby, a usual density ${\rho }_{hom}$ is a density below an ultrahigh critical density ${\rho }_{cr.,symmetry}$ at which the symmetry of space breaks in a phase transition. This can occur in a phase transition from space to matter in the Higgs [51] mechanism. Moreover, this can take place in a dimensional phase transition [36,40,52,53]).

If such a part $\delta V_j$ with $v_j=c$ of space would consist of smaller parts $\delta V_k$, then the following would be implied:

(2.1) Each smaller part $\delta V_k$ would have the speed $v_k=c$, as the energy and volume of space have the speed $v=c$.

(2.2) Consequently, each part $\delta V_k$ would have a velocity ${\overrightarrow{v}}_k=c·{\overrightarrow{e}}_k$, with a direction vector ${\overrightarrow{e}}_k$ with norm one.

(2.3) As the considered universe is homogeneous (see part (2)), there is no source that could provide a uniform direction of the direction vectors ${\overrightarrow{e}}_k$.

(2.4) Hence, the velocity ${\overrightarrow{v}}_j$ of the considered part $\delta V_j$ with $v_j=c$ would be an average of the velocities ${\overrightarrow{v}}_k$. Thereby, as a consequence of the different direction vectors ${\overrightarrow{e}}_k$ in part (2.3), the velocity ${\overrightarrow{v}}_j$ would have an absolute value smaller than c, i. e. $|{\overrightarrow{v}}_j|=v_j<c$. This would contradict the speed $v_j=c$ in Eq. (19).

(2.5) Therefore, the parts $\delta V_j$ with speeds $v_j=c$ cannot consist of smaller parts. This is the answer to the question in (2). This implies that the parts $\delta V_j$ with $v_j=c$ are indivisible. Such a part $\delta V_j$ with its speed $v_j=c$ is called indivisible volume portion, indivisible VP.

(3) Next, it is shown how the indivisible VPs solve the space paradox:

(3.1) The energy and volume of space have the speed c, and the energy of space obeys $E^2·\left(1-{\displaystyle \frac{v^2}{c^2}}\right)=E_0^2=0$, as space consists of indivisible VPs $\delta V_j$ with the speed $v_j=c$.

(3.2) Moreover, the velocities ${\overrightarrow{v}}_j=c·{\overrightarrow{e}}_j$ of the indivisible VPs have stochastic direction vectors ${\overrightarrow{e}}_j$, that are distributed isotropically. Hence, these velocities average to zero.

(3.3) As a consequence, space is isotropic at a universal scale, see Figure 2. In this manner, the space paradox is solved.

Therefore, we obtain the following deep insight, the stochastic property of space:

In a homogeneous and isotropic universe, space is a stochastic average of many indivisible volume portions $\delta V_j$, each with the speed $v_j=c$. Hereby, the velocities ${\overrightarrow{v}}_j$ of the volume portions average to zero.

(4) Next, the solution is generalized to heterogeneous space: The early universe was very homogeneous and isotropic [22]. The heterogeneity of the mass distribution in the universe increased gradually, and thereby the heterogeneity of space evolved gradually [23,36,48,54,55]. Therefore, the natural heterogeneous space is a slight variation of the natural homogeneous and isotropic space. Details of that variation will be derived in the solution of the Hubble tension below.

3.3. Examples of Parts of Space

In this section, essential parts of natural space with the volume V are analyzed.

(1) Additional volume in the vicinity of a mass M:

In the vicinity of a mass M, there occurs additional volume $\delta V$, see section (Section 1.1.4). It is at rest relative to M. Moreover, in the vicinity of M, the ACS (see Section 1.1.5) [23,24,39]. is nearly at rest at M. Consequently, the speed of the additional volume in the vicinity of a mass is clearly smaller than c, i. e. $v<c$. Each additional volume with a speed $v<c$ must be a stochastic average of the indivisible VPs $\delta V_j$ with their speeds $v_j=c$, as space with its volume V consists of indivisible VPs $\delta V_j$ with their speeds $v_j=c$. This is the case for homogeneous and isotropic space and for the case of heterogeneous space which is a slight variation of homogeneous and isotropic space.

Altogether, additional volume that is at rest in the vicinity of a mass M is a stochastic average of indivisible VPs.

(2) Relative additional volume ${\epsilon }_L$:

In general, a VP $\delta V$ is located within an underlying VP $\Delta V_L$. The relative additional volume ${\epsilon }_L$ is the following ratio of the VP $\delta V$ and of its underlying VP $\Delta V$, see section (Section 1.1.4):

$${\epsilon }_L:={\displaystyle \frac{\delta V}{\Delta V_L}}={\displaystyle \frac{\Delta L·\Delta x·\Delta y-\Delta R·\Delta x·\Delta y}{\Delta L·\Delta x·\Delta y}}={\displaystyle \frac{\Delta L-\Delta R}{\Delta L}}={\displaystyle \frac{\delta L}{\Delta L}},\mathrm{with}\delta L:=\Delta L-\Delta R.$$

(20)

Thereby, the ratio ${\displaystyle \frac{\delta L}{\Delta L}}$ is usually interpreted as a tensor element, whereby the L - direction is the z - direction or the 3 - direction:

$${\epsilon }_{zz}:={\displaystyle \frac{\delta z}{\Delta z}}={\epsilon }_{jj},\mathrm{with}j=3.$$

(21)

In general, a volume portion VP $\delta V$ represents a change of an underlying VP $\Delta V$, and this change represents a tensor element or tensor. Thereby, typically, the change of each VP $\Delta V$ has a quadrupolar structure. A dipolar structure is excluded, as volume cannot be negative. Therefore, each change of an underlying VP $\Delta V$ can be described by a tensor of rank two. It is called change tensor [23,36] ${\epsilon }_{ij}$. In general, an element ${\epsilon }_{ij}$ of a change tensor is the ratio of the change $\delta L_i$ divided by the underlying length $\Delta L_j$:

$${\epsilon }_{ij}:={\displaystyle \frac{\delta L_i}{\Delta L_j}}.$$

(22)

Hereby, for each normalized direction vector ${\overrightarrow{e}}_j$, the underlying length $\Delta L_j$ is the sum of the original length $\Delta R_j$ and the change $\delta L_j$:

$$\Delta L_j:=\Delta R_j+\delta L_j.$$

(23)

In general, indivisible VPs can have the structure of a change tensor as well, see Figure 3.

(3) Gravitational wave:

Without loss of generality, a gravitational wave can be described as follows [50]: It has an angular frequency $\omega$. At a location, a gravitational wave has one direction of propagation ${\overrightarrow{e}}_z$, and two transverse directions ${\overrightarrow{e}}_x$ and ${\overrightarrow{e}}_y$. There are two possible modes. In a first mode, the elongations are ${\epsilon }_{xx}·cos\left(\omega t\right)$ and ${\epsilon }_{yy}·cos\left(\omega t\right)$, with ${\epsilon }_{xx}={\epsilon }_{yy}$, see Figure 3. The second mode is equal to the first mode rotated by 45^o around ${\overrightarrow{e}}_z$.

The elongations and the velocity of the gravitational wave can be measured with help of a Michelson interferometer. For instance, Abbott et al. [33] measured the amplitude ${\epsilon }_{xx,max}=1·{10}^{21}$.

In the theory of waves, the above observed gravitational wave is a wave with a coherence length that amounts several wave lengths. Accordingly, a gravitational wave could be interpreted as a coherent state in the framework of quantum physics, if quantum physics is applicable.

3.4. On Quantum Properties of an Indivisible VP

The indivisible VP in homogenous space is very founded. According to this indivisibility, a minimal extension of an indivisible VP is estimated with help of the Heisenberg [56] uncertainty relation of quantum physics:

In general, an indivisible VP can have very different forms, and matter or radiation can be placed in the VP. As an example, and as a very simple model, an indivisible VP is analyzed, that has the form of a ball with a radius $\Delta L$, and that contains no radiation or matter.

Consequently, the volume is

$$\Delta V_L={\displaystyle \frac{4\pi }{3}}\Delta L^3.$$

(24)

Thus, the VP has the following energy:

$$\Delta E_L={\displaystyle \frac{4\pi }{3}}\Delta L^3·u_{DE}.$$

(25)

As the VP has the speed $v=c$. the energy momentum relation of special relativity theory (SRT) provides the following momentum:

$$\Delta p_L={\displaystyle \frac{\Delta E_L}{c}}={\displaystyle \frac{4\pi }{3}}\Delta L^3·{\displaystyle \frac{u_{DE}}{c}}.$$

(26)

In the rest system of the VP, the momentum is zero, so that the standard deviation alias uncertainty of momentum is estimated by $\Delta p_L$. Similarly, the spatial standard deviation alias uncertainty of the indivisible VP is estimated by

$${\sigma }_L=\Delta L.$$

(27)

The Heisenberg [56] uncertainty relation for these standard deviations is as follows:

$$\Delta p_L·\Delta L\ge {\displaystyle \frac{\hslash }{2}}.$$

(28)

The estimated standard deviations in Eqs. (26 and 27) are inserted into the above uncertainty relation:

$${\displaystyle \frac{4\pi }{3}}\Delta L^4·{\displaystyle \frac{u_{DE}}{c}}\ge {\displaystyle \frac{\hslash }{2}}.$$

(29)

This uncertainty relation is solved for the spatial uncertainty $\Delta L$:

$$\Delta L\ge \sqrt[4]{{\displaystyle \frac{3\hslash ·c}{8\pi ·u_{DE}}}}=3.957·{10}^{-5}\mathrm{m}.$$

(30)

Altogether, the very particular considered indivisible VP, that does not contain any matter or radiation, has a minimal spatial uncertainty of $\Delta L\approx 0.03957\mathrm{mm}.$

3.5. Empirical Evidence for Indivisible Volume Portions

The derivation of indivisible VPs is based on isotropy at small scales. Accordingly, empirical evidence for indivisible VPs is of interest. Such evidence is presented in this section.

3.5.1. Estimated Time Uncertainty of Indivisible Volume Portions

In four-dimensional spacetime, the length $\Delta L$ of an indivisible VP is estimated by Eq. (30). It is the standard deviation according to the Heisenberg [56] uncertainty relation. In four-dimensional spacetime, the corresponding time uncertainty $\Delta t$ of an indivisible volume portion is estimated by the ratio of the length and the velocity of light c:

$$\Delta t_{indivisibleVP}={\displaystyle \frac{\Delta L}{c}}\ge {\displaystyle \frac{3.957·{10}^{-5}\mathrm{m}}{c}}=1.319·{10}^{-13}\mathrm{s}.$$

(31)

For instance, for the case of an averaging time of one second, ${\tau }_{av}=1\mathrm{s}$, the fractional uncertainty is estimated as follows

$$\Delta t_{indivisibleVP,frac}\ge \approx 1.319·{10}^{-13}.$$

(32)

3.5.2. Time Uncertainty of an Atomic Clock Using Gas

Many atomic clocks use gas atoms [57,58]. As these atoms move in natural space, and as an atom is very small compared to the estimated size of an indivisible VP, the clock’s uncertainty is larger or equal to the uncertainty of an indivisible VP in homogeneous natural space, in general. Similarly, if an object moves within a ship, then the object’s uncertainty is larger or equal to the ship’s uncertainty, in general.

For the case of natural space consisting of indivisible VPs, the uncertainty of space is estimated by $\Delta t_{indivisibleVP,frac}$ in Eq. (32). Therefore, for the case of averaging of one second,

$$\Delta t_{atomicgasclock,frac}\ge \Delta t_{indivisibleVP,frac}\ge \approx 1.319·{10}^{-13}\mathrm{s}.$$

(33)

In general, the uncertainty of a clock can be reduced by averaging during a time ${\tau }_{av}$. Thereby, according to statistics, and according to observation, the uncertainty decreases by the factor $1/\sqrt{{\tau }_{av}}$ [57,59]. Empirical data show the following [57]: Atomic clocks that use gas atoms, that are not confined to any particular location or trajectory, and that are averaged at most one second, ${\tau }_{av}\le 1\mathrm{s}$, exhibit time uncertainties larger than the estimated uncertainty of indivisible VPs in Eq. (32). This provides evidence for the existence of indivisible VPs. Moreover, a control experiment is available:

3.5.3. Time Uncertainty of an Atomic Lattice Clock

In an atomic lattice clock, the used atoms are confined to the potential minima of a standing wave of laser light. Hereby, the standing wave, and the device that generates that wave, are large compared to the estimated size of an indivisible VP. As a consequence, these atoms do not move freely in an indivisible VP of homogeneous natural space, but in artificially generated potential minima. Therefore, the atomic lattice clock’s uncertainty can be smaller than the estimated uncertainty of indivisble VPs in Eq. (32). In fact, measurements show that this is clearly the case. There is even a local maximum of the uncertainty as a function of the time ${\tau }_{av}$ of averaging [60]:

$$\Delta t_{atomiclatticeclock,frac}\le \Delta t_{maximumatomiclatticeclock,frac}\approx 3·{10}^{-16}.$$

(34)

This control experiment provides evidence for the following: The independence of the uncertainty of natural space and of indivisible VPs can provide a very small uncertainty of an atomic lattice clock.

$$\Delta t_{atomiclatticeclock,frac}\ll \Delta t_{indivisibleVP,frac}$$

(35)

4. On the Dynamics of Volume Portions

In this section, a very valuable and insightful description of VPs is developed. With it, a very general differential equation (DEQ) of the dynamics of VPs is derived.

Here and in the following, mathematically, a VP could be arbitrarily small. Physically, the Heisenberg [56] uncertainty relation limits the standard deviation of a VP from below. A particular example is analyzed in section (Section 3.4).

4.1. Additional Volume

In this section, the increase $\delta V$ of the volume $\Delta V_R$ of a VP is analyzed. For it, the difference of the increased volume $\Delta V_L$ and the original volume $\Delta V_R$ of the VP is used:

$$\delta V:=\Delta V_L-\Delta V_R$$

(36)

Hereby and in the following, a light travel distance $\Delta L$ is larger or equal to the corresponding gravitational parallax distance $\Delta R$, i. e. $\Delta L\ge \Delta R$, so the particular case without curvature is included. The above difference $\delta V$ is called additional volume, see section (Section 1.1.4).

Similarly as in section (Section 1.1.3), according to the Hacking [38] criterion, the enlarged volume $\Delta V_L$ and the additional volume $\delta V$ are real, as they can be manipulated. In contrast, the original volume $\Delta V_R$ is an idealization corresponding to the idealization of flat space:

Each VP has a real additional volume$\delta V$ and a real enlarged volume $\Delta V_L$, according to the Hacking [38] criterion.

In order to derive general laws of physics, this difference is normalized in the next section:

4.2. Relative Additional Volume

In general, in order to derive general laws of physics, it is valuable to use intensive quantities rather than extensive quantities [61]. In the present case of a VP, it is useful to utilize the ratio of its real additional volume $\delta V$ and its real enlarged volume $\delta V_L$. Such ratios are formed and analyzed in detail in this section:

That ratio is called relative additional volume ${\epsilon }_L$, see Eq. (9):

$${\epsilon }_L:={\displaystyle \frac{\delta V}{\Delta V_L}}.$$

(37)

The relation to the metric tensor is achieved by inserting Eqs. (7 and 36) into Eq. (37):

$${\epsilon }_L:={\displaystyle \frac{\Delta V_L-\Delta V_R}{\Delta V_L}}=1-{\displaystyle \frac{\Delta V_R}{\Delta V_L}}=1-{\displaystyle \frac{1}{\sqrt{g_{RR}}}}.$$

(38)

This is an example for the fact that curvature can be described by the metric tensor or by the relative additional volume. Moreover, the relative additional volume of a VP is real, as it is a ratio of real quantities of that VP:

Each VP has a real relative additional volume${\epsilon }_L$.

Furthermore, the description with the additional volume is compatible with the volume portions that become necessary for the solution of the space paradox. In contrast, the metric tensor does not include the concept of volume portions, and it does not provide the dynamics of the volume portions. As a consequence, the description with the volume portions provides the additional possibility to derive the dynamics of volume portions. Of course, the metric tensor provides the description of time dilation directly. In the case of volume portions, the Schwarzschild [28] metric is used. Thereby, the tensor element of the time $g_{tt}={\displaystyle \frac{1}{g_{RR}}}$ is utilized. With it, an interval of coordinate time $dt$ is transformed to an interval of own time $d\tau =dt·g_{tt}$ [20]. With help of the volume portions, the dynamics of volume portions is derived next:

4.3. Dynamics of Volume Portions

In this section, the dynamics of an arbitrary VP is described by its relative additional volume. The result is achieved with help of calculus or standard analysis only. As a consequence, the dynamics of VPs derived here is very general.

Firstly, the applicability of calculus or standard analysis is investigated:

Calculus or analysis are a mathematical tool, such as algebra and stochastics. Thereby, calculus or analysis do not include a prejudice about the continuity of space and time. The reason is that in the present investigation, space is a stochastic average of VPs. Hereby, VPs will be characterized by eigenvalues with a spectrum of eigenvalues. This spectrum can turn out to be discrete, continuous or partially discrete and partially continuous. As calculus or analysis are used in this study, these fields of mathematics do not necessarily include a prejudice about the discreteness or continuity of space.

In contrast, an exclusion of calculus and analysis would include a prejudice about the discreteness or continuity of space.

In fact, the space paradox and the implied structure of space as a stochastic average of VPs does already deduce an essential degree of discreteness of space. And it is important to investigate the amount of discreteness and continuity of these VPs in the following.

Moreover, in this paper, the physical reality of the used and deduced concepts is permanently tested with help of the Hacking [38] criterion.

Secondly, the differential equation, DEQ, of VPs is derived:

Each localized VP (see Section 3.2, part (1)) has a local maximum of its relative additional volume ${\epsilon }_L$. It is a function of its three-dimensional position vector $\overrightarrow{L}$ and of the time $\tau$. It is illustrated in Figure 4, whereby the three-dimensional position vector is summarized by a position L. Altogether, a localized VP can be described by a function ${\epsilon }_L(\tau ,\overrightarrow{L})$ with a local maximum. If there should be several local maxima or a set of local maxima, then one local maximum can be chosen as a convention.

As a fact of calculus or of analysis, at the local maximum, the change of ${\epsilon }_L(\tau ,\overrightarrow{L})$ is zero. Thus, the total derivative is zero:

$$d{\epsilon }_L(\tau ,\overrightarrow{L}\left(\tau \right))=0$$

(39)

That derivative is evaluated with help of partial derivatives:

$$d{\epsilon }_L(\tau ,\overrightarrow{L}\left(\tau \right))={\displaystyle \frac{\partial }{\partial \tau }}{\epsilon }_L(\tau ,\overrightarrow{L})d\tau +{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}{\epsilon }_L(\tau ,\overrightarrow{L})d\overrightarrow{L}=0.$$

(40)

The VP moves parallel to a corresponding direction unit vector ${\overrightarrow{e}}_v$ of its velocity $\overrightarrow{v}={\displaystyle \frac{\partial \overrightarrow{L}}{\partial \tau }}$. Therefore, during a time $d\tau$, the vector $\overrightarrow{L}$ changes by the amount $d\overrightarrow{L}$ = $v·d\tau ·{\overrightarrow{e}}_v$. With it, the total derivative in Eq. (40) is

$${\displaystyle \frac{\partial }{\partial \tau }}{\epsilon }_L(\tau ,\overrightarrow{L})d\tau +v·{\overrightarrow{e}}_v·{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}{\epsilon }_L(\tau ,\overrightarrow{L})d\tau =0.$$

(41)

The above Eq. is divided by $d\tau$. Moreover, the Eq. is solved for ${\displaystyle \frac{\partial }{\partial \tau }}{\epsilon }_L$:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial }{\partial \tau }}{\epsilon }_L(\tau ,\overrightarrow{L})=-v·{\overrightarrow{e}}_v·{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}{\epsilon }_L(\tau ,\overrightarrow{L}),\mathrm{each}\mathrm{indivisible}\mathrm{VP}\mathrm{has}v=c\end{array}$$

(42)

This is the differential equation, DEQ, of VPs or of volume dynamics (VD). A Lorentz invariant form of the DEQ is achieved as follows. The square is applied to Eq. (42), and the right hand side is subtracted,

$${\left({\displaystyle \frac{\partial {\epsilon }_L}{\partial \tau }}\right)}^2-v^2·{\left({\displaystyle \frac{\partial {\epsilon }_L}{\partial \overrightarrow{L}}}\right)}^2=0,\mathrm{each}\mathrm{indivisible}\mathrm{VP}\mathrm{has}v=c$$

(43)

Each localized VP fulfills the volume dynamics in Eq. (42) or in the Lorentz invariant Eq. (43).

For the following reasons, the derived dynamics is very founded and insightful: The derived DEQ of VD describes the dynamics of a VP with at least one local maximum. The derivation uses no postulate or unfounded hypothesis. In contrast, general relativity uses postulates such as the Einstein Hilbert action or the Einstein field equation [5,6]. Similarly, quantum physics uses ’guessed’ postulates [62,63,64]. Also gravity uses ’guessed’ postulates or restrictions. Examples are the restriction to physics without quanta in general relativity [5], and in Newton’s gravity [1]. Another example is the graviton hypothesis. Thereby, gravity uses hypothetic quanta [65].

Indeed, we will show later that the DEQ of VD implies gravity and curvature of space and time. Moreover, we will show that the DEQ of VD implies the postulates of quantum physics. In particular, based on the VD, we derive the Schrödinger equation in the next section.

5. Derivation of the Schrödinger Equation

In this section, we show that each VP fulfills a generalized Schrödinger equation (GSEQ), which implies the usual Schrödinger equation (SEQ), which holds for the special case of a non-relativistic mass M.

5.1. The Volume Dynamics Implies the GSEQ

In this section it is shown, that VPs with their VD imply the GSEQ.

(1) In a first investigation, the geometry of relative additional volume is analyzed:

For each VP, the DEQ (42) of VD is fulfilled. Thereby, the VP moves in the direction ${\overrightarrow{e}}_v$ of its velocity, see Figure 4.

In general, a relative additional volume with an increase $\delta L_3$ with the normalized direction vector ${\overrightarrow{e}}_3$ and with a propagation of indivisible VPs in the same direction, and with an underlying length $\Delta L_3$, is called unidirectional relative additional volume ${\epsilon }_{L,33}$, see Eqs. (21, 22 and 23). More information about such tensors can be found in the literature [23,36,50,66,67].

(2) Next, each VP is described by the DEQ of VD. In that DEQ, $v=c$ is inserted. Additionally, the time derivative is applied, so that the relative additional volume ${\epsilon }_{L,jj}$ becomes ${\displaystyle \frac{\partial }{\partial \tau }}{\epsilon }_{L,jj}$, which is usually expressed by ${\dot{\epsilon }}_{L,jj}$. As a consequence, the DEQ of VD implies the following DEQ:

$${\displaystyle \frac{\partial }{\partial \tau }}{\dot{\epsilon }}_{L,jj}=-c·{\overrightarrow{e}}_v·{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}{\dot{\epsilon }}_{L,jj}$$

(44)

(3) Next, as an equivalence transformation of the above DEQ, the factor $i\hslash$ is multiplied. This multiplication is also physically equivalent, as the system of units can be chosen freely. And the factor ℏ is one in natural units [68]. Consequently, the DEQ of VD implies the following DEQ:

$$i\hslash ·{\displaystyle \frac{\partial }{\partial \tau }}{\dot{\epsilon }}_{L,jj}=c·{\overrightarrow{e}}_v·\left[-i\hslash ·{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}\right]{\dot{\epsilon }}_{L,jj}$$

(45)

Moreover, for the case of an indivisible VP, this indivisibility corresponds to the quantum property with its universal unit of quantization, the Planck [69] constant h or its reduced version $\hslash :={\displaystyle \frac{h}{2\pi }}$.

Accordingly, the correspondence principle is applicable [68]. Consequently, the rectangular bracket is identified with the momentum operator[67] chapter 9:

$$i\hslash ·{\displaystyle \frac{\partial }{\partial \tau }}{\dot{\epsilon }}_{L,jj}={\overrightarrow{e}}_v·c·\widehat{\overrightarrow{p}}·{\dot{\epsilon }}_{L,jj}$$

(46)

In this DEQ, ${\dot{\epsilon }}_{L,jj}$ represents a rate. That rate is normalized by a factor $t_n$. In physics, $t_n$ has the dimension time and the unit second. Consequently, the normalized rate $t_n·{\dot{\epsilon }}_{L,jj}$ is dimensionless and has the unit one. It will be shown that the normalized rate has the role of a wave function in the above DEQ. Accordingly, the normalized rate is called wave function $\Psi$. Of course, this can be regarded as an abbreviation, if desired. As a consequence, the DEQ of VD implies the following DEQ:

$$i\hslash ·{\displaystyle \frac{\partial }{\partial \tau }}\Psi =c·{\overrightarrow{e}}_v·\widehat{\overrightarrow{p}}·\Psi$$

(47)

$$\Psi :=t_n·{\dot{\epsilon }}_{L,jj}$$

(48)

The product of the momentum operator and the direction vector of propagation, ${\overrightarrow{e}}_v·\widehat{\overrightarrow{p}}$, is the operator of the absolute value of the momentum $\widehat{p}$:

$$i\hslash ·{\displaystyle \frac{\partial }{\partial \tau }}\Psi =c·\widehat{p}·\Psi$$

(49)

In the present case of a VP that propagates with the speed c, special relativity implies that the product of c and the momentum p is the energy E. Consequently, according to the correspondence principle [68], pages 673-674, the product of c and the momentum operator is the energy operator:

$$i\hslash ·{\displaystyle \frac{\partial }{\partial \tau }}\Psi =\widehat{E}·\Psi$$

(50)

This Eq. has the form of a Schrödinger equation, SEQ. However, the SEQ holds for non-relativistic objects. In contrast, this DEQ holds for relativistic objects too, and it implies the SEQ for non-relativistic objects, see next section (Section 5.2). Thus, this DEQ is the GSEQ. Moreover, ${\dot{\epsilon }}_{L,rr}$ is real, as it is the derivative of the real ${\epsilon }_{L,rr}$. As a consequence, the wave function $\Psi$ is real, as it is the normalized form of the real ${\dot{\epsilon }}_{L,rr}$.

Each VP fulfills the GSEQ (50) and has a physically real wave function$\Psi \propto {\dot{\epsilon }}_{L,rr}$ in Eq. (48). Thereby, according to the Hacking [38] criterion, a wave function has an extraordinary physical reality, as it can be manipulated even in a nonlocal manner [71].

5.2. The Volume Dynamics Implies the SEQ

In this section it is shown, that VPs with their VD imply the SEQ.

For each localizable quantum object at $v\le c$, the following is implied:

(1) For the case of ultrafast objects, with $p^2{c}^2\gg m_0^2{c}^4$[21] an energy eigenvalue is obtained by the following linear approximation of the energy momentum relation $E=\sqrt{p^2{c}^2+m_0^2{c}^4}$ with respect to the small ratio ${\displaystyle \frac{m_0^2{c}^4}{p^2·c^2}}$:

$$E\dot{=}p·c+{\displaystyle \frac{m_0^2{c}^4}{2·p·c}}$$

(51)

Hereby, $\dot{=}$ marks the first order approximation for small ${\displaystyle \frac{m_0^2{c}^4}{p^2·c^2}}$. The corresponding linear approximation of the GSEQ is obtained by replacing the eigenvalue p by its operator $\widehat{p}$:

$$i\hslash {\displaystyle \frac{\partial }{\partial \tau }}\Psi \dot{=}\left(\widehat{p}·c+{\displaystyle \frac{m_0^2{c}^4}{2·\widehat{p}·c}}\right)·\Psi$$

(52)

(2) For the case of slow objects, with $p^2{c}^2\ll m_0^2{c}^4=:E_0^2$, the following holds:

(2a) An energy eigenvalue of the energy is obtained by the following linear approximation of the energy momentum relation $E=\sqrt{p^2{c}^2+m_0^2{c}^4}$ with respect to the small ratio ${\displaystyle \frac{p^2·c^2}{E_0^2}}$:

$$E\dot{=}{E}_0+{\displaystyle \frac{p^2}{2·m_0}}$$

(53)

(2b) The corresponding linear approximation of the GSEQ is obtained by replacing the eigenvalue p by its operator $\widehat{p}$.

$$i\hslash {\displaystyle \frac{\partial }{\partial \tau }}{\Psi }_{E_0}\dot{=}\left(E_0+{\displaystyle \frac{{\widehat{p}}^2}{2·m_0}}\right)·{\Psi }_{E_0}$$

(54)

Hereby, the wave function includes the rest energy $E_0$. Accordingly, the wave function is named ${\Psi }_{E_0}$. In general, the following squares are equal:

$${\widehat{p}}^2={\widehat{\overrightarrow{p}}}^2$$

(55)

(2c) The wave function is factorized:

$${\Psi }_{E_0}=\Psi ·exp\left({\displaystyle \frac{E_0\tau }{i\hslash }}\right)$$

(56)

The left hand side of Eq. (54) is evaluated with the product rule:

$$E_0{\Psi }_{E_0}+exp\left({\displaystyle \frac{E_0\tau }{i\hslash }}\right)i\hslash {\displaystyle \frac{\partial \Psi }{\partial \tau }}\dot{=}\left(E_0+{\displaystyle \frac{{\widehat{p}}^2}{2m_0}}\right)·{\Psi }_{E_0}$$

(57)

(2d) In the above DEQ, $E_0{\Psi }_{E_0}$ is subtracted. The resulting DEQ is divided by $exp\left({\displaystyle \frac{E_0\tau }{i\hslash }}\right)$. As a consequence, the SEQ proposed or postulated by Schrödinger [72] is derived from the VD:

$$i\hslash {\displaystyle \frac{\partial }{\partial \tau }}\Psi \dot{=}{\displaystyle \frac{{\widehat{p}}^2}{2·m_0}}·\Psi =\widehat{H}\Psi$$

(58)

Additionally, $\widehat{H}$ can include a potential energy:

$$i\hslash {\displaystyle \frac{\partial }{\partial \tau }}\Psi \dot{=}{\displaystyle \frac{{\widehat{p}}^2}{2·m_0}}\Psi +E_{pot}\Psi =\widehat{H}\Psi$$

(59)

5.3. Interpretation of VPs and Masses

In this section, the relation between VPs and masses is elaborated on the basis of the above dynamics of the VD, the GSEQ and the SEQ, and of the Higgs [51] mechanism:

Some elementary particles form their mass by a phase transition [21,51,73,74,75]:

In physics [9,68,76], empty space is called vacuum, and its energy density is the density $u_{DE}$ of dark energy [11,77]. In the above phase transition, the vacuum transforms to a mass.

As shown by the space paradox, the vacuum is a stochastic average of indivisible VPs. As a consequence, the above phase transition transforms indivisible volume portions to a mass.

In a typical phase transition, objects change from one phase to another phase. Thereby, these objects are described by the same fundamental dynamics in the first phase, in the second phase and during the transition. An example is the phase transition of condensation [78,79].

In the present case, such a fundamental dynamics that holds in the first phase, in the second phase and during the transition has been derived. It is the DEQ of VD. It holds for VPs in the first phase, and it implies the SEQ that holds for the masses in the second phase. A description of the phase transition in the framework of the VPs is elaborated in Carmesin [75].

Of course, the question remains how a mass can emit its wave function. This will be derived in the next section: In part (Section 6), it is shown that the VPs provide gravity as well as the local curvature of space and time as a byproduct. It has already been shown that a mass causes additional volume and VPs, see sections (Section 1.1.3 and Section 4.1). In section (Section 7), the process of local formation of volume (LFV) and of VPs is described, and a corresponding DEQ of the LFV is derived. These VPs formed by a mass M represent the wave function of that mass. In part (Section 10), it is shown for the case of the homogeneous universe, that this DEQ of LFV provides the emergence of the space of the universe and of the energy density $u_{vol}$ of that space in a homogeneous universe. More generally, in a heterogeneous universe, the energy density of space is $u_{DE}$, and the difference of $u_{vol}$ and $u_{DE}$ increases gradually with the heterogeneity of the universe, and this difference remained relatively small during the time from the Big Bang until today.

Both results are in precise accordance with observation. Therefore, these results provide a clear evidence for the present theory of VPs.

Each mass M fulfills the SEQ (59) implied by the GSEQ. M can be formed from VPs via a phase transition [51,53,75].

6. Gravity and Curvature

In the vicinity of a mass M, there occurs a curvature of space, as well as an exact gravitational potential and field, see Figure 1. Next it is shown how these phenomena are implied by the DEQ of VD:

6.1. Potential and Field

In this section, an exact generalized potential and generalized field are derived from the volume portions.

6.1.1. Generalized Potential and Field

In the vicinity of a mass M, see Figure 5, the unidirectional radial relative additional volume ${\epsilon }_{L,rr}$ exhibits the following properties. Hereby, spherical polar coordinates $(r,\vartheta ,\phi )$ with M at the origin, $dR$ at $M\to 0$ and $dL$ at $M\ne 0$ in Figure 5 are used:

(1) For each indivisible VP $\delta V_j$, the relative additional volume ${\epsilon }_{L,rr,j}(\tau ,\overrightarrow{L})$ propagates according to the DEQ of VD.

(1.1) That DEQ is multiplied by c:

$$c·{\displaystyle \frac{\partial }{\partial \tau }}{\epsilon }_{L,rr,j}(\tau ,\overrightarrow{L})={\overrightarrow{e}}_v·{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}\left(-c^2·{\epsilon }_{L,rr,j}(\tau ,\overrightarrow{L})\right)$$

(60)

(1.2) At an event $(\tau ,\overrightarrow{L})$, including the set $\mathcal{S}$ of its surrounding events in a time interval ${\tau }_i\in [\tau -\Delta \tau ,\tau +\Delta \tau ]$ and in a ball $|{\overrightarrow{L}}_i-\overrightarrow{L}|\le \Delta L$, with $\overrightarrow{L}$ in the vicinity of the mass, the sum of the relative additional volume of all indivisible VPs $\delta V_j$ is applied:

$$c·{\displaystyle \frac{\partial }{\partial \tau }}\sum _{jin\mathcal{S}}{\epsilon }_{L,rr,j}(\tau ,\overrightarrow{L})={\overrightarrow{e}}_v·{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}\left(-c^2·\sum _{jin\mathcal{S}}{\epsilon }_{L,rr,j}(\tau ,\overrightarrow{L})\right)$$

(61)

(1.3) The bracket in the above DEQ has the form of a generalized potential ${\Phi }_{gen}(\tau ,\overrightarrow{L})$

$${\Phi }_{gen}(\tau ,\overrightarrow{L}):=-c^2·\sum _{jin\mathcal{S}}{\epsilon }_{L,rr,j}$$

(62)

Hereby, the potential is generalized, as it describes volume portions, since ${\epsilon }_{L,rr,j}$ is the relative additional volume of an indivisible VP.

(1.4) The negative gradient of that generalized potential is the generalized field ${\overrightarrow{G}}_{gen}$, see Figure 5:

$${\overrightarrow{G}}_{gen}(\tau ,\overrightarrow{L}):=-{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}\left(-c^2·\sum _{jin\mathcal{S}}{\epsilon }_{L,rr,j}\right)=-{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}{\Phi }_{gen}(\tau ,\overrightarrow{L})$$

(63)

(1.5) Therefore, the DEQ of VD in Eq. (60) takes the form of the following rate gravity relation:

$$c·{\displaystyle \frac{\partial }{\partial \tau }}\sum _{jin\mathcal{S}}{\epsilon }_{L,rr,j}={\overrightarrow{e}}_v·{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}{\Phi }_{gen}(\tau ,\overrightarrow{L})=-{\overrightarrow{e}}_v{\overrightarrow{G}}_{gen}(\tau ,\overrightarrow{L})$$

(64)

The potential and field in the above equation are generalized to the respective quantities for one indivisible VP $\delta V_j$. Thereby, the potential is

$${\Phi }_{gen,j}(\tau ,\overrightarrow{L})=-c^2{\epsilon }_{L,rr,j}(\tau ,\overrightarrow{L}),$$

(65)

and the field is as follows:

$${\overrightarrow{G}}_{gen,j}(\tau ,\overrightarrow{L})=-{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}{\Phi }_{gen,j}(\tau ,\overrightarrow{L})=c^2{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}{\epsilon }_{L,rr,j}.$$

(66)

These relations are results of the VD. Formally, these results can be obtained by an application of the above average with one indivisible VP only.

For comparison, expectation values of the field have been derived from the VD as follows: Firstly, a quantum field theory has been derived from the VD. Secondly, the expectation value of a field has been derived from the quantum field theory [23,67].

(2) For these indivisible VPs, and for each event $(\tau ,\overrightarrow{L})$, that rate gravity relation can be expressed with help of the following rate gravity scalar$RG{S}_{gen}$:

$$RG{S}_{gen}:={\left(c·{\displaystyle \frac{\partial }{\partial \tau }}\sum _{jin\mathcal{S}}{\epsilon }_{L,rr,j}\right)}^2-{\overrightarrow{G}}_{gen}^2,\mathrm{thus}$$

(67)

$$RG{S}_{gen}={\left(c·{\displaystyle \frac{\partial }{\partial \tau }}\sum _{jin\mathcal{S}}{\epsilon }_{L,rr,j}\right)}^2-\sum _{k=1}^{dimensionD}{G}_{gen,k}^2\mathrm{and}$$

(68)

$$RG{S}_{gen}={\left(c·{\displaystyle \frac{\partial }{\partial \tau }}\sum _{jin\mathcal{S}}{\epsilon }_{L,rr,j}\right)}^2-{\left(c{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}{\Phi }_{gen}\right)}^2\mathrm{and}$$

(69)

$$RG{S}_{gen}=0$$

(70)

(3) For each underlying volume $\Delta V$, and for each event $(\tau ,\overrightarrow{L})$, with a gravitational parallax distance R from M, the generalized field is proportional to ${\displaystyle \frac{1}{R^2}}$:

$$|{\overrightarrow{G}}_{gen}|\propto {\displaystyle \frac{1}{R^2}},\mathrm{for}D=3,\mathrm{and}\mathrm{for}\Delta V$$

(71)

This result is derived as follows:

(3.1) Eq. (64) is multiplied by ${\overrightarrow{e}}_v$. Hence, the field is as follows:

$${\overrightarrow{e}}_v·c·{\displaystyle \frac{\partial }{\partial \tau }}\sum _{jin\mathcal{S}}{\epsilon }_{L,rr,j}=-{\overrightarrow{G}}_{gen}(\tau ,\overrightarrow{L})$$

(72)

(3.2) Integration with respect to $\tau$ from zero to a time $\delta \tau$ yields:

$${\overrightarrow{e}}_v·c·\sum _{jin\mathcal{S}}{\epsilon }_{L,rr,j}\left(\delta \tau \right)=-{\int }_0^{\delta \tau }{\overrightarrow{G}}_{gen}(\tau ,\overrightarrow{L})d\tau$$

(73)

The time $\delta \tau$ is chosen so small that the integral in the above Eq. is approximated by $\delta \tau ·{\overrightarrow{G}}_{gen}$. Thus, the field is as follows:

$${\overrightarrow{e}}_v·c·\sum _{jin\mathcal{S}}{\epsilon }_{L,rr,j}\left(\delta \tau \right)=-\delta \tau ·{\overrightarrow{G}}_{gen}$$

(74)

(3.3) The definition ${\epsilon }_{L,rr,j}={\displaystyle \frac{\delta V_{L,rr,j}}{d{V}_L}}$ is used. The energy density $u_{vol}$ of volume is nonzero, as it is approximately the same as $u_{DE}$, which is nonzero [11,12,16]. Therefore, the indivisible VP $\delta V_{L,rr,j}$ is proportional to the corresponding energy $\delta E_j$. The latter is proportional to the momentum $\delta p_j=\delta E_j/c$, as each VP propagates with the speed c, that is: $\delta V_{L,rr,j}={\displaystyle \frac{\delta E_j}{u_{vol}}}={\displaystyle \frac{c·\delta p_j}{u_{vol}}}$.

(3.4) The underlying volume $d{V}_L$ of a shell with center M is considered. It is as follows: $d{V}_L=A_D·R^{D-1}·dL$. Thus, the field is as follows:

$$-{\overrightarrow{e}}_v·{\displaystyle \frac{c^2}{u_{vol}·A_D·dL}}·{\displaystyle \frac{{\sum }_{jin\mathcal{S}}\delta p_j}{\delta \tau }}·{\displaystyle \frac{1}{R^2}}={\overrightarrow{G}}_{gen}$$

(75)

Hereby, the thickness $dL$ of each shell is chosen constant, so that it does not dependent on R. Thence, the first fraction is constant. The 2^nd fraction is the momentum current flowing through each shell. It is constant, as no shell causes any momentum. Consequently, ${\displaystyle \frac{1}{R^2}}\propto \left|{\overrightarrow{G}}_{gen}\right|$. q. e. d.

A version of the corresponding result for a dimension $D>3$ is shown in Carmesin[67] THM 9.

(4) As M is the source of the field ${\overrightarrow{G}}_{gen}\left(R\right)$, that field is proportional to M: $\left|{\overrightarrow{G}}_{gen}\left(R\right)\right|\propto {\displaystyle \frac{M}{R^2}}$.

Thus, there is a universal constant $G_{gen}$ of proportionality:

$$\left|{\overrightarrow{G}}_{gen}\left(R\right)\right|={\displaystyle \frac{G_{gen}M}{R^2}},\mathrm{for}D=3.$$

(76)

In general, the value of a universal constant, such as $G_{gen}$, must be obtained from observation. Accordingly, $G_{gen}$ is obtained in the next section. Additionally, the curvature of space is analyzed:

6.1.2. Spin, Statistics and the Additive Structure of VPs, Potentials and Fields

In general, a VP has the tensor property of a quadrupolar structure, see section (Section 3). Consequently, it is represented by a tensor of rank two.

Therefore, at the level of quantum physics, an indivisible VP has an integer valued spin, see Landau and Lifschitz [81], §58, Carmesin [82]:

$$S=n·\hslash ,\mathrm{with}\mathrm{a}\mathrm{natural}\mathrm{number}n.$$

(77)

As a consequence, at the level of quantum physics, an indivisible VP is a boson, see Landau and Lifschitz [81], §64, Carmesin [82]. Consequently, at the level of quantum physics, an indivisible VP obeys the Bose [83] statistics, alias Bose - Einstein statistics, see Landau and Lifschitz [81], §64, Sakurai and Napolitano [63], section 7.2.

The Bose - Einstein statistics implies that several bosons can exist at the same place. Consequently, the additional volumes ${\epsilon }_{L,rr,j}$ caused by different masses $m_j$ can exist simultaneously at each point P in the universe, and these ${\epsilon }_{L,rr,j}$ add up at P. This, in turn, implies that the potential ${\Phi }_{gen}\left(P\right)$ at P is the sum of these additional volumes ${\epsilon }_{L,rr,j}\left(P\right)$ multiplied by $-c^2$. This founds Eq. (62) at the level of quantum physics. As a consequence of this potential, the generalized field ${\overrightarrow{G}}_{gen}\left(P\right)={\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}{\Phi }_{gen}\left(P\right)$ has the same additive structure.

6.2. Curvature in the Vicinity of a Mass

The DEQ of VD provides the curvature in the vicinity of a mass M as follows:

(1) For the case of a shell with the center M and with the gravitational parallax radius R, the relative additional volume ${\epsilon }_{L,rr}$ is as follows:

$${\epsilon }_{L,rr}={\displaystyle \frac{d{V}_L-d{V}_R}{d{V}_L}}=1-{\displaystyle \frac{d{V}_R}{d{V}_L}}=1-{\displaystyle \frac{4\pi R^{2}dR}{4\pi R^{2}dL}}=1-{\displaystyle \frac{dR}{dL}}.$$

(78)

The resulting fraction ${\displaystyle \frac{dR}{dL}}$ is called position factor [67]:

$${\epsilon }_E\left(R\right):={\displaystyle \frac{dR}{dL}}=1-{\epsilon }_{L,rr}$$

(79)

The fraction ${\displaystyle \frac{dL}{dR}}$ is identified with the root of the radial tensor element of the metric tensor. It occurs in the vicinity of a mass M.

$$\sqrt{g_{rr}}:={\displaystyle \frac{dL}{dR}}={\displaystyle \frac{1}{{\epsilon }_E\left(R\right)}}.$$

(80)

More generally, at each R, or at each event $(\tau ,\overrightarrow{L})$ with $|\overrightarrow{L}|\ge R$, the curvature can be generalized for the case of a single indivisible VP $\delta V_j$, with the relative additional volume ${\epsilon }_{L,rr,j}$, as follows:

$$g_{rr,j}:={\displaystyle \frac{1}{{\epsilon }_{E,j}^2}}:={\displaystyle \frac{1}{{(1-{\epsilon }_{L,rr,j})}^2}}.$$

(81)

(2) A DEQ for the position factor is derived: For it, ${\displaystyle \frac{\partial }{\partial L}}$ is applied to Eq. (79). This implies:

$${\displaystyle \frac{\partial }{\partial L}}{\epsilon }_E={\displaystyle \frac{\partial R}{\partial L}}{\displaystyle \frac{\partial }{\partial R}}{\epsilon }_E={\epsilon }_E{\displaystyle \frac{\partial }{\partial R}}{\epsilon }_E=-{\displaystyle \frac{\partial {\epsilon }_{L,rr}}{\partial L}}$$

(82)

The potential ${\Phi }_{gen}=-c^2{\epsilon }_{L,rr}$ is solved for ${\epsilon }_{L,rr}$, and this is inserted into Eq. (82):

$${\epsilon }_E\left(R\right){\displaystyle \frac{\partial {\epsilon }_E}{\partial R}}={\displaystyle \frac{\partial {\Phi }_{gen}/c^2}{\partial L}}$$

(83)

The gradient ${\displaystyle \frac{\partial }{\partial L}}={\overrightarrow{e}}_v{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}$ is applied:

$${\epsilon }_E\left(R\right){\displaystyle \frac{\partial {\epsilon }_E}{\partial R}}={\overrightarrow{e}}_v{\displaystyle \frac{\partial {\Phi }_{gen}/c^2}{\partial \overrightarrow{L}}}$$

(84)

The field $-{\displaystyle \frac{\partial {\Phi }_{gen}}{\partial \overrightarrow{L}}}={\overrightarrow{G}}_{gen}$ is identified:

$$-{\overrightarrow{e}}_v{\displaystyle \frac{1}{c^2}}{\overrightarrow{G}}_{gen}={\epsilon }_E\left(R\right){\displaystyle \frac{\partial {\epsilon }_E}{\partial R}}$$

(85)

The field and the direction vector are antiparallel. Consequently, the field is as follows:

$${\displaystyle \frac{1}{c^2}}\left|{\overrightarrow{G}}_{gen}\right|={\epsilon }_E\left(R\right){\displaystyle \frac{\partial {\epsilon }_E}{\partial R}}$$

(86)

The field as a function of the mass in Eq. (76) is used:

$${\displaystyle \frac{G_{gen}M}{R^2{c}^2}}={\epsilon }_E\left(R\right){\displaystyle \frac{\partial {\epsilon }_E}{\partial R}}$$

(87)

(3) The DEQ for the position factor is solved:

Integration by parts yields:

$$\int {\displaystyle \frac{G_{gen}M}{R^2{c}^2}}dR=\int {\epsilon }_E\left(R\right)d{\epsilon }_E$$

(88)

The integral is evaluated with a constant K of integration:

$$K-{\displaystyle \frac{G_{gen}M}{R{c}^2}}={\displaystyle \frac{1}{2}}{\epsilon }_E^2$$

(89)

That result is solved for the position factor:

$${\epsilon }_E=\sqrt{2K-{\displaystyle \frac{2G_{gen}M}{c^2}}{\displaystyle \frac{1}{R}}}$$

(90)

In the limit $R\to \infty$, there is no curvature. Consequently, ${\epsilon }_E={\displaystyle \frac{dR}{dL}}=1$. As a consequence, $2K=1$. Therefore, the solution of the DEQ provides the position factor as follows:

$${\epsilon }_E=\sqrt{1-{\displaystyle \frac{2G_{gen}M}{c^2}}{\displaystyle \frac{1}{R}}}$$

(91)

(4) The position factor in Eq. (91) is compared with observation. For it, the position factor is replaced by the inverse root of the radial tensor element (see Eq. 80):

$${\epsilon }_E=\sqrt{1-{\displaystyle \frac{2G_{gen}M}{c^2}}{\displaystyle \frac{1}{R}}}={\displaystyle \frac{1}{\sqrt{g_{rr}}}}$$

(92)

Moreover, observation shows that this inverse root of the radial tensor element is as follows [20,84]:

$$\sqrt{1-{\displaystyle \frac{2GM}{c^2}}{\displaystyle \frac{1}{R}}}={\displaystyle \frac{1}{\sqrt{g_{rr}}}}=\sqrt{1-{\displaystyle \frac{R_S}{R}}}.$$

(93)

Hereby, we use the definition of the Schwarzschild radius $R_S:={\displaystyle \frac{2GM}{c^2}}$. The comparison of the two relations for the tensor element in Eqs. (92 and 93) shows that the generalized universal constant $G_{gen}$ is the same as Newton’s constant of gravitation G. Thus, the generalized field is identified with the exact gravitational field and the generalized potential is identified with the exact gravitational potential. These identified potential and field are exact, as they are derived without any approximation, and as they provide the correct curvature. This exact gravitation, derived here exactly, differs from Newton’s law of gravitation, which is an approximation.

In the vicinity of a mass, the indivisible VPs cause a generalized potential, a generalized field, the gravitational field and the curvature of space and time. The respective Eqs. are derived.

6.3. Discussion of Gravity and Curvature

In the vicinity of a mass M, the VD provides the relative additional volume ${\epsilon }_{L,rr}\left(r\right)$ as a function of r. That ${\epsilon }_{L,rr}\left(r\right)$ provides the exact gravitational potential ${\Phi }_{exact}=-c^2·{\epsilon }_{L,rr}\left(r\right)$. That exact gravitational potential provides the exact gravitational field ${\overrightarrow{G}}_{exact}^{*}=-{\displaystyle \frac{\partial }{\partial \overrightarrow{L}}}{\Phi }_{exact}$. In the following, these valuable and insightful properties are analyzed and interpreted:

6.3.1. Transmission of the Potential and Field

The indivisible VPs $\delta V_j$ with their relative additional volume ${\epsilon }_{L,rr,j}\left(r\right)$ provide a net outward propagation. Thereby, these indivisible VPs transmit a nonzero momentum, as the energy density $u_{vol}$ is positive. As a consequence, these indivisible VPs transmit the gravitational interaction. This confirms the idea of the graviton hypothesis proposed by Blokhintsev and Galperin [65]. Moreover, these indivisible VPs explicate the mechanism of the transmission of gravity.

In addition, these indivisible VPs cause and explain the curvature of space. Thereby, the curvature is explained with help of the sum of indivisible VPs. More generally, the curvature of a single indivisible VP has been generalized, see Eqs. (80 and 81).

6.3.2. On the Exactness of the Potential and Field

The generalized potential and field derived here are exact. In contrast, the gravitational potential is only an approximation in Newton’s theory. For instance, correction terms depending on the gravitational parallax distance R and on the velocity $\overrightarrow{v}$ have been elaborated in Post-Newtonian approximations [85,86], Eq. (2.49). Accordingly, the following question arises: How is the exactness achieved here?

Essentially, this is achieved here by the application of especially useful distance measures and coordinates systems:

Firstly, for each point P in the universe, there is an adequate coordinate system (ACS), so that an object at rest in the ACS has the absolute zero of velocity, see section (Section 1.1.5) or Carmesin [23,24,39]. This ACS is used here. As a consequence, the velocity-terms in Post-Newtonian approximation are zero.

Secondly, two measurable distance measures are used, see Figure 1: the light travel distance $d_{LT}$[87], and the gravitational parallax distance $d_{GP}$ [23,36,40], it can also be measured as a circumferential distance [88,89], section 2.6.

Hereby, according to the Hacking [38] criterion, the light travel distance $d_{LT}$ to a field generating mass M is real, as an increase of M can change that distance $d_{LT}$. In contrast, the gravitational parallax distance $d_{GP}$ to a field generating mass M is idealized, as it represents the limit M to zero of the light travel distance:

$$d_{GP}=\underset{M\to 0}{lim}{d}_{LT}.$$

(94)

This is a typical idealization based on a limit [46]. Though the gravitational parallax distance $d_{GP}$ is idealized and not real, that distance $d_{GP}$ can be measured, and that distance $d_{GP}$ provides the ${\displaystyle \frac{1}{R^2}}$ law, see Figure 5.

Thirdly, the exact potential and field are determined as follows: For the case of a point P, the idealized gravitational parallax distance $d_{GP}$ from P to the field generating mass M is measured or determined by other means. With it, the potential and the field are determined as a function of $d_{GP}=R$, by using the respective equations in this section and paper. The result is exact, as no approximation has been used in the derivation of these equations.

In contrast, in Newton’s theory, the flatness of space has been introduced as a postulate. Accordingly, a user might use that postulate and the light travel distance $d_{LT}\ne R$, and the equations for potentials and fields in Newton’s mechanics. In such a postulate based determination of the potential or field, the result is an approximation only.

6.3.3. Advantage of the Exact Potential and Field

Altogether, the indivisible VPs cause the transmission of gravity, the exact gravitational potential, the exact gravitational field and the exact curvature of space, in an indivisible and impartible manner. Thereby, by using the adequate coordinate system and the measurable idealized gravitational parallax distance, relatively short, highly structured, and clarifying equations can be used. Moreover, the results are parts of the unification of relativity, gravity and quanta. This unification uses the relative difference ${\epsilon }_{L,rr}$, which is based on both distance measures: the real $d_{LT}$ and the idealized $d_{GP}$.

7. Local Formation of Volume in Nature

In this section, the dynamics of the local formation of volume (LFV) is derived.

In the vicinity of a mass M, additional volume $\delta V$ propagates outwards in a radial direction. Thereby, the amount of additional volume increases. Consequently, there occurs locally formed volume, LFV, $\underline{\delta }V$ or $\underline{\delta }{V}_{rr}$ in the radial direction r. Hereby and in the following, an underlined variable marks the formed volume or the process of formation of volume. Such LFV can be caused by the mass M.

More precisely, that LFV occurs at each location. At each location, there is a gradient of the relative additional volume ${\epsilon }_{L,jj}$, or of the potential ${\Phi }_L=-c^2·{\epsilon }_{L,jj}$, or there is a gravitational field ${\overrightarrow{G}}^{*}$. As a consequence, more generally, locally, the LFV is caused by a local gravitational field. In this section, the relation between the LFV $\underline{\delta }{V}_{jj}$ and its cause is analyzed: the field ${\overrightarrow{G}}^{*}$ or $G_j^{*}$.

7.1. Definition of Locally Formed Volume

If additional volume $\underline{\delta }{V}_{jj}$ forms in a volume $d{V}_L$ and in a direction ${\overrightarrow{e}}_j$ during a time $\underline{\delta }\tau$, then this process can be described by the following normalized rate of unidirectional LFV:

$${\underline{\dot{\epsilon }}}_{L,jj}:={\displaystyle \frac{\underline{\delta }{V}_{jj}}{\underline{\delta }\tau ·d{V}_L}}$$

(95)

That LFV ${\underline{\dot{\epsilon }}}_{L,jj}$ is described by a general law, which is derived in the next section:

7.2. Law of Locally Formed Volume

In this section, the mechanism of the local formation of volume is explained and formulated. This law of the local formation of volume is derived in section (Section 7.3).

In the vicinity of a mass M or an effective mass $M_{eff}$, and at a $d_{GP}$ based distance R from M or $M_{eff}$, the following holds for the normalized rate:

(1) In the far distance approximation, FDA, the ratio $R_S/R$ is relatively small compared to 1. Thereby, at first order in that ratio $R_S/R$, the normalized rate is as follows:

$${\underline{\dot{\epsilon }}}_{L,rr}^2·c^2=G_{gen,r}^2$$

(96)

Hereby, $G_{gen,r}$ is the component parallel to ${\overrightarrow{e}}_r$ of the generalized field. $G_{gen,r}$ is the cause of the rate of LFV ${\underline{\dot{\epsilon }}}_{L,rr}$. More generally, each field ${\overrightarrow{G}}_{gen}$ in a direction ${\overrightarrow{e}}_j$ causes a unidirectional normalized rate ${\underline{\dot{\epsilon }}}_{L,jj}$ in that direction. Moreover, this field ${\overrightarrow{G}}_{gen}$ is equal to the exact gravitational field ${\overrightarrow{G}}^{*}$, see section (Section 6):

$${\underline{\dot{\epsilon }}}_{L,jj}^2·c^2=G_{gen,j}^2={\left({\overrightarrow{G}}_j^{*}\right)}^2\mathrm{with}{\overrightarrow{G}}_{gen}=-G_{gen,j}·{\overrightarrow{e}}_j$$

(97)

(2) As a consequence, the non-diagonal components ${\underline{\dot{\epsilon }}}_{L,ij,i\ne j}$ do not provide additional volume.

(3) The exact value of the rate ${\underline{\dot{\epsilon }}}_{L,rr}$ is:

$${\underline{\dot{\epsilon }}}_{L,rr}=c·{\displaystyle \frac{2}{R}}·{\epsilon }_E·\left(1-{\epsilon }_E-{\displaystyle \frac{1}{4{\epsilon }_E^2·\frac{R}{R_S}}}\right)$$

(98)

(4) More generally, ${\displaystyle \frac{dR}{dL}}$ is a function ${\epsilon }_F:={\displaystyle \frac{dR}{dL}}$ that has to be determined. The definition yields ${\underline{\dot{\epsilon }}}_{L,rr}$ = ${\displaystyle \frac{\frac{\partial }{\partial \tau }\delta V\underline{\delta }\tau }{d{V}_L\underline{\delta }\tau }}$. The substitution ${\displaystyle \frac{\partial }{\partial \tau }}$ = ${\displaystyle \frac{\partial L}{\partial \tau }}{\displaystyle \frac{\partial }{\partial L}}$ = $c·{\displaystyle \frac{\partial }{\partial L}}$ yields ${\underline{\dot{\epsilon }}}_{L,rr}$ = $c{\displaystyle \frac{\frac{\partial }{\partial L}\delta V}{d{V}_L}}$. The substitution ${\displaystyle \frac{\partial }{\partial L}}$ = ${\displaystyle \frac{\partial R}{\partial L}}{\displaystyle \frac{\partial }{\partial R}}$ = ${\epsilon }_{F}c·{\displaystyle \frac{\partial }{\partial R}}$ yields ${\underline{\dot{\epsilon }}}_{L,rr}$ = ${\epsilon }_{F}c{\displaystyle \frac{\frac{\partial }{\partial R}\delta V}{d{V}_L}}$. Using $d{V}_L=4\pi R^{2}dL=4\pi R^{2}dR/{\epsilon }_F$, and $\delta V=4\pi R^2(dL-dR)$ = $4\pi R^{2}dR(1/{\epsilon }_F-1)$ yields: ${\underline{\dot{\epsilon }}}_{L,rr}$ = ${\epsilon }_F^{2}c{\displaystyle \frac{4\pi dR\frac{\partial }{\partial R}{R}^2(1/{\epsilon }_F-1)}{4\pi R^{2}dR}}$ = ${\epsilon }_F^{2}c{\displaystyle \frac{\frac{\partial }{\partial R}{R}^2(1/{\epsilon }_F-1)}{R^2}}$. Evaluation of the derivative yields ${\underline{\dot{\epsilon }}}_{L,rr}$ = ${\epsilon }_F^{2}c{\displaystyle \frac{2R(1/{\epsilon }_F-1)-R^2{\epsilon }_F^{\prime }/{\epsilon }_F^2}{R^2}}$ = ${\epsilon }_{F}c{\displaystyle \frac{2(1-{\epsilon }_F)}{R}}$ - $c{\epsilon }_F^{\prime }$. ${\epsilon }_L$ = ${\displaystyle \frac{dL-dR}{dL}}=1-{\epsilon }_F$ and ${\epsilon }_F^{\prime }=-{\epsilon }_L^{\prime }$ imly

$${\underline{\dot{\epsilon }}}_{L,rr}={\displaystyle \frac{2c}{R}}{\epsilon }_L(1-{\epsilon }_L)+c{\epsilon }_L^{\prime }.$$

(99)

(5) Eq. (99) can be solved numerically and provides the metric in a rotation symmetric system:

$${\displaystyle \frac{dR}{dL}}=1-{\epsilon }_L\mathrm{or}{\displaystyle \frac{dL}{dR}}={\displaystyle \frac{1}{1-{\epsilon }_L}}=\sqrt{|g_{rr}|}={\displaystyle \frac{1}{\sqrt{|g_{tt}|}}}$$

(100)

7.3. Derivation of the Law of LFV

In this section, the mechanism and the law of local formation of volume are derived.

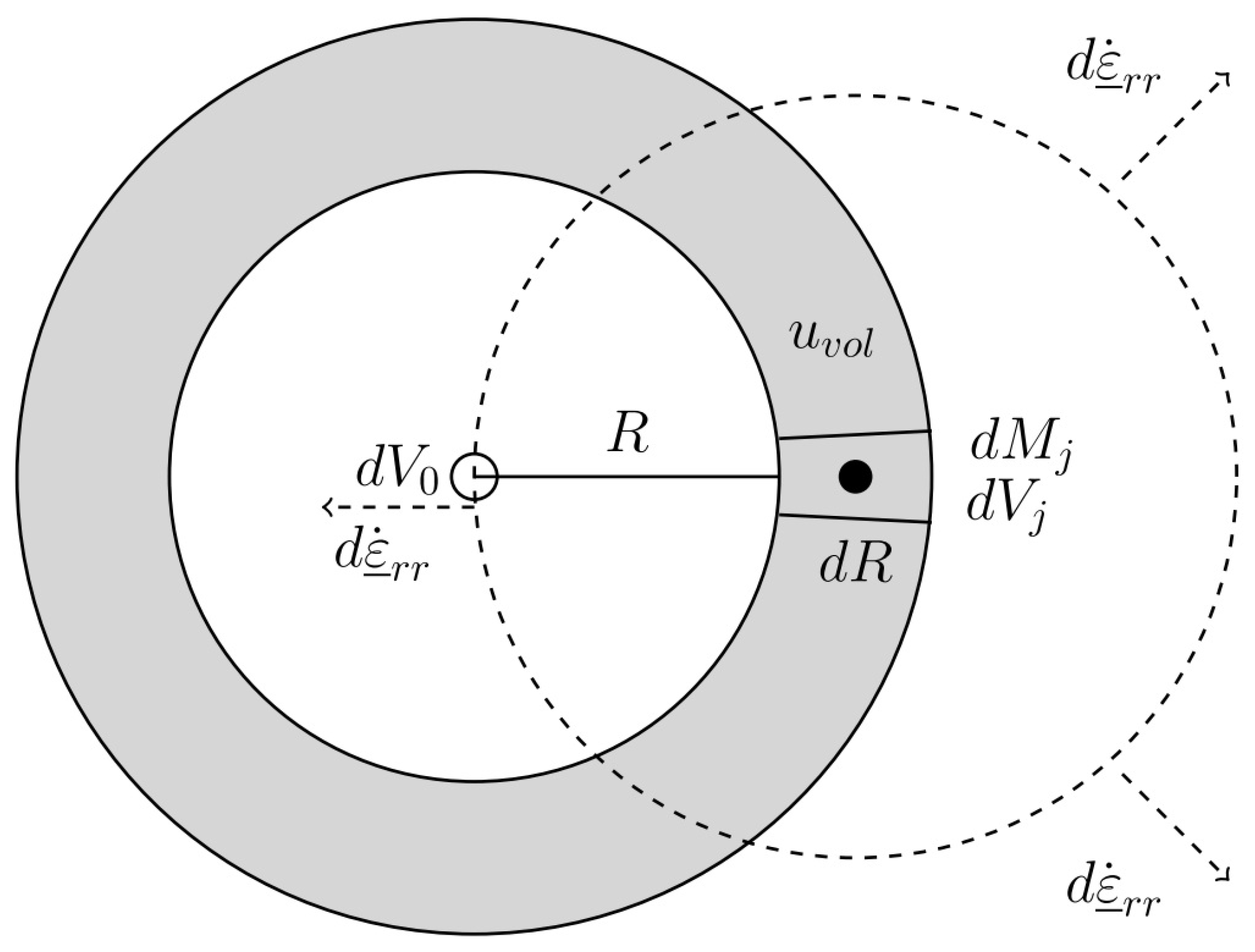
Part (1): At each radial coordinate R, a shell with center at M, and with thickness $dL$ represents the analyzed volume $d{V}_L$. Thereby, the additional volume $\delta V$ is in a shell with radius R, thickness $\delta R$, and volume $\delta V=4\pi R^2\delta R$. Similarly, the LFV $\underline{\delta }V$ is in a shell with radius R, thickness $\underline{\delta }R$, and volume $\underline{\delta }V=4\pi R^2\underline{\delta }R$.

The LFV is analyzed at leading order in the increment $dR$. This is exact, as the increment can be made as small as desired. If the additional volume $\delta V\left(R\right)$ increases as a function of R, then there occurs formed volume $\underline{\delta }{V}_{rr}$, whereby the direction r is equal to the radial direction.

In general, the observable additional volume $\delta V$ in a shell with center N, with radius R, and with thickness $dR$ is a function of R. Consequently, the LFV is the change of $\delta V$ as a function of R. Therefore, the change $\underline{\delta }{V}_{rr}$ of volume in a shell with thickness $\underline{\delta }R$ is equal to the derivative of the observable additional volume ${\displaystyle \frac{\partial }{\partial R}}\delta V$ multiplied by that thickness $\underline{\delta }R$:

$$\underline{\delta }{V}_{rr}:=\underline{\delta }R{\displaystyle \frac{\partial }{\partial R}}\delta V$$

(101)

Thereby, $\delta V$ is as follows:

$$\delta V=d{V}_L-d{V}_R=4\pi R^2·(dL-dR)=4\pi R^{2}dR·({\epsilon }_E^{-1}-1)$$

(102)

In the far distance approximation, FDA, in leading order in ${\displaystyle \frac{R_S}{R}}<<1$, ${\epsilon }_E^{-1}$ is as follows:

$${\epsilon }_E^{-1}\dot{=}1+{\displaystyle \frac{1}{2}}·{\displaystyle \frac{R_S}{R}}$$

(103)

With it, the derivative in Eq. (101) is as follows:

$${\displaystyle \frac{\partial }{\partial R}}\delta V={\displaystyle \frac{\partial }{\partial R}}\left(4\pi R^{2}dR·{\displaystyle \frac{1}{2}}·{\displaystyle \frac{R_S}{R}}\right)=2\pi ·dR·R_S$$

(104)

With it, the change in Eq. (101) is as follows:

$$\underline{\delta }{V}_{rr}:=2\pi ·dR·R_S·\underline{\delta }R$$

(105)

With it, and with $\underline{\delta }\tau ={\epsilon }_E\underline{\delta }R/c$, and with $dL=dR/{\epsilon }_E$, the normalized rate of unidirectional LFV in Eq. (95) is as follows:

$${\underline{\dot{\epsilon }}}_{L,rr}\widehat{=}{\displaystyle \frac{\underline{\delta }{V}_{rr}}{\underline{\delta }\tau ·d{V}_L}}={\displaystyle \frac{2\pi ·dR·R_S·\underline{\delta }R}{\underline{\delta }R/c·4\pi R^{2}dR}}={\displaystyle \frac{R_S·c}{2R^2}}$$

(106)

With it, and with $R_S=2GM/c^2$, the normalized rate of unidirectional LFV in Eq. (106) is as follows:

$$c·{\underline{\dot{\epsilon }}}_{L,rr}\dot{=}{\displaystyle \frac{G·M}{R^2}}$$

(107)

The above fraction is the absolute value of the field. Thereby, the field is antiparallel to the radial unit vector ${\overrightarrow{e}}_r$:

$${\overrightarrow{G}}^{*}={\overrightarrow{G}}_{gen}=-{\displaystyle \frac{G·M}{R^2}}·{\overrightarrow{e}}_r=-G_{gen,r}·{\overrightarrow{e}}_r$$

(108)

Application of the square yields Eq. (97):

$${\underline{\dot{\epsilon }}}_{L,rr}^2·c^2={\overrightarrow{G}}_{gen,r}^2$$

(109)

In the case of an effective mass, there is no rotational invariance with respect to $M_{eff}$, in general. In that case, the proof is performed for each angular direction separately[89] chapter 9. Moreover, each field ${\overrightarrow{G}}_{gen}$ parallel to a direction ${\overrightarrow{e}}_j$ causes a unidirectional rate ${\underline{\dot{\epsilon }}}_{L,jj}$, according to Eq. (97).

Part (3): We analyze the rate in Eq.(95):

$${\underline{\dot{\epsilon }}}_{L,rr}={\displaystyle \frac{\underline{\delta }{V}_{rr}}{\underline{\delta }\tau }}{\displaystyle \frac{1}{d{V}_L}}$$

(110)

The change $\underline{\delta }{V}_{rr}$ is the change of $\delta V_{rr}$

$${\underline{\dot{\epsilon }}}_{L,rr}={\displaystyle \frac{1}{d{V}_L}}{\displaystyle \frac{\delta V_{rr}({\tau }_0+\underline{\delta }\tau )-\delta V_{rr}\left({\tau }_0\right)}{\underline{\delta }\tau }}$$

(111)

As the time of propagation $\underline{\delta }\tau$ is incremental, and since a field in the radial direction causes changes in the radial direction only, we can express the difference at linear order in $\underline{\delta }\tau$:

$${\underline{\dot{\epsilon }}}_{L,rr}={\displaystyle \frac{1}{d{V}_L}}{\displaystyle \frac{\frac{\partial }{\partial \tau }\delta V_{rr}·\underline{\delta }\tau }{\underline{\delta }\tau }}={\displaystyle \frac{1}{d{V}_L}}{\displaystyle \frac{\partial }{\partial \tau }}\delta V_{rr}={\displaystyle \frac{1}{d{V}_L}}\underset{c}{\underbrace{{\displaystyle \frac{\partial L}{\partial \tau }}}}{\displaystyle \frac{\partial }{\partial L}}\delta V_{rr}$$

(112)

Next, L is substituted by R:

$${\underline{\dot{\epsilon }}}_{L,rr}={\displaystyle \frac{c}{d{V}_L}}\underset{{\epsilon }_E}{\underbrace{{\displaystyle \frac{\partial R}{\partial L}}}}{\displaystyle \frac{\partial }{\partial R}}\delta V_{rr}={\displaystyle \frac{{\epsilon }_{E}c}{d{V}_L}}{\displaystyle \frac{\partial }{\partial R}}\delta V_{rr}$$

(113)

Next, $\delta V_{rr}=4\pi R^2\delta R=4\pi R^2(dL-dR)=4\pi R^{2}dR({\epsilon }_E^{-1}-1)$ is used, as well as $d{V}_L=4\pi R^{2}dR/{\epsilon }_E$:

$${\underline{\dot{\epsilon }}}_{L,rr}={\displaystyle \frac{{\epsilon }_{E}c}{4\pi R^{2}dR/{\epsilon }_E}}4\pi dR{\displaystyle \frac{\partial }{\partial R}}[R^2·({\epsilon }_E^{-1}-1)]$$

(114)

The derivative is evaluated:

$${\underline{\dot{\epsilon }}}_{L,rr}={\displaystyle \frac{{\epsilon }_E^{2}c}{R^2}}[2R·({\epsilon }_E^{-1}-1)-{\epsilon }_E^{-3}{R}_S/2]\mathrm{or}$$

(115)

$${\underline{\dot{\epsilon }}}_{L,rr}={\displaystyle \frac{2{\epsilon }_{E}c}{R}}\left[1-{\epsilon }_E-{\displaystyle \frac{R_S}{4{\epsilon }_E^{2}R}}\right].$$

(116)

Each mass and each effective mass cause a gravitational field. At each location, the local gravitational field causes local formation of volume. The respective rates are expressed in Eqs. (96, 98, 99 and 107).

8. Energy Density of the Gravitational Field

In this section, the energy density $u_f$ of a gravitational field ${\overrightarrow{G}}^{*}$ is introduced and derived.

8.1. Measurement of the energy density of the field

The energy density of the field can be measured as follows: A rest mass $M_{rest}$ is distributed uniformly in a shell with a radius R and a small thickness $dR$, see Figure 6. That mass is lifted by a radial difference $\Delta R$. Thereby, the required energy $\Delta E_M$ is measured. This energy is located in the field within the shell with center M, thickness $\Delta R$ and radius R, see Figure 6. That shell has the volume

$$\Delta V=4\pi R^2\Delta R.$$

(117)

Consequently, the absolute value of the measured energy density is as follows:

$$|u_f|={\displaystyle \frac{\Delta E_M}{\Delta V}}$$

(118)

The positive required energy compensates the energy of the field in the shell, as the field in the shell with volume $\Delta V$ is eliminated in the process of lifting the mass. Consequently, the sign of the field is negative:

$$u_f=-{\displaystyle \frac{\Delta E_M}{\Delta V}}$$

(119)

Alternatively, this measured energy can be calculated:

8.2. Derivation of the Energy Density of the Field

The required energy $\Delta E_M$ can be calculated [67]:

$$\Delta E_M={\displaystyle \frac{G·M^2\Delta R}{2R^2}}.$$

(120)

The measured energy density in Eq. (119) can be calculated by inserting Eqs. (120 and 117) into Eq. (119):

$$u_f=-{\displaystyle \frac{G·M^2}{8\pi R^4}}=-{\displaystyle \frac{{\left({\overrightarrow{G}}^{*}\right)}^2}{8\pi G}}$$

(121)

For comparison, [91] derived the same formula for the energy density

$$u_f=-{\displaystyle \frac{{\left({\overrightarrow{G}}^{*}\right)}^2}{8\pi G}}.$$

(122)

Peters [91] derived this result in a Newtonian approximation.

In contrast, the exact energy density $u_f$ is derived here. This is achieved with help of the exact field, since no approximation is used here. This exactness is achieved here with help of the distinction between the two distance measures: the gravitational parallax distance $\Delta R$ and the corresponding light travel distance $\Delta L$.

8.3. Compensation of the Negative Field

The RGS in Eqs. (67 and 70) is divided by $8\pi G$, and ${\overrightarrow{G}}_{gen}={\overrightarrow{G}}^{*}$ is used:

$$0={\displaystyle \frac{{\left(c·\frac{\partial }{\partial \tau }{\sum }_{jin\mathcal{S}}{\epsilon }_{L,rr,j}\right)}^2}{8\pi G}}-{\displaystyle \frac{{\left({\overrightarrow{G}}^{*}\right)}^2}{8\pi G}}$$

(123)

The sum in the above Eq. is identified with the summed relative additional volume of the indivisible VPs:

$${\epsilon }_{L,rr,indivisibleVPs}:=\sum _{jin\mathcal{S}}{\epsilon }_{L,rr,j}$$

(124)

With it, the RGS in Eq. (123) is as follows:

$$0={\displaystyle \frac{c^2·{\dot{\epsilon }}_{L,rr,indivisibleVPs}^2}{8\pi G}}+{\displaystyle \frac{-{\left({\overrightarrow{G}}^{*}\right)}^2}{8\pi G}}$$

(125)

The second fraction in the above Eq. is identified with the energy density of the gravitational field $u_f$.

$$0={\displaystyle \frac{c^2·{\dot{\epsilon }}_{L,rr,indivisibleVPs}^2}{8\pi G}}+u_f$$

(126)

As a consequence, the fraction in the above Eq. is an energy density u. That fraction describes indivisible VPs $\delta V_j$ that cause the field. Therefore, that fraction describes the energy density of the indivisible VPs $\delta V_j$:

$$u_{indivisibleVPs}={\displaystyle \frac{c^2·{\dot{\epsilon }}_{L,rr,indivisibleVPs}^2}{8\pi G}}.$$

(127)

Consequently, the sum of the two energy densities is zero:

$$u_{indivisibleVPs}+u_f=0.$$

(128)

The energy density of one indivisible VP is obtained by using ${\overrightarrow{G}}_{gen,j}={\overrightarrow{G}}_j^{*}$ and by inserting the field in Eq. (66) into Eq. (122):

$$u_{f,j}=-{\displaystyle \frac{{\left({\overrightarrow{G}}_j^{*}\right)}^2}{8\pi G}}.$$

(129)

Next, the rate gravity relation (see Eqs. 67 and 70) is generalized to one indivisible VP:

$$c^2{\dot{\epsilon }}_{L,rr,indivisibleVP,j}^2={\left({\overrightarrow{G}}_j^{*}\right)}^2.$$

(130)

Similarly, Eq. (128) is generalized to one indivisible VP:

$$u_{indivisibleVP,j}+u_{f,j}=0.$$

(131)

With these generalizations, the energy density in Eq. (129) implies the energy density $u_{indivisibleVP,j}$ of one indivisible VP $\delta V_j$ as follows:

$$u_{indivisibleVP,j}=-u_{f,j}={\displaystyle \frac{c^2·{\dot{\epsilon }}_{L,rr,indivisibleVP,j}^2}{8\pi G}}.$$

(132)

These relations are results of the VD.

For comparison, expectation values of the field have been derived from the VD as follows: Firstly, a quantum field theory has been derived from the VD. Secondly, the expectation value of a field has been derived from the quantum field theory [23,67].

Each indivisible VP has the energy density $u_{indivisibleVP,j}$ based on its rate. Moreover, each indivisible VP causes the energy density $u_{f,j}$ based on its gravity. Furthermore, each indivisible VP propagates at the speed c. Accordingly, such an indivisible VP can be called rate gravity wave, RGW.

9. Derivation of the Quantum Postulates

The VD, the dynamics of the indivisible VPs, implies the SEQ, see section (Section 5.2), the fundamental deterministic dynamics of quantum physics. Accordingly, the following question arises: Does the VD imply the stochastic dynamics of quantum systems and the complete system of quantum postulates?

In order to answer this question, the deterministic time evolution is summarized in a postulate (see Section 9.1), and mathematical consequences (see Section 9.2 and Section 9.3) are derived first.

Then the stochastic dynamics (see Section 9.4) and the complete system (see Section 9.5) of the quantum postulates are derived.

Additional rules about mixed states and about entanglement [64] p. 46] have been derived from the VD [67].

9.1. Postulate about the Deterministic Time Evolution

The VD implies the postulate about the deterministic time evolution of quanta[93] p. 170:

Postulate about the deterministic time evolution

’The time evolution of the state vector is governed by the time-dependent Schrödinger equation, SEQ[72] Eq. (4”):

$$\begin{array}{c}\hfill i\hslash {\partial }_t|\psi \rangle =\widehat{H}|\psi \rangle ,\end{array}$$

(133)

where $\widehat{H}$ is the Hamilton operator corresponding to the total energy of the system.’

More generally, the VD implies the GSEQ, see section (Section 5.2).

9.2. On Hilbert space

In this section, the solution spaces of the SEQ and of the GSEQ are analyzed, in order to derive quantum postulates in later sections. In section (Section 5.2) it is shown, that indivisible VPs can be described by the DEQ of VD, and that indivisible VPs as well as objects at the speed $v=c$ are described by the quantum physical GSEQ. In particular, objects with relatively small momentum, ${\displaystyle \frac{p^2}{m_0^2{c}^2}}<<1$, in leading order in ${\displaystyle \frac{p^2}{m_0^2{c}^2}}$, are described by the SEQ.

In this section, it is shown that the solutions of the SEQ, of the GSEQ and of the DEQ of VD form Hilbert spaces:

As usual, the Dirac notation is used: A wave function $\Psi$ is expressed by a so-called ket $|\Psi \rangle$.

Moreover, two wave functions, ${\Psi }_1(\tau ,\overrightarrow{L})$ and ${\Psi }_2(\tau ,\overrightarrow{L})$, form a scalar product as follows:

$$\begin{array}{c}\hfill \langle {\Psi }_1|{\Psi }_2\rangle =\int d^{3}L{\Psi }_1^{*}(\tau ,\overrightarrow{L})·{\Psi }_2(\tau ,\overrightarrow{L})\end{array}$$

(134)

Hereby, the superscript * marks the complex conjugate value, this notation is nowadays usual in quantum physics [64,93,96,97].

Based on that scalar product, a state $|\Psi \rangle$ is multiplied by a normalization factor $t_n$ so that the following scalar product is equal to one:

$$\begin{array}{c}\hfill \langle \Psi ·t_n|\Psi ·t_n\rangle =\int d^{3}r{\Psi }^{*}(\tau ,\overrightarrow{L})·\Psi (\tau ,\overrightarrow{L})·{\left|t_n\right|}^2=1\end{array}$$

(135)

Next, it is shown that these states form a Hilbert space $\mathcal{H}$:

The states $\Psi (\tau ,\overrightarrow{L})$ form a complete vector space, as they are solutions of the (linear DEQ) SEQ. As a consequence, they form a linear vector space, whereby they include all linear combinations of states $\Psi (\tau ,\overrightarrow{L})$, including Fourier integrals, for instance. These form a complete Hilbert space $\mathcal{H}$, see e. g. Teschl[98] p. 47 or Sakurai and Napolitano[63] p. 57.

Generalization: The above derivation holds as well for the GSEQ, including rates of change tensors ${\dot{\epsilon }}_{L,p}·t_n$. Consequently, such wave functions form a Hilbert space as well.

Altogether, the solutions of the DEQ of volume dynamics (VD) form a Hilbert space $\mathcal{H}$, the solutions of the GSEQ form a Hilbert space $\mathcal{H}$, and the solutions of the SEQ form a Hilbert space $\mathcal{H}$. These DEQs and their respective Hilbert spaces, can describe VPs, indivisible VPs, matter, and radiation (the case of radiation is analyzed [67]).

9.3. On Measurements, Operators, and Possible Outcomes

In this section, the modeling of measurements with help of the above Hilbert space of the solutions of the deterministic dynamics of the GSEQ or of the SEQ is elaborated. This will be used in later sections in order to derive quantum postulates.

Firstly, the possible outcomes of a single measurement process are derived.

Secondly, the necessity of an additional dynamics is identified.

(1) In physics, in general, a measurement is described as follows:

(1.1) A measurable physical quantity A of an object is a function f of the mathematical description of that object.

(1.2) Thereby, a change of the state should be as small as possible.

(1.3) In general, the function f can be described in linear order by an operator $\widehat{A}$ in Hilbert space, and by a Taylor series thereof: $f={\sum }_{k=0}^{\infty }{c}_k{\widehat{A}}^k$. Thereby, the zeroth order is not essential in physics. Thus, $f={\sum }_{k=1}^{\infty }{c}_k{\widehat{A}}^k$.

Therefore, a measurable physical quantity A of an object is described by a linear operator $\widehat{A}$ in the Hilbert space of the states of the object.

(1.4) In the present case, the mathematical description is a state $|\Psi \rangle$ in a Hilbert space.

(1.5) In linear order in $\widehat{A}$, the function applied to the state can be expressed as follows:

$$\begin{array}{c}\hfill f_{linear}\left(\right|\Psi \rangle )=\widehat{A}|\Psi \rangle ,\mathrm{in}\mathrm{linear}\mathrm{order}.\end{array}$$

(136)

(1.6) In general, each state $|\Psi \rangle$ can be expressed as a linear combination of eigenvectors $|{\Psi }_{A,n}\rangle$ with eigenvalues $a_n$. Here, the case of discrete and different eigenvalues $a_n$, each with one eigenvector, is analyzed in detail, as other cases can be analyzed analogously:

$$\begin{array}{c}\hfill f_{linear}\left(\right|\Psi \rangle )=\widehat{A}|\sum _n{\Psi }_{A,n}\rangle =\sum _n{a}_n|{\Psi }_{A,n}\rangle \end{array}$$

(137)

(1.7) In order to keep the state unchanged in a single measurement process, see part (1.2), that process must act upon an eigenvector:

$$\begin{array}{c}\hfill f_{linear}\left(\right|{\Psi }_{A,n}\rangle )=\widehat{A}|{\Psi }_{A,n}\rangle =a_n|{\Psi }_{A,n}\rangle ,\mathrm{single}\mathrm{measurement}\mathrm{process}.\end{array}$$

(138)

Therefore, the outcome of a single measurement process of a quantity A of an object, is one of the eigenvalues of the operator $\widehat{A}$ corresponding to A.

(2) In general, a state is a linear combination of eigenvectors. But a possible outcome of each single measurement process is one of the eigenvalues. As a consequence, there must be a second dynamics that provides the choice of the eigenvalue that occurs in the measurement.

(2.1) The derivation of the deterministic dynamics of indivisible VPs is completely general, as only analysis alias calculus has been used in the derivation. As a consequence, a second dynamics would be deterministic, it would reduce the generality of the deterministic dynamics.

(2.2) Therefore, a general second dynamics must be a stochastic dynamics.

This stochastic dynamics is derived next:

9.4. On the Stochastic Dynamics

In this section, the stochastic dynamics is derived from the properties of the indivisible VPs.

(1) For the case of a single indivisible VP $\delta V_j$, the probability to measure an indivisible VP at an event $(\tau ,\overrightarrow{L})$ is proportional to the energy density $u_{indivisibleVP,j}$ of the indivisible VP $\delta V_j$ at that event $(\tau ,\overrightarrow{L})$.

(2) The energy density $u_{indivisibleVP,j}$ is related to the wave function as follows:

(2.1) For the case of a single indivisible VP $\delta V_j$, the wave function is the time derivative of its relative additional volume, multiplied by a normalization factor $t_n$, see section (Section 5.2):

$$\begin{array}{c}\hfill |{\Psi }_{indivisibleVPj}\rangle =t_n·{\dot{\epsilon }}_{indivisibleVPj}.\end{array}$$

(139)

(2.2) The absolute square is applied to the above equation:

$$\begin{array}{c}\hfill |{\Psi }_{indivisibleVPj}^2|=\langle {\Psi }_{indivisibleVPj}|{\Psi }_{indivisibleVPj}\rangle =t_n^2·{\dot{\epsilon }}_{indivisibleVPj}^2.\end{array}$$

(140)

(2.3) The above equation is multiplied by $1={\displaystyle \frac{8\pi G}{c^2}}·{\displaystyle \frac{c^2}{8\pi G}}$:

$$\begin{array}{c}\hfill |{\Psi }_{indivisibleVPj}^2|={\displaystyle \frac{8\pi G}{c^2}}{t}_n^2·{\displaystyle \frac{c^2{\dot{\epsilon }}_{indivisibleVPj}^2}{8\pi G}}.\end{array}$$

(141)

(2.4) In the above equation, the second fraction is identified with the energy density of the indivisible VP $\delta V_j$:

$$\begin{array}{c}\hfill |{\Psi }_{indivisibleVPj}^2|={\displaystyle \frac{8\pi G}{c^2}}{t}_n^2·u_{indivisibleVPj}.\end{array}$$

(142)

(3) As a consequence, the probability $P_{indivisibleVPj}$ to measure an indivisible VP at an event $(\tau ,\overrightarrow{L})$ is proportional to the absolute square of the wave function:

$$\begin{array}{c}\hfill P_{indivisibleVPj}\propto \left|{\Psi }_{indivisibleVPj}^2\right|.\end{array}$$

(143)

(4) For each measurable quantity A, and for the corresponding operator $\widehat{A}$, the probability to measure an eigenvalue $a_n$ of an eigenvector $|{\Psi }_{A,n}\rangle$ has been derived from the result in part (3) or in Eq. (143) [67].

Therefore, the result in part (3) or in Eq. (143) is the fundamental stochastic dynamics of quantum physics.

(5) As a consequence, the VD implies both, deterministic time evolution as well as the stochastic dynamics of quantum physics. Consequently, the VD implies the full dynamics of quantum physics. This is the case, as for their respective systems, quantum field theory and the Dirac theory can both be derived with help of the above deterministic and stochastic dynamics [23,63,67,89,101].

Using the above mathematical results as well as the deterministic and stochastic dynamics, the postulates of quantum physics are derived next:

9.5. Derivation of the Postulates

In this section, it is shown how the quantum postulates [93] are implied by the VD:

(1) The postulate about the deterministic time evolution has been derived in sections (Section 5.2 and Section 9.1).

(2) The postulate about probabilistic outcomes of measurements is as follows[93] p. 169, 170:

’If a measurement of an observable A is made in a state $|\Psi (t)\rangle$ of the quantum mechanical system, then the following holds:

[1] The probability of obtaining one of the non-degenerate discrete eigenvalues $a_j$ of the corresponding operator $\widehat{A}$ is given by

$$\begin{array}{c}\hfill P\left(a_j\right)={\displaystyle \frac{|\langle {\varphi }_j|\Psi \rangle {|}^2}{\langle \Psi |\Psi \rangle }},\end{array}$$

(144)

where $|{\varphi }_j\rangle$ is the eigenfunction of $\widehat{A}$ with the eigenvalue $a_j$. If the state vector is normalized to unity, $P\left(a_j\right)={\left|\langle {\varphi }_j|\Psi \rangle \right|}^2$.

[2] If the eigenvalue $a_j$ is $m_j$-fold degenerate, this probability is given by

$$\begin{array}{c}\hfill P\left(a_j\right)={\displaystyle \frac{{\Sigma }_{i=1}^{m_j}{\left|\langle {\varphi }_{j,i}|\Psi \rangle \right|}^2}{\langle \Psi |\Psi \rangle }},\end{array}$$

(145)

[3] If the operator $\widehat{A}$ possesses a continuous eigenspectrum $\left\{a\right\}$, the probability that the result of a measurement will yield a value between a and $a+da$ is given by

$$\begin{array}{c}\hfill P\left(a\right)={\displaystyle \frac{{\left|\langle \varphi \left(a\right)|\Psi \rangle \right|}^2}{\langle \Psi |\Psi \rangle }}·da={\displaystyle \frac{{\left|\langle \varphi \left(a\right)|\Psi \rangle \right|}^2}{{\int }_{-\infty }^{\infty }{|\Psi \left(a^{\prime }\right)|}^{2}d{a}^{\prime }}}·da\end{array}$$

(146)

This postulate can be derived from the stochastic dynamics in section (Section 9.4). The derivation is presented in Carmesin [67,101,103].

(3) The postulate about Hilbert space is as follows[93] p. 168:

’The state of a quantum mechanical system, at a given instant of time, is described by a vector $|\Psi (t)\rangle$, in the abstract Hilbert space $\mathcal{H}$ of the system.’

For each given state of a quantum mechanical system, the full dynamics should be determined. It is the deterministic and stochastic dynamics in the above postulates (1) and (2). It has been shown here, that the states of the respective Hilbert space provide the full information to derive the deterministic time evolution (with the SEQ or with the GSEQ, more generally), and to derive the correct probabilities for the probabilistic outcomes. Therefore, ’the state of a quantum mechanical system, at a given instant of time, is described by a vector $|\Psi (t)\rangle$, in the abstract Hilbert space $\mathcal{H}$ of the system’.

Moreover, it is insightful to realize that the correct probabilistic outcomes are a consequence of the gravitational properties of the VD. Therefore, it is enlightening to understand that the basis of the quantum postulates is a quantum gravitational foundation. As a consequence, a deep and fundamental understanding of quantum physics without understanding gravity and quantum gravity is hardly possible.

(4) The postulate about the relation between observables and operators is as follows[93] p. 169:

’A measurable physical quantity A (called an observable or dynamic physical quantity), is represented by a linear and hermitian operator $\widehat{A}$ acting in the Hilbert space of state vectors.’

This postulate is founded by the VD, as described in section (Section 9.3).

(5) The postulate about the postulate about the relation between the possible outcomes of a measurement and the eigenvalues is as follows[93] p. 169:

’The measurement of an observable A in a given state may be represented formally by the action of an operator $\widehat{A}$ on the state vector $|\Psi (t)\rangle$. The only possible outcome of such a measurement is one of the eigenvalues, $\left\{a_j\right\},j=1,2,3,\dots ,\mathrm{of}\widehat{A}$.’

This postulate is founded by the VD, as described in section (Section 9.3).

10. Emergence of Volume in Nature and of Its Energy Density

In this section, the following results are derived: For the case of a homogeneous and empty universe, the process of the global formation of the volume (GFV) of the universe is elaborated on the basis of the local formation of volume (LFV), everywhere in the universe. Moreover, it is shown that this process provides exactly the complete volume of the universe. Furthermore, it is shown that this process provides an energy density of volume, $u_{vol}={lim}_{heterogeneity\to 0}{u}_{DE}$. Additionally, it is shown that this $u_{vol}$ is in precise accordance with the observed dark energy $u_{DE}$ or $u_{\Lambda }$. These results are very insightful, as they show how the complete and global volume of the universe emerges from a local process: LFV.

10.1. On the Development and Improvements of the Lambda-CDM Model

In this section, the development of the basic model of cosmology, the $\Lambda$CDM - model, is summarized and related to the new results derived in this paper.

Einstein [15] realized that general relativity theory (GRT) implies an expansion of space since a Big Bang, in general. Thereby, he introduced the cosmological constant $\Lambda$. Zeldovich [10] showed that corresponds to an energy density of space:

$$u_{\Lambda }={\displaystyle \frac{\Lambda c^4}{8\pi G}}$$

(147)

Hubble [7] discovered the expansion of space and its rate H at the present - day time $t_0$ after the Big Bang $t_{BigBang}=0$. That present - day rate $H\left(t_0\right)=H_0$ is called Hubble constant. Thereby, the expansion is modeled by homogeneous and isotropic universe. Hereby, the expansion is modeled by a uniform scaling described by a scale radius R:

$$H:={\displaystyle \frac{\dot{R}}{R}}.$$

(148)

Based on GRT, Friedmann [17] and Lemaître [19] derived the dynamics of that expansion as a function of the dynamic density $\rho ={\displaystyle \frac{u}{c^2}}$ and a global curvature parameter k in the form of the Friedmann Lemaître equation (FLE):

$$H^2={\displaystyle \frac{8\pi G}{3}}·\rho -{\displaystyle \frac{k·c^2}{R^2}}.$$

(149)

Thereby, the global curvature parameter is zero, according to observation [22], and as a result of a derivation [89,107]. The corresponding density is called critical density:

$$H^2={\displaystyle \frac{8\pi G}{3}}·{\rho }_{cr},\mathrm{and}{H}_0^2={\displaystyle \frac{8\pi G}{3}}·{\rho }_{cr,0}.$$

(150)

Hereby and in general, present - day values are marked by a subscript zero. A good approximation of $t_0$ is the Hubble time$t_{H_0}:=1/H_0$ [20,40] and Eq. (150):

$$t_0\approx t_{H_0}:={\displaystyle \frac{1}{H_0}}=\sqrt{{\displaystyle \frac{3·{\rho }_{cr,0}}{8\pi G}}}.$$

(151)

FLE - insight: This Eq. shows that the Hubble time and the age of the universe cannot be chosen arbitrarily, these are results of the dynamic density $\rho$ and of the dynamics of the FLE.

Therefore, the time evolution and dynamics of the density are essential. For its analysis, the density is a sum of parts with particular dynamical properties, $\rho ={\rho }_r+{\rho }_m+{\rho }_{\Lambda }$:

${\rho }_r$ is the dynamic density of radiation with ${\rho }_r\propto {(R_0/R)}^4$,

${\rho }_m$ is the density of matter, including cold dark matter, CDM [21,22], with ${\rho }_m\propto {(R_0/R)}^3$

${\rho }_{\Lambda }={\displaystyle \frac{u_{\Lambda }}{c^2}}$ is the dynamic density of the cosmological constant $\Lambda$, with ${\rho }_{\Lambda }\propto {(R_0/R)}^0$. That density has been discovered [11,12,16].

Therefore, the density is the following function of the scale radius R and the density parameters ${\Omega }_j:={\rho }_J/{\rho }_{cr,0}$:

$$\rho ={\rho }_{r,0}·{(R_0/R)}^4+{\rho }_{m,0}·{(R_0/R)}^3+{\rho }_{\Lambda }={\rho }_{cr,0}·({\Omega }_r{(R_0/R)}^4+{\Omega }_m·{(R_0/R)}^3+{\Omega }_{\Lambda })$$

(152)

$\Lambda$CDM - insight: The above components of the density are underlying the name of the $\Lambda$CDM model, it is the cosmological model that includes the visible densities of radiation and of visible matter, as well as the dark densities that are not visible with help of electromagnetic radiation, the cold dark matter and the dark energy $u_{\Lambda }$ alias $u_{DE}$. Additionally, the $\Lambda$CDM model uses the following idealizations:

(1) a homogeneous and isotropic space,

(2) the classical GRT without using the quantum dynamics,

(3) a space described as one entity without using volume portions.

In this paper, these three idealizations are overcome. Thereby, precise accordance with observation is achieved, and a high predictive power is provided. Hereby, the energy density of volume is derived from first principles and in three-dimensional space for the first time with this method.

In this section, VPs are used in order to derive the value of the dark energy $u_{DE}$. Thereby, as a first step, a homogeneous universe is modeled. Therefore, $u_{DE}$ is derived for the case with zero heterogeneity. The result is an idealized value $u_{vol}={lim}_{heterogeneity\to 0}{u}_{DE}$ of the density of space. Accordingly, the derived result is compared with an observation that is based on radiation emitted at a highly homogeneous universe, the early universe. This radiation is the cosmic microwave background (CMB). The observation based on the CMB provides the following value of the energy density [22]:

$$u_{\Lambda ,obs}=5.133(\pm 0.2432)·{10}^{-10}{\displaystyle \frac{\mathrm{J}}{{\mathrm{m}}^3}}$$

(153)

The emergence of the volume of the universe and of its energy density in Eq. (153) are derived and explained in this section (Section 10).

10.2. Process of Local Formation of Volume in the Universe

In this section, the process of local formation of volume that provides the complete volume of the universe is described. This description makes possible a test of the completeness of the formed volume. Moreover, this description makes possible the derivation of the energy density of the volume $u_{vol}$, and the comparison of $u_{vol}$ with the observed energy density in Eq. (153).

Firstly, that process uses the global flatness of space, the curvature parameter is zero, see Eqs. (149, 150 and 151):

Secondly, the description of that process uses a probe volume:

As a consequence of translation invariance, the formation of volume in the universe can be analyzed with help of the formation of a probe volume $d{V}_0$, see Figure 7. Thereby, $d{V}_0$ describes a fixed amount of three-dimensional size that has been filled with volume of nature during the Hubble time $t_{H_0}$:

$$d{V}_0\mathrm{has}\mathrm{been}\mathrm{filled}\mathrm{with}\mathrm{volume}\mathrm{of}\mathrm{nature}\mathrm{during}{t}_{H_0}$$

(154)

Thirdly, that process is described as follows:

(1) Local origin of the rate of LFV at $d{V}_0$:

As the considered universe is empty, the only source for the LFV at $d{V}_0$ are the volume increments or VPs $d{V}_j$, see Figure 7. The corresponding energy is described by the energy $d{E}_j$ or equivalently by the dynamic mass $d{M}_j=d{E}_j/c^2$. Each $d{M}_j$ causes a rate ${\underline{\dot{\epsilon }}}_{L,rr,atd{V}_0}\left(d{M}_j\right)$ of LFV at $d{V}_0$, according to the law of LFV.

$$d{M}_j\mathrm{causes}{\underline{\dot{\epsilon }}}_{L,rr,atd{V}_0}\left(d{M}_j\right)$$

(155)

(2) Complete rate of LFV at $d{V}_0$:

(2.1) The complete rate ${\underline{\dot{\epsilon }}}_{L,rr,atd{V}_0}$ of LFV at $d{V}_0$ is the sum of all rates in the above part (1).

(2.2) The complete rate is identified with the Hubble constant $H_0$:

The present-day normalized rate ${\underline{\dot{\epsilon }}}_{L,rr,atd{V}_0}\left(t_0\right)$ of LFV at $d{V}_0$ is equal to one third of the normalized isotropic rate of formation of volume ${\underline{\dot{\epsilon }}}_{L,iso,atd{V}_0}$:

$${\underline{\dot{\epsilon }}}_{L,rr,atd{V}_0}={\displaystyle \frac{1}{3}}·{\underline{\dot{\epsilon }}}_{L,iso,atd{V}_0}={\displaystyle \frac{1}{3}}·\left({\underline{\dot{\epsilon }}}_{L,xx,atd{V}_0}+{\underline{\dot{\epsilon }}}_{L,yy,atd{V}_0}+{\underline{\dot{\epsilon }}}_{L,zz,atd{V}_0}\right).$$

(156)

The present-day normalized rate $H_0$ is equal to one third of the normalized isotropic rate of formation of volume [67]:

$$H_0=H\left(t_0\right)={\displaystyle \frac{1}{3}}·{\displaystyle \frac{\dot{V}}{V}}.$$

(157)

As the rates ${\displaystyle \frac{\dot{V}}{V}}$ and ${\underline{\dot{\epsilon }}}_{L,iso,atd{V}_0}$ describe the same formation of isotropic volume in nature at $d{V}_0$, these rates are equal [67]:

$$H_0={\displaystyle \frac{1}{3}}·{\displaystyle \frac{\dot{V}}{V}}={\displaystyle \frac{1}{3}}·{\underline{\dot{\epsilon }}}_{L,iso,atd{V}_0}={\underline{\dot{\epsilon }}}_{L,rr,atd{V}_0}=·{\displaystyle \frac{\dot{R}}{R}}.$$

(158)

(3) The complete rate provides the complete volume of nature in $d{V}_0$:

By definition, the rate ${\underline{\dot{\epsilon }}}_{L,rr,atd{V}_0}$ of LFV is the volume $\underline{\delta }{V}_{rr}$ that forms in a considered volume $d{V}_0$ during a time $\underline{\delta }t$:

$${\underline{\dot{\epsilon }}}_{L,rr,atd{V}_0}={\displaystyle \frac{\underline{\delta }{V}_{rr}}{\underline{\delta }t·d{V}_0}}$$

(159)

In order to derive the complete volume formed in $d{V}_0$ during the complete Hubble time $t_{H_0}$, this Eq. is solved for the formed volume, the rate ${\underline{\dot{\epsilon }}}_{L,rr,atd{V}_0}=H_0$ is used, and the complete time $\underline{\delta }t=t_{H_o}$ is utilized:

$$\underline{\delta }{V}_{rr}=\underset{1}{\underbrace{H_0·t_{H_0}}}·d{V}_0=d{V}_0.$$

(160)

Therefore, the complete probe volume $d{V}_0$ is filled with LFV. As a consequence of translation invariance, the probe volume represents the complete volume of the universe. Consequently, the complete volume of the universe forms during the Hubble time.

Altogether, this is the above introduced first test of the process:

The described process shows how the LFV forms exactly the GFV. Thereby, the LFV takes place in the complete space inside the Hubble radius and during the complete Hubble time. This result provides a great additional evidence for the theory of VPs derived above.

10.3. Derivation of the Energy Density of Volume

In this section, the process in section (Section 10.2) of formation of the volume of the universe on the basis of local formation of volume is elaborated in more quantitative detail. Thereby, the energy density $u_{vol}={lim}_{heterogeneity\to 0}{u}_{DE}$ of volume is derived, and it is shown that $u_{vol}$ is in precise accordance with observation.

10.3.1. Rate of Formation of Volume by a Volume Portion

An incremental volume or VP $d{V}_j$ has the dynamic mass $d{M}_j$:

$$\begin{array}{c}\hfill d{M}_j=d{V}_j·{\rho }_{vol}\end{array}$$

(161)

According to exact gravity shown above [67], each dynamic mass $d{M}_j$ causes the following exact field in its near vicinity:

$$\begin{array}{c}\hfill |d{\overrightarrow{G}}_j^{*}|\left(R\right)={\displaystyle \frac{G·d{M}_j}{R^2}}\end{array}$$

(162)

As a part of a RGW, this field can propagate. Thereby, the RGWs of different dynamic masses $d{M}_j$ do not cancel each other, see part (8) in section (Section 10.2), see Figure 7.

According to the law of unidirectional formation of volume, see Eqs. (96 and 107), at the probe volume $d{V}_0$, each dynamic mass $d{M}_j$ at a distance R causes the following normalized rate of unidirectional formation of volume:

$$\begin{array}{c}\hfill d{\dot{\underline{\epsilon }}}_{L,rr,atd{V}_0}(R,d{M}_j)={\displaystyle \frac{|d{\overrightarrow{G}}_j^{*}|\left(R\right)}{c}}={\displaystyle \frac{G·d{M}_j}{R^2·c}}\end{array}$$

(163)

10.3.2. Rate of Formation of Volume by One Shell

The volume that is caused by the $d{M}_j$ in the shell in Figure 7 is derived next:

10.3.2.1. Shell Around $d{V}_0$:

The dynamic masses $d{M}_j$ at a distance R from $d{V}_0$ constitute a shell with center $d{V}_0$, and with a distance R from $d{V}_0$, and with a thickness $dR$, so that the dynamic mass of the shell is the sum of the dynamic masses $d{M}_j$ in the shell, see Figure 7:

$$\begin{array}{c}\hfill dM(R,dR)=\sum _{j,R_j\in \mathrm{shell}}d{M}_j\end{array}$$

(164)

10.3.2.2. Rate Caused by a Shell Around $d{V}_0$:

The rates in Eq. (163), that are caused in the shell in Eq. (164), are added:

$$\begin{array}{c}\hfill \sum _{j,R_j\in \mathrm{shell}}d{\dot{\underline{\epsilon }}}_{L,rr,atd{V}_0}(R,d{M}_j)={\displaystyle \frac{G·{\sum }_{j,R_j\in \mathrm{shell}}d{M}_j}{R^2·c}}\end{array}$$

(165)

In the above Eq., the sum of the masses is identified with $dM(R,dR)$ in Eq. (164). Consequently, the rate is as follows:

$$\begin{array}{c}\hfill d{\dot{\underline{\epsilon }}}_{L,rr,atd{V}_0}(R,dR)={\displaystyle \frac{G·dM(R,dR)}{R^2·c}}\end{array}$$

(166)

10.3.2.3. Application of the Dynamic Density:

According to the global flatness, the dynamic mass $dM(R,dR)$ is equal to the product of the dynamic density ${\rho }_{vol}$ and the volume $dV=4\pi ·R^2·dR$ of the shell, see Figure 7:

$$dM(R,dR)={\rho }_{vol}·4\pi ·R^2·dR$$

(167)

As a consequence, the rate in Eq. (166) is as follows:

$$\begin{array}{c}\hfill d{\dot{\underline{\epsilon }}}_{L,rr,atd{V}_0}(R,dR)={\displaystyle \frac{4\pi ·G·{\rho }_{vol}·dR·R^2}{R^2·c}}\end{array}$$

(168)

It is instructive to realize that the rate caused by a shell is not a function of the radius of the shell, as the terms $R^2$ cancel out. This cancellation does also take place, if R is replaced by the comoving distance[87] section 4.3. Consequently, the rate is as follows:

$$\begin{array}{c}\hfill d{\dot{\underline{\epsilon }}}_{L,rr,atd{V}_0}\left(dR\right)={\displaystyle \frac{4\pi ·G·{\rho }_{vol}·dR}{c}}\end{array}$$

(169)

10.3.3. Light - Travel Time of One Shell

In this section, the indivisible VPs emitted in the shell in Figure 7 are characterized by the time $t_{LT}$, in which they travel to the probe volume $d{V}_0$.

A VP travels with the speed $v=c$. Therefore, a VP travels through the shell with the thickness $dR$ during the light travel time $d{t}_{LT}=dR/c$:

$$\begin{array}{c}\hfill d{t}_{LT}={\displaystyle \frac{dR}{c}}\end{array}$$

(170)

Accordingly, $dR/c$ in Eq. (169) is substituted by $d{t}_{LT}$:

$$\begin{array}{c}\hfill d{\dot{\underline{\epsilon }}}_{L,rr,atd{V}_0}\left(d{t}_{LT}\right)=4\pi ·G·{\rho }_{vol}·d{t}_{LT}\end{array}$$

(171)

Thereby, since the Big Bang until today, the light travel times range from $d{t}_{LT}=0$ to the Hubble time $d{t}_{LT}=t_{H_0}$:

10.3.4. Spatial Integration of the Shells

In this section, the shells in Figure 7 are integrated: Thereby, all VPs $d{V}_j$ that emit volume portions that can propagate to the probe volume are included. Therefore, the integration includes exactly the sources in space that provide a rate of LFV at the probe volume $d{V}_0$. Practically, this complete spatial integral is executed by the integration variable time according to the substitution in section (Section 10.3.3).

Consequently, the time increments are integrated from zero to the maximum $t_{H_0}$, and the rate increments are integrated from zero to the resulting integrated rate ${\dot{\underline{\epsilon }}}_{L,rr,atd{V}_0}$. These integrals are applied to the rate in Eq. (171):

$$\begin{array}{c}\hfill {\int }_0^{{\dot{\underline{\epsilon }}}_{L,rr,atd{V}_0}}d{\dot{\underline{\epsilon }}}_{L,rr,atd{V}_0}=4\pi ·G·{\rho }_{vol}·{\int }_0^{t_{H_0}}d{t}_{LT}\end{array}$$

(172)

The above integral is evaluated:

$$\begin{array}{c}\hfill {\dot{\underline{\epsilon }}}_{L,rr,atd{V}_0}=4\pi ·G·{\rho }_{vol}·t_{H_0}\end{array}$$

(173)

The above rate is identified with $H_0$, see Eq. (158):

$$\begin{array}{c}\hfill H_0=4\pi ·G·{\rho }_{vol}·t_{H_0}\end{array}$$

(174)

The above Eq. is divided by $t_{H_0}$:

$$\begin{array}{c}\hfill {\displaystyle \frac{H_0}{t_{H_0}}}={\rho }_{vol}·4\pi ·G\end{array}$$

(175)

According to the FLE - insight in section (Section 10.1), the values of $H_0$ and $t_{H_0}$ are functions of the density. Therefore, the result in Eq. (175) is valid and derived in our universe.

Next, the above Eq. is solved for the dynamic density ${\rho }_{vol}=u_{vol}/c^2$. Consequently, the dynamic density of volume is as follows:

$$\begin{array}{c}\hfill {\rho }_{vol}={\displaystyle \frac{H_0}{t_{H_0}}}·{\displaystyle \frac{1}{4\pi ·G}}\end{array}$$

(176)

Next, the Hubble constant is identified with the inverse Hubble time in Eqs. (175, 176). Moreover, the equality of rates ${\underline{\dot{\epsilon }}}_{L,rr,atd{V}_0}=H_0$ in Eq. (158) is used:

$$\begin{array}{c}\hfill {\rho }_{vol}={\displaystyle \frac{H_0^2}{4\pi ·G}}\mathrm{or}{u}_{vol}={\displaystyle \frac{H_0^2{c}^2}{4\pi ·G}}\end{array}$$

(177)

10.3.5. Comparison with Observation

In a universe consisting of volume only, the process of global formation of volume, GFV, from LFV causes the following energy density of volume:

$$u_{vol}={\displaystyle \frac{c^2{H}_{0,empty}^2}{4\pi G}}$$

(178)

Hereby, $H_{0,empty}$ denotes the Hubble constant in the empty universe, i. e. the universe without matter and radiation. The energy density of volume has the following amount:

$$u_{vol}={\displaystyle \frac{c^2{H}_{0,empty}^2}{4\pi G}}=5.034(\pm 0.1395)·{10}^{-10}{\displaystyle \frac{\mathrm{J}}{{\mathrm{m}}^3}},\mathrm{with}{H}_{0,empty}=66.88(\pm 0.92){\displaystyle \frac{\mathrm{km}}{\mathrm{s}·\mathrm{Mpc}}}$$

(179)

Hereby, the Hubble constant $H_0$ is taken from observation [22], as $H_0$ represents a calendar date, the age of the universe $t_0\approx 1/H_0$. A precise relation is provided in Carmesin [40]. The observed value $u_{\Lambda ,obs}$ is as follows [22]:

$$u_{\Lambda ,obs}=5.133(\pm 0.2432)·{10}^{-10}{\displaystyle \frac{\mathrm{J}}{{\mathrm{m}}^3}}$$

(180)

Hereby, it is important that $H_0$ and $u_{\Lambda ,obs}$ are observed in a very homogeneous state of the universe. Such a homogeneous state of the universe is the very early universe that can be observed with help of the Cosmic Microwave Background (CMB). Such an observation is provided in a very precise manner [22], whereby the $H_0$ - value in Eq. (179) and the $u_{\Lambda ,obs}$ value in Eq. (180) have been obtained.

Discussion of the results of this section (Section 10.1): The derived result $u_{vol}$ is in precise accordance with the observed value $u_{\Lambda ,obs}$, within the error of measurement $\pm 0.2432$. Therefore, the derived energy density $u_{vol}$ of volume is a second test of the process of formation of volume in this section (Section 10.1). Together with the first test of the exact amount of formed volume, both tests provide a clear evidence for that process of formation of volume and for the theory of VPs. For the first time, a fundamental, founded and very general theory based on derived discrete volume portions provides the functional relation for $u_{vol}$, see Eq. (179).

11. Emergence of Volume in a Homogeneous Universe

In section (Section 10), the density $u_{vol}$ of volume has been derived for the case of an empty universe. In this section (Section 11), the density $u_{vol}$ of volume is derived for the case of a homogeneous non-empty universe. Therefore, the model used in section (Section 10) is supplemented by a homogeneous density ${\rho }_{hom}$ of radiation and matter, whereby the heterogeneity of radiation and matter is not included. For it, it is essential to summarize the concepts of averaging in cosmology first, see section (Section 11.1):

11.1. Spatial Averages in Cosmology

Idea: In order to measure a homogeneous density ${\rho }_{\mathrm{hom}}$, it is necessary to execute an average in a volume $L_{box}^3$, see Figure 8. In this section, we summarize methods of such averaging in cosmology [36,47,109,110], see Figure 8.

Boxes: As a convention, the spatial average is performed in a cubic volume $V_{win}=L_{box}^3$, related to 8 Mpc as follows [36,109]1:

$$L_{box}=8h^{-1}\mathrm{Mpc}\mathrm{with}h=H_0·{\displaystyle \frac{1}{100}}{\displaystyle \frac{\mathrm{km}}{\mathrm{s}·\mathrm{Mpc}}}$$

(181)

Local density: A box has a location $\overrightarrow{r}$. A local density at a time t is measured for each box:

$$\mathrm{local}\mathrm{density}{\rho }_m(t,\overrightarrow{r})$$

(182)

Global density: The globally averaged density is introduced:

$$\mathrm{global}\mathrm{density}{\rho }_{m,hom}\left(t\right)$$

(183)

Overdensity: The overdensity is introduced as follows:

$$\mathrm{overdensity}\delta (t,\overrightarrow{r}):={\displaystyle \frac{{\rho }_m(t,\overrightarrow{r})-{\rho }_{m,hom}\left(t\right)}{{\rho }_{m,hom}\left(t\right)}}$$

(184)

The density ${\rho }_{m,het}(t,\overrightarrow{r})$ of the heterogeneity is the product of ${\rho }_{m,hom}\left(t\right)$ and the overdensity:

$${\rho }_{m,het}(t,\overrightarrow{r})={\rho }_{m,hom}\left(t\right)·\delta (t,\overrightarrow{r})$$

(185)

We summarize the densities in the surroundings of the volume:

$$\rho ={\rho }_{m,hom}\left(t\right)+{\rho }_{m,het}(t,\overrightarrow{r})+{\rho }_r+{\rho }_{\Lambda }$$

(186)

11.1.1. Averages of Fluctuations

In this section, we summarize spatial averaging of fluctuations in cosmology [36,47,109].

A spatial average of a function $f\left(\overrightarrow{r}\right)$ is applied within a volume $V_{window}$ or $V_{win}$ of a considered region (window) of averaging:

$${\langle f\left(\overrightarrow{r}\right)\rangle }_{V_{win}}={\displaystyle \frac{{\int }_{V_{win}}f\left(\overrightarrow{r}\right)d{r}^3}{{\int }_{V_{win}}1d{r}^3}}$$

(187)

Fluctuations of a function $f\left(\overrightarrow{r}\right)$ are usually described by the standard deviation ${\sigma }_{V_{win}}$:

$${\sigma }_{V_{win}}^2={\langle {[f\left(\overrightarrow{r}\right)-{\langle f\left(\overrightarrow{r}\right)\rangle }_{V_{win}}]}^2\rangle }_{V_{win}}={\langle f^2\left(\overrightarrow{r}\right)\rangle }_{V_{win}}-{\langle f\left(\overrightarrow{r}\right)\rangle }_{V_{win}}^2$$

(188)

As a convention, the spatial average is performed within a cubic volume $V_{win}=L_{box}^3$, related to 8 Mpc as follows, see Eq. (181) [36,109]2. In that case, the standard deviation is named ${\sigma }_8\left(t\right)$ or $\delta \left(t\right)$:

$${\sigma }_8\left(t\right)=\delta \left(t\right)={\sigma }_{\delta ,V_{win}}\left(t\right)\mathrm{with}{\sigma }_{8,0}={\sigma }_8\left(t_0\right)$$

(189)

11.2. Expectation Values of Fields

In order to observe densities in cosmology, more local observations are averaged as outlined in section (Section 11.1). The corresponding theoretical values are expectation values. Those expectation values are investigated in this section, that are essential for the LFV at the probe volume $d{V}_0$. That LFV is based on Eq. (97):

$${\underline{\dot{\epsilon }}}_{L,ii}^2·c^2={\left({\overrightarrow{G}}_i^{*}\right)}^2$$

(190)

Therefore, for various objects, the important expectation values are derived, and an overview is presented in Table 1:

(1) For the case of a single and separate mass $m_j$, the gravitational field is classical. Consequently, it is described by a coherent state [23,64,67,82,112,113]. Thus, the expectation value $\langle \Psi \left|{\overrightarrow{G}}_j\right|\Psi \rangle$ of the field is nonzero, and the standard deviation $\sigma =\langle \Psi |{\overrightarrow{G}}_j^2|\Psi \rangle -\langle \Psi |{\overrightarrow{G}}_j{|\Psi \rangle }^2$ of the field is nearly zero.

In this study, the classical expectation values for one mass are not essential (see columns five and six in Table 1):

(1.1) In empty space, there is no mass.

(1.2) In the non-empty homogeneous universe, the fields of masses are completely averaged to zero.

(1.3) In the case of a heterogeneous density, there are many masses, whereby their fields average to zero, and the standard deviations of the fields remain.

Consequently, the nonzero expectation value of the field is not averaged out to zero. Therefore, such a mass contributes to the LFV at the probe mass (see column seven in Table 1). Such a single mass is not essential at the large scales of several Megaparsecs considered here. This case is included for comparison only.

(2) For the case of an indivisible VP, the gravitational field is not classical. Accordingly, it is described by a number state [23,64,67,82,112,113]. Thence, the expectation value $\langle \Psi \left|{\overrightarrow{G}}_j\right|\Psi \rangle$ of the field is zero, but the standard deviation is nonzero, $\sigma =\langle \Psi \left|{\overrightarrow{G}}_j^2\right|\Psi \rangle -0\ne 0$. The classical expectation values are not essential for an indivisible VP, as no classical fields can cancel out. Similarly, the quanta of light propagate from the Sun to Earth, without cancellation - otherwise it would be dark at Earth at night and at day. Consequently, the nonzero standard deviation contributes to the LFV at the probe mass (see column seven in Table 1).

(3) For the case of the heterogeneous density, radiation is not essential. The reason is, that in our universe, heterogeneity developed at a time, at which the density of radiation was already negligible. Accordingly, the heterogeneous density is analyzed for masses only. Similarly, the homogeneous density is analyzed for masses only. In the case of the heterogeneous density, gravitational fields are classical. Consequently, they are described by coherent states [23,64,67,82,112,113]. Thus, the expectation value $\langle \Psi \left|{\overrightarrow{G}}_j\right|\Psi \rangle$ of the field of one mass $m_j$ is nonzero, and the standard deviation is negligible. The classical expectation value of all fields are zero. But the classical expectation value of all squared fields are nonzero. Therefore, the heterogeneous density contributes to the LFV at the probe mass (see column seven in Table 1).

(4) For the case of the homogeneous density, gravitational fields are classical. Consequently, they are described by coherent states [23,64,67,82,112,113]. Thus, the expectation value of the field of one mass $m_j$ is nonzero, and the standard deviation is negligible. But the classical expectation values of all fields and of all squared fields are zero. Therefore, the homogeneous density does not contribute to the LFV at the probe mass (see column seven in Table 1).

11.3. Energy Density of Volume

As the homogeneous density ${\rho }_{\mathrm{m},\mathrm{hom}}$ of matter does not contribute to the LFV at $d{V}_0$, the energy density $u_{vol}$ of volume is the same as in the case of the empty universe in Eq. (179).

In the case of the homogeneous universe, there is sufficient content, that the density parameter can be derived in a meaningful manner:

$${\Omega }_{vol}:={\displaystyle \frac{u_{vol}}{u_{cr,0}}}={\displaystyle \frac{{\rho }_{vol}}{{\rho }_{cr,0}}}$$

(191)

The respective terms in Eqs. (150 and 177) are inserted:

$${\Omega }_{vol}={\displaystyle \frac{\frac{H_0^2}{4\pi ·G}}{\frac{3H_0^2}{8\pi ·G}}}={\displaystyle \frac{2}{3}}$$

(192)

This is in precise accordance with the observed value [22], table 2, column 2, within the error of measurement:

$${\Omega }_{\Lambda }=0.679\pm 0.013$$

(193)

Therefore, this result of the homogeneous universe provides clear additional evidence for the present mechanism of formation and for the theory of volume portions.

12. Emergence of Volume in a Heterogeneous Universe

In the cases of the empty and of the homogeneous universe, the flatness of space can be used, see sections (Section 10 and Section 11). On that basis, and by using adequate coordinate systems (ACS), it is possible to use a regular and constant evolution of time.

In general, the density of space or volume is different in the heterogeneous universe and in the homogeneous universe. The density of space or volume in the heterogeneous universe and in the present-day universe is marked by $u_{DE}$. The density of space or volume in the homogeneous universe and in the very early universe is denoted by $u_{vol}$. The cosmological constant $\Lambda$ and the corresponding energy density of space or volume $u_{\Lambda }$ describe the present-day universe, since Einstein [15] proposed $\Lambda$ without any specification of the early universe or of a particularly homogeneous universe different from the present-day universe. In each case, the ratio of an energy density $u_j$ and the critical energy density $u_{cr.}={\rho }_{cr.}·c^2$ is the respective density parameter:

$${\Omega }_j={\displaystyle \frac{u_j}{u_{cr.}}}.$$

(194)

Moreover, in the cases of the empty and of the homogeneous universe, the energy density $u_{DE}$ of volume is a constant, so that the essential density parameters ${\Omega }_m:={\displaystyle \frac{{\rho }_m}{{\rho }_{cr,0}}}$ of matter and ${\Omega }_{\Lambda }={\displaystyle \frac{{\rho }_{\Lambda }}{{\rho }_{cr,0}}}$ of the cosmological constant are essentially constant.

However, in the heterogeneous universe, ${\rho }_{\Lambda }$ and ${\Omega }_{\Lambda }$ increase. This causes an increase of the Hubble constant $H_0$. Indeed, that increase has been observed [13,22]. Consequently, the Hubble time $t_{H_0}$ decreases.

For these reasons, the changes of ${\Omega }_{\Lambda }$ and of $t_{H_0}$ are analyzed simultaneously in this section.

12.1. VPs Field and Rate Caused by Heterogeneity

In this section, based on the LFV in the homogeneous universe, the additional LFV is derived, which is caused by heterogeneity.

(1) Overdensity ${\delta }_j$ of a dynamic mass in a shell:

A mass $d{M}_j$ in a shell with a mass $dM(R,dR)$ is considered. Thereby, the shell has a $d_{GP}$ distance R from the probe volume $d{V}_0$ in Figure 7, a thickness $dR$, a volume $dV=4\pi R^{2}dR$, and a density ${\rho }_{m,hom}$. According to section (Section 11.1), the overdensity of $d{M}_j$ is as follows, see Eq. (184):

$${\delta }_j={\displaystyle \frac{d{M}_j/d{V}_j-{\rho }_{m,hom}}{{\rho }_{m,hom}}}$$

(195)

The above fraction is expanded by $dV$:

$${\delta }_j={\displaystyle \frac{d{M}_j·\frac{dV}{d{V}_j}-dM(R,dR)}{dM(R,dR)}}\mathrm{with}dM(R,dR)=4\pi R^{2}dR{\rho }_{m,hom}=dV{\rho }_{m,hom}$$

(196)

(2) Rate caused by the overdensity ${\delta }_j$:

The overdensity ${\delta }_j$ in Eq. (196) multiplied by the mass $dM(R,dR)$ is the mass of heterogeneity. According to the $1/R^2$ law of the field (${\overrightarrow{G}}^{*}=-{\displaystyle \frac{GM}{R^2}}{\overrightarrow{e}}_R$), that mass causes the following field:

$$d{\overrightarrow{G}}_{gen,j}=-G{\displaystyle \frac{d{M}_j·\frac{dV}{d{V}_j}-dM(R,dR)}{R^2}}{\overrightarrow{e}}_R=-G{\displaystyle \frac{{\delta }_j·dM(R,dR)}{R^2}}{\overrightarrow{e}}_R$$

(197)

The average ${\langle ...\rangle }_{s,R}$ with respect to the shell in part (1) at a radius R and with a thickness $dR$ is derived for the square of the field in Eq. (197):

$${\langle d{\overrightarrow{G}}_{gen,j}^2\rangle }_{s,R}={\left(G{\displaystyle \frac{dM(R,dR)}{R^2}}\right)}^2·{\langle {\delta }_j^2\rangle }_{s,R},\mathrm{with}$$

(198)

$${\langle {\delta }_j^2\rangle }_{s,R}={\displaystyle \frac{{\int }_{shell}{\delta }_j^2{d}^{3}x}{{\int }_{shell}1d^{3}x}}$$

(199)

According to the law of LFV in Eq. (190), the squared field causes the following squared rate:

$$d{\overrightarrow{G}}_{gen,j}^2=c^{2}d{\dot{\underline{\epsilon }}}_{L,rr}^2,\mathrm{therefore},$$

(200)

$${\left(G{\displaystyle \frac{dM(R,dR)}{R^2}}\right)}^2·{\langle {\delta }_j^2\rangle }_{s,R}=c^2{\langle d{\dot{\underline{\epsilon }}}_{L,rr}^2\rangle }_{s,R}$$

(201)

In the above Eq., the root is applied, and $dM(R,dR)$ is replaced according to Eq. (196). Additionally, the propagation according to $dR=c·dt$ is used:

$$4\pi Gdt{\rho }_{m,hom}·\sqrt{{\langle {\delta }_j^2\rangle }_{s,R}}=\sqrt{{\langle d{\dot{\underline{\epsilon }}}_{L,rr}^2\rangle }_{s,R}}$$

(202)

The standard deviations (or uncertainties such as $\Delta {\dot{\underline{\epsilon }}}_{het}$ or $d{\dot{\underline{\epsilon }}}_{het}$, in the language of physics) in the above Eq. are abbreviated:

$${\sigma }_m:=\sqrt{{\langle {\delta }_j^2\rangle }_{s,R}}$$

(203)

$$d{\dot{\underline{\epsilon }}}_{het}:=\sqrt{{\langle d{\dot{\underline{\epsilon }}}_{L,rr}^2\rangle }_{s,R}}$$

(204)

Rate caused by heterogeneity: The rate in Eqs. (202 and 204) caused by ${\rho }_{m,het}$ is the standard deviation $d{\dot{\underline{\epsilon }}}_{het}$. It is expressed in terms of the usual density parameters of homogeneous densities:

$${\Omega }_{vol}={\displaystyle \frac{{\rho }_{vol}}{{\rho }_{cr,0}}}$$

(205)

$${\Omega }_m={\displaystyle \frac{{\rho }_{m,hom}}{{\rho }_{cr,0}}}$$

(206)

As a consequence, the densities are related as follows:

$${\rho }_{m,hom}={\rho }_{vol}·{\displaystyle \frac{{\Omega }_m}{{\Omega }_{vol}}}$$

(207)

With it, and with the standard deviations in Eqs. (203, 204), the LFV - relation in Eq. (202) is as follows:

$$4\pi Gdt{\rho }_{vol}·{\displaystyle \frac{{\Omega }_m}{{\Omega }_{vol}}}{\sigma }_m=d{\dot{\underline{\epsilon }}}_{het}$$

(208)

In the evolution of the universe, gravity accumulated matter. As a consequence, the standard deviation of matter fluctuations ${\sigma }_m$ increased as a function of time. This increase is modeled next in part (3):

(3) Linear growth theory:

Linear growth theory provides the standard deviation of matter fluctuations $\sigma$ as a function of the scale radius $\tilde{a}$ [36,48,110]:

$${\sigma }_m={\sigma }_8·\tilde{a}$$

(209)

In the matter era, the scale radius $\tilde{a}$ is the scaled time $\tilde{t}$ to the power $2/3$, see Karttunen et al. [114] Eq. 19.33 or Carmesin[116] p. 297:

$$\tilde{a}={\tilde{t}}^{q_a}\mathrm{with}{q}_a={\displaystyle \frac{2}{3}}$$

(210)

With it, the standard deviation of matter fluctuations in Eq. (209) is as follows:

$${\sigma }_m={\sigma }_8·{\tilde{t}}^{2/3}$$

(211)

(4) Time integral of the rate caused by heterogeneity:

The time evolution in Eq. (211) is inserted into the rate $d{\dot{\underline{\epsilon }}}_{het}$ caused by heterogeneity in Eq. (208) is as follows:

$$d{\dot{\underline{\epsilon }}}_{het}=4\pi G{\rho }_{vol}·{\displaystyle \frac{{\Omega }_m}{{\Omega }_{vol}}}·{\sigma }_8·{\tilde{t}}^{2/3}·dt$$

(212)

(4.1) Different Hubble times: In general, the Hubble time derived in the heterogeneous universe $t_{H_{0,het}}=1/H_{0,het}$ differs from the Hubble time derived in the homogeneous universe $t_{H_{0,hom}}=1/H_{0,hom}$. The ratio of these values is defined:

$$q_t:={\displaystyle \frac{t_{H_{0,het}}}{t_{H_{0,hom}}}}$$

(213)

The value is derived by an iteration. As a first step, the value $0.881$ is chosen. That value has to be compared with the values of $t_{H_{0,hom}}$ and $t_{H_{0,het}}$ that will be derived:

$$q_t^{\left(1\right)}=0.881,\mathrm{as}\mathrm{a}\mathrm{first}\mathrm{step}.$$

(214)

(4.2) Scaled time: The present day time $t_0$ is equal to the Hubble time multiplied by $I_0=0.9455$, see [40], Eq. (2.32)

$$t_0=t_{H_0}·I_0,\mathrm{with}{I}_0=0.9455.$$

(215)

The rate in Eq. (212) and in general, the increment of time $dt$ is scaled by the Hubble time. The idealized value is $t_{H_{0,hom}}$. The realistic value is $t_{H_{0,het}}$, which must be multiplied by $I_0$. Consequently, the realistic scaled increment is as follows:

$$d\tilde{t}={\displaystyle \frac{dt}{t_{H_{0,het}}·I_0}}$$

(216)

This Eq. is solved for $dt$, and the ration in Eq. (213) is used:

$$dt=d\tilde{t}·t_{H_{0,hom}}·I_0·q_1$$

(217)

This realistic scaling is applied to the rate in Eq. (212):

$$d{\dot{\underline{\epsilon }}}_{het}=\left[4\pi G{t}_{H_{0,hom}}{\rho }_{vol}\right]·{\displaystyle \frac{{\Omega }_m{\sigma }_8}{{\Omega }_{vol}}}·q_1·I_0·{\tilde{t}}^{2/3}·d\tilde{t}$$

(218)

Hereby, the rectangular bracket is identified with the rate ${\dot{\underline{\epsilon }}}_{L,rr,atd{V}_0}$ in the homogeneous universe. This rate is abbreviated by ${\dot{\underline{\epsilon }}}_{hom}$. Therefore, the rate in the heterogeneous universe in Eq. (218) has the following relation to the rate in the homogeneous universe:

$$d{\dot{\underline{\epsilon }}}_{het}={\dot{\underline{\epsilon }}}_{hom}·{\displaystyle \frac{{\Omega }_m{\sigma }_8}{{\Omega }_{vol}}}·q_1·I_0·{\tilde{t}}^{2/3}·d\tilde{t}$$

(219)

(4.3) Integration: The integral is applied to the above Eq.:

$${\int }_0^{\Delta {\dot{\underline{\epsilon }}}_{het}}d{\dot{\underline{\epsilon }}}_{het}={\dot{\underline{\epsilon }}}_{hom}·{\displaystyle \frac{{\Omega }_m·{\sigma }_8}{{\Omega }_{vol}}}·q_1·I_0·{\int }_0^{{\tilde{t}}_{em}}{\tilde{t}}^{2/3}·d\tilde{t}$$

(220)

The integrals are evaluated:

$$\Delta {\dot{\underline{\epsilon }}}_{het}={\dot{\underline{\epsilon }}}_{hom}·{\displaystyle \frac{{\Omega }_m·{\sigma }_8}{{\Omega }_{vol}}}·q_1·I_0·{\displaystyle \frac{3}{5}}·{\tilde{t}}_{em}^{5/3}$$

(221)

The ratio ${\displaystyle \frac{\Delta {\dot{\underline{\epsilon }}}_{het}}{{\dot{\underline{\epsilon }}}_{hom}}}$ of the rates of the heterogeneous and of the homogeneous universe is formed, and it is named ${\kappa }_{q_t}$. Moreover, the scaled time is expressed by the scaled scale radius with the relation $\tilde{t}={\tilde{a}}^{3/2}$ in Eq. (210):

$$\begin{array}{c}\hfill {\kappa }_{q_t}\left({\tilde{t}}_{em}\right):={\displaystyle \frac{\Delta {\dot{\underline{\epsilon }}}_{het}\left({\tilde{t}}_{em}\right)}{{\dot{\underline{\epsilon }}}_{hom}}}={\tilde{a}}_{em}^{5/2}·{\displaystyle \frac{{\Omega }_m{\sigma }_8}{2{\Omega }_{vol}}}·\underset{1}{\underbrace{{\displaystyle \frac{6q_t^{\left(1\right)}{I}_0}{5}}}}·{\displaystyle \frac{q_t^{\left(n\right)}}{q_t^{\left(1\right)}}}\end{array}$$

(222)

Hereby, $q_t^{\left(n\right)}$ is determined by an iteration, here a fixed point iteration will be performed. The fixed point iteration is a valid mathematical method to solve the physically based equations of this section (Section 12) simultaneously. Thereby, the first value for $q_t^{\left(n\right)}$ is $q_t^{\left(1\right)}$. With it and Eq. (213), the Hubble times are obtained, and with these, the new value $q_t^{\left(2\right)}{\displaystyle \frac{t_{H_{0,het}}}{t_{H_{0,hom}}}}$ is calculated numerically. This procedure is repeated, until the n-th value $q_t^{\left(n\right)}$, at which $q_t^{\left(n\right)}$ and the following value $q_t^{(n+1)}$ are equal for the first time, up to an accepted numerical error.

Next, the scaled scale radius is expressed by the redshift with the relation ${\tilde{a}}^{5/2}={\left({\displaystyle \frac{1}{1+z}}\right)}^{5/2}$:

$$\begin{array}{c}\hfill {\kappa }_{q_t}\left(z_{em}\right)={\displaystyle \frac{{\Omega }_m·{\sigma }_8}{2{\Omega }_{vol}{(1+z_{em})}^{2.5}}}·{\displaystyle \frac{q_t^{\left(n\right)}}{q_t^{\left(1\right)}}}\end{array}$$

(223)

12.2. Complete Rate in the Heterogeneous Universe

In this section, the sum of the rate of the homogeneous and of the heterogeneous universe are formed and studied.

(1) Sum of rates:

Both rates $\Delta {\dot{\underline{\epsilon }}}_{het}\left({\tilde{\overline{t}}}_{em}\right)$ and ${\dot{\underline{\epsilon }}}_{hom}$ add up to the sum, describing the complete rate in the heterogeneous universe:

$${\dot{\underline{\epsilon }}}_{sum}:=\Delta {\dot{\underline{\epsilon }}}_{het}+{\dot{\underline{\epsilon }}}_{hom}={\dot{\underline{\epsilon }}}_{hom}·(1+\kappa )$$

(224)

Hereby and in the following, the ration ${\kappa }_{q_t}$ is abbreviated by $\kappa$, as a short notation.

(2) Rate of LFV for the sum of rates:

The integrated rate ${\dot{\underline{\epsilon }}}_{L,rr,atd{V}_0}$, shortly called ${\dot{\underline{\epsilon }}}_{hom}$ in Eq. (173) is used:

$$\begin{array}{c}\hfill {\dot{\underline{\epsilon }}}_{hom}=4\pi ·G·{\rho }_{vol}·t_{H_{0,hom}}\end{array}$$

(225)

The corresponding rate in the heterogeneous universe is the complete rate ${\dot{\underline{\epsilon }}}_{sum}$. The above relation (Eq. 225) is transferred to the complete rate by replacing corresponding terms: The rate ${\dot{\underline{\epsilon }}}_{hom}$ corresponds to ${\dot{\underline{\epsilon }}}_{sum}$. The density ${\rho }_{vol}=u_{vol}/c^2$ corresponds to ${\rho }_{\Lambda }=u_{\Lambda }/c^2$. The Hubble time $t_{H_{0,hom}}$ corresponds to $t_{H_{0,het}}$. Therefore, the above relation is transferred to the following rate:

$$\begin{array}{c}\hfill {\dot{\underline{\epsilon }}}_{sum}=4\pi ·G·{\rho }_{\Lambda }·t_{H_{0,het}}\end{array}$$

(226)

(3) Ratio of rates:

The ratio of the rates in Eqs. (225 and 226) is formed:

$$\begin{array}{c}\hfill \underset{1+\kappa }{\underbrace{{\displaystyle \frac{{\dot{\underline{\epsilon }}}_{sum}}{{\dot{\underline{\epsilon }}}_{hom}}}}}=\underset{{\displaystyle \frac{H_{0,hom}}{H_{0,het}}}}{\underbrace{{\displaystyle \frac{t_{H_{0,het}}}{t_{H_{0,hom}}}}}}·\underset{{(1+\kappa )}^{\xi \left(z\right)}}{\underbrace{{\displaystyle \frac{{\rho }_{\Lambda }}{{\rho }_{vol}}}}}\end{array}$$

(227)

Hereby, the first fraction is the rate ratio, it is implied by Eq. (224). Similarly, the second ratio of Hubble times is equal to the corresponding ratio Hubble constants, as $t_{H_0}=1/H_0$. For each redshift $z_{em}$ or z (in a short notation), the third ratio of dynamic densities is an unknown number, which is a function of the redshift z:

$$\begin{array}{c}\hfill {\displaystyle \frac{{\rho }_{\Lambda }}{{\rho }_{vol}}}=\mathrm{unknown}\left(z\right)={(1+\kappa )}^{\xi },\mathrm{with}\xi =\xi \left(z\right)\mathrm{and}\kappa =\kappa \left(z\right).\end{array}$$

(228)

Hereby, without loss of generality and for each z, the unknown is expressed with help of another unknown $\xi$. In particular, the unknown$\left(z\right)$ is replaced by the term ${(1+\kappa \left(z\right))}^{\xi \left(z\right)}$.

(4) Ratio of Hubble constants:

As a consequence of the FLE at $k=0$ and of Eq. (152), the squared Hubble parameter is as follows:

$$H^2={\displaystyle \frac{8\pi G}{3}}·{\rho }_{cr,0}·\left({\Omega }_r·{\displaystyle \frac{R_0^4}{R^4}}+{\Omega }_m·{\displaystyle \frac{R_0^3}{R^3}}+{\Omega }_{\Lambda }\right)$$

(229)

Next, the Hubble rate is used at the present - day time $t=t_0$, so that $r=r_0$:

$$H_{0,het}^2=\underset{H_{0,hom}^2}{\underbrace{{\displaystyle \frac{8\pi G}{3}}·{\rho }_{cr,0}}}·\left({\Omega }_r+{\Omega }_m+{\Omega }_{\Lambda }\right)$$

(230)

Hereby, the Hubble constant of the homogeneous universe in Eq. (150) is identified in the underbrace in the above equation. The above Eq. is solved for the ratio of Hubble constants in the ratio in Eq. (227):

$${\displaystyle \frac{H_{0,hom}}{H_{0,het}}}={\displaystyle \frac{1}{\sqrt{{\Omega }_r+{\Omega }_m+{\Omega }_{\Lambda }}}}\mathrm{or}{H}_{0,het}=H_{0,hom}\sqrt{{\Omega }_r+{\Omega }_m+{\Omega }_{\Lambda }}$$

(231)

Moreover, the ratio of dynamic densities,

$${\displaystyle \frac{{\rho }_{\Lambda }}{{\rho }_{vol}}}={(1+\kappa )}^{\xi },$$

(232)

is equal to ratio of the corresponding density parameters:

$${\displaystyle \frac{{\Omega }_{\Lambda }}{{\Omega }_{vol}}}={(1+\kappa )}^{\xi },\mathrm{or}{\Omega }_{\Lambda }={\Omega }_{vol}·{(1+\kappa )}^{\xi }$$

(233)

These results are inserted in the rate ratio in Eq. (227):

$$\begin{array}{c}\hfill 1+\kappa ={\displaystyle \frac{1}{\sqrt{{\Omega }_r+{\Omega }_m+{\Omega }_{\Lambda }}}}·{(1+\kappa )}^{\xi },\mathrm{or}(1+\kappa )·\sqrt{{\Omega }_r+{\Omega }_m+{\Omega }_{vol}·{(1+\kappa )}^{\xi }}={(1+\kappa )}^{\xi }\end{array}$$

(234)

In order to solve this equation, a term for the exponent $\xi$ is derived:

(6) Derivation of the exponent $\xi$:

In order to solve Eq. (234), the square is applied. Additionally, $1+\kappa \left(z_{\mathrm{em}}\right)$ is abbreviated by y, and $y^{\xi }$ is abbreviated by w:

$$\begin{array}{c}\hfill y^2({\Omega }_m+{\Omega }_{vol}·w)=w^2\mathrm{or}\end{array}$$

(235)

$$\begin{array}{c}\hfill 0=w^2-w·{\Omega }_{vol}·y^2-{\Omega }_m·y^2\mathrm{with}\end{array}$$

(236)

$$\begin{array}{c}\hfill y=1+\kappa \left(z_{\mathrm{em}}\right)\mathrm{and}w=y^{\xi }\end{array}$$

(237)

The above quadratic equation has the following two solutions:

$$\begin{array}{c}\hfill w_{\pm }={\displaystyle \frac{{\Omega }_{vol}·y^2}{2}}·\left(1\pm \sqrt{1+{\displaystyle \frac{4{\Omega }_m}{{\Omega }_{vol}^2·y^2}}}\right)\end{array}$$

(238)

The solution $w_{-}$ is negative. Thus, it does not provide a real exponent, see Eq. (237). Accordingly, the above equation is solved for the exponent $\xi$ by using the solution $w_{+}$ (see Eq. 237):

$$\begin{array}{c}\hfill \xi ={\displaystyle \frac{ln\left(w_{+}\right)}{ln\left(y\right)}}\mathrm{and}y=1+\kappa \left(z_{\mathrm{em}}\right)\mathrm{with}\end{array}$$

(239)

$$\begin{array}{c}\hfill w_{+}={\displaystyle \frac{{\Omega }_{vol}·y^2}{2}}·\left(1+\sqrt{1+{\displaystyle \frac{4{\Omega }_m}{{\Omega }_{vol}^2·y^2}}}\right)\end{array}$$

(240)

12.3. Comparison with Observation

In this section, values of the Hubble constant $H_{0,het}\left(z\right)$ of the heterogeneous universe are studied as a function of the redshift z. Thereby, values derived with the volume dynamics (VD) are compared with observed values in Figure 9. For a huge range of redshifts, corresponding to time ranging from $380000\mathrm{years}$ after the Big Bang until the present - day time, the derived results are in precise accordance with the observed values. In this section, no fit is executed, no assumption is made, and no new hypothesis is proposed. This provides a clear evidence for the presented theory of volume portions.

Additionally, the numerical study is outlined in detail for the case of the CMB (see part 1) and for the case of the redshift $z=0.055$ (see part 2). Also in these cases, the values are in precise accordance with the observed values.

(1) Relation of $H_0\left(z_{CMB}\right)$ and $H_{0,hom}$ alias $H_{0,\Lambda CDM}$:

At $z_{CMB}$, the universe was almost homogeneous.

Consequently, the density parameter ${\Omega }_{vol}$ of the homogeneous universe is applied:

${\Omega }_{vol}={\displaystyle \frac{2}{3}}$, consequently, ${\Omega }_m=1-{\Omega }_{vol}={\displaystyle \frac{1}{3}}$. Moreover,

${\sigma }_{8,CMB}=2.34·{10}^{-4}$[22] table 2,

$z_{\mathrm{CMB}}=1090.3\pm 0.41$[22] table 2,

$H_0\left(z_{CMB}\right)=66.88(\pm 0.92){\displaystyle \frac{\mathrm{km}}{\mathrm{s}·\mathrm{Mpc}}}$[22] table 2.

Hereby, the value $q_t=q_t^{\left(1\right)}$ is chosen at sufficient accuracy.

Thus, the ratio $\kappa \left(z_{\mathrm{CMB}}\right)$ in Eq. (222) has the following value:

$$\kappa \left(z_{\mathrm{CMB}}\right)={\displaystyle \frac{0.000234·1/3}{2·2/3·{(1+1090.3)}^{2.5}}}=1.5·{10}^{-12}$$

(241)

With it, we evaluate $\xi$, see Eqs. (239, 240):

$$\begin{array}{c}\hfill {\xi }_{\mathrm{CMB}}=1.5\end{array}$$

(242)

Consequently, the Hubble constant $H_{0,het}\left(z_{CMB}\right)$ is derived with help of $\kappa \left(z_{\mathrm{CMB}}\right)=\mathcal{O}\left({10}^{-12}\right)$, see Eq. (241):

$$H_{0,het}\left(z_{CMB}\right)=H_{0,hom}·(1+\mathcal{O}\left({10}^{-12}\right))\approx H_{0,hom}=:H_{0,\Lambda CDM}$$

(243)

This relation is informative and helpful, as it shows that the Hubble constant observed with the CMB, $H_{0,het}\left(z_{CMB}\right)$ is almost the same as the Hubble constant $H_{0,\Lambda CDM}$ in the $\Lambda$CDM model. This result confirms that the $\Lambda$CDM model is an idealization.

(2) Hubble constant $H_{0,het}\left(z_{late}\right)$ at $z_{late}=0.055$ or $z_{near}=0.055$:

At the redshift $z=0.055$, the universe is relatively heterogeneous. Consequently, the Hubble constant is derived with help of Eq. (231):

$$H_{0,het}=H_{0,\Lambda CDM}·\sqrt{{\Omega }_m+{\Omega }_{vol}·{(1+\kappa )}^{\xi }}$$

(244)

The other terms in Eq. (244) are as follows:

${\Omega }_{vol}={\displaystyle \frac{2}{3}}$, ${\Omega }_m=1-{\Omega }_{vol}={\displaystyle \frac{1}{3}}$,

${\sigma }_8=0.8118\pm 0.0089$[22] table 2.

As a consequence, the ratio $\kappa \left(z_{\mathrm{late}}\right)$ is as follows:

$$\kappa \left(z_{\mathrm{late}}\right)={\displaystyle \frac{0.8118·1/3}{2·2/3·{(1+0.055)}^{2.5}}}·{\displaystyle \frac{q_t^{\left(n\right)}}{q_t^{\left(1\right)}}}=0.1842\pm 0.003$$

(245)

Hereby, the numerical investigation provides the following values of $q_t^{\left(n\right)}$: $q_t^{\left(1\right)}=0.881$, $q_t^{\left(2\right)}=0.916$, $q_t^{\left(3\right)}=0.913$, $q_t^{\left(4\right)}=0.914$, $q_t^{\left(5\right)}=0.91398$, $q_t^{\left(6\right)}=0.91399$ = $q_t^{\left(7\right)}$. This value is used as a fixed point, at sufficient numerical accuracy.

With it, the idealized value ${\xi }_{CMB}=1.5$ is improved to the realistic value of $\xi$, see Eqs. (239, 240):

$$\begin{array}{c}\hfill {\xi }_{\mathrm{late}}=1.532\end{array}$$

(246)

Consequently, the theoretical value of the Hubble constant is as follows:

$$\begin{array}{ccc}\hfill H_{0,het}\left(z_{\mathrm{near}}\right)& =& H_{0,\Lambda CDM}\sqrt{{\displaystyle \frac{1}{3}}+{\displaystyle \frac{2}{3}}·1.{1842}^{1.532}}\hfill \end{array}$$

(247)

$$\begin{array}{ccc}& =& 73.174\pm 1.08{\displaystyle \frac{\mathrm{km}}{\mathrm{s}·\mathrm{Mpc}}}\hfill \end{array}$$

(248)

As a consequence, the derived theoretical result is in precise accordance (within errors of measurement) with the currently most precise observation in Eq. (14):

$$H_{0,obs}\left(z_{late}\right)=73.04(\pm 1.01){\displaystyle \frac{\mathrm{km}}{\mathrm{s}·\mathrm{Mpc}}}\mathrm{at}\langle z\rangle =0.055$$

(249)

This is the baseline result[13] sections 5.1 and 5.2, obtained at the ’near field’ or ’low redshift’ $\langle z\rangle =0.055$.

The relative difference between theory and measurement is very low at 0.134 %:

$$\begin{array}{ccc}\hfill {\Delta }_{obs,theo}& =& {\displaystyle \frac{H_{0,obs}\left(z_{late}\right)-H_{0,het}\left(z_{\mathrm{late}}\right)}{H_{0,obs}\left(z_{late}\right)}}={\displaystyle \frac{73.174-73.04}{73.04}}=0.18\%\hfill \end{array}$$

(250)

13. Discussion

13.1. The Problem Is Solved with Derived Indivisible Portions of Space

The problem of the Hubble - tension has been addressed and solved. Thereby, a critically discussed method is used, and an explanation is derived. The Hubble - tension is the following finding: Significantly different values have been measured for the rate of expansion $H_0$ of space since the Big Bang.

In order to solve that problem, essential fundamental properties of space have been used: The energy density $u_{DE}$ of space is important, as it shows that space has a real energy. Moreover, the space has no rest mass. On that basis, a very enlightening and momentous result has been derived: A space paradox and its solution are derived: Space is not a single entity, but space is a stochastic average of volume portions propagating at $v=c$.

As a consequence, for the case of homogeneous space, by using a local isotropy, the indivisibility of volume portions with $v=c$ is derived. Additionally, empirical evidence has been provided for it. Therefore, these results are very founded.

13.2. Portions of Space Imply a Momentous Unification

The derived volume portions have many insightful and momentous implications: For mathematical reasons, these volume portions obey a differential equation of volume dynamics. In particular for the case of an indivisible volume portion $\delta V_j$, this differential equation implies the Schrödinger equation and a generalization thereof. Thereby, the corresponding wave function $\Psi$ is the relative additional volume ${\epsilon }_{L,rr,j}$ divided by a normalization constant $t_n$. According to the Higgs [51] mechanism, this derived Schrödinger equation includes the case of matter, as matter is formed from space via a phase transition.

Furthermore, the volume dynamics implies gravity. Moreover, on the basis of that implied gravity, the volume dynamics implies the quantum postulates. Altogether, this shows that the volume dynamics implies the deeply founded unification of quantum physics, gravity and relativity. This foundation of the unification is very fundamental, as gravity is needed for the derivation of the quantum postulates. This provides the clarifying insight that quantum physics can hardly be understood without gravity at a fundamental level. Accordingly, the more general volume dynamics of indivisible volume portions is a theory of quantum gravity. An additional consequence is the local formation of volume (LFV).

13.3. The Unification Implies Values for Homogeneous Space

On the basis of that unification, and for the case of the homogeneous universe, the following results have been derived: the global formation of volume (GFV) since the Big Bang, and the density of volume $u_{DE,hom}=u_{vol}$. These results are in precise accordance with the corresponding observed values, the values of the very early universe, which was very homogeneous. The Hubble constant $H_{0,hom}$ represents a calendar date $t_0\approx t_{H_{0,hom}}={\displaystyle \frac{1}{H_{0,hom}}}$, therefore, $H_{0,hom}$ cannot be derived from fundamental physical constants only.

13.4. The Unification Implies Values for Heterogeneous Space

The heterogeneity in the universe increased gradually in the course of time. That time can be described in an especially robust manner as a function of the cosmological redshift z: The present - day universe has $z=0$, and the emission of the Cosmic Microwave Background (CMB) in the very early universe occurred at $z=1090$.

On the basis of the above unification, the results in section (Section 13.3) have been generalized by including heterogeneity. In this manner, the following results have been derived as a function of the redshift: the global formation of volume (GFV) since the Big Bang, the density of volume $u_{DE}$ and the Hubble constant $H_0\left(z\right)$. These results are in precise accordance with the corresponding observed values, see Figure 9. Moreover, the derived Hubble constant $H_0\left(z\right)$ as a function of z includes many values that have not yet been observed. These values are predicted.

13.5. Very Convincing Evidence Is Achieved

In this paper, all results have been derived without using any unfounded hypothesis, without proposing any postulate, and without executing any fit. Thereby, a precise accordance with observation is achieved within the errors of measurement.

Therefore, the comparison of theory and observations provides a very convincing evidence for the developed and derived theory. That theory includes the following essential results: indivisible volume portions, volume portions, the volume dynamics, the derivation of the quantum postulates, the derivation of exact gravity, the derived unification of quantum physics, relativity and gravity, the energy density of space $u_{DE}$, the energy density of homogeneous space $u_{DE,hom}=u_{vol}$ as an insightful ideal value, the explanation of the Hubble tension by the gradual increase of the heterogeneity in the universe, since the Big Bang.