Submitted:
21 November 2025
Posted:
24 November 2025
You are already at the latest version
Abstract
In this article we want to present a thorough overview about the well known technique known as the Reaction Coordinate Mapping which is one of the most used theoretical tool in the context of Open quantum system and Quantum thermodynamics of quantum systems which is not weakly coupled to the reservoir. Here we discuss different aspects of the Reaction Coordinate mapping along with detailed mathematical derivations for the Bosonic and Fermionic mappings which can be achieved through the Symplectic and unitary transformations. In the later part of this article we discuss the derivation of the Quantum master equation for the extended systems (System+Reaction Coordinate) coupled to the residual reservoir in the weak coupling limit described by the usual Redfield Quantum Master equation. We observe that though the dynamics of the Extended system is Markovian in nature because of the weak coupling between the extended system and the Residual reservoir but the Reaction coordinate transformation enables us to analyses the dynamics of the system which is essentially non-Markovian. The idea of the mesoscopic lead construction and brute force chain mapping techniques has been introduced which can be used to bypass the strong system bath coupling situations.
Keywords:
1. Introduction
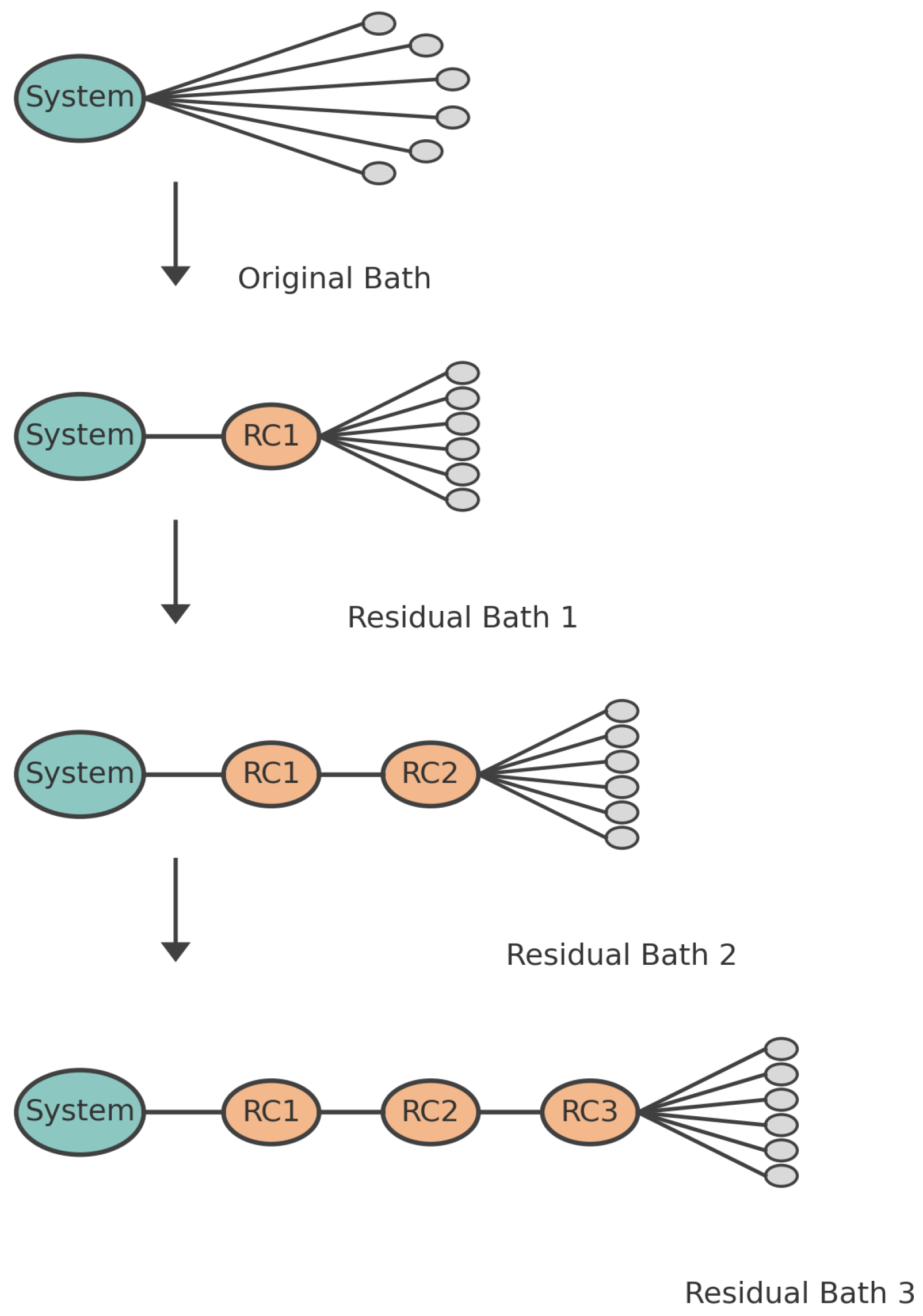
2. Reaction Coordinate Mapping
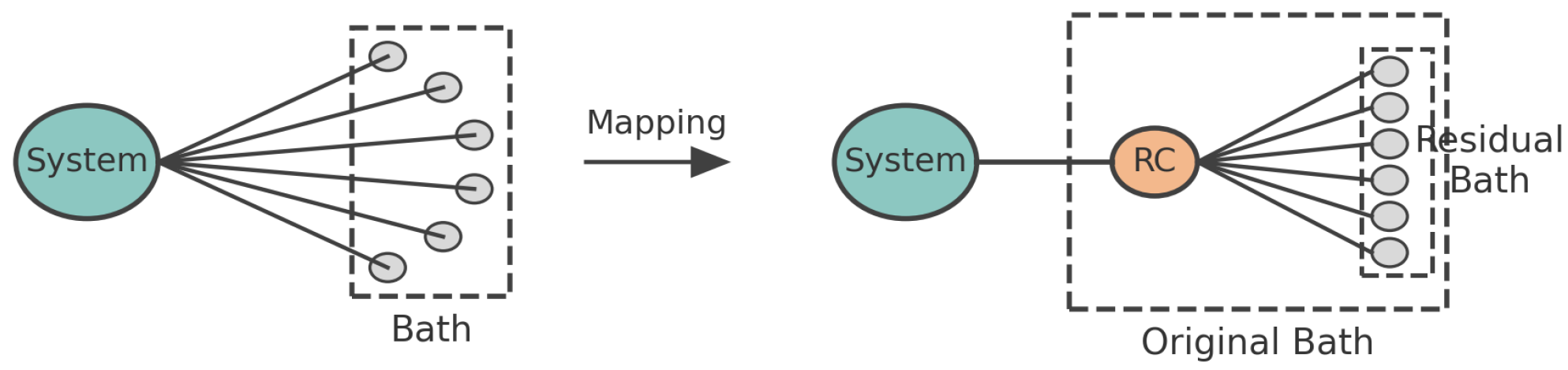
2.1. Establishing the Relation Between the Spectral Function of the Residual Bath and the Old Bath After One Step of Reaction Coordinate Mapping
2.2. Equation of Motion Technique to Find the Relation Between the Residual Bath Spectral Function and the Initial Spectral Function for the Case of Particle and Phonon Mapping
2.2.1. Heisenberg Equation of Motion Technique for the Phonon Mapping
2.2.2. Heisenberg Equation of Motion Technique for the Particle Mapping in the Bosonic Context
2.3. Heisenberg Equation of Motion Technique for Fermionic Particle Mapping Case
3. Quantum Master Equation Using the Reaction Coordinate Mapping
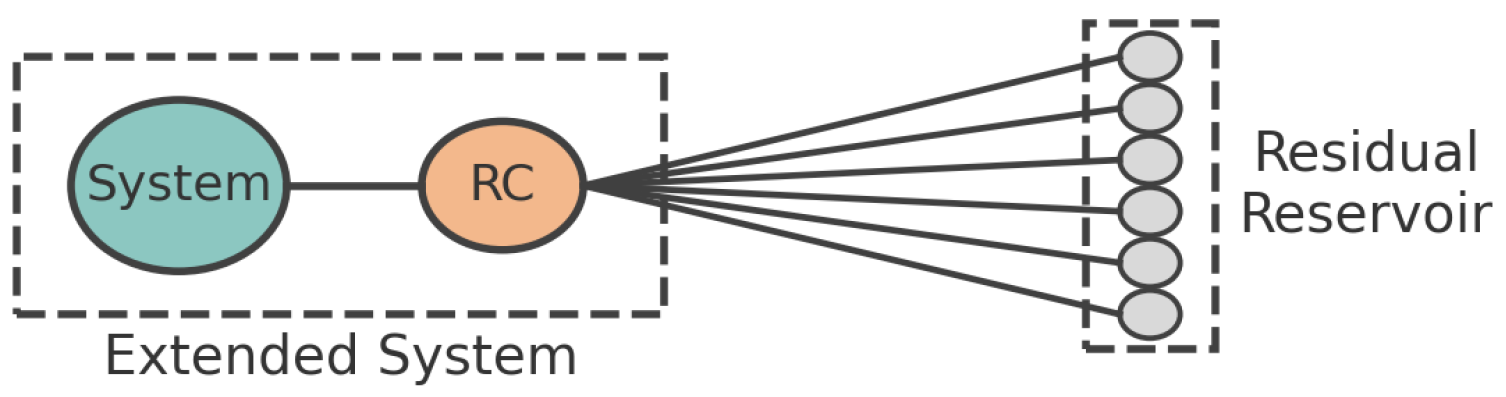
3.1. Three Level Atom Connected to Two Independent Bosonic Reservoirs
3.1.1. Modeling of the Interaction Hamiltonian for Three Level Atom Set-Up
3.1.2. Quantum Master Equation for the Three Level Atom Without Reaction Coordinate Mapping
3.1.3. Quantum Master Equation for Three Level Atom with Reaction Coordinate Mapping
3.1.4. Quantum Master Equation with Strong Coupling
3.2. Theory of Mesoscopic Lead Construction
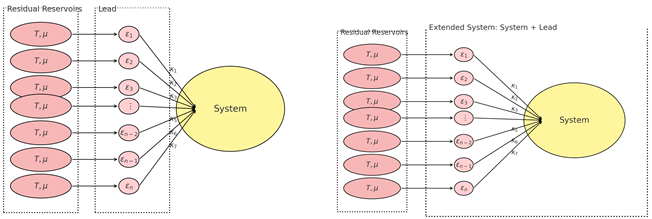
3.2.1. Mesoscopic Lead Construction for Multiple Connected Baths
3.3. Chain Mapping Technique

3.4. Single Electron Transistor
Funding
Acknowledgments
Appendix A.
Appendix A.1. Derivation of Quantum Master Equation for Mesoscopic Leads
References
- Martinazzo, R.; Vacchini, B.; Hughes, K.H.; Burghardt, I. Communication: Universal Markovian reduction of Brownian particle dynamics. The Journal of Chemical Physics 2011, 134. [Google Scholar] [CrossRef] [PubMed]
- Nazir, A.; McCutcheon, D.P.S. Modelling exciton–phonon interactions in optically driven quantum dots. Journal of Physics: Condensed Matter 2016, 28, 103002. [Google Scholar] [CrossRef] [PubMed]
- Nazir, A.; Schaller, G. , The Reaction Coordinate Mapping in Quantum Thermodynamics. In Thermodynamics in the Quantum Regime; Springer International Publishing, 2018; p. 551–577. [CrossRef]
- Anto-Sztrikacs, N.; Nazir, A.; Segal, D. Effective-Hamiltonian Theory of Open Quantum Systems at Strong Coupling. PRX Quantum 2023, 4, 020307. [Google Scholar] [CrossRef]
- Strasberg, P.; Schaller, G.; Lambert, N.; Brandes, T. Nonequilibrium thermodynamics in the strong coupling and non-Markovian regime based on a reaction coordinate mapping. New Journal of Physics 2016, 18, 073007. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




