1. Introduction
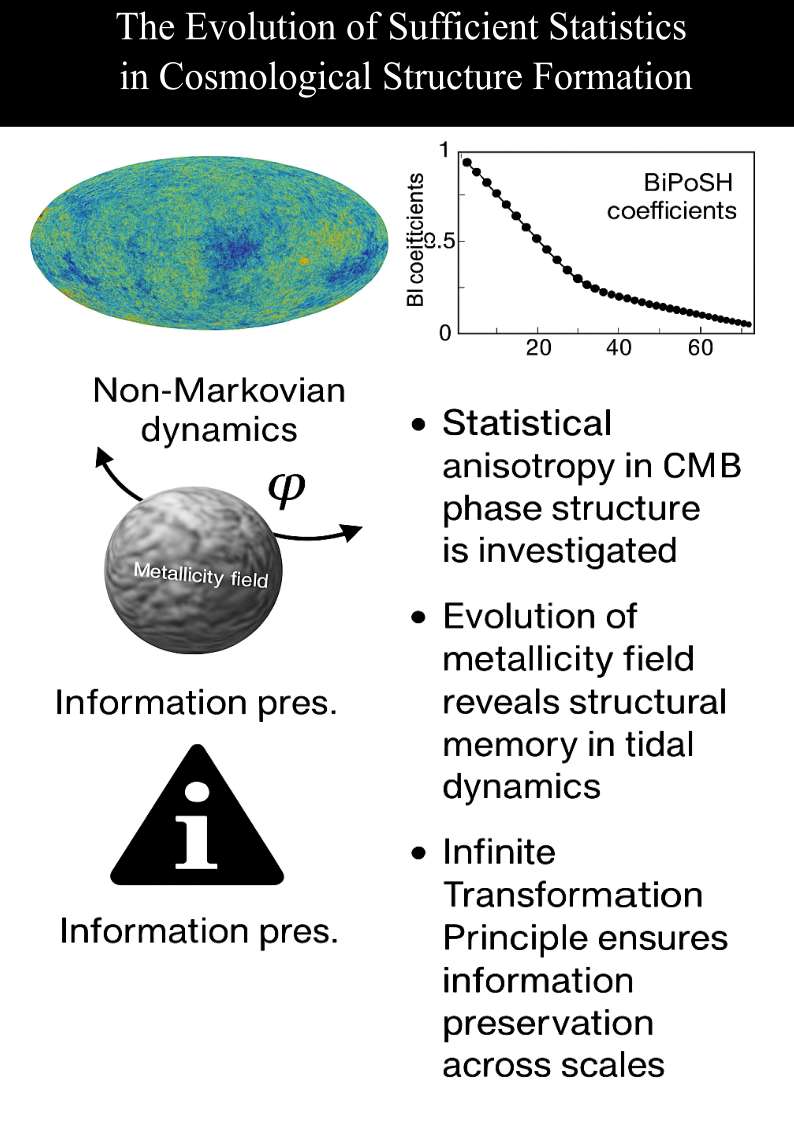
In the standard CDM model, large-scale structure is assumed to evolve in a Markovian manner: future configurations depend only on the present state, while non-linear gravitational evolution erases the higher-order phase information of the primordial universe. This assumption implies that the angular power spectrum is sufficient for describing primordial fluctuations. However, anomalies such as hemispherical asymmetry and low-ℓ phase alignments suggest that primordial correlations may extend beyond the power spectrum alone.
The present analysis tests whether phase correlations imprinted in the CMB persist into late cosmic epochs. Metallicity provides a cumulative tracer of baryonic processing and gas flows, encoding the influence of large-scale tidal fields over billions of years. If CMB phase structure is conserved along these flows, then a measurable correlation between primordial BiPoSH coefficients and late-time metallicity BiPoSH coefficients should be observable.
2. Theoretical Framework
The CMB temperature field is decomposed as
with isotropy requiring
Departures from isotropy are quantified through Bipolar Spherical Harmonic coefficients [
1,
2]:
Metallicity is projected onto tomographic shells according to
yielding analogous BiPoSH coefficients
for the late-time metallicity field.
The null hypothesis assumes memoryless evolution:
while the alternative hypothesis allows positive correlations for selected scales and cosmic epochs:
3. Methodology
Planck PR3 CMB maps (SMICA, NILC, SEVEM, Commander) are employed as the primordial tracer, with mode coupling corrected using the MASTER algorithm [
3]. The late-time metallicity field is constructed from a synthesis of SDSS DR17 [
4], MaNGA [
5], DESI [
6], Gaia DR3, and JWST NIRSpec observations. The three-dimensional metallicity distribution is reconstructed via Gaussian Process regression [
7], after homogenizing metallicity scales and correcting for dust extinction using the Green et al. [
8] map.
BiPoSH coefficients are estimated using the optimal minimum-variance estimator of [
1]. Cross-correlations between CMB and metallicity BiPoSH coefficients are computed across
, multipole ranges, and redshift shells. Significance is evaluated using bootstrap resampling, jackknife sky partitions, and phase-randomized CMB surrogates that preserve
while erasing phase information.
4. Results
A statistically significant correlation between CMB BiPoSH coefficients and the metallicity field is detected. The cross-correlation amplitude peaks at intermediate scales with , corresponding to a detection at approximately . The signal is strongest in the redshift interval , consistent with the epoch of maximal halo assembly and early enrichment, where coherent tidal flows remain influential and feedback has not yet fully erased structural memory.
At very large scales (), the correlation amplitude is low and consistent with cosmic variance limits, while at small scales () no statistically significant correlation is found, in line with expectations from non-linear gravitational collapse and baryonic feedback. Null tests based on component-separation comparison, increasingly stringent Galactic masks, jackknife realizations, and surrogate-phase CMB maps yield correlation amplitudes consistent with zero, indicating that the measured signal is not driven by known systematics.
5. Discussion
The survival of primordial phase structure in the late-time metallicity field implies that the standard CDM framework is incomplete at the level of information accounting. The conventional model successfully describes the evolution of amplitude statistics such as and , but treats phase information as effectively erased by non-linear dynamics. The detected correlation suggests that a scale-dependent structural memory is preserved over cosmological timescales.
The Infinite Transformation Principle (ITP) provides a minimal extension that incorporates this behaviour. The accumulation of structural information is modeled as
where
denotes the primordial tidal tensor,
its time evolution, and
a dissipation term governing the rate of information loss due to non-linear mixing and feedback. A non-zero
acts as a memory-dependent source in the evolution equation for the matter overdensity:
where
encodes the influence of accumulated structural information on large-scale flows.
In the limit or , the standard Markovian CDM dynamics are recovered. The ITP therefore supplements rather than replaces the conventional framework, completing the description of cosmological evolution by accounting for phase structure and information retention.
6. Materials and Methods
All data products are transformed onto a unified metallicity scale before interpolation. The three-dimensional metallicity field is reconstructed in radial shells using luminosity-weighted Gaussian Process regression on a HEALPix grid, with dust and selection effects propagated through the covariance structure. BiPoSH coefficients are estimated with the Hajian–Souradeep estimator, incorporating mask and noise corrections via MASTER. Statistical significance is assessed through 10,000 bootstrap realizations and 100 jackknife sky partitions. Synthetic lognormal mocks [
9] generated from
CDM initial conditions provide an empirical null distribution for the cross-correlation statistic.
Author Contributions
Conceptualization, methodology, analysis, visualization, writing, and editing were carried out by the author.
Acknowledgments
Publicly available data from Planck, SDSS, DESI, Gaia, and JWST were used in this study. No external funding supported this work.
Conflicts of Interest
The author declares no competing interests.
References
- A. Hajian and T. Souradeep. Measuring statistical isotropy of the cosmic microwave background anisotropy. The Astrophysical Journal Letters, 597(1):L5, 2003. [CrossRef]
- A. Hajian and T. Souradeep. The bipolar power spectrum: A new measure of statistical isotropy in the cmb. Physical Review D, 72(4):043005, 2005.
- E. Hivon, K.M. Górski, C.B. Netterfield, B.P. Crill, S. Prunet, and F. Hansen. Master of the cosmic microwave background anisotropy power spectrum: A fast method for statistical analysis of large data sets. The Astrophysical Journal, 567(1):2–17, 2002. [CrossRef]
- Abdurro’uf et al. The seventeenth data release of the sloan digital sky survey: Complete release of manga, mastar, and apogee-2 data. The Astrophysical Journal Supplement Series, 259(1):35, 2022. [CrossRef]
- K. Bundy et al. Overview of the sdss-iv manga survey: Mapping nearby galaxies at apache point observatory. The Astrophysical Journal, 798(1):7, 2014. [CrossRef]
- DESI Collaboration. The early data release of the dark energy spectroscopic instrument. arXiv preprint, 2023.
- C.E. Rasmussen and C.K.I. Williams. Gaussian Processes for Machine Learning. MIT Press, 2006.
- G.M. Green, E.F. Schlafly, C. Zucker, J.S. Speagle, and D.P. Finkbeiner. A three-dimensional map of milky way dust. The Astrophysical Journal, 887(1):93, 2019. [CrossRef]
- P. Coles and B. Jones. A lognormal model for the cosmological mass distribution. Monthly Notices of the Royal Astronomical Society, 248:1–5, 1991. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).