Submitted:
14 November 2025
Posted:
18 November 2025
You are already at the latest version
Abstract
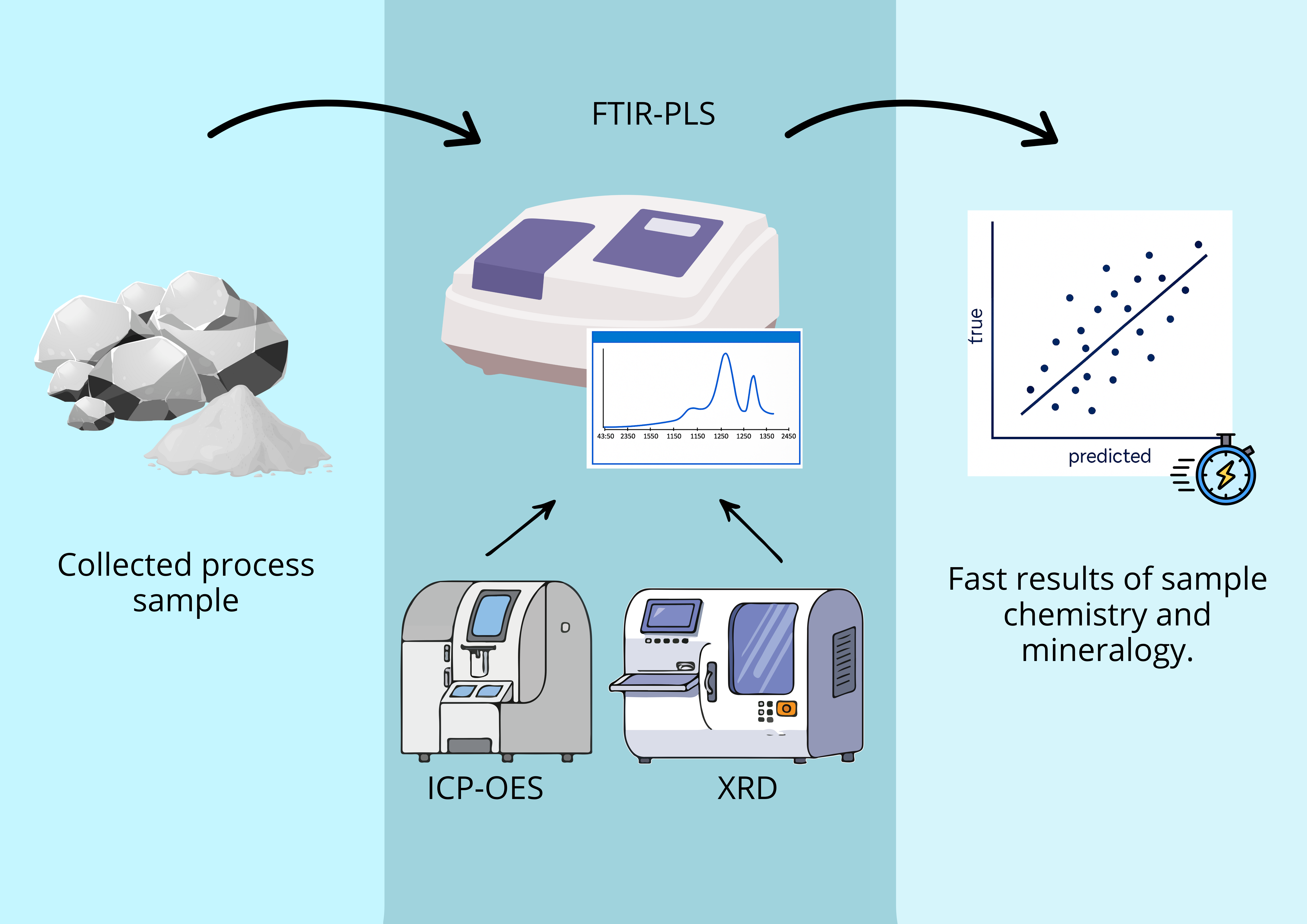
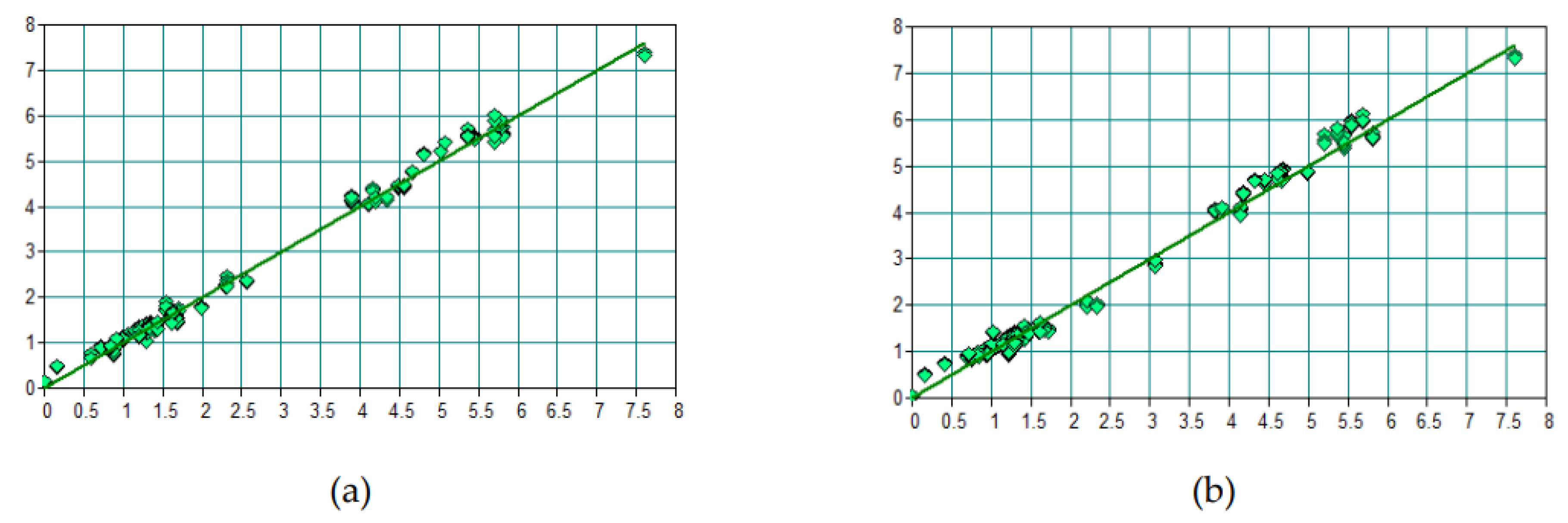
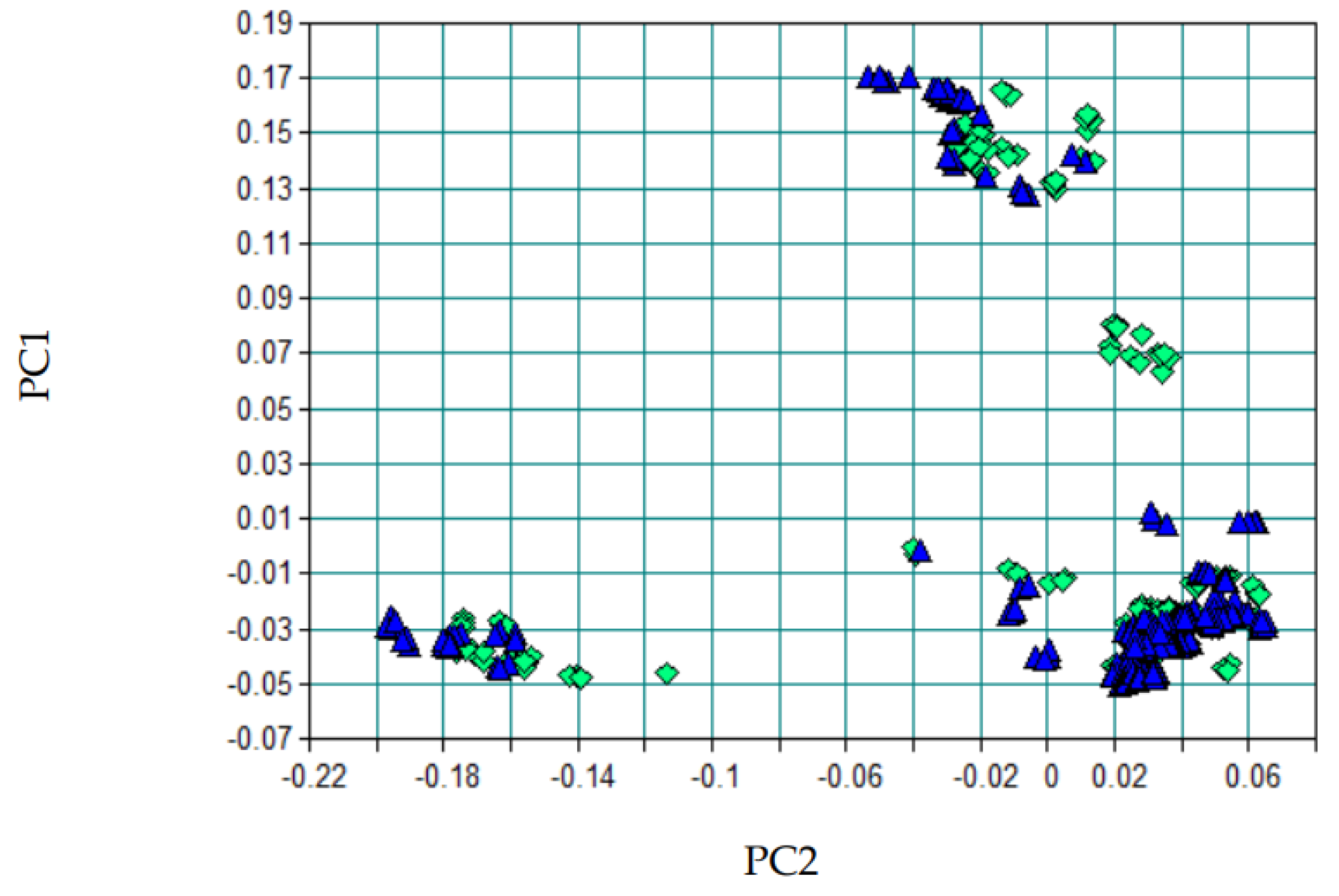
The growing global demand for strategic minerals such as lithium, driven primarily by the battery industry, has made rapid and effective control of mineral quality an urgent necessity. Conventional analytical methods, although accurate, often require considerable time and complex sample preparation, which can delay process control. To overcome this challenge, this work proposes the use of Fourier Transform Infrared (FTIR) spectroscopy combined with Partial Least Squares (PLS) modeling as an efficient alternative. This approach aims to provide immediate response for predicting grades in lithium-bearing ores, such as spodumene, ensuring agility and precision to meet industry demands. This study evaluated the application of FTIR spectroscopy coupled with chemometric modeling for the simultaneous prediction of lithium oxide (Li₂O) and spodumene contents in pegmatitic samples. Two independent PLS models were developed, using spectra preprocessed with first derivative and/or Standard Normal Variate (SNV). Spectral regions were selected based on the structural response of Al–O, Si–O, and OH⁻ groups, which are indirectly influenced by the presence of lithium. The spectral datasets were split into calibration and external test sets, and the models were evaluated based on statistical metrics and Principal Component Analysis (PCA). The Li₂O model achieved an R² of 0.9934 and an RMSEP of 0.185 in external validation, with a mean absolute error below 0.15%. The spodumene model achieved an R² of 0.9961, an RMSEP of 1.79, and a mean absolute error of 2.80%. The results indicate that the FTIR-PLS approach enables efficient quantitative estimation of lithium-bearing minerals, with reduced analytical time, good accuracy, and feasibility for application in process control and mineralogical sorting environments. PCA confirmed the statistical representativeness of the test sets, with no occurrence of spectral extrapolation.
Keywords:
lithium
; spodumene
; PLS modeling
; chemometrics
; multivariate analysis
; mineral process control
1. Introduction
Advances in the mineralogical characterization of strategic ores, such as those bearing lithium, have demanded the development of faster, more representative analytical methods that can be integrated into operational routines. The growing demand for lithium, driven by the battery and energy technology industries, reinforces the need for tools that enable rapid, inexpensive, and efficient monitoring of grades throughout the beneficiation chain, especially in complex geological contexts such as lithium-bearing pegmatites [1,2,3].
Fourier Transform Infrared (FTIR) spectroscopy has emerged as a viable alternative to conventional analysis due to its speed, low operational cost, and ability to detect structural and chemical changes in silicate materials. The spectral response in FTIR arises from the vibrations of functional groups within the mineral structure, particularly in the 1100-400 cm⁻¹ range, associated with the stretching and bending of Si–O and Al–O groups, as well as bands around 3600-3200 cm⁻¹, attributed to OH⁻ groups. Lithium itself does not exhibit direct vibrational bands in the infrared; however, its presence affects the intensity and position of structural bands and can be inferred indirectly in regions correlated with the aluminosilicate structure [2,3,4,5,6,7].
Nevertheless, the direct application of spectra for grade prediction presents challenges, such as band overlap, the presence of accessory phases, and physical interferences (particle size, moisture, crystal orientation). To mitigate these effects, it is necessary to apply mathematical preprocessing techniques like Standard Normal Variate (SNV), aiming to enhance relevant chemical patterns and reduce instrumental noise [3,5,8].
Using the preprocessed spectra, multivariate regression tools can be employed, with Partial Least Squares (PLS) regression being the most widely used in spectroscopic analyses. This technique projects spectral data onto latent variables that explain the variance in both the spectral matrix and the variable of interest (analytical response). The generated models are evaluated using statistical parameters such as the coefficient of determination (R²), Root Mean Square Error (RMSE), and bias, which indicate their precision, stability, and applicability [5,6]. To ensure model reliability, it is essential that the grades used as the response are obtained by validated reference analytical methods. The integration of reference laboratory data with spectra enables the development of robust predictive models that associate rapid FTIR measurements with precise mineral and chemical grade results [3,6].
Assessing the generalization capability of spectral models is fundamental for their application in mineral process control. The use of independent test sets allows for verifying model robustness against the variability of new samples. Among the applied statistical tools, Principal Component Analysis (PCA) is widely used to verify the multivariate representativeness of the data and the stability of the distribution between calibration and test sets [5,9]. The integrated use of FTIR, Inductively Coupled Plasma Optical Emission Spectrometry (ICP-OES), X-ray Diffraction (XRD), and PLS modeling, coupled with multivariate evaluation via PCA, enables the establishment of a protocol for mineralogical and chemical prediction with potential application in operational environments. This approach contributes to reduced response time, increased monitoring frequency, and improved control over mining, blending, separation, and final product shipment decisions.
The objective of this work was to develop and validate predictive models for the quantification of lithium oxide (Li₂O) and spodumene from FTIR spectra, using ICP-OES and XRD data as reference. The models were applied to an independent test set and evaluated using statistical metrics and PCA analysis, with a view to their practical application in mineral process control.
2. Materials and Methods
The samples analyzed in this study were sourced from different stages of exploration and beneficiation of a lithium pegmatite deposit. For FTIR analysis, spectra were acquired in the range of 4000 to 400 cm⁻¹ using Attenuated Total Reflectance (ATR) mode on a Bruker Alpha II spectrometer equipped with a diamond ATR crystal. Spectral files were processed using the OPUS software (Bruker), applying preprocessing with first derivative and Standard Normal Variate (SNV) normalization. Subsequently, spectral regions of higher analytical relevance were selected based on band intensity and stability for each model.
Lithium oxide (Li₂O) grade readings were performed by ICP-OES using an Agilent 5110 instrument. Sample preparation involved alkaline fusion with sodium peroxide (Na₂O₂) and sodium hydroxide (NaOH) in a zirconium crucible at 550 °C, followed by digestion with nitric acid (HNO₃, 2 mol/L) and tartaric acid (C₄H₆O₆). Spodumene grade readings were obtained by XRD using a Panalytical Aeris diffractometer with Cu Kα radiation (λ = 1.5406 Å), a nickel Kβ filter, a PIXcel 1D detector, and a scanning range from 5° to 70° (2θ). Refinement of crystalline phases was conducted using the Rietveld method in the HighScore software (Malvern Panalytical), utilizing crystal structures from the Crystallography Open Database (COD).
The FTIR data were correlated with the ICP-OES and XRD results to construct two Partial Least Squares (PLS) regression models, one for Li₂O and one for spodumene. Both models were calibrated using preprocessed spectra and validated internally. Subsequently, they were applied to an external test set, composed of samples not used in the calibration, to evaluate their generalization capability. The division into calibration and test sets was performed randomly, ensuring a representative distribution of grades in the analyzed samples. Model quality was assessed using statistical metrics: coefficient of determination (R²), Root Mean Square Error (RMSE), and bias.
Finally, Principal Component Analysis (PCA) was performed on the preprocessed spectra to verify the representativeness of the test set within the model’s multivariate space. The score distribution was used to identify clustering, data spread, and potential extrapolation. Compatibility between the calibration and test sets was considered an indicator of modeling robustness.
3. Results
3.1. Prediction of Li₂O by FTIR
The multivariate model for predicting Li₂O content was constructed using 446 FTIR spectra from 119 samples, with 219 spectra allocated to calibration and 227 to the external test set. The spectra were preprocessed using the first derivative and SNV. The spectral ranges used for calibration were 1627.6 to 1369.7 cm⁻¹ and 1103.5 to 665.4 cm⁻¹, as shown in Figure 1.
The final model was fitted and yielded an R² of 99.34%, an RMSEE of 0.144. Application to the external test set resulted in an R² of 98.93%, an RMSEP of 0.185, and a bias of -0.0385. The relationship between predicted and observed values is shown in Figure 2.
Principal Component Analysis (PCA), illustrated in Figure 3, demonstrated a partial overlap between the calibration (green diamonds) and test (blue triangles) sets, with a homogeneous distribution and an absence of identifiable outliers.
The comparison (see Supplementary Material) between the actual and predicted values for Li₂O content in the external validation set confirms the model’s good accuracy, with a mean absolute error of less than 0.15%, low bias, and a homogeneous distribution of residuals around the trend line. The linear correlation between the observed and estimated values, as previously illustrated in Figure 2, reflects the model’s statistical stability even outside the calibration database.
3.2. Spodumene Prediction by FTIR
For the model predicting spodumene content (% by weight), 238 spectra from 78 samples were used, with 121 spectra in the calibration set and 117 in the external validation set. The selected spectral ranges (3756.9-3056.7 cm⁻¹, 2450.7-2207 cm⁻¹, and 1265.3-534.4 cm⁻¹) are highlighted in Figure 4.
The model was fitted using 9 latent factors. The calibration resulted in an R² of 99.61%, an RMSEE of 1.79, and the external validation yielded an R² of 98.6%, an RMSEP of 3.53, and a bias of 0.0706. Figure 5 shows the linear relationship between the predicted and observed values in the test set.
The multivariate separation between the calibration and test sets was verified by PCA, presented in Figure 6, which showed a centered distribution of scores and an absence of extreme dispersions.
The external test set (see Supplementary Material) for the spodumene model exhibited a mean absolute error of less than 2.80%, which is compatible with industrial applications. The residuals remained symmetrically distributed with no systematic trend, reinforcing the model’s performance on samples not included in the calibration.
4. Discussion
The development of multivariate models based on FTIR spectroscopy demonstrated high statistical performance for the prediction of Li₂O and spodumene, validating the applicability of this approach in routine mineral characterization and process control contexts. Modeling with Partial Least Squares (PLS) regression enabled the capture of spectral variations indirectly associated with the presence of lithium and the proportion of spodumene, even in the absence of specific vibrational bands for the Li⁺ cation. In the spodumene model, the utilized spectral regions included stretching and bending bands of the aluminosilicate structure, as well as signals related to OH⁻ groups. The spectral response demonstrated good correlation with the content of the target mineral phase, albeit subject to the influence of co-occurring minerals such as micas. The greater dispersion of the residuals suggests the model is more sensitive to compositional variations and structural interferences. Nevertheless, principal component analysis indicated compatibility between the datasets.
The robustness of the models developed here is associated with the combination of adequate preprocessing techniques, such as the first derivative and SNV, the careful selection of spectral windows, and validation with a representative external set. The obtained RMSEP values classify them as reliable for analytical application. The results of R² values of 0.986 and 0.989 and RMSEP values of 3.53 and 0.185 demonstrate a predictive accuracy that aligns well with data found in the literature for FTIR analyses. For instance, models reported in the literature show R² values of 0.98 and RMSEP of 6.0 [10]; R² between 0.86 and 0.99 and RMSEP between 1.2 and 4.3 [4]; and R² values from 0.86 to 0.99 and RMSEP from 0.9 to 5.1 [2]. The performance of the current models is comparable or superior, which validates their reliability for predicting the studied parameters.
From a technical standpoint, the results demonstrate that FTIR spectroscopy coupled with PLS modeling is a viable alternative for the partial replacement of destructive and/or costly methods, such as ICP-OES and XRD with Rietveld refinement, for the characterization of pegmatitic ores. The methodology demonstrated sufficient sensitivity to capture complex structural variations in minerals with spectral similarity, while maintaining statistical stability and reducing analytical response time. Although the model’s statistical precision is acceptable for exploratory applications and mineralogical sorting, the mean absolute error of 2.80% indicates room for improvement. The potential spectral interference from co-occurring phases may contribute to residual variations and reduced accuracy. Expanding the calibration database, coupled with complementary mineralogical characterization, could increase the model’s selectivity and robustness in operational scenarios.
5. Conclusions
The application of FTIR spectroscopy, combined with multivariate PLS regression modeling, demonstrated high performance in predicting Li₂O and spodumene grades in pegmatitic samples, using spectral preprocessing with first derivative and/or SNV. The selected spectral windows effectively captured relevant structural variations, even in the absence of specific vibrational bands for the lithium cation.
The externally calibrated and validated models exhibited statistical metrics compatible with analytical requirements for process control, with coefficients of determination (R²) greater than 0.98 and low Root Mean Square Errors of Prediction (RMSEP), characterizing high predictive capability. Exploratory analysis by Principal Component Analysis (PCA) confirmed the statistical representativeness of the test sets, with no occurrence of extrapolation or formation of outliers.
The achieved accuracy, with mean absolute errors below 0.15% for Li₂O and 2.8% for spodumene, demonstrates the robustness of the developed models and their suitability for operational applications, such as sample sorting, mineralogical assessment of blends, and monitoring of intermediate product quality. Therefore, the results confirm the technical feasibility of the FTIR-PLS approach as a fast, non-destructive, and low-cost alternative method for the simultaneous estimation of Li₂O and spodumene in lithium-bearing minerals, with potential for direct application in production environments and mineralogical research.
Although the results for spodumene were satisfactory in the test set, the magnitude of the mean absolute error indicates the need for future adjustments. The presence of interfering minerals and sample compositional variability can impact the spectral response. Expanding the sample database and refining spectral selection are promising pathways for model improvement.
Author Contributions
Author Contributions: Conceptualization, B.O. and E.S.; Methodology, B.O.; Validation, B.O.; Formal analysis, B.O.; Investigation, B.O.; Resources, E.L.; Data curation, B.O.; Writing—original draft preparation, B.O.; Writing—review and editing, B.O.; Supervision, E.S.; Project administration, E.S. and E.L. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
The authors thank SGS Geosol Laboratórios for providing the samples and the laboratory infrastructure necessary for conducting the spectroscopic and chemical analyses.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ATR | Attenuated Total Reflectance |
| FTIR | Fourier Transform Infrared |
| ICP-OES | Inductively Coupled Plasma Optical Emission Spectrometry |
| PCA | Principal Component Analysis |
| PLS | Partial Least Squares |
| RMSE | Root Mean Square Error |
| RMSEE | Root Mean Square Error of Calibration |
| RMSEP | Root Mean Square Error of Prediction |
| SNV | Standard Normal Variate |
| XRD | X-ray Diffraction |
Appendix A
Appendix A.1
Table A1.
Comparison between actual and predicted Li₂O values (% by weight) in the external validation set, based on the PLS model applied to the preprocessed FTIR spectra.
Table A1.
Comparison between actual and predicted Li₂O values (% by weight) in the external validation set, based on the PLS model applied to the preprocessed FTIR spectra.
| Test Set Validation | ||||
|---|---|---|---|---|
| Sample | Spectrum | Reference Value | Predicted Value | Difference |
| 1 | 1 | 2,20 | 2,01 | 0,19 |
| 1 | 2 | 2,20 | 2,02 | 0,18 |
| 1 | 3 | 2,20 | 1,95 | 0,25 |
| 1 | 4 | 2,20 | 2,08 | 0,12 |
| 2 | 5 | 1,20 | 1,31 | -0,11 |
| 2 | 6 | 1,20 | 1,22 | -0,02 |
| 2 | 7 | 1,20 | 1,27 | -0,07 |
| 2 | 8 | 1,20 | 1,26 | -0,06 |
| 3 | 9 | 0,70 | 0,89 | -0,19 |
| 3 | 10 | 0,70 | 0,88 | -0,18 |
| 3 | 11 | 0,70 | 0,90 | -0,20 |
| 3 | 12 | 0,70 | 0,85 | -0,15 |
| 4 | 13 | 1,30 | 1,36 | -0,06 |
| 4 | 14 | 1,30 | 1,42 | -0,12 |
| 4 | 15 | 1,30 | 1,39 | -0,09 |
| 4 | 16 | 1,30 | 1,38 | -0,08 |
| 5 | 17 | 1,00 | 1,08 | -0,08 |
| 5 | 18 | 1,00 | 1,11 | -0,11 |
| 5 | 19 | 1,00 | 1,09 | -0,05 |
| 5 | 20 | 1,00 | 1,05 | -0,05 |
| 6 | 21 | 1,40 | 1,45 | -0,05 |
| 6 | 22 | 1,40 | 1,49 | -0,09 |
| 6 | 23 | 1,40 | 1,49 | -0,09 |
| 6 | 24 | 1,40 | 1,47 | -0,07 |
| 7 | 25 | 0,93 | 0,92 | 0,01 |
| 7 | 26 | 0,93 | 0,94 | -0,01 |
| 7 | 27 | 0,93 | 0,95 | -0,02 |
| 7 | 28 | 0,93 | 0,95 | -0,02 |
| 8 | 29 | 1,22 | 0,95 | 0,27 |
| 8 | 30 | 1,22 | 0,93 | 0,29 |
| 8 | 31 | 1,22 | 0,93 | 0,29 |
| 8 | 32 | 1,22 | 0,98 | 0,24 |
| 9 | 33 | 1,73 | 1,42 | 0,31 |
| 9 | 34 | 1,73 | 1,43 | 0,30 |
| 9 | 35 | 1,73 | 1,46 | 0,27 |
| 9 | 36 | 1,73 | 1,40 | 0,33 |
| 10 | 37 | 2,33 | 2,00 | 0,34 |
| 10 | 38 | 2,33 | 1,98 | 0,35 |
| 10 | 39 | 2,33 | 2,00 | 0,33 |
| 10 | 40 | 2,33 | 1,93 | 0,40 |
| 11 | 41 | 4,98 | 4,82 | 0,16 |
| 11 | 42 | 4,98 | 4,82 | 0,16 |
| 11 | 43 | 4,98 | 4,85 | 0,14 |
| 11 | 44 | 4,98 | 4,84 | 0,14 |
| 12 | 45 | 1,67 | 1,48 | 0,20 |
| 12 | 46 | 1,67 | 1,50 | 0,17 |
| 12 | 47 | 1,67 | 1,45 | 0,22 |
| 12 | 48 | 1,67 | 1,45 | 0,22 |
| 13 | 49 | 1,61 | 1,60 | 0,01 |
| 13 | 50 | 1,61 | 1,60 | 0,01 |
| 13 | 51 | 1,61 | 1,62 | 0,00 |
| 13 | 52 | 1,61 | 1,61 | 0,00 |
| 14 | 53 | 0,92 | 1,02 | -0,10 |
| 14 | 54 | 0,92 | 0,99 | -0,07 |
| 14 | 55 | 0,92 | 1,02 | -0,10 |
| 14 | 56 | 0,92 | 1,04 | -0,12 |
| 15 | 57 | 0,84 | 0,88 | -0,04 |
| 15 | 58 | 0,84 | 0,90 | -0,06 |
| 15 | 59 | 0,84 | 0,88 | -0,04 |
| 15 | 60 | 0,84 | 0,87 | -0,03 |
| 16 | 61 | 1,29 | 1,33 | -0,03 |
| 16 | 62 | 1,29 | 1,31 | -0,02 |
| 16 | 63 | 1,29 | 1,35 | -0,06 |
| 16 | 64 | 1,29 | 1,31 | -0,02 |
| 17 | 65 | 5,45 | 5,37 | 0,08 |
| 17 | 66 | 5,45 | 5,62 | -0,17 |
| 17 | 67 | 5,45 | 5,42 | 0,03 |
| 17 | 68 | 5,45 | 5,48 | -0,03 |
| 18 | 69 | 5,82 | 5,64 | 0,18 |
| 18 | 70 | 5,82 | 5,54 | 0,28 |
| 18 | 71 | 5,82 | 5,69 | 0,13 |
| 18 | 72 | 5,82 | 5,58 | 0,24 |
| 19 | 73 | 1,34 | 1,34 | 0,00 |
| 19 | 74 | 1,34 | 1,37 | -0,03 |
| 19 | 75 | 1,34 | 1,37 | -0,03 |
| 19 | 76 | 1,34 | 1,33 | 0,01 |
| 20 | 77 | 1,27 | 1,27 | 0,00 |
| 20 | 78 | 1,27 | 1,25 | 0,02 |
| 20 | 79 | 1,27 | 1,22 | 0,05 |
| 20 | 80 | 1,27 | 1,19 | 0,08 |
| 21 | 81 | 1,05 | 1,08 | -0,03 |
| 21 | 82 | 1,05 | 1,09 | -0,04 |
| 21 | 83 | 1,05 | 1,11 | -0,06 |
| 21 | 84 | 1,05 | 1,11 | -0,06 |
| 22 | 85 | 1,09 | 1,13 | -0,04 |
| 22 | 86 | 1,09 | 1,11 | -0,02 |
| 22 | 87 | 1,09 | 1,12 | -0,03 |
| 22 | 88 | 1,09 | 1,13 | -0,04 |
| 23 | 89 | 1,00 | 1,09 | -0,09 |
| 23 | 90 | 1,00 | 1,10 | -0,10 |
| 23 | 91 | 1,00 | 1,06 | -0,06 |
| 23 | 92 | 1,00 | 1,10 | -0,10 |
| 24 | 93 | 0,76 | 0,84 | -0,08 |
| 24 | 94 | 0,76 | 0,83 | -0,07 |
| 24 | 95 | 0,76 | 0,81 | -0,05 |
| 24 | 96 | 0,76 | 0,84 | -0,08 |
| 25 | 97 | 4,18 | 4,41 | -0,23 |
| 25 | 98 | 4,18 | 4,36 | -0,18 |
| 25 | 99 | 4,18 | 4,40 | -0,22 |
| 25 | 100 | 4,18 | 4,39 | -0,21 |
| 26 | 101 | 3,82 | 3,98 | -0,16 |
| 26 | 102 | 3,82 | 3,99 | -0,17 |
| 26 | 103 | 3,82 | 4,06 | -0,24 |
| 26 | 104 | 3,82 | 4,00 | -0,18 |
| 27 | 105 | 3,91 | 4,03 | -0,12 |
| 27 | 106 | 3,91 | 4,09 | -0,18 |
| 28 | 107 | 4,67 | 4,73 | -0,05 |
| 28 | 108 | 4,67 | 4,72 | -0,05 |
| 28 | 109 | 4,67 | 4,75 | -0,08 |
| 28 | 110 | 4,67 | 4,66 | 0,01 |
| 28 | 111 | 4,67 | 4,75 | -0,08 |
| 29 | 112 | 4,69 | 4,93 | -0,24 |
| 29 | 113 | 4,69 | 4,90 | -0,21 |
| 29 | 114 | 4,69 | 4,88 | -0,19 |
| 29 | 115 | 4,69 | 4,70 | -0,01 |
| 30 | 116 | 4,65 | 4,88 | -0,23 |
| 30 | 117 | 4,65 | 4,86 | -0,21 |
| 30 | 118 | 4,65 | 4,84 | -0,19 |
| 30 | 119 | 4,65 | 4,87 | -0,22 |
| 31 | 120 | 4,61 | 4,70 | -0,09 |
| 31 | 121 | 4,61 | 4,73 | -0,12 |
| 31 | 122 | 4,61 | 4,70 | -0,09 |
| 31 | 123 | 4,61 | 4,83 | -0,22 |
| 32 | 124 | 4,45 | 4,60 | -0,15 |
| 32 | 125 | 4,45 | 4,66 | -0,21 |
| 32 | 126 | 4,45 | 4,68 | -0,23 |
| 32 | 127 | 4,45 | 4,69 | -0,24 |
| 33 | 128 | 4,33 | 4,65 | -0,32 |
| 33 | 129 | 4,33 | 4,66 | -0,33 |
| 33 | 130 | 4,33 | 4,67 | -0,34 |
| 33 | 131 | 4,33 | 4,61 | -0,28 |
| 34 | 132 | 0,16 | 0,50 | -0,34 |
| 34 | 133 | 0,16 | 0,48 | -0,32 |
| 34 | 134 | 4,14 | 4,01 | 0,13 |
| 34 | 135 | 4,14 | 4,06 | 0,08 |
| 35 | 136 | 4,14 | 4,09 | 0,05 |
| 35 | 137 | 4,14 | 3,93 | 0,22 |
| 36 | 138 | 1,61 | 1,62 | -0,01 |
| 36 | 139 | 1,61 | 1,60 | 0,01 |
| 36 | 140 | 1,61 | 1,58 | 0,03 |
| 36 | 141 | 1,61 | 1,61 | 0,00 |
| 37 | 142 | 1,00 | 1,12 | -0,12 |
| 37 | 143 | 1,00 | 1,10 | -0,10 |
| 37 | 144 | 1,00 | 1,09 | -0,09 |
| 37 | 145 | 1,00 | 1,13 | -0,13 |
| 38 | 146 | 0,95 | 0,99 | -0,04 |
| 38 | 147 | 0,95 | 0,98 | -0,03 |
| 38 | 148 | 0,95 | 0,90 | 0,05 |
| 38 | 149 | 0,95 | 0,93 | 0,02 |
| 39 | 150 | 0,83 | 0,96 | -0,13 |
| 39 | 151 | 0,83 | 0,91 | -0,08 |
| 39 | 152 | 0,83 | 0,90 | -0,07 |
| 39 | 153 | 0,83 | 0,92 | -0,09 |
| 40 | 154 | 0,71 | 0,91 | -0,20 |
| 40 | 155 | 0,71 | 0,94 | -0,23 |
| 40 | 156 | 0,71 | 0,93 | -0,22 |
| 40 | 157 | 0,71 | 0,95 | -0,24 |
| 41 | 158 | 5,20 | 5,64 | -0,44 |
| 41 | 159 | 5,20 | 5,52 | -0,32 |
| 41 | 160 | 5,20 | 5,44 | -0,24 |
| 42 | 161 | 1,02 | 1,37 | -0,35 |
| 42 | 162 | 1,02 | 1,40 | -0,38 |
| 42 | 163 | 1,02 | 1,37 | -0,35 |
| 42 | 164 | 1,02 | 1,41 | -0,39 |
| 43 | 165 | 1,29 | 1,25 | 0,04 |
| 43 | 166 | 1,29 | 1,25 | 0,04 |
| 43 | 167 | 1,29 | 1,28 | 0,01 |
| 43 | 168 | 1,29 | 1,35 | -0,06 |
| 44 | 169 | 1,32 | 1,21 | 0,11 |
| 44 | 170 | 1,32 | 1,14 | 0,18 |
| 44 | 171 | 1,32 | 1,27 | 0,05 |
| 44 | 172 | 1,32 | 1,20 | 0,12 |
| 45 | 173 | 5,55 | 5,94 | -0,39 |
| 45 | 174 | 5,55 | 5,92 | -0,37 |
| 45 | 175 | 5,55 | 5,96 | -0,41 |
| 45 | 176 | 5,55 | 5,87 | -0,32 |
| 45 | 177 | 5,55 | 5,83 | -0,28 |
| 45 | 178 | 5,55 | 5,91 | -0,36 |
| 45 | 179 | 5,55 | 5,84 | -0,29 |
| 46 | 180 | 5,68 | 5,94 | -0,26 |
| 46 | 181 | 5,68 | 6,08 | -0,40 |
| 46 | 182 | 5,68 | 5,98 | -0,30 |
| 46 | 183 | 5,68 | 5,95 | -0,27 |
| 47 | 184 | 1,42 | 1,54 | -0,12 |
| 47 | 185 | 1,42 | 1,27 | 0,16 |
| 47 | 186 | 1,42 | 1,33 | 0,09 |
| 47 | 187 | 1,42 | 1,25 | 0,17 |
| 48 | 188 | 5,37 | 5,64 | -0,27 |
| 48 | 189 | 5,37 | 5,69 | -0,32 |
| 48 | 190 | 5,37 | 5,78 | -0,41 |
| 49 | 191 | 1,59 | 1,42 | 0,17 |
| 49 | 192 | 1,59 | 1,45 | 0,14 |
| 49 | 193 | 1,59 | 1,44 | 0,15 |
| 49 | 194 | 1,59 | 1,42 | 0,17 |
| 50 | 195 | 1,44 | 1,27 | 0,17 |
| 50 | 196 | 1,44 | 1,31 | 0,13 |
| 50 | 197 | 1,44 | 1,31 | 0,13 |
| 50 | 198 | 1,44 | 1,26 | 0,18 |
| 51 | 199 | 1,33 | 1,27 | 0,07 |
| 51 | 200 | 1,33 | 1,24 | 0,09 |
| 51 | 201 | 1,33 | 1,33 | 0,00 |
| 51 | 202 | 1,33 | 1,36 | -0,02 |
| 52 | 203 | 1,47 | 1,40 | 0,08 |
| 52 | 204 | 1,47 | 1,38 | 0,09 |
| 52 | 205 | 1,47 | 1,44 | 0,03 |
| 52 | 206 | 1,47 | 1,36 | 0,11 |
| 53 | 207 | 1,14 | 1,11 | 0,03 |
| 53 | 208 | 1,14 | 1,11 | 0,03 |
| 53 | 209 | 1,14 | 1,10 | 0,04 |
| 53 | 210 | 1,14 | 1,13 | 0,01 |
| 54 | 211 | 1,29 | 1,16 | 0,13 |
| 54 | 212 | 1,29 | 1,11 | 0,18 |
| 54 | 213 | 1,29 | 1,20 | 0,09 |
| 54 | 214 | 1,29 | 1,16 | 0,13 |
| 55 | 215 | 7,61 | 7,35 | 0,26 |
| 55 | 216 | 7,61 | 7,29 | 0,32 |
| 56 | 217 | 3,06 | 2,88 | 0,18 |
| 56 | 218 | 3,06 | 2,84 | 0,22 |
| 56 | 219 | 3,06 | 2,82 | 0,24 |
| 56 | 220 | 3,06 | 2,94 | 0,12 |
| 57 | 221 | 0,42 | 0,71 | -0,29 |
| 57 | 222 | 0,42 | 0,74 | -0,32 |
| 57 | 223 | 0,42 | 0,73 | -0,31 |
| 57 | 224 | 0,42 | 0,70 | -0,28 |
| 58 | 225 | 1,61 | 1,42 | 0,20 |
| 59 | 226 | 0,00 | 0,01 | -0,01 |
| 59 | 227 | 0,00 | 0,03 | -0,03 |
Table A2.
Comparison between actual and predicted spodumene values (% by weight) in the external validation set, obtained from processed FTIR spectra modeled by PLS regression.
Table A2.
Comparison between actual and predicted spodumene values (% by weight) in the external validation set, obtained from processed FTIR spectra modeled by PLS regression.
| Test Set Validation | |||||
|---|---|---|---|---|---|
| Sample | Spectrum | Reference Value | Predicted Value | Difference | |
| 1 | 1 | 9,60 | 4,67 | 4,93 | |
| 2 | 2 | 6,60 | 8,29 | -1,69 | |
| 2 | 3 | 6,60 | 7,36 | -0,76 | |
| 2 | 4 | 6,60 | 7,88 | -1,28 | |
| 2 | 5 | 6,60 | 8,86 | -2,26 | |
| 3 | 6 | 2,70 | 3,63 | -0,93 | |
| 3 | 7 | 2,70 | 3,72 | -1,02 | |
| 3 | 8 | 2,70 | 4,80 | -2,10 | |
| 3 | 9 | 2,70 | 3,05 | -0,35 | |
| 4 | 10 | 11,90 | 14,10 | -2,20 | |
| 4 | 11 | 11,90 | 13,70 | -1,80 | |
| 4 | 12 | 11,90 | 13,69 | -1,79 | |
| 4 | 13 | 11,90 | 14,17 | -2,27 | |
| 5 | 14 | 7,00 | 5,49 | 1,51 | |
| 5 | 15 | 7,00 | 7,13 | -0,13 | |
| 5 | 16 | 7,00 | 6,32 | 0,68 | |
| 5 | 17 | 7,00 | 6,79 | 0,21 | |
| 6 | 18 | 0,00 | 1,76 | -1,76 | |
| 6 | 19 | 0,00 | 1,83 | -1,83 | |
| 7 | 20 | 15,00 | 6,05 | 8,96 | |
| 7 | 21 | 15,00 | 6,54 | 8,46 | |
| 7 | 22 | 15,00 | 10,05 | 4,95 | |
| 8 | 23 | 29,00 | 23,17 | 5,83 | |
| 8 | 24 | 29,00 | 24,00 | 5,00 | |
| 8 | 25 | 29,00 | 25,49 | 3,51 | |
| 8 | 26 | 29,00 | 22,50 | 6,50 | |
| 9 | 27 | 17,30 | 15,72 | 1,58 | |
| 9 | 28 | 17,30 | 14,72 | 2,58 | |
| 9 | 29 | 17,30 | 14,74 | 2,56 | |
| 9 | 30 | 17,30 | 14,52 | 2,78 | |
| 10 | 31 | 17,70 | 15,64 | 2,06 | |
| 10 | 32 | 17,70 | 14,29 | 3,41 | |
| 10 | 33 | 17,70 | 14,57 | 3,13 | |
| 10 | 34 | 17,70 | 15,04 | 2,66 | |
| 11 | 35 | 9,10 | 9,22 | -0,12 | |
| 11 | 36 | 9,10 | 9,92 | -0,82 | |
| 11 | 37 | 9,10 | 10,25 | -1,15 | |
| 11 | 38 | 9,10 | 9,95 | -0,85 | |
| 12 | 39 | 9,40 | 11,17 | -1,77 | |
| 12 | 40 | 9,40 | 10,96 | -1,56 | |
| 12 | 41 | 9,40 | 10,84 | -1,44 | |
| 12 | 42 | 9,40 | 10,11 | -0,71 | |
| 13 | 43 | 12,40 | 13,87 | -1,47 | |
| 13 | 44 | 12,40 | 14,11 | -1,71 | |
| 13 | 45 | 12,40 | 13,52 | -1,12 | |
| 13 | 46 | 12,40 | 13,34 | -0,94 | |
| 14 | 47 | 69,70 | 64,76 | 4,94 | |
| 14 | 48 | 69,70 | 65,92 | 3,78 | |
| 14 | 49 | 69,70 | 65,39 | 4,31 | |
| 14 | 50 | 69,70 | 65,51 | 4,19 | |
| 15 | 51 | 15,26 | 14,10 | 1,16 | |
| 15 | 52 | 15,26 | 14,42 | 0,84 | |
| 15 | 53 | 15,26 | 16,07 | -0,81 | |
| 15 | 54 | 15,26 | 15,37 | -0,11 | |
| 16 | 55 | 13,14 | 14,67 | -1,53 | |
| 16 | 56 | 13,14 | 15,98 | -2,84 | |
| 16 | 57 | 13,14 | 15,14 | -2,00 | |
| 16 | 58 | 13,14 | 13,95 | -0,81 | |
| 17 | 59 | 8,38 | 9,84 | -1,46 | |
| 17 | 60 | 8,38 | 9,30 | -0,92 | |
| 17 | 61 | 8,38 | 8,44 | -0,06 | |
| 17 | 62 | 8,38 | 10,86 | -2,48 | |
| 18 | 63 | 9,92 | 10,44 | -0,52 | |
| 18 | 64 | 9,92 | 11,18 | -1,26 | |
| 18 | 65 | 9,92 | 10,52 | -0,60 | |
| 18 | 66 | 9,92 | 10,56 | -0,64 | |
| 19 | 67 | 9,19 | 10,59 | -1,40 | |
| 19 | 68 | 9,19 | 11,62 | -2,43 | |
| 19 | 69 | 9,19 | 11,50 | -2,31 | |
| 19 | 70 | 9,19 | 9,93 | -0,74 | |
| 20 | 71 | 19,60 | 12,78 | 6,82 | |
| 20 | 72 | 19,60 | 13,66 | 5,94 | |
| 20 | 73 | 19,60 | 16,60 | 3,00 | |
| 21 | 74 | 11,50 | 8,29 | 3,21 | |
| 21 | 75 | 11,50 | 9,01 | 2,49 | |
| 21 | 76 | 11,50 | 7,25 | 4,25 | |
| 21 | 77 | 11,50 | 8,83 | 2,67 | |
| 22 | 78 | 0,70 | 4,89 | -4,19 | |
| 22 | 79 | 0,70 | 5,81 | -5,11 | |
| 22 | 80 | 0,70 | 5,07 | -4,37 | |
| 22 | 81 | 0,70 | 5,76 | -5,06 | |
| 23 | 82 | 72,00 | 76,45 | -4,45 | |
| 23 | 83 | 72,00 | 76,50 | -4,50 | |
| 24 | 84 | 67,00 | 74,76 | -7,76 | |
| 24 | 85 | 67,00 | 74,24 | -7,24 | |
| 24 | 86 | 67,00 | 72,11 | -5,11 | |
| 25 | 87 | 23,00 | 17,82 | 5,18 | |
| 25 | 88 | 23,00 | 18,73 | 4,27 | |
| 25 | 89 | 23,00 | 18,19 | 4,81 | |
| 26 | 90 | 72,00 | 75,62 | -3,62 | |
| 26 | 91 | 72,00 | 76,49 | -4,49 | |
| 27 | 92 | 48,00 | 50,81 | -2,81 | |
| 27 | 93 | 48,00 | 51,22 | -3,22 | |
| 28 | 94 | 89,00 | 91,64 | -2,64 | |
| 28 | 95 | 89,00 | 93,86 | -4,86 | |
| 29 | 96 | 74,00 | 82,68 | -8,68 | |
| 29 | 97 | 74,00 | 83,00 | -9,00 | |
| 30 | 98 | 54,00 | 53,34 | 0,66 | |
| 30 | 99 | 54,00 | 53,28 | 0,72 | |
| 31 | 100 | 78,00 | 77,01 | 0,99 | |
| 31 | 101 | 78,00 | 79,18 | -1,18 | |
| 32 | 102 | 92,00 | 95,64 | -3,64 | |
| 32 | 103 | 92,00 | 96,93 | -4,93 | |
| 33 | 104 | 65,00 | 64,11 | 0,89 | |
| 33 | 105 | 65,00 | 64,23 | 0,77 | |
| 34 | 106 | 84,00 | 77,14 | 6,86 | |
| 34 | 107 | 84,00 | 76,29 | 7,71 | |
| 35 | 108 | 80,00 | 79,37 | 0,63 | |
| 35 | 109 | 80,00 | 77,99 | 2,01 | |
| 36 | 110 | 94,00 | 92,25 | 1,75 | |
| 36 | 111 | 94,00 | 90,29 | 3,71 | |
| 37 | 112 | 51,00 | 52,48 | -1,48 | |
| 37 | 113 | 51,00 | 49,93 | 1,07 | |
| 38 | 114 | 93,00 | 90,29 | 2,71 | |
| 38 | 115 | 93,00 | 89,62 | 3,38 | |
| 39 | 116 | 0,00 | -1,16 | 1,16 | |
| 39 | 117 | 0,00 | 2,86 | -2,86 | |
References
- Sardisco, L.; et al. Multi-Technique Analytical Approach to Quantitative Analysis of Spodumene. Minerals, 2022, 12, 175. [Google Scholar] [CrossRef]
- Vahur, S.; Et al Quantitative mineralogical analysis of clay-containing materials using ATR-FT-IR spectroscopy with PLS method. Analytical and Bioanalytical Chemistry, 2021.
- Guatame-García, A.; Buxton, M. Prediction of Soluble Al2O3 in Calcined Kaolin Using Infrared Spectroscopy and Multivariate Calibration. Minerals, 2018, 8, 136. [Google Scholar] [CrossRef]
- Müller, M. M.; et al. Infrared Attenuated Total Reflectance Spectroscopy: An Innovative Strategy for Analyzing Mineral Components in Energy Relevant Systems. Scientific Reports, 2014, 4, 6764. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; et al. Detection of soil organic matter from laser-induced breakdown spectroscopy (LIBS) and mid-infrared spectroscopy (FTIR-ATR) coupled with multivariate techniques. Geodema, 2019, 355, 113905. [Google Scholar] [CrossRef]
- Zhao, M.; et al. Quantification of calcium in infant formula using laser-induced breakdown spectroscopy (LIBS), Fourier transform mid-infrared (FT-IR) and Raman spectroscopy combined with chemometrics including data fusion. Food Chemistry 2020, 320, 126639. [Google Scholar] [CrossRef] [PubMed]
- RITZ, M.; et al. Determination of Chlorite, Muscovite, Albite and Quartz in Claystones and Clay Shales By Infrared Spectroscopy and Partialleast-Squares Regression. Acta Geodyn. Geomater. 2012, 9, 9–4. [Google Scholar]
- Dehaine, Q.; et al. Geometallurgical Characterisation with Portable FTIR: Application to Sediment-Hosted Cu-Co Ores. Minerals 2022, 12, 15. [Google Scholar] [CrossRef]
- Stacey, P.; Clegg, F.; Sammon, C. Multicomponent Measurement of Respirable Quartz, Kaolinite and Coal Dust using Fourier Transform Infrared Spectroscopy (FTIR): A Comparison Between Partial Least Squares and Principal Component Regressions. Annals of Work Exposures and Health, 2022, 66- 5, pp 644–655.
- Weakley, A.T.; et al. Quantifying silica in filter-deposited mine dusts using infrared spectra and partial least squares regression 2014, Anal Bioanal Chem 406, 4715–4724.
Figure 1.
Spectral region selected for the calibration of the Li₂O prediction model, after preprocessing the FTIR spectra with first derivative and SNV.
Figure 1.
Spectral region selected for the calibration of the Li₂O prediction model, after preprocessing the FTIR spectra with first derivative and SNV.
Figure 2.
Relationship between predicted and observed values for Li₂O content in the external test set: (a) Calibration and (b) Validation.
Figure 2.
Relationship between predicted and observed values for Li₂O content in the external test set: (a) Calibration and (b) Validation.
Figure 3.
Distribution of principal component scores (PC1 vs. PC2) for calibration and test samples in the Li₂O model.
Figure 3.
Distribution of principal component scores (PC1 vs. PC2) for calibration and test samples in the Li₂O model.
Figure 4.
Spectral ranges used for constructing the spodumene prediction model.
Figure 5.
Relationship between predicted and observed values for spodumene content in the external test set: (a) Calibration and (b) Validation.
Figure 5.
Relationship between predicted and observed values for spodumene content in the external test set: (a) Calibration and (b) Validation.
Figure 6.
Principal component scores (PC1 vs. PC2) for the spodumene model, showing overlap between calibration and test sets.
Figure 6.
Principal component scores (PC1 vs. PC2) for the spodumene model, showing overlap between calibration and test sets.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
