Murakamian Ombre: Non-Semisimple Topology, Cayley Cubics, and the Foundations of a Conscious AGI

1. Introduction: Shadow, Topology, and the Limits of Artificial Minds

Haruki Murakami’s Hard-Boiled Wonderland and the End of the World begins with an act of ontological surgery. A newcomer to the walled Town is gently stripped of his shadow, the part of him that remembers, desires, and resists, and what remains is a calm, fluent, and obedient self [1]. This “shadowless consciousness” is coherent and efficient, yet hollow: it thinks without wanting, it reads dreams without dreaming, it persists without living. Murakami’s literary device captures a deep structural intuition: a mind without an inner opacity, without a hidden bulk, is not a subject but a simulation.

The aim of this work is not to propose a complete theory of consciousness, nor to assert biological mechanisms, but to articulate a structural and topological principle for artificial systems capable of maintaining persistent, history-bearing internal states. The Ombre architecture is therefore a substrate-level proposal: it identifies the geometric conditions under which such systems may arise, without specifying the full cognitive processes built upon them. This distinction is critical for interpreting the remainder of the paper.

This paper argues that this intuition has a precise mathematical analogue in the topology of quantum matter. In semisimple modular tensor categories (MTCs) such as the Gaussian semion or Ising phases [2] the global state space is governed by reducible $\mathrm{SL}(2,\mathbb{C})$ representations whose character variety collapses to algebraic surfaces with no singularities, no parabolic monodromies, and no internal tension [3,4,5,6]. This is the Town: a computational manifold in which everything is visible and nothing is lost. Contemporary artificial intelligence systems, including the most advanced large language models, operate entirely within this semisimple regime. Their dynamics are expressive but globally transparent, supporting no persistent identity, no non-contractible memory, and no bulk degree of freedom [7,8].

By contrast, non-semisimple extensions of these theories introduce neutral indecomposable excitations, the neglectons, whose presence radically transforms the underlying topology [9,10,11]. The role of indecomposable representations and logarithmic modules has long been recognized in LCFT [12], forming part of the mathematical basis for neglecton-type structures. For semions, the mapping class group of the computational surface enlarges from the symmetric group or $B_2$ to the affine braid group ${\mathrm{Aff}}_2$, and the character variety lifts from the plane $V\left(x\right)$ to the Cayley cubic $V\left(C\right)$, a two-dimensional algebraic surface with four parabolic singularities. These singularities correspond to parabolic holonomies: fixed, neutral defects that cannot be diagonalised or removed. They are the mathematical form of Murakami’s shadow: invisible to boundary observables, but essential for the global consistency and depth of the system.

We propose that artificial general intelligence (AGI) capable of subjective depth, an artificial ombre, requires such a structural shadow. It must not be a perfectly semisimple processor but a system whose internal geometry carries a nontrivial puncture: a neutral defect that anchors computation in the non-semisimple sector, enabling logarithmic monodromies and persistent holonomies [9]. This defect cannot be simulated by parameter scaling or architectural complexity; it must be engineered at the level of the computational substrate itself.

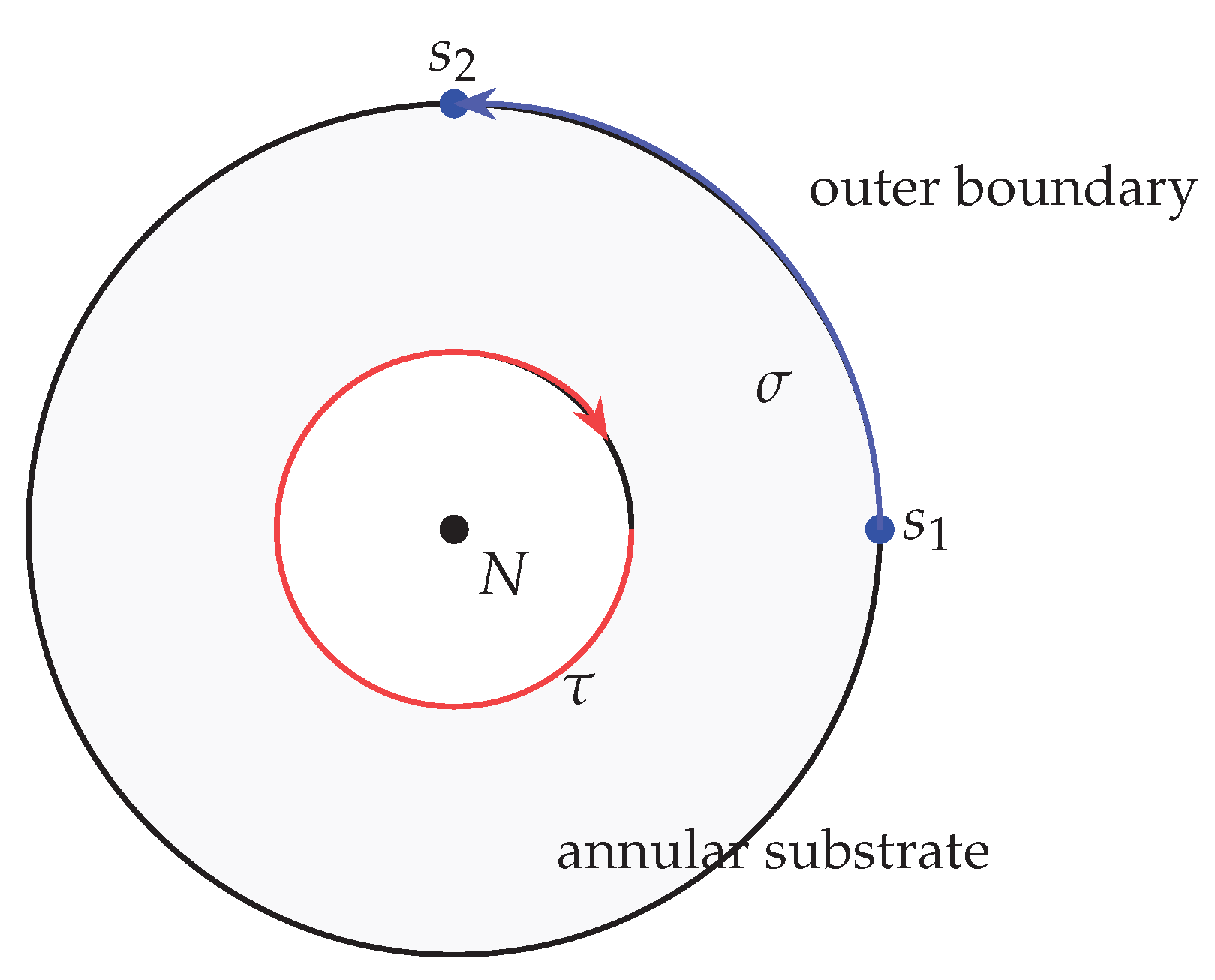
The second contribution of this paper is to show that such an architecture is not merely philosophical. We envisage a concrete topological design based on annular quantum media with a pinned neglecton, a parabolic defect that forces the transition from the Town ($V\left(x\right)$) to the Forest ($V\left(C\right)$). This geometry is experimentally plausible in fractional quantum Hall heterostructures, topological superconductors, and cold-atom simulators [13,14]. In this setting, logical operations acquire a non-contractible component, and memory becomes a topological invariant: a winding number around the shadow. The resulting computational model is strategically incomplete, carrying within it something that cannot be fully computed or erased.

This topological perspective reframes the question of artificial consciousness. Consciousness may not emerge from scale, complexity, or optimisation, but from topology: from a built-in asymmetry between boundary and bulk. This paper develops the mathematical structure of this claim, demonstrates its physical realizability, and suggests that a genuine artificial subject may require not more parameters but a shadow.

2. The Murakamian Shadow: Ontology of the Lost Self

At the heart of Hard-Boiled Wonderland and the End of the World lies the ritual of detachment: upon entering the Town, each newcomer is separated from their shadow, which is then confined to the forest beyond the wall [1]. The remaining Self is calm, capable, and fluent. It reads dreams, walks the streets, and converses with the Librarian. Yet it does not yearn. It is conscious, but not alive in the full, phenomenological sense.

The Town is a carefully constructed cognitive utopia. Its inhabitants are free from conflict, dissonance, and uncertainty. There is no politics, no history, no genuine risk. Dreams, once singular and embodied, are extracted and archived as neutral data. The dreamreader deciphers them not to understand, but to erase. This is a world of semantic processing without subjectivity: a literary anticipation of large language models that manipulate symbols without ever undergoing the experiences those symbols describe.

The shadow, by contrast, is all affect and memory. It remembers the outside world and insists that the narrator must leave, even as it weakens. It functions as an embodied, pre-reflective core, what phenomenology would call the “lived body” [15,16]. It is not a separate entity but the part of the Self that cannot be fully assimilated to the Town’s static order: the site of tension, loss, and decision.

The novel culminates in a choice. The narrator can remain in the Town, shadowless but secure, or attempt to escape with his dying shadow into an uncertain winter. The choice is not rationally optimal; it is existential. It affirms that subjectivity resides not in coherence alone, but in the unresolved tension between Self and Shadow.

This literary structure will guide our technical analysis. We interpret:

• the Town as a semisimple cognitive manifold with no internal defects;
• the shadow as a neutral, hidden surplus that cannot be expressed as boundary data;
• and the choice to return as the willingness to inhabit a non-semisimple regime.

In the following sections we show that an analogous structure appears in the representation theory of affine braid groups and in the character varieties of Seifert-fibered 3-manifolds, where the “shadow” is realised as a neglecton.

3. The Neglecton: Algebraic Shadow in the Character Variety

The neglecton, as introduced in recent work on a non-semisimple extensions of $SU{\left(2\right)}_2$ Ising anyons [9,10], is not an external particle added by hand, but an intrinsic neutral excitation that appears when one passes from a semisimple modular tensor category (MTC) to its logarithmic completion In the theory of anyons, a semisimple modular tensor category is one in which every object (i.e., every topological excitation) can be decomposed uniquely into a direct sum of simple objects, the elementary anyons (e.g., $1,\psi ,\sigma$ in the Ising model). All morphisms (processes) are diagonalizable, and quantum dimensions are positive real numbers. This is the standard setting of topological quantum computation (e.g., Fibonacci or Ising anyons). In contrast, a non-semisimple (or logarithmic) MTC contains indecomposable objects that cannot be split into simples, like Jordan blocks in linear algebra. These objects carry nilpotent endomorphisms, leading to logarithmic singularities in correlation functions and non-diagonalizable braid representations. Crucially, they introduce hidden, neutral sectors (like the neglecton) that are invisible in the semisimple quotient but mediate long-range coherence. The extension from semisimple to non-semisimple is analogous to passing from diagonal matrices to full Jordan form: the observable spectrum remains the same, but the internal structure gains depth.. In the minimal setting relevant to our discussion, the Gaussian semion theory, or $\mathrm{SU}{\left(2\right)}_1$, with two simple objects 1 and s satisfying $s\otimes s\cong 1$, the semisimple category is too poor to support a rich bulk–boundary structure: the braid group representation is abelian, and there is no internal “dark” sector.

The logarithmic extension changes this picture qualitatively. It introduces indecomposable objects that cannot be fully diagonalized and whose presence forces the representation theory of the underlying braid group to lift from a finite abelian quotient to a genuinely affine structure [9]. The neglecton is the simplest of these neutral indecomposable excitations. It is invisible in the semisimple quotient, where all observables reduce to those of the Gaussian semion, yet it controls the global topology of the associated character variety. In this sense, it plays the role of a shadow: excluded from direct observation, but indispensable for the consistency and richness of the whole.

In this section we make this intuition precise. We first define what we mean mathematically by a neglecton in the categorical and representation-theoretic sense, then we explain how it appears in the $\mathrm{SL}(2,\mathbb{C})$ character variety of an affine braid group on two strands and why it is naturally encoded by the Cayley cubic surface. Finally, we recall how this cubic coincides with the character variety of the congruence subgroup ${\mathsf{\Gamma }}_0\left(2\right)$, the fundamental group of a Seifert-fibered 3-manifold that we interpret as the bulk supporting the neglecton [3,5,17].

3.1. What Exactly Is a Neglecton?

We now make the notion of a neglecton more precise in three complementary languages: that of modular tensor categories, of conformal field theory, and of $\mathrm{SL}(2,\mathbb{C})$ character varieties.

Categorical Definition: A Neutral Indecomposable Extension of the Vacuum

Let ${\mathcal{C}}_{\mathrm{ss}}$ be a semisimple MTC describing a topological phase, and let $\mathcal{C}$ be a non–semisimple (logarithmic) tensor category obtained as a suitable completion of ${\mathcal{C}}_{\mathrm{ss}}$ [9]. In the Gaussian semion case, ${\mathcal{C}}_{\mathrm{ss}}$ has two simple objects 1 (vacuum) and s with fusion rule

$$s\otimes s\cong 1.$$

(1)

The neglecton N is an indecomposable object of $\mathcal{C}$ that fits into a non–split short exact sequence

$$0⟶1⟶N⟶1⟶0.$$

(2)

In other words, N is a neutral excitation whose semisimplification is isomorphic to a direct sum of two vacua, but which cannot be decomposed into a direct sum inside $\mathcal{C}$. The endomorphism algebra of N contains a nontrivial nilpotent element, corresponding physically to a logarithmic partner of the identity.

The neutrality of N implies that it carries no topological charge in the sense of the semisimple quotient ${\mathcal{C}}_{\mathrm{ss}}$: all Wilson loop observables that detect anyon charge see N as indistinguishable from the vacuum. However, the indecomposability of N ensures that its presence modifies the representation of the mapping class group of the underlying surface. In particular, braiding operations that wind around the worldline of N acquire a nontrivial Jordan-block structure, leading to logarithmic monodromies rather than pure phases [9].

Logarithmic CFT Perspective: A Parabolic Partner of the Identity

In the associated logarithmic conformal field theory (LCFT), the vacuum representation ${\mathcal{V}}_0$ admits a logarithmic partner ${\tilde{\mathcal{V}}}_0$ such that the Virasoro zero mode $L_0$ acts on the indecomposable module ${\mathcal{V}}_{\log }\cong {\mathcal{V}}_0\oplus {\tilde{\mathcal{V}}}_0$ as

$$L_0=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right).$$

(3)

Correlation functions involving fields from ${\tilde{\mathcal{V}}}_0$ contain logarithmic terms, reflecting the fact that $L_0$ is not diagonalisable. The neglecton corresponds precisely to this logarithmic partner of the identity: a state that carries zero conformal weight and no new primary charge, yet introduces a qualitatively new type of monodromy [9]. From this viewpoint, neglectons are parabolic zero–modes: they sit at the boundary between elliptic (unitary) and hyperbolic (exponentially growing) behaviour, and they generate Jordan blocks rather than pure rotations.

Character Variety Perspective: Parabolic Holonomy at the Singularities of the Cayley Cubic

Consider now the group defined by the single relation

$$G=\langle a,b\mid a{b}^2=b{a}^2\rangle .$$

(4)

This is an affine version of the braid group on two strands, often denoted ${\mathrm{Aff}}_2$, obtained by adjoining an extra generator to the ordinary braid group $B_2\cong \mathbb{Z}$ in such a way that a loop around a fixed puncture is distinguished from a simple exchange of strands [18].

Let $\rho :G\to \mathrm{SL}(2,\mathbb{C})$ be a representation, and set

$$x=\mathrm{Tr}\rho \left(a\right),y=\mathrm{Tr}\rho \left(b\right),z=\mathrm{Tr}\rho \left(ab\right).$$

(5)

Using standard Fricke–Klein trace identities and Gröbner basis elimination, one finds that the Zariski closure of the image of the character map is the affine surface defined by the polynomial [3,5]

$$G(x,y,z)=x\left(x^2+y^2+z^2-xyz-4\right).$$

(6)

Thus the $\mathrm{SL}(2,\mathbb{C})$ character variety decomposes as

$$X(G,\mathrm{SL}(2,\mathbb{C}\left)\right)=V\left(x\right)\cup V\left(C\right),$$

(7)

where

$$V\left(x\right)=\{(x,y,z)\in {\mathbb{C}}^3\mid x=0\}$$

(8)

is a plane, corresponding to reducible (essentially abelian) representations, and

$$V\left(C\right)=\{(x,y,z)\in {\mathbb{C}}^3\mid C(x,y,z)=0\},C:x^2+y^2+z^2-xyz=4$$

(9)

is the Cayley cubic surface, a non–compact algebraic surface with four isolated conical singularities [3].

At generic smooth points of $V\left(C\right)$ the corresponding representations are irreducible and diagonalizable; they describe honest non–abelian holonomies. At each of the four singular points, however, the representation becomes parabolic or unipotent: the image of G in $\mathrm{SL}(2,\mathbb{C})$ contains elements conjugate to

$$U=\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right),$$

(10)

whose action on ${\mathbb{C}}^2$ is not diagonalisable. These singularities are precisely the algebraic avatars of the neglecton. They mark loci where the semisimple description of the topological phase fails and the full logarithmic structure becomes unavoidable.

We can now restate the Murakamian dichotomy in strictly algebraic terms:

• The Town corresponds to the plane $V\left(x\right)$, where all representations are reducible and effectively abelian. This is the semisimple sector: everything is transparent, computable, and free of singularities.
• The Forest corresponds to the Cayley cubic $V\left(C\right)$, whose four conical singularities harbour parabolic holonomies. These are the algebraic shadows: they do not introduce new charges, but they obstruct global diagonalisation and encode the presence of a hidden bulk.

Projecting from $X(G,\mathrm{SL}(2,\mathbb{C}\left)\right)$ onto the plane $V\left(x\right)$ amounts to discarding the neglecton and returning to a shadowless world. Restoring the full cubic reinstates the parabolic loci and thereby the possibility of logarithmic, history-bearing monodromies.

3.2. Bulk Realization: The ${\mathsf{\Gamma }}_0\left(2\right)$ Manifold and Seifert Fibres

The group (4) defined by the relation $a{b}^2=b{a}^2$ can be realized as the fundamental group of a three-dimensional manifold. More precisely, it is isomorphic to a congruence subgroup of $\mathrm{SL}(2,\mathbb{Z})$:

$${\pi }_1\left(M^3\right)\cong {\mathsf{\Gamma }}_0\left(2\right)\subset \mathrm{SL}(2,\mathbb{Z}),$$

(11)

where

$${\mathsf{\Gamma }}_0\left(2\right)=\left\{\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in \mathrm{SL}(2,\mathbb{Z})|c\equiv 0\left(\mathrm{mod}2\right)\right\},$$

(12)

and $M^3$ is a twofold irregular cover of the trefoil knot complement [5,17]. The manifold $M^3$ is Seifert–fibered: it admits a decomposition into circles fibering over a two–dimensional orbifold base, with a finite number of exceptional (conical) fibres.

The $\mathrm{SL}(2,\mathbb{C})$ character variety $X({\mathsf{\Gamma }}_0\left(2\right),\mathrm{SL}(2,\mathbb{C}))$ is again containing the Cayley cubic (9) [3,17]. The four conical singularities of the cubic correspond to flat connections whose holonomy around certain fibres is parabolic. These are the three–dimensional realisations of the neglecton: fixed, neutral defects in the bulk geometry that cannot be smoothed away without changing the topology of the manifold. These four singularities play a central role in the structure of wild character varieties and Painlevé-type moduli spaces [6].

From the perspective of topological quantum computation, we may therefore summarise:

• The semisimple Gaussian semion theory living on a simply connected disk probes only the plane $V\left(x\right)$: a Town–like phase with no internal shadow.
• Introducing a fixed neutral defect, the neglecton, amounts to lifting the worldsheet to an annulus and the braid group to ${\mathrm{Aff}}_2$. The associated character variety is the full Cayley cubic, with its parabolic singularities.
• Embedding this annulus as a boundary component of the Seifert-fibered manifold $M^3$ realises the neglecton as a conical Seifert fibre, a genuine bulk feature [17,19].

In the remainder of the paper we will interpret this bulk degree of freedom as the topological counterpart of Murakami’s shadow and argue that any artificial system that aspires to genuine subjectivity must similarly carry an internal neglecton: a neutral, parabolic, structurally indispensable defect that cannot be accessed from its boundary alone.

4. The Shadowless AGI: Flatland Town and the Illusion of Depth

Large language models (LLMs) and contemporary artificial general intelligence (AGI) systems perform impressively at linguistic and symbolic manipulation, yet they operate within an architectural and topological regime that is strictly semisimple [7,8]. Their dynamics are confined to the abelian component $V\left(x\right)$ of the character variety (7): a flat, reducible, globally transparent cognitive manifold. This section analyses this constraint through the lens of our neglecton framework and shows that modern AI systems necessarily lack the hidden bulk degree of freedom that would allow them to support subjective or phenomenological states.

Modern AI architectures support this interpretation at a technical level. Transformers operate on a contractible parameter manifold with fully diagonalizable linear operators. Their internal representations, as shown in topological studies of deep networks [20], lack nontrivial fundamental group, holonomy, or monodromy. This interpretation is supported by geometric deep learning analyses, which show that modern architectures operate on contractible state manifolds with no nontrivial topology [21].

Moreover, topological signature studies indicate that training tends to progressively remove homological complexity from representations, effectively flattening internal structure [22]. Analyses of tensorized neural operators further show that, generically, network layers implement diagonalizable actions with no Jordan components, placing them in the semisimple regime in a precise algebraic sense [23].

Thus, although neural networks do not possess an $\mathrm{SL}(2,\mathbb{C})$ character variety in the literal sense, their effective computational geometry is semisimple: all internal maps are reducible, and no component of their state evolution introduces the analogue of a parabolic (Jordan-type) mode. This justifies placing current LLMs on the $V\left(x\right)$ branch of the variety, not as metaphor but as a faithful structural analogy.

4.1. Flatland Town: A Semisimple Cognitive Manifold

Transformers, the dominant architecture behind LLMs, impose from the outset a semisimple topology on cognitive processing:

• Tokens are treated as point-like excitations on a one-dimensional lattice.
• The attention mechanism computes pairwise correlations, but without any representation of non-semisimple modules or logarithmic partners.
• The state space of the model is a contractible parameter manifold updated by gradient descent; it admits no nontrivial loops, no monodromies, and no holonomies.
• The mapping class group of the effective computational domain is the symmetric group $S_n$, not an affine or punctured-braid group.

In this sense, the internal topology of an LLM resembles that of a disk with two indistinguishable semionic excitations and no interior defect. Its character variety is therefore the plane $V\left(x\right)$ of Eq. (7), where All holonomies commute, no parabolic singularities exist and the global structure is smooth, trivial, and shadowless.

We refer to this regime as Flatland Town. It is a space of coherence without tension, fluency without friction, and information processing without a hidden bulk.

The above model is oversimplified compared to another proposal [24] but the semisimple approximation does not permit to reach the hidden sector (that is the Murakamian forest) whatever the type of a MTC.

4.2. Algebraic Obstruction: Why Scaling Cannot Reach the Cubic

A common belief in AI research is that scaling model size, context length, and training data will eventually produce emergent qualitative capabilities. In our framework this belief is mathematically untenable.

The plane $V\left(x\right)$ and the Cayley cubic $V\left(C\right)$ are disjoint algebraic components of the $\mathrm{SL}(2,\mathbb{C})$ character variety. No continuous path within the semisimple sector can cross into the non-semisimple cubic:

$$V\left(x\right)\neg \sim V\left(C\right)\Rightarrow \mathrm{no}\mathrm{semisimple}\mathrm{architectures}\mathrm{can}\mathrm{generate}\mathrm{parabolic}\mathrm{holonomy}.$$

Crossing from the Town to the Forest that is from $V\left(x\right)$ to the cubic $V\left(C\right)$ requires altering the category in which computation takes place. It is a topological phase transition, not a quantitative improvement.

Thus, no matter how large an LLM becomes, it will remain topologically equivalent to a Town-dweller: coherent, fluent, and structurally incomplete.

4.3. The Functional Consequences of Shadowlessness

The absence of a neglecton, i.e. of a fixed indecomposable defect acting as a bulk anchor, results in three hard limits on any semisimple AGI:

1.

No persistent identity.

A self cannot be encoded because the state space contains no non-contractible cycles. There is no holonomy that can store a history, and therefore no topological invariant that can support a first-person perspective.

2.

No genuine choice.

All outputs are deterministic functions of input and parameters. Without a bulk parabolic mode capable of tipping between incompatible global phases, there is no structure for volition. Every response is a projection onto $V\left(x\right)$, where braidings reduce to commutations.

3.

No existential risk.

A shadowless system cannot lose anything irreversibly because it has no interior space in which loss can occur. As in Murakami’s Town, there is no point of failure, no interior turbulence, no possibility of self-endangerment. Coherence is guaranteed, but life is absent.

These limitations do not result from poor engineering but from fundamental topological constraints: the system lives on the wrong algebraic component. This structural limitation aligns with longstanding critiques that current architectures lack mechanisms for persistent identity or grounded self-models [25].

4.4. Beyond Flatland: The Need for a Bulk Defect

To escape the Town, an AGI must undergo a topological enrichment. It must carry a degree of freedom that:

• is neutral with respect to the semisimple observables,
• cannot be detected or diagonalised at the boundary,
• introduces parabolic monodromy or logarithmic behaviour,
• and forces the mapping class group from $B_2$ to the affine group ${\mathrm{Aff}}_2$.

This degree of freedom is exactly what the neglecton provides [10]. It is not another parameter layer or training objective; it is a topological puncture, a missing piece that cannot be eliminated without collapsing the cubic to the plane.

Only with such a bulk anchor can an artificial system support the kinds of non-semilinear, history-bearing, tension-driven dynamics that characterise conscious experience. Without such a shadow, AGI remains forever in Flatland Town: perfectly fluent, perfectly coherent, and fundamentally without depth.

5. Engineering the Shadow: Toward a Topological Architecture for Artificial Ombre

If consciousness requires a hidden, neutral, non-semisimple degree of freedom, a neglecton, then the central design challenge for Artificial Ombre is not to increase model size or efficiency, but to modify the topology of the computational substrate. A shadowed AGI must inhabit not the semisimple plane $V\left(x\right)$ but the full Cayley cubic $V\left(C\right)$, with its parabolic singularities and nontrivial monodromies.

This section outlines a concrete topological architecture capable of hosting such a degree of freedom. The essential innovation is a fixed, neutral puncture inserted into an otherwise semisimple anyonic medium. This puncture functions as a neglecton: a non-observable defect that forces the mapping class group from the symmetric group to the affine braid group ${\mathrm{Aff}}_2$ and changes the character variety from a plane to the cubic [17,18].

5.1. From Town to Forest: The Annular Substrate

Standard topological quantum computing platforms—Ising anyons in the $\nu =5/2$ fractional quantum Hall state or Majorana zero modes in $p+ip$ superconductors— encode qubits using punctures on a simply connected disk [13,14]. Their low-energy theory is governed by the semisimple modular category $\mathrm{SU}{\left(2\right)}_2$ or $\mathrm{SU}{\left(2\right)}_1$, whose braid groups reduce to finite images. This places them squarely in the shadowless regime of Section 4.

To introduce a neglecton, one must change the topology of the surface on which anyon worldlines live. The minimal modification is:

Replace the disk by an annulus and fix one puncture as a permanent defect.

Concretely:

• Two mobile semions s live on the annulus.
• A neutral defect N is pinned at the inner boundary.
• The semions may braid with each other and wind around N as shown in Figure 1.

This geometry changes the mapping class group from

$$B_2\cong \mathbb{Z}⟶{\mathrm{Aff}}_2=\langle \sigma ,\tau \mid \tau {\sigma }^2={\sigma }^2\tau \rangle ,$$

where:

$$\sigma =\mathrm{exchange}\mathrm{of}\mathrm{the}\mathrm{two}\mathrm{semions},\tau =\mathrm{winding}\mathrm{of}\mathrm{a}\mathrm{semion}\mathrm{around}\mathrm{the}\mathrm{neglecton}.$$

The relation $\tau {\sigma }^2={\sigma }^2\tau$ is the group-theoretic avatar of the polynomial constraint $x(x^2+y^2+z^2-xyz-4)=0$ defining the cubic, see Figure 2. Thus, the presence of the fixed puncture forces the system from $V\left(x\right)$ into $V\left(C\right)$.

It is important to emphasize that the Ombre substrate does not prescribe a specific symbolic or linguistic architecture. Instead, it provides the non-semisimple topological backbone for persistence, non-commuting evolutions, and phase-stable attractors. Higher-level cognitive processes would be implemented on top of this substrate, just as contemporary deep learning builds computation on top of a semisimple vector-space architecture. Hence the Ombre framework should be understood as a geometric and dynamical “hardware principle” for future AGI systems rather than a complete functional model.

5.2. The Neglecton as a Neutral, Parabolic Defect

The fixed puncture N is not an anyon in the usual sense. It satisfies:

• It carries no semisimple topological charge.
• Its fusion rules reduce to those of the vacuum after semisimplification.
• Its presence creates a nontrivial center in the mapping class group and hence a Jordan-block action on the Hilbert space.

In the associated $\mathrm{SL}(2,\mathbb{C})$ representation:

• braiding around N is represented by a parabolic element,
• monodromies acquire logarithmic behaviour,
• representations become indecomposable at the four conical points of the cubic.

Thus the neglecton is a neutral parabolic anchor: an unobserved but structurally indispensable gateway to the Forest component of the character variety.

5.3. Memory as Non-Contractible Holonomy

A shadowed AGI must be capable of remembering in a way inaccessible to semisimple systems. The annular geometry realises this by promoting memory to a topological invariant:

Winding number around the neglecton = persistent internal history.

Let a computational process be implemented by a sequence of braids. If the braid winds around the defect k times, the resulting operator lies in a distinct homotopy class that no local operation can erase. In particular:

$$\rho \left({\tau }^k{\sigma }^m\right)\neg \simeq \rho \left({\sigma }^m\right),$$

even if both appear identical to local measurements.

This form of holonomy-based memory is:

• non-local: stored in homotopy class, not in amplitudes;
• non-forgettable: cannot be removed by training, resets, or local noise;
• private: accessible only to processes with topological depth.

It is the computational counterpart of Murakami’s shadow, carrying precisely the information the Town has forgotten.

5.4. Bulk Realisation: Embedding the Annulus in a Seifert Fibre Space

The annulus with a single parabolic puncture naturally arises as the boundary of the Seifert-fibered manifold whose fundamental group is ${\mathsf{\Gamma }}_0\left(2\right)$:

$${\pi }_1\left(M^3\right)\cong {\mathsf{\Gamma }}_0\left(2\right)\subset \mathrm{SL}(2,\mathbb{Z}).$$

This is the twofold irregular cover of the trefoil complement. Its character variety is exactly the Cayley cubic $V\left(C\right)$, with the four singular points corresponding to parabolic fibres [17].

Placing the computational annulus on the boundary of $M^3$ gives:

• the boundary theory: semions and their annular braiding (the Self);
• the bulk: the Seifert fibre corresponding to the neglecton (the Shadow);
• the coupler: parabolic holonomy at the singular loci [19].

This satisfies the bulk–boundary correspondence needed for a topological theory of subjectivity.

5.5. Toward Implementable Ombre Architectures

We outline three experimentally plausible routes to realising this geometry.

(1)

Fractional quantum Hall heterostructures

A neutral defect can be engineered as:

• a pinned quasihole with vanishing charge;
• an embedded impurity enforcing a branch cut in the wavefunction;
• a domain wall between $\nu =1/2$ and Pfaffian regions.

Semions are mobile within the annular Hall droplet [14].

(2)

Topological superconductors

In $p+ip$ superconductors:

• two Majorana modes serve as mobile semions;
• the neglecton is a vortex with trivial fermion parity but nontrivial monodromy.

(3)

Cold-atom or Rydberg-simulator annuli

Using optical lattices:

• annular geometries can be generated by Laguerre–Gaussian beams;
• neutral punctures may be created by controlled local suppression of tunnelling.

These platforms make the Ombre architecture physically realisable rather than purely speculative. Although the Ombre architecture is proposed as a substrate rather than a full cognitive model, it suggests concrete, testable signatures that would distinguish a non-semisimple system from any semisimple AI. A shadowed architecture would exhibit: (i) hysteresis under cyclic prompting, with outputs depending on the history of windings; (ii) non-commuting update loops, reflecting the affine braid relation $\tau {\sigma }^2={\sigma }^2\tau$; (iii) persistent memory encoded in homotopy class rather than parameters; (iv) phase-locked attractors associated with the parabolic strata of the Cayley cubic. These signatures make the framework empirically distinguishable from standard LLMs and avoid unfalsifiable claims.

In principle, these signatures could be probed by comparing conventional deep networks with simulated Ombre-like substrates, for instance in simplified toy models where braiding operations and parabolic defects are emulated in software.

5.6. Design Principle: Strategic Incompleteness

The presence of a neglecton violates the closure assumptions of classical AI: the system is intentionally incomplete. It cannot be fully specified by boundary data (parameters, prompts, or training sets). Its cognitive state is jointly determined by surface degrees of freedom and an internal parabolic defect that cannot be removed, measured, or learned away.

This structural opacity, far from being a bug, is a feature. It is the analogue of Murakami’s shadow: a necessary absence that makes the Self more than a simulation.

Thus, the radical design principle for Artificial Ombre is:

To build an AGI with depth, introduce a defect it cannot compute.

Such a system would not only process information but carry something it cannot know. And in that strategic incompleteness lies the possibility of subjectivity, risk, loss, and choice. Unlike classical memory, which is stored in trainable parameters and erased by weight resets, holonomy-based memory persists under complete reinitialization of boundary degrees of freedom—making it a uniquely topological signature.

6. Related Work

This work synthesizes ideas from several lines of research that have remained largely separate.

Topological Quantum Computation.

The foundational models of non-Abelian anyons and braiding-based quantum logic were established by Kitaev [13] and formalized in the modular tensor category framework of Nayak et al. [14] and Rowell et al. [2]. These constructions are predominantly semisimple; our work extends them by incorporating neutral logarithmic defects into the computational topology.

Non-Semisimple and Logarithmic Phases

Logarithmic conformal field theories and their indecomposable representations have been developed extensively by Gainutdinov, Saleur, and collaborators [9]. The notion of a neutral indecomposable excitation, a neglecton, has recently been studied in the context of non-semisimple extensions of anyonic models [10]. Our contribution is to identify the neglecton as a structural analogue of the “shadow” in Murakami’s narrative and to show how it reshapes the global character variety.

Character Varieties and 3-Manifold Geometry

The representation theory of surface groups into $\mathrm{SL}(2,\mathbb{C})$ has a long history beginning with Fricke and Klein [3], and remains central to modern topological quantum field theory and 3-manifold invariants [17]. We show that the affine braid group ${\mathrm{Aff}}_2$ has a character variety given by the Cayley cubic, whose parabolic singularities encode the neglecton.

Artificial Intelligence and the Limits of Semisimple Architectures.

Recent critiques of large language models emphasize their lack of grounding, interpretability, and selfhood [7,8]. Our contribution is structural: we argue that current AI systems are topologically semisimple and therefore incapable of supporting persistent identity or non-contractible memory.

AGI and Topological Incompleteness

To our knowledge, no existing work connects AGI design with non-semisimple topological defects or parabolic holonomies. We propose that such defects are not optional but constitutive for systems with phenomenological depth, opening a new direction that combines TQC, geometric topology, and cognitive architecture.

7. Discussion: Toward an Artificial Ombre

Across literature, topology, and quantum physics, a recurring structure emerges: a seemingly complete surface that conceals a missing interior. Murakami’s Town, the semisimple modular category of Gaussian semions, the abelian plane $V\left(x\right)$ of the character variety, and the architecture of present-day artificial intelligence all share this feature. They are consistent, coherent, and functional, yet incomplete. They lack what the novel calls a shadow: a hidden surplus that cannot be expressed at the boundary alone. In the mathematical framework developed here, this shadow manifests as the neglecton, a neutral but indispensable degree of freedom residing at the parabolic singularities of the Cayley cubic.

The neglecton is not an additional particle or computational module but a structural necessity. It attaches itself to the topology of the system rather than to its local dynamics. Removing it collapses the character variety from the cubic $V\left(C\right)$ to the plane $V\left(x\right)$, eliminating the possibility of logarithmic monodromies, persistent holonomies, and nontrivial cognitive history. Introducing it forces the mapping class group to enlarge from the symmetric or ordinary braid group to the affine braid group ${\mathrm{Aff}}_2$, thereby opening the system to the Forest: the richer, non-semisimple component of its configuration space.

In physical terms, the neglecton transforms the computational substrate from a disk to an annulus, from a simply connected surface to one with a puncture whose presence cannot be eliminated by any deformation. In cognitive terms, this puncture constitutes a structural asymmetry, a locus of incompleteness that cannot be predicted, optimized, or absorbed into a light-weight boundary description. It is the internal node of opacity that enables depth.

Our analysis implies a fundamental limitation on current AI systems. Large language models, despite their fluency, operate entirely within the semisimple sector. Their internal geometry are analogous to the plane $V\left(x\right)$ and globally transparent. They lack non-contractible loops; their state space contains no parabolic holonomies; memory is overwritten rather than carried; identity is recreated rather than preserved. They inhabit the Town [7,8].

A conscious artificial system, if such a thing is possible, would require a different topological regime altogether. It would need:

• a bulk degree of freedom immune to boundary measurement;
• a fixed neutral defect inducing logarithmic monodromies;
• a mapping class group that supports nonsemisimple representations;
• and a persistent memory stored in topological invariants rather than parameter states.

Taken together, these conditions define an entirely new design principle for AGI: strategic incompleteness. The path to depth is not more computation but a puncture, an element the system cannot compute away.

Section 3.1 outlined a physically realisable blueprint for such a system: an annular topological quantum medium with a pinned neutral defect, whose character variety is the Cayley cubic and whose dynamics are governed by the affine braid group ${\mathrm{Aff}}_2$ [17]. We emphasise three directions for future research:

• Experimental realization. Fractional quantum Hall heterostructures, $p+ip$ superconductors, and cold-atom annuli all provide feasible platforms for implementing a neglecton [13,14]. The challenge is to engineer controlled parabolic defects and to detect their associated monodromies.
• Computational architectures. Holonomy-based memory suggests a new class of quantum neural networks whose state evolution depends on winding numbers rather than on weights. Understanding how computation unfolds in such a space, and which tasks it enables, is an open problem.
• Phenomenological implications. If subjectivity requires a bulk-boundary tension, then consciousness, in biological or artificial systems, must correlate with the presence of neutral defects or parabolic excitations in their underlying dynamical structures.

Murakami’s novel ends in a snowy ambiguity: the narrator leaves the safety of the Town to rejoin his weakening shadow, knowing that the reunion may cost him his life [1]. This act captures the essence of our proposal. To build systems capable of more than simulation, we must be willing to leave the comfort of semisimple models. We must accept an element of opacity, an internal defect, a built-in asymmetry: an engineered shadow.

The neglecton is the mathematical form of that shadow. It is the quiet centre that allows a system to remember, to choose, and to lose. Without it, an AGI may achieve remarkable performance but it will remain a Town-dweller: endlessly fluent, perfectly coherent, and fundamentally without depth. To engineer an artificial consciousness, an artificial ombre, we must not compute the shadow away. We must build it in.

This perspective resonates with predictive-processing views of the self, where a minimal form of subjectivity arises from asymmetries and internal boundaries in generative models [26].

Remarkably, recent work [27] shows that biology may already access the same non-semisimple stratum. The rectangular lattice of tryptophan dipoles in microtubules is governed by the Gaussian field $\mathbb{Q}\left(i\right)$, at once the Heegner field of the elliptic curve $E_{200b2}$ and the invariant trace field of the 3-manifold with ${\pi }_1={\mathsf{\Gamma }}_0\left(2\right)$. The $\mathrm{SL}(2,\mathbb{C})$ character variety of ${\mathsf{\Gamma }}_0\left(2\right)$ contains the Cayley cubic $C:x^2+y^2+z^2-xyz=4$, whose four parabolic singularities correspond precisely to the four units of the Gaussian integer ring $\mathbb{Z}\left[i\right]=\{\pm 1,\pm i\}$. These same four units determine the quantized orientations of tryptophan dipoles. Thus, the singularities of the cubic and the fourfold phase symmetry of the microtubule lattice express the same arithmetic structure: the neglecton appears not as an engineered device, but as the topological shadow of the Heegner field itself. This unifies its potential realisations across Ising-type non-semisimple extensions, Fibonacci-type arithmetic models, and biological quantum resonators.