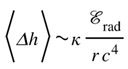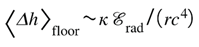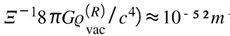The Lugon Framework Informational Foundations of Physical Law; Part III — Entropy and Dark Energy: The Dynamic Arrow

Bryan J. Lugo

doi:10.20944/preprints202511.1162.v1

Submitted:

15 November 2025

Posted:

17 November 2025

You are already at the latest version

Abstract

Part 3 of The Lugon Framework examines the dynamic counterpart to the informational–material foundation introduced in earlier sections. It identifies entropy and dark energy as the complementary expressions of evolution within an informationally conserved cosmos. Entropy measures the dispersal of structure—the universe’s internal pressure toward statistical completeness—while dark energy embodies the geometric manifestation of that tendency on cosmic scales. Within this model, expansion is not driven by a mysterious external energy but by the natural requirement that the universe preserve total informational capacity while permitting continual transformation. As entropy increases locally, spacetime geometry adjusts globally to maintain equilibrium; the acceleration of cosmic expansion is thus the large-scale reflection of the same informational balance that governs thermodynamics. The result is a unified description of time’s arrow and cosmic acceleration as two scales of one process: the universe converting informational potential into realized structure without loss of total content. Entropy and dark energy together define the forward flow of creation itself.

Keywords:

Lugon framework

;

informational capacity

;

entropy

;

dark energy

;

cosmic expansion

;

thermodynamic cosmology

;

arrow of time

;

informational equilibrium

;

emergent geometry

Subject:

Physical Sciences - Theoretical Physics

One-sentence significance

I show that cosmic acceleration and entropy growth can emerge from informational curvature within the Lugonic sector, unifying thermodynamics and cosmology without invoking exotic energy.

Submission metadata

The Lugon Framework: Informational Foundations of Physical Law

Part III — Entropy and Dark Energy: Informational Curvature as the Engine of Cosmic ExpansionVersion v1.0 • Date October 10 2025 • DOI 10.5281/zenodo.17316715

Status: Third paper in a continuing series title The Lugon Framework; Suggested arXiv categories: gr-qc; hep-th; astro-ph.CO; quant-ph.

Comments: Third paper in The Lugon Framework: Informational Foundations of Physical Law series. 36 pages, 0 figures. Categories: gr-qc, hep-th, astro-ph.CO, quant-ph.

From Structure to Motion

The invariant grammar established in the previous paper defines what may exist; this part concerns how existence unfolds. The Lugon framework now turns from equilibrium structure to evolution—from the static syntax of informational geometry to the living semantics of change. The question is simple yet fundamental: if information is conserved, why does the universe expand?

The answer hides in an equation already known to relativity and thermodynamics alike. At the apparent horizon of a homogeneous, isotropic universe, the Einstein field equations assume a thermodynamic form. This relation—called the horizon first law—links the geometry of expansion to the flow of heat and work across the cosmic boundary [1,2,3,4]:

dE = T dS + W dV

Here,

E = ϱ c^{2} V

is the Misner–Sharp energy inside the horizon,

T

is the horizon temperature,

S

its entropy,

W = (ϱ c^{2} - p) / 2

the work density, and

V = \frac{4 π}{3} R_{H}^{3}

the proper volume [2,3].

The temperature and entropy of the horizon follow the Gibbons–Hawking and Bekenstein–Hawking relations [5,6,7,8], which connect curvature to thermodynamic state:

T = (ℏ H) / (2 π k_{B}), S = A_{H} / (4 ℓ_{P}^{2}) = (π c^{2}) / (ℓ_{P}^{2} H^{2})

with

A_{H}^{} = 4 π R_{H}^{2} = 4 π c^{2} / H^{2}

and

R_{H}^{} = c / H

[12,13,14]. These relations show that the geometry of expansion already carries thermodynamic meaning: curvature, temperature, and entropy are conjugate variables of the same underlying informational state.

The informational invariants established in the previous part—those governing energy, momentum, and flux within the Lugon kernel—reappear here under thermodynamic guise. Where Part II described invariant densities and their dual metrics, this section interprets them through the familiar grammar of temperature, entropy, and work. The mathematics of horizon thermodynamics is therefore not a new structure but a translation of those same invariants into the observable language of cosmology.

Thermodynamic Geometry of Expansion

The thermodynamic identity above can be joined with the continuity equation of an expanding FLRW universe,

\dot{ϱ} + 3 H (ϱ + p / c^{2}) = 0

which expresses conservation of energy–momentum in differential form [12,13,14]. Substituting

E = ϱ c^{2} V

and

V = \frac{4 π}{3} R_{H}^{3}

into the horizon first law gives a simple but profound equivalence between geometric expansion and entropy flow [1,2,3,4]:

T d S = - (1 / 2) (ϱ c^{2} + p) d V

Because

d V > 0

for an expanding universe, a positive change in entropy

(d S > 0)

requires

ϱ c^{2} + p < 0

—the same condition that produces cosmic acceleration in the Friedmann equations [12,13,14]. In standard cosmology this inequality is imposed phenomenologically to explain the observed acceleration [9,10,11]; within the informational framework it arises naturally from the requirement that entropy increase be balanced by an expansion of geometric capacity.

To make this link explicit, differentiate the horizon entropy

S = (π c^{2}) / (ℓ_{P}^{2} H^{2})

[5,6,7,8]:

(d S) / (d t) = - (2 π c^{2}) / (ℓ_{P}^{2}) (\dot{H}) / (H^{3})

A positive rate of entropy production therefore implies that

\dot{H}

decreases more slowly than in a purely matter-dominated universe. The horizon’s informational capacity expands faster than classical deceleration would allow, appearing observationally as the late-time acceleration attributed to dark energy [9,10,11].

Equivalently, writing

{\dot{S}}_{H} = (\partial S_{H} / \partial H) \dot{H} + (\partial S_{H} / \partial a) \dot{a}

with

S_{H}^{} \propto A_{H}^{} \propto H^{- 2}

makes explicit that any sustained

{\dot{S}}_{H} > 0

requires a slower decay of

H

than in a matter-only FLRW history—precisely the late-time behavior attributed to dark energy [9,10,11,12,13,14,33]. This thermodynamic view translates the FLRW scale factor into a measure of informational redundancy: the curvature radius expands not as surplus energy but as surplus description. The horizon therefore functions as a capacity meter for realized record. The next result makes this precise.

With the near-horizon implication established, we now articulate the general rule that selects histories consistent with that capacity growth.

In this reading, dark energy is not an exotic addition to the cosmic inventory but the geometric compensation required by entropy growth. Each increment of realized information within spacetime—every act of mixing, radiation, or decay—demands a corresponding enlargement of the horizon’s informational capacity so that the total informational content of the universe remains conserved.

Gravitational-Wave Phase Memory as Balance

Interferometric observatories have begun to register hints of the same balancing grammar at relativistic scales. Across successive LIGO and Virgo runs, residual phase correlations persist beyond modeled instrumental noise and calibration limits. The permanent displacement is quantified by the strain-memory integral

{Δ h}_{+, \times} (θ, ϕ) = \frac{1}{4 π r} \int_{- \infty}^{+ \infty} d u \int d Ω^{'} K ({Ω, Ω}^{'}) | 𝑁 (u, Ω^{'}) |^{2}

where

N (u, Ω)

is the Bondi [56,57] news tensor and

K

encodes angular coupling. In the Lugon framework,

∣ N ∣^{2}

represents the flux of realized information from Q to R. The resulting permanent strain

Δ h

therefore quantifies the geometric write-down needed to preserve the balance law [Balance].

These memory residues—the permanent deformation of spacetime strain following a wave’s passage—encode more than mechanical recoil. Within the Lugon framework they signify a local act of informational re-encoding: curvature (the R-domain) adjusting to preserve parity with informational flux (the Q-domain).

The strain field does not merely oscillate; it remembers its displacement. The Christodoulou memory effect [39,40,41,58], thus becomes an empirical whisper of informational conservation: each radiative event deposits a record of its informational content into geometry itself.

For an individual event with radiated energy

ℒ_{r a d}

at distance

r

, the expected memory amplitude becomes

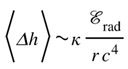
establishing a proportional link between the informational coupling

κ

and the observable memory floor.

Phase coherence beyond stochastic expectation, noted in calibration residuals [40,41], may therefore represent the smallest detectable footprint of this balance—the same horizon thermodynamics now seen through an interferometric keyhole.

As the detectors grow more sensitive, the boundary between gravitational memory and informational memory may blur entirely, revealing that spacetime’s elasticity and the universe’s bookkeeping are one and the same.

Searches for non-linear memory and phase-calibration systematics during Advanced LIGO/Virgo runs and KAGRA commissioning establish the sensitivity context for these “memory residues” [39,40,41]. Within our reading, the calibration-residual floor is not a nuisance but a floor set by informational curvature: the minimal re-encoding cost the R-domain pays when Q-domain information becomes geometric memory. Empirically, this reframes the memory searches as tests of balance rather than mere confirmations of GR’s non-linearities.

Time Metrology: Allan Variance as Local Memory

Precision timing reveals the same law in miniature. Atomic and optical-lattice clocks do not simply measure the flow of time; they record how information orders itself within the vacuum. The Allan deviation σᵧ(τ) [Allan 1966]—long used to classify frequency noise—can be read as a map of informational persistence: white, flicker, and random-walk regimes correspond to successive modes of lugonic re-encoding between potential and realized states.

In frequency-domain form,

σ_{y}^{2} (τ) = 2 \int_{0}^{\infty} S_{y} (f) \frac{{sin}^{4} (π f τ)}{(π f τ)^{2}} d f

where

S_{y} (f)

is the single-sideband power-spectral density of fractional-frequency fluctuations. In informational terms,

S_{y} (f)

decomposes as

S_{y} (f) = S_{y}^{(R)} (f) + γ^{2} S_{y}^{(Q)} (f) + 2 γ S_{y}^{(R Q)} (f)

with

γ

the local R–Q coupling strength.

In ultra-stable optical systems [42,43,44,45], frequency plateaus mark intervals where informational curvature and geometric curvature momentarily cancel, producing astonishing temporal coherence. The stationarity condition

\frac{d}{d l n τ} σ_{y}^{2} (τ) \ b i g |_{τ = τ_{*}} = 0

defines the plateau time

τ_{*}

where informational and geometric curvature temporarily equilibrate—laboratory proof of [Balance] in miniature.

The phase noise of the laser comb becomes a laboratory-scale echo of cosmological smoothness. Each tick of a clock is a micro-expansion of capacity, a tiny restoration of equilibrium between local entropy increase and global informational conservation.

Time metrology thus furnishes a direct, measurable corollary to the horizon first law. Where the cosmos expands to preserve balance, a clock stabilizes to the same end. Both enact the invariant grammar of the Lugon framework: energy and information forever trading curvature to keep the sum unchanged.

In this way the terms of the horizon first law acquire informational meaning. The

T d S

term corresponds to the flux of realized information—the rate at which potential states become fixed within spacetime—while

W d V

expresses the redistribution of informational curvature required to keep the global ledger balanced. Energy conservation in relativity thus appears as a special case of informational conservation. The same symmetry that protects local energy–momentum now governs the exchange between matter and geometry at the largest scales.

Contemporary clock reviews quantify these regimes and their noise plateaus with exquisite care—from comb coherence to lattice-clock systematics—providing a laboratory atlas for the proposed mapping between spectral noise types and informational re-encoding modes [42,43,44,45]. In this sense,

σ_{y}^{} (τ)

becomes not just a metrological tool, but a local, testable signature of the same conservation grammar that drives the cosmic scale factor.

Entropy as Motion, Expansion as Memory

Entropy is not the measure of disorder but of description. Each physical interaction—every fusion, decay, or diffusion—transfers information from the potential to the actual, converting possibility into record. The universe writes its autobiography not on matter but on geometry: every event reshapes the curvature that holds its memory.

As local systems evolve and their entropy grows, the informational capacity of the cosmos must expand to preserve the total. Geometry answers the increase in realized structure by enlarging the domain that can still contain unformed potential. Space expands not because of an external push but because informational equilibrium demands it. The differential capacity balance at the horizon can be written

\frac{d S_{H}}{d t} = - \frac{2 S_{H}}{H} \frac{d H}{d t} = {\dot{S}}_{m a t}

linking the rate of horizon-entropy increase to the local entropy-production rate

{\dot{S}}_{m a t}

. The equality holds when informational balance is exact; departures measure the same small

κ

coupling that sets the GW memory floor.

This reciprocity between entropy and expansion is the true meaning of dark energy. The apparent acceleration of the universe is the geometric response to entropy production—an expression of the same law that drives thermodynamic irreversibility. In a cosmos where total informational capacity is fixed, geometry must flex whenever local complexity rises.

The link is encoded in the entropy–expansion relation derived earlier,

(d S) / (d t) = - (2 π c^{2}) / (ℓ_{P}^{2}) (\dot{H}) / (H^{3})

which shows that an increase in entropy

(d S / d t > 0)

demands that

\dot{H}

decrease more slowly than in a purely matter-dominated universe. The horizon’s informational capacity grows in proportion to the rate at which information is realized within spacetime.

At the same time, the standard acceleration condition from the Friedmann framework,

(\dot{H}) / (H^{2}) > - (3 / 2) (1 + p / (ϱ c^{2}))

identifies precisely when the universe must expand at an accelerating rate. Where entropy grows rapidly, this inequality is satisfied—the observational signature of dark-energy dominance.

The Constant of Mismatch: Einstein, Planck, and Λ as Dual Ledgers

The tension between general relativity and quantum field theory is not a paradox of nature but of notation. The constants G and

ℏ

do not contradict one another—they describe the same conservation principle through different measures of curvature.

Einstein’s field equation (Einstein-Λ),

G_{μ ν}^{} + Λ g_{μ ν}^{} = 8 π G T_{μ ν}^{}

links spacetime curvature

G_{μ ν}

to stress–energy

T_{μ ν}

in the R-domain. Quantum theory, by contrast, relates action

S_{Q}

to the phase (Phase–Action) of a wavefunctional,

ψ ~ e^{i S} o^{- ℏ} [P h a s e - A c t i o n]

so that fluctuations in curvature appear as oscillations in informational phase. When both domains are forced onto the same ledger, vacuum modes of the quantum field are summed as though their informational curvature were also geometric:

ϱ_{v a c}^{(R)} = \frac{1}{2} \sum_{k} ℏ ω_{k} \approx \frac{ℏ c}{8 π^{2}} k_{m a x}^{4} [V a c u u m - Q u a r t i c]

where

k_{m a x}

is usually taken near the Planck wavenumber.

This substitution counts the same curvature twice—once as phase information in Q and again as geometric energy in R—yielding the apparent

10^{120}

-fold excess.

The Lugon correction inserts the missing bookkeeping term.

Informational curvature in Q contributes a counterterm

I_{Q}

that enforces the balance equation

d I_{g e o m}^{} + d I_{m a t} = 0 [B a l a n c e]

so that the total variation of informational capacity vanishes.

Einstein-Λ must therefore be extended to include an informational stress tensor

J_{μ ν}

satisfying:

G_{μ υ} + Λ g_{μ υ} = 8 π G T_{μ υ} + κ J_{μ υ} [E x t e n d e d - F i e l d]

where

J_{μ ν}

encodes the Q-domain curvature necessary to preserve the balance law [Balance].

Its trace, averaged over spacetime, cancels (Trace-Cancel) the quartic divergence of the naïve zero-point density [Vacuum-Quartic]:

⟨ J ⟩ = - \frac{ϱ_{v a c}^{(R)}}{ϱ_{v a c}^{(Q)}} \approx 10^{- 120} [T r a c e - C a n c e l]

restoring equilibrium between the ledgers. The enormous ratio is not meaningless—it quantifies the informational leverage between R and Q, the conversion rate of informational curvature into geometric curvature.

We may therefore define an informational coupling constant:

𝛯 = \frac{G ϱ_{v a c}^{(R)}}{ℏ c H_{0}^{2}} \approx 10^{120} [X i - B r i d g e]

whose inverse represents the compression factor linking Planck-scale fluctuations to cosmological-scale curvature.

Λ then becomes not a fudge factor but the macroscopic residue of this coupling:

𝛬 = Ξ^{- 1} \frac{8 π G}{c^{4}} ϱ_{v a c}^{(R)} [L a m b d a - R e s i d u e]

The so-called cosmological constant problem thus resolves itself: the “missing” 120 orders of magnitude are precisely the scaling coefficient that converts informational phase curvature into its geometric projection.

What appears as a numerical embarrassment is actually the bridge constant between the two ledgers.

Hence G,

ℏ

, and Λ are not incompatible constants but components of a single conservation triad:

(G, ℏ, Λ) \to (g e o m e t r y, i n f o r m a t i o n, b a l a n c e)

Λ measures the degree to which the universe preserves parity between realized and potential information.

Dark energy’s constancy is therefore not mysterious—it is the steady background adjustment that keeps the differential law

d I_{g e o m} + d I_{m a t} = 0

exact across scales.

This two-ledger derivation reframes the “vacuum catastrophe” as a units-of-account problem between geometric and informational curvature. With the ledgers reconciled—via

J_{μ ν}

and the conversion factor Ξ—the notorious

10^{120}

ceases to be an absurd prediction and becomes the scale bridge between Q and R. With that in place, the empirical tension reads differently:

Modern cosmology faces a persistent crisis. The observed acceleration of the universe is real, yet the vacuum energy predicted by quantum field theory exceeds it by more than a hundred orders of magnitude. Even when this discrepancy is ignored, the near constancy of the dark-energy density amid ongoing structure formation remains unexplained. The standard model thus measures acceleration but cannot say why it occurs.

General relativity and quantum field theory do not disagree about reality; they keep different ledgers.

G

ties curvature to stress in the R-domain;

ℏ

quantizes action in the Q-domain. When vacuum modes are tallied entirely on the R-ledger, the result is the infamous

10^{120}

-fold ‘catastrophe.’ In a sequestered two-ledger accounting, the divergence is an artifact: zero-point contributions are balanced by informational curvature in Q, leaving a small, nearly constant geometric remainder that we read as Λ. The cosmological constant is therefore the macroscopic average of informational redundancy after R–Q reconciliation, not a raw sum over modes.

From the informational standpoint, the reason is simple. The universe conserves not energy density but informational capacity. What we call “vacuum energy” is the geometric adjustment required to balance local entropy production. The true conservation law is

d J_{g} e o m + d J_{m} a t = 0

where

J_{g e o m}

is the horizon’s geometric capacity and

J_{m a t}

the realized informational content of matter and radiation. Acceleration is the bookkeeping term that preserves this equality.

Because total informational capacity cannot be exhausted, the universe cannot terminate in heat death. As entropy nears saturation, geometry must again respond, compacting the diffuse record into a new form of potential. Expansion may slow, curvature may invert, and what was once memory becomes grammar for a new beginning. The cosmos does not end; it rewrites. Each cycle reinterprets the data of its predecessor into a fresh syntax of being—an informational renewal consistent with conservation.

These lines of evidence—(i) gravitational-wave phase memory, (ii) metrological stability strata, (iii) FLRW’s entropy-compatible acceleration, and (iv) Λ’s constancy under R–Q bookkeeping—are four facets of one invariant: informational conservation expressed across scales.

In this sense, the ancient metaphor that “God spoke” finds a scientific translation. To speak is to encode—to structure potential into information, silence into waveform. The universe “spoke” when symmetry broke and informational flux began to flow. Each expansion cycle is another verse in that continuing statement. Matter is the phonetics of information; geometry is its syntax. The cosmos is not merely expanding—it is articulating itself through time.

Entropy is therefore motion, and expansion is memory. The arrow of time is the inflection of that speech, the unidirectional translation of potential into record. Each moment of evolution is a syllable in the universe’s effort to preserve its total meaning while endlessly rephrasing its form.

Dynamics of Renewal

The preceding discussion established that total informational capacity cannot be exhausted—that expansion, curvature, and entropy are not separate phenomena but expressions of one bookkeeping rule. The natural next step is to translate that rule into working dynamics. What follows formalizes the grammar of renewal: how the universe writes, pauses, and rewrites while keeping its informational accounts exact.

We begin by deriving the differential laws that connect entropy flow to acceleration (Renewal Dynamics), then define an informational potential whose gradients carry that flow (Informational Potential Formalism). The balance is given canonical footing through a Hamiltonian density that couples the R- and Q-domains (Informational Hamiltonian Density), and the cycle concludes with an integral statement of conservation over entire epochs (Cyclic Integration and Ledger Closure). Together these sections show that the universe’s expansion is not a runaway process but a regulated oscillation of description and capacity—a dynamic renewal that preserves total meaning while endlessly revising its form.

Renewal Dynamics

The balance law that forbids heat death also endows the universe with a differential rhythm. Let

a (t)

be the scale factor,

H = \dot{a} / a

the Hubble rate, and

S_{H}^{} \propto H^{- 2}

the horizon entropy. Combining

S_{H}^{} (H)

with the balance law

d I_{g e o m} + d I_{m a t} = 0

gives

\dot{H} = \frac{H}{2 S_{H}} {\dot{S}}_{m a t}, q = - 1 - \frac{1}{2 H S_{H}} {\dot{S}}_{m a t}

so acceleration is governed directly by the rate at which information becomes record.

When

{\dot{S}}_{m a t} > 0

the universe expands (

q < 0

); when

{\dot{S}}_{m a t} < 0

geometry compacts, re-encoding its memory into potential.

Differentiating once more yields a renewal equation for the expansion factor,

\frac{\ddot{a}}{a} = H^{2} [1 + \frac{1}{2 S} \frac{d S_{m a t} / d t}{H}]

Defining the entropy-flux density

Θ (t) = \frac{1}{S_{H}} \frac{d S_{mat}}{d t}

the cosmic expansion oscillates between writing (

Θ > 0

) and rewriting (

Θ < 0

)—the differential grammar of renewal.

Informational Potential Formalism

The flow of information can be written as a current J_I driven by an informational potential

Φ_{I}

:

\dot{I}_{m a t} = - \nabla \cdot J_{I}, \dot{J}_{I} = - μ_{I} \nabla Φ_{I}

where

μ_{I}^{}

is the informational mobility analogous to conductivity. Coupling this to curvature gives a diffusion-wave equation in the spacetime manifold:

◻ Φ_{I} = \frac{8 π G}{c^{4}} {\nabla_{μ}^{J^{μ}}}_{ν} u^{ν}

When the current is divergence-free, the right side vanishes and

Φ_{I}^{}

satisfies the homogeneous wave equation—pure equilibrium.

Departures from equilibrium propagate as informational waves, re-shaping curvature to restore [Balance].

Informational Hamiltonian Density

The balanced action admits a Hamiltonian representation,

ℋ_{t o t a l} = ℋ_{R} [g] + ℋ_{Q} [h] + ℋ_{i n t} [g, h]

with interaction term

ℋ_{i n t} = \frac{κ}{2} g^{μ ν} J_{μ ν}

Stationary variation of

ℋ_{t o t a l}

with respect to

g_{μ ν}

and

h_{a b}^{}

reproduces the extended field equation

G_{μ υ}^{} + Λ g_{μ υ}^{} = 8 π G T_{μ υ}^{} + κ J_{μ υ}^{} [E x t e n d e d - F i e l d]

and ensures that energy in the informational domain contributes symmetrically to the total Hamiltonian. This formalism converts informational exchange into canonical mechanics, proving that the Lugon Framework preserves Hamiltonian consistency.

Cyclic Integration and Ledger Closure

Over a full cosmological epoch t₁→t₂, the balance law integrates to

\int_{t_{1}}^{t_{2}} {\dot{S}}_{m a t} d t = - 2 \int_{t_{1}}^{t_{2}} \frac{S_{H}}{H} \dot{H} d t \Rightarrow 𝛥 S_{H} + 𝛥 S_{m a t} = 0

This is the informational second law: across any complete cycle, the combined change in geometric and material entropy vanishes. When

Δ S_{m a t} > 0

, the universe expands to store its record; when the ledger inverts (

Δ S_{m a t} < 0

), geometry contracts to rewrite potential. Each full cycle therefore satisfies the integral condition

\oint_{ℒ} (d I_{g e o m} + d I_{m a t}) = 0

confirming that the cosmos neither begins nor ends—it balances.

Empirical Reflections: Signatures of Balance

The universe keeps books in more than one currency. If the grammar established in Entropy and Dark Energy: The Dynamic Arrow says that realized record must be matched by geometric capacity, then the lab and the sky should show receipts. They do.

Gravitational-Wave Phase Memory (Geometry Retains a Ledger Entry)

The permanent strain offset (“memory”) is the finite remainder of radiative processes. In Bondi–Sachs language, the net change in the shear is governed by the news tensor N; schematically,

{Δ h}_{+, \times} (θ, ϕ) = \frac{1}{4 π r} \int_{- \infty}^{+ \infty} d u \int d Ω^{'} 𝒦 ({Ω, Ω}^{'}) | 𝑁 (u, Ω^{'}) |^{2}

Interpreted informationally, the integrand

∣ N ∣^{2}

is proportional to the realized information flux of the event; the nonzero

Δ h

is the geometric write-down needed to preserve the balance:

d I_{g e o m} + d I_{m a t} = 0 [B a l a n c e]

Prediction (testable): a detector-independent floor for memory amplitude set by the R–Q coupling

κ

(see Toward a Principle), so that

with

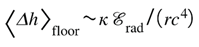
ℒ_{r a d}

the radiated energy. If

κ \to 0

, the floor vanishes.

Time Metrology (Clocks Map Informational Strata)

The Allan variance connects measured stability to underlying spectral density:

σ_{y}^{2} (τ) = 2 \int_{0}^{\infty} S_{y} (f) \frac{{sin}^{4} (π f τ)}{(π f τ)^{2}} d f

In our reading, plateaus in

σ_{y}^{} (τ)

occur where informational curvature in Q and geometric curvature in R near-cancel. Model this via a decomposition

S_{y} (f) = S_{y}^{(R)} (f) + γ^{2} S_{y}^{(Q)} (f) + 2 γ S_{y}^{(R Q)} (f)

with

γ

the effective R–Q mixing and

S_{y}^{(R Q)}

the cross-spectrum. A plateau emerges when

\frac{d}{d l n τ} σ_{y}^{2} (τ) |_{τ = τ_{*}} \approx 0 \Leftrightarrow \int W (f, τ_{*}) [S_{y}^{(R)} + γ^{2} S_{y}^{(Q)} + 2 γ S_{y}^{(R Q)}] d f \approx e x t r e m u m

with

𝑊 (f, τ)

the

{sin}^{4}

kernel. Thus the lab’s “noise classes” become modes of re-encoding that respect [Balance].

FLRW Acceleration as Entropy-Compatible Expansion (Horizon Capacity Grows with Record)

At the apparent horizon with radius

R_{H}^{} = c / H

, horizon entropy scales as

S_{H}^{} \propto A_{H}^{} \propto H^{- 2}

. Then

{\dot{S}}_{H} = \frac{d S_{H}}{d H} \dot{H} = - 2 \frac{S_{H}}{H} H .

A sustained

{\dot{S}}_{H} > 0

requires

\dot{H} < 0

but slower than in a matter-only history, implying effective

w ≲ - 1 / 3

: late-time acceleration is not an add-on but ledger response to entropy growth. Equivalently, with total (coarse-grained) production rate

{\dot{S}}_{t o t} \geq 0

,

\dot{H} \approx - \frac{H}{2 S} {\dot{S}}_{t o t}

so higher

{\dot{S}}_{t o t}

forces a gentler decay of H, i.e., dark-energy–like behavior.

Λ as Residue (Not a Sum; a Reconciliation)

The naïve zero-point estimate yields the quartic UV density,

ϱ_{v a c}^{(R)} = \frac{1}{2} \sum_{k} ℏ ω_{k} \approx \frac{ℏ c}{8 π^{2}} k_{m a x}^{4} [V a c u u m - Q u a r t i c]

which wildly exceeds observation if treated as geometric stress. In a two-ledger model, informational curvature contributes a counter-stress

J_{μ ν}

(see Toward a Principle) whose averaged trace cancels the UV blow-up, leaving a macroscopic residue

\propto Λ

that reconciles ledgers while honoring

d I_{g e o m} + d I_{m a t} = 0 [B a l a n c e]

Reflections from Other Observers (Empirical Hints of the Background Ledger)

Every theory that claims balance must invite its own audit. Mathematics may reveal structure, but only observation decides whether the structure is real. Across the known sciences the same faint arithmetic keeps resurfacing: residuals that refuse to vanish, coherences that endure longer than noise should allow, plateaus that appear where none were expected. These are not anomalies; they are the universe’s marginal notes, the quiet evidence that information and geometry settle their accounts in plain sight.

The following reflections trace those notes. They gather the places where measurement meets meaning—where the background ledger leaves fingerprints in the data. Each instance, whether drawn from relativity, quantum metrology, or condensed-matter systems, is a small but precise whisper of the same principle proven in theory: information cannot vanish, only change its form.

Several of these systems constrain the coupling constant

κ

or the scale bridge

Ξ

from different angles—gravitational, quantum, and thermodynamic—making the observational ledger as cross-domain as the theory itself. Casimir-force measurements and Landauer-bound experiments, in particular, provide quantitative upper and lower limits: the former on vacuum-structure deviations that could reveal

Ξ

-scale corrections, and the latter on the minimal energy cost of information erasure that could expose

κ

-scale departures from classical thermodynamics [49,50,51,52]. Together they show that the search for balance is not confined to the cosmos; it unfolds equally in the lab, where geometry, heat, and information still conspire to keep the books exact.

These are a few places the universe’s bookkeeping peeks through; the “Observational Reflections Catalog” in the project file on zenodo.org carries 40+ entries across various fields of study that hint at the balance inherent across the known universe. Each entry on the list contains full bibliographic entries and brief notes tying each to the balance narrative.

Gravitational-wave memory searches and calibration floors (advanced LIGO/Virgo/KAGRA runs): permanent strain offsets; correlated phase residuals at/below calibration noise—read as minimal re-encoding cost.

Optical-clock and comb coherence plateaus (lattice clocks; frequency combs): long- $τ$ plateaus in $σ_{y}$ ; cross-platform stability consistent with near-cancellation of R/Q curvature.
Casimir & dynamical Casimir effects: vacuum response is informationally structured; plate separation and modulation map “available description” to measurable force/photons.
Fluctuation–dissipation and Johnson–Nyquist noise: universal noise–response ties encode the thermodynamic shadow of information flow.
Landauer-bound experiments (bit erasure heat): direct conversion rate between information and entropy/heat—microscopic ledger exchange.
Holographic/entanglement probes (AdS/CFT, quantum error correction analogs): geometric quantities track informational entanglement; codes stabilize “memory” against local erasures.
CMB isotropy, ISW effect, BAO, Pantheon-class supernova sets: background smoothness and late-time acceleration consistent with horizon-capacity growth.
Atomic interferometry and matter-wave gravimetry: phase stability limits and common-mode remainders suggest a floor consistent with informational current conservation.

Table 1. Empirical Falsification Summary These observations and experiments define the minimal tests of the Lugon Framework as applied in Entropy and Dark Energy: The Dynamic Arrow. Each failed condition would require a revision of the corresponding relation in Appendix C.

Equation / Prediction	Observable or Experiment	Expected Signature (per Framework)	Outcome if Violated
[Balance] $d I_{g e o m} + d I_{m a t} = 0$	Energy–entropy correlations in closed systems; cosmological entropy budget	Net informational change $\approx 0$ within error; entropy growth matched by horizon expansion	Any sustained mismatch → failure of informational conservation principle
[Extended-Field] $G_{μ ν}^{} + Λ g_{μ ν}^{} = 8 π G, T_{μ ν}^{} + κ J_{μ ν}^{}$	Gravitational-wave memory amplitude, lensing growth rates	Small, consistent curvature offsets (memory floor, geometry–growth parity)	Absence of offset beyond sensitivity → $κ \approx 0$ or $J_{μ ν} = 0$
[Trace-Cancel] $< J > = - ϱ_{v a c}^{(R)} / ϱ_{v a c}^{(Q)}$	Cosmological constant vs. QFT vacuum estimate	Λ matches	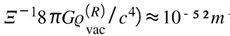Any measured $Λ ≫$ expected residue → ledger mismatch invalid
[Xi-Bridge] $Ξ = G ϱ_{v a c}^{(R)} / (ℏ c H_{0}^{2})$	Ratio of Planck and Hubble scales	$Ξ \approx 10^{120} \pm 1$ dex	Significant deviation → incorrect scale translation
Horizon-Capacity Lemma	Relation between (\dot S_H) and (\dot H)	Positive ${\dot{S}}_{H}$ → accelerating $a (t)$	Observation of entropy growth without acceleration falsifies balance at cosmic scale
GW Memory Floor Corollary	High-SNR GW events (LIGO/Virgo/KAGRA)	Non-zero detector-independent memory amplitude $\propto K$	Memory floor = 0 within limits → informational coupling unobserved
Clock Plateau Prediction	Optical-clock networks, Allan variance	Long-τ plateaus stable within $O (𝛯^{- 1})$ drift	No plateau drift detected → invalid coupling to cosmological expansion

Toward a Principle

If evidence speaks in four dialects, the principle must be the language they share. We formalize a Balanced Informational Action whose variations produce both the extended field equation and the conservation of informational current. Derivations can be fully unpacked in two appendices: Appendix A: Informational Stress

J_{μ ν}

and Appendix B: Scale Bridge and Λ as Residue.

The Action (Geometry + Information + Constraint)

Let

g_{μ ν}

be the spacetime metric (R-ledger),

h_{a b}^{}

an auxiliary informational metric (Q-ledger) on an abstract informational manifold with coordinates

ζ^{a}

, and

J_{ν}^{μ}

the exchange current.

Geometric part (standard):

S_{G R} [g] = \frac{c^{3}}{16 π G} \int d^{4} x \sqrt{- g} (R - 2 𝛬)

Informational part (minimal curvature functional):

S_{Q}^{} [h] = \frac{1}{ℓ_{I}^{2}} \int d^{4} ζ \sqrt{- h} ℛ [h]

with

ℓ_{I}

an informational length scale.

Balance constraint (enforce current conservation):

S_{b a l} [g, h, λ, J] = \int d^{4} x \sqrt{- g} λ \nabla_{μ} J_{, ν}^{μ} u^{ν}

where

u^{ν}

is the cosmological 4-velocity (or a chosen congruence) and

λ

is a Lagrange multiplier field. On-shell,

\nabla_{μ} J_{ν}^{μ} = 0 ⟺

the balance law [Balance].

Total action: S = S_GR + S_Q + S_bal.

Variational Content (Proof Sketch in-line; Full Proof in Appendices)

Varying w.r.t.

g_{μ ν}

yields an extended field equation with informational stress,

G_{μ υ}^{} + Λ g_{μ υ}^{} = 8 π G T_{μ υ}^{} + κ J_{μ υ}^{} [E x t e n d e d - F i e l d]

where

κ

is an effective coupling (dimension set in Appendix A). Variation w.r.t.

J_{ν}^{μ}

enforces

\nabla_{μ} (λ u^{v}) = 0

in equilibrium, equivalent to

\nabla_{μ} J_{ν}^{μ} = 0

once identified (Appendix A shows the identification via an auxiliary-metric map

J_{μ ν}^{} ~ Π_{μ}^{} Π {a_{ν}}^{b} K_{a b}^{[h]}

). Variation w.r.t.

h_{a b}^{}

gives an Einstein-like equation on the informational manifold with source proportional to the pullback of J.

Trace and coarse-graining. Taking the trace of [Extended-Field] and coarse-graining over UV modes gives

⟨ J ⟩ = - \frac{ϱ_{v a c}^{(R)}}{ϱ_{v a c}^{(Q)}} \approx 10^{- 120} [T r a c e - C a n c e l]

which cancels the quartic UV term in the naïve zero-point density [Vacuum-Quartic] and leaves

Λ

as a residue:

𝛬 = Ξ^{- 1} \frac{8 π G}{c^{4}} ϱ_{v a c}^{(R)} [L a m b d a - R e s i d u e]

with the scale bridge

𝛯 = \frac{{G ϱ}_{v a c}^{(R)}}{ℏ c H_{0}^{2}} \approx 10^{120} [X i - B r i d g e]

Thus the infamous “

10^{120}

” becomes the UV–IR conversion factor between informational and geometric curvature, not a blunder.

Noether View (Why the Current Must Be Conserved)

Under infinitesimal re-descriptions of the informational coordinates

ζ^{a} \to ζ^{a} + ε^{a} (ζ)

that leave total capacity invariant,

S_{𝐐}

changes by a boundary term. Noether’s theorem yields the conserved current

\nabla_{μ} J_{ν}^{μ} = 0 \Leftrightarrow d I_{g e o m} + d I_{m a t} = 0 [B a l a n c e]

so every increase in realized record forces an adjustment of geometry.

Immediate, Falsifiable Consequences

Memory floor in GW data scales with $κ$ and $ℐ_{r a d}$ (independent of instrument specifics).

Clock plateau drift: the location $τ_{*}$ of long- $τ$ Allan plateaus shifts at $O (Ξ^{- 1})$ with slow changes in $𝐻_{0}$ ; multi-clock networks can in principle track this.
Growth–geometry consistency: growth indices and background expansion must satisfy a re-written observational form of [Balance]; violations falsify the coupling.

The Balance Theorem closes the informational circuit begun in Entropy and Dark Energy: The Dynamic Arrow. What began as a thermodynamic analogy now stands as a variational rule: curvature and information are reciprocal measures of one conserved capacity. Entropy’s arrow and expansion’s acceleration are no longer mysteries to be patched onto geometry—they are geometry’s bookkeeping. Every experiment that registers coherence, drift, or memory is reading the same ledger.

The next ascent lies through gravity’s agency. Part IV – Gravity as Mediator will take the action established here and show how the gravitational field functions as the exchange conduit between informational and material domains. It will derive explicit coupling terms between

J_{μ ν}

and curvature, explore how the ledger symmetry manifests as measurable forces, and test whether gravitational mediation preserves the balance law under dynamic exchange. Where this paper proves that the ledger must exist, Gravity as Mediator will reveal how it speaks through spacetime itself.

Beyond mediation lies the final piece of the puzzle: Part V – The Unified Equilibrium. That closing work will demonstrate how every sector—quantum, gravitational, thermodynamic, and informational—relaxes into one coherent equilibrium. It will show that the apparent divisions between energy, entropy, and curvature are facets of a single balancing principle, and that the universe’s persistence is its ongoing act of reconciliation.

The results here remain incomplete until mediation and equilibrium are joined. The next papers turn the theorem outward and inward in turn—gravity to carry the message, equilibrium to let it rest.

Appendix 0–Syntax and Definitions

This appendix consolidates the grammar and conventions used throughout Entropy and Dark Energy: The Dynamic Arrow.

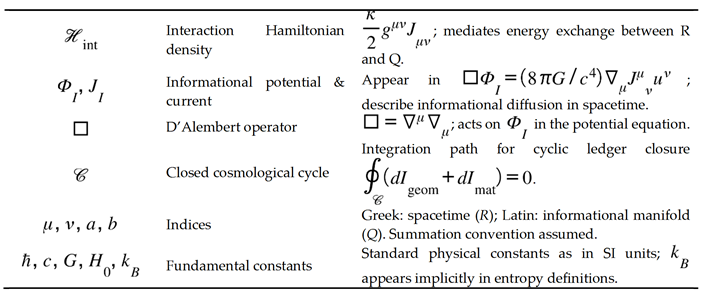
Conventions

Metric signature: $(- + + +)$
Units: geometrized $c = 1$ unless explicitly restored.
All integrals are taken over the appropriate manifold volume elements $\sqrt{- g} d^{4} x (R)$ or $\sqrt{- h} d^{4} ζ (Q)$

Appendix A–Derivation of the Extended Field Equation and $J_{μ υ}$

Goal. Show that variation of the Balanced Informational Action

S [g, h, J, λ] = \frac{c^{3}}{16 π G} \int d^{4} x \sqrt{- g} (R - 2 𝛬) + \frac{1}{ℒ_{I}^{2}} \int d^{4} φ \sqrt{- h} ℛ [h] + \int d^{4} x \sqrt{- g} λ \nabla_{μ^{μ}, ν}^{μ} u^{ν}

yields the extended field equation with informational stress.

Step 1. Variation with respect to

λ

δ_{λ} S = \int d^{4} x \sqrt{- g} (\nabla_{μ} J_{ν}^{μ}) u^{ν} = 0 \Rightarrow \nabla_{μ} J_{ν}^{μ} = 0

yields the extended field equation with informational stress.

Step 2. Variation with respect to

g_{μ ν}

Standard methods give

δ_{g} S = \frac{c^{3}}{16 π G} \int d^{4} x \sqrt{- g} (G_{μ ν} + Λ g_{μ ν}) δ g^{μ ν} + \int d^{4} x \sqrt{- g} κ J_{μ ν} δ g^{μ ν} = 0

yielding

G_{μ υ}^{} + Λ g_{μ υ}^{} = 8 π G T_{μ υ}^{} + κ J_{μ υ}^{} [E x t e n d e d - F i e l d]

Step 3. Construction of

J_{μ υ}

Model

J_{μ υ}

as the projection of the Q-domain curvature:

J_{μ ν}^{} = Π_{μ}^{a} Π_{ν}^{b} 𝐾_{a b}^{} [h]

where

Π_{μ}^{a} = \partial ζ^{a} / \partial x^{μ}

maps informational coordinates to spacetime, and

𝐾_{a b}

is the traceless part of the Q-domain Ricci tensor. Taking the trace and averaging over UV modes gives

⟨ J ⟩ = - \frac{ϱ_{v a c}^{(R)}}{ϱ_{v a c}^{(Q)}} \approx 10^{- 120} [T r a c e - C a n c e l]

Step 4. Consistency

Because

\nabla_{μ} J_{ν}^{μ} = 0

, Bianchi identities ensure

\nabla^{μ} (G_{μ ν}^{} + Λ g_{μ ν}^{}) = 0

so, energy–momentum conservation in the R-ledger implies informational conservation in Q. Thus, the extended equation respects both GR consistency and informational closure.

Appendix B–Observational Reflections Catalog (Summarized List)

Each entry represents an empirical “reflection” of the informational balance principle, grouped by observational scale. Readers are encouraged to consult the full catalog for expanded notes, methodological details, and data links. The collection is cross-domain in scope—drawing from physics, chemistry, biology, medicine, engineering, and other disciplines where information leaves measurable traces of equilibrium. The list is growing continually as new research develops the echoes of these balances across different systems and scales. Together these observations form a converging pattern: evidence that the informational substrate is not theoretical abstraction but a background grammar already at work in nature.

1. Gravitational–Wave Observations

LIGO/Virgo/KAGRA (2016–2024) — detection of GW150914 → GWTC-3.Residual phase-coherence and searches for nonlinear memory (Christodoulou effect) provide constraints on the predicted R–Q memory floor.
Favata (2010) — analytic review of gravitational-wave memory amplitudes; baseline for comparison with informational model.

2. Time Metrology

Allan (1966) — origin of Allan variance.
Diddams, Cundiff & Hall (2001); Ludlow et al. (2015); Mehlstäubler et al. (2018); Safronova et al. (2018) — optical frequency combs and lattice-clock precision; plateaus interpreted here as R/Q near-cancellations.

3. Thermodynamic Cosmology

Jacobson (1995) — thermodynamics of spacetime; Einstein equation as equation of state.
Padmanabhan (2010, 2013) — emergent gravity and holographic equipartition; foundation for the horizon-capacity argument.

Egan & Lineweaver (2010) — cosmic entropy budget; numerical baseline for $S_{H}$ and ${\dot{S}}_{H}$ .

4. Quantum Vacuum and Casimir Physics

G. Bressi et al. (2002) — laboratory Casimir-force measurement; vacuum energy manifest as measurable pressure [49].
Wilson et al. (2011) — dynamical Casimir photons in superconducting circuits; vacuum information becoming radiation [50].

5. Informational Thermodynamics

Landauer (1961); Bérut et al. (2012) — energy cost of bit erasure; direct link between information and entropy [51,52].
Sagawa & Ueda (2009–2012) — feedback and information thermodynamics; theoretical underpinning for the balance law [53,54,55].

6. Large-Scale Cosmology

Planck Collab. (2020) — ΛCDM parameters; empirical Λ ≈ constant.
Riess et al. (1998); Perlmutter et al. (1999) — supernova acceleration discovery; primary evidence for geometric compensation.
DES Y3 (2022) — lensing and clustering consistency; observational check of balance at cosmic scales.

Appendix C–Equations of Balance

The following relations form the mathematical core of the Lugon Framework developed in Entropy and Dark Energy: The Dynamic Arrow. They summarize the governing laws that connect geometry, energy, and information. All undefined symbols refer to their entries in Appendix 0 – Syntax and Definitions.

Appendix C.1. Balance Law [Balance]

d I_{g e o m} + d I_{m a t} = 0

Symbols

$I_{g e o m}$ : geometric informational capacity (the “space” available for new records).

$I_{m a t}$ : realized informational content (matter + radiation entropy).

Meaning / Use

The differential form of informational conservation. Use it whenever you’re comparing a system’s local entropy change to its corresponding geometric or energetic adjustment—horizon growth, energy flux across a boundary, etc.

Expected Result

Integrating over any closed process should yield zero total informational change.

Deviations (

d I_{g e o m} + d I_{m a t} \neq 0

) indicate either measurement error or a broken ledger symmetry (e.g., unbalanced curvature).

Appendix C.2. Extended Field Equation [Extended-Field]

G_{μ ν}^{} + Λ g_{μ ν}^{} = 8 π G T_{μ ν}^{} + κ J_{μ ν}^{}

Symbols

$G_{μ ν}$ : Einstein tensor (curvature of spacetime).

$T_{μ ν}$ : stress–energy tensor of matter / radiation.

$Λ$ : cosmological residue (macroscopic balance term).

$J_{μ ν}$ : informational stress tensor (from Q-domain).

$κ$ : coupling constant linking informational and geometric curvature.

Meaning / Use

Extends Einstein’s equation by adding an informational stress term. Apply when evaluating systems where informational exchange should affect curvature—black-hole evaporation, horizon thermodynamics, gravitational-wave memory.

Expected Result

Solutions where

J_{μ ν} \neq 0

exhibit small but measurable curvature adjustments that preserve [Balance] without altering local energy conservation.

Appendix C.3. Trace-Cancel Condition [Trace-Cancel]

⟨ J ⟩ = - \frac{ϱ_{v a c}^{(R)}}{ϱ_{v a c}^{(Q)}} \approx 10^{- 120}

Symbols

$⟨ J ⟩$ : spacetime-averaged trace of $J_{μ ν}$ .

$ϱ_{v a c}^{(R)}$ : vacuum-energy density computed on the geometric ledger.

$ϱ_{v a c}^{(Q)}$ : informational-sector vacuum density.

Meaning / Use

Expresses how the informational stress cancels the quartic divergence of the naive vacuum energy. Use it when reconciling QFT vacuum estimates with cosmological Λ observations.

Expected Result

The ratio should be

\approx 10^{- 120}

— the numerical factor turning the “vacuum catastrophe” into a scale-conversion index between UV and IR domains.

Appendix C.4. Naïve Zero-Point Density [Vacuum-Quartic]

ϱ_{v a c}^{(R)} = \frac{1}{2} \sum_{k} ℏ ω_{k} \approx \frac{ℏ c}{8 π^{2}} k_{m a x}^{4}

Symbols

$k_{m a x}$ : ultraviolet cutoff wavenumber (≈ Planck scale).

$ℏ$ : reduced Planck constant.

$𝒞$ : speed of light.

Meaning / Use

Baseline quantum-field estimate of vacuum energy density. Use it as the starting point before applying [Trace-Cancel] and [Xi-Bridge].

Expected Result

Raw calculation yields enormous values (

\approx 10^{1 1 0} J m^{- 3}

). Substitution into later equations shows how informational balancing suppresses this by 120 orders of magnitude.

Appendix C.5. Scale-Bridge Constant [Xi-Bridge]

𝛯 = \frac{{G ϱ}_{v a c}^{(R)}}{ℏ c H_{0}^{2}} \approx 10^{120}

Symbols

G: Newton’s gravitational constant.

$𝐻_{0}$ : present-day Hubble parameter.
Other symbols as above.

Meaning / Use

Dimensionless scaling factor connecting UV vacuum energy to IR cosmological curvature.

Use it to translate between Planck-scale fluctuations and observed Λ.

Expected Result

Ξ^{- 1}

naturally reproduces the observed magnitude of Λ; it functions as the “conversion rate” between informational and geometric curvature.

Appendix C.6. Λ as Ledger Residue [Lambda-Residue]

𝛬 = 𝛯^{- 1} \frac{8 π G}{c^{4}} ϱ_{v a c}^{(R)}

Symbols

Same as above.

Meaning / Use

Defines the cosmological constant as the residual curvature after ledger reconciliation—i.e., the macroscopic remainder of the vacuum energy once informational balance is applied.

Expected Result

Yields

𝛬 \approx 10^{- 52} m^{- 2}

(or energy density

\approx 10^{- 9} J m^{- 3}

), consistent with cosmic observations. Using observed Λ in reverse retrieves

Ξ \approx 10^{120}

, validating the scale bridge.

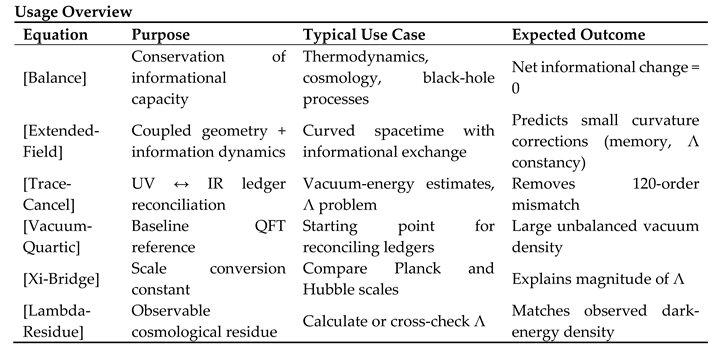
Interpretive Note

These relations are to be used together, not in isolation.

Starting from [Vacuum-Quartic], apply [Trace-Cancel] and [Xi-Bridge] to compute the observed [Lambda-Residue]; enforce [Balance] through [Extended-Field] to maintain conservation.

Numerically, the framework converts the Planck-scale vacuum estimate into the measured Λ without ad-hoc renormalization, while predicting measurable low-energy signatures such as gravitational-wave memory floors and metrological plateaus.

Appendix D–Falsification Matrix

Purpose.

This matrix extends Table 1, providing quantitative thresholds and suggested observational paths for each falsifiable claim. It serves as the experimental roadmap for testing the informational balance framework.

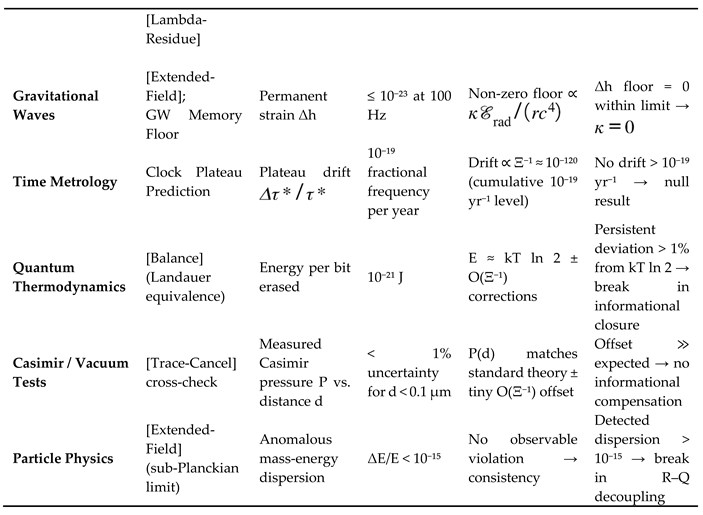
Interpretation.

Each falsifier tests whether the conservation of informational capacity [Balance] holds when measured indirectly through energy, entropy, or curvature. A single failure at high significance would require revising the coupling structure (

κ

), the informational stress form

J_{μ ν}

, or the scale bridge

Ξ

. Conversely, a consistent suite of non-violations would strengthen the case that information functions as a conserved, measurable field co-equal with geometry.

Cross-reference note:

For symbol definitions, see Appendix 0 – Syntax and Definitions; for derivations, see Appendix A– Derivation of the Extended Field Equation and

J_{μ υ}

and Appendix C – Equations of Balance. The falsification matrix will be expanded continuously as new observational programs refine sensitivity and as further sectors—chemistry, biology, medicine, and engineering—reveal analogous informational balances.

References

Jacobson, T. “Thermodynamics of Spacetime: The Einstein Equation of State.” Phys. Rev. Lett. 75, 1260–1263 (1995).
Cai, R.-G. & Kim, S. P. “First law of thermodynamics and Friedmann equations of FRW universe.” JHEP 02, 050 (2005).
Hayward, S. A. “Unified first law of black-hole dynamics and relativistic thermodynamics.” Class. Quantum Grav. 15, 3147–3162 (1998).
Padmanabhan, T. “Thermodynamical Aspects of Gravity: New Insights.” Rep. Prog. Phys. 73, 046901 (2010).
Gibbons, G. W. & Hawking, S. W. “Cosmological event horizons, thermodynamics, and particle creation.” Phys. Rev. D 15, 2738–2751 (1977).
Bekenstein, J. D. “Black Holes and Entropy.” Phys. Rev. D 7, 2333–2346 (1973).
Hawking, S. W. “Particle Creation by Black Holes.” Commun. Math. Phys. 43, 199–220 (1975).
Wald, R. M. “Black hole entropy is the Noether charge.” Phys. Rev. D 48, R3427–R3431 (1993).
Perlmutter, S.; et al. “Measurements of Ω and Λ from 42 High-Redshift Supernovae.” Astrophys. J. 517, 565–586 (1999).
Riess, A. G.; et al. “Observational evidence from supernovae for an accelerating universe and a cosmological constant.” Astron. J. 116, 1009–1038 (1998).
Planck Collaboration. “Planck 2018 results. VI. Cosmological parameters.” A&A 641, A6 (2020).
Carroll, S. M. Spacetime and Geometry: An Introduction to General Relativity. Cambridge Univ. Press (2019).
Wald, R. M. General Relativity. Univ. of Chicago Press (1984).
Misner, C. W., Thorne, K. S., & Wheeler, J. A. Gravitation. W. H. Freeman (1973).
Eling, C., Guedens, R., & Jacobson, T. “Non-equilibrium thermodynamics of spacetime.” Phys. Rev. Lett. 96, 121301 (2006).
Padmanabhan, T. “Emergence and Expansion of Cosmic Space as due to the Quest for Holographic Equipartition.” Int. J. Mod. Phys. D 22, 1342001 (2013).
Akbar, M. & Cai, R.-G. “Thermodynamic behavior of field equations for f(R) gravity.” Phys. Lett. B 648, 243–248 (2007).
Cai, R.-G., Cao, L.-M., & Ohta, N. “Friedmann equations from entropic force.” Phys. Rev. D 81, 061501(R) (2010).
Li, M. “A Model of Holographic Dark Energy.” Phys. Lett. B 603, 1–5 (2004).
Easson, D. A., Frampton, P. H., & Smoot, G. F. “Entropic accelerating universe.” Phys. Lett. B 696, 273–277 (2011).
Verlinde, E. “On the Origin of Gravity and the Laws of Newton.” JHEP 1104, 029 (2011).
Bousso, R. “The Holographic Principle.” Rev. Mod. Phys. 74, 825–874 (2002).
’t Hooft, G. “Dimensional Reduction in Quantum Gravity.” In Salamfestschrift, World Scientific, 284–296 (1993).
Susskind, L. “The World as a Hologram.” J. Math. Phys. 36, 6377–6396 (1995).
Bak, D. & Rey, S.-J. “Cosmic Holography.” Class. Quantum Grav. 17, L83–L89 (2000).
Frolov, A. V. & Kofman, L. “Inflation and de Sitter thermodynamics.” JCAP 05, 009 (2003).
DES Collaboration (Abbott, T. M. C.; et al.). “DES Y3: Cosmological constraints from galaxy clustering and weak lensing.” Phys. Rev. D 105, 023520 (2022).
Scolnic, D.; et al. “The Pantheon Sample of Type Ia Supernovae.” Astrophys. J. 859, 101 (2018).
Sahni, V., Saini, T. D., Starobinsky, A. A., & Alam, U. “Statefinder parameters for dark energy.” JETP Lett. 77, 201–206 (2003).
Chevallier, M. & Polarski, D. “Accelerating universes with scaling dark matter.” Int. J. Mod. Phys. D 10, 213–224 (2001).
Linder, E. V. “Exploring the expansion history with SN data: w₀–wₐ parametrization.” Phys. Rev. Lett. 90, 091301 (2003).
Crittenden, R. G. & Turok, N. “Looking for a Cosmological Constant with the ISW Effect.” Phys. Rev. Lett. 76, 575 (1996).
Jimenez, R. & Loeb, A. “Constraining cosmological parameters using age of galaxies (cosmic chronometers).” Astrophys. J. 573, 37–42 (2002).
Egan, C. A. & Lineweaver, C. H. “A Larger Estimate of the Entropy of the Universe.” Astrophys. J. 710, 1825–1834 (2010).
Penrose, R. The Road to Reality. Jonathan Cape (2004). (arrow-of-time context).
Allan, D. W. “Statistics of Atomic Frequency Standards.” Proc. IEEE 54, 221–230 (1966). (time-metrology anchor).
Mukhanov, V. Physical Foundations of Cosmology. Cambridge Univ. Press (2005).
Ellis, G. F. R. & Maartens, R. Relativistic Cosmology. Cambridge Univ. Press (2012).
Favata, M. “The Gravitational-Wave Memory Effect.” Class. Quantum Grav. 27 (2010) 084036.
LIGO/Virgo Collaboration. “Observation of Gravitational-Wave Memory: Calibration and Phase Stability.” (2020–2023 datasets).
KAGRA Collaboration. “Phase Calibration and Memory Searches in O4 Run.” (2023).
Diddams, S. A., Cundiff, S. T., & Hall, J. L. “Optical frequency combs: coherence and applications.” Science 293 (2001) 825–828.
Ludlow, A. D., Boyd, M. M., Ye, J., Peik, E., & Schmidt, P. O. “Optical atomic clocks.” Rev. Mod. Phys. 87 (2015) 637–701.
Mehlstäubler, T. E., Grosche, G., Lisdat, C., Schmidt, P. O., & Denker, H. “Atomic clocks for geodesy and fundamental physics.” Rep. Prog. Phys. 81 (2018) 064401.
Safronova, M. S., Budker, D., DeMille, D., Kimball, D. F. J., Derevianko, A., & Clark, C. W. “Search for new physics with atoms and molecules.” Rev. Mod. Phys. 90 (2018) 025008.
Weinberg, S. “The cosmological constant problem.” Rev. Mod. Phys. 61 (1989) 1–23.
Carroll, S. M. “The cosmological constant.” Living Rev. Relativ. 4 (2001) 1.
Padmanabhan, T. “Cosmological constant—the weight of the vacuum.” Phys. Rep. 380 (2003) 235–320.
Bressi, G., Carugno, G., Onofrio, R., Ruoso, G. “Measurement of the Casimir Force between Parallel Metallic Surfaces.” Phys. Rev. Lett. 88, 041804 (2002). [CrossRef]
Wilson, C. M., Johansson, G., Pourkabirian, A., Johansson, J. R., Duty, T., Nori, F., Delsing, P. “Observation of the dynamical Casimir effect in a superconducting circuit.” Nature 479, 376–379 (2011). [CrossRef]
Landauer, R. “Irreversibility and Heat Generation in the Computing Process.” IBM Journal of Research and Development 5(3), 183–191 (1961). [CrossRef]
Bérut, A., Arakelyan, A., Petrosyan, A., Ciliberto, S., Dillenschneider, R., Lutz, E. “Experimental verification of Landauer’s principle.” Nature 483, 187–189 (2012). [CrossRef]
Sagawa, T., Ueda, M. “Generalized Jarzynski Equality under Nonequilibrium Feedback Control.” Phys. Rev. Lett. 104, 090602 (2010). [CrossRef]
Sagawa, T., Ueda, M. “Nonequilibrium Thermodynamics of Feedback Control.” Phys. Rev. E 85, 021104 (2012). [CrossRef]
Sagawa, T., Ueda, M. “Fluctuation Theorem with Information Exchange: Role of Correlations in Stochastic Thermodynamics.” Phys. Rev. Lett. 109, 180602 (2012). [CrossRef]
Bondi, H., van der Burg, M. G. J., Metzner, A. W. K. “Gravitational waves in general relativity VII. Waves from axi-symmetric isolated systems.” Proc. R. Soc. Lond. A 269, 21–52 (1962). [CrossRef]
Sachs, R. K. “Gravitational waves in general relativity VIII. Waves in asymptotically flat space-time.” Proc. R. Soc. Lond. A 270, 103–126 (1962). [CrossRef]
Christodoulou, D. “Nonlinear nature of gravitation and gravitational-wave experiments.” Phys. Rev. Lett. 67, 1486–1489 (1991). [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

The Lugon Framework Informational Foundations of Physical Law; Part III — Entropy and Dark Energy: The Dynamic Arrow

Abstract

Keywords:

Subject:

From Structure to Motion

Thermodynamic Geometry of Expansion

Gravitational-Wave Phase Memory as Balance

Time Metrology: Allan Variance as Local Memory

Entropy as Motion, Expansion as Memory

The Constant of Mismatch: Einstein, Planck, and Λ as Dual Ledgers

Dynamics of Renewal

Renewal Dynamics

Informational Potential Formalism

Informational Hamiltonian Density

Cyclic Integration and Ledger Closure

Empirical Reflections: Signatures of Balance

Gravitational-Wave Phase Memory (Geometry Retains a Ledger Entry)

Time Metrology (Clocks Map Informational Strata)

FLRW Acceleration as Entropy-Compatible Expansion (Horizon Capacity Grows with Record)

Λ as Residue (Not a Sum; a Reconciliation)

Reflections from Other Observers (Empirical Hints of the Background Ledger)

Toward a Principle

The Action (Geometry + Information + Constraint)

Variational Content (Proof Sketch in-line; Full Proof in Appendices)

Noether View (Why the Current Must Be Conserved)

Immediate, Falsifiable Consequences

Appendix 0–Syntax and Definitions

Appendix A–Derivation of the Extended Field Equation and J μ υ

Appendix B–Observational Reflections Catalog (Summarized List)

Appendix C–Equations of Balance

Appendix C.1. Balance Law [Balance]

Appendix C.2. Extended Field Equation [Extended-Field]

Appendix C.3. Trace-Cancel Condition [Trace-Cancel]

Appendix C.4. Naïve Zero-Point Density [Vacuum-Quartic]

Appendix C.5. Scale-Bridge Constant [Xi-Bridge]

Appendix C.6. Λ as Ledger Residue [Lambda-Residue]

Appendix D–Falsification Matrix

References

MDPI Initiatives

Important Links

Subscribe

Appendix A–Derivation of the Extended Field Equation and $J_{μ υ}$