1. Introduction
A psychrometer determines relative humidity (RH) from two temperatures: the dry-bulb temperature (
) and the wet-bulb temperature (
) [
1,
2]. The dry-bulb measures the ambient air temperature, while the wet-bulb, covered with a moistened wick, registers a lower temperature due to water evaporation. The rate of evaporation depends on both temperature and RH: as RH increases, the evaporation rate decreases, causing
to rise and the psychrometric depression (
) to approach zero. In air saturated with water vapor (RH = 100%), the evaporation rate equals the condensation rate, and the wet-bulb temperature converges to the dry-bulb temperature, so that
. The psychrometer can measure RH only up to 100%; values above 100% indicate that the condensation rate exceeds the evaporation rate, meaning the wet-bulb temperature would exceed the dry-bulb temperature. In such cases, psychrometer equations are generally not applicable. A more detailed description of psychrometers and relative humidity can be found in the work of Araújo [
3].
For an ambient temperature of 292.15 K, a relative humidity of 66.8%, and a pressure of 101,325 Pa, an uncertainty of ±1 K in the temperature measurements of the transducers can lead to a maximum absolute error in relative humidity () of up to 15.6%. This work demonstrates that, by performing a simple calibration procedure of one temperature transducer relative to the other, it is possible to reduce the error in determining RH by up to 75× for temperatures in the range 274.15 K < T < 334.15 K and relative humidities of 10% < RH < 90%.
To calculate the air RH (Eq. 1), it is necessary to know the ratio between the saturation vapor pressure (
) and the partial vapor pressure (
). Both pressures are determined empirically; however, knowing an expression for the latent heat makes it possible to obtain
using the Clausius-Clapeyron relationship [
4]. Several empirical equations exist in the literature to calculate
and
; Araújo [
3] present 56 relations to obtain RH. In this work, the equations of Tetens[
5] and the British United Turkeys [
6] are used.
Just as represents the error in relative humidity, corresponds to the temperature error of the wet-bulb transducer; that is, is equal to the temperature indicated by the wet-bulb transducer minus the true wet-bulb temperature. Similarly, represents the temperature error of the dry-bulb transducer.
A decrease in the wet-bulb temperature indicates an increase in the rate of energy demand, which may correspond to an increase in the rate of evaporation due to a decrease in RH. Therefore, readings of the wet-bulb shifted to lower values () result in relative humidity readings shifted to lower values (). Conversely, dry-bulb readings shifted to higher values () also indicate lower relative humidity readings.
In the case of a transducer with wet-bulb readings shifted to higher values (), the environment captures less energy from the evaporation of water at the wet-bulb, resulting in relative humidity readings shifted to higher values (). Similarly, a transducer with dry-bulb readings shifted to lower values () again leads to relative humidity readings shifted to higher values.
Disregarding other sources of error, the magnitude and direction of and define the magnitude and direction of . While the individual influences of temperature uncertainties on the relative humidity error were discussed above, in a more general case must be considered as the result of the combined effects of and , since one contributes in a direction opposite to the other. If both errors are in the same direction, the effect of one can partially offset the interference of the other.In this context, the present work proposes a simple procedure to minimize through the calibration of one transducer relative to the other, ensuring that both have the same direction and magnitude of error.
The variation in pressure has a small influence on the determination of RH compared to the variation in temperature. For example, an uncertainty of ±1 kPa may correspond to an error in RH determination of up to 0.15% [
3], whereas an uncertainty of ±1 K can generate an
of up to 30.5% within the temperature and relative humidity ranges mentioned previously.
3. Results and Analysis
The data collected comprise two sets, with durations of 60 and 63 hours, respectively, conducted in a closed laboratory room throughout both collection periods. The sampling rate of the reference Pt100 transducers was approximately 2 Hz, with 24-bit resolution provided by the ADS1248 converter. Each data point transmitted from the Arduino to the PC corresponded to a simple average of ten samples.
For the LM35D transducers, measurements were performed using the Arduino’s internal 10-bit ADC, with each transmitted point representing the simple average of 1,000 samples. The data transfer rate from the Arduino to the PC was 0.088 Hz. Subsequently, an additional average of 100 points was applied for graph construction and psychrometer error analysis. Each point in
Figure 4 and
Figure 5, referring to any psychrometer equipped with LM35D transducers, corresponds to a relative humidity value calculated from the average of 100,000 dry-bulb and 100,000 wet-bulb readings. For the reference psychrometer using Pt100 sensors, each point represents an average of 1,000 readings.
The observed humidity range was approximately 62 % to 82 %, calculated using Equations (2), (1), and (3), for temperatures between 288.65 K and 292.15 K, and under a constant local pressure of 98,000.88 Pa.
Calibration of the LM35D temperature transducers was performed over the range of 280 K to 307 K in a thermostatic bath using four controlled temperature setpoints, aimed at obtaining the data points used to generate the calibration curves. Each point consisted of the average of several hundred measurements at each temperature level. A summary of the results is presented in
Table 2 for the dry-bulb transducers and
Table 3 for the wet-bulb transducers.
The columns labeled
Pt100m in
Table 2 and
Table 3 represent the average temperatures measured by two Pt100 Class AA sensors at the four temperature setpoints, which are the same Pt100 sensors used in the reference psychrometer assembly (PsyPt).
Using the data from
Table 2 and
Table 3, the temperature errors of transducers S1d to S7w were calculated by averaging the four temperature steps and referencing the results to the Pt100 measurements.
Table 4 summarizes the errors obtained for the LM35D sensors. These absolute errors are not used directly in the calibration procedure proposed for the psychrometer; rather, they serve to indicate the absolute deviation of the transducers relative to an accurate reference. The proposed calibration method involves calibrating one transducer relative to the other—for example, the dry-bulb sensor with respect to the wet-bulb sensor.
Each dry-bulb sensor (S1d, S2d, S3d, and S4d) was paired with each wet-bulb sensor (S5w, S6w, and S7w), resulting in twelve psychrometer combinations. The thermal calibration of these twelve psychrometers was carried out in two modes: the first using linear regression adjustments, and the second applying a simple offset correction between the dry-bulb and wet-bulb transducers.
In the first calibration mode,
linear adjustment, four calibration curves were generated: dry-bulb versus wet-bulb, wet-bulb versus dry-bulb, and both versus their mean, using the average values from the calibration setpoints listed in
Table 2 and
Table 3.
In the second mode, the differences between the dry-bulb and wet-bulb transducers were determined based on the absolute errors presented in
Table 4. These differences were then applied as correction factors for the dry-bulb relative to the wet-bulb, for the wet-bulb relative to the dry-bulb, and for both using the mean of the differences. It is worth noting that comparison with a reference sensor is not required; the calibration can be performed simply by subtracting the mean readings of one transducer from the other.
Since the LM35D transducers exhibit good linearity (typically ±0.25 K), as confirmed by the collected data, it can be concluded that both calibration approaches are equivalent. However, because the second approach is simpler to implement, it is adopted for the subsequent analyses. It should be emphasized that the equivalence between the two methods depends on the linearity of the transducers used
Table 5 summarizes the values of
for two regions:
Low, representing relative humidity in the range of 61–63%, and
High, representing 79–81%, based on the 123 hours of data collected from the two datasets. From left to right, the first column identifies the psychrometers; the tenth and unit at most left column (the 1st) indicate the dry-bulb and wet-bulb transducers, respectively. For example, Psy15 consists of transducers S1d (dry-bulb) and S5w (wet-bulb).
The second and third columns present the errors of the psychrometers without applying any correction to the temperature transducers, i.e., without implementing any of the suggested thermal calibration procedures. The fourth and fifth columns show the errors after applying corrections to both dry- and wet-bulb transducers using their average as a reference. The sixth and seventh columns display the errors obtained when only the wet-bulb transducer is corrected using the dry-bulb as a reference.
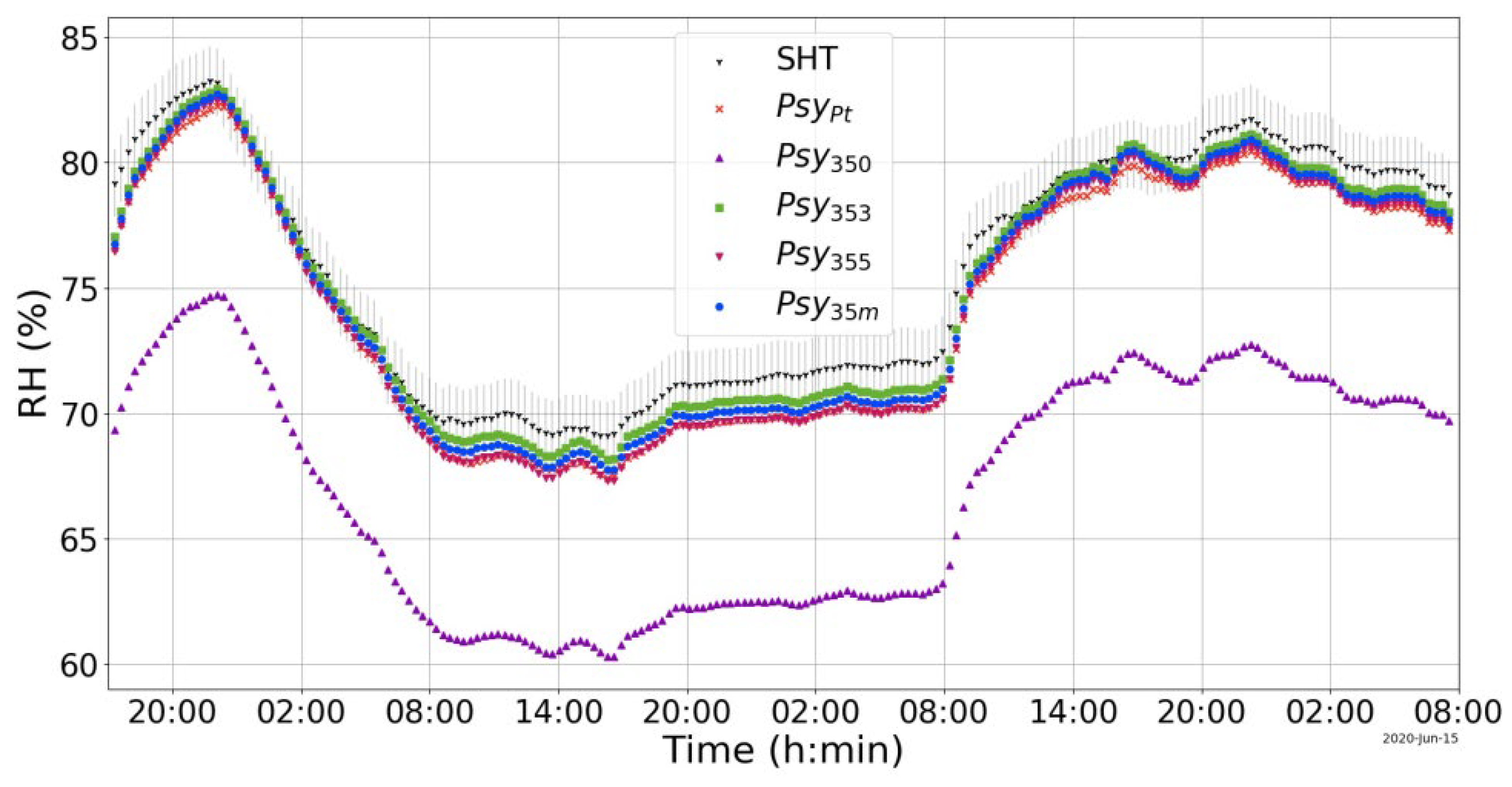
Among the twelve psychrometers, two representative cases, Psy35 and Psy25, were selected for detailed analysis. The results for Psy35, composed of S3d (dry-bulb) and S5w (wet-bulb), are shown in
Figure 4. The six relative humidity curves in
Figure 4, from bottom to top, correspond to Psy350 (purple upward triangle), representing the uncorrected psychrometer; PsyPt (red ‘X’), the reference psychrometer using Pt100 sensors; Psy355 (magenta downward triangle), the dry-bulb corrected psychrometer with S3d corrected relative to S5w; Psy35m (blue circle), the psychrometer corrected using the mean of S3d and S5w; Psy353 (green square), the wet-bulb corrected psychrometer with S5w corrected relative to S3d; and the SHT average (black ‘Y’), representing the average of the SHT75 and SHT31 sensors, with the vertical bars indicating their combined uncertainty.
The psychrometer Psy35 without correction (curve Psy350 in
Figure 4) exhibited a relative humidity difference of approximately −7.6% compared to the reference psychrometer, PsyPt. Among the corrected versions, the Psy355 curve most closely matched the reference, followed by Psy35m and Psy353. It is noted that throughout the measurement interval, all curves tracked the relative humidity variations indicated by the SHT75 and SHT31 sensors. According to
Table 5, the improvement in measurement accuracy for Psy35 using the calibration based on the average (Psy35m) was approximately 25× for the lowest recorded humidity values (RH = 62 ± 1%) and 18× for the highest values (RH = 80 ± 1%).
Figure 4 also shows that there are no significant differences between the three correction methods. The case of Psy35 corresponds to the scenario presented in the last row of
Table 1 from the theoretical simulation, in which the dry-bulb transducer error is positive while the wet-bulb transducer error is negative, resulting in a negative relative humidity error, maintaining the appropriate amplitude proportions.
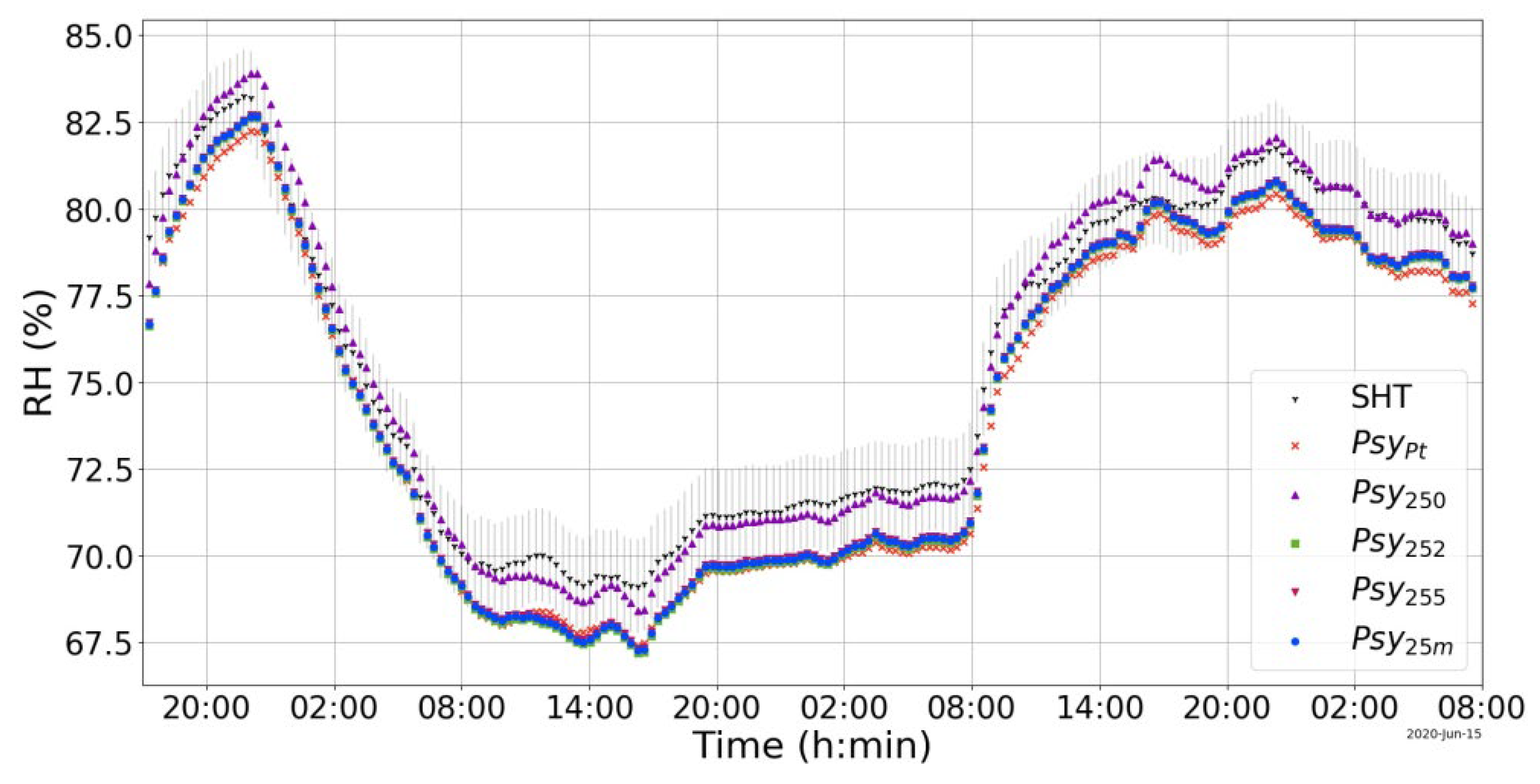
Figure 5 shows Psy25, composed of sensors S2d and S5w, with respective errors of −0.85 ± 0.15 K and −0.71 ± 0.08 K. In this case, although the transducer errors are significant, they do not substantially affect the psychrometer error because the errors have the same sign (negative) and similar magnitude relative to the reference. For this reason, applying corrections to the LM35D transducers - whether based on the dry-bulb, wet-bulb, or their average - reduces the relative humidity error by 1.25%, corresponding to an approximate 5× improvement in
at RH = 70%. Thus, the proposed correction method also enhances the psychrometer’s performance.
The humidity sensors SHT31 and SHT75, manufactured by Sensirion, were evaluated against four saturated reference solutions, and the results are summarized in
Table 6.
The results presented in
Table 6 are consistent with the error specifications provided in the datasheets, except for the temperature errors of the SHT75 sensor. The saturated solutions were prepared using reagents with a purity greater than 97%, with a mass of 10 g, dissolved in distilled and deionized water at a mass ratio of 0.25 to 0.35 (water to reagent). Glass containers with plastic lids and silicone rubber seals, having a volume of 630 cm
3 and a base area of 126 cm
2, were used. The values in
Table 6 represent the statistical analysis of 3,365 to 10,704 data points collected over 1–5 hours, depending on the solution. Temperature stability ranged from ±0.025 K to ±0.05 K depending on the solution, in accordance with ASTM E104-20 standards [
19]. The RH values of the saturated solutions in
Table 6 were adapted from Greenspan [
13]. With the exception of the NaOH solution, the remaining solutions—MgCl
2, NaCl, and KCl—correspond to Humidity Fixed Points (HPF) HPF33, HPF75, and HPF85, respectively, as defined in ASTM E104-20
Figure 1.
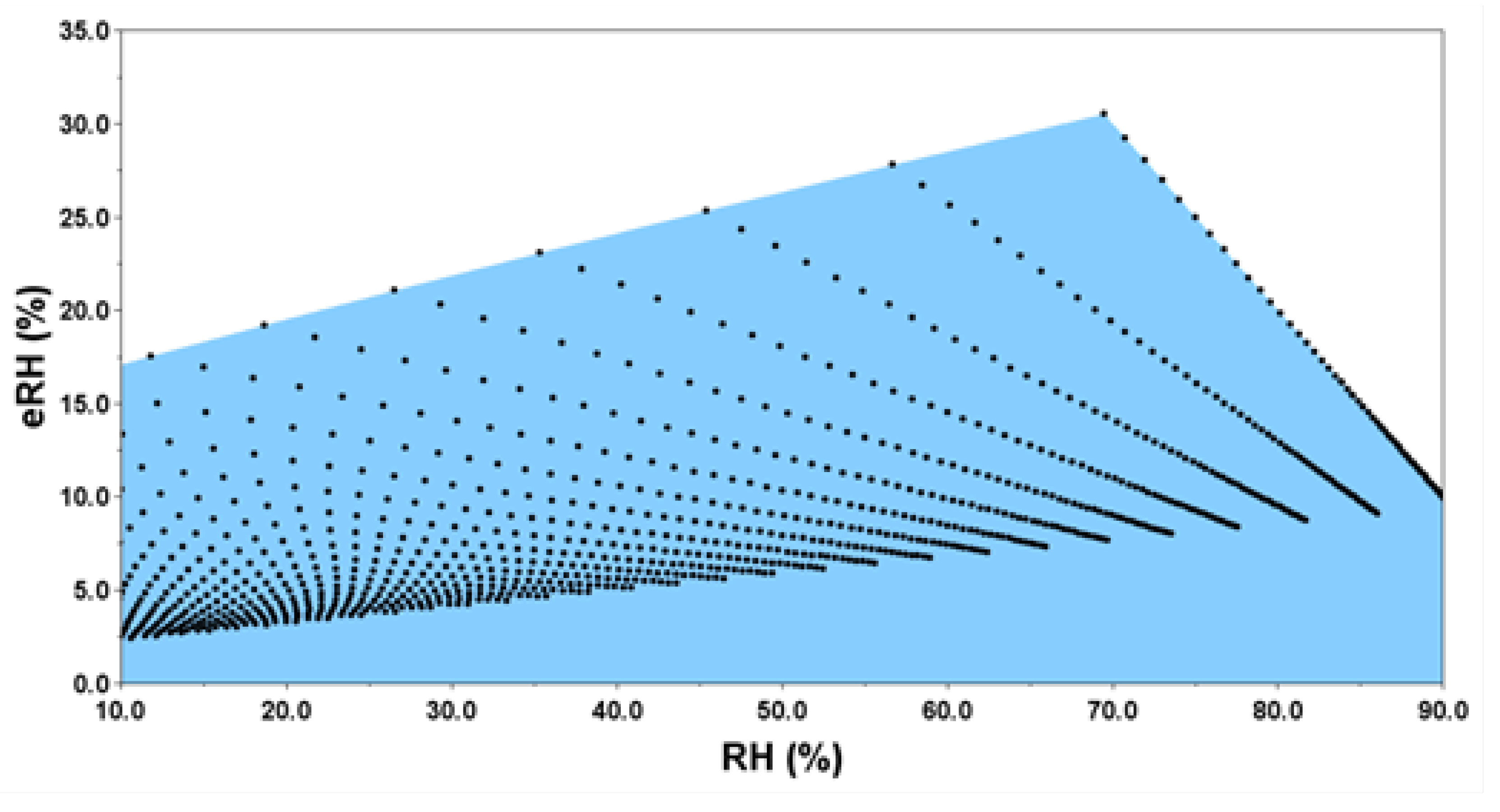
Simulation of the propagation of the temperature error in the determination of RH, using the equations of Tetens and British United Turkeys from reference [
5] and [
6]. With an uncertainty of -1K in the dry-bulb and an uncertainty +1K in the wet-bulb, the error in determining RH varies from approximately 2.5 to 30.5 in units of RH (%), in the range from 10% to 90% of RH.
Figure 1.
Simulation of the propagation of the temperature error in the determination of RH, using the equations of Tetens and British United Turkeys from reference [
5] and [
6]. With an uncertainty of -1K in the dry-bulb and an uncertainty +1K in the wet-bulb, the error in determining RH varies from approximately 2.5 to 30.5 in units of RH (%), in the range from 10% to 90% of RH.
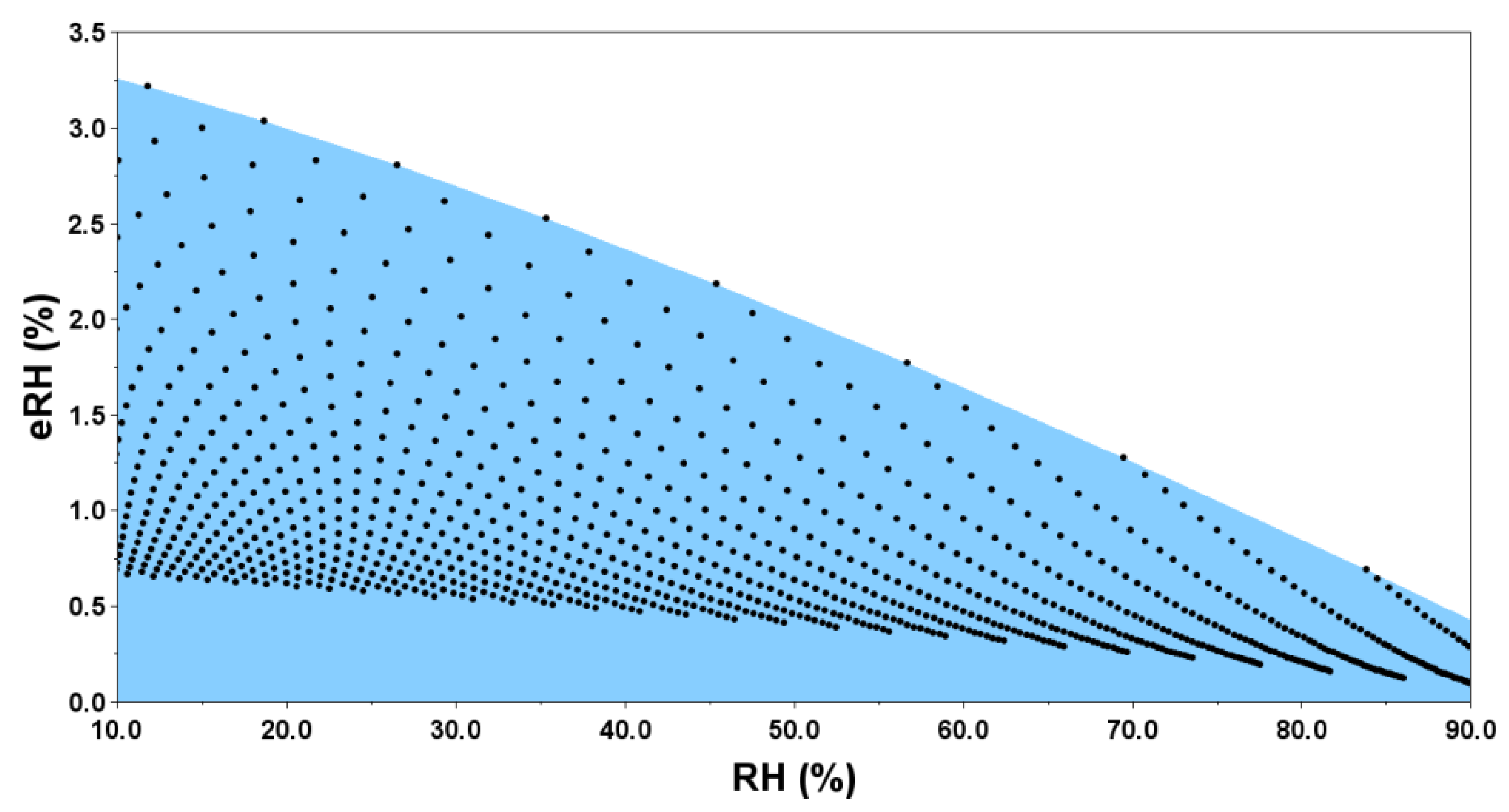
Figure 2.
Simulation of the propagation of the temperature error in the determination of RH, using the equations of Tetens and British United Turkeys. With an uncertainty of +1K in the dry-bulb and an uncertainty +1K in the wet-bulb, the error in determining the RH can vary approximately from 3.2 to 0.1 in units of RH (%), in the range of 10% to 90% of RH.
Figure 2.
Simulation of the propagation of the temperature error in the determination of RH, using the equations of Tetens and British United Turkeys. With an uncertainty of +1K in the dry-bulb and an uncertainty +1K in the wet-bulb, the error in determining the RH can vary approximately from 3.2 to 0.1 in units of RH (%), in the range of 10% to 90% of RH.
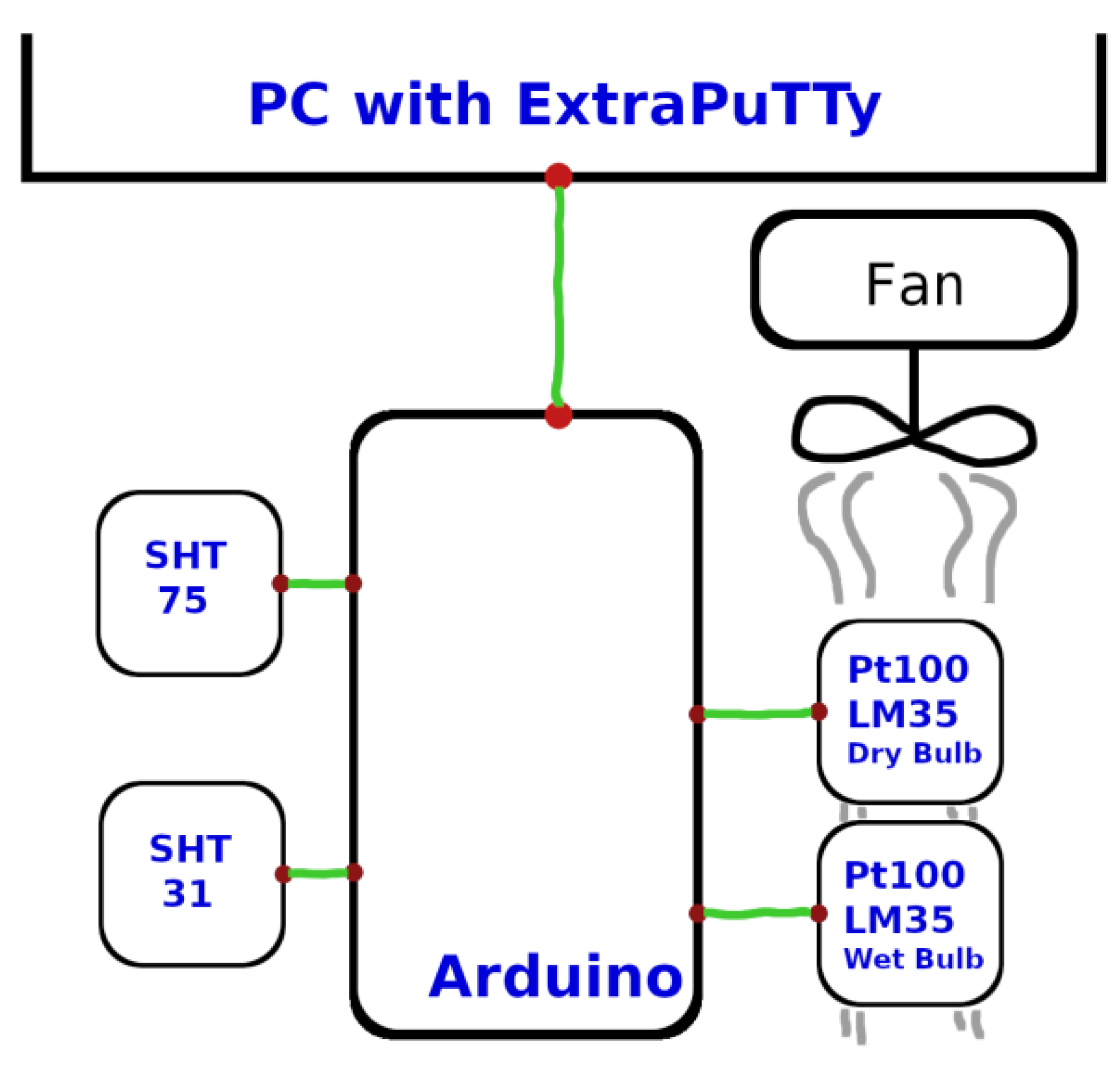
Figure 3.
Block diagram of experimental setup for psychrometer error measurement.
Figure 3.
Block diagram of experimental setup for psychrometer error measurement.
Figure 4.
Psychrometer graph Psy35, without thermal transducer correction, Psy350, and with correction, Psy353, Psy355 and Psy35m, in addition to the reference curves, SHT and Psy Pt, along 63h.
Figure 4.
Psychrometer graph Psy35, without thermal transducer correction, Psy350, and with correction, Psy353, Psy355 and Psy35m, in addition to the reference curves, SHT and Psy Pt, along 63h.
Figure 5.
Psychrometer graph Psy25, without thermal transducer correction, Psy250, and with correction, Psy252, Psy255 and Psy25m, in addition to the reference curves, SHT and PsyPt, along 63h.
Figure 5.
Psychrometer graph Psy25, without thermal transducer correction, Psy250, and with correction, Psy252, Psy255 and Psy25m, in addition to the reference curves, SHT and PsyPt, along 63h.
Table 1.
Summary of the simulation results. eTd represents the error imposed on the dry-bulb temperature, eTw represents the error imposed on the wet-bulb temperature, eRH10 corresponds to the error computed for a relative humidity (RH) of 10%, and eRHx corresponds to the error computed for a relative humidity of x%.
Table 1.
Summary of the simulation results. eTd represents the error imposed on the dry-bulb temperature, eTw represents the error imposed on the wet-bulb temperature, eRH10 corresponds to the error computed for a relative humidity (RH) of 10%, and eRHx corresponds to the error computed for a relative humidity of x%.
| eTd (K) |
eTw (K) |
eRH10 (%) |
eRHx (%) |
| -1 |
+1 |
+17 |
+30.5 (70%) |
| -1 |
0 |
+6.5 |
+16.0 (84%) |
| -1 |
-1 |
-3.5 |
-0.50 (90%) |
| 0 |
+1 |
+9.5 |
+16.0 (84%) |
| 0 |
-1 |
-9.0 |
-16.0 (90%) |
| +1 |
+1 |
+3.2 |
+0.40 (90%) |
| +1 |
0 |
-6.0 |
-15.0 (90%) |
| +1 |
-1 |
-10 |
-30.0 (90%) |
Table 2.
Checkpoints of the LM35D transducers, used in the dry-bulb, referenced to the average of Pt100, the uncertainty is expressed in ±2 sigma.
Table 2.
Checkpoints of the LM35D transducers, used in the dry-bulb, referenced to the average of Pt100, the uncertainty is expressed in ±2 sigma.
| Pt100m (K) |
S1d (K) |
S2d (K) |
S3d (K) |
S4d (K) |
| 280.77 ± 0.07 |
- |
279.86 ± 0.05 |
281.00 ± 0.05 |
280.72 ± 0.06 |
| 288.69 ± 0.00 |
288.41 ± 0.02 |
287.80 ± 0.01 |
288.90 ± 0.02 |
288.43 ± 0.01 |
| 293.36 ± 0.02 |
- |
292.53 ± 0.03 |
293.61 ± 0.03 |
293.11 ± 0.03 |
| 307.07 ± 0.06 |
- |
306.34 ± 0.06 |
307.38 ± 0.04 |
306.77 ± 0.06 |
Table 3.
Checkpoints for the LM35 transducers, used in the wet-bulb, referenced to the average of Pt100, the uncertainty is expressed in ±2 sigma.
Table 3.
Checkpoints for the LM35 transducers, used in the wet-bulb, referenced to the average of Pt100, the uncertainty is expressed in ±2 sigma.
| Pt100m (K) |
S5w (K) |
S6w (K) |
S7w (K) |
Pt100m (K) |
| 280.77 ± 0.07 |
280.10 ± 0.06 |
281.17 ± 0.05 |
280.15 ± 0.06 |
280.77 ± 0.07 |
| 288.69 ± 0.00 |
287.96 ± 0.02 |
288.89 ± 0.02 |
288.10 ± 0.02 |
288.69 ± 0.00 |
| 293.36 ± 0.02 |
292.65 ± 0.03 |
293.56 ± 0.02 |
292.81 ± 0.03 |
293.36 ± 0.02 |
| 307.07 ± 0.06 |
306.35 ± 0.06 |
307.22 ± 0.07 |
306.57 ± 0.05 |
307.07 ± 0.06 |
Table 4.
Errors of thermal transducers, LM35, referenced to the average of two Pt100, the uncertainty is expressed in ±2 sigma.
Table 4.
Errors of thermal transducers, LM35, referenced to the average of two Pt100, the uncertainty is expressed in ±2 sigma.
| Error on dry-bulb transductor, eTd |
| S1d |
S2d |
S3d |
S4d |
| - 0.29 |
- 0.85 ± 0.15 |
+ 0.24 ± 0.10 |
0.23 ± 0.19 |
| Error on wet-bulb transductor, eTw |
| S4w |
S6w |
S7w |
|
| 0.71 ± 0.08 |
+ 0.22 ± 0.19 |
0.57 ± 0.11 |
|
Table 5.
Summary of relative humidity errors, eRH, of the twelve mounted psychrometers, from Psy15 to Psy47, uncertainty is expressed in ±2 sigma.
Table 5.
Summary of relative humidity errors, eRH, of the twelve mounted psychrometers, from Psy15 to Psy47, uncertainty is expressed in ±2 sigma.
Psy
Id.
|
eRH (%)
Low |
eRH (%)
High |
eRHm (%)
Low |
eRHm (%)
High |
eRHd (%)
Low |
eRHd (%)
High |
| 15 |
-3.77±0.16 |
-3.53±0.22 |
-0.38±0.20 |
+0.14±0.16 |
-0.62±0.20 |
+0.02±0.16 |
| 16 |
+5.17±0.28 |
+5.39±0.64 |
+1.01±0.32 |
+0.89±0.50 |
+1.27±0.32 |
+1.02±0.50 |
| 17 |
-2.45±0.30 |
-2.01±0.54 |
-0.17±0.30 |
+0.46±0.62 |
-0.33±0.30 |
+0.38±0.62 |
| 25 |
+0.47±0.20 |
+1.57±0.18 |
-0.68±0.18 |
+0.32±0.18 |
-0.60±0.18 |
+0.36±0.18 |
| 26 |
+9.74±0.26 |
10.8±0.86 |
+0.72±0.34 |
+1.07±0.56 |
1.30±0.32 |
+1.35±0.58 |
| 27 |
+1.84±0.24 |
+3.15±0.74 |
-0.47±0.24 |
+0.64±0.66 |
-0.31±0.24 |
+0.72±0.66 |
| 35 |
-7.68±0.12 |
-7.60±0.26 |
-0.31±0.12 |
+0.42±0.20 |
-0.84±0.12 |
+0.16±0.20 |
| 36 |
+0.94±0.34 |
+1.03±0.64 |
+1.06±0.34 |
+1.16±0.66 |
+1.05±0.34 |
+1.16±0.66 |
| 37 |
-6.41±0.32 |
-6.13±0.56 |
-0.11±0.28 |
+0.74±0.76 |
-0.56±0.28 |
+0.52±0.76 |
| 45 |
-4.36±0.12 |
-3.82±0.12 |
-0.52±0.16 |
+0.36±0.12 |
+0.80±0.16 |
+0.23±0.14 |
| 46 |
+4.53±0.30 |
+5.08±0.74 |
+0.86±0.34 |
+1.10±0.62 |
+1.10±0.34 |
+1.22±0.62 |
| 47 |
-3.05±0.30 |
-2.30±0.64 |
-0.32±0.30 |
+0.68±0.74 |
-0.51±0.30 |
+0.58±0.74 |
Table 6.
Measurement of the SHT75 and SHT31 transducers referenced standard saturation solutions and a Pt100 AA. Values of RH for the standard solutions taken from Greenspan [
18].
Table 6.
Measurement of the SHT75 and SHT31 transducers referenced standard saturation solutions and a Pt100 AA. Values of RH for the standard solutions taken from Greenspan [
18].
| Solution |
Table Value
(% RH) |
Temperature
PT100 (K) |
SHT31
(% RH) |
SHT75
(% RH) |
SHT31
(K) |
SHT75
(K) |
| NaOH |
8.8±2.4 |
293.95±0.04 |
12.21±0.07 |
13.05±0.06 |
293.86±0.04 |
293.28±0.04 |
| MgCl2 |
32.9±0.17 |
295.17±0.03 |
39.23±0.06 |
38.10±0.02 |
295.09±0.04 |
294.68±0.04 |
| NaCl |
75.40±0.13 |
295.76±0.04 |
77.66±0.08 |
76.28±0.1 |
295.67±0.05 |
295.27±0.04 |
| KCl |
85.43±0.31 |
291.36±0.05 |
85.97±0.23 |
85.05±0.18 |
291.27±0.05 |
290.88±0.05 |