1. Introduction
Starch is one of the most important polysaccharides and a basic constituent of our everyday diet. It is found in potatoes, wheat, rice and corn, and it is laid down in the form of granules. It consists of two types of molecules, amylose and amylopectin. The extensive degree of crystallinity in starch granules originates from the amylopectin molecules which are oriented radially with their non-reducing chain ends pointing towards the outer surface of the granule. This spherocrystalline assembly when observed under polarized light, shows a Maltese cross [
1]. Furthermore, using a λ/4 waveplate, polarized light shows the positive birefringence which theoretically indicates radial orientation of the principal axis of the crystallites [
2]. The crystalline structure of starch varies by botanical origin and falls into three general types: A-type, B-type, and C-type. Corn starches, belong to the orthorhombic A-type crystal structure [
3,
4]. Starch molecules are organized in alternating con-centric crystalline and amorphous domains that form growth rings. The crystalline layer consists of ordered regions composed of double helices formed by short amylopectin branches, most of which are further ordered into structures known as the crystalline lamellae [
5]. The outer layer of starch granules (shell) seems to differ from the inner portion (core), although the chemical composition is basically the same. The remnant of this envelope structure, commonly called a “ghost”, has been found to comprise primarily amylopectin (as determined by iodine staining) [
6,
7]. Techniques like electron microscopy [
8], X-ray scattering [
9] and nuclear magnetic resonance [
10] are used to characterize the structure of starch granules. Optical approaches, like second-harmonic generation (SHG) microscopy, also offer valuable information on the structure of starch granules [
11,
12,
13,
14]. Lately, non-linear optical third harmonic generation (THG) microscopy is used to image starch [
15,
16,
17]. In THG, three photons are combined to produce one of triple energy. THG signals are coherent with well-defined polarizations. The power of the THG signals depends on the state of the excitation polarization and the structure of the interacted samples.
In the present study polarization-dependent THG (P-THG) microscopy is performed in corn starch granules. By rotating the direction of the excitation linear polarization, series of images of the granules are acquired, for different directions of polarization. In these P-THG images, the THG signals’ intensity is modulating with the rotation of the polarization, giving rise to characteristic P-THG patterns. Importantly, the THG signals originating from the shell of the granule, modulate in a different manner than those originating from the core of the granule. After a point-by-point analysis, distinct P-THG modulation profiles are revealed. These emerge from different regions of the corn starch granules (i.e. the shell and the core). A theoretical framework is introduced for interpreting P-THG signals originating from an orthorhombic crystal symmetry, characteristic of corn starches. The ratios of the susceptibility tensor elements are extracted, from fits to the P-THG intensity profiles. An anisotropy ratio AR=/ is introduced and used as a metric of the molecular arrangement in the granules. Our analysis reveals distinct AR values for the cores and shells, reflecting structural anisotropy on molecular arrangements within single granules.
2. Materials and Methods
2.1. Sample Preparation
The corn starch was purchased from the local food store. It was embedded with distilled water between two 25mm diameter, No.0 thickness, microscope cover glasses (Menzel Gläser), sealed with grease. The addition of water has significant effect on starch structure. Hydration self organizes amylopectin molecules in a more uniform spherical granule shape. Specifically, water allows the amylopectin helices to organize side by side in a smectic A-type structure [
18].
2.2. Polarization-Dependent THG Microscope
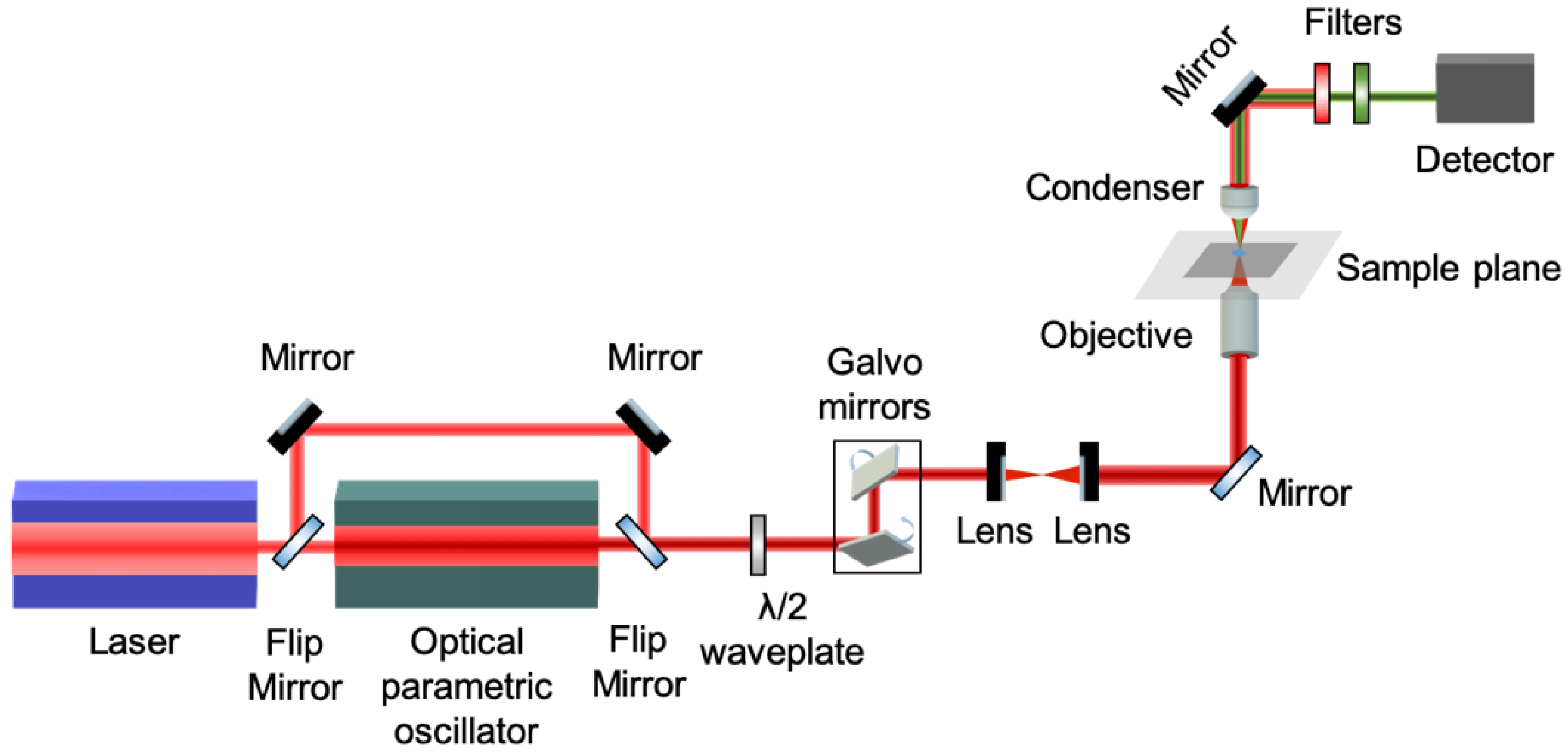
The experimental setup of our custom-build non-linear microscope is schematically shown in
Figure 1 [
19]. The excitation source is a femtosecond oscillator (FLINT, Light Conversion) centered at 1030nm, with repetition rate 80MHz and pulse duration 50fs (manufacturer specifications). The output beam is directed into an optical parametric oscillator (OPO) (Levante IR, APE) tuned to emit at 1542nm for THG excitation. The linear polarization state of the excitation beam is controlled by a half-wave retardation plate (AHWP10M-1600, ThorLabs) placed on a motorized rotational stage (8MRU, Standa). Raster-scanning of the beam is performed using a pair of galvanometric mirrors (6215H, Cambridge Technology). Using a pair of achromatic doublet lenses (forming a telescope), the beam emerging from the galvanometric mirrors is expanded approximately 7 times in order to fill the back aperture of the objective lens. Exiting the telescope, the beam is reflected on a mirror, at 45° (PFR10-P01, ThorLabs), placed at the motorized turret box of the microscope, just below the objective (Plan-Apochromat 40x/1.3NA, Carl Zeiss).
The THG (at 514 nm wavelength) is collected in the forward direction with a high-numerical aperture condenser lens (achromatic - aplanatic, 1.4NA, Zeiss) and is detected, after passing through a short-pass filter (FES0800, ThorLabs) and a band-pass filter (FF01-514/3, Semrock), by a photomultiplier tube (H9305-04, Hamamatsu). The galvanometric mirrors and the PMT are connected to a connector block (BNC-2110, National Instruments), which is interfaced to a PC through a DAQ (PCI 6259, National Instruments). Coordination of PMT recordings with the galvanometric mirrors for the image formation, as well as the movements of all the microscope motors, is carried out using LabView (National Instruments) software. One image of 500x500 pixels (measurements) is recorded in approximately 1s.
2.3. Theoretical Model of Polarization-Dependent THG in Starch
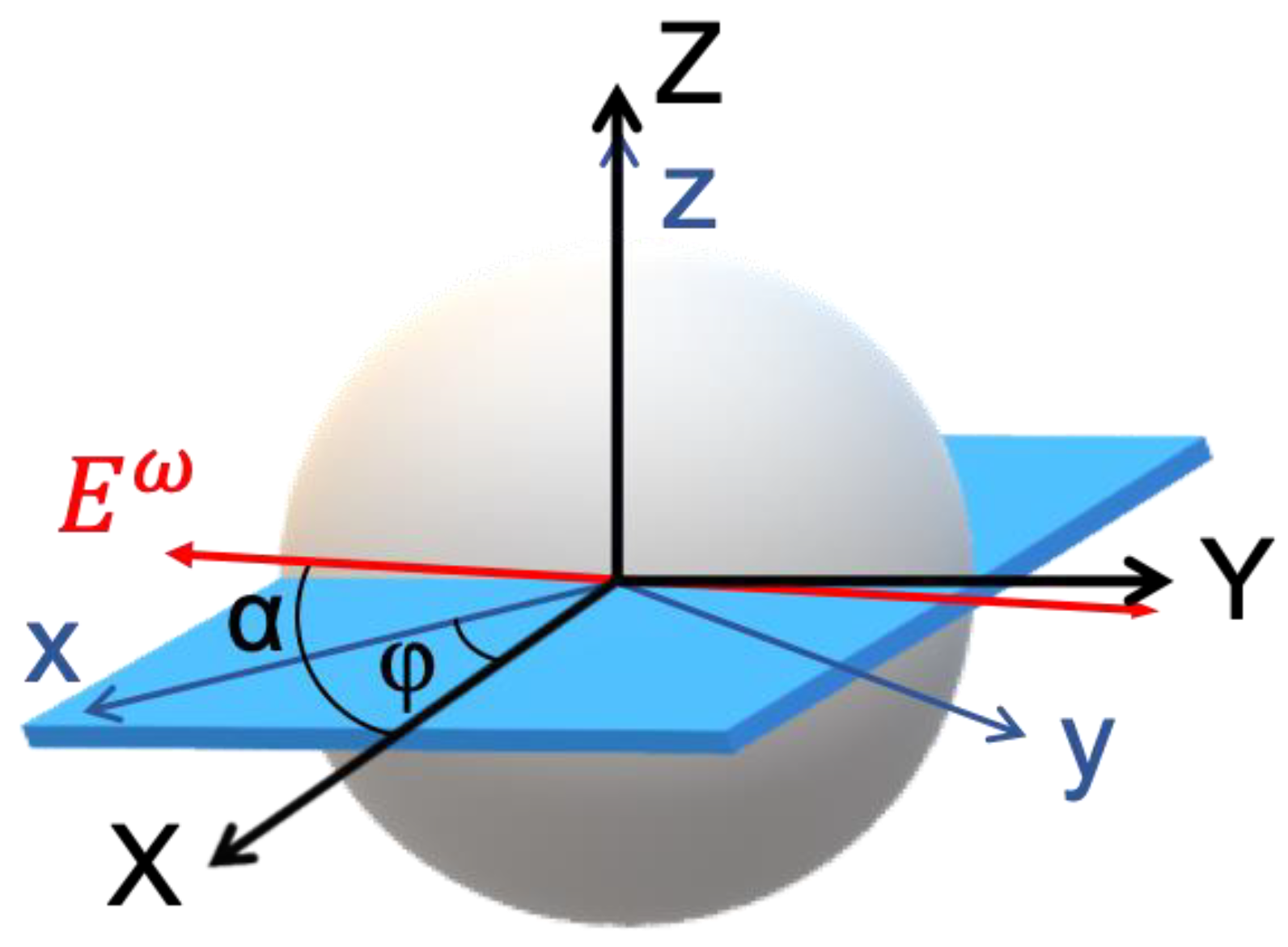
To model P-THG in starch granules two coordinate systems are introduced (
Figure 2): the laboratory frame (X-Y-Z), and the sample frame (x-y-z). The laser beam propagates along the laboratory Z-axis, and its electric field is linearly polarized in the X–Y plane. The polarization angle, denoted by α, is defined with respect to the X-axis and is varied systematically during THG intensity measurements.
is linearly polarized and rotates within the X–Y plane at an angle α relative to the X-axis. The orientation of the sample is defined by the angle φ, representing the rotation of the sample x-axis relative to the lab X-axis. This geometric configuration enables modeling of the P-THG signals in a system with radial molecular organization like in the starch granules.
Based on polarization-dependent SHG studies, starch granules exhibit radial molecular organization in both the shell and the core [
11]. An equatorial plane of the granule, where the long axes of the starch molecules predominantly lie in the sample’s x–y plane (because of the radial organization), is considered. At this equator, the sample and laboratory planes are aligned such that z=Z, and the x–y plane of the sample is coplanar with the X–Y plane of the laboratory frame. The orientation of the sample frame with respect to the laboratory frame is defined by an in-plane rotation angle φ between the sample x-axis and the laboratory X-axis. In the sample frame, the incident electric field components are expressed as:
where
is the amplitude of the incident electric field. Effects such as birefringence and diattenuation due to scattering [
20], and axial field components due to tight focusing [
21] are neglected in this model for simplicity.
The induced third-order nonlinear polarization (
) in the sample is governed by a third-order susceptibility tensor
[
22]. For convenience, the contracted notation
is adopted where the index i∈{1,2,3} corresponds to x, y z , respectively, and the multi-index
jkl is mapped to a single index
m using standard nonlinear optics conventions [
22]:
| jkl |
xxx |
yyy |
zzz |
yzz |
yyz |
xzz |
xxz |
xyy |
xxy |
xyz |
| m |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9 |
0
|
Because corn starch granules are SHG active (
Figure S1), the orthorhombic crystal symmetry (
mm2) that allows SHG [
22] is chosen. Assuming the orthorhombic (
mm2), as appropriate for corn starch [
3,
4], only a subset of the
tensor components are non-zero. Specifically, the following nine elements contribute to the third-order response [
19]:
,
,
,
,
,
,
,
. With these non-zero elements and the field components defined above, the third-order polarization
in the sample can be explicitly calculated as a function of the input polarization angle α and the sample orientation φ:
where,
denotes the permittivity of free space. Substituting Equation (1) into Equation (2), we obtain:
Then, in the laboratory coordinate system (X-Y-Z), the third-order polarization
can be expressed as:
The detected THG is given by:
By combining Equations (3), (4), and (5), the expression describing the P-THG response at the equator of a starch granule is derived:
This forms the theoretical basis for interpreting the P-THG signal modulations measured experimentally in corn starch granules. Using the above notations the anisotropy ratio (AR) is defined as follows:
The AR describes the ratio of the contribution of relative to the contribution of to the produced THG signal.
2.4. Arithmetic Simulations of P-THG Modulation
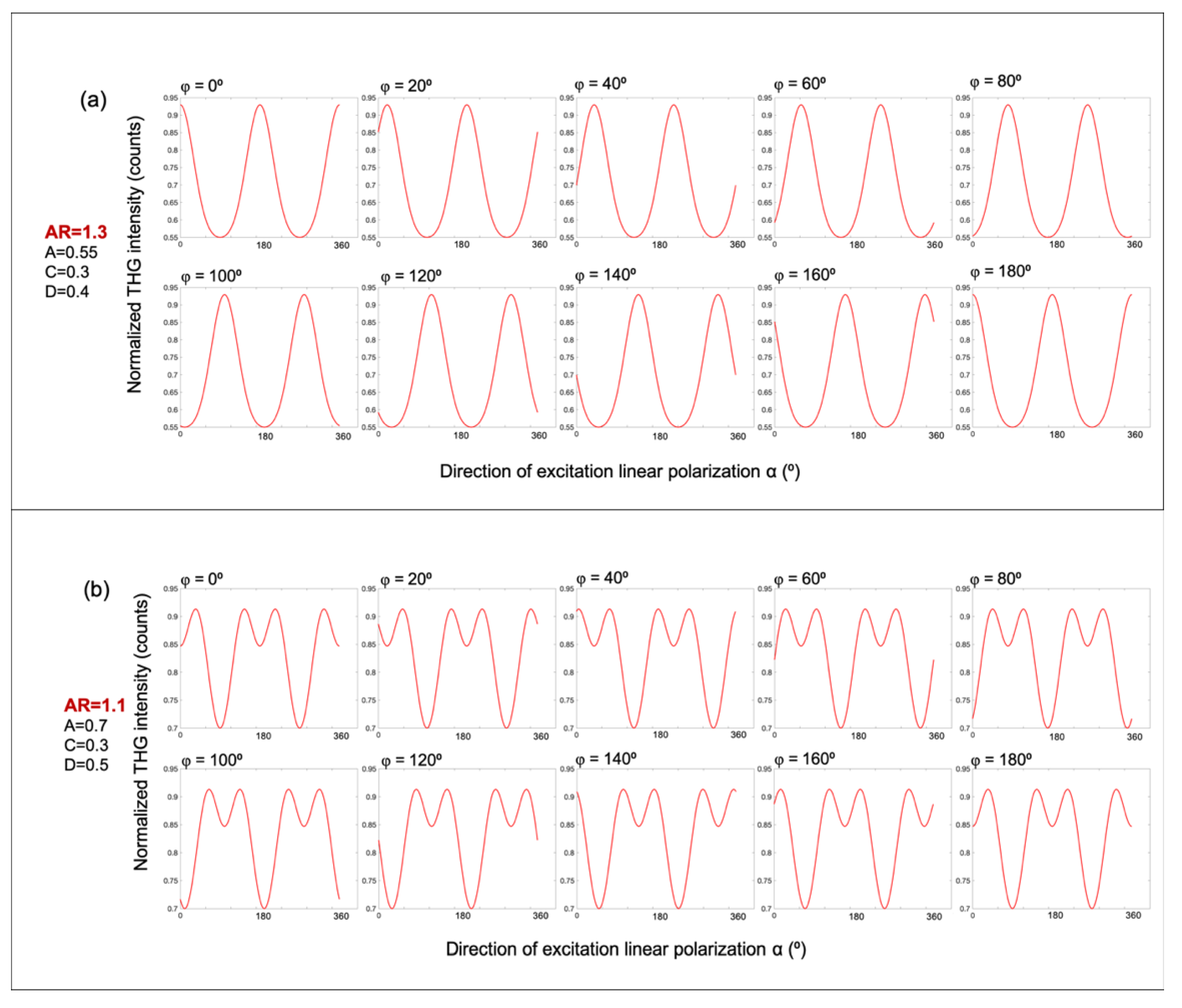
Figure 3 presents simulated polarization-dependent THG intensity profiles based on Equation (6), which models the angular modulation of the THG signal as a function of excitation polarization. These simulations explore the role of free parameters in shaping the modulation patterns observed in starch granules. In
Figure 3a, the anisotropy ratio is set to
AR=1.3, and the remaining fitting parameters are fixed as A=0.55, C=0.3, and D=0.4. The modulation curves are computed for sample orientations φ ranging from 0° to 180°, in steps of 20°. In
Figure 3b, a different set of parameters is chosen:
AR=1.1, A=0.7, C=0.3, and D=0.5. Importantly, due to the symmetry of the underlying equation, the curves for φ=0° and φ=180°, are identical in both simulation sets. This suggests that the modulation patterns possess a modulo of 180°. These simulations demonstrate how variations in the anisotropy ratio AR and other fitting parameters control the emergence of distinct modulation profiles, offering a robust means of distinguishing structurally different regions within starch granules.
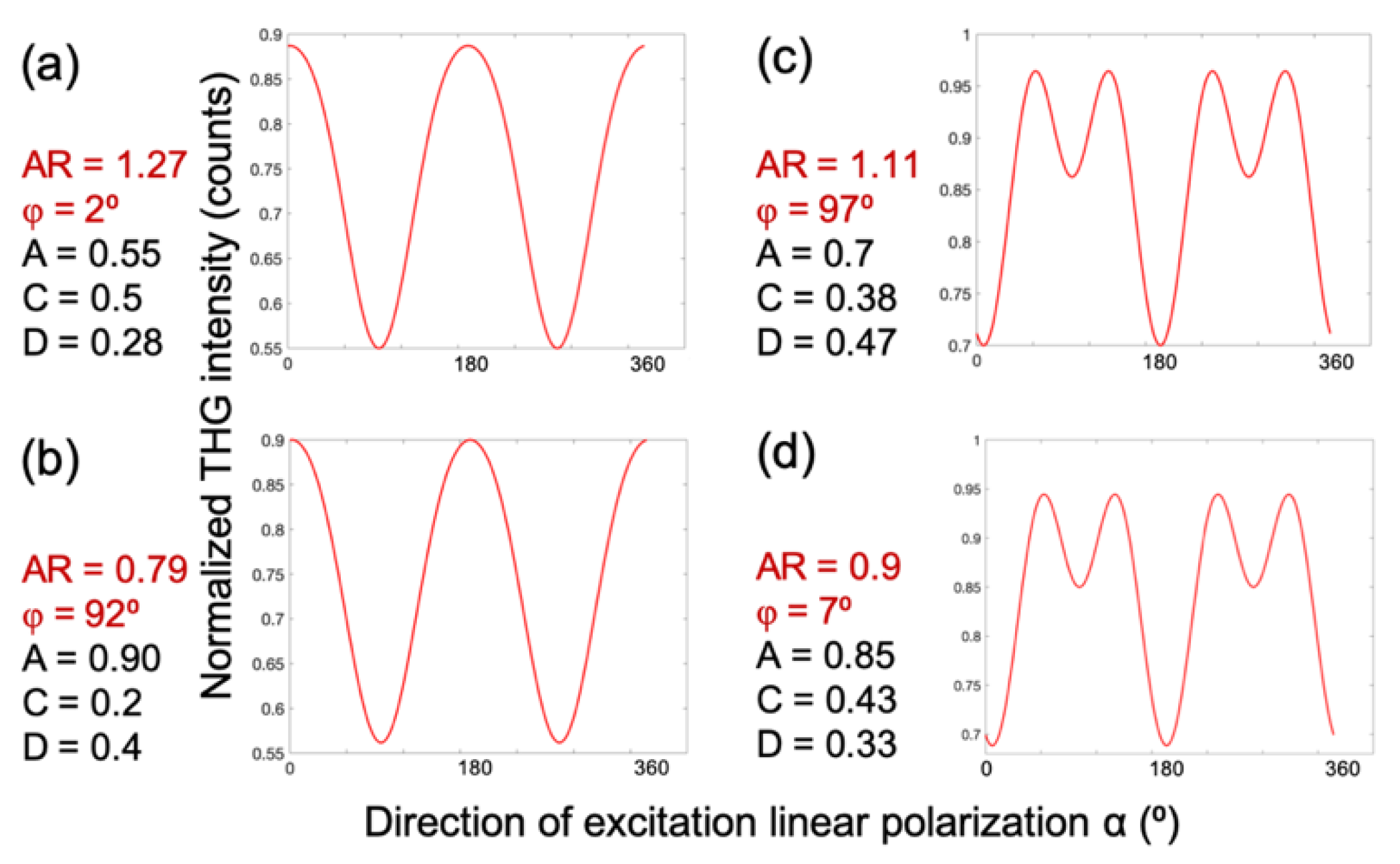
To generate a P-THG modulation curve, the free parameters in Equation (6) are set to the following values:
AR=1.27,
φ=2°, A=0.5, C=0.5, and D=0.28, as shown in
Figure 4a. Interestingly, a similar modulation profile can be obtained with a different parameter set:
AR=0.79,
φ=92°, A=0.9, C=0.2, and D=0.4 (
Figure 4b). Likewise, a different modulation pattern is reproduced in
Figure 4c using parameters
AR=1.1,
φ=97°, A=0.7, C=0.38, and D=0.47, which closely resembles the result in
Figure 4d, where the values are
AR=0.9,
φ=7°, A=0.85, C=0.43, and D=0.33. These comparisons reveal that the modulation curves remain nearly invariant when φ is shifted by 90° and the anisotropy ratio is simultaneously inverted (i.e., AR→1/AR). This degeneracy suggests that when fitting the experimental data, the iteration algorithm might converge to two different sets of values for the free parameters in Equation (6), that nevertheless describe the same data. To resolve this ambiguity during data fitting, and to obtain comparable values for the free parameters, the criterion AR>1 is imposed to the fitting algorithm.
3. Results and Discussion
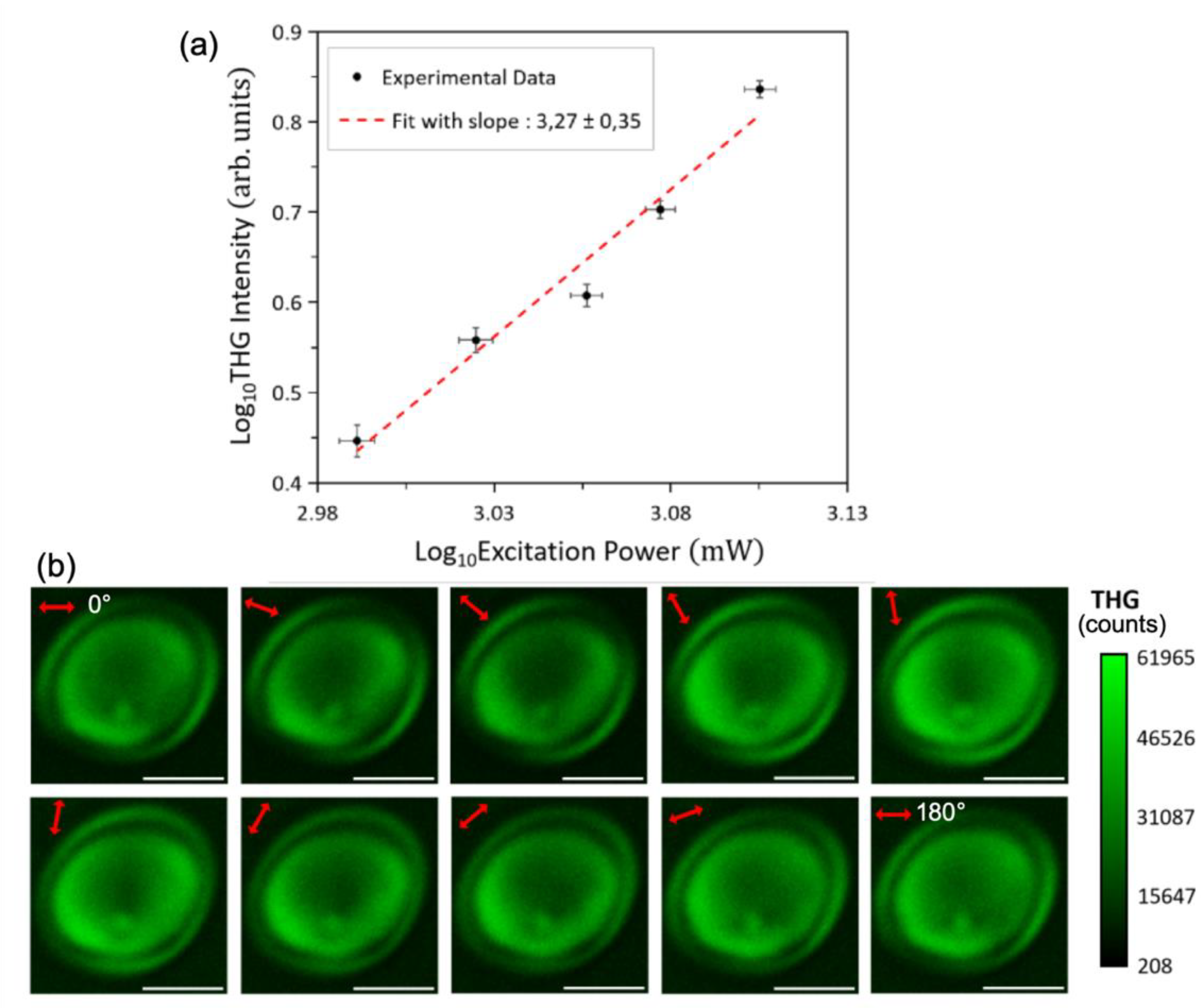
Figure 5a shows the THG signal intensity from corn starch as a function of excitation laser power, plotted on a double logarithmic scale. The observed slope of approximately 3 confirms the cubic power-law dependence, characteristic of a third-order nonlinear optical process like THG [
22].
In
Figure 5b, a series of THG images, produced by a corn starch granule, recorded while rotating the excitation linear polarization angle
(indicated by the red double-arrow), between 0° and 180° with step 20°, is presented. The images clearly show that the THG signal intensity modulates as a function of the polarization angle
. Notably, the image at α=0° is identical to that at α=180°, consistent with the modulo of 180° predicted by our simulations (see
Figure 3a and
Figure 3b). The THG imaging is performed close to the equator of the granule and both the shell and the core of the granule can be clearly visualized. Importantly, the THG signals originating from the shell of the granule, modulate in a different manner than those originating from the core of the granule. This behavior is more clearly demonstrated in Supporting Video S1, which shows 37 THG images acquired as α varies from 0° to 360° in 10° increments. The modulation patterns observed experimentally match well with our numerical simulations (
Figure 3a and
Figure 3b), where different parameter sets in Equation (6) yield distinct P-THG modulation profiles.
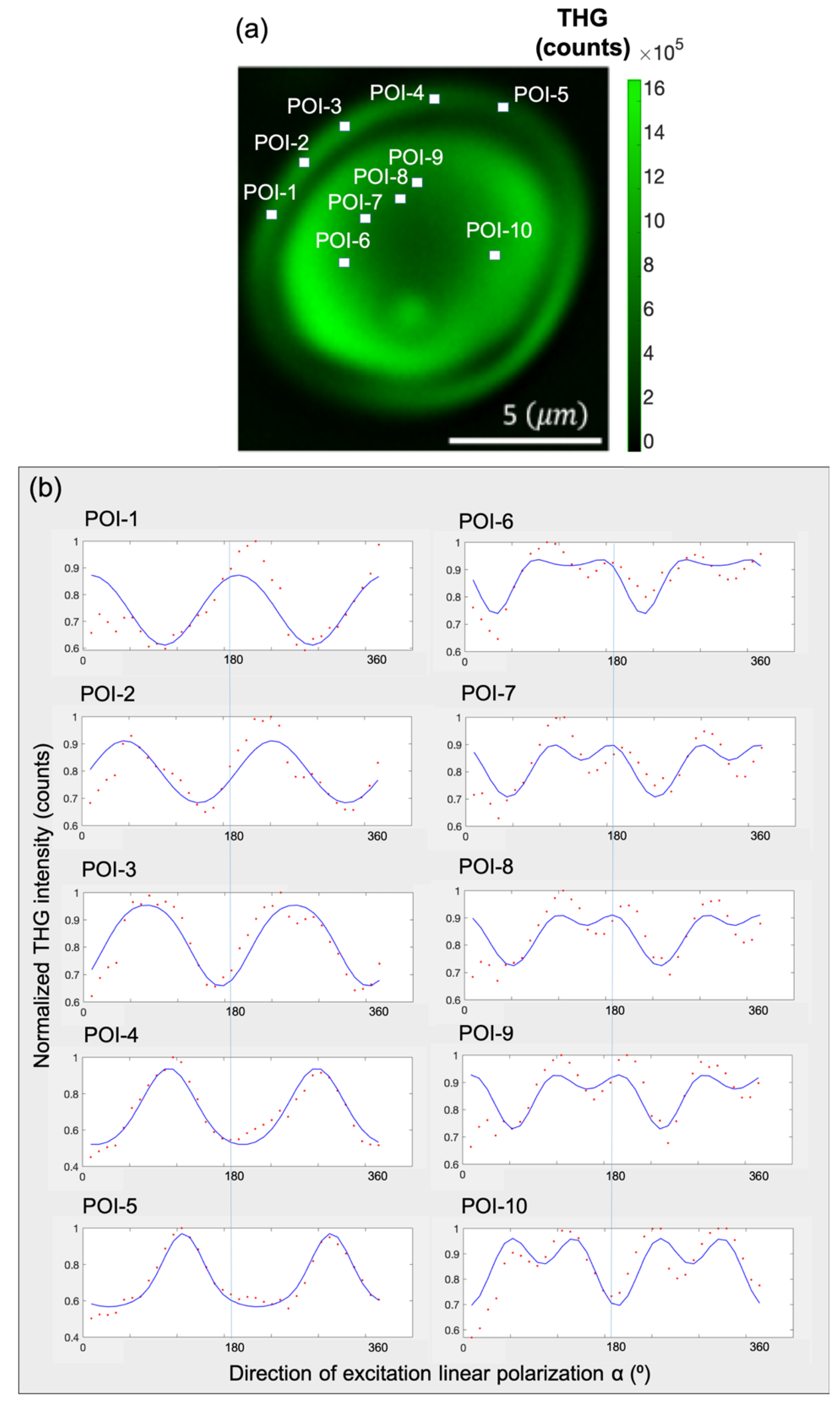
To investigate this further, in
Figure 6a five points of interest (POIs) are selected in the shell and five POIs in the core of the granule. In
Figure 6b, the P-THG modulations from each POI, are presented (angle
ϵ [0°, 360°], with a step of 10°). Then, the P-THG experimental data from each POI (
Figure 6a) is fitted with Equation (6), using the criterion AR>1 and the P-THG modulation curves shown in
Figure 6b are obtained. The values of the free parameters AR, φ, A, C, and D of Equation (6), after fitting the P-THG experimental data with Equation (6), are presented in
Table 1. As seen in
Table 1, POIs 1-5, which belong to the shell of the granule, exhibited AR values greater than 1.25 whereas the POIs 6-10, which belong to the core of the granule, exhibited AR values less than 1.25.
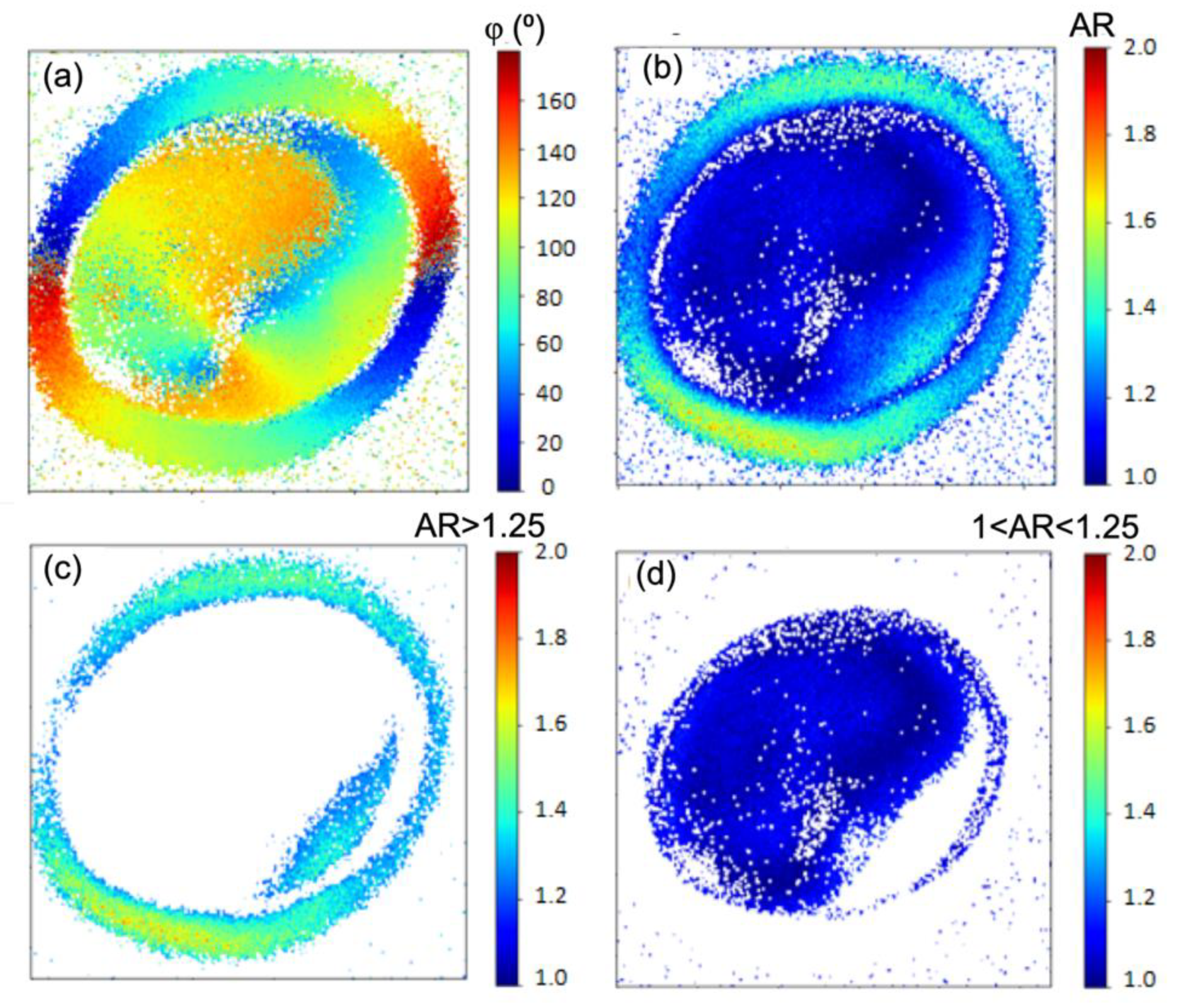
Figure 7a presents a pixel-by-pixel map of the molecular orientation angle φ, obtained by fitting the experimental data from Video S1 using Equation (6). The color scale represents molecular angles from 0° (blue, left side) to 180° (red, right side), illustrating a clockwise evolution of orientation consistent with the rotation of the excitation linear polarization. This continuous color progression across the shell indicates a radial molecular arrangement. Notably, on the right side of the granule, red regions (φ ≈ 180°) are immediately followed by blue regions (φ ≈ 0°). This apparent discontinuity arises from the modulo of 180° in the P-THG signal described in
Figure 3a. Since φ and φ + kπ (where k is an integer) produce identical P-THG responses, molecular orientations between 180° and 360° are effectively mapped to the 0°–180° range. For example, φ = 190° is equivalent to φ = 10°, and φ = 360° is equivalent to φ = 180°.
Moreover, in
Figure 7a, the molecular orientation in the core appears less uniform, likely reflecting deviations from perfect radial molecular arrangement in the granule. Moreover, it is noted that the evolution of the molecular directions in the core has an ~90° shift with the evolution of the molecular directions in the shell. This is the result of the anisotropic P-THG behavior of the granule between the shell and its core.
In
Figure 7b where a map of the AR parameter is presented, it is noted that the shell predominantly presents AR values bigger than 1.25, while the core of the granule shows mainly AR<1.25. In
Figure 7c by selecting pixels with AR>1.25 the shell of the granule is exposed, while in
Figure 7d for 1<AR<1.25 the core of the granule is exposed. In the shell (
Figure 7c) the mean of the AR values is <AR>=1.37, with standard-deviation σ=0.11, while in the core <AR>=1.14 with σ=0.06. The <AR>=1.37 in the shell implies that the
contributes 1.37 times more in THG, than the
. While, the <AR>=1.14 in the core of the granule implies that the
contributes 1.14 times more in THG, than the
.
The mean AR values in the shell of the granule are different than the mean AR values in the core. This directly implies that the molecular structure in the shell differs from the molecular structure in the core of the granule. The fact that the “ghost” envelope structure of granules discussed above, has a different structure than the core [
7], is clearly reflected in the AR values of polarization-dependent THG microscopy. In
Figure S2 and in Video S2, P-THG imaging is presented in another corn starch granule, yielding similar results with those presented above.
4. Conclusions
In this study the structural anisotropy between the shell and the core of corn starch granules is probed using P-THG microscopy. By rotating the direction of the excitation linear polarization, the THG signals originating from the shell, modulate in a different manner than the THG signals originating from the core of the granules. A theoretical framework is developed, which describes the P-THG using orthorhombic symmetry, characteristic of corn starch. After pixel-by-pixel fitting of the model and rendering of the retrieved molecular angles, the radial distribution of the molecules is revealed. An anisotropy-ratio, AR=/, which compares the contribution of the to the THG signals with the contribution of the , is introduced. The structural anisotropy between the shell and the core is reflected in the AR. By segmenting the values of the AR, the shell and core are discriminated, probing their different molecular architecture. This work provides a label-free methodology to identify structural anisotropy in biological samples and demonstrates how P-THG contrast can reveal different molecular arrangements, beyond what is accessible through intensity-only THG microscopy.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: Corn starch granules are SHG active; Figure S2: P-THG analysis of another corn starch granule; Video S1: P-THG starch 1; Video S2: P-THG starch 2.
Funding
This work was funded by the project MAYA – Project number: 014772. This project is carried out within the framework of the National Recovery and Resilience Plan Greece 2.0, funded by the European Union – NextGenerationEU (Implementation body: HFRI).
Data Availability Statement
Data underlying the results presented in this study are not publicly available at this time but may be obtained from the authors upon reasonable request.
Acknowledgments
Maria Kefalogianni acknowledges the project Brainprecision - TAEDR-0535850. This project is carried out within the framework of the National Recovery and Resilience Plan Greece 2.0, funded by the European Union – NextGenerationEU. Sotiris Psilodimitrakopoulos acknowledges the project MAYA – Project number: 014772. This project is carried out within the framework of the National Recovery and Resilience Plan Greece 2.0, funded by the European Union – NextGenerationEU (Implementation body: HFRI).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gallant, D. J.; Bouchet, B.; Baldwin, P. M. Microscopy of starch: Evidence of a new level of granule organization. Carbohydr. Polym. 1997, 32, 177–191. [Google Scholar] [CrossRef]
- Gallant, D. J.; Bouchet, B.; Buleon, A.; Perez, S. Physical characteristics of starch granules and susceptibility to enzymatic degradation. Eur. J. Clin. Nutr. 1992, 46, S3–S16. [Google Scholar] [PubMed]
- Rodriguez-Garcia, M. E.; Hernandez-Landaverde, M. A.; Delgado, J. M.; et al. Crystalline structures of the main components of starch. Curr. Opin. Food Sci. 2021, 37, 107–111. [Google Scholar] [CrossRef]
- Ouyang, Q.; Wang, X.; Xiao, Y.; et al. Structural changes of A-, B- and C-type starches of corn, potato and pea as influenced by sonication temperature and their relationships with digestibility. Food Chem. 2021, 358, 129858. [Google Scholar] [CrossRef] [PubMed]
- Oostergetel, G. T.; van Bruggen, J. E. F. The crystalline domains in potato starch granules are arranged in a helical fashion. Carbohydr. Polym. 1993, 21, 7–12. [Google Scholar] [CrossRef]
- Prentice, D. R. M.; Stark, J. R.; Gidley M., J. Granule residues and ‘ghosts’ remaining after heating A-type barley starch granules in water. Carbohydr. Res. 1992, 227, 121–130. [Google Scholar] [CrossRef]
- Obanni, M.; BeMiller, J.N. Ghost microstructures of starch from different botanical sources. Cereal Chem. 1996, 73(3), 333–337. [Google Scholar]
- de Miranda, J. A. T.; de Carvalho, L. M. J.; de, M. Vieira, A. C. et al. Scanning electron microscopy and crystallinity of starches granules from cowpea, black and carioca beans in raw and cooked forms. Brazilian Food Science and Technology 2019, 39, 718–724. [Google Scholar] [CrossRef]
- Martínez-Sanz, M.; Gidley, M. J.; Gilbert, E. P. Application of X-ray and neutron small angle scattering techniques to study the hierarchical structure of plant cell walls: A review. Carbohydr. Polym. 2015, 125, 120–134. [Google Scholar] [CrossRef] [PubMed]
- Kovrlija, R.; Rondeau-Mouro, C. Multi-scale NMR and MRI approaches to characterize starchy products. Food Chem. 2017, 236, 2–14. [Google Scholar] [CrossRef] [PubMed]
- Psilodimitrakopoulos, S.; Amat-Roldan, I, Santos, Starch granules as a probe for the polarization at the sample plane of a high resolution multiphoton microscope. In Proceedings of the SPIE Photonics West, San Jose, USA, 6860, 68600E, 2008.
- Psilodimitrakopoulos, S.; Amat-Roldan, I.; Loza-Alvarez, P.; Artigas, D. Estimating the helical pitch angle of amylopectin in Starch using polarization second harmonic generation microscopy. J. Opt. 2010, 12(8), 084007. [Google Scholar] [CrossRef]
- Psilodimitrakopoulos, S.; Amat-Roldan, I.; Loza-Alvarez, P.; Artigas, D. Effect of molecular organization on the image histograms of polarization SHG microscopy, Biomed. Opt. Express. 2012, 3, 2681. [Google Scholar] [CrossRef] [PubMed]
- Cisek, R.; Tokarz, D.; Kontenis, L.; et al. Polarimetric second harmonic generation microscopy: An analytical tool for starch bioengineering. Starch/Staerke 2018, 70, 1700031. [Google Scholar] [CrossRef]
- Chouët, A.; Chevallier, S.; Fleurisson, R.; et al. Label-free fried starchy matrix: Investigation by harmonic generation microscopy. Sensors. 2019, 19(9), 2024. [Google Scholar] [CrossRef] [PubMed]
- Psilodimitrakopoulos, S.; Gavgiotaki, E.; Melessanaki, K.; et al. Polarization second harmonic generation discriminates between fresh and aged, starch-based adhesives used in cultural heritage. Microsc. Microanal. 2016, 22, 1072. [Google Scholar] [CrossRef]
- Morizet, J.; Ducourthial, G.; Supatto, W.; et al. High-speed polarization-resolved third-harmonic microscopy. Optica. 2019, 6(3), 385–388. [Google Scholar] [CrossRef]
- Waigh, T. A.; Hopkinson, I.; Donald, A. M.; et al. Analysis of the native structure of starch granules with X-ray microfocus diffraction. Macromolecules 1997, 30, 3813–3820. [Google Scholar] [CrossRef]
- Maragkakis, G. M.; Psilodimitrakopoulos, S.; Mouchliadis, L.; et al. Anisotropic Third Harmonic Generation in 2D Tin Sulfide. Adv. Opt. Mater. 2024, 12(29), 2401321. [Google Scholar] [CrossRef]
- Gusachenko, I.; Latour, G.; Schanne-Klein, M.-C. Polarization-resolved second harmonic microscopy in anisotropic thick tissues. Opt. Express. 2010, 18(18), 19339–19352. [Google Scholar] [CrossRef] [PubMed]
- Teulon, C.; Gusachenko, I.; Latour, G.; et al. Theoretical, numerical and experimental study of geometrical parameters that affect anisotropy measurements in polarization-resolved SHG microscopy. Opt. Express. 2015, 23(7), 9313–9328. [Google Scholar] [CrossRef] [PubMed]
- Boyd, R. W. Nonlinear Optics, 2nd ed.Elsevier, 2003. [Google Scholar]
Figure 1.
Schematic representation of the experimental setup for P-THG imaging. It is based on a fs laser beam coupled to a microscope. The fundamental, 1030 nm, pulses are converted to 1542 nm, by means of an optical parametric oscillator. Starch granules, excited by this wavelength, generate THG centered at 514 nm. The THG signals are recorded for different directions of the linear polarization of the excitation beam, via a rotating a half-wave plate. A pair of galvanometric mirrors enables raster-scanning of the fs beam, obtaining P-THG images of the starch granules, for every direction of polarization.
Figure 1.
Schematic representation of the experimental setup for P-THG imaging. It is based on a fs laser beam coupled to a microscope. The fundamental, 1030 nm, pulses are converted to 1542 nm, by means of an optical parametric oscillator. Starch granules, excited by this wavelength, generate THG centered at 514 nm. The THG signals are recorded for different directions of the linear polarization of the excitation beam, via a rotating a half-wave plate. A pair of galvanometric mirrors enables raster-scanning of the fs beam, obtaining P-THG images of the starch granules, for every direction of polarization.
Figure 2.
Coordinate systems used in the theoretical description of polarization-dependent THG in starch granules. The schematic illustrates the relationship between the laboratory coordinate system (X–Y–Z) and the sample coordinate system (x–y–z). At the equatorial plane of the granule, where the molecular axes lie predominantly in the x–y plane, the sample and laboratory coordinate planes (x–y and X–Y, respectively) are considered parallel (z=Z). The excitation electric field
Figure 2.
Coordinate systems used in the theoretical description of polarization-dependent THG in starch granules. The schematic illustrates the relationship between the laboratory coordinate system (X–Y–Z) and the sample coordinate system (x–y–z). At the equatorial plane of the granule, where the molecular axes lie predominantly in the x–y plane, the sample and laboratory coordinate planes (x–y and X–Y, respectively) are considered parallel (z=Z). The excitation electric field
Figure 3.
Simulated polarization-dependent THG intensity profiles based on Equation (6), illustrating the effect of the anisotropy ratio AR and molecular orientation φ. (a) Simulated P-THG modulation curves for an anisotropy ratio AR=1.3, with fixed parameters A=0.5, C=0.3 and D=0.4. The molecular orientation angle φ varies from 0° to 180°, in 20° increments. (b) Corresponding simulations for AR=1.1, with A=0.7, C=0.3, and D=0.5. In both panels, the modulation curves for φ=0° and φ=180° are identical, reflecting the modulo of 180° in the calculation of angle φ.
Figure 3.
Simulated polarization-dependent THG intensity profiles based on Equation (6), illustrating the effect of the anisotropy ratio AR and molecular orientation φ. (a) Simulated P-THG modulation curves for an anisotropy ratio AR=1.3, with fixed parameters A=0.5, C=0.3 and D=0.4. The molecular orientation angle φ varies from 0° to 180°, in 20° increments. (b) Corresponding simulations for AR=1.1, with A=0.7, C=0.3, and D=0.5. In both panels, the modulation curves for φ=0° and φ=180° are identical, reflecting the modulo of 180° in the calculation of angle φ.
Figure 4.
Two sets of free parameters in Equation (6) describe the same P-THG data. The P-THG modulation curve for a) molecular angle φ=2° and AR=1.27, is similar to the b) molecular angle φ=92° and AR=0.79. The P-THG modulation curve for c) molecular angle φ=97° and AR=1.11, is similar to the d) molecular angle φ=7° and AR=0.9. Consequently, for the same experimentally retrieved P-THG data, the fitting algorithm might provide two different values for φ and AR. In order to solve this ambiguity and to obtain comparable values of the free parameters, we force the algorithm to provide fitting values with AR>1.
Figure 4.
Two sets of free parameters in Equation (6) describe the same P-THG data. The P-THG modulation curve for a) molecular angle φ=2° and AR=1.27, is similar to the b) molecular angle φ=92° and AR=0.79. The P-THG modulation curve for c) molecular angle φ=97° and AR=1.11, is similar to the d) molecular angle φ=7° and AR=0.9. Consequently, for the same experimentally retrieved P-THG data, the fitting algorithm might provide two different values for φ and AR. In order to solve this ambiguity and to obtain comparable values of the free parameters, we force the algorithm to provide fitting values with AR>1.
Figure 5.
Power-law dependency of detected signals and P-THG imaging microscopy of starch and P-THG imaging. a) Log-log plot of the THG intensity from starch as a function of the incident pump power. Black data points with error bars represent the experimental measurements, while the red doted-line shows the linear fit. The slope of approximately 3 confirms the third-harmonic generation process. b) Series of THG images acquired as the excitation linear polarization angle α (indicated by the red double arrow) is rotated from 0° to 180° in 20° increments. It is noted that the image when α is 0° is similar with the image when α is 180°, verifying the modulo of 180° described in the arithmetic simulations. Scale bars: 5μm.
Figure 5.
Power-law dependency of detected signals and P-THG imaging microscopy of starch and P-THG imaging. a) Log-log plot of the THG intensity from starch as a function of the incident pump power. Black data points with error bars represent the experimental measurements, while the red doted-line shows the linear fit. The slope of approximately 3 confirms the third-harmonic generation process. b) Series of THG images acquired as the excitation linear polarization angle α (indicated by the red double arrow) is rotated from 0° to 180° in 20° increments. It is noted that the image when α is 0° is similar with the image when α is 180°, verifying the modulo of 180° described in the arithmetic simulations. Scale bars: 5μm.
Figure 6.
Experimental P-THG from selected points-of-interest (POIs) and fitting with the model. a) Composite image formed by summing all the THG images seen in
Figure 5b. Five POIs are selected within the shell of the granule and five POIs within its core. b) P-THG modulation curves for each POI, obtained by fitting the experimental data using Equation (6). The POIs 1-5, (shell), present different AR values from POIs 6-10 (core), highlighting the structural anisotropy between the two regions.
Figure 6.
Experimental P-THG from selected points-of-interest (POIs) and fitting with the model. a) Composite image formed by summing all the THG images seen in
Figure 5b. Five POIs are selected within the shell of the granule and five POIs within its core. b) P-THG modulation curves for each POI, obtained by fitting the experimental data using Equation (6). The POIs 1-5, (shell), present different AR values from POIs 6-10 (core), highlighting the structural anisotropy between the two regions.
Figure 7.
Pixel-by-pixel mapping of the molecular orientation angle and the anisotropy ratio. a) Pixel-wise map of the molecular orientation angle φ. The evolution of the colors in the granule shows a radial distribution of the molecular structures. b) Pixel-wise map of the anisotropy-ratio AR. c) Mapping of regions with AR>1.25 highlighting the shell of the granule. (b) Mapping of regions with 1<AR<1.25 exposes the core of the granule.
Figure 7.
Pixel-by-pixel mapping of the molecular orientation angle and the anisotropy ratio. a) Pixel-wise map of the molecular orientation angle φ. The evolution of the colors in the granule shows a radial distribution of the molecular structures. b) Pixel-wise map of the anisotropy-ratio AR. c) Mapping of regions with AR>1.25 highlighting the shell of the granule. (b) Mapping of regions with 1<AR<1.25 exposes the core of the granule.
Table 1.
Values of the free parameters AR, φ, A, C, and D, obtained after fitting the experimental P-THG data of the POIs seen in
Figure 6a, using Equation (6). The R
2 denotes the quality of fitting.
Table 1.
Values of the free parameters AR, φ, A, C, and D, obtained after fitting the experimental P-THG data of the POIs seen in
Figure 6a, using Equation (6). The R
2 denotes the quality of fitting.
| |
POI-1 |
POI-2 |
POI-3 |
POI-4 |
POI-5 |
POI-6 |
POI-7 |
POI-8 |
POI-9 |
POI-10 |
| AR |
1.2±0.03 |
1.16±0.04 |
1.3±0.05 |
1.35±0.06 |
1.27±0.04 |
1.12±0.02 |
1.091±0.03 |
1.097±0.03 |
1.096±0.03 |
1.11±0.03 |
|
φ (°)
|
8.8±0.04 |
51.9±0.04 |
75.1±0.03 |
104.9±0.03 |
121.7±0.03 |
126.8±0.02 |
141.7±0.03 |
147.9±0.03 |
152.4±0.03 |
96.8±0.03 |
| A |
0.61±0.02 |
0.68±0.03 |
0.56±0.03 |
0.52±0.03 |
0.61±0.02 |
0.87±0.02 |
0.71±0.02 |
0.73±0.02 |
0.73±0.02 |
0.69±0.02 |
| C |
0.26±0.02 |
0.37±0.03 |
0.26±0.04 |
0.31±0.05 |
0.12±0.03 |
-0.06±0.02 |
0.22±0.02 |
0.24±0.02 |
0.01±0.02 |
0.38±0.03 |
| D |
0.48±0.02 |
0.35±0.03 |
0.55±0.03 |
0.42±0.04 |
0.5±0.03 |
0.68±0.02 |
0.54±0.02 |
0.52±0.02 |
0.66±0.02 |
0.47±0.02 |
| R2
|
0.59 |
0.65 |
0.88 |
0.92 |
0.93 |
0.64 |
0.5 |
0.47 |
0.43 |
0.6 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).