Submitted:
06 November 2025
Posted:
07 November 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
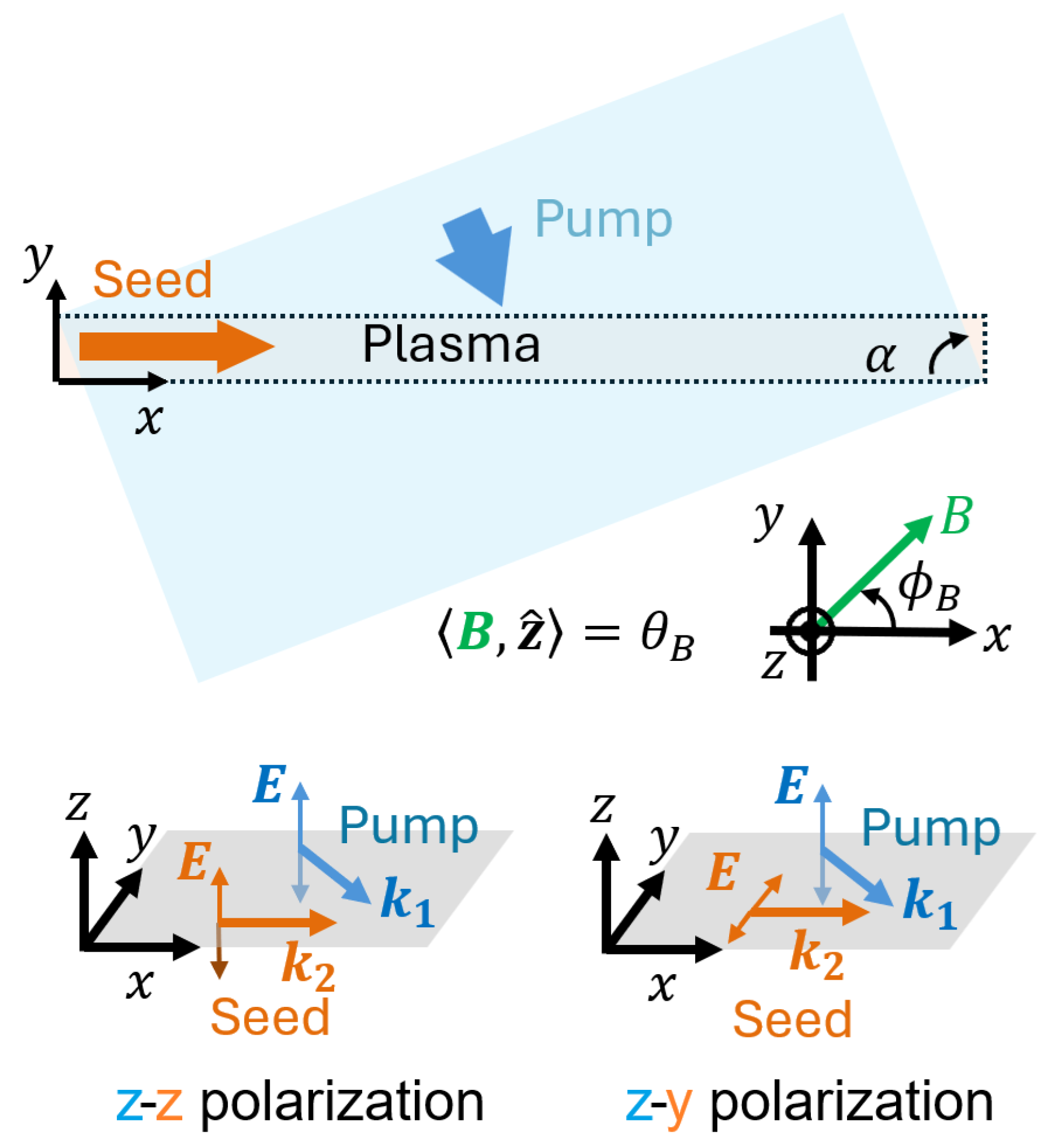
2. Simulation Setup
3. Data Analysis
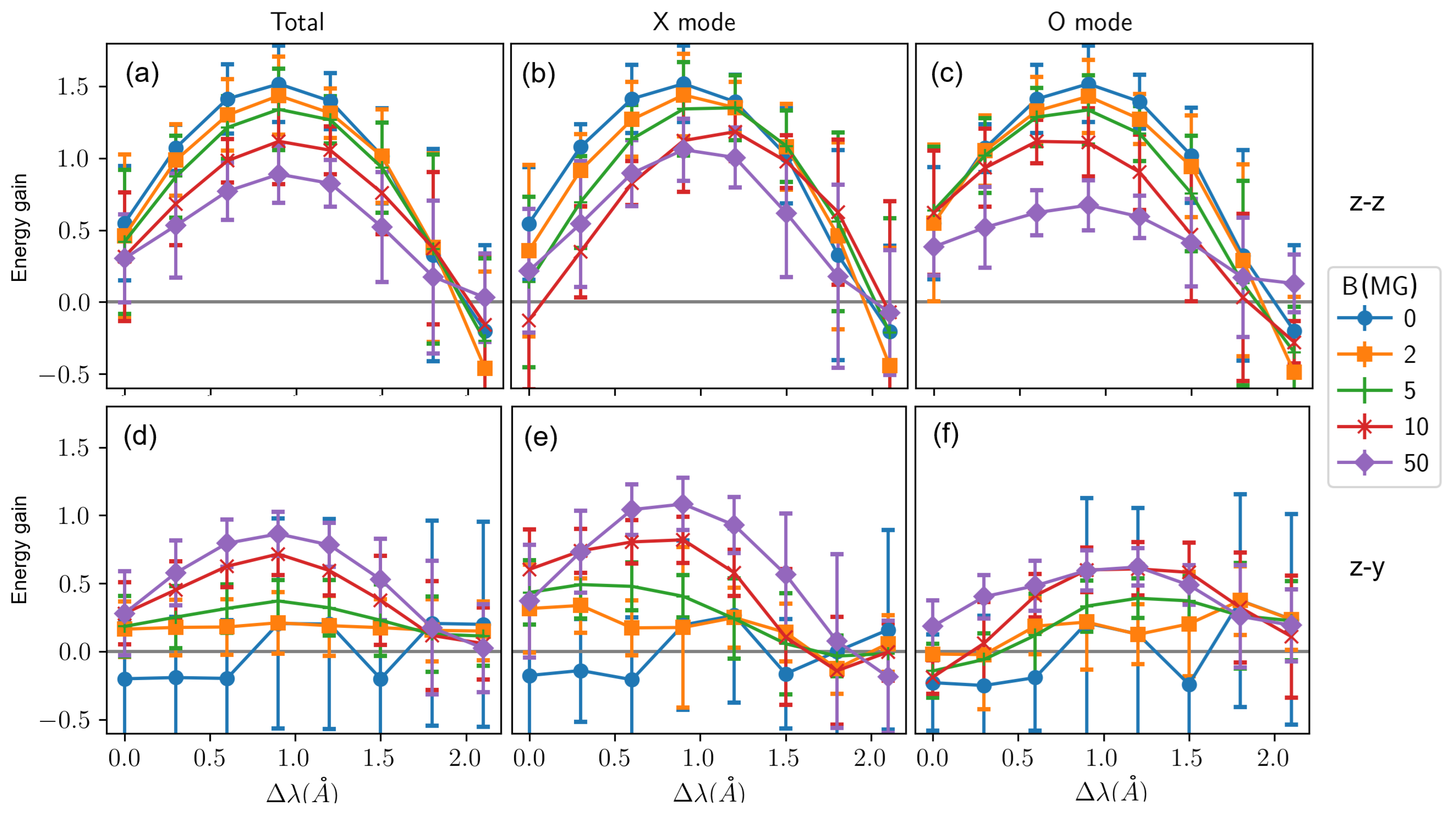
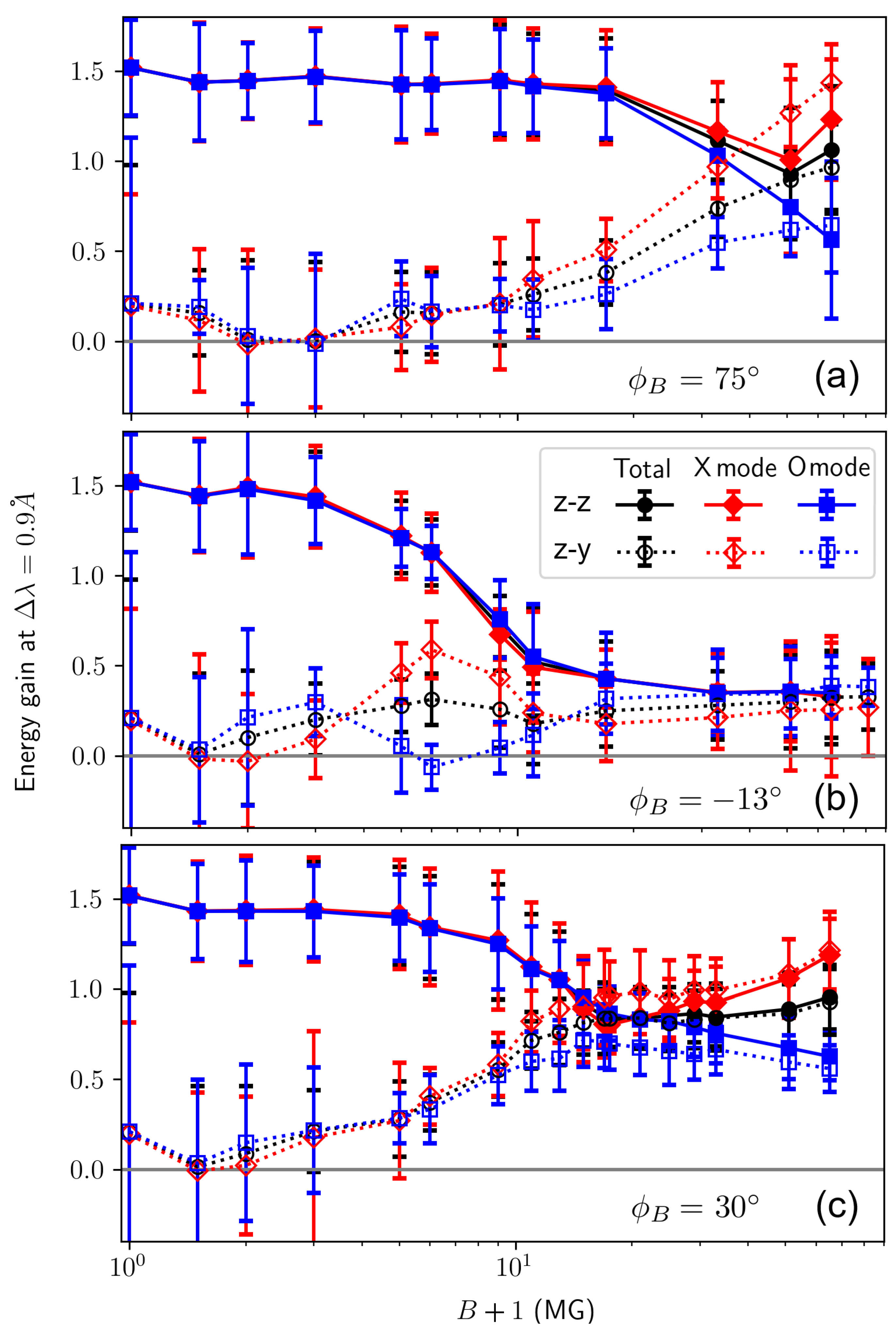
4. Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, P.Y.; Fiksel, G.; Hohenberger, M.; Knauer, J.P.; Betti, R.; Marshall, F.J.; Meyerhofer, D.D.; Séguin, F.H.; Petrasso, R.D. Fusion Yield Enhancement in Magnetized Laser-Driven Implosions. Physical Review Letters 2011, 107, 035006. [Google Scholar] [CrossRef]
- Hohenberger, M.; Chang, P.Y.; Fiksel, G.; Knauer, J.P.; Betti, R.; Marshall, F.J.; Meyerhofer, D.D.; Séguin, F.H.; Petrasso, R.D. Inertial confinement fusion implosions with imposed magnetic field compression using the OMEGA Lasera. Physics of Plasmas 2012, 19, 056306. [Google Scholar] [CrossRef]
- Hansen, E.C.; Davies, J.R.; Barnak, D.H.; Betti, R.; Campbell, E.M.; Glebov, V.Y.; Knauer, J.P.; Leal, L.S.; Peebles, J.L.; Sefkow, A.B.; et al. Neutron yield enhancement and suppression by magnetization in laser-driven cylindrical implosions. Physics of Plasmas 2020, 27, 062703. [Google Scholar] [CrossRef]
- Moody, J.D.; Pollock, B.B.; Sio, H.; Strozzi, D.J.; Ho, D.D.M.; Walsh, C.A.; Kemp, G.E.; Lahmann, B.; Kucheyev, S.O.; Kozioziemski, B.; et al. Increased Ion Temperature and Neutron Yield Observed in Magnetized Indirectly Driven D2-Filled Capsule Implosions on the National Ignition Facility. Physical Review Letters 2022, 129, 195002. [Google Scholar] [CrossRef] [PubMed]
- Peebles, J.L.; Davies, J.R.; Barnak, D.H.; Glebov, V.Y.; Hansen, E.C.; Heuer, P.V.; Leal, L.S.; Bonino, M.J.; Harding, D.R.; Sefkow, A.B.; et al. Demonstration of neutron-yield enhancement by laser preheating and magnetization of laser-driven cylindrical implosions. Physics of Plasmas 2023, 30, 082703. [Google Scholar] [CrossRef]
- Perkins, L.J.; Ho, D.D.M.; Logan, B.G.; Zimmerman, G.B.; Rhodes, M.A.; Strozzi, D.J.; Blackfield, D.T.; Hawkins, S.A. The potential of imposed magnetic fields for enhancing ignition probability and fusion energy yield in indirect-drive inertial confinement fusion. Physics of Plasmas 2017, 24, 062708. [Google Scholar] [CrossRef]
- Walsh, C.A.; O’Neill, S.; Chittenden, J.P.; Crilly, A.J.; Appelbe, B.; Strozzi, D.J.; Ho, D.; Sio, H.; Pollock, B.; Divol, L.; et al. Magnetized ICF implosions: Scaling of temperature and yield enhancement. Physics of Plasmas 2022, 29, 042701. [Google Scholar] [CrossRef]
- Strozzi, D.J.; Sio, H.; Zimmerman, G.B.; Moody, J.D.; Weber, C.R.; Djordjević, B.Z.; Walsh, C.A.; Hammel, B.A.; Pollock, B.B.; Povilus, A.; et al. Design and modeling of indirectly driven magnetized implosions on the NIF. Physics of Plasmas 2024, 31, 092703. [Google Scholar] [CrossRef]
- Walsh, C.A.; O’Neill, S.T.; Strozzi, D.J.; Leal, L.S.; Spiers, R.; Crilly, A.J.; Pollock, B.; Sio, H.; Hammel, B.; Djordjević, B.Z.; et al. Magnetized ICF implosions: Ignition at low laser energy using designs with more ablator mass remaining. Physics of Plasmas 2025, 32, 072715. [Google Scholar] [CrossRef]
- Appelbe, B.; Velikovich, A.L.; Sherlock, M.; Walsh, C.; Crilly, A.; O’ Neill, S.; Chittenden, J. Magnetic field transport in propagating thermonuclear burn. Physics of Plasmas 2021, 28, 032705. [Google Scholar] [CrossRef]
- O’Neill, S.T.; Appelbe, B.D.; Crilly, A.J.; Walsh, C.A.; Strozzi, D.J.; Moody, J.D.; Chittenden, J.P. Burn propagation in magnetized high-yield inertial fusion. Physics of Plasmas 2025, 32, 022703. [Google Scholar] [CrossRef]
- Stamper, J.A. Review on spontaneous magnetic fields in laser-produced plasmas: Phenomena and measurements. Laser and Particle Beams 1991, 9, 841–862. [Google Scholar] [CrossRef]
- Sherlock, M.; Bissell, J.J. Suppression of the Biermann Battery and Stabilization of the Thermomagnetic Instability in Laser Fusion Conditions. Physical Review Letters 2020, 124, 055001. [Google Scholar] [CrossRef] [PubMed]
- Walsh, C.; Sadler, J.; Davies, J. Updated magnetized transport coefficients: impact on laser-plasmas with self-generated or applied magnetic fields. Nuclear Fusion 2021, 61, 116025. [Google Scholar] [CrossRef]
- Campbell, P.T.; Walsh, C.A.; Russell, B.K.; Chittenden, J.P.; Crilly, A.; Fiksel, G.; Gao, L.; Igumenshchev, I.V.; Nilson, P.M.; Thomas, A.G.R.; et al. Measuring magnetic flux suppression in high-power laser–plasma interactions. Physics of Plasmas 2022, 29, 012701. [Google Scholar] [CrossRef]
- Cattani, D.; Sacchi, C. A theory on the creation of stellar magnetic fields. Il Nuovo Cimento B (1965-1970) 1966, 46, 258–272. [Google Scholar] [CrossRef]
- Munirov, V.R.; Fisch, N.J. Radiative transfer dynamo effect. Physical Review E 2017, 95, 013205. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, G.F. Self-generated magnetic field in laser plasma with super-Gaussian distributed electrons. Physics of Plasmas 2024, 31, 092303. [Google Scholar] [CrossRef]
- Gotchev, O.V.; Chang, P.Y.; Knauer, J.P.; Meyerhofer, D.D.; Polomarov, O.; Frenje, J.; Li, C.K.; Manuel, M.J.E.; Petrasso, R.D.; Rygg, J.R.; et al. Laser-Driven Magnetic-Flux Compression in High-Energy-Density Plasmas. Physical Review Letters 2009, 103, 215004. [Google Scholar] [CrossRef]
- Knauer, J.P.; Gotchev, O.V.; Chang, P.Y.; Meyerhofer, D.D.; Polomarov, O.; Betti, R.; Frenje, J.A.; Li, C.K.; Manuel, M.J.E.; Petrasso, R.D.; et al. Compressing magnetic fields with high-energy lasers. Physics of Plasmas 2010, 17, 056318. [Google Scholar] [CrossRef]
- Farmer, W.A.; Koning, J.M.; Strozzi, D.J.; Hinkel, D.E.; Berzak Hopkins, L.F.; Jones, O.S.; Rosen, M.D. Simulation of self-generated magnetic fields in an inertial fusion hohlraum environment. Physics of Plasmas 2017, 24, 052703. [Google Scholar] [CrossRef]
- Sio, H.; Moody, J.D.; Ho, D.D.; Pollock, B.B.; Walsh, C.A.; Lahmann, B.; Strozzi, D.J.; Kemp, G.E.; Hsing, W.W.; Crilly, A.; et al. Diagnosing plasma magnetization in inertial confinement fusion implosions using secondary deuterium-tritium reactions. Review of Scientific Instruments 2021, 92, 043543. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Qin, H.; Fisch, N.J. Laser-plasma interactions in magnetized environment. Physics of Plasmas 2018, 25, 055706. [Google Scholar] [CrossRef]
- Edwards, M.R.; Shi, Y.; Mikhailova, J.M.; Fisch, N.J. Laser Amplification in Strongly Magnetized Plasma. Physical Review Letters 2019, 123, 025001. [Google Scholar] [CrossRef]
- Manzo, L.; Edwards, M.R.; Shi, Y. Enhanced collisionless laser absorption in strongly magnetized plasmas. Physics of Plasmas 2022, 29, 112704. [Google Scholar] [CrossRef]
- Shi, Y. Plasma physics in strong-field regimes. PhD thesis, Princeton University, 2018.
- Shi, Y.; Qin, H.; Fisch, N.J. Plasma physics in strong-field regimes: Theories and simulations. Physics of Plasmas 2021, 28, 042104. [Google Scholar] [CrossRef]
- Shi, Y. Benchmarking magnetised three-wave coupling for laser backscattering: analytic solutions and kinetic simulations. Journal of Plasma Physics 2023, 89, 905890305. [Google Scholar] [CrossRef]
- Boyd, T.J.M.; Rankin, R. Kinetic theory of stimulated Raman scattering from a magnetized plasma. Journal of Plasma Physics 1985, 33, 303–319. [Google Scholar] [CrossRef]
- Yao, W.; Higginson, A.; Marquès, J.R.; Antici, P.; Béard, J.; Burdonov, K.; Borghesi, M.; Castan, A.; Ciardi, A.; Coleman, B.; et al. Dynamics of Nanosecond Laser Pulse Propagation and of Associated Instabilities in a Magnetized Underdense Plasma. Physical Review Letters 2023, 130, 265101. [Google Scholar] [CrossRef]
- Winjum, B.J.; Tsung, F.S.; Mori, W.B. Mitigation of stimulated Raman scattering in the kinetic regime by external magnetic fields. Physical Review E 2018, 98, 043208. [Google Scholar] [CrossRef]
- Laham, N.M.; Nasser, A.S.A.; Khateeb, A.M. Effects of Axial Magnetic Fields on Backward Raman Scattering in Inhomogeneous Plasmas. Physica Scripta 1998, 57, 253. [Google Scholar] [CrossRef]
- Galloway, J.J.; Kim, H. Lagrangian approach to non-linear wave interactions in a warm plasma. Journal of Plasma Physics 1971, 6, 53–72. [Google Scholar] [CrossRef]
- Boyd, T.J.M.; Turner, J.G. Three- and four-wave interactions in plasmas. Journal of Mathematical Physics 1978, 19, 1403–1413. [Google Scholar] [CrossRef]
- Liu, C.; Tripathi, V. Parametric instabilities in a magnetized plasma. Physics Reports 1986, 130, 143–216. [Google Scholar] [CrossRef]
- Cohen, B.I. Compact dispersion relations for parametric instabilities of electromagnetic waves in magnetized plasmas. The Physics of Fluids 1987, 30, 2676–2680. [Google Scholar] [CrossRef]
- Porkolab, M. Parametric processes in magnetically confined CTR plasmas. Nuclear Fusion 1978, 18, 367. [Google Scholar] [CrossRef]
- Grebogi, C.; Liu, C.S. Brillouin and Raman scattering of an extraordinary mode in a magnetized plasma. The Physics of Fluids 1980, 23, 1330–1335. [Google Scholar] [CrossRef]
- Hansen, S.K.; Nielsen, S.K.; Salewski, M.; Stejner, M.; Stober, J.; the ASDEX Upgrade team. Parametric decay instability near the upper hybrid resonance in magnetically confined fusion plasmas. Plasma Physics and Controlled Fusion 2017, 59, 105006. [Google Scholar] [CrossRef]
- Platzman, P.M.; Wolff, P.A.; Tzoar, N. Light Scattering from a Plasma in a Magnetic Field. Physical Reviews 1968, 174, 489–494. [Google Scholar] [CrossRef]
- Stenflo, L. Comments on stimulated scattering of electromagnetic waves by electron Bernstein modes in a plasma. Physical Review A 1981, 23, 2730–2731. [Google Scholar] [CrossRef]
- Kasymov, Z.Z.; Näslund, E.; Starodub, A.; Stenflo, L. Upper hybrid turbulence in a plasma with magnetized electrons. Physica Scripta 1985, 31, 201. [Google Scholar] [CrossRef]
- Hasegawa, A.; Chen, L. Kinetic processes in plasma heating by resonant mode conversion of Alfvén wave. The Physics of Fluids 1976, 19, 1924–1934. [Google Scholar] [CrossRef]
- Wong, H.K.; Goldstein, M.L. Parametric instabilities of circularly polarized Alfvén waves including dispersion. Journal of Geophysical Research: Space Physics 1986, 91, 5617–5628. [Google Scholar] [CrossRef]
- Viñas, A.F.; Goldstein, M.L. Parametric instabilities of circularly polarized large-amplitude dispersive Alfvén waves: excitation of parallel-propagating electromagnetic daughter waves. Journal of Plasma Physics 1991, 46, 107–127. [Google Scholar] [CrossRef]
- Sjölund, A.; Stenflo, L. Non-linear coupling in a magnetized plasma. Zeitschrift für Physik A Hadrons and Nuclei 1967, 204, 211. [Google Scholar] [CrossRef]
- Sjölund, A.; Stenflo, L. Parametric coupling between transverse electromagnetic and longitudinal electron waves. Physica 1967, 35, 499–505. [Google Scholar] [CrossRef]
- Stenflo, L.; Weiland, J.; Wilhelmsson, H. A solution of equations describing explosive instabilities. Physica Scripta 1970, 1, 46. [Google Scholar] [CrossRef]
- Stenflo, L.; Wilhelmsson, H.; Östberg, K. Non-linear Instabilities in Streaming Plasmas. Physica Scripta 1971, 3, 231. [Google Scholar] [CrossRef]
- Stenflo, L. Three-wave interaction in cold magnetized plasmas. Planetary and Space Science 1973, 21, 391–397. [Google Scholar] [CrossRef]
- Larsson, J.; Stenflo, L. Three-wave interactions in magnetized plasmas. Beiträge aus der Plasmaphysik 1973, 13, 169–181. [Google Scholar] [CrossRef]
- Stenflo, L. Kinetic theory of three-wave interaction in a magnetied plasma. Journal of Plasma Physics 1970, 4, 585. [Google Scholar] [CrossRef]
- Stenflo, L. Effect of collisions on resonant three-wave interaction. Plasma Physics 1970, 12, 509. [Google Scholar] [CrossRef]
- Shukla, P.K.; Stenflo, L. Modulational instabilities of electromagnetic waves in a collision-dominated dust-electron plasma. IEEE transactions on plasma science 2002, 29, 267–270. [Google Scholar] [CrossRef]
- Larsson, J.; Stenflo, L.; Tegeback, R. Enhanced fluctuations in a magnetized plasma due to the presence of an electromagnetic wave. Journal of Plasma Physics 1976, 16, 37–45. [Google Scholar] [CrossRef]
- Stenflo, L. Comments on Stimulated Electromagnetic Emissions in the Ionospheric Plasma. Physica Scripta 2004, 2004, 262. [Google Scholar] [CrossRef]
- Kaufman, A.N.; Stenflo, L. Wave Coupling in Cold Nonuniform Magnetoplasma. Physica Scripta 1979, 19, 523. [Google Scholar] [CrossRef]
- Linden, T.; Larsson, J.; Stenflo, L. Three-wave interaction in plasmas with sharp boundaries. Plasma Physics 1982, 24, 1177. [Google Scholar] [CrossRef]
- Lindgren, T.; Stenflo, L.; Kostov, N.; Zhelyazkov, I. Three-wave interaction in a cold plasma column. Journal of Plasma Physics 1985, 34, 427–434. [Google Scholar] [CrossRef]
- Axelsson, P.; Larsson, J.; Stenflo, L. Nonlinear interaction between acoustic gravity waves. In Proceedings of the Annales Geophysicae. Springer Verlag Göttingen, Germany, Vol. 14; 1996; pp. 304–308. [Google Scholar]
- Stenflo, L.; Shukla, P.K. Nonlinear acoustic–gravity waves. Journal of Plasma Physics 2009, 75, 841–847. [Google Scholar] [CrossRef]
- Vladimirov, S.V.; Stenflo, L. Three-wave processes in a turbulent nonstationary plasma. Physics of Plasmas 1997, 4, 1249–1256. [Google Scholar] [CrossRef]
- Brodin, G.; Stenflo, L. Three-wave interaction between transverse and longitudinal waves. Journal of plasma physics 1989, 42, 187–191. [Google Scholar] [CrossRef]
- Brodin, G.; Stenflo, L.; Shukla, P.K. Nonlinear interactions between three inertial Alfvén waves. Journal of plasma physics 2007, 73, 9–13. [Google Scholar] [CrossRef]
- Brodin, G.; Stenflo, L. A new decay channel for upper-hybrid waves. Physica Scripta 2016, 91, 104005. [Google Scholar] [CrossRef]
- Larsson, J.; Stenflo, L. Parametric instabilities of waves in magnetized plasmas. Beitraege Plasmaphysik 1976, 16, 79–85. [Google Scholar] [CrossRef]
- Stenflo, L. Resonant three-wave interactions in plasmas. Physica Scripta 1994, 1994, 15. [Google Scholar] [CrossRef]
- Stenflo, L.; Brodin, G. The three-wave coupling coefficients for a cold magnetized plasma. Journal of plasma physics 2006, 72, 143–147. [Google Scholar] [CrossRef]
- Brodin, G.; Stenflo, L. Three-wave coupling coefficients for a magnetized plasma. Physica Scripta 2012, 85, 035504. [Google Scholar] [CrossRef]
- Stenflo, L. Stimulated scattering of large amplitude waves in the ionosphere. Physica Scripta 1990, 1990, 166. [Google Scholar] [CrossRef]
- Stenflo, L. Self-consistent Vlasov description of a magnetized plasma in a large amplitude circularly polarized wave. Physica Scripta 1981, 23, 779. [Google Scholar] [CrossRef]
- Brodin, G.; Stenflo, L. Wave Generation in a Warm Magnetized Multi-Component Plasma. Contributions to Plasma Physics 2014, 54, 623–625. [Google Scholar] [CrossRef]
- Stenflo, L.; Shukla, P. Wave-wave interactions in plasmas. In Proceedings of the AIP Conference Proceedings. American Institute of Physics, Vol. 1177; 2009; pp. 4–9. [Google Scholar]
- Moody, J.D.; Shi, Y. Vlasov theory of magnetized cross-beam energy transfer in a high energy densityplasma. To be submitted 2025. [Google Scholar]
- Randall, C.J.; Albritton, J.R.; Thomson, J.J. Theory and simulation of stimulated Brillouin scatter excited by nonabsorbed light in laser fusion systems. The Physics of Fluids 1981, 24, 1474–1484. [Google Scholar] [CrossRef]
- Michel, P. Introduction to laser-plasma interactions; Springer Nature, 2023.
- Seka, W.; Edgell, D.H.; Knauer, J.P.; Myatt, J.F.; Maximov, A.V.; Short, R.W.; Sangster, T.C.; Stoeckl, C.; Bahr, R.E.; Craxton, R.S.; et al. Time-resolved absorption in cryogenic and room-temperature direct-drive implosion. Physics of Plasmas 2008, 15, 056312. [Google Scholar] [CrossRef]
- Froula, D.H.; Igumenshchev, I.V.; Michel, D.T.; Edgell, D.H.; Follett, R.; Glebov, V.Y.; Goncharov, V.N.; Kwiatkowski, J.; Marshall, F.J.; Radha, P.B.; et al. Increasing Hydrodynamic Efficiency by Reducing Cross-Beam Energy Transfer in Direct-Drive-Implosion Experiments. Physical Review Letters 2012, 108, 125003. [Google Scholar] [CrossRef] [PubMed]
- Marozas, J.A.; Hohenberger, M.; Rosenberg, M.J.; Turnbull, D.; Collins, T.J.B.; Radha, P.B.; McKenty, P.W.; Zuegel, J.D.; Marshall, F.J.; Regan, S.P.; et al. First Observation of Cross-Beam Energy Transfer Mitigation for Direct-Drive Inertial Confinement Fusion Implosions Using Wavelength Detuning at the National Ignition Facility. Physical Review Letters 2018, 120, 085001. [Google Scholar] [CrossRef] [PubMed]
- Michel, P.; Divol, L.; Town, R.P.J.; Rosen, M.D.; Callahan, D.A.; Meezan, N.B.; Schneider, M.B.; Kyrala, G.A.; Moody, J.D.; Dewald, E.L.; et al. Three-wavelength scheme to optimize hohlraum coupling on the National Ignition Facility. Physical Review E 2011, 83, 046409. [Google Scholar] [CrossRef]
- Moody, J.; Michel, P.; Divol, L.; Berger, R.; Bond, E.; Bradley, D.; Callahan, D.; Dewald, E.; Dixit, S.; Edwards, M.; et al. Multistep redirection by cross-beam power transfer of ultrahigh-power lasers in a plasma. Nature Physics 2012, 8, 344–349. [Google Scholar] [CrossRef]
- Pickworth, L.A.; Döppner, T.; Hinkel, D.E.; Ralph, J.E.; Bachmann, B.; Masse, L.P.; Divol, L.; Benedetti, L.R.; Celliers, P.M.; Chen, H.; et al. Application of cross-beam energy transfer to control drive symmetry in ICF implosions in low gas fill Hohlraums at the National Ignition Facility. Physics of Plasmas 2020, 27, 102702. [Google Scholar] [CrossRef]
- Arber, T.D.; Bennett, K.; Brady, C.S.; Lawrence-Douglas, A.; Ramsay, M.G.; Sircombe, N.J.; Gillies, P.; Evans, R.G.; Schmitz, H.; Bell, A.R.; et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Physics and Controlled Fusion 2015, 57, 1–26. [Google Scholar] [CrossRef]
- Turnbull, D.; Colaïtis, A.; Hansen, A.M.; Milder, A.L.; Palastro, J.P.; Katz, J.; Dorrer, C.; Kruschwitz, B.E.; Strozzi, D.J.; Froula, D.H. Impact of the Langdon effect on crossed-beam energy transfer. Nature Physics 2020, 16, 181–185. [Google Scholar] [CrossRef]
- Hansen, A.M.; Nguyen, K.L.; Turnbull, D.; Albright, B.J.; Follett, R.K.; Huff, R.; Katz, J.; Mastrosimone, D.; Milder, A.L.; Yin, L.; et al. Cross-beam energy transfer saturation: ion heating and pump depletion. Plasma Physics and Controlled Fusion 2022, 64, 034003. [Google Scholar] [CrossRef]
- Seaton, A.G.; Yin, L.; Follett, R.K.; Albright, B.J.; Le, A. Cross-beam energy transfer in direct-drive ICF. I. Nonlinear and kinetic effects. Physics of Plasmas 2022, 29, 042706. [Google Scholar] [CrossRef]
- Yin, L.; Nguyen, T.B.; Chen, G.; Chacon, L.; Stark, D.J.; Green, L.; Haines, B.M. Time-dependent saturation and physics-based nonlinear model of cross-beam energy transfer. Physics of Plasmas 2023, 30, 042706. [Google Scholar] [CrossRef]
- Shi, Y. Particle-in-cell simulations of magnetized crossbeam energy transfer [Data set]. Zenodo. 2025. [CrossRef]
- Taflove, A.; Hagness, S.C.; Piket-May, M. Computational electromagnetics: the finite-difference time-domain method. The Electrical Engineering Handbook 2005, 3, 15. [Google Scholar]
- Shi, Y. Three-wave interactions in magnetized warm-fluid plasmas: General theory with evaluable coupling coefficient. Physical Review E 2019, 99, 063212. [Google Scholar] [CrossRef]
- Shi, Y. MATLAB code for evaluating three-wave coupling in magnetized warm-fluid plasmas. https://gitlab.com/seanYuanSHI/three-wave-matlab, 2022.
- Shi, Y. MATLAB code for analyzing particle-in-cell simulations for magnetized crossbeam energy transfer. https://gitlab.com/seanYuanSHI/magnetized-cross-beam-energy-transfer, 2022.
- Shi, Y.; Qin, H.; Fisch, N.J. Three-wave scattering in magnetized plasmas: From cold fluid to quantized Lagrangian. Physical Review E 2017, 96, 023204. [Google Scholar] [CrossRef]
- Shi, Y.; Fisch, N.J. Amplification of mid-infrared lasers via backscattering in magnetized plasmas. Physics of Plasmas 2019, 26, 072114. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




