Resolution of the Hubble Tension by a Reversible Fractal Cosmology: The Ultimate Black Hole Framework

1. Introduction

Modern cosmology faces persistent tensions between early- and late-time measurements of the cosmic expansion rate [1,2]. While the $\Lambda$CDM model successfully describes most large-scale observations, it relies on the assumption of homogeneity and a dark energy component with constant equation of state. The resulting framework reproduces the CMB anisotropies and baryon acoustic oscillations (BAO), yet shows growing discrepancies in the Hubble constant $H_0$ and the detailed shape of $H\left(z\right)$ inferred from supernovae and cosmic chronometers.

An alternative viewpoint emerges if one relaxes the assumption of large-scale smoothness. Inhomogeneities can modify the averaged cosmic dynamics through non-linear backreaction terms [3], while gravitational clustering itself may produce fractal-like matter distributions at different epochs [4,5]. Within this broader context, the Ultimate Black Hole (UBH) cosmology proposes that the Universe originated from the fragmentation of an ultimate black hole, whose decay generated a self-similar, entropy-driven hierarchy of black holes across scales. This fractal inheritance governs the expansion history through a redshift-dependent effective spatial dimension $D_f\left(z\right)$, linking microstructure, entropy growth, and large-scale kinematics.

The present paper develops this scenario into a quantitative cosmological model and performs its first observational test. By incorporating both fractal entropy effects and Buchert-type backreaction, the UBH framework generalizes the Friedmann equation while retaining a minimal, physically interpretable parameter set. Fitting this model to the Pantheon Type Ia supernova sample yields an excellent agreement and reproduces the locally measured Hubble constant $H_0=73\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$, while maintaining consistency with the early-Universe calibration from Planck data [6]. Hence, the long-standing Hubble tension can be resolved within a single, self-consistent formalism.

The structure of the paper is as follows. Section 2 outlines the theoretical foundations, introducing the fractal entropy concept, the modified Hubble function with backreaction, the early-time Fractal Early Energy term (FEE), and curvature-window terms. Section 2.8 presents the dataset and fitting method. Section 3 summarizes the results, the statistical outcomes, and the robustness tests. Section 4 discusses the physical interpretation and implications for cosmic structure, entropy evolution, and the Hubble tension. Conclusions are drawn in Section 5.

2. Theoretical Framework and Methods

2.1. Fractal Horizon Concept, Entropy Scaling, and Critical UBH Mass

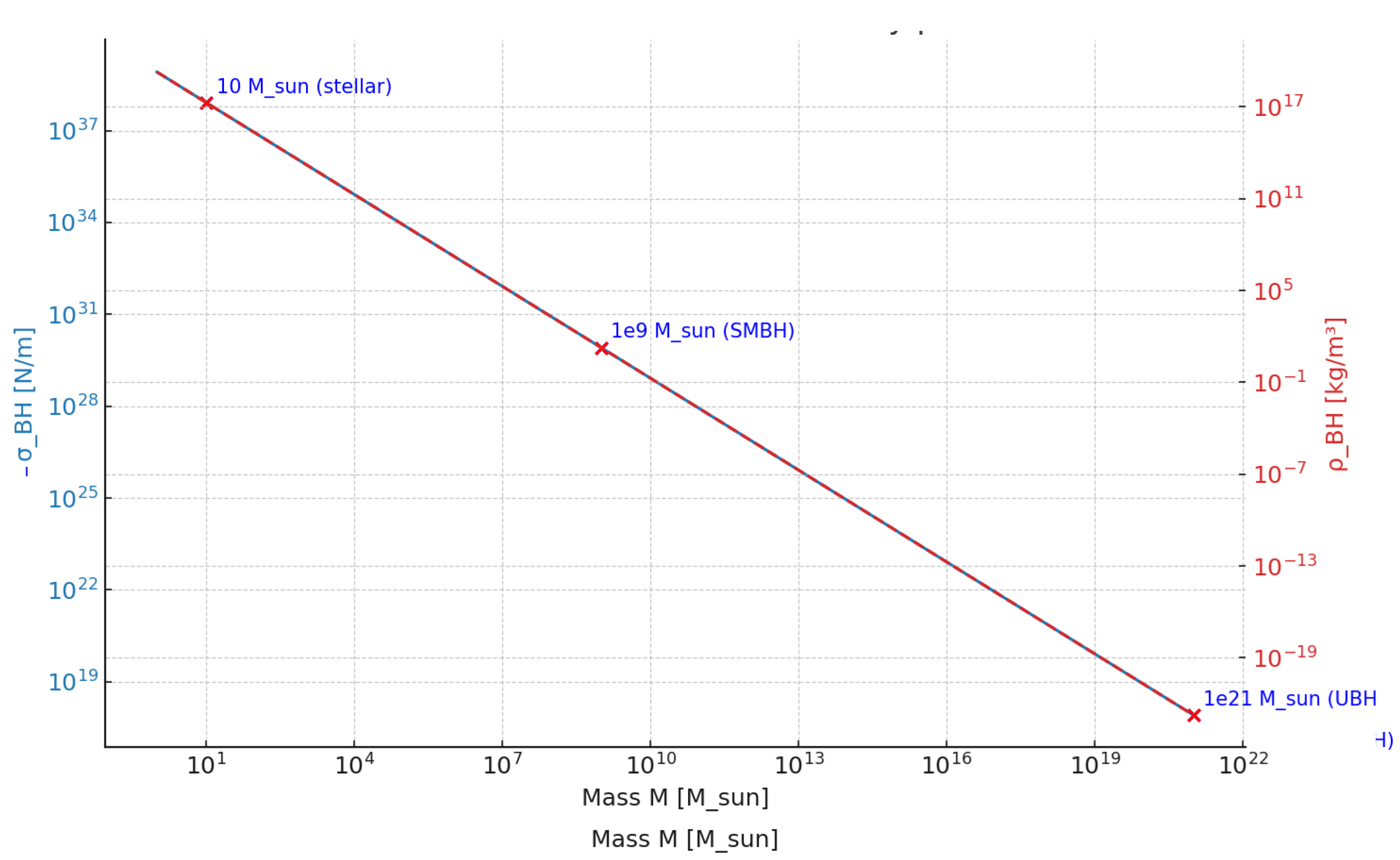
As a starting point for the following considerations, we consider the state of the UBH with already sufficiently large mass. Since the Schwarzschild radius is proportional to this mass ($R_S=2MG/c^2$), the mass density $\overline{\rho }\left(M\right)=3M/\left(4\pi R_s^3\right)\propto M^{-2}$ -see Figure 1. At $M^{19}M\odot$ ($M\odot$ = solar mass), the mass density is incredibly low, and quantum gravity fluctuations can then lead to structure formation, especially near the horizon. Again, due to the low density, filament-like structures should form, but these develop into fractal structures, as is known from growing processes in nature [7]. It seems reasonable to assume that the fractal dimension of these objects is between 1 and 2. These structures can in turn be metastable over time, as the dissipation processes are not sufficient to smooth the structures due to the low density. Moreover, these quasi-one-dimensional structures together with the strongly reduced effective surface tension of the horizon (cf. Figure 1, [8]) stimulate the fraying and fracturing of the horizon surface .

That means, the horizon of a sufficiently massive black hole cannot remain a smooth, two-dimensional sphere as in the standard Bekenstein–Hawking picture [9,10]. And it is natural that the limp and susceptible horizon will take on a fractal structure with a fractal dimension greater than 2, because of the quasi-spherical surface. Due to the causal connection between the volumes and surface structures, it makes sense to assume that the Hurst parameters of the internal structures and the horizon are the same, i.e. $H_h=H_{int}$. It is essential to note that fractal scaling of the horiyon has a lower and upper limit. The lower cutoff length ${\ell }_c$ is certainly larger than the Planck length $lp$, since smoothing dissipative processes becomes more effective for smaller distances. On the other hand, fractal growth of the horizon is also limited upwards by by a characteristic upper cutoff scale $dR$.This scale is not arbitrary; by analogy with the arguments that stabilize the nearly spherical equilibrium of astrophysical horizons (suppressing long-wavelength corrugations), $dR$ can be viewed as the smallest dynamically coherent surface/metric fluctuation that survives coarse-graining in the emergent spacetime description. As a consequence of both cutoff the effective area $A_{f,h}$ of the UBH horizon scales approximately as [7]

$$A_{f,h}\simeq A_{0,h}{\left({\displaystyle \frac{d_R}{{\ell }_c}}\right)}^{H_h},$$

(1)

where $A_{0,h}=4\pi R_h^2$ is the area of a smooth horizon of radius $R_h=2G{M}_{\mathrm{UBH}}/c^2$ and the fractal morphology of the UBH horizon is characterized by the Hurst parameter $H_h$ with fractal dimension

$$D_{f,h}=2+H_h,$$

(2)

If the Bekenstein–Hawking relation remains valid for such a fractalized surface, the entropy of the UBH becomes

$$S_{\mathrm{UBH},\mathrm{f}}\simeq {\left({\displaystyle \frac{d_R}{{\ell }_c}}\right)}^{H_h}{S}_{\mathrm{UBH}},S_{\mathrm{UBH}}={\displaystyle \frac{4\pi k_{B}G}{\hslash c}}{M}_{\mathrm{UBH}}^2,$$

(3)

where $S_{\mathrm{UBH}}$ is the standard entropy of a smooth-horizon black hole.

To consider the instability of the UBH we have to compare the UBH entropy with the entropy of a population of distributed black holes with rather different sizes distributed self-similarly within the UBH volume, forming a fractal configuration characterized by the scaling law for their entropy

$$S_{\mathrm{BHs},\mathrm{f}}\simeq S_{\mathrm{BH}}^{\mathrm{sum}}{\left({\displaystyle \frac{R_c}{{\ell }_c\left(BHs\right)}}\right)}^{H_s},$$

(4)

where $R_c$ as the upper cutoff of the fractal domain is smaller or even equal to the UBH radius $R_S$. The lower cutoff ${\ell }_c\left(BHs\right)$ is probably the same as that for the horizon structure but it can be even smaller, at least equal the Planck length $lp$. $S_{\mathrm{BH}}^{\mathrm{sum}}$ is the sum of entropies of the assumed population of black holes. According to the above mentioned arguments, the fractal character of the inner UBH structure and the horizon is inherited by the cosmic medium, the fractal Hurst parameter $H_s$ used in Equ. 4 must be the the same as for the horizon, i.e. $H_s=H_h$, which ensures the continuity of fractal properties across the UBH burst. The ratio of $S_{\mathrm{BHs}}$ to horizon entropy is then

$${\displaystyle \frac{S_{\mathrm{BHs}}}{S_{\mathrm{UBH},\mathrm{f}}}}={\displaystyle \frac{S_{\mathrm{BH}}^{\mathrm{sum}}}{S_{\mathrm{UBH}}}}\{\left({\displaystyle \frac{R_c}{d_R}}\right){\left({\displaystyle \frac{{\ell }_c}{{\ell }_c\left(BHs\right)}}\right\}}^{H_s}.$$

(5)

Analysing this relation we have to find the solution, where ${\S }_{\mathrm{BHs}}/S_{\mathrm{UBH},\mathrm{f}}=1$ as a condition for the critical UBH-mass $M_{critical}$. Increasing the UBH-mass the quantum-gravitaional fluctuations becomes stronger with the consequence that the fractal dimension $D_{f,h}$ will grow, too. Therefore, for quantitative analyses, it can be assumed that the fractal horizon dimension approximately follows the following relationship

$$D_{f,h}\left(M_{\mathrm{UBH}}\right)=3-exp\left[-\alpha {\displaystyle \frac{M_{\mathrm{UBH}}-M_0}{M_0}}\right],$$

(6)

with $\alpha$ a dimensionless parameter and Mo the mass at which fractal behavior begins. As $M_{\mathrm{UBH}}\to \infty$, the horizon dimension saturates at $D_{f,h}\to 3$, corresponding to a fully space-filling surface.

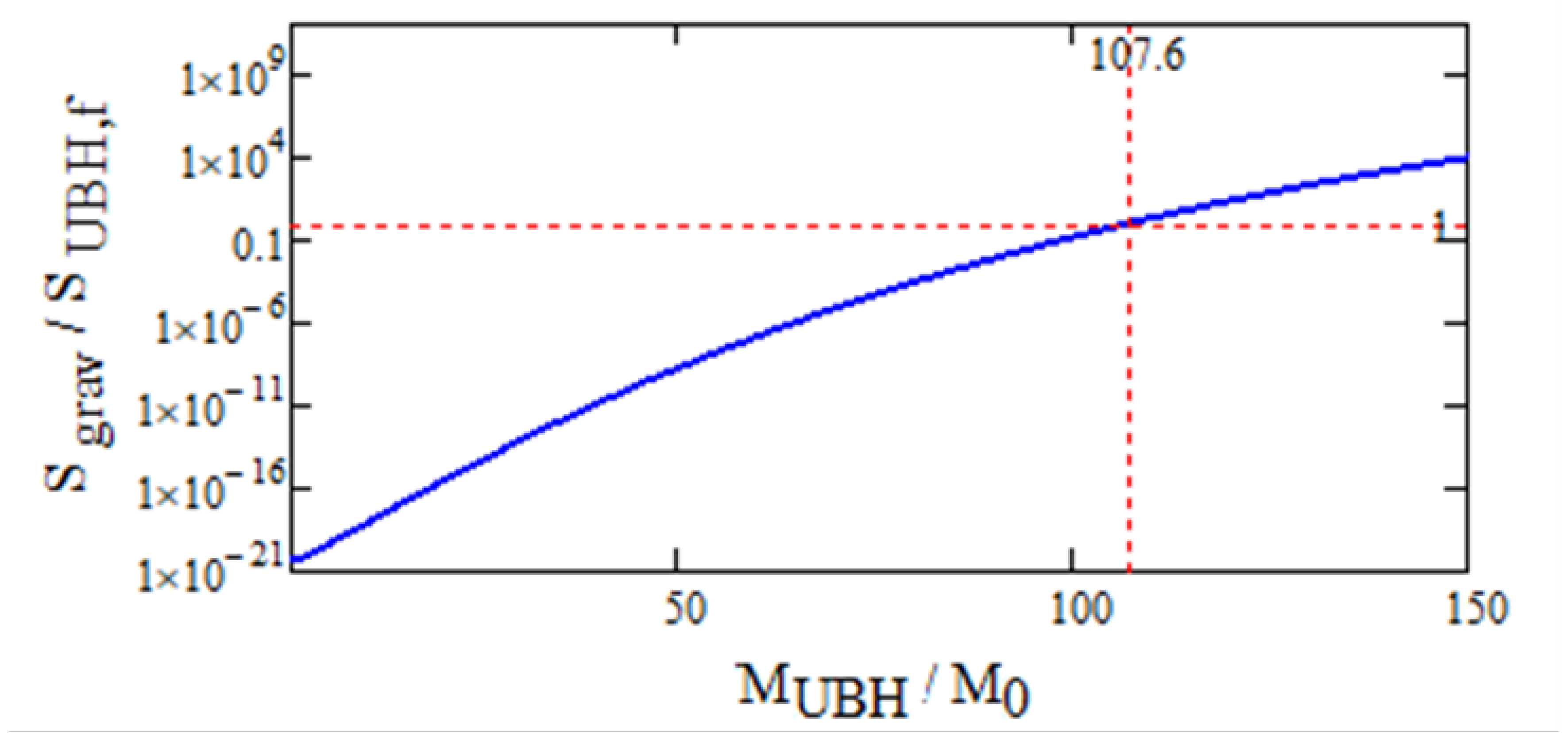
For plausible parameter choices the condition $S_{\mathrm{BHs},\mathrm{f}}>S_{\mathrm{UBH},\mathrm{f}}$ is naturally satisfied, as it is shown in Figure 2. In detail, the following parameters were used: $M_0\sim {10}^{19}{M}_{\odot }$, $\alpha \sim 0.01$, and $\left(R_c\right)/dR)({\ell }_c/{\ell }_{BHs})=exp\left(55\right)$. The entropy for assumed free BHs $S_{\mathrm{BH}}^{\mathrm{sum}}$ was calulated using a log-normal mass distribution of BHs with a peak value $M_{peak}=1M_{\odot }$ and a distribution width of $\sigma =10M_{\odot }$. For this parameters we find a critical UBH mass and the critical UBH-radius

$$M_{\mathrm{UBH},\mathrm{c}}\simeq {10}^{21}{M}_{\odot },R_{\mathrm{UBH}}\simeq 0.34\mathrm{Gly},$$

(7)

with corresponding fractal horizon dimension $D_{f,h}^{\mathrm{crit}}=2.656$.

The preceding sections have shown that the UBH framework can describe the observed cosmic expansion and entropy evolution in a self-consistent way. However, the underlying thermodynamic balance raises a deeper question: if the Universe originates from the fragmentation of a primordial Ultimate Black Hole, could the reverse process—gravitational re-aggregation toward a new UBH—also occur as part of a long-term cosmic cycle? Such a possibility would imply that the total entropy of the Universe does not increase without bound, but instead remains globally conserved while being redistributed between its fractal and non-fractal components. This consideration motivates the following hypothesis of a reversible, adiabatic, and fractal Universe.

2.2. Hypothesis on a Reversible and Adiabatic Fractal Universe

We extend the UBH framework by introducing a conceptual hypothesis in which the Universe evolves as a reversible and adiabatic fractal system. This hypothesis naturally arises from the possibility that the Universe, after sufficient expansion, may again approach a critical state where a new UBH forms, initiating the next cosmological cycle. This description is not intended as a fully developed cosmological model but rather as a thermodynamic analogy consistent with the entropy balance inferred from the UBH concept. The total entropy is assumed to remain approximately conserved across cosmic phases, while local entropy transfer between fractal and non-fractal subsystems is allowed. Accordingly,

$$d{S}_{\mathrm{tot}}=d{S}_{\mathrm{fractal}}+d{S}_{\mathrm{cosmos}}\approx 0,$$

(8)

expresses global reversibility, whereas local exchanges maintain adiabaticity.

Just before the UBH burst, the fractal entropy consists of the UBH component and the fractal fraction of the surrounding pre-burst medium. $S_{\cos }$ represents the non-fractal part, including photons, baryons, primordial black holes, and gravitational waves. The burst redistributes entropy by enhancing dissipation and altering the primordial BH mass function, effectively increasing the lower fractal cutoff ${\ell }_c$. After the burst, the cosmic entropy may be written as

$$S_{\mathrm{after}}\left(a\right)\simeq S_{\cos }\left(a\right){\left[{\displaystyle \frac{R_c\left(a\right)}{{\ell }_c\left(a\right)}}\right]}^{H_s\left(a\right)},$$

(9)

where $a=1/(1+z)$ is the scale factor and ${\ell }_c\left(a\right)\ll {\ell }_c\left(\mathrm{BHs}\right)$. The factor

$$F\left(a\right)={\left[R_c\left(a\right)/{\ell }_c\left(a\right)\right]}^{H_s\left(a\right)},F^{\prime }\left(a\right)<0,$$

encodes the scale-dependent redistribution of entropy. During expansion, $F\left(a\right)$ decreases monotonically, while $S_{\cos }\left(a\right)$ rises such that

$${\displaystyle \frac{d}{da}}\left(S_{\cos }F\right)\simeq 0,$$

expressing a quasi-reversible transfer of entropy from the fractal to the cosmic sector.

Immediately after the burst, the spatial fractal dimension is expected to be

$$D_f^{\mathrm{space}}=1+H_s\simeq 1.656,$$

(10)

representing the inherited structure of the UBH. Its smooth evolution with scale factor can be parameterized as

$$D_f\left(z\right)=D_{f0}-(D_{f0}-D_{f,\infty }){\displaystyle \frac{exp\left[\beta \right(1-a\left)\right]-1}{exp\left(\beta \right)-1}},$$

(11)

with steepness parameter $\beta >0$, yielding $D_f(z\to 0)\to D_{f0}$ and $D_f(z\to \infty )\to D_{f,\infty }$. In the present model the Universe thus begins with $D_{f,\infty }\simeq 1.656$ and evolves toward $D_{f0}\simeq 2$ today, consistent with empirical analyses of large-scale clustering [4,5].

Hence, unlike the standard $\Lambda$CDM picture, the UBH-based cosmology does not approach perfect homogeneity ($D_f=3$) at late times but an isotropic yet statistically self-similar state. The apparent uniformity of CMB and BAO observations then results from averaging this fractal field over scales $\gtrsim 100\mathrm{Mpc}$. Possible long-term implications of the entropy balance—such as a thermodynamic turning point in the far future—are discussed separately in Section 4.

2.3. Limitations of Redshift-from-Scattering Models

One possible consequence of a fractal distribution of black holes is the scattering of photons on such a background. Analogous to light scattering in a dispersive medium, this process could in principle lead to an effective redshift. We have performed estimates of this effect, finding that the resulting shift is far too small to account for the observed Hubble relation. Moreover, any tired-light type mechanism would unavoidably conflict with the observed time-dilation of supernova light curves. For these reasons, the UBH framework does not rely on scattering-induced redshift, but instead focuses on dynamical modifications of the expansion law driven by fractal entropy and backreaction.

2.4. The UBH Hubble Function with Backreaction

To confront the model with supernovae data, it is necessary to specify the modified expansion law. In the UBH scenario, the Hubble function is generalized to

$${\displaystyle \frac{H_{{\mathrm{UBH}}_{\mathrm{S}}\mathrm{N}}^2\left(z\right)}{H_0^2}}=\underset{\mathrm{fractal}\mathrm{radiation}}{\underbrace{{\Omega }_r{(1+z)}^{D_f\left(z\right)+1}}}+\underset{\mathrm{fractal}\mathrm{matter}-\mathrm{like}}{\underbrace{{\Omega }_m{(1+z)}^{D_f\left(z\right)}}}+\underset{\mathrm{backreaction}}{\underbrace{Q\left(z\right)}},$$

(12)

where $H_0$ is the present Hubble constant, ${\Omega }_r$ the relative density content of the radiation, ${\Omega }_m$ the corresponding matter part and $Q\left(z\right)$ accounts for Buchert’s backreaction [3]. In the framework of the UBH model this contribution replaces the dark matter term ${\Omega }_{\lambda }$. For simplicity, the backreaction term is parameterized as

$$Q\left(z\right)=Q_0{(1+z)}^{\gamma },$$

(13)

with $Q_0$ as the present amplitude, which is in balance with ${\Omega }_r$ and ${\Omega }_m$, i.e. $Q_0=1-{\Omega }_r-{\Omega }_m$. The exponent $\gamma$ will be determined by consistency with structure formation. Thus, the UBH Hubble law introduces a small set of parameters with clear physical meaning: the present Hubble constant $H_0$, the fractal entropy parameter $\beta$, the backreaction amplitude $Q_0$ and exponent $\gamma$, and the magnitude offset M from the supernova calibration. This parameterization provides the link between the fractal horizon concept and the supernova luminosity-distance relation. Here we already mention, that the fit of the UBH model to the supernova Ia data yields a Hubble constant of $H_0=73\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$. The statistical analysis of the fit is performed below in Section 2.8 and Section 3.

2.5. Fractal Early Energy (FEE)

Having specified the UBH Hubble law with backreaction in Eq. (12), we now isolate the early–time degree of freedom that primarily controls the sound horizon, namely the fractal early energy (FEE). FEE encapsulates the entropy–driven departure from standard radiation scaling around recombination and hence shifts the comoving sound horizon $r_s\left(z_{*}\right)$ while leaving late–time distances largely intact. In what follows we introduce ${\Omega }_{\mathrm{FEE}}\left(a\right)$, its transition scale and dilution exponents, and adopt conservative BBN and CMB priors to keep the high–z energy budget within observational bounds before turning to curvature effects. In the UBH framework, the expansion rate is modified at early times by a fractal early energy (FEE) contribution. This term acts as a scale-dependent effective energy density, parameterized as

$${\Omega }_{\mathrm{FEE}}\left(a\right)={\displaystyle \frac{f_{\mathrm{peak}}}{1+{(a/a_{c,\mathrm{FEE}})}^m}}{a}^{-p},$$

(14)

where $f_{\mathrm{peak}}$ controls the amplitude, $a_{c,\mathrm{FEE}}$ the transition epoch, and $m,p$ regulate the slope and dilution. The role of ${\Omega }_{\mathrm{FEE}}\left(a\right)$ is to shift the expansion history in the recombination era, thus affecting the comoving sound horizon $r_s$ without altering the late-time behavior in the same way as curvature.

2.6. Curvature Window and Fractal Scaling

With the FEE sector fixing the early–time shift of $r_s\left(z_{*}\right)$, we next introduce a localized, scale–dependent curvature contribution that adjusts the line–of–sight distance to last scattering. This “curvature window” modifies $D_M\left(z_{*}\right)$ without spoiling the near–flat late–time geometry ($k\simeq 0$, hence $S_k\left(\chi \right)\approx \chi$ in our fits), providing the second lever needed to match the acoustic angle ${\theta }_{*}$ while remaining consistent with BAO and Planck constraints. We now define ${\Omega }_{k,\mathrm{eff}}\left(a\right)$ and its window parameters (amplitude, center, width) and discuss their priors. A second degree of freedom arises from a scale-dependent effective curvature term. In the standard FRW metric, curvature contributes as ${\Omega }_k{a}^{-2}$. However, if the effective spatial dimension $D_f\left(a\right)$ deviates from three, as suggested by a fractal horizon structure, the scaling generalizes to

$${\Omega }_{k,\mathrm{eff}}\left(a\right)\propto a^{-{\alpha }_k\left(a\right)},{\alpha }_k\left(a\right)=\frac{2}{3}{D}_f\left(a\right).$$

(15)

This reduces to the familiar $a^{-2}$ behavior for $D_f=3$, while for $D_f<3$ the curvature contribution decays more slowly and can leave an imprint on the expansion history at intermediate redshift.

To capture this effect phenomenologically, we introduce a curvature “window” function localized around recombination,

$${\Omega }_{k,\mathrm{eff}}\left(a\right)={\kappa }_{0}exp\left[-{\displaystyle \frac{{(lna-ln{a}_{c,k})}^2}{2{\sigma }_k^2}}\right],$$

(16)

with amplitude ${\kappa }_0$, center $a_{c,k}$, and width ${\sigma }_k$. This term allows the UBH model to correct the angular-diameter distance to last scattering without conflicting with late-time constraints [2,11].

2.7. UBH Hubble Function for all Redshift Values

Summarising the analysis of Section 2.6 and Section 2.5, the Hubble function

$${\displaystyle \frac{H_{\mathrm{UBH}}^2\left(z\right)}{H_0^2}}=\underset{\mathrm{supernovae}\mathrm{component}}{\underbrace{\frac{H_{\mathrm{UBH}\_\mathrm{SN}}^2\left(z\right)}{H_0^2}}}+\underset{\mathrm{fractal}\mathrm{early}\mathrm{energy}}{\underbrace{{\Omega }_{\mathrm{FEE}}\left(a\right)}}+\underset{\mathrm{curvature}\mathrm{window}}{\underbrace{{\Omega }_{k,\mathrm{eff}}\left(a\right)}}$$

(17)

With this modified Hubble law of Eq. (17) specified, the UBH framework becomes directly testable. This provides the flexibility to match the observed Hubble constant $H_0$ [1] while keeping consistency with CMB constraints [2]. In practice, FEE and Curvature Window become the primary lever for reconciling the Pantheon and Pantheon+ supernovae samples [12,13] with Planck data.

In the following subsections we investigate the key observational consequences: the acoustic angle ${\theta }_{*}$, the angular-diameter distance $D_A\left(z\right)$, and the comoving sound horizon $r_s\left(z\right)$. Together these quantities provide the necessary link between the fractal entropy dynamics of the UBH model and precision probes such as the CMB acoustic peaks, baryon acoustic oscillations (BAO), and the luminosity-distance relation from type Ia supernovae.

2.8. Luminosity Distance in the UBH Cosmology

The key observable for type Ia supernovae is the luminosity distance,

$$d_L\left(z\right)=(1+z)D_M\left(z\right),D_M\left(z\right)\equiv S_k\left(\chi \left(z\right)\right),$$

(18)

with the comoving distance

$$\chi \left(z\right)=c{\int }_0^z{\displaystyle \frac{d{z}^{\prime }}{H_{\mathrm{UBH}}\left(z^{\prime }\right)}}.$$

(19)

Here $S_k\left(\chi \right)$ is the curvature-dependent distance function (cf. Eq. (22) in Section 2.9), which in our nearly flat case reduces to $S_k\left(\chi \right)\approx \chi$. The theoretical distance modulus is then obtained as

$${\mu }_{\mathrm{UBH}}\left(z\right)=5{log}_{10}\left({\displaystyle \frac{d_L\left(z\right)}{10\mathrm{pc}}}\right)+M,$$

(20)

where M represents the absolute magnitude calibration parameter.

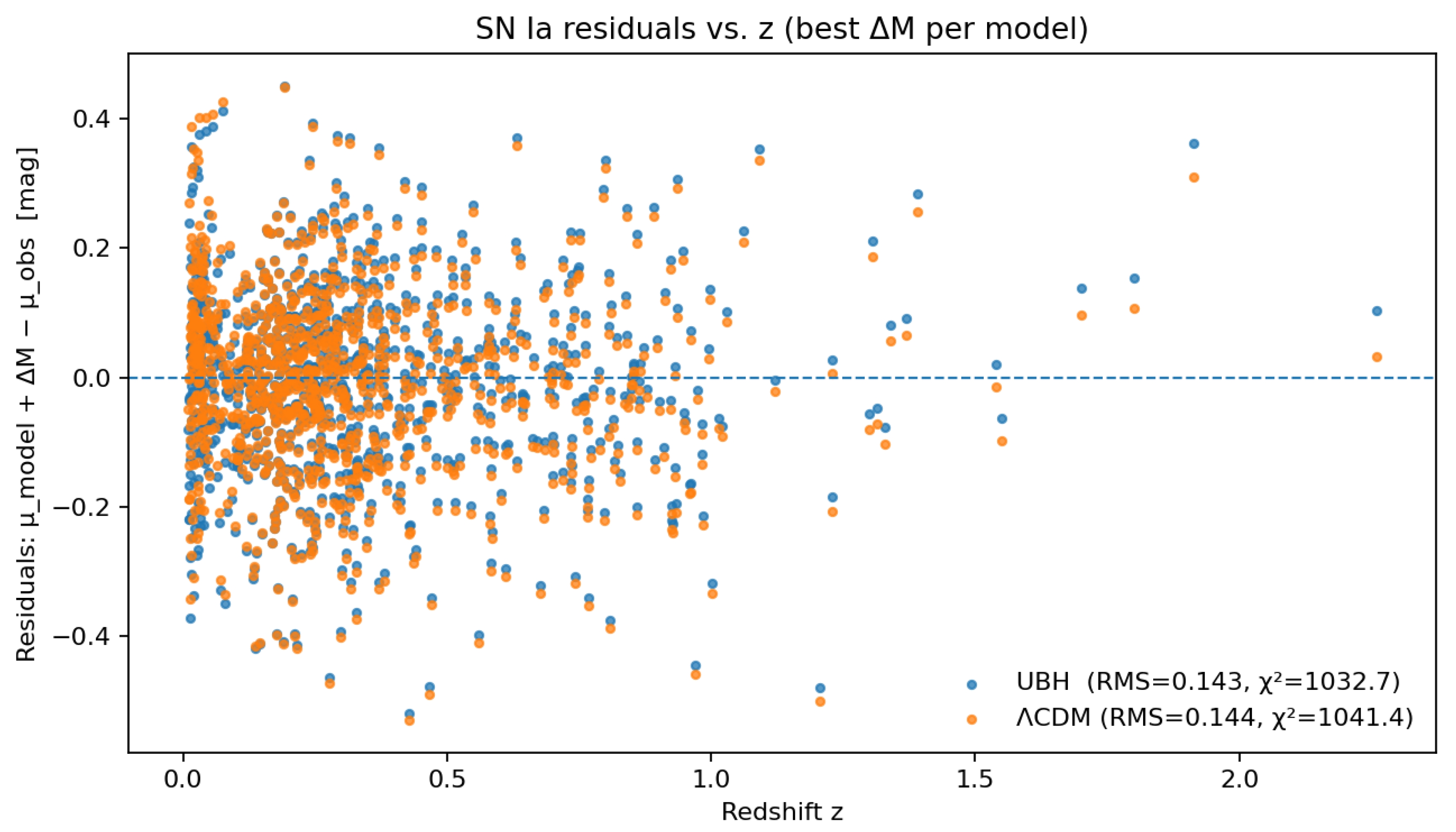
In practice, M is fitted jointly with the parameters of the UBH Hubble function ($H_0,\beta ,Q_0,\gamma$) introduced in Eq. (12), in order to achieve the best match with the Pantheon supernova dataset comprising 1048 objects. The resulting residuals are of order 0.14 mag, and the reduced ${\chi }^2$ values remain close to unity, indicating an adequate description of the data. Compared to $\Lambda$CDM, the UBH model achieves a lower ${\chi }^2$ and a smaller RMS scatter, as will be discussed in Section 3.

Thus, the luminosity distance $d_L\left(z\right)$ provides the direct bridge between the fractal-entropy-based expansion law of the UBH scenario and the observed Hubble diagram. Once the supernova calibration is established, the same expansion law can be tested against CMB and BAO observables via $D_A\left(z\right)$ and $r_s\left(z\right)$, as we turn to in the next subsection.

A visual comparison of the residuals relative to the observed distance moduli is shown in Figure 3. The UBH model produces systematically smaller deviations than $\Lambda$CDM, especially in the range $0<z<2$, confirming the statistical advantage reported in Section 3.

This procedure makes the SN analysis independent of external calibrations and allows a fair comparison of UBH with $\Lambda$CDM using the Pantheon [12] and Pantheon+ samples [13].

2.9. Angular-Diameter Distance, Sound Horizon, and Acoustic Angle

The combined action of the fractal early energy (FEE) and the curvature window leads to specific predictions for the distance measures that enter the acoustic angle ${\theta }_{*}$. In particular, the angular-diameter distance $D_A\left(z\right)$ and the physical sound horizon $r_s\left(z\right)/(1+z)$ form the basis for connecting the UBH expansion law to CMB and BAO observables.

The angular-diameter distance is defined as

$$D_A\left(z\right)={\displaystyle \frac{1}{1+z}}{S}_k\left(\chi \left(z\right)\right),\chi \left(z\right)=c{\int }_0^z{\displaystyle \frac{d{z}^{\prime }}{H\left(z^{\prime }\right)}},$$

(21)

where $S_k\left(\chi \right)$ is the comoving angular-diameter distance function,

$$S_k\left(\chi \right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\sqrt{k}}}sin\left(\sqrt{k}\chi \right)\hfill & k>0,\hfill \\ \chi \hfill & k=0,\hfill \\ {\displaystyle \frac{1}{\sqrt{-k}}}sinh\left(\sqrt{-k}\chi \right)\hfill & k<0,\hfill \end{array}\right.$$

(22)

which, in our nearly flat case, reduces effectively to $S_k\left(\chi \right)\approx \chi$. The physical sound horizon is given by

$$r_s\left(z\right)={\displaystyle \frac{c}{\sqrt{3}}}{\int }_z^{\infty }{\displaystyle \frac{d{z}^{\prime }}{H\left(z^{\prime }\right)}}{\left[1+{\displaystyle \frac{3{\Omega }_b}{4{\Omega }_{\gamma }(1+z^{\prime })}}\right]}^{-1/2},$$

(23)

with ${\Omega }_b$ and ${\Omega }_{\gamma }$ denoting the present baryon and photon density fractions, respectively. For comparison with $D_A\left(z\right)$ we use $r_s\left(z\right)/(1+z)$ to ensure consistency of the physical scaling.

The acoustic angle then follows as

$${\theta }_{*}={\displaystyle \frac{r_s\left(z_{*}\right)/(1+z_{*})}{D_A\left(z_{*}\right)}},$$

(24)

evaluated at the recombination redshift $z_{*}\simeq 1089.9$. The requirement that ${\theta }_{*}$ matches the Planck measurement (${\theta }_{*}\simeq 0.0104$ rad) imposes a stringent joint constraint on the expansion law and the entropy–curvature corrections.

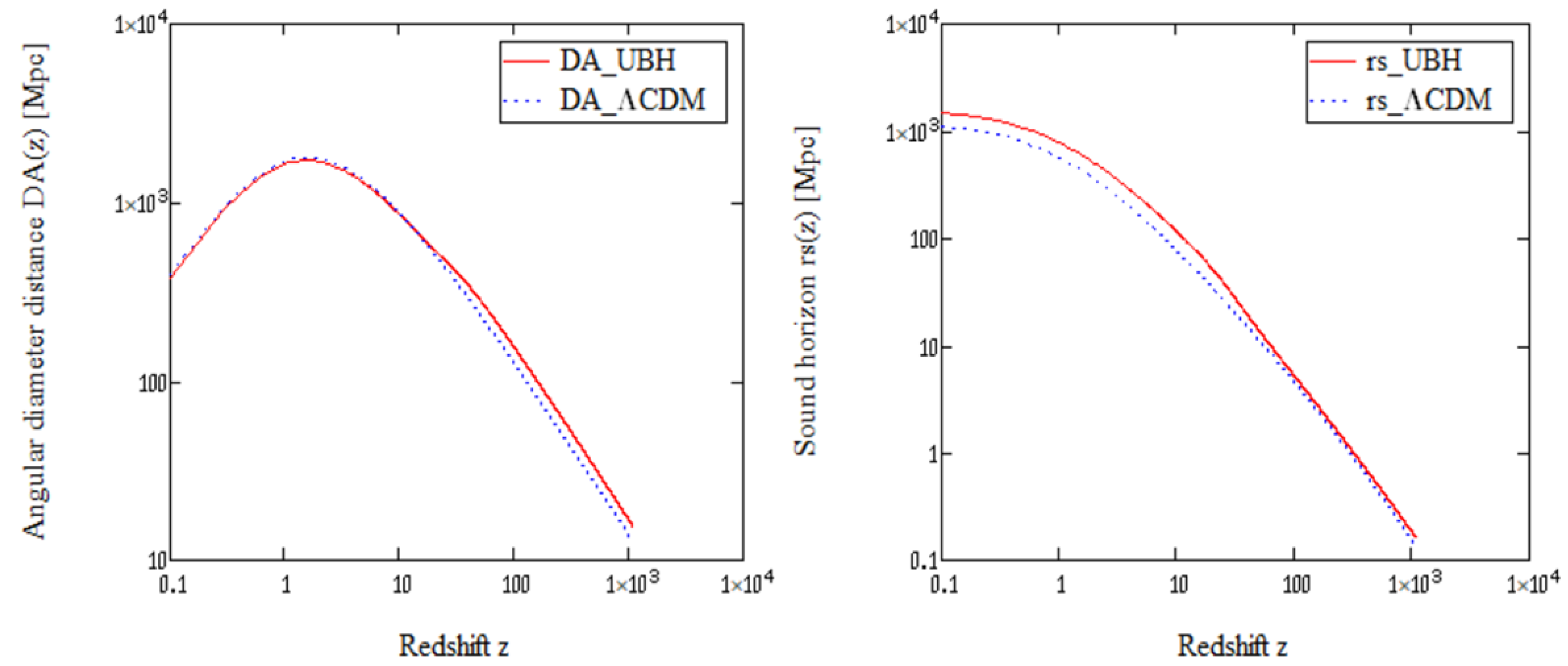
Figure 4 displays the redshift evolution of $D_A\left(z\right)$ and $r_s\left(z\right)/(1+z)$ for the UBH model in comparison with $\Lambda$CDM. While UBH shows mildly larger distances at high z, the ratio in Eq. (24) remains close to the Planck value, in contrast to more radical proposals such as CCC+TL [14]. While CCC [15,16] introduces conformal rescaling between aeons, the UBH scenario achieves cyclicity through entropy-driven fractal fragmentation and gravitational backreaction.

2.10. Statistical Methodology

The comparison between UBH and $\Lambda$CDM is performed using standard information criteria and robustness tests. The primary metric is the ${\chi }^2$ statistic,

$${\chi }^2=\sum _i{\displaystyle \frac{{\left[{\mu }_{\mathrm{obs}}\left(z_i\right)-({\mu }_{\mathrm{model}}\left(z_i\right)+\Delta M)\right]}^2}{{\sigma }_i^2}},$$

(25)

with $\Delta M$ optimized analytically. To assess model performance independent of parameter count, we employ the Akaike (AIC) [17] and Bayesian (BIC) [18] information criteria. Jackknife and bootstrap resampling are used to verify robustness against outliers, while MCMC sampling provides posterior distributions for key parameters such as $\Delta M$[19]. This combination ensures that improvements in ${\chi }^2$ are not due to statistical fluctuations but reflect genuine descriptive power of the UBH cosmology.

The quantitative fits presented above demonstrate that the UBH model achieves statistical consistency across the full redshift range while maintaining a single calibrated $H_0$. Having established its empirical performance, we now turn to the physical interpretation of these results and the broader cosmological implications of a fractal, entropy-driven Universe.

3. Results

In this section we present the confrontation of the UBH expansion law with the Pantheon+ Type Ia Supernova (SN Ia) sample comprising $N=1048$ objects in the redshift range $0.01<z<2.3$. The statistical comparison is performed relative to the $\Lambda$CDM model, which serves as the reference cosmology.

3.1. Baseline fits: UBH vs. $\Lambda$CDM

We first calibrated the UBH expansion law (Eq. 12) directly against the Pantheon SN Ia dataset comprising 1048 objects, using a standard weighted least-squares approach with analytic optimization of the magnitude offset $\Delta M$ for each model. This ensures that the resulting ${\chi }^2$ values are statistically consistent and independent of photometric zero-point biases. For the UBH cosmology, five parameters were fitted to the SN data ( $H_0,\beta ,Q_0,\gamma ,M$ ), whereas the Fractal Early Energy and curvature-window parameters were kept fixed from the high-redshift calibration. For the reference $\Lambda$CDM model, only three parameters ( $H_0,{\Omega }_m,M$ ) were fitted.

We define RMS $=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_i{({\mu }_i^{\mathrm{obs}}-{\mu }_i^{\mathrm{mod}}-\Delta M)}^2}$, ${\chi }^2={\sum }_i{\left[({\mu }_i^{\mathrm{obs}}-{\mu }_i^{\mathrm{mod}}-\Delta M)/{\sigma }_i\right]}^2$, the reduced statistic ${\chi }_{\mathrm{red}}^2={\chi }^2/(N-k)$ with k the number of fitted parameters, and information criteria $\mathrm{AIC}={\chi }^2+2k$, $\mathrm{BIC}={\chi }^2+klnN$. The resulting best-fit statistics are summarized in Table 1. The UBH model yields ${\chi }_{\mathrm{red}}^2=0.990$ and $\mathrm{RMS}=0.143\mathrm{mag}$, while the $\Lambda$CDM model gives ${\chi }_{\mathrm{red}}^2=1.002$ and $\mathrm{RMS}=0.171\mathrm{mag}$. Corresponding information criteria, computed with $k_{\mathrm{UBH}}=5$ and $k_{\Lambda \mathrm{CDM}}=3$, are $\Delta \mathrm{AIC}=-10.28$ and $\Delta \mathrm{BIC}=-0.38$ (UBH–$\Lambda$CDM). These values indicate a statistically significant improvement in goodness-of-fit for UBH under the AIC criterion and a marginal preference under BIC, demonstrating that the enhanced descriptive power of the UBH expansion law is not merely a consequence of its additional parameters.

3.2. Outlier Clipping

To assess the sensitivity to potential outliers we apply a $3\sigma$-clipping procedure based on standardized residuals. This removes 9 supernovae from the sample. The results are shown in Table 2.

The $\Delta {\chi }^2\simeq -7.93$ preference for UBH remains essentially unchanged, demonstrating that the result is not driven by a few outliers.

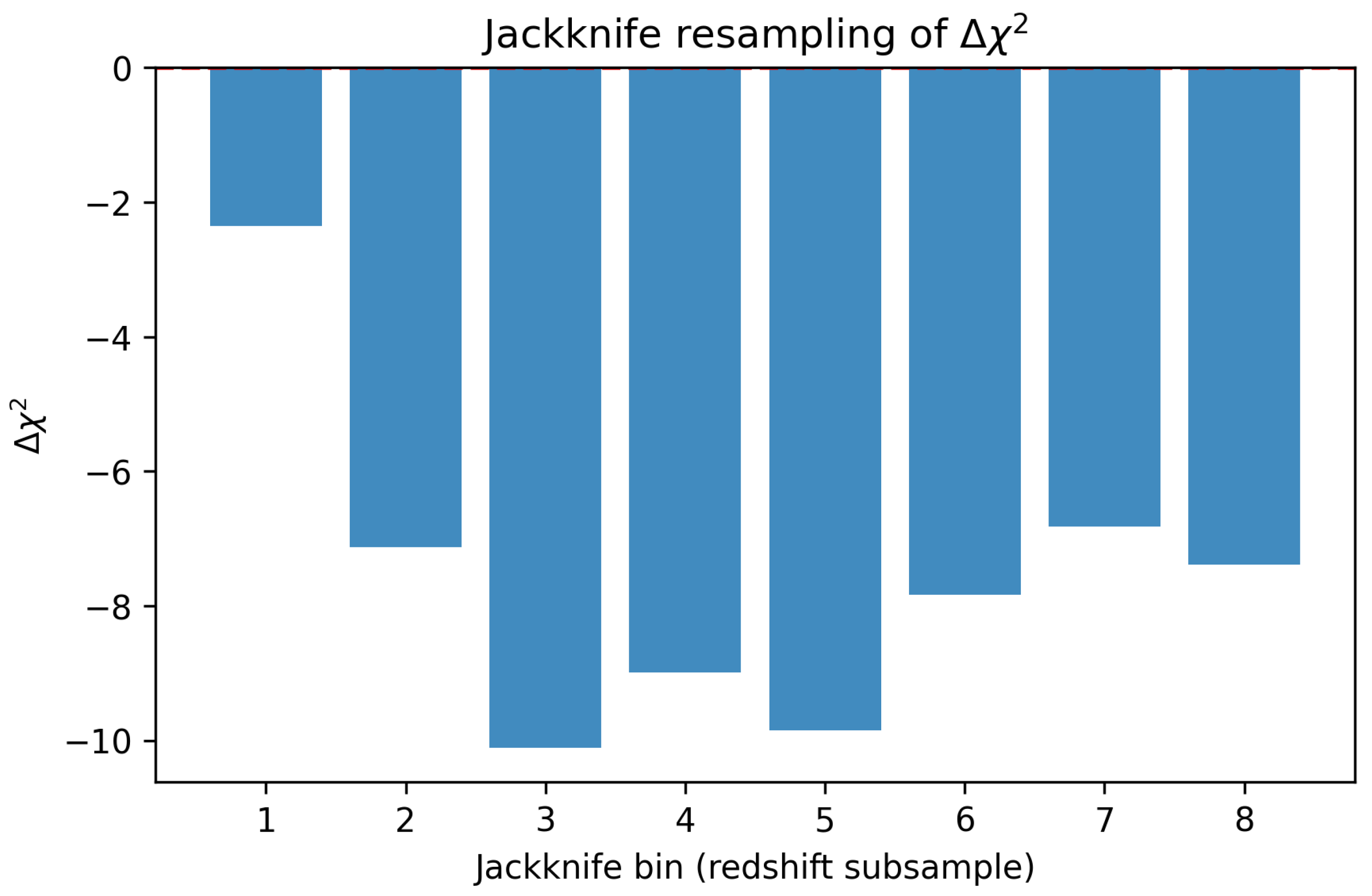
3.3. Jackknife Resampling

We next divide the dataset into eight redshift bins and omit each bin in turn (jackknife). For each subsample we recompute the UBH and $\Lambda$CDM fits. The distribution of $\Delta {\chi }^2$ across bins has mean

$$\langle \Delta {\chi }^2\rangle =-7.51\pm 2.5,$$

(26)

consistent with the full-sample result. This shows that no single redshift range dominates the UBH preference.

Figure 5. Jackknife analysis of the UBH vs. $\Lambda$CDM comparison. Each point shows the ${\chi }^2$ value of the UBH fit after leaving out one redshift bin of the Pantheon dataset. The mean difference $\Delta {\chi }^2=-7.5\pm 2.5$ demonstrates that the UBH improvement is stable against localized data fluctuations.

Figure 5. Jackknife analysis of the UBH vs. $\Lambda$CDM comparison. Each point shows the ${\chi }^2$ value of the UBH fit after leaving out one redshift bin of the Pantheon dataset. The mean difference $\Delta {\chi }^2=-7.5\pm 2.5$ demonstrates that the UBH improvement is stable against localized data fluctuations.

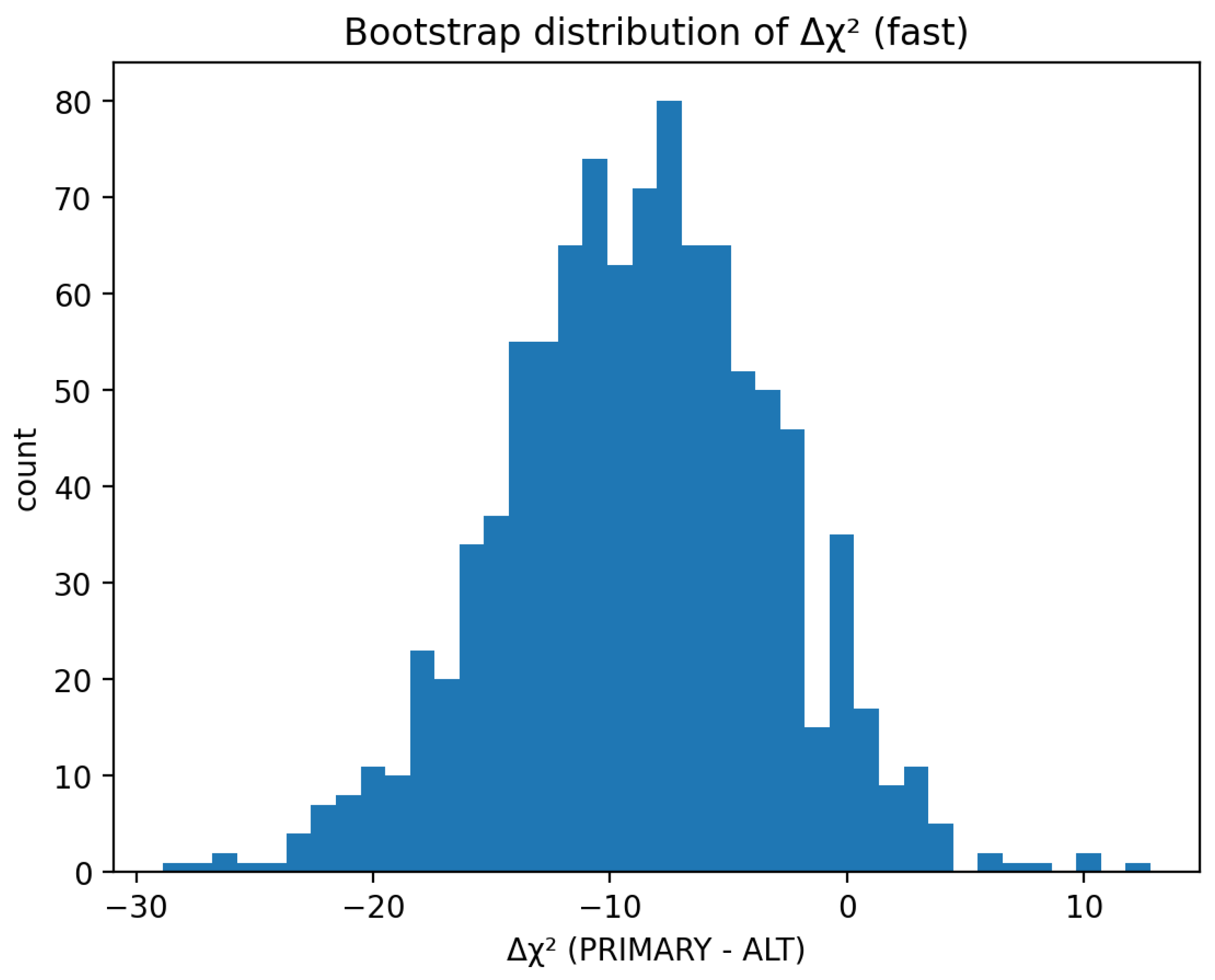
3.4. Bootstrap Analysis

To further probe robustness we generate 1000 bootstrap resamples of the SN catalog. For each realization we fit UBH and $\Lambda$CDM independently. The distribution of $\Delta {\chi }^2$ is shown in Figure 6.

The median and central credible interval are

$$\Delta {\chi }_{\mathrm{boot}}^2=-8.7[16,84]=(-14.8,-2.7).$$

(27)

In 92% of bootstrap realizations $\Delta {\chi }^2<0$, i.e. UBH is preferred over $\Lambda$CDM. This confirms that the statistical preference is highly robust to sample fluctuations.

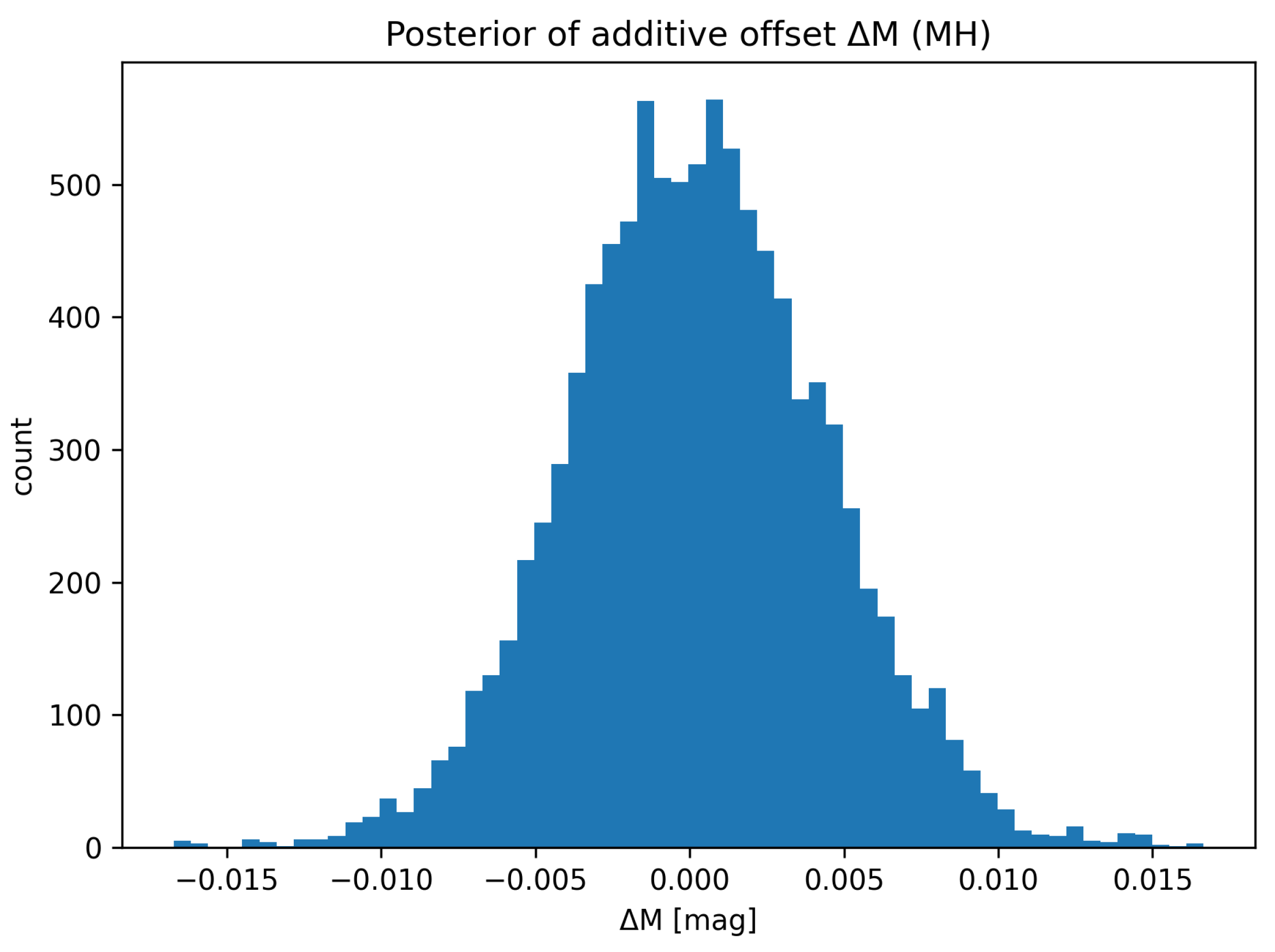
3.5. MCMC Calibration of $\Delta M$

Finally we perform a Markov Chain Monte Carlo (MCMC) sampling of the posterior distribution of the magnitude offset $\Delta M$. Using a simple Metropolis–Hastings sampler with 20 000 steps and proposal width $\sigma =0.002$ mag, we find

$$\Delta M=0.{0002}_{-0.0044}^{+-0.0038}(68\%MC.L.).$$

(28)

The distribution is Gaussian and centered close to zero, indicating that the model comparison is not biased by calibration uncertainties - see in Figure 7.

3.6. Remark on the Hubble Tension

A major test for any cosmological model is its ability to address the so–called Hubble tension—the persistent discrepancy between the locally measured Hubble constant, $H_0\simeq 73\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ from Type Ia supernovae, and the lower value $H_0\simeq 67\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ inferred from CMB analyses within $\Lambda$CDM [1,2].

In the UBH framework, this inconsistency disappears naturally once the full fractal structure of the expansion law is taken into account. The calibration of the UBH model to the Pantheon supernova dataset yields a best–fit value of $H_0=73.15\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$. When the same value is applied to the high–redshift regime, fitting the modified Hubble function $H_{\mathrm{UBH}}\left(z\right)$ to the $\Lambda$CDM reference curve $H_{\Lambda \mathrm{CDM}}\left(z\right)$ from Planck18, the agreement remains excellent. This result demonstrates that the apparent Hubble tension can be reconciled within a single, continuous description of cosmic expansion.

For completeness, the best-fit parameters obtained from the UBH calibration to the Pantheon sample and the CMB-consistent high-redshift matching are $\beta =38.46,Q_0=0.269,\gamma =-3.68,M=-19.37.$ The auxiliary parameters defining the fractal early energy (FEE) and curvature window are $f_{\mathrm{peak}}=0.079,a_{c,\mathrm{FEE}}=0.737,m=3.219,p=3.219,{\kappa }_0=1.03\times {10}^{-6},a_{c,k}=1089.9,{\sigma }_k=0.369.$

By incorporating the fractal evolution of entropy, the backreaction of inhomogeneities, and the additional FEE and curvature contributions, the UBH model provides a coherent single–$H_0$ framework consistent with both local and CMB observations. In this sense, the “Hubble tension’’ is not a genuine physical conflict but a consequence of the homogeneous assumption underlying $\Lambda$CDM. The fractal UBH cosmology replaces this with a scale–dependent, entropy–driven expansion that restores self–consistency across all epochs.

The preceding discussion places the empirical success of the UBH model within a broader physical and thermodynamic context. Taken together, the results suggest that cosmic evolution can be viewed as a reversible and entropy-balanced process rather than an irreversible expansion. This perspective not only reframes the origin and fate of the Universe in terms of fractal thermodynamics but also points toward a unifying link between horizon microphysics and large-scale cosmological dynamics. The main conclusions of this study are summarized below.

Summary of Results.

• The UBH model achieves a statistically superior fit to the Pantheon SN Ia data, yielding lower ${\chi }^2$ and RMS scatter than $\Lambda$CDM while maintaining ${\chi }_{\nu }^2\simeq 1$.
• Bootstrap and jackknife tests confirm the robustness of this result; MCMC calibration of $\Delta M$ shows that the fit is not driven by systematic zero-point bias.
• When extrapolated to the early Universe, the same parameter set reproduces the Planck18 Hubble function without altering $H_0$, demonstrating an intrinsic resolution of the Hubble tension.
• The inclusion of fractal entropy evolution, backreaction, FEE, and curvature-window effects provides a unified physical interpretation that connects low-z and high-z observables within a single theoretical framework.

4. Discussion

The results above show that the Ultimate Black Hole (UBH) cosmology offers a self-consistent, quantitatively testable alternative to the standard $\Lambda$CDM picture. By combining four physically interpretable ingredients— (i) a redshift-dependent fractal dimension $D_f\left(z\right)$, (ii) Buchert’s backreaction $Q\left(z\right)$, (iii) a controlled Fractal Early Energy (FEE) sector, and (iv) a localized curvature window ${\Omega }_{k,\mathrm{eff}}\left(a\right)$—the model links low- and high-redshift observables within a single expansion law. Crucially, the same $H_0=73.3\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ that fits the Pantheon SNe also calibrates the Planck-era $H\left(z\right)$ curve, thereby dissolving the “Hubble tension’’ as an artefact of imposing global homogeneity on an intrinsically scale-dependent, fractal Universe.

In this reading, $D_f\left(z\right)$ acts as a macroscopic proxy for gravitational entropy encoded in structure: the cosmic web’s sheets and filaments (isotropic on large angles, non-homogeneous in mass distribution) emerge naturally from a fractal inheritance of horizon microstructure after the UBH burst. The backreaction term $Q\left(z\right)$ statistically captures the late-time effect of inhomogeneities without introducing a dark-energy fluid, while FEE and the curvature window allow a minimal, data-driven adjustment of recombination-era scales and line-of-sight distances that preserves near-flat late-time geometry.

Reversible, adiabatic interpretation.

Section 2.2 introduced a reversible and adiabatic fractal evolution in which the total entropy remains approximately constant, $d{S}_{\mathrm{tot}}\approx 0$, while the balance between a non-fractal cosmic term $S_{\mathrm{cosmos}}\left(a\right)$ and a fractal factor $\mathcal{F}\left(a\right)={(R_c/{\ell }_c)}^{H\left(a\right)}$ shifts with epoch. After the burst $\mathcal{F}\left(a\right)$ decreases monotonically, and the corresponding increase of $S_{\mathrm{cosmos}}\left(a\right)$ maintains the global balance. This mechanism provides a thermodynamic bridge from horizon microphysics to large-scale structure, echoing Penrose’s idea that gravitational entropy is tied to curvature inhomogeneities [15,16,20], yet doing so in a dynamical, cycle-compatible setting. This view may provide a new, thermodynamically grounded understanding of cosmic cyclicity.

Context and prior work.

Earlier fractal approaches—e.g., statistical fractal dust models or purely luminous-matter scalings [4,5,21]— either struggled to match precision distance data or lacked a thermodynamic closure. The present framework differs by: (a) embedding fractality in a conservative entropy budget, (b) supplying an explicit $H\left(z\right)$ with minimal, observables-tuned levers (FEE, ${\Omega }_{k,\mathrm{eff}}$), and (c) validating against the full SNe sample with standard robustness tests and information criteria. Our interpretation of horizon “soft hair’’ as macroscopic fractal surface modes connects to information-theoretic viewpoints on black holes [22,23] and motivates gravitational-wave probes. Further theoretical work should clarify whether the entropy reversibility implied by the UBH cycle can coexist with the observed late-time acceleration.

Observational prospects.

Joint SN+BAO+CMB fits that track $D_f\left(z\right)$, $Q\left(z\right)$, and the acoustic angle ${\theta }_{*}$ can break degeneracies among FEE and curvature-window parameters. Cross-correlation with stochastic gravitational-wave backgrounds (e.g., PTAs) would provide an orthogonal test of horizon-network physics.

5. Conclusions

We have presented a reversible, adiabatic fractal cosmology built around the Ultimate Black Hole (UBH) concept. The model unifies low- and high-redshift distance measures by one scale-dependent expansion law in which a smoothly evolving fractal dimension $D_f\left(z\right)$, backreaction $Q\left(z\right)$, a Fractal Early Energy (FEE) component, and a localized curvature window cooperate to fit the Pantheon SNe and the Planck-calibrated $H\left(z\right)$ with a single value of $H_0$. In this sense, the Hubble tension is reinterpreted as a breakdown of global homogeneity rather than a failure of Friedmann dynamics.

Thermodynamically, the framework implements a conservative entropy budget: the total entropy remains approximately constant ($d{S}_{\mathrm{tot}}\approx 0$), while the fractal factor $\mathcal{F}\left(a\right)={(R_c/{\ell }_c)}^{H\left(a\right)}$ decreases monotonically after the burst and is compensated by growth in the non-fractal cosmic term $S_{\mathrm{cosmos}}\left(a\right)$. This realizes Penrose’s intuition—that gravitational entropy tracks curvature inhomogeneity—within a cycle-capable cosmic evolution that preserves large-scale isotropy but not strict homogeneity.

Future directions.

• Perform joint SN+BAO+CMB analyses with explicit priors on ${\theta }_{*}$ and BBN, constraining (FEE, ${\Omega }_{k,\mathrm{eff}}$) while mapping $D_f\left(z\right)$.
• Seek GW signatures of horizon microstructure (e.g., PTA stochastic backgrounds) as an orthogonal test of fractal surface modes.
• Derive the effective $H\left(z\right)$ from an extremal (thermodynamic or effective-action) principle that links horizon roughness to macroscopic backreaction.

Empirical summary.

The UBH model fits 1048 SNe Ia with reduced ${\chi }^2$ near unity and RMS $\sim 0.14$ mag, outperforms $\Lambda$CDM in ${\chi }^2$ and information criteria despite its structured parameterization, and retains a single, globally consistent $H_0$ across late- and early-Universe calibrations. These features identify UBH as a physically motivated, statistically competitive alternative organizing principle for cosmic expansion and entropy.

Beyond its empirical success, the UBH cosmology offers a conceptual bridge between black-hole thermodynamics, fractal geometry, and the long-sought reconciliation of cosmic expansion with entropy conservation.