Submitted:
01 November 2025
Posted:
03 November 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Foundations: Hypothesis Grammars for Cell Behavior Modeling
2.1. Concept and Rationale
2.2. Implementation Frameworks and Platforms
2.3. Applications and Case Studies
2.4. Toward Digital Cell Repositories
3. Digital Twins: Predicting Cellular Futures with Patient Genomics
3.1. Weather-like Cellular Forecasts
3.2. Digital Tumor Twins
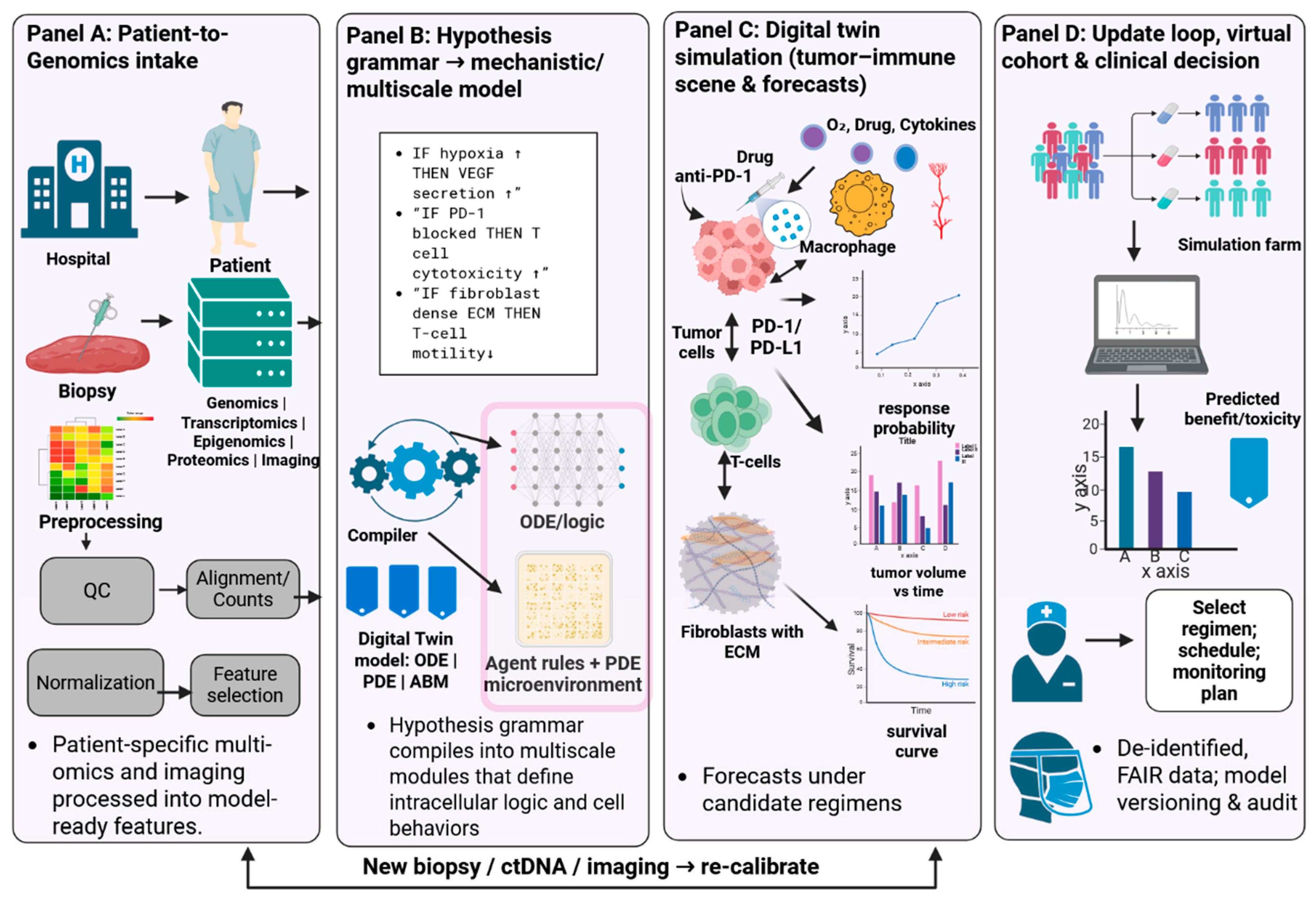
3.3. Integrative Modeling of Tumor–Immune Evolution
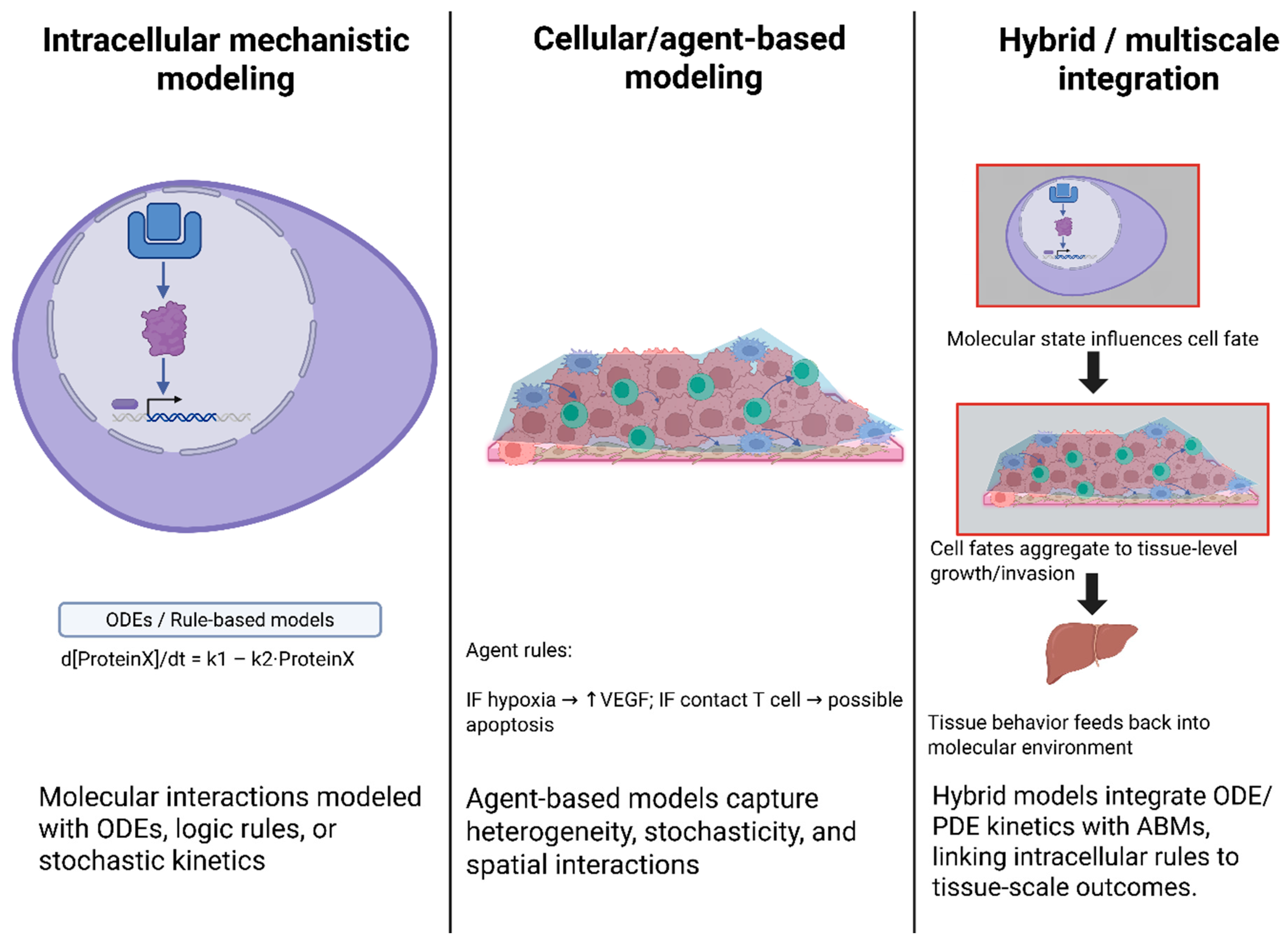
4. Mechanistic and Multiscale Modeling in Systems Biology
4.1. Systems-Scale Modeling Foundations
4.2. Rule-Based, Agent-Based, and Hybrid Multiscale Formalisms
4.3. Machine Learning with Mechanistic Multiscale Models
4.4. Inference of Biological Networks & Regulatory Programs
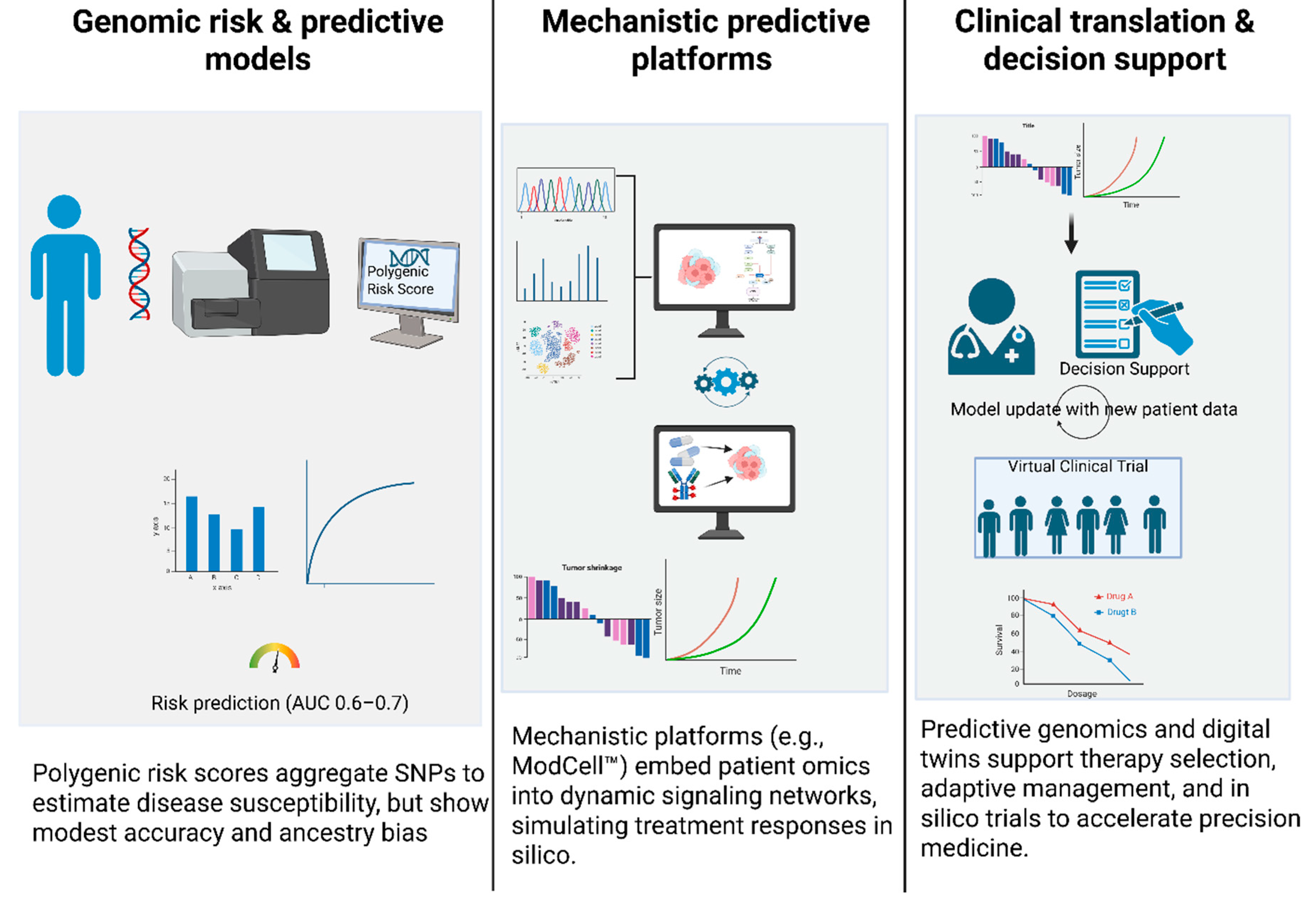
5. Predictive Genomics & Clinical Translation
5.1. Genomic Risk and Predictive Models
5.2. Mechanistic Predictive Platforms and Clinical Translation
6. Emerging Technologies & Future Directions
6.1. Integrating LLMs with Hypothesis Grammars
6.2. Community Repositories, Standards, and Reproducibility
6.3. Benchmarking, Verification/Validation, and Regulatory Pathways
7. Challenges, Limitations, Ethical Considerations & Conclusions
7.1. Technical and Clinical Challenges
7.2. Ethical and Societal Considerations
8. Conclusions and Future Outlook
9. Declaration
9.1. Funding
9.2. Authorship Contribution Statement
9.3. Declaration of Competing Interest
9.4. Acknowledgement
9.5. Ethical Statements
9.6. Declaration of Generative AI and AI-Assisted Technologies in the Writing Process
References
- Altschuler, S.J.; Wu, L.F. Cellular Heterogeneity: Do Differences Make a Difference? Cell 2010, 141, 559–563. [Google Scholar] [CrossRef] [PubMed]
- Stuart, T.; Satija, R. Integrative single-cell analysis. Nat. Rev. Genet. 2019, 20, 257–272. [Google Scholar] [CrossRef]
- Macklin, P.; Edgerton, M.E.; Thompson, A.M.; Cristini, V. Patient-calibrated agent-based modelling of ductal carcinoma in situ (DCIS): From microscopic measurements to macroscopic predictions of clinical progression. J. Theor. Biol. 2012, 301, 122–140. [Google Scholar] [CrossRef]
- Johnson, J.A.I.; Bergman, D.R.; Rocha, H.L.; Zhou, D.L.; Cramer, E.; Mclean, I.C.; Dance, Y.W.; Booth, M.; Nicholas, Z.; Lopez-Vidal, T.; et al. Human interpretable grammar encodes multicellular systems biology models to democratize virtual cell laboratories. Cell 2025, 188, 4711–4733. [Google Scholar] [CrossRef]
- Rahbar, S.; Shafiekhani, S.; Allahverdi, A.; Jamali, A.; Kheshtchin, N.; Ajami, M.; Mirsanei, Z.; Habibi, S.; Makkiabadi, B.; Hadjati, J.; et al. Agent-based Modeling of Tumor and Immune System Interactions in Combinational Therapy with Low-dose 5-fluorouracil and Dendritic Cell Vaccine in Melanoma B16F10. Iran. J. Allergy Asthma Immunol. 2022, 21, 151–166. [Google Scholar] [CrossRef]
- Stamatakos, G.; Kolokotroni, E.; Panagiotidou, F.; Tsampa, S.; Kyroudis, C.; Spohn, S.; Grosu, A.L.; Baltas, D.; Zamboglou, C.; Sachpazidis, I. In silico oncology: a mechanistic multiscale model of clinical prostate cancer response to external radiation therapy as the core of a digital (virtual) twin. Sensitivity analysis and a clinical adaptation approach. Front. Physiol. 2025, 16. [Google Scholar] [CrossRef]
- Corral-Acero, J.; Margara, F.; Marciniak, M.; Rodero, C.; Loncaric, F.; Feng, Y.; Gilbert, A.; Fernandes, J.F.; Bukhari, H.A.; Wajdan, A.; et al. The ‘Digital Twin’ to enable the vision of precision cardiology. Eur. Heart J. 2020, 41, 4556–4564. [Google Scholar] [CrossRef]
- Regev, A.; Teichmann, S.A.; Lander, E.S.; Amit, I.; Benoist, C.; Birney, E.; Bodenmiller, B.; Campbell, P.; Carninci, P.; Clatworthy, M.; et al. The Human Cell Atlas. eLife 2017, 6, e27041. [Google Scholar] [CrossRef]
- Rackauckas, C.; Ma, Y.; Martensen, J.; Warner, C.; Zubov, K.; Supekar, R.; Skinner, D.; Ramadhan, A.; Edelman, A. Universal Differential Equations for Scientific Machine Learning. arXiv 2020, arXiv:2001.04385. [Google Scholar]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Topol, E.J. High-performance medicine: the convergence of human and artificial intelligence. Nat. Med. 2019, 25, 44–56. [Google Scholar] [CrossRef] [PubMed]
- Glen, C.M.; Kemp, M.L.; Voit, E.O. Agent-based modeling of morphogenetic systems: Advantages and challenges. PLOS Comput. Biol. 2019, 15, e1006577. [Google Scholar] [CrossRef]
- Wolkenhauer, O.; Auffray, C.; Jaster, R.; Steinhoff, G.; Dammann, O. The road from systems biology to systems medicine. Pediatr. Res. 2013, 73, 502–507. [Google Scholar] [CrossRef] [PubMed]
- Ullah, M.; Wolkenhauer, O. Stochastic approaches in systems biology. Wiley Interdiscip. Rev. Syst. Biol. Med. 2010, 2, 385–397. [Google Scholar] [CrossRef]
- Ghaffarizadeh, A.; Heiland, R.; Friedman, S.H.; Mumenthaler, S.M.; Macklin, P. PhysiCell: An open source physics-based cell simulator for 3-D multicellular systems. PLoS Comput. Biol. 2018, 14, e1005991. [Google Scholar] [CrossRef]
- Alamoudi, E.; Schälte, Y.; Müller, R.; Starruß, J.; Bundgaard, N.; Graw, F.; Brusch, L.; Hasenauer, J. FitMultiCell: simulating and parameterizing computational models of multi-scale and multi-cellular processes. Bioinformatics 2023, 39, btad674. [Google Scholar] [CrossRef] [PubMed]
- Macklin, P.; Frieboes, H.B.; Sparks, J.L.; Ghaffarizadeh, A.; Friedman, S.H.; Juarez, E.F.; Jonckheere, E.; Mumenthaler, S.M. Progress Towards Computational 3-D Multicellular Systems Biology. Adv. Exp. Med. Biol. 2016, 936, 225–246. [Google Scholar]
- Vodovotz, Y.; An, G. Systems Biology and Inflammation. In: Yan Q, editor. Systems Biology in Drug Discovery and Development [Internet]. Totowa, NJ: Humana Press; 2010 [cited 2025 Sept 4]. p. 181–201. Available from: http://link.springer.com/10.1007/978-1-60761-800-3_9.
- Letort, G.; Montagud, A.; Stoll, G.; Heiland, R.; Barillot, E.; Macklin, P.; Zinovyev, A.; Calzone, L. PhysiBoSS: a multi-scale agent-based modelling framework integrating physical dimension and cell signalling. Bioinformatics 2019, 35, 1188–1196. [Google Scholar] [CrossRef]
- Malik-Sheriff, R.S.; Glont, M.; Nguyen, T.V.N.; Tiwari, K.; Roberts, M.G.; Xavier, A.; Vu, M.T.; Men, J.; Maire, M.; Kananathan, S.; et al. BioModels—15 years of sharing computational models in life science. Nucleic Acids Res. 2019, 48, D407–D415. [Google Scholar] [CrossRef]
- Cristini, V.; Lowengrub, J. Multiscale Modeling of Cancer: An Integrated Experimental and Mathematical Modeling Approach; Cambridge University Press: Cambridge, UK, 2010; p. 278. [Google Scholar]
- Viceconti, M.; Hunter, P. The Virtual Physiological Human: Ten Years After. Annu. Rev. Biomed. Eng. 2016, 18, 103–123. [Google Scholar] [CrossRef]
- Van Liedekerke, P.; Palm, M.M.; Jagiella, N.; Drasdo, D. Simulating tissue mechanics with agent-based models: concepts, perspectives and some novel results. Comput. Part. Mech. 2015, 2, 401–444. [Google Scholar] [CrossRef]
- Cess, C.G.; Finley, S.D. Multi-scale modeling of macrophage—T cell interactions within the tumor microenvironment. PLoS Comput. Biol. 2020, 16, e1008519. [Google Scholar] [CrossRef]
- An, G.; Mi, Q.; Dutta-Moscato, J.; Vodovotz, Y. Agent-based models in translational systems biology. WIREs Mech. Dis. 2009, 1, 159–171. [Google Scholar] [CrossRef]
- Stein-O’Brien, G.L.; Clark, B.S.; Sherman, T.; Zibetti, C.; Hu, Q.; Sealfon, R.; Liu, S.; Qian, J.; Colantuoni, C.; Blackshaw, S.; et al. Decomposing Cell Identity for Transfer Learning across Cellular Measurements, Platforms, Tissues, and Species. Cell Syst. 2019, 8, 395–411. [Google Scholar] [CrossRef] [PubMed]
- Chattopadhyay, S.; Karlsson, J.; Ferro, M.; Mañas, A.; Kanzaki, R.; Fredlund, E.; Murphy, A.J.; Morton, C.L.; Andersson, N.; Woolard, M.A.; et al. Evolutionary unpredictability in cancer model systems. Sci. Rep. 2025, 15, 20334. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, K.; Kananathan, S.; Roberts, M.G.; Meyer, J.P.; Sharif Shohan, M.U.; Xavier, A.; Maire, M.; Zyoud, A.; Men, J.; Ng, S.; et al. Reproducibility in systems biology modelling. Mol. Syst. Biol. 2021, 17, e9982. [Google Scholar] [CrossRef] [PubMed]
- Sansone, S.A.; McQuilton, P.; Rocca-Serra, P.; Gonzalez-Beltran, A.; Izzo, M.; Lister, A.L.; Thurston, M. FAIRsharing as a community approach to standards, repositories and policies. Nat. Biotechnol. 2019, 37, 358–367. [Google Scholar] [CrossRef]
- Stamatakos, G. The Oncosimulator - Combining Clinically Driven and Clinically Oriented Multiscale Cancer Modeling with Information Technology in the In Silico Oncology Context. Research Journal of Clinical Pediatrics [Internet]. 2021 Oct 1 [cited 2025 Sept 14];2021. Available from: https://www.scitechnol.com/abstract/the-oncosimulator-combining-clinically-driven-and-clinically-oriented-multiscale-cancer-modeling-with-information-technology-in-th-17191.html.
- Mollica, L.; Leli, C.; Sottotetti, F.; Quaglini, S.; Locati, L.D.; Marceglia, S. Digital twins: a new paradigm in oncology in the era of big data. ESMO Real World Data Digit. Oncol. 2024, 5, 100056. [Google Scholar] [CrossRef]
- Björnsson, B.; Borrebaeck, C.; Elander, N.; Gasslander, T.; Gawel, D.R.; Gustafsson, M.; Jörnsten, R.; Lee, E.J.; Li, X.; Lilja, S.; et al. Digital twins to personalize medicine. Genome Med. 2020, 12, 4. [Google Scholar] [CrossRef]
- Jenner, A.L.; Smalley, M.; Goldman, D.; Goins, W.F.; Cobbs, C.S.; Puchalski, R.B.; Chiocca, E.A.; Lawler, S.; Macklin, P.; Goldman, A.; et al. Agent-based computational modeling of glioblastoma predicts that stromal density is central to oncolytic virus efficacy. iScience 2022, 25, 104395. [Google Scholar] [CrossRef]
- Love, N.R.; Williams, C.; Killingbeck, E.E.; Merleev, A.; Saffari Doost, M.; Yu, L.; McPherson, J.D.; Mori, H.; Borowsky, A.D.; Maverakis, E.; et al. Melanoma progression and prognostic models drawn from single-cell, spatial maps of benign and malignant tumors. Sci. Adv. 2024, 10, eadm8206. [Google Scholar] [CrossRef]
- Stamatakos, G.S.; Perez, M.A.; Radhakrishnan, R. Editorial: Multiscale cancer modeling, in silico oncology and digital (virtual) twins in the cancer domain. Front. Physiol. 2025, 16, 1614235. [Google Scholar] [CrossRef]
- Alarcón, T.; Byrne, H.M.; Maini, P.K. A mathematical model of the effects of hypoxia on the cell-cycle of normal and cancer cells. J. Theor. Biol. 2004, 229, 395–411. [Google Scholar] [CrossRef]
- Thorsson, V.; Gibbs, D.L.; Brown, S.D.; Wolf, D.; Bortone, D.S.; Ou Yang, T.H.; Porta-Pardo, E.; Gao, G.F.; Plaisier, C.L.; Eddy, J.A.; et al. The Immune Landscape of Cancer. Immunity 2018, 48, 812–830. [Google Scholar] [CrossRef] [PubMed]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. arXiv 2020, arXiv:2005.14165. [Google Scholar] [CrossRef]
- Pleyer, J.; Fleck, C. Agent-based models in cellular systems. Front. Phys. 2023, 10, 968409. [Google Scholar] [CrossRef]
- Altrock, P.M.; Liu, L.L.; Michor, F. The mathematics of cancer: integrating quantitative models. Nat. Rev. Cancer 2015, 15, 730–745. [Google Scholar] [CrossRef]
- ModCell [Internet]. ALACRIS Theranostics. 2024 [cited 2025 Sept 14]. Available from: https://www.alacris.de/modcell/.
- Fridman, W.H.; Zitvogel, L.; Sautès–Fridman, C.; Kroemer, G. The immune contexture in cancer prognosis and treatment. Nat. Rev. Clin. Oncol. 2017, 14, 717–734. [Google Scholar] [CrossRef] [PubMed]
- Hiam-Galvez, K.J.; Allen, B.M.; Spitzer, M.H. Systemic immunity in cancer. Nat. Rev. Cancer 2021, 21, 345–359. [Google Scholar] [CrossRef]
- Binnewies, M.; Roberts, E.W.; Kersten, K.; Chan, V.; Fearon, D.F.; Merad, M.; Coussens, L.M.; Gabrilovich, D.I.; Ostrand-Rosenberg, S.; Hedrick, C.C.; et al. Understanding the tumor immune microenvironment (TIME) for effective therapy. Nat. Med. 2018, 24, 541–550. [Google Scholar] [CrossRef]
- Bagaev, A.; Kotlov, N.; Nomie, K.; Svekolkin, V.; Gafurov, A.; Isaeva, O.; Osokin, N.; Kozlov, I.; Frenkel, F.; Gancharova, O.; et al. Conserved pan-cancer microenvironment subtypes predict response to immunotherapy. Cancer Cell 2021, 39, 845–865. [Google Scholar] [CrossRef]
- Li, B.; Li, T.; Pignon, J.C.; Wang, B.; Wang, J.; Shukla, S.; Dou, R.; Chen, Q.; Hodi, F.S.; Choueiri, T.K.; et al. Landscape of tumor-infiltrating T cell repertoire of human cancers. Nat. Genet. 2016, 48, 725–732. [Google Scholar] [CrossRef]
- Raue, A.; Schilling, M.; Bachmann, J.; Matteson, A.; Schelke, M.; Kaschek, D.; Hug, S.; Kreutz, C.; Harms, B.D.; Theis, F.J.; et al. Lessons Learned from Quantitative Dynamical Modeling in Systems Biology. PLoS ONE 2013, 8, e74335. [Google Scholar] [CrossRef]
- Deisboeck, T.S.; Wang, Z.; Macklin, P.; Cristini, V. Multiscale cancer modeling. Annu. Rev. Biomed. Eng. 2011, 13, 127–155. [Google Scholar] [CrossRef]
- Gerlinger, M.; Rowan, A.J.; Horswell, S.; Larkin, J.; Endesfelder, D.; Gronroos, E.; Martinez, P.; Matthews, N.; Stewart, A.; Tarpey, P.; et al. Intratumor Heterogeneity and Branched Evolution Revealed by Multiregion Sequencing. N. Engl. J. Med. 2012, 366, 883–892. [Google Scholar] [CrossRef] [PubMed]
- Norton, K.A.; Gong, C.; Jamalian, S.; Popel, A.S. Multiscale Agent-Based and Hybrid Modeling of the Tumor Immune Microenvironment. Processes 2019, 7, 37. [Google Scholar] [CrossRef]
- Swat, M.H.; Thomas, G.L.; Belmonte, J.M.; Shirinifard, A.; Hmeljak, D.; Glazier, J.A. Multi-scale modeling of tissues using CompuCell3D. Methods Cell Biol. 2012, 110, 325–366. [Google Scholar]
- Stoll, G.; Caron, B.; Viara, E.; Dugourd, A.; Zinovyev, A.; Naldi, A.; Kroemer, G.; Barillot, E.; Calzone, L. MaBoSS 2.0: an environment for stochastic Boolean modeling. Bioinformatics 2017, 33, 2226–2228. [Google Scholar] [CrossRef]
- Hucka, M.; Finney, A.; Sauro, H.M.; Bolouri, H.; Doyle, J.C.; Kitano, H.; Arkin, A.P.; Bornstein, B.J.; Bray, D.; Cornish-Bowden, A.; et al. The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics 2003, 19, 524–531. [Google Scholar] [CrossRef] [PubMed]
- Hasin, Y.; Seldin, M.; Lusis, A. Multi-omics approaches to disease. Genome Biol. 2017, 18, 83. [Google Scholar] [CrossRef] [PubMed]
- Gyori, B.M.; Bachman, J.A.; Subramanian, K.; Muhlich, J.L.; Galescu, L.; Sorger, P.K. From word models to executable models of signaling networks using automated assembly. Mol. Syst. Biol. 2017, 13, 954. [Google Scholar] [CrossRef]
- Rule-Based Modelling of Cellular Signalling. In: Caires L, Vasconcelos VT, editors. CONCUR 2007 – Concurrency Theory [Internet]. Berlin, Heidelberg: Springer Berlin Heidelberg; 2007 [cited 2025 Sept 4]. p. 17–41. Available from: http://link.springer.com/10.1007/978-3-540-74407-8_3.
- Harris, L.A.; Hogg, J.S.; Tapia, J.J.; Sekar, J.A.P.; Gupta, S.; Korsunsky, I.; Arora, A.; Barua, D.; Sheehan, R.P.; Faeder, J.R. BioNetGen 2.2: advances in rule-based modeling. Bioinformatics 2016, 32, 3366–3368. [Google Scholar] [CrossRef]
- Lopez, C.F.; Muhlich, J.L.; Bachman, J.A.; Sorger, P.K. Programming biological models in Python using PySB. Mol. Syst. Biol. 2013, 9, 646. [Google Scholar] [CrossRef]
- Heiland, R.; Bergman, D.; Lyons, B.; Waldow, G.; Cass, J.; Rocha, H.L.; Ruscone, M.; Noël, V.; Macklin, P. PhysiCell Studio: a graphical tool to make agent-based modeling more accessible. Gigabyte 2024, 2024, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Starruß, J.; de Back, W.; Brusch, L.; Deutsch, A. Morpheus: a user-friendly modeling environment for multiscale and multicellular systems biology. Bioinformatics 2014, 30, 1331–1332. [Google Scholar] [CrossRef] [PubMed]
- Stoll, G.; Viara, E.; Barillot, E.; Calzone, L. Continuous time boolean modeling for biological signaling: application of Gillespie algorithm. BMC Syst. Biol. 2012, 6, 116. [Google Scholar] [CrossRef] [PubMed]
- Norton, K.A.; Gong, C.; Jamalian, S.; Popel, A.S. Multiscale Agent-Based and Hybrid Modeling of the Tumor Immune Microenvironment. Processes 2019, 7, 37. [Google Scholar] [CrossRef]
- Mirams, G.R.; Arthurs, C.J.; Bernabeu, M.O.; Bordas, R.; Cooper, J.; Corrias, A.; Davit, Y.; Dunn, S.J.; Fletcher, A.G.; Harvey, D.G.; et al. Chaste: An Open Source C++ Library for Computational Physiology and Biology. PLoS Comput. Biol. 2013, 9, e1002970. [Google Scholar] [CrossRef]
- Toni, T.; Welch, D.; Strelkowa, N.; Ipsen, A.; Stumpf, M.P.H. Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. J. R. Soc. Interface 2009, 6, 187–202. [Google Scholar] [CrossRef]
- Razavi, S.; Tolson, B.A.; Burn, D.H. Review of surrogate modeling in water resources. Water Resour. Res. 2012, 48, W07401. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Lim, G.J. A reinforcement learning approach for finding optimal policy of adaptive radiation therapy considering uncertain tumor biological response. Artif. Intell. Med. 2021, 121, 102193. [Google Scholar] [CrossRef]
- Yang, C.Y.; Shiranthika, C.; Wang, C.Y.; Chen, K.W.; Sumathipala, S. Reinforcement learning strategies in cancer chemotherapy treatments: A review. Comput. Methods Programs Biomed. 2023, 229, 107280. [Google Scholar] [CrossRef]
- Willard, J.; Jia, X.; Xu, S.; Steinbach, M.; Kumar, V. Integrating Physics-Based Modeling with Machine Learning: A Survey. arXiv 2020, arXiv:2003.04919. [Google Scholar]
- Chen, S.; Mar, J.C. Evaluating methods of inferring gene regulatory networks highlights their lack of performance for single cell gene expression data. BMC Bioinformatics 2018, 19, 232. [Google Scholar] [CrossRef]
- Andrews, T.S.; Hemberg, M. Identifying cell populations with scRNASeq. Mol. Aspects Med. 2018, 59, 114–122. [Google Scholar] [CrossRef] [PubMed]
- Margolin, A.A.; Nemenman, I.; Basso, K.; Wiggins, C.; Stolovitzky, G.; Favera, R.D.; Califano, A. ARACNE: An Algorithm for the Reconstruction of Gene Regulatory Networks in a Mammalian Cellular Context. BMC Bioinformatics 2006, 7, S7. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, H.; Kiryu, H.; Furusawa, C.; Ko, M.S.H.; Ko, S.B.H.; Gouda, N.; Hayashi, T.; Nikaido, I. SCODE: an efficient regulatory network inference algorithm from single-cell RNA-Seq during differentiation. Bioinformatics 2017, 33, 2314–2321. [Google Scholar] [CrossRef]
- Peng, J.; Serrano, G.; Traniello, I.M.; Calleja-Cervantes, M.E.; Chembazhi, U.V.; Bangru, S.; Ezponda, T.; Rodriguez-Madoz, J.R.; Kalsotra, A.; Prosper, F.; et al. SimiC enables the inference of complex gene regulatory dynamics across cell phenotypes. Commun. Biol. 2022, 5, 351. [Google Scholar] [CrossRef]
- Lopez, R.; Regier, J.; Cole, M.B.; Jordan, M.I.; Yosef, N. Deep generative modeling for single-cell transcriptomics. Nat. Methods 2018, 15, 1053–1058. [Google Scholar] [CrossRef]
- Huynh-Thu, V.A.; Irrthum, A.; Wehenkel, L.; Geurts, P. Inferring Regulatory Networks from Expression Data Using Tree-Based Methods. PLoS ONE 2010, 5, e12776. [Google Scholar] [CrossRef]
- Weinreb, C.; Wolock, S.; Klein, A.M. SPRING: a kinetic interface for visualizing high dimensional single-cell expression data. Bioinformatics 2018, 34, 1246–1248. [Google Scholar] [CrossRef]
- Singer, M.; Wang, C.; Cong, L.; Marjanovic, N.D.; Kowalczyk, M.S.; Zhang, H.; Nyman, J.; Sakuishi, K.; Kurtulus, S.; Gennert, D.; et al. A Distinct Gene Module for Dysfunction Uncoupled from Activation in Tumor-Infiltrating T Cells. Cell 2016, 166, 1500–1511. [Google Scholar] [CrossRef]
- Saez-Rodriguez, J.; Simeoni, L.; Lindquist, J.A.; Hemenway, R.; Bommhardt, U.; Arndt, B.; Haus, U.U.; Weismantel, R.; Gilles, E.D.; Klamt, S.; et al. A Logical Model Provides Insights into T Cell Receptor Signaling. PLoS Comput. Biol. 2007, 3, e163. [Google Scholar] [CrossRef]
- Cusanovich, D.A.; Hill, A.J.; Aghamirzaie, D.; Daza, R.M.; Pliner, H.A.; Berletch, J.B.; Filippova, G.N.; Huang, X.; Christiansen, L.; DeWitt, W.S.; et al. A Single-Cell Atlas of In Vivo Mammalian Chromatin Accessibility. Cell 2018, 174, 1309–1324. [Google Scholar] [CrossRef]
- Eng, C.H.L.; Lawson, M.; Zhu, Q.; Dries, R.; Koulena, N.; Takei, Y.; Yun, J.; Cronin, C.; Karp, C.; Yuan, G.C.; et al. Transcriptome-scale super-resolved imaging in tissues by RNA seqFISH+. Nature 2019, 568, 235–239. [Google Scholar] [CrossRef]
- Marbach, D.; Costello, J.C.; Küffner, R.; Vega, N.M.; Prill, R.J.; Camacho, D.M.; Allison, K.R.; Kellis, M.; Collins, J.J.; Stolovitzky, G. Wisdom of crowds for robust gene network inference. Nat. Methods 2012, 9, 796–804. [Google Scholar] [CrossRef] [PubMed]
- Lewis, C.M.; Vassos, E. Polygenic risk scores: from research tools to clinical instruments. Genome Med. 2020, 12, 44. [Google Scholar] [CrossRef] [PubMed]
- Inouye, M.; Abraham, G.; Nelson, C.P.; Wood, A.M.; Sweeting, M.J.; Dudbridge, F.; Lai, F.Y.; Kaptoge, S.; Brozynska, M.; Wang, T.; et al. Genomic Risk Prediction of Coronary Artery Disease in 480,000 Adults. J. Am. Coll. Cardiol. 2018, 72, 1883–1893. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, N.; Shi, J.; García-Closas, M. Developing and evaluating polygenic risk prediction models for stratified disease prevention. Nat. Rev. Genet. 2016, 17, 392–406. [Google Scholar] [CrossRef] [PubMed]
- Martin, A.R.; Kanai, M.; Kamatani, Y.; Okada, Y.; Neale, B.M.; Daly, M.J. Clinical use of current polygenic risk scores may exacerbate health disparities. Nat. Genet. 2019, 51, 584–591. [Google Scholar] [CrossRef] [PubMed]
- Schlüter, J.; Schönhuth, A. Genetic features for drug responses in cancer — Investigating an ensemble-feature-selection approach. Comput. Biol. Med. 2025, 196, 110572. [Google Scholar] [CrossRef]
- Willard, J.; Jia, X.; Xu, S.; Steinbach, M.; Kumar, V. Integrating Scientific Knowledge with Machine Learning for Engineering and Environmental Systems. arXiv 2020, arXiv:2003.04919. [Google Scholar] [CrossRef]
- Lorenzo, G.; Ahmed, S.R.; Hormuth, D.A.; Vaughn, B.; Kalpathy-Cramer, J.; Solorio, L.; Yankeelov, T.E.; Gomez, H. Patient-Specific, Mechanistic Models of Tumor Growth Incorporating Artificial Intelligence and Big Data. Annu. Rev. Biomed. Eng. 2024, 26, 529–560. [Google Scholar] [CrossRef]
- Pellman, J.; Sheikh, F. Atrial Fibrillation: Mechanisms, Therapeutics, and Future Directions. Compr. Physiol. 2015, 5, 649–665. [Google Scholar] [CrossRef] [PubMed]
- Heman-Ackah, S.M.; Bassett, A.R.; Wood, M.J.A. Precision Modulation of Neurodegenerative Disease-Related Gene Expression in Human iPSC-Derived Neurons. Sci. Rep. 2016, 6, 28420. [Google Scholar] [CrossRef] [PubMed]
- Vlachogiannis, G.; Hedayat, S.; Vatsiou, A.; Jamin, Y.; Fernández-Mateos, J.; Khan, K.; Lampis, A.; Eason, K.; Huntingford, I.; Burke, R.; et al. Patient-derived organoids model treatment response of metastatic gastrointestinal cancers. Science 2018, 359, 920–926. [Google Scholar] [CrossRef] [PubMed]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef]
- Kim, J.I.; Maguire, F.; Tsang, K.K.; Gouliouris, T.; Peacock, S.J.; McAllister, T.A.; McArthur, A.G.; Beiko, R.G. Machine Learning for Antimicrobial Resistance Prediction: Current Practice, Limitations, and Clinical Perspective. Clin. Microbiol. Rev. 2022, 35, e00179–21. [Google Scholar] [CrossRef]
- Thorogood, A.; Dalpé, G.; Knoppers, B.M. Return of individual genomic research results: are laws and policies keeping step? Eur. J. Hum. Genet. 2019, 27, 535–546. [Google Scholar] [CrossRef]
- Cuellar, A.A.; Lloyd, C.M.; Nielsen, P.F.; Bullivant, D.P.; Nickerson, D.P.; Hunter, P.J. An Overview of CellML 1.1, a Biological Model Description Language. SIMULATION 2003, 79, 740–747. [Google Scholar] [CrossRef]
- Lewis, P.; Perez, E.; Piktus, A.; Petroni, F.; Karpukhin, V.; Goyal, N.; Küttler, H.; Lewis, M.; Yih, W.; Rocktäschel, T.; et al. Retrieval-Augmented Generation for Knowledge-Intensive NLP Tasks. arXiv 2020, arXiv:2005.11401. [Google Scholar]
- Schick, T.; Dwivedi-Yu, J.; Dessì, R.; Raileanu, R.; Lomeli, M.; Zettlemoyer, L.; Cancedda, N.; Scialom, T. Toolformer: Language Models Can Teach Themselves to Use Tools. arXiv 2023, arXiv:2302.04761. [Google Scholar] [CrossRef]
- Friedman, S.H.; Anderson, A.R.A.; Bortz, D.M.; Fletcher, A.G.; Frieboes, H.B.; Ghaffarizadeh, A.; Grimes, D.R.; Hawkins-Daarud, A.; Hoehme, S.; Juarez, E.F.; et al. MultiCellDS: a standard and a community for sharing multicellular data. bioRxiv 2016, 090696. [Google Scholar]
- Wilkinson, M.D.; Dumontier, M.; Aalbersberg, I.j.J.; Appleton, G.; Axton, M.; Baak, A.; Blomberg, N.; Boiten, J.W.; Da Silva Santos, L.B.; Bourne, P.E.; et al. The FAIR Guiding Principles for scientific data management and stewardship. Sci. Data 2016, 3, 160018. [Google Scholar] [CrossRef] [PubMed]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer [Internet]. 1st ed. Wiley; 2007 [cited 2025 Sept 4]. Available from: https://onlinelibrary.wiley.com/doi/book/10.1002/9780470725184.
- Kennedy, M.C.; O’Hagan, A. Bayesian calibration of computer models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2001, 63, 425–464. [Google Scholar] [CrossRef]
- American Society of Mechanical Engineers. Assessing Credibility of Computational Modeling Through Verification and Validation: Application to Medical Devices: ASME V&V 40 - 2018; ASME: New York, NY, USA, 2018; p. 47. [Google Scholar]
- Galluppi, G.R.; Ahamadi, M.; Bhattacharya, S.; Budha, N.; Gheyas, F.; Li, C.C.; Chen, Y.; Dosne, A.G.; Kristensen, N.R.; Magee, M.; et al. Considerations for Industry—Preparing for the FDA Model-Informed Drug Development (MIDD) Paired Meeting Program. Clin. Pharmacol. Ther. 2024, 116, 282–288. [Google Scholar] [CrossRef] [PubMed]
- Viceconti, M.; Pappalardo, F.; Rodriguez, B.; Horner, M.; Bischoff, J.; Musuamba Tshinanu, F. In silico trials: Verification, validation and uncertainty quantification of predictive models used in the regulatory evaluation of biomedical products. Methods 2021, 185, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Raue, A.; Kreutz, C.; Maiwald, T.; Klingmüller, U.; Timmer, J. Addressing parameter identifiability by model-based experimentation. IET Syst. Biol. 2011, 5, 120–130. [Google Scholar] [CrossRef]
- Gutenkunst, R.N.; Waterfall, J.J.; Casey, F.P.; Brown, K.S.; Myers, C.R.; Sethna, J.P. Universally Sloppy Parameter Sensitivities in Systems Biology Models. PLoS Comput. Biol. 2007, 3, e189. [Google Scholar] [CrossRef]
- Kammoun, A.; Slama, R.; Tabia, H.; Ouni, T.; Abid, M. Generative Adversarial Networks for face generation: A survey. ACM Comput. Surv. 2022, 55, 1–37. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated Machine Learning: Concept and Applications. ACM Trans. Intell. Syst. Technol. 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Stamatakos, G.S.; Dionysiou, D.D.; Graf, N.M.; Sofra, N.A.; Desmedt, C.; Hoppe, A.; Uzunoglu, N.K.; Tsiknakis, M. The “Oncosimulator”: a multilevel, clinically oriented simulation system of tumor growth and organism response to therapeutic schemes. In Towards the clinical evaluation of in silico oncology. In Proceedings of the 2007 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 6629–6632. [Google Scholar]
- Gymrek, M.; McGuire, A.L.; Golan, D.; Halperin, E.; Erlich, Y. Identifying Personal Genomes by Surname Inference. Science 2013, 339, 321–324. [Google Scholar] [CrossRef] [PubMed]
- Popejoy, A.B.; Fullerton, S.M. Genomics is failing on diversity. Nature 2016, 538, 161–164. [Google Scholar] [CrossRef]
- Morley, J.; Machado, C.C.V.; Burr, C.; Cowls, J.; Joshi, I.; Taddeo, M.; Floridi, L. The ethics of AI in health care: A mapping review. Soc. Sci. Med. 2020, 260, 113172. [Google Scholar] [CrossRef]
- Bekisz, S.; Geris, L. Cancer modeling: From mechanistic to data-driven approaches, and from fundamental insights to clinical applications. J. Comput. Sci. 2020, 46, 101198. [Google Scholar] [CrossRef]
- Brown, L.V.; Gaffney, E.A.; Wagg, J.; Coles, M.C. Applications of mechanistic modelling to clinical and experimental immunology: an emerging technology to accelerate immunotherapeutic discovery and development. Clin. Exp. Immunol. 2018, 193, 284–292. [Google Scholar] [CrossRef]
- Hunter, A.; Lewis, C.; Hill, M.; Chitty, L.S.; Leeson-Beevers, K.; McInnes-Dean, H.; Harvey, K.; Pichini, A.; Ormondroyd, E.; Thomson, K. Public and patient involvement in research to support genome services development in the UK. J. Transl. Genet. Genom. 2023, 7, 17–26. [Google Scholar] [CrossRef]
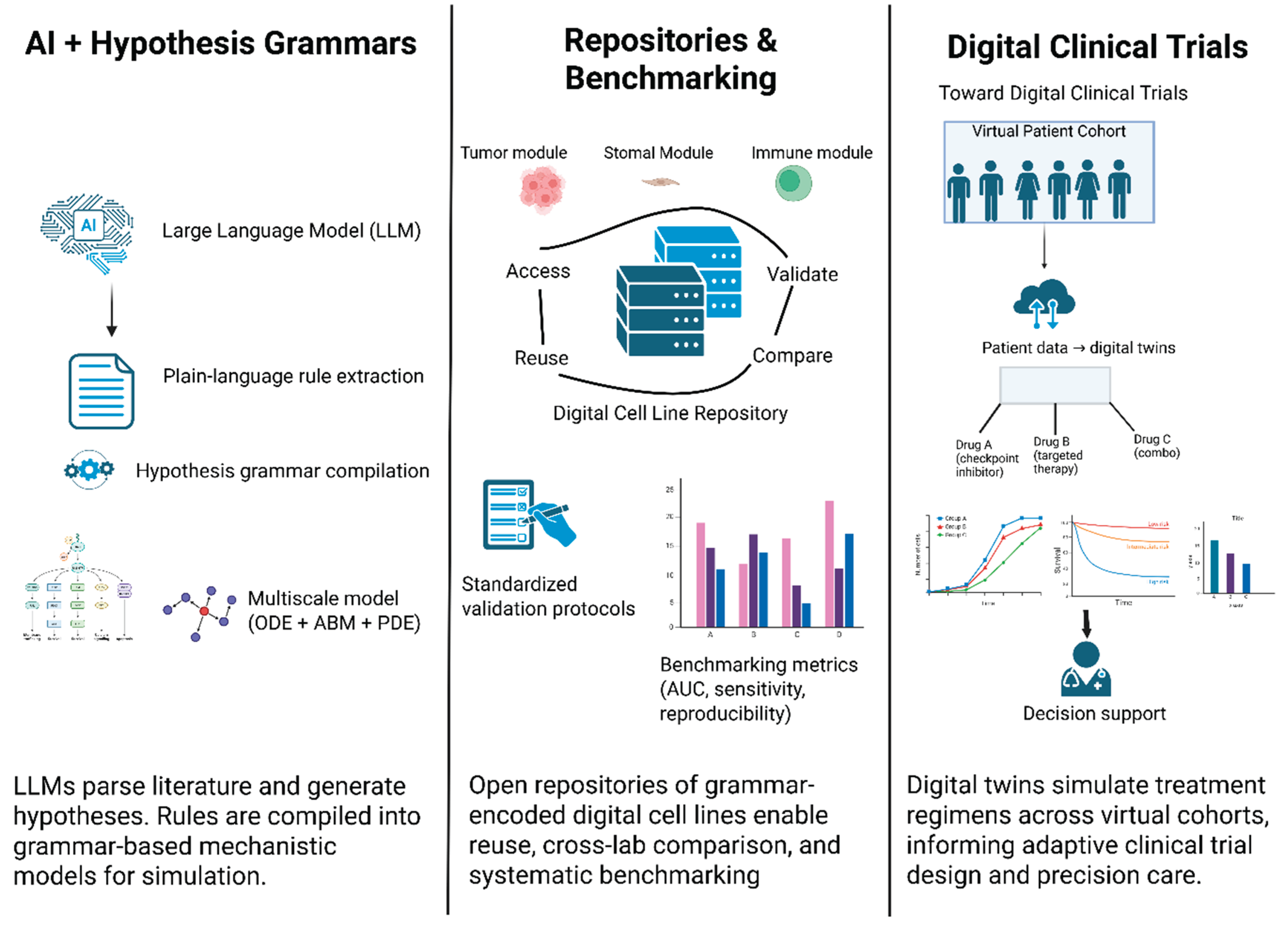
| Framework/Tool | Description | Application Examples | Key Features |
|---|---|---|---|
| PhysiCell (CBHG) | Agent-based modeling platform with built-in cell-behavior hypothesis grammar [15]. | Cancer-immune simulations; liver metastasis; brain cortical development. | Human-readable rule language; handles diffusion, mechanics, and cell rules [15,18]. |
| PhysiBoSS | ABM platform coupling PhysiCell with MaBoSS (Boolean network simulator) [19]. | Multi-scale cancer models combining cell agents with intracellular signaling. | Integrates Boolean GRNs into each agent; enables cell decisions based on signaling [19,20]. |
| Custom Hypothesis Engines | Standalone scripts or libraries that parse plain-language rules into ODEs/ABMs [21,22]. | Prototype tools in research labs for specialized tissue models (no community name). | Often tailored to a project, focus on readability over performance [17]. |
| Framework/Platform | Modeling Approach | Data Inputs | Representative Application |
|---|---|---|---|
| TumorTwin | Modular Python toolkit for patient-specific tumor models. Combines PDE solvers (diffusion, reaction) with imaging-derived geometries [7,37]. | Patient imaging (MRI/CT) + molecular profiles (for parameter fitting). | In silico high-grade glioma growth (radiation therapy planning). |
| ModCell™ (Alacris) | Large-scale ODE signaling network mechanistic model. High-dimensional parametric model of pathways with omics-driven parameterization [20,38]. | Tumor omics (genome, transcriptome, proteome) + known drug targets/kinetics. | Predicted to kill the patient's tumor. |
| PhysiCell + Grammar | Agent-based modeling with hypothesis-grammar rules. Spatial tumor microenvironment with immune/CAF agents (cells) and diffusing molecules [25,39]. | Patient biopsy data (cell counts, expression) to set rule parameters. | Breast and pancreatic tumor models combining patient transcriptomics and spatial data to predict invasion and therapy response |
| Digital Twin Cloud Platforms | (Emerging) Hybrid models integrating ML forecasts with mechanistic simulators [7,8,37]. | Real-time patient monitoring data (future). | Promised for predictive monitoring (no specific example yet in published literature). |
| Modeling Approach | Spatial Scale | Key Components | Representative Tools |
|---|---|---|---|
| Agent-Based (Discrete) | Cellular (µm) | Individual cells serve as agents, governed by rules that regulate proliferation, death, motility, and signaling. Nutrient/cytokine fields via PDEs [21]. | PhysiCell, CompuCell3D, Morpheus; used in GBM invasion, TME studies. |
| Reaction–Diffusion PDE | Tissue (mm) | Continuum fields for growth factors, drugs, and oxygen. Averaged cell densities or ignored individual cells [21,50,51]. | Custom PDE solvers, often coupled with ABM for nutrients. |
| ODE/Boolean (Intracellular) | Subcellular | Gene/protein network dynamics within each cell (mass-action ODEs or Boolean rules) [38,51,52]. | COPASI, MaBoSS, BioNetGen (Rule-based), CellNOpt. |
| Hybrid (ABM + Signaling) | Multi-scale | Coupled systems: e.g., ABM for cell positions + Boolean/ODE networks per agent [40,51,53,54]. | PhysiCell+MaBoSS, CHASTE (multi-scale configs), Elecans. |
| Machine Learning (Data-driven) | Varies | Statistical/ML models trained on data (lacking explicit physics). May incorporate mechanistic features [32,51,54,55]. | Random forests, Neural nets, and Physics-Informed neural networks. |
| Modeling Paradigm | Core Mechanism | Scale of Focus | Key Strengths | Key Weaknesses |
|---|---|---|---|---|
| Agent-Based Models (ABMs) | Individual, rule-based agents (cells) interacting locally. | Cellular, Tissue | Captures emergent properties, exhibits high biological interpretability, is modular, and is flexible [25,39]. | High computational cost, difficult to calibrate parameters, not feasible for large-scale, homogeneous systems. |
| Continuum Models | PDEs/ODEs representing tissue as a continuous medium. | Tissue, Organ | Computationally efficient, well-established mathematical theory, effective for bulk phenomena [21,22]. | Obscures individual cell heterogeneity and is limited in capturing stochasticity and emergent behaviors. |
| Hybrid Models | Combines discrete agents with a continuous field. | Cellular to Tissue | Balances computational efficiency and mechanistic detail, allowing for the modeling of heterogeneous and critical regions [38,45,88]. | Increased model complexity, difficult to integrate different mathematical formalisms seamlessly. |
| Method | Type | Interpretability Strength | Example Usage |
|---|---|---|---|
| Decision Trees | Tree-based (white-box) | Moderate (paths give logic) | Classify tumor subtypes by gene expression thresholds [76]. |
| Rule Lists | Sequence of if-then rules | High (short, readable rules) | Identified antibiotic-resistance markers via k-mer rules [56,58]. |
| Rule Ensembles (e.g., RuleFit) | Weighted rules | Moderate (composite rules) | Aggregate multiple simple rules for robust classification [56,57,58]. |
| Sparse Linear Models | e.g., LASSO (intrinsic) | High (coefficients as effects) | PRS models: linear combo of variant effects [83]. |
| Global Surrogate | Interpretable model fitted to black-box outputs | Moderate | Fit a decision tree on predictions of a deep net to approximate its logic [4,93]. |
| Challenge Category | Specific Barrier | Description of Issue | Proposed Direction for Resolution |
|---|---|---|---|
| Technical | Parameter Identifiability | High-dimensional models often have multiple parameter sets that fit the data, leading to non-unique solutions [7,108,109]. | Development of new computational methods (e.g., Bayesian approaches, ML integration) that can handle large parameter spaces and incorporate prior knowledge to constrain solutions. |
| Data Granularity | Current omics data are often static "snapshots" that fail to capture the full temporal dynamics of cellular processes[54,110,111,112]. | Increased focus on time-series and longitudinal data collection, as well as new methods to infer dynamic trajectories from static data (e.g., pseudo-time analysis). | |
| Computational Complexity | Large-scale, 3D simulations are computationally prohibitive, limiting the scope of models and the speed of simulations [22,25,44]. | Investment in high-performance computing (HPC) infrastructure and the use of ML to create efficient "surrogate models" that can run simulations at a fraction of the cost. | |
| Ethical & Clinical | Algorithmic Bias | Models trained on unrepresentative or biased data can perpetuate or amplify existing health inequities [113]. | A multidisciplinary approach to model development that includes diverse teams, representative datasets, and a focus on transparency and fairness metrics. |
| Patient Privacy & Consent | Genomic data is intrinsically identifiable, making it difficult to balance data sharing for research with a patient's right to privacy [109]. | Adoption of ethical frameworks like GDPR, robust de-identification and encryption techniques, and new models for data ownership and federated learning that keep data local. | |
| Regulatory Validation | Lack of a clear, standardized framework for validating and approving predictive models for clinical use[8,105]. | Collaborative efforts between academia, industry, and regulatory bodies (e.g., FDA) to establish clear guidelines, standardized benchmarking protocols, and community-wide acceptance criteria. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





