Doubts About the Expansion of the Universe Derived from Einstein's Field Equations

1. Introduction

General relativity [1] is a theory that describes the gravitational interaction between matter. In 1915, Einstein's field equations were published, marking the completion of the foundation of general relativity. The general theory of relativity was officially published in 1916. This theory equates the gravitational field to the curvature of space-time for the first time.

The standard form of Einstein’s field equation [2] is:

$$R_{\mu v}-{\displaystyle \frac{1}{2}}{g}_{\mu v}R={\displaystyle \frac{8\pi G}{c^4}}{T}_{\mu v}$$

(1)

In the formula, Ruv is the Ricci tensor condensed from the Riemann tensor, which represents the curvature of space. R is the curvature scalar condensed from the Ricci tensor, guv is the metric tensor, and Tuv is the energy and momentum tensor, which represents the distribution and motion of matter. G is the gravitational constant, and c is the speed of light in vacuum.

The article "Revisiting the Space-time Structure of General Relativity" [3] states that in general relativity, Einstein equated gravity to the curvature of space-time, and from this he deduced that gravity will bend light and gravitational lensing. At that time, Einstein did not describe the structure of space-time, nor did he explain how gravity bends space-time, so the curved space-time structure can only be said to be a hypothesis. We know that light is propagated by photons, and gravity is propagated by gravitons. Photons and gravitons basically do not interact, so the gravity bending of light cannot be explained from the microscopic mechanism. Light can interfere, diffract, and interfere with the same frequency. Therefore, this article believes that light bending is the result of the continuous interaction between visible light and the electromagnetic waves emitted by the luminous planet when the visible light passes next to a massive luminous planet (explanation of the same-frequency mutual winding of light bending). Observations of colliding galaxies show that there is a large amount of non-luminous hot gas during the galaxy collision process. At the same time, there is a gravitational lensing phenomenon in visible light observations. The mass distribution of the galaxy inverted by the gravitational lens is separated from the mass distribution of the hot gas. The traditional view is that this is strong evidence of dark matter. This article believes that the non-luminous hot gas does not contribute to the gravitational lensing phenomenon, which means that the non-luminous hot gas does not bend visible light, which means that the non-luminous hot gas does not bend the space-time around it. Only then will the mass distribution of galaxies inverted by gravitational lensing be separated from the mass distribution of hot gas. This phenomenon shows that the space-time structure of general relativity does not exist. The explanation of the same-frequency mutual winding of light bending is that the degree of bending of light is directly proportional to the brightness of the luminous planet and inversely proportional to the distance between visible light and the center of the planet. Generally, the light-to-quality ratio of high-brightness planets is much greater than that of the sun. The degree of bending of visible light by high-brightness luminous planets is much greater than the degree of bending of visible light by the sun. The dark matter in colliding galaxies is caused by the gravitational lens's insufficient calculation of the degree of bending of visible light by massive luminous planets.

Generally speaking, general relativity is correct in most cases and has been verified in many ways.

In 1917, Soviet physicist Alexander Friedmann established a dynamic universe model framework based on Einstein's field equations. After that, American physicist HP Robertson and British mathematician Arthur Walker independently derived a complete mathematical form of a four-dimensional space-time metric describing a uniform isotropic universe. Belgian astronomer Georges Lemaître also made important contributions, thus forming the famous Friedmann-Lemaître-Robertson-Walker metric [4] (FLRW metric).

The FLRW metric has the following form:

$$d{s}^2=R^2\left(t\right)\left({\displaystyle \frac{d{r}^2}{1-k{r}^2}}+r^{2}d{\theta }^2+r^2{\sin }^2\theta d{\phi }^2\right)-c^{2}d{t}^2$$

(2)

In the formula, R(t) is the universe scaling factor, r, θ, and ∅ are spherical coordinate variables, t is the universe, and k is the space curvature.

The value of the curvature term k needs to be determined by observing the ratio of critical density to actual density Ω(t).

When k=1, the three-dimensional space is spherical, the total volume is finite, and its value is 2R(t).

When k=-1, the three-dimensional space is a hyperbolic space and the total volume is infinite.

When k=0, the three-dimensional space is flat and the total volume is infinite.

The FLRW metric is widely used in constructing mainstream universe models and can explain the cosmic microwave background radiation and the formation of large-scale structures. It can also be used to explore the distribution of dark matter and dark energy through this metric.

In 1922, Soviet physicist Alexander Friedman derived the core equation that describes the evolution of a uniform and isotropic expanding universe - the Friedman equation [5]. This equation is based on the FLRW metric, which reflects the expansion rate of the universe through the scaling factor a(t). The core parameters include the curvature constant k (which determines the geometry of the universe) and energy density.

The Friedmann equation can be derived through Newton's theory of gravity, or through the Einstein field equations of general relativity. Down

Let’s first look at the derivation process of Newton’s universal gravitation [6]. Figure 1 is an imaginary diagram of deriving the Friedman equation from universal gravitation.

From the law of universal gravitation, we know that the gravitational force of an object with mass M (universe) on an object with mass m is:

$$F={\displaystyle \frac{GMm}{r^2}}$$

(3)

where r is the distance between objects and G is Newton's gravitational constant. We all know that gravitational potential energy is:

$$V=-{\displaystyle \frac{GMm}{r}}$$

(4)

Assume that the density of M is ρ and the volume is ${\displaystyle \frac{4}{3}}\pi r^3$. Therefore $M={\displaystyle \frac{4}{3}}\pi r^3\rho$, substituting into the above two equations, we have:

$$F={\displaystyle \frac{Gm}{r^2}}{\displaystyle \frac{4}{3}}\pi r^3\rho ={\displaystyle \frac{4\pi G\rho rm}{3}}$$

(5)

$$V=-{\displaystyle \frac{4\pi G\rho r^{2}m}{3}}$$

(6)

According to the law of conservation of energy, now that we have gravitational potential energy, we need to know its kinetic energy. Because r is distance, the speed at which objects move away from each other should be the derivative of distance r with respect to time t, dr/dt. Writing this as $\dot{r}$:

$$T={\displaystyle \frac{1}{2}}m{\dot{r}}^2$$

(7)

Assuming the total energy is U, then there is:

$$U=T+V$$

(8)

Obviously U should be a constant. Substituting T and U, we get:

$$U={\displaystyle \frac{1}{2}}m{\dot{r}}^2-{\displaystyle \frac{4\pi }{3}}G\rho r^{2}m$$

(9)

Here a parameter a is introduced, which is called the universe scale factor. Because the universe is expanding, the distance between two points is not in a constant coordinate system, but in an expanding coordinate system (comoving coordinate system). The relationship between the real distance r and the co-moving distance x is:

$$\overrightarrow{r}=a\left(t\right)\overrightarrow{x}$$

(10)

Since the expansion rate of the universe changes with time, a is a function of t, and the derivation of x with respect to t is dx/dt=0, that is to say:

$$\dot{r}={\displaystyle \frac{d\left(ax\right)}{dt}}=a{\displaystyle \frac{dx}{dt}}+x{\displaystyle \frac{da}{dt}}=\dot{a}x$$

(11)

Substitute (10) (11) into (9) to get

$$U={\displaystyle \frac{1}{2}}m{\dot{a}}^2{x}^2-{\displaystyle \frac{4\pi }{3}}G\rho a^2{x}^{2}m$$

(12)

Multiply both sides simultaneously$2/m{a}^2{x}^2$：

$${\displaystyle \frac{2U}{m{a}^2{x}^2}}={\left({\displaystyle \frac{\dot{a}}{a}}\right)}^2-{\displaystyle \frac{8\pi }{3}}G\rho$$

(13)

we order $-2U/m{x}^2=k{c}^2$, Obtained after transfer：

$${\left({\displaystyle \frac{\dot{a}}{a}}\right)}^2={\displaystyle \frac{8\pi }{3}}G\rho -{\displaystyle \frac{k{c}^2}{a^2}}$$

(14)

This is the standard form of the Friedmann equation, where c is the speed of light and k is the geometric curvature of the universe. Transferring items results in:

$${\left({\displaystyle \frac{\dot{a}}{a}}\right)}^2-{\displaystyle \frac{8\pi }{3}}G\rho =-{\displaystyle \frac{k{c}^2}{a^2}}$$

(15)

The letter a is called the scale factor, and it represents the size of the universe, more accurately thought of as the average distance between galaxies. The Friedmann equation also tells us how a changes with time. The one point on a is the derivative of a with respect to time, which represents the expansion rate of the universe.

The first term on the left side of the Friedmann equation is similar to the kinetic energy of expansion, but this kinetic energy is resisted by the gravitational effect of the energy of the second term on the left, where ρ is the matter density of the universe. So the second term represents the ability of the universe to slow down itself, similar to gravitational potential energy. The right-hand term describes the shape (curvature) of space, which depends on the value of k, which is the shape of the universe in the sense that k can be +1, -1, or 0.

The Friedmann equation can also be derived through the general theory of relativity. The process is as follows:

First, simplify Einstein’s field equations to:

$$G_{\mu v}=8\pi T_{\mu v}$$

(16)

In cosmology, the FRW metric (Friedmann-Lemaître-Robertson-Walker metric) is used：

$$d{s}^2=c^{2}d{t}^2-a^2\left(t\right)\left({\displaystyle \frac{d{r}^2}{k}}+r^{2}d{\theta }^2+r^2{\sin }^2\theta d{\phi }^2\right)$$

(17)

where a(t) is the universe scaling factor, and k is the curvature constant (values ​​0, 1, and -1 correspond to flat, closed, and open universes).

Calculate the Ricci tensor Rμν through the metric tensor, and its non-zero components include:

$$R_{00}=-3{\displaystyle \frac{\ddot{a}}{a}}$$

(18)

$$R_{ii}=g_{ii}\left(2{\displaystyle \frac{\ddot{a}}{a}}+2{\displaystyle \frac{{\dot{a}}^2}{a^2}}+2k\right)$$

(19)

where i=1,2,3.

Substituting the Ricci tensor into Einstein's field equations we get：

$$-{\displaystyle \frac{3\ddot{a}}{a}}=8\pi G\left(\rho c^2-3p\right)$$

(20)

Right now：

$${\displaystyle \frac{\ddot{a}}{a}}={\displaystyle \frac{4\pi G}{3c^2}}\left(3p+\rho c^2-3k\right)$$

(21)

The Friedmann equation describes the relationship between the acceleration of the expansion of the universe and the density, pressure and curvature of matter. When ${\displaystyle \frac{\ddot{a}}{a}}$>0, the universe continues to expand; when ${\displaystyle \frac{\ddot{a}}{a}}$<0, the expansion will slow down and may turn to contraction.

The two methods agree in the simple case of a flat universe (k=0), but the derivation of general relativity has wider applicability, especially the precise description of accelerated expansion and space-time geometry.

For a long time, scientists believed that the ultimate fate of the universe lay in its density ρ. So for decades, astronomers have been trying to measure the total mass of matter and dark matter across large swaths of the universe. It turns out that the density of the universe is too low, only a quarter of the density required for torsional expansion. Therefore, the left-hand term of Friedmann's equation is positive and the universe will expand forever.

2. Curvature of Space and Time (Gravity) and Distance

General relativity, the FRW metric and the Friedman equation, from a mathematical point of view, there is absolutely no problem with them. The FRW metric and the Friedman equation are both developed on the basis of the general theory of relativity. Their most fundamental idea is that massive objects will bend the space-time around them. Let's review the relationship between the curvature of space-time (gravity) and distance.

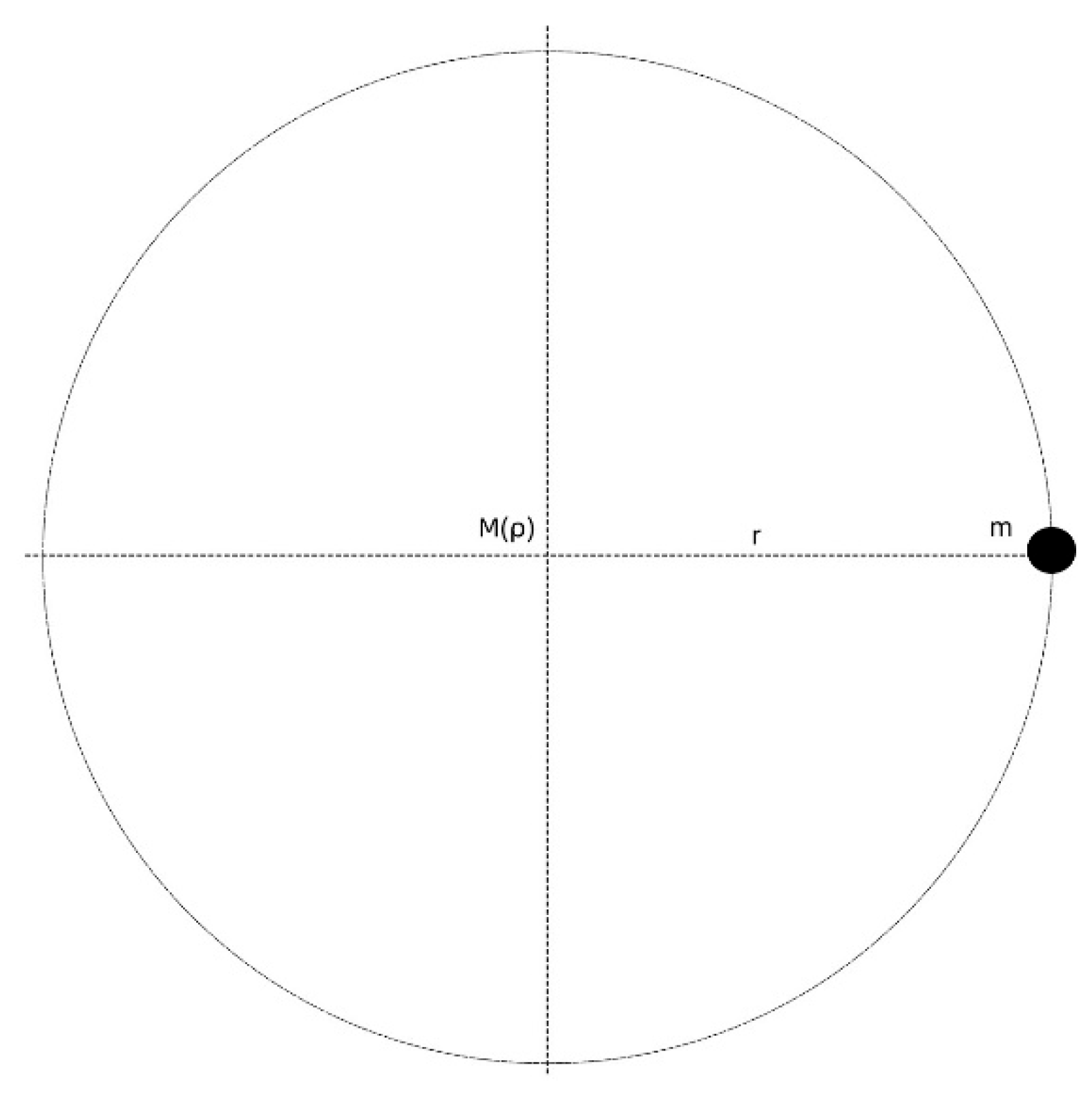
From Newton's universal gravitation, we know that gravity is inversely proportional to the square of the distance between two planets. The article "Gravity, Gravitational Field and Gravitons - Inference on the Frequency of Gravitational Energy Waves" [7] believes that the distance over which gravity acts is limited, and its average maximum distance Rmax is 7.94 light-years. In the generalized phase, The theory of reciprocity holds that a massive planet can bend the space-time around it, but the degree of curvature will decrease as the distance increases. When the distance increases to a certain extent (Rmax), the degree of curvature of space-time will tend to 0. At this time, the degree of curvature of the planet for space-time greater than Rmax distance is k=0.

Figure 2 Schematic diagram of the relationship between space-time curvature (gravity) and distance. According to the general theory of relativity, the planet with mass M in the figure bends the space-time around it. As the distance R increases, the gravity of the object M will become smaller and smaller, and the curvature of space-time will also become smaller and smaller. When the distance exceeds the maximum distance of gravity, the gravity of the object M can be ignored, and the curvature of the space-time of the object M will be small enough to be ignored. At this time, it can be said that the object M has no impact on the space-time with a distance greater than Rmax. Of course, any movement of the object M will also have no impact on space-time.

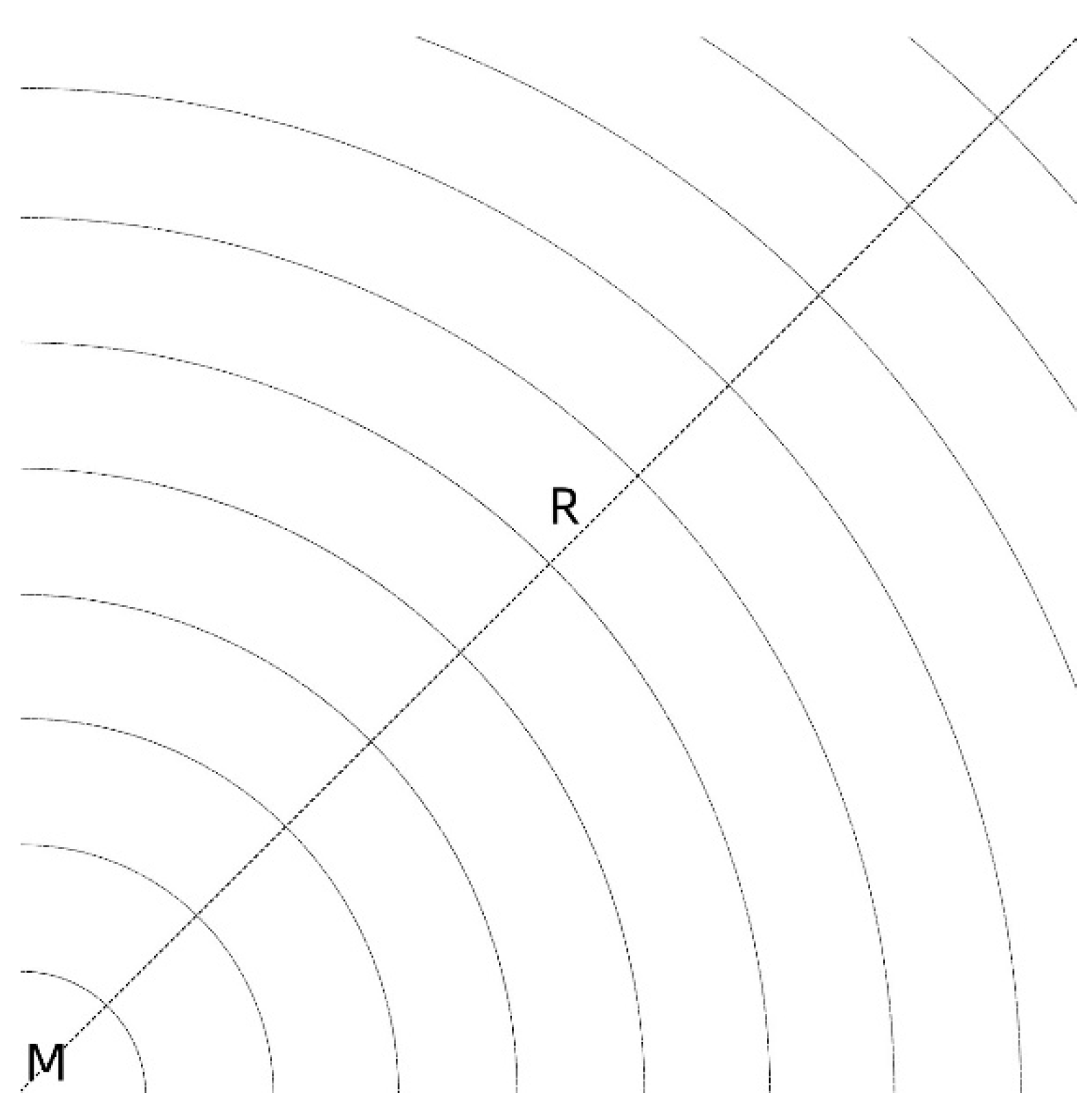
Figure 3 is a three-dimensional schematic diagram of the curved space-time of a massive planet. It can be seen from the figure that when the distance is large, the massive planet has no impact on its space-time. Of course, any movement of the object M also has no impact on space-time.

3. Space-Time Curvature (Gravity) and Galaxies

For galaxies with a diameter less than 10 light-years (such as the solar system), the mass is mainly concentrated on the central planet (the sun). All planets in the entire galaxy are affected by the gravity of the central planet. Although the degree of curvature of space-time by the central planet becomes smaller as the distance increases, this degree of curvature cannot be ignored even when it reaches the edge of the galaxy.

For large galaxies or galaxy clusters (such as the Milky Way), there is usually a cantilever. At this time, the planets at the edge of the galaxy or galaxy cluster are usually at the end of the cantilever. Since most of the planets in the galaxy are quite far away from the edge planets, their gravitational pull on the edge planets can be ignored, and the degree of space-time curvature of the edge planets is also negligible. Therefore, it can be said that it has no impact on the movement of the edge planets. At this time, only the gravity of the planets that are relatively close to the edge planet (less than 10 light years) will have an impact on the movement of the edge planet. That is to say, only the stars that are relatively close to the edge star (less than 10 light years) will have an impact on the curvature of space-time at the edge planet.

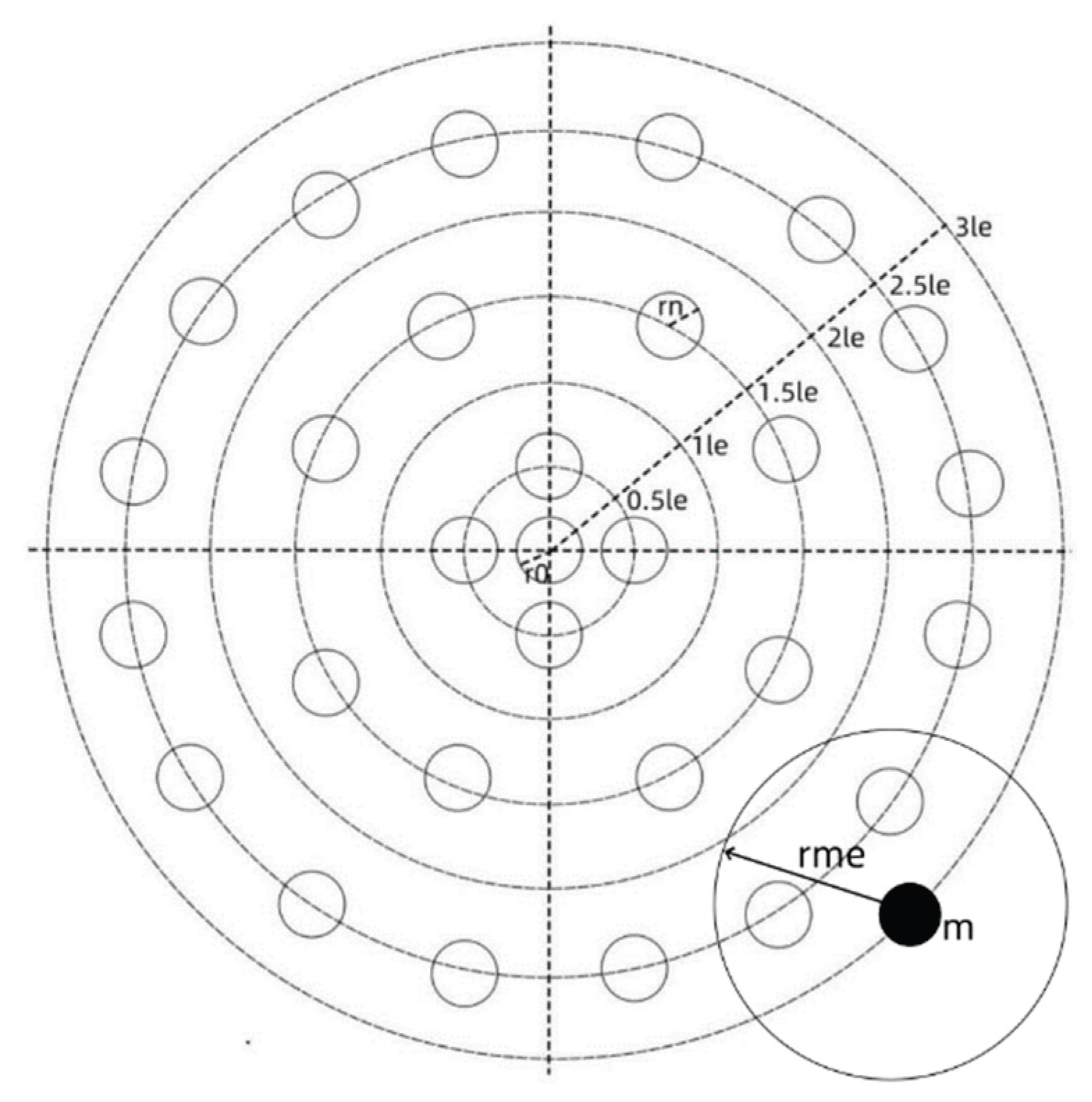
Figure 4 is a force diagram on the edge planets of the galaxy (universe). The figure assumes that the planets are evenly distributed in space, rn is the radius of each planet, le is the equivalent distance between the planets, all planets are on spheres at different distances, m is the edge planet with mass m on the edge of the galaxy or galaxy cluster, rme is the maximum radius that will affect the edge planet, that is, it will have an impact on the space and time of the edge planet m. As for the maximum radius, it can be seen from the figure that the gravitational pull of most planets in a galaxy or galaxy cluster on the edge planet m is negligible. That is to say, the degree of space-time curvature of the vast majority of planets in a galaxy or galaxy cluster on the edge planet m is negligible. Only planets within the radius rme will exert gravitational attraction on the edge planet, and only planets within the radius rme will cause space-time curvature at the location of the edge planet. At this time, we cannot equate the distribution of matter in the entire galaxy to the center of the galaxy to calculate the gravitational pull of the entire galaxy on the edge planets, nor can we equate the distribution of matter in the entire galaxy to the center of the galaxy to calculate the degree of space-time curvature of the entire galaxy on the edge planets.

4. The Expansion of the Universe

Regarding the universe, the first question is the question of finiteness and infinity. So far, although we have launched the Hubble Telescope and the Webb Telescope, the observation distance is far beyond the era of human eye observation, but we still have not observed the edge and end of the universe. So we cannot determine whether the universe is limited or infinite.

For an infinite universe, there is no problem of the entire universe affecting the space and time around it.

For the finite universe, it can be considered that there is no matter outside the universe, so there is no problem of the gravity of the entire universe on the objects around it. Generally, the curvature of space-time is manifested by changes in the orbits of surrounding objects affected by the gravitational pull of the central object. At this time, it is impossible to know whether the entire universe has an impact on the surrounding space-time.

As for the influence of the entire universe on its edge planets, as shown in Figure 4, we can also easily obtain: the gravitational pull of the vast majority of planets in the universe on edge planet m is negligible, which means that the vast majority of planets in the universe have negligible space-time curvature at edge planet m. Only planets within the radius rme will exert gravitational force on the edge planet, and only planets within the radius rme will cause space-time curvature at the location of the edge planet. At this time, we cannot equate the distribution of matter in the entire universe to the center of the universe to calculate the gravitational pull of the entire universe on the edge planets, nor can we equate the distribution of matter in the entire universe to the center of the universe to calculate the degree of space-time curvature of the entire universe on the edge planets.

The main observational evidence of the expansion of the universe is the phenomenon of galaxy redshift: in 1929, Hubble discovered through observations that the spectra of almost all distant galaxies were shifted toward red light (i.e., redshift). The mainstream view is that this is because the galaxy is far away from the earth, causing the light waves to be elongated, which is consistent with the principle of the Doppler effect. The farther a galaxy is from the earth, the more obvious the red shift phenomenon is. The regression speed is linearly related to the distance, which directly proves that the universe is expanding. There is a very loose logical error in this reasoning: the retrogression of galaxies can produce red shifts, but red shifts are not necessarily caused by the retrogression of galaxies. Just like an apple orchard with A1, A2, A3, A4, A5, ..., A20 apple trees, each apple tree can produce apples, but we cannot say that these apples are all produced by a certain apple tree (such as A1). There are many reasons that can produce redshift in the universe. Since the publication of Hubble's law, many scholars have proposed different redshift theories. Louis Mamet, an adjunct professor of physics and astronomy at York University in Toronto, Canada, published in January 2018: A review of 59 mechanisms of spectral redshift in astrophysics [8]. Doppler redshift is only one of them, so we cannot conclude that galaxies are regressing and the universe is expanding through Hubble redshift.

The article "Hubble's Law, Universe Expansion Contradicts Observations of Pulsar Time Stability" [9] calculated the pulsar time stability caused by Hubble's law. According to Hubble's law, the 10-year change value of the pulsar period should be on the order of 10^-10. The actual observed value of the pulsar time stability is on the order of 10^-15, which is more than 5 orders of magnitude smaller than the change in pulsar period inferred by Hubble's law. This shows that the galaxy is not regressing as Hubble inferred, and the universe is not expanding.

General relativity believes that the degree of curvature of space-time is mainly related to the mass and density of the central planet. The greater the mass, the more significant the curvature of space-time around it is. Although high-density celestial bodies (such as neutron stars) are small in size, their mass is concentrated in a smaller space, causing the surface gravitational acceleration to be much greater than that of lower-density celestial bodies (such as stars). Therefore, high-density celestial bodies bend the space-time around them more significantly, so it should be easier for larger galaxies to form around neutron stars. Actual observations show that no large galaxies with neutron stars as their centers have been found in the universe.

Since its launch at the end of 2021, the James Webb Space Telescope has used its infrared eyes to penetrate cosmic dust, pushing the limits of human observation to hundreds of millions of years after the Big Bang. In just a few years, it observed that mature galaxies that should have formed only after billions of years had quietly bloomed when the universe had just passed three percent of its lifespan [10].

According to the mainstream Λ-cold dark matter model, about 380,000 years after the Big Bang, neutral atoms began to gather, and the universe entered a long "dark age." Under the gravitational pull of dark matter, it took hundreds of millions of years for the gas to gradually collapse and give birth to the first generation of stars and galaxies. This theory is like the "standard answer" to the evolution of the universe and has been recognized by the academic community for decades. However, the data returned by the Webb Telescope shows that when the universe was only about 500 million years old, galaxies with a mass comparable to the Milky Way and complete structures had already appeared. They were quietly suspended in the early universe, as if silently questioning our inherent understanding of the evolution of the universe.

Since scientific observations began in 2022, the number of early galaxies discovered by the Webb Telescope far exceeds astronomers' expectations. It captures galaxies with redshift values exceeding 10, such as GN-z11, whose redshift value reaches 11.09, corresponding to the age of the universe is only about 400 million years; and the MoM-z14 galaxy, whose redshift value soars to 14.44, indicating its birth 280 million years after the Big Bang - at this point in time, the universe was still in its "infancy", and even the first generation of stars should have just begun to shine. However, this galaxy has already shown an astonishing brightness, suggesting that violent star formation activities are taking place within it.

Even more astonishing are the early galaxies with mature structures. When the universe was about 500 million years old, the mass of the ZF-UDS-7329 galaxy reached 10 billion times that of the sun, and star formation activity had basically stopped and entered a "quiet state." You must know that according to traditional theory, galaxies require at least billions of years of evolution from formation to cessation of stellar activity; there is also a giant galaxy chain known as the "cosmic vine", which connected 20 galaxies and spanned 13 million light-years when the universe was only 2 billion years old. Such a scale should have only appeared 5 billion years after the birth of the universe. At a redshift of 7.88, the Webb Telescope also confirmed a primordial galaxy cluster through spectral analysis, with seven galaxies crowded within a diameter of 60 kiloparsecs. The density is 20 times the average density of the universe, and the mass of its dark matter halo exceeds 40 billion times that of the sun. These data continue to impact the boundaries of existing theories.

In June 2025, Alicia Wang, a professor of astronomy at the California Institute of Technology, led a team to analyze data from the Webb Telescope and found that in the first billion years after the Big Bang, the formation rate and number of galaxies far exceeded the predictions of current mainstream models. Specifically, in the range of redshift 5 to 11, the number density of galaxies is about 10 times higher than predicted by the Λ-cold dark matter model - this means that a large number of galaxy cluster structures have been formed in the early universe, which directly conflicts with the hierarchical structure theory of "small galaxies gradually merge into large galaxies" in the standard model.

Not only were these early galaxies numerous in number, but their mass and evolutionary state were also "abnormal." The Webb-CEERS-93316 galaxy was formed about 600 million years after the Big Bang, but its mass reaches 50 billion times that of the sun, which is equivalent to the combined mass of 50 galaxies. Although the MoM-z14 galaxy is compact in size, it is extremely bright. Astronomers have used light to Spectral analysis found that its internal star formation efficiency is extremely high, converting almost all the surrounding gas and dust into stars. However, at such an early stage of the universe, these gases and dust, which are the "raw materials" for stars, should have been slowly gathering, and there was no time to form a star group of this size.

Even more complex is the chemical makeup of these galaxies. Spectroscopic analysis of galaxies shows that they contain a large amount of heavy elements such as carbon and oxygen, and these elements can only be formed through nuclear fusion inside stars, and are spread into interstellar space in the form of supernova explosions when stars die. This means that when the universe was only 280 million years old, it had already gone through the "birth-death" cycle of multiple generations of stars - the first generation of stars formed, glowed, exploded, and spread heavy elements; the second generation of stars formed based on heavy elements and then went through the same process... Such a cycle would take at least billions of years, but the early universe did not have such a long time window.

Some early galaxies also exhibit a disk-like structure and orderly rotation similar to the Milky Way, such as galaxies known as "cosmic vineyards." When the research team compared its observation data with the current most advanced cosmological simulations (SERRA, FIRE and TNG50), they found that the galaxies in the simulation could either only form a small number of clumps but maintain a rotating disk structure, or form a large number of clumps but fall into chaotic motion, and could never reproduce the observed characteristics of "rich clumps + orderly rotation" at the same time.

These findings put the mainstream Λ-cold dark matter model into trouble. This model believes that the universe is composed of about 5% ordinary matter, 27% dark matter and 68% dark energy, and the structure is formed in a hierarchical aggregation from small to large. However, the observations of the Webb Telescope have thrown up four unavoidable contradictions: In terms of time, early galaxies were formed much earlier than model expectations, and the universe had complex structures when it was only 280 million years old; in terms of mass, the mass of galaxies like MoM-z14 far exceeded model predictions, and it should not have been possible when the universe was 600 million years old. There are objects with a mass of 50 billion times that of the sun. Structurally, the disk-like structure and orderly rotation of early galaxies are completely inconsistent with the "loose small galaxies" predicted by the model. Quantitatively, the number of galaxies in the redshift range of 5 to 11 is ten times that predicted by the model. The "crowding" of the early universe is beyond imagination.

The theory of galaxy formation faces the same crisis. Traditional theories believe that the star formation efficiency of early galaxies is low because of the lack of heavy elements to help cool the gas. However, the star formation efficiency of the early galaxies observed by the Webb Telescope reached almost 100%. Theoretically, it takes a long time for the gas and dust in the early universe to accumulate, but these galaxies can gather enough "raw materials" in a short time. ; In terms of chemical evolution, the heavy element content in early galaxies shows that multi-generational stellar cycles have long been completed, which is seriously inconsistent with the time scale of the early universe; What is even more difficult is the problem of dark matter halo matching. The mass of the ZF-UDS-7329 galaxy even exceeds the mass of the dark matter halo in which it is located as estimated by the standard model, which completely goes against common sense.

Even the understanding of the reionization history of the universe has been rewritten by the Webb telescope. Traditional theory holds that reionization (the transition from a neutral state to an ionized state) of the universe mainly occurs near redshift 6 and is dominated by young, massive stars. However, observations from the Webb Telescope show that there is a large amount of star formation activity at redshifts above 10, and the reionization process may be much earlier than expected. The new study also found that faint galaxies are the main force in providing reionization photons, and the production efficiency of these photons is much higher than previous observations. Its efficiency is directly related to the history of star formation explosions in galaxies. This means that the "dark ages" of the universe may not be that dark, and the "first light" of stars shines earlier than we imagined.

The Webb Telescope discovered striking similarities between early quasars in the universe and recent quasars [11]. All of this shows that the distance and time are basically the same everywhere in the universe, and there is no expansion process in the universe.

5. Conclusion

From Newton's universal gravitation, we can know that the gravitational force between two planets is inversely proportional to the square of the distance. When the distance is large, the gravitational force between the two planets will become very small. At this time, it can be considered that the two planets are no longer affected by each other's gravity. Einstein's general theory of relativity believes that a massive planet can bend the space-time around it, and the degree of curvature decreases with distance. When the distance is large, the degree of the planet's curvature of its space-time will also become very small, or even negligible. For a large galaxy or galaxy cluster, there are many planets in it. Their gravitational pull on the edge planets of the galaxy or galaxy cluster varies with the distance. For most planets, because the distance is quite far, it has no impact on the edge planets of the galaxy or galaxy cluster. It can also be said that most of the stars in the galaxy or galaxy cluster Numerous planets have no impact on the space-time where the edge planets are located. Only a few planets that are close to the edge planets of the galaxy or galaxy cluster will have an impact on it. Therefore, we cannot equate the distribution of all the planets in the galaxy or galaxy cluster to the center of the galaxy or galaxy cluster to analyze its impact on the edge planets of the galaxy or galaxy cluster. For the entire universe, we are currently unable to determine whether its size is finite or infinite. Even if we regard it as a finite sphere, we cannot equate the planets in the entire universe to the center of the universe to analyze its impact on the planets (space-time) at the edge of the universe. Therefore, we cannot derive the results of the expansion of the universe from Einstein's field equations. We know that the field equations of Einstein's general theory of relativity evolved from the bending of the space-time around a massive planet. This article believes that it is only suitable for calculating the impact of a specific planet on the surrounding space-time. It is not applicable to the calculation of the impact of galaxies or galaxy clusters on the surrounding space-time, let alone the calculation of the evolution of the entire universe. Observations by the Webb Telescope have shown that the characteristics of galaxies in the early universe are surprisingly similar to those of recent galaxies, indicating that there is no expansion process in the universe.