Submitted:
29 October 2025
Posted:
30 October 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Chiral Perturbation Theory with Resonances
3. Study of the Decay into Within
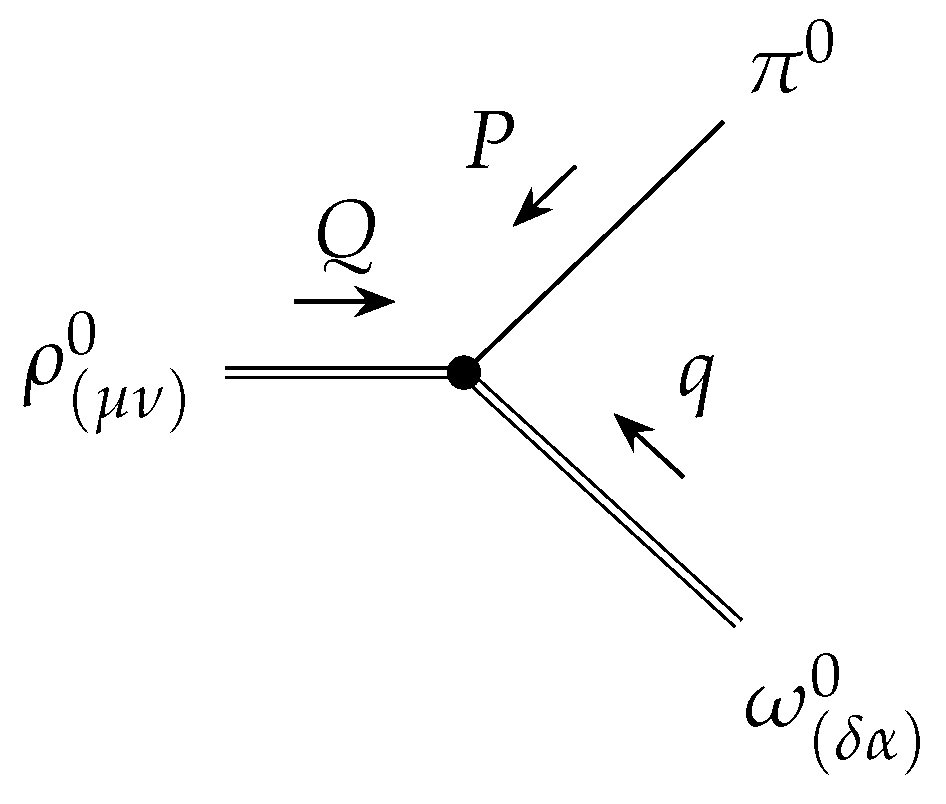
3.1. Interaction Vertex Among the , , and Particles
3.1.1. On-Shell Vertex
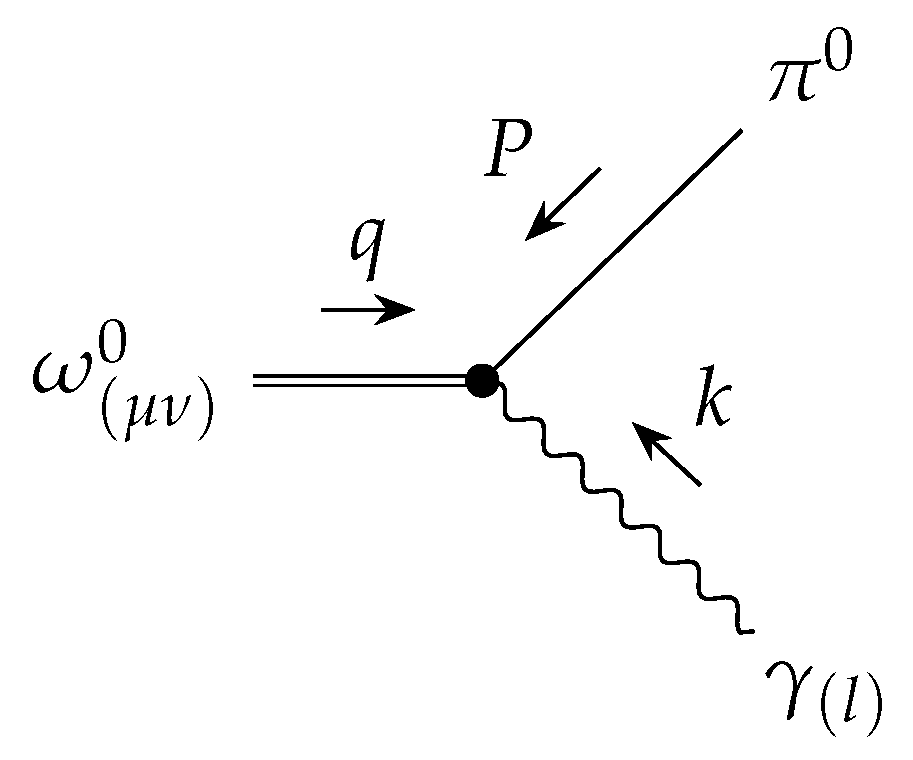
3.2. Interaction Vertex Among the , , and Particles
3.2.1. On-Shell Vertex
3.3. Decay into
Scenario 1: The Decay via Purely on-Shell Vertices
Scenario 2: The decay via the on-shell vertex
Scenario 3: The Decay via the on-Shell vertex
Scenario 4: The Decay with Off-Shell Vertices
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BR | Branching Ratio. |
| dBR | Differential Branching Ratio. |
| LEC | Low-energy Coupling Constant. |
| SM | Standard Model. |
| EFT | Effective Field Theory. |
| ChPT | Chiral Perturbation Theory. |
| QCD | Quantum Chromodynamics. |
| Resonance Chiral Theory. | |
| VVP | Two vector sources and a pseudoscalar source. |
| VJP | A vector source, an external source and pseudoscalar source. |
Appendix A. Detailed and Supplementary Expressions
References
- Schwartz, M.D. Quantum Field Theory and the Standard Model; Cambridge University Press, 2014.
- Grossman, Y.; Nir, Y. The Standard Model: From Fundamental Symmetries to Experimental Tests; Princeton University Press, 2023.
- Navas, S.; et al. Review of particle physics. Phys. Rev. D 2024, 110, 030001. [Google Scholar] [CrossRef]
- Weinberg, S. Phenomenological Lagrangians. Physica A: Statistical Mechanics and its Applications 1979, 96, 327–340. [Google Scholar] [CrossRef]
- Scherer, S.; Schindler, M. A Primer for Chiral Perturbation Theory; Lecture Notes in Physics, Springer Berlin Heidelberg, 2011. [CrossRef]
- Pich, A. Chiral perturbation theory. Reports on Progress in Physics 1995, 58, 563. [Google Scholar] [CrossRef]
- Ecker, G.; Gasser, J.; Pich, A.; De Rafael, E. The role of resonances in chiral perturbation theory. Nuclear Physics B 1989, 321, 311–342. [Google Scholar] [CrossRef]
- Ruiz-Femenía, P.D.; Pich, A.; Portolés, J. Odd-intrinsic-parity processes within the resonance effective theory of QCD. Journal of High Energy Physics, 2003; 003. [Google Scholar] [CrossRef]
- Miranda, J.A.; Roig, P. New τ-based evaluation of the hadronic contribution to the vacuum polarization piece of the muon anomalous magnetic moment. Phys. Rev. D 2020, 102, 114017. [Google Scholar] [CrossRef]
- Aliberti, R.; et al. The anomalous magnetic moment of the muon in the Standard Model: an update. Phys. Rept. 2025, 1143, 1–158. [Google Scholar] [CrossRef]
- Chen, C.; Duan, C.G.; Guo, Z.H. Triple-product asymmetry in the radiative two-pion tau decay. JHEP 2022, 08, 144. [Google Scholar] [CrossRef]
- Ecker, G.; Gasser, J.; Leutwyler, H.; Pich, A.; De Rafael, E. Chiral Lagrangians for massive spin-1 fields. Physics Letters B 1989, 223, 425–432. [Google Scholar] [CrossRef]
- Roig, P.; Cillero, J.J.S. Consistent high-energy constraints in the anomalous QCD sector. Physics Letters B 2014, 733, 158–163. [Google Scholar] [CrossRef]
- Kampf, K.; Novotný, J. Resonance saturation in the odd-intrinsic parity sector of low-energy QCD. Phys. Rev. D 2011, 84, 014036. [Google Scholar] [CrossRef]
- Cirigliano, V.; Ecker, G.; Eidemüller, M.; Kaiser, R.; Pich, A.; Portolés, J. Towards a consistent estimate of the chiral low-energy constants. Nuclear Physics B 2006, 753, 139–177. [Google Scholar] [CrossRef]
- Gómez Dumm, D.; Roig, P. Resonance Chiral Lagrangian analysis of τ-→η(′)π-π0ντ. Phys. Rev. D 2012, 86, 076009. [Google Scholar] [CrossRef]
- Gómez Dumm, D.; Pich, A.; Portolés, J. τ→πππντ decays in the resonance effective theory. Phys. Rev. D 2004, 69, 073002. [Google Scholar] [CrossRef]
- Cirigliano, V.; Ecker, G.; Eidemüller, M.; Pich, A.; Portolés, J. 〈VAP〉Green function in the resonance region. Physics Letters B 2004, 596, 96–106. [Google Scholar] [CrossRef]
- Achasov, M.; et al. The e+e-→π0π0γ process below 1.0 GeV. Journal of Experimental and Theoretical Physics Letters 2000, 71, 355–358. [Google Scholar] [CrossRef]
- Bramon, A.; Escribano, R.; Napsuciale, M.; et al. Scalar σ meson effects in ρ and ω decays into π0π0γ. Physics Letters B 2001, 517, 345–354. [Google Scholar] [CrossRef]
- Achasov, M.; et al. Experimental study of ρ→π0π0γ and ω→π0π0γ decays. Physics Letters B 2002, 537, 201–210. [Google Scholar] [CrossRef]
- Gokalp, A.; Yilmaz, O. The decay ρ0→π0π0γ and the role of σ-meson. Physics Letters B 2001, 508, 25–30. [Google Scholar] [CrossRef]
- Marco, E.; Hirenzaki, S.; Oset, E.; Toki, H. Radiative decay of ρ0 and φ mesons in a chiral unitary approach. Physics Letters B 1999, 470, 20–26. [Google Scholar] [CrossRef]
- Gokalp, A.; Solmaz, S.; Yilmaz, O. Scalar σ meson effects in radiative ρ0-meson decays. Phys. Rev. D 2003, 67, 073007. [Google Scholar] [CrossRef]
- Akhmetshin, R.; et al. Study of the process e+e-→π0π0γ in c.m. energy range 600–970 MeV at CMD-2. Physics Letters B 2004, 580, 119–128. [Google Scholar] [CrossRef]
- Shtabovenko, V.; Mertig, R.; Orellana, F. FeynCalc 10: Do multiloop integrals dream of computer codes? Computer Physics Communications 2025, 306, 109357. [Google Scholar] [CrossRef]
- Mertig, R.; Böhm, M.; Denner, A. FeynCalc - Computer-algebraic calculation of Feynman amplitudes. Computer Physics Communications 1991, 64, 345–359. [Google Scholar] [CrossRef]
| 1 | The chiral limit denotes the theoretical scenario in which the light quarks u, d, and s are massless. |
| 2 | see discussion in appendix B of Ref. [11]) |
| 3 | Tr denotes the trace. |
| 4 | The symmetry group is referred to as the Chiral Symmetry |
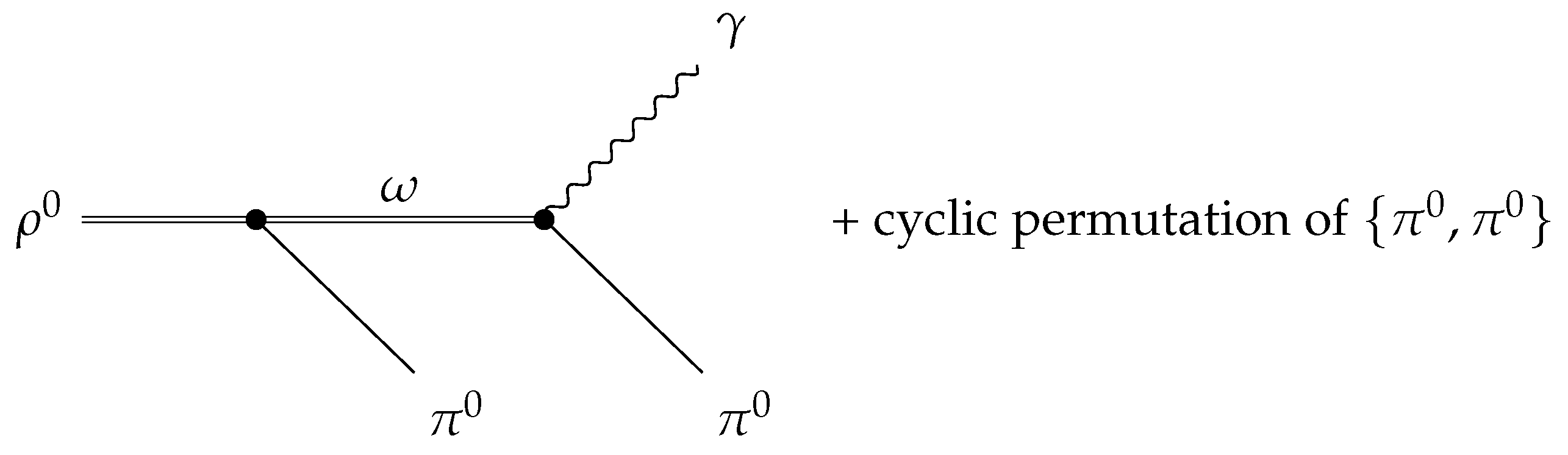

| Constraints (38)–(43) | Constraints (44)–(46) | ||||
|---|---|---|---|---|---|
| 0.032(3) | 0.901(54) | 0.030(3) | 1.059(65) | ||
| -0.025(3) | 0.901(54) | -0.025(3) | 1.059(65) | ||
| 0.032(3) | -0.221(54) | 0.030(3) | -0.327(65) | ||
| -0.025(3) | -0.221(54) | -0.025(3) | -0.327(65) | ||
| -0.98 | 0.03 | -0.03 |
| 0.90 | 0.03 | -0.03 |
| -0.80 | 0.03 | -0.03 |
| -0.70 | 0.04 | -0.03 |
| -0.60 | 0.04 | -0.04 |
| -0.50 | 0.05 | -0.04 |
| -0.40 | 0.06 | -0.05 |
| -0.30 | 0.07 | -0.06 |
| -0.20 | 0.09 | -0.08 |
| -0.10 | 0.12 | -0.10 |
| 0.02 | 0.20 | -0.18 |
| 0.10 | 0.33 | -0.31 |
| 0.20 | 0.44 | -0.53 |
| 0.30 | 0.21 | -0.25 |
| 0.40 | 0.12 | -0.15 |
| 0.50 | 0.09 | -0.10 |
| 0.60 | 0.07 | -0.08 |
| 0.70 | 0.05 | -0.07 |
| 0.80 | 0.05 | -0.05 |
| 0.90 | 0.04 | -0.05 |
| 0.98 | 0.04 | -0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





