Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Einstein and Debye Temperatures, Electron-Phonon Coupling Constant and a Probable Mechanism for Ambient-Pressure Room-Temperature Superconductivity in Intercalated Graphite

Submitted:

01 November 2025

Posted:

04 November 2025

You are already at the latest version

Abstract
Recently, Ksenofontov et al. (arXiv:2510.03256) observed ambient pressure room-temperature superconductivity in graphite intercalated with lithium-based alloys with transition temperature (according to magnetization measurements) \( T_{c} =330K \). Here, I analyzed the reported temperature dependent resistivity data \( \rho(T) \) in these graphite-intercalated samples and found that \( \rho(T) \) is well described by the model of two series resistors, where each resistor is described as either an Einstein conductor or a Bloch-Grüneisen conductor. Deduced Einstein and Debye temperatures are \( \Theta_{E,1} \approx 250~\text{K} \) and \( \quad \Theta_{E,2} \approx 1600~\text{K} \), and \( \quad \Theta_{D,1} \approx 300~\text{K} \) and \( \quad \Theta_{D,2} \approx 2200~\text{K} \), respectively. Following the McMillan formalism, from the deduced \( \quad \Theta_{E,2} \) and \( \quad \Theta_{D,2} \), the electron-phonon coupling constant \( \lambda_{e-ph} \approx 2.2 \) was obtained. This value of \( \lambda_{e-ph} \) is approximately equal to the value of \( \lambda_{e-ph} \) in highly compressed superconducting hydrides. Based on this, I can propose that the observed room-temperature superconductivity in intercalated graphite is localized in nanoscale Sr-Ca-Li metallic flakes/particles, which adopt the phonon spectrum from the surrounding bulk graphite matrix, and as a result, conventional electron-phonon superconductivity arises in these nano-flakes/particles at room temperature. Experimental data reported by Ksenofontov et al. (arXiv:2510.03256) on trapped magnetic flux decay in intercalated graphite samples supports the proposition.
Keywords: 
room-temperature superconductivity
;  
ambient pressure superconductivity
;  
Debye temperature
;  
electron-phonon coupling constant
Subject: 
Physical Sciences  -   Condensed Matter Physics
Einstein and Debye temperatures, electron-phonon coupling constant and a probable mechanism for ambient-pressure room-temperature superconductivity in intercalated graphite

I. Introduction

Near-room-temperature superconductivity in hydrides was experimentally discovered by Drozdov et al. [1] in highly compressed H3S. Over the past decade, the joint efforts of the high-pressure physics and first-principles calculations communities have led to the experimental discovery of dozens highly compressed hydride superconductors [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45], including the ternary hydride LaSc2H24 with a zero-resistance superconducting transition temperature T c , z e r o P = 262   G P a = 292   K [46]. Several new experimental techniques have been developed during this journey [47,48,49,50,51,52,53,54,55,56,57,58,59]. The exploration of this scientific terra incognita is continuing by first-principles calculations [60,61,62,63,64,65,66], as well as detailed characterization of the superconducting state in highly compressed hydrides [55,67,68,69].
While superhydrides remain the main family in which superconductivity is expected to be found at room temperature and ambient pressure [60,61,62,63,64,70,71,72], Ksenofontov et al. [73] recently reported the discovery of a new class of superconductors at ambient pressure, in which the zero-field cooling (ZFC) and field cooling (FC) magnetization curves show a transition temperature up to T c , d i a m a g n e t P = 0.1   M P a = 330   K . These superconductors [73] are the graphite intercalated with strontium-calcium-lithium alloys.
Here, in an attempt to determine fundamental superconducting properties of this new class of superconductors, I analyzed the reported temperature dependent resistivity data ρ T and found that ρ T is well described by the two-component Bloch-Grüneisen equation. Deduced Debye temperatures are Θ D , 1 = 240 − 340   K and Θ D , 2 = 2,200 − 2,700   K . Following advanced McMillan formalism [74,75,76], the Debye temperature of Θ D , 2 ≅ 2,200   K and transition temperature of T c = 330   K mean that the intercalated graphite has an electron-phonon coupling constant λ e − p h ≅ 2.15 , which is a typical value for highly compressed near-room-temperature superconducting hydrides [10,76,77,78,79,80,81,82,83,84].
II. Two Series Resistors Model
The Debye temperature Θ D can be derived from fitting the specific heat data C p T to the Debye equation [85,86,87]:
C p , D T = γ × T + 9 × R g c × N × T Θ D 3 ∫ 0 Θ D T x 4 e x e x − 1 2 d x
where γ is the Sommerfeld coefficient, R g c = 8.31   J K − 1 m o l − 1 is the universal gas constant. Some research groups [88] utilized multichannel Debye equation proposed by Bouquet et al. [89]:
C p T = γ × T + 9 × R g c × ∑ i = 1 M A i T Θ D , i 3 ∫ 0 Θ D , i T x 4 e x e x − 1 2 d x
where A i are constants (depended from given crystalline structure and chemical composition), M is a number of the channels for the Debye modes.
Wälti et al. [90] proposed a combined Debye-Einstein model, which is also in use [91,92]:
C p T = γ × T + α × C p , D T + 1 − α × C p , E T
where the third term represents the optical phonon-mode contributions and it is described by Einstein equation for heat capacity:
C p , E T = 3 × R g c × Θ E T 2 e Θ E T e Θ E T − 1 2
For multichannel case, Eq. 3 can be rewritten as following:
C p T = γ × T + 9 × R g c × ∑ i = 1 M A i T Θ D , i 3 ∫ 0 Θ D , i T x 4 e x e x − 1 2 d x + 3 × R g c × ∑ j = 1 P B j Θ E , j T 2 e Θ E , j T e Θ E , j T − 1 2
where A i and B j are constants, M and P are number of the channels for the Debye modes and the Einstein modes, respectively; Θ D , i is the Debye temperature of the i-channel, Θ E , j is the Einstein temperature of the j-channel.
The Debye temperature Θ D can also be derived from fitting temperature-dependent resistivity ρ T to the Bloch-Grüneisen [93,94] equation (where the Debye temperature, Θ D , is one of free-fitting parameters):
ρ T = ρ 0 + A × T Θ D 5 × ∫ 0 Θ D T x 5 e x − 1 1 − e − x d x
where ρ 0 , and A other are free-fitting parameters. Eq. 6 is one of the approaches to determine the Debye temperature from experimental data [76,77,78,92,95,96,97,98,99,100,101,102,103]. Wiesmann et al [104] advanced this model by assuming that there is an additional conduction channel with a temperature-independent resistance R s a t that is connected in parallel with the resistor described by Equation 1:
1 ρ T = 1 ρ s a t +   1 ρ 0 + A × T Θ D 5 × ∫ 0 Θ D T x 5 e x − 1 1 − e − x d x
Based on the Matthiessen rule, Varshney [105] proposed an alternative model for the ρ T in MgB2. This model is based on the assumption (which is similar to one made in Ref. [90]) that the phonon spectrum consists of two parts: an acoustic branch of the Debye type (which is characterized by the Debye temperature Θ D ) and an optical mode with characteristic Einstein temperature, Θ E . In the result, the proposed equation [105] is:
ρ T = ρ 0 + A × T Θ D 5 × ∫ 0 Θ D T x 5 e x − 1 1 − e − x d x + B × Θ E 2 T e Θ E T − 1 1 − e − Θ E T
where the third term is the Einstein resistivity model [106,107], and ρ 0 , A , Θ D , B , Θ E are free fitting parameters.
Because there is no additional information on the phonon spectrum in the intercalated graphite, I employed three two-series resistances models to fit the ρ T data reported by Ksenofontov et al. [73] for graphite intercalated with lithium-based alloys:
ρ T = ρ 0 + ∑ i = 1 2 A i × T Θ D , i 5 × ∫ 0 Θ D , i T x 5 e x − 1 1 − e − x d x
this model is designated as the 2BG model, where ρ 0 , A i , Θ D , i are free-fitting parameters;
ρ T = ρ 0 + ∑ i = 1 2 B i × Θ E , i 2 T e Θ E , i T − 1 1 − e − Θ E , i T
this model is designated as the 2E model, where ρ 0 , B i , Θ E , i are free-fitting parameters; and Eq. 9 is designated as the BGE model.

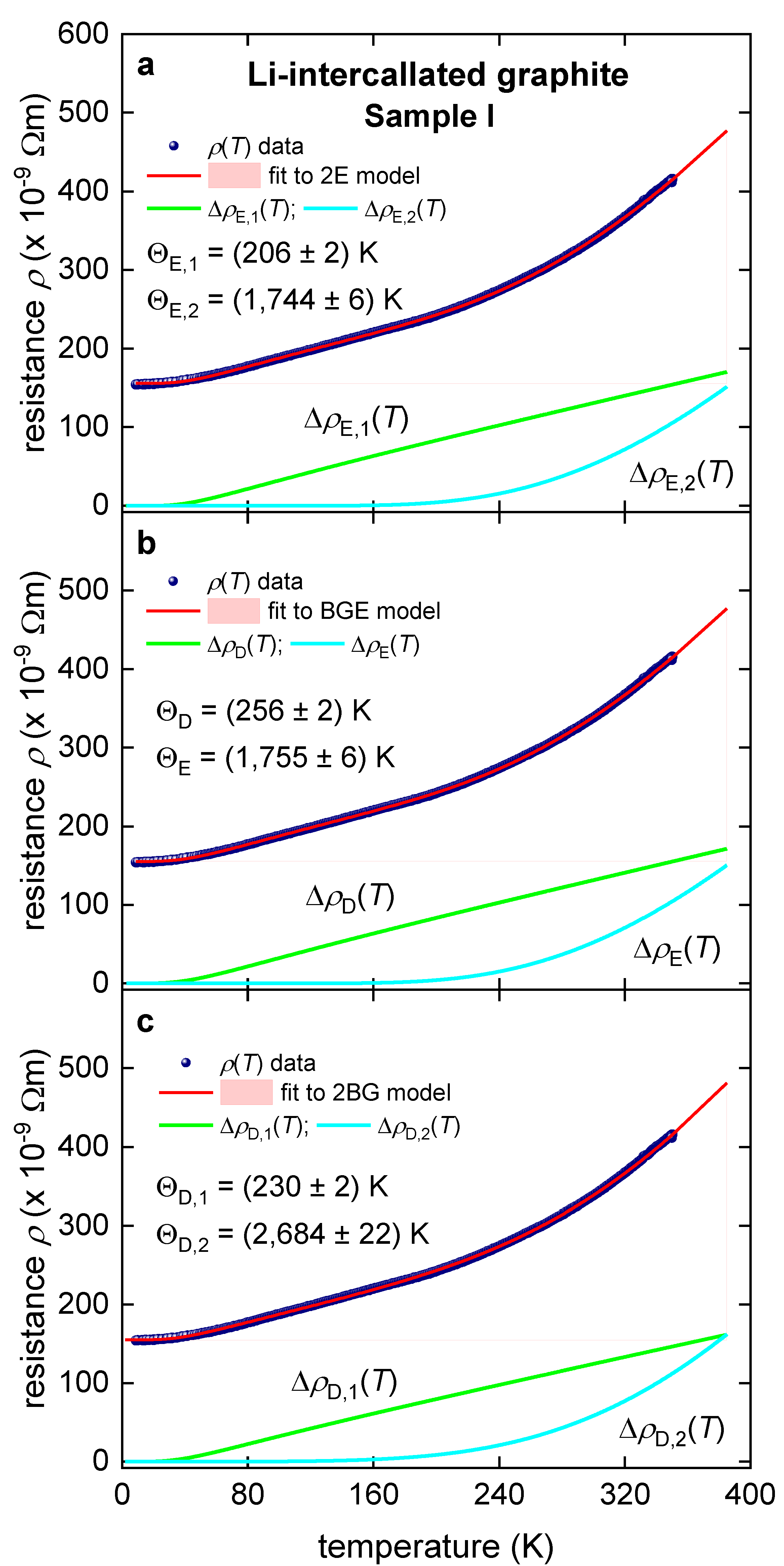
III. Einstein and Debye Temperatures in Intercalated Graphite Samples

Sample I (in the report by Ksenofontov et al. [73]) is Li-intercalated graphite sample. Figure 1 shows fits of the ρ T data for this sample Sample I [73] to three models (Eqs. 9-11). Deduced characteristic temperatures and temperature dependent contributions of each term are shown in each panel of Figure 1. The derived temperatures Θ E , Θ E , 2 , and Θ D , 2 are approximately in the same range with the Debye temperature in graphene [108,109,110,111] Θ D ≅ 1,700 − 2300   K . At the same time, Θ D , Θ E , 1 , and Θ D , 1 are close to the reported in-plane [112] Debye temperature in the LiCn (n = 6, 12) Θ D , | | ≅ 350   K .
Sample IIId (in the report by Ksenofontov et al. [73]) is Sr-Ca-Li-intercalated graphite sample, which showed the diamagnetic superconducting transition T c , d i a = 330   K . Figure 2 shows fits of the ρ T data for this sample Sample IIId [73] to three models (Eqs. 9-11).
T c = Θ E 1.20 × e − 1.04 1 + λ e − p h , E λ e − p h , E − μ * × 1 + 0.62 × λ e − p h , E × f 1 × f 2 *                         f 1 = 1 + λ e − p h , E 2.46 × 1 + 3.8 × μ * 3 / 2 1 / 3                                                                               f 2 * = 1 + 0.0241 − 0.0735 × μ * × λ e − p h , E 2                                      
and
T c = Θ D 1.45 × e − 1.04 1 + λ e − p h , D λ e − p h , D − μ * × 1 + 0.62 × λ e − p h , D × f 1 × f 2 *                 f 1 = 1 + λ e − p h , D 2.46 × 1 + 3.8 × μ * 3 / 2 1 / 3                                                                             f 2 * = 1 + 0.0241 − 0.0735 × μ * × λ e − p h , D 2                                      
where μ * is the Coulomb pseudopotential parameter (ranging within [114] μ * = 0.10 − 0.15 ). In Figure 2, the derived λ e − p h , E and λ e − p h , D values were calculated in the assumption of μ * = 0.10 .

V. Discussion

Based on results reported by Ksenofontov et al. [73] and results reported above, I can hypothesize that the observed room-temperature superconductivity in intercalated graphite is localized in nanoscale Sr-Ca-Li metallic flakes/particles, which cannot exhibit their own phonon spectrum and thus receive the phonon spectrum from the surrounding graphite matrix (with Einstein temperature Θ E , 2 ≅ 1,600   K , or Debye temperature Θ D , 2 ≅ 2,500   K ). Such high Θ E and Θ D bust superconducting transition temperature T c within electron-phonon phenomenology [74,75,113,115,116] (Eqs. 12,13).
In addition to these high Θ E and Θ D , intercalated graphite has a prominent low frequency part of the phonon spectrum with Θ E , 1 ≅ 250   K or Θ D , 1 ≅ 350   K , which boosts the electron-phonon coupling constant λ e − p h :
λ e − p h = 2 × ∫ 0 ∞ α 2 ω × F ω ω d ω
where ω is the phonon frequency, F() is the phonon density of states, and α 2 ω × F ω is the electron-phonon spectral function (more details can be found elsewhere [74,75,113,114,116]).
Thus, combined action of low- and high-frequency phonons causes the emergence of room-temperature superconductivity in nano-flakes/particles, because these objects cannot maintain their own phonon spectrum, and they adopt the spectrum from the surrounding graphite matrix.
Further confirmation of this hypothesis is the fact that superconducting diamagnetism is observed in ~ 0.1% of the sample volume, which can be explained by the assumption that the superconducting phase is nanoscale flakes/particles dispersed throughout the sample volume. Small flakes/particles cannot have their independent phonon spectrum from surrounding graphite matrix, and, therefore, the flakes/particles more or less adopt the phonon spectrum of the graphite. Thus, the emergence of superconductivity in these nanoscale flakes/particles depends on the match between the phonon spectrum of the graphite, density of states at the Fermi level of the flakes/particles, etc.
In overall, the superconducting state in these nano-flakes/particles can be detected by magnetic measurements (by ZFC and FC protocols), but because of the small volume fraction of these nano-flakes/particles (~ 0.1%), the percolation path [117,118] cannot be formed, and thus, the resistance measurements R T will not show the zero-resistance state in the intercalated graphite.
Additional support for this model can be found in time-dependent magnetic measurements of the trapped magnetic flux in intercalated graphite, m t r a p T . Truly, each nano-flake/particle exhibits room-temperature superconductivity, and, thus, integrated trapped magnetic flux of the sample should exhibit the logarithmic time dependence [119,120,121,122,123]. And exact this dependence was demonstrated by Ksenofontov et al. [73] (in their Figure 4 [73]). m t r a p T data fit to the logarithmic time dependence [119,120,121,122,123] showed that the decay rate is S = 0.005 − 0.013 [73], which is in a ballpark of typical values for other high-temperature superconductors [119,120,121,122,123,124,125,126].

4. Conclusions

In this paper, I analyze recently reported data [73] on ρ T measured in an ambient-pressure room-temperature superconductor Li- and Sr-Ca-Li-intercalated graphite. The experimental data on ρ T are well described by the model of two series resistors, and the derived values of the Einstein and Debye temperatures allow us to calculate the electron-phonon coupling constant in intercalated Sr-Ca-Li graphite: λ e − p h , D ≅ 2.2 . The obtained value is typical for highly compressed hydride superconductors [10]. Based on the currently available data, I propose a probable mechanism for the emergence of room-temperature superconductivity in ambient-pressure intercalated graphite.

Acknowledgements

The author thanks Dr. V. Ksenofontov (Max Planck Institute for Chemistry, Mainz, Germany) and all co-workers of the original study [73] for providing raw experimental ρ T
data for the analysis. The work was carried out within the framework of the state assignment of the Ministry of Science and Higher Education of the Russian Federation for the IMP UB RAS. The author gratefully acknowledged the research funding from the Ministry of Science and Higher Education of the Russian Federation under Ural Federal University Program of Development within the Priority-2030 Program.

References

  1. Drozdov, A. P., Eremets, M. I., Troyan, I. A., Ksenofontov, V. & Shylin, S. I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 525, 73–76 (2015).
  2. Liu, H., Naumov, I. I., Hoffmann, R., Ashcroft, N. W. & Hemley, R. J. Potential high- T c superconducting lanthanum and yttrium hydrides at high pressure. Proceedings of the National Academy of Sciences 114, 6990–6995 (2017).
  3. Drozdov, A. P. et al. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 569, 528–531 (2019).
  4. Somayazulu, M. et al. Evidence for Superconductivity above 260 K in Lanthanum Superhydride at Megabar Pressures. Phys Rev Lett 122, 027001 (2019).
  5. He, X.-L. et al. Predicted hot superconductivity in LaSc 2 H 24 under pressure. Proceedings of the National Academy of Sciences 121, (2024).
  6. Minkov, V. S., Prakapenka, V. B., Greenberg, E. & Eremets, M. I. A Boosted Critical Temperature of 166 K in Superconducting D 3 S Synthesized from Elemental Sulfur and Hydrogen. Angewandte Chemie 132, 19132–19136 (2020).
  7. Sun, D. et al. High-temperature superconductivity on the verge of a structural instability in lanthanum superhydride. Nat Commun 12, 6863 (2021).
  8. Cai, W.; et al. Superconductivity above 180 K in Ca-Mg Ternary Superhydrides at Megabar Pressures. http://arxiv.org/abs/2312.06090 (2023).
  9. Kong, P. et al. Superconductivity up to 243 K in the yttrium-hydrogen system under high pressure. Nat Commun 12, 5075 (2021).
  10. Lilia, B. et al. The 2021 room-temperature superconductivity roadmap. Journal of Physics: Condensed Matter 34, 183002 (2022).
  11. Drozdov, A. P. , Eremets, M. I. & Troyan, I. A. Superconductivity above 100 K in PH3 at high pressures. http://arxiv.org/abs/1508.06224 (2015).
  12. Chen, W. et al. High-Temperature Superconducting Phases in Cerium Superhydride with a Tc up to 115 K below a Pressure of 1 Megabar. Phys Rev Lett 127, 117001 (2021).
  13. Troyan, I. A., Semenok, D. V., Sadakov, A. V., Lyubutin, I. . S. & Pudalov, V. M. PROGRESS, PROBLEMY I PERSPEKTIVY KOMNATNO-TEMPERATURNOY SVERKhPROVODIMOSTI. Žurnal èksperimentalʹnoj i teoretičeskoj fiziki 166, 74–88 (2024).
  14. Chen, W. et al. Enhancement of superconducting properties in the La–Ce–H system at moderate pressures. Nat Commun 14, 2660 (2023).
  15. Zhou, D. et al. Superconducting praseodymium superhydrides. Sci Adv 6, 1–9 (2020).
  16. Guo, J. et al. Unusual metallic state in superconducting A15-type La4H23. Natl Sci Rev. [CrossRef]
  17. Semenok, D. V. et al. Superconductivity at 161 K in thorium hydride ThH10: Synthesis and properties. Materials Today 33, 36–44 (2020).
  18. Troyan, I. A. et al. High-temperature superconductivity in hydrides. Physics-Uspekhi 65, 748–761 (2022).
  19. Chen, W. et al. Synthesis of molecular metallic barium superhydride: pseudocubic BaH12. Nat Commun 12, 1–9 (2021).
  20. Guo, J.; et al. Soft superconductivity in covalent bismuth dihydride BiH$_2$ under extreme conditions. http://arxiv.org/abs/2505.12062 (2025).
  21. Troyan, I. A. et al. Non-Fermi-Liquid Behavior of Superconducting SnH 4. Advanced Science 10, (2023).
  22. Semenok, D. V. et al. Superconductivity at 253 K in lanthanum–yttrium ternary hydrides. Materials Today 48, 18–28 (2021).
  23. Troyan, I. A. et al. Anomalous High-Temperature Superconductivity in YH 6. Advanced Materials 33, 2006832 (2021).
  24. Semenok, D. V. et al. Effect of Magnetic Impurities on Superconductivity in LaH10. Advanced Materials 34, 2204038 (2022).
  25. Song, Y. et al. Stoichiometric Ternary Superhydride LaBeH8 as a New Template for High-Temperature Superconductivity at 110 K under 80 GPa. Phys Rev Lett 130, 266001 (2023).
  26. Ma, C. et al. Synthesis of medium-entropy alloy superhydride with high-temperature superconductivity under high pressure. Phys Rev B 111, 024505 (2025).
  27. Bi, J. et al. Giant enhancement of superconducting critical temperature in substitutional alloy (La,Ce)H9. Nat Commun 13, 5952 (2022).
  28. Duan, D. et al. Pressure-induced metallization of dense (H2S)2H2 with high-Tc superconductivity. Sci Rep 4, 6968 (2014).
  29. Song, X. et al. Superconductivity above 105 K in Nonclathrate Ternary Lanthanum Borohydride below Megabar Pressure. J Am Chem Soc 146, 13797–13804 (2024).
  30. Ma, L. et al. High-Temperature Superconducting Phase in Clathrate Calcium Hydride CaH6 up to 215 K at a Pressure of 172 GPa. Phys Rev Lett 128, 167001 (2022).
  31. Sun, Y., Lv, J., Xie, Y., Liu, H. & Ma, Y. Route to a Superconducting Phase above Room Temperature in Electron-Doped Hydride Compounds under High Pressure. Phys Rev Lett 123, 097001 (2019).
  32. Bi, J. et al. Stabilization of superconductive La–Y alloy superhydride with Tc above 90 K at megabar pressure. Materials Today Physics 28, 100840 (2022).
  33. He, X. et al. Superconductivity discovered in niobium polyhydride at high pressures. Materials Today Physics 40, 101298 (2024).
  34. Wang, Y. et al. Synthesis and superconductivity in yttrium superhydrides under high pressure. Chinese Physics B 31, 106201 (2022).
  35. Li, X. et al. Polyhydride CeH9 with an atomic-like hydrogen clathrate structure. Nat Commun 10, 3461 (2019).
  36. Hong, F. et al. Possible superconductivity at ∼70 K in tin hydride SnHx under high pressure. Materials Today Physics 22, 100596 (2022).
  37. Salke, N. P. et al. Synthesis of clathrate cerium superhydride CeH9 at 80-100 GPa with atomic hydrogen sublattice. Nat Commun 10, 4453 (2019).
  38. Zhang, C. L. et al. Superconductivity above 80 K in polyhydrides of hafnium. Materials Today Physics 27, 100826 (2022).
  39. Shan, P. et al. Molecular Hydride Superconductor BiH 4 with T c up to 91 K at 170 GPa. J Am Chem Soc 147, 4375–4381 (2025).
  40. Huang, G. et al. Synthesis of superconducting phase of La 0.5 Ce 0.5 H 10 at high pressures. Journal of Physics: Condensed Matter 36, 075702 (2024).
  41. Chen, L.-C. et al. Synthesis and superconductivity in yttrium-cerium hydrides at high pressures. Nat Commun 15, 1809 (2024).
  42. Cao, Z.-Y. et al. Probing superconducting gap in CeH$_9$ under pressure. ArXiv http://arxiv.org/abs/2401.12682 (2024).
  43. Ma, C. et al. Hydrogen-Vacancy-Induced Stable Superconducting Niobium Hydride at High Pressure. J Am Chem Soc 147, 11028–11035 (2025.
  44. Racioppi, S. & Zurek, E. Quantum Effects or Theoretical Artifacts? A Computational Reanalysis of Hydrogen at High-Pressure. ArXiv http://arxiv.org/abs/2510.02098 (2025).
  45. Ma, L. et al. High Pressure Superconducting transition in Dihydride BiH$_2$ with Bismuth Open-Channel Framework. Phys Rev Lett. [CrossRef]
  46. Song, Y. et al. Room-Temperature Superconductivity at 298 K in Ternary La-Sc-H System at High-pressure Conditions. ArXiv.
  47. Du, F. et al. Tunneling Spectroscopy at Megabar Pressures: Determination of the Superconducting Gap in Sulfur. Phys Rev Lett 133, 036002 (2024).
  48. Du, F. et al. Superconducting gap of H3S measured by tunnelling spectroscopy. Nature 641, 619–624 (2025).
  49. Bhattacharyya, P. et al. Imaging the Meissner effect in hydride superconductors using quantum sensors. Nature 627, 73–79 (2024).
  50. Marathamkottil, A. H. M. et al. X-ray Diffraction and Electrical Transport Imaging of Superconducting Superhydride (La,Y)H10. (2025).
  51. Liu, L. et al. Evidence for the Meissner Effect in the Nickelate Superconductor Single Crystal Using Diamond Quantum Sensors. Phys Rev Lett 135, 096001 (2025).
  52. Ku, C. et al. Point-contact Andreev reflection spectroscopy of layered superconductors with device-integrated diamond anvil cells. Review of Scientific Instruments 96, (2025).
  53. Rietwyk, K. J. et al. Practical limits to spatial resolution of magnetic imaging with a quantum diamond microscope. AVS Quantum Science 6, (2024).
  54. Chen, Y. et al. Imaging magnetic flux trapping in lanthanum hydride using diamond quantum sensors. ArXiv http://arxiv.org/abs/2510.21877 (2025).
  55. Eremets, M. I., Minkov, V. S., Drozdov, A. P. & Kong, P. P. The characterization of superconductivity under high pressure. Nat Mater 23, 26–27 (2024).
  56. Minkov, V. S., Ksenofontov, V., Bud’ko, S. L., Talantsev, E. F. & Eremets, M. I. Magnetic flux trapping in hydrogen-rich high-temperature superconductors. Nat Phys 19, 1293–1300 (2023.
  57. Minkov, V. S. et al. Revaluation of the lower critical field in superconducting H$_3$S and LaH$_{10}$ (Nature Comm. 13, 3194, 2022). http://arxiv.org/abs/2408.12675 (2024).
  58. Minkov, V. S. et al. Magnetic field screening in hydrogen-rich high-temperature superconductors. Nat Commun 13, 3194 (2022).
  59. Hao, Q. et al. Diamond quantum sensing at record high pressure up to 240 GPa. ArXiv.
  60. Cerqueira, T. F. T., Fang, Y., Errea, I., Sanna, A. & Marques, M. A. L. Searching Materials Space for Hydride Superconductors at Ambient Pressure. Adv Funct Mater 34, (2024).
  61. Wei, X. et al. Design of High- T c Quaternary Hydrides Under Moderate Pressures Through Substitutional Doping. Adv Funct Mater 35, (2025).
  62. Jiang, Q. et al. Prediction of Room-Temperature Superconductivity in Quasi-Atomic H 2 -Type Hydrides at High Pressure. Advanced Science 11, (2024).
  63. Belli, F., Torres, S., Contreras-García, J. & Zurek, E. Refining T c Prediction in Hydrides via Symbolic-Regression-Enhanced Electron-Localization-Function-Based Descriptors. Ann Phys. [CrossRef]
  64. Hansen, M. F. et al. Synthesis of : A potential pathway to high- TC hydride superconductivity at ambient pressure. Phys Rev B 110, 214513 (2024).
  65. Rastkhadiv, M. A. Revisiting YH$_9$ Superconductivity and Predicting High-T$_c$ in GdYH$_5$. ArXiv.
  66. Mishra, S. B. & Margine, E. R. Nonadiabatic and anharmonic effects in high-pressure H3S and D3S superconductors. ArXiv.
  67. Talantsev, E. F. Primary Superconducting Parameters of Highly Compressed Nonclathrate Ternary Hydride LaB2H8. Physics of Metals and Metallography 126, 493–500 (2025).
  68. Minkov, V. S.; et al. Long-Term Stability of Superconducting Metal Superhydrides. http://arxiv.org/abs/2507.08009 (2025).
  69. Talantsev, E. F. Structural and superconducting parameters of highly compressed H3S. SSRN. [CrossRef]
  70. Wrona, I. A., Niegodajew, P. & Durajski, A. P. A recipe for an effective selection of promising candidates for high-temperature superconductors among binary hydrides. Materials Today Physics 46, 101499 (2024).
  71. Liu, S. et al. High-Throughput Study of Ambient-Pressure High-Temperature Superconductivity in Ductile Few-Hydrogen Metal-Bonded Perovskites. Adv Funct Mater 34, (2024).
  72. Huang, H. et al. High-Temperature Superconductivity of Thermodynamically Stable Fluorite-Type Hydrides at Ambient Pressure. Advanced Science. [CrossRef]
  73. Ksenofontov, V., Minkov, V. S., Drozdov, A. P., Pöschl, U. & Eremets, M. I. Signs of Possible High-Temperature Superconductivity in Graphite Intercalated with Lithium-Based Alloys. ArXiv.
  74. McMillan, W. L. Transition Temperature of Strong-Coupled Superconductors. Physical Review 167, 331–344 (1968).
  75. Dynes, R. C. McMillan’s equation and the Tc of superconductors. Solid State Commun 10, 615–618 (1972).
  76. Talantsev, E. F. Advanced McMillan’s equation and its application for the analysis of highly-compressed superconductors. Supercond Sci Technol 33, 094009 (2020).
  77. Talantsev, E. F. & Stolze, K. Resistive transition of hydrogen-rich superconductors. Supercond Sci Technol 34, 064001 (2021).
  78. Talantsev, E. F. The electron–phonon coupling constant and the Debye temperature in polyhydrides of thorium, hexadeuteride of yttrium, and metallic hydrogen phase III. J Appl Phys 130, 195901 (2021).
  79. Errea, I. Superconducting hydrides on a quantum landscape. Journal of Physics: Condensed Matter 34, 231501 (2022).
  80. Pickard, C. J., Errea, I. & Eremets, M. I. Superconducting Hydrides Under Pressure. Annu Rev Condens Matter Phys 11, 57–76 (2020).
  81. Errea, I. et al. High-Pressure Hydrogen Sulfide from First Principles: A Strongly Anharmonic Phonon-Mediated Superconductor. Phys Rev Lett 114, 157004 (2015).
  82. Errea, I. et al. Quantum hydrogen-bond symmetrization in the superconducting hydrogen sulfide system. Nature 532, 81–84 (2016).
  83. Errea, I. et al. Quantum crystal structure in the 250-kelvin superconducting lanthanum hydride. Nature 578, 66–69 (2020).
  84. Gao, K.; et al. The Maximum $T_c$ of Conventional Superconductors at Ambient Pressure. http://arxiv.org/abs/2502.18281 (2025).
  85. Pallecchi, I. et al. Experimental investigation of electronic interactions in collapsed and uncollapsed LaFe2As2 phases. Phys Rev B 108, 014512 (2023).
  86. Yang, K. et al. Charge fluctuations above TCDW revealed by glasslike thermal transport in kagome metals AV3Sb5 (A=KRb,Cs). Phys Rev B 107, 184506 (2023).
  87. Poole, C. P., Farach, H., Creswick, R. & Prozorov, R. Superconductivity. (Academic Press, London, UK, 2007).
  88. Ni, D. et al. Layered polymorph of titanium triiodide. Phys Rev Mater 6, 124001 (2022).
  89. Bouquet, F. et al. Phenomenological two-gap model for the specific heat of MgB 2. Europhysics Letters (EPL) 56, 856–862 (2001).
  90. Wälti, Ch. et al. Strong electron-phonon coupling in superconducting MgB2: A specific heat study. Phys Rev B 64, 172515 (2001).
  91. Wang, A. et al. Magnetic mixed valent semimetal EuZnSb2 with Dirac states in the band structure. Phys Rev Res 2, 033462 (2020).
  92. Shang, T. et al. Enhanced T c and multiband superconductivity in the fully-gapped ReBe 22 superconductor. New J Phys 21, 073034 (2019).
  93. Bloch, F. Zum elektrischen Widerstandsgesetz bei tiefen Temperaturen. Zeitschrift f�r Physik 59, 208–214 (1930).
  94. Grüneisen, E. Die Abhängigkeit des elektrischen Widerstandes reiner Metalle von der Temperatur. Ann Phys 408, 530–540 (1933).
  95. Talantsev, E. F. An approach to identifying unconventional superconductivity in highly-compressed superconductors. Supercond Sci Technol 33, 124001 (2020).
  96. Talantsev, E. F. The dominance of non-electron–phonon charge carrier interaction in highly-compressed superhydrides. Supercond Sci Technol 34, 115001 (2021).
  97. Klimczuk, T., Królak, S. & Cava, R. J. Superconductivity of Ta-Hf and Ta-Zr alloys: Potential alloys for use in superconducting devices. Phys Rev Mater 7, 064802 (2023).
  98. Ma, K.; et al. Superconductivity with High Upper Critical Field in the Cubic Centrosymmetric η-Carbide Nb 4 Rh 2 C 1−δ. ACS Materials Au.
  99. Jonas, D. G. C., Biswas, P. K., Hillier, A. D., Mayoh, D. A. & Lees, M. R. Quantum muon diffusion and the preservation of time-reversal symmetry in the superconducting state of type-I rhenium. Phys Rev B 105, L020503 (2022).
  100. Hu, Z. et al. Robust three-dimensional type-II Dirac semimetal state in SrAgBi. NPJ Quantum Mater 8, 20 (2023).
  101. Susner, M. A., Bhatia, M., Sumption, M. D. & Collings, E. W. Electrical resistivity, Debye temperature, and connectivity in heavily doped bulk MgB2 superconductors. J Appl Phys 105, (2009).
  102. Putti, M. et al. Electron transport properties of MgB2 in the normal state. Eur Phys J B 25, 439–443 (2002).
  103. Jiang, H. et al. Physical properties and electronic structure of Sr2Cr3As2 containing CrO2 and Cr2As2 square-planar lattices. Phys Rev B 92, 205107 (2015).
  104. Wiesmann, H. et al. Simple Model for Characterizing the Electrical Resistivity in A−15 Superconductors. Phys Rev Lett 38, 782–785 (1977).
  105. Varshney, D. Impurity, phonon and electron contributions to the electrical resistivity of single-crystal MgB 2. Supercond Sci Technol 19, 685–694 (2006).
  106. Cooper, J. R. Electrical resistivity of an Einstein solid. Phys Rev B 9, 2778–2780 (1974.
  107. Pinsook, U. & Tanthum, P. Universal resistivity from electron-phonon interaction based on Einstein model: Application to near-room temperature superconductors. Next Materials 6, 100302 (2025).
  108. Xie, Y. et al. The defect level and ideal thermal conductivity of graphene uncovered by residual thermal reffusivity at the 0 K limit. Nanoscale 7, 10101–10110 (2015).
  109. Ren, X.-X., Kang, W., Cheng, Z.-F. & Zheng, R.-L. Temperature-Dependent Debye Temperature and Specific Capacity of Graphene. Chinese Physics Letters 33, 126501 (2016).
  110. Pop, E., Varshney, V. & Roy, A. K. Thermal properties of graphene: Fundamentals and applications. MRS Bull 37, 1273–1281 (2012).
  111. Tewary, V. K. & Yang, B. Singular behavior of the Debye-Waller factor of graphene. Phys Rev B 79, 125416 (2009).
  112. Moreh, R., Shnieg, N. & Zabel, H. Effective and Debye temperatures of alkali-metal atoms in graphite intercalation compounds. Phys Rev B 44, 1311–1317 (1991).
  113. Allen, P. B. & Dynes, R. C. Transition temperature of strong-coupled superconductors reanalyzed. Phys Rev B 12, 905–922 (1975).
  114. Semenok, D. Computational design of new superconducting materials and their targeted experimental synthesis. PhD Thesis; Skolkovo Institute of Science and Technology. [CrossRef]
  115. Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Theory of Superconductivity. Physical Review 108, 1175–1204 (1957).
  116. G. M. Eliashberg. Interactions between Electrons and Lattice Vibrations in a Superconductor. Sov. Phys.–JETP 11, 696 (1960).
  117. Riley, G. N., Malozemoff, A. P., Li, Q., Fleshler, S. & Holesinger, T. G. The freeway model: New concepts in understanding supercurrent transport in Bi-2223 tapes. JOM 49, 24–27 (1997).
  118. Nadifi, H. et al. Superconductive percolation in Bi-based superconductor/Bi-based insulator composites: case of Bi-2223/Bi-2310 and Bi-2212/BiFeO 3. Supercond Sci Technol 13, 1174–1179 (2000).
  119. Yeshurun, Y., Malozemoff, A. P. & Shaulov, A. Magnetic relaxation in high-temperature superconductors. Rev Mod Phys 68, 911–949 (1996).
  120. McElfresh, M. W., Yeshurun, Y., Malozemoff, A. P. & Holtzberg, F. Remanent magnetization, lower critical fields and surface barriers in an YBa2Cu3O7 crystal. Physica A: Statistical Mechanics and its Applications 168, 308–318 (1990).
  121. Eley, S., Miura, M., Maiorov, B. & Civale, L. Universal lower limit on vortex creep in superconductors. Nat Mater 16, 409–413 (2017).
  122. MCHENRY, M. & SUTTON, R. Flux pinning and dissipation in high temperature oxide superconductors. Prog Mater Sci 38, 159–310 (1994).
  123. Maley, M. P., Willis, J. O., Lessure, H. & McHenry, M. E. Dependence of flux-creep activation energy upon current density in grain-aligned YBa2Cu3O7-x. Phys Rev B 42, 2639–2642 (1990).
  124. Eley, S., Willa, R., Chan, M. K., Bauer, E. D. & Civale, L. Vortex phases and glassy dynamics in the highly anisotropic superconductor HgBa2CuO4+δ. Sci Rep 10, 10239 (2020).
  125. Cole, H. M. et al. Plastic vortex creep and dimensional crossovers in the highly anisotropic superconductor HgBa2CuO4+x. Phys Rev B 107, 104509 (2023).
  126. Iida, K., Hänisch, J. & Tarantini, C. Fe-based superconducting thin films on metallic substrates: Growth, characteristics, and relevant properties. Appl Phys Rev 5, 031304 (2018).
Preprints 183276 g001
Figure 1. ρ T , B = 0 of the graphite intercalated with lithium (Sample I [73] fabricated and measured by Ksenofontov et al. [73]) and fits to (a) double Einstein model (Eq. 11, the goodness of fit R-square COD = 0.99992); (b) combined Bloch-Grüneisen and Einstein model [105] (Eq. 9, the goodness of fit is 0.99993); and (c) double Bloch-Grüneisen model (Eq. 10, the goodness of fit is COD = 0.99991). The thickness of 95% confidence bands (pink shadow areas) is narrower than the width of the fitting lines.
Figure 1. ρ T , B = 0 of the graphite intercalated with lithium (Sample I [73] fabricated and measured by Ksenofontov et al. [73]) and fits to (a) double Einstein model (Eq. 11, the goodness of fit R-square COD = 0.99992); (b) combined Bloch-Grüneisen and Einstein model [105] (Eq. 9, the goodness of fit is 0.99993); and (c) double Bloch-Grüneisen model (Eq. 10, the goodness of fit is COD = 0.99991). The thickness of 95% confidence bands (pink shadow areas) is narrower than the width of the fitting lines.
Preprints 183276 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated