Time-Varying Feedback for Rigid Body Attitude Control

1. Introduction

Vehicles moving in three spatial dimensions, which include aerial, space and underwater vehicles, require attitude control. The vehicles can be modeled as a rigid body with actuators that are used for attitude and translational motion. In this work, we consider control of the attitude motion for maneuverable vehicles without any constraints on the motion. Rigid body attitude is uniquely and globally represented on the Lie group SO(3), which is a compact manifold and not a vector (linear) space. This makes control of rigid body rotational motion on the state space TSO(3), the tangent bundle of SO(3) consisting of all attitudes (orientations) and angular velocities, an inherently nonlinear control problem. Prior research on attitude stabilization and control has shown that global stabilization on TSO(3) with continuous state feedback is not possible [1,2,3].

Instead, the best possible outcome with continuous state feedback is almost global asymptotic stability of desired trajectories or states on TSO(3) [2,3,4]. This best possible outcome is achieved by use of Morse or Morse-Bott functions on SO(3), as part of Lyapunov functions on the state space TSO(3). Consequently, Morse and Morse–Bott functions are necessary to design Lyapunov functions for rigid body control and estimation with guarantees of almost global domains of convergence. Polar Morse functions on SO(3) have a critical set with cardinality four, while Morse-Bott functions on SO(3) have a connected set of critical points; the sets of critical points for both these types of functions are of zero (Lebesgue) measure on SO(3). Their use as part of Lyapunov functions produce feedback systems whose equilibria on TSO(3) correspond to the critical points (attitudes) of the Morse (or Morse–Bott) function on SO(3). The existence of multiple equilibria precludes global asymptotic stability of a single equilibrium state of the continuous state feedback system. By formulating the function appropriately, one can obtain almost global asymptotic stability (AGAS) for the desired attitude state as an equilibrium, while the other equilibria are confined to a set of measure zero in TSO(3).

Designs using constant gain Morse functions have a limitation in certain applications for attitude control that involve large rotations but need fast convergence to a desired attitude. The control approach given in this work is also robust to external disturbance torques due to its rapid convergence and large domain of attraction. In this sense, it is complementary to our previous work on attitude control on SO(3) using integral feedback [5]. Another use case for the control scheme given here is for attitude synchronization of multi-agent rigid body systems (MARBS), where certain network topologies admit stable but undesirable non-consensus equilibria that correspond to critical points of the Morse or Morse-Bott function that prevent convergence to the consensus configuration for the MARBS network [6,7]. Constant gains fix the Hessian of the Morse function at each critical point, and therefore limit our ability to alter stability properties of the crtical point without changing the function’s continuity and resorting to hybrid switching strategies. Recent works on feedback reshaping, multi-agent relative attitude control, and continuous distributed synchronization have demonstrated the need for more flexible approaches to avoid or destabilize undesired equilibria [8,9].

In this work, we design and analyze a new class of Morse functions that have continuously time-varying positive gains, for stable and robust attitude control. The principal motivations are two-fold. The time-dependence of gains in the Morse function modifies the local properties (the gradient and Hessian) at each critical point, and this changes the properties of the dynamics near these equilibria, without altering the global stability properties or using discontinuous or hybrid control. The second motivation of practical interest is the use of these functions for attitude synchronization in multi-agent systems. We hypothesize that including time-varying Morse functions for relative attitude measure a network can remove or destabilize undesirable non consensus and partial consensus [7] equilibria arising from certain graph topologies and thus recover almost global synchronization without hybrid switching or global coordination. Preliminary related ideas have appeared in feedback-reshaping and time-varying formation control literature [10,11,12], but a systematic analysis of Morse functions with continuous time-varying gains for single rigid body control and attitude synchronization for MARBS is, to the best of our knowledge, unexplored. This work, which concentrates on developing important fundamental results for single rigid-body attitude control with a continuous time-varying state feedback, can serve as a foundation for future work on attitude synchronization and control of MARBS.

The remainder of this article is organized as follows. Section 2 defines the problem statement followed by Section 3 containing analysis and some basic results from prior research using (constant gain) Morse functions. It also introduces time-varying Morse functions, establishes some important results and contrasts it with results obtained using constant Morse functions. This section lays the groundwork for the attitude control approach presented in this article. Next, Section 4 formulates a time-varying controller using a Morse function with time-varying gains for attitude control. This is followed by Section 5, which provides numerical simulation results for the designed controller, highlighting the advantages of the proposed time-varying Morse function. Lastly, Section 6 concludes this article by summarizing contributions and giving planned future directions.

2. Problem Statement

Consider a rigid body with a body-fixed coordinate frame $\mathcal{B}$ centered at the center of mass. Let R be the rotation matrix from $\mathcal{B}$ frame to an inertial coordinate frame $\mathcal{N}$. The attitude kinematics and dynamics are described by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{R}& =R_i{\Omega }^{\times },\hfill \\ \hfill J\dot{\Omega }& =-{\Omega }^{\times }J\Omega +\mathrm{T}u,\hfill \end{array}\end{array}$$

(1)

where $\Omega$ is the angular velocity of the rigid body in frame $\mathcal{B}$, $J\subseteq {\mathbb{R}}^{3\times 3}$ is the inertia-like matrix of the rigid body, and $\mathrm{T}u\in {\mathbb{R}}^3$ is the external torque acting on that rigid body in frame $\mathcal{B}$. If $R\left(t\right)$ denotes a trajectory on SO(3), the tangent vector at $R\left(t\right)$ is given by:

$$\dot{R}=R{\Omega }_i^{\times }, \mathrm{where} {\Omega }^{\times }=\left[\begin{array}{ccc}0& -{\Omega }_3& {\Omega }_2\\ {\Omega }_3& 0& -{\Omega }_1\\ -{\Omega }_2& {\Omega }_1& 0\end{array}\right]\in \mathfrak{s}\mathfrak{o}(3),$$

(2)

where ${\Omega }^{\times }\in \mathfrak{so}\left(3\right)$ and $\mathfrak{so}\left(3\right)$ is the Lie algebra of SO(3), represented by $3\times 3$ skew-symmetric matrices. This Lie algebra corresponds to the three-dimensional Euclidean vector space ${\mathbb{R}}^3$, with the angular velocity vector $\Omega =\left[{\Omega }_1{\Omega }_2{\Omega }_3\right]\in {\mathbb{R}}^3$ being mapped by the ${(·)}^{\times }:{\mathbb{R}}^3\to \mathfrak{so}\left(3\right)$ map. This map is a vector space isomorphism from 3D vectors in ${\mathbb{R}}^3$ to $3\times 3$ skew-symmetric matrices in $\mathfrak{so}\left(3\right)$, and the cross superscript is used as this is equivalent to the cross product operator matrix, i.e., $a^{\times }b=a\times b$ for vectors $a,b\in {\mathbb{R}}^3$.

3. Morse Function on SO(3) with Time-Varying Gains

Let $\langle ·,·\rangle :{\mathbb{R}}^{3\times 3}\to \mathbb{R}$ denote the trace inner product defined by:

$$<A,B>=tr\left(A^{\text{T}}B\right),$$

(3)

where $(·)$ denotes the trace of a matrix. Consider a Morse function defined on the Lie group SO(3) as:

$$U_0\left(R\right)=\langle K,I_3-R\rangle =\left(K(I_3-R)\right),$$

(4)

where $R\in \mathrm{SO}\left(3\right)$ is a rotation matrix, and $K\in {\mathbb{R}}^{3\times 3}$ is a positive diagonal matrix with $k_1>k_2>k_3>0$. A perturbation (variation) of R on $\mathrm{SO}\left(3\right)$ is given by:

$$\delta R=R{\Sigma }^{\times },{\Sigma }^{\times }\in \mathfrak{so}\left(3\right),$$

(5)

where $\Sigma \in {\mathbb{R}}^3$ and ${\Sigma }^{\times }\in \mathfrak{so}\left(3\right)$ is the skew-symmetric cross-product operator matrix associated with $\Sigma$.

3.1. First Variation of the Morse Function

The first variation of $U_0\left(R\right)$ is given by:

$$\begin{array}{cc}\hfill \delta U_0(R,\Sigma )& =\delta \langle K,I_3-R\rangle =-\langle K,\delta R\rangle =-\langle K,R{\Sigma }^{\times }\rangle .\hfill \end{array}$$

(6)

Using the commutative property of trace operator and orthogonality of symmetric and skew-symmetric matrices under the trace inner product, eq. (6) simplifies to:

$$\begin{array}{cc}\hfill \delta U_0(R,\Sigma )& ={\displaystyle \frac{1}{2}}\langle KR-R^{T}K,{\Sigma }^{\times }\rangle .\hfill \end{array}$$

(7)

Now consider $K=K\left(t\right)$, a time-varying positive diagonal matrix. Then the Morse function becomes:

$$U(R,t)=\langle K\left(t\right),I_3-R\rangle .$$

(8)

Next we evaluate the first variation of U, due to variations in R. That is, we compute:

$$\delta U(R,\Sigma ,t)={\left.{\displaystyle \frac{d}{dϵ}}\right|}_{ϵ=0}U(R\left(ϵ\right),t),$$

(9)

where $R\left(ϵ\right)$ is a curve on $\mathrm{SO}\left(3\right)$ with $R\left(0\right)=R$ and ${\left.{\displaystyle \frac{d}{dϵ}}\right|}_{ϵ=0}R\left(ϵ\right)=R{\Sigma }^{\times }$, for some ${\Sigma }^{\times }\in \mathfrak{so}\left(3\right)$. Thus, the first variation of U with respect to R is:

$$\begin{array}{cc}\hfill \delta U(R,\Sigma ,t)& =-\langle K\left(t\right),R{\Sigma }^{\times }\rangle \hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & ={\displaystyle \frac{1}{2}}\langle K\left(t\right)R-RK\left(t\right),{\Sigma }^{\times }\rangle .\hfill \end{array}$$

(11)

As the Morse function in (4) varies explicitly with time, its gradient on SO(3) also varies explicitly with time.

3.2. Analysis of Equilibria on SO(3)

Using the identity: $\left(a^{\times }{b}^{\times }\right)=-2ab$ , eq. (10) simplifies to

$$\delta U=\left(S_{K\left(t\right)}\left(R\right)\right)\Sigma ,$$

(12)

where $S_{K\left(t\right)}\left(R\right)=(K\left(t\right)R-RK\left(t\right))$ and $\left({\chi }^{\times }\right)=\chi =[{\chi }_1,{\chi }_2,{\chi }_3]\in {\mathbb{R}}^3$. It can be readily verified by inspection that

$$S_{K\left(t\right)}\left(R\right)=\sum _{l=1}^3{k}_l\left(t\right)\left(R{e}_l\right)\times e_l,$$

(13)

where $e_l,l=1,2,3$, are the column vectors of the $3\times 3$ identity matrix.

The necessary condition for critical points of the Morse function in eq. (4) is $\delta U(R,t)=0$, which implies that $S_{K\left(t\right)}\left(R\right)=0$, or equivalently $K\left(t\right)R=RK\left(t\right)$, at the critical points. Therefore, the set of critical points is

$${\mathcal{S}}_c:=\left\{R\in \mathrm{SO}\left(3\right)\mid S_{K\left(t\right)}\left(R\right)=0\right\}.$$

(14)

Moreover, from eq. (13), $S_{K\left(t\right)}\left(R\right)=0$ implies that $R{e}_l=\pm e_l\iff e_l=\pm R{e}_l$. Therefore, set ${\mathcal{S}}_c$ in eq. (14) is given by its elements as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{S}}_c=\{& I=[e_1,e_2,e_3],E_1=[e_1,-e_2,-e_3],\hfill \\ \hfill & E_2=[-e_1,e_2,-e_3],E_3=[-e_1,-e_2,e_3]\}\subset \mathrm{SO}\left(3\right).\hfill \end{array}\end{array}$$

(15)

$E_2$, $E_3$, and $E_4$ denote ${180}^{\circ }$ ($\pi$ rad) rotations about the body frame’s first, second and third coordinate axes, respectively. Note that this set of critical points with time-varying $K\left(t\right)$ is identical to that obtained with constant K, which can be readily obtained by setting the right side of eq. (7) to zero. The second variation of eq. (4) is obtained by applying the variation operator to eq. (10), as:

$${\delta }^{2}U(R,\Sigma ,\delta \Sigma ,t)=\langle K\left(t\right),-R{\left({\Sigma }^{\times }\right)}^2-R\delta {\Sigma }^{\times }\rangle ,$$

(16)

where $\delta \Sigma$ denotes the differential of $\Sigma \in {\mathbb{R}}^3$. Using the trace orthogonality property of symmetric and skew-symmetric matrices, eq. (16) further simplifies to

$$\begin{array}{cc}\hfill {\delta }^{2}U& ={\displaystyle \frac{1}{2}}\left[\langle K\left(t\right)R-RK\left(t\right),\delta {\Sigma }^{\times }\rangle -\langle RK\left(t\right)+K\left(t\right)R,{\left({\Sigma }^{\times }\right)}^2\rangle \right].\hfill \end{array}$$

(17)

Evaluating the second variation of the Morse function given by eq. (4) on the set ${\mathcal{S}}_c$ at an instant of time, gives:

$${\left.{\delta }^{2}U\left(t\right)\right|}_{{\mathcal{S}}_c}={\left.-\langle K\left(t\right)R,{\left({\Sigma }^{\times }\right)}^2\rangle \right|}_{R\in {\mathcal{S}}_c}.$$

(18)

Evaluating eq. (15) at each of the four critical points, we get:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\left.{\delta }^{2}U\left(t\right)\right|}_I=& k_1\left(t\right)({\Sigma }_2^2+{\Sigma }_3^2)+k_2\left(t\right)({\Sigma }_3^2+{\Sigma }_1^2)+k_3\left(t\right)({\Sigma }_1^2+{\Sigma }_2^2),\hfill \\ \hfill {\left.{\delta }^{2}U\left(t\right)\right|}_{E_1}=& k_1\left(t\right)({\Sigma }_2^2+{\Sigma }_3^2)-k_2\left(t\right)({\Sigma }_3^2+{\Sigma }_1^2)-k_3\left(t\right)({\Sigma }_1^2+{\Sigma }_2^2),\hfill \\ \hfill {\left.{\delta }^{2}U\left(t\right)\right|}_{E_2}=& -k_1\left(t\right)({\Sigma }_2^2+{\Sigma }_3^2)+k_2\left(t\right)({\Sigma }_3^2+{\Sigma }_1^2)-k_3\left(t\right)({\Sigma }_1^2+{\Sigma }_2^2),\hfill \\ \hfill {\left.{\delta }^{2}U\left(t\right)\right|}_{E_3}=& -k_1\left(t\right)({\Sigma }_2^2+{\Sigma }_3^2)-k_2\left(t\right)({\Sigma }_3^2+{\Sigma }_1^2)+k_3\left(t\right)({\Sigma }_1^2+{\Sigma }_2^2).\hfill \end{array}\end{array}$$

(19)

We evaluate the Hessian matrix evaluated for $R\in S_c$ by taking second partial derivatives of ${\delta }^{2}U$ with respect to ${\Sigma }_i,i=1,2,3$. Denote the Hessian of the Morse function $U\left(R\right)$ by:

$$H_U(R,t){|}_{R\in {\mathcal{S}}_c}={\partial }^{2}U(R,t){|}_{R\in S_c}$$

We define it as:

$$H_U(R,t){|}_{R\in {\mathcal{S}}_c}={\left[{\displaystyle \frac{{\partial }^2}{\partial {\Sigma }_i\partial {\Sigma }_j}}\mathrm{trace}{\left(-L\left(t\right){\Sigma }^{\times }\right)}^2\right]}_{ij}$$

where $L\left(t\right)=K\left(t\right)R$. For $R\in {\mathcal{S}}_c\left(t\right)$,

$$L\left(t\right)=\left({\ell }_i\left(t\right)\right),where{\ell }_i\left(t\right)=k_i\left(t\right)R_{ii},i\in \{1,2,3\},$$

and $R_{ij}$ is the $(i,j)$ component of R. In addition, $(-L\left(t\right){\left({\Sigma }^{\times }\right)}^2)=({\ell }_2\left(t\right)+{\ell }_3\left(t\right)){\Sigma }_1^2+({\ell }_3\left(t\right)+{\ell }_4\left(t\right)){\Sigma }_2^2+({\ell }_1\left(t\right)+{\ell }_2\left(t\right)){\Sigma }_3^2$, we get the following expression given by,

$$H_U(R,t){|}_{R\in {\mathcal{S}}_c}=2\left[\begin{array}{ccc}{\ell }_2\left(t\right)+{\ell }_3\left(t\right)& 0& 0\\ 0& {\ell }_3\left(t\right)+{\ell }_1\left(t\right)& 0\\ 0& 0& {\ell }_1\left(t\right)+{\ell }_2\left(t\right)\end{array}\right]$$

The Hessian matrices for each $R\in {\mathcal{S}}_c\subset \mathrm{SO}\left(3\right)$ are given by:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill H_U(I,t)=& 2[k_2\left(t\right)+k_3\left(t\right),k_3\left(t\right)+k_1\left(t\right),k_1\left(t\right)+k_2\left(t\right)],\hfill \\ \hfill H_U(E_1,t)=& 2[-(k_2\left(t\right)+k_3\left(t\right)),k_1\left(t\right)-k_3\left(t\right),k_1\left(t\right)-k_2\left(t\right)],\hfill \\ \hfill H_U(E_2,t)=& 2[k_2\left(t\right)-k_3\left(t\right),-(k_3\left(t\right)+k_1\left(t\right)),-(k_1\left(t\right)-k_2\left(t\right))],\hfill \\ \hfill H_U(E_3,t)=& 2[-(k_2\left(t\right)-k_3\left(t\right)),-(k_1\left(t\right)-k_3\left(t\right)),-(k_1\left(t\right)+k_2\left(t\right))].\hfill \end{array}\end{array}$$

(20)

Equation (20) readily reveals that the Hessian of the Morse function evaluated at critical points in the set (14) depends on time because of $K\left(t\right)$; this is unlike the case with constant K. This directly affects the indices of these critical values on SO(3), which in turn influences the stability properties of the equilibria on TSO(3) that these critical points correspond to in the feedback system. This is due to the fact that the eigenvalues of $H_U(R,t)$ for $R\in S_c$ are time-varying and may be positive, negative or even momentarily zero depending on the relative values of the $k_i\left(t\right)$. The only critical point that has a positive definite Hessian and therefore a zero index for all time is the identity $I\in \mathrm{SO}\left(3\right)$, which corresponds to the desired equilibrium state $(I,0)\in \mathrm{T}\mathrm{SO}\left(3\right)\simeq \mathrm{SO}\left(3\right)\times \mathfrak{so}\left(3\right)$. In summary, the time-varying positive diagonal gain matrix $K\left(t\right)$ ensures that all critical points of the Morse function that are in the set $S_c\setminus I$, have time-varying indices.

Remark: The index of a critical point of the Morse function is the number of negative eigenvalues of its Hessian, $H_U(R,t)$, for $R\in S_c$. If $K\left(t\right)=K$ is constant, then the indices of $I,E_1,E_2,$ and $E_3$ are 0, 1, 2 and 3, respectively with the minimum attained at $R=I$, given that $k_1>k_2>k_3>0$. However, when $K\left(t\right)$ is time-varying, the number of positive and negative eigenvalues of the Hessian at any of the three critical points of the Morse function (i.e., any point in the set $S_c\setminus I$), switch with time depending on $K\left(t\right)$. As the index values can vary with time for $R\in S_c\setminus I$, the dimensions of stable and unstable manifolds associated with these critical points also switch with time. As can be seen from eq. (20), a switch in the index of one of these three critical points occurs when $k_i\left(t\right)=k_j\left(t\right)$ for $i\ne j$, $i,j\in \{1,2,3\}$. This results in discrete switching of the index values at these critical points depending on the instantaneous inequality constraint between diagonal elements of $K\left(t\right)$. The index values of the critical points give the dimensions of the stable manifolds of the equilibria of the feedback system corresponding to these critical points. The dimension of the stable manifold $\mathcal{S}\left(E_i\right)$ is calculated as $dim\left(\mathcal{S}\left(E_i\right)\right)=6-Index\left(E_i\right)$, where 6 is the total dimension of the state-space $\mathrm{T}\mathrm{SO}\left(3\right)\simeq \mathrm{SO}\left(3\right)\times \mathfrak{so}\left(3\right)$. Therefore, the stable manifolds and their dimensions vary over time for these equilibrium points on TSO(3) corresponding to the critical points in $S_c\setminus I$.

4. AGAS Attitude Control Law

The following statement gives a feedback control law on the state space TSO(3) to asymptotically stabilize the desired attitude and angular velocity state $(I,0)$.

Theorem 1. 

Consider a positive diagonal time-varying $K\left(t\right)\in {\mathbb{R}}^{3\times 3}$ such that $K\left(t\right)=\overline{K}+\tilde{K}\left(t\right)$ where $\overline{K},\tilde{K}\left(t\right)\in {\mathbb{R}}^{3\times 3}$ are diagonal and $k_i={\overline{k}}_i+{\tilde{k}}_i\left(t\right)>0$, $i=1,2,3$, and ${\tilde{k}}_i\left(t\right)={\tilde{k}}_i(t+T)$ is ${\mathcal{C}}^1$ continuous and time-periodic with period T. Consider the attitude control law for the rigid body given by:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{T}u=& J{\dot{\Omega }}_d+{\Omega }_d\times J\Omega -L{\displaystyle \frac{\tilde{\Omega }}{{\left(\tilde{\Omega }L\tilde{\Omega }\right)}^{(1-1/p)}}},\hfill \\ \hfill {\Omega }_d=& -S_{K\left(t\right)}\left(R\right)and\tilde{\Omega }:=\Omega -{\Omega }_d,\hfill \end{array}\end{array}$$

(21)

where $p\in ]1,2[$, $L-J⪰0$. This control law makes the state $(R,\Omega )=(I,0)$ almost globally aymptotically stable (AGAS) and locally exponentially stable.

Proof. 

The proof is given in two steps. The first step considers the velocity kinematics, where we define a desired angular velocity ${\Omega }_d$ profile that is guaranteed to steer the attitude R towards the identity attitude I. In the second step, the attitude dynamics is considered, where we formulate the control torque law $\mathrm{T}u$ that forces the true angular velocity $\Omega$ of the rigid body to follow the desired angular velocity ${\Omega }_d$ with finite-time stable (FTS) convergence.

Consider the polar Morse function on SO(3) given by

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{U}}_{\overline{K}}\left(R\right)=\langle \overline{K},I-R\rangle ,\end{array}\end{array}$$

(22)

which depends on the constant part of $K\left(t\right)$ as defined in the statement. The time derivative of (22) is given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{\mathcal{U}}}_{\overline{K}}=& \langle \overline{K},-R{\Omega }^{\times }\rangle ,(1/2)\langle \overline{K}R-R\overline{K},{\Omega }^{\times }\rangle \hfill \\ \hfill =& {\left(S_{\overline{K}}\left(R\right)\right)}^T\Omega =\Omega S_{\overline{K}}\left(R\right),\hfill \end{array}\end{array}$$

(23)

where $S_{\overline{K}}\left(R\right)=vex(\overline{K}R-R\overline{K})={\sum }_{i=1}^3{\overline{k}}_i{e}_i\times R{e}_i$ and $vex(·):\mathfrak{so}\left(3\right)\to {\mathbb{R}}^3$ is the inverse of the cross-product operator map ${(·)}^{\times }$ defined by eq. (2). A kinematic control law that leads to almost global asymptotically stable (AGAS) convergence of R to $I\in \mathrm{SO}\left(3\right)$ described by (1) is given by

$$\begin{array}{c}\hfill {\Omega }_d=-S_{K\left(t\right)}\left(R\right)=-\sum _{i=1}^3{k}_i\left(t\right)(e_i\times R{e}_i),\end{array}$$

(24)

where $k_i\left(t\right)={\overline{k}}_i+{\tilde{k}}_i\left(t\right)>0$ according to the properties of $K\left(t\right)$. Setting the true angular velocity equal to the desired angular velocity ${\Omega }_d$, and substituting (24) into the expression (23) for the time derivative of ${\mathcal{U}}_{\overline{K}}\left(R\right)$, gives:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\dot{\mathcal{U}}}_{\overline{K}}=-\left(S_{K\left(t\right)}\left(R\right)\right)S_{\overline{K}}\left(R\right).\end{array}\end{array}$$

(25)

Simplifying (25) using (24) by observing that the vectors $(e_i\times R{e}_i),i=1,2,3$, are mutually orthogonal, leads to:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\dot{\mathcal{U}}}_{\overline{K}}=-\sum _{i=1}^3({\overline{k}}_i^2+{\overline{k}}_i{\tilde{k}}_i\left(t\right)){\parallel e_i\times R{e}_i\parallel }^2.\end{array}\end{array}$$

(26)

Eq. (26) can be rewritten as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{\mathcal{U}}}_{\overline{K}}=& -\sum _{i=1}^3{\overline{k}}_i({\overline{k}}_i+{\tilde{k}}_i\left(t\right)){\parallel e_i\times R{e}_i\parallel }^2\le 0.\hfill \end{array}\end{array}$$

(27)

In eq. (27), ${\dot{\mathcal{U}}}_{\overline{K}}=0$ when $R\in {\mathcal{S}}_c$. The only (global) minimum of ${\mathcal{U}}_{\overline{K}}$ is at $R=I$, while $E_1$ and $E_2$ give saddle points with one- and two-dimensional stable manifolds, respectively. The global maximum of ${\mathcal{U}}_{\overline{K}}$ over SO(3) is attained at $E_3$. Therefore, with the kinematic control law (24), all trajectories on SO(3) that do not start on the stable manifolds of $E_1$ and $E_2$, or at $E_3$, converge to $R=I$. This leads to $R=I$ being the AGAS equilibrium for this kinematic (velocity level) control system on SO(3).

The next step of this control scheme is to track the desired angular velocity profile given by the kinematic-level control law (24) so that the true angular velocity converges to this desired profile in a finite time interval. For this, we define the angular velocity tracking error as $\tilde{\Omega }:=\Omega -{\Omega }_d$. Consider the attitude dynamics of the body given by the second of eqs. (1), where $J=J\succ 0$ is the inertia matrix. Define the following energy-like Lyapunov function of the angular velocity tracking error:

$$V:={\displaystyle \frac{1}{2}}\tilde{\Omega }J\tilde{\Omega }=V\left(\tilde{\Omega }\right).$$

(28)

The time derivative of this Lyapunov function along the trajectories of (1) is given by:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{V}=& \tilde{\Omega }(J\Omega \times \Omega +\mathrm{T}u-J{\dot{\Omega }}_d).\hfill \end{array}\end{array}$$

(29)

Substituting the finite-time stable $\mathrm{T}u$ control law (21) into expression (29) for $\dot{V}$ results in,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{V}=& -{\left(\tilde{\Omega }L\tilde{\Omega }\right)}^{1/p}\le -{\left(\tilde{\Omega }J\tilde{\Omega }\right)}^{1/p}\hfill \\ \hfill \Rightarrow & \dot{V}\le -{\left(2V\right)}^{1/p}.\hfill \end{array}\end{array}$$

(30)

Therefore, from (30) and [13], we conclude that $\Omega \to {\Omega }^d$ in finite time, with the settling time upper-bounded as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill T_s\le {\displaystyle \frac{V{\left({\tilde{\Omega }}_0\right)}^{1-(1/p)}}{2^{1/p}(1-(1/p))}}={\displaystyle \frac{V_0^{1-(1/p)}}{2^{1/p}(1-(1/p))}},\end{array}\end{array}$$

(31)

where $V_0=V\left({\tilde{\Omega }}_0\right)$ is the initial value of the Lyapunov function in (28) and ${\tilde{\Omega }}_0$ is the initial tracking error in angular velocity. In summary, the control law (21) ensures FTS convergence of $\Omega$ to ${\Omega }^d$, which in turn ensures AGAS convergence of $(R,\Omega )$ to $(I,0)$ according to the kinematic control law (24). □

For numerical simulation studies, this work considers a particular structure of $K\left(t\right)$ given by:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill K\left(t\right)=[& C_1+a_{1}cos{({\omega }_{1}t+{\varphi }_1)}^2,C_2+a_{2}cos{({\omega }_{2}t+{\varphi }_2)}^2,\hfill \\ & C_3+a_{3}cos{({\omega }_{3}t+{\varphi }_3)}^2],\hfill \end{array}\end{array}$$

(32)

where $C_i>0$, $a_i>0$, ${\omega }_i$ is the oscillation frequency and ${\varphi }_i$ is an initial phase, for $i=1,2,3$.

5. Numerical Simulation Results

In this section, a comparative set of numerical simulations with constant gain K and time-varying gain $K\left(t\right)$ of the Morse function is presented. The continuous time dynamics is discretized for numerical simulations in computer. The resulting discrete time dynamics is in the form of a Lie group variational integrator (LGVI) [14], obtained by applying the discrete Lagrange–d’Alembert principle [15,16,17]. Consider an interval of time $[t_0,T]\in {\mathbb{R}}^{+}$ separated into N equal-length subintervals $[t_n,t_{n+1}]$ for $n=0,1,2,\dots ,l$, with $t_{l+1}=T$ and $\Delta t=t_{n+1}-t_n$ is the time step size. The discrete-time equations are:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\left(J{\Omega }_n\right)}^{\times }& ={\displaystyle \frac{1}{\Delta t}}\left(F_n\mathcal{J}-\mathcal{J}{F}_n\right),\hfill \\ \hfill \mathcal{J}& ={\displaystyle \frac{1}{2}}\left[J\right]I_3-J,\hfill \\ \hfill R_{n+1}& =R_n{F}_n,\hfill \\ \hfill J{\Omega }_{n+1}& =F_n\left(J{\Omega }_n\right)+\Delta t\mathrm{T}{u}_n,\hfill \\ \hfill \mathrm{T}{u}_n& =\mathrm{T}u(R_n,{\Omega }_n).\hfill \end{array}\end{array}$$

(33)

For the time-varying gains of the Morse function, we choose the $K\left(t\right)$ as described in (32), with:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill K\left(t\right)=0.5*[& 0.55+0.2cos{(0.04\pi t+\pi /2)}^2,\hfill \\ & 0.52+0.15cos{(0.12\pi t+\pi /3)}^2,\hfill \\ & 0.5+cos{(0.2\pi t+\pi /4)}^2].\hfill \end{array}\end{array}$$

(34)

For the constant gain Morse function, the gains are selected as $K=0.5*[0.55+0.2/2,0.52+0.15/2,0.5+1/2]$. The simulated time period is 250 seconds. The gain matrix for the dynamic level controller (21) is $L=J_1+0.03I_3$ with $p=1.01$. The inertia tensor of the rigid body is $J_1=diag\left(\left[345\right]\right)$ ${\mathrm{kgm}}^2$. The initial attitude of the rigid body is $R_0=E_2$, and the initial angular velocity is ${\Omega }_0=\left[{10}^{-5}{10}^{-5}0\right]$$rad/s$. 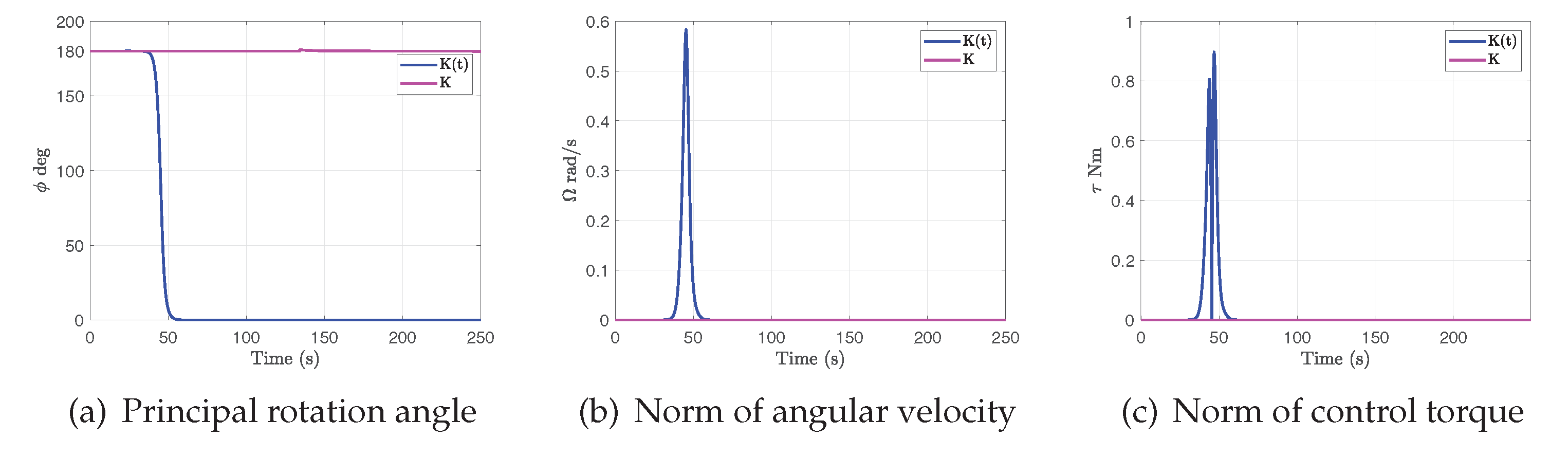Figure 1 shows comparative simulation results for constant K versus time-varying $K\left(t\right)$. In Figure 1(a) the principal rotation angle for time-varying $K\left(t\right)$ converges to zero (corresponding to identity attitude $R=I_3$), whereas with the constant K it remains at the initial attitude $R_0=E_2$. Figure 1(b) and (c) show the angular velocity and control torque profiles. This numerical simulation demonstrate the usefulness of time-varying gains for the Morse function as an attitude measure, and the role of the resulting time-varying state feedback controller in destabilizing the local stable manifolds of unstable equilibria.

6. Conclusion

This work provides a continous time-varying state dependent feedback attitude controller on TSO(3) based on Morse functions with time-varying gains. As a result, undesirable equilibria for the feedback system of the rigid body are avoided because the indices of these equilibrium points switch discretely in time, and the only always minimum equilibrium on TSO(3) is the identity attitude with zero angular velocity. Simulation results confirm that the time-varying Morse function can prevent system response from “getting stuck" near undesired equilibria of the feedback system and can achieve convergence to the identity attitude. Future work will focus on extending the analysis and results to coordinated relative attitude control of network of unmanned aerial vehicles modeled as multi-agent rigid body systems (MARBS). Distributed gain design for Morse functions for a network of MARBS, integration with observers, and experimental validation on small UAVs, are other future research directions.