Alternating Causality: Reversible Information Flow and the Arrow of Time in Communication Channels

1. Introduction

Shannon’s Mathematical Theory of Communication [1] presumes a unidirectional, forward flow of information from transmitter to receiver. Time is treated as an external ordering parameter along which signals propagate, with a fixed and globally well-defined causal order. The framework is therefore silent on regimes in which the direction of time may be indefinite or even reversible. Such regimes, once thought purely speculative, now appear in quantum information theory and quantum foundations [2,3,4,5,6,7,8,9].

To restore symmetry without invoking quantum superposition, we replace the one-way channel with a bidirectional shannon channel: every forward symbol is immediately echoed on a reverse channel as a symbol-level acknowledgement. In the ideal deterministic (noise-free) limit, the receiver’s information gain about the forward message is exactly matched by the sender’s information gain from the echo, so that over a complete forward–echo cycle the net mutual information across the pair is zero while both endpoints attain certainty. We call this Perfect Information Feedback (PIF).

We cast the bidirectional echo channel as an instance of Alternating Causality (AC): a reversible, symmetric process whose deterministic microdynamics alternate sender/receiver roles according to a fixed schedule. A single causal transmission collapses an oscillating arrow of causality into one of four directions: Alice to Alice, Alice to Bob, Bob to Alice, Bob to Bob. The AC/PIF primitive avoids baking a global forward-in-time assumption into the model; any macroscopic arrow emerges from boundary conditions and control objectives. Physically, one can view AC as the classical, buildable analogue of time-symmetric “mirror” interactions (e.g., photon reflections), but our formal results rely only on the deterministic alternation, making the construction auditable and composable at network scale.

2. From Minkowski Spacetime to Alternating Causality

In Minkowski spacetime, time-separated events are represented along the $ct$ axis, while spatial separations are measured along x, y, and z. In this framing, “instants” are meaningless: a single point in spacetime carries no temporal reality independent of the intervals that connect it to others. An interval in Minkowski spacetime,

$$d{s}^2=c^{2}d{t}^2-d{x}^2-d{y}^2-d{z}^2,$$

(1)

is therefore not the same as the interval measured on a local clock. Only the invariant proper time $\tau$, defined along a timelike worldline by

$$c^{2}d{\tau }^2=c^{2}d{t}^2-d{x}^2-d{y}^2-d{z}^2,$$

(2)

corresponds to the physical time experienced by an observer. For a photon, however, the proper time is identically zero:

$$d\tau =0,$$

(3)

A photon therefore experiences no passage of time between emission and absorption. Its worldline connects two events without internal duration, leaving its “distance traveled” undefined from the photon’s own perspective. The frequency $\nu$ of light conveys energy ($E=h\nu$), not elapsed time; only ensembles of photons, averaged statistically, generate measurable temporal frequencies [10].

In general relativity, causal structure is encoded geometrically through causal diamonds: regions defined by the intersection of the future of one event and the past of another [2,3]. Each diamond represents the set of all spacetime points that can both influence and be influenced between two events. While such constructions elegantly capture local causal order, they are insufficient to describe processes where causal order itself becomes indefinite or reversible.

Recent developments in quantum foundations have challenged this classical assumption. Work by Oreshkov, Brukner, and collaborators has shown that quantum theory can accommodate processes in which the order of operations is not fixed but exists in superposition, a regime known as indefinite causal order (ICO) [4,5,6,7]. In the ICO framework, operations performed by two parties A and B may coexist coherently in both $A\prec B$ and $B\prec A$ configurations. Such processes are represented not by a single causal relation but by a higher-order process matrix, which encodes all admissible temporal configurations consistent with local quantum operations.

2.1. The Photon Clock Model

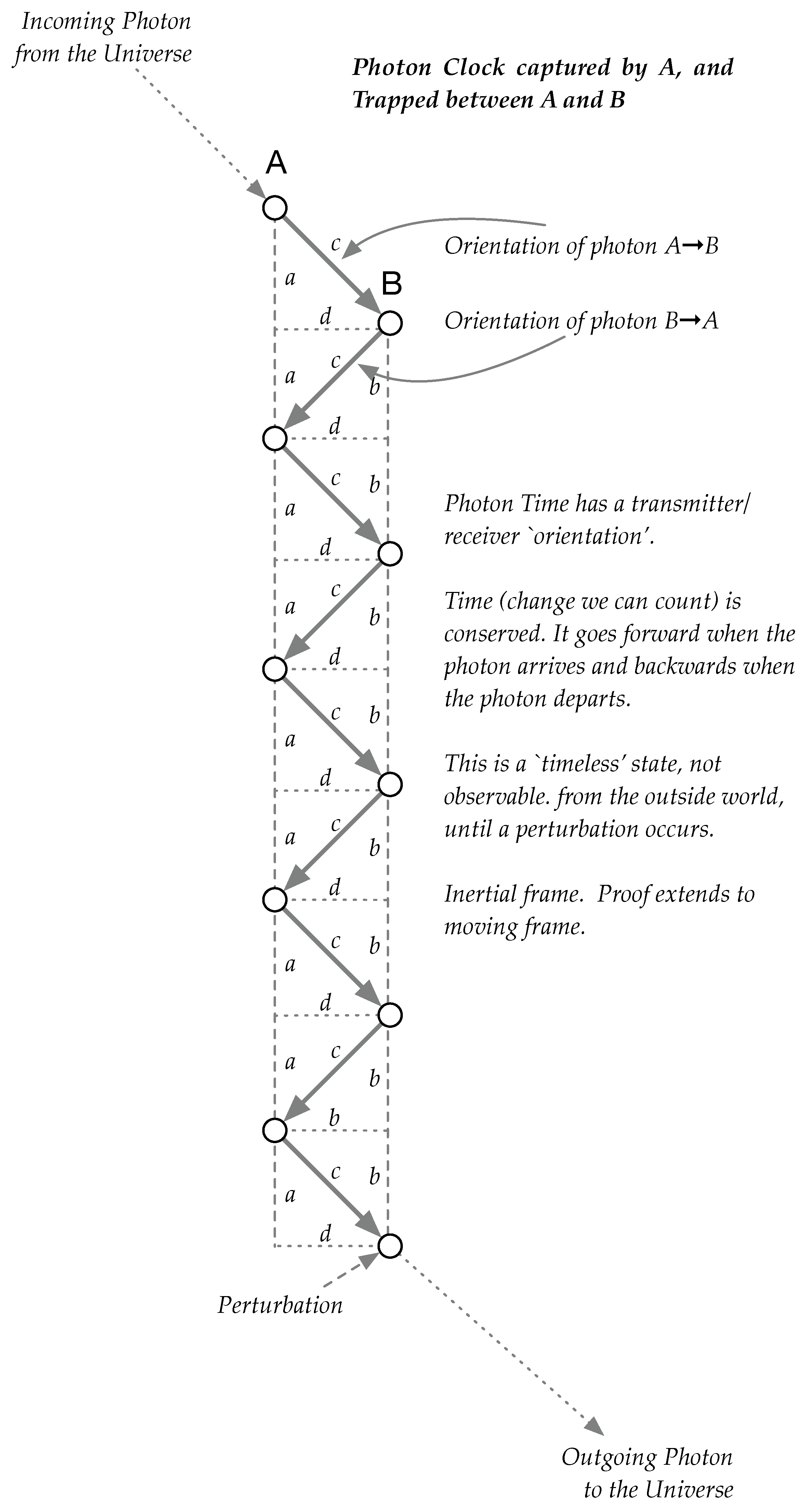
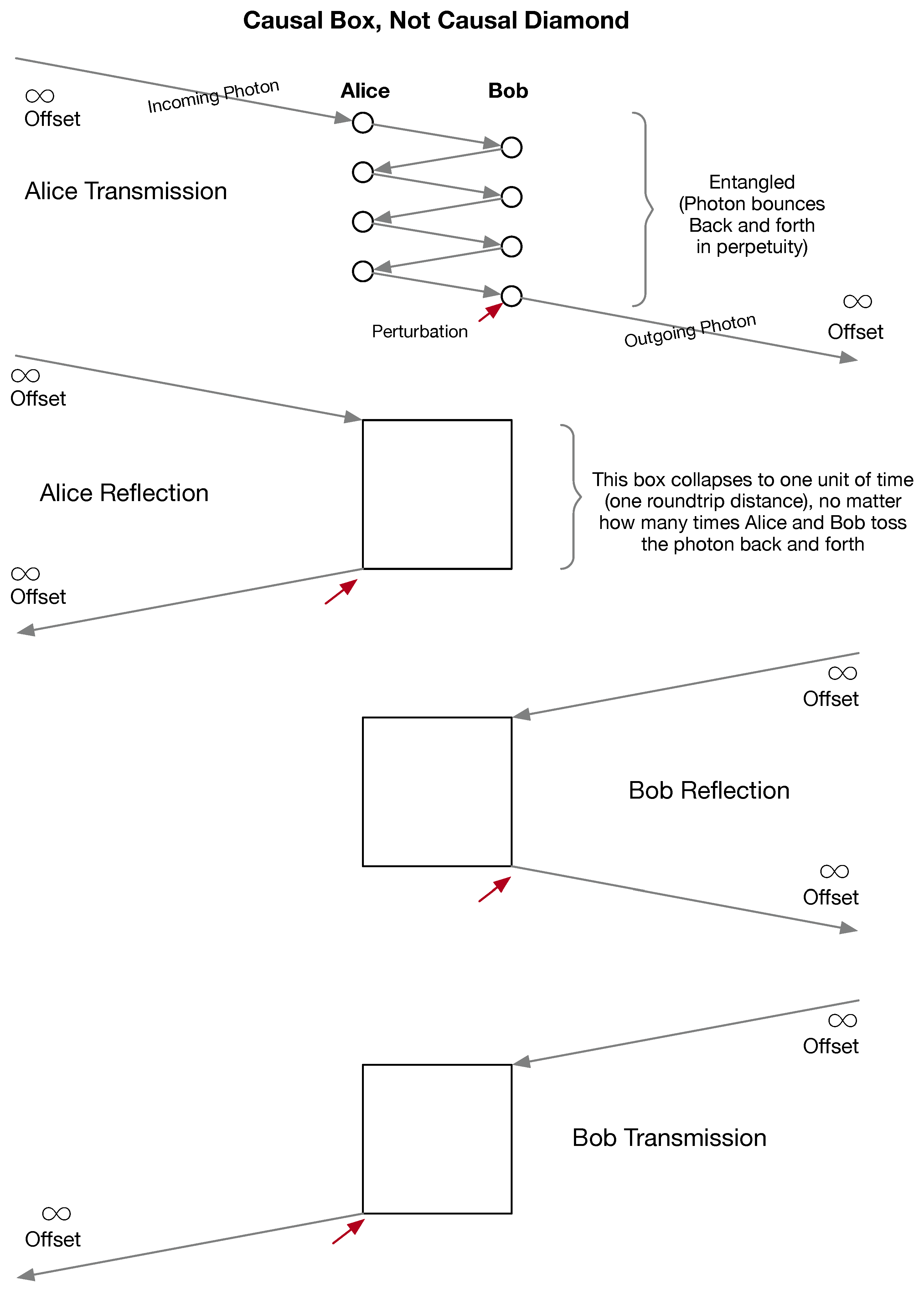
To operationalize this idea within a relativistic setting, consider a single photon confined between two ideal mirrors, representing observers A (Alice) and B (Bob). Each reflection constitutes a lightlike exchange event. As long as the photon remains trapped, the system exists in an alternating causality regime: causal influence oscillates reversibly between A and B, without a definite direction of time.

Figure 1. A photon confined between two mirrors forms a closed causal system.

Figure 1. A photon confined between two mirrors forms a closed causal system.

When Alice first encounters the photon, she has no knowledge of how far or for how long it has traveled. She reflects it perfectly toward Bob, reversing both momentum and phase. From her standpoint, no local time elapses between emission and reception. The photon’s worldline is a single, lightlike event with zero proper duration. When Bob receives and reflects the photon, he too possesses no information about Alice’s existence—only that a photon arrived with proper time zero. Only after multiple exchanges can either observer infer a round-trip duration using their own local clock. This measured interval defines an emergent geometric separation between A and B, effectively reconstructing spacetime distance from the statistics of information exchange [8,9].

The confined photon and its two mirrors together form an entangled, time-symmetric system. As long as the photon remains within, its causal configuration is reversible; no absolute ordering between Alice and Bob exists. When a perturbation allows the photon to escape by absorption, decoherence, or asymmetry, the system’s causal symmetry collapses. The external observer then perceives one of four possible classical configurations, corresponding to distinct, definite arrows of time.

This photon-clock model thus provides a minimal physical realization of indefinite causal order. It extends the causal-diamond construction by embedding within it a reversible, quantum-causal interior termed a “causal box.” When projected outward, the box behaves as a single classical causal diamond with a fixed orientation; internally, however, it encodes a superposition of time directions. Alternating Causality (AC) therefore serves as a bridge between general relativity’s local causal geometry and quantum theory’s process-based indeterminacy.

A perturbation such as absorption, decoherence, or asymmetry, breaks this interaction, collapsing the system into a definite causal order (Figure 2). The alternating forward–backward structure of influence can be represented geometrically as two joined causal triangles (Fig. ??), capturing the oscillatory exchange of causal orientation between A and B.

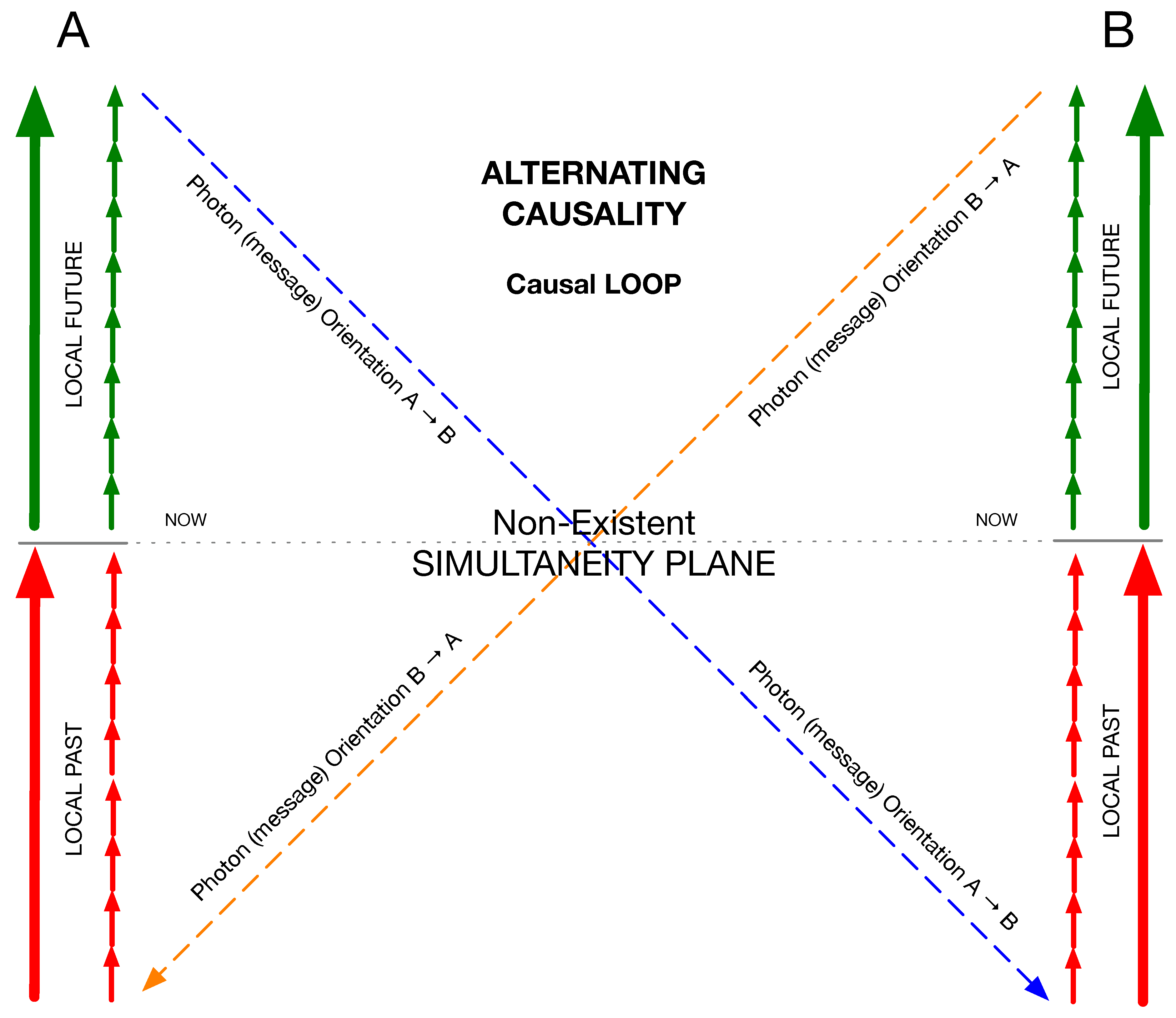
2.2. Barukčić Triangles, Radar Time, and the Non-Existence of a Simultaneity Plane

Consider a single photon bouncing back and forth between two timelike worldlines A (Alice) and B (Bob). Each bounce is the junction of two null legs: $A\to B$ and $B\to A$. Between Alice’s emission and her reception, all causal communication across the gap is lightlike; the only timelike accumulation occurs on the local clocks along A and B.

From Alice’s perspective, if the emission and echo-reception occur at proper times $T_{-}^A$ and $T_{+}^A$, the radar-time construction assigns the reflection event R the coordinates

$$t_A=\frac{1}{2}\left(T_{+}^A+T_{-}^A\right),{\displaystyle \frac{x_A}{c}}=\frac{1}{2}\left(T_{+}^A-T_{-}^A\right),$$

(4)

or, in light-cone form, $u_A=T_{+}^A$, $v_A=T_{-}^A$. The only invariant extracted from this single echo is

$${\tau }_A^2=t_A^2-{\left({\displaystyle \frac{x_A}{c}}\right)}^2=u_A{v}_A=T_{+}^A{T}_{-}^A,$$

(5)

Where:

$T_{-}^A$: Alice’s proper time at the emission event: when the photon leaves her worldline toward Bob.

$T_{+}^A$: Alice’s proper time at the reception event: when the reflected photon returns from Bob.

$t_A$: the radar time coordinate of the reflection event R, defined as the midpoint between emission and reception times on Alice’s clock.

${\displaystyle \frac{x_A}{c}}$: the radar distance to the reflection event R, equal to half the round-trip light time expressed in light-seconds.

$u_A=t_A+{\displaystyle \frac{x_A}{c}}=T_{+}^A$: the forward light-cone coordinate, representing the outgoing null leg ($A\to B$).

$v_A=t_A-{\displaystyle \frac{x_A}{c}}=T_{-}^A$: the backward light-cone coordinate, representing the return null leg ($B\to A$).

${\tau }_A$: Alice’s proper-time interval accumulated between emission and reception; the invariant tick of her local clock satisfying ${\tau }_A^2=t_A^2-{(x_A/c)}^2=T_{+}^A{T}_{-}^A$.

which equals the proper time that Alice’s clock accrues over the closed send–reflect–receive loop. An identical statement holds for Bob with ${\tau }_B^2=T_{+}^B{T}_{-}^B$. Thus, the null legs and the local proper-time altitudes are the physically meaningful pieces.

Figure 3. Each event is registered only against its own local clock: the emission and reception of a photon define proper-time intervals for the participating observers, but not a shared global schedule. No observer can assert that distant clocks advance in lock step with a single transmission or echo; the notion of simultaneity exists only within each worldline’s local frame.

Figure 3. Each event is registered only against its own local clock: the emission and reception of a photon define proper-time intervals for the participating observers, but not a shared global schedule. No observer can assert that distant clocks advance in lock step with a single transmission or echo; the notion of simultaneity exists only within each worldline’s local frame.

A “simultaneity plane’’ would be a spacelike slice $\Sigma$ that intersects both worldlines between emission and reception and is supposed to represent a shared “now.” Inside the causal diamond of the echo, there is no observer independent way to pick such a slice. Any slice of simultaneity must be defined by a foliation, e.g., $t=\mathrm{const}$ for some inertial frame. Lorentz boosts tilt this foliation: one null leg appears longer while the other appears shorter, so which pair of points on A and B are “simultaneous’’ changes with the frame. The diamond’s null boundaries are preserved; a spacelike simultaneity cut is not.

The only operational way for Alice to nominate a “midpoint time’’ for R is the average $t_A=\frac{1}{2}(T_{+}^A+T_{-}^A)$. Bob can do the same on his clock. These constructions are private coordinate choices: they depend on each party’s synchronization convention and, in general, yield different slices. Nothing inside the two-party photon exchange selects one foliation over another. Physically, the interior dynamics oscillate their causal orientation: $A\to B$ on one leg, $B\to A$ on the next. That alternation supplies a discrete global order (bounce number) but not a continuous, frame-invariant “time sheet’’ spanning both worldlines.

The averages $\frac{1}{2}(T_{+}^A+T_{-}^A)$ and $\frac{1}{2}(T_{+}^B+T_{-}^B)$ are perfectly meaningful as local coordinates (they define each party’s radar chart), but they have no observer-independent status between the parties. They cannot be promoted to a common “now’’ because a change of inertial frame changes which distant events are simultaneous. By contrast, the products $T_{+}^A{T}_{-}^A$ and $T_{+}^B{T}_{-}^B$ (and the count of bounces) are invariant and exhaust what the echo itself can certify.

2.3. Construction (Barukčić Triangle)

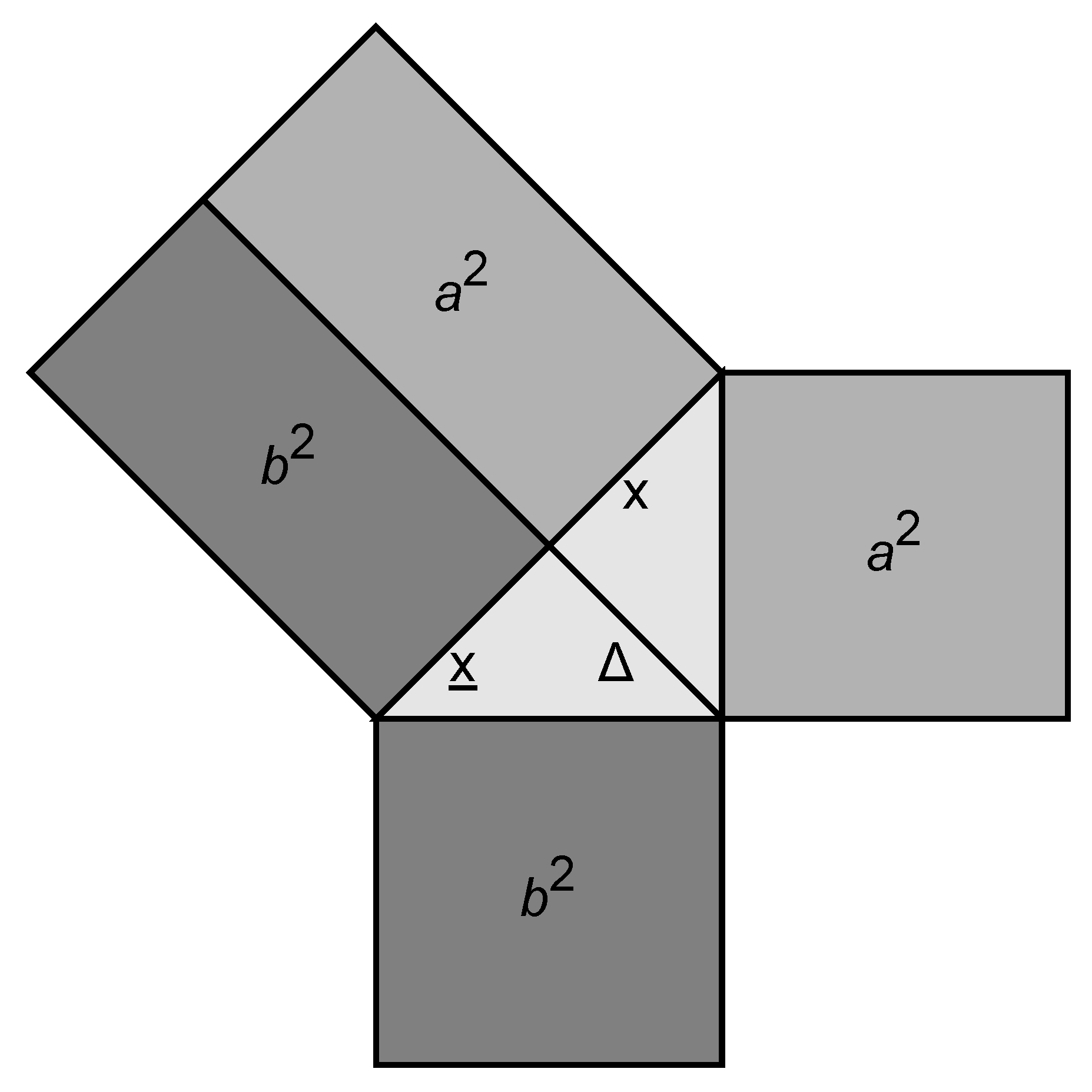
To visualize the invariant relationship between Alice’s local proper time and the photon’s forward–backward propagation, we recast the radar-time equations into a simple geometric form. The idea is to represent the two null exchanges ($A\to B$ and $B\to A$) as the sides of a right triangle, and Alice’s proper-time interval as its altitude. In this construction, the photon’s outward and return legs define the boundaries of a causal diamond, while the altitude corresponds to the invariant tick of Alice’s local clock. The resulting triangle provides a Euclidean analogue of the Minkowski relation ${\tau }_A^2=T_{+}^A{T}_{-}^A$, allowing the null and timelike components of a single photon exchange to be expressed in one compact geometric identity.

Draw a right triangle whose hypotenuse is partitioned into two contiguous segments of lengths

$$p:=T_{+}^A,q:=T_{-}^A.$$

(6)

Drop the altitude $\Delta$ from the right angle to the hypotenuse. By the right-triangle altitude (geometric-mean) theorem,

$${\Delta }^2=pq=T_{+}^A{T}_{-}^A.$$

(7)

Comparing (7) with (5), we identify

$$\Delta ={\tau }_A.$$

(8)

0.9

Where:

$p=T_{+}^A$: the forward light-cone coordinate measured on Alice’s clock, corresponding to the photon’s outgoing leg ($A\to B$). It represents the null interval from emission to reflection as perceived by Alice.

$q=T_{-}^A$: the backward light-cone coordinate measured on Alice’s clock, corresponding to the photon’s return leg ($B\to A$). It represents the null interval from reflection to reception.

$\Delta$: the altitude of the right triangle, dropped from the right angle to the hypotenuse. It represents the geometric mean of the two null intervals and corresponds physically to Alice’s proper-time tick between emission and reception: $\Delta ={\tau }_A=\sqrt{T_{+}^A{T}_{-}^A}$.

${\tau }_A$: the proper-time interval accumulated on Alice’s worldline between the emission and reception events. It is the invariant part of the exchange, equal to the altitude $\Delta$ of the triangle.

$(p,q)$: the two contiguous segments of the hypotenuse, together forming the radar-defined worldline interval between the two null legs. They encode the forward and backward propagation times of the photon as projected onto Alice’s clock.

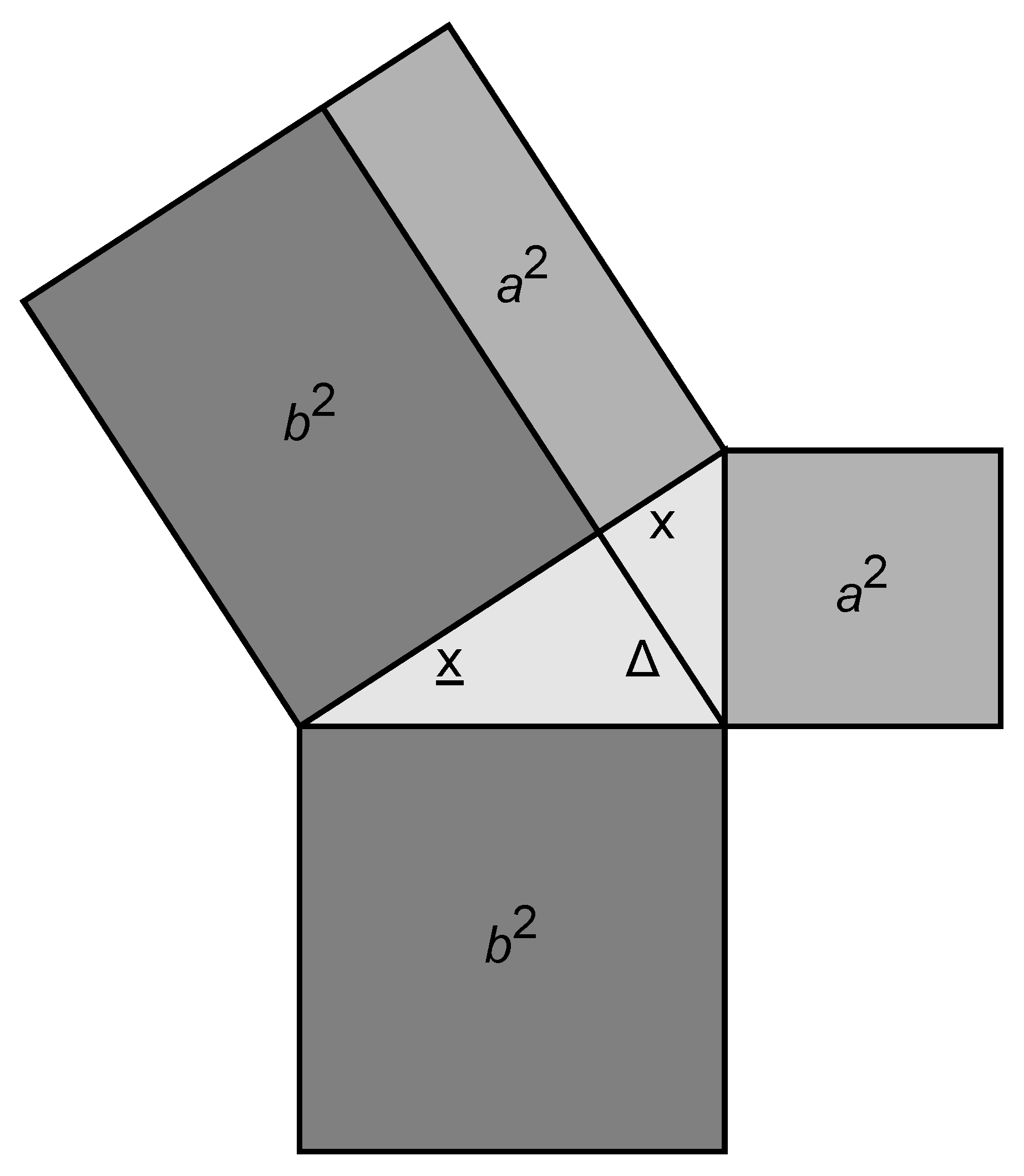
Tiling the worldsheet with back-to-back copies of this triangle (forward and return) as in Figure 4 gives a photon clock: each bounce contributes one invariant “tick’’ equal to the altitude $\Delta ={\tau }_A$. Repeating the same construction using Bob’s times $T_{-}^B,T_{+}^B$ yields an analogous triangle with altitude ${\Delta }_B={\tau }_B$. In a stationary two-mirror configuration ${\tau }_A={\tau }_B$, but the mapping $(p,q)\mapsto \Delta$ remains invariant in general because (5) is local to each radar cycle.

Figure 5. Non-inertial frame: the photon clock experiences asymmetric bounces.

Figure 5. Non-inertial frame: the photon clock experiences asymmetric bounces.

Figure 6. Inertial frame: two local clocks in uniform motion, no global simultaneity.

Figure 6. Inertial frame: two local clocks in uniform motion, no global simultaneity.

This construction emphasizes that the photon exchange defines only local relations between emission and reception events. Each worldline measures its own proper-time altitude $\Delta ={\tau }_A$ or ${\tau }_B$, derived from its own pair of null intervals $(T_{-}^A,T_{+}^A)$ or $(T_{-}^B,T_{+}^B)$. However, no single “horizontal’’ plane of simultaneity can be drawn through the triangle that both observers would agree upon. The forward and backward null legs constrain what each observer can signal or know, but not how distant clocks advance in relation to one another. The midpoint of a round-trip echo, defined by the average $\frac{1}{2}(T_{+}^A+T_{-}^A)$, is a convention internal to Alice’s frame, not a global timestamp shared with Bob.

In this sense, the Barukčić triangle captures more than a geometric mean: it visualizes the limits of simultaneity. Each observer constructs time from the closed loop of its own emissions and receptions, anchored only by local invariants. The proper-time altitude $\Delta$ is therefore the sole physically meaningful measure inside the triangle, while any attempt to project a global “now’’ across both worldlines is coordinate-dependent and physically unobservable. The photon clock, built from these alternating null exchanges, thus enforces a fundamentally background-independent notion of time: one defined locally by causal contact, not globally by synchronized ticks.

3. Alternating Causality and the Process Matrix Formalism

Oreshkov, Costa, and Brukner (OCB, 2012) introduced the process matrix formalism to describe correlations among quantum operations without assuming a fixed global causal order [11]. Within that framework, two operations A and B can exist in a coherent superposition of causal sequences:

$$A\prec B\mathrm{and}B\prec A.$$

(9)

The process matrix W generalizes the concept of a quantum channel by encoding all physically admissible correlations consistent with local quantum operations but independent of a global temporal reference frame.

Alternating Causality (AC) builds upon this foundation but differs conceptually from indefinite causal order. Whereas ICO describes a probabilistic or coherent superposition of orders, AC represents a deterministic, time-symmetric oscillation of causal direction. Instead of an indeterminate mixture of $A\to B$ and $B\to A$, AC describes a periodic, reversible exchange of influence between the two parties.

A link state is x: classically a probability vector (entries $\ge 0$, sum 1); quantum mechanically a density operator (positive, trace 1). AC specifies two maps on states: forward F ($A\to B$) and reverse R ($B\to A$). One cycle is F then R.

Alternating Causality is defined by three simple principles. First, the forward and reverse maps F and R must preserve the set of valid states. Probabilities remain normalized in the classical case, and density operators remain positive and unit-trace in the quantum case. Second, the dynamics proceed in two consecutive halves, with each complete cycle consisting of a forward transformation F immediately followed by its reverse R. Third, the reverse half exactly undoes the forward half, expressed algebraically as

$$R\circ F=\mathbb{I}.$$

(10)

Together these axioms ensure that a full forward–reverse cycle restores the system to its initial state while maintaining internal consistency and causal definiteness.

In the classical setting, F may be taken as a permutation on microstates—a bijective stochastic update—so that $R=F^{-1}$. In the quantum setting, the natural reversible half is unitary conjugation, $F\left(x\right)=Ux{U}^{†}$ with inverse $R\left(x\right)=U^{†}xU$. In both cases, the two halves are exact inverses, and a complete forward–reverse cycle therefore acts as the identity on the state space.

3.1. From Indefinite to Alternating Order

Table 1. Comparison between Indefinite Causal Order (ICO) and Alternating Causality (AC).

Concept	Indefinite Causal Order (ICO)	Alternating Causality (AC)
Relation between $A,B$	Superposition of $A\to B$ and $B\to A$	Oscillation between $A\to B$ and $B\to A$
Temporal model	Non-factorizable process matrix	Periodic reversible process tensor
Reversibility	Implicit via linearity	Explicit via phase alternation
Information flow	Coherent mixture of directions	Deterministic bidirectional feedback

Table 1. Comparison between Indefinite Causal Order (ICO) and Alternating Causality (AC).

Concept	Indefinite Causal Order (ICO)	Alternating Causality (AC)
Relation between $A,B$	Superposition of $A\to B$ and $B\to A$	Oscillation between $A\to B$ and $B\to A$
Temporal model	Non-factorizable process matrix	Periodic reversible process tensor
Reversibility	Implicit via linearity	Explicit via phase alternation
Information flow	Coherent mixture of directions	Deterministic bidirectional feedback

The bidirectional symmetry of Alternating Causality mirrors the Wheeler–Feynman absorber picture, in which every exchange consists of two complementary causal halves: one propagating forward in time and its counterpart propagating in reverse [12]. A causal initiator is the side that emits first; operationally this is a local CPTP perturbation $P_A$ (or $P_B$) inserted before the reversal:

$${\Phi }_A:=R\circ P_A\circ F,P_A=\mathrm{id}+\epsilon {\mathcal{K}}_A+O\left({\epsilon }^2\right),\mathrm{Tr}\circ {\mathcal{K}}_A=0.$$

(11)

In the unperturbed loop $R\circ F=\mathrm{id}$; the insertion (11) sets the time orientation of that cycle. Let $H(·)$ be Shannon/VN entropy and $I(A:B)$ the mutual information across the link’s cut (definitions in Appendix A). With a unitary dilation of the full cycle, total entropy is conserved, $\Delta H_{AB}=0$, and at the instant of initiation the phasewise information flux satisfies

$$J_{A\to B}\left(t\right):={\displaystyle \frac{d}{dt}}I{(A:B)}_t,{\overline{J}}_{A\to B}+{\overline{J}}_{B\to A}=0,$$

(12)

so the initiator’s local entropy increase is balanced by an equal information gain on the opposite side:

$$\Delta H_A=-\Delta H_B,\Delta H_A+\Delta H_B=0(\mathrm{over}\mathrm{a}\mathrm{full}F+R\mathrm{cycle}).$$

(13)

The resulting causal arrow collapses into one of four deterministic modes, represented by idempotent selectors $\{{\Pi }_{\mathrm{AB}},{\Pi }_{\mathrm{BA}},{\Pi }_{\mathrm{AA}},{\Pi }_{\mathrm{BB}}\}$ with $\sum {\Pi }_{\mu }=\mathbb{I}$:

$${\Phi }_{\mathrm{AB}}={\Pi }_{\mathrm{AB}}(R\circ F),{\Phi }_{\mathrm{BA}}={\Pi }_{\mathrm{BA}}(R\circ F),{\Phi }_{\mathrm{AA}}={\Pi }_{\mathrm{AA}}(R\circ F),{\Phi }_{\mathrm{BB}}={\Pi }_{\mathrm{BB}}(R\circ F),$$

(14)

corresponding to forward transfer $A\to B$, reverse transfer $B\to A$, and the two self-mirror cases $A\leftrightarrow A$, $B\leftrightarrow B$. Equations (12)–(13) make it clear that the initiator exports uncertainty (positive $\Delta H$) while the partner imports information, yet the composite evolution remains entropy balanced and time–symmetric.

The Wheeler–Feynman picture let us treat a single exchange as two time-symmetric halves (forward, then echo), with a local initiator choosing which half fires first. That is a dynamical account: phase by phase, one side exports uncertainty while the other imports information, yet the complete forward/echo cycle is entropy balanced and reversible. If we now coarse-grain this cycle to a single “use’’ of the link—suppressing the internal timing and tracing out the microdynamics—we obtain a static object that only answers the operational question: which pairs of local instruments at A and B are jointly compatible? This is precisely what the Oreshkov–Costa–Brukner (OCB) process matrix formalism captures.

Seen this way, Alternating Causality produces (after coarse-graining) a process description that may look like a mixture of different effective orders, because the time labels that distinguished the forward and echo halves have been hidden. Crucially, however, that appearance comes from classical averaging over which half went first in each cycle; the underlying dynamics remained deterministic and time-symmetric. By contrast, Indefinite Causal Order (ICO) refers to situations where no underlying time-resolved account can select a single order or a classical mixture of orders: operational statistics themselves witness causal nonseparability that cannot be explained by coarse-graining a definite alternating sequence. In the next subsection, we switch fully to the OCB language, introduce process matrices, and use them to distinguish this genuinely indefinite regime from the alternating (but ultimately definite) reversible dynamics above.

3.2. Process Tensor Perspective

The OCB process matrix formalism provides a static snapshot of causal relations between two parties: a single-use map that specifies how operations at A and B can be probabilistically composed without presupposing a definite temporal order. In contrast, a physical interaction proceeds through a sequence of locally timed operations. Each node advances according to its own proper-time clock, which defines when inputs are received and outputs are emitted. A full description must therefore account for how causal influence propagates across these discrete local intervals and how earlier exchanges leave traces that shape subsequent ones. The process tensor extends the process matrix into this temporally resolved regime: it records correlations among interventions occurring at successive clock ticks, thereby describing the flow of information between parties as their local clocks advance step by step. This elevates the static W-matrix of OCB into a structured object ${\mathcal{T}}_{k:0}$ that specifies not only who influences whom, but also when each influence occurs within the synchronized lattice of local proper times.

Within Alternating Causality, this tensor naturally splits into two complementary phases,

$${\mathcal{T}}_{k:0}\in \mathcal{L}\left(\underset{i=0}{\overset{k-1}{⨂}}\left({\mathcal{H}}_i^{\mathrm{in}}\otimes {\mathcal{H}}_i^{\mathrm{out}}\right)\right)$$

(15)

$${\mathcal{T}}_{k:0}={\mathcal{T}}_{+}+{\mathcal{T}}_{-}$$

(16)

Where:

$\mathcal{L}(·)$: the space of linear operators on the given Hilbert space (analogous to $B\left(\mathcal{H}\right)$ in operator algebra).

${\mathcal{H}}_i^{\mathrm{in}}$: the input Hilbert space at time step i, representing the system space before an operation.

${\mathcal{H}}_i^{\mathrm{out}}$: the output Hilbert space at time step i, representing the system space after that operation.

${\displaystyle \underset{i=0}{\overset{k-1}{⨂}}}$: the tensor product over all steps $i=0,1,\dots ,k-1$, capturing the multi-time correlations across the entire process.

The transition from a symmetric, oscillatory regime to an observed, directional one marks the emergence of irreversibility. When the causal cavity is closed and perfectly balanced, information circulates without dissipation, maintaining a steady equilibrium between the two halves of the link. When the balance is perturbed by measurement, emission, or boundary asymmetry, one side acquires informational surplus while the other incurs uncertainty, and a local arrow of time appears. To formalize this transition, we now quantify how entropy and information flux behave within a complete alternating cycle and show that, under unitary dilation, the global process remains exactly reversible even though each half may appear thermodynamically biased from its own frame.

3.3. Reversibility and Entropy Production

We adopt the formal definitions of entropy and mutual information from Appendix A, where $H\left(a\right)$ denotes the Shannon entropy of a source, $H\left(a\right|b)$ its conditional entropy, $I\left(ab\right)$ their mutual information, and $H\left(ab\right)$ the joint entropy [1,13,14]. Throughout, logarithms are taken base 2 and all entropies are expressed in bits.

  Entropy balance. Let ${\rho }_{SE}\left(t\right)$ be the joint state of the system S (comprising the nodes $A,B$) and its environment E at time t. If the combined evolution over a cycle of duration $2\tau$ is unitary, ${\rho }_{SE}\left(2\tau \right)=U_{\mathrm{cycle}}{\rho }_{SE}\left(0\right)U_{\mathrm{cycle}}^{†}$, then von Neumann entropy is invariant:

$$S\left({\rho }_{SE}\left(2\tau \right)\right)=S\left({\rho }_{SE}\left(0\right)\right).$$

(17)

Differentiating and integrating over one period gives the fundamental conservation law

$${\Sigma }_{[0,2\tau )}={\int }_0^{2\tau }{\displaystyle \frac{d}{dt}}{S}_{SE}\left(t\right)dt=\Delta S_{\mathrm{sys}}+\Delta S_{\mathrm{env}}=0.$$

(18)

Equation (18) expresses the vanishing of total entropy production: although the subsystem entropies $S_S$ and $S_E$ may vary during each half-cycle, their changes exactly cancel under global unitarity. This condition is the information-theoretic analogue of Clausius’ equality for a reversible thermodynamic cycle.

  Information flux. Let $I{(A:B)}_t=H{\left(A\right)}_t+H{\left(B\right)}_t-H{\left(AB\right)}_t$ be the mutual information between the nodes at local proper time t. The rate of change of $I{\left(AB\right)}_t$ defines an information flux across the causal cut,

$$J_{A\to B}\left(t\right)={\displaystyle \frac{d}{dt}}I{\left(AB\right)}_t,$$

(19)

whose temporal average over a half-cycle is

$${\overline{J}}_{A\to B}={\displaystyle \frac{1}{\tau }}{\int }_0^{\tau }{J}_{A\to B}\left(t\right)dt.$$

(20)

Alternating Causality imposes a strict flux balance:

$${\overline{J}}_{A\to B}+{\overline{J}}_{B\to A}=0.$$

(21)

Equation (21) guarantees that information exchanged in one temporal direction is returned in the next, establishing a steady-state equilibrium analogous to the zero-net-energy condition of a standing electromagnetic wave. Local entropic gradients may exist transiently, but their integral over a full cycle vanishes, confirming that no information is created or destroyed.

  Operator symmetry. The microscopic origin of this balance is the operator identity

$$W_{BA}\left(t\right)=W_{AB}{(-t)}^{†},$$

(22)

which enforces exact time-reversal duality between the forward and reverse causal phases. Each half-cycle corresponds to a completely positive, trace-preserving map on its respective subsystem, while the composite process is unitary on the joint $S+E$ Hilbert space. Any local entropy increase at one node is offset by a corresponding decrease at the other, preserving Eq. (18) and ensuring the process remains on the reversible manifold of the CPTP set.

  Logical reversibility and causal computation. This structure realizes Bennett’s principle of logical reversibility: each causal operation has a unique inverse and thus erases no information [15]. The forward transformation F and its reverse R satisfy

$$R\circ F=\mathbb{I}.$$

(23)

Here F plays the role of a computational write step, encoding the mapping $A\to B$; R performs the exact uncomputation, restoring the pre-image by reversing the order of local operations. Viewed dynamically, the causal channel behaves as a Turing machine with two time-reversed tapes evolving along opposite directions of proper time. At the midpoint of the cycle, the two tapes coincide, no net entropy is produced, and all logical states remain accessible from both temporal boundaries. This correspondence extends Bennett’s reversible computation to physical causation: Alternating Causality acts as a reversible information engine in which entropy is not dissipated but exchanged symmetrically between temporal phases, conserving total information and maintaining exact time-reversal symmetry.

3.4. Geometric Interpretation

In Indefinite Causal Order, causal direction is undefined: the underlying structure exists in a superposition of orders. In Alternating Causality, causal direction is phase-linked: it alternates coherently, like a standing wave exchanging energy between two reflectors. Each causal link thus behaves as a causal resonator, sustaining equilibrium between forward and backward propagation.

This viewpoint connects directly to time-symmetric electrodynamics and to the reversible signaling logic used in Open Atomic Ethernet (OAE) link design.

The causal resonator picture also provides a geometric analogue of the “photon clock” model: a photon confined between two mirrors embodies a reversible, alternating causal process whose external measurement collapses to a single direction of time.

Alternating Causality therefore unifies two paradigms: the quantum-informational notion of causal symmetry and the computational requirement of logical reversibility. In this sense, AC can be regarded as the causal analogue of a unitary gate: time evolution preserves information and admits a well-defined inverse.

Section 4 will develop the information-theoretic realization of Alternating Causality as Perfect Information Feedback (PIF) on reversible physical links, demonstrating that the framework is not only mathematically self-consistent but also physically implementable in deterministic signaling networks.

4. Perfect Information Feedback: Constructing the Bidirectional Channel

While Section 3 treated Alternating Causality (AC) as a generalization of the Oreshkov–Costa–Brukner process matrix, we now translate it into the language of information theory. The central idea is that every reversible causal interaction can be described as a form of Perfect Information Feedback (PIF): a closed two-way channel in which the receiver continuously confirms the sender’s transmitted state.

This feedback symmetry provides an explicit physical mechanism for alternating causality. Where ordinary communication channels rely on error detection and correction that operate after the fact, a PIF channel maintains instantaneous correlation between transmission and reception, producing a self-verifying exchange.

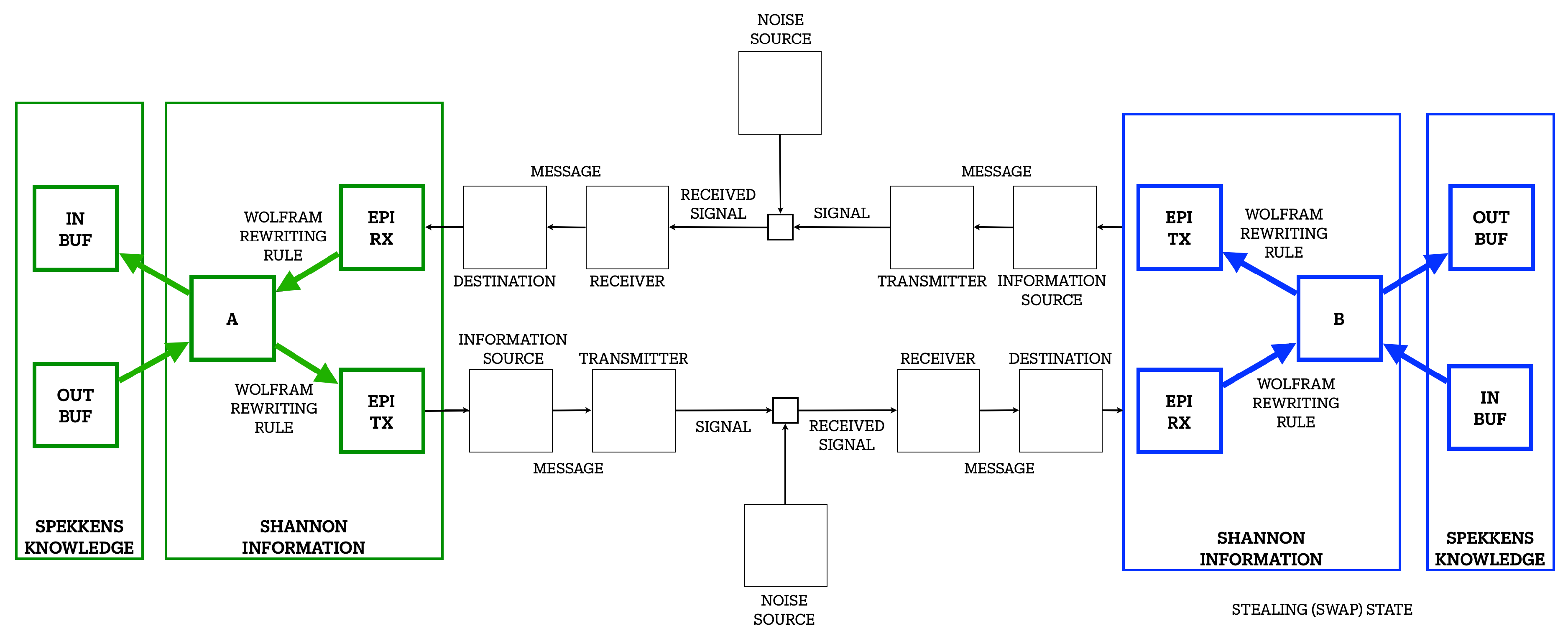
The bidirectional channel of Figure 6 establishes the physical foundation of Perfect Information Feedback: two conjugate communication paths maintaining mutual state through continuous reflection. We now translate this symmetry into information-theoretic form. In Shannon’s original formulation, the information content of an event is given by the term $-plogp$, defined for a single, forward-directed flow of probability. However, a reversible channel necessarily contains both the forward and its conjugate, retrocausal component. Each transmitted symbol therefore carries a pair of informational amplitudes—p for the forward half and $-p$ for the reverse—whose contributions cancel when combined.

In what follows, this idealized construction serves as the reference frame for analyzing real channels. Introducing noise, delay, or partial reflection will be shown to break the conjugate symmetry between $p_i^{(+)}$ and $p_i^{(-)}$, producing finite entropy and an apparent arrow of time.

4.1. Information Theoretic Model of PIF

Figure 7. Shannon communication system extended to a bidirectional Perfect Information Feedback (PIF) configuration. Forward and reverse channels form conjugate halves of a reversible exchange. In the noise-free limit, total information flux is conserved; symmetric perturbations (${\delta }_i,{ϵ}_i$) from the shared noise source break this balance, producing entropy.

Figure 7. Shannon communication system extended to a bidirectional Perfect Information Feedback (PIF) configuration. Forward and reverse channels form conjugate halves of a reversible exchange. In the noise-free limit, total information flux is conserved; symmetric perturbations (${\delta }_i,{ϵ}_i$) from the shared noise source break this balance, producing entropy.

We begin by constructing the simplest reversible communication link: two conjugate channels operating in opposite directions. Each endpoint alternately acts as transmitter and receiver, so that every symbol launched in one direction is immediately mirrored by a corresponding acknowledgment in the other. This closed loop forms a self-consistent, bidirectional channel analogous to a standing electromagnetic cavity. No external clock or global time reference is required; synchronization arises naturally from the mutual reflection of state between the two sides.

Let $X\left(t\right)$ and $Y\left(t\right)$ denote the instantaneous logical states of the two agents. In a conventional forward-in-time channel, information flows only from X to Y:

$$X\to Y,I\left(XY\right)=H\left(X\right)-H\left(XY\right).$$

(24)

To complete the feedback loop, we introduce the reverse channel $Y\to X$ that carries the conjugate correlation:

$$I_{+}\left(XY\right)=I_{-}\left(YX\right),{\displaystyle \frac{d{I}_{+}}{dt}}+{\displaystyle \frac{d{I}_{-}}{dt}}=0.$$

(25)

Together these two directions form a closed informational system in which the total mutual information is conserved. In the ideal, noise-free limit, the forward and reverse probability amplitudes are exact conjugates,

$$p_i^{(-)}=-p_i^{(+)},$$

(26)

so that their informational contributions cancel,

$$I_{\mathrm{total}}=-\sum _i\left[p_i^{(+)}log{p}_i^{(+)}+p_i^{(-)}log\left|p_i^{(-)}\right|\right]=0.$$

(27)

This condition defines the Perfect Information Feedback (PIF) limit: a fully reversible, two-way Shannon channel in which uncertainty and confirmation are perfectly balanced.

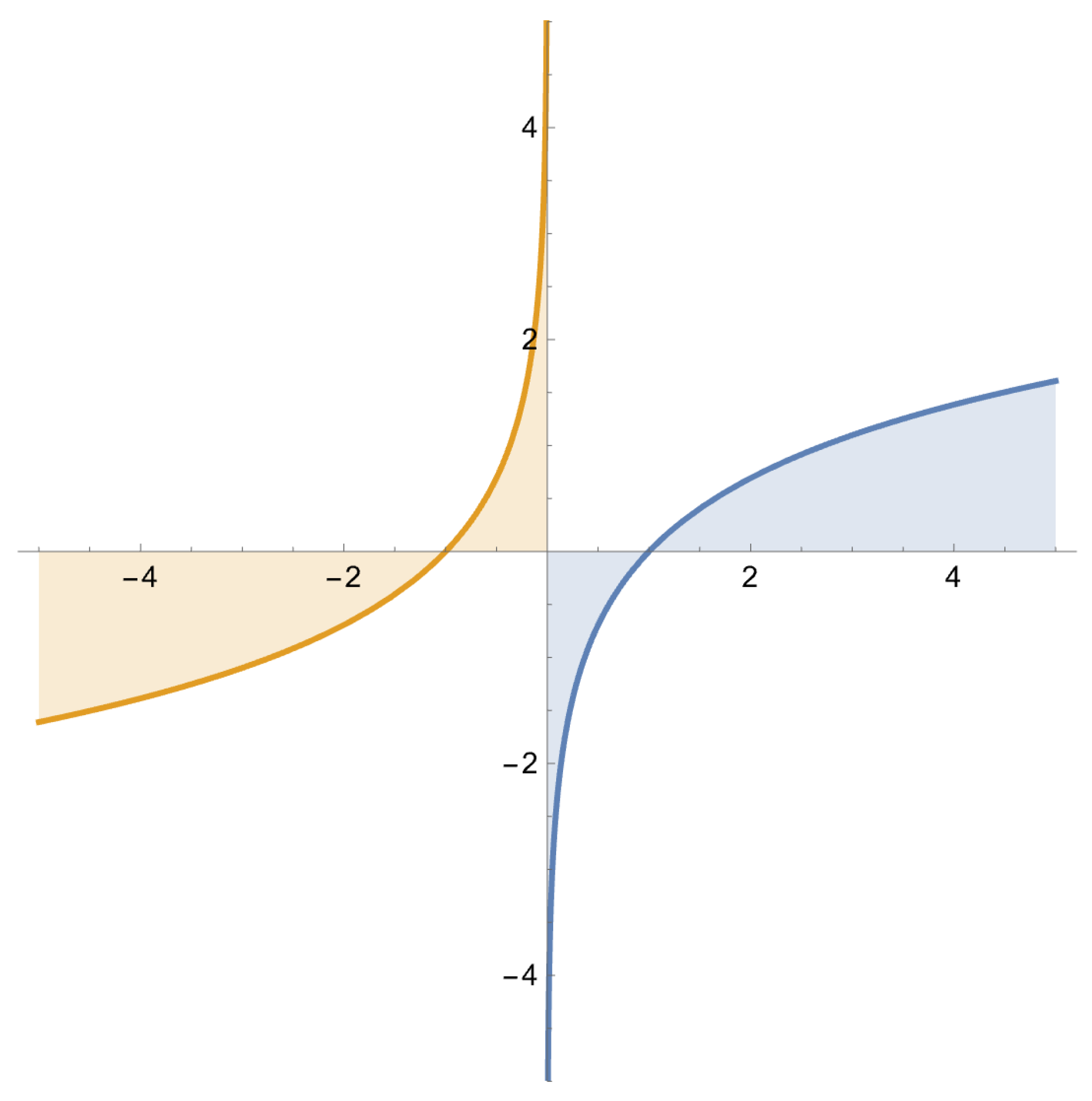
Figure 8. In Shannon’s formulation, each event with probability p contributes an information term $-plogp$, representing the expected surprise associated with its occurrence. Log is undefined for $p<0$, so $-log(-p)$ corresponds to a reflection across $y=x$, and the inverse of $log\left(p\right)$.

Figure 8. In Shannon’s formulation, each event with probability p contributes an information term $-plogp$, representing the expected surprise associated with its occurrence. Log is undefined for $p<0$, so $-log(-p)$ corresponds to a reflection across $y=x$, and the inverse of $log\left(p\right)$.

Following Shannon, view a channel as a sequence of discrete uses (slots) indexed by $n\in \mathbb{Z}$. Let $I_n(A:B)$ denote the mutual information across a chosen cut during slot n. For each edge e of the link graph, define the slot flux

$$J_e\left[n\right]:=I_{n+1}\left(AB\right){|}_e-I_n\left(AB\right){|}_e,$$

(28)

the net information pushed across e from $n\to n+1$ (edge–resolved contribution to the cut). In the noise free PIF regime, conservation holds slotwise at every internal node v:

$$\sum _{e\in \mathrm{in}\left(v\right)}{J}_e\left[n\right]=\sum _{e\in \mathrm{out}\left(v\right)}{J}_e\left[n\right]\forall n,$$

(29)

and reversibility enforces a loop constraint on any closed causal cycle $\Gamma$ within one forward–echo pair:

$$\sum _{e\in \Gamma }\Delta {\Phi }_e\left[n\right]=0,\Delta {\Phi }_e\left[n\right]:={\Phi }_e[n+1]-{\Phi }_e\left[n\right],$$

(30)

where ${\Phi }_e$ is an information potential attached to e (e.g., surprisal $-logp$ or a log–likelihood ratio). Together, (29)–(30) state that, per slot, information neither accumulates at nodes nor builds net “bias” around loops: the standing–wave picture of PIF.

4.2. Effects of Noise

With noise (erasures, phase slips, timing jitter), forward and reverse path weights on e need not match. Define the information affinity

$${\mathcal{A}}_e\left[n\right]:=ln{\displaystyle \frac{{\mathbb{P}}_e^{(+)}\left[n\right]}{{\mathbb{P}}_e^{(-)}\left[n\right]}},$$

(31)

and the (Schnakenberg-type) slot entropy production

$$\sigma \left[n\right]=\sum _e{J}_e\left[n\right]{\mathcal{A}}_e\left[n\right]\ge 0.$$

(32)

Node balance then includes an environmental leak $J_{E,v}\left[n\right]\ge 0$:

$$\sum _{e\in \mathrm{in}\left(v\right)}{J}_e\left[n\right]-\sum _{e\in \mathrm{out}\left(v\right)}{J}_e\left[n\right]=-J_{E,v}\left[n\right],$$

(33)

and loop sums register the net affinity,

$$\sum _{e\in \Gamma }\Delta {\Phi }_e\left[n\right]=\sum _{e\in \Gamma }{\mathcal{A}}_e\left[n\right]\ne 0.$$

(34)

In the ideal PIF limit, ${\mathcal{A}}_e\left[n\right]=0$ for all $e,n$, so $\sigma \left[n\right]=0$ and both Kirchhoff laws (29)–(30) are restored per slot. Intuition. PIF behaves like a lossless AC network at steady state whereas noise introduces resistive drops that convert balanced standing waves into directed, entropy-producing flow.

An incorrect symbol is not “pure loss”; it is a surprisal event1. Its likelihood $p_{\mathrm{err}}$ contributes evidence $-log{p}_{\mathrm{err}}$ that something in the forward–echo pair has decohered. In a hardware implementation, the slice-level echo and comparator turn that evidence into a local trigger: the nodes can (i) mark the offending slot/slice, (ii) exchange minimal reverse messages (ACK/NACK, checksums, or syndrome bits), and (iii) roll back only the affected portion and replay with stronger protection (re-encode, interleave, escalate redundancy). This successive reversibility confines repair to the smallest inconsistent region, converting raw surprisal into guidance for recovery. Thus even when the original payload instance is unrecoverable in that pass, the event itself supplies the side information needed to restore information balance and alignment on the next pass.

4.3. Capacity and Composition in Slots

Let $C_{+}$ and $C_{-}$ be the forward/reverse capacities in bits/slot. A phase-locked PIF link satisfies $C_{\mathrm{PIF}}=C_{+}+C_{-}$ with $C_{+}=C_{-}$ in the balanced case; noise reduces $C_{\mathrm{PIF}}$ via the penalty $\langle \sigma \left[n\right]\rangle$. Series/parallel composition of links preserves equations (29)–(30) when interfaces are slot and phase aligned, so contracting any zero-EP subgraph yields an equivalent PIF edge. This forms the basis of a “nestable, composable” Alternating Causal Graph in discrete time.

In the Shannon sense, the channel capacity for such a reversible link doubles the degrees of freedom available for encoding:

$$C_{\mathrm{PIF}}=2C_{\mathrm{one}-\mathrm{way}},$$

(35)

4.4. Nestability and Composability of PIF Links

Let $L_1$ and $L_2$ be PIF links with forward/reverse halves $(F_1,R_1)$ and $(F_2,R_2)$. They are compatible when their boundary clocks and phases align so that the downstream reverse half mirrors the upstream forward half:

$$\mathrm{Clock}/\mathrm{phase}\mathrm{lock}\text{:}{\varphi }_1\left(t\right)={\varphi }_2\left(t\right),\mathrm{and}{R}_1\simeq F_2^{-1}(\mathrm{up}\mathrm{to}\mathrm{slot}\mathrm{delay}).$$

(36)

More generally, for multi-rate operation there exist integers $m_1,m_2\ge 1$ such that one outer slot equals $m_1$ inner slots of $L_1$ and $m_2$ of $L_2$, with phase alignment at the shared boundary.

Series composition (closure).: If $L_1,L_2$ are compatible and each satisfies $R_i\circ F_i=\mathrm{id}$, then the series composite

$$F_{\mathrm{series}}:=F_2\circ F_1,R_{\mathrm{series}}:=R_1\circ R_2$$

(37)

is again PIF:

$$R_{\mathrm{series}}\circ F_{\mathrm{series}}=(R_1\circ R_2)\circ (F_2\circ F_1)=\mathrm{id}.$$

(38)

Hence, with slotwise conservation (29)–(30) holding on each link, entropy production and mutual-information flux sum to zero over the composite cycle.

Parallel composition (independent branches): For disjoint links $L_a,L_b$,

$$(F_a\otimes F_b,R_a\otimes R_b),(R_a\otimes R_b)\circ (F_a\otimes F_b)=\mathrm{id},$$

(39)

and capacities add while ideal entropy production remains zero:

$$C_{\mathrm{tot}}=C_a+C_b,{\Sigma }_{\mathrm{tot}}=0.$$

(40)

Nested composition (encapsulation): A PIF module is any subgraph G with boundary ports $\partial G=\{p_{\mathrm{in}},p_{\mathrm{out}}\}$ that, over an integer number of inner slots per outer slot, satisfies: (i) slotwise node balance and loop neutrality (29)–(30) at the boundary, and (ii) zero net entropy production per complete forward–echo pair at the boundary. Such a module is contractible: there exists an effective edge $E\left(G\right)$ with halves $(F_G,R_G)$ whose boundary traces reproduce the observed boundary fluxes and echoes of G. Contractibility is associative and context-preserving: replacing any subgraph by $E\left(G\right)$ leaves all external measurements of flux, capacity, and (ideal) entropy balance unchanged. Thus, a bidirectional channel can be built out of bidirectional channels: PIF is closed under hierarchical encapsulation.

Nesting supports multiple levels of semantic and informational reversibility. A lower layer (symbols/slices) provides immediate echoes to detect physical mismatches; a middle layer (frames/transactions) aggregates slice-level surprisal into targeted rollbacks; an upper layer (application semantics) confirms invariants (e.g., exactly-once) via lightweight reverse checks. Errors are not “pure loss’’—they are surprisal events that supply side information to localize and repair. Because each layer is itself a PIF module, recovery remains confined to the smallest inconsistent region and composes cleanly: inner-layer corrections restore alignment so outer layers rarely need to escalate. In this way, bidirectional links within bidirectional links yield robust, nestable channels whose reversibility extends from bits on the wire to application APIs.

4.5. Alternating Causal Graphs

On an Alternating Causal Graph (ACG) with nodes $\mathcal{V}$ and oriented edges $\mathcal{E}$, let ${\overline{J}}_e$ be the half-cycle–averaged flux on e. PIF imposes a Kirchhoff-like conservation at every internal node v:

$$\sum _{e\in \mathrm{in}\left(v\right)}{\overline{J}}_e-\sum _{e\in \mathrm{out}\left(v\right)}{\overline{J}}_e=0,$$

(41)

and along any closed cycle $\Gamma$,

$${\oint }_{\Gamma }Jdt=0.$$

(42)

If a nested subgraph obeys these boundary equalities over whole-slot pairs (possibly at a slower outer timescale), it may be contracted to a single PIF edge without changing the rest of the graph.

4.6. Thermodynamic Perspective

In ordinary communication theory, entropy production is tied to irreversible encoding, lossy decisions, and noise dissipation. In a PIF system, the budget is ideally zero: each forward update is immediately mirrored, so exchange is balanced slot by slot and the composite evolution is reversible.2

Figure 9. Shannon Slots.

Figure 9. Shannon Slots.

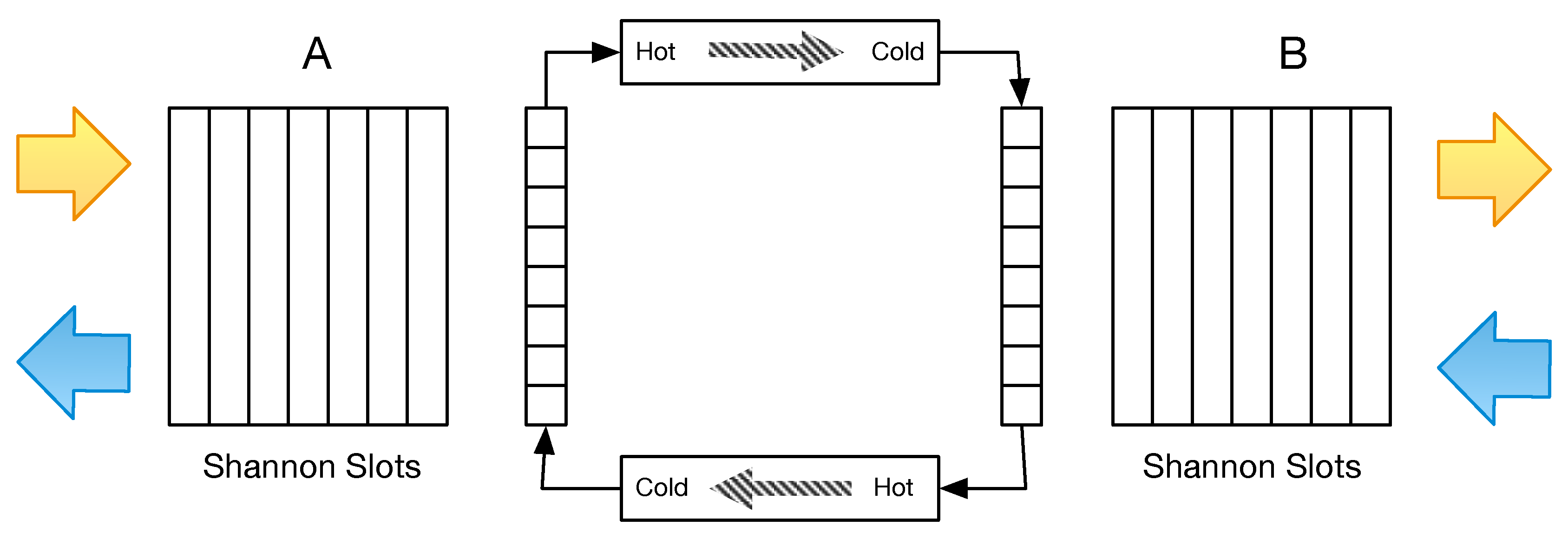
A transmitter (HOT) injects quanta into a guided cavity (cable/fiber pair, connectors, package parasitics) while a receiver (COLD) absorbs a small fraction. During each bit period, the cavity modes fill to a quasi-steady standing wave set by the SERDES bit clock and the ASIC clock tree. Energy flows down the HOT→COLD gradient, yet time’s direction is not fixed by the physics of the cavity: it is imposed operationally by how we terminate the ports and schedule who “goes first.”

The receiver does not read the waveform continuously; it takes discrete samples at instants defined by its local clock. A clock-and-data recovery (CDR) loop derives and continuously adjusts this clock so those sampling instants land near the center of each symbol’s eye: a phase detector measures timing error between signal transitions and the local oscillator, a loop filter integrates that error (storing soft timing evidence), and a VCO/DLL shifts the sampling phase until the eye is centered. Once aligned, bits are decided at those instants and transferred across a small elastic buffer into the digital clock domain. In a one-way link, any sampling mistake is resolved by a hard decision at the slicer, discarding soft evidence and dissipating heat. In a PIF link, the echo returns the same timing evidence to the initiator; both ends co-adjust and co-lock on the common standing wave so their sampling instants are mirror-matched across the cavity. Small phase disturbances then circulate as reversible, reactive corrections rather than being burned away as resistive heat.

Figure 10. Transmitting creates entropy. Receiving increases information and decreases entropy.

Figure 10. Transmitting creates entropy. Receiving increases information and decreases entropy.

Landauer’s bound penalizes logically irreversible steps; PIF neither denies nor violates this—it rearranges the pipeline so that soft information is preserved in echoes and loop states, corrections are targeted at the smallest inconsistent slice/slot, and only the net irreversibility appears where synchronization fails or a deliberate final decision is taken. In the reversible limit (no slips, no erasures, soft inference), the link behaves like a conservative dynamical system: information is shuttled, not destroyed, and slotwise conservation (cf. (29)–(30)) holds at the boundary.

Noise, shot fluctuations, phase slips, and timing jitter break detailed balance: forward and reverse paths no longer carry identical weights, and an unexpected symbol or timing excursion occurs—a surprisal event. Surprisal is not “pure loss’’; its improbability is diagnostic. With an echo and comparator, the nodes treat that event as side information: they localize the fault (which edge, which slice/slot) and trigger the minimal reverse exchange (ACK/NACK, syndrome, re-timing) that rolls back only the affected micro-interval. Even when a particular payload instance is unrecoverable in that pass, the event seeds the next pass with exactly the evidence needed to realign.

Two PLLs facing each other across a bidirectional cavity are thermodynamically analogous to reactive tanks coupled by an ideal transformer: the forward drive builds phase on one side while the echo builds the equal-and-opposite mirror on the other. At two-sided lock, the net entropy flow over a forward–echo pair is zero; only imbalance introduces a resistive component, visible as loop error, excess jitter, or decoding heat. Conventional Alternating Bit Protocols (ABP) handles that imbalance after the fact with bulk retransmissions; PIF addresses it in the act at slice granularity, confining dissipation to the smallest place and time.

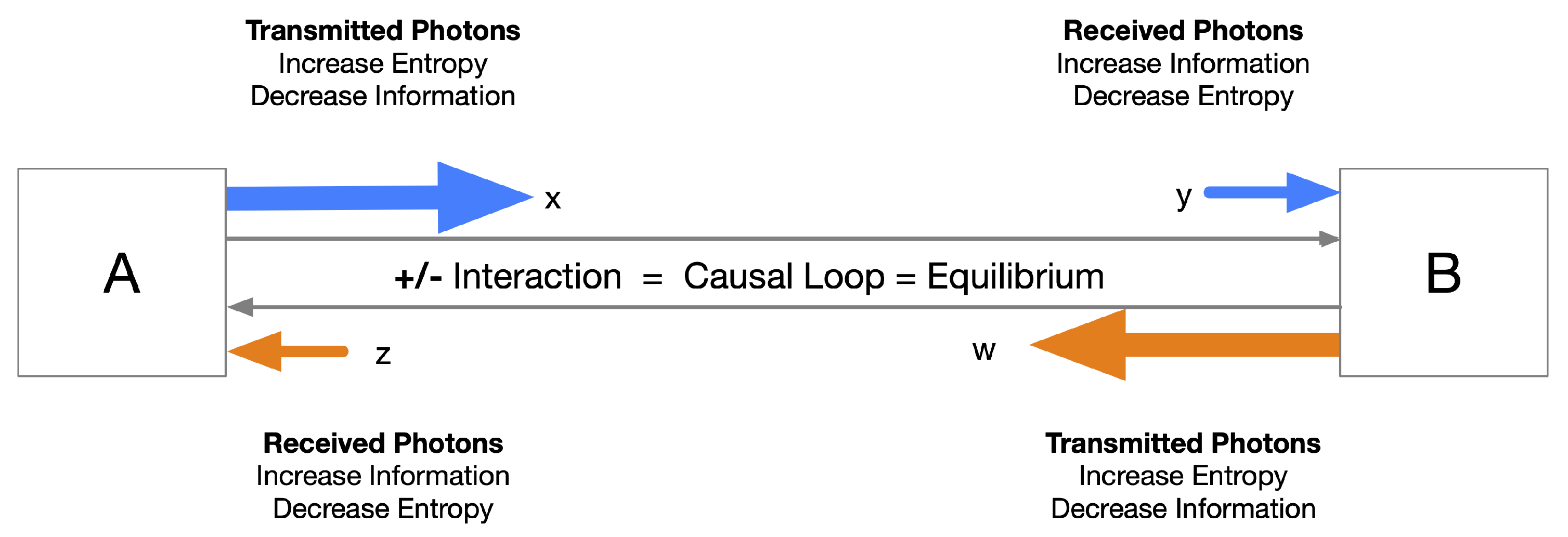
There is no intrinsic direction of time in this picture. The apparent arrow of causality is imposed by the designer who connects TX/RX asymmetrically. A pair of back-to-back channels naturally reflects TX/RX symmetry, turning each Shannon channel (originally one-way) into a bidirectional flow between Alice and Bob. Alice’s entropy becomes Bob’s information, and Bob’s information becomes Alice’s entropy; in the ideal, phase-locked regime these balance exactly over each forward–echo cycle.

5. Toward a Unified Reversible Causal Principle

This section consolidates the preceding analyses into a single formal symmetry: the Reversible Causal Principle (RCP). Sections 3–4 examined Alternating Causality from four complementary domains—the formal structure of process matrices, the informational symmetry of Perfect Information Feedback, the time-symmetric dynamics of physical fields, and the topology of Alternating Causal Graphs. RCP unifies these views by asserting that every causal interaction $A\leftrightarrow B$ admits a time-reversed conjugate satisfying

$${\mathcal{P}}_{BA}\left(t\right)={\mathcal{P}}_{AB}{(-t)}^{†},$$

and that any closed causal loop obeys

$${\oint }_{\Gamma }d\varphi =0.$$

These relations express local reversibility and global causal neutrality, extending Noether’s logic from mechanics to information:

$$\mathrm{time}-\mathrm{symmetry}\Rightarrow \mathrm{energy}\mathrm{conservation},\mathrm{causal}-\mathrm{symmetry}\Rightarrow \mathrm{information}\mathrm{conservation}.$$

The principle is cast in an operator form

$$\mathcal{R}\left(t\right)={\mathcal{T}}_{+}\left(t\right)+{\mathcal{T}}_{-}{(-t)}^{†},$$

whose unitarity condition,

$$\langle \psi \left|{\mathcal{R}}^{†}\mathcal{R}\right|\psi \rangle =\mathrm{const}.,$$

guarantees conservation of total informational amplitude. Departures from unitarity correspond to entropy generation or causal decoherence. A cross-domain correspondence links this invariance to familiar constructs: Hermitian process matrices in quantum theory, mutual-information balance in Shannon channels, advanced–retarded field superposition in electrodynamics, and zero net causal flux in topological cycles. In each case, irreversibility appears as the non-vanishing of an asymmetry term.

Within this framework, the arrow of time emerges from the entropy generated around the network rather than axiomatically. When boundary conditions or noise impede perfect reflection

$${\mathcal{T}}_{-}{(-t)}^{†}\ne {\mathcal{T}}_{+}\left(t\right)$$

(43)

a small imaginary term $iϵ$ enters the action, breaking time-reversal invariance and yielding measurable entropy. The macroscopic flow of time thus represents the universe’s imperfect causal echo [2,16]. RCP therefore provides a compact grammar linking Shannon’s communication symmetry [1], Wheeler–Feynman absorber dynamics, and Bennett’s reversible computation [15,17,18] under a single conservation law of information.

6. Conclusions

Under the Reversible Causal Principle (RCP) explored in this work, symmetry in causal direction elevates information to the status of a conserved quantity. In a perfectly time-symmetric (reversible) interaction, the present state retains all the encoded details of its past states. Nothing of the initial information is truly lost or irretrievably dissipated; the evolution is invertible, and every effect can in principle be traced back to its cause. In this sense, information behaves analogously to an invariant of motion, preserved by the bidirectional symmetry of cause and effect

For a more concrete intuition, we can draw an analogy with communication theory. Reliable communication protocols intrinsically rely on two-way exchange: a sender transmits data and the receiver returns an acknowledgment, incurring a measurable round-trip latency. This bidirectional feedback loop ensures that information sent is information received and confirmed. Every bit of data is effectively “spoken” by the sender and “heard” by the receiver, who then responds with an ACK. In effect, the channel enforces a causal symmetry: the forward flow of information is mirrored by a return flow, preventing a one sided dissipation of the message. Such mechanisms guarantee that no information is lost in transit without leaving a trace, much like a reversible physical process guarantees that no information vanishes without a record in the system’s state. What might appear as a mere engineering detail (the necessity of acknowledgments and handshakes) is, in essence, the communication system’s insistence on a minimal form of causal reversibility to preserve information.

At steady state, a well-designed channel operates in a mode akin to detailed balance in physics: for every packet or signal sent from one end, an acknowledgement or return signal is sent from the other, so that each elementary “action” is paired with an opposing action. No unbounded accumulation of unacknowledged packets occurs; likewise, no net loss of information transpires. In this ideal lossless exchange, the information flow reaches a kind of dynamic equilibrium, maintaining maximum throughput without degradation. By contrast, delays, packet loss, or dissipation of signals indicate a breach of this symmetry and a departure from equilibrium. An unacknowledged or lost message is the communication analog of an irreversible process: information escapes into an unrecoverable form (noise or delay), much as erasing a bit of information in a computational system dissipates a minimum amount of heat into the environment.

The experimental test of RCP lies in systems that sustain near-perfect bidirectional feedback: reversible digital links, quantum-switch interferometers, and symmetric electromagnetic or superconducting cavities. The predicted signature is not merely energy conservation but the suppression of informational entropy through phase coherence between alternating directions.

RCP reframes reliability as a symmetry law: a link is “good” not merely when signals are strong in the forward direction but when every assertion is promptly closed by a confirmation. Practically, this means designing for echo quality as carefully as for SNR, budgeting latency as the unavoidable price of certainty, and treating acknowledgments and handshakes as constitutive features of a lossless medium. Whether implemented as slice-by-slice echo verification in digital links, echo-locked electromagnetic cavities, or protocol stacks that preserve invertibility at each slot, the prescription is the same: maximize alternating causality to conserve information.

Appendix A.1. Local Observer Entropy

Entropy in network theory is typically taken to be Shannon Information Entropy [1]. Rényi Entropy generalizes this to an infinte class of entropy measures with values of $\alpha \in \mathbb{R}$ where $0\le \alpha \le \infty ]$.

In [13] Rényi defined an expression for the entropy of order $\alpha$ of a distribution X where X is represented as a list of probabilties $X=(p_1,\dots ,p_n)$

$$H_{\alpha }\left(X\right)=H_{\alpha }(p_1,\dots ,p_n)={\displaystyle \frac{1}{1-\alpha }}{log}_2\left(\sum _{i=1}^n{P}_i^{\alpha }\right),\alpha \ge 0,\alpha \ne 1$$

From this infinite set of entropy measures, the two measures of interest for communications networks are Shannon Information Entropy with $\alpha =1$ and Min Entropy with $\alpha =\infty$ which gives a measure of the security of secret values such as keys used in cryptographic protocols.

$$H_1\left(X\right)=H_1(p_1,\dots ,p_n)=-\sum _{i=1}^n{p}_i{log}_2\left(p_i\right)$$

$$H_{\infty }\left(X\right)=H_{\infty }(p_1,\dots ,p_n)=-{log}_2\left(max\left(p_i\right)\right)$$

A notable feature of all Rényi entropy measures is that they are all a function of a static distribution.

A sequence of symbols transmitted over a network is not constrained to be I.I.D. (Independent and Identically Distributed) and so does not typically have a static distribution. Quantum entanglement behavior in physical systems mean that no generator is free of correlation and so no generator is genuinely I.I.D. while extractor theory permits methods to approximate an I.I.D. distribution arbitrarily closely.

Any sequence of random symbols that can be generated from a birth-death Markov chain generator will, except for 2 state, fully symmetric configurations, be non I.I.D. and so will have a distribution that changes with the reception of each symbol, which gives the receiver information about the current active state in the Markov generator [19].

For the purposes of practically characterizing entropy of a Shannon channel or a sequence of non I.I.D. symbols, it is sufficient to average over a number of symbols where a static distribution will be asymptotically reached as the number of symbols increases.

For example, a simple 2 state Markov generator creating binary symbols with equal probability of 0.5 and a negative serial correlation coefficient of 0.2. The min entropy of a generated bit will be 1 bit when the observer is ignorant of the previous bit but the min entropy will be lower if the previous bit is taken into account [20].

$$P_{max}=max{\left(\left({\displaystyle \frac{SCC}{2}}+0.5\right),1-\left({\displaystyle \frac{SCC}{2}}+0.5\right)\right)}^n$$

$$H_{\infty }\left(X\right)=-lo{g}_2\left(P_{max}\right)$$

In the example with $SCC=-0.2$ and single bit symbols, the entropy per bit is:

$$P_{max}=max\left(\left({\displaystyle \frac{-0.2}{2}}+0.5\right),1-\left({\displaystyle \frac{-0.2}{2}}+0.5\right)\right)=0.6$$

$$H_{\infty }\left(X\right)=-lo{g}_2\left(0.6\right)\approx 0.737$$

However the most probable symbol is alternating between 0 and 1.

Accumulating generated bits into groups of 8 bits forming bytes for symbols, we find the most probable symbols will be 0x55 and 0xAA representing the alternating bits patterns of 01010101 and 10101010. These symbols are equiprobable and so the distribution of most probable symbols is static, even though the underlying single bit distribution is not static.

In our example, the 8 bit min entropy per symbol will be:

$$P_{max}=max{\left(\left({\displaystyle \frac{-0.2}{2}}+0.5\right),1-\left({\displaystyle \frac{-0.2}{2}}+0.5\right)\right)}^8$$

$$H_{\infty }\left(X\right)=-lo{g}_2\left(P_{max}\right)\approx 4.087$$

These equations can be extended for more complex Markov models of generator processes. An example analyzing a physical bit generator with an infinite Markov model as the limit is given in [21].

In this paper, where the term entropy is used without qualification, it is referring to Shannon Entropy.

Another variation on terminology is "Entropy Rate" which is defined as the Entropy in a group of n symbols divided by n. This corresponds to the average entropy per symbol.

$$\mathrm{Entropy}\mathrm{Rate}\mathrm{of}X={\displaystyle \frac{H_{\alpha }\left(X\right)}{n}}$$

Appendix A.2. Mutual Information

In the context of Shannon entropy, we have source x and receiver y entropy defined as:

$$\begin{array}{cc}\hfill H\left(x\right)=& -\sum p\left(x\right)log\left(p\right(x\left)\right)\hfill \end{array}$$

(A1)

$$\begin{array}{cc}\hfill H\left(y\right)=& -\sum p\left(y\right)log\left(p\right(y\left)\right)\hfill \end{array}$$

(A2)

From this we can derive the two equivocations $H\left(x\right|y)$ and $H\left(y\right|x)$ :

$$\begin{array}{cc}\hfill H\left(x\right|y)=& -\sum \sum \left(p\right(xy\left)log\right(p(x/y)\left)\right)\hfill \end{array}$$

(A3)

$$\begin{array}{cc}\hfill H\left(y\right|x)=& -\sum \sum \left(p\right(y\left|x\right)log\left(p\right(y/x\left)\right)\hfill \end{array}$$

(A4)

We can derive information transfer $I\left(xy\right)$ :

$$\begin{array}{cc}\hfill I\left(xy\right)=& \sum \sum (p\left(xy\right)log\left({\displaystyle \frac{p\left(xy\right)}{p\left(x\right)p\left(y\right)}}\right)\hfill \end{array}$$

(A5)

$$\begin{array}{cc}\hfill =& H\left(x\right)-H(x/y)\hfill \end{array}$$

(A6)

$$\begin{array}{cc}\hfill =& H\left(y\right)-H(y/x)\hfill \end{array}$$

(A7)

From these we can define joint or mutual entropy $H\left(xy\right)$ as:

$$\begin{array}{cc}\hfill H\left(xy\right)=& -\sum \sum (p\left(xy\right)log\left({\displaystyle \frac{p\left(xy\right)}{p\left(xy\right)}}\right)\hfill \end{array}$$

(A8)

$$\begin{array}{cc}\hfill =& H(x/y)+H(y/x)+I\left(xy\right)\hfill \end{array}$$

(A9)

In this paper, $H\left(a\right)$, $H\left(a\right|b)$, $I\left(ab\right)$ and $H\left(ab\right)$ are used with these definitions [14].