Buckling Analysis of Extruded Polystyrene Columns with Various Slenderness Ratios

1. Introduction

Foamed plastics have been conventionally used as heat-insulating materials and cushioning materials, owing to their high thermal insulation and lightweight properties, respectively [1,2]. In addition, they have found use in construction for floors and walls in housing because they are free from formaldehyde, a cause of sick building syndrome, as well as efficiently attenuating seismic forces [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. As the use of foamed plastics in construction increases, it is essential to gain a deeper insight into their mechanical properties. In particular, when they are used for walls, axial load is inevitably applied along the length direction, raising concerns of collapse owing to buckling deformation. To address this, it is important to characterize the buckling properties of foamed plastics.

Several studies have investigated the buckling properties of composite materials where foamed plastics were used as a sandwich core [20,21,22], but few have explored the buckling properties of the foamed plastics themselves. Their buckling behaviors have often been ignored because they have not conventionally been used as structural materials but rather as thermal insulation materials, as described above. In fact, it is difficult to find characterization methods in major standards, including the International Organization for Standardization (ISO), ASTM International, and Japanese Industrial Standards (JIS). Although a method for detecting buckling load is standardized for continuous ceramic matrix composites in ISO 20504:2006 [23] and JIS R 1673:2007 [24], the principal aim of these standards is the prevention of buckling. This lack of standardization for foamed plastics specifically makes characterizing their buckling properties more difficult. In addition, the methods typically applied to analyze buckling behavior are well-established; therefore, many researchers might not consider buckling analysis to be novel. However, as described above, buckling behaviors cannot be ignored, as the frequency of using foamed plastics as construction materials is increasing. When foamed plastics are used for walls, it is important to analyze plate buckling behaviors, which are more complex than column buckling behaviors, but even the latter remain insufficiently elucidated.

The buckling properties of columns are usually characterized using the buckling stress (or buckling load) corresponding to the slenderness ratio. In this characterization, actual buckling tests are performed and the relationship between the load and loading-line displacement or that between load and lateral deflection is often used [26,27,28,29]. Otherwise, the strains of the column are measured on both side surfaces, and the buckling is determined when the strain reversal is induced in one surface [30,31]. However, it is often difficult to determine buckling stress precisely using these methods, as detailed below. In previous studies, the authors proposed a method for determining buckling stress using solid wood and cardboard samples with a high slenderness ratio [32,33,34]. This method is promising for determining the buckling stress of foamed plastics while reducing the drawbacks of the conventional methods described above.

Instead of performing buckling tests, buckling stress can be predicted using the stress–strain relationship obtained from compression tests of short columns [25]. In this method, when the slenderness ratio is sufficiently large, the buckling stress is predicted based on classical Euler theory. In contrast, when the slenderness ratio is regarded to be intermediate, the buckling stress is predicted using Engesser–Kármán theory or other empirical formulas [25]. However, the applicability of these methods for foamed plastics, including extruded polystyrene (XPS), has not been well verified

In this study, buckling tests were performed using XPS columns with various slenderness ratios, ranging from intermediate to long, and the buckling stress was analyzed using different three methods. In addition, compression and three-point bending tests were performed independently of the buckling tests, and the data obtained from them were also used to predict buckling stress.

2. Theoretical Background

2.1. Buckling Stress Determination

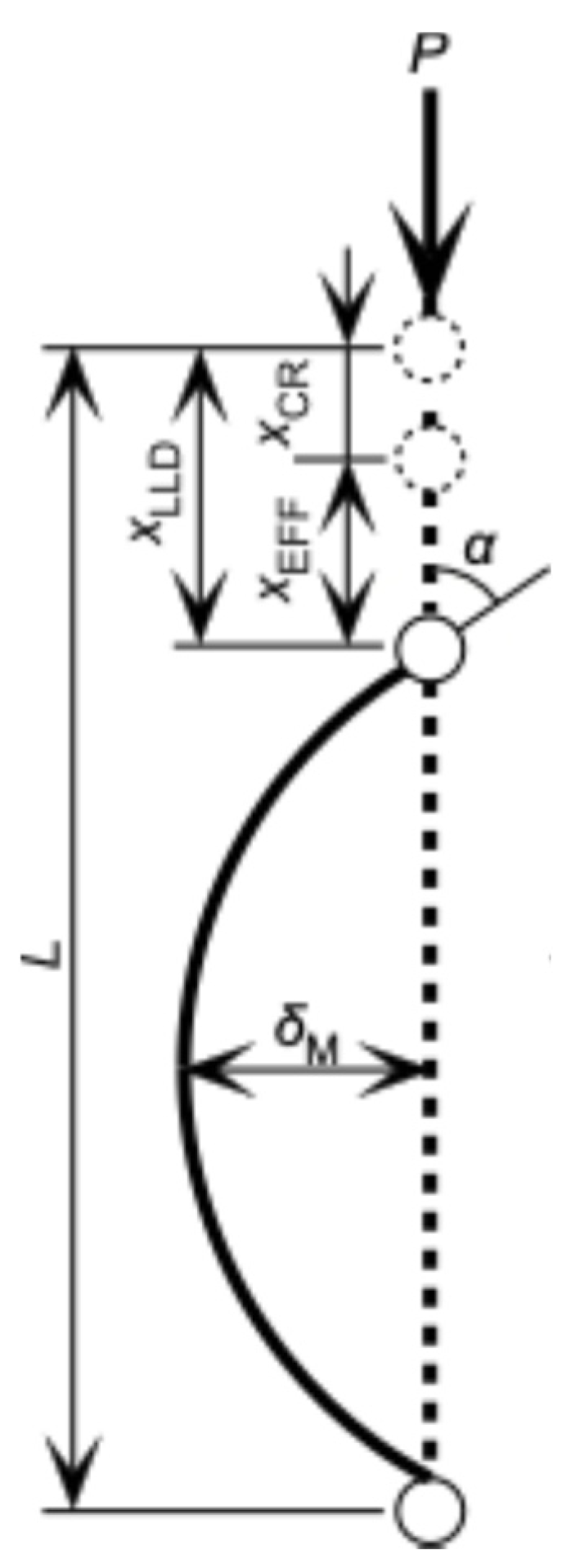
Figure 1 represents a diagram of the column in the pre- and post-buckling conditions. The length, width, and depth of the column are defined as L, B, and H, respectively, whereas the axial load applied to the column and loading-line displacement are defined as P and x_lld, respectively. Based on these definitions, the axial stress induced in the column s_AX is derived as P/(BH). Buckling is induced when s_AX reaches the critical stress for buckling (i.e., buckling stress) s_cr, whereas x_lld at s_AX = s_cr is defined as x_CR

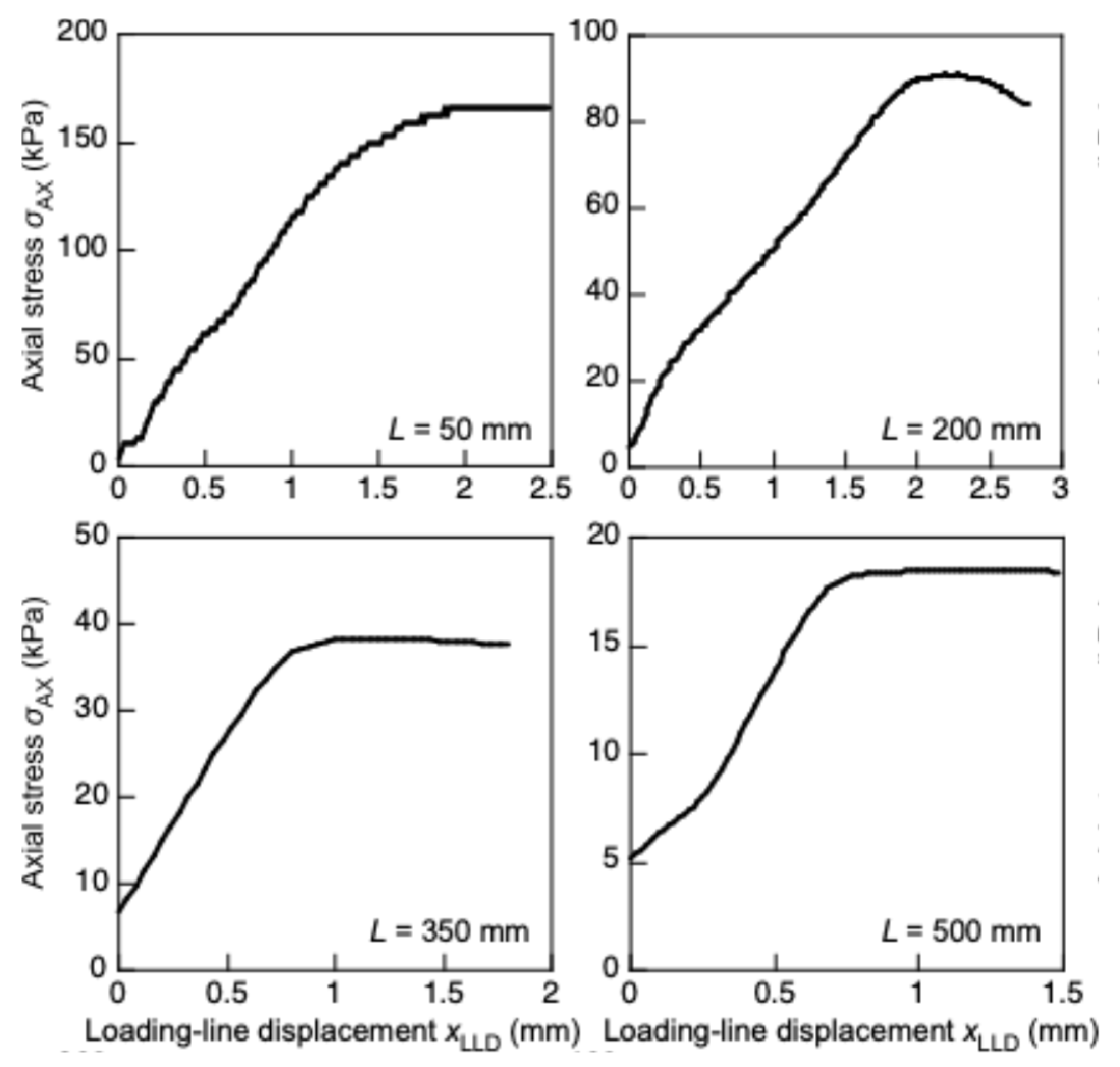
Figure 2 shows the typical s_AX-x_lld relationships obtained under various L in this study, with these relationships including significantly nonlinear and plateau portions. In this experiment, flexural deformation was not visually observed in the linear portion of the relationship. Therefore, buckling was supposed to be induced at a certain load in the post-linear portion. Several methods have been suggested to determine the s_cr value using the s_AX-x_lld relationship. Kúdela and Slaninka [27] and Kotšmíd and Beňo [29] determined buckling stress using the stress at the proportional limit in the s_AX-x_lld relationship. In their method, a straight-line is drawn onto the linear segment in the s_AX-x_lld curve. Based on visual observation, the deviation point between the straight-line and s_AX-x_lld curve is determined to be s_cr. However, this determination is often prone to error owing to the subjectivity in the visual observation. In contrast, Fairker [26] and Koczan and Kozakiewicz [28] determined buckling stress as the maximum of s_AX. However, in the buckling test, flexural deformation is often induced prior to the maximum s_AX. Instead of using the s_AX-x_lld relationship, buckling stress can be determined from the strains obtained using strain gauges bonded on both surfaces of the sample [30,31]. In the pre-buckling condition, compressive strains are induced on both surfaces. After flexural deformation is induced, the polarity of the strain at the convex surface inverts, and s_cr is determined from s_AX at the occurrence of the strain inversion. However, this method is not always suitable for porous materials such as XPS because the strain cannot be precisely measured using strain gauges [35]. Due to the aforementioned drawbacks, these conventional methods are not always relevant for determining the s_cr value of XPS.

There are several methods of making it easier to determine s_cr using the load–deflection relationship in the post-buckling condition. As shown in Figure 1, the deflection at the mid-length of the sample is defined as d_M, whereas the angle between the loading line and sample length is defined as a. The radius of curvature at the mid-length is denoted as k_M. The effective displacement for inducing the deflection is defined as x_eff and is obtained by subtracting x_CR from x_lld, as shown in Figure 1. According to elastica theory, a = 0-30°, 30-60°, and 60-90° correspond to x_eff/L = 0-0.0676, 0.0676-0.259, and 0.259-0.543, respectively, and the d_M/L- x_eff/L and k_ML-x_eff/L relationships under a pin-pin end condition are approximated as follows [32,33,34]:

$${\displaystyle \frac{{\delta }_{\mathrm{M}}}{L}}=\left\{\begin{array}{c}0.624{\left({\displaystyle \frac{x_{\mathrm{E}\mathrm{F}\mathrm{F}}}{L}}\right)}^{0.497}\left(0\le x/L\le 0.0676\right)\\ 0.549{\left({\displaystyle \frac{x_{\mathrm{E}\mathrm{F}\mathrm{F}}}{L}}\right)}^{0.450}\left(0.0676<x/L\le 0.259\right)\\ 0.473{\left({\displaystyle \frac{x_{\mathrm{E}\mathrm{F}\mathrm{F}}}{L}}\right)}^{0.340}\left(0.259<x/L\le 0.543\right)\end{array}\right.$$

(1)

and

$${\kappa }_{\mathrm{M}}L=\left\{\begin{array}{c}6.36{\left({\displaystyle \frac{x_{\mathrm{E}\mathrm{F}\mathrm{F}}}{L}}\right)}^{0.502}\left(0\le x/L\le 0.0676\right)\\ 6.87{\left({\displaystyle \frac{x_{\mathrm{E}\mathrm{F}\mathrm{F}}}{L}}\right)}^{0.530}\left(0.0676<x/L\le 0.259\right)\\ 7.51{\left({\displaystyle \frac{x_{\mathrm{E}\mathrm{F}\mathrm{F}}}{L}}\right)}^{0.596}\left(0.259<x/L\le 0.543\right)\end{array}\right.$$

(2)

The flexural stress and longitudinal strain at the mid-length surface, s_FLEX and e_FLEX, respectively, are derived as

$${\sigma }_{\mathrm{F}\mathrm{L}\mathrm{E}\mathrm{X}}={\displaystyle \frac{6P{\delta }_{\mathrm{M}}}{B{H}^2}}$$

(3)

and

$${\epsilon }_{\mathrm{F}\mathrm{L}\mathrm{E}\mathrm{X}}={\displaystyle \frac{{\kappa }_{\mathrm{M}}H}{2}}$$

(4)

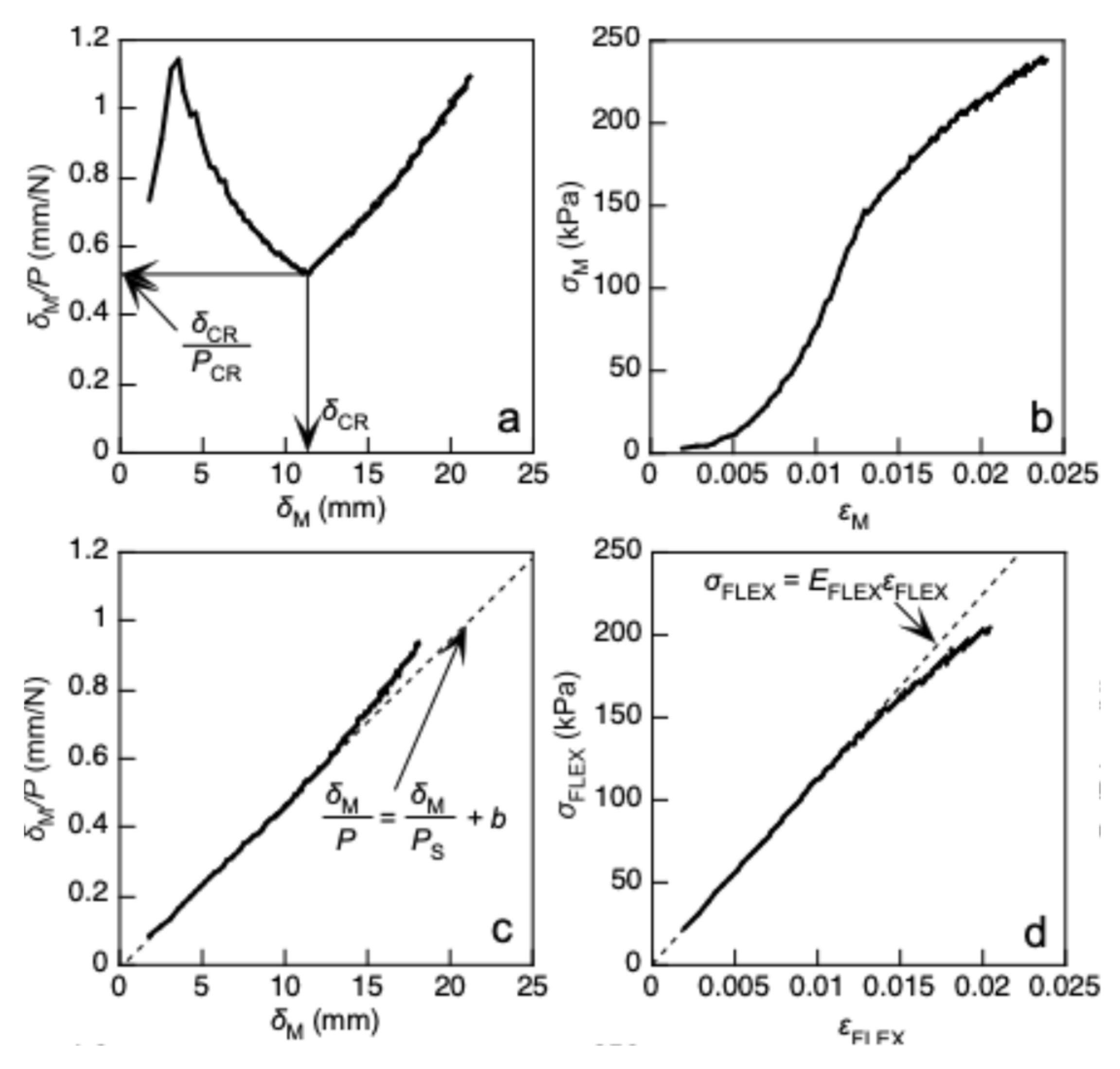
Figure 3a and b show the d_M/P-d_M and s_FLEX-e_FLEX relationships obtained directly by substituting x_lld into x_eff in Equations (1) and (2), respectively; both relationships showed anomalous tendencies. In a previous study, x_CR was determined by deriving the minimum value of d_M/P, as shown in Figure 3a [32,33,34]. The P and d_M values at x_lld = x_CR are denoted as P_CR and d_CR, respectively. Figure 3c and d illustrate the d_M/P-d_M and s_FLEX-e_FLEX relationships obtained by substituting x_eff (= x_lld - x_CR) into Equations (1) and (2), respectively. The anomalous tendencies found in Figure 3a and b are effectively reduced. Using this method, s_cr is derived as P_CR/(BH). Hereafter, this method is denoted as Method (A).

When using the buckling test data, the s_cr value can be evaluated using the following two classical methods in addition to Method (A):

(B) Southwell’s method:

In Southwell’s method, the buckling load is determined using the d_M/P-d_M relationship. As represented in Figure 3c, the d_M/P-d_M relationship is linear at the initiation of flexural deformation; therefore, it can be regressed into the following equation [25]:

$${\displaystyle \frac{{\delta }_{\mathrm{M}}}{P}}={\displaystyle \frac{{\delta }_{\mathrm{M}}}{P_{\mathrm{S}}}}+b$$

(5)

where 1/P_S and b correspond to the slope and intercept of the regressed relationship, respectively; therefore, P_CR is obtained from the inverse of the slope (= P_S). Similar to Method (A), s_cr is derived as P_CR/(BH).

(C) Modified Euler method:

According to classical Euler theory, s_cr is predicted using data obtained from compression tests using a short column, which is performed independently of the buckling test, as follows [25]:

$${\sigma }_{\mathrm{C}\mathrm{R}}={\displaystyle \frac{{\pi }^2{E}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}{{\lambda }^2}}$$

(6)

where E_comp is the Young’s modulus determined using the compression test, and l is the slenderness ratio. For a sample with a rectangular cross section, l is derived using the cross-sectional area A and secondary moment of area I as follows:

$$\lambda ={\displaystyle \frac{L}{\sqrt{\frac{I}{A}}}}={\displaystyle \frac{2\sqrt{3}L}{H}}$$

(7)

As shown in Figure 3d, the initial slope of the s_FLEX-e_FLEX relationship is denoted as E_FLEX, and s_cr is derived using E_FLEX instead of E_comp in Equation (6) as follows:

$${\sigma }_{\mathrm{C}\mathrm{R}}={\displaystyle \frac{{\pi }^2{E}_{\mathrm{F}\mathrm{L}\mathrm{E}\mathrm{X}}}{{\lambda }^2}}$$

(8)

2.2. Buckling Stress Predicted from the Compression Test Using Short Column

As described above, s_cr can be predicted using E_comp obtained from the compression tests of short columns based on classical Euler theory. Although classical Euler theory is applicable alone for a slender column where the buckling is induced prior to the onset of nonlinearity, it was extended to Engesser–Kármán theory to predict the buckling stress of a column across a wide range of slenderness ratio. To predict s_cr according to Engesser–Kármán theory, the stress–strain relationship obtained using compression tests should be formulated into an equation. The relationship between the compression stress s_comp and compression strain e_comp is approximated into the following Ramberg–Osgood type equation [36]:

$${\epsilon }_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}={\displaystyle \frac{{\sigma }_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}{E_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}}+K_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}{\left({\displaystyle \frac{{\sigma }_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}{F_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}}\right)}^{n_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}$$

(9)

where F_comp is the compressive strength, and K_comp and n_comp are the parameters obtained by regression. Using Equation (9), the tangent modulus, denoted as E_TAN, is derived as follows:

$$E_{\mathrm{T}\mathrm{A}\mathrm{N}}={\displaystyle \frac{d{\sigma }_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}{{d\epsilon }_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}}={\displaystyle \frac{1}{\frac{1}{E_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}+n_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}{K}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}{\left(\frac{{\sigma }_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}{F_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}\right)}^{n_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}-1}}}$$

(10)

According to Engesser–Kármán theory, s_cr is represented using E_TAN instead of E_comp in Equation (6) as follows:

$${\sigma }_{\mathrm{C}\mathrm{R}}={\displaystyle \frac{{\pi }^2{E}_{\mathrm{T}\mathrm{A}\mathrm{N}}}{{\lambda }^2}}={\displaystyle \frac{{\pi }^2}{{\lambda }^2\left[\frac{1}{E_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}+n_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}{K}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}{\left(\frac{{\sigma }_{\mathrm{C}\mathrm{R}}}{F_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}\right)}^{n_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}-1}\right]}}$$

(11)

The s_cr value can be obtained by solving Equation (11) numerically. This method is defined as Method (D).

Method (D) is not always convenient because of the complexity in solving Equation (11). Several methods have been proposed to address this, such as the Johnson–Euler method, in which the s_cr is derived using the following two formulas [37]:

$${\sigma }_{\mathrm{C}\mathrm{R}}=\left\{\begin{array}{c}{F}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}-{\displaystyle \frac{1}{E_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}}{\left({\displaystyle \frac{F_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}{2\pi }}\right)}^2{\lambda }^2\left(0\leqq \lambda \leqq {\lambda }_{\mathrm{y}}\right)\\ {\displaystyle \frac{{\pi }^2{E}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}{{\lambda }^2}}\left(\lambda \geqq {\lambda }_{\mathrm{y}}\right)\end{array}\right.$$

(12)

where l_y is the slenderness ratio at the intersectional point between the two formulas in Equation (11); therefore,

$$F_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}-{\displaystyle \frac{1}{E_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}}{\left({\displaystyle \frac{F_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}{2\pi }}\right)}^2{\lambda }_{\mathrm{y}}^2={\displaystyle \frac{{\pi }^2{E}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}{{\lambda }_{\mathrm{y}}^2}}$$

(13)

The method for determining the s_cr-l relationship using Equation (12) is defined as Method (E).

3. Materials and Methods

3.1. Materials

An XPS panel (STYROFOAM IB; Dupont Styro Corporation, Tokyo, Japan) was used for the tests. It had initial dimensions of 1820, 910, and 25 mm in length, width, and thickness, respectively, the directions of which are denoted as the L-, T-, and Z-axes, respectively. The panel was roughly cut using a heat cutter into smaller dimensions, and the final dimensions of the sample were cut using a heat wire. The density of the sample was 28.7 ± 0.4 kg/m³. The length direction of the sample coincided with the L- and T-axes of the panel. The former and latter samples were defined as L- and T-type samples, respectively. In both types, the width direction coincided with the Z-axis. Five samples were used for each test condition. A universal testing machine (AUTOGRAPH AG-100kNG, Shimadzu Corporation, Kyoto, Japan) was used for all the tests.

2.2. Buckling Tests

Buckling tests were performed using the L- and T-type samples with various slenderness ratios. The value of L varied from 50 mm to 500 mm at intervals of 50 mm, whereas the values of B and H were fixed at 25 and 20 mm, respectively. From Equation (7), l varied from approximately 8.66 to 86.6 at intervals of 8.66.

Figure 4 shows a photograph of the buckling test performed in this study. An axial load P was applied via the cylindrical attachment equipped on both ends of the sample to realize the pin–pin end condition. The test was continued after the flexural deformation was significantly induced as shown in Figure 4.

The rate of loading-line displacement (= crosshead speed) is denoted as ${\dot{x}}_{\mathrm{L}\mathrm{L}\mathrm{D}}$. When L was greater than 250 mm, ${\dot{x}}_{\mathrm{L}\mathrm{L}\mathrm{D}}$ was determined from the rate of flexural strain in the post-buckling condition ${\dot{\epsilon }}_{\mathrm{F}\mathrm{L}\mathrm{E}\mathrm{X}}$. When x_eff/L is in the range of 0 to 0.0676, ${\dot{x}}_{\mathrm{E}\mathrm{F}\mathrm{F}}$ is obtained using Equations (2) and (4) as follows:

$${\dot{x}}_{\mathrm{E}\mathrm{F}\mathrm{F}}=L{\left({\displaystyle \frac{0.314{\dot{\epsilon }}_{\mathrm{F}\mathrm{L}\mathrm{E}\mathrm{X}}L}{H}}\right)}^{1.99}\left(0\le x/L\le 0.0676\right)$$

(14)

Because x_lld is derived by summing x_CR and x_eff, ${\dot{x}}_{\mathrm{E}\mathrm{F}\mathrm{F}}$ is equal to ${\dot{x}}_{\mathrm{L}\mathrm{L}\mathrm{D}}$. Therefore, ${\dot{x}}_{\mathrm{L}\mathrm{L}\mathrm{D}}$ was derived by substituting ${\dot{\epsilon }}_{\mathrm{F}\mathrm{L}\mathrm{E}\mathrm{X}}$ = 0.015 /min into Equation (14) for the samples with L greater than 250 mm. However, when ${\dot{x}}_{\mathrm{L}\mathrm{L}\mathrm{D}}$ was determined using Equation (14) for the samples with L lower than 200 mm, the flexural deformation was not induced easily, and the testing time often exceeded 15 min. Therefore, the crosshead speed was fixed at 0.87 mm/min when L was lower than 250 mm. Table 1 lists the values of ${\dot{x}}_{\mathrm{L}\mathrm{L}\mathrm{D}}$ corresponding to L. The total testing time was approximately 5 min under these testing conditions.

When x_lld was directly substituted into x_eff in Equations (1) and (2), the d_M/P-d_M relationship was obtained as shown in Figure 3a. Therefore, by substituting x_lld directly into x_eff in Equations (1) and (2), the x_CR, d_CR, and s_cr values were determined using this d_M/P-d_M relationship at the minimum of d_M/P, according to Method (A). Then the s_cr values were determined according to Methods (B) and (C) based on the aforementioned procedures.

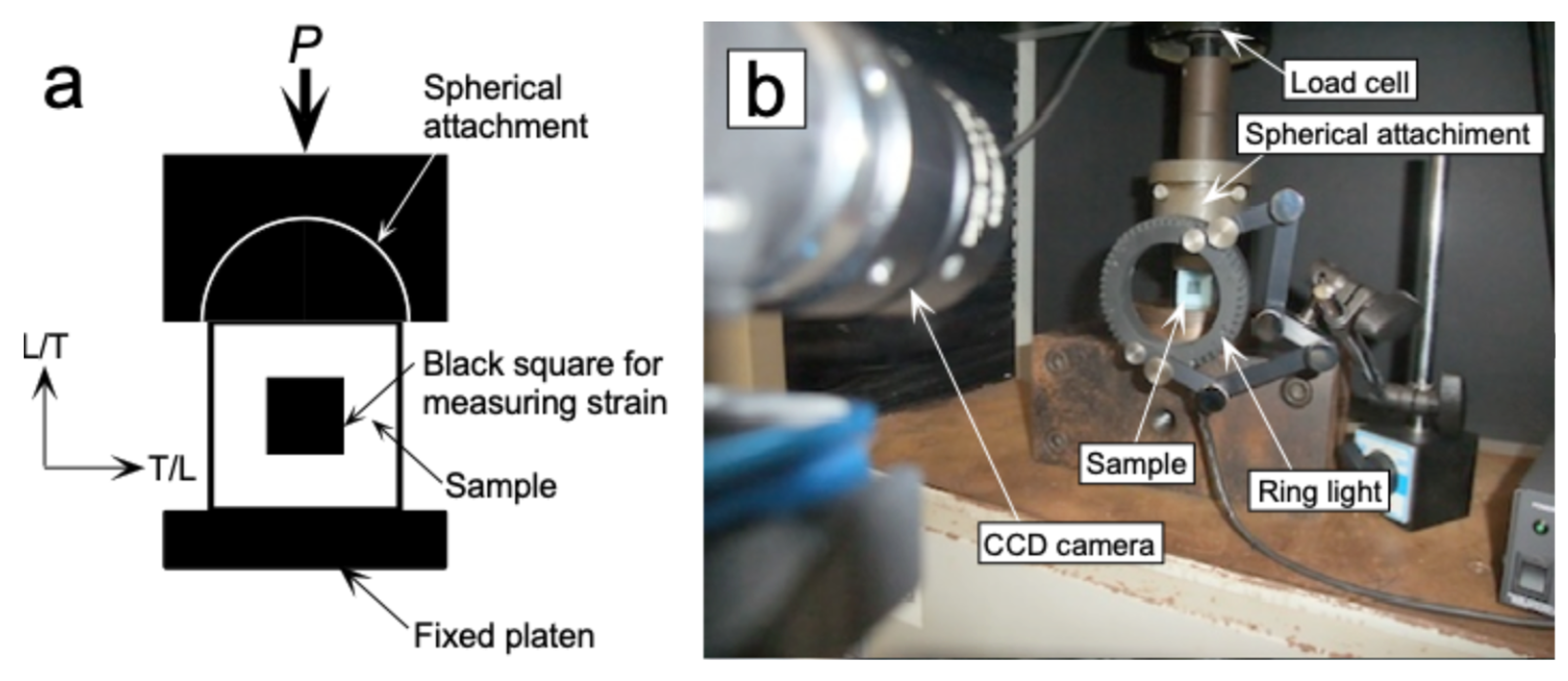
2.2. Compression Tests Using Cubic Samples

Compression tests were performed using short columns (cubic samples) to obtain the s_comp-e_comp relationship. Figure 5a and b show the detail and setup for the compression test, respectively. A cubic sample with dimensions of 25, 25, and 25 mm was used. As shown in Figure 5a, a black square with dimensions of 10 and 10 mm was marked using a stamp at the center of an LT-plane to measure e_comp. A load was applied along the L- or T-direction of the sample via a spherical attachment to reduce the bending moment at both ends of the sample with a crosshead speed of 0.5 mm/min, and s_comp was obtained. During the test, the length along the loading direction of the black square was measured using a CCD camera at intervals of 0.5 sec (Figure 5b), and e_comp was analyzed using a high-speed digital image sensor (Keyence CV-5000, Keyence Corporation, Osaka, Japan). The s_comp-e_comp relationship was regressed into Equation (9), and the E_comp, F_comp, n_comp, and K_comp values were obtained. Using these properties, the s_cr-l relationships were determined according to Methods (D) and (E).

2.3. Three-Point Bending Tests

The s_cr-l relationship could not be obtained accurately using the Engesser–Kármán and Johson–Euler methods when using the properties obtained from the compression tests. To improve the accuracy, three-point bending tests were performed in addition to the compression tests, and the properties obtained from the former were also used to determine the s_cr-l relationships using the Engesser–Kármán and Johson–Euler methods.

Figure 6 shows the setup for the three-point bending test. The length, depth, and width of the sample were 400, 10, and 25 mm, respectively. Similar to the buckling test, the length direction of the sample corresponded to the L- or T-axes. The distance between the supports l was 300 mm, and a load P_TPB was applied to the midspan with a crosshead speed of 50 mm/min until the load reached its maximum. The bending stress and bending strain at the outer surface of the midspan, s_TPB and e_TPB, respectively, are derived as follows:

$$\left\{\begin{array}{c}{\sigma }_{\mathrm{T}\mathrm{P}\mathrm{B}}={\displaystyle \frac{{3P}_{\mathrm{T}\mathrm{P}\mathrm{B}}l}{2b{h}^2}}\\ {\epsilon }_{\mathrm{T}\mathrm{P}\mathrm{B}}={\displaystyle \frac{6b{\delta }_{\mathrm{T}\mathrm{P}\mathrm{B}}}{h^2}}\end{array}\right.$$

(15)

where b and h are the width and depth of the sample, respectively, and d_TPB is the deflection at the midspan. Similar to Equation (9), the s_TPB-e_TPB relationship was regressed into the following Ramberg–Osgood-type equation [36]:

$${\epsilon }_{\mathrm{T}\mathrm{P}\mathrm{B}}={\displaystyle \frac{{\sigma }_{\mathrm{T}\mathrm{P}\mathrm{B}}}{E_{\mathrm{T}\mathrm{P}\mathrm{B}}}}+K_{\mathrm{T}\mathrm{P}\mathrm{B}}{\left({\displaystyle \frac{{\sigma }_{\mathrm{T}\mathrm{P}\mathrm{B}}}{F_{\mathrm{T}\mathrm{P}\mathrm{B}}}}\right)}^{n_{\mathrm{T}\mathrm{P}\mathrm{B}}}$$

(16)

where E_TPB and F_TPB are the bending Young’s modulus and bending strength, respectively, and K_TPB and n_TPB are the parameters obtained by regression. The s_cr-l relationship was determined based on Methods (D) using the properties obtained from the three-point bending tests as follows:

$${\sigma }_{\mathrm{C}\mathrm{R}}={\displaystyle \frac{{\pi }^2}{{\lambda }^2\left[\frac{1}{E_{\mathrm{T}\mathrm{P}\mathrm{B}}}+n_{\mathrm{T}\mathrm{P}\mathrm{B}}{K}_{\mathrm{T}\mathrm{P}\mathrm{B}}{\left(\frac{{\sigma }_{\mathrm{T}\mathrm{P}\mathrm{B}}}{F_{\mathrm{T}\mathrm{P}\mathrm{B}}}\right)}^{n_{\mathrm{T}\mathrm{P}\mathrm{B}}-1}\right]}}$$

(17)

In contrast, Equation (12) was modified using E_TPB and F_TPB as follows:

$${\sigma }_{\mathrm{C}\mathrm{R}}=\left\{\begin{array}{c}{F}_{\mathrm{T}\mathrm{P}\mathrm{B}}-{\displaystyle \frac{1}{E_{\mathrm{T}\mathrm{P}\mathrm{B}}}}{\left({\displaystyle \frac{F_{\mathrm{T}\mathrm{P}\mathrm{B}}}{2\pi }}\right)}^2{\lambda }^2\left(0\leqq \lambda \leqq {\lambda }_{\mathrm{y}}\right)\\ {\displaystyle \frac{{\pi }^2{E}_{\mathrm{T}\mathrm{P}\mathrm{B}}}{{\lambda }^2}}\left(\lambda \geqq {\lambda }_{\mathrm{y}}\right)\end{array}\right.$$

(18)

The s_cr-l relationship was also determined using Equations (17) and (18).

3. Results and Discussion

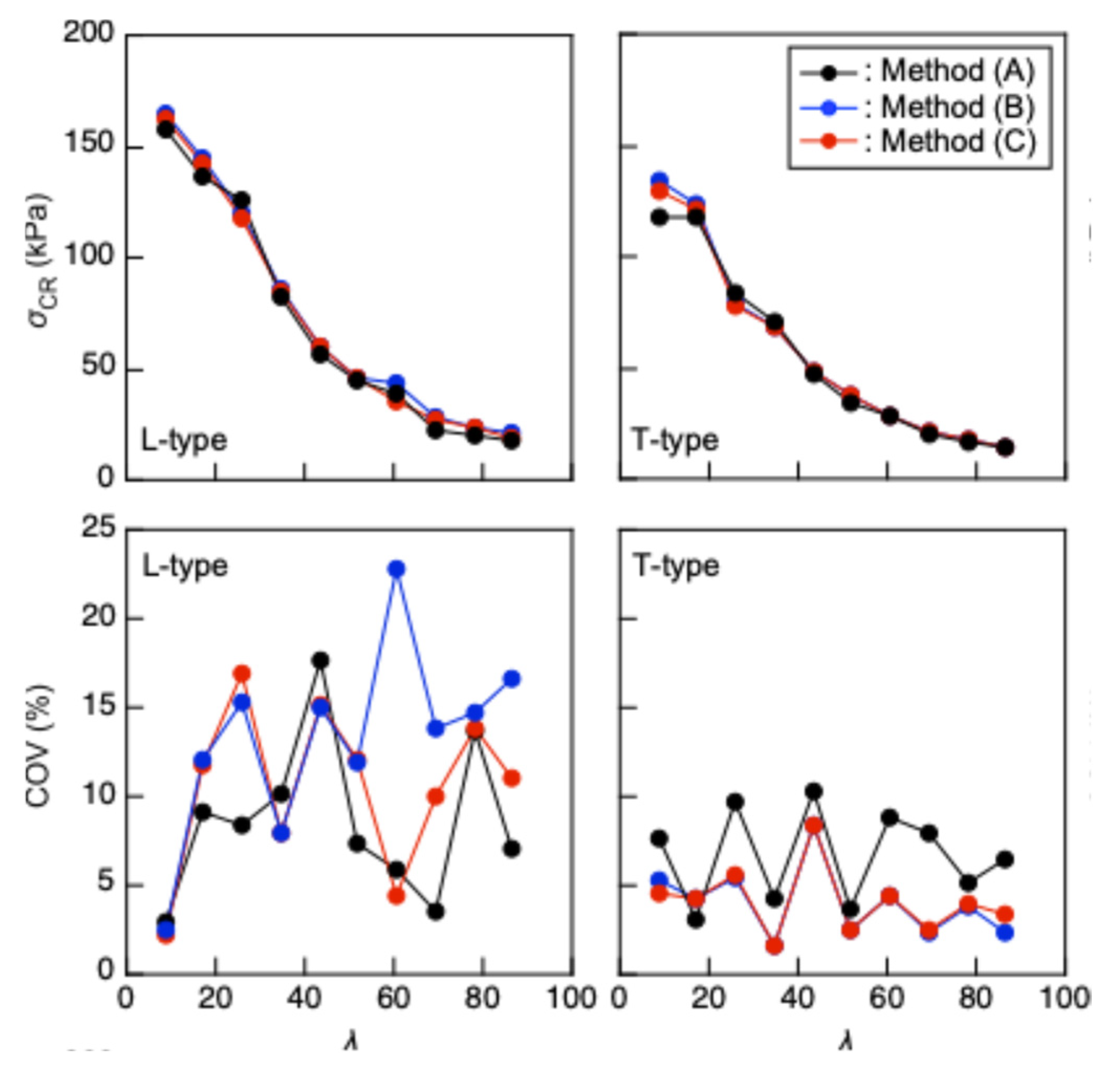
3.1. Buckling Stress Obtained from Actual Buckling Test

Figure 7 illustrates comparisons of the s_cr-l and coefficient of variation (COV)-l relationships obtained using Methods (A), (B), and (C). Analysis of variance (ANOVA, Tukey tests) was performed on s_cr corresponding to l using EZR [37], and the s_cr-l relationships obtained using the different three methods statistically coincided with each other. In a previous study, buckling analyses were performed using a slender column of solid wood and cardboard, whose l exceeded 100 and 200, respectively [32,33]. There, the buckling preceded the onset of nonlinearity induced by the compressive force axially applied to the material. 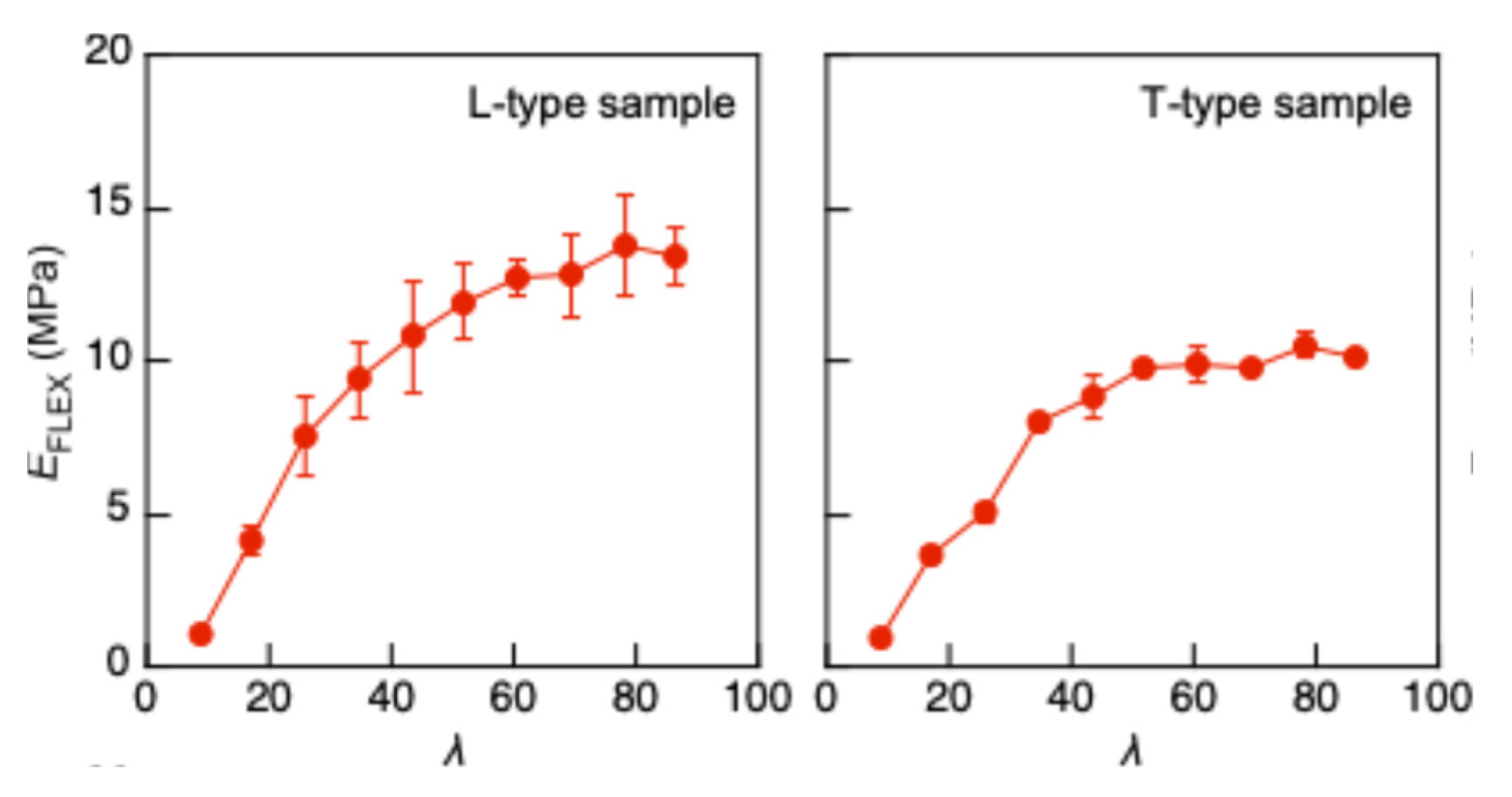In contrast, l was lower than 100 in this study, and the buckling was often induced after the onset of material nonlinearity. When the buckling is induced in the elastic condition, E_FLEX obtained from the s_FLEX-e_FLEX relationship should be constant. However, as shown in Figure 8, the E_FLEX value decreased as l decreased. Tukey tests were also performed, and the decreasing tendency was significant when l was lower than 52.0, corresponding to L = 300 mm. Therefore, the buckling was induced after the material nonlinearity when l was lower than 52.0, and the coincidence of the results obtained using Methods (A), (B), and (C) indicates the validity of these analysis methods. In particular, Method (A) is simpler and easier than Methods (B) and (C); therefore, it is recommended to determine the buckling stress of XPS using the actual buckling test data in a wide range of slenderness ratio.

Figure 7 also indicates that the COV values calculated using the L-type samples were often greater than those calculated using the T-type samples. The anisotropic cell arrangement in XPS may partly explain this difference, but further research involving microscopic observation is required to elucidate this phenomenon.

3.2. Buckling Stress Predicted Using the Compression and Three-Point Bending Test Data

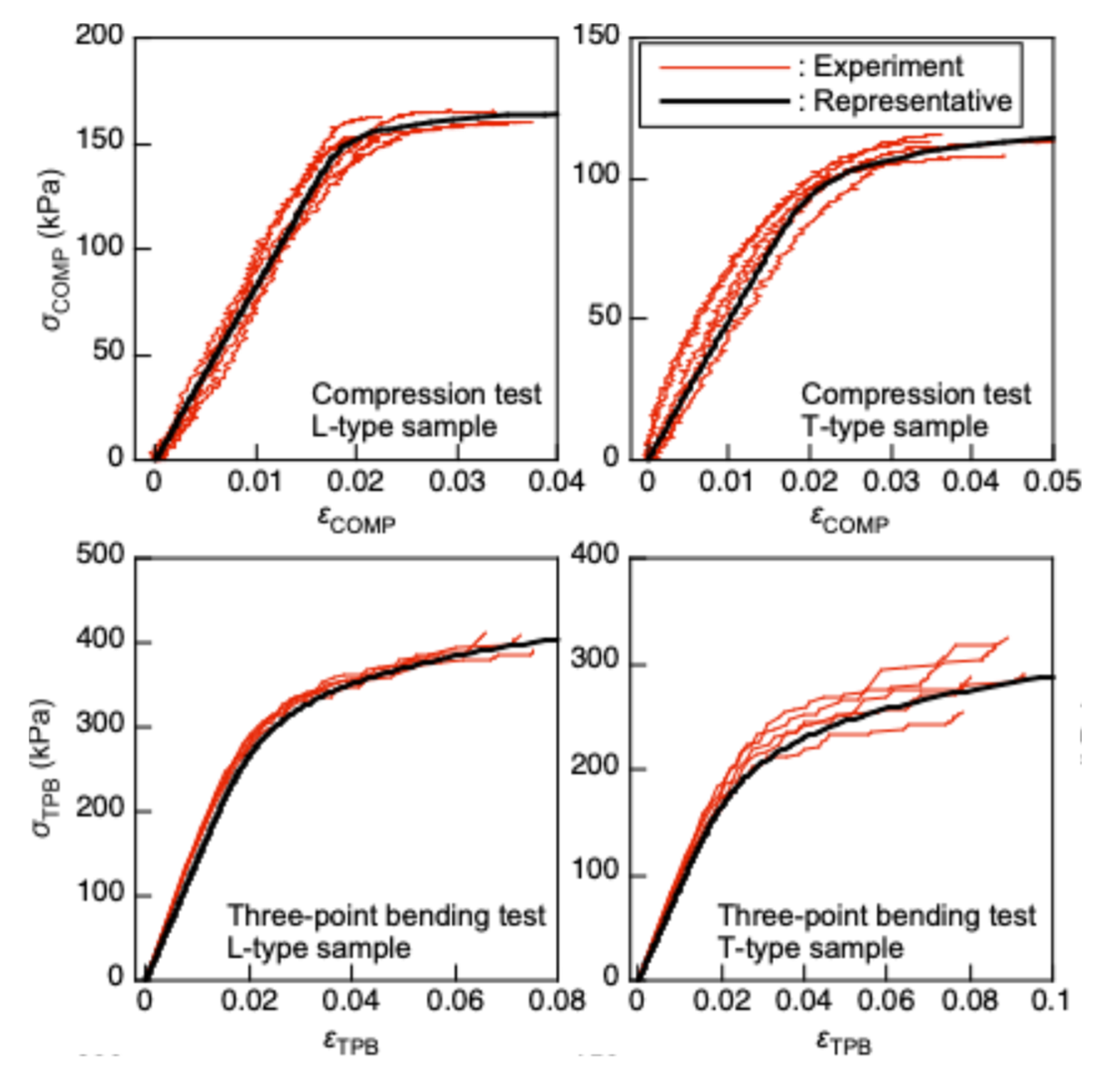
Figure 9 illustrates the representative s_comp-e_comp and s_TPB-e_TPB relationships obtained from the compression and three-point bending tests, respectively, depicted using black solid lines. These relationships were determined as follows:

(a) The F_comp value corresponding to each sample was determined using the maximum value of s_comp.

(b) The experimentally obtained s_comp-e_comp relationship was regressed into Equation (9), and the values of E_comp, n_comp, and K_comp were calculated for each sample.

(c) The average value of F_comp, defined as ${\overline{F}}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}$, was calculated using five samples. Then the e_comp value corresponding to s_comp = ${N\overline{F}}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}/100$ (N = 1, 2, …, 100) was calculated by substituting E_comp, n_comp, and K_comp into Equation (9).

(d) The e_comp values at NF_comp/100 obtained using five samples were averaged, and the averaged value was defined as ${\overline{\epsilon }}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}$.

(d) The ${N\overline{F}}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}/100$-${\overline{\epsilon }}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}$ relationship was regressed again into Equation (9). The properties obtained from this procedure, defined as ${\overline{E}}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}$, ${\overline{n}}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}$, and ${\overline{K}}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}$, are listed in Table 2, as well as ${\overline{F}}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}$.

(e) The abovementioned process was also performed using the data obtained from the three-point tests. The values of ${\overline{E}}_{\mathrm{T}\mathrm{P}\mathrm{B}}$, ${\overline{n}}_{\mathrm{T}\mathrm{P}\mathrm{B}}$, ${\overline{K}}_{\mathrm{T}\mathrm{P}\mathrm{B}}$ and ${\overline{F}}_{\mathrm{T}\mathrm{P}\mathrm{B}}$ are also listed in Table 2.

Table 2 indicates that the anisotropy of XPS affected the properties. Additionally, the properties obtained using compression and three-point bending tests are significantly different from each other. In particular, the E_comp values are approximately half the E_TPB values, and these differences affect the prediction of the s_cr-l relationship.

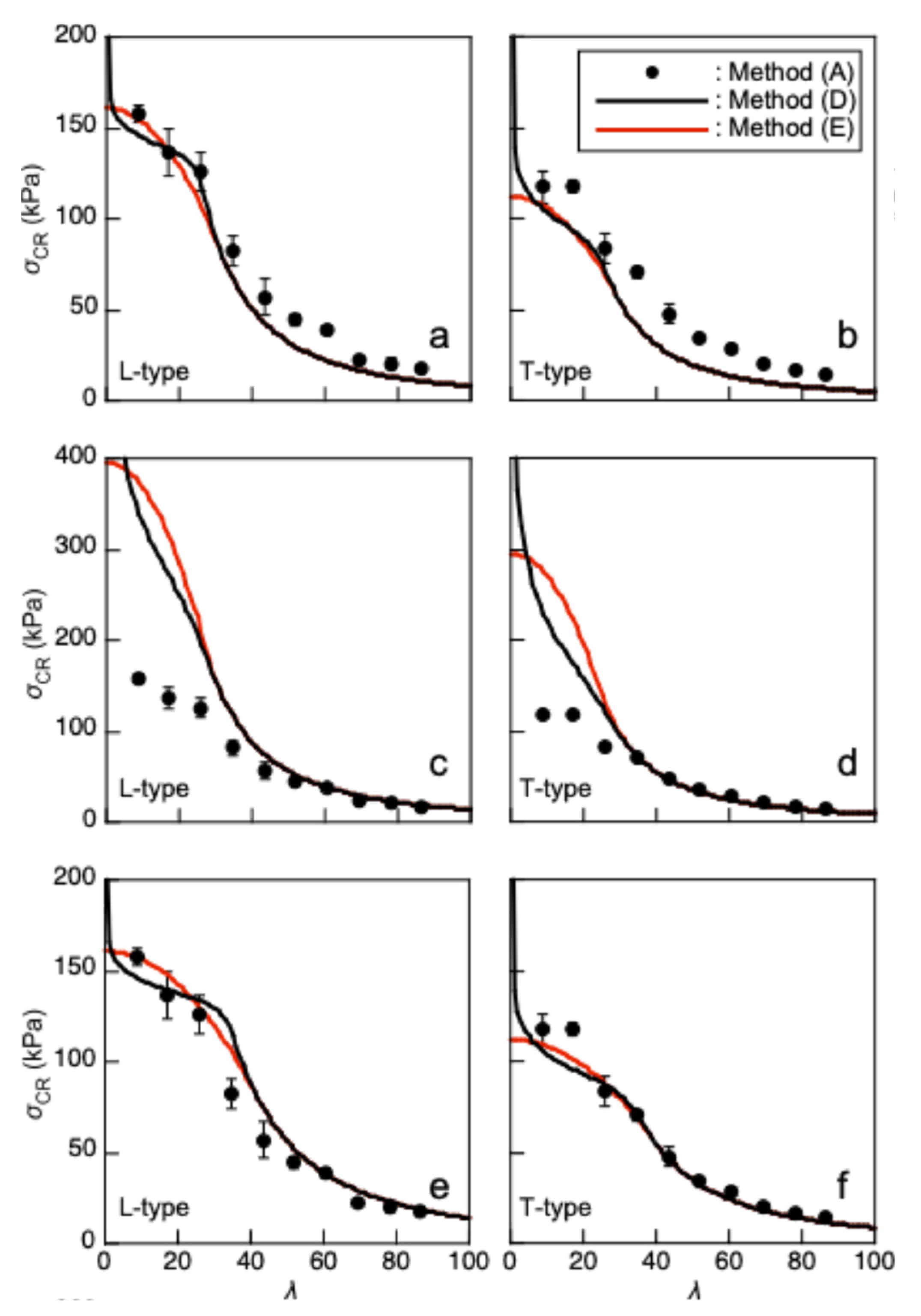
Figure 10a and b show the s_cr-l relationships predicted by Methods (D) and (E) using Equations (12) and (13), respectively. In contrast, Figure 10c and d show the relationships predicted using Equations (17) and (18). In addition to these predictions, the results obtained using Method (A), which are close to those obtained using Methods (B) and (C), are included in these figure panels. Figure 10a and b indicate that the predictions using the properties obtained from the compression tests are close to the s_cr-l relationship obtained using Method (A) when l is not sufficiently great. However, this closeness is not applicable as l increases. In contrast, the inverse tendencies are significant when using the properties obtained from the three-point bending tests as shown in Figure 10c and d.

When l is sufficiently great, the Young’s modulus is dominant in determining s_cr; therefore, the use of E_TPB is more appropriate than that of E_comp. In contrast, as l decreases, the inelastic component in the stress–strain relationship becomes dominant. Considering these tendencies, Equations (12), (13), (19), and (20) were modified as follows:

$${\sigma }_{\mathrm{C}\mathrm{R}}={\displaystyle \frac{{\pi }^2}{{\lambda }^2\left[\frac{1}{E_{\mathrm{T}\mathrm{P}\mathrm{B}}}+n_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}{K}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}{\left(\frac{{\sigma }_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}{F_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}\right)}^{n_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}-1}\right]}}$$

(19)

and

$${\sigma }_{\mathrm{C}\mathrm{R}}=\left\{\begin{array}{c}{F}_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}-{\displaystyle \frac{1}{E_{\mathrm{T}\mathrm{P}\mathrm{B}}}}{\left({\displaystyle \frac{F_{\mathrm{C}\mathrm{O}\mathrm{M}\mathrm{P}}}{2\pi }}\right)}^2{\lambda }^2\left(0\leqq \lambda \leqq {\lambda }_{\mathrm{y}}\right)\\ {\displaystyle \frac{{\pi }^2{E}_{\mathrm{T}\mathrm{P}\mathrm{B}}}{{\lambda }^2}}\left(\lambda \geqq {\lambda }_{\mathrm{y}}\right)\end{array}\right.$$

(20)

Figure 10e and f represent the s_cr-l relationships predicted using Equations (19) and (20). The coincidence is more significant than that when using the properties obtained from the compression or three-point bending tests alone. Buckling analyses of solid wood were performed in several previous studies, and it was found that the buckling stress of long and intermediate columns could be predicted appropriately using compression test data for a short column alone [39,40]. However, as shown in Table 2, the properties of XPS obtained using the compression and bending tests were significantly different from each other. In particular, XPS can be regarded as a bi-modular material in that the tensile and compressive Young’s moduli are different from each other. Such bi-modular characteristics are commonly found in several rocks [41], and further research should be conducted to reveal the bi-modular nature of XPS. However, when both the properties obtained using compression tests and those obtained using bending tests are combined, the buckling stress of XPS can be appropriately predicted under various slenderness ratios based on Engesser–Kármán theory and the Johnson–Euler method.

4. Conclusions

In this study, buckling tests were performed using extruded polystyrene (XPS) samples with various slenderness ratios to determine their buckling stress. In addition to the buckling tests, compression and three-point bending tests were performed independently, and the buckling stress was also predicted using the properties obtained from these tests. The dependence of the buckling test on the slenderness was analyzed, and the following results were obtained:

(1) Buckling stress could be effectively determined via the actual buckling test using our proposed method, Southwell’s method, and the modified Euler method across a wide range of slenderness ratios, whether buckling occurred in the elastic or inelastic region.

(2) Among the three methods mentioned in (1), our proposed method was superior to the other two, owing to its simplicity.

(3) It was difficult to predict the buckling stress using the properties obtained from the compression tests alone or those obtained from the bending tests alone.

(4) The buckling stress could be appropriately determined when using the properties obtained from both the compression and three-point bending tests together.