Models and Formulae of the Galactic Electrostatic Field

1. Introduction

The main reasons to admit a permanent electric field in the Milky Way Galaxy have been reported at the 37$th$ $ICRC$ held in Berlin in 2021, Germany [1]. These reasons, arranged in a logical inference and based on experimental data, take advantage of the energy density of cosmic rays, about 1 $eV$/$c{m}^3$, and the $Virial$ $Theorem$ applied to a system of charged particles. Cosmic nuclei are fully ionized atomic nuclei and globally form a huge system of charged particles extended up to the Galaxy radius of $4.6\times {10}^{20}$m, 15 $kpc$, and elevations above the Galactic midplane of 2 $kpc$. Electrons are only 1.5 per cent of the cosmic-ray population at about 10 $GeV$ and still less electron fractions are observed at higher energies up to 1 $TeV$ [2,3] and above. Recently (2024), in Namibia, the HESS gamma-ray telescope observed an electron fraction of about 0.02 per cent of the proton flux at 40 $TeV$.

This work, in order to redundantly prove the existence of the $Galactic$ $electric$ $field$, contrary to the previous one [1], makes the opposite move: electric fields of simple charge configurations are reliably computed from $Electrostatics$ and, then, patiently connected to pertinent features of $Galactic$ cosmic rays measured by many experiments.

The two essential pertinent features are: ($F1$ ) the position of cosmic-ray sources in spiral galaxies. The $Milky$ $Way$ $Galaxy$ is a spiral galaxy. Its radio emission and that from nearby spiral galaxies as well, particularly synchrotron emission, unambiguously determine the position of the sources (see, for example, ref. [4,5,6]). Sources are located in molecular and atomic clouds and store the negative charge $Q_w$ (the subscript w is for widow electrons). Orbital electrons lost by the accelerated cosmic-ray nuclei leaving the sources retain the negative charge $Q_w$ and are referred to as $widow$ $electrons$. Cosmic-ray nuclei are fully stripped nuclei and transport the charge $Q_{cr}$ (the subscript cr is for cosmic rays) being, $Q_w$= -$Q_{cr}$.

($F2$) Cosmic nuclei do have overwhelming kinetic energies in comparison to any sort of cosmic materials. These high energies enable cosmic-ray nuclei to propagate far away from the sources where they are generated. As a consequence, the motion of the nuclei creates a halo of positive electric charge around the negatively charged sources because cosmic-ray nuclei transport and disseminate only positive charge. In essence: halo size is larger than source size both structures storing the same opposite charge, $Q_{cr}$ = - $Q_w$ and this spatial mismatch, ultimately, generates the Galactic electric field.

All cosmic-ray nuclei circulating in the $Galaxy$ transport the total positive charge $Q_{cr}$ in the range ${10}^{31}$- ${10}^{32}$C evaluated elsewhere [1]. In order to easily intercompare the results of different calculations, the nominal charge $Q_{cr}$ = - $Q_w$ = $2.585252\times {10}^{31}$C 1 is arbitrarily adopted lying in the range ${10}^{31}$- ${10}^{32}$ [1] and nominally and shortly set at $2.58\times {10}^{31}$C. The total number of cosmic rays, $N_{cr}$, circulating at a given instant in the $Galaxy$ is about $N_{cr}$ ≃ $Q_{cr}$/q${\overline{Z}}_{cr}$ = $2.58\times {10}^{31}$ /($1.602\times {10}^{-19}$)×(1.21) = $1.34\times {10}^{50}$ $particles$ where q${\overline{Z}}_{cr}$ is the average electric charge per cosmic-ray nucleus and ${\overline{Z}}_{cr}$ = $1.21$ from cosmic-ray data. Here $N_{cr}$ is an order of magnitude estimate.

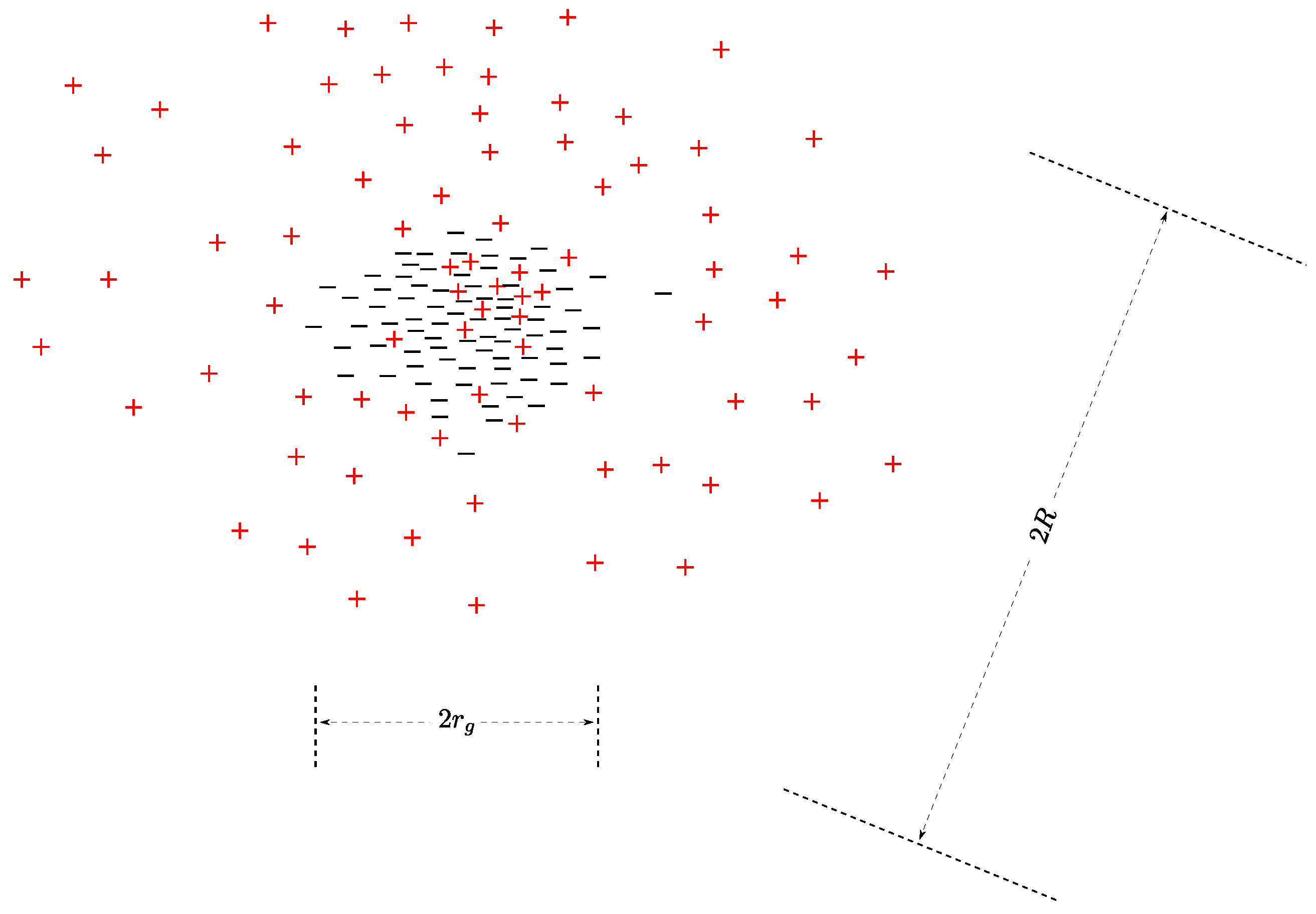
A highly schematic picture of the positions of the negative $Q_w$ and positive $Q_{cr}$ charges in the arbitrary spherical volume of galactic size is in Figure 1. This picture reflects the facts $F1$ and $F2$ in the sense that the negative charge occupies the central region while the positive charge lies peripherally.

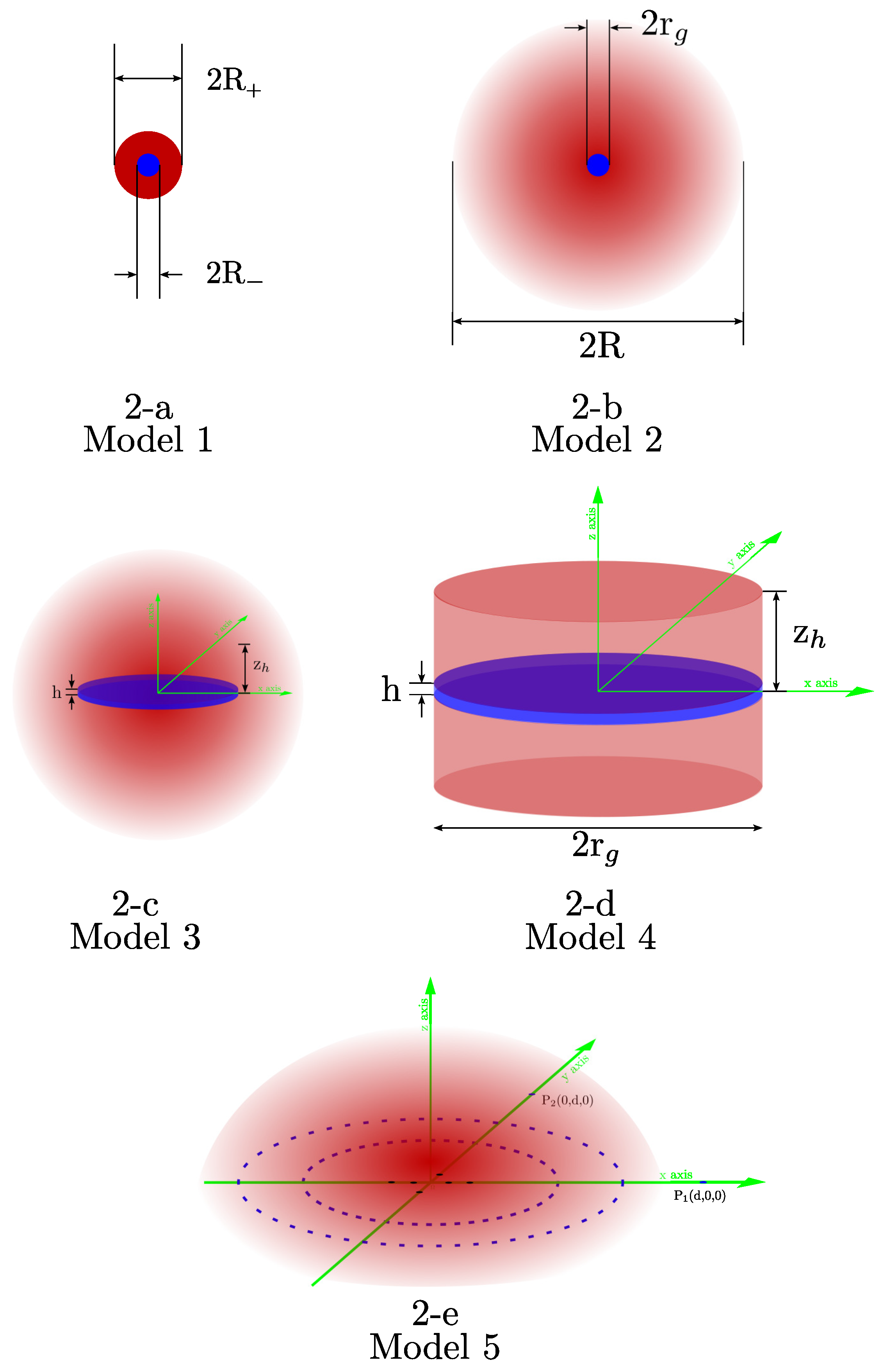
Five diverse charge configurations (Figure 2) are examined in this study, all with total zero charge, namely, $Q_{cr}$ = -$Q_w$. The simplest charge configuration is the double, concentric spheres with constant charge density shown in Figure 2-a (Section 2). The second configuration (Section 3) consists of two concentric spheres: a uniformly negatively charged sphere surrounded by positively charged spherical halo with decreasing density from the center (Figure 2-b).

The third configuration (Section 4) derives from the second one: the internal sphere storing the negative charge $Q_w$ is replaced by a flat disk of volume $\pi$$r_g^2$ 2 h where h is the half thickness of the disk and $r_g$ its radius (Figure 2-c).

The fourth configuration (Figure 2-d and Section 5) has no spherical form : it consists of two highly squashed, concentric cylinders with the same radius and different heights, h and $z_h$ (h for halo of positive charge). The fifth configuration (Figure 2-e and Section 6) consists of six discrete negative pointlike charges constrained by the charge equality $Q_{cr}$ = -$Q_w$ = $2.58\times {10}^{31}$C and a size of about 15 $kpc$. The number of six charges is thoroughly arbitrary but uncritical. A positively charged halo with decreasing charge density from the center (Figure 2-e) completes the structure.

Why the $Galactic$ electric field cannot be dissolved in time and space is dealt with in Section 7. $Compendium$, $conclusion$ and $context$ closes this study (Section 8) highlighting its empirical basis.

2. The Electric Field Of Two Concentric Uniformly Charged Spheres

Imagine a sphere of radius $R_{-}$ with negative electric charge $Q_{-}$ uniformly distributed over its volume. The intensity of the electric field $E_{-}$(r) is straightforwardly determined from elementary $Electrostatics$:

$$E_{-}\left(r\right)={\displaystyle \frac{{\rho }_{-}r}{3{ϵ}_0}}$$

(1-a)

$$E_{-}\left(r\right)={\displaystyle \frac{Q_{-}}{4\pi {ϵ}_0}}{\displaystyle \frac{1}{r^2}}$$

(1-b)

where ${ϵ}_0$ = $8.8541\times {10}^{-12}$F/m and ${\rho }_{-}$ = $Q_{-}$ / (4/3) $\pi$$R_{-}^3$ is the negative charge density in the sphere. Equation (1-a) applies in the range r≤$R_{-}$ while (1-b) in r≥$R_{-}$. Here, of course, it is $Q_{-}$ = $Q_w$ = - $2.58\times {10}^{31}$C.

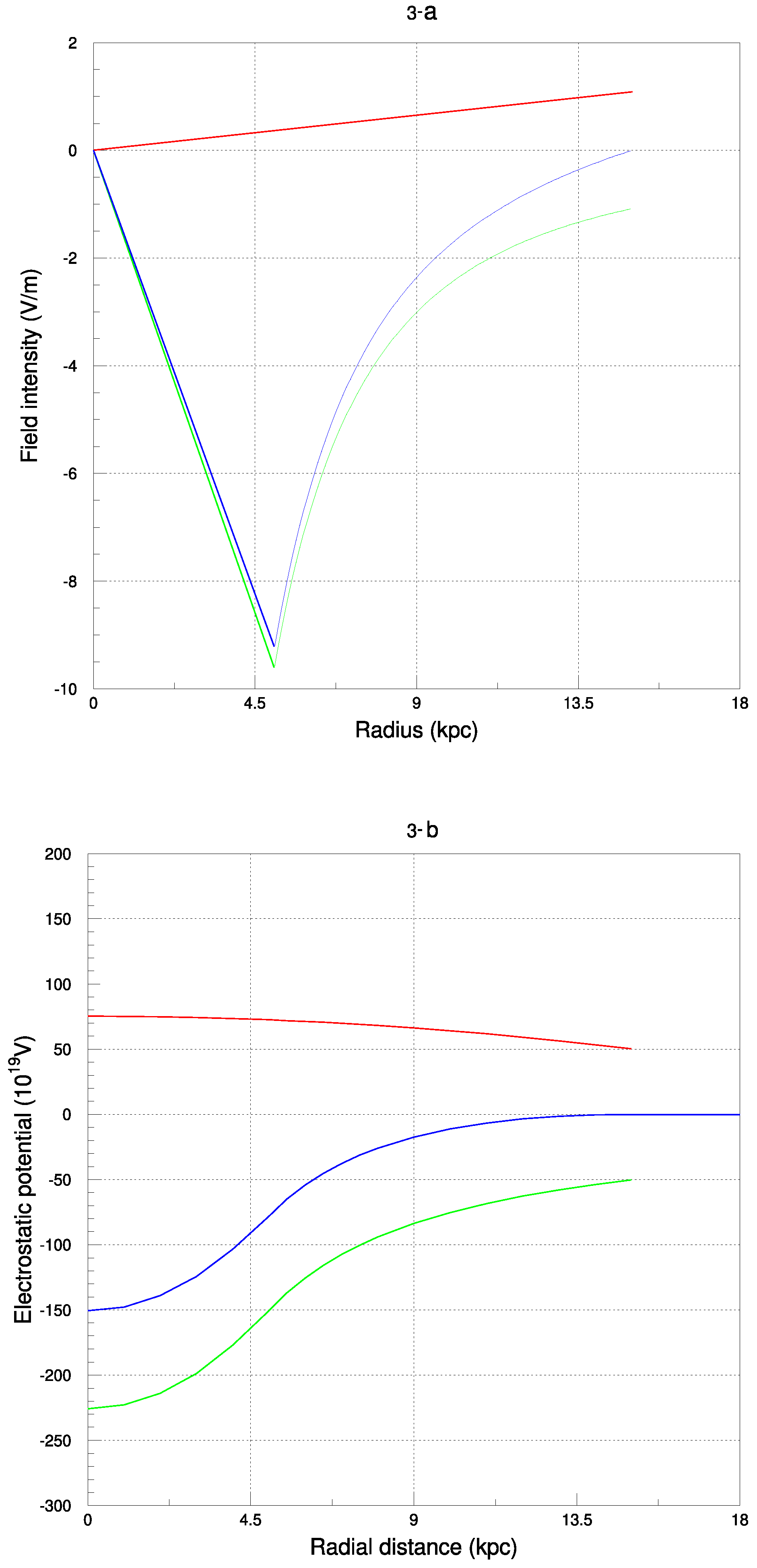
Due to the spherical symmetry, the field intensity $E_{-}$(r) is zero at the center, then, it augments with increasing radial distance r according to (1-a) up to the sphere radius $R_{-}$ as displayed in Figure 3-a. At radial distance r ≥$R_{-}$ the field strength decreases as 1/$r^2$ as it is well known.

Consider further a second sphere of radius $R_{+}$ of positive electric charge $Q_{+}$ and density ${\rho }_{+}$ = $Q_{+}$ / (4/3) $\pi$$R_{+}^3$ concentric to the sphere of radius $R_{-}$. The corresponding electric field $E_{+}$(r) has expressions analogous to those (1-a) and (1-b) except for the positive charge sign, ${\rho }_{+}$ and $Q_{+}$.

The total field E(r) is the sum of two components: E(r)= $E_{-}($r) + $E_{+}($r) at any distance r from the sphere center. If $Q_{-}$ = - $Q_{+}$ and $R_{-}$ = $R_{+}$ the field strength is, of course, null everywhere. Whenever a slight offset in the positive and negative charge distributions occurs, a finite electric field sets on inside the sphere.

For example, the arbitrary parameters, $R_{-}$ = 5 $kpc$, $R_{+}$ = 3 $R_{-}$ = 15 $kpc$, $Q_{+}$ = - $Q_{-}$ = $2.58\times {10}^{31}$C yield charge densities ${\rho }_{-}$ = - $1.677\times {10}^{-30}$C/$m^3$, ${\rho }_{+}$ = $6.22\times {10}^{-32}$C/$m^3$ and field intensities $E_{+}$(15 $kpc$) = 1.0819 V/m and $E_{-}$(5 $kpc$) = - $9.76$V/m, respectively. The radial profile of the total electric field, E(r), is shown in Figure 3-a (blue curve) along with $E_{+}$(r) (red curve) and $E_{-}$(r) (green curve). The field vanishes beyond $R_{+}$ = 3$R_{-}$ = 15 $kpc$ as shown in same figure.

The potential for the negative charge $Q_{-}$ reads:

$$V\left(r\right)={\displaystyle \frac{Q_{-}}{8\pi {ϵ}_0{R}_{-}}}(3-{\displaystyle \frac{r^2}{R_{-}^2}})$$

(2-a)

$$V\left(r\right)={\displaystyle \frac{Q_{-}}{4\pi {ϵ}_0}}{\displaystyle \frac{1}{r}}$$

(2-b)

Equation (2-a) applies in the interval r ≤$R_{-}$ while (2-b) in r≥$R_{-}$. Analogous equations hold for the positive charge $Q_{+}$.

This is the simplest conceivable charge configuration with a vague kinship to cosmic-ray data. The vague kinship are facts $F1$ and $F2$ (Section 1), namely, the negative charge predominates in the core of the spherical volume while the positive charge in the periphery.

3. Two Concentric Spheres With Unequal Profiles Of Charge Densities

A step forward from the previous charge configuration toward physical reality is the removal of the uniform charge distribution of the positive charged halo of the cosmic-ray nuclei.

The displacement of cosmic-ray nuclei from the sources of finite size produces a charge density2 featured by 1/r where r is the distance from the source up to a characteristic distance R. The simple behavior 1/r is in the radial interval $0<$r< R. Accordingly, the positive electric charge density per unitary volume, ${\rho }_{cr}$(r), reads:

$${\rho }_{cr}\left(r\right)={\displaystyle \frac{k}{r}}$$

(3)

where k is a constant. From elementary $Electrostatics$ the electric field intensity $E_{+}$(r) generated by the charge distribution (3) is constant, directed outwardly and it is:

$$E_{+}\left(r\right)={\displaystyle \frac{k}{2{ϵ}_0}}={\displaystyle \frac{Q_{cr}}{4\pi {ϵ}_0{R}^2}}$$

(4)

where $Q_{cr}$ is the total positive electric charge transported by cosmic rays and $R_{dis}$ the characteristic distance of the propagation. For example, with $Q_{cr}$ = $2.58\times {10}^{31}$ C and R = 300 $kpc$, at any arbitrary radial distance satisfying, $0<$$r<R$, it turns out: $E_{+}$ = $2.711\times {10}^{-3}$V/m.

As cosmic-ray sources of this $Model$ 2 retain a total negative electric charge, $Q_w$=$-Q_{cr}$ having spherical symmetry of diameter 2$r_g$, in a generic point r such that $r_g<r<R$, the intensity of the resulting electric field E(r) is:

$$E\left(r\right)=E_{-}\left(r\right)+E_{+}\left(r\right)={\displaystyle \frac{-Q_{rc}}{4\pi {ϵ}_0}}\left({\displaystyle \frac{1}{r^2}}-{\displaystyle \frac{1}{R^2}}\right)$$

(5)

where $Q_{cr}$ / $4\pi {ϵ}_0$$r^2$ is the field strength of the negative charge only, designated by $E_{-}$(r). Because of the postulated spherical symmetries of the positive and negative charge distributions and the common origin $\Omega$, the electric field $\overrightarrow{E}$ (r) vanishes beyond the distance R.

Inside the sphere, 0 ≤r≤$r_g$, the field intensity $E_{-}$ is: $-r{Q}_{rc}$/ 4 $\pi {ϵ}_0$ $r_g^3$ similarly to Equation (1). Accordingly:

$$E\left(r\right)=E_{-}\left(r\right)+E_{+}\left(r\right)={\displaystyle \frac{-Q_{rc}}{4\pi {ϵ}_0}}\left({\displaystyle \frac{r}{r_g^3}}-{\displaystyle \frac{1}{R^2}}\right)$$

(6)

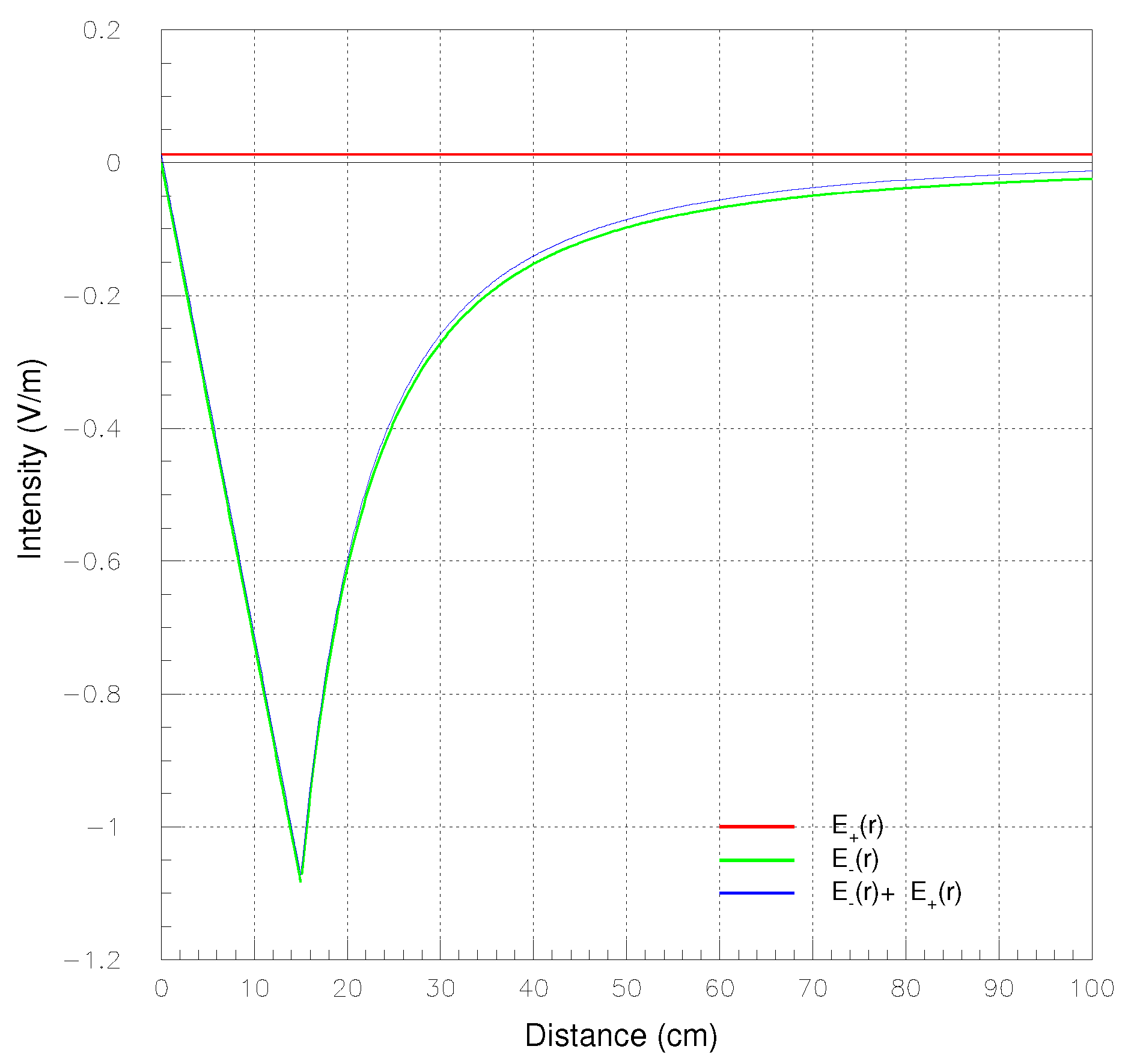
which coincides with the outer field given by Equation (5) at the point r = $r_g$ = 15 $kpc$. Hence, the electric field intensity E(r) for r<R is always less than $E_{-}$(r) by the constant amount $E_{+}$ = $Q_{cr}$/ 4$\pi$${ϵ}_0$$R^2$. The profile of E(r) versus radius is shown in Figure 4. For example at the distance r = $r_g$ = 15 $kpc$ it turns out, $E_{-}$($r_g$) = $1.083$V/m, which is about 400 times greater than $E_{+}$(r) of Equation (6) with R = 300 $kpc$. For any other distances r<$r_g$ the ratio $E_{-}$(r)/ $E_{+}$(r) decreases.

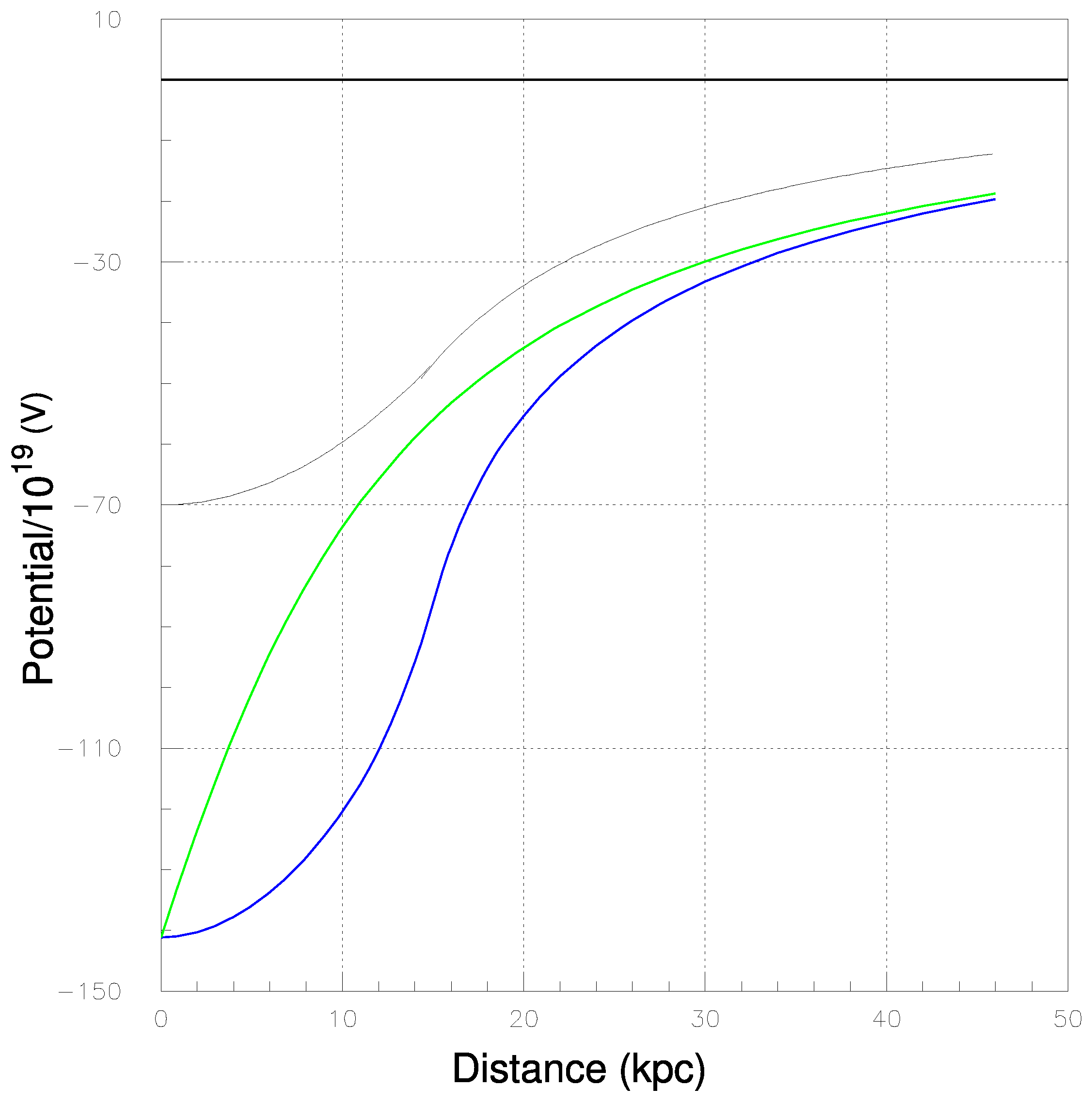
In the region, 0 ≤r≤ $r_g$ = 15 $kpc$ of the spherical volume (4/3) $\pi$ $r_g^3$ = $4.153\times {10}^{68}$$c{m}^3$, the mean energy of the electrostatic field given by equation (5) is $0.506\times {10}^{68}$$eV$ and, accordingly the mean electrostatic energy density is $0.12$$eV$/$c{m}^3$.

The radial profile of the electrostatic potential related to the electric field represented by Equation (5) and (6) , in the same conditions specified above, setting D≡$Q_{rc}$/4 $\pi$${ϵ}_0$$r_g$ = $50.1998716\times {10}^{19}$V takes the form:

$$V_e\left(r\right)=D\left(-{\displaystyle \frac{r_g}{r}}-{\displaystyle \frac{r}{n^2{r}_g}}+{\displaystyle \frac{2}{n}}\right)$$

(7-a)

$$V_e\left(r\right)=D\left(-{\displaystyle \frac{3}{2}}+{\displaystyle \frac{2}{n}}-{\displaystyle \frac{r}{n^2{r}_g}}+{\displaystyle \frac{r^2}{2r_g^2}}\right)$$

(7-b)

Equation (7-a) holds for $r_g<$$r<R$ while the (7-b) for $0<$$r<r_g$. Figure 5 shows the profile of the potential (black curve) in the range, $0<$$r<r_g$ for $r_g$ = 15 $kpc$ and n = 20 being n = R/$r_g$. The classical normalization condition of zero electrostatic potential at very large distances has been adopted.

4. A Positively Charged Sphere Concentric To A Negatively Charged Disk

Sources of cosmic rays in the Milky Way Galaxy like other nearby spiral galaxies are distributed on a thin disk. This fact is proved by redundant evidence via radio, infrared and optical emission from $HII$ regions, molecular clouds and neutral Hydrogen clouds as recapitulated in Section 1 by the fact $F1$. As a consequence, a thin disk, instead of a sphere, better adheres to the spatial dissemination of the cosmic-ray sources.

An artistic view of this charge configuration ($Model$ 3) is delineated in Figure 2-c.

The negative charge $Q_w$ has a cylindrical symmetry and, therefore, the electric field and potential have two components: radial r and elevation z (Figure 2-c).

Consider a disk of center $\Omega$, radius $r_g$ and thickness 2h with $r_g$ = 15000 $pc$ and h=125 $pc$. Let the negative charge $Q_w$= - $2.58\times {10}^{31}$C be uniformly distributed inside the disk volume, and assume further, that the positive charge of the cosmic rays (positively charged nuclei) diminishes in the whole space as k/r following equation (3) up to the maximum distance from the center R. Here r is the generic distance from the center $\Omega$ and k a suitable constant. The calculation adopts, R = 300 $kpc$, k = - $Q_w$/2 $\pi$$R_g^2$ = -$1.506\times {10}^{22}$C/$m^2$ and a total positive charge $Q_{cr}$ equal to that of widow electrons, $Q_w$. This geometrical form with the negative electric charge $Q_w$ enshrouded by the charged cocoon of cosmic nuclei $Q_{cr}$ would imitate the electrostatic structure of a common disk galaxy like the Milky Way Galaxy or $Andromeda$ better than the concentric double sphere with zero charge previously examined ($Model$ 2 in Section 3).

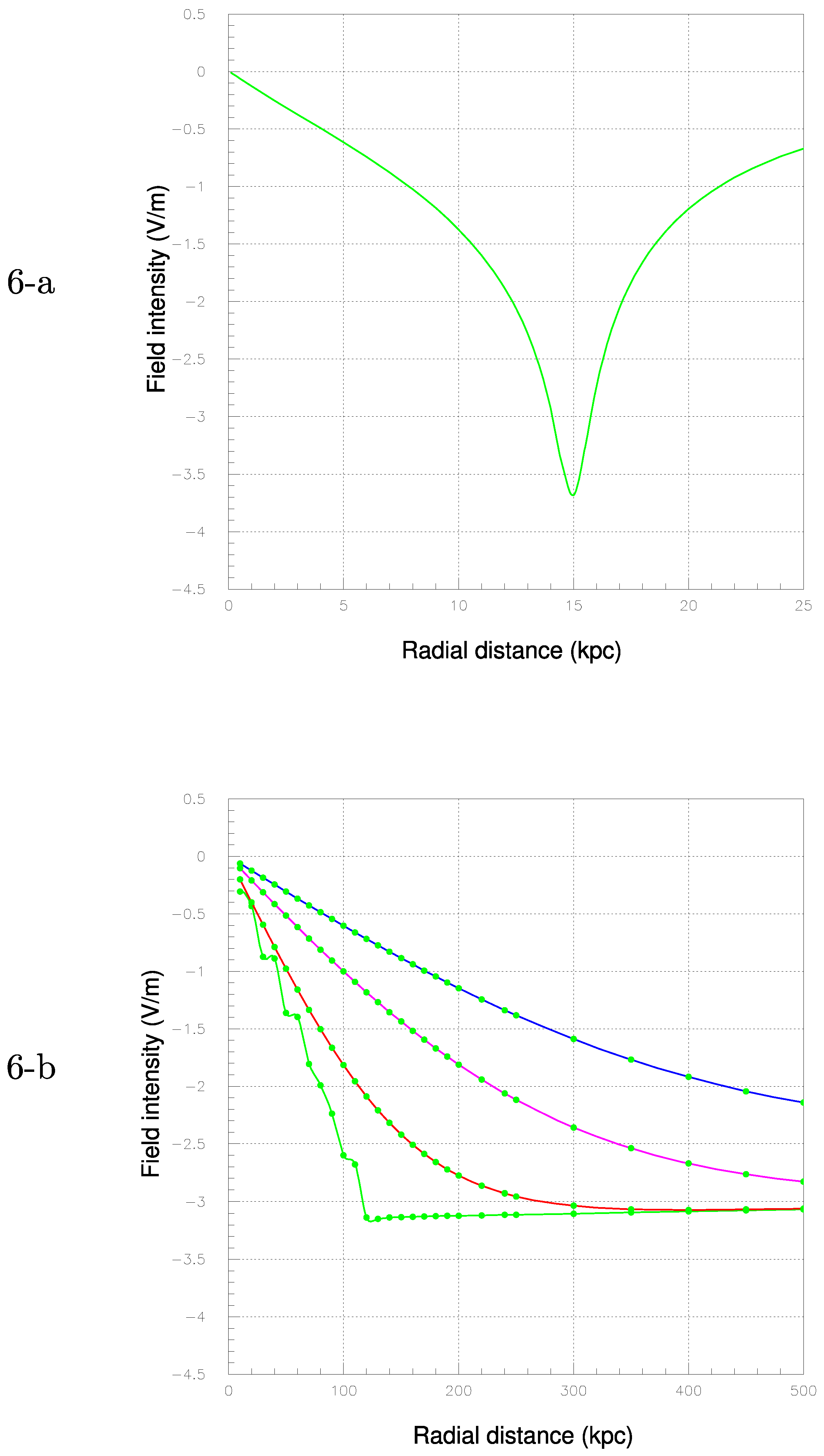
The function k/r is equal to that of the crude surrogate of the spherical galaxy expressed by Equation (3) and it produces a constant electric field intensity of $2.711\times {10}^{-3}$V/m if $Q_{cr}$ = $2.58\times {10}^{31}$C and R = 300 $kpc$, always directed outwardly, as previously remarked.

The electric field of this structure denoted by ${\overrightarrow{E}}_g$ can be decomposed in a radial and vertical (also elevation z) components, ${\overrightarrow{E}}_r$ and ${\overrightarrow{E}}_z$, respectively, in such a way that: ${\overrightarrow{E}}_g$ = ${\overrightarrow{E}}_r$ + ${\overrightarrow{E}}_z$. The intensity $E_r$ versus radius r up to 25 $kpc$ is shown in Figure 6-a. As it is quickly realized, in the range 0 <r<$r_g$ the field profile turns out to be concave relative to a linear trend (for instance the trends represented in Figure 3-a and 4 in the radial range 0 <r< 15 $kpc$). Thus, the field strength ${\overrightarrow{E}}_r$ vanishes at the origin $\Omega$ and takes the maximum value of - 3.7 V/m on the rim e. g. r = $r_g$ = 15 $kpc$.

The intensity $E_z$ versus elevation z at the four arbitrary radii r = 0, r= $3.5$, r = $8.5$ and r = $13.5$ $kpc$ are shown in Figure 6-b. The $E_z$ profile for r = 0 (green curve) joins the profile in Figure 6-a (green curve) in the range $0.25$<r< 250 $pc$ and completes it. For r = 0 the $E_z$ field strength attains its maximum of 3.38 V/m at elevations z above 125 $pc$. As expected for an ideal, infinite uniformly charged slab, the field strength $E_z$ is almost constant close to the slab (highly flat cylinder in the present case) even with a finite slab.

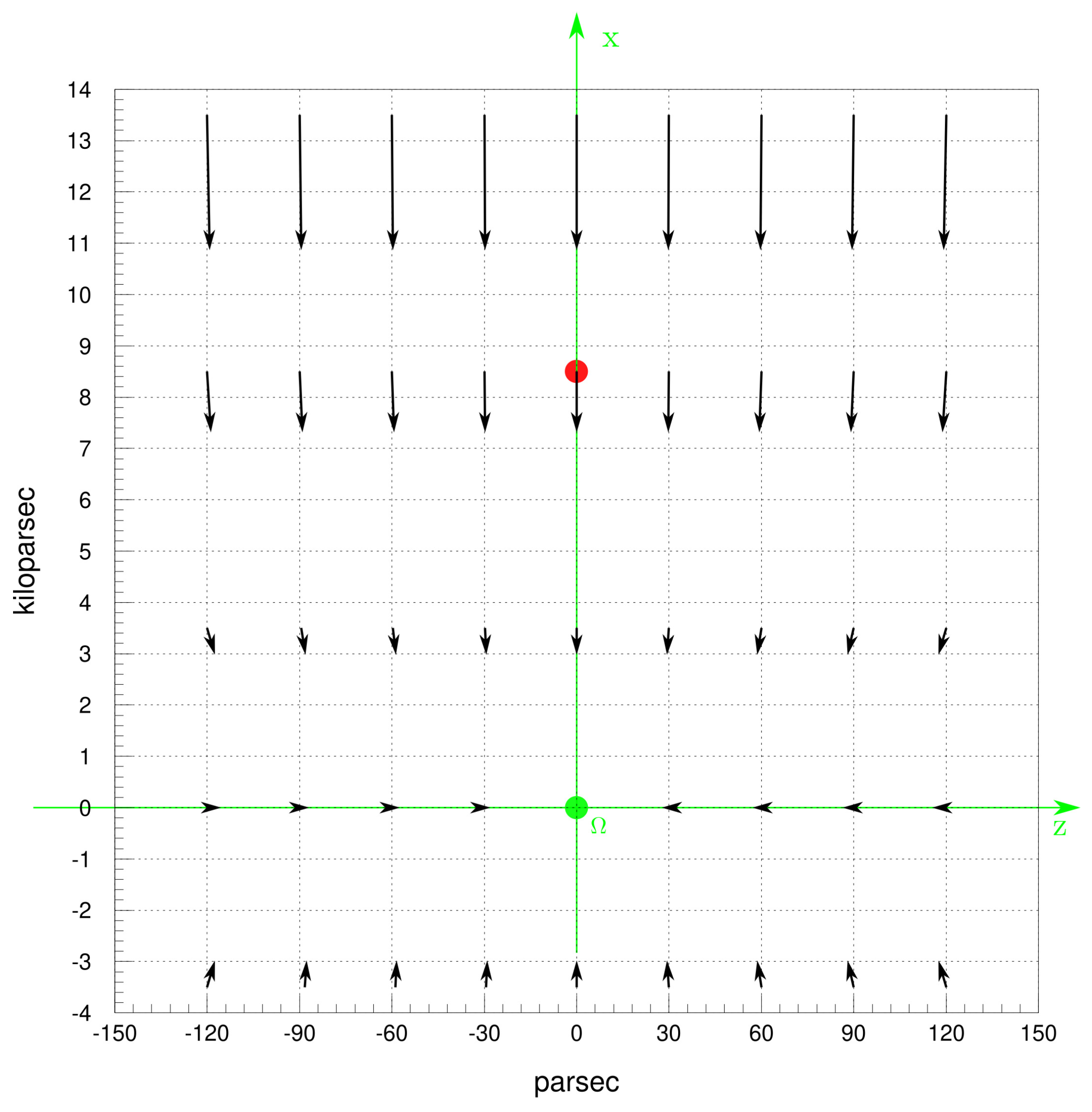
Assimilating the Milky Way Galaxy to this structure ($Model$ 3), in the nominal position of the solar system, i. e. r = $8.5$$kpc$ and z = 0 it is: $E_r$ = $1.1$V/m. The electric field ${\overrightarrow{E}}_g$ inside the disk, around the solar system (r = $8.5$$kpc$ and z = 0) in the plane xz normal to the Galactic midplane xy is visualized by the vector array in Figure 7. Note that the unit length in the x and z axes differ by a factor 80.

The electric field of $Model$ 3 has an approximate spherical symmetry in regions far away from the center and imitates the spherical symmetry of the double sphere with zero charge ($Model$ 2 in Section 3). For example, in the position z = 400 $kpc$ and r = 0 it results, $E_z$ = $1.232\times {10}^{-5}$ V/m while for r = 400 $kpc$ and z = 0 it results: $E_r$ = $1.236\times {10}^{-5}$V/m so that: $\mid E_r\mid$ - $\mid E_z\mid$ = $0.04$$\mu$V/m. Given the smallness of this difference it turns out that at large distance from the center $\Omega$ the field strength $E_g$ is almost independent from the direction.

5. Two Concentric Squashed Cylinders With Positive And Negative Charge

In $Model$ 4 the electrostatic field $\overrightarrow{E}$(r,z) results from the sum of the fields of two separate single disks which are denoted by ${\overrightarrow{E}}_{-}$(r,z) for the charge $Q_w$ and ${\overrightarrow{E}}_{+}$(r,z) for the charge $Q_{cr}$ being $\overrightarrow{E}$ = ${\overrightarrow{E}}_{-}$ + ${\overrightarrow{E}}_{+}$. For sake of simplicity,

two uniform charge distributions in the two volumes $\pi$$r_g^2$2h (disk) and $\pi$$r_g^2$2$z_h$ (halo) are used in the calculation having, respectively, charge densities ${\rho }_{-}$ = $4.979\times {10}^{-30}$C/$m^3$ and ${\rho }_{+}$ = $0.3111\times {10}^{-30}$C/$m^3$.

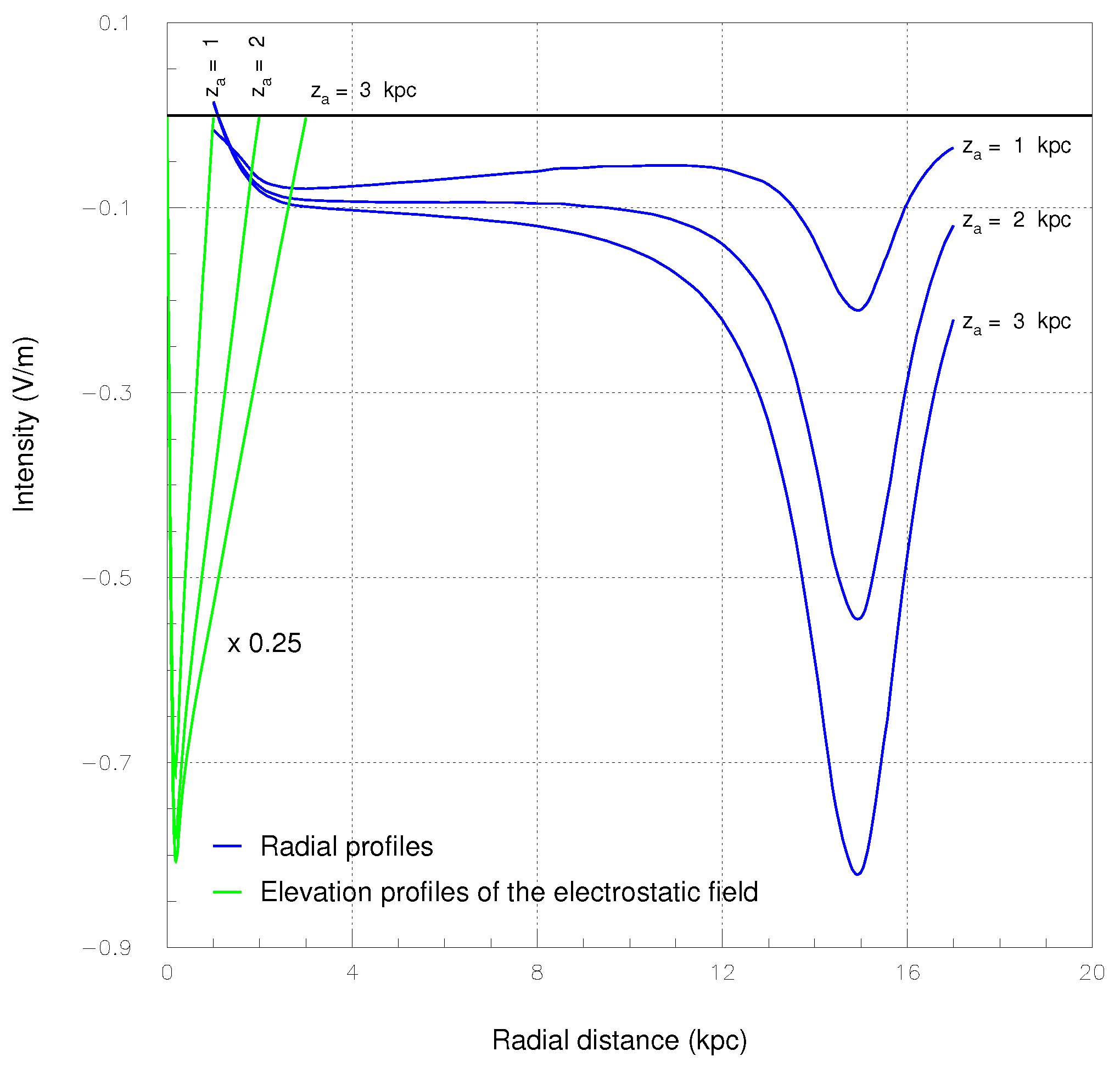
To begin with, the field strength E(r,0) along the radial direction for z = 0, and E(0,z) along the z axis for r = 0 are calculated. The x axis is chosen as generic radial direction. This choice does not lack of generality as the field $\overrightarrow{E}$(r,z) has cylindrical symmetry. These two field profiles, to be evaluated along two particular directions, facilitate the description of $\overrightarrow{E}$(r,z) at any space point inside and outside the $Galaxy$.

Radial field profiles, E(r,0) versus r, are shown in Figure 8 (blue curves) for $z_h$ = 1, 2 and 3 $kpc$. For example, for $z_h$ = 2 the field intensity is almost constant in the range 3 ≤r≤ 9 $kpc$, then rapidly increases, reaching the maximum of 0.55 V/m at the radial distance r=$r_g$=15 $kpc$, then, as expected, attenuates as any electrostatic body with of finite roundish form.

The field profiles in elevation, E(0,z)/4 versus z, are shown in Figure 8 (green curves) for $z_h$ = 1, 2 and 3 $kpc$. Field strengths are reduced by a round factor 4 to facilitate the visual comparison with radial strength E(r,0) in the same figure. The field $\overrightarrow{E}$(0,z) has maximum intensity for z≤ 1 $kpc$ and direction toward the disk interior. For instance, at $z_h$ = 1 $kpc$ the maximum of E(0,z) is $2.84$ $mV$/m at the elevation z= ± 175 $pc$. Beyond the distance of 1 $kpc$ the direction of the field $\overrightarrow{E}$(0,z) points toward the exterior. Field intensity spans the interval 1-5 $mV$/m, lower by 3 orders of magnitude than that in the range r≤ 1 $kpc$ which however is not visible in Figure 8.

Let us examine some aspects of the individual fields ${\overrightarrow{E}}_{-}$ and ${\overrightarrow{E}}_{+}$ quite useful in the following. Generally, for a preassigned radial distance and a halo size $z_h$, the field intensity $E_{+}$(0,z) decreases if z ≤ $z_h$. For instance, for z = 1 $kpc$ and $z_h$ = 3 $kpc$, the field intensity $E_{+}$(0,3) is $0.85$$mV$/m while for z = 1 $kpc$ and $z_h$ = 5 $kpc$ the field intensity $E_{+}$(0,5) is $0.43$$mV$/m.

Whenever $z_h$ is greater than h, the intensity $E_{+}$(0,z) in the range z≤$z_h$ is lower than ∣ $E_{-}$(0,z) ∣ in the same range and the resulting field $\overrightarrow{E}$ = ${\overrightarrow{E}}_{-}$ + ${\overrightarrow{E}}_{+}$ is directed toward the disc midplane. On the contrary, for z≥$z_h$ the inequality, $E_{+}$(0,z) ≥ ∣ $E_{-}$(0,z) ∣ holds and the direction of the field $\overrightarrow{E}$ is points outwardly. In the specified conditions E(0,z) vanish and changes sign. Consequently, there exists a coordinate ±z labelled $z_{inv}$ for which the field $\overrightarrow{E}$(0,z) vanishes and changes sign. Of course, $z_{inv}$ is a function of r.

The numerical example just discussed is very general indeed and the field inversion $\overrightarrow{E}$ takes place in the whole range 0 <r≤ 15 $kpc$ and not only at r = 0. The behavior $z_{inv}$ versus r for $z_h$= 1,2,3 and 4 $kpc$ is shown in Figure 26 of ref. 8.

If the field configuration $\overrightarrow{E}$ is examined not only for r = 0 but for an arbitrary value of r in the intervals, 0 <r≤ 15 $kpc$ and z≤$z_{inv}$ it results that the field is directed toward the center (exactly toward the Galactic midplane) and for z≥$z_{inv}$ the field is directed toward the exterior.

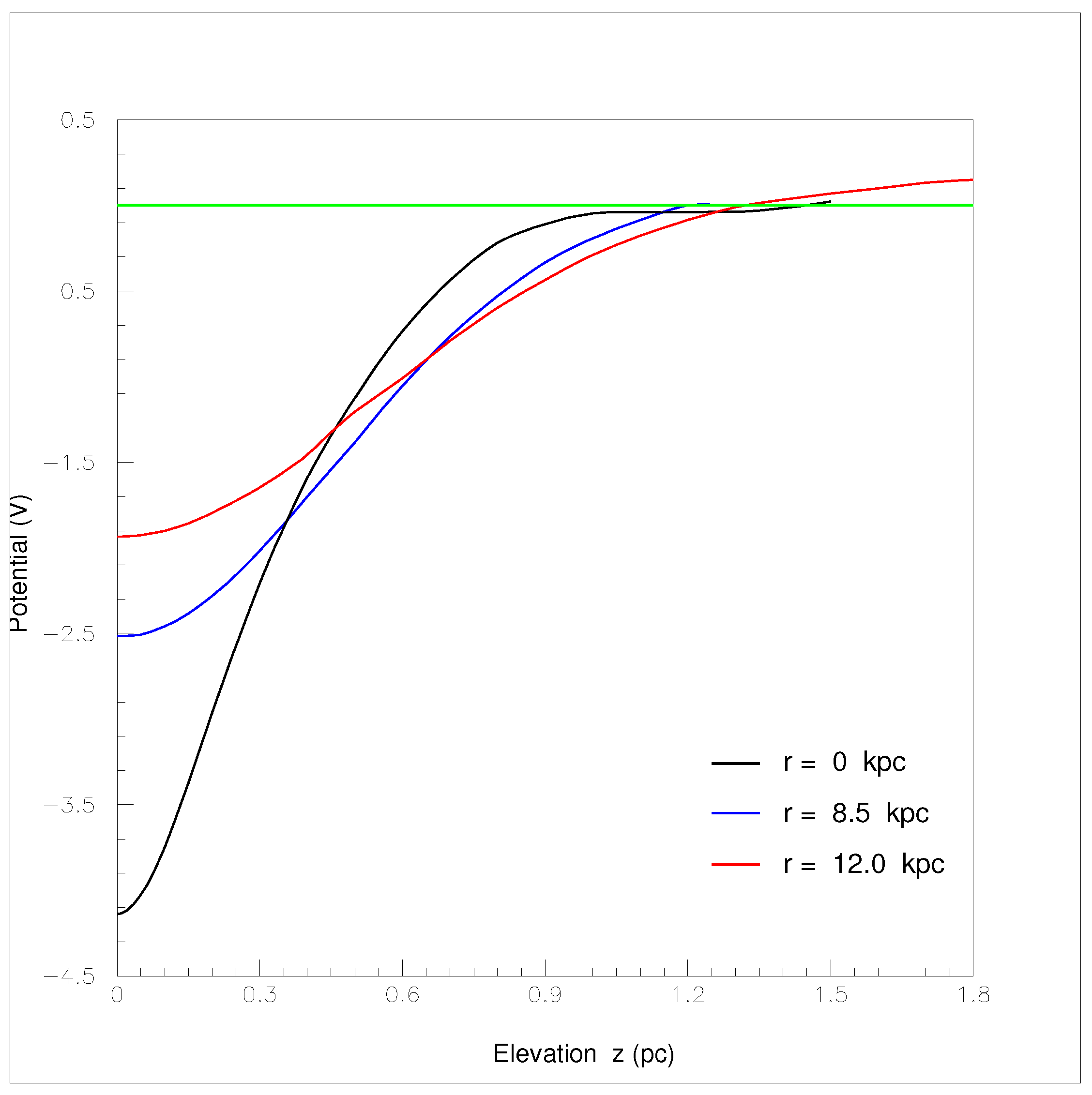
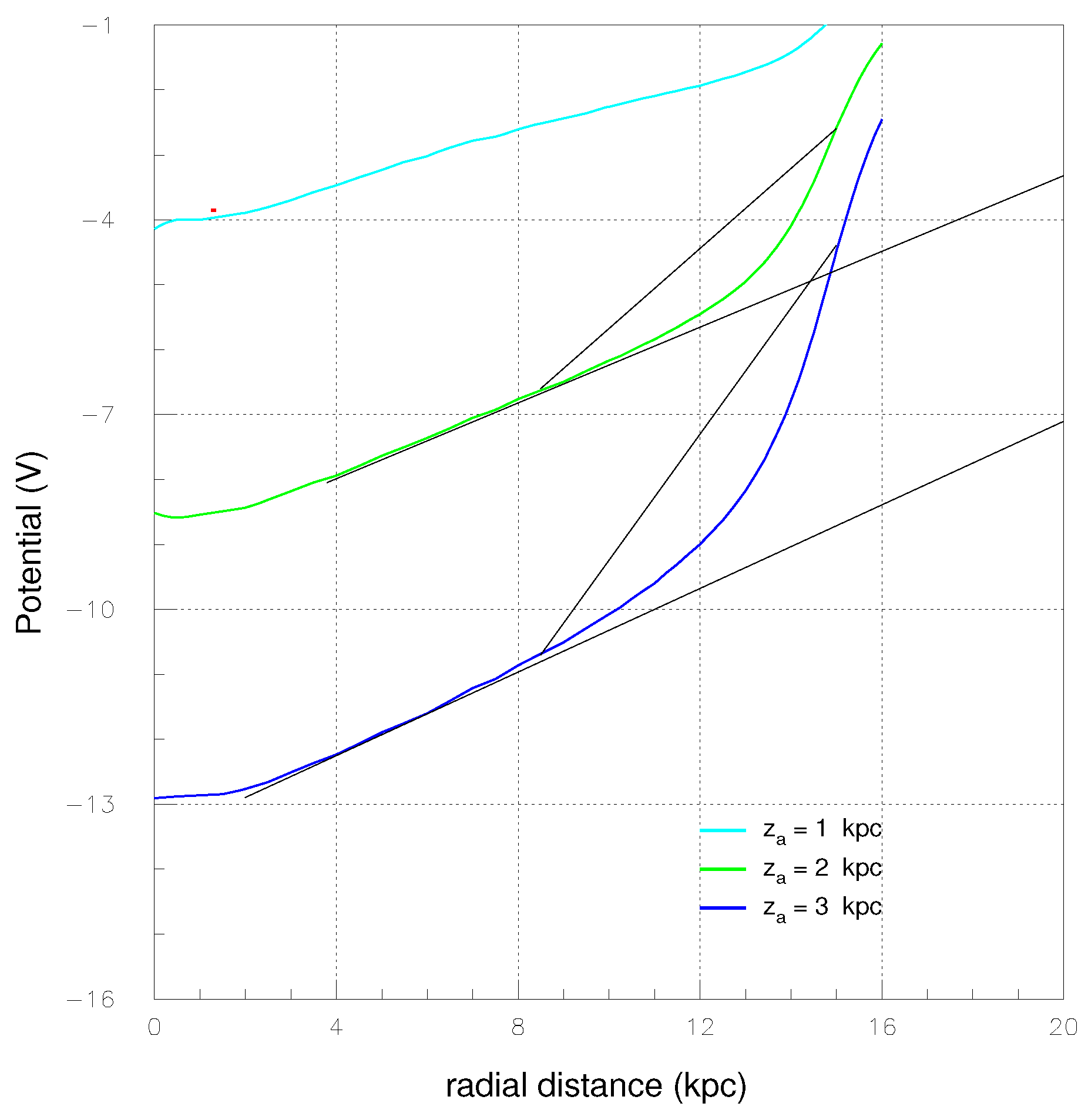
Notice that the values of the electrostatic potential V(r,z) for the two squashed, concentric, coaxial cylinders (Figure 9 and Figure 10 of $Model$ 4) are thoroughly different from those of the Models 1 and 2 (Figure 3-b and Figure 5). As an example, the potential difference onto the Galactic midplane between the disc rim $r_g$= 15 $kpc$ and the solar system at $r_s$ =$8.5$$kpc$, namely, [V($r_g$,0) - V($r_s$,0)] is $21.34\times {10}^{19}$V for $Model$ 1, $16.98\times {10}^{19}$V for Model 2 with R = 300 $kpc$, $r_g$ = 15 $kpc$ and n = R/$r_g$ = 20, $15.68\times {10}^{19}$V with R = 60 $kpc$, $r_g$ = 15 $kpc$, n = 4 and, finally, $1.67\times {10}^{19}$V for $Model$ 4 with $z_h$ = 1 $kpc$ and $4.04\times {10}^{19}$V for $Model$ 4 with $z_h$ = 2 $kpc$. Such differences are intuitively and qualitatively expected from the charge distribution sizes.

Improvements of $Model$ 4 based on observational Astronomy are suggested in the legend of Figure 11.

6. Discrete Charge Array Of Galactic Dimension

The electrostatic structures of $Models$ 1 and 2 have a perfect radial symmetry. This implies $inter$$alia$ that the electric field is strictly zero beyond the radius R, namely, beyond the maximum extension of the halo of positive electric charge transported by cosmic nuclei. What happens instead, if the radial symmetry is altered, yet maintaining the condition $Q_{cr}$ = -$Q_w$ ?

A multipolar electric field extending in all the space is generated. Here it is desired to familiarize with this assertion with a numerical example by the examination

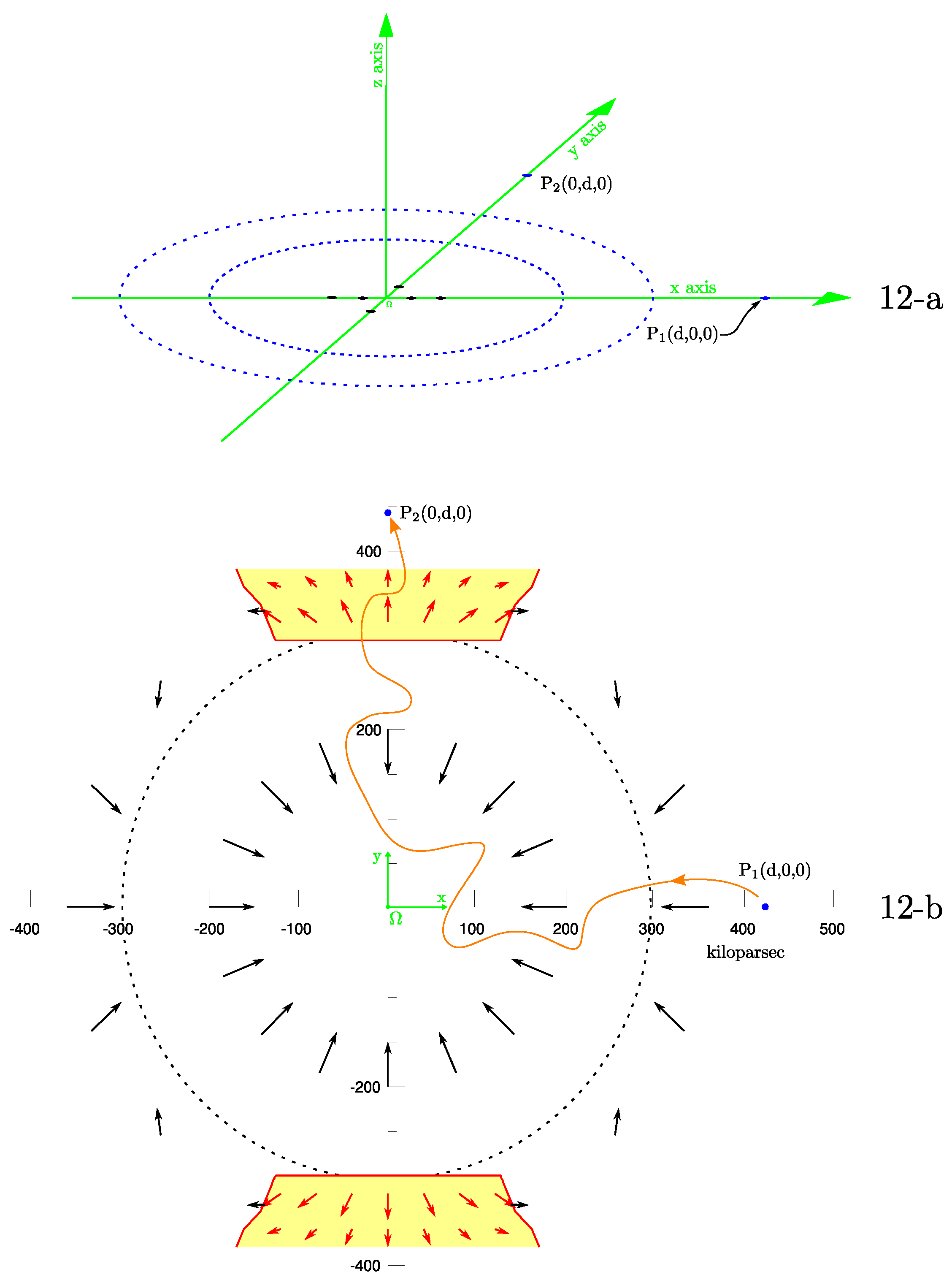
of a very simple electrostatic structure devoid of planar and spherical symmetries. A system of six pointlike negative charges is shown in Figure 12-a. The total amount of negative charge is $Q_w$ = - $2.58\times {10}^{31}$ C. The six spheres lie in the xy plane with origin $\Omega$ as shown in the same figure. Each sphere stores the charge $Q_w$/6 and it is placed at the following (x, y, z) coordinates: (-$2a$,0, 0); ($-a$,0, 0); (a,0, 0); ($2a$,0, 0), (0,$-a$, 0) and (0,a, 0) being a the characteristic size of the system. Setting a = $7.5$ $kpc$ the maximum extension of the structure is 2 a = 15 $kpc$. The spherical halo of positive charge with density $\rho$(r) given by the Equation (5) with R = 300 $kpc$ overlaps the negative charge. The total charge within R is zero i. e. $Q_{cr}$ = -$Q_w$. To simplify Figure 12-a the positive charged halo is not shown but it is sketched in Figure 2-c.

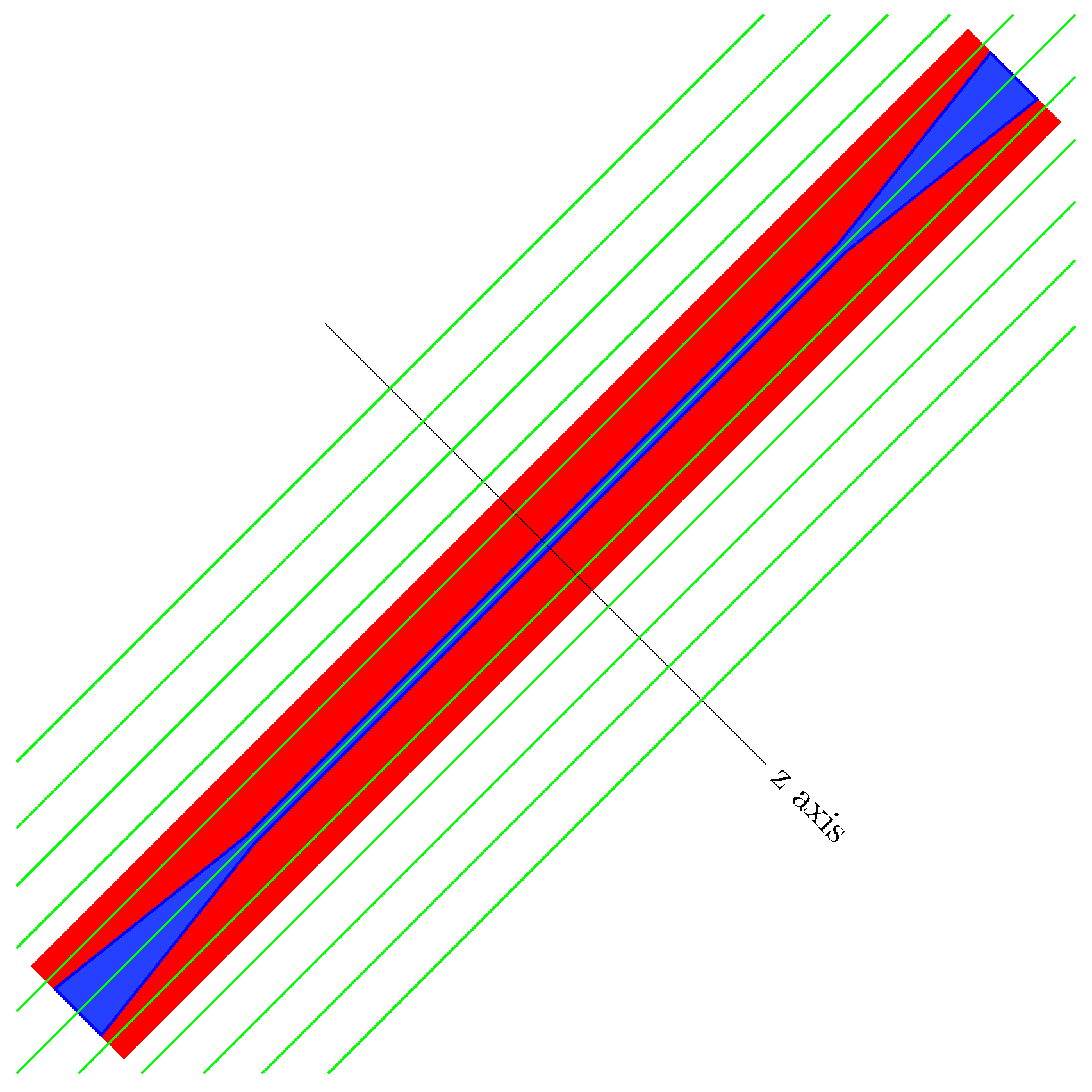
Beyond 2a and within R that is, between 15 and 300 $kpc$ the electric field strength behaves similarly to that of Figure 3 of the double concentric sphere with zero charge. There are however slight differences due to the absence of the radial symmetry of the system shown in Figure 12-a. The electric field on the xy plane at the two radial distances 200 and 300 $kpc$ is shown in Figure 12-b by a vector array.

The direction of the electric field along the x axis points always to the center $\Omega$ while along the y axis, at the characteristic distance R - i (i for inversion and i> 0) the field changes direction. In the specified conditions it turns out, i = $140.06$$pc$. Beyond the distance R - i = $299859.$94 $pc$ along the y axis, the electric field points always outwardly. The electric field can be decomposed in a radial $E_r$ and normal $E_n$ component. In xy plane at the approximate distance R (Figure 12-b) there is a line defined by all the points for which the radial electric field $E_r$ vanishes. This line intercepts the coordinate y = $R_g$ - i = $299859.$94 $pc$ and x = 0 and mimics a geographical divide: cosmic nuclei born and emitted beyond the line are accelerated toward the exterior. This region and the symmetric one are colored by yellow in Figure 12-b and filled with red arrows.

On the contrary a cosmic nucleus, initially at rest and located at any arbitrary point along the x axis, will encounter an electric field always in the same favorable direction, precipitating toward the center of the electrostatic structure. This occurs not only along the x axis but in the entire annular region around the x axis beyond R = 300 $kpc$.

The electrostatic potential generated by the 6 negative charges in a generic point $P_1$ along the x axis at the distance d from the center $\Omega$ is:

$$V_{-}\left(P\right)={\displaystyle \frac{Q_w}{4\pi {ϵ}_0}}\left({\displaystyle \frac{1}{d-2a}}+{\displaystyle \frac{1}{d-a}}+{\displaystyle \frac{1}{d+a}}+{\displaystyle \frac{1}{d+2a}}+{\displaystyle \frac{2}{\sqrt{d^2+a^2}}}\right)$$

(8)

Here it is desired to compare the electrostatic potential of the point $P_1$ (d, 0, 0) with that in the point $P_2$(0, d, 0) of coordinate d in the vicinity of R= 300 $kpc$ as Figure 12-a (not in scale) shows. Setting arbitrarily d = 300 $kpc$ then, it turns out: $V_{-}\left(P_1\right)$ = - $2.51235\times {10}^{19}$V. The potential $P_1$ generated by the positive charge is given by the Equation (7-a), $V_{+}\left(P_1\right)$ = $2.50999\times {10}^{19}$V and, hence, the resulting potential in $P_1$ is: $V\left(P_1\right)$ = $V_{+}\left(P_1\right)$ - $V_{-}\left(P_1\right)$ = -$2.23852\times {10}^{16}$V. Thus, if this enormous electrostatic potential were converted into kinetic energy of a cosmic proton traveling between $P_1$ and $P_2$ the acquired energy is $2.2\times {10}^{16}$$eV$. This elementary example highlights the huge energy gains and losses of cosmic nuclei roaming Galactic and intergalactic regions.

As the ideal and smooth charge distributions of Models 1,2,3 and 4 do not perfectly materialize in real galaxies, some features of the discrete charge distribution of $Model$ 5 highlight the prominent common features of the other four models. For instance, galactic electric fields extend to all the space and do not vanish beyond the typical sizes of the charge distributions as it occurs in $Model$ 1 and $Model$ 2 ( i.e., beyond 30 $kpc$ and 300 $kpc$, respectively).

Notice, finally, that both the electric field intensity and related electrostatic potential of the $Model$ 5, inside and outside its characteristic size 2a = 15 $kpc$, are comparable to those of the four models 1, 2, 3 and 4.

7. The Permanent Regeneration Of The Galactic Electric Field

In order to dissolve or nullify the $Galactic$ electric field, ${\overrightarrow{E}}_g$, either the electric charge of the cosmic rays $Q_{cr}$ and that at the sources $Q_w$ have to disappear from the $Galaxy$ or the electric generator powering cosmic-ray circulation has to cease operation.

The disappearance of $Q_{cr}$ could occur only by charge neutralization accomplished by a hypothetical particle population transporting negative electric charges $Q_w$ = - $Q_{cr}$ = -$2.58\times {10}^{31}$ C. This hypothetical population of negative charged particles has to exactly and finely compensate the positive charge $Q_{cr}$ = $2.58\times {10}^{31}$ C over the entire $Galactic$ volume. The compensation mechanism has to accomplish charge neutralization at any sites of the $Galaxy$, not only globally. In fact, any disjoint charge distributions would generate a global electric field as it simply and unquestionably emerges from the two concentric charged spheres having an arbitrary offset in the charge distributions (Figure 2-a and Section 2).

The only negative charged particles with infinite lifetimes are electrons and antiprotons out of more than 300 elementary charged particles presently known. Electrons due to synchrotron emission in the $Galactic$ magnetic field neither spatially nor energetically could accomplish such a chimeric compensation. The flux of cosmic-ray antiprotons are 4 orders of magnitude lower than those of cosmic-ray nuclei and, therefore, do not dissolve whatsoever the $Galactic$ electric field.

Without an appropriate refurbishment of fresh cosmic rays, the electric field ${\overrightarrow{E}}_g$ would disappear in a cosmic-ray lifetime of (10-20) $million$ years . The observed stability of the cosmic-ray intensity dictates that the field ${\overrightarrow{E}}_g$ is continuously regenerated by new born cosmic rays. The existence of cosmic rays and the stability of their intensity in the last billion years is a fact (see, for example, potassium data [10]) which necessarily implies the existence and stability of the $Galactic$ electrostatic field.

The energy source powering cosmic-ray circulation ultimately derives from stars via photon ionization of interstellar gaseous materials. This theme is outside the perimeter of this work and is dealt with in [8] (see $Chaper$ 10 for the energy sources and $Chapter$ 12 for an electric circuit imitating the cosmic-ray circulation through the $Galaxy$).

The arguments above lead to the plain conclusion that the $Galactic$ electric field not only exists but it is an inviolable structure of the $Galaxy$.

8. Compendium, Context And Conclusion

$Galactic$ electric fields and related potentials have been computed with a $Galaxy$ size of $4.86\times {10}^{20}$m (15 $kpc$) and the total electric charge $Q_{cr}$ transported by cosmic rays which is in the range ${10}^{31}$-${10}^{32}$C [1], nominally set in this and other studies at $2.58\times {10}^{31}$C (see footnote 1). These two input data have a solid, irrefutable empirical basis [1,8]. The computed intensities of the electric field span from fractions of V/m up to a few V/m and they are shown in Figure 3-a, Figure 4, Figure 6 and Figure 8. These field intensities through the $Galactic$ size of $4.86\times {10}^{20}$m generate electrostatic potentials in the interval ${10}^{19}$-${10}^{20}$V shown in Figure 3-b, Figure 5, Figure 9 and Figure 10.

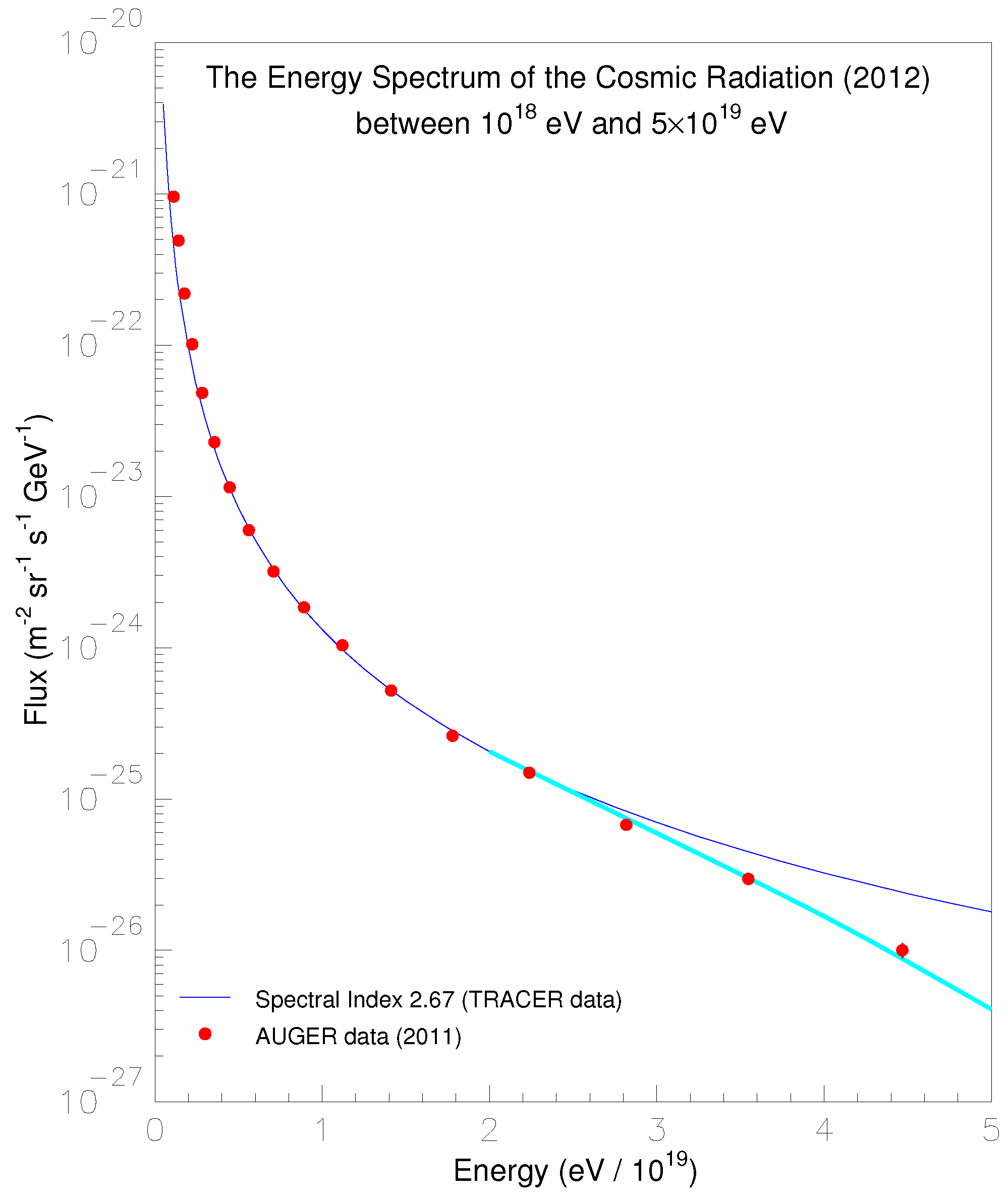
As far as the existence of the $Galactic$ electric field is at stake, all the geometrical forms of the five models presented in this paper produce similar results. Only when fine features of the $Galactic$ electric field have to be discerned, different models become relevant. For example, if the spectral index

of 2.65 of the cosmic-ray energy spectrum has to be predicted and correctly calculated, model 4 (two highly squashed concentric cylinders) offers the best agreement with cosmic-ray data (see [8] $Chapters$ 9 and 13).

Notice that quiescent, unbound protons with charge q prone to the $Galactic$ electrostatic potential, V(r), convert in cosmic-ray protons of maximum energies, q$\Delta$V = q [V($r_2$) - V($r_1$) ] where V($r_1$) and V($r_2$) are the potentials at the radial distances $r_1$ and $r_2$, respectively. Adopting the electrostatic potentials evaluated in this work and the Galactic disk radius of 15 $kpc$, it turns out: q$\Delta$V≃${10}^{19}$-${10}^{20}$$eV$, order of magnitude. From this, it descends a precious signature in the cosmic-ray energy spectrum: above the energy q$\Delta$V no cosmic-ray proton is expected to circulate in the $Galaxy$ because q$\Delta$V is the maximum energy achievable by protons. For instance, if $r_1$ = $8.5$ $kpc$ (solar circle radius) and $r_2$ = 15 $kpc$ (disk rim) then, in the $Model$ 4, $\Delta$V = V($r_2$) - V($r_1$) = -$2.588\times {10}^{19}$ V + $6.626\times {10}^{19}$ V = $4.04\times {10}^{19}$ V for a halo hight $z_h$ = 2 $kpc$ and $\Delta$V = $1.67\times {10}^{19}$V for a halo hight $z_h$ = 1 $kpc$. These maximum energies entail a recognizable break or suppression in the smooth cosmic-ray energy spectrum above the ankle energy of $3.0\times {10}^{18}$$eV$ as displayed in Figure 13.

It is a notable fact that these maximum cosmic-ray energies have been observed with the precise and unsurpassed energy resolution of the Auger experiment [12] in the range 7-16 per cent in the energy band ${10}^{18}$-${10}^{20}$$eV$. The break reported by the Auger experiment is at $2.7\times {10}^{19}$$eV$ [11] as attested by Figure 13. Only the unsurpassed energy resolution of the Auger experiment made possible the identification of the break in terms of the $Galactic$ electrostatic potential and, concomitantly, to dismiss the GZK [13,14] interpretation of the same break. The HiRes Collaboration observed the $suppression$ or $break$ at the energy of $6.3\times {10}^{19}$$eV$[15] and interpreted it as $GZK$ effect. This interpretation was reiterated by the Telescope Array (hereafter TA) experiment [16]. The critical theme of energy scales of the $TA$ and $Auger$ instruments has been discussed elsewhere [17]. The nature of the spectral break at $2.7\times {10}^{19}$$eV$ has been elucidated in 2013 [18], in 2017 [19,20] and precognized in 2009 [21].

The break in the energy spectrum represents a direct, solid and unmistakable support to the present evaluation of the $Galactic$ electrostatic potentials. It is direct because, given the electrostatic potential V(r), the energy achieved by cosmic-ray nuclei of atomic number Z is just Zq$\Delta$V as detailed above. It is solid because the break [12,15] has been reconfirmed by the Telescope Array collaboration [16]. 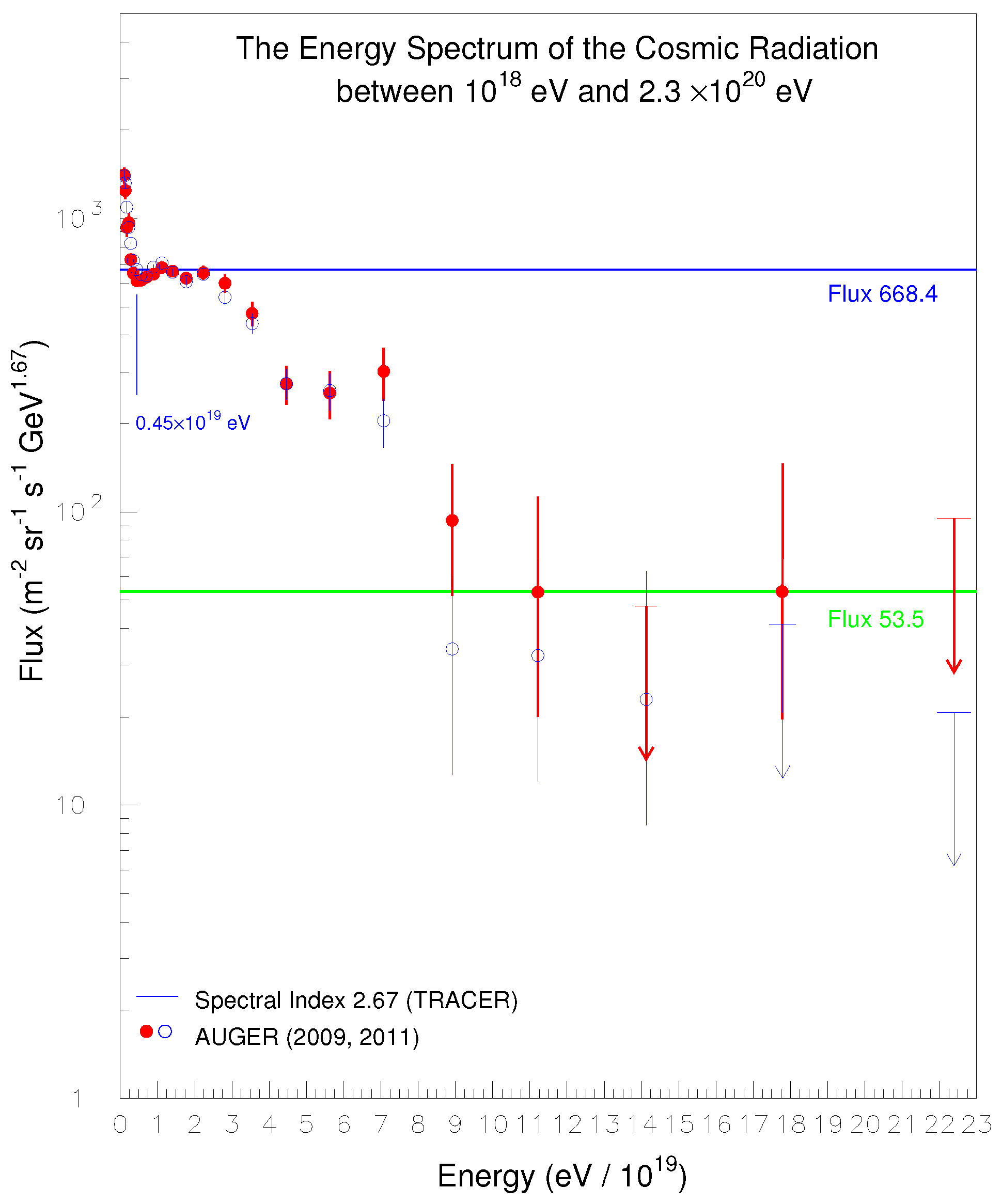It is unmistakable because the Telescope Array collaboration [16]. It is unmistakable because cosmic-ray Helium of charge 2q produces a second break in the spectrum exactly where expected, namely, at the energy of $2\times$ ( $2.7\times {10}^{19}$ ) $eV$ = $5.4\times {10}^{19}$$eV$ as displayed in Figure 14 (on this issue see $Chapter$ 13, Section $13.3$ in [8]).

In this and other works [1,8,18,21] the observation of the spectral break at $2.7\times {10}^{19}$$eV$ is regarded as a major discovery in $Cosmic$ $Ray$ $Physics$ in the last half century but neither the discoverers (the HiRes, Auger and Telescope Array Collaborations) nor the presently prevailing cosmic-ray community recognized it as an effect of the $Galactic$ electrostatic potential. The spectral break was erroneously ascribed to the $GZK$ effect [13,14] even if the stunning and unpredicted heavy chemical composition of the cosmic rays above $3.0\times {10}^{18}$ $eV$ [24,25] and the spectral break at $2.7\times {10}^{19}$$eV$ (Figure 13) are blatantly inconsistent with the $GZK$ effect.

Closing this work it is proper to recognize and acknowledge its ultimate empirical foundation.

The negative electric charge, $Q_w$ = - $2.58\times {10}^{31}$C from which the $Galactic$ electric field partially originates, resides on the thin disk made of stars, molecular and atomic Hydrogen and heavier elements. As the negative charge $Q_w$ rotates with the disk at about 240 $km$/s, a Galactic magnetic field is generated (here labeled first component). The magnetic field strength resulting from the rotating charge $Q_w$ is about 1 $\mu$G [1,8] in agreement with the reiterated measurements of about 1 $\mu$G performed during half a century by optical [26,27] and radio astronomers [28,29,30,31].

In addition to the first component, the circulation of $1.34\times {10}^{50}$ cosmic-ray particles through the Galaxy (see Section 1) generates a second component of the $Galactic$ magnetic field of about 1 $\mu$G derived elsewhere (see $Chapters$ 14 and 15 of ref. [8]). The derivation is simple but lengthy3.

Adding the first component (rotating electric charge stored in the Galactic disk) to the second component (cosmic-ray circulation), the strength and magnetic filed line pattern (geometry) of the global, regular, Galactic magnetic field is obtained. The accordance of the magnetic field strength and its geometry with observations, due to its unique and variegated signature, is the ultimate empirical foundation the $Galactic$ electrostatic field and of this work4.