Root Mean Square Error as a Robust Index of Gradient Speech Perception

Bing Cheng; Xiangrong Dai; Xi Xiang; Xiaojuan Zhang; Yang Zhang

doi:10.20944/preprints202510.1806.v1

Submitted:

22 October 2025

Posted:

24 October 2025

You are already at the latest version

Abstract

This study introduces the root mean square error (RMSE) as a new metric for quantifying gradient speech perception in visual analog scale (VAS) tasks. By measuring the deviation of individual responses from an ideal linear mapping between stimulus and percept, RMSE offers a theoretically transparent alternative to traditional metrics like slope, response consistency, and the quadratic coefficient. To validate these metrics, we first used simulated data representing five distinct perceptual response profiles: ideal gradient, categorical, random, midpoint-biased, and conservative. The results revealed that only RMSE correctly tracked the degree of true gradiency, increasing monotonically from the ideal gradient profile (RMSE = 5.48) to random responding (RMSE = 42.16). In contrast, traditional metrics failed critically; for example, slope misclassified non-gradient, midpoint-biased responding as highly gradient (slope = 0.24). When applied to published empirical VAS data, RMSE demonstrated strong convergent validity, correlating robustly with response consistency (r ranging from -0.44 to -0.89) while avoiding the ambiguities of other measures. Crucially, RMSE exhibited moderate-to-high cross-continuum stability (mean r = 0.51), indicating it captures a stable, trait-like perceptual style. By providing a more robust and interpretable measure, RMSE offers a clearer lens for investigating the continuous nature of phonetic categorization and individual differences in speech perception.

Keywords:

phonetic categorization

;

gradient perception

;

categorical perception

;

visual analog scale (VAS)

;

root mean square error (RMSE)

Subject:

Social Sciences - Language and Linguistics

Introduction

Categorical and Gradient Processing in Speech Perception

A foundational concept in speech science is categorical perception (CP), a perceptual mechanism by which listeners map continuous acoustic variations onto discrete phonological categories (Liberman et al., 1957). For example, along a synthesized speech continuum from /da/ to /ta/ characterized by systematic manipulation of the voice onset time (VOT), listeners typically exhibit a sharp categorical shift in identification from /da/ to /ta/ at a specific boundary region (Abramson & Lisker, 1970). This sudden crossover pattern in the continuum indicates that the perceptual system prioritizes efficient categorization over precise tracking of within-category acoustic details.

To quantify CP, researchers commonly employ binary forced-choice paradigms, such as the two-alternative forced-choice (2AFC) identification task, in which participants assign each acoustic stimulus to one of two mutually exclusive phonological categories. This is coupled with a discrimination task (e.g., the ABX paradigm), in which participants judge whether a target stimulus (X) is more similar to one of two preceding stimuli (A or B). CP is then inferred from two key characteristics (see Figure 1): (1) a steep identification function, which reflects a clear categorical boundary, and (2) a peak in discrimination accuracy for paired stimuli that straddle this boundary. These metrics have played a pivotal role in demonstrating the robustness and efficiency of phoneme categorization, particularly under conditions of temporal constraint or acoustic noise (Pisoni, 1973; Winn et al., 2013).

However, the very design of these forced-choice paradigms obscures the processing of within-category detail. By compelling a discrete judgment, such tasks cannot reveal whether listeners perceive an acoustically ambiguous stimulus as intermediate or simply less prototypical (Apfelbaum et al., 2022; McMurray, 2022). To address this limitation, researchers have increasingly adopted graded-response paradigms, including the four-alternative forced choice (4AFC) task (McMurray et al., 2008; Ou et al., 2021) and the visual analog scale (VAS) task (Massaro & Cohen, 1983). Such paradigms enable participants to express graded levels of confidence or perceptual similarity to target categories.

The VAS, in particular, employs a continuous response format: a linear scale anchored by labels for the two target categories, on which participants mark the position corresponding to their perceptual judgment of the stimulus. This approach unveils a more nuanced understanding of speech perception, wherein the response profile is not rigidly step-like but may exhibit smooth transitions or inter-individual variability in the mapping between acoustic inputs and phonological categories (Honda et al., 2024; Kong & Edwards, 2016; McMurray et al., 2010; Myers et al., 2024; Ou et al., 2021). These findings have driven a theoretical paradigm shift toward recognizing gradient perception (GP) as a core characteristic of the speech perceptual system. Instead of collapsing acoustic stimuli into discrete categorical bins, listeners may encode sub-phonemic acoustic details, including VOT (Lisker & Abramson, 1964), fundamental frequency (F0) (Ohde, 1984), spectral tilt (Stevens & Klatt, 1974), and vowel formants (Flege et al., 1997), and retain this information to support downstream cognitive processes, such as lexical access (Kapnoula et al., 2021; McMurray et al., 2002), word segmentation (Kapnoula & McMurray, 2021), and talker adaptation (Goldinger et al., 1991). Empirical research in this domain has demonstrated that GP is particularly advantageous in uncertain or variable listening contexts where acoustic cues are degraded or categorical boundaries exhibit flexibility (Clayards et al., 2008).

Notably, GP is not just the antithesis of CP; rather, it represents a distinct cognitive strategy that can coexist with categorical processing mechanisms. Neurocognitive evidence (Kapnoula & McMurray, 2021; Ou & Yu, 2022; Sarrett et al., 2020) supports a dual-route framework of speech perception, in which discrete categorical and gradient representations emerge in parallel, potentially engaging distinct brain regions or temporal profiles. This emerging framework positions GP as a fundamental and functionally significant component of speech perceptual processing.

This paradigm shift toward studying gradient phenomena has introduced a critical methodological challenge: how can we best quantify the degree of gradiency in a listener’s perception? While VAS tasks provide richer data, the metrics used to analyze them have not always kept pace, often carrying assumptions inherited from the categorical framework. A more robust quantitative approach is needed to fully characterize how listeners map continuous acoustic variation onto their internal perceptual space.

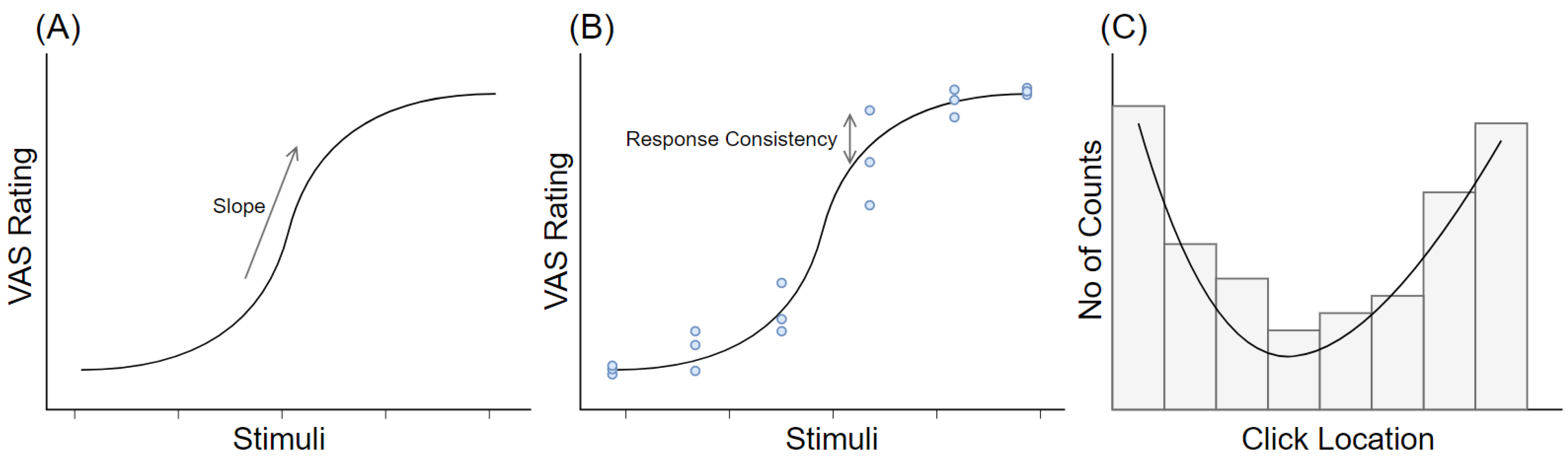
Existing Metrics and Their Limitations

As VAS tasks have become increasingly common in studies of fine-grained perceptual processes, particularly in speech perception research (Honda et al., 2024; Munson & Carlson, 2016), three primary metrics have emerged to quantify the degree of gradient perception from continuous response data. Each provides a distinct analytical lens of how individuals map acoustic variation onto perceptual ratings: slope-based metrics derived from sigmoid curve fitting, residual-based metrics of response consistency, and distribution-focused metrics involving curve fitting. Collectively, they provide distinct analytical lenses for determining whether perceptual responses exhibit smooth continuity (gradient characteristics) or sharp discreteness (categorical characteristics). However, each metric is susceptible to artifacts that can misrepresent listeners’ underlying perceptual processing.

One widely adopted approach in speech perception research draws on the theoretical logic of sigmoid fitting, a method frequently used to model categorical perception shifts. A four-parameter logistic function (Kapnoula et al., 2017; McMurray et al., 2010) is fitted to average VAS ratings across stimulus steps, generating an estimate of the curve’s steepness at its midpoint. This slope steepness (see Figure 2A) is typically interpreted as an indicator of perceptual gradiency. A shallower slope denotes a more gradual, continuous transition between categories, reflecting a smoother, gradient-driven response pattern in listeners. In contrast, a steeper slope implies an abrupt categorical shift, consistent with CP, wherein listeners transition sharply between categories as stimulus properties change. This method aligns with the established mathematical framework of categorical shifts, rendering it intuitive and closely aligned with theoretical models of CP.

Another prominent approach centers on response consistency (variability), redirecting the analytical focus from the overall shape of the response curve to the variability of individual responses (see Figure 2B). Researchers have proposed metrics such as residual standard deviation and mean squared residuals to quantify the extent to which a participant’s ratings deviate from a smooth regression line (linear or non-linear) fitted to their data (Fuhrmeister et al., 2023; Myers et al., 2024). This approach yields a measure of internal perceptual consistency: the lower the variability in a participant’s judgments across repeated presentations of the same stimulus, the more consistent and stable their perceptual processing. Reduced residual variance indicates a more uniform response pattern, a characteristic feature of gradient perceivers who apply a consistent perceptual criterion across the stimulus continuum. Conversely, higher variability often indicates boundary effects, in which participants show uncertainty or fluctuation between categories.

A third strategy involves analyzing response histograms across VAS steps (Kong & Edwards, 2016; Lee & Park, 2024), with a focus on the distributional shape of responses (see Figure 2C). Some individuals exhibit a tendency to cluster responses at the two endpoints of the scale, producing a bimodal distribution that indicates a propensity for categorical responding. Others distribute responses more evenly across the entire scale, reflecting a more gradual, gradient-like response pattern. To quantify these differences, researchers fit a second-order polynomial function to response distributions and use the quadratic coefficient as an index of gradiency (Kong & Edwards, 2011; Kong, 2019). A larger concave-up quadratic coefficient corresponds to a peaked (categorical) distribution, while a flatter curve indicates a more uniform, continuous distribution of responses. This method is particularly valuable as it directly links to the shape of the response distribution, providing a visual and intuitive means of assessing how evenly participants map acoustic variation onto perceptual categories. It offers a straightforward approach to distinguishing between more categorical and more gradient-like response profiles based on distributional curvature.

Despite their wide use, each of these metrics is vulnerable to specific confounds that can lead to misleading interpretations of perceptual gradiency. Slope-based metrics, for example, are susceptible to non-perceptual artifacts; a listener who strategically compresses their responses may produce an artificially shallow slope, giving the false appearance of gradiency. A related, but more paradoxical, issue plagues consistency metrics. Specifically, a highly categorical listener who consistently chooses only the endpoints will produce minimal residuals, leading to the misclassification of their categorical strategy as highly consistent or gradient. Conversely, a listener making subtle, fine-grained distinctions might exhibit more trial-to-trial variability, which could be incorrectly labeled as “noisy” processing. Finally, distributional metrics introduce a problem of ambiguity. Because they collapse data into a single curvature index, they cannot distinguish between principled, linear gradiency and simple random responding, as both can produce the same flat, low-curvature signature. These examples reveal a common weakness: existing metrics act as indirect proxies for gradiency and can be biased by the very behavioral patterns they were intended to detect. This underscores the need for a metric that moves beyond inferring gradiency from slope, consistency, or distribution, and instead directly quantifies the fidelity of listeners’ responses to the underlying acoustic continuum.

The Present Study: RMSE as a Measure of Deviation from Linearity

A central challenge in quantifying gradient perception lies in d establishing a theoretical benchmark for “ideal gradiency.” Whereas a categorical perceiver is expected to produce a step-like function, an ideal linear-gradient perceiver would map each incremental acoustic change onto a proportionally graded judgment. On a VAS task, this translates to a perfectly linear response pattern, where the endpoints correspond to the category prototypes and all intermediate stimuli are spaced evenly between them. This idealized mapping represents a perceptual system that tracks acoustic detail with perfect fidelity, free from categorical compression or random noise. As such, it provides a powerful and theoretically grounded benchmark against which a real listener’s performance can be measured.

While existing metrics like slope, consistency, and the quadratic coefficient provide partial insights, none directly quantifies how closely a listener’s responses adhere to this linear ideal. Each is limited by restrictive assumptions or a sensitivity to artifacts that can obscure the underlying perceptual strategy. What is needed is a metric that measures the deviation from ideal linearity itself.

To address this gap, we introduce the Root Mean Square Error (RMSE) as a formal measure of this deviation. The core idea is simple: gradient perception is the inverse of deviation from linearity. The smaller the discrepancy between listeners’ observed responses and the ideal linear pattern, the more gradient their perception. Formally, RMSE is defined as:

R M S E = \sqrt{\frac{1}{N} \sum_{i = 1}^{N} (y_{i} - {\hat{y}}_{i})^{2}},

where

y_{i}

is the observed VAS rating for trial

i

,

{\hat{y}}_{i}

is the ideal rating predicted by the linear mapping between stimulus step and response scale, and

N

is the total number of trials. This formula yields a single, continuous value representing the average magnitude of error (deviation) between a participant’s actual responses and those of an ideal gradient perceiver. By squaring the deviations, the metric gives greater weight to large errors and prevents positive and negative errors from canceling out, making it a highly sensitive index of non-linearity.

A key advantage of RMSE is that it holistically captures the two fundamental sources of error: systematic bias and random variance. This property can be illustrated by its mathematical decomposition, analogous to mean squared error in statistical theory (Walther & Moore, 2005):

R M S E^{2} = B i a s^{2} + V a r i a n c e .

Here, Bias quantifies systematic departures from ideal linearity, the S-shaped curve of a categorical perceiver or the flat line of a conservative responder, while Variance captures trial-to-trial inconsistency or random noise in responses, independent of their overall shape. This dual sensitivity to both bias and variance is what distinguishes RMSE from traditional metrics. Traditional metrics, by contrast, are ill-equipped to handle this dual challenge. Response consistency, for example, captures low variance but is completely blind to bias, leading to the paradoxical result where a categorical perceiver who uses only the endpoints is favorably scored as highly consistent. On the other hand, slope and quadratic coefficients are designed to detect bias but are easily confounded by variance, making them unable to distinguish principled linearity from simple random responding. By integrating these two distinct sources of error, RMSE provides a more robust and theoretically complete measure of how faithfully listeners tracks a continuous acoustic signal.

The primary goal of this study is to validate RMSE against these traditional metrics. To achieve this, our investigation follows a two-pronged approach. First, we used simulations to establish the theoretical validity of each metric. We generated data from five distinct response profiles, i.e., ideal gradient, categorical, random, midpoint-biased, and conservative, to assess how each metric behaves under these known ground-truth conditions. We hypothesized that while traditional metrics would yield ambiguous or misleading values for some profiles, RMSE would uniquely maintain a clear, monotonic relationship with the degree of deviation from ideal gradiency.

Second, we applied this analytical framework to human VAS data collected across multiple speech continua. This allowed us to evaluate the convergent validity of the metrics and, crucially, to assess their stability. If gradiency is a stable, trait-like perceptual style, a robust metric should yield consistent scores for an individual across different tasks. We predicted that RMSE, by measuring deviation from a fixed ideal, would demonstrate higher cross-continuum stability than metrics more susceptible to task-specific response biases. Together, these analyses position RMSE not just as another calculation, but as a theoretically grounded tool for quantifying how accurately listeners’ perception maps onto the physical reality of the speech signal.

Method

Data Source and Participants

All human participant data for the present study were sourced from Kim et al. (2025). Participants were recruited via the online research platform Prolific (www.prolific.com), provided informed consent in compliance with the requirements of the University of Iowa Institutional Review Board, and were compensated at a rate of $12 per hour.

Initially, 78 participants completed all experimental tasks. To ensure data validity, raw VAS ratings were preprocessed at the individual level: participants with near-flat response slopes (a marker of random or unreliable perceptual judgments) were excluded. The exclusion criterion specifically targeted participants whose responses at step 1 (the extreme lower end of the scale) exceeded 25% and those at step 9 (the extreme upper end) accounted for less than 75%. This step eliminated individuals who failed to discriminate unambiguous stimuli or provided arbitrary responses. Ten participants were excluded, resulting in a final sample of 68 native speakers of American English (33 female). None of the participants reported speech, hearing, or neurological impairments, and the sample had a mean age of 32.2 years (SD = 4.9).

Stimuli

Stimuli comprised eight speech continua, each spanning a set of monosyllabic minimal pairs. These continua covered three phonetic categories: five vowel pairs (e.g., beet–boot, bet–bat), two stop voicing pairs (e.g., beach–peach, dime–time), and one fricative place pair (sip–ship). Certain continua were phonetically proximal (e.g., sharing phonemic components), while others were phonetically distal (e.g., /s/~/ʃ/ vs. /b/~/p/); this design was intended to explore how phonetic proximity influences the stability of perceptual traits.

All minimal pair tokens were recorded by a native male speaker of American English within the carrier sentence “He said ____.” Target words were excised from the carrier sentences and manipulated to create nine equidistant steps per continuum, utilizing phonetically validated techniques customized to each phonetic category (e.g., cross-splicing for stop consonants, spectral averaging for fricatives). Detailed procedures for stimulus development are available in the supplementary materials of the original study.

Phonetic analysis confirmed acoustic distinguishability between the extreme steps of each continuum: vowel continua differed primarily in formant frequencies or vowel duration; stop continua differed in VOT and post-stop vowel duration; fricative continua differed in the spectrum of frication noise (a key cue for sibilant discrimination).

Procedure

Experimental procedures adhered to the design outlined in the original data source. Tasks were constructed using Gorilla Experiment Builder (Anwyl-Irvine et al., 2020) and were completed by participants on personal computers (mobile devices were prohibited to ensure consistent task presentation).

Participants first completed a headphone/earphone check to verify audio playback quality. Participants who failed this check (due to insufficient audio quality, which would compromise stimulus perception) were excluded from further participation. Finally, participants completed the VAS task to assess gradient perception.

The VAS task served as the source of gradient perception data. On each trial, a horizontal line was displayed, with clipart corresponding to the endpoint words of the current continuum positioned at each end of the line. Participants listened to the stimulus binaurally, then selected a position on the line to rate the stimulus’s similarity to the two endpoint words. Participants were permitted to revise their responses with no time constraint, and the next trial initiated 300 ms after the final response was confirmed.

Trials were organized into blocks by continuum (to minimize cognitive demands associated with endpoint remapping), and the left/right assignment of continuum endpoints was reversed across two experimental sessions. Each participant completed 432 trials in total, calculated as follows: 9 stimulus steps × 8 continua × 3 repetitions × 2 sessions. The order of continua was randomized for each participant in each session. Prior to the main task, participants completed three practice trials (utilizing endpoint stimuli) to familiarize themselves with the response format. The VAS task required approximately 20 minutes to complete.

Data Analysis

For each speech continuum, an ideal response mapping was established to represent maximally gradient perception. In this mapping, the 0–100 VAS range was linearly assigned to the nine stimulus steps (e.g., step 1 = 0, step 9 = 100). This ideal linear gradiency captures the theoretical pattern of a perceiver who tracks acoustic variation continuously, without categorical discontinuities or random variability, and serves as a benchmark for evaluating individual response patterns.

To compute the RMSE, which quantifies each participant’s deviation from the ideal mapping, each observed VAS value was paired with the corresponding ideal value for its stimulus step. Squared deviations were then averaged, and the square root of this average produced the RMSE. The resulting value reflects the average magnitude of deviation between participants’ observed responses and the theoretical ideal gradient across all trials. A more detailed rationale for this formula and its theoretical grounding is provided in the section The present study: RMSE as a measure of deviation from linearity.

Three traditional gradiency metrics were also computed, with detailed procedures as follows: Slope and response consistency, derived from a four-parameter logistic function fitted to the mean VAS responses across stimulus steps. The logistic function (McMurray et al., 2010) takes the form:

p (x) = b_{1} + \frac{b_{2} - b_{1}}{1 + \exp (- 4 s \cdot \frac{x - c}{b_{2} - b_{1}})},

where

b_{1}

and

b_{2}

are the lower and upper asymptotes,

s

is the slope parameter, and

c

is the estimated boundary location (the inflection point). The slope parameter (

s

) is used as a traditional index of categoricality, where a higher value indicates a steeper, more binary transition. Additionally, we calculated response consistency as the reverse of residual standard deviations from this logistic model. This ratio captures within-step variability relative to the fit, providing a signal of perceptual uncertainty.

Quadratic coefficient was obtained by fitting a second-order polynomial function (Kong & Edwards, 2016) to the complete histogram of VAS responses across the continuum. The quadratic term of the function (i.e., the coefficient of x²) was used as an index of categoricality: higher positive coefficients correspond to more U-shaped, endpoint-biased distributions (signaling a stronger tendency toward categorical responding), while lower coefficients indicate responses are spread more uniformly across the VAS range (reflecting stronger gradient perception).

To evaluate the relationships between the RMSE and traditional metrics, and to verify the convergent validity of the new RMSE indicator, analyses focused on within-continuum associations. For each of the eight continua, pairwise Pearson correlation coefficients were computed between all four gradiency metrics. To identify the metric with the highest consistency across continua (a critical criterion for a robust gradiency measure), each metric was computed for all eight continua per participant. For each participant, pairwise Pearson correlation coefficients were then calculated across all possible continuum pairs. The average of these correlation coefficients per participant generated a stability score for each metric. Stability scores were subsequently compared across the four metrics: higher average correlation values indicated greater cross-continuum consistency.

Additionally, to assess the theoretical validity and sensitivity of each gradiency metric prior to applying them to human data, we generated simulated datasets representing canonical perceptual response profiles. Five synthetic participant types were defined: ideal gradient, categorical, random, midpoint-biased, and conservative responders. Each simulated participant produced responses for nine stimulus steps with six repetitions per step, and responses were drawn from predefined response functions with additive Gaussian noise (SD = 5).

The ideal gradient profile represented a listener who tracks the acoustic continuum in a perfectly proportional manner. Responses increased linearly with stimulus step, reflecting a one-to-one mapping between acoustic variation and perceived category strength. This pattern served as the theoretical benchmark of maximal gradiency, where deviations from linearity are minimal.

The categorical profile modeled a listener who enforces a sharp perceptual boundary between categories. Responses followed a four-parameter logistic function with a steep slope at the midpoint, yielding near-zero ratings for stimuli below the boundary and near-100 ratings above it. This function captures the canonical signature of categorical perception while retaining minor variability from added noise.

The random profile simulated an inattentive or disengaged participant whose responses bear no relation to the acoustic input. Each trial’s response was sampled from a uniform distribution spanning the full 0–100 VAS range, resulting in a flat, unstructured distribution that serves as a baseline for evaluating the metrics’ susceptibility to non-perceptual noise.

The midpoint-biased profile reflected a listener who consistently avoids strong category judgments, perhaps due to indecision or misunderstanding of task demands. Responses were normally distributed around the scale midpoint (mean = 50), independent of step number, producing an apparent flat function that could superficially resemble weak gradiency.

Finally, the conservative profile represented a listener who underutilizes scale extremes, systematically hedging ratings toward intermediate values. Early continuum steps received ratings shifted upward from 0 (e.g., ~20) and late steps received ratings shifted downward from 100 (e.g., ~80), compressing the response range. This produces a shallower slope driven by categorical uncertainty rather than gradient perception.

All four gradiency metrics were computed for each simulated dataset using the same analysis pipeline applied to the human data. This simulation framework provided a controlled benchmark for testing whether each metric responds systematically to known perceptual structures and whether it remains interpretable under non-ideal response behaviors.

Results

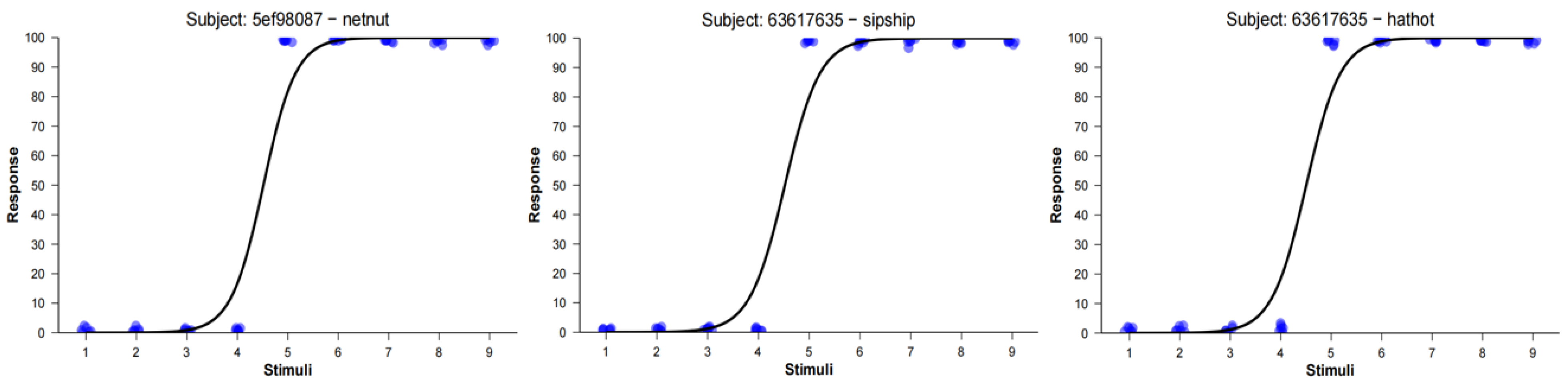
Simulated Data

To benchmark the validity of each metric, we first tested them against simulated listeners with five theoretically defined response profiles: ideal gradient, categorical, random, midpoint-biased, and conservative. These simulations serve as a proof of concept, allowing us to assess how each metric performs under known and perfectly controlled conditions. The characteristic response patterns for each profile are illustrated in Figure 3, with their corresponding metric values presented in Table 1.

The RMSE metric successfully and unambiguously identified the ideal gradient perceiver. As predicted, the ideal gradient profile yielded the lowest RMSE value (5.481), reflecting minimal deviation from the expected linear response structure. Critically, RMSE values increased monotonically in a manner that tracked the theoretical degree of structured perception: conservative responding showed modest elevation (13.378), categorical perception demonstrated substantial deviation (26.194), and unstructured patterns (midpoint-biased: 32.063; random: 42.159) registered the highest values. This result demonstrates that RMSE provides a clear, graded index that correctly maps onto the theoretical continuum from perfect gradiency to unstructured noise.

In stark contrast, the traditional metrics exhibited misclassifications. Slope proved unreliable, yielding a near-zero value for the midpoint-biased profile (0.241) that was even shallower than both the ideal gradient (12.781) and conservative (11.129) patterns, creating the false impression of gradiency. It also produced an extremely high, uninterpretable value for the random profile (81.936). Response consistency failed to distinguish between the categorical perception (-2.285) and ideal gradient perception (-5.263), assigning them similarly favorable scores despite them representing fundamentally opposite perceptual modes. This limited discriminative power makes response consistency inadequate for distinguishing continuous from categorical phonetic processing. The quadratic coefficient was similarly problematic, producing nearly identical near-zero values for both ideal gradient (0.189) and random (0.070) profiles, rendering it incapable of distinguishing structured perception from noise. This coefficient also failed to clearly distinguish the artifactual curvature in midpoint-biased responding (-1.515) from meaningful nonlinearity. Collectively, these simulations demonstrate that only RMSE possesses the diagnostic specificity required to isolate true gradient perception from all alternative response strategies. This ability to avoid misclassification is essential for its valid application to empirical data.

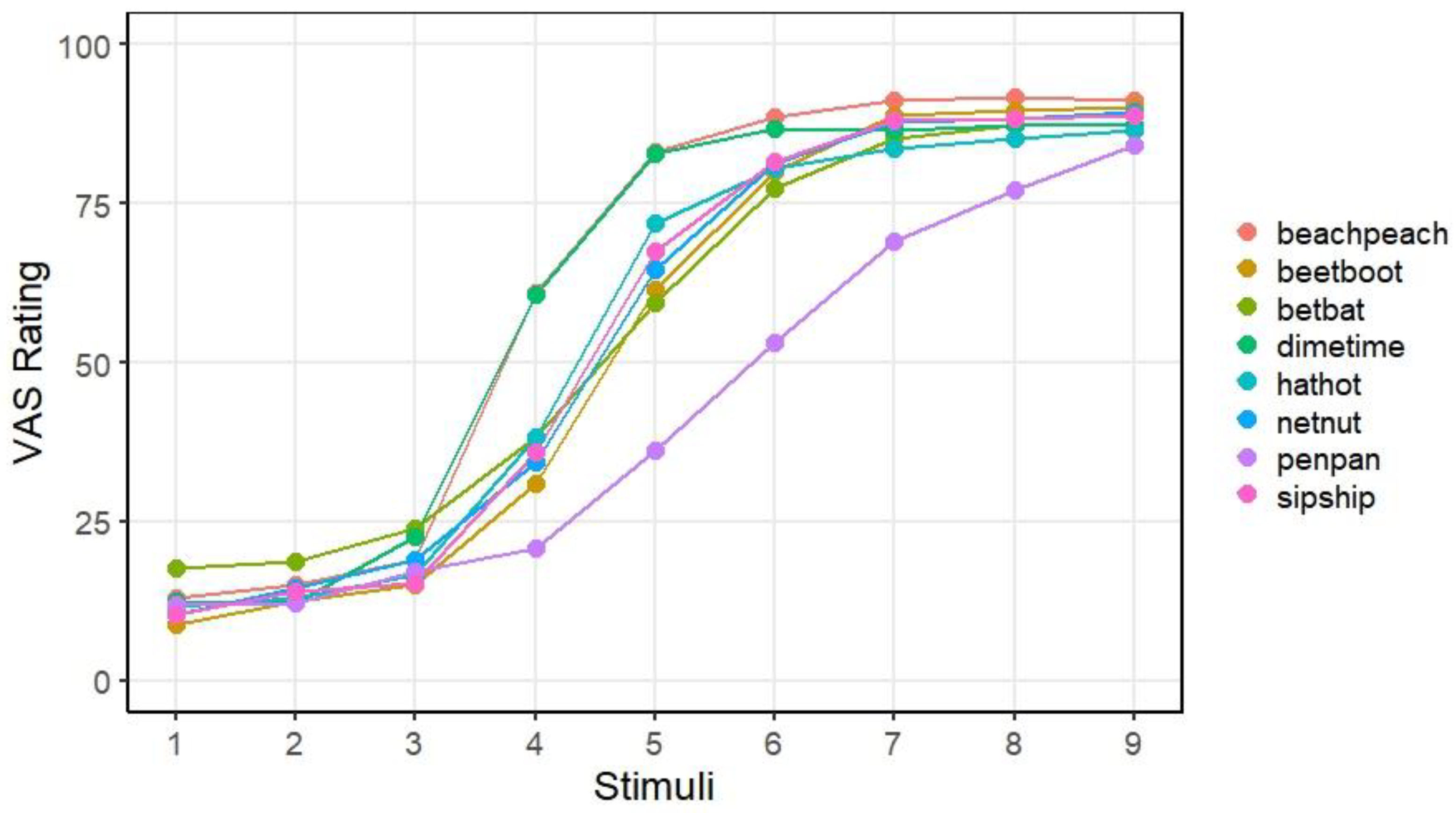
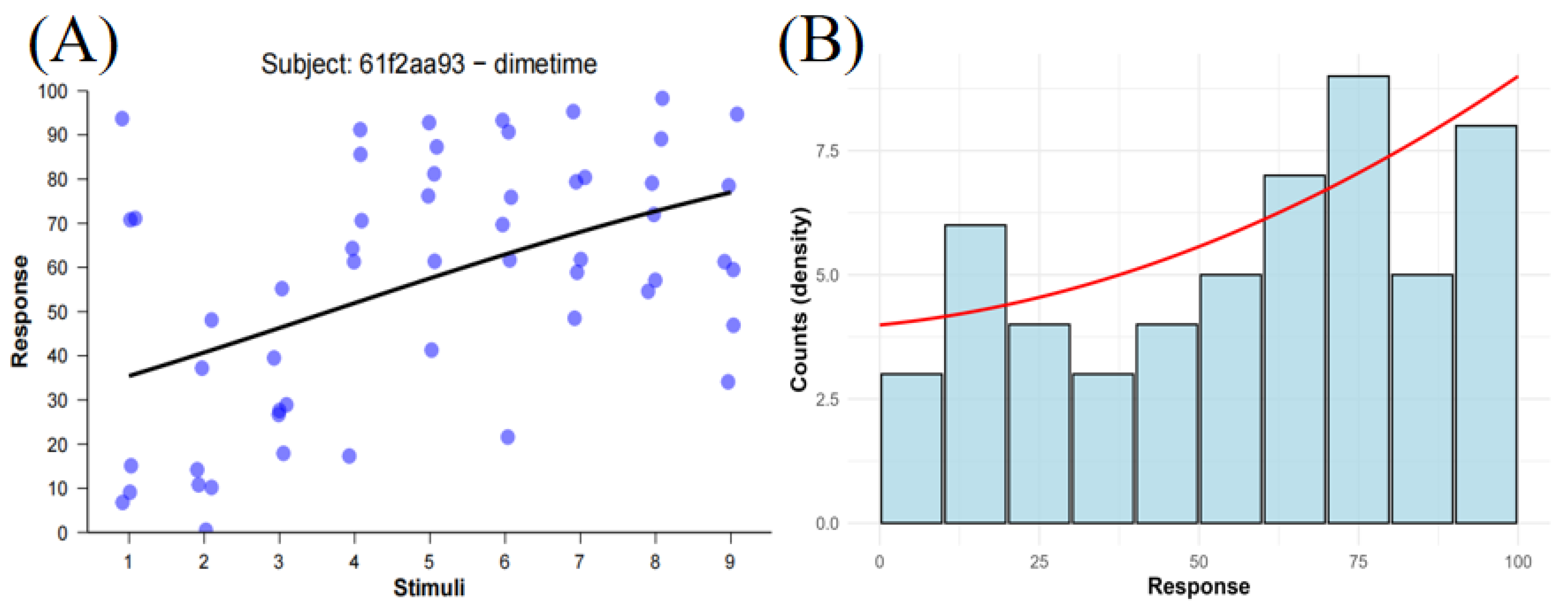
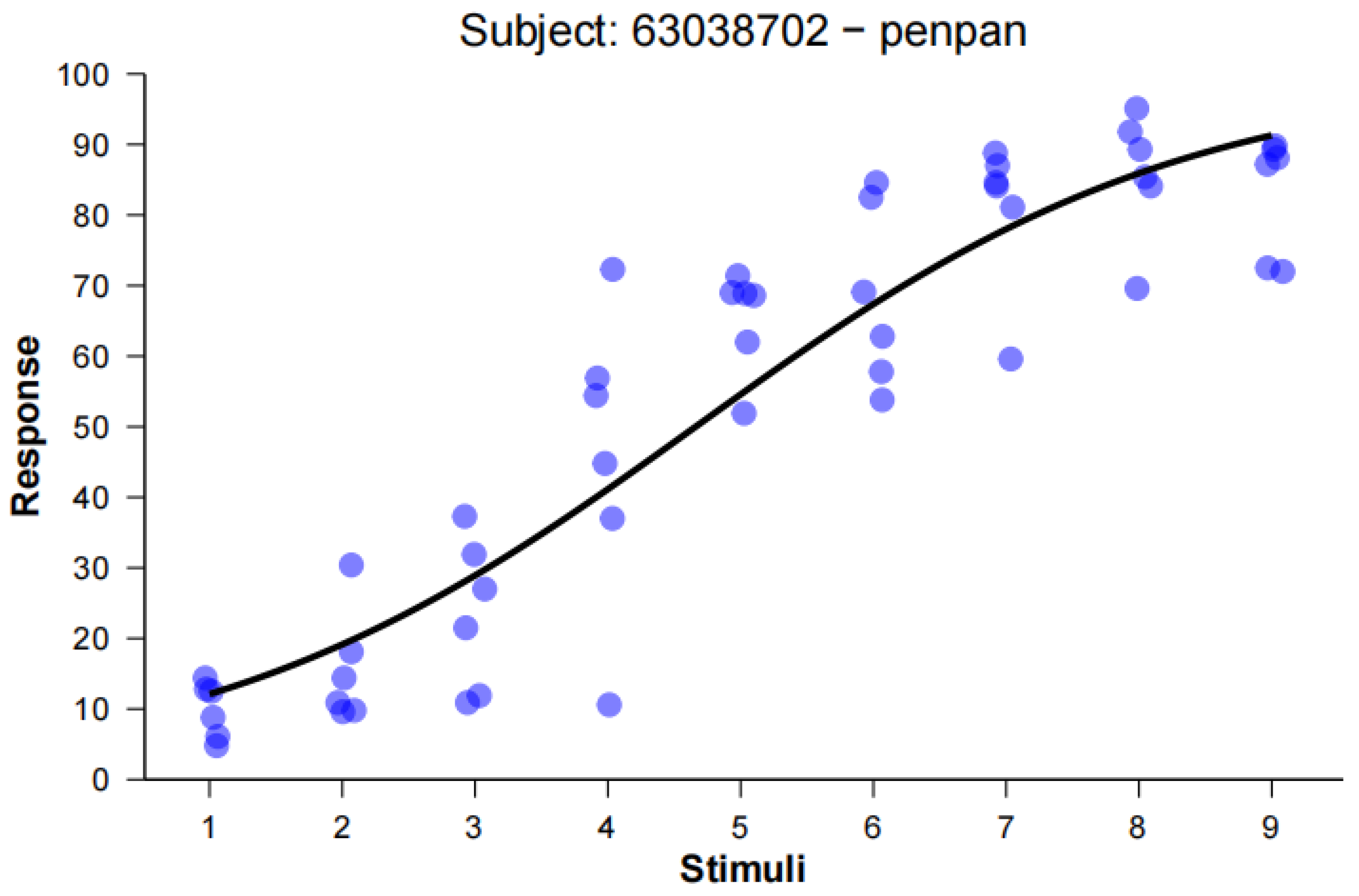
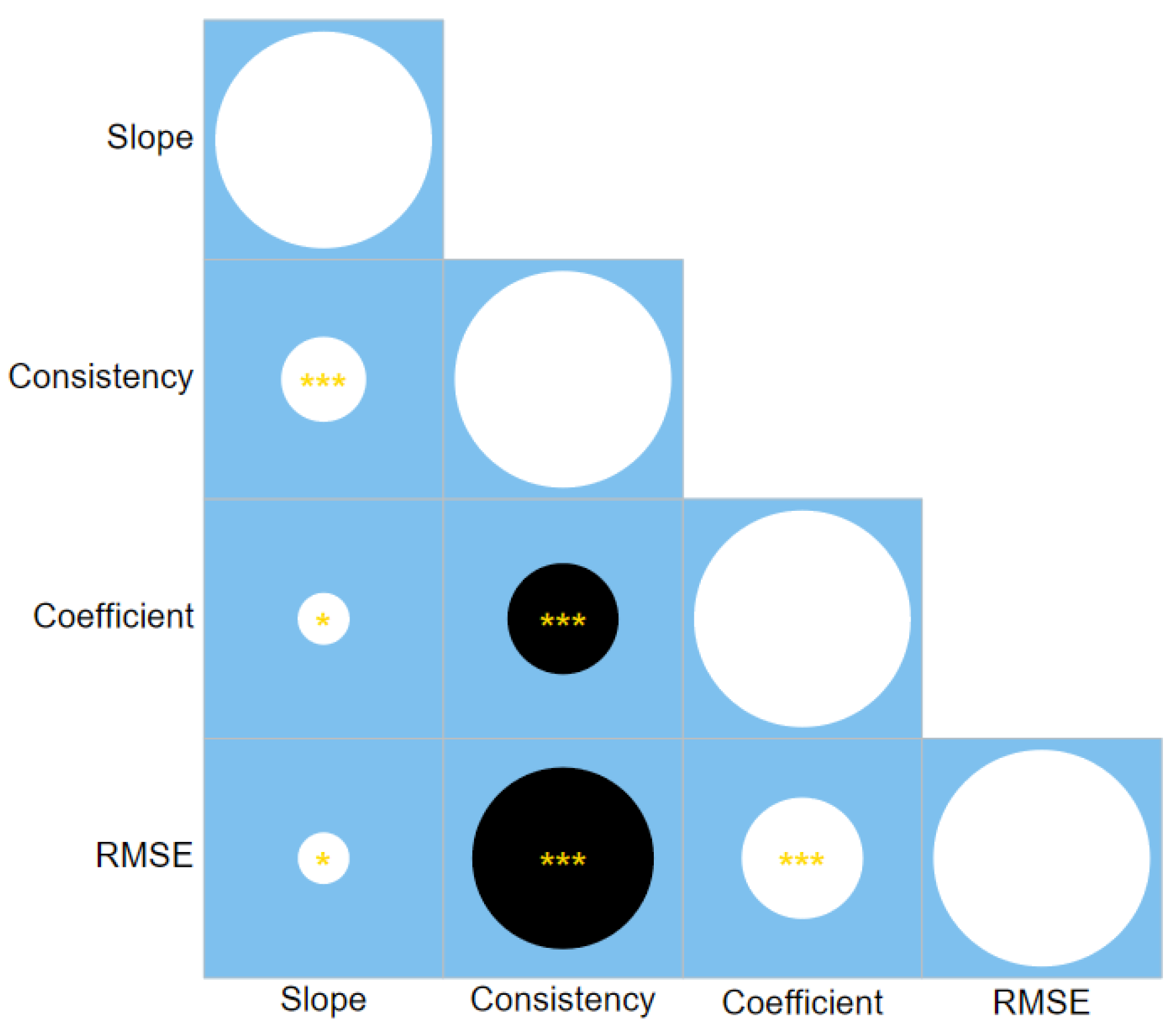
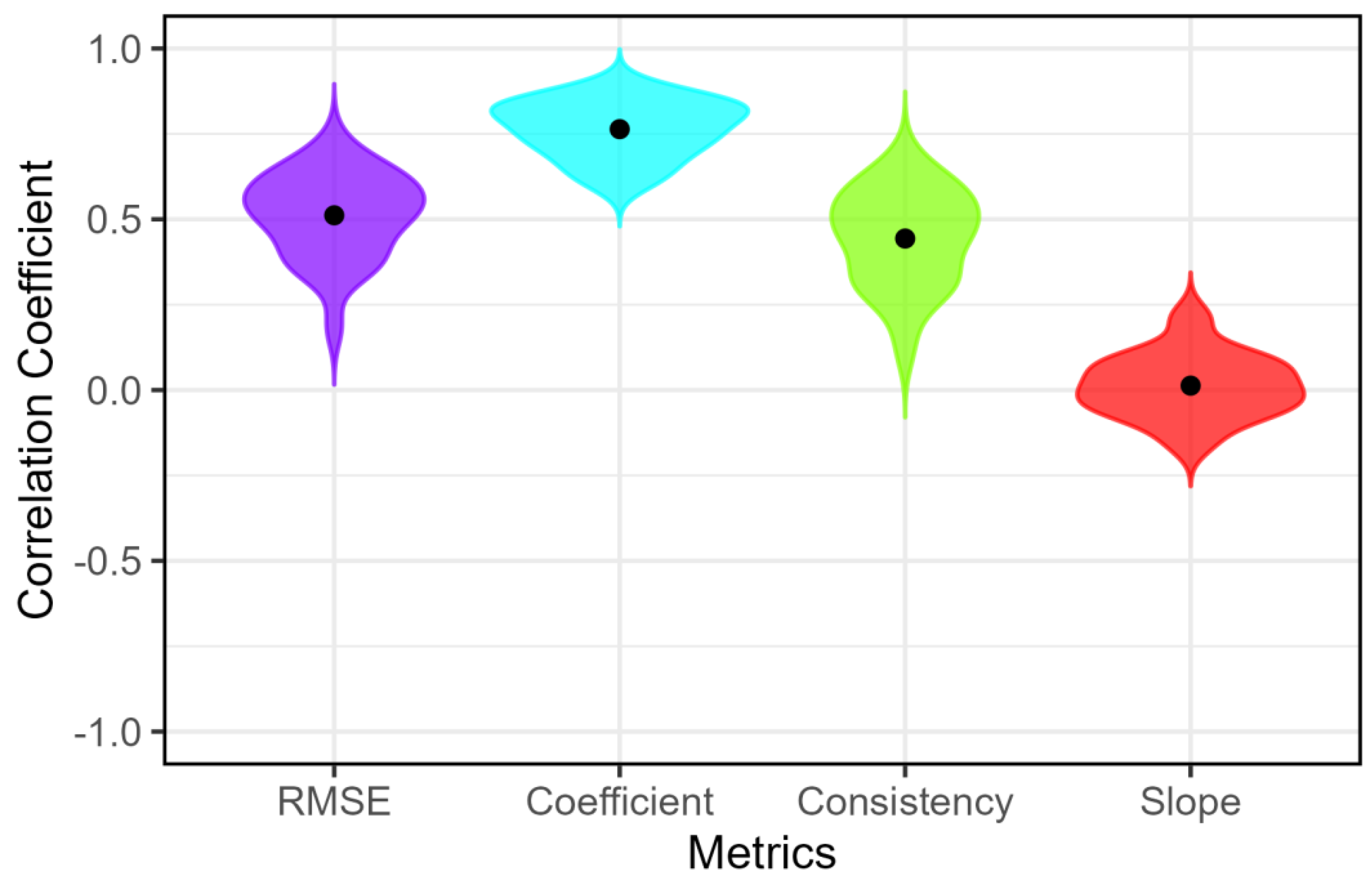
Empirical Data

Having established the theoretical validity of RMSE, we next applied all four metrics to the human VAS data. As a descriptive overview, Figure 4 shows average VAS responses as a function of continuum step for each contrast. As expected, most continua produced monotonically increasing response functions, with higher VAS ratings assigned to later steps along the acoustic continuum. However, the steepness and shape of these curves varied by contrast. Voicing continua such as beach–peach and dime–time showed the steepest slopes, indicating strong categorical responding. In contrast, vowel and fricative continua, particularly pen–pan, produced shallower response functions, consistent with more gradient or variable perceptual patterns. These data provide a rich and realistic testbed for evaluating how each metric captures this behavioral diversity.

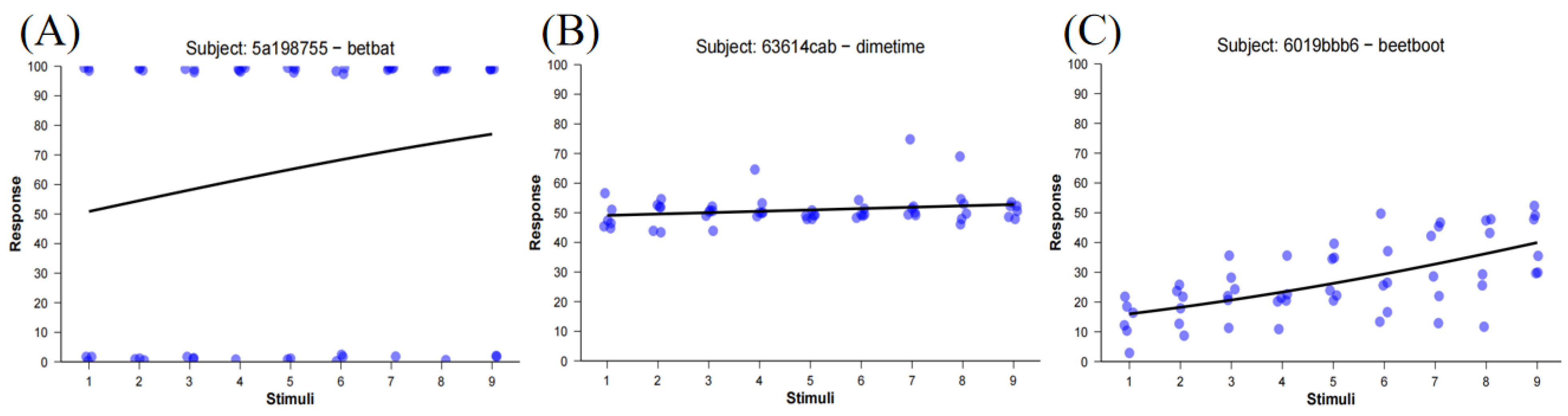
Failures of Traditional Metrics in Practice

The empirical data reveal that the theoretical flaws of traditional metrics lead to systematic misinterpretations of listener behavior. A critical flaw of the slope metric is its ambiguity. While a shallow slope is often assumed to indicate gradiency, it more frequently signals a distortion of the response space rather than superior perceptual sensitivity. As shown in Figure 5, extremely shallow slopes often arise from clearly non-gradient behaviors. For instance, a participant responding randomly by choosing only the endpoints (0 or 100) in roughly equal proportions produced a near-zero slope of 0.041 (Figure 5A). Similarly, a listener who conservatively clustered all responses around the scale’s midpoint generated a very shallow slope of 0.634 (Figure 5B). Finally, a participant who used only a compressed portion of the scale, likely due to inattention, produced a reduced slope of 3.306 (Figure 5C). In each of these real-world cases, a shallow slope did not reflect principled gradient perception but rather a failure to map the acoustic continuum onto the response scale.

The response consistency metric is undermined by a central paradox: it often assigns the most favorable scores to the most categorical listeners. Because categorical responders concentrate their choices at the scale’s endpoints, their responses show very little deviation from a fitted sigmoid curve, except at the boundary. This results in minimal residuals and, consequently, a high consistency score (Figure 6). In contrast, a truly gradient perceiver making fine-grained distinctions may exhibit more trial-to-trial variability as a natural consequence of the higher cognitive demand, leading to a worse consistency score. The metric thus systematically mistakes rigid, categorical behavior for stable, gradient perception, making it an unreliable index on its own.

The quadratic coefficient’s primary limitation is its inability to distinguish a principled, uniform use of the scale from a random one. A U-shaped response distribution (many endpoint responses) yields a large positive coefficient, while a flat distribution yields a near-zero coefficient. Although an ideal gradient perceiver might produce a flat distribution, so too will a participant responding randomly across the entire scale (Figure 7). Therefore, a small quadratic coefficient is a necessary but insufficient condition for gradiency, also making it an ambiguous and unreliable index on its own.

RMSE as a Valid and Stable Index of Gradiency

In contrast to these flawed metrics, RMSE robustly quantifies the degree to which a listener’s responses approximate the ideal linear mapping. Figure 8 shows an exemplar participant whose profile was identified by a very low RMSE score (13.769). This individual’s responses are tightly distributed around the ideal linear function, spanning the full scale and showing progressive differentiation between steps, which perfectly embodies the theoretical ideal of gradient perception. The other metrics for this same participant (slope = 19.216, response consistency = -10.647, quadratic coefficient = 0.147) fail to capture this near-ideal performance with the same clarity.

To further validate RMSE, we assessed its convergent validity and cross-continuum stability. Within-continuum correlations (Figure 9) revealed that RMSE’s relationships with other metrics were both logical and informative. RMSE showed a strong negative correlation with response consistency across all eight continua (rs ranging from -0.44 to -0.89, all ps < .001), confirming that lower deviation from linearity aligns with more stable responding. Likewise, RMSE correlated positively with the quadratic coefficient in six of the eight continua (rs ranging from 0.260 to 0.442, ps < .05), indicating that more U-shaped, categorical distributions are appropriately associated with higher error. In contrast, correlations between slope and RMSE were inconsistent and largely non-significant (rs ranging from -0.357 to 0.233, ps > .05), with the exception of the bet–bat continuum (r = −0.357, p < .01), suggesting that RMSE is not susceptible to the artifacts that make shallow slopes ambiguous. This overall pattern shows that RMSE selectively integrates the valid information from other metrics while successfully rejecting their noise.

A second line of evidence comes from cross-continuum stability (Figure 10), which assess whether a metric captures a stable, trait-like perceptual style. RMSE demonstrated moderate-to-high stability (mean r = 0.512), significantly outperforming slope (mean r = 0.013) and response consistency (mean r = 0.444). While the quadratic coefficient showed the highest stability (mean r = 0.764), its stability likely reflects a consistent response bias (e.g., a tendency to use endpoints) rather than a consistent perceptual strategy. RMSE’s stability, however, is more meaningful: it demonstrates that individuals who faithfully track the acoustic continuum in one task tend to do so in others. In sum, the empirical analyses confirm the findings from our simulations. Traditional metrics are prone to systematic misinterpretations, whereas RMSE provides a direct, robust, and stable quantification of gradient perception that is grounded in a clear theoretical ideal.

Discussion

The present study introduced and validated the RMSE as a theoretically grounded metric for quantifying gradient perception. Across both simulated and empirical data, RMSE proved to be a uniquely robust measure of how faithfully a listener’s responses track a continuous acoustic signal. Unlike traditional metrics that act as indirect proxies, RMSE directly operationalizes gradiency as the deviation from an ideal linear mapping. Our results demonstrate that while metrics like slope, consistency, and the quadratic coefficient capture certain aspects of perceptual behavior, they are systematically vulnerable to confounds that can lead to misleading conclusions. In contrast, RMSE provides a single, interpretable, and stable index that successfully distinguishes principled gradient perception from categorical, random, or biased responding.

Reinterpreting the Field: How RMSE Resolves Critical Flaws in Traditional Metrics

The significance of RMSE extends beyond being a numerically superior tool; it exposes and resolves systemic interpretive flaws in how gradiency has been conceptualized and measured. The slope of a logistic function, long inherited from categorical perception paradigms, is often treated as an inverse proxy for gradiency. Our analyses show this assumption to be untenable. We found that shallow slopes routinely emerge from non-gradient behaviors like random responding, conservative midpoint clustering, or inattentive scale use. This finding offers a new lens through which to interpret prior work (e.g., Kutlu et al. (2024); Theodore et al. (2015) where participants with unusually flat slopes may not have been “hyper-gradient” perceivers, but rather individuals exhibiting non-systematic response patterns. RMSE corrects this by correctly identifying such patterns as having high error, providing a principled distinction between genuine gradiency and task-related noise.

Metrics of response consistency, computed as the inverse of residual variability, have been used to capture the internal stability of perception, under the assumption that gradient perceivers are more consistent. Our results reveal the opposite: the highest consistency scores were achieved by strongly categorical responders who rigidly selected the endpoints. This occurs because making fine-grained gradient judgments is cognitively demanding and naturally invites more trial-to-trial variability than low-effort categorical choices. This insight suggests that studies interpreting low residual variance as a sign of gradiency (e.g., Fuhrmeister et al. (2023) Myers et al. (2024) may have inadvertently prioritized categorical behavior. RMSE sidesteps this “consistency paradox” entirely by rewarding stimulus-response fidelity, not mere response uniformity.

Finally, the quadratic coefficient, while intuitive, discards the essential stepwise relationship between stimulus and response. By collapsing all responses into a single histogram, it cannot distinguish a truly gradient perceiver from a participant responding randomly across the scale. This limitation suggests that listeners previously classified as gradient based on flat response distributions (e.g., Kong and Edwards (2016); Lee and Park (2024) may have included a mix of genuine gradient perceivers and random responders. RMSE circumvents this issue by preserving the trial-level correspondence between stimulus step and percept, ensuring that gradiency is defined by structured sensitivity to acoustic variation, not just distributional shape.

Theoretical and Practical Contributions of RMSE

By addressing these pitfalls, RMSE offers more than a methodological fix; it provides a conceptual refinement. By computing the root mean square deviation between observed and ideal responses, RMSE directly penalizes both random responding and categorical endpoint compression, resolving the flat slope and distribution fallacies. Because it does not assume that lower variability is better, it also avoids the consistency paradox, providing a measure that rewards accurate, stepwise mapping rather than effortless uniformity. Importantly, RMSE redefines the measurement of gradient perception to align with its theoretical meaning: the faithful encoding of continuous acoustic detail. This has profound implications for the field.

For individual differences research, RMSE offers a “purer” measure of gradiency. A large body of work has linked gradient speech perception to cognitive and linguistic factors such as executive function and phonological awareness (Honda et al., 2024; Kapnoula et al., 2021; Kapnoula & McMurray, 2021; Kapnoula & Samuel, 2024; Kapnoula et al., 2017; Kim et al., 2020; Lee & Park, 2024; McMurray et al., 2010; McMurray et al., 2002). However, given that traditional metrics are contaminated by noise and response bias, some of these reported associations may be artifacts. As demonstrated in our simulated results and analysis with human data, RMSE offers a promising solution. By quantifying how closely a listener’s responses align with a continuous, idealized perceptual function rather than assuming an underlying categorical boundary, RMSE provides a cleaner, less biased estimate of genuine gradient perception. Re-analyzing existing datasets using RMSE might therefore reveal more accurate relationships between continuous perception and higher-level cognitive abilities that underpin individual differences in speech perception. Such analyses would help clarify whether gradiency represents a general perceptual sensitivity, a domain-specific phonological trait, or a flexible processing strategy shaped by task demands.

For theoretical models of speech perception, RMSE provides a much-needed tool to test core hypotheses. While slope and consistency often show weak stability across different phonetic continua, our results show that RMSE captures a moderate yet meaningful degree of stability. This suggests that RMSE indexes not only enduring individual tendencies but also context-sensitive adaptation, making it uniquely suited to capture the dual nature of speech perception as both structured and fluid. These methodological clarifications have direct theoretical implications. The dual-route framework (Kapnoula & McMurray, 2021; Ou & Yu, 2022; Sarrett et al., 2020) proposes that categorical and gradient processes operate in parallel, each supporting distinct functional roles in speech understanding. Yet empirical tests of this model have been hindered by metrics that have some difficulties to isolate the gradient and categorical components. RMSE, by virtue of its grounding in continuous response patterns and its resistance to categorical contamination, provides a principled behavioral index of the gradient route for testing dual-route predictions in both behavioral and neurocognitive studies. For example, in neuroimaging research, RMSE could serve as a behavioral covariate to disentangle neural activity associated with gradient versus categorical processing streams. This would enable more precise localization of subphonemic representations and clarify how the brain balances discrete categorization with fine-grained acoustic sensitivity.

Looking ahead, RMSE opens new avenues for investigating the dynamics of perceptual learning, adaptation, and cross-linguistic differences. Its stability across continua suggests it captures an enduring aspect of perception, making it an ideal metric for longitudinal studies. Longitudinal studies could track how RMSE changes with phonetic training or exposure to novel category boundaries, testing whether gradient perception is a stable trait or a malleable skill that develops with experience. Cross-linguistic work could determine whether gradiency stems from universal auditory principles or language-specific phonological tuning. Furthermore, integrating RMSE with measures of attention, working memory, and lexical access would show how gradient perception interfaces with broader cognitive systems to improve our understanding of how listeners resolve the tension between categorical efficiency and acoustic fidelity in real-time speech comprehension. While RMSE is not a panacea, it represents a conceptually grounded step toward more valid measurement of gradient perception. By addressing long-standing confounds in how gradiency has been operationalized, RMSE provides a clearer empirical foundation for studying individual differences, perceptual learning and the architecture of speech perception.

Conclusion

This study introduced RMSE as a principled metric for quantifying that reframes the quantification of gradient perception. Instead of relying on indirect proxies like boundary steepness or response uniformity, RMSE measures structured sensitivity by quantifying the fidelity of the mapping between a continuous acoustic stimulus and listeners’ perception. Our simulations and analyses of human data confirmed that RMSE overcomes the critical limitations of traditional metrics, successfully distinguishing genuine gradiency from artifacts arising from random responding, categorical endpoint clustering, or response bias. Furthermore, we demonstrated that RMSE is not only valid within a given task but also shows moderate-to-high stability across different phonetic continua, suggesting it captures a meaningful, trait-like aspect of individual perceptual style. While any new metric requires broad evaluation across diverse contexts, RMSE represents a significant step forward. By addressing long-standing measurement confounds, it provides a more reliable and theoretically coherent foundation for investigating individual differences, perceptual learning, and the fundamental architecture of the human speech perception system.

Acknowledgments

This work was supported by grants from the National Social Science Fund of China (22BYY160, 24CYY096), Xi’an Jiaotong University Undergraduate Teaching Reform Research Fund (2424Z), and the China Postdoctoral Science Foundation (2025T180911).

Conflicts of Interest Statement

The authors declare no conflicts of interest.

References

Abramson, A. S., & Lisker, L. (1970). Discriminability along the voicing continuum: Cross-language tests. Proceedings of the sixth international congress of phonetic sciences, 196(7), 569-573. https://www.coli.uni-saarland.de/groups/FK/speech_science/icphs/ICPhS1967/p6_569.pdf.
Anwyl-Irvine, A. L., Massonnié, J., Flitton, A., Kirkham, N., & Evershed, J. K. (2020). Gorilla in our midst: An online behavioral experiment builder. Behavior research methods, 52(1), 388-407. [CrossRef]
Apfelbaum, K. S., Kutlu, E., McMurray, B., & Kapnoula, E. C. (2022). Don’t force it! Gradient speech categorization calls for continuous categorization tasks. Journal of the Acoustical Society of America, 152(6), 3728-3745. [CrossRef]
Clayards, M., Tanenhaus, M. K., Aslin, R. N., & Jacobs, R. A. (2008). Perception of speech reflects optimal use of probabilistic speech cues. Cognition, 108(3), 804-809. [CrossRef]
Flege, J. E., Bohn, O. S., & Jang, S. (1997). Effects of experience on non-native speakers’ production and perception of English vowels. Journal of phonetics, 25(4), 437-470. [CrossRef]
Fuhrmeister, P., Phillips, M. C., McCoach, D. B., & Myers, E. B. (2023). Relationships Between Native and Non-Native Speech Perception. Journal of Experimental Psychology-Learning Memory and Cognition, 49(7), 1161-1175. [CrossRef]
Goldinger, S. D., Pisoni, D. B., & Logan, J. S. (1991). On the Nature of Talker Variability Effects on Recall of Spoken Word Lists. Journal of Experimental Psychology-Learning Memory and Cognition, 17(1), 152-162. [CrossRef]
Honda, C. T., Clayards, M., & Baum, S. R. (2024). Exploring Individual Differences in Native Phonetic Perception and Their Link to Nonnative Phonetic Perception. Journal of Experimental Psychology-Human Perception and Performance, 50(4), 370-394. [CrossRef]
Kapnoula, E. C., Edwards, J., & McMurray, B. (2021). Gradient Activation of Speech Categories Facilitates Listeners’ Recovery From Lexical Garden Paths, But Not Perception of Speech-in-Noise. Journal of Experimental Psychology-Human Perception and Performance, 47(4), 578-595. [CrossRef]
Kapnoula, E. C., & McMurray, B. (2021). Idiosyncratic use of bottom-up and top-down information leads to differences in speech perception flexibility: Converging evidence from ERPs and eye-tracking. Brain and Language, 223, 105031. [CrossRef]
Kapnoula, E. C., & Samuel, A. G. (2024). Sensitivity to Subphonemic Differences in First Language Predicts Vocabulary Size in a Foreign Language. Language learning, 74(4), 950-984. [CrossRef]
Kapnoula, E. C., Winn, M. B., Kong, E. J., Edwards, J., & McMurray, B. (2017). Evaluating the Sources and Functions of Gradiency in Phoneme Categorization: An Individual Differences Approach. Journal of Experimental Psychology-Human Perception and Performance, 43(9), 1594-1611. [CrossRef]
Kim, D., Clayards, M., & Kong, E. J. (2020). Individual differences in perceptual adaptation to unfamiliar phonetic categories. Journal of phonetics, 81, 100984. [CrossRef]
Kim, H., Mcmurray, B., Sorensen, E., & Oleson, J. (2025). The consistency of categorization-consistency in speech perception. Psychonomic Bulletin & Review. [CrossRef]
Kong, E., & Edwards, J. (2011). Individual Differences in Speech Perception: Evidence from Visual Analogue Scaling and Eye-Tracking. ICPhS, 1126-1129. https://learningtotalk.umd.edu/wp-content/uploads/2017/03/KongEJ2011.pdf.
Kong, E. J. (2019). Individual differences in categorical perception: L1 English learners’ L2 perception of Korean stops. Phonetics and Speech Sciences, 11(4), 63-70. [CrossRef]
Kong, E. J., & Edwards, J. (2016). Individual differences in categorical perception of speech: Cue weighting and executive function. Journal of phonetics, 59, 40-57. [CrossRef]
Kutlu, E., Baxelbaum, K., Sorensen, E., Oleson, J., & McMurray, B. (2024). Linguistic diversity shapes flexible speech perception in school age children. Scientific Reports, 14(1), 28825. [CrossRef]
Lee, J. U., & Park, H. (2024). Acoustic cue sensitivity in the perception of native category and their relation to nonnative phonological contrast learning. Journal of phonetics, 104, 101327. [CrossRef]
Liberman, A. M., Harris, K. S., Hoffman, H. S., & Griffith, B. C. (1957). The Discrimination of Speech Sounds within and across Phoneme Boundaries. Journal of Experimental Psychology, 54(5), 358-368. [CrossRef]
Lisker, L., & Abramson, A. S. (1964). A Cross-Language Study of Voicing in Initial Stops - Acoustical Measurements. Word-Journal of the International Linguistic Association, 20(3), 384-422. [CrossRef]
Massaro, D. W., & Cohen, M. M. (1983). Evaluation and Integration of Visual and Auditory Information in Speech-Perception. Journal of Experimental Psychology-Human Perception and Performance, 9(5), 753-771. [CrossRef]
McMurray, B. (2022). The myth of categorical perception. Journal of the Acoustical Society of America, 152(6), 3819-3842. [CrossRef]
McMurray, B., Samelson, V. M., Lee, S. H., & Tomblin, J. B. (2010). Individual differences in online spoken word recognition: Implications for SLI. Cognitive Psychology, 60(1), 1-39. [CrossRef]
McMurray, B., Spivey, M. J., Aslin, R. N., Tanenhaus, M. K., & Subik, D. (2008). Gradient Sensitivity to Within-Category Variation in Words and Syllables. Journal of Experimental Psychology-Human Perception and Performance, 34(6), 1609-1631. [CrossRef]
McMurray, B., Tanenhaus, M. K., & Aslin, R. N. (2002). Gradient effects of within-category phonetic variation on lexical access. Cognition, 86(2), B33-B42. [CrossRef]
Munson, B., & Carlson, K. U. (2016). An Exploration of Methods for Rating Children’s Productions of Sibilant Fricatives. Speech Lang Hear, 19(1), 36-45. [CrossRef]
Myers, E., Phillips, M., & Skoe, E. (2024). Individual differences in the perception of phonetic category structure predict speech-in-noise performance. Journal of the Acoustical Society of America, 156(3), 1707-1719. [CrossRef]
Ohde, R. N. (1984). Fundamental-Frequency as an Acoustic Correlate of Stop Consonant Voicing. Journal of the Acoustical Society of America, 75(1), 224-230. [CrossRef]
Ou, J. H., & Yu, A. C. L. (2022). Neural correlates of individual differences in speech categorisation: evidence from subcortical, cortical, and behavioural measures. Language Cognition and Neuroscience, 37(3), 269-284. [CrossRef]
Ou, J. H., Yu, A. C. L., & Xiang, M. (2021). Individual Differences in Categorization Gradience As Predicted by Online Processing of Phonetic Cues During Spoken Word Recognition: Evidence From Eye Movements. Cognitive science, 45(3), e12948. [CrossRef]
Pisoni, D. B. (1973). Auditory and phonetic memory codes in the discrimination of consonants and vowels. Percept Psychophys, 13(2), 253-260. [CrossRef]
Sarrett, M. E., McMurray, B., & Kapnoula, E. C. (2020). Dynamic EEG analysis during language comprehension reveals interactive cascades between perceptual processing and sentential expectations. Brain and Language, 211, 104875. [CrossRef]
Stevens, K. N., & Klatt, D. H. (1974). Role of Formant Transitions in Voiced-Voiceless Distinction for Stops. Journal of the Acoustical Society of America, 55(3), 653-659. [CrossRef]
Theodore, R. M., Myers, E. B., & Lomibao, J. A. (2015). Talker-specific influences on phonetic category structure. Journal of the Acoustical Society of America, 138(2), 1068-1078. [CrossRef]
Walther, B. A., & Moore, J. L. (2005). The concepts of bias, precision and accuracy, and their use in testing the performance of species richness estimators, with a literature review of estimator performance. Ecography, 28(6), 815-829. [CrossRef]
Winn, M. B., Chatterjee, M., & Idsardi, W. J. (2013). Roles of voice onset time and F0 in stop consonant voicing perception: effects of masking noise and low-pass filtering. J Speech Lang Hear Res, 56(4), 1097-1107. [CrossRef]

Figure 1. Canonical patterns of categorical perception. The figure illustrates a steep identification (ID) function (dotted line) that establishes a sharp perceptual boundary, and a corresponding peak in discrimination (DIS) accuracy (solid line) for stimulus pairs that straddle this boundary.

Figure 2. Indices of categorization and possible patterns in the VAS data. (A) Schematic of averaged responses with indicators of slope. (B) Individual responses overlaid on an average curve illustrating a shallow slope due to high response consistency. (C) Histograms of click locations across listeners with quadratic regression curves overlaid.

Figure 3. The five simulated perceptual profiles. These idealized response patterns provide a ground truth for evaluating the diagnostic accuracy of each gradiency metric.

Figure 4. Average VAS ratings from human participants across eight phonetic continua. The functions show clear variability in steepness and shape, with voicing continua (e.g., beach–peach) appearing more categorical than vowel continua (e.g., pen–pan).

Figure 5. Examples of non-gradient response patterns that produce misleadingly shallow slopes, including (A) random endpoint responding, (B) clustering around the midpoint, and (C) restricted use of the scale.

Figure 6. Examples of a highly categorical response pattern that yields a high score for response consistency (i.e., low residual variance), illustrating the metric’s failure to distinguish rigid categorical responding from true gradiency.

Figure 7. A random response pattern (A) produces a uniform response distribution (B), resulting in a small quadratic coefficient that is indistinguishable from that of an ideal gradient perceiver.

Figure 8. A participant response profile identified by RMSE as near-ideal gradient perception. Note the even, linear progression of responses that are tightly clustered around the ideal diagonal and span the full scale.

Figure 9. Within-continuum correlation matrix for all four metrics, averaged across eight continua. Circle size and darkness reflect the strength of the negative correlation. RMSE shows robust negative correlations with consistency (lower deviation aligns with higher consistency) but is largely independent of slope.

Figure 10. Cross-continuum stability for each metric, displayed as violin plots of correlation coefficients. RMSE demonstrates high stability, comparable to the quadratic coefficient but without its interpretive flaws, indicating it reliably captures a trait-like perceptual style.

Table 1. Comparison of metric performance on simulated data. Only RMSE correctly identifies the ideal gradient profile (lowest value) while maintaining a clear, monotonic separation from all other theoretically defined response patterns.

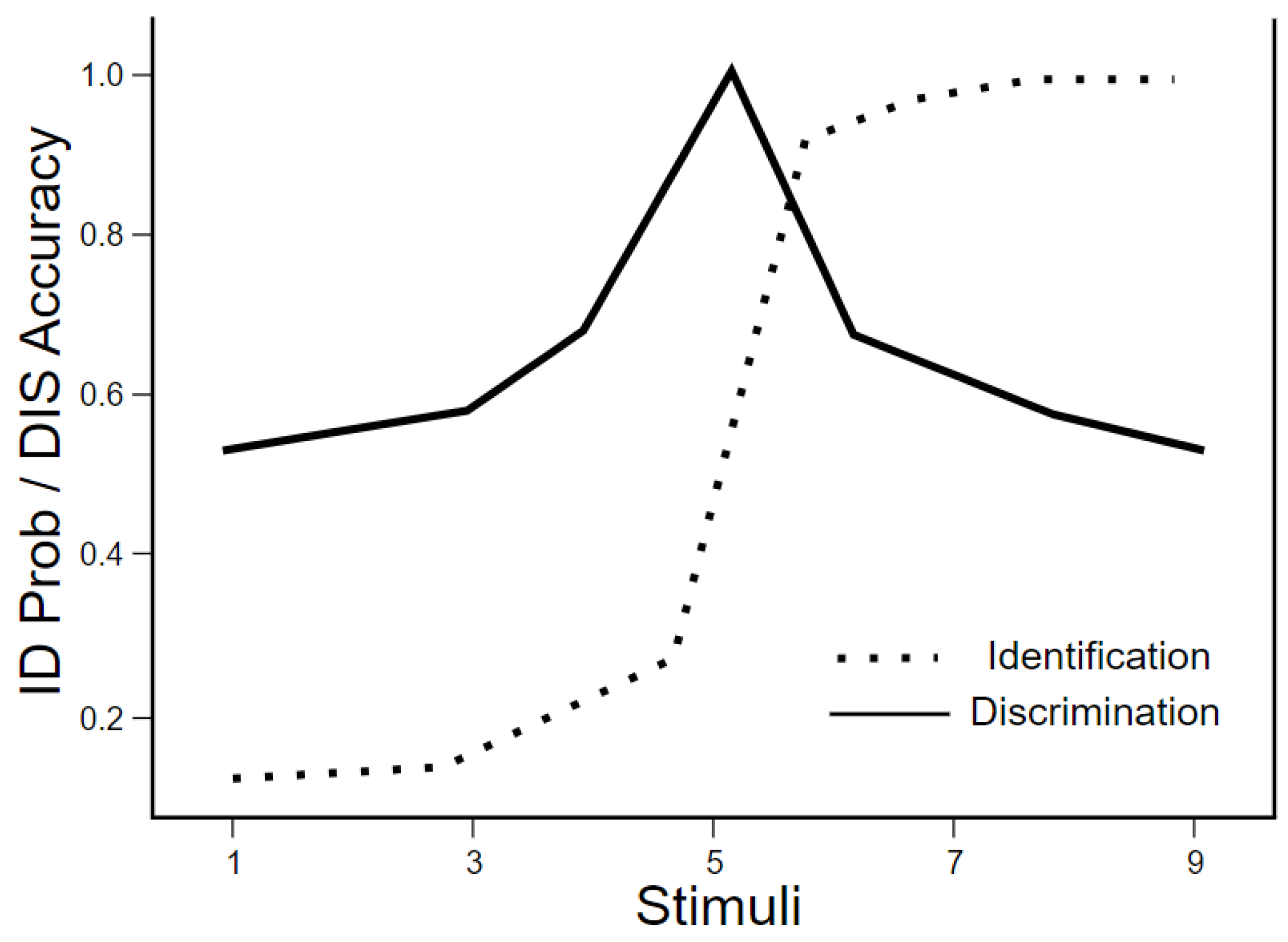
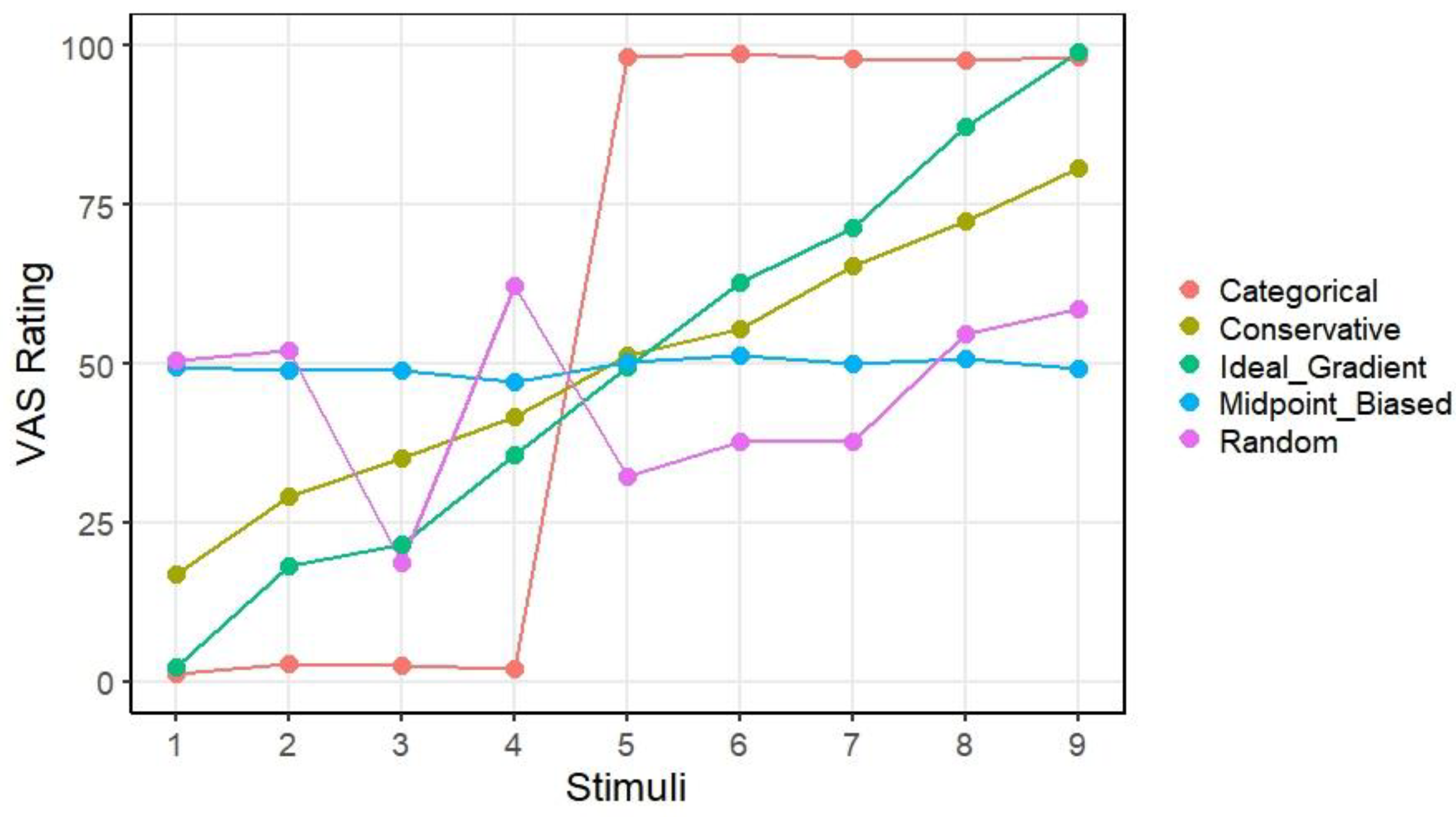
Response Pattern	Slope	Response Consistency	Quadratic Coefficient	RMSE
Ideal Gradient	12.781	-5.263	0.189	5.481
Categorical	570.263	-2.285	2.273	26.194
Random	81.936	-28.934	0.070	42.159
Midpoint-Biased	0.241	-4.038	-1.515	32.063
Conservative	11.129	-4.736	-0.765	13.378

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.