A Blended Extended Kalman Filter Approach for Enhanced AGV Localization in Centralized Camera-Based Control Systems

1. Introduction

A centralized, vision-based control architecture for Autonomous Guided Vehicles (AGVs) offers a cost-effective alternative to systems reliant on expensive onboard sensors like LIDAR [9]. In industrial environments, positioning accuracy is critical [21]. This approach, often termed "infrastructure-based control," transfers complex navigation and fleet management tasks from individual vehicles to a powerful central server, enabling sophisticated coordination while reducing per-vehicle hardware costs [13]. The system’s core components include a network of CCTV cameras, a central processing server, a wireless communication network, and the vehicles themselves. The cameras provide a global "God’s-eye view" of the operational area, tracking vehicles and obstacles in real-time. This centralized vision approach leverages advances in computer vision and deep learning techniques for robust localization, as demonstrated by recent work combining imaging sensors with deep convolutional neural networks (DCNNs) for AGV pose estimation [9]. The central server processes this visual data through fleet management software that handles localization, path planning, and traffic management using AI [6] and computer vision techniques [2]. The server then transmits simple motion commands, such as "move forward 5 meters," to the AGVs via wireless communication networks. Recent infrastructure-based vision studies demonstrate that overhead or roadside cameras can detect and track mobile robots reliably in real time, underscoring the practicality of centralized, vision-first approaches [20,25]. Yet long-term localization remains challenging due to illumination changes, occlusions, and drift. A systematic review highlights the need for robust filtering, cross-sensor redundancy, and adaptive models to sustain performance over extended periods [17]. The vehicles execute these commands precisely by utilizing onboard sensor fusion techniques, integrating data from multiple sensors including encoders for distance measurement and Inertial Measurement Units (IMUs) for orientation tracking [24]. Recent advances in sensor fusion have shown that passive wheel odometry can outperform traditional drive-wheel odometry in many scenarios, while IMU/AHRS integration significantly improves accuracy during angular motion [2]. Advanced filtering techniques, including hybrid Kalman-particle filters and trainable Extended Kalman Filters with adaptive noise models, have demonstrated improved localization accuracy and robustness in indoor AGV environments [13,24]. Ultrasonic sensors act as a final safety measure, preventing collisions with unforeseen obstacles that may be in the camera’s blind spots. This hybrid model significantly reduces the cost per vehicle by replacing expensive onboard LIDAR systems with lower-cost sensor combinations and allows for sophisticated, system-wide traffic optimization through centralized path planning algorithms [22]. Modern optimization approaches, such as hybrid Grey Wolf Optimization combined with Kalman corrections, have shown improved path predictability and collision avoidance capabilities for dense warehouse AGV operations [16,22]. However, this centralized approach relies heavily on the central infrastructure, making it vulnerable to single-point failures and potentially less flexible in dynamic environments compared to fully autonomous, SLAM-based robots that maintain complete onboard sensing and processing capabilities. Although the Extended Kalman Filter (EKF) has been widely used for AGV positioning [19] , its performance may degrade when raw sensor data have different characteristics, such as camera (CAM) data with high noise and low update rate, compared to Dead Reckoning data with high update rate but prone to accumulated errors (drift). The normal EKF implementations often treat each sensor measurement update independently, which can lead to inconsistencies and non-smooth trajectory estimates, particularly when one sensor is prone to high noise or sudden disturbances. This highlights the research gap in developing an efficient data fusion strategy that can blend data from different sensors before feeding it to the filter update stage. Therefore, the contribution of this paper is to propose and evaluate a novel Blended EKF, which pre-fuses CAM and DR data using a weighted blending strategy before sending the data to the EKF. It is hypothesized that this approach not only reduces the positioning error but also produces smoother and more stable trajectories compared to the Normal EKF in an indoor environment.

2. Materials and Methods

This research presents an integrated approach for indoor localization of automated guided vehicles (AGVs) using multiple low-cost sensors, including cameras (CAMs), encoders, inertial measurement units (IMUs), and approximate positioning (Dead Reckoning - DR) [7].

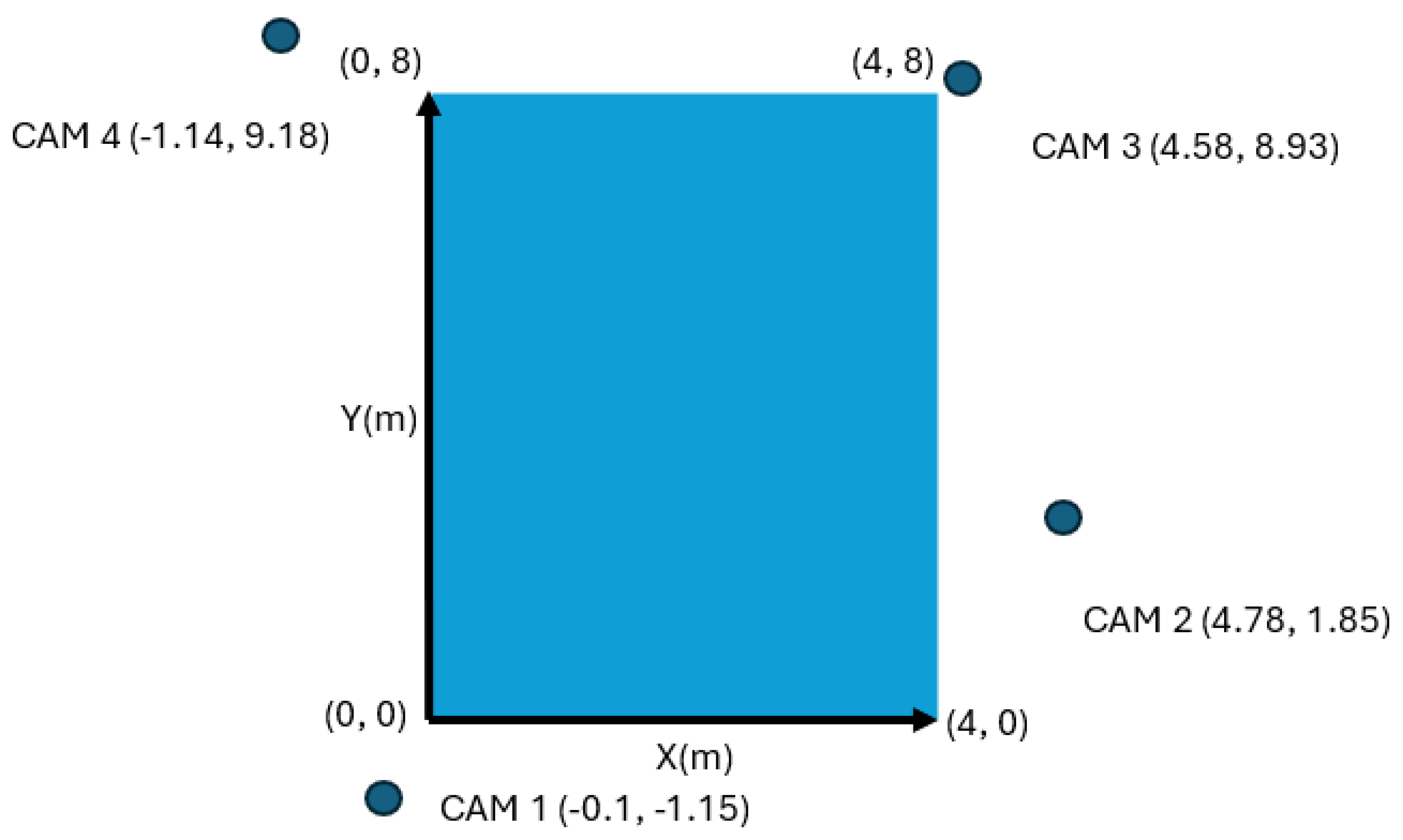
2.1. Preparation and Equipment Used in the Experiment

2.1.1. Preparation Used in the Experiment

The BALTY AGV robot used in the experiment were equipped with specified sensors. Data from the encoder and IMU were recorded at a sampling rate of 10 Hz (every 0.1 s), while data from the camera (CAM) for absolute positioning were recorded at a rate of 5 Hz (every 0.2 s) [12]. To ensure the accuracy and consistency of the data used in the data fusion process, two data sampling scenarios were defined: (1) using the original sampling rate, with the IMU and Wheel Encoder set at 10 Hz and the CAM at 5 Hz, and (2) adjusting the sampling rate of all sensors to 5 Hz to create temporal consistency and facilitate efficient joint processing. Since the data from each sensor is collected asynchronously, a temporal alignment using an event-based synchronization method was performed in the post-processing step, with the “AGV starting point” set as the reference marker for synchronizing the entire dataset. For data communication between sensors, the MQTT protocol is used, which is set to a basic Quality of Service (QoS) level, prioritizing data transmission speed. However, this approach may result in some data loss in cases of unstable Wi-Fi network signals. The Ground Truth (GT) data is obtained by recording the AGV movement video using a top-view camera. Then, the image is processed frame by frame to extract the AGV position using Camera Calibration and Coordinate Transformation [3]. Reference positions on the experimental field are established as ground truth coordinates, which serve as a reference data set to assess the accuracy and errors of the sensors, as well as to perform error correction and evaluate the overall system performance [21].

2.1.2. Equipment Used in the Experiment

In this experiment, various sensors were installed to determine the grid position at (Table 1). An encoder coupled to a DC motor (JGB37-520) provides an AB-phase quadrature signal of 90 pulses per revolution, which is used to calculate the distance and direction of rotation. The WitMotion WT901C Inertial Measurement Unit (IMU) is a 9-DOF sensor that can measure linear acceleration (±16 g) and rotation rate (up to ±2000 °/s) and is set to output data at a frequency of 10 Hz. For image sensing, a TP-Link Tapo C200 camera was installed in a 4x8m the experimental area (Figure 1), which supports Full HD (1080p) recording at 30 frames per second. The data from these three sensors is used to integrate the data, which helps the system determine the position of the AGV.

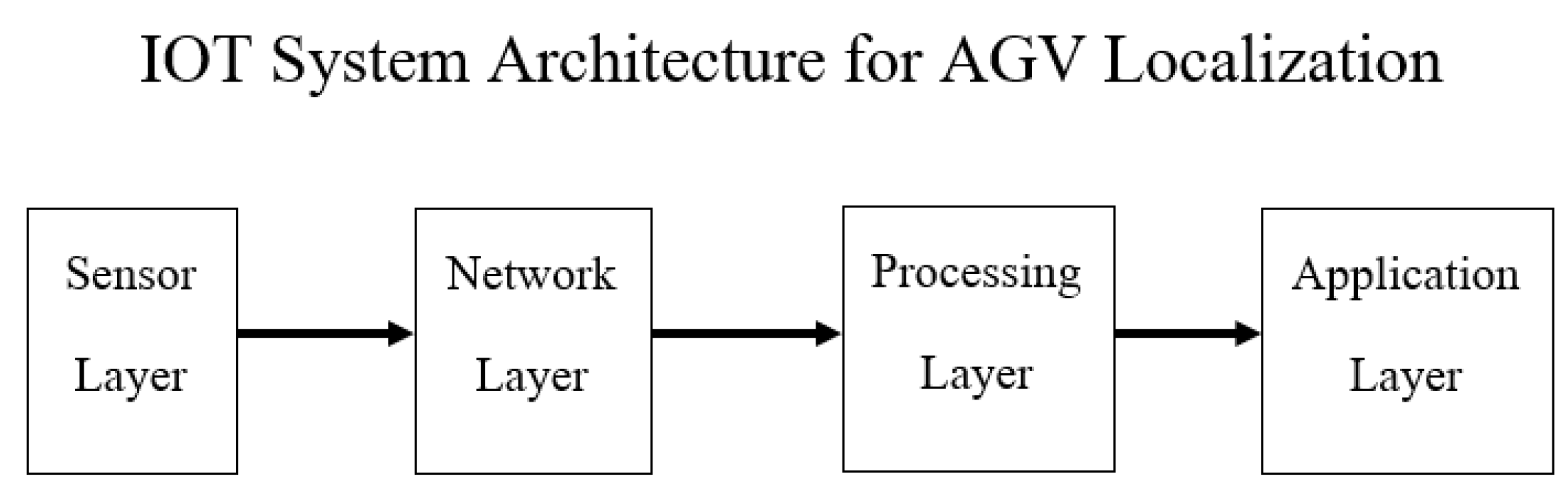
2.1.3. IoT System Architecture Concepts

The conceptual framework for the IoT system architecture for AGV localization (Figure 2) is designed to collect, synchronize, and integrate data between multiple sensors and a central processing unit. This architecture consists of four main layers:

• Sensor (Sensor) Layer: Consists of the encoder + IMU and a CCTV camera that records data from the experimental area.
• Network (Communication) Layer: Uses Wi-Fi wireless communication with the MQTT protocol for lightweight messaging to exchange sensor data with low latency.
• Processing Layer (Central Server): The central server collects sensor data streams, performs synchronization, integrates the data, and stores the records for analysis.
• Application Layer: Provides visualization and location identification for the experimental area.

2.2. Localization Methods

Multi-sensor fusion works to determine the position and orientation of the AGV by combining data from internal sensors (e.g., encoder, IMU) with external sensors (e.g., camera) using EKF [11] with encoder, IMU, and camera.

2.2.1. Dead Reckoning Localization

Dead Reckoning estimation, which estimates the position of an AGV based on its previous state and movement data, is divided into two parts: measuring the distance from the wheels (encoder)and the direction from the IMU. This method is widely used in positioning research [5,18,23]. The state vector for Dead Reckoning is defined as

$$\mathbf{X}=\left[\begin{array}{c}x\\ y\\ \theta \end{array}\right],$$

(1)

which represents the Cartesian coordinates and heading angle of the AGV. The AGV’s motion can be estimated using a kinematic motion model using the linear velocity v and angular velocity $\omega$ data from the sensors, as shown in the equation:

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{c}vcos\theta \\ vsin\theta \\ \omega \end{array}\right],$$

(2)

When integrating this equation with respect to time $\mathsf{\Delta }t$, the state update is obtained as follows:

$$\left[\begin{array}{c}{x}_k\\ y_k\\ {\theta }_k\end{array}\right]=\left[\begin{array}{c}{x}_{k-1}+v_k\mathsf{\Delta }tcos\left({\theta }_{k-1}\right)\\ y_{k-1}+v_k\mathsf{\Delta }tsin\left({\theta }_{k-1}\right)\\ {\theta }_{k-1}+{\omega }_k\mathsf{\Delta }t\end{array}\right],$$

(3)

where k is the current time index and $k-1$ is the previous time index. The data $v_k$ and ${\omega }_k$ are obtained by fusing data from:

• Distance measurement from encoder: An encoder mounted to the drive motor provides wheel rotation data that is converted to linear velocity $v_o$ and angular velocity ${\omega }_o$ using the vehicle kinematics model. However, This method is limited by accumulated errors caused by wheel slip, calibration inaccuracies, and surface irregularities [18,23].
• Direction from IMU: A 9-DOF IMU provides angular velocity ${\omega }_{imu}$ and linear acceleration $a_{imu}$. The gyroscope output is crucial for direction calculations, as accelerometer data is highly sensitive to noise and bias errors that increase with time [8].

A limitation of the DR method is the continuous error introduced by the time integral, which leads to an infinitely increasing error [11,14]. Therefore, periodic corrections from external sensors are required.

2.2.2. Camera Localization

To address the accumulated drift of Dead Reckoning (DR) that cannot be corrected with internal sensor data, external sensors, such as cameras, LiDAR, or CCTV, are used to measure the position based on world coordinates, thus correcting the position estimate. [5]. The process is as follows:

• Feature Detection: The system detects the features of the AGV to be located using standard computer vision algorithms.
• Coordinate Transformation: The AGV’s position in the image plane is converted to its real-world coordinates (world frame) via perspective transformation or a pre-calibrated homography matrix.

The measurement values obtained from this camera, $z_{CAM}$, are crucial for making the system observable, meaning that important system states (such as position and velocity) can be estimated. [8]

The measurement values, $z_k$, are fed into a filter for interpolation and prediction of ${\widehat{x}}_{k|k-1}$ through a nonlinear measurement model, h, noise, $w_k$ as shown in the equation:

$$z_k=h\left({\mathbf{x}}_k\right)+w_k,$$

(4)

These measurement values are then used in a Kalman Filter to calculate the innovation or error of the measurement, $y_k$:

$${\mathbf{y}}_k={\mathbf{z}}_k-h\left({\widehat{\mathbf{x}}}_{k|k-1}\right),$$

(5)

The accuracy of coordinate transformation and feature detection is crucial because they affect the accuracy of $z_k$, which is a key factor in reducing the cumulative error of the DR.

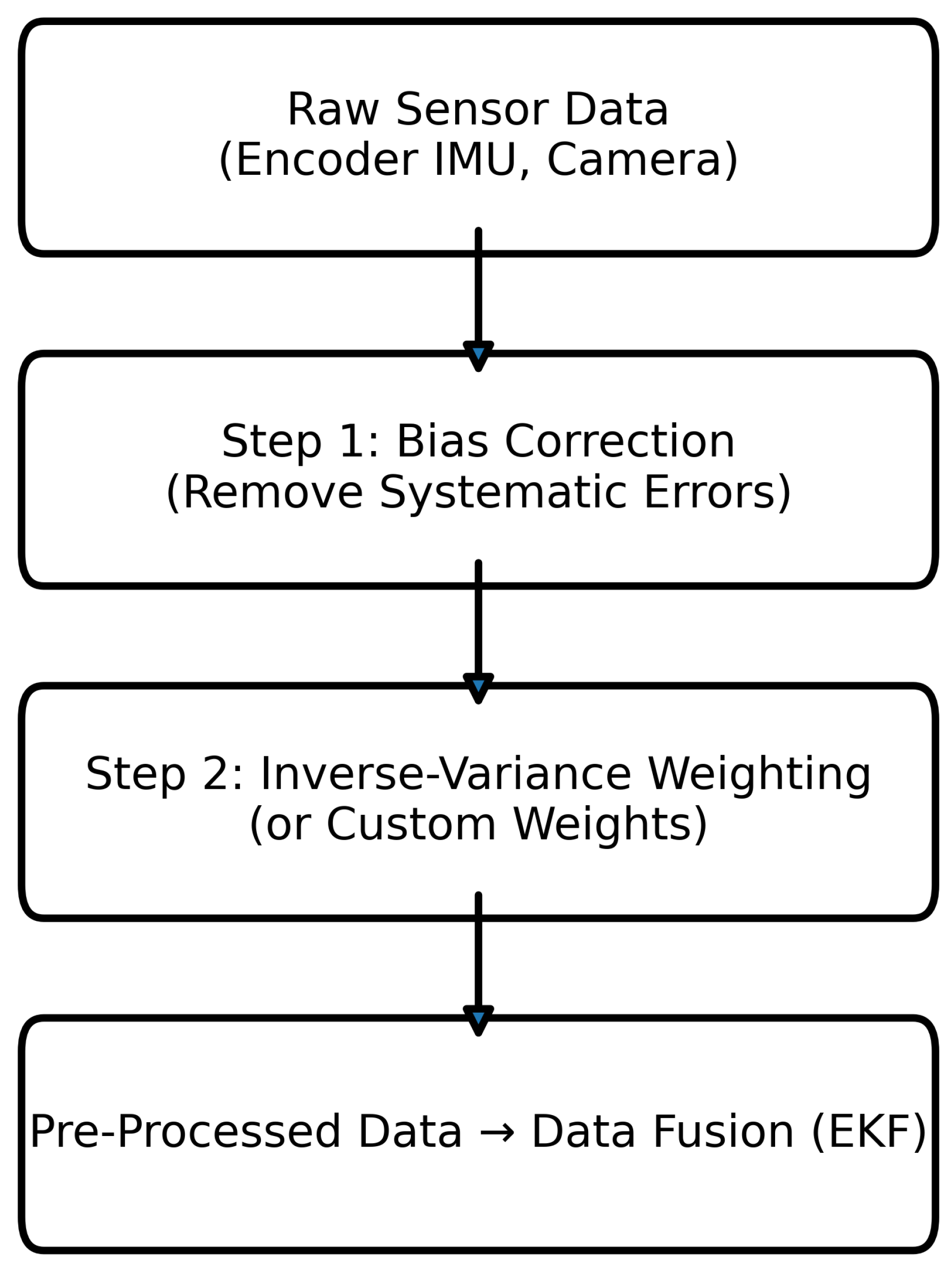
2.3. Pre-Processing Data Analysis

Before data from different sensors can be fed through the data fusion process, it is essential to perform a pre-processing step to reduce bias and increase the reliability of the input data. This step consists of two main steps designed to apply bias correction and appropriately weight each sensor based on its statistical variance. An overview of all these pre-processing steps is shown in Figure 3 . The next subsections describe each step in detail.

2.3.1. Bias Correction

Before using the raw sensor data in the fusion process, the systematic bias of each sensor is assessed and corrected [15]. This is done by calculating the average deviation between the measured sensor value S and the reference value from the Ground Truth (GT) according to the equation:

$${\overline{b}}_s={\displaystyle \frac{1}{N}}\sum _{t=1}^N\left(S_t-G{T}_t\right),$$

(6)

Where $S_t$ is the measured value from the sensor at time t and $G{T}_t$ is the reference value from the true path GT at the same time. The corrected value $S_t^{\prime }$ is then given by:

$$S_t^{\prime }=S_t-{\overline{b}}_s,$$

(7)

This process reduces the Root Mean Squared Error (RMSE) of the raw data and improves the reliability of the data. [10].

2.3.2. Inverse-Variance Weighting

Data from the error-corrected sensors are weighted statistically using the Inverse-Variance Weighting [4] method. This method assumes that sensors with low error variance are given higher weights during data fusion. The weight $w_i$ for each sensor i is calculated from the error variance ${\sigma }_i^2$ as follows:

$$w_i={\displaystyle \frac{1}{{\sigma }_i^2}},$$

(8)

The weights are then normalized to Normalized Weights so that the sum of all weights is 1, defined as:

$$w_i^{\prime }={\displaystyle \frac{w_i}{{\sum }_{j=1}^M{w}_j}},$$

(9)

where M is the total number of sensors.

2.4. Extended Kalman Filter (EKF)

This research developed and compared the performance of two Extended Kalman Filter (EKF) models to estimate the state of an AGV, consisting of its position (X, Y axes) and heading. The state equations and measurement equations used in the EKF system can be written in the following general form: [13]:

$${\mathbf{x}}_k=f({\mathbf{x}}_{k-1},{\mathbf{u}}_k)+{\mathbf{w}}_k,$$

(10)

$${\mathbf{z}}_k=h\left({\mathbf{x}}_k\right)+{\mathbf{v}}_k,$$

(11)

Where: ${\mathbf{x}}_k$ is the AGV state vector (position and direction), $f(·)$ is the state transition function, ${\mathbf{u}}_k$ is the control data from the IMU and encoder, ${\mathbf{w}}_k$ is the process noise, ${\mathbf{z}}_k$ is the measured value from the sensor, $h(·)$ is the measurement function, ${\mathbf{v}}_k$ is the measurement noise.

2.4.1. Normal Series Fusion EKF (Normal EKF)

A typical EKF operates using an iterative process consisting of two main steps: Prediction Step and Update Step[1] Prediction Step:

In this step, the EKF uses the AGV’s motion model, combined with data from the IMU and DR (encoder) sensors to predict the AGV’s next state (position and direction) based on the predicted state values. ${\widehat{\mathbf{x}}}_{k|k-1}$ and the variance of the estimate (covariance) ${\mathbf{P}}_{k|k-1}$ According to the equation:

$${\widehat{\mathbf{x}}}_{k|k-1}=f({\widehat{\mathbf{x}}}_{k-1|k-1},{\mathbf{u}}_k),$$

(12)

$${\mathbf{P}}_{k|k-1}={\mathbf{F}}_{k-1}{\mathbf{P}}_{k-1|k-1}{\mathbf{F}}_{k-1}^{\mathrm{T}}+{\mathbf{Q}}_{k-1},$$

(13)

where ${\widehat{\mathbf{x}}}_{k|k-1}$ and ${\mathbf{P}}_{k|k-1}$ is the predicted state and covariance, ${\mathbf{F}}_{k-1}$ is the Jacobian matrix of the state transition function f, and ${\mathbf{Q}}_{k-1}$ is the process noise covariance of the system.

Update Step:

When new measurements from a sensor (e.g., a CAM) are received, the EKF uses them to update the predictions.

The Kalman Gain ${\mathbf{K}}_k$ is calculated to determine the appropriate weight between the predicted and actual measured values. Then, the state and covariance are updated according to the equation:

$${\mathbf{K}}_k={\mathbf{P}}_{k|k-1}{\mathbf{H}}_k^{\mathrm{T}}{\left({\mathbf{H}}_k{\mathbf{P}}_{k|k-1}{\mathbf{H}}_k^{\mathrm{T}}+{\mathbf{R}}_k\right)}^{-1},$$

(14)

$${\widehat{\mathbf{x}}}_{k|k}={\widehat{\mathbf{x}}}_{k|k-1}+{\mathbf{K}}_k\left({\mathbf{z}}_k-h\left({\widehat{\mathbf{x}}}_{k|k-1}\right)\right),$$

(15)

$${\mathbf{P}}_{k|k}=\left(\mathbf{I}-{\mathbf{K}}_k{\mathbf{H}}_k\right){\mathbf{P}}_{k|k-1},$$

(16)

where ${\mathbf{H}}_k$ is the Jacobian matrix of the measurement function h, and ${\mathbf{R}}_k$ is the measurement noise covariance.

A conventional EKF updates its values using measurements from each sensor separately. In sequential updating.

2.4.2. Blended EKF

The purpose of Blended EKF is to correct for the characteristics of Camera-Based Reckoning (CAM) and Dead Reckoning (DR) measurements. While CAM provides drift-free absolute position data, it suffers from high noise, inconsistent update rates, and occasional occlusions. DR, on the other hand, provides relative motion estimates, but inevitably accumulates drift over time. The raw data causes EKF to be unsmooth, as it alternates between noisy camera updates and drifting DR estimates. To correct for this, CAM and DR measurements are pre-blended prior to the update step. This blending produces a more stable and consistent measurement input, which reduces oscillations and produces a smoother trajectory.

The Blended EKF method fuses measurements from the Camera (CAM) and Dead Reckoning (DR) before the update process. User-defined weights are used to control the proportion of influence of each measurement source. This can be written as the following equation:

$${\overrightarrow{\mathbf{z}}}_{\mathrm{blend}}={\alpha }_{\mathrm{cam}}{\overrightarrow{\mathbf{z}}}_{\mathrm{cam}}+{\alpha }_{\mathrm{dr}}{\overrightarrow{\mathbf{z}}}_{\mathrm{dr}},$$

(17)

where:

• ${\alpha }_{cam}$ is the weight assigned to the Camera (CAM) measurements
• ${\alpha }_{dr}$ is the weight assigned to the Dead Reckoning (DR) measurements

To achieve balance in the aggregation, the following conditions are defined. Normalization:

$${\alpha }_{\mathrm{cam}}+{\alpha }_{\mathrm{dr}}=1,$$

(18)

The uncertainty of the mixed measurement covariance, or ${\mathbf{R}}_{blend}$, can be estimated as:

$${\mathbf{R}}_{\mathrm{blend}}={\alpha }_{\mathrm{cam}}^2{\mathbf{R}}_{\mathrm{cam}}+{\alpha }_{\mathrm{dr}}^2{\mathbf{R}}_{\mathrm{dr}},$$

(19)

The selection of the values of ${\alpha }_{cam}$ and ${\alpha }_{dr}$ may be based on experimental testing or tuning to suit the actual application environment.

3. Experimental Design

This experiment aimed to evaluate the performance of AGV location identification using fusion of data from multiple sensors.The main equipment used in this experiment is the AGV BALTY and various sensors, shown in Figure 4. The experimental design was structured and controlled to generate reliable data for analysis. The experimental data processing steps consisted of the following:

• Bias Correction Analysis: The raw data obtained from each sensor type were analyzed against Ground Truth (GT) data, which is akin to the "true path," to determine the systematic bias and variance.
  This step is crucial in reducing the Root Mean Squared Error (RMSE) of the raw data and enhancing the reliability of the data before further use.
• Weighting with Inverse-Variance Weighting: The error-corrected data were then statistically weighted. The principle is that sensors with lower bias variance (which means higher reliability) will receive higher weight in data fusion.
• Data Fusion with EKF: The pre-processed data is fed into the EKF system to estimate the state (position and orientation). Two EKF models have been developed and compared: (1) a conventional EKF and (2) a blended EKF, which fuses measurements from the CAM and DR sensors before the update process.

To ensure that the performance evaluation covers real-world application scenarios, the AGV was tested to move along a specially designed route, which consists of two main parts:

• Straight Section: This movement involves constant speed and no sudden changes of direction to assess the ability to maintain a precise position under normal conditions.
• Curved Section: It is a dynamic movement, which easily causes accumulated drift in the dead reckoning system to assess the system capability and stability under the condition of changing direction of movement.

The experiment starts at x=0, y=7, moves in a straight line, stops at position x=1, y=7, then rotates and moves in a straight line again, then stops the movement, which is a comprehensive experiment to test the accuracy and stability under the conditions of movement.

4. Results and Discussion

This section presents and discusses experimental results obtained from sensor data analysis and data fusion, focusing on evaluating the performance of the designed algorithmic location system.

4.1. Analysis of bias correction (BC) results

Bias correction improves the accuracy of the sensor, particularly its positioning. The analysis of the average bias errors of each sensor used in the experiment reveals the limitations and basic accuracy of the sensor before its application. Table 2 shows the average sensor error values at two sampling rates (dt), 0.1 s and 0.2 s, the sensor’s data acquisition frequency.

• Camera Sensor (CAM): The bias error values in the X-axis (Mean Error X) and Y-axis (Mean Error Y) were found to be positive in both cases ($dt$ = 0.1 and 0.2). The position was higher than the actual values in both axes. However, the camera sensor did not measure the rotation angle, so there was no error for the Mean Error $\theta$.
• Dead Reckoning (DR) Sensor: For DR, the error values in the X-axis (Mean Error X) were negative, while the Y-axis (Mean Error Y) were positive, indicating that there was error in both directions.
• Inertial Measurement Unit (IMU) Sensors: IMU sensors are used to measure changes in angle ($\theta$). The only error is the Mean Error ($\theta$).

Different types of sensors have different bias tolerances, both in direction (positive/negative) and magnitude. This information is used to develop bias correction algorithms, and the analysis, using Root Mean Square Error (RMSE) values, was calculated for two sampling intervals: dt = 0.1 s and dt = 0.2 s (Table 3).

• Camera Sensor (CAM):

  −

  Before Correction (Raw): CAM had RMSE X values of 0.0617 m and 0.0483 m, and RMSE Y values of 0.0467 m and 0.0459 m for $dt=0.1$ s and $dt=0.2$ s, respectively.

  −

  After Correction (Corrected): RMSE values significantly decreased, with RMSE X decreasing to 0.0536 m and 0.0414 m, and RMSE Y decreasing to 0.0382 m and 0.0355 m, respectively.

• Dead Reckoning (DR) Sensor:

  −

  Before Correction (Raw): DR had RMSE X values of 0.0792 m and 0.0780 m, and RMSE Y values of 0.0241 m and 0.0255 m.

  −

  After Correction (Corrected): Error correction significantly reduced the RMSE of DR. RMSE X decreased to 0.0497 m and 0.0495 m, while RMSE Y decreased to 0.0148 m and 0.0157 m, respectively.

• Inertial Measurement Unit (IMU) Sensor:

  −

  Before Correction (Raw): The IMU is used to measure the rotation angle ($\theta$). The RMSE $\theta$ values before correction were approximately 0.2256 rad and 0.2317 rad.

  −

  After Correction (Corrected): The RMSE $\theta$ values decreased to approximately 0.2018 rad and 0.2072 rad.

The trajectories of the CAM and DR sensors before and after the aberration correction, compared to the ground truth (GT) trajectories at dt=0.1s and dt=0.2s, are shown Figure 5 and Figure 6 respectively.

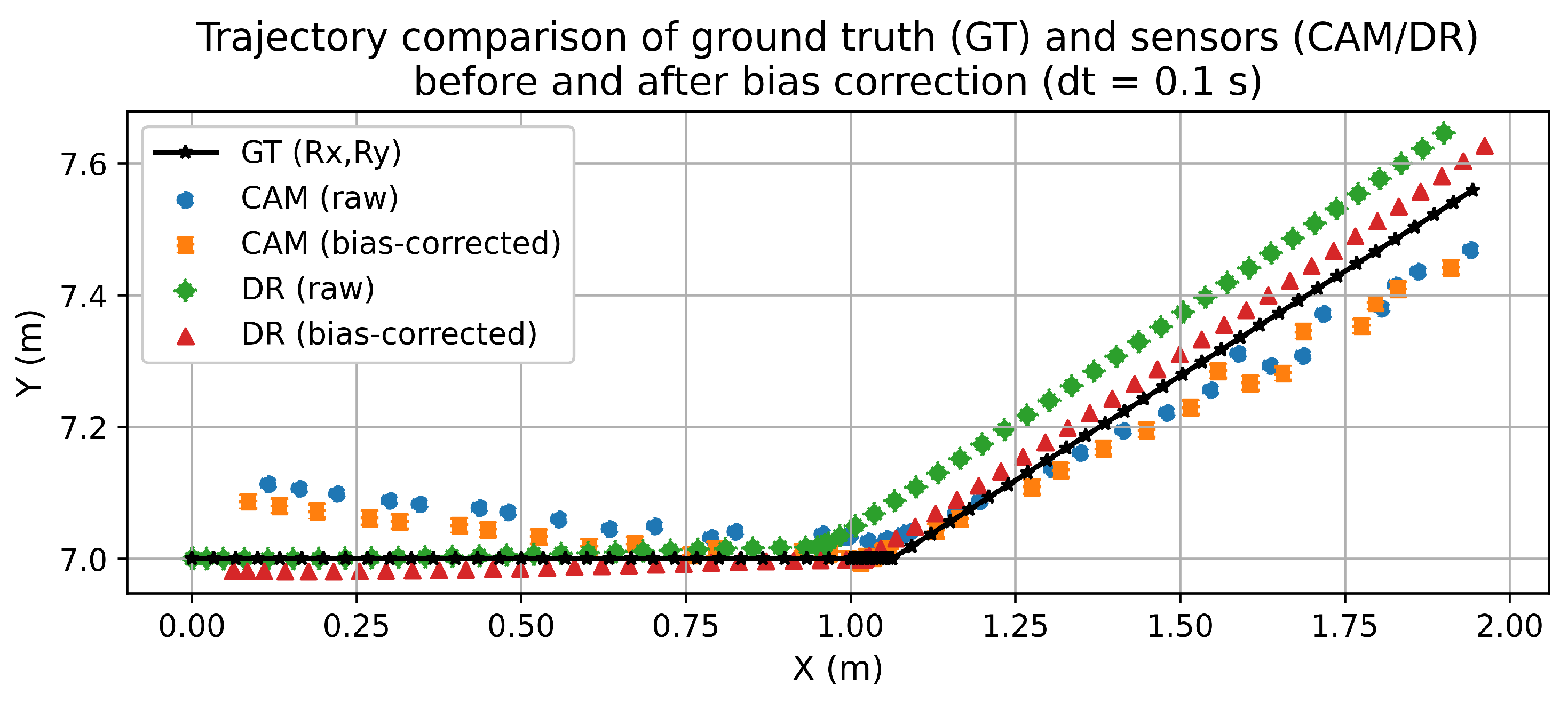
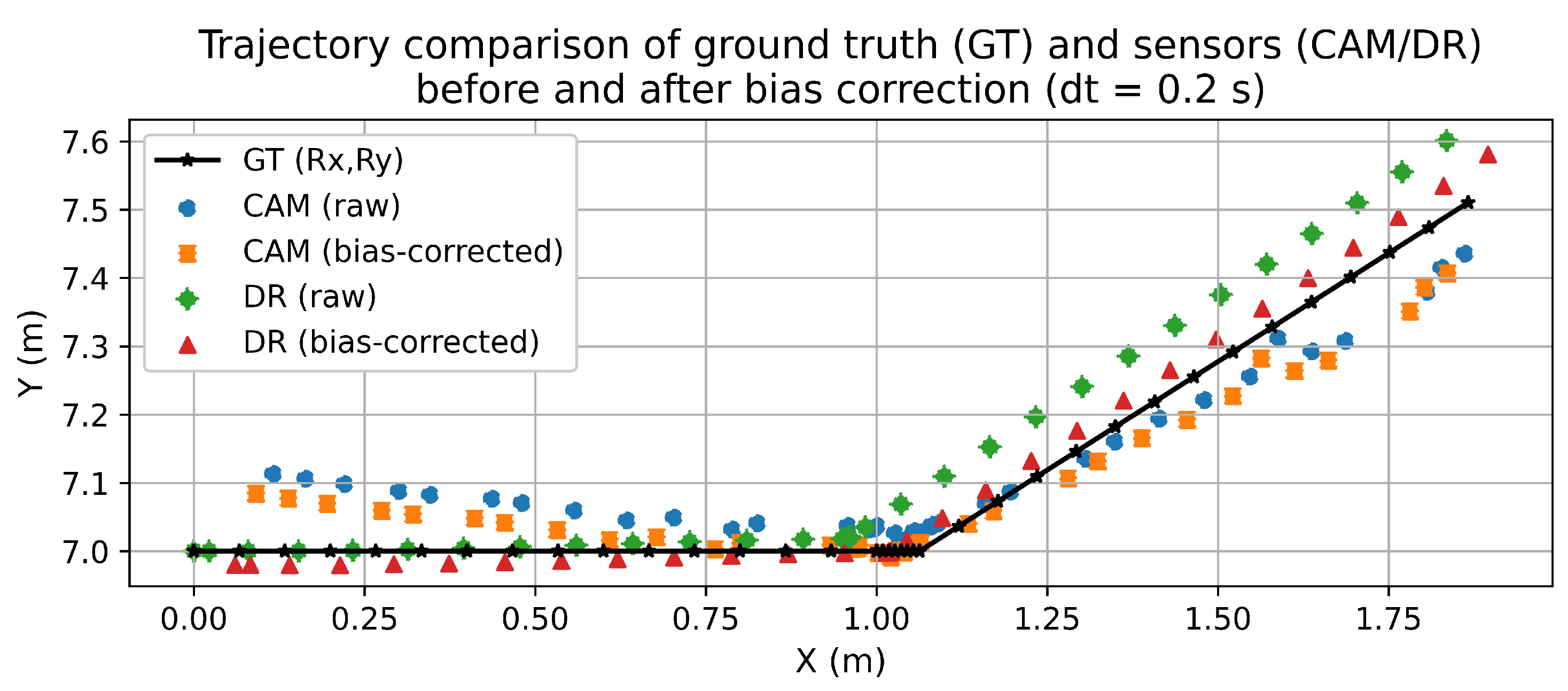
• True Trajectory (GT): The blue line represents the actual trajectory of the object, which is the reference line.
• CAM (Raw): The dark blue dots represent the CAM path before correction.
• CAM (Bias-Corrected): The orange dots represent the CAM path after correction.
• DR (Raw): The green dots represent the DR path before correction.
• DR (Bias-Corrected): The red dots represent the DR path after correction.

Bias correction reduces sensor errors. The apparent decrease in RMSE values corresponds to a closer match of the corrected trajectory to the ground truth, demonstrating the importance of performing bias correction before data acquisition.

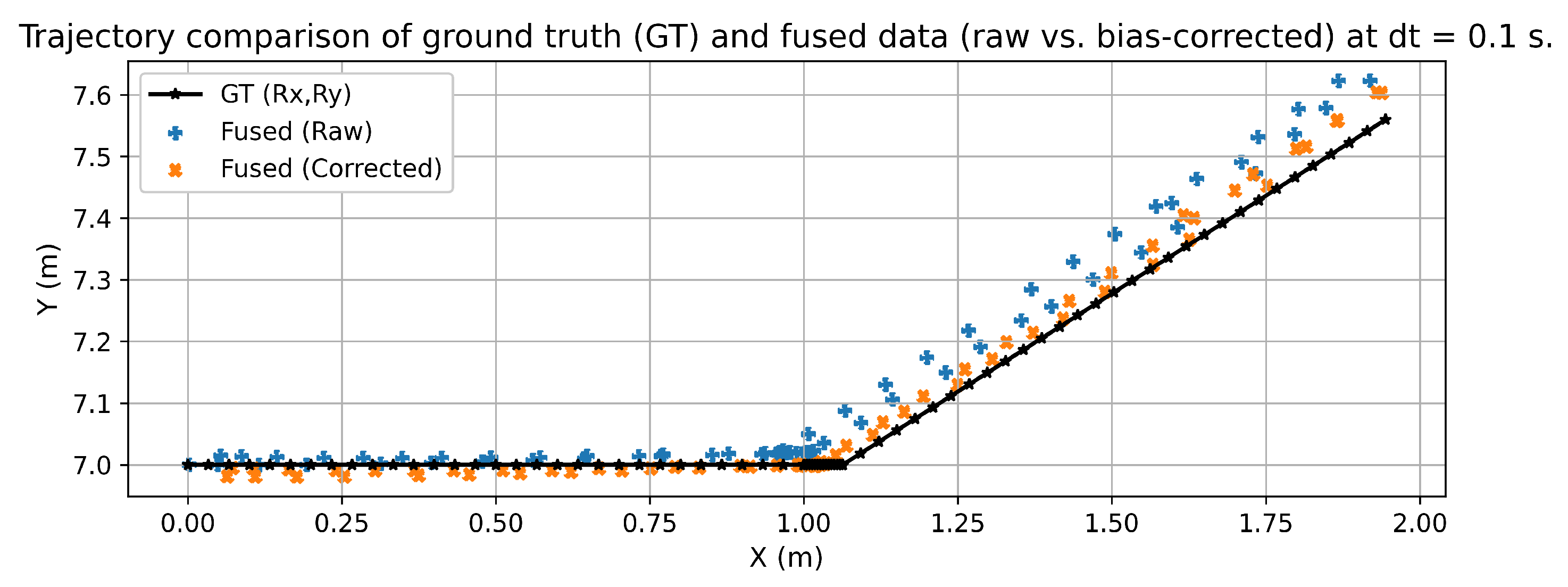
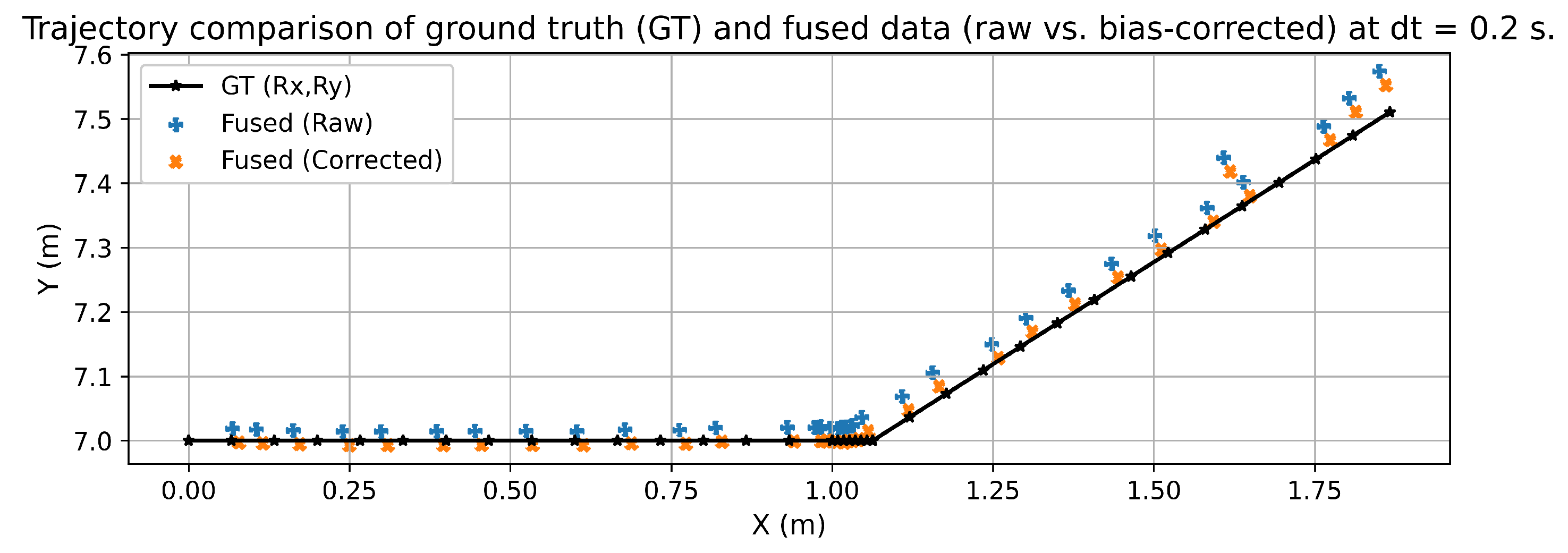
4.2. Analysis of the results of sensor data fusion using Inverse-Variance Weighting

Data from multiple sensors is combined using Inverse-Variance Weighting, a method that prioritizes low variance (i.e. high accuracy) data. Data from cameras (CAM), dead reckoning (DR), and inertial measurement units (IMU) are compared between raw data and bias corrected at dt=0.1s and dt=0.2s.

From Table 4 and Table 5, the variance values were used to determine the sensor weights via inverse-variance weighting, which assigns larger weights to measurements with lower variance. In particular, the dead reckoning (DR) sensor, having a very low Y-axis variance (${\mathrm{Var}}_Y\approx 0.0002$), receives a high Y-axis weight ($W_Y\approx 0.87$). Conversely, the camera (CAM) has a higher Y-axis variance, resulting in a lower weight ($W_Y\approx 0.13$), while along the X-axis the similar variances lead to more balanced weights. For the rotation angle ($\theta$), the inertial measurement unit (IMU)—as the sole information source—receives a weight of 1. These findings are consistent with the trajectory comparison in Figure 7 and Figure 8, where the bias-corrected trajectories lie closer to the ground truth.

Table 6, which shows the root mean square error (RMSE) values of the sensor data fusion, shows that bias-corrected data were obtained before fusion. Comparing the raw data and the fused data after bias correction, the RMSE of the bias-corrected data decreased on both the X and Y axes.

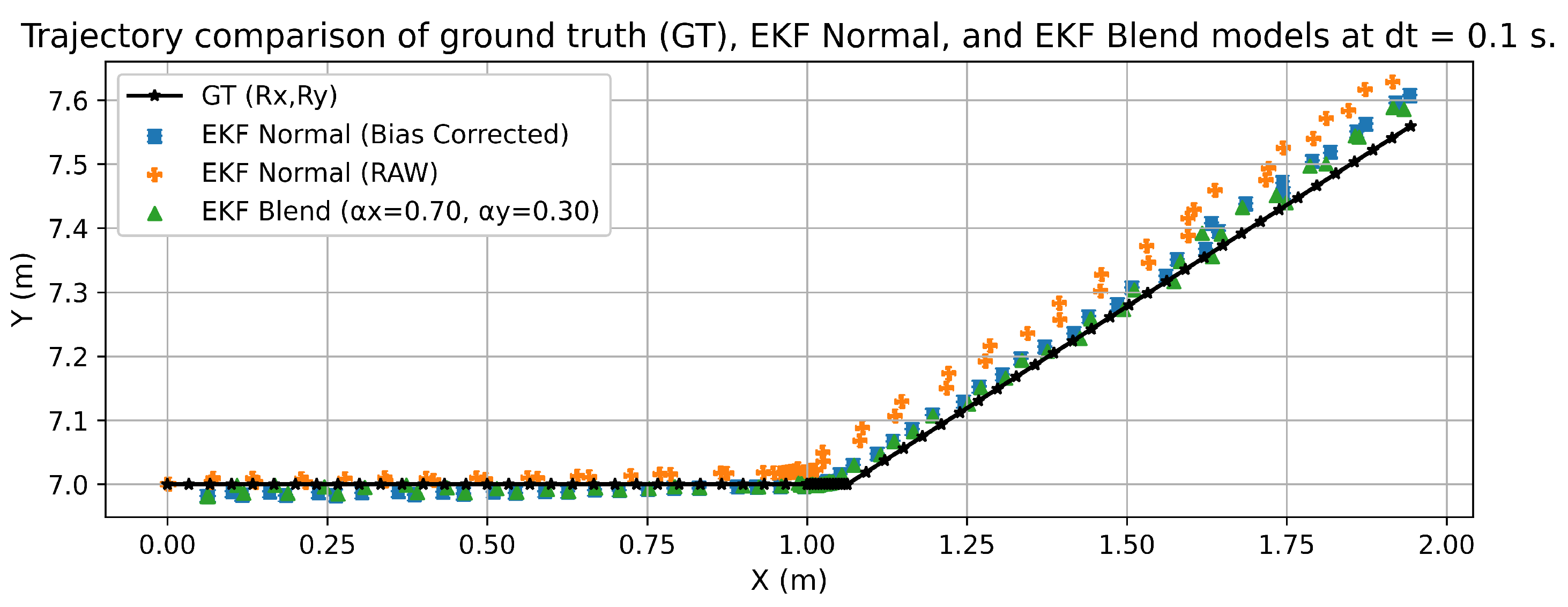
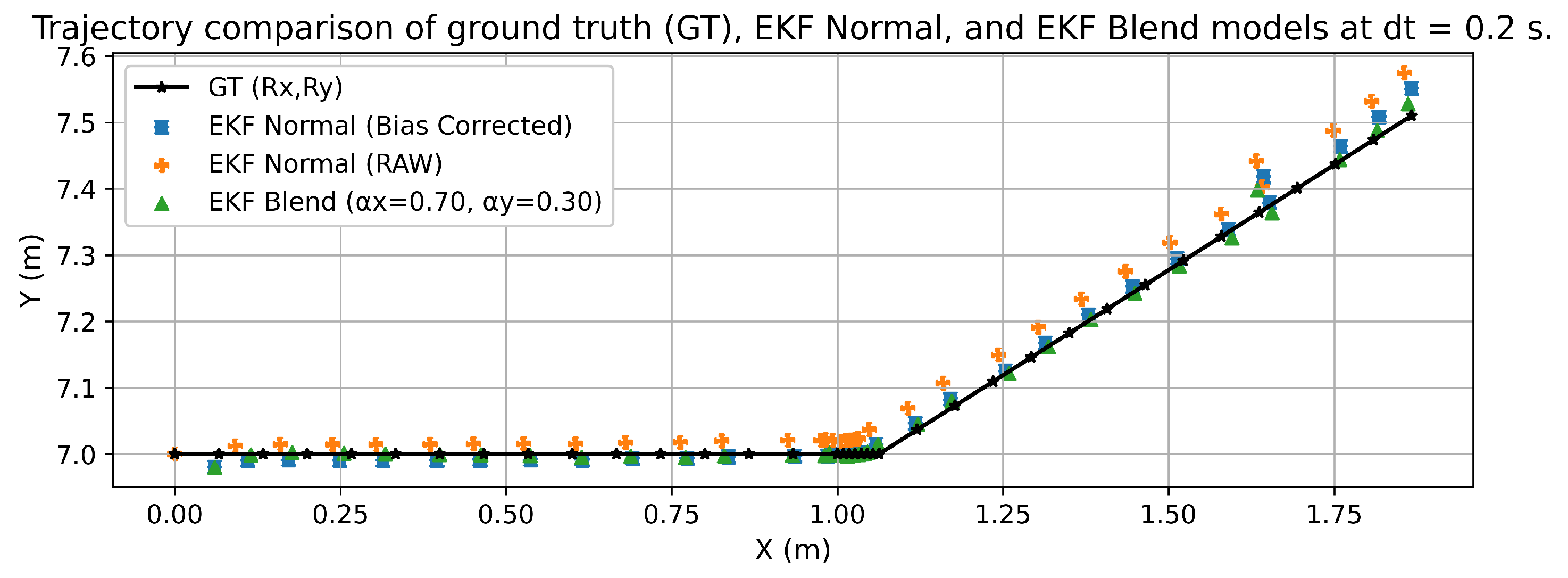
4.3. Analysis of data integration results using EKF

Indoor localization of an Automated Guided Vehicle (AGV) involves the fusion of data from multiple sensor sources to improve accuracy. The Extended Kalman Filter (EKF) is a popular choice due to its capability of handling nonlinearities. Therefore, two EKF models were compared: the EKF Normal (original, both raw and bias-corrected) and the EKF Blended (weighted with sensor values based on the parameters ${\alpha }_x$ and ${\alpha }_y$).

From Table 7, it can be seen that using the EKF with bias correction effectively reduces the RMSE error. The RMSE for $XY$ is significantly reduced when using the corrected data compared to the raw data, both at $dt=0.1\mathrm{s}$ and $dt=0.2\mathrm{s}$. Furthermore, applying the blended EKF provides even better results, minimizing the RMSE for $XY$ when appropriate weighting coefficients (${\alpha }_x$, ${\alpha }_y$) are selected.

From Figure 9 and Figure 10, which compare the trajectories of the EKF filter, it is found that the trajectory obtained from the raw data (Normal RAW) deviates the most from the ground truth (GT), especially at dt=0.1s. However, when the data is normal bias corrected, the trajectory becomes closer to the GT, and the Blended EKF performs better, giving a smoother trajectory that is closest to the GT. Comparing the sampling periods (dt), it is found that at dt=0.1s, although it provides more detailed trajectory details, it also has more pronounced noise, while at dt=0.2s, it is smoother.

It is noteworthy that some weighting configurations of Blended EKF give lower RMSE values. Fusing higher ${\alpha }_x$ and lower ${\alpha }_y$ values leads to better performance. This result can be explained by Table 4 and Table 5, which shows that Dead Reckoning (DR) sensors have lower variance along the Y-axis compared to cameras (CAM), thereby increasing the reliability of DR measurements in that direction. Therefore, it is more prudent to assign more weight to DR along the Y-axis, which relies more on stable sensors, while CAM still performs better along the X-axis, which is comparable to DR. The importance of adjusting the blending coefficients to match the statistical values of each sensor to increase the accuracy and stability of the positioning.

4.4. Discussion and suggestions

The experiments demonstrate the advantages of Blended EKF, but there are some limitations. First, the experiment was conducted indoors in a controlled environment with fixed camera positions, which may not capture complex real-world conditions or have uncaptured points. Second, this analysis assumes that the deviations of each sensor are constant. In practice, sensor characteristics may change due to temperature, wear, or other disturbances, which may affect the bias correction process. Third, the blending coefficients (${\alpha }_x$, ${\alpha }_y$) were selected based on experimental performance.

This limitation provides a useful guideline for future research. Future studies could expand the experiments to larger or more complex environments and incorporate dynamic simulations, such as moving obstacles or the interaction of multiple automated guided vehicles (AGVs). Developing methods and compensating for time-varying biases is also important. Furthermore, adopting adaptive or machine-learning mechanisms to automatically adjust blending weights may contribute to the practical application of the proposed Blended EKF in industrial and logistics contexts.

5. Conclusions

This research has demonstrated an effective data fusion framework for the localization of Automated Guided Vehicles (AGVs) in indoor environments. The core of this framework, which incorporates bias correction and inverse-variance weighting, yielded a significant reduction in the Root Mean Square Error (RMSE) across all sensors, causing the corrected trajectories to align more closely with the ground truth (GT). This weighting method strategically assigns greater influence to more reliable sensor data, such as the high weight given to the Dead Reckoning (DR) sensor’s stable Y-axis measurements. The proposed Blended EKF methodology proved superior to the standard EKF. Not only did it achieve a lower RMSE in key scenarios, but it also produced a markedly smoother trajectory that demonstrated the highest fidelity to the ground truth. Furthermore, this study confirmed that fine-tuning the blending coefficients to reflect the statistical properties of each sensor enhances both accuracy and stability. Specifically, assigning greater weight to the DR sensor for the Y-axis and the Camera (CAM) for the X-axis minimized the overall RMSE.

In conclusion, the experimental results indicate that the proposed approach provides a low-cost, accurate, and robust localization solution, making it highly suitable for practical AGV applications in indoor settings.