Submitted:
13 October 2025
Posted:
14 October 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Set Up of the Model
3. Results
3.1. First Principle and Entropy of Macro-Gas
3.2. Free Energy
3.3. Gibbs Potential
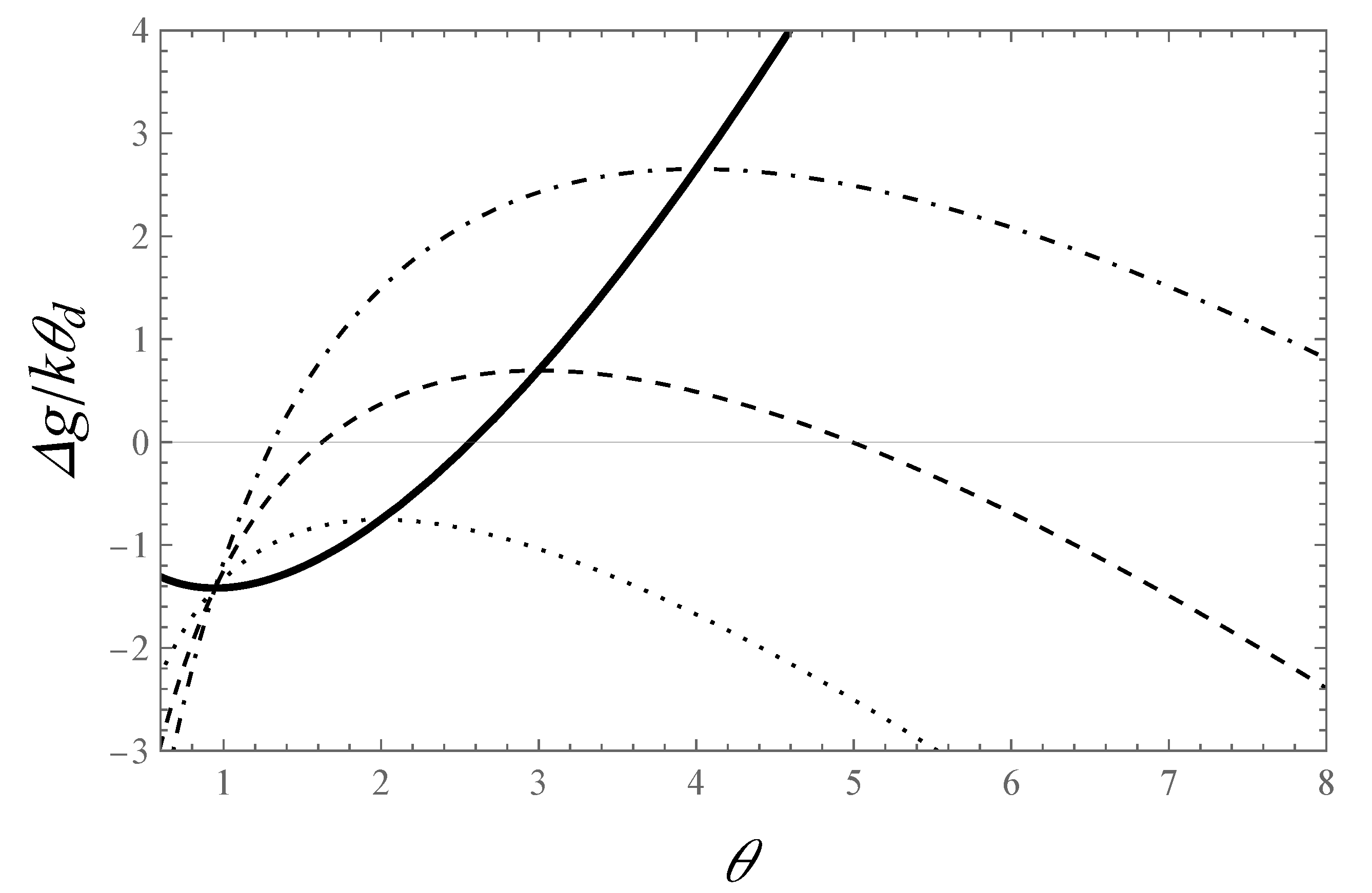
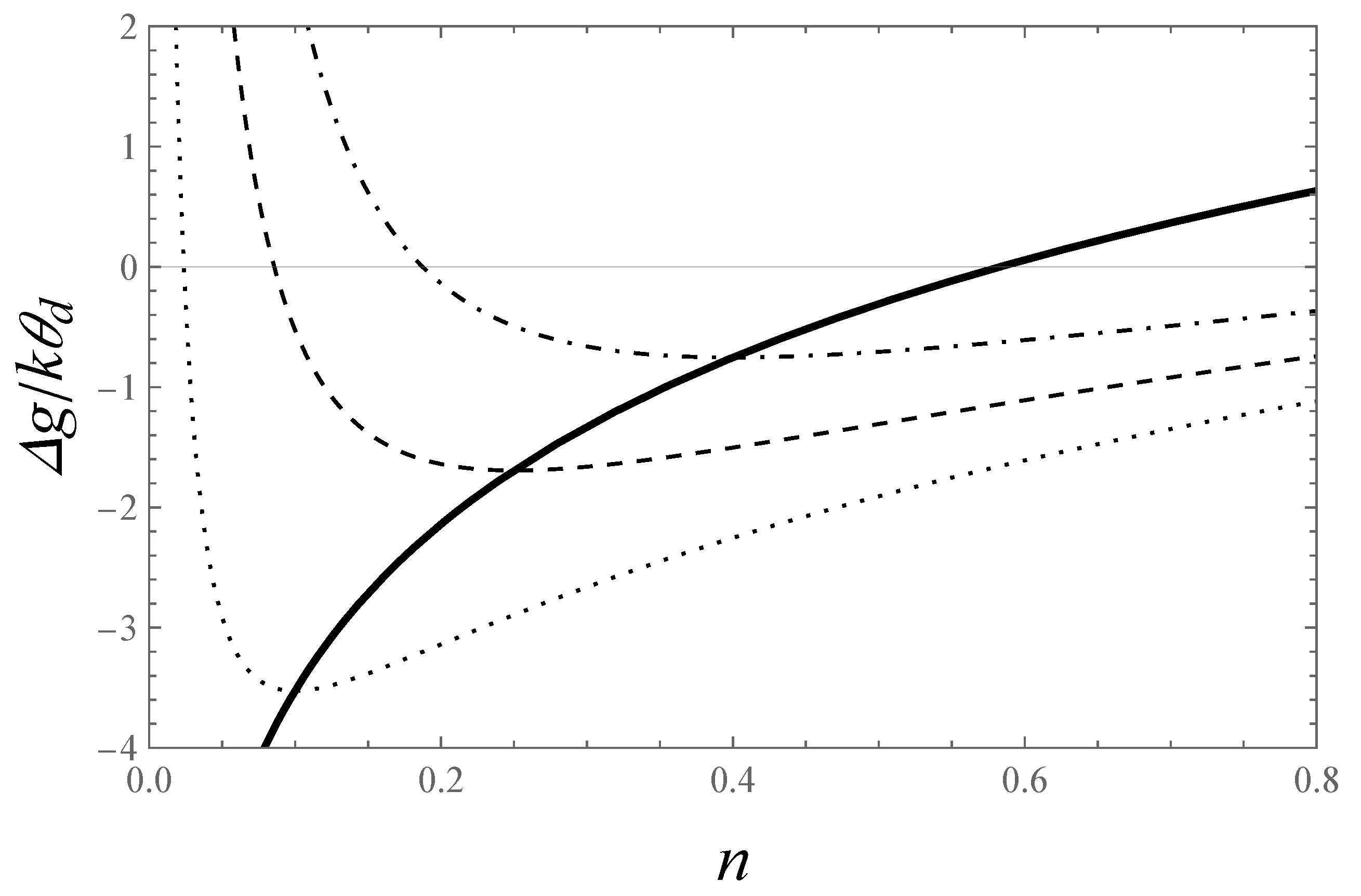
3.4. Stability Analysis
3.4.1. Micro-Canonical Ensemble
3.4.2. Canonical Ensemble
3.4.3. Grand Canonical Ensemble
3.5. The Origin of the Entropy Change
4. Discussion
4.1. Basic Assumptions and Main Results
4.2. Caveats
5. Conclusions
Author Contributions
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MC(s) | Molecular Cloud(s) |
| 3D | three-dimensional space |
References
- Antonov, V. A. Most probable phase distribution in spherical star systems and conditions for its existence. Vest. Leningr. Gos. Univ. 1962, 7, p.135. [Google Scholar] [CrossRef]
- Katz, J. On the number of unstable modes of an equilibrium. Monthly Notices of the Royal Astronomical Society 1978, 183, 765–770. [Google Scholar] [CrossRef]
- Lynden-Bell, D. , Wood, R. The gravo-thermal catastrophe in isothermal spheres and the onset of red-giant structure for stellar systems. Monthly Notices of the Royal Astronomical Society 1968, 138, 495–525. [Google Scholar] [CrossRef]
- Padmanabhan, T. Antonov Instability and Gravothermal Catastrophe–Revisited. Astrophysical Journal Supplement, 1989, 71, p.651. [Google Scholar] [CrossRef]
- Padmanabhan, T. Statistical mechanics of gravitating systems. Physics Reports 1990, 188, 285–362. [Google Scholar] [CrossRef]
- Chavanis, P-H. Gravitational instability of finite isothermal spheres. Astronomy & Astrophysics 2002, 381, 340–356. [Google Scholar]
- Chavanis, P-H. Gravitational instability of isothermal and polytropic spheres. Astronomy & Astrophysics 2003, 401, 15–42. [Google Scholar] [CrossRef]
- Chavanis, P-H. Dynamical stability of collisionless stellar systems and barotropic stars: the nonlinear Antonov first law Astronomy & Astrophysics 2006, 451, 109–123.
- de Vega, H. J. , Sanchez, N., Combes, F. Self-gravity as an explanation of the fractal structure of the interstellar medium. Nature 1996, 383, 56–58. [Google Scholar] [CrossRef]
- de Vega, H. J. , Sanchez, N., Combes, F. Fractal dimensions and scaling laws in the interstellar medium: A new field theory approach. Physical Review D 1996, 54, 6008–6020. [Google Scholar] [CrossRef]
- de Vega, H. J. , Sanchez, N. The statistical mechanics of the self-gravitating gas: equation of state and fractal dimension. Physics Letters B 2000, 490, 180–186. [Google Scholar] [CrossRef]
- Sormani, M. C. , Bertin, G. Gravothermal catastrophe: The dynamical stability of a fluid model. Astronomy & Astrophysics 2013, 552, id–A37. [Google Scholar]
- Keto, E. , Field, G., B., Blackman, E., G. A turbulent-entropic instability and the fragmentation of star-forming clouds. Monthly Notices of the Royal Astronomical Society 2020, 492, 5870–5877. [Google Scholar] [CrossRef]
- Elmegreen, B. , Scalo, J. Interstellar Turbulence I: Observations and Processes. Annual Review of Astronomy & Astrophysics 2004, 42, 211–273. [Google Scholar]
- Hennebelle, P. & Falgarone, E. Turbulent molecular clouds. The Astronomy & Astrophysics Review 2012, 20, id–55. [Google Scholar]
- Klessen, R. S., & Glover, S. C. O. Physical Processes in the Interstellar Medium. Star Formation in Galaxy Evolution: Connecting Numerical Models to Reality, Saas-Fee Advanced Course; ISBN 978-3-662-47889-9; Springer-Verlag: Berlin Heidelberg, Germany, 2016, pp. 85-249.
- Ferriere, K. M. The interstellar environment of our galaxy. Reviews of Modern Physics 2001, 73, 1031–1066. [Google Scholar] [CrossRef]
- Frisch, U. , Donnelly, R.J. Turbulence: The Legacy of A. N. Kolmogorov. Physics Today 1995, 49, p.82. [Google Scholar] [CrossRef]
- Kolmogorov, A. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Dokl. Akad. Nauk SSSR 1941, 30, 301–305. [Google Scholar]
- Galtier, S. , Banerjee, S. Exact Relation for Correlation Functions in Compressible Isothermal Turbulence. Physical Review Letters 2011, 107, id–134501. [Google Scholar] [CrossRef]
- Kritsuk, A. , Norman, M., Padoan, P., & Wagner, R. The Statistics of Supersonic Isothermal Turbulence. The Astrophysical Journal 2007, 665, 416–431. [Google Scholar]
- Aluie, H. Compressible Turbulence: The Cascade and its Locality. Physical Review Letters 2011, 106, id–174502. [Google Scholar] [CrossRef] [PubMed]
- Federrath, C. , Roman-Duval, J., Klessen, R., Schmidt, W., Mac Low, M.-M. Comparing the statistics of interstellar turbulence in simulations and observations. Solenoidal versus compressive turbulence forcing. Astronomy & Astrophysics 2010, 512, id–81. [Google Scholar]
- Padoan, P. , Juvela, M., Kritsuk, A., Norman, M. The Power Spectrum of Supersonic Turbulence in Perseus. The Astrophysical Journal 2006, 653, L125–L128. [Google Scholar] [CrossRef]
- Keto, E. Scales of Stability and Turbulence in the Molecular ISM. Astronomische Nachrichten 2024, 345, id–e20240044. [Google Scholar] [CrossRef]
- Donkov, S. , Stefanov I.Zh., Kopchev V., Thermodynamics of Fluid Elements in the Context of Turbulent Isothermal Self-Gravitating Molecular Clouds. Universe 2025, 11(6), 184. [Google Scholar] [CrossRef]
- Larson, R. Turbulence and star formation in molecular clouds. Monthly Notices of the Royal Astronomical Society 1981, 194, 809–826. [Google Scholar] [CrossRef]
- Callen, H. B. Thermodynamics and an introduction to Thermostatistics ISBN 978-0471862567. Published by John Wiley & Sons, Inc., 2nd Edition, 1991, pp. 203-207.
- Reif, F. Fundamentals of Statistical and Thermal Physics ISBN 978-1-57766-612-7. Published by Waveland Press, Inc., Nong Grove, IL USA, 1965, pp. 288-319.
- Donkov, S. , Stefanov, I. Z., Veltchev, T. V. Thermodynamics of fluid elements in the context of saturated isothermal turbulence in molecular clouds. Bulgarian Astronomical Journal 2023, 38, 91–97. [Google Scholar]
- Aschwanden, M.J. , Scholkmann, F., Bethune, W., et al. Order out of Randomness: Self-Organization Processes in Astrophysics. Space Science Reviews 2018, 214, article. [Google Scholar] [CrossRef]
- Cover, T.M., Thomas, J.A. Elements of Information Theory, Second Edition, ISBN-13 978-0-471-24195-9. Published by A John Wiley & Sons, Inc., Hoboken, New Jersey, 2006, pp. 13-103.
- Vázquez-Semadeni, E. , Palau, A., Ballesteros-Paredes, J., Gómez, G., Zamora-Aviles, M. Global hierarchical collapse in molecular clouds. Towards a comprehensive scenario. Monthly Notices of the Royal Astronomical Society 2019, 490, 3061–3097. [Google Scholar] [CrossRef]
- Binney, J. , Tremaine, S. Galactic dynamics. Galactic Dynamics (Princeton Series in Astrophysics); Princeton, N.J.: Princeton University Press, USA, 1987; pp. 567–573. [Google Scholar]
| 1 | This range roughly spans between and
|
| 2 | To avoid the so called "Jeans swindle": the assumption for infinite homogeneous medium is actually not really consistent, because the Poisson equation cannot be solved unless the medium density is zero. |
| 3 |
We can easily obtain that in canonical variables and v the conclusion for the stability will be the same. If one accounts for the differential relations and , defining the change of variables in s, obtains:
The conditions for stability of the system according to Callen [28] are violated, due to the derivative regarding , the derivative in regard to v is right. Hence, the instability is caused by the energy (temperature).
|
| 4 | The detailed derivation of the off-equilibrium form for the Gibbs potential is performed in App.B of the previous paper [26]. The derivation for the free energy is not made, because the calculations in the case of canonical ensemble are (a subcase and) simpler than that for the grand canonical ensemble. |
| 5 | We must note here that similar consideration of the canonical ensemble, without varying density n, had to be done in Section 4.4.1 of our previous work [26], too. The right application of the method of off-equilibrium potentials, presented in Reif [29], implies that in the case of the canonical ensemble the off-equilibrium free energy must be varied only in regard to the temperature, although the equilibrium potential is a function of two variables. Therefore, by the consideration in Section 4.4.1 of [26] we must conclude that the system is in a stable equilibrium state at temperature , due to the minimum of the free energy. |
| 6 | See the App.B in [26]. |
| 7 | See, also, the assessment for the macro-temperature made in our previous paper [26], Section 4.4.2 there. |
| 8 | Here we must note that in [26], Section 4.1, there is a mistake. We consider virialization in the form , which means a strong self-gravitating cloud, like in the present work. The right hypothesis is an equipartition (at all the scales of the inertial range) with a strong domination of the turbulent kinetic energy (i.e. ). The considerations in Section 4.1, there, are in accordance with the latter presumption. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




