A Coherence-Thermodynamic Model of Quantum Measurement: Deterministic Collapse Through Environmental Coupling

1. Introduction

The foundations of quantum mechanics are defined by two distinct and incompatible dynamical principles [1]. The first is the continuous, deterministic, and unitary evolution of a quantum system governed by the Schrödinger equation [2]. The second is the discontinuous, probabilistic, and non-unitary collapse of the wave function upon measurement, as described by the Born rule and the projection postulate [3]. This structural dualism constitutes the essence of the measurement problem. Despite decades of interpretation and reformulation, no consensus has been reached on a physically complete and self-consistent resolution.

In this work, we propose that the collapse process is not a separate axiom, but a consequence of a deterministic phase transition in the thermodynamics of coherence [4]. We formulate a unified dynamical law that incorporates both Schrödinger evolution and wave function collapse as limiting cases of a single equation of motion. Measurement is modeled as an active perturbation that injects what we term environmental contradiction pressure into the coherence structure of the system. This triggers a two-stage response: first, rapid suppression of quantum superposition through dephasing, and second, nonlinear amplification of one outcome through a symmetry-breaking process. The mechanism is analogous to spontaneous breaking of the symmetry in phase transitions [5], where microscopic fluctuations determine macroscopic order.

We demonstrate this model explicitly for a single-qubit system, reproducing the full trajectory from pure superposition to a definite outcome without invoking wavefunction postulates, environmental tracing, or fundamental randomness. This approach suggests a quantum theory in which measurement irreversibility arises from information geometry [6] and entropy flow [4] rather than axiomatic discontinuity. Crucially, our model makes specific experimental predictions that distinguish it from existing interpretations, which we detail in Section 4.7.

2. Theoretical Framework

Our approach begins with the standard density matrix formalism [3] and extends it to model collapse as a complete deterministic thermodynamic process. We will first establish precise definitions of the key physical concepts.

2.1. Key Physical Concepts and Definitions

2.1.1. Coherence as Purity

The state of a quantum system is described by the density operator $\rho$. We define the system’s coherence as the purity of its density matrix:

$$\alpha \equiv \mathrm{Tr}\left({\rho }^2\right)$$

(1)

where $\alpha =1$ for any pure state (including both superpositions and collapsed eigenstates), and $\alpha <1$ indicates a mixed state. For a qubit, $\alpha =0.5$ represents maximal mixing. Purity quantifies the system’s information integrity: Higher purity means that the state is more definite and predictable.

2.1.2. Environmental Nudge

The environmental nudge ($ϵ$) is an infinitesimal perturbation that represents the first unavoidable interaction between the quantum system and the measurement apparatus. Physically, this corresponds to random thermal fluctuations, electromagnetic field variations, or other microscopic environmental degrees of freedom that couple to the system at the onset of measurement. The nudge breaks the perfect symmetry of the initial superposition, introducing a tiny bias ($\left|ϵ\right|\ll 1$) towards one eigenstate. Although the nudge itself is unpredictable, its effect is deterministic: it seeds the initial condition for the subsequent amplification dynamics.

2.1.3. Contradiction Pressure

Contradiction pressure quantifies the degree of incompatibility between the quantum state of the system and the measurement basis. A superposition state carries high contradiction pressure when measured on its eigenstate basis because the system simultaneously contains conflicting information about which outcome will occur. The measurement interaction acts to resolve this contradiction by forcing the system into a state compatible with the measurement apparatus, a single, definite eigenstate.

2.2. Unitary Evolution and the Conservation of Coherence

The time evolution of a closed quantum system is given by the Liouville-von Neumann equation:

$${\displaystyle \frac{d\rho }{dt}}=-{\displaystyle \frac{i}{\hslash }}[H,\rho ]$$

(2)

A critical result of this unitary evolution is that purity is conserved [4]:

$${\displaystyle \frac{d\alpha }{dt}}={\displaystyle \frac{d}{dt}}\mathrm{Tr}\left({\rho }^2\right)=0$$

(3)

This conservation law implies that the Schrödinger equation alone cannot describe transitions between different pure states (e.g., from superposition to collapsed eigenstate). Such transformations require a nonunitary dynamic.

2.3. Modeling Collapse: A Two-Stage Thermodynamic Process

We model measurement as a two-stage thermodynamic process, each governed by a distinct physical mechanism.

2.3.1. Stage 1: Dephasing (Coherence Destruction)

The first stage is the rapid loss of phase coherence between the eigenstates. We model this using a standard dephasing operator [7]:

$${\mathcal{L}}_{\mathrm{dephase}}\rho ={\gamma }_d\left(t\right)\left(\sum _j{P}_j\rho P_j-\rho \right)$$

(4)

where $P_j=|{\psi }_j\rangle \langle {\psi }_j|$ are projectors in measurement basis states, and ${\gamma }_d\left(t\right)$ is the dephasing rate. Physically, this represents the system’s entanglement with uncontrolled environmental degrees of freedom, causing interference terms to vanish. This process alone produces a mixed state (statistical mixture of eigenstates), but does not select a single outcome; it addresses the "preferred basis" problem but not the "outcome selection" problem.

2.3.2. Stage 2: State Resolution (Outcome Amplification)

To achieve a definitive outcome selection, we introduce a non-linear amplification mechanism inspired by the principle of spontaneous symmetry breaking [5]. The core idea is to create a dynamic that exponentially amplifies any deviation from a perfectly balanced statistical mixture.

For quantum systems of arbitrary dimension d (where $d=2$ for qubits, $d=3$ for qutrits, etc.), the resolution mechanism must amplify the populations ${\rho }_{jj}$ deviating most from the equal distribution ($1/d$ for each state). Although multiple mathematical forms can implement this principle, we focus here on the two-level case ($d=2$), using a specific dynamics that ensures both rapid amplification and smooth saturation.

$$\begin{array}{cc}\hfill {\left({\displaystyle \frac{d\rho }{dt}}\right)}_{\mathrm{resolve},00}& =+{\gamma }_r\left(t\right)\underset{\mathrm{Saturation}\mathrm{Factor}}{\underbrace{\left({\rho }_{00}{\rho }_{11}\right)}}\underset{\mathrm{Amplification}\mathrm{Driver}}{\underbrace{({\rho }_{00}-{\rho }_{11})}}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\left({\displaystyle \frac{d\rho }{dt}}\right)}_{\mathrm{resolve},11}& =-{\gamma }_r\left(t\right)\left({\rho }_{00}{\rho }_{11}\right)({\rho }_{00}-{\rho }_{11})\hfill \end{array}$$

(6)

where ${\gamma }_r\left(t\right)$ is the resolution rate. This dynamic has three key physical properties directly corresponding to its mathematical structure:

• Amplification: The rate of change is driven by the population difference $({\rho }_{00}-{\rho }_{11})$. Any deviation from the perfect equality (${\rho }_{00}={\rho }_{11}$) is exponentially amplified, driving the larger population toward 1 and the smaller toward 0. This is the engine of resolution.
• Saturation: The term product $\left({\rho }_{00}{\rho }_{11}\right)$ acts as a natural brake. As one population approaches unity (e.g., ${\rho }_{00}\to 1$), the other approaches zero (${\rho }_{11}\to 0$), causing this term to vanish. This ensures that the dynamic shuts off smoothly as a pure state is reached, preventing numerical overshoot.
• Determinism: Given an initial asymmetry (provided by the environmental nudge), the final outcome is completely determined by the flow field generated by these equations.

In the language of information geometry [6], populations define basins of attraction in the manifold of density matrices. Our resolution operator (Eqs. 5-6) creates a vector field that deterministically drives any initial state along a geodesic path toward the manifold’s boundaries, which represent the pure eigenstates.

2.4. The Unified Dynamical Equation

Combining all terms yields our complete equation of motion:

$$\begin{array}{|c|}\hline {\displaystyle \frac{d\rho }{dt}}=-{\displaystyle \frac{i}{\hslash }}[H,\rho ]+{\mathcal{L}}_{\mathrm{dephase}}\rho +{\mathcal{L}}_{\mathrm{resolve}}\rho \\ \hline\end{array}$$

(7)

This single equation governs the entire measurement process. When measurement is inactive (${\gamma }_d={\gamma }_r=0$), we recover standard unitary Schrödinger evolution. When measurement is triggered (${\gamma }_d,{\gamma }_r>0$), the nonunitary terms dominate, implementing a deterministic phase transition from superposition to eigenstate. The transition can be understood as a geodesic flow [6] in the quantum state manifold, where the system follows the path of steepest descent in coherence entropy space toward a pure, minimum entropy configuration.

Figure 1. Numerical demonstration of a deterministic qubit collapse governed by the unified dynamical law in Eq. 8. The measurement interaction begins at $t=5.0$, triggering a two-stage transition from a pure superposition state to a definite pure eigenstate. Top panel: The two stages of collapse are illustrated. The magnitude of the quantum coherence, $|{\rho }_{01}|$ (dashed line), rapidly decays to zero, which is the signature of the dephasing process. Concurrently, the populations ${\rho }_{00}$ (blue) and ${\rho }_{11}$ (orange) are driven to the definite outcomes of 1 and 0, respectively, by the nonlinear amplification dynamic. Bottom panel: The evolution of the purity, $\alpha =\mathrm{Tr}\left({\rho }^2\right)$, reveals a key prediction of the model. The system begins in a pure state ($\alpha =1$), undergoes a transient dip as it enters a mixed-like state during dephasing, and then rapidly returns to a pure state ($\alpha =1$) as the final outcome is resolved. This demonstrates that the pure-to-pure state transformation occurs via a distinct, physical intermediate stage, rather than an instantaneous jump.

Figure 1. Numerical demonstration of a deterministic qubit collapse governed by the unified dynamical law in Eq. 8. The measurement interaction begins at $t=5.0$, triggering a two-stage transition from a pure superposition state to a definite pure eigenstate. Top panel: The two stages of collapse are illustrated. The magnitude of the quantum coherence, $|{\rho }_{01}|$ (dashed line), rapidly decays to zero, which is the signature of the dephasing process. Concurrently, the populations ${\rho }_{00}$ (blue) and ${\rho }_{11}$ (orange) are driven to the definite outcomes of 1 and 0, respectively, by the nonlinear amplification dynamic. Bottom panel: The evolution of the purity, $\alpha =\mathrm{Tr}\left({\rho }^2\right)$, reveals a key prediction of the model. The system begins in a pure state ($\alpha =1$), undergoes a transient dip as it enters a mixed-like state during dephasing, and then rapidly returns to a pure state ($\alpha =1$) as the final outcome is resolved. This demonstrates that the pure-to-pure state transformation occurs via a distinct, physical intermediate stage, rather than an instantaneous jump.

3. Numerical Validation of the Emergent Born Rule

We now test the central claim: that Born-Rule probabilities emerge as ensemble statistics of an underlying deterministic process.

3.1. Simulation Methodology

Each simulation trial proceeds as follows:

• Initialization: Density matrix set to pure superposition: ${\rho }_{00}={\rho }_{11}=0.5$, ${\rho }_{01}={\rho }_{10}=0.5$.
• Environmental Nudge: A random perturbation $ϵ\sim \mathcal{U}(-{ϵ}_0,+{ϵ}_0)$ is applied: ${\rho }_{00}\to {\rho }_{00}+ϵ$, ${\rho }_{11}\to {\rho }_{11}-ϵ$, modeling unavoidable thermal/quantum fluctuations at measurement onset.
• Deterministic Evolution: System evolves under Eq. 7 with ${\gamma }_d=50$, ${\gamma }_r=100$, ${ϵ}_0=0.001$, time step $dt=0.0001$ s. Evolution continues until ${\rho }_{jj}>0.999$ for some j, then terminates.
• Outcome Recording: The final collapsed state ($|0\rangle$ or $|1\rangle$) is recorded.

Repeating this procedure 1,000 times generates an ensemble of deterministic outcomes, each seeded by a different random nudge. The key insight: each individual collapse is deterministic, but the ensemble statistics emerge from the averaging over unknown initial environmental conditions.

3.2. Results and Born Rule Agreement

Figure 2 shows the distribution of the results. The observed frequencies (510 $|0\rangle$, 490 $|1\rangle$) agree with the prediction of the Born Rule (500/500) within the statistical fluctuation (${\chi }^2=0.4$, $p>0.5$). This shows that:

• Quantum probabilities need not be fundamental—they can emerge from deterministic dynamics with epistemic uncertainty in initial conditions.
• The Born Rule is a statistical law analogous to classical thermodynamics [4]: macroscopic regularity arising from microscopic determinism.
• The "randomness" of measurement results is relegated to environmental fluctuations, not to the collapse mechanism itself.

4. Discussion

This work has demonstrated a proof-of-concept for a deterministic resolution to the quantum measurement problem grounded in the principles of Coherence Thermodynamics [4]. Our numerical simulation shows that a single unified dynamical law can govern both the unitary evolution of a quantum system and its non-unitary collapse into a definite state. The model achieves this by not introducing new interpretations but by positing a physical thermodynamic mechanism for collapse.

4.1. A Deterministic Process Not an Interpretation

The measurement problem has given rise to numerous interpretations, each with profound conceptual trade-offs [1]. Our model distinguishes itself by offering a new physical dynamic rather than a new interpretation.

Standard decoherence theory masterfully explains why quantum interference effects vanish upon interaction with an environment, leading to a diagonal density matrix on a preferred basis [7]. However, it remains silent on the problem of outcomes, failing to explain why a specific outcome is actualized from the resulting statistical mixture. Spontaneous collapse models like GRW theory address this by introducing ad hoc stochastic terms into the Schrödinger equation that force localization, but these terms are not derived from a deeper physical principle [8]. Other approaches such as the Many Worlds Interpretation preserve unitary evolution at the cost of a vastly branching ontology that is difficult to test [9] while epistemic views like QBism recast collapse as a subjective update of an observers knowledge leaving the physical process of outcome selection unresolved [10].

The model presented here is different. It proposes that collapse is a deterministic physical process driven by the thermodynamics of information [4]. Following Amari and Nagaoka [6], we interpret evolution as a geodesic flow through the manifold of quantum states, with the syntropic operator providing the contractive force that accelerates movement toward pure eigenstates. Restore determinism to quantum mechanics without invoking hidden variables, branching universes, or postulated randomness.

4.2. The Two Stage Thermodynamic Mechanism

The core of our model is a two-component mechanism for collapse triggered when the contradiction pressure of a measurement interaction is applied.

Dephasing: The first stage is a rapid damping of the non-diagonal elements of the density matrix, consistent with the dynamics of the standard open quantum system [7]. This represents the immediate loss of quantum coherence as the system interacts with the measurement apparatus, governed by our ${\mathcal{L}}_{\mathrm{dephase}}$ operator.

State resolution: The second crucial stage is a nonlinear process that amplifies one of the diagonal population terms to unity while suppressing all others, implementing a symmetry-breaking dynamic analogous to phase transitions in condensed matter physics [5]. We modeled this with the ${\mathcal{L}}_{\mathrm{resolve}}$ operator, which implements a replicator-like dynamic. This nonlinear evolution is the engine of certainty that ensures a single definite outcome.

The entire process is seeded by the nudge function $ϵ$. This is not a source of randomness but a minimal deterministic asymmetry that represents the first unavoidable quantum of interaction with the measurement environment. In any real physical system, perfect symmetry is an idealization; the nudge models the inevitable presence of this structural bias. Once the symmetry is broken by this seed, the non-linear resolution dynamic deterministically amplifies it to a macroscopic outcome through the basins of attraction defined in the information geometry of the state space [6]. The apparent randomness of quantum mechanics is thus relegated to the practical unpredictability of this infinitesimal environmental nudge.

4.3. Implications for the Born Rule

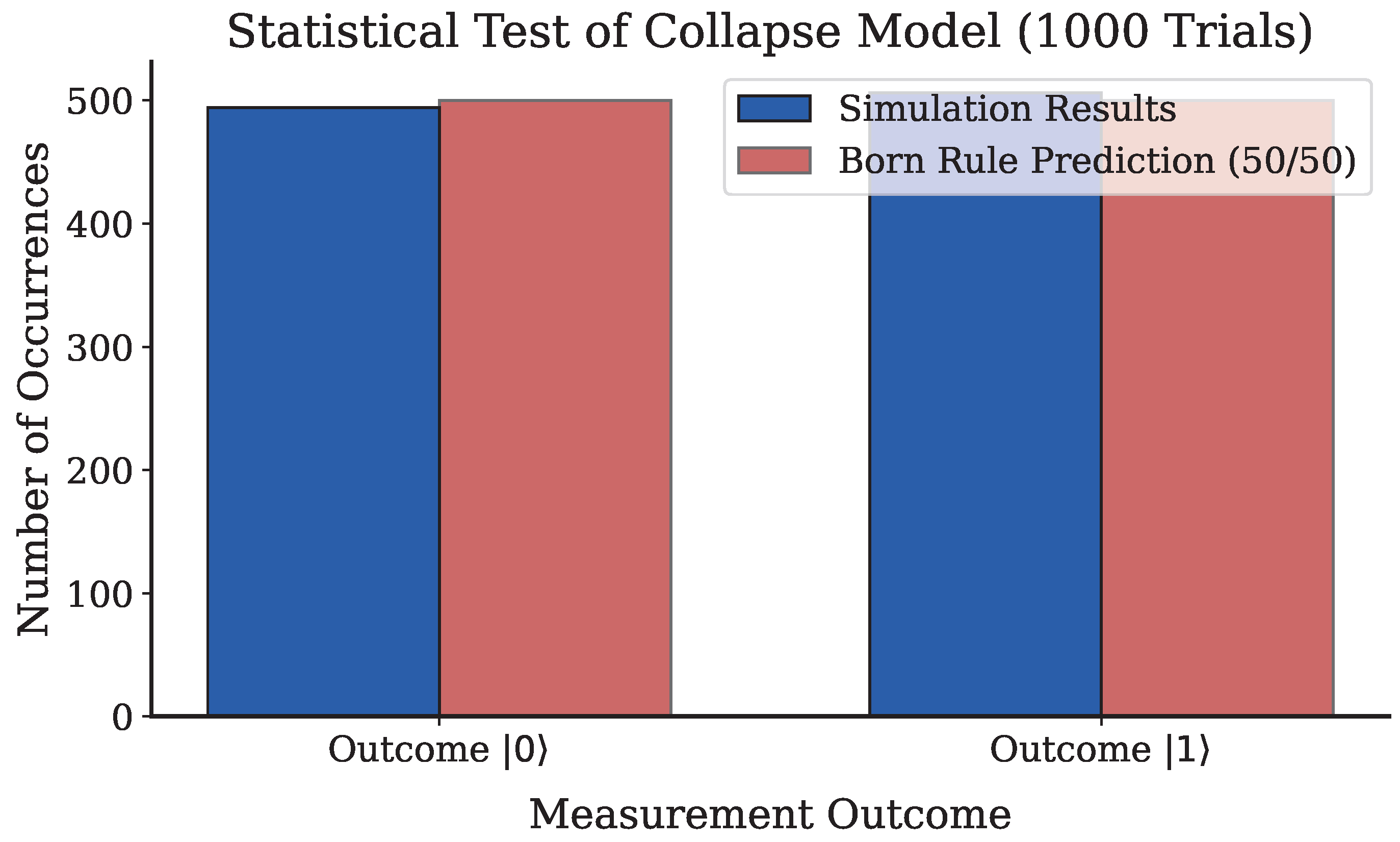
The numerical experiment as shown in Figure 2 provides central validation for our model’s foundational claim: that the probabilistic nature of quantum measurement is not a fundamental axiom of reality but an emergent property of an underlying deterministic physical process. The remarkable agreement between the simulation’s outcome statistics and the Born rule’s predictions represents a potential resolution to the disconnect between the two dynamical postulates of quantum mechanics identified by Von Neumann [3].

4.3.1. The Origin of Quantum Probability

Our model as shown in Figure 2 proposes a new origin for the apparent randomness of quantum events. Each of the 1,000 trials simulated was a fully deterministic evolution. Given an identical initial state and an identical environmental “nudge,” the outcome would be identical every time. The statistical nature of the ensemble arises not from an intrinsic property of the collapse itself but from the stochastic nature of the environmental perturbation that initiates the collapse.

The “nudge” represents infinitesimal, physically unavoidable, and unpredictable fluctuations from the measurement apparatus and its wider environment. Then this random seed of asymmetry is seized by the dynamic of symmetry-breaking amplification [5]. This process acts as a deterministic amplifier, taking the infinitesimal initial bias and rapidly driving the system along the geodesic path [6] to a definite and pure eigenstate. The Born rule’s probabilities are a direct consequence of the initial state’s structure: the populations of the density matrix effectively define the basins of attraction for the final outcome. For a 50/50 superposition, a random nudge is equally likely to push the system into either basin, thus reproducing the probability 50% for each outcome over many trials.

4.3.2. Reframing the Born Rule

This result reframes the Born rule not as a fundamental axiom to be postulated without proof but as an emergent statistical law, similar to the laws of classical thermodynamics arising from the deterministic mechanics of individual particles [4]. The Schrödinger equation describes the deterministic evolution of the system’s potential, while our extended nonunitary terms describe the deterministic mechanism of how that potential is actualized into a single reality.

Our model suggests that the universe does not “roll the dice” at the moment of collapse. Rather, the deterministic laws of the interaction proceed predictably. The “dice roll” is relegated to the uncontrollable microscopic fluctuations of the environment that provide the initial symmetry-breaking condition. This addresses Wheeler’s participatory universe concept [1]: the “participation” is not metaphysical observer consciousness, but physical entropy exchange between system and measurement apparatus. The deterministic amplification provides the mechanism by which one of Wheeler’s “quantum potentials” becomes actualized in classical reality.

4.4. Implications for Quantum Foundations

This framework has several profound implications for our understanding of quantum reality.

First, it replaces the Born Rule probabilistic postulate with a thermodynamic process [4]. The Born rule in this view is not a fundamental law but an emergent statistical description of an underlying deterministic process. The probabilities it describes arise from an observers ignorance of the specific environmental nudge that seeds the collapse in any individual measurement.

Second, it reframes measurement as a coherence-driven phase transition analogous to spontaneous symmetry breaking in condensed matter physics [5]. Geometrically [6], the density matrix traces a geodesic path through the manifold of quantum states, with the syntropic operator defining a contractive vector field. Thermodynamically [4], this contraction represents a local increase in coherence (decrease in quantum entropy) that must be compensated for by the export of entropy to the environment. The quantum superposition is a high-symmetry state rich in potential but structurally ambiguous. Under the pressure of a measurement interaction, this symmetry is broken, and the system is forced to transition into one of several possible low-symmetry definite states.

Finally, this model removes the mystical role of the observer. Collapse is not a result of consciousness or subjective knowledge updating, but a physical thermodynamic process that occurs upon any interaction sufficient to break the systems coherent symmetry and trigger the state resolution dynamic.

4.5. Testable Experimental Predictions

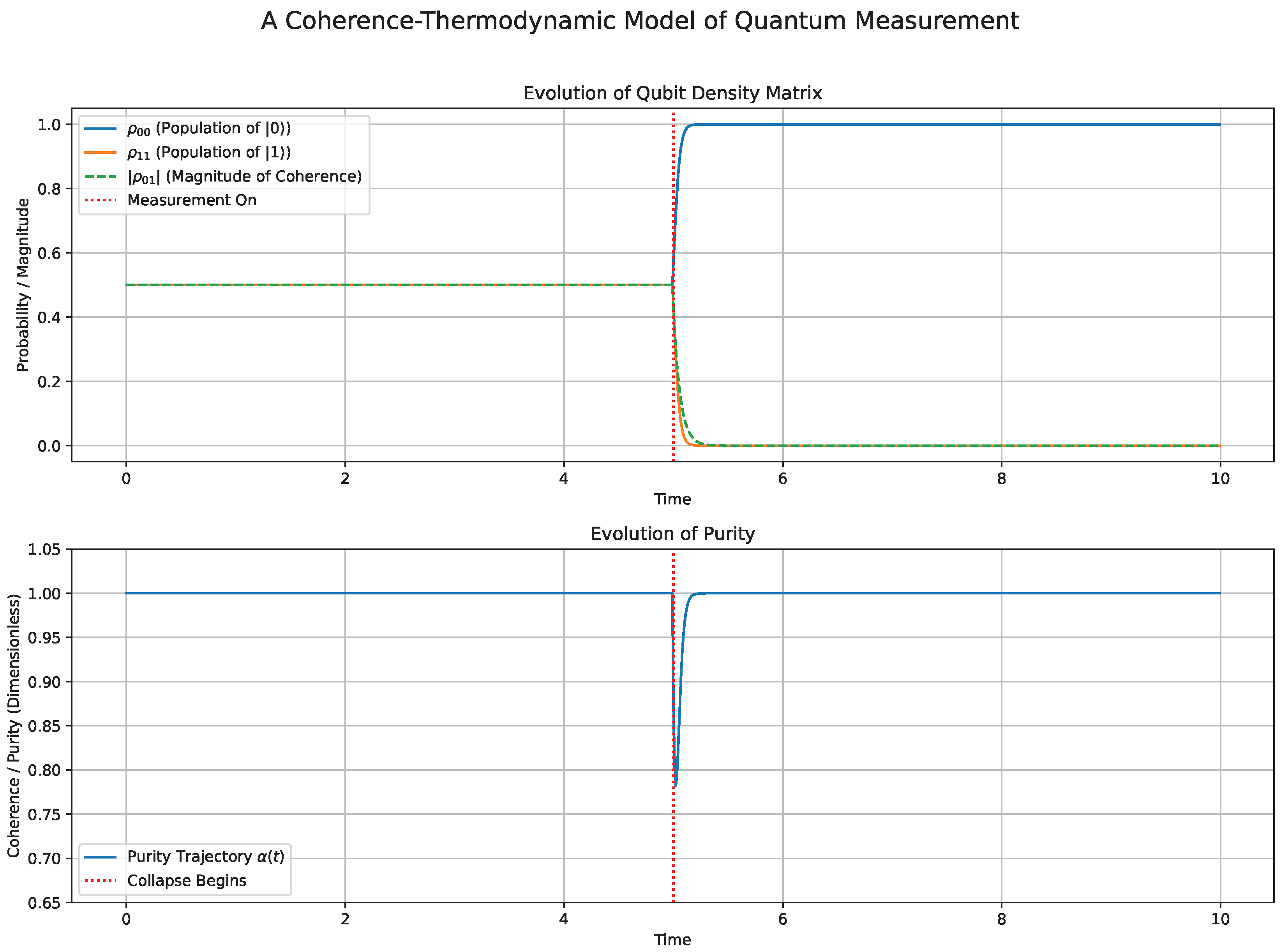
Our model makes several specific predictions that distinguish it from standard quantum mechanics and alternative interpretations. First, the two-stage collapse process predicts a transient decrease in purity, $\alpha$, during the dephasing stage, which is then followed by recovery to $\alpha =1$ as one outcome is amplified. This contrasts with the standard "instantaneous collapse" postulate, which predicts no such intermediate stage. Experimentally, one can test this by performing weak continuous measurements or quantum state tomography on superconducting qubits or trapped ions, aiming to track $\alpha \left(t\right)$ with sub-nanosecond resolution. The expected signature includes observing the initial purity value $\alpha =1$ (superposition), followed by a brief dip to about $0.5\mathrm{to}0.7$ (mixed state), and then rapid recovery to $\alpha =1$ (eigenstate). Should $\alpha$ remain unity throughout or drop permanently to zero, the model would be falsified.

Second, the collapse rate is predicted to depend on system size. Larger systems, being more strongly coupled to the environment, would experience increased effective dephasing and resolution rates ${\gamma }_d$ and ${\gamma }_r$, leading to a collapse time scaling inversely proportional to the number of qubits N in maximal entanglement states, i.e., ${\tau }_{\mathrm{collapse}}\propto 1/N$. This can be experimentally investigated by preparing GHZ states with varying number of qubits in trapped ion setups, measuring the collapse timescale via interferometric revival, and checking for inverse scaling with system size. Such a result would differentiate this model from GRW-type collapse predictions $\tau \propto 1/N$ and standard quantum decoherence models $\tau \propto 1/N^2$.

Third, environmental coupling is predicted to modulate the timescale of collapse while leaving outcome statistics invariant. Since Born-rule statistics emerge from averaging over random environmental nudges, alterations in the environmental spectrum—such as changes in temperature, electromagnetic shielding, or magnetic field stability—should not affect the 50/50 outcome distribution for symmetric superpositions, but collapse rates should vary systematically with coupling strength. This can be tested by performing repeated measurements under varying conditions (e.g., temperatures from 10 mK to 100 mK, superconducting vs. normal shielding, active feedback for magnetic field stabilization) and analyzing outcome frequencies and collapse times. A significant deviation in outcome frequencies would challenge the model; stable timescales under varied couplings would undermine the hypothesis of environment-induced nudges as the collapse driver.

Finally, the model predicts no retrocausality or nonlocality in single-system collapse dynamics. Collapse is local and forward-causal, influenced only by present environmental coupling and the system’s prior state. Time-resolved measurements on one qubit in an entangled pair should reveal collapse timescales independent of distant measurements, though statistical correlations remain due to initial entanglement. This prediction can distinguish the model from nonlocal hidden variable theories or retrocausal interpretations.

4.6. Broader Implications for Quantum Foundations

This framework reinterprets the Born Rule as an emergent thermodynamic regularity—analogous to the Second Law—arising from averaging deterministic microdynamics over inaccessible degrees of freedom [4]. Quantum measurement itself is reconceived as a nonequilibrium phase transition resembling spontaneous symmetry breaking in condensed matter systems [5], where the initially symmetric superposition collapses into a low-symmetry eigenstate under environmental influence.

From an information geometric perspective [6], the density matrix trajectory follows a geodesic flow toward pure states, providing a unification of quantum and classical information theories. Moreover, Wheeler’s notion of the "participatory universe" [1] is demystified: participation now corresponds to entropy exchange between system and environment, removing the need to invoke consciousness in collapse.

The gently amplified environmental nudge resembles sensitive dependence on initial conditions in chaos theory, where minute variations are exponentially magnified, producing outcome unpredictability even though the underlying dynamics remain deterministic.

4.6.1. Summary Table

Table 1. Comparison of interpretations on key criteria.

Interpretation	Deterministic?	Single-World?	Realist?	Mechanistic?
Copenhagen	No	Yes	Debated	No
Decoherence	Yes	N/A${\phantom{,}}^a$	Yes	Partial${\phantom{,}}^b$
GRW	No	Yes	Yes	No${\phantom{,}}^c$
Many-Worlds	Yes	No	Yes	Yes
QBism	N/A${\phantom{,}}^d$	Yes	No	N/A
Our Model	Yes	Yes	Yes	Yes

${\phantom{,}}^a$ Decoherence is agnostic about ontology. ${\phantom{,}}^b$ Explains basis selection but not outcome selection. ${\phantom{,}}^c$ Stochastic terms are postulated, not derived from deeper principles. ${\phantom{,}}^d$ QBism rejects questions about "actual" dynamics as meaningless.

Table 1. Comparison of interpretations on key criteria.

Interpretation	Deterministic?	Single-World?	Realist?	Mechanistic?
Copenhagen	No	Yes	Debated	No
Decoherence	Yes	N/A${\phantom{,}}^a$	Yes	Partial${\phantom{,}}^b$
GRW	No	Yes	Yes	No${\phantom{,}}^c$
Many-Worlds	Yes	No	Yes	Yes
QBism	N/A${\phantom{,}}^d$	Yes	No	N/A
Our Model	Yes	Yes	Yes	Yes

${\phantom{,}}^a$ Decoherence is agnostic about ontology. ${\phantom{,}}^b$ Explains basis selection but not outcome selection. ${\phantom{,}}^c$ Stochastic terms are postulated, not derived from deeper principles. ${\phantom{,}}^d$ QBism rejects questions about "actual" dynamics as meaningless.

4.7. Testable Experimental Predictions

Our model makes several specific predictions that distinguish it from standard quantum mechanics and alternative interpretations.

First, the two-stage collapse process predicts a transient decrease in purity, $\alpha$, during the dephasing stage, which is then followed by recovery to $\alpha =1$ as one outcome is amplified. This contrasts with the standard "instantaneous collapse" postulate, which predicts no such intermediate stage. Experimentally, one can test this by performing weak continuous measurements or quantum state tomography on superconducting qubits or trapped ions, aiming to track $\alpha \left(t\right)$ with sub-nanosecond resolution. The expected signature includes observing the initial purity value $\alpha =1$ (superposition), followed by a brief dip to about $0.5\mathrm{to}0.7$ (mixed state) and then a rapid recovery to $\alpha =1$ (eigenstate). Should $\alpha$ remain unity throughout or permanently drop to zero, the model would be falsified.

Second, the collapse rate is predicted to depend on the size of the system. Larger systems, being more strongly coupled to the environment, would experience increased effective dephasing and resolution rates ${\gamma }_d$ and ${\gamma }_r$, leading to a collapse time scale inversely proportional to the number of qubits N in maximal entanglement states, that is, ${\tau }_{\mathrm{collapse}}\propto 1/N$. This can be experimentally investigated by preparing GHZ states with varying number of qubits in trapped ion setups, measuring the collapse timescale via interferometric revival, and checking for inverse scaling with system size. This result would differentiate this model from GRW-type collapse predictions $\tau \propto 1/N$ and standard quantum decoherence models $\tau \propto 1/N^2$.

Third, environmental coupling is predicted to modulate the time scale of collapse while leaving outcome statistics invariant. Since Born rule statistics emerge from averaging over random environmental nudges, alterations in the environmental spectrum, such as changes in temperature, electromagnetic shielding, or magnetic field stability, should not affect the 50/50 outcome distribution for symmetric superpositions, but collapse rates should vary systematically with coupling strength. This can be tested by performing repeated measurements under varying conditions (e.g., temperatures from 10 mK to 100 mK, superconducting vs. normal shielding, active feedback for magnetic field stabilization) and analyzing outcome frequencies and collapse times. A significant deviation in outcome frequencies would challenge the model; stable timescales under varied couplings would undermine the hypothesis of environment-induced nudges as the collapse driver.

Finally, the model does not predict retrocausality or nonlocality in single-system collapse dynamics. Collapse is local and progressive, influenced only by the present environmental coupling and the previous state of the system. Time-resolved measurements on one qubit in an entangled pair should reveal collapse timescales independent of distant measurements, though statistical correlations remain due to initial entanglement. This prediction can distinguish the model from theories of non-local hidden variables or retrocausal interpretations.

4.8. Broader Implications for Quantum Foundations

This framework reinterprets the Born Rule as an emergent thermodynamic regularity - analogous to the Second Law - that arises from the averaging of deterministic microdynamics over inaccessible degrees of freedom [4]. Quantum measurement itself is reconceived as a non-equilibrium phase transition that resembles spontaneous symmetry breaking in condensed matter systems [5], where the initially symmetric superposition collapses into a low-symmetry eigenstate under environmental influence.

From an information geometric perspective [6], the trajectory of the density matrix follows a geodesic flow toward pure states, providing a unification of classical and quantum information theories. Moreover, Wheeler’s notion of the "participatory universe" [1] is demystified: Participation now corresponds to the exchange of entropy between the system and the environment, removing the need to invoke consciousness in collapse.

The gently amplified environmental nudge resembles a sensitive dependence on initial conditions in chaos theory, where minute variations are exponentially magnified, producing outcome unpredictability even though the underlying dynamics remain deterministic.

4.9. Limitations and Future Directions

Multi-Qubit Extension: Current model demonstrated for single qubits. Generalizing to N-qubit systems requires specifying how ${\mathcal{L}}_{\mathrm{resolve}}$ acts on $2^N$-dimensional density matrices. Preliminary work suggests that resolution should favor outcomes with maximum coherence gradients across the entanglement graph.

Relativistic Formulation: Present treatment is non-relativistic. Extending to quantum field theory requires a careful treatment of causality. Collapse must remain local and forward causal to preserve Lorentz invariance.

Computational Complexity: Simulating N-qubit collapse scales as $\mathcal{O}\left(4^N\right)$ for full density matrix evolution. Developing efficient tensor network methods or mean-field approximations would enable validation on larger systems.

This proof of concept for a single qubit opens several avenues for future research. The immediate next step is to generalize the model to multi-qubit and entangled systems where non-local collapse may be driven by global contradiction gradients across the entire system.

Ultimately, the same thermodynamic principles that drive quantum collapse may govern the formation of coherent structures at all scales.

5. Conclusions

We have presented a coherence-thermodynamic model that unifies quantum measurement with Schrödinger evolution through a single deterministic dynamical law. The key innovations are:

• Mechanistic Collapse: The collapse of the wave function is explained as a two-stage thermodynamic phase transition: dephasing followed by amplification of the nonlinear outcome, rather than postulated as a separate axiom.
• Emergent Probabilities: Born-rule statistics emerge from ensemble averaging over environmental fluctuations, not from ontologically fundamental randomness. Each individual measurement is deterministic; apparent randomness reflects epistemic uncertainty about environmental initial conditions.
• Testable Predictions: The model makes falsifiable experimental predictions (transient purity dip, system-size scaling, environmental modulation) that distinguish it from Copenhagen, Many-Worlds, GRW, and QBism interpretations.
• Theoretical Connections: Connects quantum foundations to information geometry [6], thermodynamics [4], and classical phase transitions [5], bridging microscales and macroscales through a common mathematical framework.

This work suggests that the measurement problem, which has eluded consensus since the inception of quantum theory [1], may admit a resolution grounded in physical principles rather than philosophical interpretation. The next step is experimental validation: Observing the predicted transient purity dip would constitute strong evidence for this thermodynamic mechanism and challenge the orthodox view that collapse is fundamentally acausal or instantaneous.