Interference with Individual Elementary Particles

1. Introduction

Quantum mechanics encompasses various interpretations, including the Copenhagen, de Broglie–Bohm, von Neumann–Wigner, stochastic mechanics, and many worlds theories [1,2,3,6,7,8,9,10,11,12,13,14]. Despite these interpretations, challenges remain with the ontological duality of elementary particles. When detected individually, these particles appear as distinct entities, but their collective detection reveals wave-like distributions, such as interference patterns. Some researchers have suggested that individual particles carry phase information, which is gathered by specialized detectors [3,4,11,15]. These detectors only exhibit wave-like characteristics after processing a significant number of particles. [4,5] concluded that interference phenomena may be explained classically, and wave-like behavior may just be an illusion of our detectors.

In [5] and in the present work, we diverge from the model of [4] because we realised that elementary particles like photons cannot carry any phase information. Instead, we propose that the phase information is carried collectively by the time series of these particles. As we saw in [5], this information may be transferred to the detector if the latter is in resonance with the source that produces these time series. We would like to once again ask the question

"is it possible to manifest interference with non-interacting elementary particles?",

where by elementary we mean classical particles with no internal degrees of freedom, i.e. with no hidden variables. Feynman famously quoted that wave-like characteristics are ‘impossible, absolutely impossible to explain in any classical way’ (Feynman Lectures on Physics; [16]). We have already challenged this statement with our model of the Source–Detector Resonance (hereafter SDR, first described in [5]) according to which wave-like characteristics manifest themselves due to the collective response of a series of oscillators to their periodic forcing by a resonant periodic stream of elementary particles.

In the next sections, we perform a numerical double-slit experiment with two resonant streams of individual particles, and show that we are able to reproduce a particle-conserving interference pattern with a finite thickness detector. We reach the same conclusion as [4], namely, that wave phenomena may reflect the nature of detectors rather than fundamental laws of physics.

2. An Oscillator Driven by a Resonant Stream of Particles

Let us consider a classical oscillator with damping and an external periodic forcing. This is described by the equation

$${\displaystyle \frac{{\mathrm{d}}^{2}y\left(t\right)}{\mathrm{d}{t}^2}}+{\omega }_0^{2}y\left(t\right)+2\zeta {\omega }_0{\displaystyle \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}}=fsin\left(\omega t\right),$$

(1)

where y is the amplitude of oscillation, ${\omega }_0\equiv 2\pi /P_0$ where $P_0$ is the eigenperiod of the oscillator, $\zeta$ is the damping ratio, $\omega \equiv 2\pi /P$ is the frequency of the forcing where P is the period of the periodic forcing, and f is the amplitude of the forcing which is equal to the transfer of velocity per unit time by the driver. The above oscillator reaches an asymptotic oscillating state described by

$$y\left(t\right)={\displaystyle \frac{f}{\sqrt{{\left(2\omega {\omega }_0\zeta \right)}^2+{({\omega }_0^2-{\omega }^2)}^2}}}sin(\omega t+\varphi )$$

(2)

where $\varphi =arctan[2\omega {\omega }_0\zeta /({\omega }^2-{\omega }_0^2)]+\pi$. When the forcing is at or close to resonance, the above expressions simplify to

$$y\left(t\right)\approx Acos\left({\omega }_{0}t\right),$$

(3)

where

$$A\equiv {\displaystyle \frac{f}{2{\omega }_0^2\zeta }}$$

(4)

is the asymptotic amplitude of the driven damped resonant oscillation.

Let us now consider a stream of elementary particles that reach the oscillater randomly at times equal to random integer multiples of the eigenperiod $P_0$. This is equivalent to a stream of particle expressed as the time series

$$\eta \left(t\right)=\sum _j{\alpha }_j\delta (t-j{P}_0),$$

(5)

where ${\alpha }_j$ is a random variable that is equal to 1 with a certain probability $\mathrm{Prob}({\alpha }_j=1)$, and 0 with probability $\mathrm{Prob}({\alpha }_j=0)=1-\mathrm{Prob}({\alpha }_j=1)$. Let us also assume that, when the particles reach the oscillator, they change its velocity by $+\delta v$. This means that, on average, the oscillator experiences a resonant transfer of velocity per unit time equal to

$$f=\mathrm{Prob}({\alpha }_j=1){\displaystyle \frac{\delta v{\omega }_0}{2\pi }},$$

(6)

and the oscillator reaches an asymptotic amplitude of oscillation equal to

$$A\approx \mathrm{Prob}({\alpha }_j=1){\displaystyle \frac{\delta v}{4\pi {\omega }_0\zeta }}.$$

(7)

If one wants to integrate eq. (1) numerically, this may be expressed mathematically by rewritting it as the following set of equations:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}}& =& -{\omega }_0^{2}y\left(t\right)-2\zeta {\omega }_0{\displaystyle \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}}+\mathrm{Prob}({\alpha }_j=1){\displaystyle \frac{\delta v{\omega }_0}{2\pi }}sin\left({\omega }_{0}t\right)\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}}& =& v\left(t\right)+\delta v·\delta (t-t_j),\hfill \end{array}$$

(8)

where again $t_j$ are the random arrival times when particles reach the oscillator. We will next consider an oscillator that is driven by two independent periodic streams of particles.

3. An Oscillator Driven by Two Resonant Streams of Particles

Let us now place our classical oscillator at position $x=x_0$ and $y=0$ in a cartesian system of coordinates $(x,y)$. We will also consider two point sources of classical particles at positions $y=-L$, $x=\pm d/2$, with $d\ll L$. The particles are emitted randomly either from the left or the right source at times equal to random integer multiples of the period P with $P\approx P_0$. Therefore, each point source emits a time series of particles equal to

$$\begin{array}{ccc}\hfill {\eta }_{-d/2}\left(t\right)& =& \sum _j{\alpha }_j\delta (t-jP)\hfill \\ \hfill {\eta }_{+d/2}\left(t\right)& =& \sum _j(1-{\alpha }_j)\delta (t-jP)\hfill \end{array}$$

(9)

where ${\alpha }_j$ is equal to either 1 or 0 with $50\%$ random probability each.

For simplicity, we will also assume that particles travel with constant velocity v towards the screen with a Gaussian spread with dispersion $\pm \sigma$ around $x=0$ at $y=0$. When particles reach the oscillator, they change its velocity by $+\delta v$ at random arrival times $t_i$. We will assume that the particles interact with the oscillator if they approach to within an interval $\delta x$ centered around the position $x=x_0$ of the oscillator. According to the above scenario, the oscillator is driven by the following time series:

$$\eta \left(t\right)={\displaystyle \frac{\delta x}{\sqrt{2\pi }\sigma }}\left({\eta }_{-d/2}\left(t\right)+{\eta }_{+d/2}\left(t\right)\right){\mathrm{e}}^{-{\displaystyle \frac{x_0^2}{2{\sigma }^2}}}$$

(10)

at each position $x=x_0$ and $y=0$. What is important for driving the oscillator is the number of particles that reach it per period $P_0$ at the resonance frequency ${\omega }_0$. On average, this number is equal to the total number of particles that reach it per period $P_0$, multiplied by the ratio of the Probability Spectral Distribution (hereafter PSD) of $\eta \left(t\right)$ at the resonance frequency, over the PSD of $\eta \left(t\right)$ at $\omega =0$ (the latter is proportional to the total number of particles that reached this particular position over the time t of the experiment). Putting everything together we obtain the resonant driving

$$f={\displaystyle \frac{2\delta x{\mathrm{e}}^{-\frac{x_0^2}{2{\sigma }^2}}}{\sqrt{2\pi }\sigma }}{\displaystyle \frac{\mathrm{PSD}\left({\omega }_0\right)}{\mathrm{PSD}\left(0\right)}}{\displaystyle \frac{\delta v{\omega }_0}{2\pi }}.$$

(11)

With this forcing, the oscillator reaches an asymptotic amplitude of oscillation given by eq. (4), i.e.

$$A\left(x\right)\approx {\displaystyle \frac{\delta x\delta v{\mathrm{e}}^{-\frac{x_0^2}{2{\sigma }^2}}}{2\pi \sqrt{2\pi }\sigma \zeta }}{\displaystyle \frac{\mathrm{PSD}\left({\omega }_0\right)}{\mathrm{PSD}\left(0\right)}}$$

(12)

where the power spectrum of the time series $\eta \left(t\right)$ is calculated at the position $x=x_0,y=0$ of the oscillator. It is straightforward to see that the pattern of $A\left(x\right)$ is what would result from adding the two independent particles streams ${\eta }_{\pm d/2}\left(t\right)$, namely

$${\displaystyle \frac{2\delta x}{\sqrt{2\pi }\sigma }}{\mathrm{e}}^{-{\displaystyle \frac{x_0^2}{2{\sigma }^2}}},$$

(13)

modulated by the ratio of the PSDs as those are calculated from the total particle stream $\eta \left(t\right)={\eta }_{-d/2}\left(t\right)+{\eta }_{+d/2}\left(t\right)$ that reaches the position of the oscillator.

If the particles reach the oscillator in phase, i.e. with arrival time differences that are integer multiples of the period $P_0$, the oscillator will be resonantly excited. If the particles reach the oscillator out of phase, i.e. with arrival time differences that are odd multiples of $P_0/2$, the oscillator will be de-excited because the PSD of the particle stream $\eta \left(t\right)$ will be zero at the resonance frequency (see [5]). When the oscillator is placed at the resonance positions $x_{\lambda }$ where the differences of the two travel times are equal to integer multiples of the period $P_0$, namely

$${\displaystyle \frac{\sqrt{L^2+{(x_{\lambda }+d/2)}^2}-\sqrt{L^2+{(x_{\lambda }-d/2)}^2}}{v}}=\pm \lambda P_0\iff$$

$${\displaystyle \frac{x_{\lambda }}{L}}\approx \pm \lambda {\displaystyle \frac{P_{0}v}{d}}forL\gg d,\left|x_{\lambda }\right|,$$

(14)

the amplitudes of oscillation grow linearly with time till they reach their corresponding locally maximum asymptotic amplitudes $A_{\lambda }$ given by eq. (4). When the oscillator is placed at the positions of destructive interference $x_{\lambda }$ where the differences of the two travel times are equal to integer multiples of the period $P_0$ plus $P_0/2$, namely

$${\displaystyle \frac{\sqrt{L^2+{(x_{\lambda }+d/2)}^2}-\sqrt{L^2+{(x_{\lambda }-d/2)}^2}}{v}}=\pm \lambda P_0+{\displaystyle \frac{P_0}{2}}\iff$$

$${\displaystyle \frac{x_{\lambda }}{L}}\approx (\pm \lambda +{\displaystyle \frac{1}{2}}){\displaystyle \frac{P_{0}v}{d}}forL\gg d,\left|x_{\lambda }\right|,$$

(15)

the amplitudes of oscillation $A_{\lambda }$ remain close to zero. In summary, we assume that each resonant oscillator is able to figure out the ratio of particles that reach it at its resonant frequency, over the total number of particles that reach it. This ratio is equal to PSD(${\omega }_0$)/PSD(0) and is of fundamental importance in determining the saturated amplitude of oscillations. As we will see next, this ratio is also crucial in generating the interference detection pattern expected to form due to the two resonant streams of particles.

4. A Numerical Experiment with a Thick Layer of Resonant Oscillators

Instead of one damped driven resonant oscillator, we will now perform a numerical experiment in a thick (two dimensional) screen of oscillators arranged in a square lattice of width $\delta x=\delta y$ beyond position $y=0$. In our numerical code, we used the following parameters:

$$P=P_0=1,v=0.1,\zeta =5\times {10}^{-6},\delta v=8\times {10}^{-5},$$

$$L=20,\delta x=0.05,\sigma =1.75$$

(16)

As before, this array of oscillators will be excitted by the same double stream of particles as before. In general, an oscillating pattern develops along the screen according to eq. (12), with local amplitude maxima along angular directions $x/(L+y)=\pm \lambda P_{0}v/d$ (eq. 14), and zeroings along angular directions $x/(L+y)=\pm (\lambda +1/2)P_{0}v/d$ (eq. 15).

What we are missing in order to reproduce the interference pattern of a double-slit experiment with elementary particles is the mechanism of detection of the particles by the oscillators. We will assume that an oscillator detects a particle with a probability

$$\mathrm{Probability} \mathrm{of} \mathrm{detection}\equiv \alpha {\left({\displaystyle \frac{\mathrm{PSD}\left({\omega }_0\right)}{\mathrm{PSD}\left(0\right)}}\right)}^2,$$

(17)

where, once again, PSD($\omega$) is the PSD of the time series of particles that reach it from the two slits. We will assume that whenever a particle is detected by a particular oscillator, it will then be absorbed and will disappear from the particle series. If it is not absorbed, it will continue its path deeper inside the stack of oscillators till it is finally absorbed. The extra factor $\alpha <1$ imposes a finite detection/absorption probability by the oscillator. As we will see below with our detection experiments, the value of $\alpha$ must be sufficiently small in order to accurately reproduce the expected interference pattern.

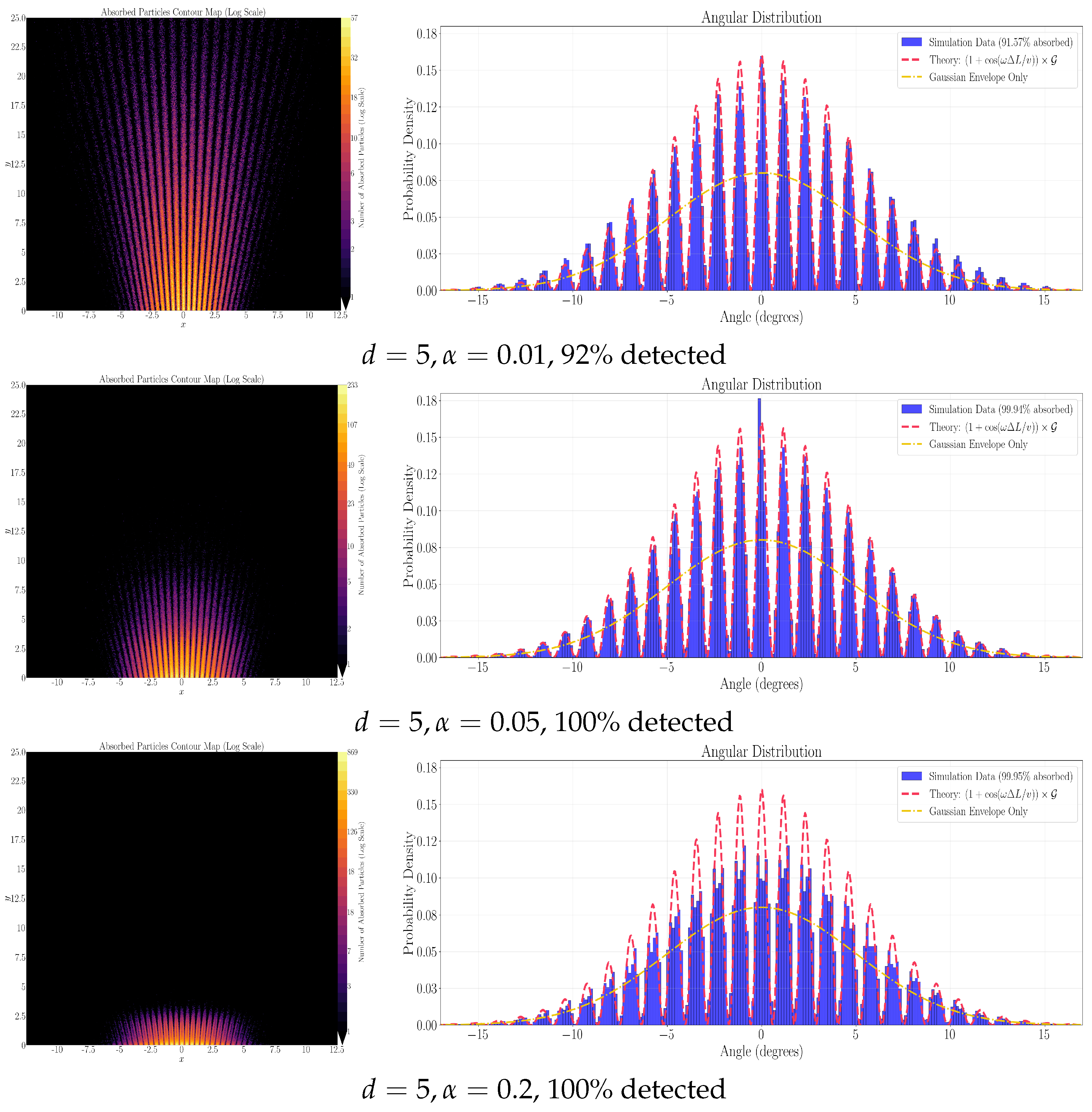
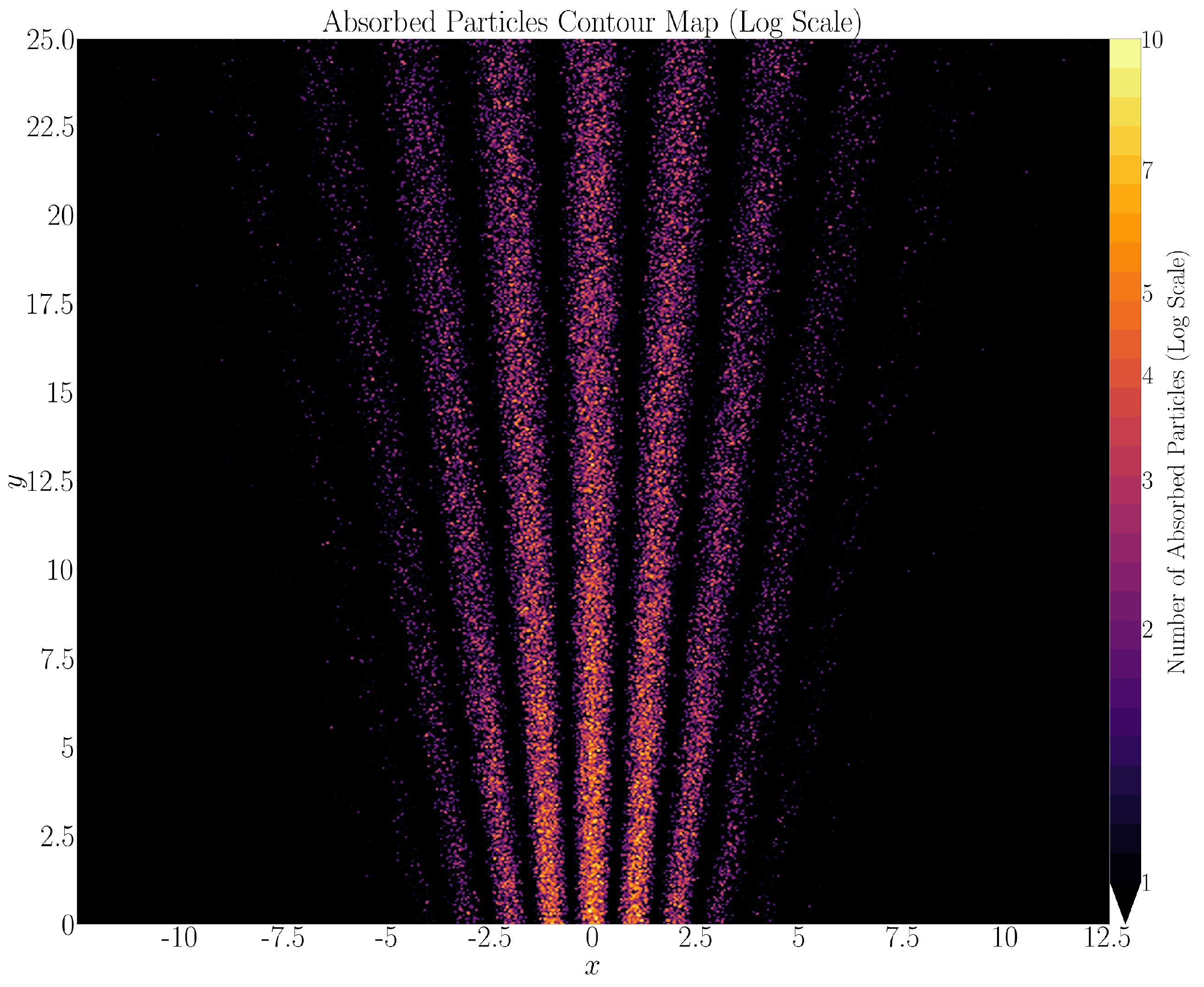
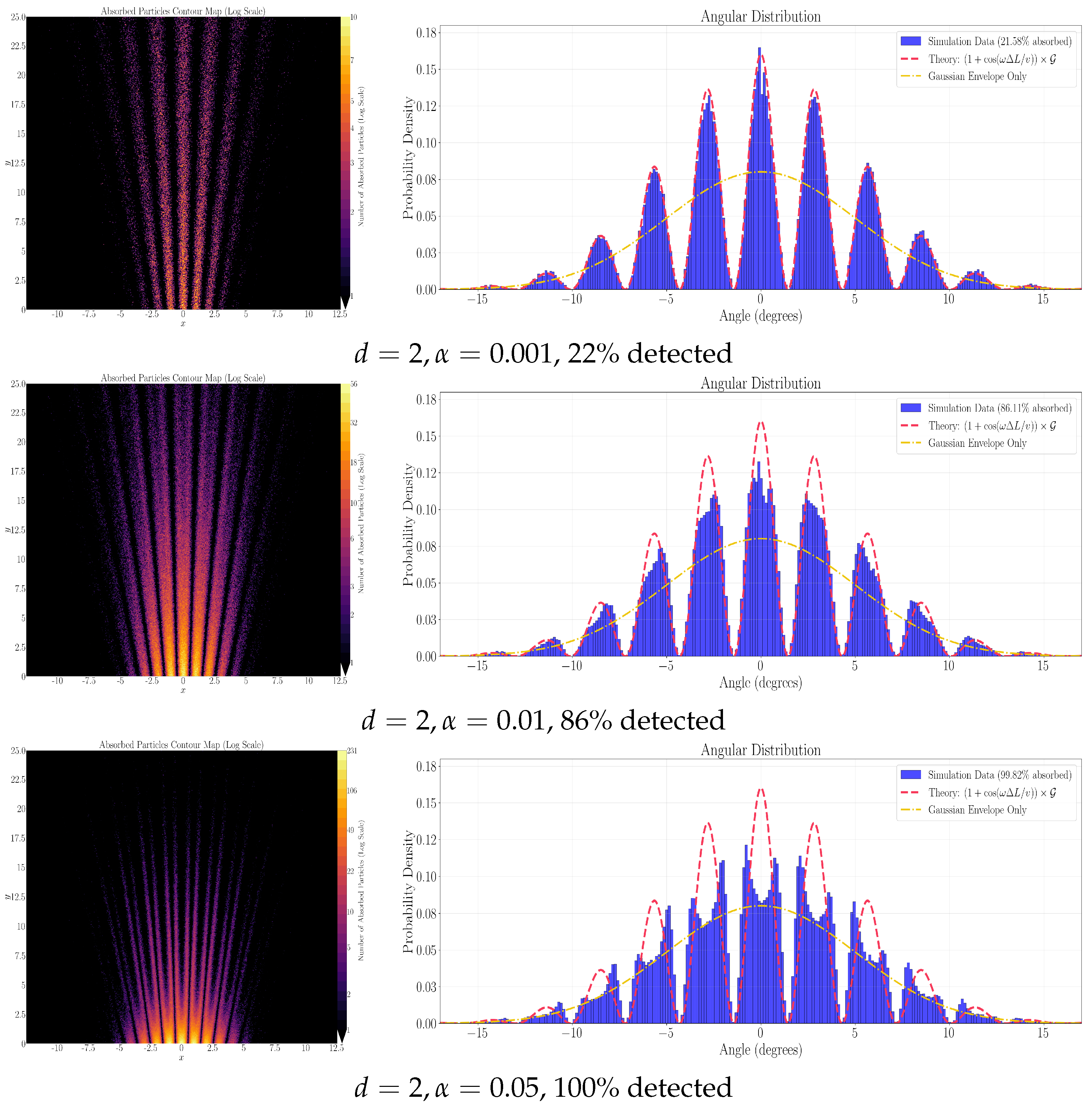
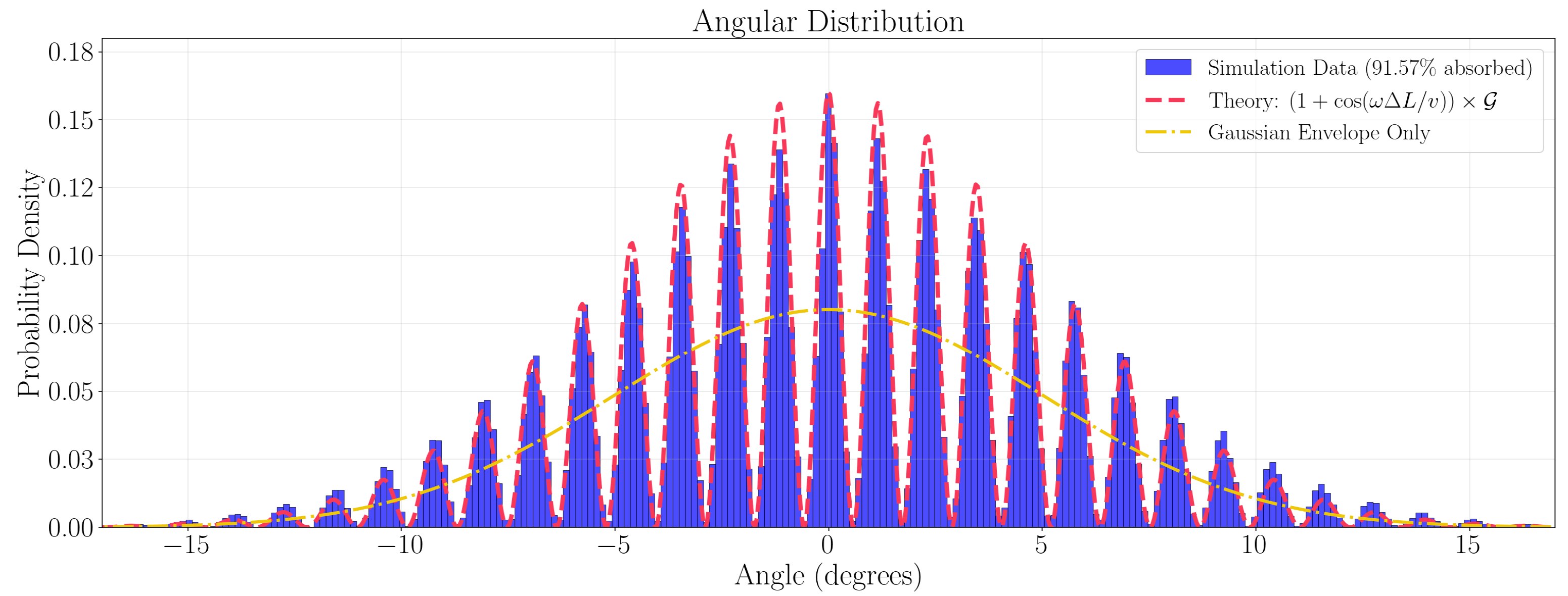
In Figure 1 we perform the numerical experiment described above for $d=5$ and for an array of oscillators deep enough for almost all particles to be detected. Particles that pass through the first layer of resonant oscillators undetected reach the next layer of oscillators. If they again remain undetected, they reach a deeper layer of oscillators and so on and so forth till they are finally detected and removed from the experiment. The integrated distribution of particle detections accross the detector thickness over angular directions $arctan(x/(L+y\left)\right)$ centered on $x=0,y=-L$ is shown in Figure 2 together with the angular distribution of particle injections (yellow line). The agreement with the classical/quantum mechanical interference result (red dashed line) is impressive. In particular, at the points of destructive interference, the two streams of undetected particles from the left and right slits will continue unimpeded deeper inside the detector. By doing so, both streams will move towards the two regions of constructive interference to the left and right of each region of deconstructive intereference. When detected there, they will add up to a number of particles detected along the region of constructive interference that is greater than the number of particles that reach the first layer of the detector in that region. This is how the blue histogram in Figure 2 and the corresponding theoretical red-dashed line lies above the Gaussian angular distribution of particles that reach the first layer of the detector (yellow line).

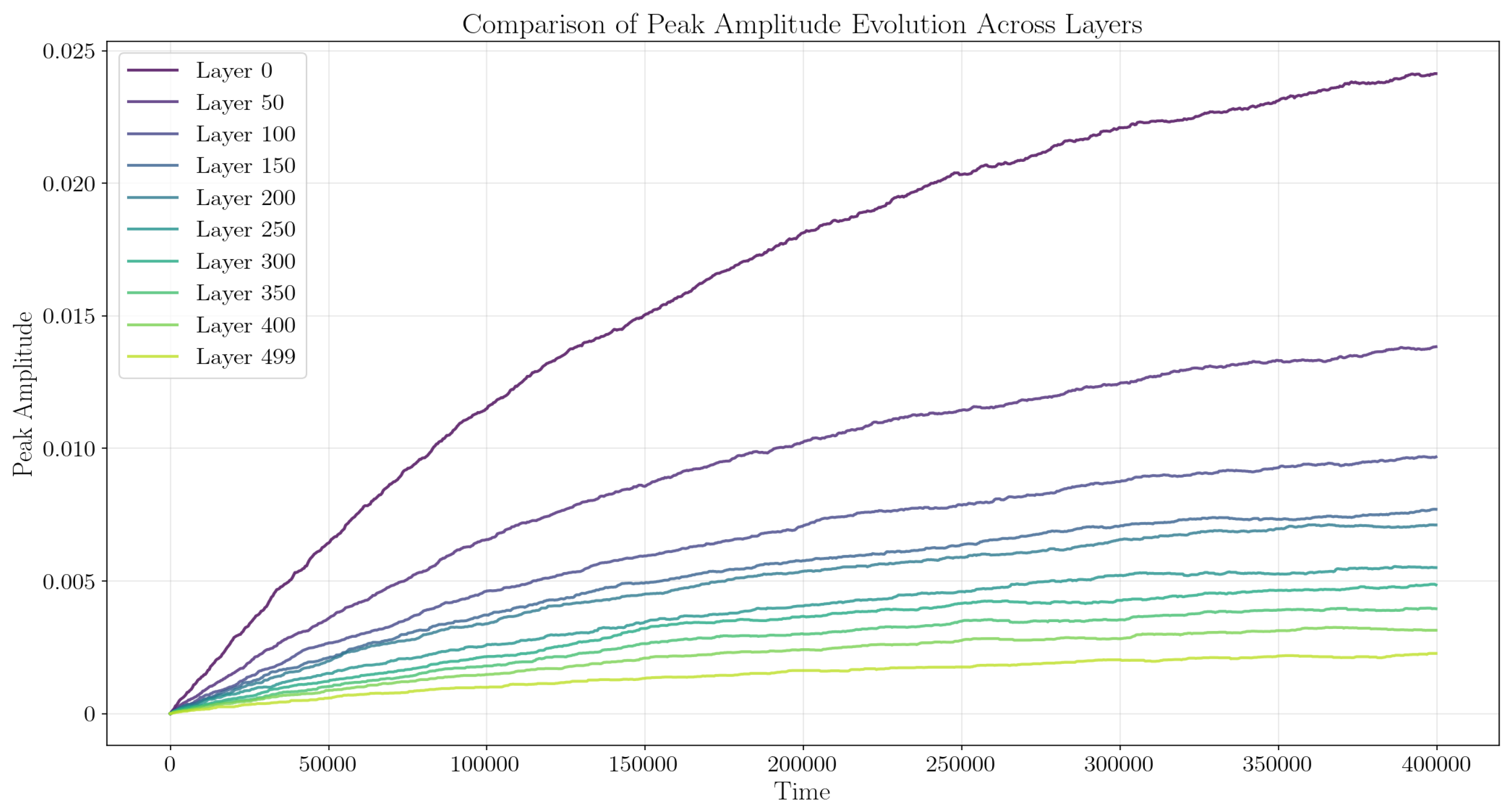
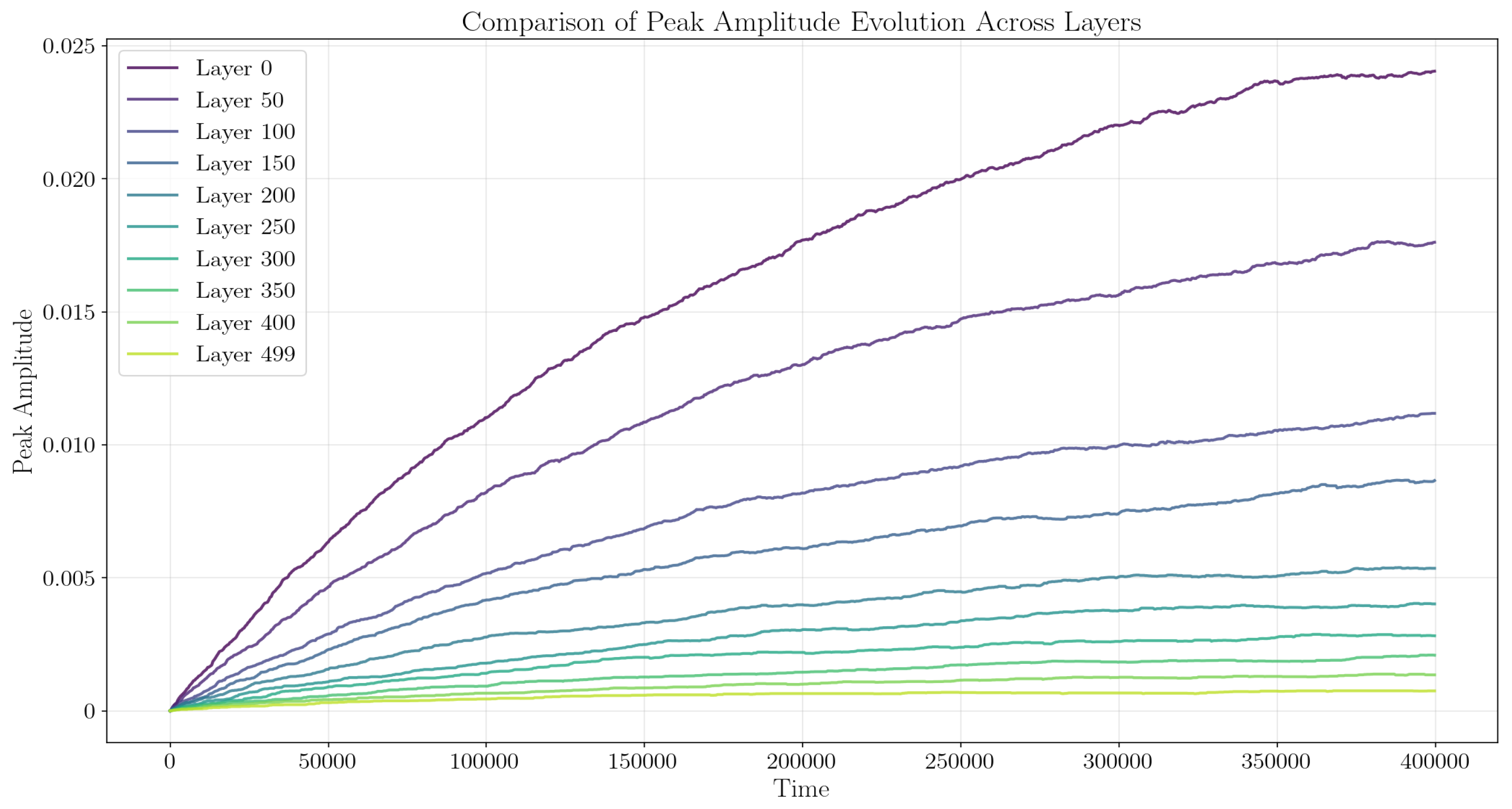
In Figure 3 we also show how the oscillation amplitudes saturate with time and depth inside the thick detector (shown only the maximum amplitudes per layer). Saturation is reached through the balance between the periodic forcing by the two particle streams and the damping of each oscillator (eq. 4). The forcing is gradually decreasing as we move deeper inside the detector since the two particle streams are gradually depleted as particles are detected in the oscillator layers closer to the surface.

In [5] we showed that, in the case of a superposition of two intermittently periodic time series with average percentages of particles per period a and b respectively, the probability of detection at position $(x,y)$ of the Resonant Detector as defined by eq. (17) is found numerically to be proportional to

$$\begin{array}{ccc}\hfill \mathrm{Probability} \mathrm{of} \mathrm{detection}(x,y)& \propto & {\left.{\left({\displaystyle \frac{\mathrm{PSD}\left({\omega }_0\right)}{\mathrm{PSD}\left(0\right)}}\right)}^2\right|}_{(x,y)}\hfill \\ & =& {\displaystyle \frac{a^2+b^2}{{(a+b)}^2}}\left(1+{\displaystyle \frac{2ab}{a^2+b^2}}cos\left(2\pi {\displaystyle \frac{\delta t}{P}}\right)\right)\hfill \\ & =& {\displaystyle \frac{1}{2}}\left(1+cos\left({\omega }_0\delta t\right)\right),\hfill \end{array}$$

(18)

since in our particular numerical experiment $a\approx b$ at all positions. Here, $\delta t\equiv (L_1-L_2)/v$ and $L_{1,2}$ are the distances of each slit from the point $(x,y)$ under consideration. It is important to understand that a finite probability of detection implies that not all particles will be detected in the first layer of the detector. Quantum Mechanics and classical interference predicts the following probability distribution along the face (the first layer) of the detector at $y=0$:

$$\mathrm{Q}\mathrm{M}\mathrm{Probability} \mathrm{of} \mathrm{detection}(x;\delta x)={\displaystyle \frac{2\delta x}{\sqrt{2\pi }\sigma }}{\mathrm{e}}^{-{\displaystyle \frac{x^2}{2{\sigma }^2}}}\left[1+cos\left({\displaystyle \frac{{\omega }_0\delta L}{v}}\right)\right]$$

(19)

Here, $\delta L$ is the difference in distance of a point $x,y=0$ of the first layer of the detector from each one of the two sources of particles at $y=-L$. In our numerical experiment we observe that this distribution (red dashed line of Figure 2) develops within a certain depth inside the detector as was schematically shown in [5].

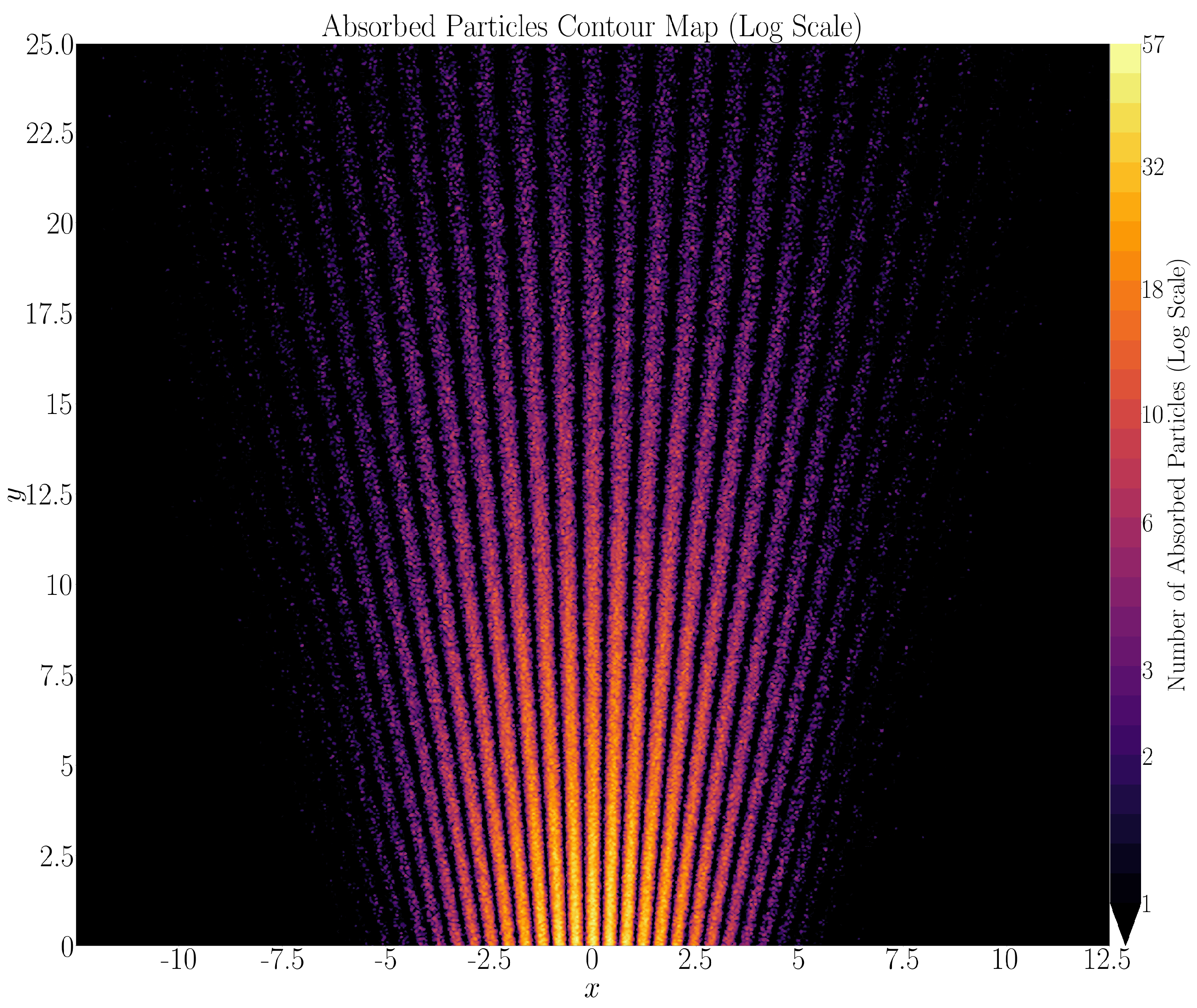
Figure 5, Figure 6, Figure 7 and Figure 8 show the results of the same numerical experiment for $d=2$. Once again, the positions of detection maxima and minima confirm eqs. 14-15. Here, the best agreement with the intereference patterns of Quantum Mechanics is obtained for values of $\alpha \ll 0.01$. Notice that the smaller the value of the detection parameter $\alpha$, the deeper the final interference pattern, and the better the agreement with the theoretical pattern predicted by Quantum Mechanics and classical interference. For larger values of $\alpha$ closer to unity, strong detection spikes develop left and right of each detection minimum, and, although the positions of detection minima are reproduced correctly, the shape of the interference pattern diverges from the theoretical one (see Figure 4 and Figure 8).

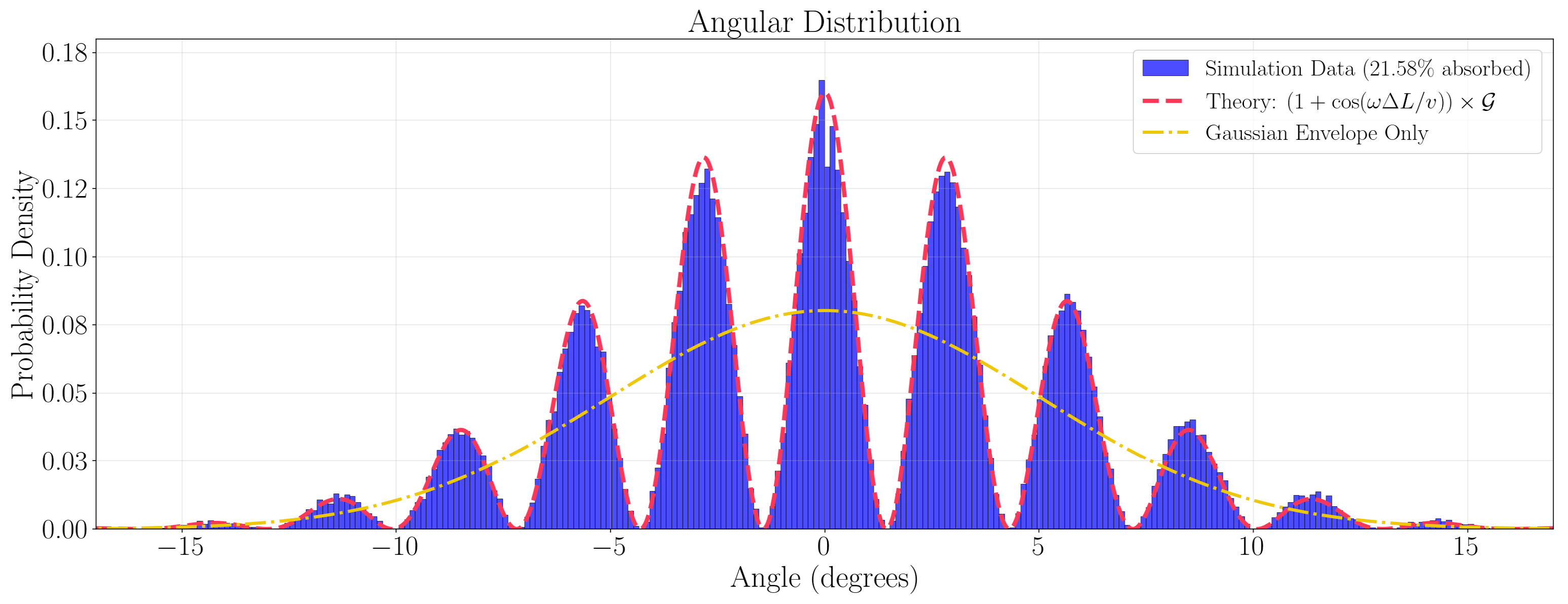
Figure 4. Same as Figure 1 & Figure 2 for $d=5$ for various values of $\alpha$. We see that the larger the value of $\alpha$, the shallower and the more distorted the absorption interference pattern.

Figure 4. Same as Figure 1 & Figure 2 for $d=5$ for various values of $\alpha$. We see that the larger the value of $\alpha$, the shallower and the more distorted the absorption interference pattern.

Figure 5. Same as Figure 1 for $d=2$ and $\alpha =0.001$.

Figure 5. Same as Figure 1 for $d=2$ and $\alpha =0.001$.

Figure 6. Same as Figure 2 for $d=2$ and $\alpha =0.001$. The positions of detection maxima and minima confirm eqs. 14-15. $22\%$ of all particles are detected.

Figure 6. Same as Figure 2 for $d=2$ and $\alpha =0.001$. The positions of detection maxima and minima confirm eqs. 14-15. $22\%$ of all particles are detected.

Figure 7. Same as Figure 3 for $d=2$ and $\alpha =0.010$.

Figure 7. Same as Figure 3 for $d=2$ and $\alpha =0.010$.

Figure 8. Same as Figure 4 for $d=2$ and $\alpha =0.001,0.01,0.05$ (from top to bottom). Here, $\alpha$ must be much smaller than about 0.01 for good agreement with the interference pattern of Quantum Mechanics.

Figure 8. Same as Figure 4 for $d=2$ and $\alpha =0.001,0.01,0.05$ (from top to bottom). Here, $\alpha$ must be much smaller than about 0.01 for good agreement with the interference pattern of Quantum Mechanics.

5. Summary and Conclusions

In [5] we first introduced the concept of SDR (the Source-Detector Resonancs) as a means to transmit some kind of ‘phase’ information to the detector. Such information cannot by carried by an individual elementary particle with no internal degrees of freedom as originally proposed in [4]. However, such information can be carried collectively by a periodic stream of particles, as long as the detector becomes aware of the periodicity of the particle stream. This is possible if the detector resonates with the particle stream, or equivalently if the eigenperiod $P_0$ of each one of its constituents (oscillators) is close to the period P of the particle stream ($P\approx P_0$). In that case, the detector identifies only the square of the fraction of particles that reach it at its resonant frequency at every position inside the detector. Obviously, this fraction is less than unity, thus a large fraction of the particles remain undetected after they reach the first layer of the detector. If the detector is deep enough, all the particles will be detected and a detection interference pattern will develop inside the detector. This is slightly different from what Quantum Mechanics predicts, namely that the interference pattern will develop even if the detector is infinitely thin, and all particles are detected along its surface. According to our scenario, the exact Quantum Mechanical interference pattern is recovered only if we are willing to integrate over the thickness of the detector the interference pattern that we obtained at all points in its interior. This prediction may be experimentally confirmed or disprooved. The reader should bear in mind that Quantum Mechanics associates with each particle the de Broglie longitudinal wavelength ${\lambda }_{\mathrm{de}\mathrm{Broglie}}=h/\left(mv\right)$ where h is the Planck constant, and if we make the association of [5] that ${\omega }_0\equiv {\displaystyle \frac{1}{2}}m{v}^2/\hslash$, in our units, the de Broglie longitudinal wavelength is equal to

$${\lambda }_{\mathrm{de}\mathrm{Broglie}}={\displaystyle \frac{h}{mv}}={\displaystyle \frac{\frac{1}{2}v}{\frac{1}{2}m{v}^2/h}}={\displaystyle \frac{1}{2}}Pv=0.05.$$

(20)

Hence, in our macroscopic detector, detection takes place within several tens of de Broglie wavelengths. This is not unreasonable physically.

The periodicity of the particle stream may hold some fundamental information about how elementary particles are generated and accelerated in nature to some kinetic energy $m{v}^2/2$ as we first discussed in [4]. In order for our numerical interference experiment to correspond to the Quantum Mechanical experiment, the kinetic energy of the emitted particles must be directly related to he eigenperiod P of their source as

$${\displaystyle \frac{1}{2}}m{v}^2={\displaystyle \frac{h}{P}}\approx {\displaystyle \frac{h}{P_0}}.$$

(21)

This is the only relation that connects our classical experiment to Quantum Mechanics. Why this is the case, we do not yet understand. If the stream of particles is generated periodically in a source oscillator with mass $M\gg m$, frequency ${\omega }_0$ and damping ratio $\zeta$, then every period, the source oscillator loses energy $\zeta M{v}_{\max }^2$ which must be equal to the kinetic energy $m{v}^2/2$ of the emitted particle. Here, $v_{\max }$ is the maximum velocity of oscillation of the source oscillator. Therefore,

$$\zeta \approx {\displaystyle \frac{1}{2}}\left({\displaystyle \frac{m}{M}}\right){\left({\displaystyle \frac{v}{v_{\max }}}\right)}^2={\displaystyle \frac{h}{M{P}_0{v}_{\max }^2}}.$$

(22)

This result agrees with the estimate of [4]. More investigation is necessary.

Finally, in order for the detector to calculate the fraction of the incoming stream of particles that reach it at its resonant frequency, it needs to collect a certain number of particles from which it will calculate the ratio PSD(${\omega }_0$)/PSD(0). This means that if one abruptly changes the experiment by e.g. closing one of the two slits, the PSD of the stream of particles that the detector sees will need some time to transition to the PSD of the new experiment. In other words, the interference pattern will require some finite amount of time to transition to the one expected in the new experiment. This transition time together with the finite thickness of the interference pattern inside the detector are two physical quantities that may be tested experimentally.