Optimized Formation Control in Undulating Fields

1. Introduction

Formation control is a cornerstone for multi-robot systems, and there is abundant literature on leader–follower and rigid formation strategies. Such existing methods usually enable coordinated multi-robot operation in a simplistic, flat space. However, when robots operate in undulating fields, the varying elevation creates challenges, such as destabilizing tilt stability and distracting robots from predetermined paths. This can compromise formation integrity and task synchronization.

Leader–follower formation control is one of the most studied topics in multi-robot coordination. Typically, a designated leader has access to the desired trajectory while follower robots track the leader’s state based on local information. Early foundational work by Fax and Murray [1] and Olfati-Saber and Murray [2] established consensus-based methods to enable coordinated motion under dynamic conditions. Wang [3] later extended these frameworks to nonholonomic systems, providing rigorous stability and convergence analyses. More recent studies have applied leader-follower strategies to unmanned vehicles to achieve efficient coordination even in the presence of uncertainties and communication constraints. A secure leader–follower formation control framework is proposed in [4] that integrates time-stamp-based replay attack detection and robust control design to address communication delays, system uncertainties, and external disturbances. Their work emphasizes the importance of security-aware control strategies, particularly in scenarios where the integrity of inter-robot communication is critical for formation stability and coordination. Waypoint instability in leader–follower formations was addressed in [5] by introducing a stabilizing area around waypoints and a velocity correction term, enabling smoother heading transitions and stable tracking, as validated in both simulations and experiments. Chain formation strategies [6] offer an effective approach for coordinating multiple differential drive mobile robots, particularly when maintaining relative spacing and alignment over time. Each robot follow the delayed trajectory of its immediate leader, and such formations naturally adapt to varying velocities and enable smooth navigation through dynamic environments using only local measurements and input histories. Formation control strategies that support flexible reconfiguration are essential for multi-agent systems operating in dynamic environments. A distributed leader–follower control framework is introduced in [7] that enables agents to achieve target formations through arbitrary linear transformations, extending traditional affine formation control to support greater adaptability and coordination. Leader-follower framework is proposed in [8] that enables consensus tracking toward a formation centroid, even when the reference trajectory is only partially available across the network. A predefined-time adaptive leader–follower control framework is introduced in [9] that integrates prescribed performance functions and observer-based techniques to achieve safe and accurate formation tracking under strict time constraints. In this paper, we use a simplistic leader-follower structure for path following. The followers gather around the leader in the local frame. The robots are close to each other, and we omit any communication constraints.

Rigid formation control usually focuses on maintaining a fixed geometric formation among robots during operations, ensuring the preservation of inter-robot distances and angles. This approach is particularly useful for applications that require precise alignment and spatial organization. Image-based visual relative information (IBVR) is used in [4] to achieve distributed rigid formation control in 3D space, and this enables agents to maintain formation using only local visual data and camera parameters. The rigid-body kinematics-based frameworks are proposed in [10] for multirobot formations to achieve coordinated translational and rotational motion, and this is supported by distributed control protocols and prescribed performance control for nonholonomic systems. Formation control under uncertainties is addressed in [11] by proposing adaptive distance-based schemes and ensuring global stability and constraint satisfaction, even when the formation is not minimally rigid. Ratio-of-distance (RoD) rigidity theory is proposed in [12] to ensure desired formation shapes, addressing both time-invariant and time-varying formation maneuvering. The proposed distributed adaptive control protocols aim to drive agents towards these formations while minimizing communication resources through a leader–follower strategy and efficient velocity communication. Roto-translation invariant (RTI) formations in [13] offer a more natural and cohesive motion pattern, enabling multiple underactuated planar rigid bodies to maintain coordinated rotation and translation simultaneously. A distributed finite-time attitude control strategy is used in [14] that effectively handles system uncertainties and external disturbances while relying only on local neighbor information, making it highly applicable to networked rigid spacecraft under directed communication topologies. In this paper, we use the leader robot as the origin of the desired formation and define the rest of the positions in its local frame. We propose a formation controller for the robots to enhance the rigidity and follow the given path.

Traditional formation control methods often assume flat terrains and structured space. Real-world applications such as military operations, environmental monitoring, and precision agriculture frequently involve undulating fields. The challenge in these scenarios is to maintain formation stability and coordinated motion despite elevated grounds and uneven surfaces. Adaptive control is integrated in [15] for a force-based control system, enabling robots to adapt to model uncertainties and rough terrain while performing dynamic gaits like fast trotting and bounding. Fast coverage and the ability to traverse harsh terrains are considered [16], which often pose significant challenges for traditional unmanned ground vehicles (UGVs). However, the development of a reliable and fully autonomous UAV system capable of navigating such environments and extracting actionable information remains a key challenge. Snake-like robots are particularly effective in navigating undulating and irregular terrains [17] due to their flexible, multi-jointed structures. Coordinated control of these robots enhances their ability to maintain stable formations in such environments while maneuvering through complex landscapes and avoiding obstacles. These approaches collectively demonstrate the importance of integrating terrain-induced disturbances into formation control strategies, setting the stage for further breakthroughs in multi-robot systems operating in complex environments. In this paper, we combine target chasing, formation consensus and path following and provide an integrated solution for robotic operation in undulating fields.

In this paper, we propose algorithms for formation control and path following for multi-robot systems in undulating fields. The contributions of this work are: 1) it extends traditional formation control methods to address the specific challenges posed by undulating terrain; 2) the desired formation is defined in the local frame for both formation consensus and path following; 3) it introduces a simplistic tilt-aware stabilization process that facilitates real-time performance. Simulation studies demonstrate that our method delivers satisfactory synchronization performance and path following in undulating terrains.

The remainder of this paper is organized as follows. Section 2 introduces the preliminary model and problem formulation, outlining the system setups and robot dynamics that lay the groundwork for formation behavior in undulating fields. Section 3 presents the main results, including the tilt stabilization design, adaptive target-robot allocation for collision avoidance, formation consensus control, and path following strategy. Section 4 showcases simulation results that validate the effectiveness of the proposed methods. Section 5 concludes the paper, discuss the limitations and outlines directions for future research. The symbols in this paper are listed in Table 1.

2. Preliminaries & Problem Description

In this section, we introduce the preliminary model and present the controller design in this paper. We will formulate the problem and propose the main assumptions. We consider the formation control for multiple robots in undulating fields. In this paper, there are two main tasks: 1) formation control, and 2) path following. The first is to gather a group of robots safely and get ready for the next step of the task. The second is to maintain the formation while the robots are roaming along the predefined path.

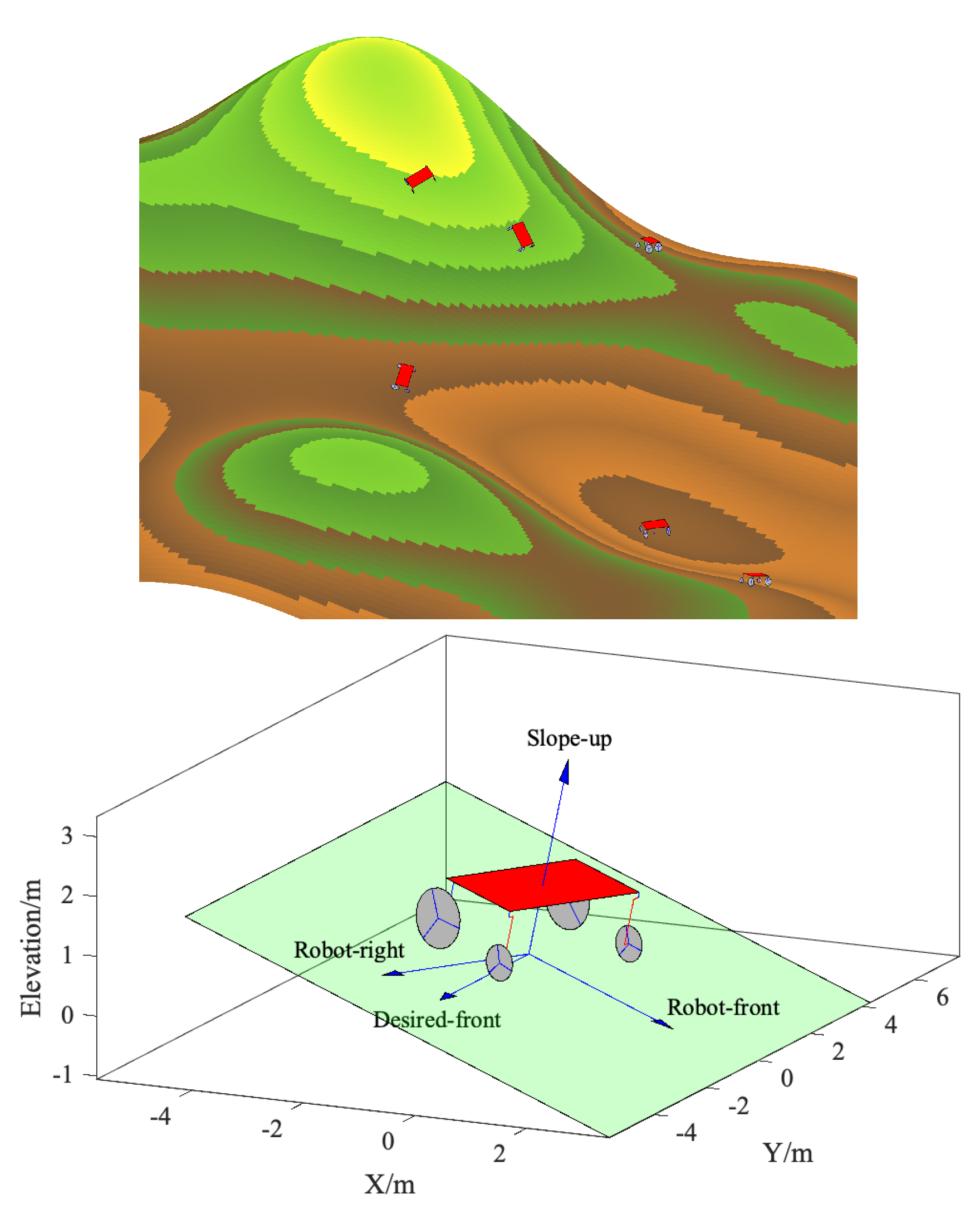
We consider the four-wheel robots in this paper, as shown in Figure 1. The robots are running across the undulating field, and for simplification, the robots will land on the tilt and will not topple throughout the simulation. The robots will move as a collective; they can avoid collisions with each other and reschedule their paths to increase tilt stability if required. The two smaller wheels (radius is $r_1$) are free-turning, and the two bigger wheels (radius is $r_2$) are driving. The centre of robot i at instant k is $x_i\left(k\right)$, and it turns when the bigger wheels have different speeds. The robot has at least three contacts with the ground, and we assume no slipping at the wheel.

The control design for target chasing is fundamental for various robotic missions. In this paper, we mainly manipulate steering to achieve this, and use speed tuning to achieve consensus in Section 3.3. Assume that the rotation of the robot i is ${\omega }_i\left(k\right)\in R$ at instant k. We have the control law below:

$$\begin{array}{ccc}\hfill {\omega }_i\left(k\right)& =& \sigma \mathrm{sign}\left({\overrightarrow{e}}_i\left(k\right)·\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]·{\overrightarrow{f}}_i{\left(k\right)}^T\right)\hfill \\ \hfill & & ·\sin \left(\arccos \left({\overrightarrow{e}}_i\left(k\right)·{\overrightarrow{f}}_i{\left(k\right)}^T\right)\right),\hfill \end{array}$$

(1)

where ${\overrightarrow{e}}_i\left(k\right)\in R^{1\times 3}$ is a unit vector pointing to robot front, and ${\overrightarrow{f}}_i\left(k\right)\in R^{1\times 3}$ is a unit vector pointing to its target $T_i\left(k\right)\in R^{1\times 3}$.

Figure 1. Four-wheel robots on the slope.

Figure 1. Four-wheel robots on the slope.

In this paper, we consider robot 1 as the leader and the rest of the robots as followers. Assume that ${\overrightarrow{e}}_r\left(k\right)\in R^3$ is a unit vector pointing to the right of robot 1. We use $d=[d_1;d_2;\dots ;d_n]\in R^{n\times 3}$ to denote the desired formation, where $d_i\in R^3$ is the target coordinate in the relative frame. We then get the target location $D=[D_1;\dots ]=d·[{\overrightarrow{e}}_i\left(k\right);{\overrightarrow{e}}_r\left(k\right)]$ in the global frame, defined by (2).

$$\begin{array}{ccc}\hfill D& =& [D_1;\dots ]=d·[{\overrightarrow{e}}_i\left(k\right);{\overrightarrow{e}}_r\left(k\right)],\hfill \\ \hfill D_i\left(k\right)& =& d_i·[{\overrightarrow{e}}_i\left(k\right);{\overrightarrow{e}}_r\left(k\right)].\hfill \end{array}$$

(2)

Note that the desired formation is defined and converted in the global coordinate system. As robot 1 moves and turns, the desired formation will change around it. The followers will then have changing targets, and this may have a negative impact on the overall performance. Further analysis is omitted in this paper.

3. Main Results

In this section, we present the main results of the paper. A two-step process is proposed to achieve formation consensus and path following.

3.1. Tilt Stability

Robots have asymmetric mass distribution, and their width-length ratios are larger than 1. As a result, they are prone to tumble on slopes. In this paper, we consider the robot in Figure 1, and it’s more likely to topple forward. We use

$${\theta }_i\left(k\right)=\left|{\overrightarrow{e}}_i\left(k\right)·\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]\right|$$

to denote the tilt stability of robot i. It is easy to see that $0\le {\theta }_i\left(k\right)\le 1$, and we assume that the smaller ${\theta }_i\left(k\right)$ is, the more stable robot i is on a tilt. We use the expression below to optimize the turning of robot i and increase its tilt stability.

$$\begin{array}{ccc}\hfill {\omega }_i{\left(k\right)}^{*}& =& max{\theta }_i(k+1),\hfill \\ \hfill \mathrm{subject}\mathrm{to}& & \left|T_i(k+1)-x_i(k+1)\right|\hfill \\ \hfill & \le & \left|T_i\left(k\right)-x_i\left(k\right)\right|,\hfill \end{array}$$

(3)

Note that (3) will help robots improve their tilt stability. The condition will guarantee that the robots still move toward their targets. When robots move away from the targets, the condition will not be satisfied and (3) will not be triggered. Instead, robots will move towards their targets by (1).

3.2. Adaptive Formation for Collision Avoidance

Collisions among the robots are mostly due to path crossovers, and reallocation of targets to robots could help reduce the likelihood of inter-robot collisions. We use the allocation function $T_k$ to determine the targets for robots at instant k. Namely, $T_i\left(k\right)=T\left(x_i\left(k\right)\right)$ for $1\le i\le n$. We use the expression below to optimize the target-robot allocation and avoid likely collisions.

$$\begin{array}{ccc}\hfill \mathrm{if}& & \left|T_k\left(x_i\left(k\right)\right)-x_i\left(k\right)\right|+\left|T_k\left(x_j\left(k\right)\right)-x_j\left(k\right)\right|\hfill \\ \hfill & & >\left|T_k\left(x_j\left(k\right)\right)-x_i\left(k\right)\right|+\left|T_k\left(x_i\left(k\right)\right)-x_j\left(k\right)\right|,\hfill \\ \hfill \mathrm{then}& & T_{k+1}\left(x_i\left(k\right)\right)=T_k\left(x_j\left(k\right)\right),\hfill \\ \hfill & & T_{k+1}\left(x_j\left(k\right)\right)=T_k\left(x_i\left(k\right)\right).\hfill \end{array}$$

(4)

Note that (4) cannot provide guaranteed collision avoidance. Inter-path distances have to be considered with advanced path-robot allocation. Further proof is omitted in this paper.

3.3. Formation Consensus

In this paper, we assume that the robots must reach the desired formation to enter the next step of the following path. To synchronize the movements of robots, we introduce formation consensus control for them to collectively reach the desired formation. We have presented the target chasing controller in (1). There is no need to change the rotational speeds, and we will help the robots reach formation consensus by tuning only the translational speeds. We have the formation control law below:

$$\begin{array}{ccc}\hfill v_1\left(k\right)& =& {\displaystyle \frac{v_{max}}{1+\frac{max\left|T_i\left(k\right)-x_i\left(k\right)\right|}{d_0}}},\hfill \\ \hfill v_i\left(k\right)& =& v_{max}\times {\displaystyle \frac{\left|T_i\left(k\right)-x_i\left(k\right)\right|}{\underset{j>1}{max}\left|T_j\left(k\right)-x_j\left(k\right)\right|}},\mathrm{for}\mathrm{i}>1,\hfill \end{array}$$

(5)

where $v_{max}$ is top speed for all robots; $d_0$ is a constant and we used it to tune the convergence rate for formation consensus. The proof is omitted.

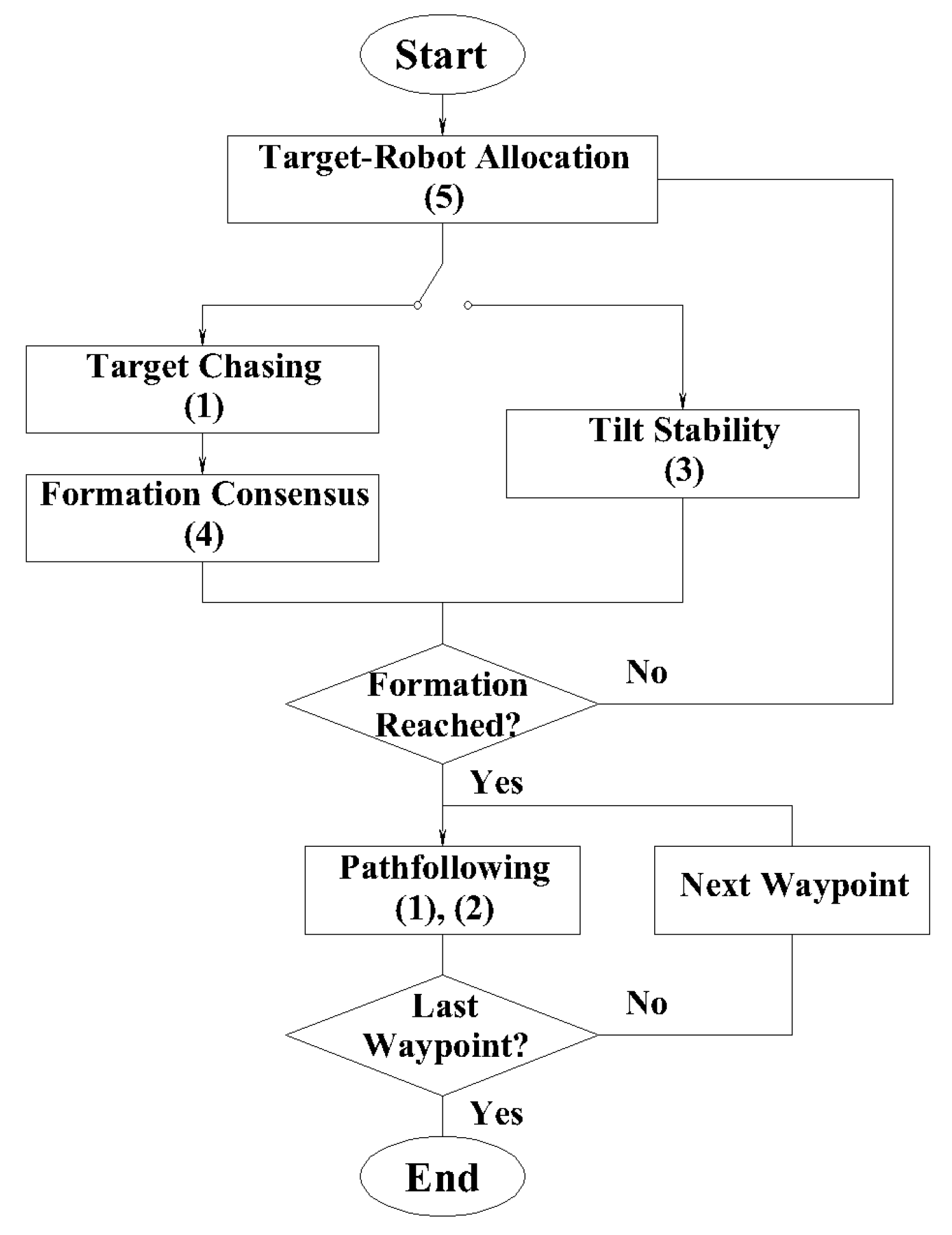
3.4. Path Following

After the follower robots gather around the leader robot, they will reach the desired formation defined by (2). As soon as the formation error is sufficiently small, the robots will follow the desired path as a collective. The process is given in the diagram Figure 2 below.

The multi-robot operation starts with a target-robot allocation, and there are two modes: the first for formation consensus and the second for maintaining tilt stability. The robots will be in the second mode as long as they are still approaching their targets; other wise they will be in the first mode. This makes sure that the robots will keep getting closer to the desired formation. Meanwhile, targets are reallocated to robots during sampling intervals, and potential collisions will be avoided. After the desired formation is reached, the robots will follow the given path until the last waypoint along the path is reached.

4. Simulation Example

To validate the proposed formation control strategy, we conduct simulations using a team of 10 four-wheeled robots traversing an undulating field. The simulation scenario reflects realistic terrain variations, with continuous changes in slope and elevation that challenge both formation integrity and tilt stability.

The simulation was run by Matlab R2023a on a Mac Mini with Apple M2 Pro and 32 GB RAM. The sampling interval is 1.2 seconds, during when the control law and target-robot allocation are updated. The desired local formation d is given below and shown in Figure 4 and the desired path is shown in Figure 6.

$$\begin{array}{ccc}\hfill d^T& =& \left[\begin{array}{c}0\\ 0\end{array}\begin{array}{c}10\\ 0\end{array}\begin{array}{c}-10\\ 0\end{array}\begin{array}{c}20\\ -10\end{array}\begin{array}{c}10\\ -10\end{array}\begin{array}{c}0\\ -10\end{array}\right.\hfill \\ \hfill & & \left.\begin{array}{c}-10\\ -10\end{array}\begin{array}{c}-20\\ -10\end{array}\begin{array}{c}10\\ -20\end{array}\begin{array}{c}-10\\ -20\end{array}\right].\hfill \end{array}$$

Note that we have omitted the heights of d as those are determined by the elevation of the field.

Each robot is modeled with two large driving wheels and two smaller free-turning wheels. The leader robot follows a predefined path, while the follower robots maintain a rigid formation defined in the leader’s local coordinate frame. The tilt-aware fitness function guides turning behavior to minimize the risk of toppling, and target allocation is dynamically adjusted to prevent inter-robot collisions. We use formation error $P\left(k\right)$ and shortest inter-robot distance $Q\left(k\right)$ at instant k in this section to demonstrate the system performance.

$$\begin{array}{ccc}\hfill P\left(k\right)& =& \stackrel{n}{\sum _{i>=1}}\left|x_i\left(k\right)-d_i\left(k\right)\right|,\hfill \\ \hfill Q\left(k\right)& =& \underset{i\ne j}{min}\left|x_i\left(k\right)-x_j\left(k\right)\right|.\hfill \end{array}$$

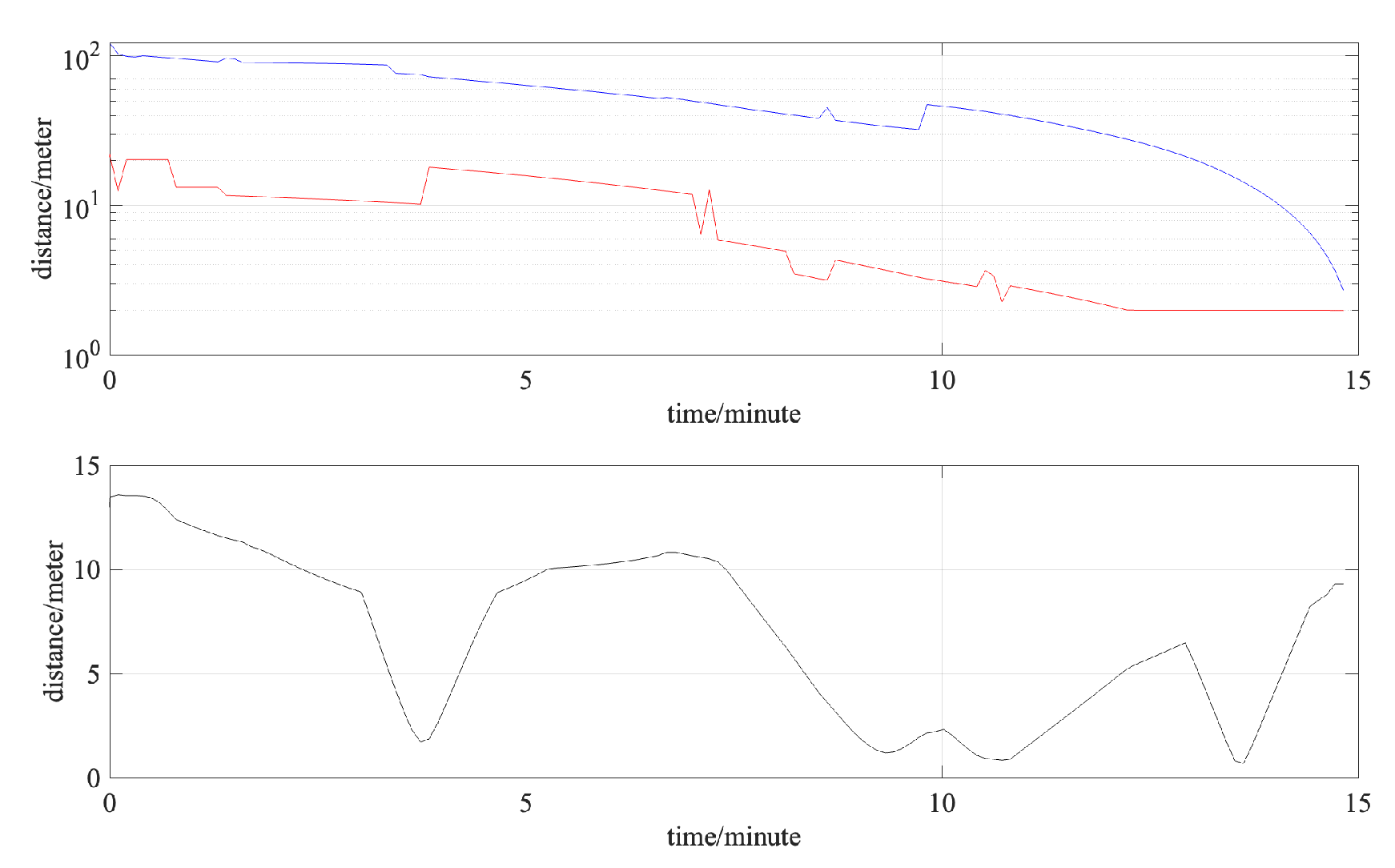
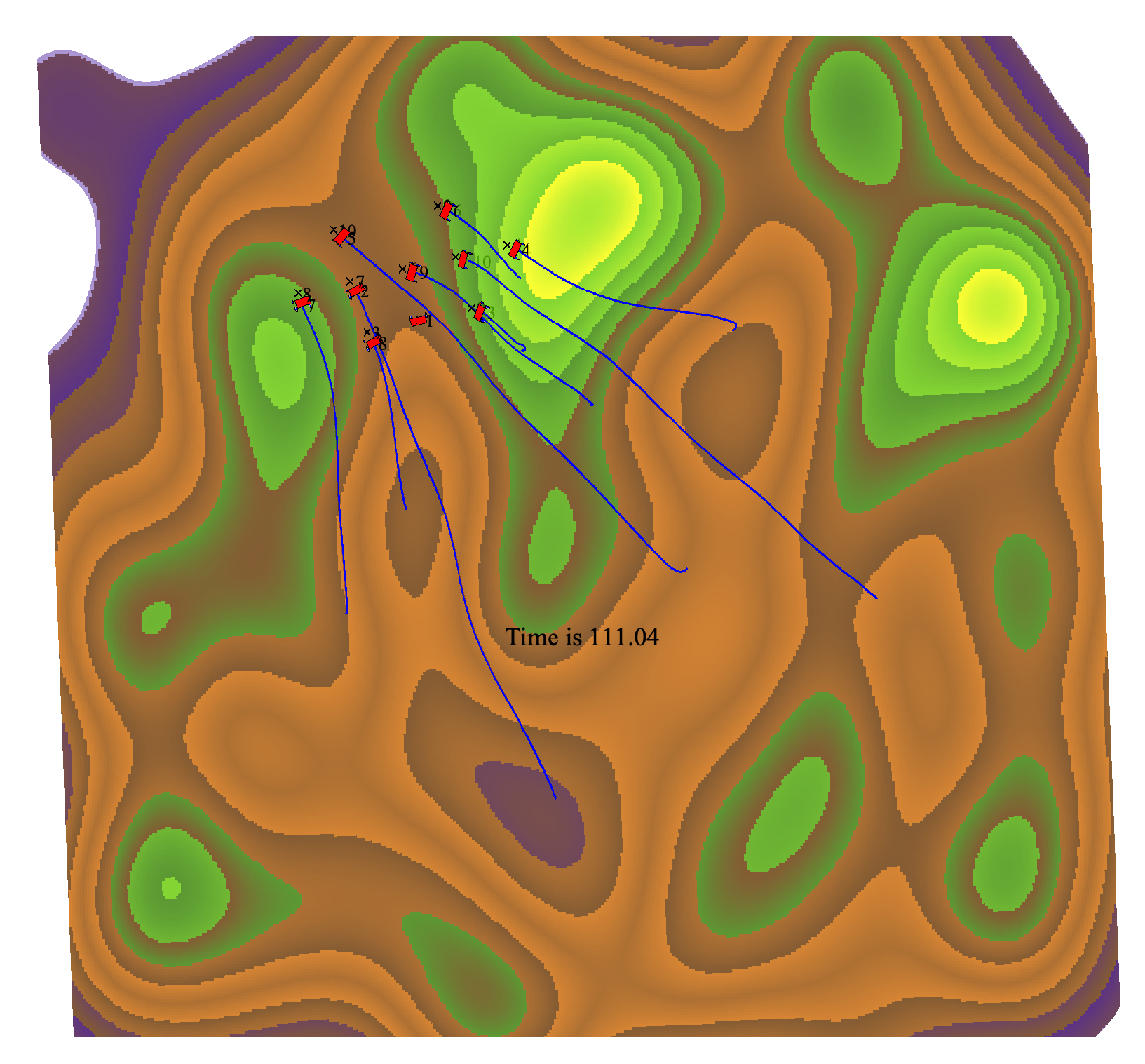
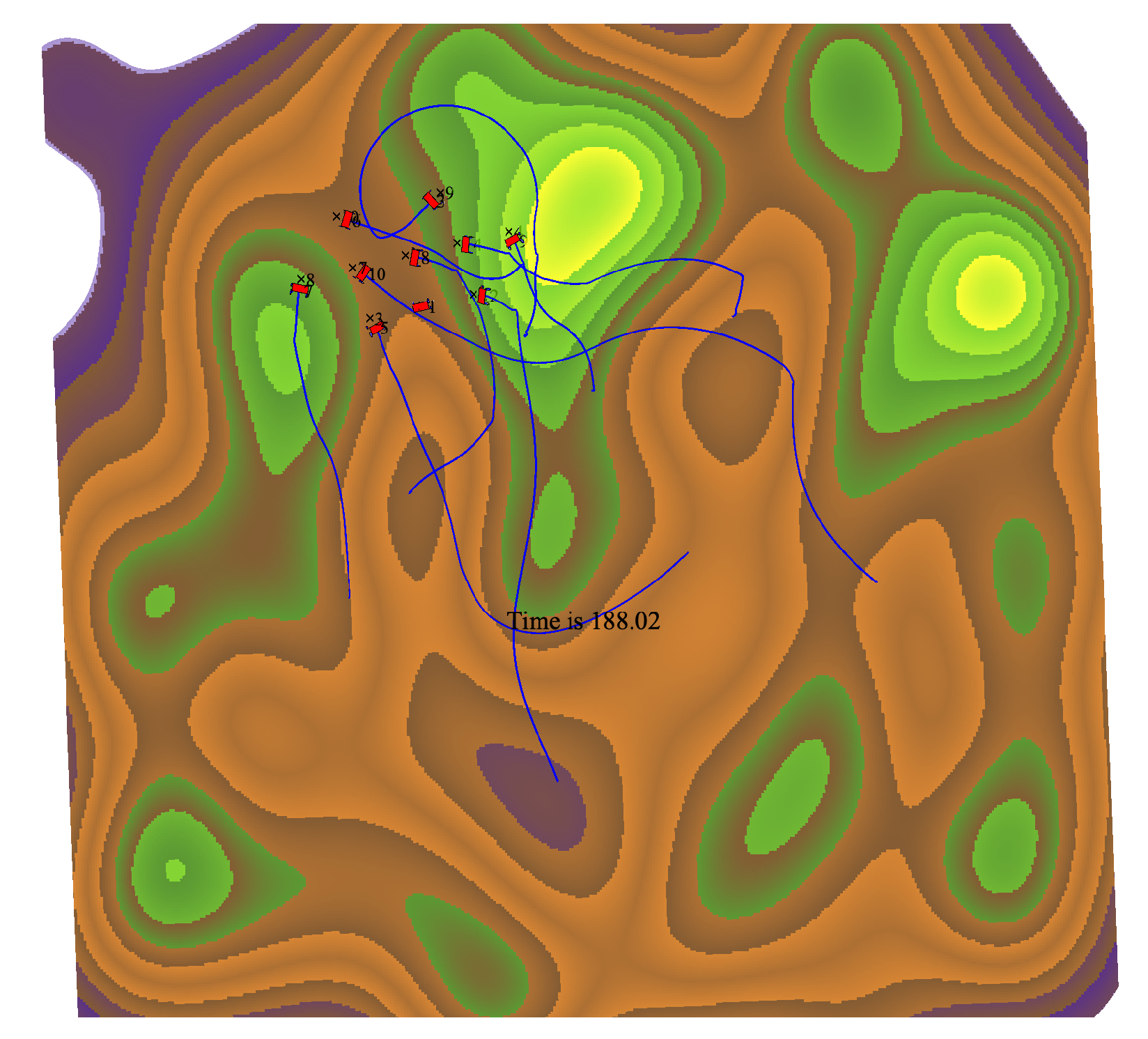
The robots can reach their targets synchronously, as shown in the upper plot in Figure 3. At the same time, robots can avoid collisions, as shown in the lower plot. Furthermore, it can be seen in Figure 4 that they could maintain tilt stability as they reach the desired formation. The whole operation takes 188 minutes, while it takes 111 minutes for robots without tilt stability, as shown in Figure 5. This means that the robots have to take some roundabouts to improve tilt stability.

Figure 3. Formation error (above) and shortest inter-robot distance (below).

Figure 3. Formation error (above) and shortest inter-robot distance (below).

Figure 4. Wandering paths of 10 robots with tilt stability.

Figure 4. Wandering paths of 10 robots with tilt stability.

Figure 5. Wandering paths of 10 robots without tilt stability.

Figure 5. Wandering paths of 10 robots without tilt stability.

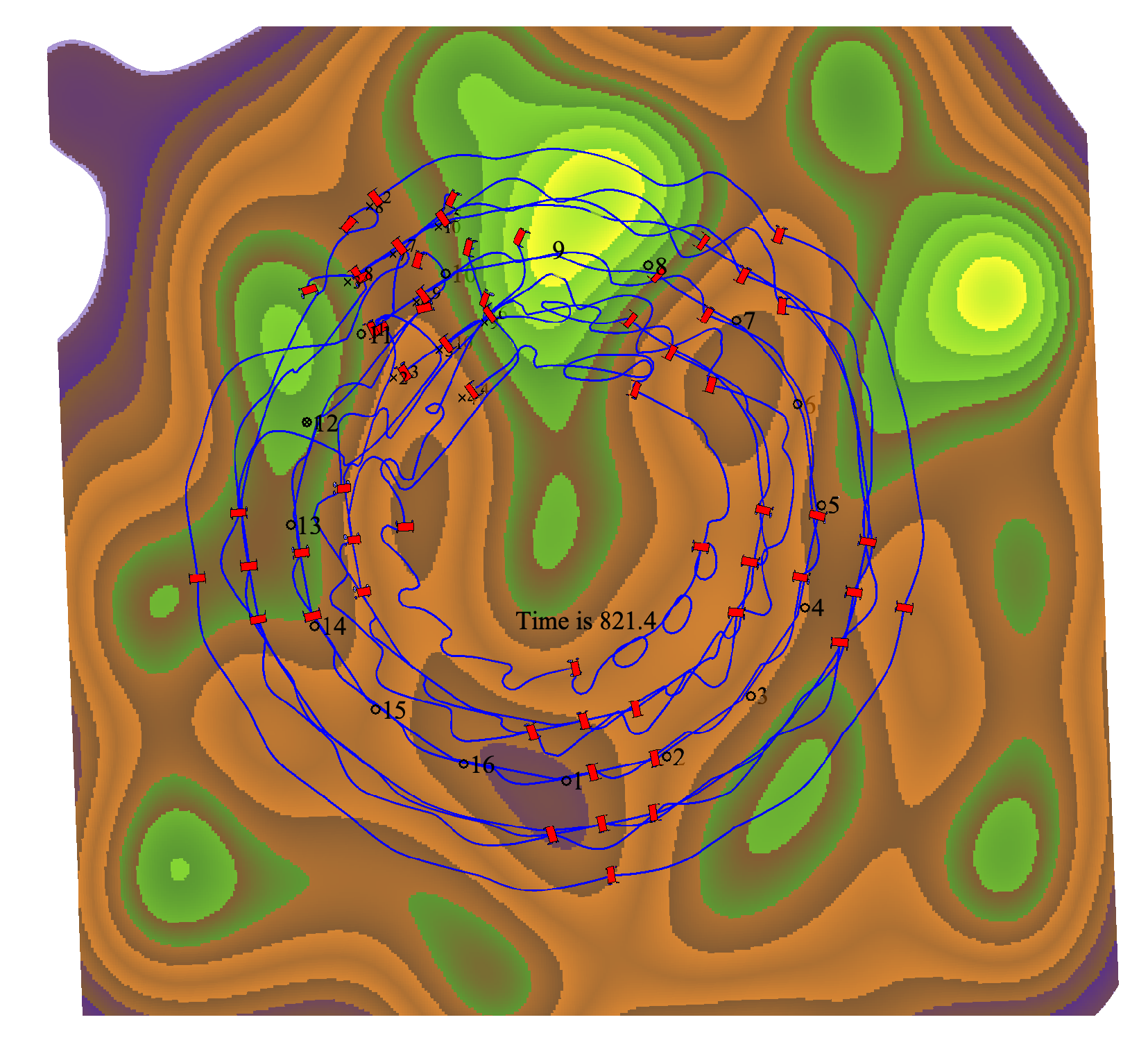
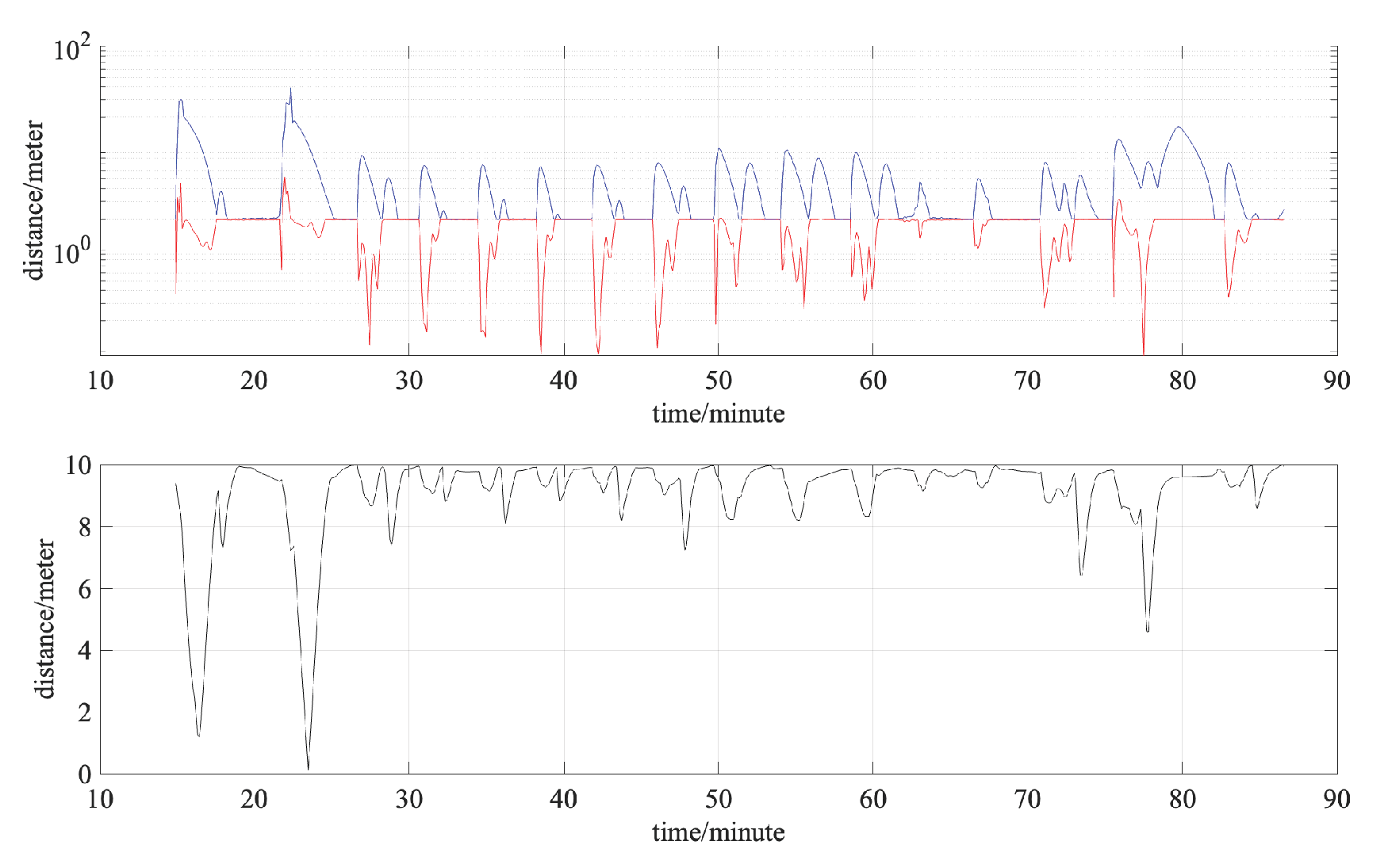
After the robots reach the desired formation, they then continue to follow the given path, as shown in Figure 6. It can be seen that the robots are able to maintain the overall formation, as demonstrated by the robot snapshots along the circular path. Moreover, the inner circle has more jittering along the path while the outer circle has less. This is due to the similar translational speeds, and the inner robots have to slow down and take detours to match the pace of the outer robots. The formation errors and shortest inter-robot distances are given in Figure 7. It can be seen in the upper picture that the formation errors are larger whenever there is a new waypoint. As the robots progress, the errors converge to zero and then move on to the next waypoint. Meanwhile, the robots have avoided collisions, as shown in the lower picture.

Figure 6. Wandering paths of 10 robots with path following.

Figure 6. Wandering paths of 10 robots with path following.

Figure 7. Formation error (above) and shortest inter-robot distance (below).

Figure 7. Formation error (above) and shortest inter-robot distance (below).

The results demonstrate that the proposed approach achieves high formation accuracy and robustness under undulating field conditions, validating its practical applicability for terrain-aware multi-robot coordination.

5. Conclusion

This paper presents a two-step formation control strategy for multi-robot systems operating in undulating fields, addressing key challenges such as formation consensus, tilt-induced instability, collision avoidance, and path following. By introducing tilt stabilization, the proposed control framework enhances the stability of robots collectively on undulating terrain while achieving the overall formation. A target chasing controller, combined with adaptive formation reassignment and speed-based formation consensus, enables robust coordination without requiring complex communication protocols. Simulation results demonstrate that the proposed methods significantly improve the tilt stability and provide accurate path following in challenging environments.

There are several limitations to this study. For example, the algorithms are designed for wheeled robots with asymmetric mass distribution, and this calls for a need to increase tilt stability in the heading direction. Few discussion is made on robots with different dynamics. A simplistic tilt stabilization process is given, which only takes immediate tilts into account. This is not sufficient to handle every possible scenario, and a comprehensive approach is required to guarantee safe operations in complex terrains. Moreover, after the robots start to follow the given path, we omit the need for tilt stabilization. This is mainly due to the limited capacity of the robots, and the priority is path following and formation maintenance. An advanced method is needed to strike a satisfactory balance among the objectives of different tasks.

Further research will explore several directions. First, the current approach assumes idealized conditions, such as no wheel slippage and constant terrain profiles; future work could incorporate more realistic models, including dynamic surface friction and terrain unpredictability. Second, while our method focuses on fixed-frequency target allocation, adaptive learning-based approaches could further improve scalability and resilience. Lastly, integrating onboard sensors for real-time terrain estimation and obstacle detection will make the system more adaptable to unstructured environments. Testing with physical robot platforms in real-world settings will be essential to validate the effectiveness and robustness of the proposed framework.