Submitted:
09 October 2025
Posted:
10 October 2025
You are already at the latest version
Abstract
Keywords:
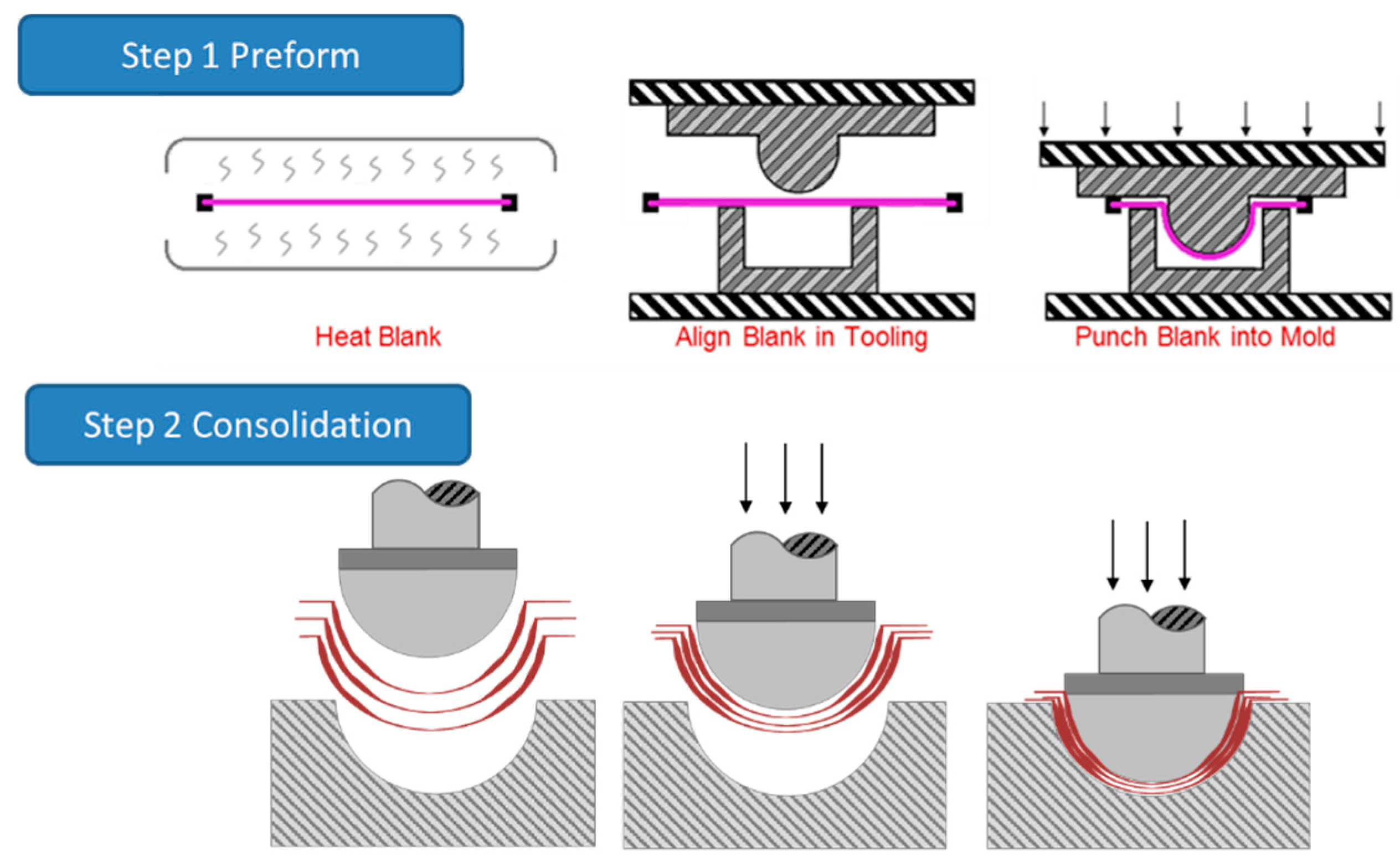
1. Introduction
2. Materials and Methods
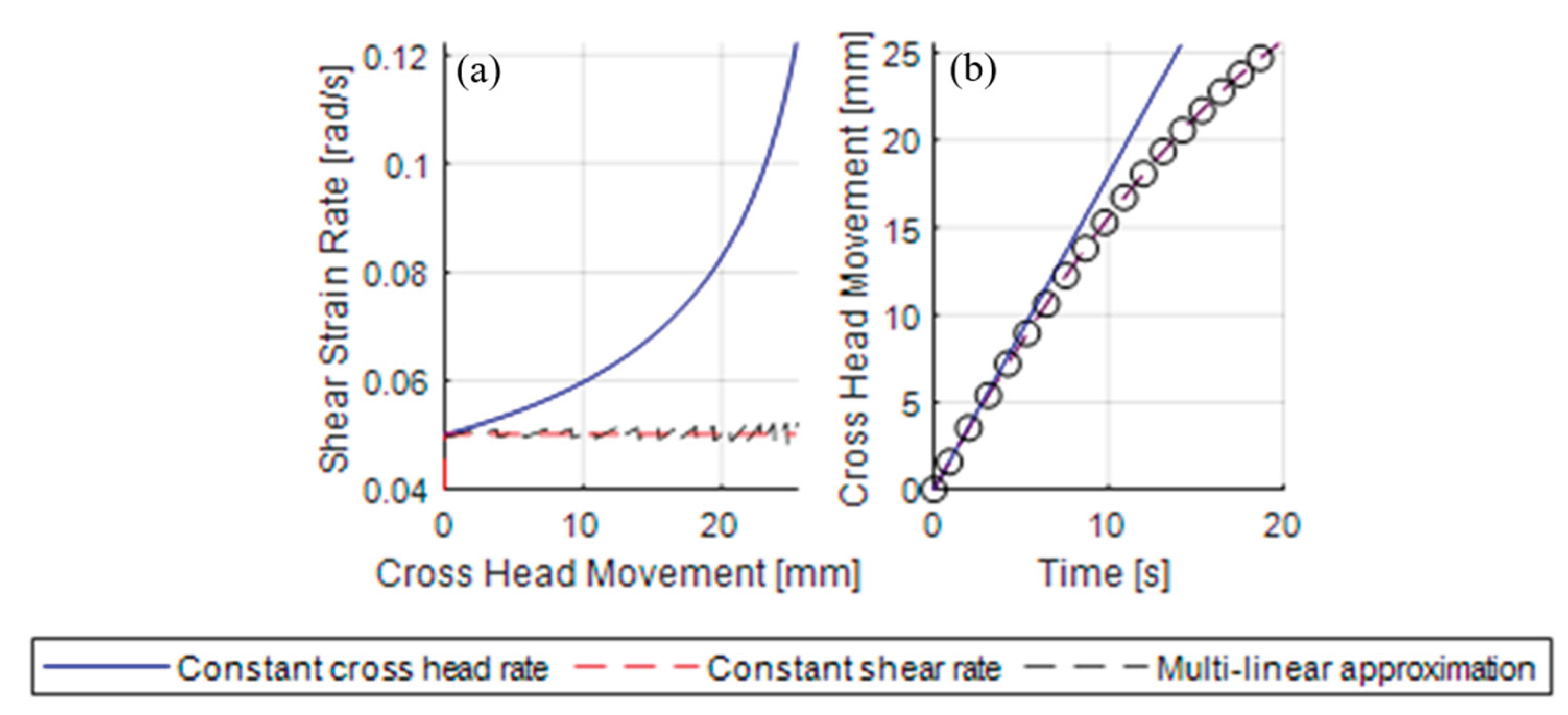
2.1. Determination of Shear Rate in Forming
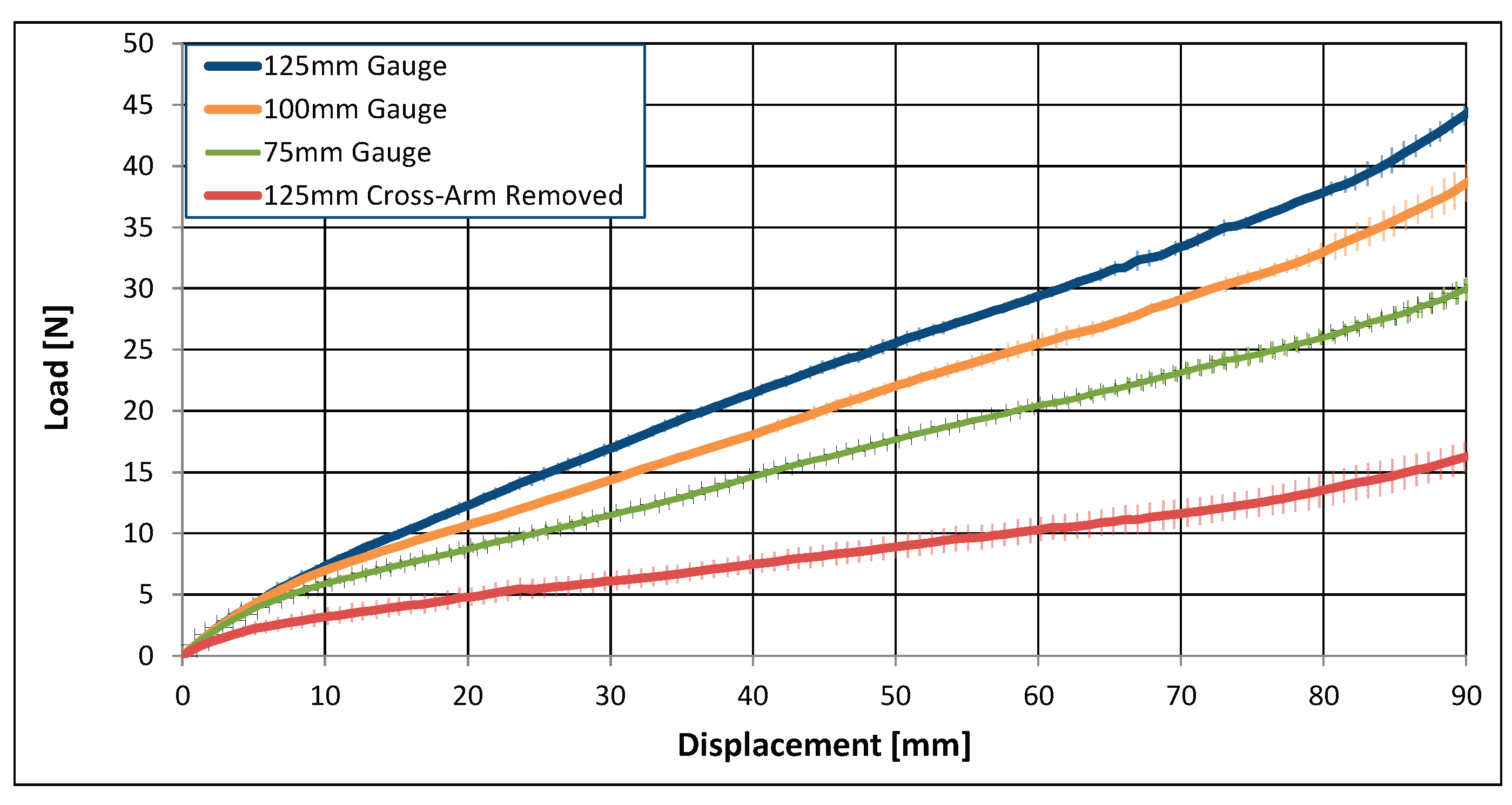
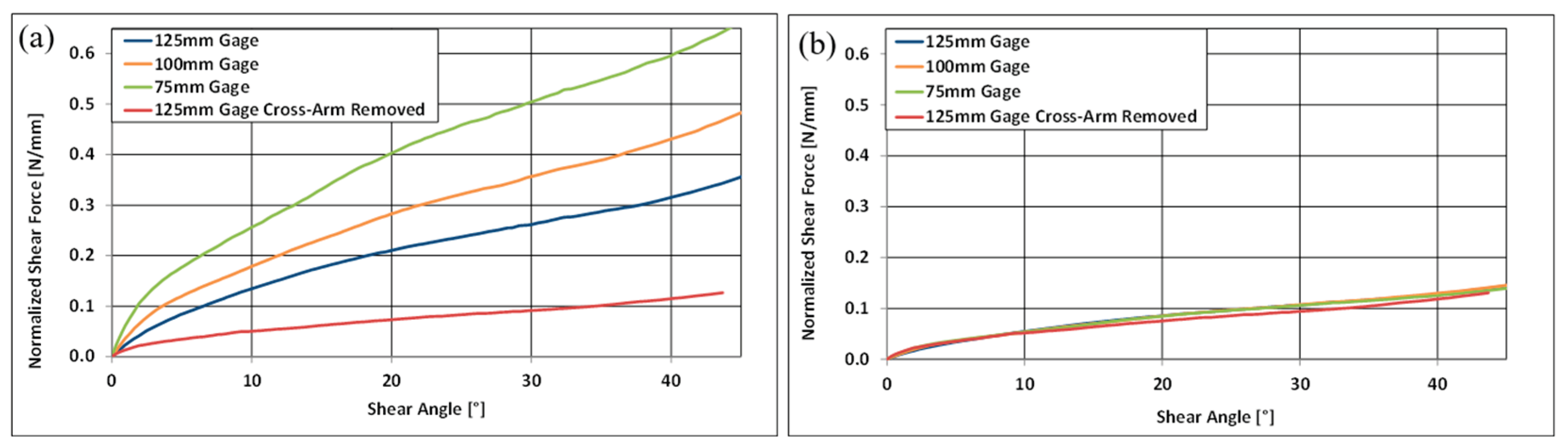
2.2. Sample Size Variation
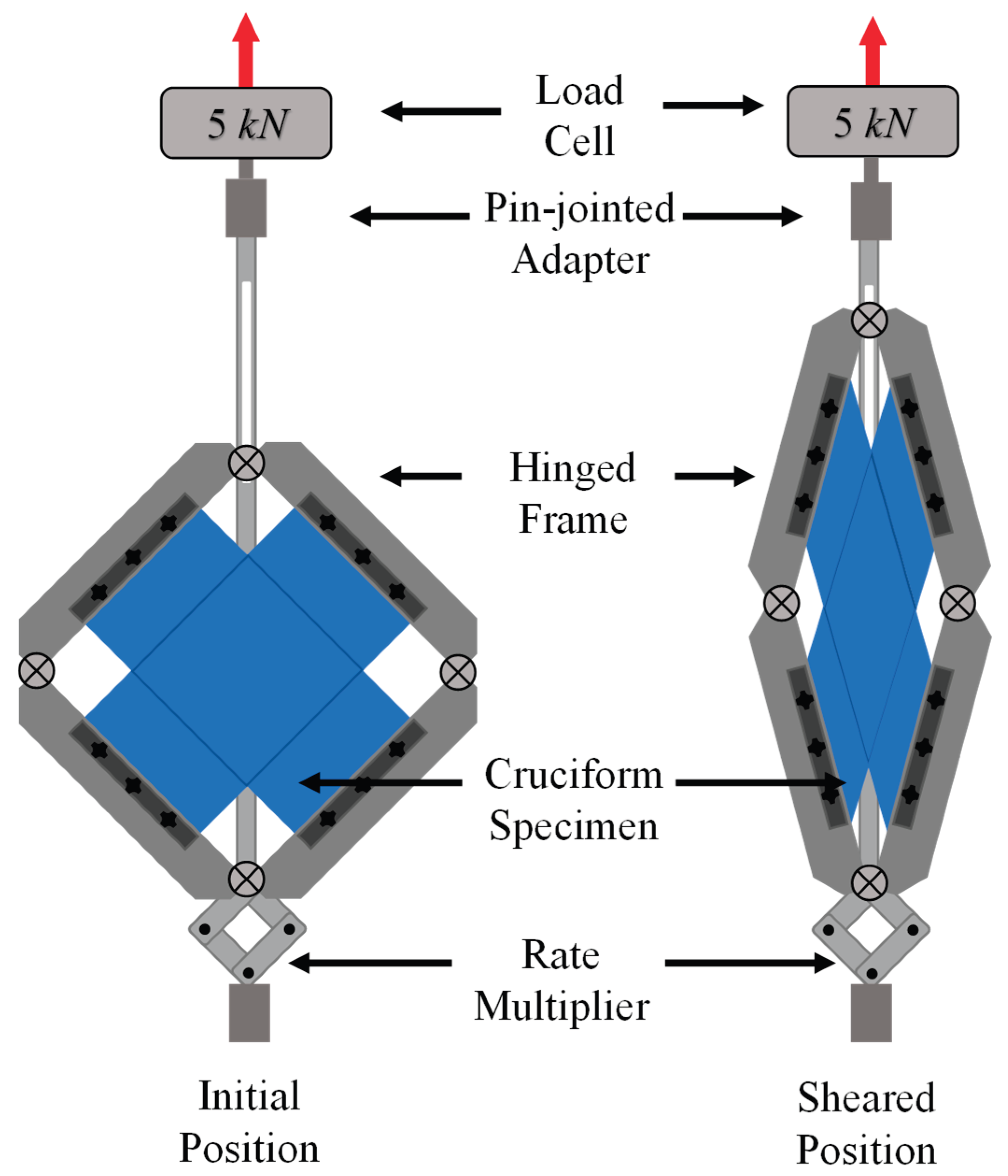
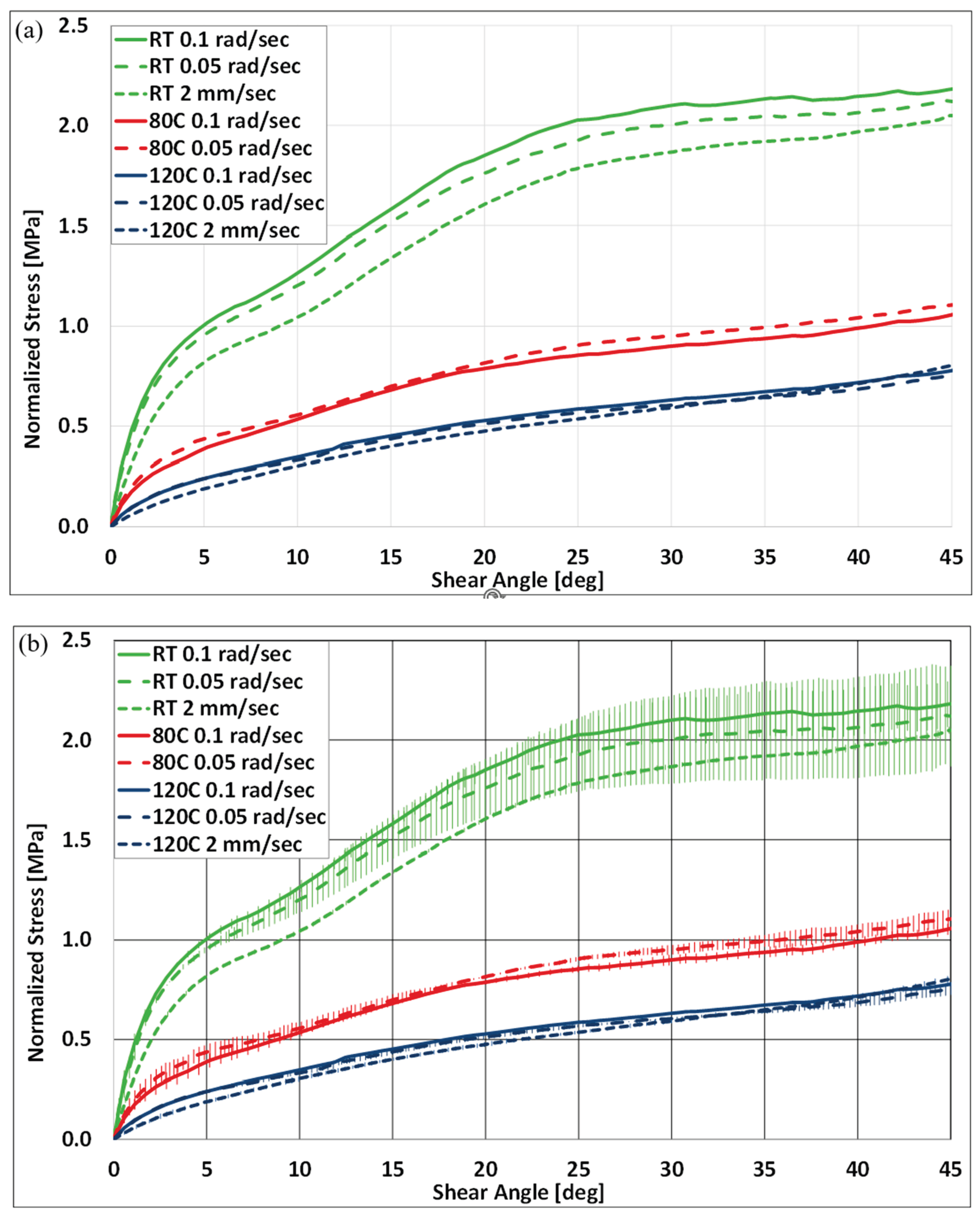
2.3. Constant Shear-Rate Testing
3. Results
3.1. Strain Rate Variation
3.2. Sample Size
3.3. Constant Shear-Rate
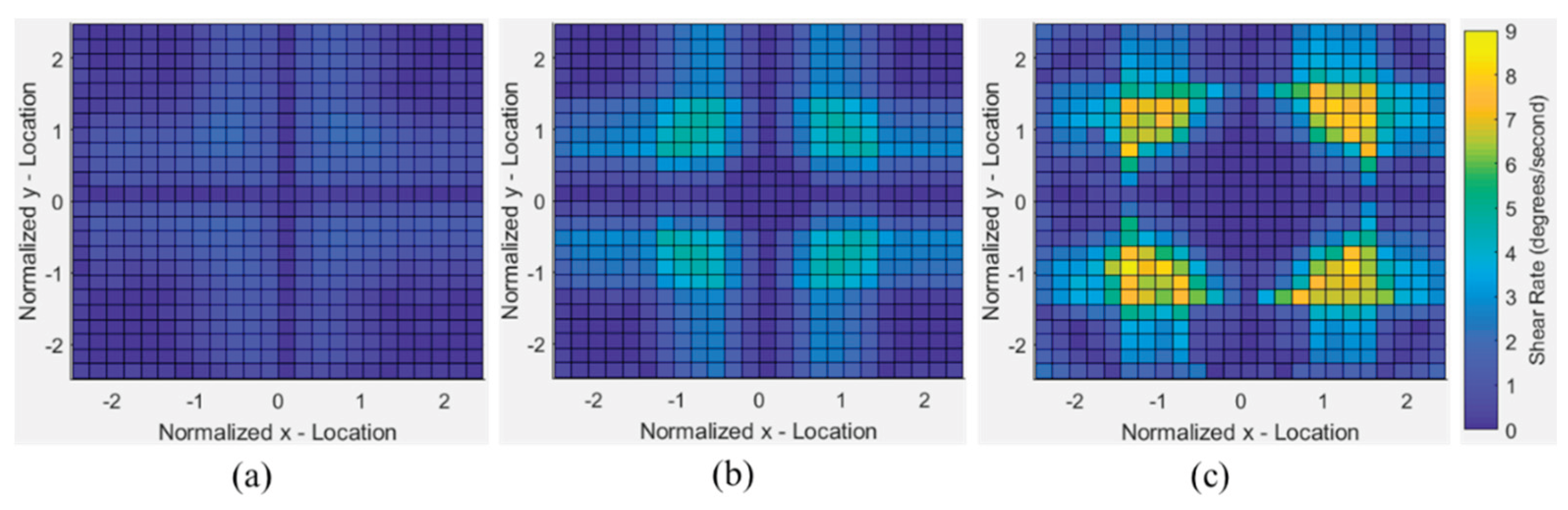
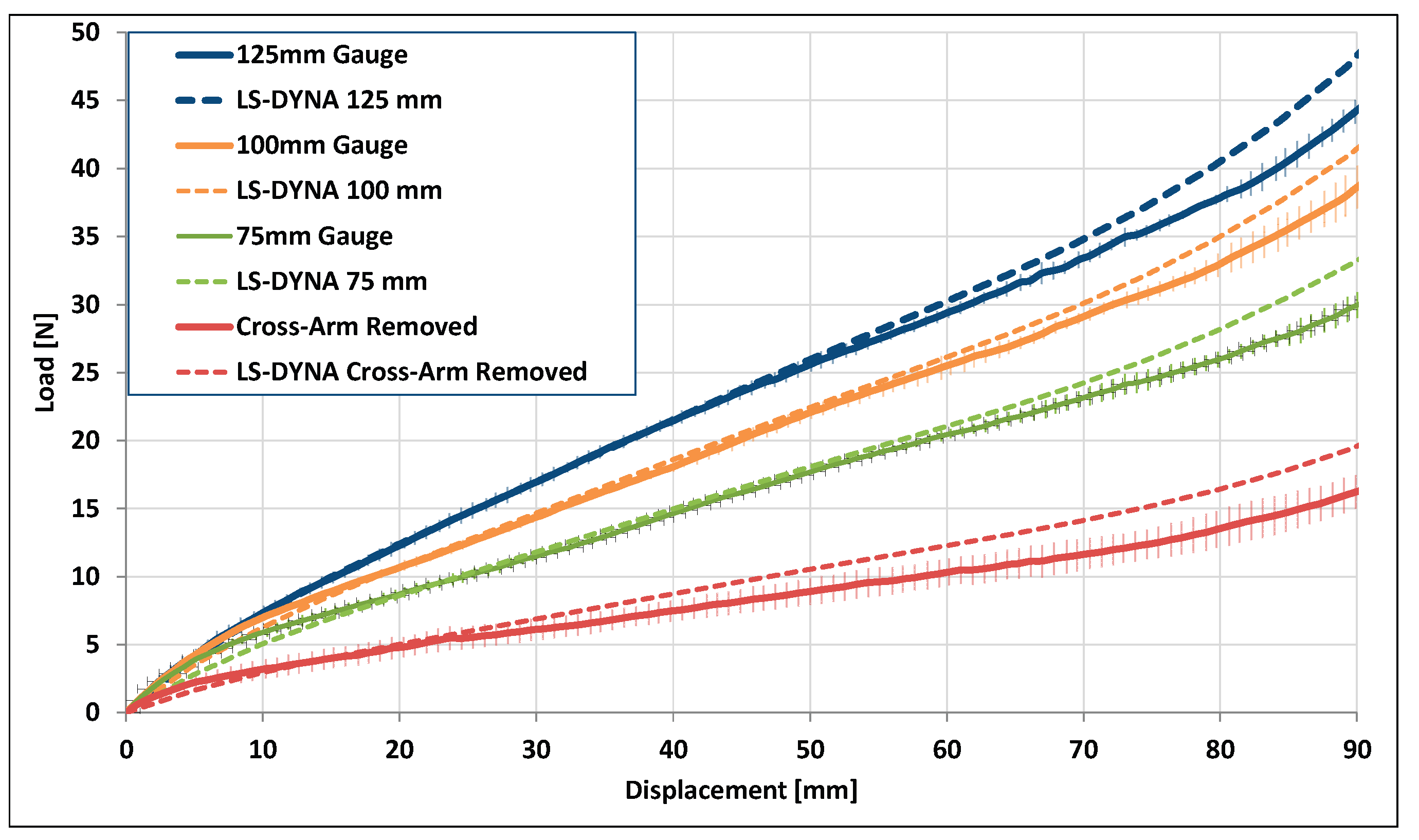
3.4. Finite Element Modeling Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dangora, L.M.; Mitchell, C.J.; Sherwood, J.A.; Parker, J.C. Deep-drawing forming trials on a cross-ply thermoplastic lamina for helmet preform manufacture. Journal of Manufacturing Science and Engineering 2017, 139, 031009. [Google Scholar] [CrossRef]
- Prodromou, A.G.; Chen, J. Relationship between shear angle and wrinkling of textile composite preforms. Composites Part A: Applied Science and Manufacturing 1997, 28A, 491–503. [Google Scholar] [CrossRef]
- McGuinness, G.B.; Brád aigh, C.M.O. Characterisation of thermoplastic composite melts in rhombus-shear. Composites Part A: Applied Science and Manufacturing 1998, 29, 509–518. [Google Scholar] [CrossRef]
- Potter, K. Bias extension measurements on cross-plied unidirectional prepreg. Composites Part A: Applied Science and Manufacturing 2002, 33, 627–634. [Google Scholar] [CrossRef]
- Lebrun, G.; Bureau, M.N.; Denault, J. Evaluation of bias-extension and picture-frame test methods for the measurement of intraply shear properties of PP/glass commingled fabrics. Composite Structures 2003, 61, 341–352. [Google Scholar] [CrossRef]
- Sharma, S.B.; Sutcliffe, M.P.F. A simplified finite element model for draping of woven material. Composites Part A: Applied Science and Manufacturing 2004, 35, 637–643. [Google Scholar] [CrossRef]
- Peng, X.Q.; Cao, J.; Chen, J.; Xue, P.; Lussier, D.S.; Liu, L. Experimental and numerical analysis on normalization of picture frame tests for composite materials. Composites Science and Technology 2004, 64, 11–21. [Google Scholar] [CrossRef]
- Cao, J.; Akkerman, R.; Boisse, P.; Chen, J.; Cheng, H.S.; de Graaf, E.F.; et al. Characterization of mechanical behavior of woven fabrics: experimental methods and benchmark results. Composites Part A: Applied Science and Manufacturing 2008, 39, 1037–1053. [Google Scholar] [CrossRef]
- Shear of woven fabrics: theoretical model, numerical experiments and full field strain measurements. In: Proc. ESAFORM-2004, 7th International Conference on Material Forming; 2004. (No DOI found). Lomov, S.V.; Stoilova, T.; Verpoest, I. (Eds.).
- Harrison, P.; Clifford, M.J.; Long, A.C. Shear characterisation of viscous woven textile composites: a comparison between picture frame and bias extension experiments. Composites Science and Technology 2004, 64, 1453–1465. [Google Scholar] [CrossRef]
- Potluri, P.; Ciurezu, D.P.; Ramgulam, R. Measurement of meso-scale shear deformations for modelling textile composites. Composites Part A: Applied Science and Manufacturing 2006, 37, 303–314. [Google Scholar] [CrossRef]
- Kawabata, S.; Niwa, M.; Kawai, H. The finite-deformation theory of plain-weave fabrics part I: the biaxial-deformation theory. Journal of the Textile Institute 1973, 64, 21–46. [Google Scholar] [CrossRef]
- Kawabata, S.; Niwa, M.; Kawai, H. The finite-deformation theory of plain-weave fabrics part III: the shear deformation theory. Journal of the Textile Institute 1973, 64, 62–85. [Google Scholar] [CrossRef]
- Long, A.; Rudd, C.; Blagdon, M.; Smith, P. Characterizing the processing and performance of aligned reinforcements during preform manufacture. Composites Part A: Applied Science and Manufacturing 1996, 27, 247–253. [Google Scholar] [CrossRef]
- Wang, J.; Page, J.; Paton, R. Experimental investigation of the draping properties of reinforcement fabrics. Composites Science and Technology 1998, 58, 229–237. [Google Scholar] [CrossRef]
- Nguyen, M.; Herszberg, I.; Paton, R. The shear properties of woven carbon fabric. Composite Structures 1999, 47, 767–779. [Google Scholar] [CrossRef]
- McGuinness, G.B.; O’Brien, M. O’B. Development of rheological models for forming flows and picture-frame shear testing of fabric reinforced thermoplastic sheets. Journal of Non-Newtonian Fluid Mechanics 1997, 72, 1–16. [Google Scholar] [CrossRef]
- Harrison, P.; Wiggers, J.; Long, A. Normalization of shear test data for rate-independent compressible fabrics. Journal of Composite Materials 2008, 42, 2315–2344. [Google Scholar] [CrossRef]
- Boisse, P.; Akkerman, R.; Carlone, P.; Kärger, L.; Lomov, S.V.; Sherwood, J.A. Advances in composite forming through 25 years of ESAFORM. International Journal of Material Forming 2022, 15, 39. [Google Scholar] [CrossRef]
- Boisse, P.; Gomes, R.; Curado-Correia, N. Press forming a 0/90 cross-ply advanced thermoplastic composite using the double-dome benchmark geometry. Composites Part A: Applied Science and Manufacturing 2013, 54, 56–69. [Google Scholar] [CrossRef]
- Boisse, P.; Hamila, N.; Guzman-Maldonado, E.; Madeo, A.; Hivet, G.; dell’Isola, F. The bias-extension test for the analysis of in-plane shear properties of textile composite reinforcements and prepregs: a review. International Journal of Material Forming 2017, 4, 473–499. [Google Scholar] [CrossRef]
- Milani, A.; Nemes, J.; Lebrun, G.; Bureau, M. A comparative analysis of a modified picture-frame test for characterization of woven fabrics. Polymer Composites 2010, 31, 561–568. [Google Scholar] [CrossRef]
- Willems, A.; Lomov, S.V.; Verpoest, I.; Vandepitte, D. Picture frame shear tests on woven textile composite reinforcements with controlled pretension. AIP Conference Proceedings 2007. [CrossRef]
- Launay, J.; Hivet, G.; Duong, A.V.; Boisse, P. Experimental analysis of the influence of tensions on in-plane shear behaviour of woven composite reinforcements. Composites Science and Technology 2008, 68, 506–515. [Google Scholar] [CrossRef]
- Krogh, C.; White, K.D.; Sabato, A.; Sherwood, J.A. Picture-frame testing of woven prepreg fabric: an investigation of sample geometry and shear angle acquisition. International Journal of Material Forming 2019, 1–13. [Google Scholar] [CrossRef]
- Liu, L.; Chen, J.; Gorczyca, J.L.; Sherwood, J.A. Modeling of friction and shear in thermostamping of composites—Part II. Journal of Composite Materials 2004, 38, 1931–1947. [Google Scholar] [CrossRef]
- Lussier, D.; Chen, J. Material characterization of woven fabrics for thermoforming of composites. Journal of Thermoplastic Composite Materials 2002, 15, 497–509. [Google Scholar] [CrossRef]
- Lomov, S.V.; Belov, E.; Bischoff, T.; Ghosh, S.B.; Chi, T.T.; Verpoest, I. Carbon composites based on multiaxial multiply stitched preforms. Part 1: geometry of the preform. Composites Part A: Applied Science and Manufacturing 2002, 33, 1171–1183. [Google Scholar] [CrossRef]
- Jauffrès, D.; Morris, C.D.; Sherwood, J.A.; Chen, J. Simulation of the thermostamping of woven composites: mesoscopic modeling using explicit finite element analysis. International Journal of Material Forming 2010, 3, S1205–S1216. [Google Scholar] [CrossRef]
- Dangora, L.M.; Hansen, C.J.; Mitchell, C.J.; Sherwood, J.A.; Parker, J.C. Challenges associated with shear characterization of a cross-ply thermoplastic lamina using picture frame tests. Composites Part A: Applied Science and Manufacturing 2015, 78, 181–190. [Google Scholar] [CrossRef]
- Chen, Q.; Boisse, P.; Park, C.H.; Saouab, A.; Bréard, J. Intra/inter-ply shear behaviors of continuous fiber reinforced thermoplastic composites in thermoforming processes. Composite Structures 2011, 93, 1692–1703. [Google Scholar] [CrossRef]
- Guzman-Maldonado, E.; Hamila, N.; Naouar, N.; Moulin, G.; Boisse, P. Simulation of thermoplastic prepreg thermoforming based on a visco-hyperelastic model and a thermal homogenization. Materials & Design 2016, 93, 431–442. [Google Scholar] [CrossRef]
- Hsiao, S.-W.; Kikuchi, N. Numerical analysis and optimal design of composite thermoforming process. Computer Methods in Applied Mechanics and Engineering 1999, 177, 1–34. [Google Scholar] [CrossRef]
- Lee, J.S.; Hong, S.J.; Yu, W.-R.; Kang, T.J. The effect of blank holder force on the stamp forming behavior of non-crimp fabric with a chain stitch. Composites Science and Technology 2007, 67, 357–366. [Google Scholar] [CrossRef]
- Lin, H.; Wang, J.; Long, A.; Clifford, M.; Harrison, P. Predictive modelling for optimization of textile composite forming. Composites Science and Technology 2007, 67, 3242–3252. [Google Scholar] [CrossRef]
- Boubaker, B.B.; Haussy, B.; Ganghoffer, J. Discrete models of woven structures: macroscopic approach. Composites Part B: Engineering 2007, 38, 498–505. [Google Scholar] [CrossRef]
- Pickett, A.K.; Creech, G.; de Luca, P. Simplified and advanced simulation methods for prediction of fabric draping. Revue Européenne des Eléments 2005, 14, 677–691. [Google Scholar] [CrossRef]
- Skordos, A.A.; Aceves, C.M.; Sutcliffe, M.P. A simplified rate dependent model of forming and wrinkling of pre-impregnated woven composites. Composites Part A: Applied Science and Manufacturing 2007, 38, 1318–1330. [Google Scholar] [CrossRef]
- Cherouat, A.; Billoët, J.L. Mechanical and numerical modelling of composite manufacturing processes: deep-drawing and laying-up of thin pre-impregnated woven fabrics. Journal of Materials Processing Technology 2001, 118, 460–471. [Google Scholar] [CrossRef]
- Dangora, L.M.; Mitchell, C.; White, K.D.; Sherwood, J.A.; Parker, J.C. Characterization of temperature-dependent tensile and flexural rigidities of a cross-ply thermoplastic lamina with implementation into a forming model. International Journal of Material Forming 2018, 11, 43–52. [Google Scholar] [CrossRef]
- Dangora, L.M.; Mitchell, C.J.; Sherwood, J.A. Predictive model for the detection of out-of-plane defects formed during textile-composite manufacture. Composites Part A: Applied Science and Manufacturing 2015, 78, 102–112. [Google Scholar] [CrossRef]
- Chen, J.; Niezrecki, C.; Sherwood, J.; Avitabile, P.; Rumsey, M.; Hughes, S.; et al. Effect of manufacturing-induced defects on reliability of composite wind turbine blades. University of Massachusetts Lowell Report 2012. (No DOI).
- Morris, C.D.; Dangora, L.; Sherwood, J. Using LS-DYNA to simulate the thermoforming of woven-fabric reinforced composites. In: Proceedings of the 13th International LS-DYNA Users Conference; Dearborn, MI; 2014. p. 1–11. (No DOI).
- Morris, C.D.; Dangora, L.; Sherwood, J. Using LS-DYNA to simulate the forming of woven-fabric reinforced composites. In: Proceedings of the 19th International Conference on Composite Materials; Montreal, Quebec, Canada; 2013.
- Yeager, M.; Cline, J.; White, K.; Bogetti, T.; Sherwood, J. Characterization and modeling of the in-plane shear deformation in ultra-high molecular weight polyethylene (UHMWPE) composites. 2019.
- DSM Dyneema® Industries. Dyneema, 2018. Available online: http://www.dsm.com/products/dyneema/en_US/home.html.
- Cline, J.; Yeager, M.; Bogetti, T. Determination of in-plane shear properties of ultra-high molecular weight polyethylene composites for input into a thermoforming model. CCDC Army Research Laboratory, Aberdeen Proving Ground, USA; 2019.
- White, K.D.; Sherwood, J.A. Characterization and modeling of a highly-oriented thin film for composite forming. AIP Conference Proceedings 2018, 1960, 020038. [Google Scholar] [CrossRef]


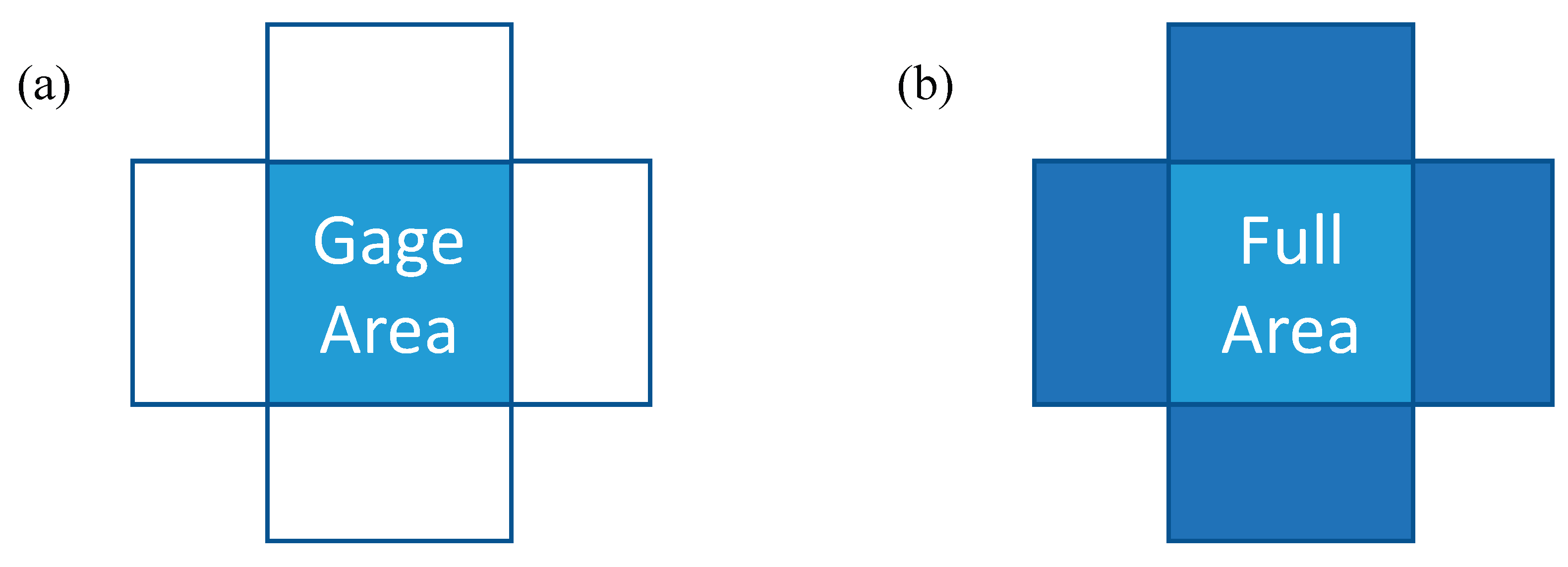




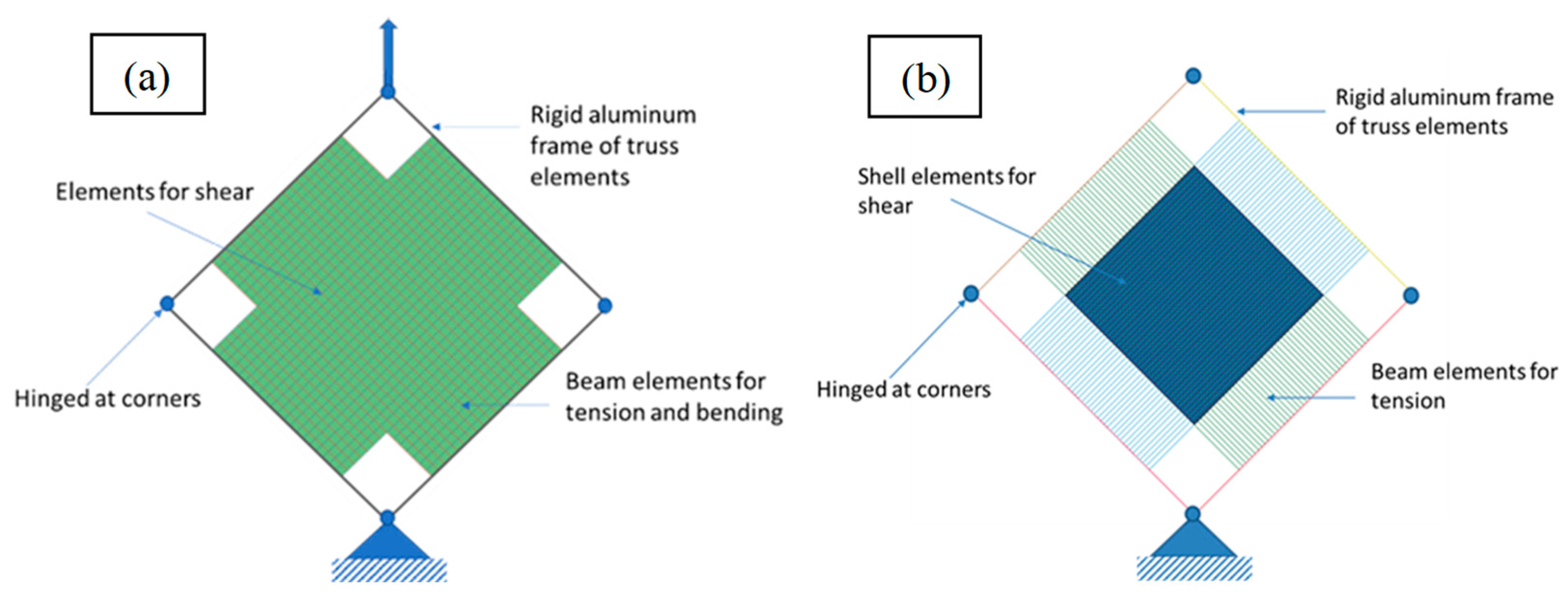
| Sample | Gage Side Length | Ratio of Arm Area / Total Area |
|---|---|---|
| A | 125 mm | 0.6 |
| B | 100 mm | 0.7 |
| C | 75 mm | 0.8 |
| Material System | Temperature (°C) |
Shear Stiffness (MPa) |
Tensile Modulus (MPa) |
|---|---|---|---|
| Dyneema HB210 | 120 | 13222 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





