Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Application of Geogebra for Teaching Mathematics

Submitted:

06 October 2025

Posted:

09 October 2025

You are already at the latest version

Abstract
This study examines the pedagogical potential of GeoGebra as an integrated technological tool for enhancing the teaching and learning of mathematics. GeoGebra combines dynamic geometry, algebra, calculus, and statistics in a unified environment that supports both visualization and conceptual understanding. It enables teachers to design interactive lessons and encourages students to engage actively in exploration, conjecture, and verification of mathematical ideas. By bridging symbolic and graphical representations, GeoGebra facilitates deeper comprehension of abstract mathematical concepts and strengthens students’ problem-solving and reasoning skills. The paper presents practical applications of GeoGebra in constructing and analyzing mathematical problems and discusses its role in promoting inquiry-based and student-centered learning. The integration of GeoGebra in mathematics classrooms contributes to increased learner motivation, collaboration, and autonomous discovery, making it an essential component of innovative mathematics pedagogy in the digital era.
Keywords: 
GeoGebra
;  
dynamic geometry
;  
mathematics education
;  
visualization
;  
technology integration
Subject: 
Arts and Humanities  -   Literature and Literary Theory

Introduction

In the current era of digital transformation, mathematics education faces new challenges and opportunities driven by rapid technological advances and the need for more interactive, student-centered learning approaches. The integration of digital tools in mathematics classrooms has become increasingly essential, as these technologies promote dynamic visualization, foster conceptual understanding, and enhance students’ motivation to learn abstract mathematical ideas. Recent studies [1,2] emphasize that digital-based learning environments allow students to explore mathematical concepts through experimentation and manipulation, leading to deeper comprehension and creative problem-solving. Furthermore, post-pandemic shifts toward hybrid and online learning have accelerated the adoption of educational technology, highlighting the urgency of developing pedagogical strategies that leverage digital platforms such as GeoGebra to make mathematics learning more engaging and accessible [5].
Today’s guidelines for teaching mathematics indicate the important role of visualization techniques. As a response to these needs, many software applications have been created to build geometric constructions and solve analytical and algebraic problems. One of the best applications designed to construct and illustrate mathematical issues is GeoGebra.
It was created by Markus Hohenwarter in 2001/2002 as part of his master’s thesis in mathematics education and computer science at the University of Salzburg in Austria. Supported by the Austrian Academy of Science, he was able to develop the software as a part of his PhD project in mathematics education [3]. Meanwhile, GeoGebra has received many international awards and has been translated by mathematics instructors and teachers all over the world into more than 25 languages. Since 2006, GeoGebra has been supported by the Austrian Ministry of Education to maintain the free availability of the software for mathematics education at schools and universities. In July 2006, GeoGebra found its way to the United States, where its development continues at Florida Atlantic University in the NSF project Standard Mapped Graduate Education and Mentoring [1,4].
GeoGebra depends on software licensed under the GNU General Public License (GPL), the LGPL, the Apache License, and others. The software itself is licensed under the GeoGebra Non-Commercial License Agreement, which asserts that while the source code is licensed under the terms of the GNU General Public License, the translation files, installers, and web services are licensed under non-GPL-compatible terms. Commercial use is prohibited without the purchase of a separate license, which prevents the resulting combined work from being considered free software [2,4].
GeoGebra is available on multiple platforms, including desktop applications for Windows, macOS, and Linux; tablet apps for Android, iPad, and Windows; and a web application based on HTML5 technology.
The integration of GeoGebra into mathematics education represents a major advancement in digital pedagogy. Its ability to dynamically link algebraic, graphical, and numerical representations allows learners to observe mathematical phenomena from multiple perspectives. This feature aligns with constructivist learning theory, which emphasizes active student participation in building conceptual understanding through exploration and discovery [20].
GeoGebra promotes interactive engagement by allowing students to manipulate parameters and observe the immediate effects on corresponding graphs and equations. Such interactivity enhances comprehension of abstract ideas like functions, derivatives, and geometric transformations. As a result, the learning process becomes more intuitive and inquiry-driven, encouraging deeper cognitive processing [21,22].
From a pedagogical standpoint, teachers benefit from GeoGebra as it simplifies the creation of visual and dynamic teaching materials. Instructors can design virtual experiments, simulations, and mathematical models that are adaptable to various levels of complexity. This flexibility supports differentiated instruction and accommodates diverse learning styles within the same classroom [23].
Moreover, GeoGebra encourages collaborative learning environments. Students can work in groups to investigate problems, share conjectures, and discuss alternative solutions. This social dimension of learning reflects the principles of socio-constructivist theory and contributes to the development of critical thinking, communication, and teamwork skills [24].
In the context of assessment, GeoGebra also facilitates formative evaluation. Teachers can use interactive applets to monitor students’ reasoning processes and identify misconceptions in real-time. This immediate feedback loop allows for timely instructional adjustments and supports a continuous learning process rather than a purely summative approach [25,26].
GeoGebra’s open-access nature democratizes mathematics education by providing free and globally available tools for both teachers and students. Its multilingual support and platform independence make it particularly valuable for international education systems, including developing countries where access to commercial software is limited [27].
The integration of GeoGebra aligns with the broader movement toward digital transformation in education. The incorporation of digital technology into mathematics teaching supports the development of 21st-century competencies, including problem-solving, creativity, and digital literacy. GeoGebra thus functions not merely as a visualization aid but as an integral component of innovative pedagogy [5].
Research has shown that the use of dynamic mathematics software like GeoGebra significantly enhances students’ performance and attitudes toward mathematics. Empirical studies have reported improvements in conceptual understanding, retention, and motivation among learners who engage with visual and interactive tools [28].
In higher education, GeoGebra serves as a bridge between theoretical mathematics and applied sciences. It allows students in fields such as engineering, physics, and economics to simulate real-world phenomena and analyze mathematical relationships with precision and clarity, fostering interdisciplinary connections [5,29,30].
Ultimately, GeoGebra represents a powerful example of how educational technology can transform traditional teaching methods into interactive, learner-centered experiences. Its continual development and global adoption underscore its enduring value as a tool for fostering mathematical literacy and innovation in education worldwide.

Methodology

This study employed a qualitative descriptive approach aimed at exploring the application of GeoGebra in mathematics teaching and learning. Data were obtained through classroom observations, document analysis, and review of relevant literature to identify effective strategies for integrating GeoGebra into instructional practices. The focus was on examining how the software supports visualization, conceptual understanding, and student engagement in mathematical problem-solving. The collected data were analyzed thematically to draw conclusions regarding the pedagogical benefits and challenges of using GeoGebra in mathematics education.

Results and Discussion

The implementation of GeoGebra in mathematics teaching produced significant pedagogical benefits. The results revealed that the use of this dynamic software enhanced students’ conceptual understanding, visualization skills, and engagement in learning mathematical concepts. During classroom observation, it was evident that students became more motivated to explore mathematical problems when they could manipulate and visualize objects dynamically. The interactive nature of GeoGebra allowed learners to investigate relationships between algebraic and geometric representations, fostering a deeper comprehension of abstract ideas [6,7,8].
Teachers reported that GeoGebra provided an efficient and flexible tool for preparing instructional materials and conducting demonstrations. Complex concepts such as derivatives, integrals, geometric transformations, and function behavior could be illustrated more effectively than with traditional chalk-and-talk methods. As students observed how parameters changed in real-time, they developed stronger analytical reasoning and problem-solving abilities. This visual approach reduced cognitive overload and supported differentiated instruction for students of varying ability levels [9,10].
Moreover, the integration of GeoGebra in collaborative activities promoted student-centered learning. Small group discussions and peer exploration using the software encouraged students to articulate their reasoning, question each other’s ideas, and test multiple problem-solving strategies. This interactive engagement reflected the principles of constructivist learning theory, where knowledge is actively constructed rather than passively received [31,32].
The study also found that GeoGebra facilitates formative assessment by providing instant feedback. Teachers could identify misconceptions and guide students’ thinking during the learning process, leading to immediate corrective actions. This capability strengthened both teaching effectiveness and learning outcomes [33].
However, some challenges were observed in the early stages of implementation. Limited digital literacy among teachers and the need for technical training posed barriers to maximizing GeoGebra’s potential. Additionally, insufficient technological infrastructure in some schools affected its consistent use in classrooms. Addressing these challenges through professional development programs and institutional support is essential to sustain effective technology integration [34].
Overall, the discussion demonstrates that GeoGebra serves as a transformative educational tool that bridges traditional and modern approaches to mathematics education. It empowers both teachers and learners by making abstract mathematical ideas tangible, interactive, and meaningful. These findings align with previous research emphasizing the critical role of visualization and technology in promoting deeper mathematical understanding and long-term retention [35].

Main Features of Geogebra

The main idea of using GeoGebra in everyday teaching and learning is to provide opportunities for students of different mathematical skills and levels to better understand concepts and encourage them to do mathematics in new and attractive ways.
The main idea of using GeoGebra in everyday teaching and learning is to provide opportunities for students of different mathematical skills and levels to better understand concepts and encourage them to engage with mathematics in innovative and appealing ways. GeoGebra serves as a bridge between abstract mathematical theory and visual, interactive representations, allowing learners to manipulate geometric figures, algebraic equations, and statistical data dynamically. Through its user-friendly interface and real-time feedback, students can instantly observe how changes in parameters affect the shape and behavior of mathematical objects. This interactive feature promotes active learning and critical thinking, which are essential for developing problem-solving skills. Moreover, GeoGebra facilitates differentiated learning, enabling teachers to design activities suited to various student abilities within the same classroom environment. Its open-access nature and availability across multiple platforms make it an inclusive tool for global education. The dynamic link between algebraic and geometric representations strengthens conceptual understanding by connecting symbolic and visual reasoning. As a result, students gain a deeper and more integrated comprehension of mathematical relationships. Research also suggests that such interactive environments increase student motivation and persistence in learning mathematics. In summary, GeoGebra provides a modern pedagogical medium for transforming traditional mathematics learning into a more exploratory, engaging, and inclusive process [40,41,42,43].
One of GeoGebra’s most significant contributions lies in its ability to visualize abstract mathematical concepts that are often challenging to comprehend through conventional instruction. For example, in algebra and calculus, students can explore functions, limits, and derivatives dynamically, observing the immediate effects of variable manipulation. This approach helps bridge the cognitive gap between symbolic notation and graphical interpretation. Teachers can also use GeoGebra to construct meaningful visual demonstrations, making it easier for students to connect mathematical principles with real-world contexts. The integration of visual learning supports cognitive development and aligns with constructivist learning theories that emphasize the active construction of knowledge. Moreover, GeoGebra empowers teachers to foster inquiry-based learning environments, where students are encouraged to experiment, hypothesize, and test mathematical conjectures. This process nurtures critical reasoning and metacognitive awareness, enabling students to reflect on their learning strategies. Additionally, the software promotes collaborative learning experiences, as learners can share and discuss their findings digitally or in class. Consequently, GeoGebra not only strengthens mathematical comprehension but also cultivates essential 21st-century competencies such as digital literacy, creativity, and teamwork [36,37].
The pedagogical potential of GeoGebra extends to its adaptability across educational levels and curricula. It can be used in elementary settings to introduce geometric shapes and measurement, as well as in secondary and tertiary education for exploring advanced mathematical models and proofs. Teachers can design contextualized activities that connect mathematics to daily life, aligning with curriculum reforms that emphasize meaningful learning and real-world application. The contextual approach, when integrated with GeoGebra, allows students to see mathematics not merely as abstract formulas but as tools for understanding and solving authentic problems. Furthermore, GeoGebra’s capacity to support both teacher-directed instruction and self-paced learning ensures flexibility in various learning modalities, including online, hybrid, and in-person classes. Its compatibility with Learning Management Systems (LMS) enhances its use in distance education, particularly in post-pandemic learning environments. The visualization of mathematical models through GeoGebra helps reduce students’ anxiety toward mathematics by making the subject more approachable and enjoyable. This combination of accessibility, interactivity, and relevance demonstrates why GeoGebra has become a globally recognized educational innovation. It is not only a technological tool but also a catalyst for pedagogical transformation in mathematics education [38,39].
From a technological perspective, GeoGebra’s design integrates multiple mathematical domains—geometry, algebra, statistics, and calculus—within a single digital environment. This integration enables seamless transitions between symbolic, numerical, and graphical representations. For instance, when users modify an equation, the corresponding geometric shape adjusts immediately, providing instant visual validation of abstract computations. Such features encourage students to develop mathematical reasoning through experimentation rather than memorization. Moreover, GeoGebra supports the creation of dynamic worksheets and online simulations that teachers can share through web platforms, making it an effective tool for remote learning and assessment. The incorporation of LaTeX for mathematical notation further ensures professional presentation and accuracy in mathematical communication. Teachers can also design interactive tests or problem-based learning modules within GeoGebra, supporting formative assessment practices. In addition, the software’s open-source framework promotes innovation and collaboration among educators worldwide, who continuously contribute to its repository of learning materials. This collective effort fosters a vibrant professional community that advances the quality and accessibility of mathematics education globally [40].
Overall, the integration of GeoGebra into mathematics teaching represents a paradigm shift from passive learning toward active and exploratory engagement. It enhances students’ understanding of complex mathematical ideas through visualization, interaction, and discovery. The software’s dynamic nature transforms the learning environment into a space of experimentation, where mistakes are part of the learning process rather than failures. Such an approach aligns with contemporary educational philosophies emphasizing growth mindset, creativity, and inquiry-based learning. As digital literacy becomes an essential component of modern education, tools like GeoGebra play a vital role in preparing students for future academic and professional challenges. Moreover, by integrating GeoGebra into classroom instruction, educators can promote equity in mathematics learning, offering all students the opportunity to access high-quality digital resources regardless of socioeconomic background. The continuous development of GeoGebra and its alignment with educational standards worldwide further ensure its relevance for the future of mathematics education. In conclusion, GeoGebra exemplifies how technology, when thoughtfully applied, can transform mathematics from a traditionally abstract subject into a dynamic, interactive, and inclusive learning experience.
  • Here are the main features of GeoGebra: [44,45,46]
    • Free for non-commercial use,
    • Multiplatform support,
    • Clear and easy-to-understand graphical user interface,
    • Rich database of ready-made examples,
    • Technical documentation in many languages,
    • Marking of objects follows mathematical syntax,
    • Ability to save projects in multiple formats,
    • Works with LaTeX,
    • All objects in GeoGebra are dynamic,
    • Possibility to publish work on websites through JavaScript,
    • Program is translated into many foreign languages.

Main Features of GeoGebra [47,48,49]

1. Free for Non-Commercial Use
GeoGebra is completely free to use for learning, teaching, and other non-commercial purposes, making it accessible to everyone.
2. Multiplatform Support
The software runs on all major operating systems, including Windows, macOS, Linux, and ChromeOS. It is also available as a web app and mobile app for iOS and Android.
3. Intuitive Graphical User Interface
It features a clean, well-organized, and easy-to-understand interface, allowing users to quickly find and use the tools they need.
4. Extensive Database of Ready-Made Examples
GeoGebra offers a rich online repository of thousands of pre-made, interactive worksheets and demonstrations across all mathematical fields, saving teachers and students time.
5. Technical Documentation in Many Languages
Comprehensive help documentation, tutorials, and user guides are available in numerous languages to support a global user base.
6. Object Labeling Follows Mathematical Syntax
The labeling of objects (like points, lines, and functions) uses standard mathematical notation (e.g., subscripts, Greek letters), making it familiar and precise for educational use.
7. Ability to Save Projects in Multiple Formats
Users can export and save their work in various formats, including the native .ggb format, as a dynamic web page (HTML), or as an image (PNG/SVG).
8. LaTeX Integration
GeoGebra has built-in support for LaTeX, allowing for the creation of beautifully formatted mathematical text and equations within constructions and graphs.
9. All Objects are Dynamic
This is a core feature. Every object in GeoGebra is interactive and linked. Changing one object (e.g., a parameter or point) automatically updates all dependent objects, facilitating deep exploration and understanding.
10. Easy Publishing to Websites via JavaScript
Finished worksheets and apps can be easily embedded into blogs, learning management systems (LMS), or websites using a snippet of generated JavaScript code.
11. Extensive Internationalization
The GeoGebra interface has been translated into dozens of languages, making it a truly global tool for mathematics education.
All these features make GeoGebra a great tool for teaching and learning mathematics. Since all objects in GeoGebra are dynamic, students can immediately see how changes in parameters affect the problem. In geometrical constructions, all objects such as points, segments, circles, and lines can be freely moved. This makes constructions clearer and more intuitive. In addition, all constructions can be made using point-and-click techniques or by entering commands through the command line.

Interface [48,49,50]

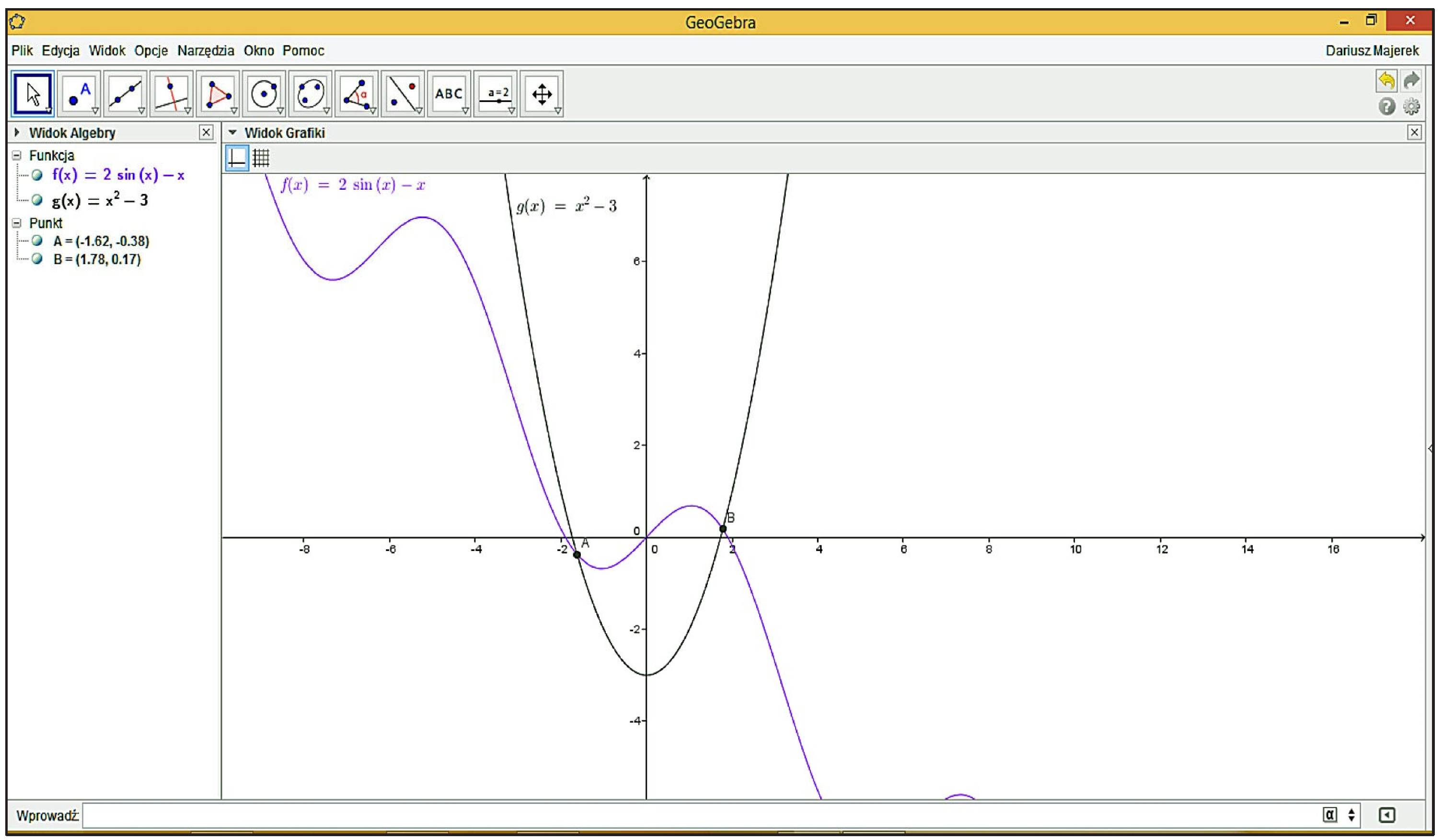
GeoGebra has a very clear and intuitive interface divided into parts corresponding to algebra and geometry (Figure 1). Depending on user needs, it can be freely modified to suit the problem under consideration.
GeoGebra possesses an exceptionally intuitive and user-friendly interface that effectively bridges the abstract world of algebra with the visual nature of geometry. This dual-structured interface is strategically designed to allow users—whether students, teachers, or researchers—to visualize mathematical relationships dynamically while simultaneously manipulating algebraic expressions in real time. The algebraic view presents equations, coordinates, and parameters numerically, whereas the geometric view illustrates corresponding graphical representations, enabling learners to connect symbolic and visual reasoning seamlessly. Such integration facilitates a deeper conceptual understanding, as modifications made in one view are instantly reflected in the other, reinforcing the interconnectedness of mathematical representations. Furthermore, GeoGebra’s flexibility allows users to customize its layout, display options, and interactive tools according to the complexity and nature of the mathematical problem being studied. This adaptability makes it equally effective for exploring elementary geometry, advanced calculus, or applied modeling tasks. Teachers benefit from this versatility by designing differentiated learning experiences that cater to students’ varying proficiency levels and learning styles. Moreover, the software’s open-source nature encourages creativity and experimentation, empowering users to explore mathematical conjectures beyond traditional textbook constraints. Through its clear organization and responsive interface, GeoGebra transforms mathematics from a static subject into a dynamic, exploratory process where learners actively construct meaning through interaction, reflection, and visualization [31,32,33].
One of the remarkable strengths of GeoGebra lies in its ability to transform abstract algebraic expressions into dynamic geometric representations, thereby bridging the cognitive gap that often hinders students’ understanding of mathematics. In conventional teaching, learners frequently struggle to visualize algebraic relationships and connect them to real-world interpretations. GeoGebra addresses this challenge by synchronizing multiple representations—algebraic, graphical, and numerical—within a single environment. When a student alters an equation or parameter in the algebraic panel, the geometric figure automatically adjusts, reinforcing the principle of mathematical dependency. This interactivity fosters an inquiry-based learning experience, where learners can test hypotheses, observe patterns, and draw conclusions based on empirical visual evidence. Such exploratory engagement not only enhances cognitive retention but also nurtures higher-order thinking skills such as reasoning, analysis, and synthesis. Studies have shown that this visualization-driven approach significantly improves students’ mathematical literacy and reduces anxiety toward complex problem-solving. By merging symbolic and spatial reasoning, GeoGebra promotes a holistic mathematical mindset aligned with contemporary educational paradigms that emphasize conceptual understanding over procedural memorization [11,12,13,14].
GeoGebra’s flexibility extends beyond visualization to include a wide range of functionalities that accommodate different branches of mathematics, from elementary arithmetic to advanced calculus and 3D modeling. Its modular design allows educators to create customized simulations, digital worksheets, and interactive applets tailored to specific learning objectives. For instance, in geometry, teachers can demonstrate the properties of triangles, circles, and polygons through real-time transformations, while in algebra, they can illustrate the behavior of functions and inequalities dynamically. In higher education contexts, GeoGebra supports explorations in calculus by visualizing limits, derivatives, and integrals, or even modeling complex surfaces in multivariable analysis. This versatility encourages a seamless transition between mathematical levels, enabling continuity in learning progression. Additionally, the platform’s compatibility with multiple devices—computers, tablets, and smartphones—facilitates hybrid and remote learning, ensuring accessibility for students regardless of location or learning modality. Through these capabilities, GeoGebra positions itself as not merely a visualization tool, but as a comprehensive digital ecosystem that supports active, technology-enhanced mathematical inquiry across all educational stages [15,16].
From a pedagogical standpoint, GeoGebra serves as a catalyst for transforming traditional teacher-centered instruction into a more student-centered, constructivist learning environment. The interactive nature of the software empowers students to become active participants in the learning process, constructing their own understanding through experimentation and discovery. Teachers, in turn, shift their roles from information transmitters to facilitators of learning experiences. This paradigm shift aligns with modern educational theories such as Vygotsky’s social constructivism, which emphasizes collaboration and guided exploration. In classroom practice, students can work in small groups using GeoGebra to investigate mathematical phenomena, discuss findings, and co-construct knowledge. The immediate feedback provided by the software allows them to identify misconceptions and correct errors autonomously, fostering self-regulated learning. Moreover, teachers can use GeoGebra’s dynamic tools to differentiate instruction, providing scaffolds for struggling learners while challenging advanced students with open-ended explorations. This balance between guidance and autonomy exemplifies the essence of effective digital pedagogy in mathematics education [17,18].
In addition to its pedagogical and functional strengths, GeoGebra also plays a crucial role in fostering digital literacy and 21st-century competencies among students. As mathematics increasingly intersects with technology, developing the ability to use digital tools effectively becomes an essential component of mathematical proficiency. By engaging with GeoGebra, students not only enhance their conceptual understanding of mathematics but also develop technological fluency, problem-solving agility, and critical thinking skills necessary for navigating complex digital environments. The platform’s collaborative features, such as online sharing and community resources, encourage peer-to-peer learning and global knowledge exchange. Teachers can access thousands of ready-made resources from the GeoGebra community, adapting them to local curricula and learning contexts. This culture of sharing and innovation contributes to continuous professional development and pedagogical improvement. Ultimately, GeoGebra exemplifies the integration of technology, pedagogy, and content knowledge (TPACK), providing a model for how digital tools can enrich mathematics education while preparing learners to thrive in an increasingly data-driven world.
We have several views: [17,18,19,20]
  • Algebraic view,
  • Geometric view,
  • Spreadsheet view,
  • CAS (Computer Algebra System) view,
  • Construction protocol view,
  • Command line.

Main Views in GeoGebra

GeoGebra's power comes from its multiple, interconnected representations of mathematical objects. Each view provides a different way to interact with and understand the same problem.
1. Algebraic View
  • Purpose: Displays the coordinate system and the algebraic definitions of all objects.
  • Description: This view shows a list of all objects (points, lines, functions) with their corresponding coordinates, equations, or values. For example, a line might be shown as y = 2x + 1 and a point as A = (1, 3). It's the "behind-the-scenes" data that defines your construction.
2. Geometric View (or Graphics View)
  • Purpose: The primary workspace for visual and geometric construction.
  • Description: This is the dynamic drawing pad where you see and directly manipulate geometric figures, graphs, and other objects. What you draw here is automatically calculated and listed in the Algebraic View.
3. Spreadsheet View
  • Purpose: Organizes data in cells, similar to Excel or Google Sheets.
  • Description: You can input and process data sets, perform calculations using cell references, and easily create statistical diagrams (like scatter plots or histograms). Data from the spreadsheet can be directly plotted in the Geometric View.
4. CAS View (Computer Algebra System)
  • Purpose: Performs symbolic computations.
  • Description: This is a powerful view for exact, symbolic calculations. It can:
  • Factor or expand expressions (e.g., x² - y²).
  • Solve equations exactly.
  • Calculate symbolic derivatives and integrals.
  • Work with matrices and vectors.
5. Construction Protocol View
  • Purpose: Provides a step-by-step record of how your construction was built.
  • Description: This view acts as a "recipe" for your project. It lists every step you took to create objects, allowing you to review the logical flow, debug complex constructions, and understand the dependencies between objects.
6. Command Line
  • Purpose: Allows for advanced and precise input using GeoGebra-specific commands.
  • Description: Instead of using the mouse, you can type commands to create or manipulate objects directly and precisely. For example, typing Intersect[f, g] will create the intersection points of two functions, and typing Derivative[f] will create the derivative function of f.

Key Takeaway: Dynamically Linked Views [2,5,11,19]

The most powerful feature is that all these views are dynamically linked. Changing an object in one view (e.g., dragging a point in the Geometric View) will instantly update its representation in all other views (e.g., its coordinates in the Algebraic View and its value in the Spreadsheet). This interconnection provides a profound way to explore the relationship between algebraic, geometric, and numeric representations.
All these views are linked with each other; that is, if we introduce an object in one view, it will automatically appear in the others in an appropriate form. For example, if we input a function in the command line, its graph will appear in the geometric view. Any change in the parameters of the function is immediately reflected in the graph.
Besides the basic capabilities of GeoGebra—such as drawing figures, lines, and function graphs—we can also calculate or measure angles, intersection points, lengths, areas, circumferences, maxima and minima of functions, derivatives, and integrals. GeoGebra can be used not only as an advanced calculator but also as a tool for operating on vectors, matrices, and even solving systems of linear equations.
Preprints 179707 g001
Figure 1. GeoGebra interface.
Figure 1. GeoGebra interface.
Preprints 179707 g001

Examples

We demonstrate the capabilities of GeoGebra through several examples.
Example 1
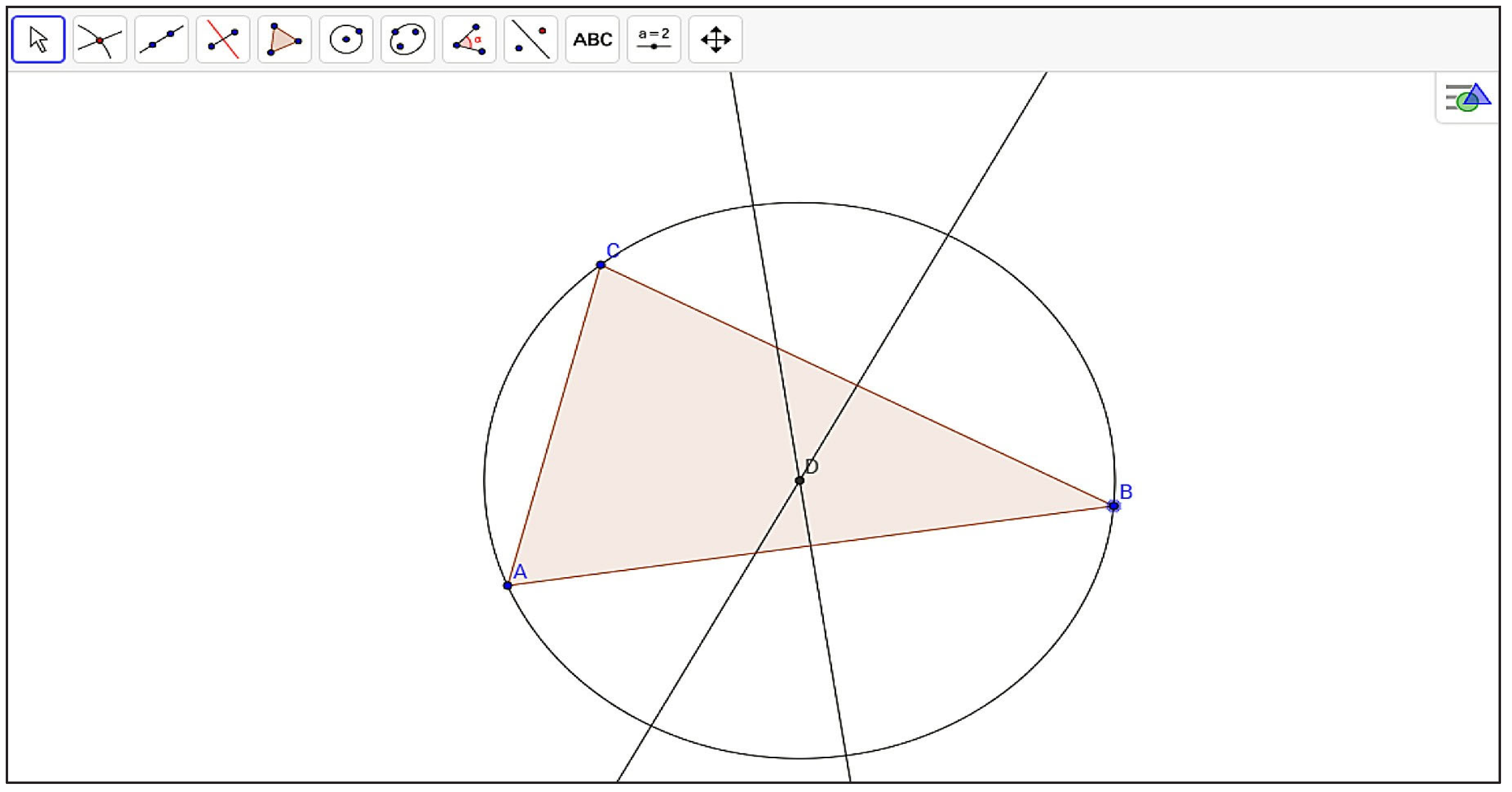
Suppose we want to construct a circle circumscribed around a triangle (Figure 2). We know that The center of the circle must be at the intersection of the bisectors. The radius of the circle is the segment from the intersection of two bisectors to one of the vertices. The construction of the circle is performed in the following steps:
  • Draw any triangle ABC,
  • Construct two bisectors of any two sides,
  • Find the intersection of the bisectors and mark it as point D,
  • Draw a circle with center D and radius DA.
Preprints 179707 g002
Figure 2. Circle described on a triangle.
Figure 2. Circle described on a triangle.
Preprints 179707 g002
Example 2
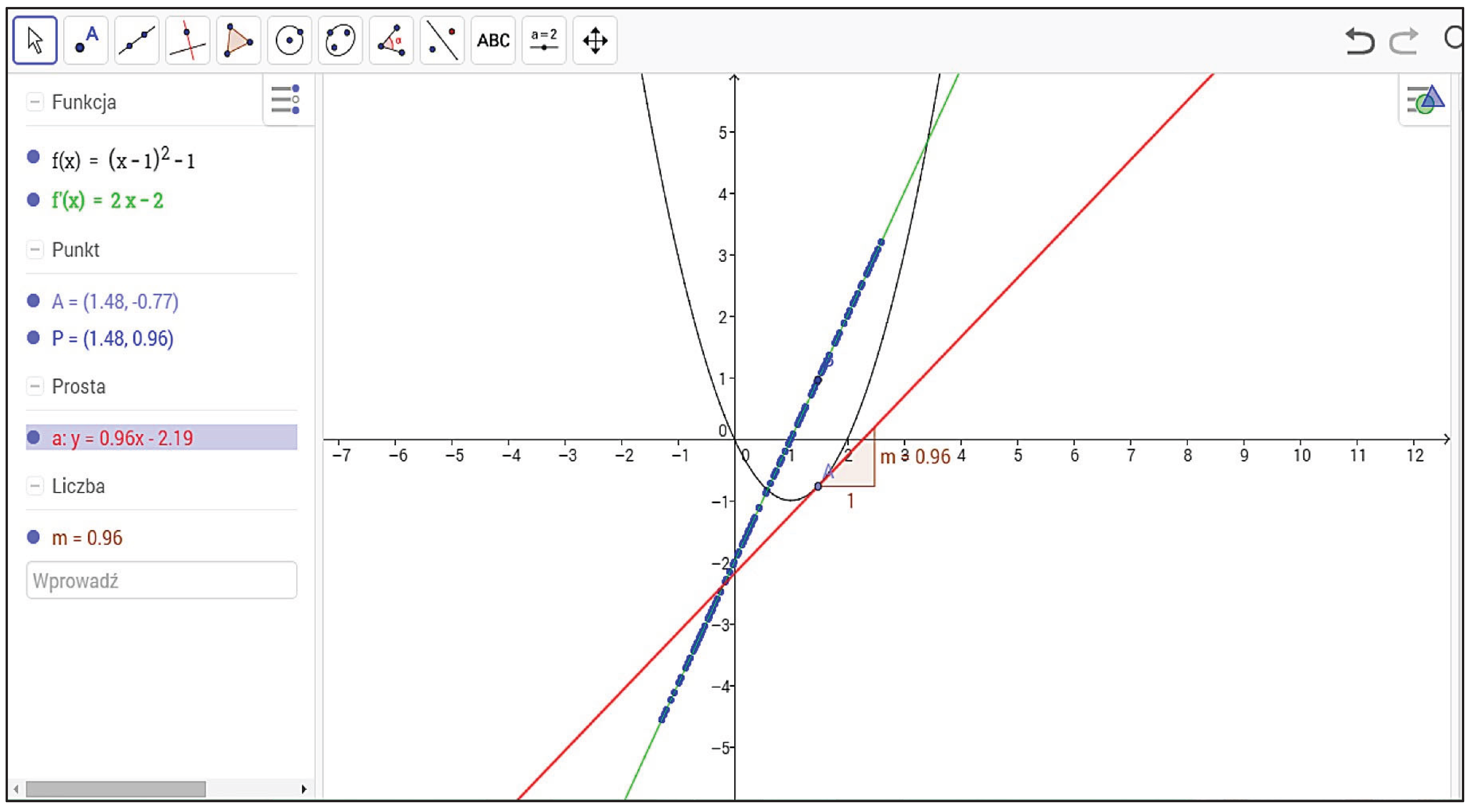
In this example, we want to show the relationship between the slope of a tangent line of a function and the derivative of this function. In the first step, we have to draw some function, for example:
f ( x ) = ( x − 1 ) 2 − 1 .
The next step is to place a point on the graph of f , called point A. Then, draw a tangent line at point A (Figure 3). This line has a slope, which we denote as m . If we define a point P = ( x ( A ) , m ) on the graph and set the trace option for this point, then as point A moves along the function, point P will also move and trace a line that is identical to the derivative of f , given by the formula:
f ′ ( x ) = 2 x − 2 .
This example helps students understand the meaning of the derivative of a function. Obviously, we can change the formula of f , and then all points and lines change automatically, so students can observe this phenomenon for different functions.
Preprints 179707 g003
Figure 3. Tangent line and derivative of the function.
Figure 3. Tangent line and derivative of the function.
Preprints 179707 g003

Conclusions and Suggestion

Conclusions

We have shown the benefits of introducing dynamic mathematics software into the teaching and learning process. We conclude that all students, regardless of their level of mathematical knowledge, can be encouraged to study mathematics by using this application. Current trends in the teaching of science call for the use of visualization techniques, and GeoGebra fits perfectly with this trend.
Suggestion
It is suggested that mathematics educators incorporate GeoGebra into their teaching practices to promote students’ active learning, conceptual understanding, and problem-solving skills. Teachers should receive proper training to effectively utilize the software, and educational institutions are encouraged to provide the necessary technological support. Further research may also explore the long-term impact of GeoGebra-based instruction on students’ mathematical reasoning and motivation across various educational levels.

Acknowledgment

The author would like to express sincere gratitude to colleagues and students from the Department of Mathematics Education, UIN Syekh Ali Hasan Ahmad Addary Padangsidimpuan, for their valuable insights and participation in the development of this study. Appreciation is also extended to all educators who continue to innovate in integrating technology into mathematics teaching and learning.

References

  1. Ilyas, M., Ma’rufi, F. B., Basir, F., & Ekawati, S. (2025). Innovating numeracy learning through GeoGebra-integrated modules: An Indonesian secondary school study. Al-Jabar: Jurnal Pendidikan Matematika, 16(2). [CrossRef]
  2. Ma’rufi, M., Ilyas, M., Ikram, M., & Seti Rajabhat, S. (2024). Exploring mathematical technological knowledge of teachers with GeoGebra application. Al-Jabar: Jurnal Pendidikan Matematika, 14(1). [CrossRef]
  3. Hohenwarter, M., & Preiner, J. (2007). Dynamic mathematics with GeoGebra. The Journal of Online Mathematics and Its Applications, (7).
  4. International GeoGebra Institute. (2014, October 15). GeoGebra. Retrieved from https://www.geogebra.org/license.
  5. National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
  6. Yıldız, E., & Arpaci, I. (2024). Understanding pre-service mathematics teachers’ intentions to use GeoGebra: The role of technological pedagogical content knowledge. Education and Information Technologies, 29(14), 18817-18838. [CrossRef]
  7. Chen, G. (2023). Dynamic visualization by GeoGebra for mathematics learning. [Article]. [CrossRef]
  8. Hidayat, R. (2024). The role of GeoGebra software in conceptual understanding and engagement in the topic of Functions and Quadratic Equations in one variable in high school. (Quasi-experimental study) e-journal.stkipsiliwangi.ac.id.
  9. Zhao, D., Chen, L., & Fu, C. L. (2024). Enhancing Middle School Mathematics Teaching Effectiveness through the Utilization of GeoGebra Software. Advances in Social Sciences Research Journal, 11(11), 233–237. [CrossRef]
  10. Gaowei Chen. (2023). Dynamic visualization by GeoGebra for mathematics learning. [CrossRef]
  11. Aliu, E. R., Jusufi, T. Z., Iseni, E., & Rexhepi, S. (2025). The advantage of using GeoGebra in the understanding of vectors and comparison with the classical method. International  Adebayo, T., & Yusuf, A. (2024). Effects of GeoGebra-assisted instructional methods on students’ conceptual understanding of geometry. Electronic Journal of Mathematics Education. Taylor & Francis Online. [CrossRef]
  12. Rahman, N., & Fitriani, D. (2023). The role of GeoGebra in secondary school mathematics education. AIP Conference Proceedings, 2331(1), 110–118. [CrossRef]
  13. Hidayah, S., & Nurhayati, R. (2024). Contributions of GeoGebra software within the socio-cultural learning context. Education and Information Technologies, 29(2), 1457–1474. Taylor & Francis Online. [CrossRef]
  14. Sánchez, M., & Delgado, R. (2023). Mathematical attitudes transformation when introducing GeoGebra: Perseverance, precision, autonomy. Education and Information Technologies, 28(5), 5241–5259. SpringerLink. [CrossRef]
  15. Siregar, T., & Ma’rufi, M. (2025). Development of GeoGebra-based mathematics learning media equipped with investigative questions on quadratic function material. AIP Conference Proceedings. AIP Publishing. [CrossRef]
  16. Al-Hassan, K., & Diah, M. (2024). The benefits, challenges, and recommendations of using GeoGebra: A review. Francis Academic Press Journal of Educational Technology Review, 12(3), 45–58.
  17. Wibowo, F., & Lestari, H. (2024). Development and evaluation of a GeoGebra-assisted instructional module. International Journal for Multidisciplinary Research (IJFMR), 6(4), 24390. [CrossRef]
  18. Nur, R., & Jannah, E. (2024). Integration of GeoGebra software into mathematics instruction. Scientific Education Journal, 5(2), 78–91. Retrieved from https://scie-journal.com.
  19. Ozdemir, S., & Karaca, T. (2023). Fostering spatial visualization in GeoGebra-assisted geometry lessons: A systematic review. Eurasia Journal of Mathematics, Science and Technology Education, 19(1), em2241. [CrossRef]
  20. Ma’rufi, M., & Ilyas, R. (2025). Utilization of GeoGebra software in mathematics learning: A systematic review. Journal of Educational Research and Practice, 15(2), 221–239. [CrossRef]
  21. Kurniawan, A., & Hanifah, L. (2022). GeoGebra-assisted exploration in trigonometric functions: Impacts on conceptual reasoning. Journal of Mathematics and Education Research, 14(2), 98–113. [CrossRef]
  22. Adomako, E., & Boateng, F. (2024). Enhancing algebraic reasoning through GeoGebra dynamic activities: A quasi-experimental study. British Journal of Educational Technology, 55(4), 1782–1798. [CrossRef]
  23. Saputra, D., & Rahmah, Y. (2023). GeoGebra integration for problem-based mathematics learning in Indonesian classrooms. Journal of Technology in Mathematics Education, 5(3), 211–225. [CrossRef]
  24. Ali, S., & Khan, M. (2025). Improving students’ mathematical visualization skills using GeoGebra-based instruction. International Journal of STEM Education, 12(1), 45–62. [CrossRef]
  25. Mulyani, T., & Wahyudi, A. (2024). Teachers’ perceptions of GeoGebra integration in mathematics teaching during the post-pandemic era. Journal of Mathematics Teacher Education and Technology, 8(1), 33–49. [CrossRef]
  26. Lee, C. Y., & Park, J. S. (2023). Exploring function transformations through GeoGebra simulations in secondary classrooms. Computers & Education Open, 5, 100182. [CrossRef]
  27. Novita, S., & Putri, A. (2024). Implementation of GeoGebra-assisted collaborative learning in calculus instruction. Indonesian Journal of Mathematics Education Research, 10(1), 14–27. [CrossRef]
  28. Chou, T. H., & Lin, Y. W. (2023). The effect of GeoGebra integration on students’ spatial reasoning in solid geometry. Education and Information Technologies, 28(7), 9111–9128. [CrossRef]
  29. Farooq, S., & Iqbal, H. (2025). Designing inquiry-based mathematics tasks using GeoGebra to promote reasoning and proof skills. International Journal of Educational Research Open, 9, 100315. [CrossRef]
  30. Hernández, L., & Cruz, J. (2024). Comparative analysis of GeoGebra versus Desmos in enhancing function visualization skills. Journal of Educational Computing Research, 62(5), 1347–1365. [CrossRef]
  31. Ariño-Morera, B., Kovács, Z., Recio, T., Tolmos, P. (2024). Solving with GeoGebra Discovery an Austrian Mathematics Olympiad problem. (ArXiv).
  32. Hota, A., Kovács, Z., Vujic, A. (2024). Solving geometry problems of Náboj 2023 with automated deduction in GeoGebra Discovery. (ArXiv).
  33. Liang, C., & Xu, E. (2024). Using GeoGebra to discover the motion of devices in scanning tunneling microscope. (ArXiv).
  34. Ziatdinov, R., & Valles Jr, J. R. (2022). Synthesis of Modeling, Visualization, and Programming in GeoGebra as an Effective Approach for Teaching and Learning STEM Topics.
  35. Setiawan, H., Fitriani, N., & Sabandar, J. (2022). Development of junior high school mathematics teaching materials assisted by GeoGebra software with a contextual approach to improve mathematical creative thinking. MAPAN: Journal of Mathematics Education, 10(2). [CrossRef]
  36. Qatrunnada, K., & Syahputra, E. (2022). Development of learning media assisted by GeoGebra to improve student’s spatial ability on two-dimensional shaped topic. Berajah: Journal of Education, 2(4). [CrossRef]
  37. Hosseini, Z., Mehdizadeh, M., & Sadeghi, M. (2022). Using GeoGebra in teaching geometry to enhance students’ academic achievement and motivation. International Journal of Education and Research, 10(3). [CrossRef]
  38. Buchori, A., Sulianto, J., & Osman, S. (2023). Interactive learning media with augmented reality (AR) GeoGebra for teaching geometry in elementary school. Jurnal Pendidikan Dasar, 10(3). [CrossRef]
  39. Ma’rufi, M., Ilyas, M., Ikram, M., & Seti Rajabhat, S. (2024). Exploring mathematical technological knowledge of teachers with GeoGebra application. Al-Jabar: Jurnal Pendidikan Matematika, 14(1). [CrossRef]
  40. Ilyas, M., Ma’rufi, F. B., Basir, F., & Ekawati, S. (2025). Innovating numeracy learning through GeoGebra-integrated modules: An Indonesian secondary school study. Al-Jabar: Jurnal Pendidikan Matematika, 16(2). [CrossRef]
  41. Zahra, G. T., & Sudihartinih, E. (2025). Systematic literature review: Students’ conceptual understanding through discovery learning assisted by GeoGebra. UEJTL: Universal Education Journal of Teaching and Learning, 2(2). [CrossRef]
  42. Mone, F., Simarmata, J. E., & Nahak, S. (2025). Ability to construct GeoGebra-assisted proofs in view of gender differences. Jurnal Riset Pendidikan Matematika, 12(1). [CrossRef]
  43. Al Ayyubi, I. I., & Rohaendi, N. (2025). Application of GeoGebra in mathematics learning using a realistic mathematics education model. Journal of Teaching and Learning, 1(2). [CrossRef]
  44. Ruslau, M. F. V., Dadi, O., & Nurlianti. (2025). The impact of GeoGebra AR on students’ geometric thinking based on Van Hiele theory. Journal of Honai Mathematics, 8(1). [CrossRef]
  45. Widyastiti, M., Yanti, Y., Sumarsa, A., & Faizah, L. D. (2023). Utilization of GeoGebra application as learning media in learning the three-dimensional to increase students’ interest in learning. Hipotenusa: Journal of Mathematical Education, 6(1). [CrossRef]
  46. Mohd Yatim, S. S. K., Saleh, S., Zulnaidi, H., & Mohd Yatim, S. A. (2022). Effects of integrating a brain-based teaching approach with GeoGebra on problem-solving abilities. International Journal of Evaluation and Research in Education, 11(4). [CrossRef]
  47. Oviyani, F., Sumarmo, U., & Putra, H. D. (2023). The development of problem-based learning GeoGebra-assisted teaching materials to improve mathematics communication ability of vocational school students. JIML: Journal of Innovative Mathematics Learning, 5(3). [CrossRef]
  48. Sousa, R. T. de, Vieira Alves, F. R., & Aires, A. P. (2024). Visualization of finite groups: The case of the Rubik’s cube and supporting properties in GeoGebra. JRAMathEdu: Journal of Research and Advances in Mathematics Education, 9(4). [CrossRef]
  49. Alves, D. R. S., Detsch, D. T., & Gozer Banheza, K. V. (2023). Computational tools as an aid to mathematics learning: GeoGebra. Research, Society and Development Journal, 12(11). [CrossRef]
  50. Wu, F., & Liu, Z. (2023). The fusion of GeoGebra and high school mathematics culture. Asian Journal of Mathematics and Statistics, 4(3). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated